Численные методы оптимизации. Методы оптимизации это

Задача оптимизации - это... Что такое Задача оптимизации?

Задача оптимизации

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.

Постановка задачи оптимизации

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

Допустимое множество — множество ;
Целевую функцию — отображение ;
Критерий поиска (max или min).

Тогда решить задачу означает одно из:

Показать, что .
Показать, что целевая функция не ограничена.
Найти .
Если , то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x0 таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Классификация методов оптимизации

Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:

Локальные методы (задача оптимизации унимодальной целевой функции).
Глобальные методы (имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.).

Существующие в настоящее время методы поиска можно разбить на три большие группы:

детерминированные;
случайные;
комбинированные.

Некоторые детерминированные методы:

Задачи оптимизации, в которых целевая функция и ограничения являются линейными функциями, разрешаются так называемыми методами линейного программирования.
В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

Помимо того, оптимизационные методы делятся на следующие группы:

Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.

Литература

Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высшая школа, 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
Растригин Л.А. Статистические методы поиска. — М.: 1968.
Абакаров А.Ш., Сушков Ю.А. Статистическое исследование одного алгоритма глобальной оптимизации. — Труды ФОРА, 2004.

Ссылки

MDOP — Поиск глобального оптимума для задач оптимального проектирования систем или определения оптимальных законов управления.

Глобальная оптимизация, принятие решений — Программные системы поддержки принятия оптимальных решений. Глобальные алгоримы.

Wikimedia Foundation. 2010.

Задача о четырёх красках
Задача трех тел

Смотреть что такое "Задача оптимизации" в других словарях:

задача оптимизации надёжности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN reliability optimization problem … Справочник технического переводчика
Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия
Задача о рюкзаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия
Задача о рюказаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия
Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия
Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр … Википедия
Задача о ранце — Пример задачи о ранце: необходимо разместить ящики в рюкзак при условии на вместимость рюкзака 15 кг, так чтобы суммарная полезность предметов в рюкзаке была максимальной. Задача о ранце (рюкзаке) (англ. … Википедия
Задача о максимальном потоке — Максимальный поток в транспортной сети. Числа обозначают потоки и пропускные способности. В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сум … Википедия

dal.academic.ru

Моделирование в электроэнергетике - Оптимизационные задачи. Общие сведения

Оптимизационные задачи. Общие сведения

Оптимизационная задача – это задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Целевая функция представляет собой набор критериев качества, которые должны быть оптимизированы одновременно. В общем случае целевая функция состоит из управляемых и неуправляемых переменных. Условие поиска экстремума целевой функции записывается в следующем виде:

Методы решения оптимизационных задач изучает математическое программирование. Математическое программирование – это математическая дисциплина, изучающая теорию и методы решения задач по определению экстремумов функций на множествах конечномерного векторного пространства, определяемых набором линейных и/или нелинейных ограничений (равенствами и/или неравенствами). Математическое программирование представляет собой, как правило, многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению. Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности:

Методы линейного программирования используются в случае, если в математической модели имеются только линейные зависимости между переменными, для решения оптимизационной задачи.
Методы нелинейного программирования используются в случае, если в математической модели имеются нелинейные зависимости между переменными, для решения оптимизационной задачи.
Методы целочисленного или дискретного программирования используются в случае, если среди переменных имеются целочисленные или дискретные переменные, соответственно.
Методы стохастического программирования используются в случае, если исходные данные или их часть являются случайными величинами.
Математический аппарат теории игр используются в случае, если задана недетерминированная (неопределенная) исходная информация.

Решение задачи оптимизации осуществляется с помощью поисковых методов, использующих предшествующую информацию для построения улучшенного решения задачи (итерационные методы расчета). К настоящему времени разработано достаточно много методов локальной оптимизации для решения задач общего вида. Большинство из них используют принцип локального спуска, когда метод последовательно на каждом шаге переходит к точкам с существенно меньшими (большим) значениями целевой функции. Данные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска. Поиск оптимального значения в таких задачах может быть представлен в виде итерационного соотношения:

где переменная - это приращение вектора управляемых параметров. В зависимости от условия поиска (поиск максимального или минимального значения целевой функции) используется либо знак «+», либо знак «-».

Приращение вектора управляемых параметров в большинстве случаях вычисляется по формуле:

В данном выражении - значение вектора управляемых параметров на k-ом шаге, - шаг расчета, а - направление поиска экстремума функции.

В зависимости от числа управляемых параметров различают методы одномерной и многомерной оптимизации (многокритериальная оптимизация). Поиск считается одномерным, в случае если аргументом целевой функции является один управляемый параметр.

Шаг расчета

Итерационная форма методов локальной оптимизации для решения задач поиска экстремума целевой функции требует выбора шага расчета вдоль заданных направлений на каждом шаге итерации. Шаг расчета может быть постоянным или переменным, но оптимальное значение длины шага определяется в результате поиска экстремума целевой функции в выбранном направлении с использованием методов одномерной оптимизации:

Другими словами, величина шага расчета вычисляется при решении следующего выражения:

В результате решения данного уравнение мы получим, что шаг расчета в символьном виде определяется следующим образом:

где - значение аргумента функции на k-ом шаге итерации;

n – количество неизвестных переменных, которые определяются в ходе решения задачи;

L – некоторая константа, которая определяется из определителя следующей матрицы:

В результате для определения оптимального шага расчета требуется выполнить большой объем вычислений целевой функции. Для снижения числа операций на практике используют другой подход: подбирают такие значения шага расчета , чтобы они удовлетворяли любому из представленных ниже условию.

Первое условие (правило Армихо) является адаптивным методом поиска величины шага расчета, которое говорит о том, что функция не должна превышать значения некоторой убывающей линейной функции, равной в нуле:

где коэффициент , а шаг расчета определяется итеративно путем умножения первоначального шага на коэффициент до тех пор пока не будет выполняться условие.

Рис.1. Критерий выбора шага расчета по правилу Армихо

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Армихо заключается в следующем:

1.Задать коэффициент в диапазоне от 0 до 1.

2.Задать начальное значение шага .

Процедура поиска (проверка выполнения условия по правилу Армихо)

3. В случае если условие по правилу Армихо не выполняется, тогда необходимо скорректировать шаг расчета , где переменная может принимать любое значение от 0 до 1, по умолчанию примем, что переменная , а - текущий шаг поиска.

4. В случае если условие по правилу Армихо выполняется, тогда в качестве шага расчета можно принять , а процедура поиска завершается.

Данное правило требует однократного вычисления градиента, после чего небольшое количество итераций затрачивается на подбор подходящего шага. Каждая из таких вложенных итераций, в свою очередь, требует вычисления значения целевой функции без градиента, то есть проводимые испытания относительно легковесны. Следует отметить, что данное условие удовлетворяется для всех достаточно малых . Правило Армихо можно расширить на многокритериальный случай: неравенство 3.19 следует понимать покомпонентно.

Второе условие (Правило Вольфе-Пауэлла - Wolfe. P) является модифицированным критерием, позволяет выбрать шаг расчета в случае выполнения двух условий:

- функция не должна превышать значения некоторой убывающей линейной функции, равной в нуле:

- величина скорости изменения функция в заданном направлении была в раз больше, чем скорость изменения функции в первоначальной точке

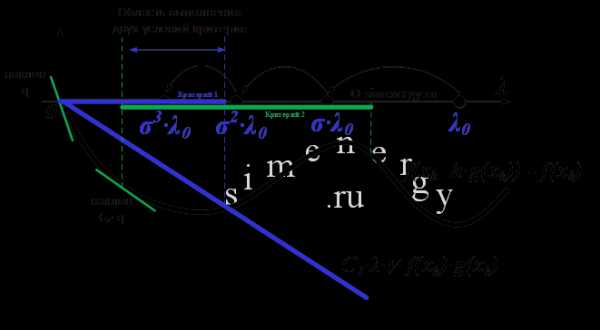
Рис.2. Критерий выбора шага расчета по правилу Вольфе-Пауэлла

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Вольфе-Пауэлла заключается в следующем:

1. Задать коэффициент и в диапазоне от 0 до 1 .

2. Задать начальное значение шага , принять коэффициент и

Процедура поиска (проверка выполнения условия по правилу Вольфе-Пауэлла)

3. В случае если первое условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент . Перейти к пункту №5.

4. В случае если второе условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент :

- в случае если , то перейти к пункту №5;

- в случае если выполнить экстраполяцию, положив , где r – коэффициент экстраполяции . Перейти к пункту №3.

5. Выполнить текущий расчет шага по формуле

где - коэффициент интерполяции, который определяется в следующем диапазоне

Перейти к пункту №3.

6. В случае если выполняются оба условия правилу Вольфе-Пауэлла, тогда в качестве шага расчета можно принять , а процедура поиска завершается.

Третье условие (правило Голдстейна-Армийо) позволяет выбрать шаг расчета, рассматривая следующее неравенство:

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Голдстейна-Армийо заключается в следующем:

1.Задать коэффициент и в диапазоне от 0 до 1 .

2. Задать начальное значение шага

3. В случае если условие по правилу Голдстейна-Армийоне выполняется, тогда необходимо скорректировать шаг расчета , где переменная может принимать любое значение от 0 до 1, по умолчанию примем, что переменная , а - текущий шаг поиска.

4. В случае если условие по правилу Голдстейна-Армийо выполняется , тогда в качестве шага расчета можно принять , а процедура поиска завершается.

Критерии останова оптимизационного процесса

Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета выполняется один (или несколько) критериев:

- траектория поиска остается в малой окрестности текущей точки поиска:

- приращение целевой функции не меняется:

- градиент целевой функции в точке локального минимума обращается в нуль:

Классификация методов оптимизации.

В настоящее время для решения задач оптимизации разработано огромное количество различных математических методов. Применение того или иного метода определяется постановкой задачи, сложностью вычисления функции и ее производных, поведением функции и т. д.

Задачи оптимизации и методы их решения можно разделить по наличию или отсутствию ограничений (задаётся системой неравенств и равенств или более сложным алгоритмом) в математических моделях на методы условной и безусловной оптимизации. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений.

Методы безусловной оптимизации

Классическая задача безусловной оптимизации формулируется следующим образом: требуется найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение

Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:

Рис.3. Задача безусловной оптимизации для функции двух переменных

Сущность метода оптимизации в первую очередь определяется способом выбора направления движения к экстремуму. В зависимости от используемого порядка производных целевой функции методы безусловной оптимизации делят на методы нулевого, первого и второго порядков. Если производные не используются, то имеет место метод нулевого порядка, если используются первые или вторые производные, то соответственно метод первого или второго порядка.

Методы нулевого порядка (методы прямого поиска) для поиска экстремума функции требуют вычисление только значений функции в точках пространства оптимизации. В данном методе информация о производных не используется и, соответственно, не требуют определения аналитического вида производных. В зависимости от количества управляемых параметров различают методы одномерного и многомерного поиска.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач нулевого порядка:

Методы одномерного поиска:

- Метод дихотомического деления и метод золотого сечения – это методы одномерной оптимизации, основанные на делении отрезка, на котором ищется экстремум, пополам или в пропорциях золотого сечения (0,382 / 0,618), соответственно.

- Метод полиномиальной аппроксимации (метод квадратичной интерполяции) – это метод одномерной оптимизации, в соответствии с которым целевая функция аппроксимируется квадратичным полиномом.

Методы многомерного поиска:

- Метод покоординатного спуска (Гаусса-Зейделя) – это метод безусловной оптимизации нулевого порядка, в котором направления поиска выбираются поочередно вдоль всех координатных осей, шаг рассчитывается на основе одномерной оптимизации.

- Метод вращающихся координат (Метод Розенброка) – это метод безусловной оптимизации нулевого порядка, в котором реализуется покоординатный спуск, но вдоль координатных осей, поворачиваемых таким образом, чтобы направление одной из осей было близко к направлению, параллельному дну оврага.

- Симплексный метод (метод деформируемого многогранника или метод Нелдера-Мида) – это метод безусловной оптимизации нулевого порядка, основанный на многократно повторяемых операциях построения многогранника с (n+1) вершинами, где n — размерность пространства управляемых параметров, и перемещения наихудшей вершины (с наихудшим значением целевой функции) в направлении центра тяжести многогранника.

Методы первого порядка (градиентные методы поиска)для поиска экстремума требуют вычисления значений функции в точках пространства оптимизации, а также определение аналитического вида производных первого порядка по управляемым параметрам. Методы первого порядка называют также градиентными, поскольку вектор первых производных функции F(X) по оптимизируемым переменным X есть градиент целевой функции:

Градиент в базовой точке строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиента), соответственно, показывает направление наискорейшего убывания функции. Градиентные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач первого порядка:

- Метод градиентного спуска – это метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента с переменным (дробным) шагом, который задается пользователем.

- Метод наискорейшего спуска – это метод нахождения локального минимума (максимума) функции при движении вдоль градиента с оптимальным шагом. Шаг расчета выбирается минимума целевой (минимизируемой) функции в направлении спуска.

- Метод сопряженных градиентов (метод Флетчера-Ривса) – это метод безусловной оптимизации первого порядка, в котором направление поиска на очередном шаге есть градиентное направление, скорректированное с учетом направления поиска на предыдущем шаге.

- Метод переменной метрики (метод Девидона-Флетчера-Пауэлла) – это метод безусловной оптимизации, в котором за основу взято решение системы уравнений, выражающих необходимые условия экстремума.

Методы второго порядка для поиска экстремума требуют вычисления значений функции в точках пространства оптимизации, а также определение аналитического вида производных первого и второго порядка по управляемым параметрам.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач второго порядка:

- Метод Ньютона – это метод безусловной оптимизации, основанный на использовании необходимых условий безусловного экстремума целевой функции: равенству нулю первой производной. В соответствии с данным методом определяют матрицу вторых частных производных целевой функции по управляемым параметрам (матрицу Гессе).

- Метод Марквардта – это метод безусловной оптимизации, направленный на решение задач о наименьших квадратах. Является альтернативой методу Гаусса – Ньютона. Может рассматриваться как комбинация последнего с методом градиентного спуска или как метод доверительных интервалов.

Методы условной оптимизации

Классическая задача условной оптимизации формулируется следующим образом: необходимо найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение

при заданных условиях (равенствами и/или неравенствами), при этом число ограничений m может быть как больше, так и меньше числа переменных n.

, j=1,2,…,m.

Другими словами, необходимо найти экстремум целевой функции при условии, что значения аргументов функции принадлежат области допустимых значений, которая образуется системой ограничений. Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:

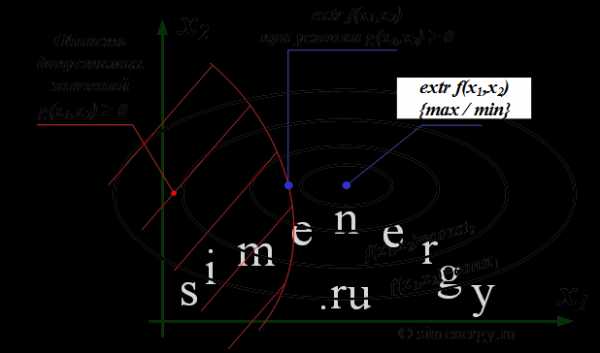
Рис.4. Задача условной оптимизации для функции двух переменных

В зависимости от используемого метода решения методы условной оптимизации можно разделить на методы сведения задачи к безусловной оптимизации и методы непосредственного решения.

Методы сведения задачи к безусловной оптимизации - это задача условной оптимизации, основанная на преобразование задачи нелинейного программирования в последовательность задач безусловной оптимизации путем построения вспомогательных функций

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач условной оптимизации:

- Метод неопределенных множителей Лагранжа – это метод условной оптимизации, ориентированный на поиск экстремума целевой функции при наличии ограничений типа равенств.

- Условия Куна-Таккера – это метод решения оптимизационной задачи математического программирования с заданными ограничениями. Метод является обобщением метода множителей Лагранжа на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.

- Метод штрафных функций – это метод или группа методов для решения задач математического программирования, основанные на преобразовании задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции, учитывающей ограничения задачи.

Методы непосредственного решения задачи условной оптимизации – это задача условной оптимизации, основанная на движении из одной допустимой точки, где выполнены все ограничения, к другой допустимой точке с лучшим значением целевой функции.

- Метод приведенного градиента – это метод условной оптимизации, ориентированный на решение задач с ограничениями типа равенств. Направление движение в данном методе определяет приведенный градиент функции.

- Метод возможных направлений (метод Зойтендейка) - этот метод решения задач математического программирования основан на движении из одной допустимой точки к другой с лучшим значением целевой функции.

Численные методы оптимизации реализованы и широко используются в различных математических пакетах. При этом наличие готовых программных средств (математических библиотек и пакетов) не только не снимает необходимость изучения методов, а наоборот, делает подготовку в этом направлении еще более актуальной. Это связано с тем, что при решении реальной задачи от специалиста требуется грамотная математическая постановка задачи, ее формализация, обоснование и выбор наиболее эффективного метода расчета, а также умение производить оценку адекватности и точности полученных результатов.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

simenergy.ru

Численные методы оптимизации - это... Что такое Численные методы оптимизации?

Численные методы оптимизации

Численные методы оптимизации [numerical optimization technique] — методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы — предмет изучения вычислительной математики. См. также Имитационные (численные) методы решения моделей.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

Четность и нечетность функции
Числовая модель

Смотреть что такое "Численные методы оптимизации" в других словарях:

численные методы оптимизации — Методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет изучения вычислительной математики … Справочник технического переводчика
Численные методы — Вычислительная математика раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика теория численных методов решения типовых математических… … Википедия
Имитационные (численные) методы решения моделей — [numerical simulation methods] последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср.… … Экономико-математический словарь
имитационные (численные) методы решения моделей — Последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср. Аналитические методы решения… … Справочник технического переводчика
Бесконечные методы математического программирования — [infinite methods in mathematical programming] – численные методы оптимизации, решения задач математического программирования (например, крупноразмерных линейных) путем последовательных шагов (итераций), дающих все более точное приближение к… … Экономико-математический словарь
бесконечные методы математического программирования — Численные методы оптимизации, решения задач математического программирования (например, крупноразмерных линейных) путем последовательных шагов (итераций), дающих все более точное приближение к искомому решению. Процесс вычислений может быть… … Справочник технического переводчика
ОВРАЖНЫХ ФУНКЦИЙ МЕТОДЫ МИНИМИЗАЦИИ — численные методы отыскания минимумов функций многих переменных. Пусть задана ограниченная снизу дважды непрерывно дифференцируемая по своим аргументам функция для к рой известно, что при нек ром векторе ( знак транспонирования) она принимает… … Математическая энциклопедия
Градиентные методы — численные методы решения с помощью градиента задач, сводящихся к нахождению экстремумов функции. Содержание 1 Постановка задачи решения системы уравнений в терминах методов о … Википедия
Задача оптимизации — Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств. Содержание … Википедия
Вычислительные методы — См. также: Вычислительная математика Вычислительные (численные) методы методы решения математических задач в численном виде (см. Компьютерная алгебра)[1] Представление как исходных данных в задаче, так и её решения в виде числа или… … Википедия

Книги

Численные методы оптимизации. Учебное пособие, Измаилов Алексей Феридович, Солодов Михаил Владимирович. Современный курс численных методов оптимизации. Основное внимание уделено методам общего назначения, ориентированным на решение гладких задач математического программирования без какой-либо… Подробнее Купить за 983 грн (только Украина)
Численные методы оптимизации. Учебник и практикум для академического бакалавриата, Тимохов А.В., Сухарев А.Г., Федоров В.В.. Учебник написан на основе курсов лекций по оптимизации, которые на протяжении ряда лет читались авторами на факультете вычислительной математики и кибернетики Московского государственного… Подробнее Купить за 976 руб
Численные методы оптимизации. Учебное пособие, Измаилов Алексей Феридович, Солодов Михаил Владимирович. Современный курс численных методов оптимизации. Основное внимание уделено методам общего назначения, ориентированным на решение гладких задач математического программирования без какой-либо… Подробнее Купить за 793 руб

Другие книги по запросу «Численные методы оптимизации» >>

economic_mathematics.academic.ru

методы оптимизации - это... Что такое методы оптимизации?

методы оптимизации

методы оптимизации —[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]

Тематики

информационные технологии в целом

EN

optimization strategy
optimization techniques

Справочник технического переводчика. – Интент. 2009-2013.

методы определения относительного возраста горных пород
методы ослабления влияния затухания в дожде

Смотреть что такое "методы оптимизации" в других словарях:

Методы оптимизации — Математическое программирование математическая дисциплина, изучающая теорию и методы решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями… … Википедия
РД 50-216-80: Методические указания. Количественные методы оптимизации параметров объектов стандартизации. Основные положения по обеспечению широкого внедрения. Направления работ и унификация методов и документов — Терминология РД 50 216 80: Методические указания. Количественные методы оптимизации параметров объектов стандартизации. Основные положения по обеспечению широкого внедрения. Направления работ и унификация методов и документов: Базовая… … Словарь-справочник терминов нормативно-технической документации
Численные методы оптимизации — [numerical optimization technique] методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет… … Экономико-математический словарь
численные методы оптимизации — Методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет изучения вычислительной математики … Справочник технического переводчика
оптимизации мышления методы — ОПТИМИЗАЦИИ МЫШЛЕНИЯ МЕТОДЫ (от лат. optimus наилучший) специальные практические психолого педагогические приемы, направленные на повышение эффективности протекания мыслительного процесса, его продуктивности. Разработка конкретного метода … Энциклопедия эпистемологии и философии науки
Методы изобретательного творчества — Методы технического творчества это совокупность последовательности операций прогнозирования оптимальных параметров, в наибольшей степени отвечающих общественным или техническим потребностям. Содержание 1 Развитие методики изобретательного… … Википедия
МЕТОДЫ ПРОЕКТИРОВАНИЯ СУДОВ — методы, используемые для определения основных элементов проектируемых судов, а также для решения ряда других задач, предусматриваемых теорией проектирования судов: разработки задания на проектирование судна; построения теоретического чертежа;… … Морской энциклопедический справочник
Методы активного обучения — (МАО) совокупность педагогических действий и приёмов, направленных на организацию учебного процесса и создающего специальными средствами условия, мотивирующие обучающихся к самостоятельному, инициативному и творческому освоению учебного материала … Википедия
методы сетевого планирования и управления — Комплекс методов построения, расчёта, анализа и оптимизации сетевых моделей [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики сетевое планирование, моделирование EN methods of network planning and control… … Справочник технического переводчика
МЕТОДЫ КЛАССИФИКАЦИИ — совокупность методов статистич. многомерного анализа. В зависимости от того, в какой области научн. знаний М.к. возникли и получили свое развитие, они наз. методами многомерной классификации, таксономии, кластерного анализа, группировки,… … Российская социологическая энциклопедия

Книги

Методы оптимизации, А. В. Аттетков, В. С. Зарубин, А. Н. Канатников. Освещается одно из важнейших направлений математики - теория оптимизации. Рассмотрены теоретические, вычислительные и прикладные аспекты методов конечномерной оптимизации. Описаны алгоритмы… Подробнее Купить за 1290 грн (только Украина)
Методы оптимизации, А. П. Смирнов. Особое внимание уделено построению алгоритмов поиска экстремума, что даст возможность студентам самостоятельно разрабатывать соответствующие программные средства в случаях, когда… Подробнее Купить за 512 руб электронная книга
Методы оптимизации, А. В. Аттетков, В. С. Зарубин, А. Н. Канатников. Освещается одно из важнейших направлений математики - теория оптимизации. Рассмотрены теоретические, вычислительные и прикладные аспекты методов конечномерной оптимизации. Описаны алгоритмы… Подробнее Купить за 402 руб

Другие книги по запросу «методы оптимизации» >>

technical_translator_dictionary.academic.ru

метод оптимизации - это... Что такое метод оптимизации?

метод определения стоимости
метод ортогонализации

Смотреть что такое "метод оптимизации" в других словарях:

МЕТОД ОПТИМИЗАЦИИ — метод построения алгоритмов нахождения максимумов функции и точек, в которых они достигаются, при наличии ограничений или без них. Обычно рассматривается случай, когда функция задана в одномерном или многомерном пространстве; однако М.о. обобщены … Большой экономический словарь
Теоретический метод оптимизации — Совокупность процедур построения или выбора математической модели оптимизации ПОС, проверки ее применимости, получения входных данных и вычисления оптимальных параметров Источник … Словарь-справочник терминов нормативно-технической документации
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Метод роя частиц — (МРЧ) метод численной оптимизации, для использования которого не требуется знать точного градиента оптимизируемой функции. МРЧ был доказан Кеннеди, Эберхартом и Ши[1] [2] и изначально предназначался для имитации социального поведения.… … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Гаусса — Ньютона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона-Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательной (Метод Ньютона) — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод касательных — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

dic.academic.ru

Основные методы оптимизации

Классические методы решения задачи оптимизации хорошо известны – поиск условных экстремумов с помощью производной. Однако подобные методы имеют ограниченное применение по ряду причин:

– когда аргументовх1, х2 , … хnмного, совместное решение системы уравнений оказывается зачастую очень сложным;

– как правило, экстремум наблюдается не в точке, где производная обращается в ноль, а на границе области принятия решений;

– производных, о которых идет речь, может не существовать, например, если аргументы х1, х2 , …, хnизменяются дискретно, или же сама функция имеет особенности.

Поэтому приходится применять численные методы оптимизации. Одним из таких методов является математическое программирование.

Математическое программирование – область математики, объединяющая различные математические методы и дисциплины: линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование и др.

Линейное программирование (ЛП) – область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными (все ограничения и целевая функция – линейные).

Линейное программирование находит применение в решении широкого класса экономических задач:

– задача об использовании ресурсов (задача планирования производства): при заданных ограничениях на ресурсы составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной;

– задача об использовании мощностей (задача о загрузке оборудования) – распределение выпуска продукции между станками, минимизирующего затраты на производство всей продукции;

– транспортная задача – задача о прикреплении поставщиков к потребителям, минимизирующем суммарные расходы на перевозки;

– задача составления рациона (задача о диете, задача о смесях): при заданном содержании питательных веществ в каждом виде продукта необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела;

– задача о назначениях – распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т. д.). То есть ресурсы неделимы между работами, а работы неделимы между ресурсами. Задача о назначениях имеет место при распределении людей на должности или работы, автомашин на маршруты, водителей на машины, групп по аудиториям, научных тем по научно-исследовательским лабораториям и т.п.

– задача о раскрое. Производство многих видов промышленной продукции начинается с раскроя материала. Кроят не только одежду и обувь, но и детали корпуса корабля, кузова автомобиля, фюзеляжа самолета. Раскраивают ткани и кожу, бумагу и стекло, металл и пластмассу. В масштабах предприятия, отрасли, страны рациональный раскрой позволяет сэкономить колоссальные средства.

Общепринятое понятие оптимальности расширяет теория игр. Принципиальным достоинством теории игр считают то, что она включает в это понятие такие важные элементы, как, например, компромиссное решение, устраивающее разные стороны в споре (игре).

Теория игр – математическая теория конфликтных ситуаций.

В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Во всех этих примерах конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неизвестные заранее решения, которые эти партнеры будут принимать.

Целью теории игр является определение оптимальных стратегий игроков. При выборе оптимальной стратегии естественно предполагать, что игроки ведут себя разумно с точки зрения своих интересов.

На практике игровые подходы используются при разработке микроэкономических моделей, в которых учитываются интересы различных звеньев (например, отраслей и экономических районов).

Кроме того, математические приемы теории игр могут применяться для решения практических экономических задач на промышленных предприятиях. Например, для выбора оптимальных решений в области повышения качества продукции или определения запасов. «Противоборство» здесь происходит в первом случае между стремлением выпустить больше продукции (затратить на нее меньше труда) и сделать ее лучше, т. е. затратить больше труда; во втором случае – между желанием запасти ресурсов побольше, чтобы быть застрахованным от случайностей, и запасти поменьше, чтобы не замораживать средства.

Дата добавления: 2015-12-08; просмотров: 261 | Нарушение авторских прав

mybiblioteka.su - 2015-2018 год. (0.007 сек.)

mybiblioteka.su