Оптимизация гиперпараметров в Vowpal Wabbit с помощью нового модуля vw-hyperopt. Байесова оптимизация гиперпараметров
Оптимизация гиперпараметров в Vowpal Wabbit с помощью нового модуля vw-hyperopt / Блог компании DCA (Data-Centric Alliance) / Хабр
 Для поиска хороших конфигураций vw-hyperopt использует алгоритмы из питоновской библиотеки Hyperopt и может оптимизировать гиперпараметры адаптивно с помощью метода Tree-Structured Parzen Estimators (TPE). Это позволяет находить лучшие оптимумы, чем простой grid search, при равном количестве итераций.
Для поиска хороших конфигураций vw-hyperopt использует алгоритмы из питоновской библиотеки Hyperopt и может оптимизировать гиперпараметры адаптивно с помощью метода Tree-Structured Parzen Estimators (TPE). Это позволяет находить лучшие оптимумы, чем простой grid search, при равном количестве итераций.
Эта статья будет интересна всем, кто имеет дело с Vowpal Wabbit, и особенно тем, кто досадовал на отсутствие в исходном коде способов тюнинга многочисленных ручек моделей, и либо тюнил их вручную, либо кодил оптимизацию самостоятельно.
Гиперпараметры
Что такое гиперпараметры? Это все «степени свободы» алгоритма, которые он напрямую не оптимизирует, но от которых зависит результат. Иногда результат зависит совсем чуть-чуть, и тогда, если это не kaggle, можно обойтись дефолтными значениями или подобрать вручную. Но иногда неудачная конфигурация может все испортить: алгоритм либо сильно переобучится, либо, наоборот, не сможет использовать большую часть информации.В узком смысле, под гиперпараметрами часто понимают лишь регуляризацию и другие «очевидные» настройки методов машинного обучения. Однако в широком смысле, гиперпараметры — это вообще любые манипуляции с данными, которые могут повлиять на результат: инжиниринг фич, взвешивание наблюдений, undersampling и т.д.
Grid Search
Конечно, было бы неплохо иметь алгоритм, который помимо оптимизации параметров, оптимизировал бы и гиперпараметры. Еще лучше, если бы мы могли доверять этому алгоритму больше, чем интуиции. Какие-то шаги в этом направлении, конечно, давно сделаны. В многие библиотеки машинного обучения встроены наивные методы: grid search — проход по сетке, либо random search — семплирование точек из фиксированного распределения (самые известные экземпляры — это GridSearchCV и RandomizedGridSearchCV в sklearn). Преимущество прохода по сетке в том, что его легко закодить самому и легко распараллелить. Однако у него есть и серьезные недостатки:- Он перебирает много заведомо неудачных точек. Допустим, уже имеется набор каких-то конфигураций с результатами или другая какая-то информация. Человек может понять, какие конфигурации точно дадут отстойный результат, и догадается не проверять лишний раз эти регионы. Grid search так делать не умеет.
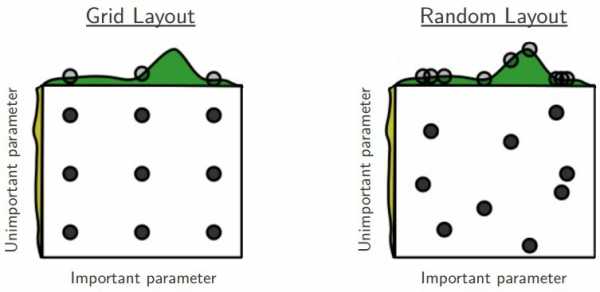
- Если гиперпараметров много, то размер «ячейки» приходится делать слишком крупным, и можно упустить хороший оптимум. Таким образом, если включить в пространство поиска много лишних гиперпараметров, никак не влияющих на результат, то grid search будет работать намного хуже при том же числе итераций. Впрочем, для random search это справедливо в меньшей степени:
Байесовские методы
Для того, чтобы уменьшить число итераций до нахождения хорошей конфигурации, придуманы адаптивные байесовские методы. Они выбирают следующую точку для проверки, учитывая результаты на уже проверенных точках. Идея состоит в том, чтобы на каждом шаге найти компромисс между (а) исследованием регионов рядом с самыми удачными точками среди найденных и (б) исследованием регионов с большой неопределенностью, где могут находиться еще более удачные точки. Это часто называют дилеммой explore-exploit или «learning vs earning». Таким образом, в ситуациях, когда проверка каждой новой точки стоит дорого (в машинном обучении проверка = обучение + валидация), можно приблизиться к глобальному оптимуму за гораздо меньшее число шагов.Подобные алгоритмы в разных вариациях реализованы в инструментах MOE, Spearmint, SMAC, BayesOpt и Hyperopt. На последнем мы остановимся подробнее, так как vw-hyperopt — это обертка над Hyperopt, но сначала надо немного написать про Vowpal Wabbit.
Vowpal Wabbit
Многие из вас наверняка использовали этот инструмент или хотя бы слышали о нем. Вкратце, это одна из наиболее быстрых (если не самая быстрая) в мире библиотека машинного обучения. Натренировать модель для нашего CTR-предиктора (бинарная классификация) на 30 миллионах наблюдений и десятках миллионах фичей занимает всего несколько гигабайт оперативной памяти и 6 минут на одном ядре. В Vowpal Wabbit реализованы несколько онлайновых алгоритмов:- Стохастический градиентный спуск с разными наворотами;
- FTRL-Proximal, о котором можно почитать здесь;
- Онлайновое подобие SVM;
- Онлайновый бустинг;
- Факторизационные машины.
FTRL и SGD могут решать задачи как регрессии, так и классификации, это регулируется только функцией потерь. Эти алгоритмы линейны относительно фичей, но нелинейность может легко быть достигнута с помощью полиномиальных фичей. Имеется очень полезный механизм ранней остановки, чтобы уберечься от переобучения, если указал слишком большое количество эпох.
Также Vowpal Wabbit знаменит своим хешированием фичей, которое выполняет роль дополнительной регуляризации, если фичей очень много. Благодаря этому удается обучаться на категориальных фичах с миллиардами редко встречающихся категорий, вмещая модель в оперативную память без ущерба для качества.
Vowpal Wabbit требует специальный входной формат данных, но в нем легко разобраться. Он естественным образом разреженный и занимает мало места. В оперативную память в любой момент времени загружена всего одно наблюдение (или несколько, для LDA). Обучение проще всего запускать через консоль.
Интересующиеся могут прочитать туториал и другие примеры и статьи в их репозитории, а также презентацию. Про внутренности Vowpal Wabbit можно подробно прочитать в публикациях Джона Лэнгфорда и в его блоге. На Хабре тоже есть подходящий пост. Список аргументов можно получить через vw --help или почитать подробное описание. Как видно из описания, аргументов десятки, и многие из них могут считаться гиперпараметрами, которые можно оптимизировать.
В Vowpal Wabbit имеется модуль vw-hypersearch, который умеет подбирать один какой-нибудь гиперпараметр методом золотого сечения. Однако при наличии нескольких локальных минимумов этот метод, скорее всего, обнаружит далеко не лучший вариант. К тому же, зачастую нужно оптимизировать сразу много гиперпараметров, и этого нет в vw-hypersearch. Пару месяцев назад я попробовал написать многомерный метод золотого сечения, но количество шагов, которые требовались ему для сходимости, превзошло любой grid search, так что этот вариант отпал. Было решено использовать Hyperopt.
Hyperopt
В этой библиотеке, написанной на питоне, реализован алгоритм оптимизации Tree-Structured Parzen Estimators (TPE). Преимущество его в том, что он может работать с очень «неуклюжими» пространствами: когда один гиперпараметр непрерывный, другой категориальный; третий дискретный, но соседние значения его коррелированы друг с другом; наконец, некоторые комбинации значений параметров могут просто не иметь смысла. TPE принимает на вход иерархическое пространство поиска с априорными вероятностями, и на каждом шаге смешивает их с Гауссовским распределением с центром в новой точке. Его автор Джеймс Бергстра утверждает, что этот алгоритм достаточно хорошо решает проблему explore-exploit и работает лучше как grid search-а, так и экспертного перебора, по крайней мере, для задач глубокого обучения, где гиперпараметров особенно много. Подробнее об этом можно почитать здесь и здесь. Про сам алгоритм TPE можно почитать здесь. Возможно, в будущем удастся написать про него подробный пост.vw-hyperopt
Перейдем к использованию модуля vw-hyperopt. Сначала нужно установить последнюю версию Vowpal Wabbit с гитхаба. Модуль находится в папке utl.Внимание! Последние изменения (в частности, новый синтаксис команды) пока что (на 15 декабря) не влиты в основной репозиторий. В ближайшие дни, надеюсь, проблема решится, а пока что можете пользоваться последней версией кода из моей ветки. EDIT: 22 декабря изменения влиты, теперь можно пользоваться основным репозиторием.
Пример использования:
./vw-hyperopt.py --train ./train_set.vw --holdout ./holdout_set.vw --max_evals 200 --outer_loss_function logistic --vw_space '--algorithms=ftrl,sgd --l2=1e-8..1e-1~LO --l1=1e-8..1e-1~LO -l=0.01..10~L --power_t=0.01..1 --ftrl_alpha=5e-5..8e-1~L --ftrl_beta=0.01..1 --passes=1..10~I --loss_function=logistic -q=SE+SZ+DR,SE~O --ignore=T~O' --plot На вход модулю требуется обучающая и валидационная выборки, а также априорные распределения гиперпараметров (закавыченные внутри --vw_space). Можно задавать целочисленные, непрерывные или категориальные гиперпараметры. Для всех, кроме категориальных, можно задавать равномерное или лог-равномерное распределения. Пространство поиска из примера преобразуется внутри vw-hyperopt приблизительно в такой объект для Hyperopt (если вы прошли туториал по Hyperopt, вы поймете это):from hyperopt import hp prior_search_space = hp.choice('algorithm', [ {'type': 'sgd', '--l1': hp.choice('sgd_l1_outer', ['empty', hp.loguniform('sgd_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('sgd_l2_outer', ['empty', hp.loguniform('sgd_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('sgd_l', log(0.01), log(10)), '--power_t': hp.uniform('sgd_power_t', 0.01, 1), '-q': hp.choice('sgd_q_outer', ['emtpy', hp.choice('sgd_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('sgd_loss', ['logistic']), '--passes': hp.quniform('sgd_passes', 1, 10, 1), }, {'type': 'ftrl', '--l1': hp.choice('ftrl_l1_outer', ['emtpy', hp.loguniform('ftrl_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('ftrl_l2_outer', ['emtpy', hp.loguniform('ftrl_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('ftrl_l', log(0.01), log(10)), '--power_t': hp.uniform('ftrl_power_t', 0.01, 1), '-q': hp.choice('ftrl_q_outer', ['emtpy', hp.choice('ftrl_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('ftrl_loss', ['logistic']), '--passes': hp.quniform('ftrl_passes', 1, 10, 1), '--ftrl_alpha': hp.loguniform('ftrl_alpha', 5e-5, 8e-1), '--ftrl_beta': hp.uniform('ftrl_beta', 0.01, 1.) } ]) Опционально можно изменить функцию потерь на валидационной выборке и максимальное количество итераций (--outer_loss_function, по умолчанию logistic, и --max_evals, по умолчанию 100). Также можно сохранять результаты каждой итерации и строить графики с помощью --plot, если установлен matplotlib и, желательно, seaborn: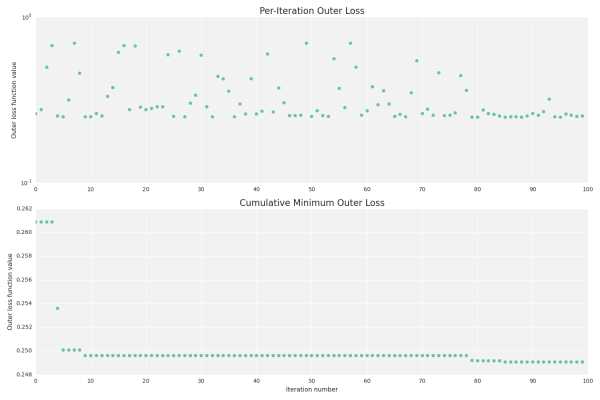
Документация
Так как на хабрахабр не принято выкладывать подробную документацию, ограничусь ссылкой на нее. Про всю семантику вы можете почитать в русскоязычной вики в моем форке или дождаться англоязычной версии в главном репозитории Vowpal Wabbit.Планы
В будущем в модуль планируется добавить:- Поддержку задач регрессии и мультиклассовой классификации.
- Поддержку «теплого старта»: выдать Hyperopt заранее оцененные точки, и начать оптимизацию уже с учетом результатов на них.
- Опцию оценки ошибки на каждом шаге на еще одной тестовой выборке (но без оптимизации гиперпараметров на ней). Это нужно, чтобы лучше оценить обобщающую способность — не переобучились ли мы.
- Поддержку бинарных параметров, которые не принимают никаких значений, таких как --lrqdropout, --normalized, --adaptive и т.д. Сейчас можно, в принципе, писать --adaptive=\ ~O, но это неинтуитивно совсем. Можно сделать что-то вроде --adaptive=~B или --adaptive=~BO.
Обновление 22.12.2015
Пулл реквест с последними изменениями вмержили в основной репозиторий Vowpal Wabbit, так что можно теперь использовать его, а не ветку.habr.com
Оптимизация гиперпараметров Википедия
В обучении машин, оптимизация гиперпараметров — это задача выбора набора оптимальных гиперпараметров[en] для обучающего алгоритма.
Одни и те же виды моделей обучения машин могут требовать различные предположения, веса или скорости обучения для различных видов данных. Эти параметры называются гиперпараметрами и их следует настраивать так, чтобы модель могла оптимально решить задачу обучения машины. Оптимизация гиперпараметров находит кортеж гиперпараметров, который даёт оптимальную модель, оптимизирующую заданную функцию потерь на заданных независимых данных[1]. Целевая функция берёт кортеж гиперпараметров и возвращает связанные с ними потери[1]. Часто используется перекрёстная проверка для оценки этой обобщающей способности[2].
Подходы
Поиск по решётке
Традиционным методом осуществления оптимизации гиперпарамеров является поиск по решётке (или вариация параметров), который просто делает полный перебор по заданному вручную подмножеству пространства гиперпараметров обучающего алгоритма. Поиск по решётке должен сопровождаться некоторым измерением производительности, обычно измеряемой посредством перекрёстной проверки на тренировочном множестве[3], или прогонкой алгоритма на устоявшемся проверочном наборе[4].
Поскольку пространство параметров обучающего машину алгоритма для некоторых параметров может включать пространства с вещественными или неограниченными значениями, вручную установить границу и дискретизацию может оказаться необходимым до применения поиска по решётке.
Например, типичный классификатор с мягким зазором на основе метода опорных векторов (МОВ), оснащённый ядерной радиально-базисной функцией[en] имеет по меньшей мере два гиперпараметра, которые необходимо настроить для хорошей производительности на недоступных данных — константа C регуляризации и гиперпараметр ядра γ. Оба параметра являются непрерывными, так что для поиска по решётке выбирают конечный набор «приемлемых» значений, скажем
C∈{10,100,1000}{\displaystyle C\in \{10,100,1000\}} γ∈{0.1,0.2,0.5,1.0}{\displaystyle \gamma \in \{0.1,0.2,0.5,1.0\}}Поиск по решётке затем прогоняет МОВ для каждой пары (C, γ) в декартовом произведении этих двух множеств и проверяет производительность при выбранных параметрах на устоявшемся проверочном наборе (или с помощью внутренней перекрёстной проверки на тренировочном наборе и в этом случае несколько МОВ прогоняют попарно). Наконец, алгоритм поиска по решётке выдаёт в качестве результата наивысший результат, достигнутый на процедуре проверки.
Поиск по решётке страдает от проклятия размерности, но часто легко параллелизуем, поскольку обычно гиперпараметрические величины, с которыми алгоритм работает, не зависят друг от друга[2].
Случайный поиск
Случайный поиск заменяет полный перебор всех комбинаций на выборку их случайным образом. Это можно легко применить к дискретным установкам, приведённым выше, но метод может быть также обобщен к непрерывным и смешанным пространствам. Случайный поиск может превзойти поиск по решётке, особенно в случае, если только малое число гиперпараметров оказывает влияние на производительность алгоритма обучения машины[2]. В этом случае говорят, что задача оптимизации имеет низкую внутреннюю размерность[5]. Случайный поиск также легко параллелизуем и, кроме того, позволяют использовать предварительные данные путём указания распределения для выборки случайных параметров.
Байесовская оптимизация
Байесовская оптимизация — это метод глобальной оптимизации для неизвестной функции (чёрного ящика) с шумом. Применённая к гиперпараметрической оптимизации байесовская оптимизация строит стохастическую модель функции отображения из значений гиперпараметра в целевую функцию, применённую на множестве проверки. Путём итеративного применения перспективной конфигурации гиперпараметров, основанной на текущей модели, а затем её обновления, байесовская оптимизация стремится собрать как можно больше информации об этой функции и, в частности, место оптимума. Метод пытается сбалансировать зондирование (гиперпараметры, для которых изменение наименее достоверно известно) и использование (гиперпараметры, которые, как ожидается, наиболее близки к оптимуму). На практике байесовская оптимизация показала[6][7][8][9] лучшие результаты с меньшими вычислениями по сравнению с поиском по решётке и случайным поиском ввиду возможности суждения о качестве экспериментов ещё до их выполнения.
Оптимизация на основе градиентов
Для конкретных алгоритмов обучения можно вычислить градиент гиперпараметров и оптимизировать их с помощью градиентного спуска. Первое использование этих техник фокусировалось на нейронных сетях[10]. Затем эти методы были распространены на другие модели, такие как методы опорных векторов[11] или логистическая регрессия[12].
Другой подход использования градиентов гиперпараметров состоит в дифференцировании шагов алгоритма итеративной оптимизации с помощью автоматического дифференцирования[en][13][14].
Эволюционная оптимизация
Эволюционная оптимизация — это методология для глобальной оптимизации неизвестных функций с шумом. При оптимизации гиперпараметров эволюционная оптимизация использует эволюционные алгоритмы для поиска гиперпараметров для данного алгоритма[7]. Эволюционная оптимизация гиперпараметров следует процессу, навеянному биологической концепцией эволюции:
- Создаём начальную популяцию случайных решений (т.е. сгенерированный случайно кортеж гиперпараметров, обычно 100+)
- Оцениваем кортежи гиперпараметров и получаем их функцию приспособленности (например, с помощью 10-кратной точности перекрёстной проверки алгоритма обучения машины с этими гиперпараметрами)
- Ранжируем кортежи гиперпараметров по их относительной пригодности
- Заменяем кортежи киперпараметров с худшей производительностью на новые кортежи гиперпараметров, образованных скрещиванием[en] и мутацией[en]
- Повторяем шаги 2—4, пока не получим удовлетворительной производительности алгоритма или пока производительность не перестанет улучшаться
Эволюционная оптимизация используется для оптимизации гиперпараметров для статистических алгоритмов обучения машин[7], автоматического обучения машин[15][16], для поиска архитектуры глубоких нейронных сетей[17][18], а также для формирования весов в глубоких нейронных сетях[19].
Другое
Развиваются также методы радиально-базисной функции (РБФ)[20] и спектральный метод[en][21].
Программное обеспечение с открытым кодом
Поиск по решётке
Случайный поиск
- hyperopt через hyperas и hyperopt-sklearn — это пакеты на языке Python, которые включают случайный поиск.
- scikit-learn[en] — это пакет на языке Python, включающий случайный поиск.
- h3O AutoML обеспечивает автоматическую подготовку данных, настройку гиперпараметров случайным поиском и многоуровневые сборки в распределённой платформе обучения машин.
- Talos включает допускающий настройку случайный поиск для Keras.
Байесовская оптимизация
- Spearmint — это пакет для байесовской оптимизации алгоритмов обучения машин.
- Bayesopt[22], эффективная имплементация байесовской оптимизации на C/C++ с поддержкой Python, Matlab и Octave.
- MOE — это библиотека для Python, C++ и системы параллельных вычислений CUDA, имплементирующая байесовскую глобальную оптимизацию, используя гауссовы процессы.
- Auto-WEKA[23] — это уровень для байесовской оптимизации поверх WEKA.
- Auto-sklearn[24] — это уровень для байесовской оптимизации поверх scikit-learn[en].
- mlrMBO с mlr — это пакет на языке R[en] для байесовской оптимизации или для оптимизации на основе модели неизвестной функции (чёрный ящик).
- tuneRanger — это пакет на языке R для настройки случайных лесов используя оптимизацию на базе модели.
- BOCS — это пакет Matlab, использующий полуопределённое программирование для минимизации неизвестной функции при дискретных входных данных.[25] Включена также имплементация для Python 3.
- SMAC — это библиотека на языках Python/Java, имплементирующая байесовскую оптимизацию[26].
Основанные на градиенте
- hypergrad — это пакет на языке Python для дифференцирования по гиперпараметрам[14].
Эволюционные методы
Другое
Коммерческие сервисы
- BigML OptiML поддерживает смешанные области поиска
- Google HyperTune поддерживает смешанные области поиска
- Indie Solver поддерживает многокритериальную и разнотипную оптимизацию и оптимизацию при ограничениях
- SigOpt поддерживает смешанные области поиска, поддерживает многокритериальную и разнотипную оптимизацию и оптимизацию при ограничениях и параллельную оптимизацию.
- Mind Foundry OPTaaS поддерживает смешанные области поиска, многокритериальную и параллельную оптимизацию, оптимизацию при ограничениях и суррогатные модели.
См. также
Примечания
- ↑ 1 2 Claesen, Marc & Bart De Moor (2015), "Hyperparameter Search in Machine Learning", arΧiv:1502.02127 [cs.LG]
- ↑ 1 2 3 Bergstra, Bengio, 2012, с. 281–305.
- ↑ Chin-Wei Hsu, Chih-Chung Chang and Chih-Jen Lin (2010). A practical guide to support vector classification. Technical Report, National Taiwan University.
- ↑ Chicco, 2017, с. 1–17.
- ↑ Ziyu, Frank, Masrour, David, de Feitas, 2016.
- ↑ Hutter, Hoos, Leyton-Brown, 2011.
- ↑ 1 2 3 Bergstra, Bardenet, Bengio, Kegl, 2011.
- ↑ Snoek, Larochelle, Adams, 2012.
- ↑ Thornton, Hutter, Hoos, Leyton-Brown, 2013.
- ↑ Larsen, Hansen, Svarer, Ohlsson, 1996.
- ↑ Chapelle, Vapnik, Bousquet, Mukherjee, 2002, с. 131–159.
- ↑ Chuong, Foo, Ng, 2008.
- ↑ Domke, 2012.
- ↑ 1 2 Maclaurin, Douglas; Duvenaud, David & Adams, Ryan P. (2015), "Gradient-based Hyperparameter Optimization through Reversible Learning", arΧiv:1502.03492 [stat.ML]
- ↑ 1 2 Olson, Urbanowicz, Andrews, Lavender, Kidd, Moore, 2016, с. 123–137.
- ↑ 1 2 Olson, Bartley, Urbanowicz, Moore, 2016, с. 485–492.
- ↑ Miikkulainen R, Liang J, Meyerson E, Rawal A, Fink D, Francon O, Raju B, Shahrzad H, Navruzyan A, Duffy N, Hodjat B (2017), "Evolving Deep Neural Networks", arΧiv:1703.00548 [cs.NE]
- ↑ Jaderberg M, Dalibard V, Osindero S, Czarnecki WM, Donahue J, Razavi A, Vinyals O, Green T, Dunning I, Simonyan K, Fernando C, Kavukcuoglu K (2017), "Population Based Training of Neural Networks", arΧiv:1711.09846 [cs.LG]
- ↑ Such FP, Madhavan V, Conti E, Lehman J, Stanley KO, Clune J (2017), "Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning", arΧiv:1712.06567 [cs.NE]
- ↑ 1 2 Diaz, Gonzalo; Fokoue, Achille; Nannicini, Giacomo & Samulowitz, Horst (2017), "An effective algorithm for hyperparameter optimization of neural networks", arΧiv:1705.08520 [cs.AI]
- ↑ 1 2 Hazan, Elad; Klivans, Adam & Yuan, Yang (2017), "Hyperparameter Optimization: A Spectral Approach", arΧiv:1706.00764 [cs.LG]
- ↑ Martinez-Cantin, 2014, с. 3915−3919.
- ↑ Kotthoff, Thornton, Hoos, Hutter, Leyton-Brown, 2017, с. 1–5.
- ↑ Feurer, Klein, Eggensperger, Springenberg, Blum, Hutter, 2015, с. 2962–2970.
- ↑ Baptista, Ricardo & Poloczek, Matthias (2018), "Bayesian Optimization of Combinatorial Structures", arΧiv:1806.08838 [stat.ML]
- ↑ Hutter, Hoos, Leyton-Brown, 2011, с. 507-523.
- ↑ Gorissen, Crombecq, Couckuyt, Demeester, Dhaene, 2010, с. 2051–2055.
Литература
- James Bergstra, Yoshua Bengio. Random Search for Hyper-Parameter Optimization // J. Machine Learning Research. — 2012. — Т. 13.
- Chicco D. Ten quick tips for machine learning in computational biology // BioData Mining. — 2017. — Декабрь (т. 10). — P. 1–17. — DOI:10.1186/s13040-017-0155-3. — PMID 29234465.
- Wang Ziyu, Hutter Frank, Zoghi Masrour, Matheson David, Nando de Feitas. Bayesian Optimization in a Billion Dimensions via Random Embeddings (англ.) // Journal of Artificial Intelligence Research. — 2016. — Vol. 55. — DOI:10.1613/jair.4806.
- James Bergstra, Remi Bardenet, Yoshua Bengio, Balazs Kegl. Algorithms for hyper-parameter optimization // Advances in Neural Information Processing Systems. — 2011.
- Jasper Snoek, Hugo Larochelle, Ryan Adams. Practical Bayesian Optimization of Machine Learning Algorithms // Advances in Neural Information Processing Systems. — 2012. — Bibcode: 2012arXiv1206.2944S. — arXiv:1206.2944.
- Chris Thornton, Frank Hutter, Holger Hoos, Kevin Leyton-Brown. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms // Knowledge Discovery and Data Mining. — 2013. — Bibcode: 2012arXiv1208.3719T. — arXiv:1208.3719.
- Jan Larsen, Lars Kai Hansen, Claus Svarer, M Ohlsson. Design and regularization of neural networks: the optimal use of a validation set // Proceedings of the 1996 IEEE Signal Processing Society Workshop. — 1996.
- Olivier Chapelle, Vladimir Vapnik, Olivier Bousquet, Sayan Mukherjee. Choosing multiple parameters for support vector machines // Machine Learning. — 2002. — Vol. 46. — DOI:10.1023/a:1012450327387.
- Chuong B., Chuan-Sheng Foo, Andrew Y Ng. Efficient multiple hyperparameter learning for log-linear models // Advances in Neural Information Processing Systems 20. — 2008.
- Justin Domke. Generic Methods for Optimization-Based Modeling // AISTATS. — 2012. — Т. 22.
- Ruben Martinez-Cantin. BayesOpt: A Bayesian Optimization Library for Nonlinear Optimization, Experimental Design and Bandits // Journal of Machine Learning Research. — 2014. — Т. 15. — С. 3915−3919. — Bibcode: 2014arXiv1405.7430M. — arXiv:1405.7430.
- Kotthoff L., Thornton C., Hoos H.H., Hutter F., Leyton-Brown K. Auto-WEKA 2.0: Automatic model selection and hyperparameter optimization in WEKA // Journal of Machine Learning Research. — 2017.
- Feurer M., Klein A., Eggensperger K., Springenberg J., Blum M., Hutter F. Efficient and Robust Automated Machine Learning // Advances in Neural Information Processing Systems 28 (NIPS 2015). — 2015.
- Hutter F., Hoos H.H., Leyton-Brown K. Sequential Model-Based Optimization for General Algorithm Configuration // Proceedings of the conference on Learning and Intelligent OptimizatioN (LION 5). — Rome, Italy: Springer-Verlag, 2011.
- Olson R.S., Urbanowicz R.J., Andrews P.C., Lavender N.A., Kidd L., Moore J.H. Automating biomedical data science through tree-based pipeline optimization // Proceedings of EvoStar 2016. — 2016. — Т. 9597. — (Lecture Notes in Computer Science). — ISBN 978-3-319-31203-3. — DOI:10.1007/978-3-319-31204-0_9.
- Olson R.S., Bartley N., Urbanowicz R.J., Moore J.H. Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. — 2016. — С. Proceedings of EvoBIO 2016. — ISBN 9781450342063. — DOI:10.1145/2908812.2908918. — arXiv:1603.06212.
- Dirk Gorissen, Karel Crombecq, Ivo Couckuyt, Piet Demeester, Tom Dhaene. A Surrogate Modeling and Adaptive Sampling Toolbox for Computer Based Design // J. Machine Learning Research. — 2010. — Т. 11. — С. 2051–2055.
wikiredia.ru
Оптимизация гиперпараметров в Vowpal Wabbit с помощью нового модуля vw-hyperopt
Привет! В этой статье речь пойдет о таком не очень приятном аспекте машинного обучения, как оптимизация гиперпараметров. Две недели назад в очень известный и полезный проект Vowpal Wabbit был влит модуль vw-hyperopt.py, умеющий находить хорошие конфигурации гиперпараметров моделей Vowpal Wabbit в пространствах большой размерности. Модуль был разработан внутри DCA (Data-Centric Alliance).

Для поиска хороших конфигураций vw-hyperopt использует алгоритмы из питоновской библиотеки Hyperopt и может оптимизировать гиперпараметры адаптивно с помощью метода Tree-Structured Parzen Estimators (TPE). Это позволяет находить лучшие оптимумы, чем простой grid search, при равном количестве итераций.
Эта статья будет интересна всем, кто имеет дело с Vowpal Wabbit, и особенно тем, кто досадовал на отсутствие в исходном коде способов тюнинга многочисленных ручек моделей, и либо тюнил их вручную, либо кодил оптимизацию самостоятельно.
Гиперпараметры
Что такое гиперпараметры? Это все «степени свободы» алгоритма, которые он напрямую не оптимизирует, но от которых зависит результат. Иногда результат зависит совсем чуть-чуть, и тогда, если это не kaggle, можно обойтись дефолтными значениями или подобрать вручную. Но иногда неудачная конфигурация может все испортить: алгоритм либо сильно переобучится, либо, наоборот, не сможет использовать большую часть информации.
В узком смысле, под гиперпараметрами часто понимают лишь регуляризацию и другие «очевидные» настройки методов машинного обучения. Однако в широком смысле, гиперпараметры — это вообще любые манипуляции с данными, которые могут повлиять на результат: инжиниринг фич, взвешивание наблюдений, undersampling и т.д.
Grid Search
Конечно, было бы неплохо иметь алгоритм, который помимо оптимизации параметров, оптимизировал бы и гиперпараметры. Еще лучше, если бы мы могли доверять этому алгоритму больше, чем интуиции. Какие-то шаги в этом направлении, конечно, давно сделаны. В многие библиотеки машинного обучения встроены наивные методы: grid search — проход по сетке, либо random search — семплирование точек из фиксированного распределения (самые известные экземпляры — это GridSearchCV и RandomizedGridSearchCV в sklearn). Преимущество прохода по сетке в том, что его легко закодить самому и легко распараллелить. Однако у него есть и серьезные недостатки:
- Он перебирает много заведомо неудачных точек. Допустим, уже имеется набор каких-то конфигураций с результатами или другая какая-то информация. Человек может понять, какие конфигурации точно дадут отстойный результат, и догадается не проверять лишний раз эти регионы. Grid search так делать не умеет.
- Если гиперпараметров много, то размер «ячейки» приходится делать слишком крупным, и можно упустить хороший оптимум. Таким образом, если включить в пространство поиска много лишних гиперпараметров, никак не влияющих на результат, то grid search будет работать намного хуже при том же числе итераций. Впрочем, для random search это справедливо в меньшей степени:
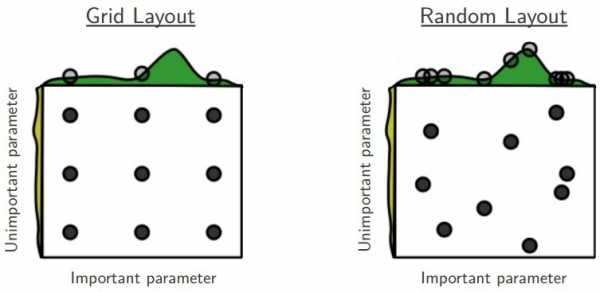
Байесовские методы
Для того, чтобы уменьшить число итераций до нахождения хорошей конфигурации, придуманы адаптивные байесовские методы. Они выбирают следующую точку для проверки, учитывая результаты на уже проверенных точках. Идея состоит в том, чтобы на каждом шаге найти компромисс между (а) исследованием регионов рядом с самыми удачными точками среди найденных и (б) исследованием регионов с большой неопределенностью, где могут находиться еще более удачные точки. Это часто называют дилеммой explore-exploit или «learning vs earning». Таким образом, в ситуациях, когда проверка каждой новой точки стоит дорого (в машинном обучении проверка = обучение + валидация), можно приблизиться к глобальному оптимуму за гораздо меньшее число шагов.
Подобные алгоритмы в разных вариациях реализованы в инструментах MOE, Spearmint, SMAC, BayesOpt и Hyperopt. На последнем мы остановимся подробнее, так как vw-hyperopt — это обертка над Hyperopt, но сначала надо немного написать про Vowpal Wabbit.
Vowpal Wabbit
Многие из вас наверняка использовали этот инструмент или хотя бы слышали о нем. Вкратце, это одна из наиболее быстрых (если не самая быстрая) в мире библиотека машинного обучения. Натренировать модель для нашего CTR-предиктора (бинарная классификация) на 30 миллионах наблюдений и десятках миллионах фичей занимает всего несколько гигабайт оперативной памяти и 6 минут на одном ядре. В Vowpal Wabbit реализованы несколько онлайновых алгоритмов:
- Стохастический градиентный спуск с разными наворотами;
- FTRL-Proximal, о котором можно почитать здесь;
- Онлайновое подобие SVM;
- Онлайновый бустинг;
- Факторизационные машины.
Помимо этого, в нем реализованы feed-forward нейронные сети, батч-оптимизация (BFGS) и LDA. Можно запускать Vowpal Wabbit в фоновом режиме и принимать на вход поток данных, либо дообучаясь на них, либо просто выдавая предсказания.
FTRL и SGD могут решать задачи как регрессии, так и классификации, это регулируется только функцией потерь. Эти алгоритмы линейны относительно фичей, но нелинейность может легко быть достигнута с помощью полиномиальных фичей. Имеется очень полезный механизм ранней остановки, чтобы уберечься от переобучения, если указал слишком большое количество эпох.
Также Vowpal Wabbit знаменит своим хешированием фичей, которое выполняет роль дополнительной регуляризации, если фичей очень много. Благодаря этому удается обучаться на категориальных фичах с миллиардами редко встречающихся категорий, вмещая модель в оперативную память без ущерба для качества.
Vowpal Wabbit требует специальный входной формат данных, но в нем легко разобраться. Он естественным образом разреженный и занимает мало места. В оперативную память в любой момент времени загружена всего одно наблюдение (или несколько, для LDA). Обучение проще всего запускать через консоль.
Интересующиеся могут прочитать туториал и другие примеры и статьи в их репозитории, а также презентацию. Про внутренности Vowpal Wabbit можно подробно прочитать в публикациях Джона Лэнгфорда и в его блоге. На Хабре тоже есть подходящий пост. Список аргументов можно получить через vw --help или почитать подробное описание. Как видно из описания, аргументов десятки, и многие из них могут считаться гиперпараметрами, которые можно оптимизировать.
В Vowpal Wabbit имеется модуль vw-hypersearch, который умеет подбирать один какой-нибудь гиперпараметр методом золотого сечения. Однако при наличии нескольких локальных минимумов этот метод, скорее всего, обнаружит далеко не лучший вариант. К тому же, зачастую нужно оптимизировать сразу много гиперпараметров, и этого нет в vw-hypersearch. Пару месяцев назад я попробовал написать многомерный метод золотого сечения, но количество шагов, которые требовались ему для сходимости, превзошло любой grid search, так что этот вариант отпал. Было решено использовать Hyperopt.
Hyperopt
В этой библиотеке, написанной на питоне, реализован алгоритм оптимизации Tree-Structured Parzen Estimators (TPE). Преимущество его в том, что он может работать с очень «неуклюжими» пространствами: когда один гиперпараметр непрерывный, другой категориальный; третий дискретный, но соседние значения его коррелированы друг с другом; наконец, некоторые комбинации значений параметров могут просто не иметь смысла. TPE принимает на вход иерархическое пространство поиска с априорными вероятностями, и на каждом шаге смешивает их с Гауссовским распределением с центром в новой точке. Его автор Джеймс Бергстра утверждает, что этот алгоритм достаточно хорошо решает проблему explore-exploit и работает лучше как grid search-а, так и экспертного перебора, по крайней мере, для задач глубокого обучения, где гиперпараметров особенно много. Подробнее об этом можно почитать здесь и здесь. Про сам алгоритм TPE можно почитать здесь. Возможно, в будущем удастся написать про него подробный пост.
Хотя Hyperopt не был встроен в исходный код известных библиотек машинного обучения, многие используют его. Например, вот замечательный туториал по hyperopt+sklearn. Вот применение hyperopt+xgboost. Весь мой вклад — эта похожая обертка для Vowpal Wabbit, более-менее сносный синтаксис для задания пространства поиска и запуска всего этого из командной строки. Так как в Vowpal Wabbit еще не было подобного функционала, мой модуль понравился Лэнгфорду, и он его влил. В действительности, каждый может попробовать Hyperopt для своего любимого инструмента машинного обучения: это несложно сделать, и все необходимое есть в этом туториале.
vw-hyperopt
Перейдем к использованию модуля vw-hyperopt. Сначала нужно установить последнюю версию Vowpal Wabbit с гитхаба. Модуль находится в папке utl.
Внимание! Последние изменения (в частности, новый синтаксис команды) пока что (на 15 декабря) не влиты в основной репозиторий. В ближайшие дни, надеюсь, проблема решится, а пока что можете пользоваться последней версией кода из моей ветки.
Пример использования:
./vw-hyperopt.py --train ./train_set.vw --holdout ./holdout_set.vw --max_evals 200 --outer_loss_function logistic --vw_space '--algorithms=ftrl,sgd --l2=1e-8..1e-1~LO --l1=1e-8..1e-1~LO -l=0.01..10~L --power_t=0.01..1 --ftrl_alpha=5e-5..8e-1~L --ftrl_beta=0.01..1 --passes=1..10~I --loss_function=logistic -q=SE+SZ+DR,SE~O --ignore=T~O' --plotНа вход модулю требуется обучающая и валидационная выборки, а также априорные распределения гиперпараметров (закавыченные внутри --vw_space). Можно задавать целочисленные, непрерывные или категориальные гиперпараметры. Для всех, кроме категориальных, можно задавать равномерное или лог-равномерное распределения. Пространство поиска из примера преобразуется внутри vw-hyperopt приблизительно в такой объект для Hyperopt (если вы прошли туториал по Hyperopt, вы поймете это):
from hyperopt import hp prior_search_space = hp.choice('algorithm', [ {'type': 'sgd', '--l1': hp.choice('sgd_l1_outer', ['empty', hp.loguniform('sgd_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('sgd_l2_outer', ['empty', hp.loguniform('sgd_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('sgd_l', log(0.01), log(10)), '--power_t': hp.uniform('sgd_power_t', 0.01, 1), '-q': hp.choice('sgd_q_outer', ['emtpy', hp.choice('sgd_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('sgd_loss', ['logistic']), '--passes': hp.quniform('sgd_passes', 1, 10, 1), }, {'type': 'ftrl', '--l1': hp.choice('ftrl_l1_outer', ['emtpy', hp.loguniform('ftrl_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('ftrl_l2_outer', ['emtpy', hp.loguniform('ftrl_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('ftrl_l', log(0.01), log(10)), '--power_t': hp.uniform('ftrl_power_t', 0.01, 1), '-q': hp.choice('ftrl_q_outer', ['emtpy', hp.choice('ftrl_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('ftrl_loss', ['logistic']), '--passes': hp.quniform('ftrl_passes', 1, 10, 1), '--ftrl_alpha': hp.loguniform('ftrl_alpha', 5e-5, 8e-1), '--ftrl_beta': hp.uniform('ftrl_beta', 0.01, 1.) } ])Опционально можно изменить функцию потерь на валидационной выборке и максимальное количество итераций (--outer_loss_function, по умолчанию logistic, и --max_evals, по умолчанию 100). Также можно сохранять результаты каждой итерации и строить графики с помощью --plot, если установлен matplotlib и, желательно, seaborn:
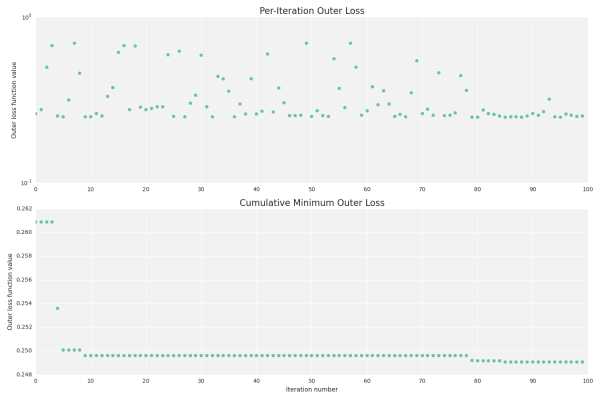
Документация
Так как на хабрахабр не принято выкладывать подробную документацию, ограничусь ссылкой на нее. Про всю семантику вы можете почитать в русскоязычной вики в моем форке или дождаться англоязычной версии в главном репозитории Vowpal Wabbit.
Планы
В будущем в модуль планируется добавить:
- Поддержку задач регрессии и мультиклассовой классификации.
- Поддержку «теплого старта»: выдать Hyperopt заранее оцененные точки, и начать оптимизацию уже с учетом результатов на них.
- Опцию оценки ошибки на каждом шаге на еще одной тестовой выборке (но без оптимизации гиперпараметров на ней). Это нужно, чтобы лучше оценить обобщающую способность — не переобучились ли мы.
- Поддержку бинарных параметров, которые не принимают никаких значений, таких как --lrqdropout, --normalized, --adaptive и т.д. Сейчас можно, в принципе, писать --adaptive= ~O, но это неинтуитивно совсем. Можно сделать что-то вроде --adaptive=~B или --adaptive=~BO.
Буду очень рад, если кто-нибудь воспользуется модулем, и кому-нибудь он поможет. Буду рад любым предложениям, идеям или обнаруженным багам. Можете писать их сюда или создавать issue на гитхабе.
Автор: DCA (Data-Centric Alliance)
Источник
www.pvsm.ru
Оптимизация гиперпараметров в Vowpal Wabbit с помощью нового модуля vw-hyperopt / СоХабр
Привет, Хабр! В этой статье речь пойдет о таком не очень приятном аспекте машинного обучения, как оптимизация гиперпараметров. Две недели назад в очень известный и полезный проект Vowpal Wabbit был влит модуль vw-hyperopt.py, умеющий находить хорошие конфигурации гиперпараметров моделей Vowpal Wabbit в пространствах большой размерности. Модуль был разработан внутри DCA (Data-Centric Alliance). Для поиска хороших конфигураций vw-hyperopt использует алгоритмы из питоновской библиотеки Hyperopt и может оптимизировать гиперпараметры адаптивно с помощью метода Tree-Structured Parzen Estimators (TPE). Это позволяет находить лучшие оптимумы, чем простой grid search, при равном количестве итераций.
Для поиска хороших конфигураций vw-hyperopt использует алгоритмы из питоновской библиотеки Hyperopt и может оптимизировать гиперпараметры адаптивно с помощью метода Tree-Structured Parzen Estimators (TPE). Это позволяет находить лучшие оптимумы, чем простой grid search, при равном количестве итераций.
Эта статья будет интересна всем, кто имеет дело с Vowpal Wabbit, и особенно тем, кто досадовал на отсутствие в исходном коде способов тюнинга многочисленных ручек моделей, и либо тюнил их вручную, либо кодил оптимизацию самостоятельно.
Гиперпараметры
Что такое гиперпараметры? Это все «степени свободы» алгоритма, которые он напрямую не оптимизирует, но от которых зависит результат. Иногда результат зависит совсем чуть-чуть, и тогда, если это не kaggle, можно обойтись дефолтными значениями или подобрать вручную. Но иногда неудачная конфигурация может все испортить: алгоритм либо сильно переобучится, либо, наоборот, не сможет использовать большую часть информации.В узком смысле, под гиперпараметрами часто понимают лишь регуляризацию и другие «очевидные» настройки методов машинного обучения. Однако в широком смысле, гиперпараметры — это вообще любые манипуляции с данными, которые могут повлиять на результат: инжиниринг фич, взвешивание наблюдений, undersampling и т.д.
Grid Search
Конечно, было бы неплохо иметь алгоритм, который помимо оптимизации параметров, оптимизировал бы и гиперпараметры. Еще лучше, если бы мы могли доверять этому алгоритму больше, чем интуиции. Какие-то шаги в этом направлении, конечно, давно сделаны. В многие библиотеки машинного обучения встроены наивные методы: grid search — проход по сетке, либо random search — семплирование точек из фиксированного распределения (самые известные экземпляры — это GridSearchCV и RandomizedGridSearchCV в sklearn). Преимущество прохода по сетке в том, что его легко закодить самому и легко распараллелить. Однако у него есть и серьезные недостатки:- Он перебирает много заведомо неудачных точек. Допустим, уже имеется набор каких-то конфигураций с результатами или другая какая-то информация. Человек может понять, какие конфигурации точно дадут отстойный результат, и догадается не проверять лишний раз эти регионы. Grid search так делать не умеет.
- Если гиперпараметров много, то размер «ячейки» приходится делать слишком крупным, и можно упустить хороший оптимум. Таким образом, если включить в пространство поиска много лишних гиперпараметров, никак не влияющих на результат, то grid search будет работать намного хуже при том же числе итераций. Впрочем, для random search это справедливо в меньшей степени:
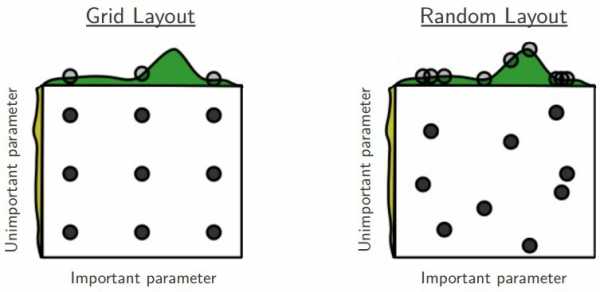
Байесовские методы
Для того, чтобы уменьшить число итераций до нахождения хорошей конфигурации, придуманы адаптивные байесовские методы. Они выбирают следующую точку для проверки, учитывая результаты на уже проверенных точках. Идея состоит в том, чтобы на каждом шаге найти компромисс между (а) исследованием регионов рядом с самыми удачными точками среди найденных и (б) исследованием регионов с большой неопределенностью, где могут находиться еще более удачные точки. Это часто называют дилеммой explore-exploit или «learning vs earning». Таким образом, в ситуациях, когда проверка каждой новой точки стоит дорого (в машинном обучении проверка = обучение + валидация), можно приблизиться к глобальному оптимуму за гораздо меньшее число шагов.Подобные алгоритмы в разных вариациях реализованы в инструментах MOE, Spearmint, SMAC, BayesOpt и Hyperopt. На последнем мы остановимся подробнее, так как vw-hyperopt — это обертка над Hyperopt, но сначала надо немного написать про Vowpal Wabbit.
Vowpal Wabbit
Многие из вас наверняка использовали этот инструмент или хотя бы слышали о нем. Вкратце, это одна из наиболее быстрых (если не самая быстрая) в мире библиотека машинного обучения. Натренировать модель для нашего CTR-предиктора (бинарная классификация) на 30 миллионах наблюдений и десятках миллионах фичей занимает всего несколько гигабайт оперативной памяти и 6 минут на одном ядре. В Vowpal Wabbit реализованы несколько онлайновых алгоритмов:- Стохастический градиентный спуск с разными наворотами;
- FTRL-Proximal, о котором можно почитать здесь;
- Онлайновое подобие SVM;
- Онлайновый бустинг;
- Факторизационные машины.
FTRL и SGD могут решать задачи как регрессии, так и классификации, это регулируется только функцией потерь. Эти алгоритмы линейны относительно фичей, но нелинейность может легко быть достигнута с помощью полиномиальных фичей. Имеется очень полезный механизм ранней остановки, чтобы уберечься от переобучения, если указал слишком большое количество эпох.
Также Vowpal Wabbit знаменит своим хешированием фичей, которое выполняет роль дополнительной регуляризации, если фичей очень много. Благодаря этому удается обучаться на категориальных фичах с миллиардами редко встречающихся категорий, вмещая модель в оперативную память без ущерба для качества.
Vowpal Wabbit требует специальный входной формат данных, но в нем легко разобраться. Он естественным образом разреженный и занимает мало места. В оперативную память в любой момент времени загружена всего одно наблюдение (или несколько, для LDA). Обучение проще всего запускать через консоль.
Интересующиеся могут прочитать туториал и другие примеры и статьи в их репозитории, а также презентацию. Про внутренности Vowpal Wabbit можно подробно прочитать в публикациях Джона Лэнгфорда и в его блоге. На Хабре тоже есть подходящий пост. Список аргументов можно получить через vw --help или почитать подробное описание. Как видно из описания, аргументов десятки, и многие из них могут считаться гиперпараметрами, которые можно оптимизировать.
В Vowpal Wabbit имеется модуль vw-hypersearch, который умеет подбирать один какой-нибудь гиперпараметр методом золотого сечения. Однако при наличии нескольких локальных минимумов этот метод, скорее всего, обнаружит далеко не лучший вариант. К тому же, зачастую нужно оптимизировать сразу много гиперпараметров, и этого нет в vw-hypersearch. Пару месяцев назад я попробовал написать многомерный метод золотого сечения, но количество шагов, которые требовались ему для сходимости, превзошло любой grid search, так что этот вариант отпал. Было решено использовать Hyperopt.
Hyperopt
В этой библиотеке, написанной на питоне, реализован алгоритм оптимизации Tree-Structured Parzen Estimators (TPE). Преимущество его в том, что он может работать с очень «неуклюжими» пространствами: когда один гиперпараметр непрерывный, другой категориальный; третий дискретный, но соседние значения его коррелированы друг с другом; наконец, некоторые комбинации значений параметров могут просто не иметь смысла. TPE принимает на вход иерархическое пространство поиска с априорными вероятностями, и на каждом шаге смешивает их с Гауссовским распределением с центром в новой точке. Его автор Джеймс Бергстра утверждает, что этот алгоритм достаточно хорошо решает проблему explore-exploit и работает лучше как grid search-а, так и экспертного перебора, по крайней мере, для задач глубокого обучения, где гиперпараметров особенно много. Подробнее об этом можно почитать здесь и здесь. Про сам алгоритм TPE можно почитать здесь. Возможно, в будущем удастся написать про него подробный пост.Хотя Hyperopt не был встроен в исходный код известных библиотек машинного обучения, многие используют его. Например, вот замечательный туториал по hyperopt+sklearn. Вот применение hyperopt+xgboost. Весь мой вклад — эта похожая обертка для Vowpal Wabbit, более-менее сносный синтаксис для задания пространства поиска и запуска всего этого из командной строки. Так как в Vowpal Wabbit еще не было подобного функционала, мой модуль понравился Лэнгфорду, и он его влил. В действительности, каждый может попробовать Hyperopt для своего любимого инструмента машинного обучения: это несложно сделать, и все необходимое есть в этом туториале.
vw-hyperopt
Перейдем к использованию модуля vw-hyperopt. Сначала нужно установить последнюю версию Vowpal Wabbit с гитхаба. Модуль находится в папке utl.Внимание! Последние изменения (в частности, новый синтаксис команды) пока что (на 15 декабря) не влиты в основной репозиторий. В ближайшие дни, надеюсь, проблема решится, а пока что можете пользоваться последней версией кода из моей ветки. EDIT: 22 декабря изменения влиты, теперь можно пользоваться основным репозиторием.
Пример использования:
./vw-hyperopt.py --train ./train_set.vw --holdout ./holdout_set.vw --max_evals 200 --outer_loss_function logistic --vw_space '--algorithms=ftrl,sgd --l2=1e-8..1e-1~LO --l1=1e-8..1e-1~LO -l=0.01..10~L --power_t=0.01..1 --ftrl_alpha=5e-5..8e-1~L --ftrl_beta=0.01..1 --passes=1..10~I --loss_function=logistic -q=SE+SZ+DR,SE~O --ignore=T~O' --plot На вход модулю требуется обучающая и валидационная выборки, а также априорные распределения гиперпараметров (закавыченные внутри --vw_space). Можно задавать целочисленные, непрерывные или категориальные гиперпараметры. Для всех, кроме категориальных, можно задавать равномерное или лог-равномерное распределения. Пространство поиска из примера преобразуется внутри vw-hyperopt приблизительно в такой объект для Hyperopt (если вы прошли туториал по Hyperopt, вы поймете это):from hyperopt import hp prior_search_space = hp.choice('algorithm', [ {'type': 'sgd', '--l1': hp.choice('sgd_l1_outer', ['empty', hp.loguniform('sgd_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('sgd_l2_outer', ['empty', hp.loguniform('sgd_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('sgd_l', log(0.01), log(10)), '--power_t': hp.uniform('sgd_power_t', 0.01, 1), '-q': hp.choice('sgd_q_outer', ['emtpy', hp.choice('sgd_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('sgd_loss', ['logistic']), '--passes': hp.quniform('sgd_passes', 1, 10, 1), }, {'type': 'ftrl', '--l1': hp.choice('ftrl_l1_outer', ['emtpy', hp.loguniform('ftrl_l1', log(1e-8), log(1e-1))]), '--l2': hp.choice('ftrl_l2_outer', ['emtpy', hp.loguniform('ftrl_l2', log(1e-8), log(1e-1))]), '-l': hp.loguniform('ftrl_l', log(0.01), log(10)), '--power_t': hp.uniform('ftrl_power_t', 0.01, 1), '-q': hp.choice('ftrl_q_outer', ['emtpy', hp.choice('ftrl_q', ['-q SE -q SZ -q DR', '-q SE'])]), '--loss_function': hp.choice('ftrl_loss', ['logistic']), '--passes': hp.quniform('ftrl_passes', 1, 10, 1), '--ftrl_alpha': hp.loguniform('ftrl_alpha', 5e-5, 8e-1), '--ftrl_beta': hp.uniform('ftrl_beta', 0.01, 1.) } ]) Опционально можно изменить функцию потерь на валидационной выборке и максимальное количество итераций (--outer_loss_function, по умолчанию logistic, и --max_evals, по умолчанию 100). Также можно сохранять результаты каждой итерации и строить графики с помощью --plot, если установлен matplotlib и, желательно, seaborn: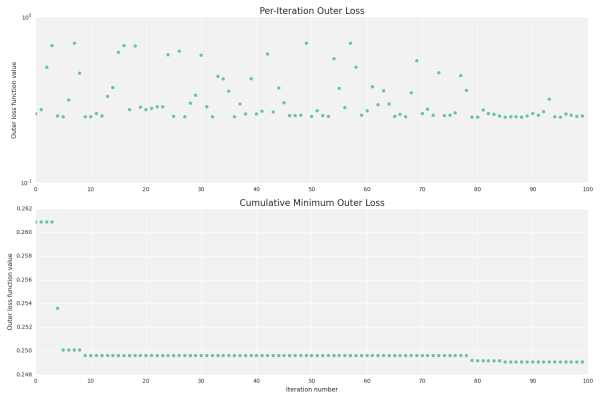
Документация
Так как на хабрахабр не принято выкладывать подробную документацию, ограничусь ссылкой на нее. Про всю семантику вы можете почитать в русскоязычной вики в моем форке или дождаться англоязычной версии в главном репозитории Vowpal Wabbit.Планы
В будущем в модуль планируется добавить:- Поддержку задач регрессии и мультиклассовой классификации.
- Поддержку «теплого старта»: выдать Hyperopt заранее оцененные точки, и начать оптимизацию уже с учетом результатов на них.
- Опцию оценки ошибки на каждом шаге на еще одной тестовой выборке (но без оптимизации гиперпараметров на ней). Это нужно, чтобы лучше оценить обобщающую способность — не переобучились ли мы.
- Поддержку бинарных параметров, которые не принимают никаких значений, таких как --lrqdropout, --normalized, --adaptive и т.д. Сейчас можно, в принципе, писать --adaptive=\ ~O, но это неинтуитивно совсем. Можно сделать что-то вроде --adaptive=~B или --adaptive=~BO.
Обновление 22.12.2015
Пулл реквест с последними изменениями вмержили в основной репозиторий Vowpal Wabbit, так что можно теперь использовать его, а не ветку.sohabr.net
Оптимизация гиперпараметров — Википедия РУ
Поиск по решётке
Традиционным методом осуществления оптимизации гиперпарамеров является поиск по решётке (или вариация параметров), который просто делает полный перебор по заданному вручную подмножеству пространства гиперпараметров обучающего алгоритма. Поиск по решётке должен сопровождаться некоторым измерением производительности, обычно измеряемой посредством перекрёстной проверки на тренировочном множестве[3], или прогонкой алгоритма на устоявшемся проверочном наборе[4].
Поскольку пространство параметров обучающего машину алгоритма для некоторых параметров может включать пространства с вещественными или неограниченными значениями, вручную установить границу и дискретизацию может оказаться необходимым до применения поиска по решётке.
Например, типичный классификатор с мягким зазором на основе метода опорных векторов (МОВ), оснащённый ядерной радиально-базисной функцией[en] имеет по меньшей мере два гиперпараметра, которые необходимо настроить для хорошей производительности на недоступных данных — константа C регуляризации и гиперпараметр ядра γ. Оба параметра являются непрерывными, так что для поиска по решётке выбирают конечный набор «приемлемых» значений, скажем
C∈{10,100,1000}{\displaystyle C\in \{10,100,1000\}} γ∈{0.1,0.2,0.5,1.0}{\displaystyle \gamma \in \{0.1,0.2,0.5,1.0\}}Поиск по решётке затем прогоняет МОВ для каждой пары (C, γ) в декартовом произведении этих двух множеств и проверяет производительность при выбранных параметрах на устоявшемся проверочном наборе (или с помощью внутренней перекрёстной проверки на тренировочном наборе и в этом случае несколько МОВ прогоняют попарно). Наконец, алгоритм поиска по решётке выдаёт в качестве результата наивысший результат, достигнутый на процедуре проверки.
Поиск по решётке страдает от проклятия размерности, но часто легко параллелизуем, поскольку обычно гиперпараметрические величины, с которыми алгоритм работает, не зависят друг от друга[2].
Случайный поиск
Основная статья: Случайный поиск
Случайный поиск заменяет полный перебор всех комбинаций на выборку их случайным образом. Это можно легко применить к дискретным установкам, приведённым выше, но метод может быть также обобщен к непрерывным и смешанным пространствам. Случайный поиск может превзойти поиск по решётке, особенно в случае, если только малое число гиперпараметров оказывает влияние на производительность алгоритма обучения машины[2]. В этом случае говорят, что задача оптимизации имеет низкую внутреннюю размерность[5]. Случайный поиск также легко параллелизуем и, кроме того, позволяют использовать предварительные данные путём указания распределения для выборки случайных параметров.
Байесовская оптимизация
Основная статья: Байесовская оптимизация
Байесовская оптимизация — это метод глобальной оптимизации для неизвестной функции (чёрного ящика) с шумом. Применённая к гиперпараметрической оптимизации байесовская оптимизация строит стохастическую модель функции отображения из значений гиперпараметра в целевую функцию, применённую на множестве проверки. Путём итеративного применения перспективной конфигурации гиперпараметров, основанной на текущей модели, а затем её обновления, байесовская оптимизация стремится собрать как можно больше информации об этой функции и, в частности, место оптимума. Метод пытается сбалансировать зондирование (гиперпараметры, для которых изменение наименее достоверно известно) и использование (гиперпараметры, которые, как ожидается, наиболее близки к оптимуму). На практике байесовская оптимизация показала[6][7][8][9] лучшие результаты с меньшими вычислениями по сравнению с поиском по решётке и случайным поиском ввиду возможности суждения о качестве экспериментов ещё до их выполнения.
Оптимизация на основе градиентов
Для конкретных алгоритмов обучения можно вычислить градиент гиперпараметров и оптимизировать их с помощью градиентного спуска. Первое использование этих техник фокусировалось на нейронных сетях[10]. Затем эти методы были распространены на другие модели, такие как методы опорных векторов[11] или логистическая регрессия[12].
Другой подход использования градиентов гиперпараметров состоит в дифференцировании шагов алгоритма итеративной оптимизации с помощью автоматического дифференцирования[en][13][14].
Эволюционная оптимизация
Эволюционная оптимизация — это методология для глобальной оптимизации неизвестных функций с шумом. При оптимизации гиперпараметров эволюционная оптимизация использует эволюционные алгоритмы для поиска гиперпараметров для данного алгоритма[7]. Эволюционная оптимизация гиперпараметров следует процессу, навеянному биологической концепцией эволюции:
- Создаём начальную популяцию случайных решений (т.е. сгенерированный случайно кортеж гиперпараметров, обычно 100+)
- Оцениваем кортежи гиперпараметров и получаем их функцию приспособленности (например, с помощью 10-кратной точности перекрёстной проверки алгоритма обучения машины с этими гиперпараметрами)
- Ранжируем кортежи гиперпараметров по их относительной пригодности
- Заменяем кортежи киперпараметров с худшей производительностью на новые кортежи гиперпараметров, образованных скрещиванием[en] и мутацией[en]
- Повторяем шаги 2—4, пока не получим удовлетворительной производительности алгоритма или пока производительность не перестанет улучшаться
Эволюционная оптимизация используется для оптимизации гиперпараметров для статистических алгоритмов обучения машин[7], автоматического обучения машин[15][16], для поиска архитектуры глубоких нейронных сетей[17][18], а также для формирования весов в глубоких нейронных сетях[19].
Другое
Развиваются также методы радиально-базисной функции (РБФ)[20] и спектральный метод[en][21].
http-wikipediya.ru
Оптимизация гиперпараметров Википедия
В обучении машин, оптимизация гиперпараметров — это задача выбора набора оптимальных гиперпараметров[en] для обучающего алгоритма.
Одни и те же виды моделей обучения машин могут требовать различные предположения, веса или скорости обучения для различных видов данных. Эти параметры называются гиперпараметрами и их следует настраивать так, чтобы модель могла оптимально решить задачу обучения машины. Оптимизация гиперпараметров находит кортеж гиперпараметров, который даёт оптимальную модель, оптимизирующую заданную функцию потерь на заданных независимых данных[1]. Целевая функция берёт кортеж гиперпараметров и возвращает связанные с ними потери[1]. Часто используется перекрёстная проверка для оценки этой обобщающей способности[2].
Поиск по решётке
Традиционным методом осуществления оптимизации гиперпарамеров является поиск по решётке (или вариация параметров), который просто делает полный перебор по заданному вручную подмножеству пространства гиперпараметров обучающего алгоритма. Поиск по решётке должен сопровождаться некоторым измерением производительности, обычно измеряемой посредством перекрёстной проверки на тренировочном множестве[3], или прогонкой алгоритма на устоявшемся проверочном наборе[4].
Поскольку пространство параметров обучающего машину алгоритма для некоторых параметров может включать пространства с вещественными или неограниченными значениями, вручную установить границу и дискретизацию может оказаться необходимым до применения поиска по решётке.
Например, типичный классификатор с мягким зазором на основе метода опорных векторов (МОВ), оснащённый ядерной радиально-базисной функцией[en] имеет по меньшей мере два гиперпараметра, которые необходимо настроить для хорошей производительности на недоступных данных — константа C регуляризации и гиперпараметр ядра γ. Оба параметра являются непрерывными, так что для поиска по решётке выбирают конечный набор «приемлемых» значений, скажем
C∈{10,100,1000}{\displaystyle C\in \{10,100,1000\}} γ∈{0.1,0.2,0.5,1.0}{\displaystyle \gamma \in \{0.1,0.2,0.5,1.0\}}Поиск по решётке затем прогоняет МОВ для каждой пары (C, γ) в декартовом произведении этих двух множеств и проверяет производительность при выбранных параметрах на устоявшемся проверочном наборе (или с помощью внутренней перекрёстной проверки на тренировочном наборе и в этом случае несколько МОВ прогоняют попарно). Наконец, алгоритм поиска по решётке выдаёт в качестве результата наивысший результат, достигнутый на процедуре проверки.
Поиск по решётке страдает от проклятия размерности, но часто легко параллелизуем, поскольку обычно гиперпараметрические величины, с которыми алгоритм работает, не зависят друг от друга[2].
Случайный поиск
Случайный поиск заменяет полный перебор всех комбинаций на выборку их случайным образом. Это можно легко применить к дискретным установкам, приведённым выше, но метод может быть также обобщен к непрерывным и смешанным пространствам. Случайный поиск может превзойти поиск по решётке, особенно в случае, если только малое число гиперпараметров оказывает влияние на производительность алгоритма обучения машины[2]. В этом случае говорят, что задача оптимизации имеет низкую внутреннюю размерность[5]. Случайный поиск также легко параллелизуем и, кроме того, позволяют использовать предварительные данные путём указания распределения для выборки случайных параметров.
Байесовская оптимизация
Основная статья
ruwikiorg.ru
Оптимизация гиперпараметров — узбекистан вики
Поиск по решётке
Традиционным методом осуществления оптимизации гиперпарамеров является поиск по решётке (или вариация параметров), который просто делает полный перебор по заданному вручную подмножеству пространства гиперпараметров обучающего алгоритма. Поиск по решётке должен сопровождаться некоторым измерением производительности, обычно измеряемой посредством перекрёстной проверки на тренировочном множестве[3], или прогонкой алгоритма на устоявшемся проверочном наборе[4].
Поскольку пространство параметров обучающего машину алгоритма для некоторых параметров может включать пространства с вещественными или неограниченными значениями, вручную установить границу и дискретизацию может оказаться необходимым до применения поиска по решётке.
Например, типичный классификатор с мягким зазором на основе метода опорных векторов (МОВ), оснащённый ядерной радиально-базисной функцией[en] имеет по меньшей мере два гиперпараметра, которые необходимо настроить для хорошей производительности на недоступных данных — константа C регуляризации и гиперпараметр ядра γ. Оба параметра являются непрерывными, так что для поиска по решётке выбирают конечный набор «приемлемых» значений, скажем
C∈{10,100,1000}{\displaystyle C\in \{10,100,1000\}} γ∈{0.1,0.2,0.5,1.0}{\displaystyle \gamma \in \{0.1,0.2,0.5,1.0\}}Поиск по решётке затем прогоняет МОВ для каждой пары (C, γ) в декартовом произведении этих двух множеств и проверяет производительность при выбранных параметрах на устоявшемся проверочном наборе (или с помощью внутренней перекрёстной проверки на тренировочном наборе и в этом случае несколько МОВ прогоняют попарно). Наконец, алгоритм поиска по решётке выдаёт в качестве результата наивысший результат, достигнутый на процедуре проверки.
Поиск по решётке страдает от проклятия размерности, но часто легко параллелизуем, поскольку обычно гиперпараметрические величины, с которыми алгоритм работает, не зависят друг от друга[2].
Случайный поиск
Основная статья: Случайный поиск
Случайный поиск заменяет полный перебор всех комбинаций на выборку их случайным образом. Это можно легко применить к дискретным установкам, приведённым выше, но метод может быть также обобщен к непрерывным и смешанным пространствам. Случайный поиск может превзойти поиск по решётке, особенно в случае, если только малое число гиперпараметров оказывает влияние на производительность алгоритма обучения машины[2]. В этом случае говорят, что задача оптимизации имеет низкую внутреннюю размерность[5]. Случайный поиск также легко параллелизуем и, кроме того, позволяют использовать предварительные данные путём указания распределения для выборки случайных параметров.
Байесовская оптимизация
Основная статья: Байесовская оптимизация
Байесовская оптимизация — это метод глобальной оптимизации для неизвестной функции (чёрного ящика) с шумом. Применённая к гиперпараметрической оптимизации байесовская оптимизация строит стохастическую модель функции отображения из значений гиперпараметра в целевую функцию, применённую на множестве проверки. Путём итеративного применения перспективной конфигурации гиперпараметров, основанной на текущей модели, а затем её обновления, байесовская оптимизация стремится собрать как можно больше информации об этой функции и, в частности, место оптимума. Метод пытается сбалансировать зондирование (гиперпараметры, для которых изменение наименее достоверно известно) и использование (гиперпараметры, которые, как ожидается, наиболее близки к оптимуму). На практике байесовская оптимизация показала[6][7][8][9] лучшие результаты с меньшими вычислениями по сравнению с поиском по решётке и случайным поиском ввиду возможности суждения о качестве экспериментов ещё до их выполнения.
Оптимизация на основе градиентов
Для конкретных алгоритмов обучения можно вычислить градиент гиперпараметров и оптимизировать их с помощью градиентного спуска. Первое использование этих техник фокусировалось на нейронных сетях[10]. Затем эти методы были распространены на другие модели, такие как методы опорных векторов[11] или логистическая регрессия[12].
Другой подход использования градиентов гиперпараметров состоит в дифференцировании шагов алгоритма итеративной оптимизации с помощью автоматического дифференцирования[en][13][14].
Эволюционная оптимизация
Эволюционная оптимизация — это методология для глобальной оптимизации неизвестных функций с шумом. При оптимизации гиперпараметров эволюционная оптимизация использует эволюционные алгоритмы для поиска гиперпараметров для данного алгоритма[7]. Эволюционная оптимизация гиперпараметров следует процессу, навеянному биологической концепцией эволюции:
- Создаём начальную популяцию случайных решений (т.е. сгенерированный случайно кортеж гиперпараметров, обычно 100+)
- Оцениваем кортежи гиперпараметров и получаем их функцию приспособленности (например, с помощью 10-кратной точности перекрёстной проверки алгоритма обучения машины с этими гиперпараметрами)
- Ранжируем кортежи гиперпараметров по их относительной пригодности
- Заменяем кортежи киперпараметров с худшей производительностью на новые кортежи гиперпараметров, образованных скрещиванием[en] и мутацией[en]
- Повторяем шаги 2—4, пока не получим удовлетворительной производительности алгоритма или пока производительность не перестанет улучшаться
Эволюционная оптимизация используется для оптимизации гиперпараметров для статистических алгоритмов обучения машин[7], автоматического обучения машин[15][16], для поиска архитектуры глубоких нейронных сетей[17][18], а также для формирования весов в глубоких нейронных сетях[19].
Другое
Развиваются также методы радиально-базисной функции (РБФ)[20] и спектральный метод[en][21].
uz.com.ru