Лабораторная работа №4 по курсу «Прикладные методы оптимизации». Лабораторные работы методы оптимизации
Программирование методов оптимизации
Федеральное агентство по образованию
––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»
––––––––––––––––––––––––––––––––––––
Методические указания
к лабораторным работам
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2004
Федеральное агентство по образованию
––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»
––––––––––––––––––––––––––––––––––––
Программирование методов оптимизации
Методические указания
к лабораторным работам
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2004
УДК 681.5.001: 621.396.6
Программирование методов оптимизации: Методические указания к лабораторным работам / Сост.: Г. Д. Дмитревич, А. И. Ларистов, В. А. Павлушин. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2004. 44 с.
Содержат описания лабораторных работ по методам оптимизации, которые лежат в основе многих экономических, производственных задач и задач оптимального проектирования.
Предназначены для студентов специальностей 220300 – «Системы автоматизированного проектирования», 220100 – «Вычислительные машины, комплексы, системы и сети», 075200 – «Компьютерная безопасность», а также для бакалавров и магистров, обучающихся по направлению 552800 – «Информатика и вычислительная техника».
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2004
Предисловие
Настоящие методические указания предназначены для обеспечения учебного процесса по курсу «Методы оптимизации», цель которого – научить разработке программ решения оптимизационных задач с применением современной технологии программирования. Изначально предполагается, что студенты владеют навыками программирования на языке C++, полученными в рамках следующих курсов: «Программирование» (250 ч) и «Структуры и алгоритмы обработки данных» (207 ч).
Курс лекций имеет четкую практическую направленность: основное внимание уделяется прикладным и вычислительным аспектам построения алгоритмов поиска оптимальных решений. Существует обширная литература [1]–[7] по вопросам доказательства сходимости методов, условий существования и единственности решения задач оптимизации, что определило отказ от изложения в лекциях теоретических вопросов в пользу удобных для реализации вычислительных схем, доведенных до уровня практических алгоритмов.
В приложениях дополнительно представлены некоторые алгоритмы, предназначенные для построения многовариантных заданий к лабораторным работам.
Лабораторная работа 1. Исследование методов одномерного поиска минимума унимодальных функций
1.1. Требования задания
Цель работы– изучение методов одномерной минимизации функций одной переменной:
М1 – метода Свенна – золотого сечения-1;
М2 – метода Свенна – золотого сечения-2;
М3 – метода Свенна – Фибоначчи-1;
М4 – метода Свенна – Фибоначчи-2;
М5 – метода Свенна – дихотомии – Ньютона;
М6 – метода Свенна – трехточечного поиска – линейной интерполяции;
М7 – метода Свенна – Больцано – золотого сечения-1;
М8 – метода Свенна – Больцано – Фибоначчи-2.
Таблица тестовых функций
| № | Функция f(x) | Начальная точка x1 | Точность локализации минимума | Значение минимума x* |
| (1) | 2x2 + 3e–x | 1 | 10–3 | 0.469150 |
| (2) | –e–хln x | 0 | 10–4 | 1.763223 |
| (3) | 2x2 – ex | 1 | 10–3 | 0.357403 |
| (4) | x4 – 14x3 + 60x2 – 70x | 2 | 10–2 | 0.780884 |
| (5) | 4x3– 3x4, еслиx ≥ 0 4x3+ 3x4, еслиx < 0 | 0.4 | 10–3 | –1.000000 |
| (6) | x2+ 2x | 4 | 10–2 | –1.000000 |
| (7) | 2x2+ 16/x | 1 | 10–2 | 1.587401 |
| (8) | (10x3+ 3x2+x+ 5)2 | 2 | 10–2 | –0.859902 |
| (9) | 3x2+ (12/x3) – 5 | 0.5 | 10–2 | 1.430969 |
Варианты задания
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Метод | М1 | М2 | М3 | М4 | | М6 | М7 | М8 |
| Тестовая функция | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
studfiles.net
Лабораторная работа №3 "Методы оптимизации первого и второго порядков"
страница 1 Лабораторная работа №3 “Методы оптимизации первого и второго порядков”Задание для лабораторной работы
- Написать условие задачи и аналитическое выражение для градиента.
- Решить задачу методом Коши, используя различные методы нахождения шага: метод квадратичной интерполяции, метод кубической интерполяции и метод первого приемлемого значения.
- Решить задачу методами Флетчера-Ривса и Полака-Рибьера.
- Решить задачу методами DFP и BFGS.
- Решить задачу методами Ньютона-Рафсона и Марквардта.
- Представить результаты решения задачи различными методами в таблице.
- Сделать выводы о влиянии способа отыскания шага на ход решения задачи.
- Сравнить результаты, полученные методами первого порядка, методами переменной метрики и методами второго порядка.
- Реализовать один из методов оптимизации в соответствии с вариантом, (см. таблицу 5). Проверить работу реализованного метода на квадратичной функции (функция вида ) и функции Розенброка (функция вида ).
- Титульный лист.
- Задание.
- Уравнение функции, подлежащей минимизации.
- Аналитическое выражение градиента.
- График поверхности минимизируемой функции
- Графики линий уровня функции с указанными на них траекториями минимизации всеми методами первого и второго порядка.
- Таблица результатов минимизации функции вышеперечисленными методами.
- Выводы о траекториях минимизации полученными различными методами.
- Текст программы реализующей один из методов оптимизации.
- Результаты оптимизации квадратичной функции и функции Розенброка реализованным методом.
- Для сравнения на линиях уровня квадратичной функции и функции Розенброка указать траектории оптимизации, полученные с помощью собственной программы и с помощью предложенной программы.
- Математическая модель задачи безусловной оптимизации.
- Аффинная модель функции многих переменных
- Квадратичная модель функции многих переменных.
- Метод Коши.
- Метод Флетчера-Ривса.
- Метод Полака-Рибьера.
- Методы DFP и BFGS.
- Методы Ньютона, Ньютона-Рафсона, Марквардта.
- Методы нахождения шага: метод первого приемлемого значения, квадратичная интерполяция, кубическая интерполяция.
- Методы нахождения градиента: численный расчет градиента, вычисление градиента с помощью метода быстрого дифференцирования.
Задача №1
Студенту специальности АС дали задание сравнить результаты минимизации функции Розенброка различными методами прямого поиска.
Функция имеет вид: .
Данные для задачи представлены в таблице 1.
Задача №2
Водный инспектор получил задание поставить опознавательный знак на самом глубоком месте некоего водоема. Площадь водоема представляет собой систему координат. Известно, что дно водоема на всей его площади может быть описано следующей функцией , указывающей глубину в метрах над уровнем моря. Найти координаты места, в котором инспектору необходимо поставить этот опознавательный знак.
Данные для задачи представлены в таблице 2.
Задача №3
1-ое тело движется по траектории вида: , 2-ое по траектории вида: . Найти наименьшее расстояние между траекториями движения тел. Т.е. необходимо решить задачу:
найти min
Данные для задачи приведены в таблице 3.
Задача №4
Эллиптический параболоид и плоскость пересекаются в точке . Определить будет ли данная точка точкой минимума этого параболоида:
.
Данные для задачи приведены в таблице 4.
Таблица 1
| № | a | b | № | a | b |
| 1 | 100 | 1 | 11 | 50 | 1 |
| 2 | 90 | 2 | 12 | 60 | 2 |
| 3 | 110 | 3 | 171 | 6 | |
| 4 | 120 | 1 | 14 | 160 | 2 |
| 5 | 80 | 4 | 15 | 90 | 5 |
| 6 | 90 | 2 | 16 | 110 | 1 |
| 7 | 100 | 3 | 17 | 80 | 2 |
| 8 | 150 | 4 | 18 | 95 | 3 |
| 9 | 145 | 5 | 19 | 100 | 4 |
| 10 | 75 | 1 | 20 | 115 | 2 |
| № | a | b | № | a | b |
| 1 | 1 | 2 | 11 | 3 | 1 |
| 2 | 1 | 3 | 12 | 3 | 2 |
| 3 | 1 | 4 | 13 | 3 | 3 |
| 4 | 1 | 5 | 14 | 3 | 4 |
| 5 | 1 | 6 | 15 | 3 | 5 |
| 6 | 2 | 1 | 16 | 4 | 1 |
| 7 | 2 | 2 | 17 | 4 | 2 |
| 8 | 2 | 3 | 18 | 4 | 3 |
| 9 | 2 | 4 | 19 | 4 | 4 |
| 10 | 2 | 5 | 20 | 5 | 1 |
| № | а | b | № | а | b |
| 1 | 4 | 3 | 11 | 3 | 17 |
| 2 | 2 | 5 | 12 | 20 | -6 |
| 3 | 6 | -4 | 13 | 1 | 3 |
| 4 | 6 | 12 | 14 | 4 | 2 |
| 5 | -5 | 3 | 15 | 11 | 2 |
| 6 | 0 | 5 | 16 | 4 | 3 |
| 7 | -3 | -6 | 17 | 2 | 5 |
| 8 | 8 | 8 | 18 | 6 | -4 |
| 9 | 5 | 5 | 19 | 0 | 1 |
| 10 | 4 | 6 | 20 | 6 | 12 |
| № | p | q | № | p | q |
| 1 | 3 | 1 | 11 | 6 | 7 |
| 2 | 4 | 0 | 12 | 23 | -8 |
| 3 | 8 | -5 | 13 | 3 | 5 |
| 4 | 3 | 14 | 14 | 2 | -9 |
| 5 | -8 | 5 | 15 | 12 | 2 |
| 6 | 0 | 5 | 16 | 18 | 2 |
| 7 | -3 | -2 | 17 | 5 | 4 |
| 8 | 5 | 8 | 18 | 7 | -1 |
| 9 | 8 | 5 | 19 | 9 | 3 |
| 10 | -4 | 6 | 20 | 6 | 0 |
| № | Метод поиска направления | Метод поиска шага |
| 1 | Метод Коши | Метод квадратичной интерполяции |
| 2 | Метод Флетчера-Ривса | Метод квадратичной интерполяции |
| 3 | Метод Полака-Рибьера | Метод квадратичной интерполяции |
| 4 | Метод DFP | Метод квадратичной интерполяции |
| 5 | Метод BFGS | Метод квадратичной интерполяции |
| 6 | Метод Ньютона-Рафсона | Метод квадратичной интерполяции |
| 7 | Метод Марквардта | |
| 8 | Метод Коши | Метод кубической интерполяции |
| 9 | Метод Флетчера-Ривса | Метод кубической интерполяции |
| 10 | Метод Полака-Рибьера | Метод кубической интерполяции |
| 11 | Метод DFP | Метод кубической интерполяции |
| 12 | Метод BFGS | Метод кубической интерполяции |
| 13 | Метод Ньютона-Рафсона | Метод кубической интерполяции |
| 14 | Метод Коши | Метод первого приемлемого значения |
| 15 | Метод Флетчера-Ривса | Метод первого приемлемого значения |
| 16 | Метод Полака-Рибьера | Метод первого приемлемого значения |
| 17 | Метод DFP | Метод первого приемлемого значения |
| 18 | Метод BFGS | Метод первого приемлемого значения |
| 19 | Метод Ньютона-Рафсона | Метод первого приемлемого значения |
- Постановка задачи
где является целевой функцией. При решении этой задачи используются методы минимизации, которые приводят к стационарной точке , определяемой уравнением . Данные методы используют первую и вторую частные производные.
Независимо от метода используют следующие условия останова:
- Достигнута заданная точность градиента: , где - малое положительное число.
- Проведено заданное количество итераций: , где - заданное количество итераций.
- Изменение значения функции и изменение вектора координат слишком мало: и , где - малое положительное число.
- Методы первого порядка
Градиентные методы носят итерационный характер и имеют единую модельную схему. Имея текущее приближение на k-ой итерации, выполняется последовательность следующих шагов:
Шаг 1. Проверка соблюдения условия остановки. Если условие выполняется, то вычисления прекратить и взять в качестве искомого решения, иначе перейти к Шагу 2.
Шаг 2. Расчет направления поиска .
Шаг 3. Расчет длины шага , обеспечивающее выполнение неравенства: .
Шаг 4. Пересчет оценки решения. Положить . Положить . Перейти на Шаг 1.
Способы определения достаточно хорошо отработаны и гарантируют убывание функции . Главной частью алгоритмов оптимизации является расчет направления . Для того чтобы был направлением минимизации функции , обычно контролируется выполнение условия
(4.1)
Метод Коши (метод наискорейшего спуска)
Применение метода наискорейшего спуска для решения задачи минимизации без ограничений было рассмотрено еще французским математиком Коши. Градиент целевой функции в любой точке есть вектор в направлении наибольшего локального увеличения . Следовательно, нужно двигаться в направлении, противоположном , т. е. в направлении наискорейшего спуска, поскольку отрицательный градиент в точке направлен в сторону наибольшего уменьшения по всем компонентам x и ортогонален линии уровня в точке . Введение направления, противоположного нормированному (единичному) градиенту , т. е. направления наискорейшего спуска, определяемого в точке по формуле
(4.2)
в дает следующую формулу перехода из в :
(4.3)
Отрицательный градиент дает только направление оптимизации, но не величину шага. При этом можно использовать различные процедуры метода наискорейшего спуска в зависимости от выбора и определения выражения . Поскольку один шаг в направлении наискорейшего спуска не приводит в точку минимума , формула (4.3) должна применяться несколько раз, до тех пор пока не будет достигнут минимум. В точке минимума все составляющие вектора градиента равны нулю.
При выборе размера шага применяются два общих метода. В первом методе при переходе из точки в точку целевая функция минимизируется по , в другом методе выбирается фиксированный или меняется от шага к шагу.
Метод Флетчера-Ривза
В методе сопряженного градиента Флетчера-Ривза строится последовательность направлений поиска s являющихся линейными комбинациями , текущего направления наискорейшего спуска, и , предыдущих направлений поиска, причем весовые коэффициенты выбираются так, чтобы сделать направления поиска сопряженными. Упомянутые веса такие, что для вычисления нового направления поиска в точке используется только текущий и предпоследний градиент.
Ниже приводятся операции этого алгоритма:
Шаг 1. В вычисляется
.
Шаг 2. На k-м шаге с помощью одномерного поиска в направлении , находим минимум . Это определяет точку .
Шаг 3. Вычисляются и .
Шаг 4. Направление определяется из соотношения
(4.4)
После (n+1) итерации (k=n) процедура циклически повторяется с заменой на .
Шаг 5. Алгоритм заканчивается, когда , где - произвольная константа.
Метод Полака-Рибьера
Метод Полака-Рибьера является разновидностью метода Флетчера-Ривза. Ниже приводятся операции этого алгоритма:
Шаг 1. В вычисляется
.
Шаг 2. На k-м шаге с помощью одномерного поиска в направлении , находим минимум . Это определяет точку .
Шаг 3. Вычисляются и .
Шаг 4. Направление определяется из соотношения
(4.5)
После (n+1) итерации (k=n) процедура циклически повторяется с заменой на .
Шаг 5. Алгоритм заканчивается, когда , где - произвольная константа.
4.2.2 Квазиньютоновские методы (методы переменной метрики)
Методы переменной метрики называют также квазиньютоновскими или градиентными с большим шагом.
В этих методах в процессе поиска осуществляется аппроксимация матрицы вторых частных производных или обратной к ней. Причем для этого используются только первые производные.
Строиться квадратичная модель оптимизируемой функции в окрестностях текущей точки.
, (4.6)
где матрица является аппроксимацией матрицы Гессе.
Квадратичная модель приводит к линейной модели для градиента.
(4.7)
Направление движения из в находят из уравнения:
(4.8)
Общий алгоритм методов оптимизации, использующих аппроксимацию матрицы вторых производных представлен ниже.
Шаг 1. Расчет матрицы .
Шаг 2. Расчет градиента в текущей точке.
Шаг 3. Расчет направления
Шаг 4. Расчет шага.
Шаг 5. Расчет новой точки .
Шаг 6. Пересчет матрицы .
Шаг 7. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
Матрица должна обладать двумя свойствами:
- Симметричность.
- Положительная определенность.
(4.9)
Если , , тогда соотношение секущих для оптимизации будет иметь вид
(4.10)
Способы пересчета породили ряд методов, которые называются квазиньютоновские методы.
Метод BFGS
В методе BFGS в качестве выбирается единичная матрица, а пересчет матрицы осуществляется по следующей формуле:
(4.11)
Данная формула гарантирует симметричность и положительную определенность матрицы секущих на каждом шаге итераций.
Метод DFP
В методе DFP в качестве также выбирается единичная матрица, но на каждой итерации сразу производится пересчет матрицы , что избавляет от необходимости обращения матрицы аппроксимации вторых производных. Пересчет матрицы осуществляется по следующей формуле:
(4.12)
4.3. Методы второго порядка
Методы второго порядка при поиске минимума используют информацию о функции и ее производных до второго порядка включительно. К этой группе относят метод Марквардта, метод Ньютона и его модификации.
В основе метода лежит квадратичная аппроксимация функции , которую можно получить, отбрасывая в рядах Тейлора члены третьего и более высокого порядков:
(4.13)
где - матрица Гессе, представляющая собой квадратную матрицу вторых частных производных в точке .
Направление поиска находится из следующего соотношения
, (4.14)
где - остаточный член разложения в ряд Тейлора до второго порядка.
Способы учета матрицы породили различные методы оптимизации второго порядка.
4.3.1. Метод Ньютона
В методе Ньютона остаточный член отбрасывается, и направление вычисляется по формуле
. (4.15)
Необходимым условием вычисления направления по формуле (4.15) является положительная определенность матрицы . Если это условие не выполняется, то направление находится по формуле
. (4.16)
Пересчет следующей точки производится следующим образом:
(4.17)
Алгоритм метода Ньютона состоит из следующих шагов:
Шаг 1. Задать начальную точку , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Проверить выполнение условия
а) если , то перейти к шагу 6
б) если нет, то перейти к шагу 7, вычислив как .
Шаг 6. Расчет направления , . Переход на шаг 8.
Шаг 7. Поиск шага из условия минимизации функции
Шаг 8. Расчет новой точки .
Шаг 9. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2. 4.3.2. Метод Ньютона-Рафсона
В методе Ньютона-Рафсона, направление поиска вычисляется, так же как и в методе Ньютона, но шаг вычисляется на каждой итерации, независимо от способа расчета направления из условия минимизации функции .
Алгоритм метода Ньютона-Рафсона состоит из следующих шагов:
Шаг 1. Задать начальную точку , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Проверить выполнение условия
а) если , то перейти к шагу 6
б) если нет, то перейти к шагу 7, вычислив как .
Шаг 6. Расчет направления .
Шаг 7. Поиск шага из условия минимизации функции
Шаг 8. Расчет новой точки .
Шаг 9. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
4.3.3. Метод МарквардтаЭтот метод является распространенной альтернативой метода Ньютона и его модификаций. Он основан на замене выражением , где
- параметр регуляризации,
- единичная матрица.
Итерационная формула имеет вид:
(4.18)
где - регулирует длину шага и корректирует направление поиска. - это последовательность положительных чисел, таких, что матрица положительна определена на каждой итерации. Как правило, число назначается как минимум на порядок больше, чем самый большой элемент матрицы , а в ряде стандартных программ полагается .
Пересчет осуществляется по следующим правилам: если , то ; в противном случае .
Алгоритм метода Марквардта состоит из следующих шагов:
Шаг 1. Задать начальную точку , , .
Шаг 2. Вычислить градиент в текущей точке .
Шаг 3. Вычислить матрицу Гессе .
Шаг 4. Вычислить матрицу .
Шаг 5. Вычислить матрицу .
Шаг 6. Вычислить
Шаг 7. Расчет новой точки .
Шаг 8. Проверить выполнение условия :
а) если неравенство выполняется, то перейти к шагу 9
б) если нет, то перейти к шагу 10.
Шаг 9.. Переход на шаг 11.
Шаг 10. . Переход на шаг 4.
Шаг 11. Проверка критерия останова. Если не выполняется, то положить и перейти на Шаг 2.
4.4. Методы поиска минимума для функции одной переменной
Для любых методов полиномиальной интерполяции необходимо выбрать такие начальные точки, чтобы оптимум был заключен в интервале ограниченном этими точками. Для этого можно использовать метод Свена или оценивать знак производной.
4.4.1. Квадратичная интерполяция
Если известны значения функции в трех различных точках , , , равные соответственно , , , то функция может быть аппроксимирована квадратичной функцией
(4.19)
где A, B и C определяются из уравнений:
(4.20)
После преобразований этих уравнений получаем
(4.21)
будет иметь минимум в точке , если A>0. Следовательно, можно аппроксимировать точку минимума функции значением
(4.22)
4.4.2. Метод первого приемлемого значения
Метод первого приемлемого значения отличается от квадратичной интерполяции тем, что полином строится исходя из значений в двух точка и и значения производной в одной из этих точек. Тогда значения коэффициентов полинома (4.13) определяются из соотношений
(4.23)
Получаем следующие значения для коэффициентов полинома:
(4.24)
(4.25)
(4.26)
4.4.3. Кубическая интерполяция
Предполагаем, что известны следующие значения:
(4.27)
Эту информацию можно использовать для построения кубического полинома
(4.28)
который будет аппроксимировать функцию . Если , то уравнения, определяющие a, b, c и d выглядят так:
(4.29)
Эти уравнения имеют следующее решение:
(4.30)
В более общем случае (для любых значений и решение системы имеет следующий вид:
(4.31)
Решение уравнения определяет стационарную точку кубического полинома.
4.5. Методы расчета градиента
4.5.1. Численный расчет градиента
Метод численного вычисления градиента основан на использовании определения производной: .
Пусть имеется функция многих переменных , тогда частные производные вычисляются по следующей формуле:
. (4.32)
Значение выбирается в каждом случае индивидуально и зависит от вида функции .
Таким образом, для вычисления значения градиента функции переменных необходимо вычислить значение функции раз.
4.5.2. Расчет градиента с помощью метода быстрого дифференцирования
Пусть - сложная функция многих переменных являющаяся комбинацией функций из множества . Для каждой функции известны выражения для частных производных .
Тогда функцию можно представить в виде ориентированного графа с входными вершинами и одной конечной вершиной. Входным вершинам соответствуют атрибуты , а остальным вершинам соответствуют функции . Пример такого графа для функции
(4.33)
представлен на рис 4.1.
Рис. 4.1. Ориентированный граф для вычисления функции (4.33).
Вычисление значения для каждой вершины графа производится по следующей формуле:
. (4.34)
С каждой вершиной графа, принадлежащей ненулевому слою, ассоциируется автомат, вычисляющий функцию , где - метка вершины. Автоматы срабатывают по слоям в дискретные моменты времени (такты) - автоматы i-го слоя в i-й момент времени. В начальный момент сформированы значения вершин нулевого слоя - известны значения переменных и констант. Они поступают на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i-го такта функционирования определены значения вершин, принадлежащих слоям . На i+1-м такте автоматы i+1-го слоя вычисляют значения вершин i+1-го слоя, получая входные сигналы с предыдущих слоев.
Вычисление градиента сложной функции многих переменных также будет представлено как некоторый вычислительный процесс, в ходе которого сигналы перемещаются в обратном направлении - от выходных элементов графа к входным. И так же, как при вычислении сложной функции, будет явно представлено прохождение каждого узла, а весь процесс в целом будет складываться из таких элементарных фрагментов за счет структуры связей между узлами. Сама эта структура - та же самая, что и для прямого процесса.
Основной инструмент при построении двойственного функционирования - формула для дифференцирования «двухслойной» сложной функции нескольких переменных:
. (4.35)
Для расчета градиента функции , представленной в виде ориентированного графа каждой вершине графа ставится в соответствие двойственная переменная . Для конечной вершины . Для остальных вычисление производится по формуле:
, (4.36)
где - соответствующая вершине функция от независимых переменных и констант, отмечающих вершины нулевого слоя , - соответствующая вершине переменная или константа. Производные в (4.36) берутся при фиксированных значениях прочих переменных и констант. Двойственные переменные вычисляются последовательно, начиная с последнего слоя и заканчивая нулевым. Двойственные переменные вершин слоя являются значениями частных производных функции по соответствующим атрибутам.
Библиографический список
- Д. Химмельблау Прикладное нелинейное программирование. – М.:Мир, 1975. – 534 с.
- Г. Рейклейтис, А. Рейвиндран, К. Рэгсдел Оптимизация в технике: В 2-х книгах. Пер. с англ. - М.:Мир 1986 г. 345 с., 320 с.
- М. Мину Математическое программирование. Теория и алгоритмы. М.:Наука. Гл. ред. физ.-мат. лит., 1990 г. 488 с.
- Б. Банди Методы оптимизации. Вводный курс: Пер. с англ. – М.:Радио и связь, 1988, - 128 с.
- А.В. Пантелеев, Т.А. Летова Методы оптимизации в примерах и задачах. Учебное пособие. М.: Высшая школа, 2002 г., 544 с.
Смотрите также:
Лабораторная работа №3 "Методы оптимизации первого и второго порядков" 242.83kb. 1 стр.
Если в десятичной записи обоих чисел использованы различные цифры и каждая цифра первого числа является делителем второго, а каждая цифра второго числа является делителем первого 43.55kb. 1 стр.
Лабораторная работа 01 Изучение электростатического поля Москва 2005 г. Лабораторная работа №01 64.11kb. 1 стр.
www.moglobi.ru
Тема 6.7. Лабораторная работа по теме «Методы оптимизации функций нескольких переменных»
Вопросы, подлежащие изучению
Постановка задачи многомерной оптимизации.
Основные понятия: выпуклое множество, целевая функция, линия уровня, градиент, локальный и глобальный минимум.
Градиентные методы: метод с дроблением шага, метод наискорейшего спуска аналитический, метод наискорейшего спуска численный.
Вычисление значений частных производных для функции нескольких переменных.
Работа с матрицами: вычисление определителя и угловых миноров.
Организация циклического алгоритма для расчета траектории спуска по методу наискорейшего спуска.
Алгоритм поиска минимума функции нескольких переменных с использованием встроенной функции Minimize.
Алгоритм поиска минимума функции нескольких переменных с использованием встроенной функции Minеrr.
Построение трехмерных графиков и графиков линий уровней.
Построение графика траектории спуска.
Задание
Выбрать индивидуальное задание по номеру варианта из табл. 1 - функцию f(x,y).
Проверить условия существования точки минимума заданной функцииf(x.y).
Решить задачу оптимизации аналитическим методом.
Выбрать начальную точкуx0, y0 для метода наискорейшего спуска.
Решить аналитически задачу оптимизации (3 итерации), методом наискорейшего спуска. Результат расчета отобразить в таблице.
Вычислить погрешности после трех итераций:
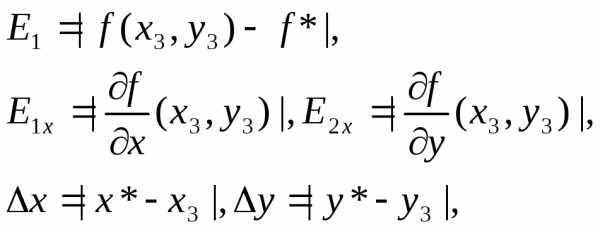
где x*, y* - координаты точки минимума;f*=f(x*,y*) - значение исследуемой функции, вычисленное в точке минимума (аналитическим методом).
Решить задачу оптимизации «расчетом на MathCad» с помощью встроенных функцийMinimize иMinerr.
Построить трехмерный график функции f(x,y).
Построить график линий уровняфункции f(x,y) и траекторию поиска минимумапо результатам ручного расчета, изобразив схематически линии уровня, проходящие через точки траектории. На графике указать точку минимума, найденную в п.3 задания.
Варианты задания
Таблица 6.7-1
| № | Функция |
| 1 | 2 x2 + 3 y2 – 5 x + 6 |
| 2 | x2 + 2 y2 – 3 y + 7 |
| 3 | 3 x2 + y2 – 15 |
| 4 | 3 x2 + 5 y2 + x – 2 |
| 5 | 2 x2 + 3 y2 + 2 x – 3 y |
| 6 | 5 x2 + 2 y2 + 3 x + 10 |
| 7 | 4 x2 + 3 y2 – 3 y – 7 |
| 8 | 5 x2 + 6 y2 + 3 x – 2 y + 3 |
| 9 | 3 x2 + y2 + - 3 x + y – 2 |
| 10 | 6 x2 + 5 y2 – 10 |
| 11 | 5 x2 + 2 y2 – 2 x |
| 12 | x2 + 2 y2 – 3 x + 5 y + 1 |
| 13 | x2 + 4 y2 – 2 x |
| 14 | 4 x2 + 3 y2 + y + 3 |
| 15 | 3 x2 + y2 + 3 |
| 16 | 6 x2 + 4 y2 – 5 x + 3 y –13 |
| 17 | 5 x2 + y2 + x |
| 18 | x2 + 4 y2 – 2 x + 3 y + 5 |
| 19 | 2 x2 + 5 y2 + 2 y + 3 |
| 20 | x2 + 3 y2 – x + 2 y + 7 |
| 21 | 3 x2 + y2 – y + 3 |
| 22 | 6 x2 + 3 y2 + 10 |
| 23 | 5 x2 + 4 y2 – 4 x – 11 |
| 24 | x2 + 2 y2 – x – y |
| 25 | 3 x2 + 2 y2 – 5 y + 1 |
| 26 | 3 x2 + 4 y2 – 2 x + 3 y – 5 |
| 27 | 4 x2 + 5 y2 + 2 x – 4 y + 12 |
| 28 | 6 x2 + 3 y2 – 4 x + 17 |
| 29 | x2 + 5 y2 – x + 2 y + 10 |
| 30 | 3 x2 + y2 – 10 |
studfiles.net
Лабораторная работа №4 по курсу «Прикладные методы оптимизации»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИНовосибирский Государственный Технический Университет
Лабораторная работа №4
по курсу «Прикладные методы оптимизации»
«Динамическое программирование»
Факультет бизнеса
Группа ФББ-12
Студенты: Березовская М., Шевченко А., Корунский В.
Преподаватель: Кириллов Ю.В.
Новосибирск
2013 г
Цели работы:
- научиться строить модели динамического программирования для задач различных классов, в которых процесс принятия решений может быть многошаговым;
- правильно определять суть и природу состояний управляемой системы, мероприятий, составляющих управление системой;
- приобрести практические навыки и опыт решения многошаговых задач методом динамического программирования.
Требуется загрузить ранец объемом А предметами n типов. Известен объем каждого предмета vi и его ценность (вес) сi (i=1…n). Требуется определить, какие предметы и в каком количестве нужно загрузить в ранец, чтобы суммарная ценность (вес) груза была максимальной.
| V | v1 | v2 | v3 | v4 | c1 | c2 | c3 | c4 |
| 69 | 15 | 12 | 9 | 7 | 46 | 35 | 30 | 20 |
X – количество загружаемых предметов k- типа, =(xk) - план загрузки, математическая модель данной задачи:
(X) = 46X1 + 35X2 + 30X3 + 20X4 max
При ограничениях:
15X1+12X2+9X3+7X4 69
X1 10
X2 10
X3 10
X4 10
Xj 0, j= 1…4
Xj - целые, j= 1…4.
Параметры состояния:
0 = 69,
1 = 69-15x1,
2 = 69-15x1-12x2,
3 = 69-15x1-12x2-9x3,
4 = 69-15x1-12x2- 9x3-7x4.
Уравнения состояний:
1 = 0-15x1,
2 = 1-12x2,
3 = 2-9x3,
4 = 3-7x4,
Решение:
1. Решение в ПЭР, как задачи динамического программирования.
2. Анализируем процесс решения. Сравниваем результат решения задачи с полученным по методу Гомори и методом ветвей и границ.
По методу Гомори:
| Базис | Сб | 46 | 35 | 30 | 20 | 0 | 0 | 0 | Bj |
| x1 | x2 | x3 | x4 | X5 | X6 | X7 | |||
| X3 | 30 | 0 | 1/2 | 1 | 0 | -1/6 | 21/2 | 11/6 | 6 |
| X4 | 20 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| X1 | 46 | 1 | 1/2 | 0 | 0 | 1/6 | -11/2 | -11/6 | 1 |
| ∆j | 0 | 3 | 0 | 0 | 22/3 | 6 | 11/3 | 226 | |
Методом ветвей и границ:
Является оптимальным решением.
Результаты решений разными методами совпадают. Максимальная величина целевой функции равна 226, ранец загружают предметами первого и третьего типа. Следовательно, все три метода одинаково хорошо подходят для решения задач подобной формулировки. Анализируя процесс решения, можно сделать вывод о том, что при решении задачи о ранце методом динамического программирования можно быстрее всего добиться желаемого результата, нежели при решении подобной задачи методом Гомори и методом ветвей и границ.
Условие задачи о выборе оптимальной траектории самолета.
Самолет, находящийся на высоте H0 и имеющий скорость V0, должен подняться на высоту Hn и набрать скорость Vm. Известен расход горючего при подъеме самолета на любую высоту ΔH при постоянной скорости, а также при увеличении скорости на любую величину ΔV при неизменной высоте.
Требуется найти оптимальный вариант управления набором высоты и скорости, при котором общий расход горючего будет оптимальным.
m=5; n=4.
Пространством возможных состояний системы будет являться прямоугольник на плоскости V0H, ограниченный прямыми V=V0= 18; H=H0=6; V=Vm=63; H=Hn=42. Разобьем это пространство координатной сеткой с интервалом дискретности по горизонтали
∆V= (Vm – V0) / m = (63 – 18)/5 = 9
и интервалом дискретности по вертикали
∆H= (Hm – H0) / n = (42 – 6)/4 = 9
Представим полученный оптимальный план в графическом виде.
Условие задачи управления запасами с исходными данными:
Предприятие производит продукцию (станки), спрос на которую в каждый из месяцев известен и составляет единиц. Запас продукции на складе предприятия на начало планируемого периода равен единиц. В начале каждого месяца, требуется переналадка оборудования, затраты на которую равны . Затраты на производство единицы продукции равны , а затраты на ее хранение – . Хранить можно не более единиц продукции. Производственные мощности также ограничены, и в каждом месяце можно изготовить не более единиц продукции.
Определить производственную программу изготовления продукции . Запас продукции на складе в конце планируемого периода должен быть равен нулю. Планируемый период составляет 4 месяца.
Исходные данные.
| № п/п | I0 | B | M | c | h | p | s1 | s2 | s3 | s4 |
| 1 | 3 | 9 | 7 | 6 | 1 | 8 | 5 | 4 | 5 | 6 |
Решение:
Вывод: При выполнении данной работы мы научились строить модели динамического программирования для задач различных классов, правильно определять суть и природу состояний управляемой системы, мероприятий, составляющих управление системой. Приобрели практические навыки и опыт в решении многошаговых задач методом динамического программирования.
add.coolreferat.com
Лабораторная работа по "Методам Оптимизации" — лабораторная работа
Лабораторная работа по курсу «Методы Оптимизации»
Численные методы нулевого порядка
Общая характеристика методов 0-го порядка
К численным методам оптимизации нулевого порядка относятся вычислительные алгоритмы поиска экстремума, не использующие информации о производных целевой функции. По сравнению с методами более высоких порядков, они отличаются большей вычислительной устойчивостью, но, в большинстве случаев, более медленной сходимостью (сходимость типичных методов нулевого порядка линейная, то есть с каждым шагом точность вычислений возрастает примерно в k раз, где константа k зависит от метода и свойств целевой функции). Кроме того, методы нулевого порядка – единственные методы, которые применимы к функциям, производные которых не определены во всех или в некоторых точках.
В данной работе рассматриваются одномерные методы оптимизации, то есть целевая функция является функцией одной переменной. Формально задача ставится следующим образом:
Задана функция одной переменной f(x), где a<=x<=b. Требуется с заданной точностью ε найти значение x0, при котором f(x0) минимально.
Рис. 1. Унимодальные функции. На отрезке [a, b] функция f1(x) унимодальна, f2(x) – нет.
Метод дихотомии
Метод дихотомии также называется методом деления пополам. Необходимым условием для его применения является требование унимодальности целевой функции f(x): на рассматриваемом промежутке [a,b] функция f(x) должна иметь не более одного экстремума (см. рис 1).
Алгоритм
- На начальном этапе отрезок, на котором ищется минимум, задаётся равным интервалу допустимых значений [a,b]
- Вычисляется положение центра отрезка c=(a+b)/2 и центров его правой и левой половин: x1=(a+c)/2, x2=(c+b)/2
- Вычисляются значения целевой функции в точках f(c), f(x1), f(x2)
- Значения функции в точках c, x1, x2 сравниваются, и определяется положение нового, уточнённого интервала поиска. При этом интервал поиска уменьшается в 2 раза:
- Если f(c) > f(x1), то новый отрезок: [a,c]
- Если f(c) > f(x2), то новый отрезок: [c,b]
- Иначе новый отрезок: [x1,x2]
- Если длина отрезка меньше заданной точности ε, то алгоритм завершается, иначе осуществляется переход на шаг 2.
Алгоритм проиллюстрирован рис. 2.
Рис. 2. Метод дихотомии. Показан случай, когда f(x1)<f(c)
Для уменьшения количества вычислений можно воспользоваться тем, что на втором и последующих шагах значение функции в центре нового отрезка всегда будет вычислено на предыдущем шаге, поэтому на каждом новом шаге требуется вычислять целевую функцию только в центрах правого и левого полуотрезков.
Так как каждый последующий отрезок всегда ровно в 2 раза меньше предыдущего, метод дихотомии обеспечивает увеличение точности в 2 раза за каждые 2 вычисления целевой функции, или, в среднем, в 21/2 = 1,41... раза на 1 вычисление целевой функции.
Метод Фибоначчи
Метод Фибоначчи аналогичен методу деления пополам, но вместо деления отрезка на равные части в нём используется деление в золотой пропорции: φ = (1 + 51/2) / 2 = 1,6817…. Так же , как и метод деления пополам, метод Фибоначчи требует того, чтобы функция была унимодальной.
Алгоритм
- На начальном этапе выбирается отрезок [a,b] , на котором ищется минимум.
- Внутри отрезка выбирается точка c, делящая его в золотом отношении, то есть так, что отношение большей части отрезка к меньшей равно отношению всего отрезка к его большей части:
с = a + (b-a)/ φ
- Определяется положение дополнительной точки x, которая расположена симметрично точке c относительно центра отрезка:
x = a + b - c
- Вычисляются значения функции f(a), f(b), f(c), f(x).
- Значения функции сравниваются и определяется новое положение интервала поиска (см. рис 3):
- Если c>x:
- Если f(x) < f(c), то новый отрезок: [a, c]
- Иначе новый отрезок: [x, b]
- Если c<x: (эта ситуация может возникнуть на втором шаге и далее)
- Если f(x) < f(c), то новый отрезок: [c, b]
- Иначе новый отрезок: [a, x]
- Если длина отрезка стала меньше заранее заданной точности, алгоритм завершается, иначе итерация повторяется с шага 2.
Рис. 3. Метод Фибоначчи. Показан случай, когда f(x)<f(c).
Особенностью метода Фибоначчи, позволяющей экономить дорогостоящие вычисления целевой функции f(x), является то, что, начиная со второго шага, значение функции в точке c известно с предыдущего шага, остаётся вычислить только значение в отражённой точке x.
Например, на рис.3 f(x)<f(c), поэтому новым интервалом поиска становится интервал [a,c]. Точка x в этом случае оказывается внутри нового интервала и делит его в золотом отношении, то есть она становится новой точкой c.
Длина интервала поиска на следующем шаге всегда в φ = 1,68… раз меньше длины на предыдущем шаге. Таким образом, за одно вычисление целевой функции метод Фибоначчи увеличивает точность в 1,68… раз, что больше чем соответствующий показатель метода дихотомии (1.41…).
Задание на лабораторную работу
В лабораторной работе требуется на любом реализовать один из методов поиска экстремума. Метод поиска минимума и целевая функция указаны в варианте задания. Целевая функция содержит два свободных параметра, базовые значения которых также указаны в варианте задания.
Представленная программа должна предоставлять пользователю возможность указывать другие значения свободных аргументов (реализовывать графический интерфейс необязательно). Точность, с которой осуществляется поиск экстремума, для всех вариантов одинакова и равна 10-6. В результате выполнения программа должна вывести найденное численное значение экстремума и число шагов, за которое была достигнута требуемая точность.
Содержание отчёта
Отчет по лабораторной работе должен содержать следующие элементы:
- Постановка задания
- Данные варианта
- Эскиз графика целевой функции на заданном интервале поиска
- Аналитически найденное значение экстремума
- Текст программы (можно привести только часть кода, относящуюся непосредственно к реализации алгоритма)
- Результаты выполнения программы для базовых значений, приведенных в варианте
- Выводы
Варианты заданий
№ | Интервал поиска [a, b] | Метод оптимизации | Целевая функция f(x) | Значения свободных параметров A, B | |
A | B | ||||
1 | [-2; 2] | Дихотомия | Ax2 + Bx | 1 | -1 |
2 | [0; π/2] | Фибоначчи | A sin(x) + Bx | 1 | 0,5 |
3 | [-1; 3] | Дихотомия | Ax + Bx | 2 | -1 |
4 | [-2; 2] | Фибоначчи | 1 / (x2 + Ax + B) | 0 | 1 |
5 | [1; 5] | Дихотомия | A ln(x) + Bx | 2 | -1 |
6 | [-1; 5] | Фибоначчи | Ax2 + Bx | 2 | -4 |
7 | [1; 5] | Дихотомия | A ln(x) + Bx | 3 | -2 |
8 | [0; π/2] | Фибоначчи | A sin(x) + Bx | 2 | √2 |
9 | [0; 3] | Дихотомия | Ax + Bx | 1,5 | -2 |
10 | [-1; 3] | Фибоначчи | 1 / (x2 + Ax + B) | 1 | 1 |
11 | [-2; 3] | Дихотомия | Ax2 + Bx | 0,5 | 2 |
12 | [0; 4] | Фибоначчи | 1 / (x2 + Ax + B) | 2 | 1 |
13 | [-2; 2] | Дихотомия | Ax + Bx | ½ | 3 |
14 | [0; π/2] | Фибоначчи | A sin(x) + Bx | 1 | √3 / 2 |
15 | [-1; 4] | Дихотомия | Ax2 + Bx | 1 | -2 |
16 | [1; 5] | Фибоначчи | A ln(x) + Bx | -7 | 3 |
17 | [-3; 3] | Дихотомия | Ax + Bx | e | -1 |
18 | [-5; 0] | Фибоначчи | 1 / (x2 + Ax + B) | -2 | 5 |
19 | [1; 7] | Дихотомия | A ln(x) + Bx | 6 | -3 |
20 | [-1; 2] | Фибоначчи | Ax2 + Bx | 2 | 2 |
21 | [0; π/2] | Дихотомия | A sin(x) + Bx | 3 | √3 |
Точность, с которой необходимо искать минимум целевой функции, одинакова дял всех вариантов и равна 10-6.
student.zoomru.ru
Дисциплина “Методы оптимизации” Красноярск 2003 г (1) - Лабораторная работа
Красноярская государственная академия цветных металлов и золота
Кафедра автоматизации производственных процессов
ЦМ | Дисциплина “Методы оптимизации” Красноярск 2003 г. |
“Изучение пакета Optimization Toolbox системы MATLAB 6.5
и его применения для решения задач оптимизации”
ЦЕЛЬ РАБОТЫ
Ознакомиться с составом и назначением программного пакета Optimization Toolbox
Ознакомиться с основными командами программного пакета OptimizationToolbox в оптимизационных задачах.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Открыть рабочее окно программы MATLAB 6.
Изучая теоретические сведения о пакете OptimizationToolbox, вводите в рабочем окне команды, приводимые в описании пакета и выделенные желтым цветом. При работе необходимые m-файлы сохраняйте в папке E:\MATLAB 6\work, а затем копируйте в свои папки на сервере NT003.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Назначение и возможности пакета
Пакет оптимизации (Optimization Toolbox) – это библиотека функций, расширяющих возможности системы MATLAB по численным вычислениям и предназначенная для решения задач оптимизации и систем нелинейных уравнений. Поддерживает основные методы оптимизации функций ряда переменных:
Безусловная оптимизация нелинейных функций.
Метод наименьших квадратов.
Решение нелинейных уравнений.
Линейное программирование.
Квадратичное программирование.
Условная минимизация нелинейных функций.
Методы минимакса.
Многокритериальная оптимизация.
Рассматриваемый пакет дает возможности решать задачи минимизации функций, нахождения решений уравнений, задачи аппроксимации («подгонки» кривых под экспериментальные данные).
Различные типы таких задач вместе с применяемыми для их решения функциями пакета Optimization Toolbox приведены в таблице 1.
Таблица 1 - Типы задач, решаемых средствами пакета Optimization Toolbox
Тип задачи | Математическая запись | Функция MATLAB |
Задачи минимизации | ||
Скалярная (одномерная) минимизация | fminbnd | |
Безусловная минимизация (без ограничений) | fminunc, fminsearch | |
Линейное программирование |
| linprog |
Квадратичное программирование | при условиях A·x b, Aeq·x = beq, xL x xU, | quadprog |
Минимизация при наличии ограничений | при условиях с(x) 0, сeq(x) = 0, A·x b, Aeq·x = beq, xL x xU, | fmincon |
Достижение цели |
F(x) –wγ goal, с(x) 0, сeq(x) = 0, A·x b, Aeq·x = beq, xL x xU, | fgoalattain |
Минимакс | при условиях с(x) 0, сeq(x) = 0, A·x b, Aeq·x = beq, xL x xU, | fminimax |
Полубесконечная минимизация | при условиях K(x,w) 0 для всех w, с(x) 0, сeq(x) = 0, A·x b, Aeq·x = beq, xL x xU, | fseminf |
Нахождение решений уравнений | ||
Линейные уравнения | C(x) d , n уравнений, n переменных | \ (оператор левого деления, slash) |
Нелинейное уравнение одной переменной | f(a) = 0 | fzero |
Нелинейные уравнения многих переменных | F(x) = 0, n уравнений, n переменных | fsolve |
Задачи аппроксимации («подгонки» кривых) | ||
Линейный метод наименьших квадратов (МНК) | ,m уравнений, n переменных | \ (оператор левого деления, backslash) |
Неотрицательный линейный МНК | , при условии x ≥ 0 | lsqnonneg |
Линейный МНК при наличии ограничений | , при условиях A·x b, Aeq·x = beq, xL x xU, | lsqlin |
Нелинейный МНК | , при условии xL x xU, | lsqnonlin |
Нелинейная «подгонка» кривой | , при условии xL x xU, | lsqcurvefit |
Принятые обозначения:
а – скалярный аргумент;
 ,
,  – в общем случае векторные аргументы;
– в общем случае векторные аргументы;f(a), f(x) – скалярные функции; F(x), с(x), сeq(x), K(x,w) – векторные функции;
A, Aeq, C, H – матрицы;
b, beq, d, f, w, goal, xdata, ydata – векторы;
xL ,xU, – соответственно, нижняя и верхняя границы области изменения аргумента.
Методы оптимизации описаны в работах [1-5]:
Применяемые алгоритмы
В рамках пакета OptimizationToolbox все задачи оптимизации делятся на две группы: задачи малой и средней размерности и задачи большой размерности. Такое же деление принято для алгоритмов решения данных задач. Это не означает, что для решения задач средней размерности нельзя применять алгоритмы большой размерности и наоборот. Просто алгоритмы той или иной группы более эффективны для задач своей размерности.
В пакете Optimization Toolbox реализован широкий набор алгоритмов для решения задач оптимизации средней и малой размерности. Основными для задач без ограничений являются симплексный метод Нелдера-Мида и квазиньютоновские методы.
Для решения задач с ограничениями, минимакса, достижения цели и полубесконечной оптимизации использованы алгоритмы квадратичного программирования.
Задачи, сводящиеся к нелинейным МНК, решаются с помощью алгоритмов Ньютона-Рафсона и Левенберга-Марквардта.
Вспомогательные процедуры одномерной (скалярной) оптимизации используют алгоритмы квадратичной (параболической) и кубической интерполяции.
Общая формулировка задачи параметрической оптимизации
Задача параметрической оптимизации формулируется как задача нахождения набора параметров x = {x1, x1, …, xn}, который является оптимальным в смысле некоторого критерия. В простейшем случае такая задача сводится к минимизации или максимизации некоторой (целевой) функции без каких-либо ограничений. В более сложных ситуациях на отмеченные параметры могут быть наложены некоторые ограничения в виде равенств gi(x) = 0 (i = 1, 2, …, m), неравенств gi(x) 0 (i = me +1, …, m) и/или параметрических границ xL , xU,.
Общая формулировка задачи параметрической оптимизации представляется следующим образом: требуется найти вектор x,обеспечивающий
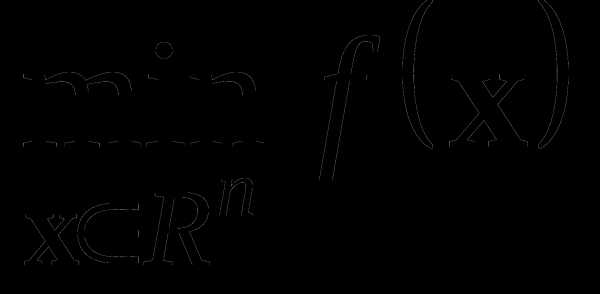
при ограничениях
gi (x) = 0 (i = 1, 2, …, m),
gi (x) 0 (i = me +1, …, m),
xL x xU,
где x – вектор оптимизируемых параметров (x Rn),f(x) – скалярная целевая функция (критерий) векторного аргумента (f (x): Rn R), Rn), gi(x) – также некоторые скалярные функции векторного аргумента (задача максимизации сводится к задаче минимизации заменой f(x) на –f(x)).
Эффективность и точность решения данной задачи зависит как от числа параметров и ограничений, так и от вида целевой функции. При линейных ограничениях и целевой функции приведенная задача оптимизации называется задачей линейного программирования, при линейных ограничениях, но при квадратичной (по аргументам) целевой функции – задачей квадратичного программирования, в общем случае это задача нелинейного программирования.
Безусловная оптимизация
Существующие алгоритмы безусловной оптимизации могут быть разделены на две группы – алгоритмы, базирующиеся на использовании производных минимизируемой функции (градиентные и методы второго порядка), и алгоритмы, использующие только значения функции (безградиентные).
Безградиентныеметоды (например, симплексный метод Нелдера-Мида) более пригодны для задач, где минимизируемая функция является существенно нелинейной или имеет разрывы. Градиентные методы (методы первого порядка) обычно эффективны в случаях целевых функций, непрерывных вместе с первыми производными. Методы второго порядка, такие как метод Ньютона, применяются реже, поскольку требуют больших вычислительных затрат для расчета матриц вторых производных.
Градиентные методы используют информацию о наклоне функции для выбора направления поиска экстремума. В одном из таких методов – наискорейшего спуска – на каждой итерации движение к точке минимума осуществляется в направлении – f(x) (где f(x) – вектор-градиент целевой функции f(x)). Этот метод неэффективен в ситуациях, когда поверхность целевой функции имеет узкие «овраги», как, например, у известной функции Розенброка
f(x) = 100 ( x1 – x22)2+ (1 – x1).
Поверхность этой функции приведена на рисунке 1.
Минимальное значение данной функции равно нулю при x1 = x2 = 1. Между тем численные эксперименты показывают, что зачастую метод наискорейшего спуска не обеспечивает нахождение точки экстремума даже после сотен и тысяч итераций.
Указанную функцию из-за своеобразной формы ее линии равного уровня часто называют «банановой» функцией и используют как тестовую при проверке эффективности различных оптимизационных алгоритмов.
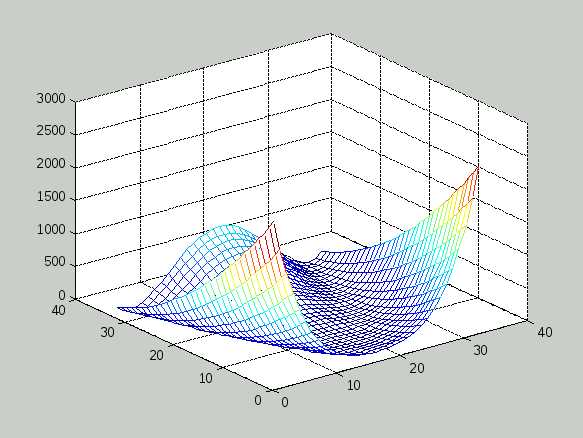
Рисунок 1 Графическое представление функции Розенброка
Квазиньютоновские алгоритмы. Среди алгоритмов, использующих информацию о градиенте, наиболее распространенными являются квазиньютоновские. В этих (итерационных) алгоритмах целевая функция в окрестностях произвольной точки аппроксимируется квадратичной функцией, при этом на каждой итерации решается задача локальной минимизации
где H – симметричная и положительно определенная матрица вторых частных и смешанных производных (матрица Гессе, или гессиан), c – постоянный вектор, b – константа.
Оптимальное решение приведенной задачи соответствует нулевым значениям первых производных, то есть
Ñf(x*) = Hx* + c = 0,
откуда
x*= –H–1c .
Ньютоновские алгоритмы
Ньютоновские алгоритмы (в отличие от квазиньютоновских) непосредственно вычисляют H (прямое вычисление матрицы H требует больших вычислительных затрат) и осуществляют движение в рассчитанном на очередной итерации направлении уменьшения целевой функции до достижения минимума (с использованием методов одномерного поиска). В квазиньютоновских алгоритмах такое вычисление не производится, а используется некоторая аппроксимация H.
Среди подобных алгоритмов одним из наиболее популярных и используемым в пакете OptimizationToolbox является так называемый BFGS-алгоритм, получивший свое название по фамилиям предложивших его авторов (Broyden, Fletcher, Goldfarb, Shanno), в котором аппроксимация H производится итерационно, по формуле
,
где
sk = xk+1 – xk,
qk = f(xk+1) – f(xk).
Более удобно использовать аппроксимацию не матрицы H, а обратной к ней матрицы H–1; приведенное рекуррентное соотношение подобную замену допускает. При этом сам алгоритм становится практически идентичным хорошо известному алгоритму Давидона-Флетчера-Пауэлла, за тем исключением, что в последнем векторы q заменены на векторы s и наоборот.
Алгоритмы Ньютона-Гаусса и Левенберга-Марквардта
Алгоритмы Ньютона-Гаусса и Левенберга-Марквардта используются в функциях рассматриваемого пакета, предназначенных для решения задачи нелинейного метода наименьших квадратов (МНК). При отсутствии ограничений указанная задача формулируется следующим образом:
.
Скалярная оптимизация в данных алгоритмах производится, соответственно, вдоль направлений
dk= –( JT(xk) J(xk))–1J(xk) F(xk) – для алгоритма Ньютона-Гаусса,
dk= –( JT(xk) J(xk) + λkI)–1J(xk) F(xk) – для алгоритма Левенберга-Марквардта,
где 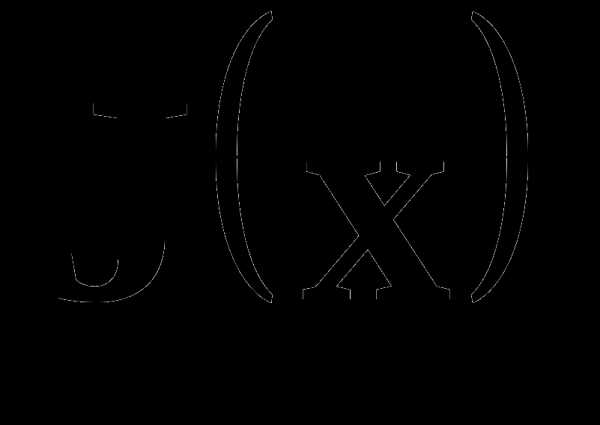 – матрица-якобиан размером mn (в пакете OptimizationToolbox под якобианом понимается матрица первых частных производных вектор-функции F(x) по векторному аргументу x, а не определитель этой матрицы, как обычно принято в математической литературе), λk – параметр алгоритма, определяемый в процессе линейной (скалярной) оптимизации вдоль выбранного направления.
– матрица-якобиан размером mn (в пакете OptimizationToolbox под якобианом понимается матрица первых частных производных вектор-функции F(x) по векторному аргументу x, а не определитель этой матрицы, как обычно принято в математической литературе), λk – параметр алгоритма, определяемый в процессе линейной (скалярной) оптимизации вдоль выбранного направления.
Минимизация при наличии ограничений
В задачах оптимизации с ограничениями (таблица 1) обычный подход к нахождению решения состоит в замене исходной задачи с ограничениями на задачу без ограничений (задачу безусловной оптимизации), например, с помощью метода штрафных функций. В настоящее время более эффективным считается применение так называемых уравнений Куна-Таккера, которые на основании вышеприведенной формулировки задачи параметрической оптимизации и при некоторых дополнительных предположениях о характере ограничений записываются в виде
,
gi (x*) = 0, (i = 1, 2, …, me),
λi* = 0, (i = me + 1, …, m),
где λi – множители Лагранжа.
Для решения данных уравнений в пакете Optimization Toolbox использован алгоритм так называемого последовательного квадратичного программирования (в оригинале – Sequential Quadratic Programming, или SQP), представляющий собой, по сути, разновидность квазиньютоновского метода. Основная идея SQP заключается в применении квадратичной аппроксимации функции Лагранжа (учитывающей ограничения)
,
так что на каждой итерации решается задача оптимизации
,
gi T(xk)d + gi(xk) = 0, i = 1, 2, …, me,
gi T(xk)d + gi(xk) 0, i = me + 1, …, m.
В последней формулировке данная задача может быть решена любым методом решения задач квадратичного программирования. В пакете OptimizationToolbox для этой цели использован комбинированный алгоритм, объединяющий алгоритм BFGS и так называемый метод проекций.
Многокритериальная оптимизация
Достаточно часто в реальных ситуациях качество работы исследуемого объекта или системы оценивается не единственным критерием или показателем качества, а совокупностью таких критериев, причем представляющихся одинаково значимыми. Это приводит к задаче оптимизации с векторной целевой функцией F(x) = {F1(x), F2(x), …, Fm(x)} и формулировкой
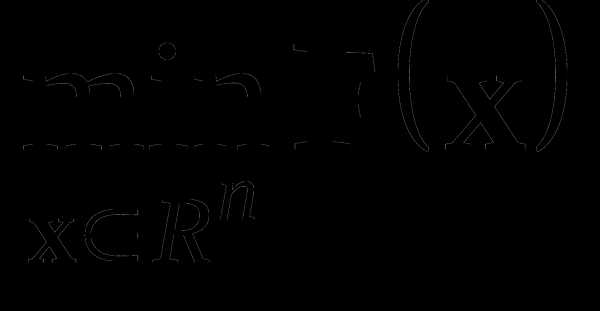
при ограничениях
gi (x) = 0, i = 1, 2, …, me,
gi (x) 0, i = me + 1, …, m.
xL x xU,
получившей название задачи многокритериальной, или векторной, оптимизации.
Известно, что решение подобной задачи сводится к нахождению множества точек неулучшаемых решений (Парето-множества), для чего используются такие, например, методы, как метод взвешенной суммы частных критериев или метод ε-ограничения.
В рассматриваемом пакете для решения задачи многокритериальной оптимизации применен так называемый метод достижения цели, предложенный Gembicki и математически описываемый соотношениями
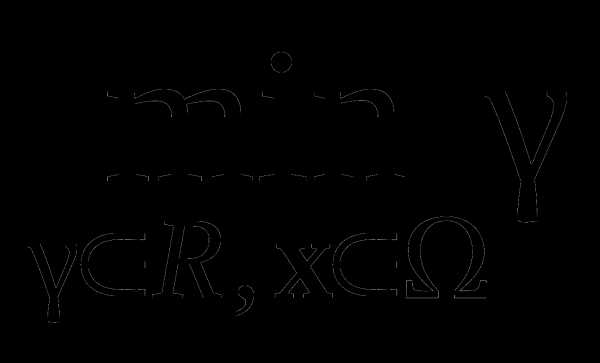
при ограничениях
Fi (x) – wi γ Fi*, i = 1, 2, …, m,
где – область допустимых значений x, wi – некоторые весовые коэффициенты, Fi* – некоторые устанавливаемые «цели» (goals).
В приведенной формулировке задача подобна задаче однокритериальной оптимизации и может решаться с помощью перечисленных алгоритмов.
textarchive.ru
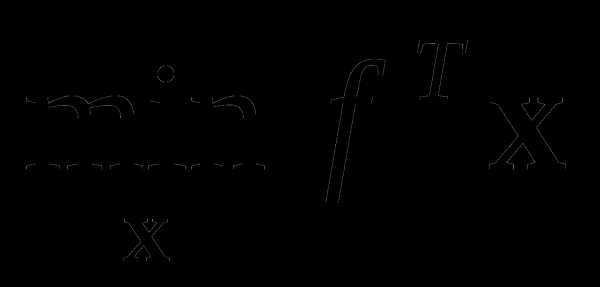 при условиях Ax b, Aeqx = beq, xL x xU
при условиях Ax b, Aeqx = beq, xL x xU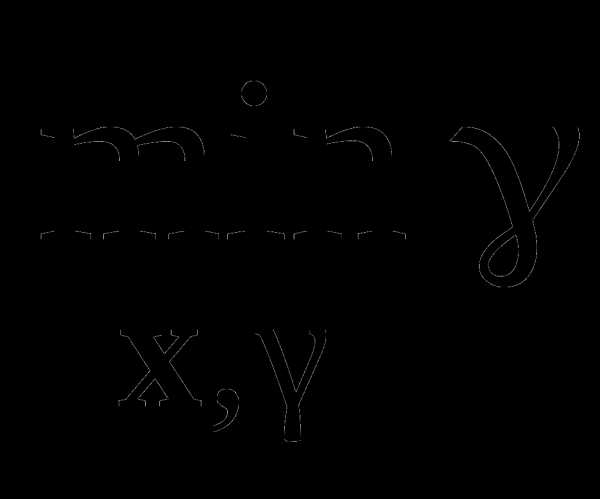 при условиях
при условиях