ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ. Экспериментальные методы оптимизации презентация

Презентация на тему: МЕТОДЫ ОПТИМИЗАЦИИ

В своей жизни человек часто сталкивается с ситуацией, когда ему из некоторой совокупности возможных вариантов своего поведения или принятия решения в какой-либообласти деятельности необходимо выбрать один вариант. Наилучший вариант поведения (принятие наилучшего решения) можно выбиратьпо-разному.Если такой выбор предусматривает проведение количественного анализа ситуации путем сравнения различных вариантов с помощьюкакой-либоколичественной оценки этих вариантов, то говорят о необходимости решениязадачи оптимизации (по латыни optimus — наилучший). Ясно, что задача оптимизации имеет смысл, если есть несколько возможных вариантов ее решения. Эти варианты обычно называютальтернативами.

По содержанию задачи оптимизации весьма разнообразны. Они могут быть связаны с проектированием технических устройств и технологических процессов, с распределением ограниченных ресурсов и планированием работы предприятий, наконец, с решением проблем, возникающих в повседневной жизни человека. Всевозможные устройства, процессы и ситуации, применительно к которым предстоит решать задачу оптимизации, объединим общим названием объект

оптимизации.

В этой главе сформулированы некоторые основные определения и понятия, играющие важную роль в дальнейшем изложении материала, даны постановки известных и достаточно простых задач поиска экстремума из геометрии, алгебры и других разделов математики, приведены примеры прикладных задач оптимального проектирования и планирования, а также перечислены классы задач оптимизации.

1.1. ОСНОВНЫЕ ПОНЯТИЯ

Обычно человек хочет сделать “как лучше”, но, чтобы не получить плохой результат при самых хороших намерениях, для решения задачи оптимизации нужно прежде всего найти ответы на следующие вопросы:

-Что значит лучше"?

-Что конкретно нужно улучшить?

- За счет чего можно добиться улучшения, что можно изменить? - В каких пределах можно производить изменения?

Отвечая на первый вопрос, необходимо сформулировать критерий оптимальности, т.е. определить те признаки и предпочтения, по которым следует провести сравнительную оценку альтернатив и выбрать среди них наилучшую с точки зрения поставленной цели оптимизации. Именно с этой точки зрения можно ответить на второй вопрос: что конкретно нужно улучшить? Это может быть повышение производительности станка или срока службы технического устройства, снижение массы конструкции летательного аппарата или затрат на его производство и т.п.

Для ответа на два последних вопроса необходимо располагать математической моделью объекта оптимизации. Эта модель описывает объект при помощи соотношений между величинами, характеризующими его свойства. Обычно хотя бы часть этих величин можно изменять в некоторых пределах, что и порождает множество альтернатив, среди которых и предстоит выбрать наилучшую. Изменяемые при оптимизации величины, входящие в математическую модель объекта оптимизации, называютпараметрами оптимизации, а соотношения, устанавливающие пределы возможного изменения этих параметров, —ограничениями. Эти ограничения могут быть заданы в форме равенств или неравенств. Их называют соответственноограничениями типа равенства или

ограничениями типа неравенства.

Если множество параметров оптимизации является подмножеством конечномерного линейного пространства, то говорят о конечномерной задаче оптимизации в отличие от бесконечномерных задач, которые рассматривают в вариационном исчислении и оптимальном управлении. При этом критерием оптимальности может быть требование достижения наибольшего или наименьшего значения одной или несколькими действительными (скалярными) функциями параметров оптимизации, выражающими количественно меру достижения цели оптимизации рассматриваемого объекта. Каждую из таких функций принято называтьцелевой. Если целевая функция единственная, то задачу конечномерной оптимизацииназывают задачей математического программирования, а в противном случае — задачей многокритериальной (векторной) оптимизации. В дальнейшем ограничимся рассмотрением задач математического программирования и методов их решения.

Если целевая функция и ограничения являются линейными относительно параметров оптимизации, то говорят о задаче линейного программирования. Одну из первых таких задач сформулировал и решил Л.В. Канторович. Задача Канторовича была связана с выбором оптимальной производственной программы, что и объясняет появление в названии этого класса задач слова “программирование”. При нелинейной зависимости целевой функции или ограничений от параметров оптимизации

1.2. НЕКОТОРЫЕ ПРОСТЫЕ ПРИМЕРЫ

Начнем с рассмотрения достаточно простых задач оптимизации из геометрии, алгебры и некоторых других разделов математики. Эти задачи обычно можно решить геометрическим или алгебраическим путем, а также при помощи необходимых и достаточных условий экстремума действительной (скалярной) функции одного переменного. Включение таких примеров в эту книгу важно по нескольким причинам.Во-первых,эти задачи тесно связаны с историей развития методов оптимизации и позволяют наглядно продемонстрировать многообразиеобъектов оптимизации. Во-вторых,на простой задаче можно более четко выявить особенности построенияматематических моделей таких объектов с точки зрения выбранногокритерия оптимальности и проследить этапы процесса формулировки

задачи математического программирования. В-третьих, знание способов и результатов решения многих из этих задач помогает при решении более сложных задач оптимизации,

задач оптимального проектирования

(см. 1.3).

Пример 1.1. Найдем стороны прямоугольника, вписанного в окружность радиусаR и имеющего наибольшую площадьS (рис. 1.1).

Эта задача известна с глубокой древности, и ее нетрудно решить геометрическим путем. Диагональ вписанного в окружность прямоугольника является диаметром окружности и имеет фиксированную длину. Площадь S прямоугольника равна половине произведения его диагоналей на синус углаφ между диагоналями, т.е.S = 2R2sinφ. Ясно, что эта площадь будет наибольшей приsinφ = 1, или приφ = π/2. В этом случае диагонали прямоугольника перпендикулярны, а сам прямоугольник представляет собой квадрат. Таким образом, прямоугольником наибольшей площади, вписанным в окружность, является квадрат со стороной и площадью 2R2.

Если в качестве параметров оптимизации выбрать длиныа≥0 иb ≥0 сторон прямоугольника, то получимцелевую функцию S = аb иограничение типа равенства, нелинейные по отношению к этим параметрам. Поэтому рассматриваемую задачу оптимизации следует отнести к задачамнелинейного программирования. Ее математическую формулировку можно представить в виде

Эту задачу можно решить одним из известных стандартных путей: либо использовать формальную процедуру поиска условного экстремума функции S =ab двух переменных с одним уравнением связи, построив функцию Лагранжа, либо выразить при помощи ограничения одно переменное через другое и перейти к поиску экстремума функции одного переменного. Отметим, что в данном случае возможен и нестандартный способ решения, связанный с построением вспомогательного соотношения 4R2 - 2S =а2 +b2- 2аb = (a -b)2, или . Отсюда следует, чтоS достигает наибольшего значенияS* = 2R2 при условииа =b, т.е. когда прямоугольник является квадратом, причема =

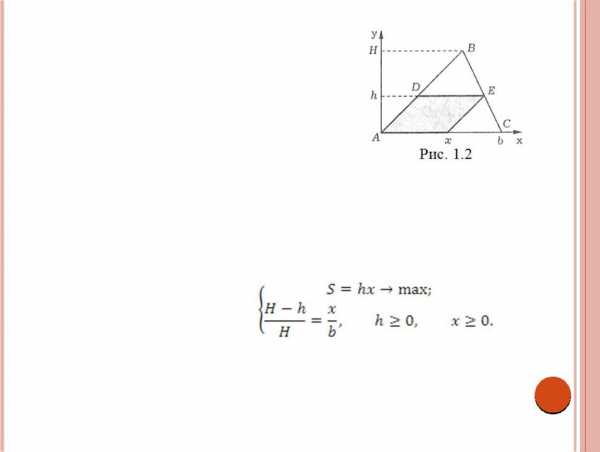
Пример 1.2 (задача Евклида).В заданный треугольник ABC с высотой Н и основанием

b вписать параллелограмм наибольшей площади, стороны которого параллельны двум сторонам треугольника (рис. 1.2).

Критерием оптимальности в этой задаче является достижение площадью параллелограмма наибольшего значения, а ограничения связаны с

условиями параллельности сторон и размещения параллелограмма в пределах заданного треугольника.

Выберем прямоугольную систему координат, совместив ее начало с общей вершиной параллелограмма и треугольника(вершина А на рис. 1.2), а ось абсцисс — с одной из сторон треугольника. В качестве параметров оптимизации выберем основаниех параллелограмма и его высотуh. Тогда площадьS параллелограмма можно записать в видеS =hx, а условие, что параллелограмм вписан в треугольник, — как ограничение типа равенства (H —h)/H =x/b, которое вытекает из подобия треугольниковDBE иABC. Итак, имеем задачу оптимизации

Эту задачу также можно решить стандартными способами (см. пример 1.1). Ее решением является параллелограмм с основанием x* =b/2 и высотойh* = (1 -x/b)H = H/2. Отметим, что выбор вершины треугольника, с которой совпадает вершина параллелограмма, не является существенным, так как в любом из трех вариантов выбора вершины треугольника площадь параллелограмма максимальной площади равна половине площади треугольникаABC.

1.3. ЗАДАЧИ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ

При создании технического устройства различного назначения обычно часть его параметров можно изменять в определенных пределах. Это приводит к тому, что при проектировании появляется некоторое множество вариантов создаваемого устройства. В результате возникает проблема выбора из этого множества

альтернатив наилучшей альтернативы с точки зрениякритерия оптимальности.

Соответствующие такому выбору задачи оптимизации часто называют задачами оптимального проектирования.

Пример 1.6. Одной из наиболее простых задач оптимального проектирования является выбор размеров емкости определенной формы, имеющей наибольший объем при заданной площади поверхности или же наименьшую площадь при заданном объеме.

Пусть требуется спроектировать бак горючего в виде прямого кругового цилиндра заданного объема V, на изготовление которого будет затрачено наименьшее количество листовой стали. В качествепараметров оптимизации выберем радиусR и высотуН цилиндра. Тогда затраты материала на изготовление бака будет определять суммарная площадьS его боковой поверхности и двух плоских днищ. Таким образом, необходимо минимизироватьцелевую функцию S = 2πR(H +R) приограничении типа равенства πR2H =V, т.е. решитьзадачу нелинейного программирования. Если из целевой функции при помощи ограничения исключитьН и записать ее в виде

то произведение слагаемых не будет зависеть от R, и для нахождения ее минимального значения удобно использовать то же неравенство между геометрическим и арифметическим средними, что и в примере 1.3:

Равенство имеет место только при равенстве слагаемых, т.е. при Учитывая ограничение, получаем

т.е. высота оптимального бака равна его диаметру.

При изготовлении одного бака нужно учитывать, что для заготовки круглого днища площадью πR2 придется взять квадратный лист площадью 4R2, причем после раскроя оставшуюся часть листа использовать будет практически невозможно. Поэтому более обоснованно в качестве целевой минимизировать функцию

при прежнем ограничении πR2H =V.

Тогда в результате процедуры, аналогичной рассмотренной, получим

Если предстоит изготовить крупную партию баков, то раскрой листовой стали при заготовке днищ можно провести более рационально, располагая соседние центры днищ в вершинах правильных треугольников со стороной 2R. Тогда расход листа на каждое днище будет соответствовать площади правильного шестиугольника, описанного около окружности радиуса Д. При этом следует

минимизировать целевую функцию	при том же
ограничении. В итоге получим

Отметим, что при постановке задач оптимального проектирования важно, чтобы

математическая модель объекта оптимизации достаточно полно отражала именно те свойства объекта, улучшение которых является целью оптимизации. Разработка такой модели обычно требует использования сведений из соответствующих инженерных дисциплин или областей техники.

1.4. ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ

Задачи математического программирования часто возникают в экономике, при планировании производственных процессов и количественной оценке альтернатив,связанных с принятием управленческих решений. Постановка этих задач обычно основана на анализе и сопоставлении расходуемых ресурсов и полученного результата. Такой подход принято называть методом “затраты — эффективность”. Применение этого подхода приводит, как правило, к двум связанным между собой типам задач: либо максимизировать эффективность при ограниченных затратах, либо обеспечивать эффективность не ниже заданной при минимальных затратах. Таким образом, критерием оптимальностиможет быть количественное выражение затрат или эффективности. Рассмотрим несколько примеров такого подхода.

Пример 1.11. Предположим, что предприятие может выпускать продукциюп наименований, для производства которой требуетсят видов

ресурсов (сырья, энергии, оборудования и т.п.). Обозначим через aij
затраты i-говида ресурсов,	на производство единицы
продукции j-гoнаименования,	,	а через bi иxj

полные объемы располагаемых ресурсов и планируемые объемы выпуска продукции соответственно. Если к тому же по каждому наименованию продукции заданы нижняя aj и верхняяAj границы объема выпуска

продукции, то можно записать ограничения типа неравенства

studfiles.net

Презентация на тему: ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Лекция 1

Константин Ловецкий [email protected]

Сентябрь 2012

1	Кафедра систем
	телекоммуникаций

Постановка задачи оптимизации

Постановка задачи оптимизации начинается с

определения набора независимых переменныхи

обычно включает условия, которые характеризуют ихприемлемые значения. Эти условия называютограничениями задачи. Еще одной обязательной компонентой описания являетсяскалярная мера «качества», именуемаяцелевой функцией и

зависящая каким-тообразом от переменных.

Решение оптимизационной задачи — это приемлемый набор значений переменных, которому отвечает оптимальное значение целевой функции. Под оптимальностью обычно понимают максимальность илиминимальность; например, речь может идти о максимизации прибыли или минимизации массы.

Постановка задачи оптимизации

Задачей оптимизации называется задача поиска минимума скалярной функции на множестве значений ее аргумента, удовлетворяющих некоторым ограничениям.

В основном речь пойдет об ограничениях, которые выражаются в терминах соотношений на значения непрерывных функций от переменных задачи; другие типы ограничений будут рассмотрены позже.

Постановка задачи оптимизации

К задачам на поиск оптимума сводятся многие из проблем математики, системного анализа, техники, экономики, медицины и статистики. В частности, они возникают при построении математических моделей.

Когда для изучения какого-нибудьсложного явления конструируется математическая модель, к оптимизации прибегают для того, чтобы определить такую структуру и такие параметры последней, которые обеспечивали бы наилучшее согласование с реальностью.

Постановка задачи оптимизации

Курс посвящен вопросам численного поиска оптимума и оптимизационным алгоритмам. При описании оптимизационных алгоритмов часто используют стандартные формы представления задач. В качестве такой формы мы будем использовать следующую:

Найти	min F (x)
	xÎ	Rn	=			=
при ограничениях i		(x)			i
	c		³	0,		1, 2,..., m¢;
	i	(x)		0,	i	= +
	c					m¢ 1,...,m;

Классификация оптимизационных задач

Подавляющее большинство оптимизационных задач, возникающих на практике, приводятся к стандартному виду. Даже те задачи, которые сами по себе в эти рамки не укладываются, часто могут быть сведены к последовательности стандартных. Однако существование столь универсальной формы представления вовсе не означает, что различиями между отдельными задачами следует пренебрегать.

Наоборот, имея дело с конкретной постановкой, всегда надо постараться использовать ее особенности для того, чтобы организовать поиск решения самым эффективным образом. К примеру, усилия можно сэкономить, отказавшись от каких-топроверок, необходимых в общем случае, но лишних в конкретном, или избежав повторных вычислений величин, являющихся константами.

Рассмотрим классификацию разнообразных задач по тем их особенностям, которые наиболее существенны для выбора алгоритма решения.

Постановка задачи оптимизации

Вначале обсудим весьма широкий класс задач,

именуемых нелинейными непрерывными задачами

условной оптимизации (NCP).

Ставятся они следующим образом:

Задача NCP.	min F (x)
	xÎ	Rn		0,	i	1, 2,..., m¢;
Найти	c (x)
при ограничениях i			=			=
		(x)	³	0,	i	= +
	i
	c					m¢ 1,...,m;

Произвольную точку х, удовлетворяющую всем ограничениям NCP, будем называть допустимой. Множества всех допустимых точек называют допустимой областью.

8	Примечание. NCP - Nonlinear Continuous Problem

Классификация оптимизационных задач

Класс задач NCP разбивают на подклассы, и делается это по ряду признаков, существенных для выбора алгоритма и метода решения.

Типы функций	Типы ограничений
Функция одной переменной	Ограничения отсутствуют
Линейная функция	Простые ограничения на
	переменные
Сумма квадратов линейных	Линейные функции
функций
Квадратичная форма	Линейные функции с
	разреженной
	матрицей коэффициентов
Сумма квадратов нелинейных	Гладкие нелинейные функции
функций
Гладкая нелинейная функция	Гладкие нелинейные функции с
	разреженной матрицей Якоби
Нелинейная функция с	Негладкие нелинейные
9 разреженной матрицей Гессе	функции
Негладкая нелинейная функция

Классификация оптимизационных задач

Определим, что понимается под «решением» задачи NCP, и выясним, какими свойствами оно обладает.

Мы будем называть решением NCP точку локального минимума целевой функции в допустимой области, т. е. точку, удовлетворяющую ограничениям задачи и отличающуюся тем, что между значениями целевой функции в ней и в соседних допустимых точках имеются специфические отношения.

Формальные определения звучат следующим образом.

studfiles.net

Презентация на тему: МЕТОДЫ ОПТИМИЗАЦИИ

8.ЦЕЛОЧИСЛЕННОЕ

ЛИНЕЙНОЕ

ПРОГРАММИРОВАНИЕ

8.1. ВВЕДЕНИЕ

Целочисленное линейное программирование (ЦЛП) ориентировано на решение задач линейного программирования, в которых все или некоторые переменные должны принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На сегодня не существует надежных вычислительных алгоритмов решения таких задач.

В настоящей главе рассматриваются сначала примеры задач целочисленного программирования, а затем методы их решения.

6.2. ПРИМЕРЫ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Рассмотрим сначала простые практические задачи, которые сводятся к задачам ЦЛП, затем обратимся к более сложным. Для удобства задачи, в которых все переменные должны быть целочисленными, называются полностью целочисленными, а задачи, в которых лишь некоторые переменные должны принимать целочисленные значения, — частично-целочисленными.

Пример 6.2-1.(Распределение капиталовложений)

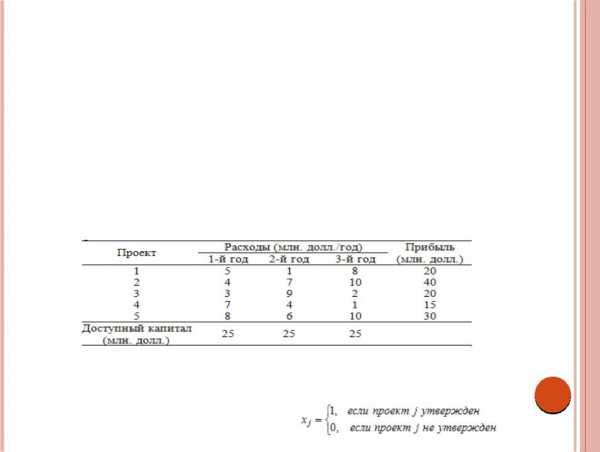
Оценивается пять проектов с точки зрения их возможного финансирования на предстоящий трехлетний период. Следующая таблица содержит ожидаемую прибыль от реализации каждого проекта и распределение необходимых капиталовложений по годам.

Предполагается, что каждый утвержденный проект будет реализован за трехлетний период. Необходимо определить совокупность проектов, которой соответствует максимум суммарной прибыли.

Задача сводится к решению типа "да - нет" относительно каждого проекта. Определим двоичные переменные хj:

Задача ЦЛП будет записана следующим образом. Максимизировать

z = 20х1 + 40х2 + 20х3 + 15х4 + 30х5 при ограничениях

5x1 + 4х2 + 3х3 + 7х4 + 8х5 25,х1 + 7х2 + 9х3 + 4х4 + 6x5 25, 8x1 + 10х2 + 2х3 +x4 + 10x5 25,х1,х2,х3,х4,x5 = 0 или 1.

Оптимальным целочисленным решением является х1 =х2 =х3 =х4 = 1,х5 = 0 сz = 95 (млн. долл.). Это решение означает, что необходимо выбрать для финансирования все проекты, кроме пятого.

Интересно сравнить решение данной задачи ЦЛП с решением "обычной" задачи ЛП с теми же ограничениями, но без условия целочисленности переменных. Задача линейного программирования получается в результате замены условия хj = 0 или 1 на ограничение 0хj 1 для всех

j. Эта задача имеет решениех1 = 0.5789,х2 =х3 =х4 = 1,х5 = 0.7368 иz =

108.68 (млн. долл.). Такое решение с точки зрения целочисленной задачи лишено смысла, так как две переменные принимают дробное значение. Можно было бы попытаться округлить полученный результат, что привело бы к х1 =х5 = 1. Полученное при этом решение является

недопустимым, так как нарушаются ограничения задачи. Более существенным в этой ситуации является то, что округление применять нельзя, так какхj представляет решение типа "да - нет", для которого

дробные значения лишены смысла.

8.3.МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Методы решения задач целочисленного линейного программирования основаны на использовании вычислительных возможностей методов линейного программирования. Обычно алгоритмы целочисленного программирования включают три шага.

Шаг 1. "Ослабление" пространства допустимых решений задачи целочисленного линейного программирования путем замены любой двоичной переменной y непрерывным ограничением 0у 1 и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача линейного программирования.

Шаг 2. Решение задачи линейного программирования и определение ее оптимального решения.

Шаг 3. Имея полученное (непрерывное) оптимальное решение, добавляем специальные ограничения, которые итерационным путем изменяют пространство допустимых решений задачи линейного программирования таким образом, чтобы, в конечном счете, получилось оптимальное решение, удовлетворяющее требованиям целочисленности.

Разработаны два общих метода генерирования специальных ограничений, о которых идет речь при реализации шага 3.

Метод ветвей и границ.

Метод отсекающих плоскостей.

Хотя ни один из упомянутых методов не дает надежных результатов при решении задачи целочисленного линейного программирования, опыт вычислений свидетельствует, что метод ветвей и границ более успешно решает задачу, чем метод отсекающих плоскостей.

Метод ветвей и границ

Основы этого метода объясним на численном примере.

Пример 6.3-1

Рассмотрим следующую задачу целочисленного линейного программирования.

Максимизировать

z = 5х1 + 4х2

при ограничениях

х1 +х2 5, 10x1 + 6х2 45,х1,х2 0 и целые.

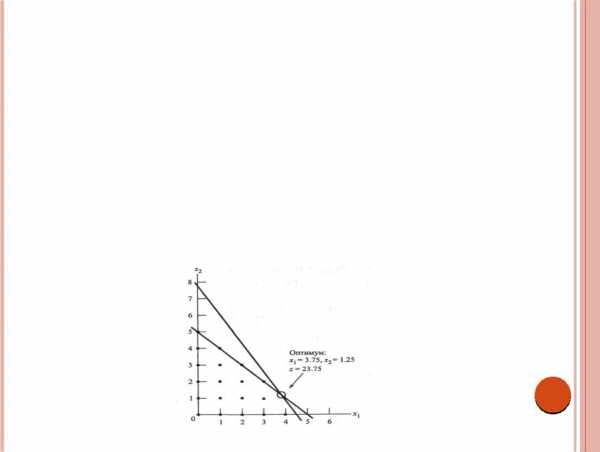
На рис. 6.6 пространство допустимых решений задачи целочисленного линейного программирования представлено точками. Соответствующая начальная задача линейного программирования (обозначим ее ЛП0)

получается путем отбрасывания условий целочисленности. Ее оптимальным решением будет х1 = 3.75,х2= 1.25 иz = 23.75.

Так как оптимальное решение задачи ЛП0 не удовлетворяет условия целочисленности, метод ветвей и границ изменяет пространство решений задачи линейного программирования так, что, в конечном счете, получается оптимальное решение задачи целочисленного линейного программирования. Для этого сначала выбирается одна из целочисленных переменных, значение которой в оптимальном решении задачи ЛП0 не является целочисленным. Например, выбирая х1 (= 3.75),

замечаем, что область 3 < х1 < 4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений переменнойх1 и, следовательно, может

быть исключена из рассмотрения, как бесперспективная. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами линейного программирования ЛП1 и ЛП2, которые определяются следующим образом:

пространство допустимых решений ЛП1 = пространство допустимых решений ЛП0 + (х1 3),

пространство допустимых решений ЛП2 = пространство допустимых решений ЛП0 + (х1 4).

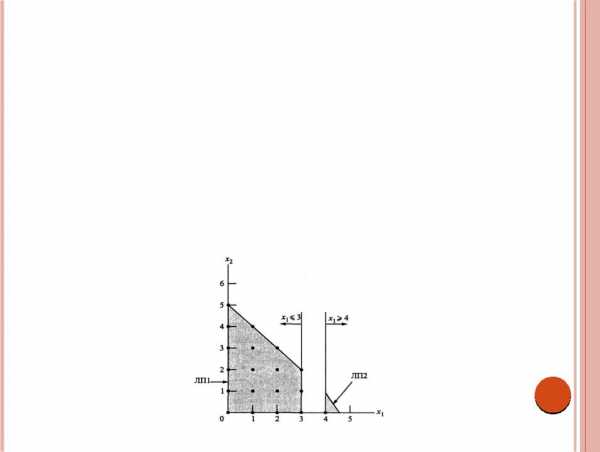
На рис. 6.7 изображены пространства допустимых решений задач ЛП1 и ЛП2. Оба пространства содержат все допустимые решения исходной задачи ЦЛП. Это означает, что задачи ЛП1 и ЛП2 "не потеряют" решения начальной задачи ЛП0.

Если мы продолжим разумно исключать из рассмотрения области, не содержащие целочисленных решений (такие, как 3 <х1 < 4), путем введения

надлежащих ограничений, то в конечном счете получим задачу линейного программирования, оптимальное решение которой удовлетворяет требованиям целочисленности. Другими словами, будем решать задачу ЦЛП путем решения последовательности непрерывных задач линейного программирования.

Новые ограничения х1 3 их1 4 взаимоисключаемы, так что задачи ЛП1 и

ЛП2 необходимо рассматривать как независимые задачи линейного программирования, что и показано на рис. 6.8. Дихотомизация задач ЛП — основа концепции ветвления в методе ветвей и границ. В этом случаех1

называется переменной ветвления.

Рис. 6.8

Оптимальное решение задачи ЦЛП находится в пространстве допустимых решений либо задачи ЛП1, либо ЛП2. Следовательно, обе подзадачи должны быть решены. Выбираем сначала задачу ЛП1 (выбор произволен), имеющую

Максимизировать z =5х1 + 4х2 при ограничениях

х1 +х2 5, 10x1 + 6х2 45,х1 3,

х1,х2 0.

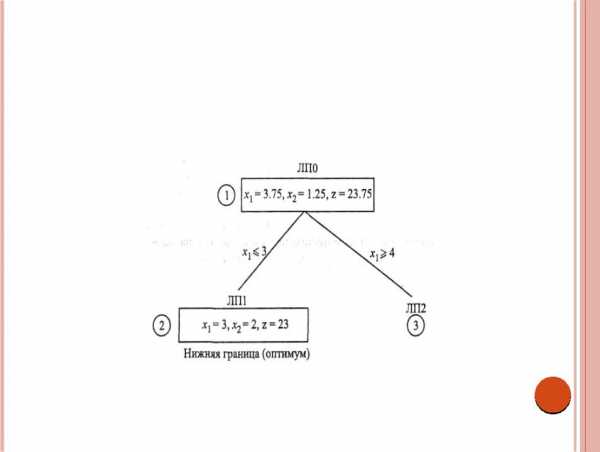
Оптимальным решением задачи ЛП1 (которое можно получить с помощью метода решения задач с ограниченными переменными, изложенного в разделе 7.5.2) является х1 = 3,х2 = 2 и

z = 23.

Оптимальное решение задачи ЛП1 удовлетворяет требованию целочисленности переменных х1 их2. В этом случае говорят, что задача ЛП1 прозондирована. Это означает,

что задача ЛП1 не должна больше зондироваться, так как она не может содержать лучшего решения задачи ЦЛП.

Мы не можем в этой ситуации оценить качество целочисленного решения, полученного из рассмотрения задачи ЛП1, ибо решение задачи ЛП2 может привести к лучшему целочисленному решению (с большим значением целевой функции z). Пока мы можем лишь сказать, что значение z = 23 является нижней границей оптимального (максимального) значения целевой функции исходной задачи ЦЛП. Это значит, что любая нерассмотренная подзадача, которая не может привести к целочисленному решению с большим значением целевой функции, должна быть исключена из рассмотрения, как бесперспективная. Если же нерассмотренная подзадача может привести к лучшему целочисленному решению, то нижняя граница должна быть надлежащим образом изменена.

При значении нижней границы z = 23 исследуем задачу ЛП2 (единственную оставшуюся нерассмотренную подзадачу). Так как в задаче ЛП0 оптимальное значение целевой функции равно 23.75 ивсе ее коэффициенты являются целыми числами, то невозможно получить целочисленное решение задачи ЛП2 (пространство решений которой более узко, чем в задаче ЛП0), которое будет лучше имеющегося. В результате мы отбрасываем подзадачу ЛП2 и считаем еепрозондированной.

Реализация метода ветвей и границ завершена, так как обе подзадачи ЛП1 и ЛП2 прозондированы (рассмотрение первой привело к нахождению целочисленного решения, а

Остались без ответа два вопроса, связанные с реализацией описанной вычислительной процедуры.

Можно ли было в задаче ЛП0 выбрать переменную х2 в качествепеременной ветвления вместох1?

Можно ли было при выборе подзадачи для зондирования решить сначала задачу ЛП2 вместо ЛП1?

Ответы на оба вопроса положительные. Однако последующие вычисления могут значительно отличаться.

Последовательность решения подзадач, показанная на рис. 6.9 (ЛП0, ЛП2, ЛП4, ЛП3, ЛП6, ЛП5, ЛП1), является наихудшей; тем не менее, она встречается на практике. Этот пример указывает на основную слабость метода ветвей и границ: как выбирать следующую подзадачу для исследования и как выбирать для нее переменную ветвления?

В процессе решения, представленного на рис. 6.8, мы случайно наткнулись на хорошую нижнюю границу значений целевой функции на самой первой подзадаче ЛП1, что позволило прозондировать ЛП2 без детальных исследований и закончить вычисления. По существу, мы завершили вычисления, решив лишь одну подзадачу. В процессе решения, представленном на рис. 6.9, мы были вынуждены исследовать семь подзадач, и лишь тогда завершились вычисления метода ветвей и границ. Хотя имеются эвристические соображения, позволяющие "угадать", какая из ветвей может привести к улучшенному решению задачи ЦЛП, не существует строгой теории, которая всегда обеспечивала бы надежные результаты.

Теперь сформулируем алгоритм метода ветвей и границ в общем случае. Предположим, что рассматривается задача максимизации. Зададим нижнюю границу оптимального значения целевой функции z задачи ЦЛП равной- .Положимi = 0.

studfiles.net

Методы оптимизации - презентация, доклад, проект

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: [email protected]

Мы в социальных сетях

Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам

ВКонтакте >

Что такое Myslide.ru?

Myslide.ru - это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.

Для правообладателей >

myslide.ru