Градиентные методы оптимизации. Метод наискорейшего спуска. Градиентные методы оптимизации

Градиентные методы оптимизации. Метод наискорейшего спуска.

Метод градиентного спуска.

Направление наискорейшего спуска соответствует направлению наибольшего убывания функции. Известно, что направление наибольшего возрастания функции двух переменных u = f(x, у) характеризуется ее градиентом:

где e1, е2 — единичные векторы (орты) в направлении координатных осей. Следовательно, направление, противоположное градиентному, укажет направление наибольшего убывания функции. Методы, основанные на выборе пути оптимизации с помощью градиента, называются градиентными.

Идея метода градиентного спуска состоит в следующем. Выбираем некоторую начальную точку

вычисляем в ней градиент рассматриваемой функции. Делаем шаг в направлении, обратном градиентному:

Процесс продолжается до получения наименьшего значения целевой функции. Строго говоря, момент окончания поиска наступит тогда, когда движение из полученной точки с любым шагом приводит к возрастанию значения целевой функции. Если минимум функции достигается внутри рассматриваемой области, то в этой точке градиент равен нулю, что также может служить сигналом об окончании процесса оптимизации.

Метод градиентного спуска обладает тем же недостатком, что и метод покоординатного спуска: при наличии оврагов на поверхности сходимость метода очень медленная.

В описанном методе требуется вычислять на каждом шаге оптимизации градиент целевой функции f(х):

Формулы для частных производных можно получить в явном виде лишь в том случае, когда целевая функция задана аналитически. В противном случае эти производные вычисляются с помощью численного дифференцирования:

При использовании градиентного спуска в задачах оптимизации основной объем вычислений приходится обычно на вычисление градиента целевой функции в каждой точке траектории спуска. Поэтому целесообразно уменьшить количество таких точек без ущерба для самого решения. Это достигается в некоторых методах, являющихся модификациями градиентного спуска. Одним из них является метод наискорейшего спуска. Согласно этому методу, после определения в начальной точке направления, противоположного градиенту целевой функции, решают одномерную задачу оптимизации, минимизируя функцию вдоль этого направления. А именно, минимизируется функция:

Для минимизации можно использовать один из методов одномерной оптимизации. Можно и просто двигаться в направлении, противоположном градиенту, делая при этом не один шаг, а несколько шагов до тех пор, пока целевая функция не перестанет убывать. В найденной новой точке снова определяют направление спуска (с помощью градиента) и ищут новую точку минимума целевой функции и т. д. В этом методе спуск происходит гораздо более крупными шагами, и градиент функции вычисляется в меньшем числе точек. Разница состоит в том, что здесь направление одномерной оптимизации определяется градиентом целевой функции, тогда как покоординатный спуск проводится на каждом шаге вдоль одного из координатных направлений.

Метод наискорейшего спуска для случая функции двух переменных z = f(x,y).

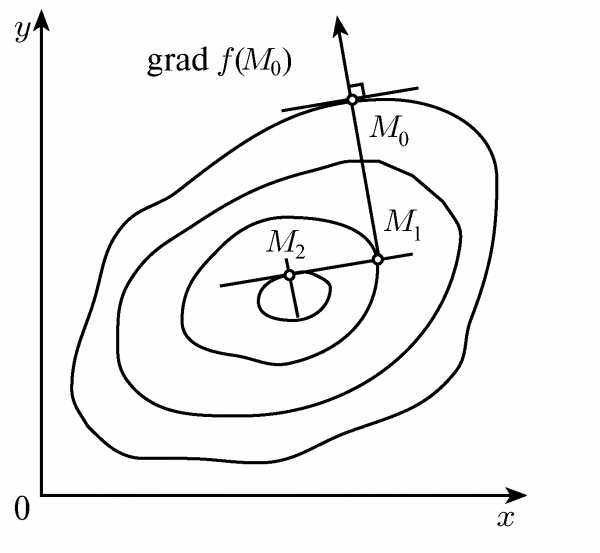
Во-первых, легко показать, что градиент функции перпендикулярен касательной к линии уровня в данной точке. Следовательно, в градиентных методах спуск происходит по нормали к линии уровня. Во-вторых, в точке, в которой достигается минимум целевой функции вдоль направления, производная функции по этому направлению обращается в нуль. Но производная функции равна нулю по направлению касательной к линии уровня. Отсюда следует, что градиент целевой функции в новой точке перпендикулярен направлению одномерной оптимизации на предыдущем шаге, т. е. спуск на двух последовательных шагах производится во взаимно перпендикулярных направлениях.

studfiles.net

Градиентные методы оптимизации — Мегаобучалка

Метод релаксации

Алгоритм метода заключается в отыскании осевого направления, вдоль которого целевая функция уменьшается наиболее сильно ( при поиске минимума). Рассмотрим задачу безусловной оптимизации

(3.6)

Для определения осевого направления в начальной точке поиска из области определяются производные , , по всем независимым переменным. Осевому направлению соответствует наибольшая по модулю производная .

Пусть – осевое направление, т.е. .

Если знак производной отрицательный, функция убывает в направлении оси, если положительный – в обратном направлении:

В точке вычисляют . По направлению убывания функции производится один шаг, определяется и в случае улучшения критерия шаги продолжаются до тех пор, пока не будет найдено минимальное значение по выбранному направлению. В этой точке вновь определяются производные по всем переменным, за исключением тех, по которой осуществляется спуск. Снова находится осевое направление наиболее быстрого убывания , по которому производятся дальнейшие шаги и т.д.

Эту процедуру повторяют до тех пор, пока не достигается оптимальная точка, при движении из которой по любому осевому направлению дальнейшего убывания не происходит. На практике критерием окончания поиска служит условие

(3.7)

которое при превращается в точное условие равенства нулю производных в точке экстремума. Естественно условие (3.7) может быть использовано только в том случае, если оптимум лежит внутри допустимой области изменения независимых переменных . Если же оптимум попадает на границу области , критерий типа (3.7) непригоден и вместо него следует применять положительности всех производных по допустимым осевым направлениям.

Алгоритм спуска для выбранного осевого направления может быть записан так

(3.8)

где -значение варьируемой переменной на каждом шаге спуска;

- величина k+1 шага, которая может изменяться в зависимости от номера шага:

– функция знака z;

- вектор точки, в которой последний раз производилось вычисление производных ;

Знак “+” в алгоритме (3.8) принимается при поиске max I, а знак “-” – при поиске min I.Чем меньше шаг h., тем больше количество вычислений на пути движения к оптимуму. Но при слишком большой величине h вблизи оптимума может возникнуть зацикливание процесса поиска. Вблизи оптимума необходимо, чтобы выполнялось условие h<E, где E- заданная погрешность определения положения оптимума.

Простейший алгоритм изменения шага h состоит в следующем. В начале спуска задается шаг , равный например, 10% от диапазона d; изменения с этим шагом производится спуск по выбранному направлению до тез пор, пока выполняется условие для двух последующих вычислений

При нарушении условия на каком-либо шаге направление спуска на оси изменяется на обратное и спуск продолжается из последней точки с уменьшенной вдвое величиной шага.

Формальная запись этого алгоритма следующая:

(3.9)

В результате использования такой стратегии ша спуска будет уменьшатся в районе оптимума по данному направлению и поиск по направлению можно прекратить, когда станет меньше E.

Затем отыскивается новое осевое направление начальный шаг для дальнейшего спуска, обычно меньший пройденного вдоль предыдущего осевого направления. Характер движения в оптимуме в данном методе показан на рисунке 3.4.

Рисунок 3.5 – Траектория движения к оптимуму в методе релаксации

Улучшение алгоритма поиска по данному методу может быть достигнуто путем применения методов однопараметрической оптимизации. При этом может быть предложена схема решения задачи:

Шаг 1. – осевое направление,

; , если ;

, если ;

или

Шаг 2. – новое осевое направление;

и т.д.

Метод градиента

В этом методе используется градиент функции . Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам (рис. 6.5)

Рисунок 3.6 – Градиент функции

Направление градиента – это направление наиболее быстрого возрастания функции (наиболее крутого “склона” поверхности отклика). Противоположное ему направление (направление антиградиента) – это направление наибыстрейшего убывания (направление наискорейшего “спуска” величин ).

Проекция градиента на плоскость переменных перпендикулярна касательной к линии уровня , т.е. градиент ортогонален к линиям постоянного уровня целевой функции (рис. 3.6).

Рисунок 3.7 – Траектория движения к оптимуму в методе

градиента

В отличие от метода релаксации в методе градиента шаги совершаются в направлении наибыстрейшего уменьшения (увеличения) функции .

Поиск оптимума производится в два этапа. На первом этапе находятся значения частных производных по всем переменным , которые определяют направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в направлении градиента при поиске максимума или в противоположном направлении – при поиске минимума.

Если аналитическое выражение неизвестно, то направление градиента определяется поиском на объекте пробных движений. Пусть начальная точка. Дается приращение величина , при этом . Определяют приращение и производную

Аналогично определяют производные по остальным переменным. После нахождения составляющих градиента пробные движения прекращаются и начинаются рабочие шаги по выбранному направлению. Причем величина шага тем больше, чем больше абсолютная величина вектора .

При выполнении шага одновременно изменяются значения всех независимых переменных. Каждая из них получает приращение, пропорциональное соответствующей составляющей градиента

, (3.10)

или в векторной форме

, (3.11)

где – положительная константа;

“+” – при поиске max I;

“-” – при поиске min I.

Алгоритм градиентного поиска при нормировании градиента (деление на модуль) применяется в виде

; (3.12)

(3.13)

определяет величину шага по направлению градиента.

Алгоритм (3.10) обладает тем достоинством, что при приближении к оптимуму длина шага автоматически уменьшается. А при алгоритме (3.12) стратегию изменения можно строить независимо от абсолютной величины коэффициента.

В методе градиента каждый разделяется один рабочий шаг, после которого вновь вычисляются производные, определяется новое направление градиента и процесс поиска продолжается (рис. 3.5).

Если размер шага выбран слишком малым, то движение к оптимуму будет слишком долгим из-за необходимости вычисления в очень многих точках. Если же шаг выбран слишком большим, в район оптимума может возникнуть зацикливание.

Процесс поиска продолжается до тех пор, пока , , не станут близки к нулю или пока не будет достигнута граница области задания переменных.

В алгоритме с автоматическим уточнением шага величину уточняют так, чтобы изменение направления градиента в соседних точках и улучшающей последовательности составляло (рис 3.7)

Рисунок 3.8 – Изменение направления градиента в соседних

точках

Должно быть

где – скалярное произведение векторов.

;

Если ;

если ;

если ,

где .

Критерии окончания поиска оптимума:

; (3.14)

, ; (3.15)

; (3.16)

; (3.17)

где – норма вектора.

Поиск завершается при выполнении одного из условий (3.14) – (3.17).

Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции . Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.

megaobuchalka.ru

Градиентный метод - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Градиентный метод - оптимизация

Cтраница 1

Градиентный метод оптимизации и его обобщения используют свойство градиента быть направленным в сторону максимального возрастания функции качества. [1]

Преимущества градиентного метода оптимизации по сравнению с методом случайного поиска возрастают в случае организации процесса спуска с переменным рабочим шагом. [2]

Общий недостаток градиентных методов оптимизации, за исключением, может быть, метода тяжелого шарика, состоит в том, что все они застревают в ближашце м локальном оптимуме, в область притяжения которого попадает выбранная начальная точка спуска. [3]

Цель работы: изучение градиентных методов оптимизации и практический поиск на ЦВМ таких значений некоторых параметров, которые обеспечивают минимум заданной функции. [4]

Алгоритм представляет собой аналог градиентных методов оптимизации для дискретного случая. [5]

Как учитывается система ограничений при использовании градиентных методов оптимизации. [6]

Значительное число весовых коэффициентов нейросетевой модели и медленная сходимость градиентного метода оптимизации затрудняют использование принципа регулирования на основе инверсных нейросетевых моделей, обучаемых в режиме реального времени. Вычислительные ( временные) затраты на обучение нейросетевой модели могут быть уменьшены путем применения обобщенного метода обучения на предварительном этапе инициализации настраиваемых параметров нейросетевой модели. Кроме того, для увеличения скорости сходимости может быть использован метод Гаусса - Ньютона. [8]

На рис. 7.4 приведена обобщенная структурная схема устройства идентификации, реализующая градиентный метод оптимизации. [10]

В составе типового комплекта ряда аналоговых машин имеется автоматический оптимизатор, реализующий, как правило, градиентный метод оптимизации. При отсутствии оптимизатора кинетические параметры, устанавливаемые в аналоговой модели, варьируют вручную. При небольшом числе искомых параметров ( до 3 - 4) используют метод проб и ошибок при периодическом режиме счета. Метод заключается в последовательном приближении кривой решения, получаемой на машине, к экспериментальным данным. После достижения удовлетворительного совпадения расчетных и экспериментальных данных константы определяют по полученным настройкам аналоговых элементов, воспроизводящих соответствующие параметры. При большом числе определяемых параметров целесообразно использовать методы планирования экспериментов. [11]

Для решения задач регулирования разработки газоконденсатных месторождений при обратной закачке в пласт сухого газа эффективным представляется использование методики расчетов на основе градиентных методов оптимизации. [12]

Введение параметра е0 в алгоритмы А 2 и А 3 вызвано следующими причинами. Естественно, что в такой ситуации ( стандартной для градиентных методов оптимизации) целесообразно ограничивать число итерации. При этом наряду с условием малости изменения / на соседних итерациях альтернативно можно использовать меру отклонения и1 и и, как, например, это сделано выше. [13]

Проблеме беспоискового решения задач оптимизации посвящена большая литература. Это направление имеет ярко выраженный математический характер, так как математическая модель объекта предполагается известной и задача оптимизации сводится к задаче построения вычислительного алгоритма решения соответствующей вариационной задачи. В свою очередь среди итерационных методов выделяются градиентные методы, которые реализуют аналитически известный градиентный метод оптимизации. Именно эти методы и образуют основу для создания беспоисковых систем экстремального управления. [14]

Выше было указано, что для улучшения точности алгоритма Пао может быть применен градиентный алгоритм Ермольева. В данном пункте приводятся методические основы спектрального метода получения оптимальных программных управлений. Этот подход может считаться альтернативой градиентному методу Ермольева, поскольку он использует параметризацию функций управления, фазовых координат, функционалов качества, а также предполагает применение градиентного метода оптимизации. Кроме того, по неклассическим равновесиям безкоалиционной игры, спектральный подход обеспечивает получение решения в виде непрерывных функций, что, как будет показано на примере, может существенно улучшить значения показателей качества, а также может быть использовано для анализа динамики конфликта и его прогноза. [15]

Страницы: 1 2

www.ngpedia.ru

Условная оптимизация градиентным методом

В случае если решение задачи достигается на границе области допустимых решений (ОДР), то градиентные методы требуют модификации с целью поиска вдоль границы ОДР. Рассмотрим задачу поиска минимума для ограничений вида gi(X)  0. Пока представляющая точка находится в ОДР, поиск произво-дится по обычной схеме. Однако как только будет нарушено хотя бы одно ограничение, то процедуру поиска нужно менять. В этом случае одним из возможных способов движения является перемещение в направлении, противоположном направлению суммы градиентов тех функций gi(X), для которых в данной точке нарушаются ограничения. В этом случае траектория движения будет представлять собой зигзагообразную траекторию вдоль ограничения (рисунок 5.1).

Рисунок 5.1  Траектория движения при поиске экстремума

Для реализации такого способа алгоритмы, основанные на методе градиента с дроблением шага или наискорейшего спуска, должны быть изменены следующим образом:

1. После каждого рабочего шага в методе с дроблением шага (или малого рабочего шага в методе наискорейшего спуска) должно проверяться выполнение ограничений gi(Xk+1)  0 в новой точке Xk+1.

2. Если ограничения выполняются, то поиск происходит по обычной схеме.

3. Если хотя бы одно из ограничений нарушено, то дальнейший поиск ведется следующим образом:

а) для всех gi(X), которые стали положительными, составляется новый комплексный критерий 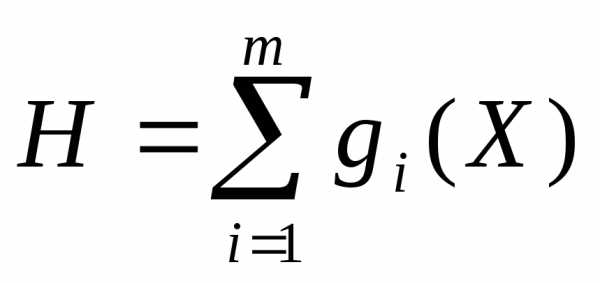, где m – число нарушенных ограничений.

б) вычисляется grad H так же, как и для F(X).

в) делается шаг в направлении grad Н до тех пор, пока все gi(X) не станут отрицательными (представляющая точка не войдет в ОДР).

4. Далее поиск происходит по обычной схеме до нового нарушения хотя бы одного из ограничений.

5.2 Порядок выполнения работы

5.2.1 Получить задание у преподавателя.

5.2.2 Написать программу поиска экстремума целевой функции заданным методом.

5.2.3 Для выданной задачи нелинейного программирования продемонст-рировать работу программы при различных стартовых точках.

Содержание отчета

5.3.1 Цель работы.

5.3.2 Исходное задание.

5.3.3 Решение задачи заданным методом.

5.3.4 Выводы по полученным результатам.

Контрольные вопросы

Куда направлен градиент скалярной функции?
Каково условие дробления параметра шага в градиентном методе с дроблением шага?
Каковы критерии остановки процесса поиска оптимума в градиентном методе?
В чем отличие метода наискорейшего спуска от градиентного метода с дроблением шага?
Какие методы могут использоваться для поиска значения параметра шага в методе наискорейшего спуска?
Как изменится основное расчетное выражение градиентных методов для определения следующей точки при решении задачи поиска максимума?
Как учесть ограничения при оптимизации с помощью градиентных методов?
Почему в задаче нелинейного программирования поисковый процесс необходимо начинать из нескольких разных точек?

studfiles.net

Решение задач многомерной оптимизации градиентными методами

1.Теория градиентного метода

Рассмотрим функцию трех переменных f(x, y, z). Вычислим частные производные: и составим с их помощью вектор, который называется градиентом функции.

Grad f(x, y, z) =

i, j, k - единичные векторы параллельные координатным осям (орты).

Частные производные характеризуют изменение функции по каждой независимой переменной в отдельности. Вектор градиента дает общее представление о поведении функции в окрестности точки (x, y, z). В направление градиента функция возрастает с максимальной скоростью. В обратном направлении, которое часто называют антиградиентным, функция убывает с максимальной скоростью.

Модуль градиента

определяет скорость возрастания и убывания целевой функции в направление градиента и антиградиента. В других направлениях целевая функция будет изменяться с меньшей скоростью. При переходе от одной точке к другой меняется как модуль градиента, так и его направление.

1.1 Метод градиентного спуска

Выбираем каким-либо способом начальную точку , выделяем в ней градиент целевой функции и сделаем небольшой шаг в антиградиентном направлении. В результате мы придем в точку, в которой целевая функция будет иметь меньшее значение. Во вновь полученной точке снова вычисляем градиент и снова делаем шаг в антиградиентном направлении. Продолжая этот процесс будем двигаться в сторону уменьшения целевой функции. Выбор направления движения позволяет надеяться, что продвижение к точке минимума в этом случае будет более быстрым, чем в методе покоординатного спуска.

Формулы для вычисления координат точек в методе градиентного спуска

Поскольку градиент - это вектор, а при выполнении каких-либо операций мы должны использовать однородные математические объекты, то вместо точки n-мерного пространства будем пользоваться понятием радиуса вектора этой точки

точка

радиус вектор

В общем виде, координата точки выражается через координату точки.

Формулы для вычисления частных производных можно получить только в том случае, если целевая функция задана аналитически.

В противном случае, эти производные вычисляются с помощью численного дифференцирования.

Поиск прекращается когда

1.2 Метод наискорейшегого спуска

При использовании градиентного спуска в задачах оптимизации основной объем вычислений приходится обычно на вычисление градиента целевой функции в каждой точке траектории спуска. Поэтому целесообразно уменьшить количество таких точек без ущерба для самого решения. Это достигается в методе наискорейшего спуска. Согласно этому методу, после определения в начальной точке антиградиентного направления, в этом направлении делают не один шаг, а двигаются до тех пор, пока целевая функция убывает, достигая таким образом минимума в некоторой точке. В этой точке снова определяют направление спуска (с помощью градиента) и ищут новую точку минимума целевой функции и т.д. В этом методе спуск происходит гораздо более крупными шагами и градиент функции вычисляется в меньшем числе точек.

Пример: целевая функция

начальная точка M0 = (2,3)

Подставим эти значения в целевую функцию:

Возьмем частную производную по и приравняв ее нулю, найдем величину шага, при котором мы приходим в точку минимума.

следовательно, точка - это точка минимума.

Повторяем процедуру, считая начальной точкой точку .

и т.д.

Удачный выбор начальной точки , может существенно сократить объем вычислительной работы.

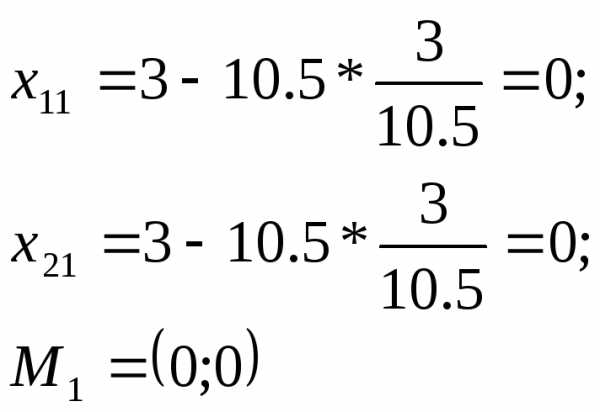
Проверим, является ли точка точкой минимума.

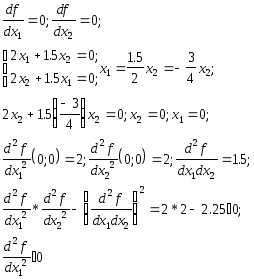
значит точка минимума.

Этот метод в литературе называется методом Коши.

studfiles.net

Градиентные методы оптимизации - Справочник химика 21

из "Методы кибернетики в химии и химической технологии 1968"

Градиентные методы оптимизации относятся к численным методам поискового типа. Эти методы универсальны, хорошо приспособлены для современных цифровых вычислительных машин и весьма эффективны в большинстве случаев поиска экстремального значения нелинейных функций с ограничениями и без них, а также, когда функция вообще аналитически неизвестна. Вследствие этого градиентные или поисковые методы широко применяются на практике. [c.126] Сущность указанных методов заключается в определении значений независимых переменных, дающих наибольшие изменения целевой функции. Обычно это достиг ается при движении вдоль градиента, ортогонального к контурной поверхности в данной точке. [c.126] Основным вопросом, решаемым в методах градиента, является определение направления градиентного вектора в базисной точке с тем, чтобы установить, как велик должен быть шаг движения по градиенту и как вести расчет. Нахождение величины шага в направлении X], Х2,. . Хп В значительной степени зависит от вида поверхности. Если шаг слишком мал, это потребует продолжительных расчетов. Если наоборот размеры шага слишком велики, можно проскочить оптимум. Размеры шага по каждой переменной Xi вычисляются из значений частных производных в базовой (начальной) точке. Только в базовой точке градиент строго ортогонален к поверхности. Если же шаги слишком велики в каждом /-м направлении, вектор из базисной точки не будет ортогонален к поверхности в новой точке. [c.127] Для нелинейной функции направление градиентного вектора зависит от точки на поверхности, в которой он вычисляется. [c.128] Несмотря на существующие между градиентными методами различия, последовательность операций при поиске оптимума в большинстве случаев одинакова и сводится к следующему а) выбирается базисная точка б) определяется направление движения от базисной точки в) находится размер шага г) определяется следующая точка поиска д) значение целевой функции в данной точке сравнивается с ее значением в предыдущей точке е) вновь определяется направление движения и т. д. до достижения оптимального значения. [c.128] Этот принцип без изменения переносится на любое число переменных, а также на любое число дополнительных условий. [c.128] Известно, что направление этого вектора (см. рис. 11-10) совпадает с направлением наиболее крутого возрастания величины/ . Противоположное ему направление — это направление наискорей-шего спуска , или, другими словами, наиболее крутого убывания величины F. [c.129] Эффективность метода крутого восхождения зависит от выбора масштаба переменных и вида поверхности отклика. Поверхность со сферическими контурами дает быстрое стягивание к оптимуму. [c.130] Метод крутого восхождения при наличии ограничений. При наличии ограничений на изменение параметров целевой функции базисная точка выбирается так, чтобы она лежала в пределах ограничений, и поиск начинают по методу крутого восхождения. После расчета следующей точки оценивается не произошло ли нарушения ограничений если нарушения нет, поиск продолжается. Когда какое-либо ограничение нарушено, производят расчет градиента в соответствии с учетом ограничений (см. ниже). [c.130] Может быть использован также метод согласно которому при одном нарушении ограничений точка возвращается на линию ограничений. Когда существует более чем одно ограничение, и в каждый момент времени новое ограничение нарушается, метод требует, чтобы точки были перенесены к новому ограничению. В этом методе принимается, что оптимум лежит на ограничении. [c.130] По методу Розенброка25 функция цели видоизменяется введением множителей. Всякий раз, как одно из переменных нарушает ограничения, множитель равен нулю, т. е. функция цели умножается на нуль и поэтому равна нулю. Если значения переменной находятся в пределах допустимого режима, множитель равен 1и целевая функция принимает ее полное значение. Однако, когда значения переменной снижаются до пределов, предписываемых пограничной зоной , множительный фактор изменяется параболически от О до 1 в пределах пограничной зоны и целевая функция изменяется от О до ее полного значения. [c.130] Начальные координаты поиска Хю=2 и Х2о=2 (точка М, рис. 11-11). [c.131] Последняя из полученных точек указывает, что мы вновь перешли минимум, так как г/а больше у . [c.132] Вновь изменяем направление (точка Q), как показано на рис. 11-11, и продолжаем подобные расчеты, пока не достигнем оптимальных условий или, в нашем случае, минимального значения у. [c.132] Пример П-7 2. Найти минимум значения функции лг + лггпри наличии ограничения л 1 + Х2 4. Начальная точка имеет координаты л 1 = 3 и д 2=1. Дать графическую интерпретацию метода. [c.132] Находим частные производные целевой функции по переменным хх и Х2. [c.132] Следовательно, отношение изменения хг к изменению равно 2Xi Для начальной точки получим 1/[(2) (3)]=1/6. [c.132] НИИ или вправо от нее, возможно решение задачи. Начальная точка есть точка 1 и следующая точка есть точка 2. На графике видно нарушение ограничений и точка 3 возвращает нас обратно в допустимую область. Решением задачи являются значения переменных д 1=0,50 и 2=3,5. [c.133] Рассмотренный метод означает движение из нежелательной области ортогонально к ограничению целевой функции. [c.133]

Вернуться к основной статье

chem21.info

Градиентная метода - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Градиентная метода - оптимизация

Cтраница 1

Градиентные методы оптимизации относятся к численным методам поискового типа. [2]

Градиентные методы оптимизации относятся к численным методам поискового типа. Эти методы универсальны, хорошо приспособлены для современных цифровых вычислительных машш и весьма эффективны в большинстве случаев поиска экстремального значения нелинейных ( функций с ограничениями и бев них, а также, когда функция вообще аналитически неизвестна. Вследствие этого поисковые методы широко применяются на практике. [6]

В задачах с нелинейными функциями многих переменных часто используется метод множителей Лагранжа, динамическое программирование и градиентные методы оптимизации. При математическом моделировании работу транспортно-складской системы описывают с помощью методов статистического моделирования, например метода Монте-Карло. [7]

Производные для функции дели / не всегда можно вычислить в явной форме, а значит, и использовать градиентные методы оптимизации. Такая ситуация возникает, когда функционал разрывен или недифференцируем, например для функционалов, которые формулируются с помощью логических операций. [8]

В рассматриваемой экстремальной задаче функционал является нелинейной функцией независимых переменных. Поэтому задача относится к задачам нелинейного программирования. Вышерассмотренные градиентные методы оптимизации оказались непригодными для поиска глобального экстремума, так как часть переменных (, dBH, Zi и Zz) дискретна и, кроме того, имеются локальные экстремумы. В каждом узле рассчитывалось значение функционала, при этом отбрасывались из расчета узлы, не удовлетворявшие вышеприведенным ограничениям, налагаемым на зависимые и независимые переменные. [9]

Страницы: 1

Градиентные методы оптимизации. Метод наискорейшего спуска. Градиентные методы оптимизации