Лекция № 8. Численные методы безусловной оптимизации. Численные методы оптимизации

Численные методы решения задач оптимизации

Численное решение задач оптимизации

Актуализация опорных знаний.

Численные методы одномерной оптимизации.

Метод дихотомии.

Метод золотого сечения.

Метод Фибоначчи.

Встроенные функции MathCAD для поиска локального минимума/максимума.

Пример использования.

Условный экстремум.

Экстремум функции многих переменных.

Контрольные вопросы.

Литература

Царегородцева, В. В. Вычислительная математика: лабораторный практикум по курсам «Численные методы» и «Вычислительная математика» для студентов всех специальностей и направлений подготовки / В. В. Царегородцева, Г. И. Севодина; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2014. – 78 с.

Актуализация опорных знаний

Постановка задачи оптимизации сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) одной или многих переменных.

Оптимизируемую функцию f(x) называют целевой функцией, или критерием оптимальности.

Рассмотрим задачу поиска минимального значения функции f(x) одной переменной и запишем эту задачу следующим образом:

Значение х*, определяющее минимум целевой функции, называется оптимальным.

Отметим, что задачу максимизации можно заменить эквивалентной ей задачей минимизации или наоборот: минимальное значение функции равно максимальному значению функции , взятому с противоположным знаком, т. е.

Если на переменную х или некоторые функции, характеризующие качественные свойства объекта, накладываются ограничения в виде равенств или неравенств, то такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.

На заданной области определения независимой переменной у функции может быть несколько локальных минимумов и максимумов, а также по одному глобальному минимуму и максимуму (рисунок 1). На отрезке – точки локального максимума, а – локального минимума. В точке реализуется глобальный максимум, а в точке – глобальный минимум.

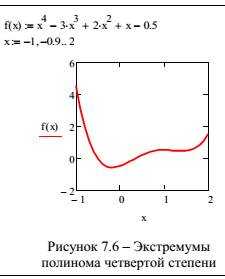
Рисунок 1 – Экстремумы функции

Как известно, в курсе математического анализа для определения точки оптимума используют необходимое условие существования экстремума – равенство нулю первой производной функции одной переменной или равенство нулю частных производных для функции многих переменных. Однако при решении практических задач вычисление производных функции бывает затруднительно или невозможно, если функция выражена неявно. В этих случаях приходится использовать аппарат численных методов для нахождения приближенного значения решения задачи с заранее заданной степенью точности.

На данном занятии рассматриваются только некоторые безградиентные методы одномерного поиска экстремума.

Численные методы одномерной оптимизации

К численным методам одномерной оптимизации относятся методы:

- дихотомического деления,

- золотого сечения,

- чисел Фибоначчи,

- полиномиальной аппроксимации

и ряд их модификаций.

Основная идея этих методов заключается в разбиении интервала поиска экстремума на несколько частей в определённом отношении, вычислении функции в этих точках и выборе наименьшего значения. После этого интервал поиска сужается, и процедура повторяется. Критерием окончания поиска может служить соотношение:

т. е. длина нового, суженного интервала поиска экстремума по модулю на i-й итерации меньше или равна заданной степени точности решения задачи.

Метод дихотомии

Пусть задан отрезок , на котором имеется один минимум (в общем случае нечетное число минимумов). Согласно методу дихотомического деления (рисунок 2, а) отрезок делят пополам и в точках, отстоящих от центра с отрезка на величину допустимой погрешности , рассчитывают значения целевой функции и .

Рисунок 2 – Одномерная минимизация: а – дихотомическое деление; б – золотое сечение

Если окажется, что , то минимум находится на отрезке , если , то минимум – на , если ) – на . Таким образом, на следующем шаге вместо отрезка нужно исследовать суженный отрезок , или . Шаги повторяются, пока длина отрезка не уменьшится до величины погрешности . Таким образом, требуется не более n шагов, где n – ближайшее к целое значение, но на каждом шаге целевую функцию следует вычислять дважды.

Пример 1. Пусть задана функция одной переменной вида

Найти её минимальное значение на интервале [2, 5 ] с заданной точностью методом дихотомического деления.

Программа, реализованная в системе MathCAD, приведена на рисунке 3. Для получения результата с заданной степенью точности потребовалось выполнить 19 итераций.

Метод золотого сечения

В соответствии с методом золотого сечения (рис. 2, б) внутри отрезка выделяют две промежуточные точки и на расстоянии от его конечных точек, где – длина отрезка. Затем вычисляют значения целевой функции в точках и . Если , то то минимум находится на отрезке , если , то на отрезке , если , то на отрезке .

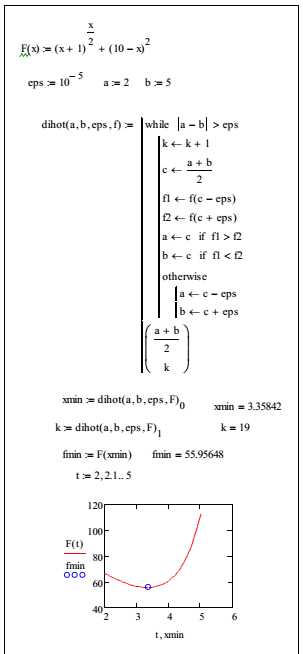
Рис. 3. Программа поиска минимума методом дихотомического деления

Следовательно, вместо отрезка теперь можно рассматривать отрезок , или , т. е. длина отрезка уменьшилась не менее чем в

раз. Если подобрать значение α так, чтобы в полученном отрезке меньшей длины одна из промежуточных точек совпадала с промежуточной точкой от предыдущего шага, т. е. в случае выбора отрезка точка будет совпадать с точкой , а в случае выбора отрезка точка – с точкой , то это позволит сократить число вычислений целевой функции на всех шагах (кроме первого) в 2 раза.

Условие получения такого значения формулируется следующим образом:

откуда с учетом (*) имеем = 0,382. Это значение и называют золотым сечением.

Алгоритм поиска экстремума складывается из следующих этапов:

1) вычисляются значения функции на концах исходного интервала ;

2) вычисляются промежуточные точки интервала по формулам:

а также значения функции в этих точках;

3) по найденным значениям функции определяется её минимальное значение на интервале;

4) в зависимости от того в какой точке расположен минимум ( или ) определяется подынтервал, в котором локализован минимум – или ;

5) в новом интервале определяется точка по одной из формул п. 2 и итерационный процесс поиска продолжается с п. 3 до тех пор пока не будет достигнут критерий окончания поиска, например, такой:

Пример 2. Для функции (см. пример 1) найти минимальное значение методом золотого сечения. Программа поиска решения приведена на рисунке 4. Здесь интервал поиска задан вектором с, а точки деления интервала в заданном соотношении заданы вектором z.

Процедура отсечения интервала задаётся функцией , в которой на каждой итерации из четырёх значений функции выбирается минимальное, а затем определяется новый соответствующий подынтервал. Координаты точек деления в новом интервале и соответствующие значения целевой функции находятся в процедуре-функции ming(eps, c, f).

Здесь задаётся число eps – точность решения задачи, вектор c и функция f. Как видно из приведенных результатов, для достижения заданной точности в методе золотого сечения требуется сделать 28 итераций. Этот метод гарантирует нахождение экстремума в самых неблагоприятных для поиска областях, однако обладает медленной сходимостью.

Рис.4. Метод золотого сечения

Метод Фибоначчи

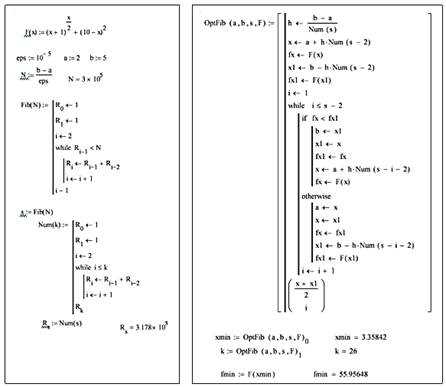
Рис. 5. Метод Фибоначчи

Встроенные функции MathCAD для поиска локального минимума/максимума

Для численного решения задач поиска локального максимума и минимума в MathCAD имеются встроенные функции Minerr, Minimize и Maximize.

Чтобы найти глобальный максимум (или минимум), требуется сначала просканировать с некоторым шагом рассматриваемую область и вычислить все локальные значения и потом выбрать из них наибольший (наименьший). Другим вариантом будет простое сканирование с вычислением значений функции, позволяющее выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности.

Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно:

Пример использования

Всем аргументам функции предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления локальных экстремумов функций одной перемен-ной показаны на рисунке 7.7.

Если начальное приближение выбрать удачно, то итерационный процесс алгоритма сойдется к экстремуму функции, а если выбрать его вдали от него, на участке, где функция неограниченно возрастает, численный метод вообще не справится с задачей, выдавая сообщение об ошибке. Например, при поиске максимума (см. рисунок 7) начальное приближение (x = 10) выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения функции.

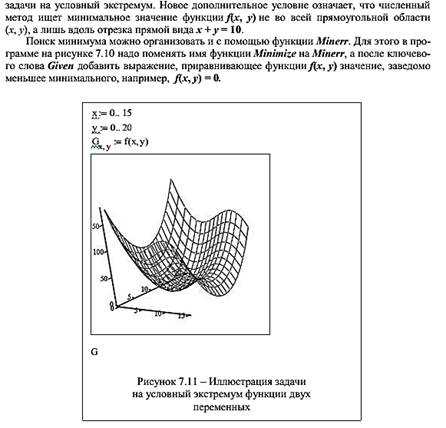
Условный экстремум

Экстремум функции многих переменных

Контрольные вопросы

1. Сформулируйте постановку задачи оптимизации.

2. Что такое локальный и глобальный экстремумы?

3. Какие ограничения имеет применение классических методов поиска оптимума?

4. Назовите численные методы поиска оптимума функции одной переменной.

5. Разберите алгоритмы методов одномерного поиска оптимума: дихотомии, золотого сечения, чисел Фибоначчи.

6. Сформулируйте критерий окончания поиска решения в итерационных методах.

7. Какие встроенные в MathCAD функции для решения задачи оптимизации вы знаете?

8. Какие функции могут применяться для решения задачи условной оптимизации?

Практическое занятие. Инструкционная карта на выполнение практического занятия по дисциплине "Компьютерная математика"

Тема: Численное решение задач оптимизации

Цель работы: освоить численное решение задач одномерной оптимизации различными методами; изучить возможности пакета MathCAD для поиска экстремума функции одной и двух переменных

Норма времени: 2 часа.

После выполненных работ студент должен

знать: основные методы одномерной оптимизации: дихотомии, золотого сечения, Фибоначчи;

уметь: решать задачи оптимизации с использованием пакета MathCAD.

Оснащение рабочего места: ПК, инструкционные карты, конспект.

Вводный инструктаж.

Метод дихотомии (половинного деления).

Метод золотого сечения.

Метод Фибоначчи.

Встроенные функции MathCAD для поиска локального минимума/максимума.

Условный экстремум.

Экстремум функции нескольких переменных.

Задания для самостоятельного выполнения.

Задание 1 . Поиск минимума функции одной переменной.

Задание 2. Поиск оптимума функции двух переменных.

Контрольные вопросы.

Литература:

Вводный инструктаж

Оптимизируемую функцию f(x) называют целевой функцией, или критерием оптимальности.

К численным методам одномерной оптимизации относятся методы: дихотомического деления; золотого сечения; чисел Фибоначчи; полиномиальной аппроксимации.

Метод дихотомии (половинного деления)

Согласно методу дихотомического деления отрезок делят пополам и в точках, отстоящих от центра с отрезка на величину допустимой погрешности , рассчитывают значения целевой функции и .

Пример программы поиска минимума методом дихотомии приведен на рис.1.

Метод золотого сечения

В соответствии с методом золотого сечения внутри отрезка выделяют две промежуточные точки и на расстоянии от его конечных точек, где – длина отрезка. Затем вычисляют значения целевой функции в точках и . Если , то то минимум находится на отрезке , если , то на отрезке , если , то на отрезке .

Алгоритм метода золотого сечения складывается из следующих этапов:

1) вычисляются значения функции на концах исходного интервала ;

2) вычисляются промежуточные точки интервала по формулам: , а также значения функции в этих точках;

3) по найденным значениям функции определяется её минимальное значение на интервале;

Пример программы приведен на рис. 2.

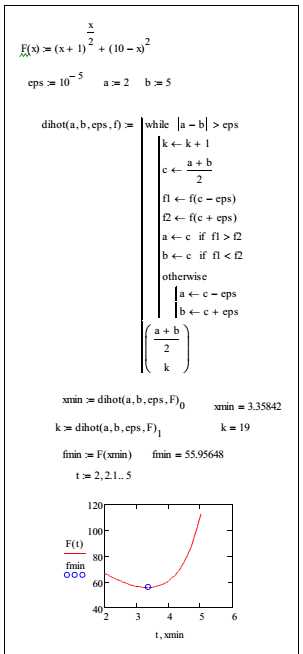
Рис. 1. Программа поиска минимума методом дихотомического деления

Рис. 2. Метод золотого сечения

Метод Фибоначчи

Согласно этому методу при разбиении отрезка используют числа Фибоначчи . Последовательность Фибоначчи образуется по правилу:

Ряд Фибоначчи имеет вид: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144 …

Алгоритм поиска с использованием числе Фибоначчи включает следующие шаги:

1) По заданной точности рассчитывается вспомогательное число ;

2) находится ближайшее к N число Фибоначчи ;

3) определяется минимальный шаг поиска по формуле ;

4) задается начальное значение счетчика шагов i = 0;

5) вычисляются значения и соответствующие значения функции в этих точках и ;

6) в зависимости от соотношения и выбирается новый интервал локализации минимума: или ;

7) внутри полученного интервала (значение счетчика i увеличивается на 1) находится новая точка (x или x1) , симметричная к уже имеющейся точке и отстоящая от конца интервала на величину , где i – номер шага. В этой точке рассчитывается значение f(x). Указанный процесс продолжается с пункта 5 до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности , i = 0; 1; 2; …, т. е. пока i не станет равно s – 2. Это будет соответствовать ситуации достижения решения с заданной точностью.

Пример программы приведен на рис. 3.

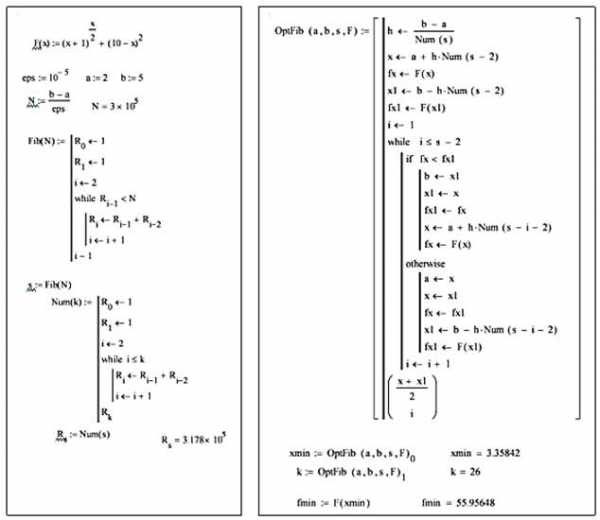
Рис. 3. Метод Фибоначчи

Встроенные функции MathCAD для поиска локального минимума/максимума

Для численного решения задач поиска локального максимума и минимума в MathCAD имеются встроенные функции Minerr, Minimize и Maximize. Пример приведен на рис.4.

Рис. 4. Поиск локальных экстремумов

Условный экстремум

В задачах на условный экстремум встроенные функции минимизации и максимиза-ции должны быть включены в вычислительный блок (solve block), который имеет следующую структуру:

Начальные приближения переменных

Given

Ограничительные условия

Выражения с функциями Minerr, Minimize или Maximize

Экстремум функции нескольких переменных

Вычисление экстремума функции многих переменных не несет принципиальных осо-бенностей по сравнению с функциями одной переменной. Пример нахождения максимума и минимума функции, показанной в виде графика трехмерной поверхности, приведен на рис. 5. Следует обратить внимание к тому, как с помощью неравенств, задается область на плоскости (x, y).

Задания для самостоятельного выполнения

Задание 1 . Поиск минимума функции одной переменной

Постройте графики функций одной переменной. Напишите программы в среде MathCAD и рассчитайте минимальное значение функции с заданной точностью методами дихотомии, золотого сечения, с использованием чисел Фибоначчи, с помощью встроенной функции Minner. Сравните результаты. Оцените количество итераций, необходимых для достижения заданной точности (таблица 1).

Задание 2. Поиск оптимума функции двух переменных

С помощью встроенных функций MathCAD решите задачу поиска оптимума функции двух переменных F(x, y), предварительно исследовав функцию графически.

Контрольные вопросы

1. Сформулируйте постановку задачи оптимизации.

2. Что такое локальный и глобальный экстремумы?

3. Какие ограничения имеет применение классических методов поиска оптимума?

4. Назовите численные методы поиска оптимума функции одной переменной.

5. Разберите алгоритмы методов одномерного поиска оптимума: дихотомии, золотого сечения, чисел Фибоначчи.

6. Сформулируйте критерий окончания поиска решения в итерационных методах.

7. Какие встроенные в MathCAD функции для решения задачи оптимизации вы знаете?

8. Какие функции могут применяться для решения задачи условной оптимизации?

zadachi-ru.com.ua

Презентация на тему: ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Оптимизация. Алгоритм Левенберга—Марквардта

Константин Ловецкий Ноябрь 2012

Кафедра систем телекоммуникаций

Метод Левенберга—Марквардта

•Алгоритм Левенберга — Марквардта — метод оптимизации, направленный на решение задач о наименьших квадратах. Является альтернативой методу Гаусса — Ньютона. Может рассматриваться как комбинация последнего с методом градиентного спуска или как метод доверительных интервалов. Алгоритм был сформулирован независимо Левенбергом (1944) и Марквардтом (1963).

•Kenneth Levenberg (1944). "A Method for the Solution of Certain NonLinear Problems in Least Squares".The Quarterly of Applied Mathematics 2:164–168.

•Donald Marquardt (1963). "An Algorithm forLeast-SquaresEstimation of Nonlinear Parameters".SIAM Journal on Applied Mathematics 11(2): 431– 441.doi:10.1137/0111030.

•Philip E. Gill and Walter Murray (1978). "Algorithms for the solution of the nonlinearleast-squaresproblem".SIAM Journal on Numerical

Analysis 15 (5): 977–992. doi:10.1137/0715063.

10/13/17	The algorithm was first published by Kenneth Levenberg, while working at the Frankford Army Arsenal. It	2
	was rediscovered by Donald Marquardt who worked as astatistician atDuPont and independently by

Girard, Wynn and Morrison.

Метод Левенберга—Марквардта

•Алгоритм Левенберга—Марквардта(LevenbergMarquardt Algorithm, LMA) является наиболее распространенным алгоритмом оптимизации. Он превосходит по производительности метод наискорейшего спуска и другие методы сопряженных

градиентов в различных задачах. Изначально считалось, что LMA – это комбинация простейшего

градиентного метода и методаГаусса-Ньютона,

однако впоследствии выяснилось, что данный алгоритм можно также рассматривать как метод доверительных интервалов.

Метод Левенберга—Марквардта

LMA решает задачу нелинейной минимизации методом наименьших квадратов. Это означает, что функция, которую необходимо минимизировать, выглядит следующим образом:

f (x) =1 å rj2		(x)
	m
	2 j=1
где x =(x1, x2 ,..., xn ) - вектор, аrj	- функция отображения из Rn вR .

Функцию rj называют невязкой в предположении, чтоm ³n . Для простоты функцияf представляется вектором невязки вида:

r(x) =(r1(x),r2	(x),...,rm (x))
10/13/17	4

Метод Левенберга—Марквардта

Теперь f можно переписать как

f(x) =12 r(x) 2 ,

аее производные представить с помощью матрицы Якоби

J (x) =	¶rj	, 1 £ j £m, 1 £i £n
	¶xi

Рассмотрим линейный случай, когда каждая функция rj линейна. Здесь якобиан равен константе,r можно представить как

гиперплоскость в пространстве, а

f (x) =12 Jx+r(0) 2

Метод Левенберга—Марквардта

Отличительной особенностью метода наименьших квадратов является то, что, имея матрицу Якоби J (x), легко получить гессианÑ2 f (x), если функцииrj можно аппроксимировать линейными приближениями

(т.е. Ñ2rj (x) малы) или еслиrj (x) малы сами по себе. Тогда гессиан, как и в линейном случае, будет равен:

Ñ2 f (x) =J (x)T J (x)

Важно отметить, что это уравнение верно только для малых невязок. Проблемы больших невязок не могут быть решены с помощью квадратичной аппроксимации, и, следовательно, производительность алгоритма, представленного выше, в таких случаях невелика.

Метод Левенберга—Марквардта

LMA как комбинация простейшего градиентного метода и метода Ньютона— Гаусса

Простейший градиентный метод – это наиболее интуитивно понятный способ нахождения минимума функции. Вычисление параметра на очередном шаге выполняется путем вычитания градиента функции, умноженного на заданный положительный

коэффициент:	xi+1	=xi -l Ñf

Однако при таком подходе имеют место различные проблемы сходимости. Логично предположить, что желательно было бы осуществлять большие шаги по направлению градиента там, где градиент мал (т.е. наклон пологий), и, наоборот, маленькие шаги там, где градиент большой, чтобы не пропустить минимум.

Однако в формуле выполняются прямо противоположные действия.

Метод Левенберга—Марквардта

Другая проблема заключается в том, что кривизна поверхности невязки может быть не одинаковой по всем направлениям. К примеру, если есть длинная и узкая впадина на поверхности невязки, компонент градиента в направлении, указывающем вдоль основания впадины, очень мал, а компонент градиента вдоль стенок впадины, наоборот, велик. Это приводит к движению по направлению к стенкам впадины, тогда как необходимо перемещаться на большие расстояния вдоль основания впадины и на малые – вдоль ее стенок.

Ситуацию можно улучшить, если учитывать информацию о кривизне и градиенте, т. е. вторые производные. Один из способов сделать это – использовать метод Ньютона для решения уравнения Ñf (x) =0 .

Раскладывая градиент f в ряд Тейлора вокруг текущего состоянияx0 , получим

Ñf (x) =Ñf (x0 ) +(x -x0 )T Ñ2 f (x0 )

Метод Левенберга—Марквардта

Пренебрегая членами более высокого порядка (считая f квадратичной вблизиx0 ) и решая задачу минимума, приравняв левую часть

уравнения	Ñf (x) =Ñf (x0 ) +(x -x0 )T Ñ2 f (x0 )

к нулю, получим правило вычисления параметра на очередном шаге по

методу Ньютона:	x	=x	- (Ñ2 f (x ))- 1	Ñf(x)

	i+1	i	i	i

Поскольку метод Ньютона напрямую использует предположение о квадратичности (пренебрегая членами более высоких порядков при разложении в ряд Тейлора), нет необходимости точно вычислять гессиан, а достаточно использовать его аппроксимацию.

Главное достоинство такого подхода – быстрая сходимость. Однако скорость сходимости зависит от начального положения (если быть более точным - от линейности вокруг начального положения).

studfiles.net

Лекция № 8. Численные методы безусловной оптимизации.

1. Унимодальные функции.

Из курса математического экстремума нам известны понятия локального и глобального экстремума функции одной переменной.

Пусть дана функция 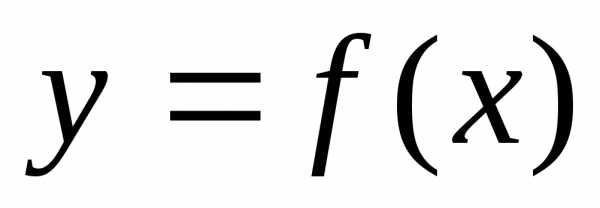, непрерывная на некотором множествеX, являющемся подмножеством множества действительных чиселR.Задачейбезусловной оптимизациидля функции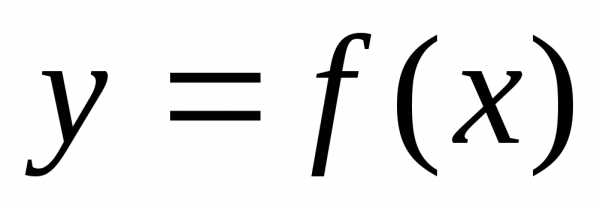называется задача отыскания всех её локальных минимумов (максимумов) в случае, если множествоX совпадает с множествомR 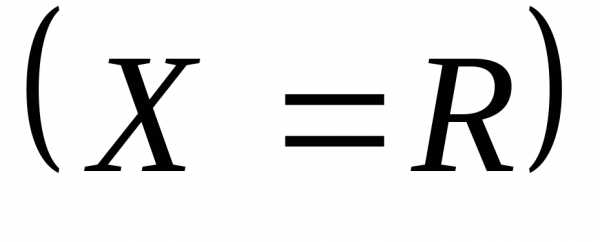. Функция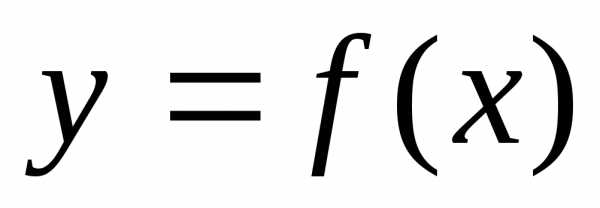называется при этомцелевой функцией.

Аналогично данная задача формулируется для функции двух и более переменных, для множества .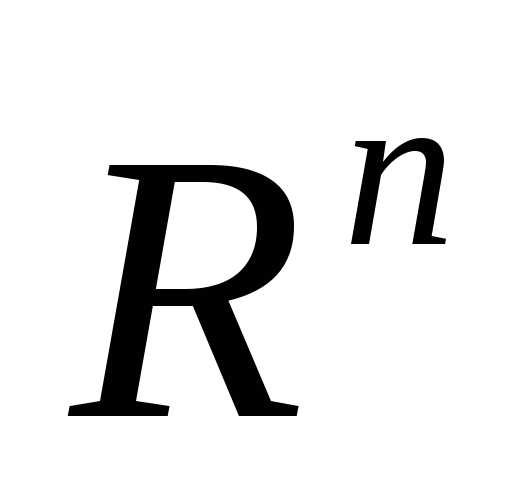

Мы рассмотрим численные методы решения данной задачи для нахождения минимума функции одной переменной. Задачу отыскания локального минимума целевой функции 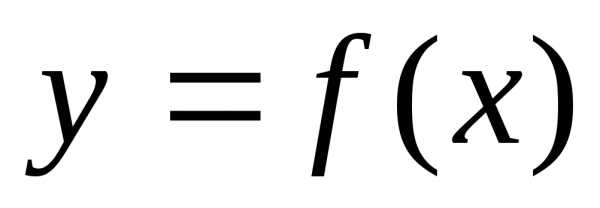символически записывают так:.

Определение.Непрерывная функция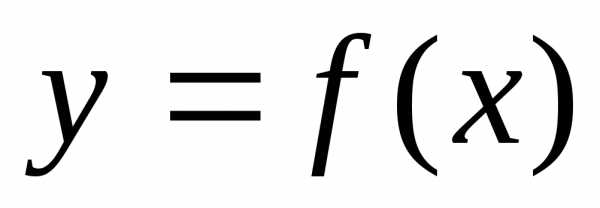называетсяунимодальной на отрезке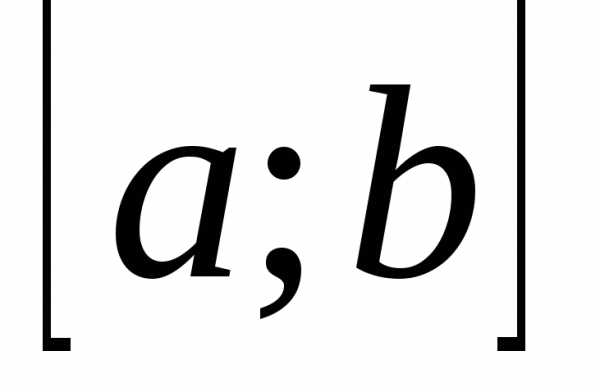, если:

точка 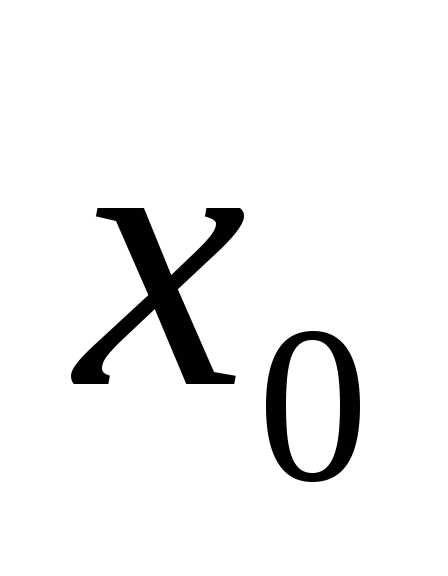локального минимума функции принадлежит отрезку;
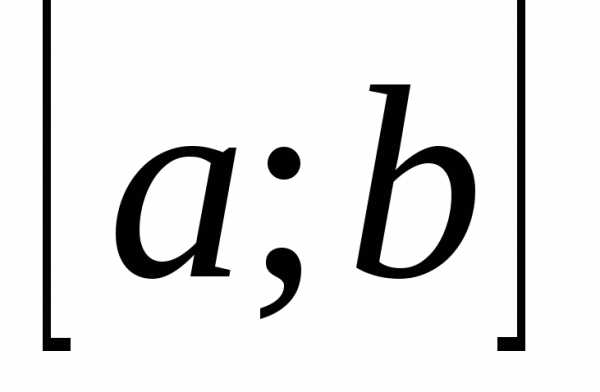для любых двух точек отрезка 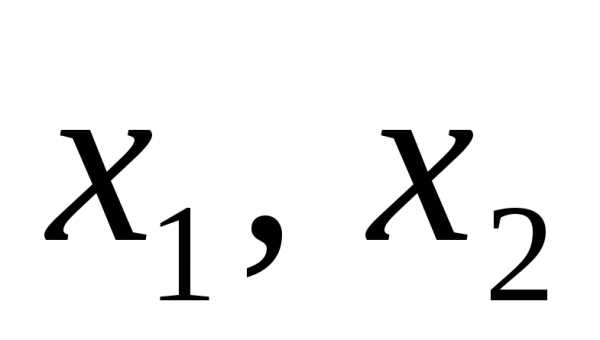взятых по одну сторону от точки минимума, точке, более близкой к точке минимума соответствует меньшее значение функции; то есть из условийилиследует условие.

Достаточное условие унимодальности функции 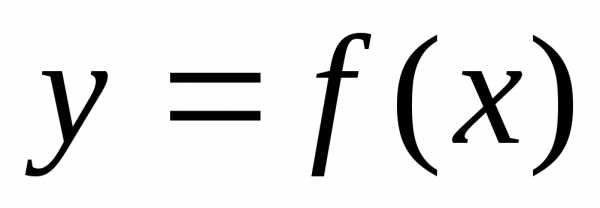на отрезке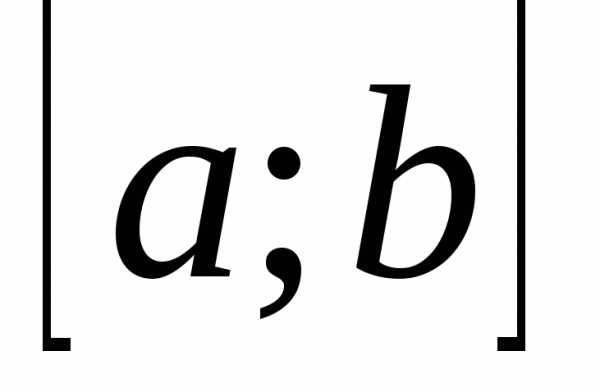содержится в следующей теореме.

Теорема. Если функция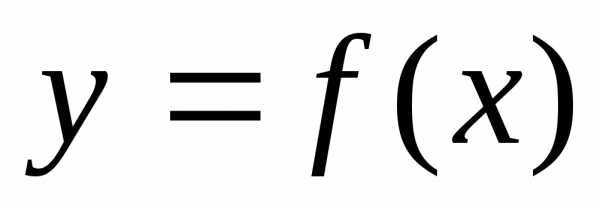дважды дифференцируема на отрезке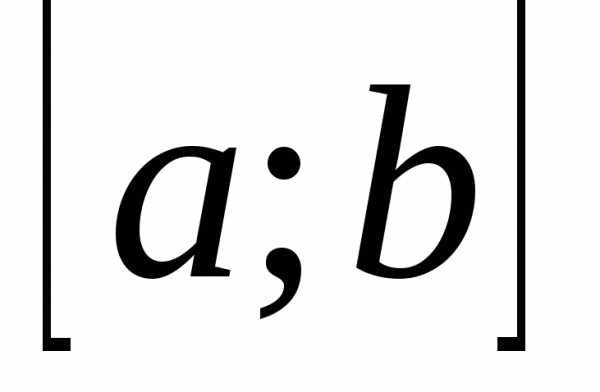и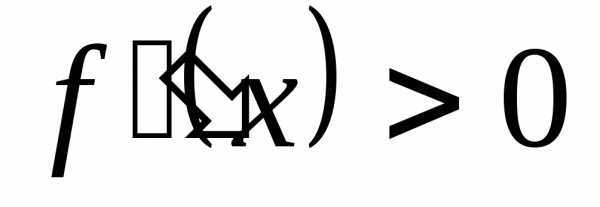в любой точке этого отрезка, то данная функция является унимодальной на отрезке.

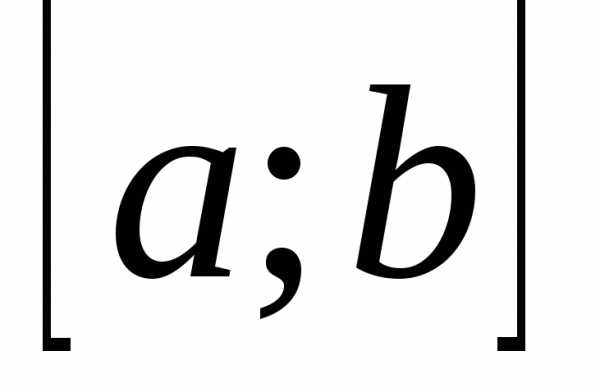Заметим, что условие 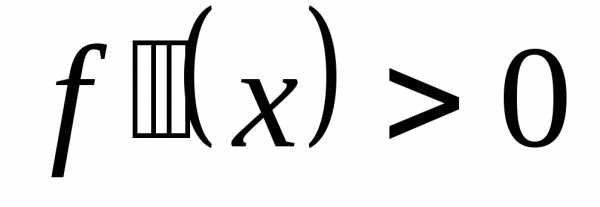определяет выпуклость вниз (вогнутость) функции на указанном отрезке.

Пример 1.Для функциинайти:

промежуток Х, на котором функция является унимодальной;
решение задачи .

Решение.

Функция 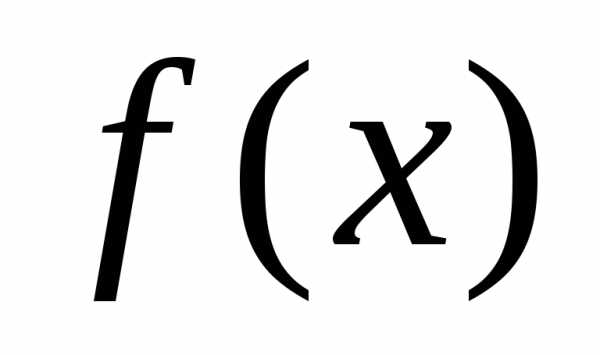определена при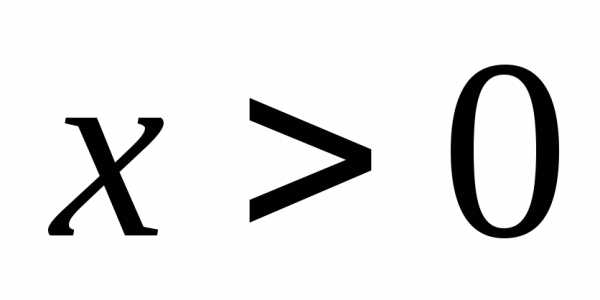; найдём её производные:. Заметим, что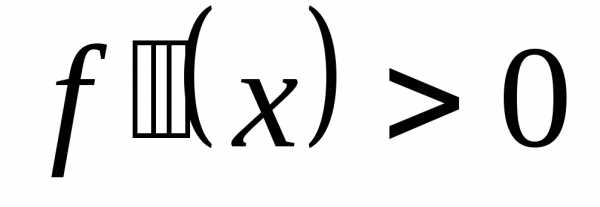при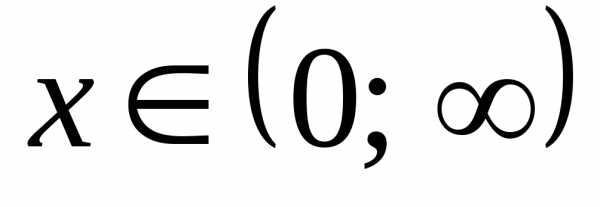. Следовательно, функция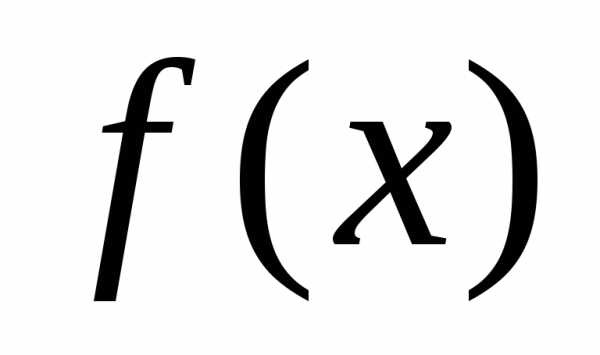унимодальна на интервале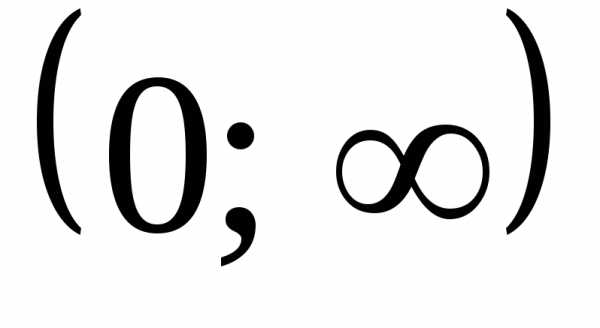. Далее,при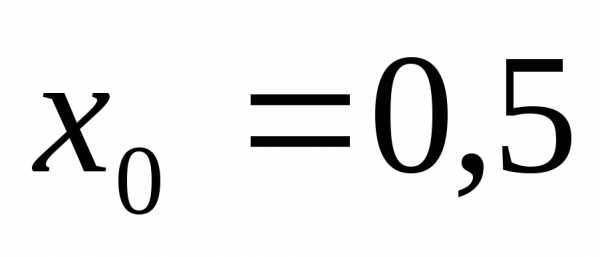. Знаки производной меняются в окрестностях точки 0,5 с “- “ на “+”, поэтому, согласно достаточном условию экстремума, данная точка является точкой локального минимума.

2. Схема сужения промежутка унимодальности функции.

Пусть требуется решить задачу

(1)

Применение численных методов для отыскания точек 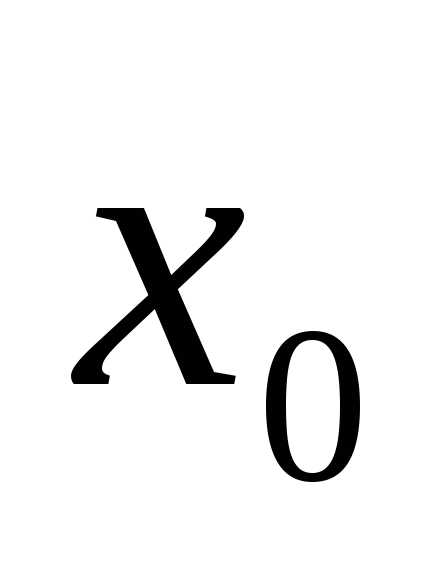локального минимума предполагает:

определение промежутков унимодальности функции, то есть нахождение отрезков, каждому из которых принадлежит одна точка локального минимума;
вычисление значения 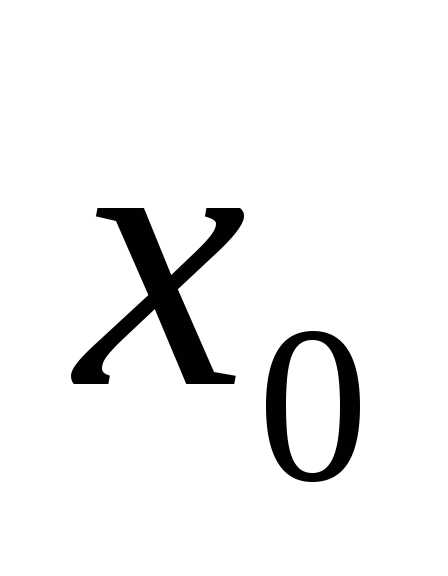, принадлежащего выбранному промежутку, с заданной точностью.

Для непрерывной функции 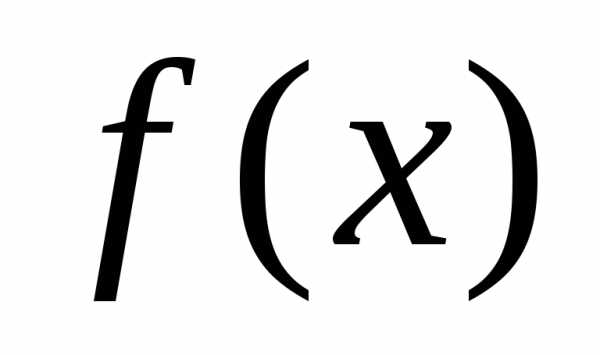строят её график на некотором отрезке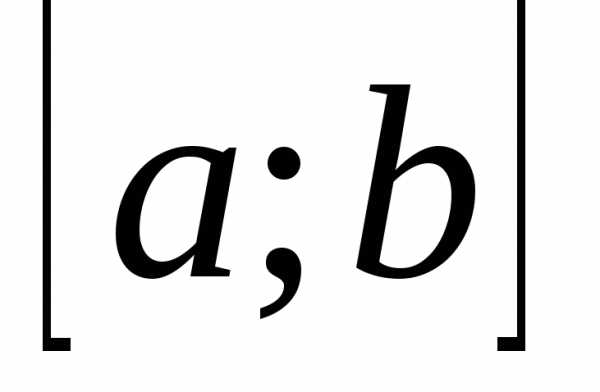и, если окажется, что на этом отрезке график функции имеет вид, изображённый на рисунке, то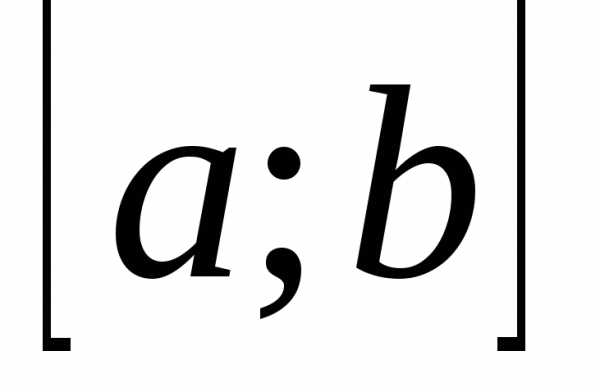- отрезок унимодальности функции. Отрезок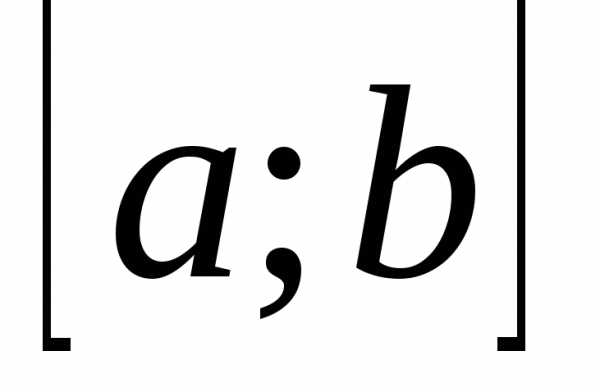берётся, по возможности, малым.

При вычислении точки минимума точность достигается последовательным уменьшением отрезка 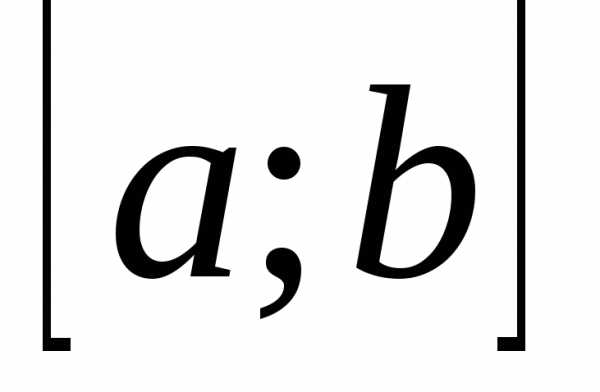, содержащего точку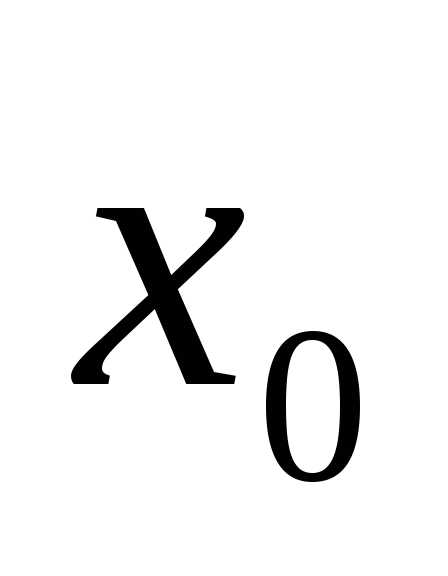, до размеров, не превышающих заданную точность.

Замечание. Если функция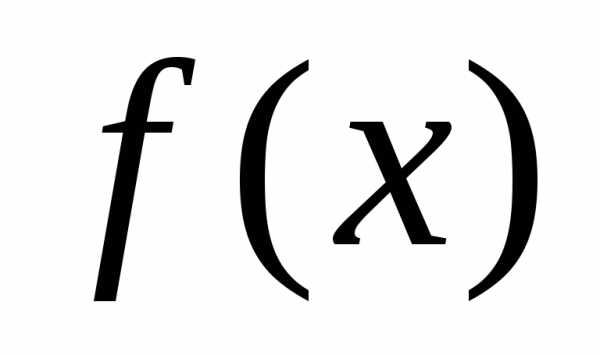имеет производную во всей области определения, то для отыскания её стационарных точек нужно решить уравнение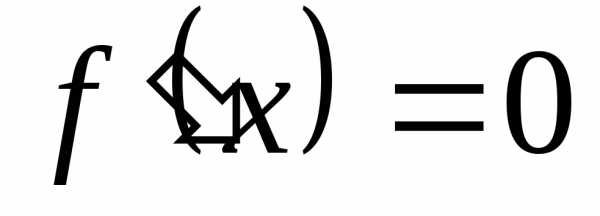. Для решения этого уравнения, как правило, необходимо использовать численные методы, описанные в лекциях 1 и 2. Однако, для решения задачи (1) проще применять прямые численные методы поиска минимума функции.

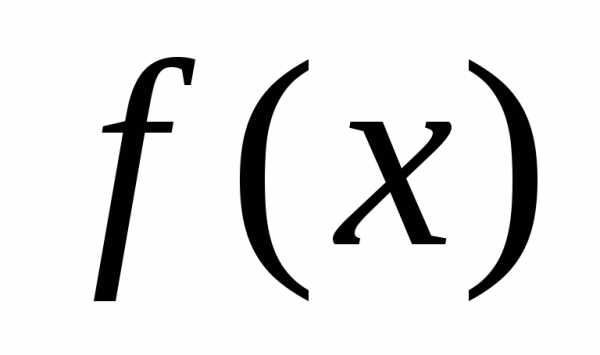Рассмотрим один из приёмов, позволяющих сузить отрезок унимодальности функции. Пусть функция 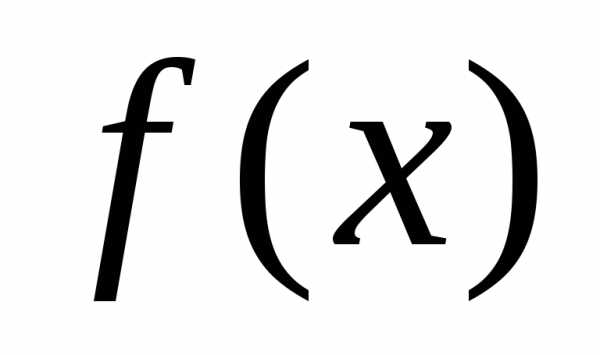унимодальна на отрезке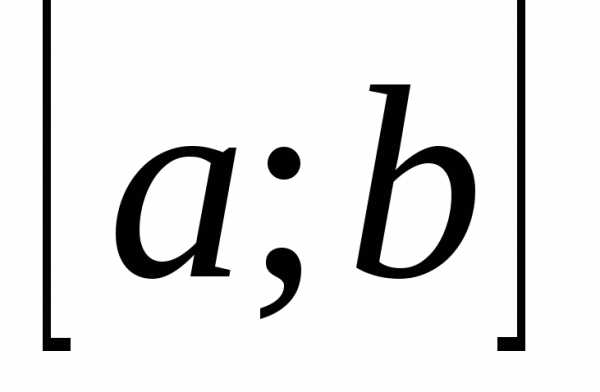. Возьмём две произвольные точк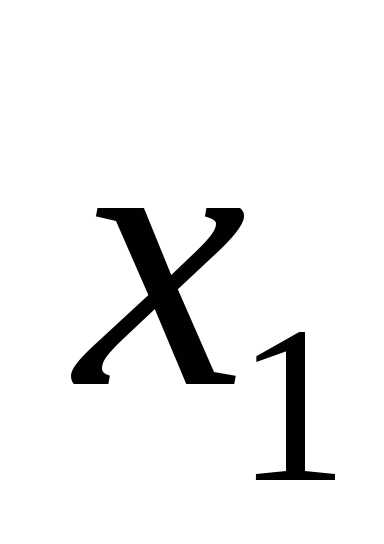ии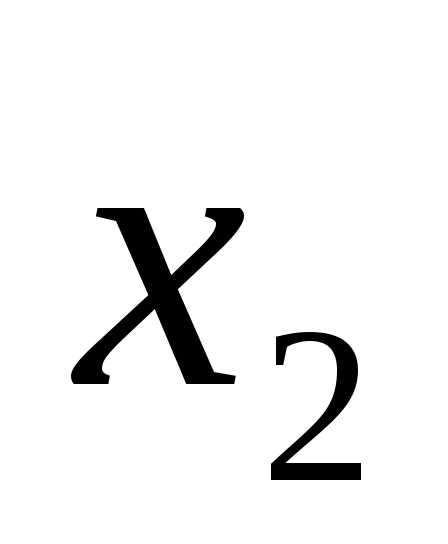, принадлежащие этому отрезку и такие, что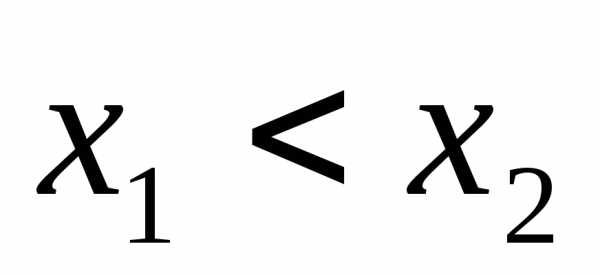. Возможны, очевидно, следующие три случая, в каждом из которых можно указать отрезок меньших размеров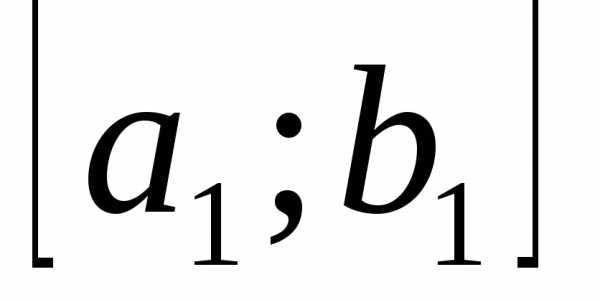, содержащий точку минимума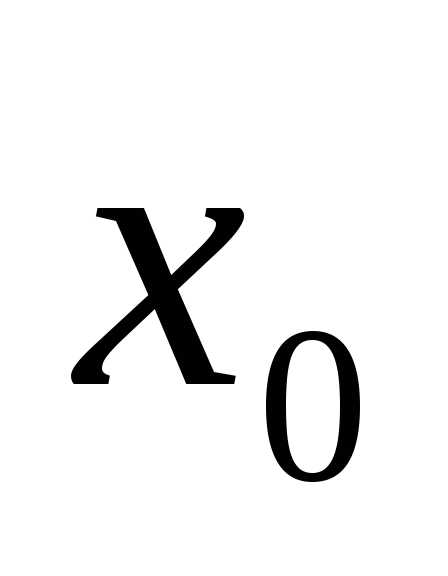и принадлежащий первоначальному отрезку.

Если , то положими получим меньший отрезок унимодальности.
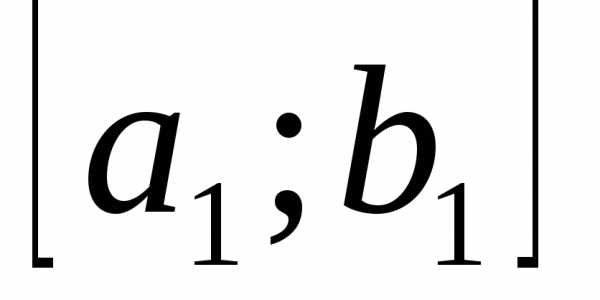Если , то положим.
Если , то, очевидно,.

Пример 2.Для функции, выбрав отрезок унимодальностии две произвольные точки, найти меньший отрезок унимодальности.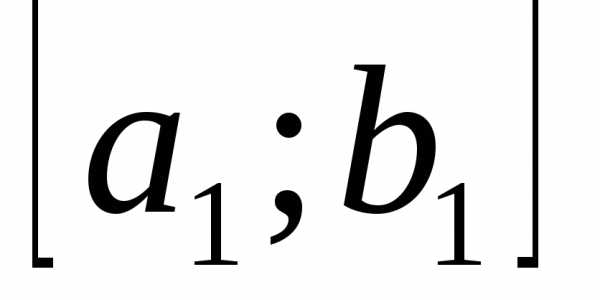

Решение.

В примере 1 было установлено, что данная функция имеет точку минимума 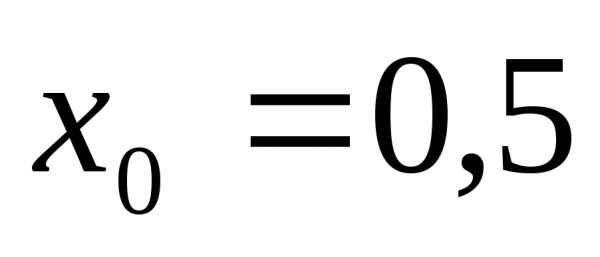и является унимодальной на любом отрезке, содержащем эту точку и лежащем в области её определения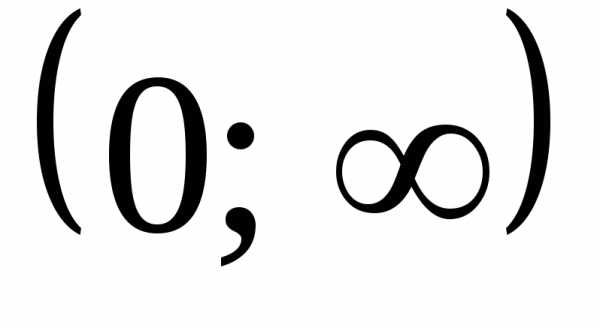. Возьмём; тогда:

Здесь естественно положить и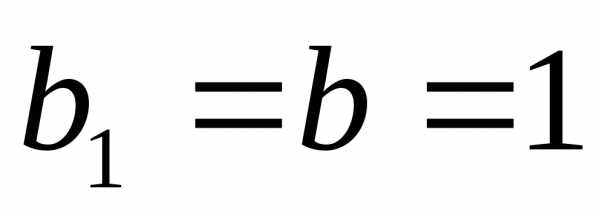(случайII). Получили новый, меньший отрезок унимодальности.

Методы, с помощью которых вычисляют значения точки минимума функции одной переменной, отличаются алгоритмами выбора точек 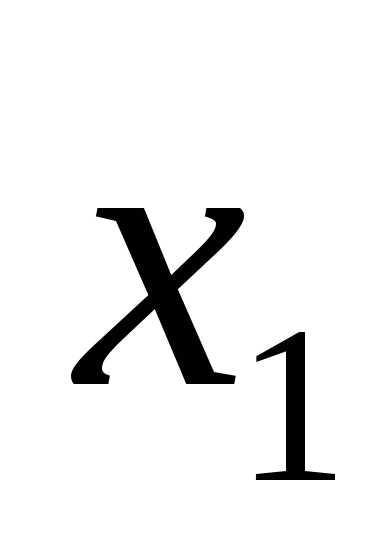и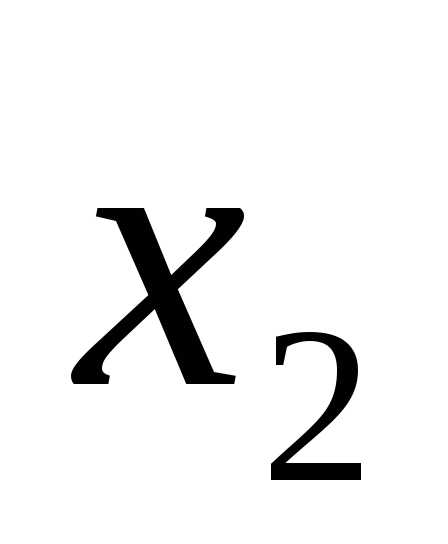для локализации точки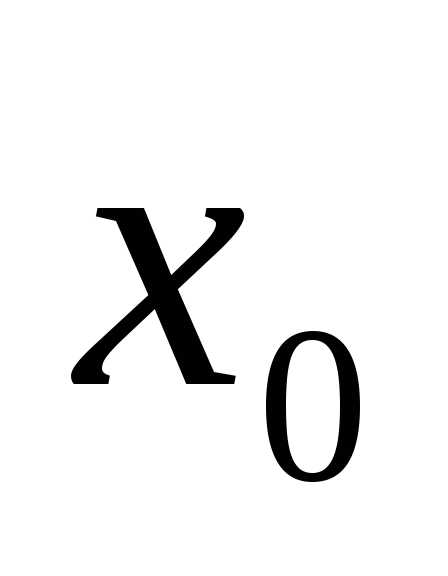с заданной точностью.

3. Метод половинного деления.

Пусть при решении задачи (1) определён отрезок 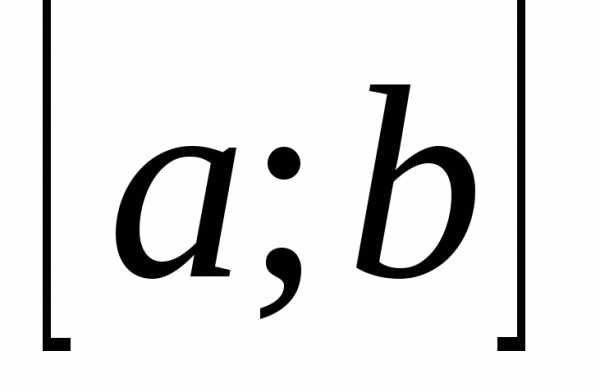, которому принадлежит точка локального минимума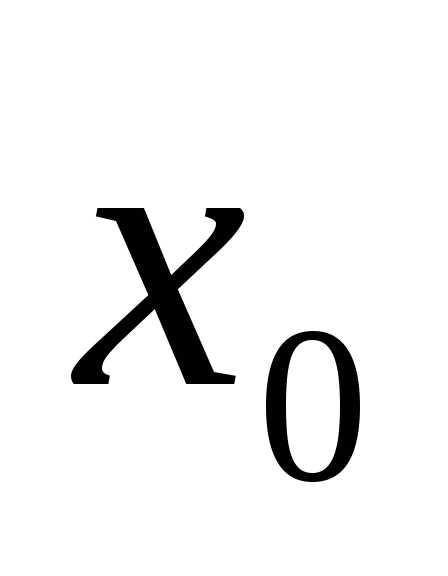, и функция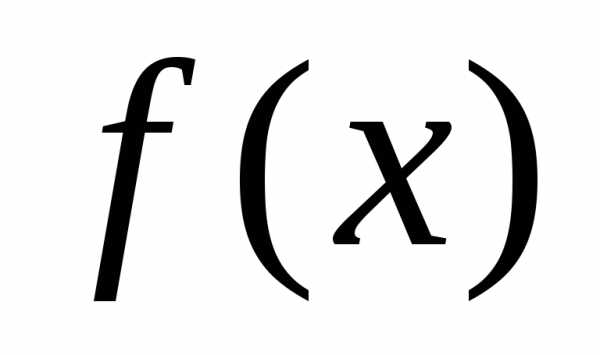унимодальна на этом отрезке.

Далее для сужения отрезка унимодальности используем точк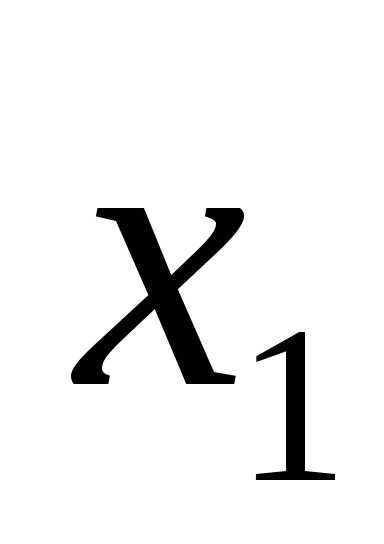и и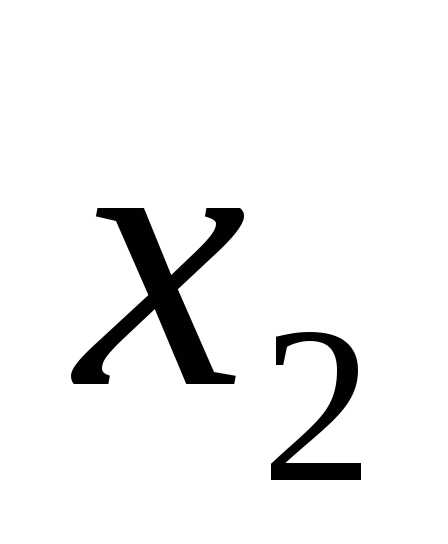, расположенные симметрично относительно середины данного отрезка:

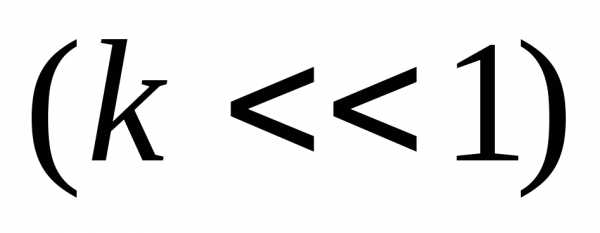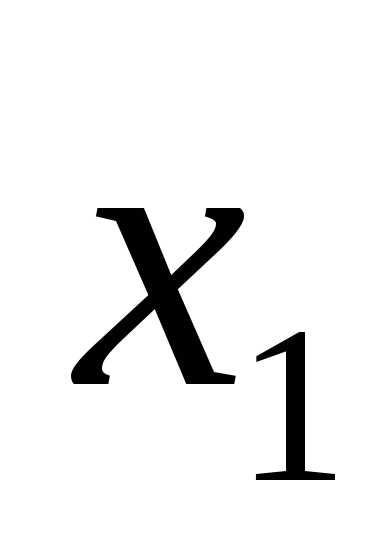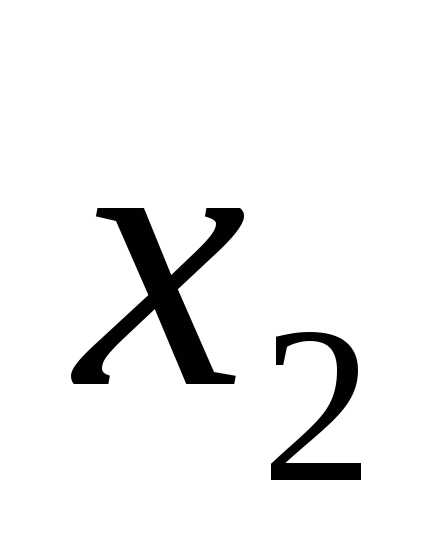Будем считать, что число k гораздо меньше единицы. Тогда точкиипринадлежат отрезку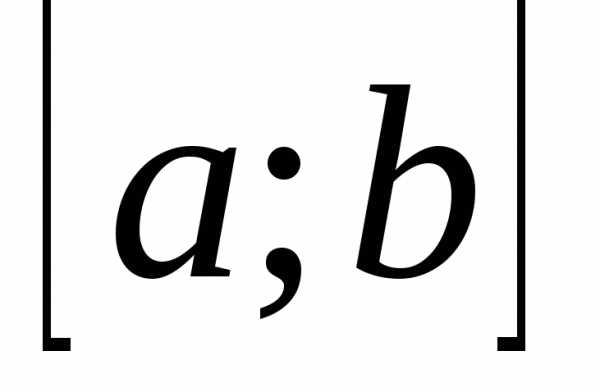и, следуя рассмотренной в предыдущем пункте схеме, получим новый суженный отрезок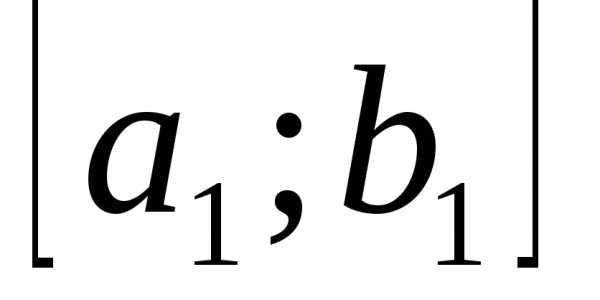и оценим его длину в каждом из трёх возможных случаев:

I.;

II.;

III..

Таким образом, после первого шага преобразований найден новый отрезок унимодальности 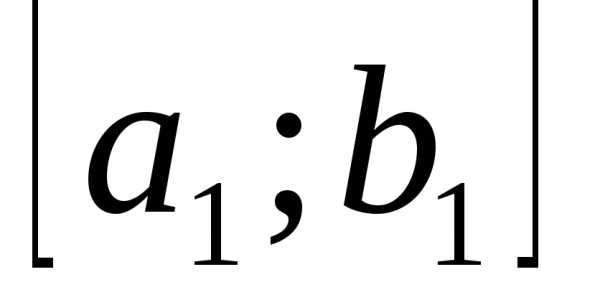, длина которого уменьшилась.

Названия метода (метод половинного деления) мотивировано тем, что если величинаkочень мала, то длина отрезка унимодальности уменьшается почти вдвое (в случаяхIиII).

Теперь в новом суженном промежутке 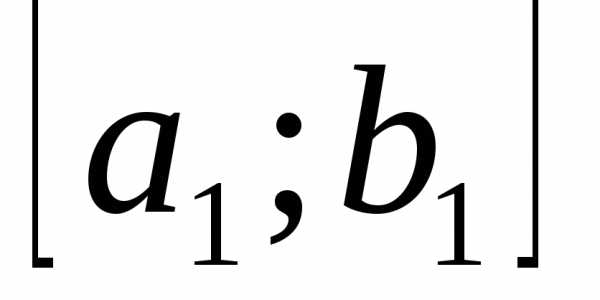выберем точк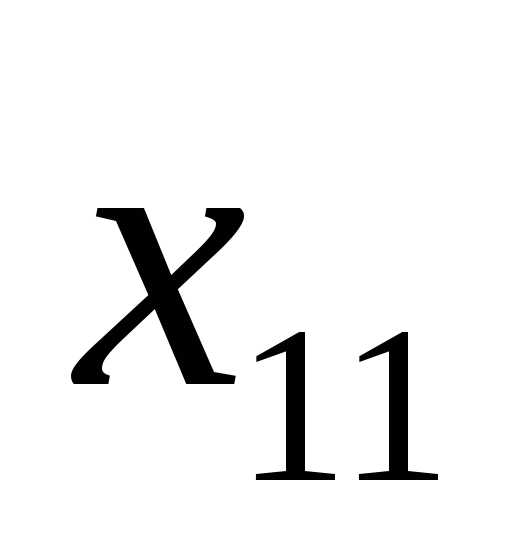ии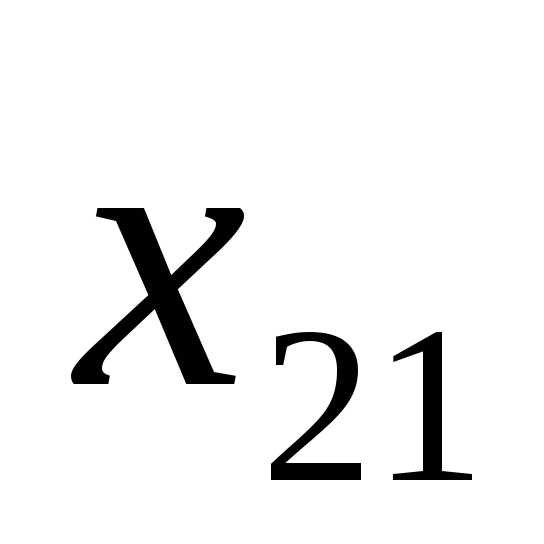, симметричные относительно его середины:

Произведя вычисления, аналогичные проделанным ранее, получаем отрезок 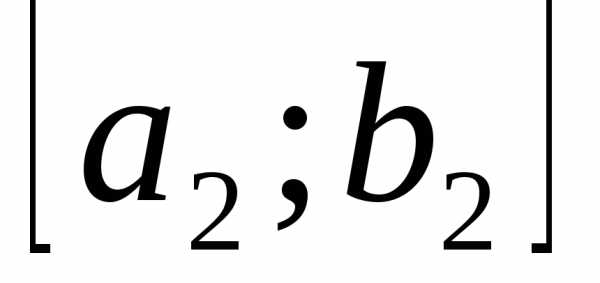, длина которого не больше, чем

и так далее.

В результате приходим к последовательности таких вложенных отрезков , что точка локального минимума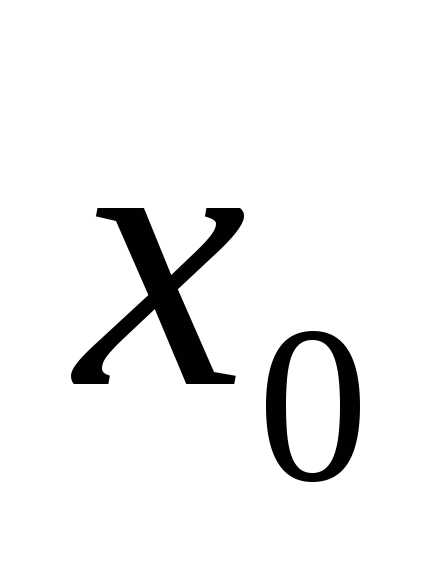функции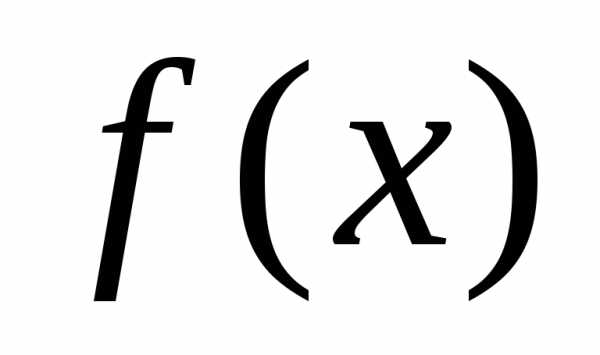принадлежит каждому из них и является общим пределом последовательносте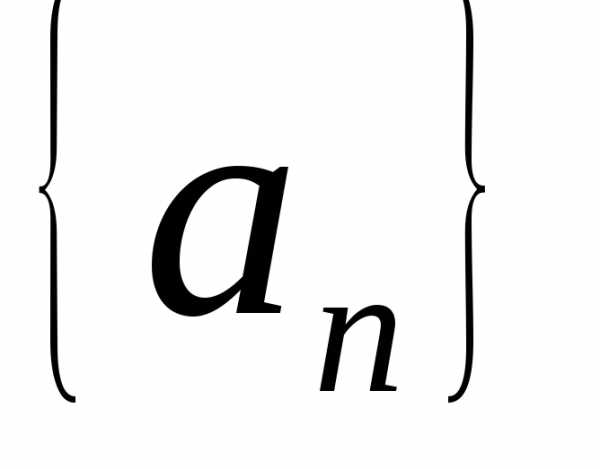йи.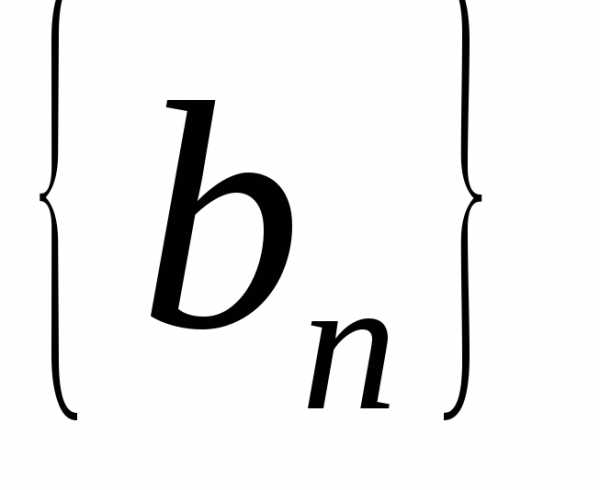

Отсюда получаются приближённые равенства: , оценить точность которых нап-м шаге вычислений можно с помощью неравенства:

Пример 3.Найти точку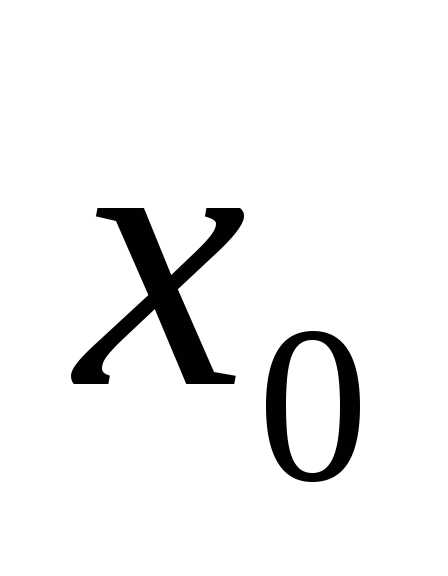локального минимума функциина отрезке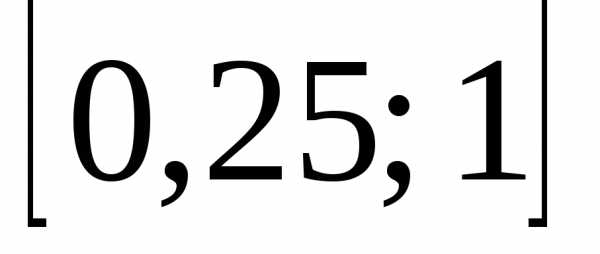методом половинного деления с точностью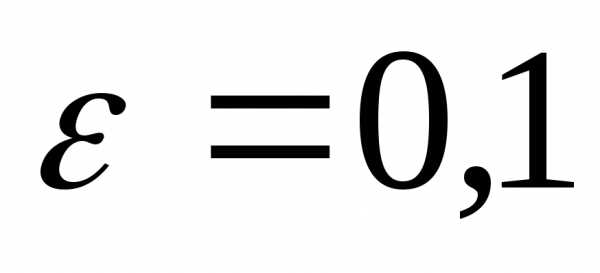. Провести вычисления, полагая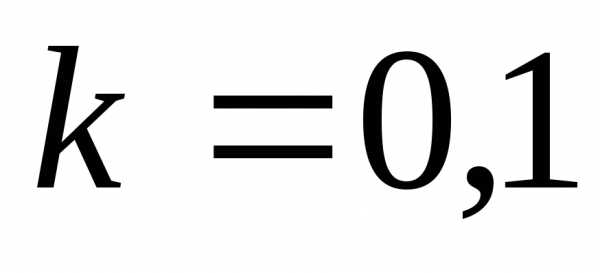и предварительно оценив минимальное число шагов, необходимое для достижения указанной точности.

Решение.

В примере 1 было установлено, что функция унимодальна на отрезке 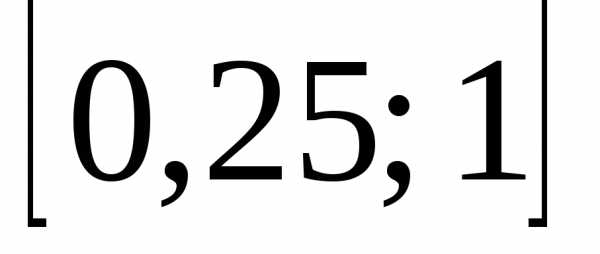; точка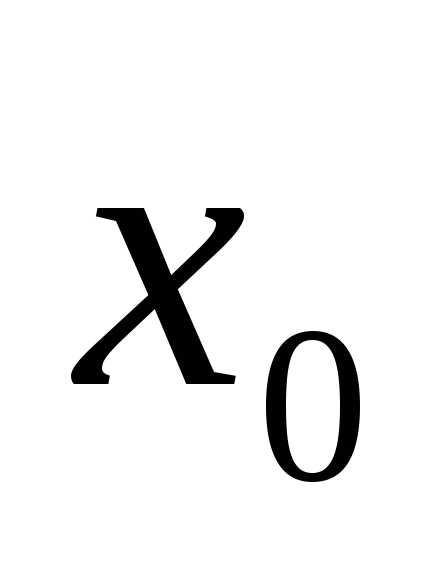принадлежит этому отрезку. Воспользуемся неравенством (2) и определим число шаговп:

Введём обозначения:

Здесь ,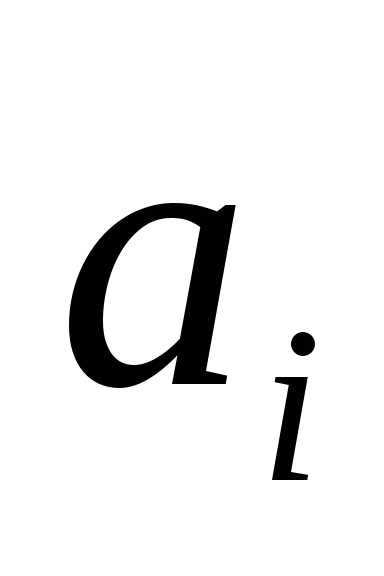и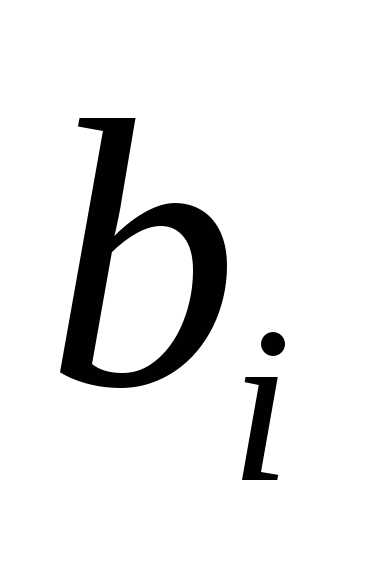- координаты начала и конца отрезка, полученного на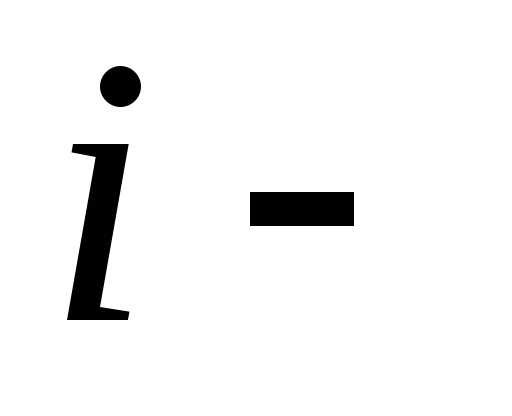м шаге вычислений, точки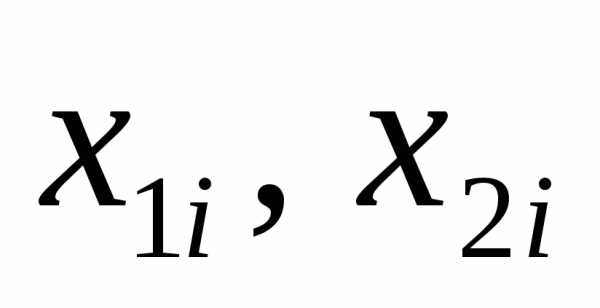принадлежат отрезку.

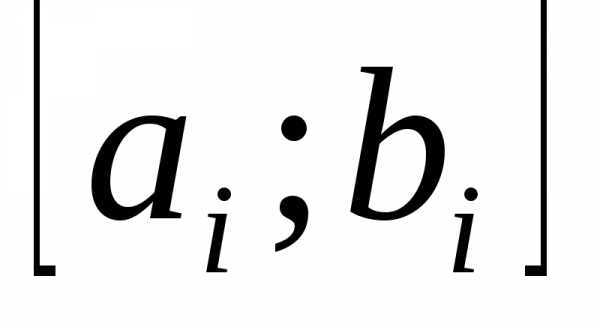Проведём последовательные вычисления.

Отрезок :

Отрезок :

Отрезок :

Отрезок :

Отрезок .

Разность . Следовательно, точкой локального минимума, найденной с заданной точностью, является.

Задание.

Для заданной целевой функции 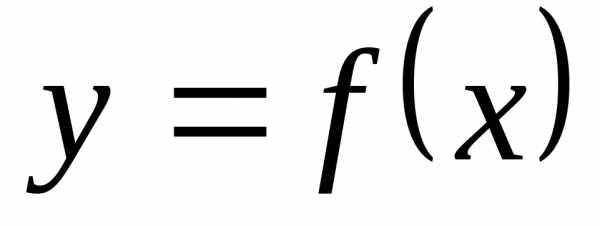найти промежуток, на котором она унимодальна. Найти точное решение задачи минимизации. Найти приближённое решение этой задачи с точностью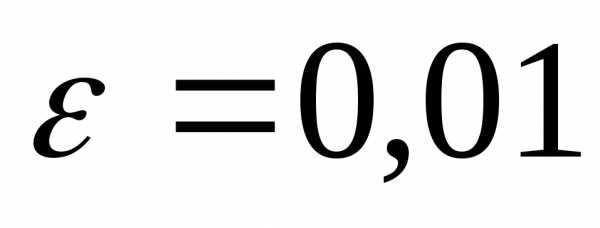методом половинного деления.

1. ;

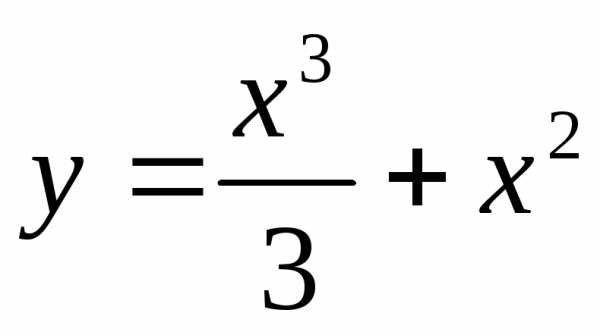2. ;

3. ;

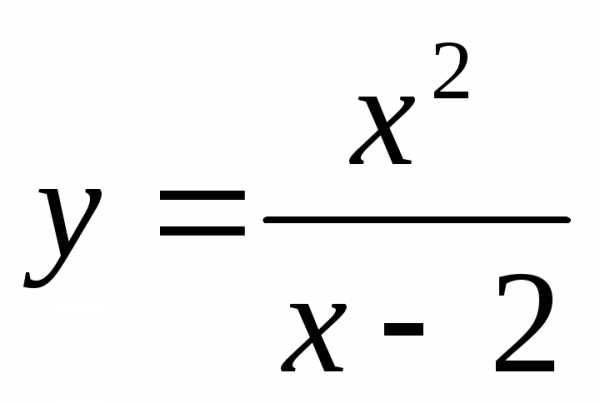4. .

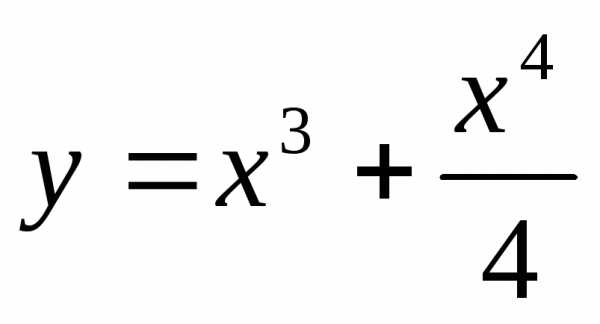Лекция № 9. Численное решение дифференциальных уравнений первого порядка.

studfiles.net

Презентация на тему: ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Применение методов оптимизации

Константин Ловецкий Декабрь 2012

Кафедра систем телекоммуникаций

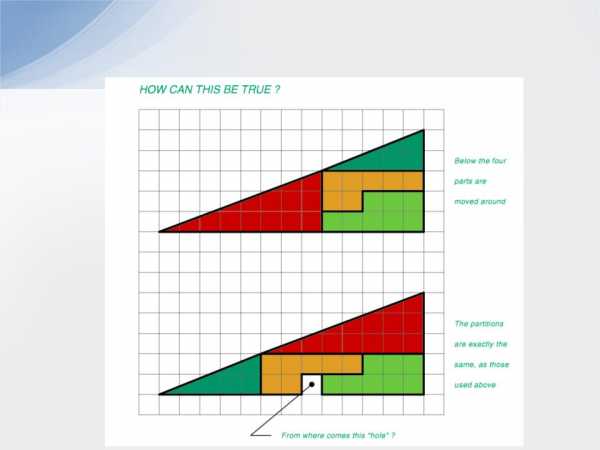
Wedge Paradox

Contributed by Carsten Kolve

Нанооптика

Проектирование тонкопленочных структур используется

впроизводстве:

•жидкокристаллических дисплеев

•солнечных батарей на основе диэлектриков

•фотоэмиссионных диодов

•просветляющих покрытий

•поляризаторов

•миниатюрных лазеров

•управляемых оптических элементов

Проектирование оптических покрытий состоит из следующих этапов

•Физическая модель

•Математическая модель

•Целевая функция – мера качества модели

•Решение оптимизационной задачи

Методы оптимизации

•Методы условной оптимизации

•Методы безусловной оптимизации

Что такое оптимизация?

Задача оптимизации: Максимизация или минимизация некоторой функции на некотором множестве, часто представляющем

собой множество выборов в определенной ситуации. Функционально существует возможность сравнения различных выборов для определения «наилучшего».

Области применения: Минимальная стоимость, максимальный доход, оптимальное управление, вариационное исчисление, создание новых конструкций и приборов.

Что такое оптимизация?

Цель изучения: Усвоение практических и теоретических аспектов:Результат моделирования: На какой результат надеяться при постановке

оптимизационной задачи? Какие свойства благоприятны, а какие нет? Что может способствовать правильной постановке задачи? К какому классу лучше

отнести конкретную задачу?

Анализ решения: Что подразумевается под «решением»?

Условия существования и единственности решения. Каким образом распознать и охарактеризовать решение? Что произойдет при возмущении исходной

задачи?

Численные методы: Итеративные схемы решения. Существуют ли способы (локального) упрощения проблемы? Сравнение различных способов оптимизации.

Свойства оптимизации как математической дисциплины

Описательная – предписывающая (конструктивная) математика:

Большая часть математических задач описывала ранее поведение

различных (физических) систем. Появление компьютеров позволяет использовать математику для проектирования систем спредсказуемым поведением, что обеспечивается оптимизацией.

Равенства - неравенства: Оптимизация обычно имеет дело с переменными, которые лежат в определенном диапазоне, диктуемом ограничениями на допустимый результат. Это приводит к тому, чтоограничения-неравенстваиспользуются гораздо чаще, чем равенства.

Свойства оптимизации как математической дисциплины

Линейные/нелинейные – выпуклые/невыпуклые: Подразделение между линейностью и нелинейностью задач гораздо менее важно при оптимизации, чем различие между выпуклостью и не выпуклостью целевых функций и ограничений. Этот факт требует от математической постановки задачи совершенно новых подходов.

Дифференцируемость - не дифференцируемость : Преобладание

неравенств вместе с такими специальными функциями как «max» и «min» приводит к тому, что методология классической математики с

опорой на гладкость поверхностей и дифференцируемость функций не

является преобладающей.

Свойства оптимизации как математической дисциплины

Конечномерная оптимизация: Случай, когда результат расчета целевой функции соответствует выбору конечного числа действительных переменных, называемых искомыми переменными. Обычно их обозначают черезx1, x2 ,..., xn

и возможный набор переменных соответствует точке x =( x1, x2 ,..., xn ) Î Rn

которая называется допустимой точкой.

Ограничения: Условия, налагаемые на искомые переменные, определяют множество допустимых точек в пространстве переменных задачи.

studfiles.net

Презентация на тему: ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Оптимизация. Метод

наименьших квадратов

Константин Ловецкий Октябрь 2012

Кафедра систем телекоммуникаций1

Метод наименьших квадратов

•Используемые в сочетании с квазиньютоновским методом процедуры линейного поиска получили широкое

применение. Эти методы также используются и в подпрограммах нелинейной оптимизации по методу наименьших квадратов. В задачахf (x)

на метод наименьших квадратов подлежащая минимизации функция представляет собой

сумму квадратов:1		F (x)	2	=	1	åi	F (x)	2

min f (x) =
xÎ Rn	2		2		2		i

Метод наименьших квадратов

Подобного типа задачи широко распространены и имеют ряд практических применений, особенно при подборе модельной функции для некого набора данных, т.е. определение нелинейных параметров модели. Эти задачи также широко распространены в теории управления, где в

конечном итоге необходимо получить некую			, соответствующую
		y(x,t)	для вектора	и скаляра
некой непрерывной модельной траектории
.	j (t)	x	t

Данная задача может быть сформулирована как:

min òt1 (y(x,t) -j (t))2 dt

xÎ Rn t2

где y(x,t) иj (t) есть некие скалярные функции.

Метод наименьших квадратов

При дискретизации интеграла посредством подходящих квадратурных формул уравнение может быть сформулировано как задача на метод наименьших квадратов:

min f (x) =		( y(x,t	) - j (t	))2
xÎ Rn	å	i	i
	i

где - y иj включают в себя веса квадратичной схемы. Отметим, что

F (x)	понимается:
в данной задаче под вектором
é y(x,t1 ) -j (t1 ) ù
ê		ú
êy(x,t2 ) -j (t2 )ú
F (x) =	...	ú
ê
ê		ú

ëy(x,tm ) -j (tm )û

Постановка задачи

Матрица Q(x) обладает тем свойством, что когдаF (x) невязка стремится к нулю при стремлении к точке решения, то и сама матрица стремится к нулю. ТакимF (x) образом, при небольших значениях

в точке решения одним из наиболее эффективных методов является использование направления Ньютона—Гауссав качестве основы для процедуры и оптимизации.

Метод Левенберга—Марквардта

•В основу метода Левенбрга-Марквардтаположено направление поиска, которое находится при решении системы линейных

уравнений:	k	k	k	I )d		k	k	k	)
(J	(x)T J	(x	) +l	I )d			=- J (x	)F(x	)
l k	задаетk				как величину, так и						k
где скалярk	задаетk				как величину, так и						k
d		l								d
направление							равенk		нулю, то
параметра	. Когда						равенk		нулю, то
направление dk								l
направление dk
будет идентично этому же параметру из
метода										8
10/13/17										8
Ньютона—Гаусса.По мере того как

Метод Левенберга—Марквардта

В данном случае предполагается, что для

достаточно	l	k	остается справедливым
больших значений
	l k (F(xk ) +dk ) <F(xk )

l	может быть
Следовательно, членk

контролируемым с целью обеспечения спуска в случае

необходимости учета членов второго порядка, которые, в свою

очередь, заметно ограничивают эффективность метода Ньютона—Гаусса.

Метод Левенберга—Марквардта

•Отсюда следует, что метод Левенберга—Марквардтаоснован на направлении поиска, являющегося сочетанием направленияНьютона—Гауссаи наискорейшего спуска. Решение для функции Розенброка сходится после 90 обращений к расчету функции по сравнению с 48 для метода Ньютона— Гаусса. Такая низкая эффективность отчасти объясняется тем, что методНьютона—Гауссаобычно более эффективен в случае, когда в решении невязка равна нулю. Однако такая информация не всегда является заранее доступной, и повышенная устойчивость методаЛевенберга—Марквардтакомпенсирует его иногда имеющую место слабую эффективность.

studfiles.net

Численные методы решения одномерных задач оптимизации

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ

В данном разделе не делается упор на поиск именно минимума, тем более что практически все методы могут искать и минимум, и максимум при незначительных изменениях в алгоритмах. Действительно для того, чтобы найти максимум (минимум) функции нужно искать минимум (максимум) целевой функции с противоположным знаком.

В данном разделе рассматриваются методы решения одномерных задач оптимизации вида

R(x) -> max , ,где х — скаляр, а и b — соответственно нижняя и верхняя граница значения переменной x.В основном рассматриваются алгоритмы, связанные с построением улучшающей последовательности. Решением задачи называется х*, при котором R(x*) > R(x) для любого значения . При практическом решении задач не будем различать два значениях и , ecли ,где — задаваемая погрешность решения.

Метод сканирования

Метод заключается в последовательном переборе всех значений с шагом (погрешность решения) с вычислением критерия оптимальности R в каждой точке. Путем выбора наибольшего из всех вычисленных значений R и находится решение задачи х *.

Достоинство метода в том, что можно найти глобальный максимум критерия, если R(x) — многоэкстремальная функция. К недостаткам данного метода относится значительное число вычислений R(x), что в случае сложной функции R(x) требует существенных затрат времени.

Метод деления пополам

Метод основан на делении текущего отрезка [a, b], где содержится искомый экстремум, на две равные части с последующим выбором одной из половин, в которой локализуется максимум в качестве следующего текущего отрезка. Экстремум локализуется путем сравнения двух значений критерия оптимальности в точках, отстоящих от середины отрезка на / 2, где — погрешность решения задачи оптимизации. Если R(x + /2) > R(x - /2), то максимум располагается на правой половине текущего отрезка [а, b],

в противном случае — на левой.

Иллюстрация метода половинного деления

Процесс поиска завершается при достижении отрезком [a, b] величины заданной погрешности .К недостаткам метода относится его работоспособность только для одноэкстремальных функций R(x) (т.е. таких, которые содержат один экстремум того типа, который мы ищем в задаче),так как в других случаях при сравнении двух критериев в соседних точках невозможно правильно выбрать следующий интервал, где находится максимум.

Пример. Дана функция R(x) = 100*sin(x+1). Найти максимум на интервале: [-1, 2]. Ошибка задается по х: =0,05.Результаты расчетов. Середина отрезка х= 0,5, значение критерия R =99.75, значение R(0,5 - /2) =R(0,475) = 97.92, значение R(0,5 + /2) =R(0,525) =99.89. Следовательно, искомый максимум лежит в правой половине отрезка, т.е. теперь отрезком является [0,5, 2J.

Метод золотого сечения

Метод основан на делении текущего отрезка [a, b] , где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для определения следующего отрезка, содержащего максимум.

Иллюстрация метода золотого сечения.

Золотое сечение определяется по правилу: отношение всего отрезка к большей его части равно отношению большей части отрезка к меньшей. Ему удовлетворяют две точки с и d, расположенные симметрично относительно середины отрезка.

Если ab=1, ad=x, тогда x=0.38197

Путем сравнения R(c) и R(d) определяют следующий отрезок, где содержится максимум. Если R(d) > R(c), то в качестве следующего отрезка выбирается отрезок [a, c],

Если же R(d) < R(c), то — отрезок [a, c].

Новый отрезок снова делится на неравные части по правилу золотого сечения. Следует отметить, что точка c и в том и другом случаях входит в интервал поиска. Поэтому на каждой следующей итерации (кроме "запуска" метода на исходном отрезке) нужно вычислять только одно значение критерия оптимальности.

Существуют аналитические формулы для расчета новой точки на отрезке, где находится максимальное значение R(x), которую нетрудно получить:

Условие окончания поиска — величина отрезка, содержащего максимум, меньше заданной погрешности.

Метод обеспечивает более быструю сходимость к решению, чем многие другие методы, и применим, очевидно, только для одноэкстремальных функций.

В практических задачах под одноэкстремальной функцией понимают функцию, содержащую один экстремум того типа, который ищется в задаче.

Пример. Дана функция R(x)=sin(x+1). Найти максимум на интервале: [-1,2]. Ошибка задается по х: e =0,05.

Результаты расчетов. Для "запуска" метода найдем две симметричные точки золотого сечения для отрезка [-1, 2]: x1 =0,146, x2 =0,854.

Значения критериев в этих точках соответственно R(x1) =0,911, R(x2 =0,960. Следовательно, новым отрезком является [0,146,2], внутри которого находится максимальное из найденных значений R. Точка золотого сечения для нового отрезка будет x3 =0,583, a R(x3) =0,999

Численная метода - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Численная метода - оптимизация

Cтраница 1

Численные методы оптимизации - бурно развивающийся в настоящее время раздел вычислительной математики. В литературе описаны десятки, если не сотни, численных методов решения экстремальных задач. Многообразие методов, вообще говоря, закономерно. Оно определяется многообразием задач, которые необходимо решать, и различием доступных методам источников информации о решаемой задаче. [1]

При численных методах оптимизации используют таблицы или графики, методы поочередного одномерного поиска, а затем более сложные методы наискорейшего спуска. [2]

В численных методах оптимизации - поиск оптимума путем последовательного деления пополам ( дихотомии) пространства решений и проверки каждой половины на наличие в ней экстремальной точки. [3]

Указанные обстоятельства позволяют рассматривать численные методы оптимизации как необходимое средство решения проблем поиска оптимума в исследованиях, различных по содержанию и сложности. [4]

Поскольку основное внимание в книге уделяется прямым численным методам оптимизации механических систем и конструкций, необходимые условия оптимальности и численные методы, основанные на них ( непрямые методы), рассматриваются менее подробно. При переводе добавлены три ссылки [199-201] на новые книги по оптимизации конструкций, в которых всесторонне исследуются необходимые условия оптимальности и непрямые численные методы. [5]

Эта книга написана на основе трудов конференции по численным методам оптимизации при ограничениях, проходившей в Национальной физической лаборатории в январе 1974 г. Ей предшествовала конференция по методам безусловной оптимизации, проведенная тремя годами ранее. [6]

Для более сложных реакций аналитическое решение невозможно; необходимо использовать численные методы оптимизации, однако приведенный выше подход, связанный с построением характеристик, может быть принципиально применен в том же виде, что и для простых реакций. [8]

Предлагаемая книга написана на основе курса лекций по теории и численным методам оптимизации, который в течение ряда лет читался авторами на факультете вычислительной математики и кибернетики МГУ им. [9]

При более сложных зависимостях, не описываемых дифференциальными уравнениями, пользуются численными методами оптимизации. Например, если целевая функция зависит от элементов решения линейно, а наложенные на них ограничения также имеют вид линейных равенств ( или неравенств), экстремум находят методом линейного программирования. [10]

Это обстоятельство не позволяет получить выражения для искомых коэффициентов в аналитической форме и заставляет пользоваться численными методами оптимизации. В задачах оптимизации алгоритмов управления оказался весьма удобным метод последовательной оптимизации, сводящий общую задачу нелинейного программирования к последовательности более простых задач. [11]

Полученные свойства выпуклых задач имеют важное значение не только в теории, но и в численных методах оптимизации. [12]

Причем во многих случаях удается перейти к задачам линейного или квадратичного программирования, для решения которых разработаны эффективные численные методы оптимизации. [13]

По сравнению с 1 - м изданием ( вышло в 1973 г.) добавлены новые разделы, посвященные теории эксперимента, численным методам оптимизации; переработано большинство разделов. Материал дополнен новыми примерами и задачами. [14]

В настоящее время активно ведутся исследования по алгоритмам оптимизации и имеется богатый материал по теории нелинейного программирования, который в будущем может привести к улучшенным численным методам оптимизации. Авторы надеются, что постановка и анализ задач проектирования механических систем и конструкций, данные в книге, помогут инженерам в использовании и улучшении методов оптимизации конструкций. [15]

Страницы: 1 2 3