ГлавнаяОптимизацияДискретная оптимизация

Большая Энциклопедия Нефти и Газа. Дискретная оптимизация


Задача - дискретная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Задача - дискретная оптимизация

Cтраница 1

Задачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации.  [1]

Задачи дискретной оптимизации часто встречаются во всех сферах практической деятельности. Ограничимся здесь одним примером ( другие см. в гл.  [2]

Для большинства задач дискретной оптимизации явный вид всех граней до настоящего времени не найден. Наиболее интересные результаты получены для многогранников задачи об упаковке, задачи о максимальном паро-сочетании графа, задачи коммивояжера, задачи о рюкзаке ( все они приводятся в гл. На принципиальную возможность получения такого описания указывает еще теорема Гильберта о конечном базисе кольца многочленов, однако эффективные методы до сих пор не получены. IV излагается подход к построению методов аналитического и параметрического описания целых точек многогранников, основанный на выделении порождающих множеств полугрупп.  [3]

Z называется задачей дискретной оптимизации.  [4]

В [13] рассматриваются задачи дискретной оптимизации, для решения которых применяется аппроксимационно-комбинаторный метод.  [5]

Рассмотрим примеры двух задач дискретной оптимизации: задачу о ранце и задачу о коммивояжере. Эти задачи часто рассматриваются как тестовые при разработке алгоритмов решения задач дискретной оптимизации.  [6]

Например, сложными являются задачи дискретной оптимизации, где точные алгоритмы имеют обычно экспоненциальную сложность и нереализуемы за приемлемое время.  [7]

Алгоритмы и программы решения задач дискретной оптимизации / Сост.  [8]

Существует несколько схем решения задач дискретной оптимизации.  [9]

Очевидно, что в задачах дискретной оптимизации область допустимых решений ( или область работоспособности) D является невыпуклой и несвязной.  [10]

Ограниченность возможностей точных методов решения задач дискретной оптимизации естественным образом приводит к идее разработки комбинированных алгоритмов, в которых объединялись преимущества методов и, по возможности, отсутствовали их недостатки.  [11]

Как следует из общей постановки задач дискретной оптимизации, основное влияние на формальную постановку таких задач имеет пространство X, в котором рассматривается данная конкретная задача, что естественным образом отражается на способе ( алгоритме) ее решения.  [12]

Учет ограничений типа неравенств в задаче дискретной оптимизации незначительно усложняет процедуру случайного поиска.  [13]

Излагаются современные комбинаторные алгоритмы для решения задач дискретной оптимизации с применением компьютерных средств. Основное внимание уделяется вычислительной реализации алгоритмов. Приводятся результаты вычислительного исследования алгоритмов для классических задач дискретной оптимизации - задачи о ранце и задачи о коммивояжере. Приведено много примеров для самостоятельной работы.  [14]

Одним из наиболее мощных методов решения задач дискретной оптимизации является метод последовательного анализа ваоиантов. В настоящем параграфе приводится общее описание метода последовательного анализа вариантов, придерживаясь работ [19, 20, 84], и иллюстрируются возможности его применения к некоторым задачам геометрического проектирования.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Дискретная оптимизация

Home Teaching Courses Дискретная оптимизация

В данный момент курс ведётся на потоке ПМИ школы ПМИ МФТИ альтернативным к курсу функционального программирования. В разных версиях курс читался в МФТИ с 2011 года в качестве спецкурса и основного курса.

Важные новости курса

Логистика курса

Задания

Лекции

План лекций

www.dainiak.com

Дискретная оптимизация - это... Что такое Дискретная оптимизация?

 Дискретная оптимизация

Дискре́тное программи́рование (дискретная оптимизация) — раздел математического программирования.

В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные значения, например, целочисленные.

Задачи комбинаторной оптимизации можно решить с помощью методов дискретного программирования. Одними из основных методов решения задач дискретного программирования являются метод ветвей и границ и динамическое программирование.

Примеры задач:

Wikimedia Foundation. 2010.

Смотреть что такое "Дискретная оптимизация" в других словарях:

Книги

Другие книги по запросу «Дискретная оптимизация» >>

dic.academic.ru

Дискретная оптимизация — Wiki - Факультет компьютерных наук

Материал из Wiki - Факультет компьютерных наук

О курсе

Курс читается для студентов 3-го курса ПМИ ФКН ВШЭ в 4 модуле.

Лектор: Игнат Колесниченко

Лекции ПМИ проходят по вторникам, 13:40 - 15:00, ауд. 622.

Полезные ссылки

Канал в телеграм для объявлений: https://t.me/joinchat/AAAAAFD1-ZdchZS1FoOduA

Таблица с оценками: TODO

Оставить отзыв на курс: TODO

Семинары

Группа Преподаватель Связь Страница Расписание
МОП 151 Лахтанов Иван telegram: @ivan_lakhtanov  ? Пятница 15:10 - 16:30
МОП 152 Колесниченко Игнат [email protected] http://wiki.cs.hse.ru/%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Ignat Вторник 15.10-16.30
АПР 153 Суханов Николай -  ?  ?
АДИС 154 Савченко Руслан -  ?  ?
РС 155 Ахмедов Максим telegram: @max_akhmedov, http://t.me/discrete_opt_155  ?  ?
ТИ 156 Саакян Вильям telegram: @wilwell  ? Вторник 10:30 - 11:50

Консультации

Консультации с преподавателями и учебными ассистентами (если иное не оговорено на странице семинаров конкретной группы) по курсу проводятся по предварительной договорённости ввиду невостребованности регулярных консультаций.

Правила выставления оценок

В курсе предусмотрено 3 домашних задания – 2 практических и 1 теоретическое. За каждое домашнее задание выставляется оценка по 10-бальной шкале, правила получения оценки будут оговариваться при публикации домашнего задания.

Итоговая оценка вычисляется исходя из оценок за домашние задания

Oитоговая = round(0.33 * OДЗ1 + 0.33 * ОДЗ2 + 0.34 * ОДЗ3), где round – это функция арифметического округления.

Также на семинарах иногда будут выдаваться небольшие домашние задания. Их решение будет засчитываться как доп. баллы в домашних заданиях (доп. баллы к исходной оценке в ДЗ, а не к результирующей).

Правила сдачи заданий

Дедлайны по всем домашним заданиям являются жёсткими, то есть после срока работы не принимаются.

При обнаружении плагиата оценки за домашнее задание обнуляются всем задействованным в списывании студентам, а также подаётся докладная записка в деканат. Следует помнить, что при повторном списывании деканат имеет право отчислить студента.

При наличии уважительной причины дедлайн по домашнему заданию может быть перенесён. Дедлайн по домашнему заданию переносится на количество дней, равное продолжительности уважительной причины. Решение о том, является ли причина уважительной, принимает исключительно учебный офис.

Лекции

Лекция 1 (3 апреля). Метод Branch&Bound решения оптимизационных задач. Задача о рюкзаке: 2-приближение, динамическое программирование по весам и по стоимостям.

Лекция 2 (10 апреля). Задача о рюкзаке: PTAS с временем работы (n^(1+1/eps)), FPTAS с временем работы O(n^3 * 1 /eps). Напоминание об переменных нежесткости и условиях дополняющей нежесткости.

Лекция 3 (17 апреля). Методика Primal-Dual построения решений для комбинаторных задач. Применение Primal-Dual к задаче о поиске кратчайших путей.

Лекция 4 (24 апреля). Задача о взвешенном паросочетании в двудольном графе, применение Primal-Dual для её решения.

Лекция 5 (15 мая). Поиск паросочетаний в недвудольных графах. Алгоритм Эдмонса. Минимаксная формула для размера паросочетания в произвольном графе (формула Татта-Бержа).

Лекция 6 (22 мая). Симплекс-метод, геометрическая интерпретация, базисные перменные и эффективная реализация (табличный симплекс-метод).

Лекция 7 (29 мая). Метод эллипсоидов, решение выпуклых задач оптимизации с помощью метода отделяющей плоскости. Задача о разрезе максимального веса, 0.5-приближение с помощью дерандомизации. Построение 0.878-приближения с помощью сведения к задаче полуопределенного программирования.

Лекция 8 (5 июня). Метод локального поиска. Применение его к задаче о ферзях. Применение к задаче о раскраске графа. Алгоритм sqrt(n) раскраски 3-раскрашиваемого графа.

Семинары

Семинар 1 (2-6 апреля). Напоминание о линейном и целочисленном программирование. Построение двойственных программ. Задача о поиске максимального паросочетания в двудольном графе.

Семинар 2 (9-13 апреля).

Семинар 3 (16-20 апреля).

Семинар 4 (23-24 апреля). Задача Set-Cover. Решение с помощью округления ЛП. Примерение Primal-Dual для построение f-приближения. Вероятностный способ округления для построения log(n)-приближения.

Семинар 5 (14-18 мая). Разложение Эдмонса-Галлаи, его полученеи из алгоритмы Эдмонса и его свойства. Задача о существовании совершенного паросочения в 3-регулярном графе без мостов.

Семинар 6 (21-25 мая). Задача о поиске упаковки вершинно-непересекающихся T-путей, минимаксная формула Галлаи. Связь с задачей о паросочетаниях.

Семинар 7 (28 мая - 1 июня). Программирование в ограничениях (CP), базовая концепция. Примеры решения задач с помощью CP: задача о ферзях, задача о магической последовательности, задача о сборке автомобилей.

Семинар 8 (4-8 июня). Задача коммивояжера. Алгоритмы для 2 и 1.5 приближений. Алгоритмы локального поиска в данной задаче: 2-OPT, 3-OPT, эвристика Ли-Кернигана.

Домашние задания

Домашнее задание 1 (практика)

Дедлайн: 14 мая 23:59

В домашнем задании требуется решить три практических задачи, архив с условием: https://yadi.sk/d/t9yrhBy-3UiVgA

Контест для сдачи задач: https://contest.yandex.ru/contest/8104/

Грейдер для задачи о рюкзаке: http://akhmedov.me:50010/knapsack

Задание следует отправлять на почту [email protected]. В заголовке письма с решением указывайте "[Название группы] ФИО Домашнее задание 1". В случае вопроса добавляйте в заголовок письма слово "вопрос".

Критерий оценки задачи о рюкзаке

Оценивание производилось на закрытых тестах. Оценка ставится в зависимости от отличия вашего решения и оптимального решения. Также в случае отсутствия отчета или плохо написанного отчета семинарист вправе снять еще до 1 балла.

Суммарная ошибка 0 – 6 баллов.

Суммарная ошибка <200 – 5 баллов.

Суммарная ошибка <1500 – 4 балла.

Суммарная ошибка <5000 – 3 балла.

Суммарная ошибка <15000 – 2 балла.

Суммарная ошибка <21000 – 1 балл.

Последняя граница выбрана исходя из того, что стандартное жадное решение имеет ошибку примерно 20800)

Приватные тесты: https://yadi.sk/d/1n9vMPTi3XLFiM

Домашнее задание 2 (теория)

Дедлайн: 2 июня 23:59

В домашнем задании требуется решить 5 теоретических задач, условия: https://yadi.sk/i/o4gtEhpA3VywLM

В качестве решения в каждой задачи должно быть подробное доказательство требуемого факта/описание работы алгоритма/структуры данных с оценкой времени его работы. При выполнении этого домашнего задания можно использовать все алгоритмы и теоремы, которые были разобраны и доказаны на лекциях и семинарах. Однако, следует подробно объяснить к чему и как они применяются.

Решения настоятельно рекомендуется записывать в latex-е.

Оценка будет выставлять по формуле min(10, баллы за решение + баллы за семинар 1 + баллы за семинар 2)

Задание следует отправлять на почту [email protected]. В заголовке письма с решением указывайте "[Название группы] ФИО Домашнее задание 2". В случае вопроса добавляйте в заголовок письма слово "вопрос".

Домашнее задание 3 (практика)

Дедлайн: 25 июня 23:59

В домашнем задании требуется решить три практических задачи, архив с условием: https://yadi.sk/d/7fEE0CuN3Xk5bJ

Контест для сдачи задач: https://contest.yandex.ru/contest/8422

Оценка будет выставлять по формуле min(10, баллы за решение)

Задание следует отправлять на почту [email protected]. В заголовке письма с решением указывайте "[Название группы] ФИО Домашнее задание 3". В случае вопроса добавляйте в заголовок письма слово "вопрос".

Пересдача

Пересдачи будут проходить 4-го и 7-го сентября. 4-го сентября пересдача будет в аудитории Кэмбридж в ШАДе в 10.00 (с 09.55 до 10.05 мы будем ждать вас у проходной). 7-го сентября пересдача будет в аудитории 435 на Кончовском в 10.00.

Правила проведения пересдачи и программа экзамена поступны тут: https://yadi.sk/d/P2NVdCGy3Zrkh9

Практика. Условие задачи и открытые тесты доступно по следующей ссылке: https://yadi.sk/d/E_h5glrb3acMWJ

Контест доступен по следующей ссылке: https://contest.yandex.ru/contest/8801/problems/

Решения принимаются до 23:59:59 2 сентября вне зависимости от даты пересдачи, на которую приходит студент. Несданное к дедлайну решение практическое части оценивается в 0 баллов.

Комиссия

Состоится 27 сентября в 10.00 в аудитории ауд.322. Формат аналогичен теоретической части на пересдаче.

Полезные материалы

Рекомендуемая литература

* "B.Korte, J.Vygen – Combinatorial optimization" – подробная книга по теории комбинаторной оптимизации (http://www.or.uni-bonn.de/~vygen/co.html). * "V. Vazirani – Approximation Algorithms" – одна из лучших книг по приближенным алгоритмам. * "H. Papadimitriou – Combinatorial Optimization: Algorithms and Complexity" – классический учебник по комбинаторной оптимизации. * "Where are the hard knapsack problems?" [David Pisinger] - интересные рассуждения по поводу того, как генерировать сложные тесты для задачи о рюкзаке. * ["Heuristics for the Traveling Salesman Problem" [Christian Nilsson]] - краткое но насыщенное описание эвристик для задачи о коммивояжёре. * "Handbook of Constraint Programming" [F. Rossi, P. van Beek and T. Walsh] - справочник по программированию в ограничениях. * "Handbook of Metaheuristics" [Michel Gendreau, Jean-Yves Potvin] - справочник с описанием эвристических алгоритмов оптимизации.

Полезные ссылки

* [Визуализатор маршрута коммивояжёра] (вершины подаются в 0-индексации) * Курс по дискретной оптимизации на [Coursera]. Содержит хорошие видео-лекции по Constraint Programming и Local Search.

Библиотеки для решения задач оптимизации

* [Google Optimization Tools] (C++, Python, Java, C#) - фреймворк для решения задач дискретной оптимизаций. Позволяет программировать в парадигме Constraint Programming. Содержит инструменты для решения задач линейного программирования. ([Более полная документация]) * [Numberjack] (Python) * [Choco] (Java) * [Gecode] (C++) * [MiniZinc] (MiniZinc) - Довольно выразительный язык для CP. Есть ((http://www.hakank.org/minizinc/ много примеров)).

wiki.cs.hse.ru

6.9. Методы дискретной оптимизации

X G,

(x )

X

допустимая область

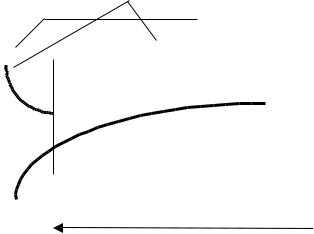
РИС. 49. ЦЕЛЕВАЯ ФУНКЦИЯ В МЕТОДЕ ВНЕШНЕЙ ТОЧКИ

Задача дискретного математического программирования – это задача (116), но с дополнительными условием дискретности пространства управляемых параметров, т.е. где G – счетное множество точек. В ряде случаев лишь часть управляемых параметров дискретна. Тогда задача оптимизации является задачей частично дискретного программирования. Обычно для параметровx i водятся двусторонние прямые ограничения (123), тогдаG – конечное множество и задача дискретного программирования становится комбинаторной.

Дискретная оптимизация сложнее непрерывной. Сложность точного решения комбинаторной задачи является экспоненциальной. Эффективные точные методы дискретной оптимизации существуют лишь для отдельных классов задач, поэтому для задач целочисленного линейного программирования и нелинейного дискретного программирования в САПР применяются

приближенные методы локальной оптимизации и ветвей и границ.

Метод локальной оптимизации характеризуется тем, что один его шаг заключается в исследовании -окрестности,текущей точки поискаX k при значении , обеспечивающем нахождение в этой окрестности по крайней мере еще одной точки. ЕслиF(X k ) F(X j ), гдеX j – любая точка в исследуемой - окрестности, тоX k принимается в качестве точки локального экстремума. Если же найдется точка с лучшим значением целевой функции, то она становится новой текущей точкой поиска и происходит переход к следующему шагу. Для реализации метода локальной оптимизации нужно установить способы выбора начальной точки поиска, величины , правила возможного изменения в процессе поиска и т.п. При больших увеличивается трудоемкость поиска, при малых снижается надежность определения глобального экстремума.

Метод ветвей и границ заключается в разбиении конечного множества, на котором ищется экстремум, на несколько подмножеств и в выяснении перспективности каждого из них. Если подмножество неперспективно, оно исключается из рассмотрения. Если в подмножестве может находиться экстремум, оно подвергается дальнейшему разбиению и исследованию. Разбиения и исследования продолжаются до тех пор, пока не будет выявлена единственная наилучшая точка. Исключение из рассмотрения неперспективных точек обусловливает направленность перебора. В большинстве задач дискретного программирования оценки перспективности подмножеств точек могут быть только приближенными. Если применяются излишне оптимистические оценки перспективности, перебор начинает приближаться к полному, увеличиваются потери на поиск. Если правила выбора перспективных ветвей излишне пессимистические, то снижается надежность определения экстремума.

Идеи метода ветвей и границ находят применение во многих алгоритмах решения комбинаторных задач в процессе автоматизированного проектирования.

литература

1. Норенков И.П., Маничев В.Б. Основы теории и проектирования САПР: Учеб. для втузов по спец. «Вычислительные машины комплексы, системы и сети». М.: Высш. шк., 1990. 335 с.

2. САПР: Учеб. пособ. для втузов / Под ред. И.П. Норенкова. Минск: Вышейш. шк., 1987. Кн. 1: Принципы построения и структура / И.П. Норенков.1987. 127 с.; Кн. 2: Технические средства и ОС / Д.М. Жук и др. 1988. 155 с.; Кн. 4: Математические модели технических объектов / В.А. Трудоношин, Н.В. Пивоварова. 1988. 158 с.; Кн. 7: Лабораторный практикум / Т.И. Булдакова и др. 1988. 143 с.; Кн. 8: Сборник примеров и задач / Д.М. Жук и др. 1988. 141 с.

3.Бугров В. Г. Основы построения САПР: Конспект лекций. Калинин: Калининский гос. ун-т.1982. 46 с.

4.Разработка САПР: В 10 кн. / Под ред. А.В. Петрова. М.: Высш. шк., 1990. Кн. 1: Проблемы и принципы создания САПР / А.В. Петров, В.М. Черненький. 1990. 144 с.

5.Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем: Пер. с англ. М.: Радио и связь, 1988. 560 с.

6.Самарский А.А., Гулин А.В. Численные методы: Учеб. пособ. для вузов.

М.: Наука, 1989. 432 с.

7.Очков В.Ф. Mathcad PLUS 6.0 для студентов и инженеров. – М.: Компьютер-Пресс,1996. – 238 с.

8.Дьяков В.П., Абраменкова Н.В. Mathcad 7.0 в математике, физике и в Internet. – М.: Нелидж, 1998. – 352 с.

9.Дьяков В.П. Mathcad 2001: Учебный курс. – СПб.: Питер, 2001. – 621 с.

10.Карлащук В.Н. Электронная лаборатория на IBM РС. Программа Electronic Workbench и ее применение. – М.: СОЛОН-Р,2000. – 506 с.

studfiles.net

Дискретная оптимизация. Задачи и методы дискретной оптимизации, страница 2

Частным случаем данной задачи является задача о выборе заявок – дано  заявок на проведение занятий в одной и той же аудитории. Для каждого занятия известно время его проведения , где  - соответственно время начала и окончания занятия. Два разных занятия не могут перекрываться по времени, но начало одного может совпадать с окончанием другого. Требуется выбрать максимальное число совместимых по времени занятий.

     К числу распространённых задач дискретной оптимизации также относятся задачи нахождения кратчайшего пути на графе и максимального потока в сети.

     Следует отметить, что для решения разных задач может быть использован один и тот же метод (в рамках которого могут быть использованы различные алгоритмы), а также – одна и та же задача может быть решена различными методами (и, соответственно, различными алгоритмами). Это обстоятельство проиллюстрируем следующим примером соответствия между задачами дискретной оптимизации и существующими методами их решения (рис. 1).

                   МЕТОДЫ                                    ЗАДАЧИ

 

  ВЕТВЕЙ И ГРАНИЦ                                     О РЮКЗАКЕ

   ДИНАМИЧЕСКОГО                                        О КРАТЧАЙШЕМ ПУТИ

ПРОГРАММИРОВАНИЯ

           ЖАДНЫЙ                                                КОММИВОЯЖЁРА

Рис. 1

   Так,  метод ветвей и границ (МВГ), упомянутый в рис. 1, относится к числу методов, учитывающих комбинаторный характер задачи оптимизации. Он основан на упорядоченном переборе вариантов, т.е. рассмотрении лишь тех из них, которые оказываются перспективными по некоторым признакам, и отбрасывании целых множеств вариантов, являющихся, соответственно, бесперспективными. Таким образом, на каждом из этапов решения задачи дискретной оптимизации с помощью МВГ множество возможных выборов сужается.

     Хорошей иллюстрацией общей идеи МВГ служит задача отыскания фальшивой монеты в мешке с монетами, если известно, что фальшивая монета весит меньше настоящей, посредством деления мешка на части и взвешивания этих частей.

          Общая схема МВГ следующая. Вначале исходное множество

решений (вариантов) по некоторым признакам разбивается на некоторое число подмножеств , одно из которых обязательно включает оптимальный вариант . (Например, в задаче о кратчайшем пути это есть подмножества тех путей, которые могут быть получены продолжением одной из исходящих из начальной вершины дуг.) Для каждого из подмножеств  находится нижняя оценка целевой функции , т.е. такие числа , что .

     Затем определяется оценка , удовлетворяющая условию

, после чего соответствующее подмножество  разбивается на некоторое число подмножеств, для каждого из которых отыскивается своя оценка, т.е. и  и т.д.

        Если после некоторого числа ветвлений, например, , получается оценка , удовлетворяющая условию , то оптимальным решением будет , т.е. соответствующему граничному подмножеству и при этом . Следует отметить, что МВГ – точный метод решения комбинаторных задач.

     В приближённых методах, исходя из определённых эвристических предпосылок по относительно простым правилам строятся допустимые решения, которые могут быть удовлетворительными с практической точки зрения, хотя они могут и не быть оптимальными.  К числу таких методов относится жадный (или метод жадного выбора решений), общая идея которого состоит в том, что на каждом шаге выбирается самый лучший вариант. При решении большинства задач данный метод будет приближённым в силу того, что при формировании окончательного решения не учитывается предистория решений, полученных на предыдущих шагах. В то же время для некоторых задач данный метод позволяет получить оптимальное решение.

В методах случайного поиска организуется случайный перебор точек множества  такой, что существует вероятность выбора любого из допустимых решений (граничных подмножеств множества ). Поэтому, при достаточно большом числе испытаний оптимальное решение будет выбрано с вероятностью, сколь угодно близкой к единице.

1      – Число рёбер полного графа с  вершинами есть .

2      – Мощность множества гамильтоновых циклов полного графа, включающего  вершин, есть , т.е. число перестановок из  элементов без повторения.

vunivere.ru

3.11 Дискретная оптимизация

Рис. 3.14

будут видеть определённые в схеме векторы. Этим переменным присвоены конкретные значения из соответствующего вектора, например, L0=Len[15], т.е. переменнойL0 присваивается значение15-гоэлемента из вектораLen, которое равно 114 (здесь все размеры в mil). Чтобы увидеть, какие конкретно значения имеют эти введённые переменные, нужно дополнительно определить такие же переменные с двоеточием, например,L0: (см. рис. 3.12). После выполнения анализа или оптимизации значения этих переменных будут показаны (см. рис. 3.13). Теперь можно присвоить значения параметрам симметричных элементов в схеме, например первому и

последнему отрезкам связанных линий присвоены значения W=W0, S=S0, L=L0 (см. схему рис. 3.12).

Установка ограничений на значения Рис. 3.13 оптимизируемых параметров и установка целей производится обычным образом, как и

при непрерывной оптимизации.

Пример 3.1.

В качестве примера рассмотрим оптимизацию фильтра из примера 2.1 предыдущей гла-

вы.

Выберите File > Open Project в выпадающем меню и откройте проектCFil.

Сделайте активным окно схемы, щёлкнув левой кнопкой мышки по видимой части этого окна, или дважды щёлкните по подгруппе Fil в окне просмотра проекта.

Назначьте переменные для оптимизации и введите ограничения на их значения. Для этого щёлкните левой кнопкой мышки по переменной s1 и затем щёлкните правой кнопкой по этой переменной. Во всплывающем меню выберитеProperties. Откроется диалоговое окноEdit Equation (Рис. 3.14). В областиMode отметьтеTune,Optimize иConstrained. Введите ниж-

нюю границу допустимого значения этой переменной 0.05 в полеLower bound и верхнюю гра-

ницу 0.2в поле Upper bound

и нажмите OK. Аналогично назначьте переменныe.s2, установив ограничения0.1 и0.5, а такжеL1, установив ограничения8 и13.

Затем назначьте для оптимизации длину среднего резонатора. Дважды щелкните по элементу среднего резонатора (TL5) и в открыв-

шемся окне Element Options

(Рис. 3.15) отметьте столбцы

Tune, Optи Limitнапротив параметра L. Введите нижнюю допустимую границу длины резонатора 8в столбце Lowerи верхнюю границу 13в столбце Upperи нажмите

OK.

Сделайте активным окно графика потерь S21, щёлкнув левой кнопкой мышки по видимой части этого окна, или дважды щёлкните по подгруппеS21 в окне просмотра проекта. Выполните анализ, щёлкнув мышкой по значкуAnalyze на панели инструментов.

Рис. 3.15

studfiles.net

Prostoy-Site | Все права защищены © 2018 | Карта сайта