Задача - дискретная оптимизация. Дискретная оптимизация это
Дискретная оптимизация.
Дискретная оптимизация — категория оптимизации, концепция которой используется в области компьютерных наук и математики. В отличие от конкретной или непрерывной оптимизации, дискретная оптимизация использует только целые числа, а не дроби, чтобы выполнить максимизацию функций, что и является целью всей оптимизации. В дальнейшем есть возможность разделить дискретную оптимизацию в целочисленное программирование и комбинаторную оптимизацию.Непрерывная оптимизация относится к максимизации функций с непрерывными, реальными цифрами, начиная от набора целых чисел и всеми значения, которые лежат между ними. Это означает, что численные значения которые используются могут представлять любое значение, которое может проявляться как в реальном физическом мире так и в абстрактном мире математики. Отрицательные числа, а также дроби и десятичные, которые работают на неопределенный срок. Эта форма оптимизации является наиболее сложной, и она принимает наиболее точный подход к математической функции.
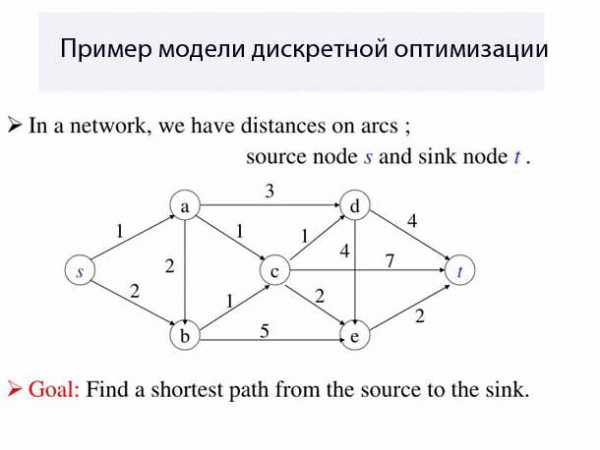
Другая ветвь дискретной оптимизации, в целом, это движущая цель оптимизации и она остаётся прежней — максимизировать результаты математических функций, так как они применяются в вычислительной технике или других областях. В отличие от своего аналога непрерывной оптимизации, этот тип оптимизации имеет дело только с дискретными численными значениями. Это конкретные числа, например, число 2 или 647. В то время как другая ветвь проходит вдоль линии, этой дискретной ветке не хватает плавных переходов от одного целого числа к другому — фракции, которые лежат между ними не в счёт.
Как и в области самой оптимизации, дискретную оптимизацию можно разделить на две категории: целочисленное программирование и комбинаторная оптимизация. В области компьютерных наук, целочисленные переменные пределы программирования находятся в программе в целых числах, то есть дроби и отрицательные числа запрещены в программе. Комбинаторная оптимизация используется в компьютерных науках, а также в области математики, и она довольно сложная. Она предполагает интеграцию операций оптимизации и решения в разных видах графики. Из-за конечного и конкретного характера дискретных числовых значений, графики не гладкие, а наоборот, подчеркивают различия на вертикальных и горизонтальных осях, которые появляются между двумя значениями.
Где и как используется непрерывная или дискретная оптимизация — это зависит исключительно от области и целей конкретного проекта. Помимо математики и компьютерных приложений, в области машиностроения, экономики, или механических наук, могут быть использованы различные виды оптимизации. Согласно проекту, это может быть, ни дискретная, ни непрерывная оптимизация — их только две и в других категориях оптимизации.
mega-obzor.ru
дискретная оптимизация - это... Что такое дискретная оптимизация?
дискретная оптимизация мат. discrete optimizationБольшой англо-русский и русско-английский словарь. 2001.
- дискретная однородность
- дискретная переменная
Смотреть что такое "дискретная оптимизация" в других словарях:
Дискретная оптимизация — Дискретное программирование (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные… … Википедия
Шевченко, Валерий Николаевич — Валерий Николаевич Шевченко Дата рождения: 17 июня 1940(1940 06 17) (72 года) Место рождения: Минск … Википедия
Асанов, Магаз Оразкимович — Магаз Оразкимович Асанов Дата рождения: 18 февраля 1951(1951 02 18) (61 год) Место рождения: Зыряновск Научная сфера: топология Место работы: Уральский университет … Википедия
Кафедра математической логики и высшей алгебры (Нижегородский государственный университет) — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/30 октября 2012. Пока процесс обсужден … Википедия
Кафедра математической логики и высшей алгебры — Нижегородский государственный университет им Н. И. Лобачевского Факультет вычислительной математики и кибернетики Заведующий кафедрой Шевченко, Валерий Николаевич … Википедия
Критерий оптимальности — Критерий оптимальности (критерий оптимизации) характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может… … Википедия
Гимади Эдуард — Эдуард Гимади (ранее Гимадутдинов) Дата рождения: 1937(1937) Место рождения: Казань Гражданство: РФ Место работы: Институт математики СОРАН Альма матер: Казанский государственный университет, физ мат Гимади (ранее Гимадутдинов)Эдуард… … Википедия
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ — раздел математического программирования, в к ром исследуется задача оптимизации (максимизации пли минимизации) функции нескольких переменных, связанных рядом уравнений и (или) неравенств и удовлетворяющих условию целочисленности (используются… … Математическая энциклопедия
Московский государственный университет приборостроения и информатики — (МГУПИ) Международное название Moscow State University of Instrument Engineering and Computer Science Год основания … Википедия
Дискретное программирование — (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные значения, например, целочисленные … Википедия
ИМИТ ОмГУ — Связать? Институт математики и информационных технологий Омский государственный университет им. Ф.М. Достоевского … Википедия
Книги
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков В.. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 643 руб
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 568 грн (только Украина)
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 552 руб
dic.academic.ru
дискретная оптимизация - это... Что такое дискретная оптимизация?
дискретная оптимизацияdiscrete optimization
Англо-русский словарь технических терминов. 2005.
- дискретная модель
- дискретная свертка
Смотреть что такое "дискретная оптимизация" в других словарях:
Дискретная оптимизация — Дискретное программирование (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные… … Википедия
Шевченко, Валерий Николаевич — Валерий Николаевич Шевченко Дата рождения: 17 июня 1940(1940 06 17) (72 года) Место рождения: Минск … Википедия
Асанов, Магаз Оразкимович — Магаз Оразкимович Асанов Дата рождения: 18 февраля 1951(1951 02 18) (61 год) Место рождения: Зыряновск Научная сфера: топология Место работы: Уральский университет … Википедия
Кафедра математической логики и высшей алгебры (Нижегородский государственный университет) — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/30 октября 2012. Пока процесс обсужден … Википедия
Кафедра математической логики и высшей алгебры — Нижегородский государственный университет им Н. И. Лобачевского Факультет вычислительной математики и кибернетики Заведующий кафедрой Шевченко, Валерий Николаевич … Википедия
Критерий оптимальности — Критерий оптимальности (критерий оптимизации) характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может… … Википедия
Гимади Эдуард — Эдуард Гимади (ранее Гимадутдинов) Дата рождения: 1937(1937) Место рождения: Казань Гражданство: РФ Место работы: Институт математики СОРАН Альма матер: Казанский государственный университет, физ мат Гимади (ранее Гимадутдинов)Эдуард… … Википедия
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ — раздел математического программирования, в к ром исследуется задача оптимизации (максимизации пли минимизации) функции нескольких переменных, связанных рядом уравнений и (или) неравенств и удовлетворяющих условию целочисленности (используются… … Математическая энциклопедия
Московский государственный университет приборостроения и информатики — (МГУПИ) Международное название Moscow State University of Instrument Engineering and Computer Science Год основания … Википедия
Дискретное программирование — (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные значения, например, целочисленные … Википедия
ИМИТ ОмГУ — Связать? Институт математики и информационных технологий Омский государственный университет им. Ф.М. Достоевского … Википедия
Книги
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков В.. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 643 руб
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 568 грн (только Украина)
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 552 руб
dic.academic.ru
Задача - дискретная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 3
Задача - дискретная оптимизация
Cтраница 3
Решение задач дискретной оптимизации связано с трудностями принципиального характера. Полный перебор точек допустимого множества, как правило, неосуществим из-за слишком большого объема вычислительной работы. [31]
Центральным алгоритмом в описываемом подходе является алгоритм кластеризации - разбиения множества точек на непересекающиеся подмножества близких точек. Задача кластеризации - это задача дискретной оптимизации, для ее решения применяются стандартные подходы: построение начального разбиения и его улучшение. [32]
Многие из методов решения задач дискретной оптимизации основаны на идее перебора вариантов, качество алгоритма оценивается числом точек х, для которых вычислялись значения f ( x) или значения некоторых других функций. Выше было отмечено, что объем вычислительной работы резко возрастает с ростом числа переменных. Поэтому перебор большого числа вариантов принципиально невозможен ни при каком быстродействии ЭВМ, хотя рост быстродействия ЭВМ позволяет решать задачи, решение которых на ЭВМ с более низким быстродействием не представлялось возможным. [33]
Далее в этой главе приводятся определения, некоторые полезные идеи и теоремы и дается краткое изложение материала, касающегося рассматриваемых здесь вопросов для непрерывного случая, когда можно использовать методы математического анализа. В конце главы приводятся примеры задач дискретной оптимизации. [34]
Задачи геометрического проектирования, как правило, имеют большую размерность. Вместе с тем эффективность точных методов решения задач дискретной оптимизации существенно зависит от размерности, причем с ее возрастанием резко увеличивается объем вычислений, необходимых для отыскания точного решения. Обычно он настолько велик, что точно решить задачу за реальное время не возможно. Поэтому возникает необходимость в выборе эффективных приближенных методов дискретной оптимизации. В настоящее время разработано большое число приближенных методов, например [5, 22, 33, 43, 44, 151, 155, 160,161] и др., успешно применяемых при решении различных практических задач, в том числе задач геометрического проектирования. Ниже описан метод вектора спада согласно работам [114, 115] и его применение иллюстрируется к задачам разбиения и покрытия. [35]
Рассмотрим примеры двух задач дискретной оптимизации: задачу о ранце и задачу о коммивояжере. Эти задачи часто рассматриваются как тестовые при разработке алгоритмов решения задач дискретной оптимизации. [36]
Задачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации. [37]
В настоящей главе приводится обзор современного состояния целочисленного программирования. Здесь излагаются идеи основных методов ( точных ( § 2) и приближенных ( § 3)) решения задач дискретной оптимизации. В § 4, 5 изложено состояние вопроса о вычислительной сложности задач целочисленного программирования. [38]
В последнее время в нашей стране создан целый ряд автоматизированных систем, в том числе систем, предназначенных для автоматизированного решения с помощью ЭВМ многих задач проектирования вычислительных средств, размещения промышленных предприятий, проектирования сложных инженерных сооружений, автоматизированной обработки данных в реальном масштабе времени, характеризующих быстропротекающие процессы различной природы. Получены интересные результаты в области разработки и исследования новых математических моделей ряда важных процессов, создания эффективных математических методов решения задач, возникающих при построении всевозможных автоматизированных систем, в частности, задач дискретной оптимизации в различных постановках, и их современного программного обеспечения. В этом интенсивно развивающемся научном направлении важные результаты получены различными коллективами ученых под руководством академиков В. М. Глушкова, А. А. Дородницына, чл. [39]
В задачах регулярного математического программирования значительная часть методов основана на следующем исходном положении: если точки ж1 Е G и х2 Е G близки, то значения / ( ж1) и / ( ж2) также близки. В задачах дискретной оптимизации это положение не имеет места. Если в этом классе задач удается ввести естественным образом понятие окрестности, то близкие точки из этой окрестности могут сколь угодно значительно отличаться по значениям функции. В некоторых задачах дискретной оптимизации не удается естественным образом ввести понятие окрестности, оно вводится с помощью искусственных построений. [40]
Алгоритмы локальной оптимизации связаны с понятием окрестности. В регулярных задачах математического программирования это понятие вводится естественным образом и является основным при разработке алгоритмов и исследовании их сходимости. Во многих задачах дискретной оптимизации понятие окрестности не удается ввести естественным образом, в этом состоит одна из принципиальных трудностей, возникающих при решении задач этого типа. [41]
В действительности схемы сетей намного сложнее, чем на рис. 4.17. В ряде узлов имеются КУ разных типов. При отказе от допущений 1) - 4) задача оптимизации становится нелинейной и сильно усложняется из-за учета напряжений и нелинейности стоимости КУ. В наиболее общем виде эта задача дискретной оптимизации, так как мощность компенсирующих устройств, например БК, меняется дискретно, а не непрерывно. [42]
В нашем случае переборный путь состоит в перечислении всех 2 подмножеств V, отборе из них / / ( G) и. Объем перебора растет при этом очень быстро - экспоненциально - с ростом числа вершин гиперграфов. Существуют различные эвристические приемы сокращения перо-бора в задачах дискретной оптимизации, фигурирующие обычно под шифром метода ветвей и границ. [43]
Задачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации. [44]
Возникает задача вычислительной оценки с предварительным исключением абсурдных и неконкурентоспособных вариантов. В основу их положен принцип представления процесса решения в виде многоступенчатой структуры. Каждая ступень связана с проверкой наличия тех или иных свойств у подмножества вариантов, по которым либо непосредственно сокращается исходное множество, либо подготавливается возможность такого сокращения в будущем. Одним из правил отсева бесперспективных вариантов является принцип монотонной рекурсивности, применяемый для решения задач дискретной оптимизации при пошаговом конструировании вариантов. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
дискретная оптимизация - это... Что такое дискретная оптимизация?
дискретная оптимизациядыскрэтная аптымізацыя
Русско-белорусский математический словарь. 2013.
- дискретная математика
- дискретная случайная величина
Смотреть что такое "дискретная оптимизация" в других словарях:
Дискретная оптимизация — Дискретное программирование (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные… … Википедия
Шевченко, Валерий Николаевич — Валерий Николаевич Шевченко Дата рождения: 17 июня 1940(1940 06 17) (72 года) Место рождения: Минск … Википедия
Асанов, Магаз Оразкимович — Магаз Оразкимович Асанов Дата рождения: 18 февраля 1951(1951 02 18) (61 год) Место рождения: Зыряновск Научная сфера: топология Место работы: Уральский университет … Википедия
Кафедра математической логики и высшей алгебры (Нижегородский государственный университет) — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/30 октября 2012. Пока процесс обсужден … Википедия
Кафедра математической логики и высшей алгебры — Нижегородский государственный университет им Н. И. Лобачевского Факультет вычислительной математики и кибернетики Заведующий кафедрой Шевченко, Валерий Николаевич … Википедия
Критерий оптимальности — Критерий оптимальности (критерий оптимизации) характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может… … Википедия
Гимади Эдуард — Эдуард Гимади (ранее Гимадутдинов) Дата рождения: 1937(1937) Место рождения: Казань Гражданство: РФ Место работы: Институт математики СОРАН Альма матер: Казанский государственный университет, физ мат Гимади (ранее Гимадутдинов)Эдуард… … Википедия
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ — раздел математического программирования, в к ром исследуется задача оптимизации (максимизации пли минимизации) функции нескольких переменных, связанных рядом уравнений и (или) неравенств и удовлетворяющих условию целочисленности (используются… … Математическая энциклопедия
Московский государственный университет приборостроения и информатики — (МГУПИ) Международное название Moscow State University of Instrument Engineering and Computer Science Год основания … Википедия
Дискретное программирование — (дискретная оптимизация) раздел математического программирования. В противоположность задачам оптимизации с непрерывными переменными, переменные в задачах дискретного программирования принимают только дискретные значения, например, целочисленные … Википедия
ИМИТ ОмГУ — Связать? Институт математики и информационных технологий Омский государственный университет им. Ф.М. Достоевского … Википедия
Книги
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков В.. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 643 руб
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 568 грн (только Украина)
- Дискретная оптимизация. Модели, методы, алгоритмы решения прикладных задач, Струченков Валерий Иванович. Эта книга для всех, кто, не имея специального математического образования, хочет узнать, как применять методы оптимизации для решения практических задач. В ней рассматриваются прикладные… Подробнее Купить за 552 руб
math_ru_be.academic.ru
|
|
|
rabotafornew.ru
Задача - дискретная оптимизация
Главная » Новости
Опубликовано: 15.10.2017
Гимади Э.Х. Алгоритмы с оценками и асимптотически точные алгоритмы для задач дискретной оптимизацииЗадачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации.
М. И. Харитонов "Задачи дискретной оптимизации маршрутизации потоков в современных сетях связи" Задачи дискретной оптимизации часто встречаются во всех сферах практической деятельности. Ограничимся здесь одним примером ( другие см. в гл. Для большинства задач дискретной оптимизации явный вид всех граней до настоящего времени не найден. Наиболее интересные результаты получены для многогранников задачи об упаковке, задачи о максимальном паро-сочетании графа, задачи коммивояжера, задачи о рюкзаке ( все они приводятся в гл. На принципиальную возможность получения такого описания указывает еще теорема Гильберта о конечном базисе кольца многочленов, однако эффективные методы до сих пор не получены. IV излагается подход к построению методов аналитического и параметрического описания целых точек многогранников, основанный на выделении порождающих множеств полугрупп. Д. С. Миненков "Задачи распределения ресурсов в сетях 4G как стохастическая оптимизация" Z называется задачей дискретной оптимизации. В [13] рассматриваются задачи дискретной оптимизации, для решения которых применяется аппроксимационно-комбинаторный метод. Рассмотрим примеры двух задач дискретной оптимизации: задачу о ранце и задачу о коммивояжере. Эти задачи часто рассматриваются как тестовые при разработке алгоритмов решения задач дискретной оптимизации. Например, сложными являются задачи дискретной оптимизации, где точные алгоритмы имеют обычно экспоненциальную сложность и нереализуемы за приемлемое время. Алгоритмы и программы решения задач дискретной оптимизации / Сост. Существует несколько схем решения задач дискретной оптимизации. Очевидно, что в задачах дискретной оптимизации область допустимых решений ( или область работоспособности) D является невыпуклой и несвязной. Ограниченность возможностей точных методов решения задач дискретной оптимизации естественным образом приводит к идее разработки комбинированных алгоритмов, в которых объединялись преимущества методов и, по возможности, отсутствовали их недостатки. Как следует из общей постановки задач дискретной оптимизации, основное влияние на формальную постановку таких задач имеет пространство X, в котором рассматривается данная конкретная задача, что естественным образом отражается на способе ( алгоритме) ее решения. Учет ограничений типа неравенств в задаче дискретной оптимизации незначительно усложняет процедуру случайного поиска. Излагаются современные комбинаторные алгоритмы для решения задач дискретной оптимизации с применением компьютерных средств. Основное внимание уделяется вычислительной реализации алгоритмов. Приводятся результаты вычислительного исследования алгоритмов для классических задач дискретной оптимизации - задачи о ранце и задачи о коммивояжере. Приведено много примеров для самостоятельной работы. Одним из наиболее мощных методов решения задач дискретной оптимизации является метод последовательного анализа ваоиантов. В настоящем параграфе приводится общее описание метода последовательного анализа вариантов, придерживаясь работ [19, 20, 84], и иллюстрируются возможности его применения к некоторым задачам геометрического проектирования. НСМ может быть применен к широкому кругу задач дискретной оптимизации и структурного синтеза, характеризуемых следующими особенностями. Основная тематика: теория графов и гиперграфов, задачи дискретной оптимизации, приложения к структурной химии; рассматриваются также вопросы обоснования теории множеств, алгебры, математической логики и специальной теории относительности. Подобная математическая модель в виде графа широко используется в задачах дискретной оптимизации. В данном учебном пособии отражен мой многолетний опыт по решению задач дискретной оптимизации. Главы 8 10 написаны на основании научных результатов, полученных мною за время многолетней работы в Вычислительном центре им. Предлагается общий подход для формирования двойственных оценок для широкого класса задач дискретной оптимизации. Подход основывается на введении разрешающей функции и трактовке каждого из рассматриваемых видов двойственности как специального случая задания этой функции. Подход позволяет с единых позиций объяснить большинство существующих видов двойственности, установить их взаимосвязь, предложить новые виды двойственности и алгоритмы на их основе. Указанные особенности обусловливают сложность решения задач синтеза расписаний, являющихся задачами дискретной оптимизации. Рассматриваются оценки отклонения некоторых приближенных решений от оптимального решения в задачах дискретной оптимизации. Особое внимание уделяется отклонению от оптимума, следующего после оптимального решения задачи. Предложена общая схема получения таких оценок, которая конкретизирована для задач о целочисленном и булевом ранце с одним ограничением и задачи коммивояжера с симметричной матрицей расстояний. Основная особенность полученных результатов состоит в том, что указанные оценки зависят лишь от параметров исходной задачи и некоторых ее решений, для нахождения которых не требуется существенных затрат вычислительных ресурсов. Сформулированные принципы носят общий характер и применяются не только в задачах дискретной оптимизации. Уравнение, являющееся математической формулировкой принципа оптимальности ( например, уравнение (4.1)), часто называют уравнением Беллмана. Данный пакет программ, как уже отмечалось, ориентирован на решение задач дискретной оптимизации, являющихся комбинаторными задачами. Переход от параметрической формы задания выпуклого многогранника к аналитической имеет большое значение для задач дискретной оптимизации, так как позволяет сформулировать их в терминах линейного программирования. При возникновении новых нестандартных задач реализация алгоритмов их решения требует информации о технологии решения задач дискретной оптимизации. Итак, основной целью данного учебного пособия является изложение современных комбинаторных алгоритмов для практического решения задач дискретной оптимизации. При этом вовсе не ставится цель разработать такой алгоритм, который решает любую задачу ( например, задачу коммивояжера) с любой заранее заданной точностью: такая цель недостижима, что следует непосредственно из результатов, полученных в теории сложности алгоритмов. Для задачи коммивояжера необходимо разработать алгоритм, расширяющийся с учетом особенностей задачи и позволяющий получить приближенное решение с оценкой отклонения от оптимума. Существуют задачи из класса NP ( например, общая задача частично целочисленного линейного программирования), для которых даже эта цель недостижима, так как трудоемкость получения хотя бы одного допустимого решения сравнима с трудоемкостью нахождения оптимального решения. Мой учитель академик Н. Н. Моисеев еще в середине 60 - х годов во время моего обучения в аспирантуре обратил внимание на задачи дискретной оптимизации. Все изложенные здесь мои результаты неоднократно обсуждались в наших беседах и докладывались на проводимых им научных школах и семинарах. Данные табл. 2.1 - 2.4 интересны также тем, что они свидетельствуют о преимуществе НСМ перед обычными эвристическими методами решения задач дискретной оптимизации. В последующих параграфах этой главы исследуются точные ( § III.1 - III.5) и приближенные ( § III.6) методы решения задач дискретной оптимизации. Решение задач дискретной оптимизации связано с трудностями принципиального характера. Полный перебор точек допустимого множества, как правило, неосуществим из-за слишком большого объема вычислительной работы. Центральным алгоритмом в описываемом подходе является алгоритм кластеризации - разбиения множества точек на непересекающиеся подмножества близких точек. Задача кластеризации - это задача дискретной оптимизации, для ее решения применяются стандартные подходы: построение начального разбиения и его улучшение. Многие из методов решения задач дискретной оптимизации основаны на идее перебора вариантов, качество алгоритма оценивается числом точек х, для которых вычислялись значения f ( x) или значения некоторых других функций. Выше было отмечено, что объем вычислительной работы резко возрастает с ростом числа переменных. Поэтому перебор большого числа вариантов принципиально невозможен ни при каком быстродействии ЭВМ, хотя рост быстродействия ЭВМ позволяет решать задачи, решение которых на ЭВМ с более низким быстродействием не представлялось возможным. Далее в этой главе приводятся определения, некоторые полезные идеи и теоремы и дается краткое изложение материала, касающегося рассматриваемых здесь вопросов для непрерывного случая, когда можно использовать методы математического анализа. В конце главы приводятся примеры задач дискретной оптимизации. Задачи геометрического проектирования, как правило, имеют большую размерность. Вместе с тем эффективность точных методов решения задач дискретной оптимизации существенно зависит от размерности, причем с ее возрастанием резко увеличивается объем вычислений, необходимых для отыскания точного решения. Обычно он настолько велик, что точно решить задачу за реальное время не возможно. Поэтому возникает необходимость в выборе эффективных приближенных методов дискретной оптимизации. В настоящее время разработано большое число приближенных методов, например [5, 22, 33, 43, 44, 151, 155, 160,161] и др., успешно применяемых при решении различных практических задач, в том числе задач геометрического проектирования. Ниже описан метод вектора спада согласно работам [114, 115] и его применение иллюстрируется к задачам разбиения и покрытия. Рассмотрим примеры двух задач дискретной оптимизации: задачу о ранце и задачу о коммивояжере. Эти задачи часто рассматриваются как тестовые при разработке алгоритмов решения задач дискретной оптимизации. Задачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации. В настоящей главе приводится обзор современного состояния целочисленного программирования. Здесь излагаются идеи основных методов ( точных ( § 2) и приближенных ( § 3)) решения задач дискретной оптимизации. В § 4, 5 изложено состояние вопроса о вычислительной сложности задач целочисленного программирования. В последнее время в нашей стране создан целый ряд автоматизированных систем, в том числе систем, предназначенных для автоматизированного решения с помощью ЭВМ многих задач проектирования вычислительных средств, размещения промышленных предприятий, проектирования сложных инженерных сооружений, автоматизированной обработки данных в реальном масштабе времени, характеризующих быстропротекающие процессы различной природы. Получены интересные результаты в области разработки и исследования новых математических моделей ряда важных процессов, создания эффективных математических методов решения задач, возникающих при построении всевозможных автоматизированных систем, в частности, задач дискретной оптимизации в различных постановках, и их современного программного обеспечения. В этом интенсивно развивающемся научном направлении важные результаты получены различными коллективами ученых под руководством академиков В. М. Глушкова, А. А. Дородницына, чл. В задачах регулярного математического программирования значительная часть методов основана на следующем исходном положении: если точки ж1 Е G и х2 Е G близки, то значения / ( ж1) и / ( ж2) также близки. В задачах дискретной оптимизации это положение не имеет места. Если в этом классе задач удается ввести естественным образом понятие окрестности, то близкие точки из этой окрестности могут сколь угодно значительно отличаться по значениям функции. В некоторых задачах дискретной оптимизации не удается естественным образом ввести понятие окрестности, оно вводится с помощью искусственных построений. Алгоритмы локальной оптимизации связаны с понятием окрестности. В регулярных задачах математического программирования это понятие вводится естественным образом и является основным при разработке алгоритмов и исследовании их сходимости. Во многих задачах дискретной оптимизации понятие окрестности не удается ввести естественным образом, в этом состоит одна из принципиальных трудностей, возникающих при решении задач этого типа. В действительности схемы сетей намного сложнее, чем на рис. 4.17. В ряде узлов имеются КУ разных типов. При отказе от допущений 1) - 4) задача оптимизации становится нелинейной и сильно усложняется из-за учета напряжений и нелинейности стоимости КУ. В наиболее общем виде эта задача дискретной оптимизации, так как мощность компенсирующих устройств, например БК, меняется дискретно, а не непрерывно. В нашем случае переборный путь состоит в перечислении всех 2 подмножеств V, отборе из них / / ( G) и. Объем перебора растет при этом очень быстро - экспоненциально - с ростом числа вершин гиперграфов. Существуют различные эвристические приемы сокращения перо-бора в задачах дискретной оптимизации, фигурирующие обычно под шифром метода ветвей и границ. Задачи дискретной оптимизации - это задачи нахождения экстремума функции, заданной на дискретном ( чаще всего - конечном) множестве точек. Если область определения функции состоит из конечного числа точек, то задачу дискретной оптимизации всегда, в принципе, можно решить перебором всего этого множества. Однако на практике это множество хоть и конечно, но может быть очень велико, так что методы перебора не эффективны. Рассмотрим несколько общих подходов к решению задач дискретной оптимизации. Возникает задача вычислительной оценки с предварительным исключением абсурдных и неконкурентоспособных вариантов. В основу их положен принцип представления процесса решения в виде многоступенчатой структуры. Каждая ступень связана с проверкой наличия тех или иных свойств у подмножества вариантов, по которым либо непосредственно сокращается исходное множество, либо подготавливается возможность такого сокращения в будущем. Одним из правил отсева бесперспективных вариантов является принцип монотонной рекурсивности, применяемый для решения задач дискретной оптимизации при пошаговом конструировании вариантов. В задачах регулярного математического программирования значительная часть методов основана на следующем исходном положении: если точки ж1 Е G и х2 Е G близки, то значения / ( ж1) и / ( ж2) также близки. В задачах дискретной оптимизации это положение не имеет места. Если в этом классе задач удается ввести естественным образом понятие окрестности, то близкие точки из этой окрестности могут сколь угодно значительно отличаться по значениям функции. В некоторых задачах дискретной оптимизации не удается естественным образом ввести понятие окрестности, оно вводится с помощью искусственных построений. В § 11.8 указано, что задачи геометрического проектирования имеют ярко выраженную дискретно-континуальную структуру. Таким образом, существует взаимосвязь непрерывной и дискретной вероятностных моделей задач геометрического проектирования. Непрерывная вероятностная модель соответствует исходной постановке задачи в непрерывной формулировке. В этом случае вероятностная мера задается на всем множестве допустимых решений. Дискретная вероятностная модель соответствует задаче дискретной оптимизации, возникающей на этапе перебора локальных экстремумов. Здесь вероятностная мера задается не на всем множестве допустимых решений целевой функция, а на дискретном множестве точек, соответствующих локальным экстремумам ( или их приближениям) этой функции.paynetsystems.ru