Программы и алгоритмы оптимизации. Алгоритмы оптимизации

6. Оптимизация алгоритмов. Оценка сложности алгоритмов

Программы и алгоритмы оптимизации

Здесь нет описаний конкретных алгоритмов и программ. Скорее - общие рассуждения на заданную тему...

Параметрическая оптимизация - тема, которой я увлеченно занимался в начале своей программистской деятельности и к которой не раз возвращался в тех или иных обстоятельствах.

От самой первой своей уже "инженерной" задачи, оказавшейся, ни много, ни мало - решением системы нелинейных алгебраических уравнений методом - только не надо смеяться, была проявлена инженерная смекалка! - дихотомии. Здесь я впервые на собственной шкуре узнал, как важно знать, где искать. И как полезно правильно определить интервал унимодальности при одномерном поиске. А заодно, с цифрами, то бишь, с распечатками в руках показал своим теоретикам, что их задача имеет в общем случае два решения. В результате родилось выдающееся открытие: оказывается прямоугольный лист можно свернуть в трубку, как по длинной, так и по короткой стороне!

До самой последней: поиска максимального замкнутого пути в связанном ориентированном графе, с последующим разбиением оного на связанные же подграфы, максимизируя суммарную длину таких подграфов. Клиринговые расчеты во вселенской клиринговой системе!

Между этими двумя точками несколько лет в разных вариантах решалась классическая задача параметрической оптимизации:

найти экстремум функции нескольких (в моем случае до 15..20) переменных, описываемой системой нелинейных алгебраических уравнений, при наличии ограничений (числом до 30), заданных функционалами, определяемых из решения нескольких (от 2 до 6) систем нелинейных дифференциальных уравнений (порядок систем 7..20).

Очень научно! Пакостность математического описания функции качества как-то сразу заставила обратиться к методам "случайного поиска с самообучением". Несколько книжек Леонарда Андреевича Расстригина были зачитаны до дыр. В результате появилась программа PSK578, в которой были скомбинированы два, предложенных Расстригиным метода: адаптированный поиск по направляющему конусу и стохастический градиентный поиск. Идея комбинированного алгоритма состоит в том, что информация, получаемая при поиске очередного направления по конусу, накапливается и, если поиск по конусу не удался, используется для вычисления статистической оценки градиента. По которой проводится исследующий поиск перед очередным уменьшением радиуса направляющего конуса и увеличением угла его раскрытия. Примерно для 8..10% таких попыток новое направление поиска оказывалось удачным, что для решавшейся задачи было не плохо. Помимо всего, в программе было заложено несколько хитрых приемов для борьбы с застреванием на границах ограничений и учета "физически не реализуемых сочетаний варьируемых переменных". Худо-бедно, но пару задач из предметной области, которой я в ту пору занимался, удалось "соптимизировать". Программа даже приобрела определенную популярность, по меньшей мере, еще в четырех работах из смежных областей ее использовали. Правда, увы, не всегда указывалось авторство.

Исходная задача была связана с попытками улучшить характеристики изделия, уже принятого на ... э-э-э в массовое производство. Поэтому пространство допустимых (по ограничениям) решений было чрезвычайно мало. Это заставило искать методы исследования пространства параметров, позволяющие определять области возможного расположения экстремума.

Первоначально, для определения "начальной точки" поиска использовался алгоритм изменения распределений случайных значений управляемых переменных. Случайные значения управляемых переменных с большей вероятностью генерируются в некоторой β-окрестности предполагаемого оптимума. Замечательное свойство алгоритма - исключительно просто реализуется анализ на "физическую реализуемость сочетания параметров" - очередная проба попросту объявляется несуществующей. При невысоких требованиях к определению оптимума алгоритм успешно реализовался как самостоятельный алгоритм оптимизации. Например, - редкий случай, когда могу явно назвать объект оптимизации, - для оптимизации параметров компрессора бытового холодильника (см. работы М.Ю.Елагина.) (К сожалению, авторов алгоритма указать не могу - был опубликован в закрытом источнике. А вот программа, его реализующая, спустя 12 лет нашлась, есть повод для разговора...)

Но появилась следующая книжка, так же, до дыр, зачитанная. Соболь И.М., Статников Р.Б. "Выбор оптимальных параметров в задачах со многими критериями". Авторы придумали "ЛП-τ" распределение, "более представительное, чем равномерное". Нетривиальный механизм генерации пробных точек в пространстве параметров использовался ими для решения многокритериальных оптимизационных задач (точнее - использовался способ интерпретации результатов исследования в ЛПτ точках). На мой взгляд, любые попытки формализовать решение подобных задач, должны сводиться скорее к предоставлению Лицу, Принимающему Решению некой дополнительной информации для принятия решения, не больше. Поэтому, алгоритм ЛПτ-поиска был использован как метод поиска начальной точки для применения программа PSK578. Попутно, накопленная информация использовалась для решения принципиально новой задачи, но об этом, если руки дойдут, потом...

Так у меня зафиксировался на некоторое время подход к оптимизационным задачам: ЛПτ-поиск для исследования пространства параметров и определения начальной точки поиска, затем - использование алгоритма самообучаемого поиска PSK578.

В самом начале 90-х, когда востребованным стало программирование уже совсем других задач, неожиданно предложили мне по старой памяти порешать одну новую задачку. Сводилась она, в конечном счете, снова к решению небольшой нелинейной системы алгебраических уравнений. Система имела достаточно мерзкую структуру, чтобы решать ее, как задачу минимизации "невязки правых частей". И порядок действий уже привычный: ЛПτ-поиск плюс что-нибудь самообучаемое... Очень удачно было отпущено время на работу - с января по июнь, как раз семестр. Решил, поиграю-ка я в руководителя проекта, и раздал куски задачи студентам в виде курсовых работ. А сам зачитался какой-то книжкой по численным методам и... призадумался. Призадумался на тему, а почему это я никогда классические методы оптимизации не использую? Пишут же умные люди, дескать, градиентные методы за n+1, что ли, шагов экстремум дают... А переменных у меня сегодня не так много... Ну да, ну да. Выражения для производных здесь не выведешь. Но ведь можно попробовать производные и численно вычислять. И, пока студиозы корпели над реализацией, настучал безыскусную процедуру численного определения градиента и градиентного поиска. Студентов я муштровал жестко и, когда они получили вожделенные пятерки, получил работающую систему. Объединил со своим градиентным поиском, запустил супер персоналку типа ДВК-3... и пошел к Заказчику объясняться. "Такой точности не бывает". Заказчик сравнил результаты со своими представлениями о счастье. И понял - счастье есть. А я отправился уже для собственного удовольствия играть в "что будет, если".

Для этой конкретной задачи получилось вот что (все цифры по памяти и применительно к упомянутой "ЭВМ"). ЛПτ-поиск занимал 20-30% общего времени решения, случайный поиск с самообучением улучшал решение после ЛПτ-поиска на 2-3 порядка. Градиентная подсистема, требовала дополнительно процентов 10 времени, точность решения увеличивалась еще на 3-5 порядков. Условимся эти результаты считать эталонными. Попытки добиться такой же точности без применения градиентной процедуры за счет ужесточения условий останова самообучающегося случайного поиска эффекта не дали. Поиск вырождался и останавливался. Отказ от предварительного этапа ЛПτ-поиска увеличивал время решения в 1.5-2 раза. Отказ от промежуточного этапа случайного поиска увеличивал время решение более чем 3 раза. При этом, так же как и в случае отказа от ЛПτ-поиска, т.е. при случайной начальной точке, градиентный поиск достаточно часто "зависал" на начальных итерациях. Заметим, что решалась задача без ограничений. Для задач условной минимизации учет ограничений в градиентной процедуре не тривиален.

А вот и мораль, свежая и оригинальная. Нет метода для любой задачи. Потребная точность, затраты на решение (время) определят выбор метода оптимизации или их сочетания и последовательности применения.Ищите, и обрящете!

alural.narod.ru

генетический алгоритм оптимизации функции / Хабр

На Хабре присутствует множество статей, посвященных эволюционным алгоритмам вообще и генетическим алгоритмам в частности. В таких статьях обычно более или менее подробно описывается общая структура и идеология генетического алгоритма, а затем приводится пример его использования. Каждый такой пример включает в себя какой-то выбранный автором вариант процедуры скрещивания особей, мутации и отбора, причем в большинстве случаев для каждой новой задачи приходится придумывать свой вариант этих процедур. Кстати, даже выбор представления элемента пространства решений вектором генов очень сильно влияет на качество получаемого алгоритма и по сути является искусством.

В то же время очень многие практические задачи легко сводятся к оптимизационной задаче на поиск минимума функции n вещественных переменных и для такого типового варианта хотелось бы иметь готовый надежный генетический алгоритм. Поскольку даже определение операторов скрещивания и мутации для векторов, состоящих из вещественных чисел, оказывается не совсем тривиальным, то «изготовление» нового алгоритма для каждой такой задачи оказывается особенно трудоемким.

Под катом приводится краткое описание одного из самых известных генетических алгоритмов вещественной оптимизации — алгоритма дифференциальной эволюции (Differential Evolution, DE). Для сложных задач оптимизации функции n переменных этот алгоритм обладает настолько хорошими свойствами, что зачастую может рассматриваться как готовый «строительный блок» при решении многих задач идентификации и распознавания образов.

Я буду считать, что читатель знаком с базовыми понятиями, используемыми при описании генетических алгоритмов, поэтому сразу перейду к сути дела, а в заключении опишу наиболее важные свойства алгоритма DE.

Генерация начальной популяции

В качестве начальной популяции выбирается случайный набор из N векторов из пространства Rn. Распределение исходной популяции должно выбираться, исходя из особенностей решаемой оптимизационной задачи — обычно используется выборка из n-мерного равномерного или нормального распределения с заданными математическим ожиданием и дисперсией.

Воспроизводство потомков

На очередном шаге алгоритма производится скрещивание каждой особи X из исходной популяции со случайно выбранной особью C, отличной от X. Координаты векторов X и C рассматриваются как генетические признаки. Перед скрещиванием применяется специальный оператор мутации — в скрещивании участвуют не исходные, а искаженные генетические признаки особи C:

Здесь A и B — случайно выбранные представители популяции, отличные от X и C. Параметр F определяет т.н. силу мутации — амплитуду возмущений, вносимых в вектор внешним шумом. Следует особо отметить, что в качестве шума, искажающего «генофонд» особи C используется не внешний источник энтропии, а внутренний — разность между случайно выбранными представителями популяции. Ниже мы остановимся на этой особенности подробнее.

Скрещивание производится следующим образом. Задается вероятность P, с которой потомок T наследует очередной (искаженный мутацией) генетический признак от родителя C. Соответствующий признак от родителя X наследуется с вероятностью 1 — P. Фактически n раз разыгрывается бинарная случайная величина с математическим ожиданием P, и для единичных ее значений производится наследование (перенос) искаженного генетического признака от родителя C (т.е. соответствующей координаты вектора C'), а для нулевых значений — наследование генетического признака от родителя X. В результате формируется вектор-потомок T.

Отбор

Отбор осуществляется на каждом шаге функционирования алгоритма. После формирования вектора-потомка T производится сравнение целевой функции для него и для его «прямого» родителя X. В новую популяцию переносится тот из векторов X и T, на котором целевая функция достигает меньшего значения (речь идет о задаче минимизации). Здесь необходимо заметить, что описанное правило отбора гарантирует неизменность размера популяции в процессе работы алгоритма.

Обсуждение особенностей алгоритма DE

В целом алгоритм DE представляет собой одну из возможных «непрерывных» модификаций стандартного генетического алгоритма. В то же время этот алгоритм имеет одну существенную особенность, во многом определяющую его свойства. В алгоритме DE в качестве источника шума используется не внешний генератор случайных чисел, а «внутренний», реализованный как разность между случайно выбранными векторами текущей популяции. Напомним, что в качестве исходной популяции используется совокупность случайных точек, выбранных из некоторого генерального распределения. На каждом шаге популяция преобразуется по некоторым правилам и в результате на следующем шаге в качестве источника шума снова используется совокупность случайных точек, но этим точкам соответствует уже некий новый закон распределения. Эксперименты показывают, что в целом эволюция популяции соответствует динамике «роя мошек» (т.е. случайного облака точек), движущегося как целое вдоль рельефа оптимизируемой функции, повторяя его характерные особенности. В случае попадания в овраг «облако» принимает форму этого оврага и распределение точек становится таким, что математическое ожидание разности двух случайных векторов оказывается направленным вдоль длинной стороны оврага. Это обеспечивает быстрое движение вдоль узких вытянутых оврагов, тогда как для градиентных методов в аналогичных условиях характерно колебательная динамика «от стенки к стенке». Приведенные эвристические соображения иллюстрируют наиболее важную и привлекательную особенность алгоритма DE — способность динамически моделировать особенности рельефа оптимизируемой функции, подстраивая под них распределение «встроенного» источника шума. Именно этим объясняется замечательная способность алгоритма быстро проходить сложные овраги, обеспечивая эффективность даже в случае сложного рельефа.

Выбор параметров

Для размера популяции N обычно рекомендуется значение Q * n, где 5 <= Q <= 10.

Для силы мутации F разумные значения выбираются из отрезка [0.4, 1.0], причем хорошим начальным значением будет 0.5, но при быстром вырождении популяции вдали от решения следует увеличить параметр F.

Вероятность мутации P изменяется от 0.0 до 1.0, причем начинать следует с относительно больших значений (0.9 или даже 1.0), чтобы проверить возможность быстрого получения решения случайным поиском. Затем следует уменьшать значения параметра вплоть до 0.1 или даже 0.0, когда в популяции практически не вносится изменчивости и поиск оказывается конвергентным.

На сходимость сильнее всего влияют размер популяции и сила мутации, а вероятность мутации служит для более тонкой настройки.

Численный пример

Особенности метода DE хорошо иллюстрируются при его запуске на стандартной тестовой функции Розенброка вида

Эта функция имеет очевидный минимум в точке x = y = 1, который лежит на дне длинного извилистого оврага с крутыми стенками и очень пологим дном.

При запуске с равномерным начальным распределением 200 точек в квадрате [0, 2] x [0, 2] после 15 шагов получаем вот такое распределение популяции:

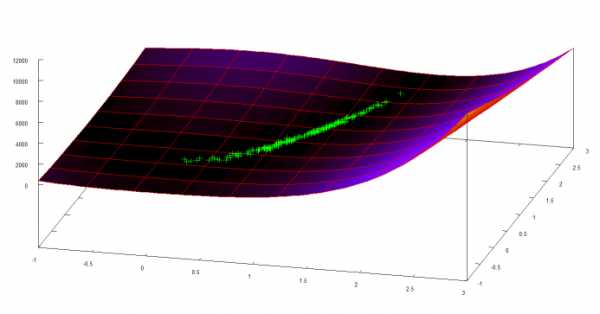
Видно, что «облако» точек расположилось вдоль дна оврага и большинство мутаций будет приводить к сдвигу точек также вдоль дна оврага, т.е. метод хорошо адаптируется к особенностям геометрии пространства решений.

Следующая анимированная картинка показывает эволюцию облака точек на первых 35 шагах алгоритма (первый кадр соответствует начальному равномерному распределению):

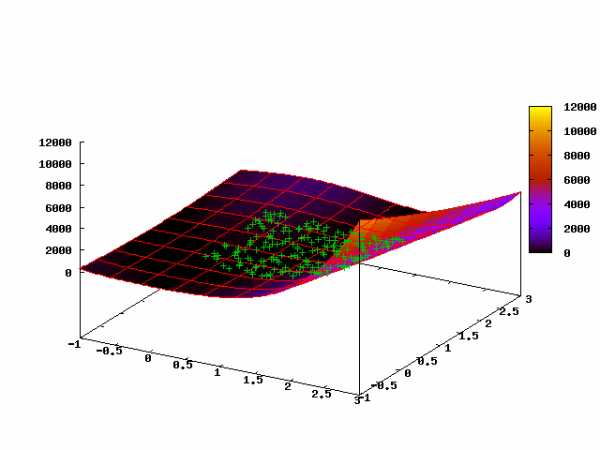
Ссылки

Дамашняя страничка алгоритма содержит много реализаций и примеров использования в разных областях.
Статья в Dr. Dobb's Journal содержит очень простую и понятную реализацию на языке C, которую можно взять за основу при использовании алгоритма DE в своих проектах.

habr.com

Алгоритм - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Алгоритм - оптимизация

Cтраница 1

Алгоритм оптимизации учитывает одно возмущающее воздействие и определяет одно управляющее воздействие. Другие возмущения не учитываются из-за малой чувствительности функции цели по отношению к этим возмущениям. Каналы управления и возмущения имеют любые передаточные функции. [2]

Алгоритм оптимизации учитывает несколько возмущений и определяет несколько управляющих воздействий. Каналы управления и возмущения представляют собой звенья запаздывания. [4]

Алгоритм оптимизации будет работать неудовлетворительно, поскольку линии равных значений ф представляют собой очень вытянутые эллипсы. Репараметризация, такая как 106pi pj, может помочь в исправлении неравномерного масштабирования. [5]

Алгоритмы оптимизации выполнены с использованием математических моделей отдельных стадий, полученных на основании уравнений кинетики, процессов массо - и теплопереноса с экспериментально определенными коэффициентами. [6]

Алгоритм оптимизации поисковый, пошаговый. Перед каждым шагом проводится автоматическая корректировка модели производства и затем определяются частные производные от целевой функции по управляющим воздействиям в данный момент времени. В зависимости от знака частных производных выдаются рекомендации об изменении управляющих воздействий. [8]

Алгоритм оптимизации этого типа применяется в случаях, когда характеристики объекта существенно изменяются с течением времени, либо при использовании упрощенных моделей, адекватных объекту лишь в малых интервалах изменения переменных состояния объекта. [9]

Алгоритмы оптимизации на данном уровне иерархии опираются на различные методы математического программирования, определяемые для каждой технологической установки индивидуально. [10]

Алгоритм оптимизации работает следующим образом. В статическом режиме работы агрегата МЭА очистки определяются значения входных параметров. Эта информация, характеризующая работу агрегата в данный момент времени, является исходной для работы алгоритма оптимизации. [11]

Алгоритм оптимизации в программе NASTRAN принадлежит к семейству методов, называемых градиентными. Эти методы в ходе численного поиска оптимальной конструкции используют кроме значений функции еще и ее градиент. Процесс численного поиска может быть кратко описан следующим образом: для данной точки в пространстве переменных определяются градиенты целевой функции и ограничений, а затем эта информация используется для определения направления поиска. В этом направлении мы двигаемся так далеко, как это возможно, после чего проверяем, найдена ли оптимальная точка. Если точка не найдена, то этот процесс повторяем до тех пор, пока не окажемся в ситуации, когда нельзя добиться улучшения без нарушения какого-либо ограничения. [12]

Алгоритм оптимизации заключается в следующем. [13]

Алгоритм оптимизации решений и способы их машинной реализации обычно включаются в подсистемы математического и программного обеспечения конкретной ЭВМ. При использовании их при совершенствовании МО эти методы отбираются специалистом-метрологом, который консультирует исполнителей и руководителей по причинам выбора того или иного метода оптимизации. [14]

Страницы: 1 2 3 4 5

www.ngpedia.ru

Разработка алгоритма оптимизации - Энциклопедия по экономике

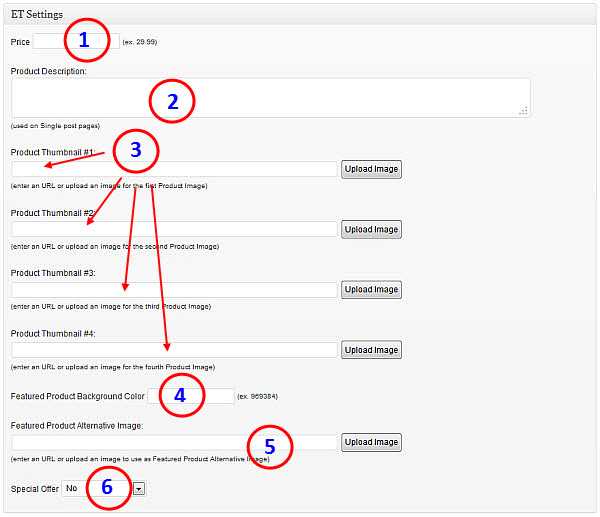
Разработка алгоритма оптимизации [c.102]

При использовании метода экспериментальной оптимизации с использование имитационной модели объекта перед исследователем помимо создания моделирующего алгоритма возникают проблемы разработки алгоритма оптимизации, включающего моделирующий алгоритм в качестве одного из элементов — этапа расчета значения целевой функции для определения значений переменных. Для этого должна быть продумана алгоритмическая и программная реализация решения оптимизационной задачи. [c.103]

Модель нефтедобывающей промышленности страны описывается блочной задачей линейного программирования. Процесс согласования решений моделей различных уровней опирается на группу управляющих параметров, которые формируются в моделях нефтедобывающих районов (в настоящей разработке они являются координаторами решений). Эти параметры представляют собой вектор дискретных оценок, возможность использования которых для согласования решений рассматривалась в работе [83], где они интерпретируются по их роли в алгоритме оптимизации, т. е. как параметры, показывающие наиболее вероятное направление изменений условий задачи, учитывающие дефицитность ресурсов, существенность ограничений, соотношение затрат и т. д. и приводящие к улучшению отраслевого плана. [c.208]

Все используемые методы разработки управленческих решений по степени формализации расчетов можно разделить на две большие группы - формализованные и эвристические. Формализованные методы имеют четкий алгоритм решения задачи в виде экономико-математических моделей, методик анализа и расчета данных, компьютерных программ, которые обеспечивают высокую точность количественной оценки разрабатываемых вариантов. Формализованные методы используются для разработки и оптимизации программных, т. е. структурированных, решений. [c.242]

После существенной оптимизации мощности тока, разработки алгоритма зарядки и объединения систем был успешно собран прототип универсального зарядного устройства для батарей (в рамках ЦРТ) и разработана технология его производства. Однако рынок электромобилей развивался не так быстро, как ожидалось, поэтому инвесторы этого проекта использовали эту технологию в другом секторе рынка. [c.103]

Разработка алгоритмов и математических программ для решения на ЭВМ задач оптимизации запасов нефтепродуктов на перевалочных нефтебазах требует совершенствования учета издержек обращения на этих базах. Так, учет издержек по приобретению и содержанию запасов нефтепродуктов (следует осуществлять раздельно по следующим группам издержки по управлению нефтеснабжением издержки содержания запасов нефтепродуктов издержки по доставке нефтепродуктов (транспортные расходы). Первую и третью группы расходов можно [c.186]

Конструктивное символическое выражение взаимосвязи факторов (разработка алгоритма) Определение коэффициентов весомости факторов Упрощение методов анализа Учет стимулирующих факторов Применение типовой схемы оптимизации [c.212]

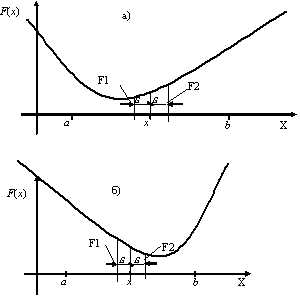
Разумеется, эта упрощенная задача пе эквивалентна исходной, но лишь аппроксимирует ее с любой необходимой точностью. Здесь открывается соблазнительная возможность унифицированного подхода как при разработке алгоритмов, так и при создании набора стандартных программ. К сожалению, эта внешняя простота не дается даром. Сведение сложной задачи к простой (9) достигается за счет резкого ухудшения дифференциальных свойств F (х) по сравнению с дифференциальными свойствами функций исходной содержательной постановки задачи. Заметим, что под дифференциальными свойствами вычислитель должен понимать не столько словесные характеристики типа непрерывная функция , дифференцируемая , дважды дифференцируемая и т. д., сколько величины констант в характеристиках непрерывности, дифференцируемости. Поэтому тот факт, что методом штрафных функций можно свести общую задачу оптимизации к задаче (9) даже с бесконечно дифференцируемой F (х), не следует переоценивать. Рассмотрим характерную для упомянутой тенденции попытку решать задачу (9) с функцией [c.412]

Однако к моменту выполнения операции раскроя эти ограничения уже фиксируются. Остается обойти пороки и максимизировать некоторый показатель суммарную кубатуру или суммарную коммерческую цену или условные цены . Лучшее решение этих задач требует совершенствования стратегии т. е, оснастки, алгоритмов оптимизации, вплоть до разработки систем автоматической оптимизации. [c.269]

Дальнейшее повышение эффективности ТПШ связано с адаптацией и оптимизацией цикла обработки деталей в условиях случайного или неопределенного характера действующих факторов на основе разработки более совершенных алгоритмов и структур САУ. По различным оценкам автоматическая оптимизация режима обработки и формообразования деталей за счет адаптации системы управления к изменяющимся условиями ТПШ способна повысить производительность в 1.5...3 раза (3). Повышение качества продукции, как главной задачи машиностроения, также немыслимо без использования адаптивных САУ. До недавнего времени при оптимизации финишных операций критерий качества выступал как ограничивающее условие при выборе типа и параметров алгоритма управления режимом обработки деталей, а целью оптимизации являлось достижение экстремальных характеристик по производительности, себестоимости, приведенным затратам и т.д. Этому способствовали как сложившаяся ориентация на валовые показатели, так и недостаточная разработка проблемы в научном и прикладном аспектах. [c.141]

Разработанный и реализованный на ЭВМ эвристический алгоритм решения задачи включает два основных блока. В процессе реализации первого из них достигается соблюдение ограничения по равномерности распределения по кварталам объемов товарной строительной продукции, второго — осуществляется выравнивание по загрузке производственной мощности в отдельные периоды года. При этом план строительства объектов в последующие годы является естественным продолжением формируемой годовой программы работ. Ее изменение как в процессе оптимизации на стадии разработки, так и в ходе реализации неминуемо отразится на показателях производственной программы последующих лет. Тем самым применение модели позволяет реализовать принцип непрерывного планирования строительного производства. [c.193]

Практическое применение экономико-математических методов в планировании нефтеперерабатывающих производств требует создания специального программного обеспечения, реализующего алгоритмы параметризации, моделирования, оптимизации НПП и анализа решений. Автоматизация процессов построения модели и интерпретации результатов решений требует, как правило, разработки оригинальных программных средств, учитывающих структурные, функциональные и информацион- [c.178]

См., разработанный Дж. Данцигом, послужил исходным пунктом для разработки целого семейства алгоритмов решения как линейных, так и нелинейных выпуклых задач оптимизации. [c.322]

Комплексный алгоритм, таким образом, органически сочетает взаимную увязку алгоритмов распределения ресурсов, расчета параметров модели и оптимизации структуры локальной разработки с организационно-техническими мероприятиями. Следует отметить, что рассмотренные задачи планирования и управления не только связаны между собой, но и логически [c.18]

Выше было показано, что системы обслуживания и, в частности, системы организации проведения ГИС и ТОР объектов добычи и транспорта нефти и газа являются по своей сути замкнутыми системами массового обслуживания, которые имеют достаточно большое количество как источников заявок (например, скважин - до нескольких сотен), так и каналов обслуживания (например, геофизических партий, ремонтных бригад), которые в процессе организации работ разбиваются на участки (например, районные насосные управления, экспедиции, площади и т.д.), образуя совокупность замкнутых параллельно работающих СМО (точнее подсистем одной замкнутой СМО). Поэтому, говоря об оптимизации планов и расписаний проведения ГИС и ТОР в рассмотренном выше смысле необходимо также, говорить и об оптимизации структуры и функционирования соответствующих им замкнутых систем массового обслуживания, Актуальность поставленной задачи - разработка эффективного алгоритма поиска оптимальной структуры системы проведения ГИС и ТОР, определяется еще и тем фактором, что в рыночных условиях функционирования этих систем, одинаково плохо иметь как недостаток, так и избыток ресурсов в системе. [c.443]

В том случае, когда снижение точности осуществляется с расходами на создание специализированных средств измерений взамен универсальных, разработку менее точного метода и алгоритма обработки результатов измерений, доля эффекта, приходящегося на работы по оптимизации, определяется по формуле (5.2.14). [c.159]

Теоретическое решение любой задачи сводится к составлению алгоритма. Этому предшествует разработка математической модели задачи и метода вычисления, понимая под математической моделью оптимизации совокупность формул, уравнений, неравенств, критерия (или условий) оптимальности, определяющую при заданной исходной информации оптимальный процесс (в неявном или явном виде), а под методом вычисления — совокупность правил определения искомых величин на основе заданной математической модели при заданной исходной информации. [c.210]

Кибернетические аспекты предусматривают совершенствование системы управления производственным коллективом путем оптимизации процесса принятия и реализации управленческих решений на основе использования обратных связей, выявления неэффективных звеньев, разработки соответствующих алгоритмов. [c.21]

Лучшее возможное решение задачи может быть найдено разнообразными способами. В некоторых случаях задача может быть решена простым методом проб и ошибок, особенно если поиск решения не полностью автоматизирован, а проводится вручную . В других случаях могут потребоваться сложные процедуры и алгоритмы. Например, симуляция процесса эволюции (в генетическом оптимизаторе) — очень мощный метод поиска качественных решений для сложных задач. В некоторых случаях лучшее решение — аналитическая (вычислительная) процедура, например метод сопряженных градиентов. Аналитическая оптимизация — эффективный подход для задач с гладкими (дифференцируемыми) функциями пригодности, например задач, встречающихся при обучении нейронных сетей или разработке множественных моделей линейной регрессии. [c.48]

Место имитационного моделирования в составе экономико-математических методов. 2.Мысленные и машинные модели социально экономических систем. 3.Социально-экономические процессы как объекты моделирования. 4. Структура и классификация имитационных моделей. 5.Основные этапы процесса имитации. 6.Определение системы, постановка задачи, формулирование модели и оценка ее адекватности. 7.Экспериментирование с использованием ИМ, механизм регламентации, интерпретация и реализация результатов. 8.Организационные аспекты имитационного моделирования. 9.Основные компоненты динамической мировой модели Форрестера. 10.Концепция петля обратной связи . И.Структура модели мировой системы. 12. Каноническая модель предприятия. 13.Моделирование затрат предприятия. 14.Моделирование налогообложения. 15.Использование имитационного моделирования для планирования. 16.Содержание процессов стратегического и тактического планирования. 17.Основные модули системы поддержки принятия решений. 18.Сущность статистического ИМ. 19.Метод Монте-Карло. 20.Идентификация закона распределения. 21.Классификация систем МО. 22.Сущность метода экспериментальной оптимизации. 23.Формирование концептуальной модели. 24.Принципы выбора критерия оптимальности, разработка алгоритма оптимизации. 25.Эвристические алгоритмы поиска решений. 26.Управленческие имитационные игры, их природа и сущность. 27. Структура и порядок разработки управленческих имитационных игр. [c.121]

Проблемы теории и практики. Решение задачи синтеза цели требует разработки методов и средств получения информации об окружающей среде и эффективной идентификации собственного состояния, как объекта управления, так и самой системы. При формировании цели возникает проблема достаточности базы знаний, а следовательно, и памяти, возможности их реализации как на содержательном, так и на конструктивном уровне. Динамическая экспертная система выполняет расчет, оптимизацию, прогноз и моделирование результатов, поэтому должна обладать высоким быстродействием. Потенциал, накопленный при разработке алгоритмов принятия решений и выработки управления, может успешно использоваться в интеллектуальных системах, однако потребуется распараллеливание алгоритмов и их мультитранспьютерная реализация и, конечно, не исключается синтез новых, эффективных параллельных алгоритмов. Источником возмущающего воздействия для интеллектуальной системы является окружающая среда, а функционирование системы должно обеспечить в конечном итоге компенсацию этого воздействия. И.П. Павлов писал Вся жизнь — от простейших до сложнейших организмов, включая, конечно, и человека, есть длинный ряд все усложняющихся до высочайшей степени уравновешиваний внешней среды. Придет время, пусть отдаленное, когда математический анализ, опираясь на естественнонаучный, осветит величественными формулами уравнений все эти уравновешивания, включая в них и самого себя (Павлов И.П. Поли. собр. соч. Т.З. С.124-125). [c.9]

Раскрой древесного ствола по длине. Очищенный от сучков ствол (хлыст) раскраивается по длине на круглые сортименты (пиловочник, шпальник, кряжи, баланс, рудстойка и т. п.). Уже эта первая операция раскроя (раскряжёвка) должна быть нацелена на максимизацию окончательной продукции. Здесь оптимизация раскроя возможна на механизированном нижнем складе леспромхоза или складе сырья лесозавода. Она требует сосредоточения разных заказов, автоматизации всех этапов работы выявления пороков, геометрических обмеров, разделки ствола, сортировки продукции по размерам и качеству. Алгоритмы оптимизации раскроя реализуемы в меру их соответствия внедренной механизации. Но опережающая разработка алгоритмов стимулирует и само развитие механизации, предсказывая ожидаемую экономию сырья. [c.266]

Анализ перечисленных и других существующих генетических пакетов программ алгоритмов многокритериальной оптимизации, а также доступного программного обеспечения показал, что разработано множество алгоритмов со своими методиками для решения различных задач оптимизации. Однако ранее не рассматривалось решение нечеткой обобщенной распределительной задачи, которая является многокритериальной, с нечетко поставленной целью и ограничениями. Все выше сказанное послужило основанием для разработки генетического алгоритма поиска оптимального решения нечеткой распределительной задачи в рамках системы MATLAB. [c.512]

По принципиальной схеме алгоритма нормирования труда различают поисковую (одновариантную) и оптимизирующую (многовариантную) системы нормирования труда [4]. Поисковая система предусматривает одновариантный расчет норм труда на основе нормативных материалов. В этом случае машинный алгоритм расчетов дублирует расчет норм вручную по нормативам. Оптимизацию режимов, технологического и трудового процессов и норм осуществляют на стадии разработки нормативных материалов. [c.308]

Другая важная проблема, тесно связанная с согласованием решений,— формирование и согласование целей (критериев оптимальности) различных уровней. При декомпозиционном подходе к построению С. о.-м. м., используемом гл. обр. для разработки моделей планирования, общая цель для всей системы задана, а целевые функции составных частей формируются исходя из этой общей цели. Методика декомпозиции целей хорошо разработана для моделей оптимального планирования, базирующихся на методах блочного программирования. При синтотич. подходе, более универсальном и реалистичном, целевые функции частей (напр., групп населения) являются исходными, заданными. Задача состоит в определении такого взаимодействия частей внутри системы и такого порядка функционирования, при к-ром вся система в целом достигла бы решения, соответствующего глобальной цели. Проблемы синтеза общем цели на основе частных ставятся и решаются в теории игр, моделях векторной оптимизации, моделях экономич. равновесия, теории принятия групповых решений, а также методами имитационного моделирования. В имитационных моделях, понимаемых достаточно широко, переменными или варьируемыми параметрами могут выступать алгоритмы принятия решений отд. подмоделями, а также алгоритмы согласования решений. Следовательно, задача состоит в нахождении такого набора алгоритмов, имитирующих функционирование экономич. системы, при к-ром получаемое общее решение наилучшим образом соответствует глобально] цели системы. [c.558]

Методы линейного программирования разработаны для проблем оптимизации, затрагивающих линейные функции пригодности или расходов с линейными ограничениями параметров или входных переменных. Линейное программирование обычно используется для решения задач по распределению активов. В мире трейдинга одно из возможных применений линейного программирования СОСТОИТЕ поиске оптимального размещения денежных средств в различные финансовые инструменты для получения максимальной прибыли. Если оптимизировать прибыль с учетом возможного риска, то применятьлинейные методы нельзя. Прибыль с поправкой нариск не является линейной функцией весов различных инвестиций в общем портфеле, здесь требуются другие методы, к примеру генетические алгоритмы. Линейные модели редко бывают полезны при разработке торговых систем и упоминаются здесь исключительно в ознакомительных целях. [c.59]

В процессе исследования и изучения математических методов [8, 48, 63, 64, 72, 73, 74, 78, 96, 114, 124, 127], а также современных подходов к ресурсному планированию MRP, ERP, SRP [11, 23, 33, 55], нами были осуществелены попытки разработки нескольких вариантов модели оптимизации ассортимента, а также целевой функции 1) на основе теории систем массового обслуживания 2) на основе ранжирования альтернатив по критериям важности, коэффициенту запаса времени и риска 3) на основе динамической оптимизации суммарного коэффициента важности, рассчитываемого с использованием матрицы рентабельность - риск . Были разработаны соответствующие алгоритмы и целевые функции оптимизации. В результате оказалось, что данные модели обладают рядом недостатков и не могут учесть ряда факторов, указанных в 4.2, и, следовательно, решить поставленных в исследовании цели и задач. [c.61]

economy-ru.info

Алгоритм оптимизации сайта под поисковые системы

Все ресурсы разные, и требуют индивидуальной оценки при раскрутке. Но общий алгоритм оптимизации сайта все же существует – это стандартизированный набор действий, обязательных для всех типов проектов. Без них привлечение трафика и рост в поисковой выдаче будет затруднен или вовсе невозможен.

Алгоритм оптимизации сайта под поисковые системы

Первый шаг, с которого начинается алгоритм оптимизации сайта – регистрация ресурса в поисковых системах, точнее, в сервисах для веб-мастеров. Чаще всего достаточно пройти ее в Яндекс.Вебмастер и в Google Search Console. Остальные поисковики обычно используют алгоритмы лидеров, поэтому специально продвигаться под них нет необходимости. Почему это нужно делать на самом начальном этапе работ? Потому что индексация новых проектов идет крайне медленно.

Алгоритм оптимизации сайта будет реализован правильно, если изначально ресурс пройдет анализ. Изучению подлежат все аспекты:

код;
скорость загрузки;
адаптивность;
мобилопригодность;
наличие дублей;
правильные ответы сервера.

В целом таких факторов достаточно много. Вместе с технической частью алгоритм оптимизации сайта включает внутреннее улучшение. Оно проводится комплексно: после изучения ниши и конкурентов формируют семантическое ядро, распределяют запросы, заполняют мета-теги, настраивают внутреннюю перелинковку и ЧПУ, проводят другие необходимые работы.

Алгоритм оптимизации сайта: работа с контентом

Современный алгоритм оптимизации сайта обязательно опирается на контент – именно информация на страницах ресурса может стать ключевым фактором успешной посещаемости. Самые распространенные варианты заполнения проекта – оптимизированные тексты и изображения. Главные требования к информации – уникальность (отсутствие копий), структурированность (в том числе с использованием тегов заголовков), удобство для просмотра и чтения.

Любая страница должна быть интересной, предоставлять максимум актуальной и полезной информации, рассчитанной в первую очередь на посетителей. Но и оптимизированность тоже важна: правильное и естественное употребление релевантных ключевых слов, по которым поисковые роботы определят принадлежность и тематику страниц. Но в целом выдача формируется по результатам посещаемости и поведенческим факторам, а не по количеству употребленных запросов.

Алгоритм оптимизации сайта: ссылочное наращивание и раскрутка проекта

После внутренней подготовки, алгоритм оптимизации сайта включает набор методик по внешнему продвижению. Одна из основных и пока что не потерявших актуальности – наращивание ссылочной массы. Для нового проекта достаточно небольшого количества ссылок, но их нужно покупать постепенно, на разные целевые страницы, и при этом тщательно отслеживать качество доноров. Это должны быть авторитетные тематические проекты или СМИ. Ссылаться лучше через контент. Со временем массу нужно постепенно увеличивать.

Алгоритм оптимизации сайта с целью внешнего продвижения включает такое понятие, как раскрутку: набор действий по повышению известности ресурса. Они могут быть разными. Самые распространенные варианты:

экспертная тема на авторитетном форуме – позволяет бесплатно размещать ссылки на свои страницы с хорошим весом и живыми переходами;
то же самое – но на сайте СМИ. Например, можно вести тематическую авторскую рубрику;
партнерский обмен ссылкам с тематическими сайтами: например, можно написать обзоры интересных ресурсов и попросить их собственников сделать то же.

Современный алгоритм оптимизации сайта обязательно включает раскрутку в социальных сетях. Сейчас это одна из наиболее эффективных методик привлечения посетителей, брендирования и быстрого контакта с аудиторией. Для этого нужно разместить кнопки «Поделиться», зарегистрировать официальные страницы и сообщества, качественно их поддерживать.

Что не рекомендуется включать в алгоритм оптимизации сайта

Чтобы раскрутка была эффективной и без рисков, не стоит включать в алгоритм оптимизации сайта следующие пункты:

большое количество ссылок с сильным приростом массы – позволяет поисковым роботам вычислить накрутку (автоматическую закупку) и наказать ресурс;
разнообразные «прогоны»: по каталогам, сайтам, доскам объявлений. Нулевой результат и впустую потраченные деньги;
накрутки поведенческих факторов. Любая эмуляция действий живых пользователей без проблем вычисляется поисковиками;
переспам – принцип «чем больше ключевых слов, тем лучше» перестал работать несколько лет назад.

Алгоритм оптимизации сайта должен включать только белые методы: естественное развитие проекта, увеличение качества, контент для людей, создание новых страниц, реагирование на потребности аудитории. Только в таком случае эффект от действий будет положительным и долговременным.

prodvizhenie-saitov.top

Алгоритм оптимизации - Энциклопедия по машиностроению XXL

Анализ чувствительности. Анализ чувствительности входит составной частью в алгоритмы решения многих задач, в частности в алгоритмы оптимизации градиентными методами. Для анализа чувствительности задаются ММ объекта и вектор тех внутренних и внешних параметров X, влияние которых на вектор выходных параметров Y требуется определить. [c.255] Выбор расчетных моделей и алгоритмов оптимизации (ч-м) [c.141]

При построении поисковых алгоритмов оптимизации следует учесть, что многообразие методов оптимального проектирования ЭМП требует их сравнительной оценки и выбора из них наиболее эффективных для решения конкретных задач. Однако достаточно полные критерии теоретической оценки методов пока не разработаны и поэтому оценка осуществляется обычно с помощью вычислительного эксперимента. Анализ работ по оптимальному проектированию ЭМП показывает, что все основные методы программирования получили практическую апробацию. Так, методы упорядоченного перебора использованы для проектирования асинхронных двигателей [42], методы случайного перебора — для проектирования асинхронных двигателей и синхронных генераторов [24], методы градиента, покоординатного поиска, динамического программирования— для проектирования синхронных машин [8], методы случайного направленного поиска —для проектирования асинхронных машин (22] и т. д. [c.144]

Начальное решение примера получено с помощью алгоритма оптимизации релейного управления для основной задачи терминального управления. При этом изменение Т осуществлялось варьированием Д/ при постоянном значении т = вО. Найденная функция опт(ДО показана на рис. 7,7, а пунктирной кривой /. Дальнейшее уточнение решения достигнуто с помощью алгоритма оптимизации релейного управления для вспомогательной задачи терминального управления (кривая 2 на рис. 7.7, а). Уточненное оптимальное управление и соответствующий переходный процесс показаны на рис. 7.7, б, в. Анализ кривых показывает, что пренебрегая погрешностями аппроксимации управления, можно отметить три стабильных интервала постоянства в управлении, т, е. два переключения, что в данном случае соответствует теореме об (п—1) переключениях. [c.219]

Важность этого вопроса применительно к поиску оптимальных проектных решений определяется массовым характером применения соответствующих программ в условиях функционирования САПР. Особенностью САПР является также многообразие требований, которые предъявляются к методам и алгоритмам оптимизации в силу разнообразия решаемых с их помощью задач. В этих условиях, исходя из сравнительной оценки эффективности различных алгоритмов, можно найти области их предпочтительного применения. [c.169]

Возможность получить устойчивое решение дают некоторые итерационные алгоритмы оптимизации, в которых происходит последовательное уточнение решения в соответствии с формулой [c.285]

Ген (в генетических алгоритмах оптимизации) - управляемый параметр Генетический алгоритм - алгоритм решения оптимизационных задач, в котором для поиска экстремума используются принципы, напоминающие принципы приспособления популяций живых организмов к особенностям окружающей среды [c.311]

Задача оптимизации отклика типа (3) при разработке алгоритма оптимизации заключается в следующем минимизировать [c.109]

АЛГОРИТМ ОПТИМИЗАЦИИ И ВЫЧИСЛЕНИЕ [c.84]

Здесь необходимо заметить, что минимальное значение продолжительности теоретического такта (получаемого при помощи алгоритма оптимизации на ЭВМ) может не совпасть с минимумом фактического такта выпуска (рис.З). [c.60]

Математическое описание объекта и системы управления представим в виде o =M(u,f), К = R(X, Л). где ЖО - символы математических моделей объекта (I) и системы ос, U - векторы выходных координат объекта и управляющих воздействий Л - вектор настроечных параметров системы ( в классе АСР Л - вектор заданий регуляторам, в классе ССО А - вектор параметров алгоритма оптимизации ). [c.52]

В более ответственных случаях применяют балансировку роторов в рабочих опорах в процессе эксплуатации, когда положение корректирующих масс в пространстве делают изменяемым. Применение микропроцессорного управления балансировкой позволяет программно реализовать различные алгоритмы оптимизации поиска положения корректирующих масс. [c.204]

Первая схема расчетов соответствует алгоритму оптимизации свойств динамических систем по запасу устойчивости с выполнением ограничений по другим свойствам с чисто случайным поиском оптимальных значений выбираемых параметров. Вторая схема расчетов совпадает с первой и отличается от нее лишь тем, что осуществляется направленный случайный поиск оптимальных значений выбираемых параметров. [c.138]

Согласно изложенной методике был разработан алгоритм оптимизации, реализованный на ЭВМ ЕС-10-20. Результаты машинной обработки по определению оптимального режима для Na- и Mg—Ма-катионитных фильтров показали, что оптимальная скорость фильтрования воды Каспийского моря через фильтры диаметром 3,4 м в обоих случаях находится в пределах 26— 27 м/ч. При этом среднечасовая производительность Na- и Mg—Na-катионитного фильтра составляет соответственно 122 и 153 м /,ч. Оптимальная высота загрузки катионита в фильтре для режимов Na- и Mg—Na-катионирования равна соответственно 7,5 и 5,5 м, т. е. значительно превосходит высоту существующих стандартных фильтров. Однако, учитывая, что условия транспортировки допускают изготовление фильтров длиной до-10 м (как, например, для горизонтальных механических фильтров), есть смысл перейти к серийному заводскому производству стандартных фильтров повышенной высоты. [c.81]

Лучшие результаты дает получение одного результата применением разных алгоритмов оптимизации при разных начальных условиях. Поэтому системы САПР обычно снабжены программными комплексами оптимизации, разрабатываемыми с тем условием, что пользователю будет предоставлена возможность в режиме диалога с ЭВМ менять алгоритмы поиска, сравнивать полученные результаты, прерывать счет при попадании в кризисные ситуации, менять направление поиска с дроблением шага на краю допустимой зоны. [c.121]

Одна из практически важных задач, решаемых на основе математической модели инерционной системы,—оптимизация настройки АСР в условиях недостаточной определенности модели объекта. В [41] рассмотрены методические основы и приведен алгоритм оптимизации настройки путем итерационной процедуры, на каждом шаге которой выполняются следующие этапы [c.462]

Конкретизируем предложенный алгоритм оптимизации ПТУ. Из всех агрегатов теплоэнергетического оборудования ПТУ в рамках уравнения (3.12) целесообразно оптимизировать лишь турбину и конденсирующий инжектор. Необходимость включения этих агрегатов обусловливается, с одной стороны, сложной зависимостью реально достижимых величин критериев их эффектив- [c.45]

Значительное место уделено освещению вычислительных приемов и методов. Излагаются алгоритмы оптимизации непрерывно и дискретно изменяющихся параметров, изучаются вопросы ускорения их сходимости. [c.2]

В главе 2 изложены методы и алгоритмы оптимизации параметров и профиля теплоэнергетических установок. Здесь дано описание алгоритма оптимизации непрерывно изменяющихся параметров, использующего идеи градиентного метода алгоритма направленного дискретного спуска, сочетающего возможности метода покоординатного спуска и метода случайного поиска метода динамического программирования в применении к оптимизации компоновки парогенератора. Обсуждаются вопросы сходимости предложенных алгоритмов, а также даны примеры их практического использование . [c.3]

Теоретические доказательства корректности применения некоторых экстремальных методов при большом числе разнородных переменных и сложности системы ограничений трудно осуществимы. В таких случаях центр тяжести доказательств корректности и эффективности используемых алгоритмов целесообразно переносить на анализ вычислительных процессов при решении задач на ЭЦВМ. Подобный анализ (см. 1 главы 2) позволил, в частности, отказаться от некоторых усложнений алгоритма оптимизации непрерывно и дискретно изменяющихся параметров реальных теплоэнергетических установок и их элементов. Необходимы дальнейшие постановки вычислительных экспериментов для определения наилучших значений критериев окончания решения отдельных подзадач и процесса оптимизации теплоэнергетической установки в целом. [c.12]

Однако при сведении задачи с непрерывными переменными к задаче с дискретными переменными теряется точность получения оптимальных значений переменных Хн, а значит и Хд. Поэтому при использовании такого приема необходимо после получения некоторого оптимума в результате решения дискретной задачи провести еще дополнительную оптимизацию по непрерывным переменным Х при некотором фиксированном векторе Хд. Таким образом, и в этом случае все равно приходим к разделению процесса решения задачи на этапы, только уже на конечной стадии полной оптимизации. При оптимизации теплоэнергетических установок этот подход не используется из-за своеобразия учета ограничивающих условий (2.8), (2.9), рассматриваемого ниже, и некоторых других особенностей задачи (2.7) — (2.10), позволяющих более эффективно применять методы типа градиентных на первом этапе ее решения. Ниже излагаются алгоритмы оптимизации по этапам. [c.17]

Алгоритм оптимизации непрерывно изменяющихся параметров. Рассмотрим задачу (2.7) — (2.9), предполагая при этом, что дискретные переменные фиксированы на определенных исходных значениях (в дальнейшем будем вместо Хд писать просто X аналогично поступим и на втором этапе). [c.17]

Алгоритм оптимизации непрерывно изменяющихся переменных опирается на некоторые идеи градиентного метода, предложенного в [29]. Вместе с тем, используя специфику поставленной задачи (2.1) — (2.4) для рассматриваемого здесь объекта, удается при движении внутри области R и, что наиболее важно, по ее границам избежать нарушения условий [c.19]

Алгоритм оптимизации дискретно изменяющихся параметров. На втором этапе решается задача дискретного нелинейного программирования для оптимизации переменных Хд (или просто X в соответствии со сказанным выше). Сформулируем эту задачу найти минимум нелинейной функции [c.24]

Задача 1. Алгоритм оптимизации непрерывно изменяющихся параметров реализуется применительно к задаче оптимизации термодинамических, расходных и конструктивных параметров тепловой электростанции с паротурбинными блоками мощностью 800 тыс. кет, имеющими весьма сложные схемы технических связей между отдельными узлами и элементами оборудования. Математическая модель такой установки вместе с табличными данными термодинамических свойств рабочих веществ занимает более 10 тысяч ячеек внутренней и внешней памяти ЭЦВМ. Время счета задачи при совместной оптимизации 20 термодинамических параметров находится в интервале 2—3 час машинного времени для случайно взятого исходного варианта и 0,3—1,0 час при обоснованно выбранном исходном варианте. Такой выбор всегда возмон[c.34]

Методика и алгоритм оптимизации. Круг задач оптимизации, решение которых возможно методом динамического программирования, определяется применимостью к ним так называемого принципа оптимальности [461 Оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения . Из этого принципа следует основная идея метода динамического программирования развернуть решение задачи в многошаговый процесс с оптимизацией всех возможных исходов каждого предыдущего шага, чтобы затем можно было выбрать искомое решение, оптимальное с точки зрения задачи в целом. [c.45]

Разработан алгоритм оптимизации суточного режима СЦТ на основе схемы динамического программирования. [c.131]

На следующем этапе осуществляют варьирование параметров Х , Х2,. ... Х24 в соответствии с выбранным алгоритмом оптимизации и вычисляют для каждой их совокупности значения целевых функций й р и С р. Процесс вычисления осуществляют до тех пор, пока В р или С р не достигнут минимального значения. Соответствующие им значения параметров являются оптимальными для данной ТЭС МК, определяют вид тепловой схемы ТЭС МК, имеющей наибольшую энергетическую эффективность. [c.263]

Для поиска локальных оптимумов используются однопарамвтрические методы оптимизации (метод покоординатного спуска в сочетанжи с методом золотого сечения), Функщюнально-технические огранячендя на систему пластин целесообразно учитывать методом штрафных функций fij. Тогда алгоритм оптимизации заключается в минимизации функции [c.131]

Рассмотренная совокупность алгоритмов оптимизации, включая и алгоритм поиска аналогов, бьша реализована в подсистеме поиска оптимальных проектных решений САПР гиродвигателей и представлена в виде соответствующего обобщенного алгоритма. Кроме того, в состав методического обеспечения подсистемы включаются методы математического моделирования основного злектромеханического и сопутствующих ему преобразований энергии, а также соответствующие алгоритмы анализа рабочих показателей проектируемых объектов. [c.229]

Метод полного перебора вариантов целесообразно использовать для решения задач небольшой размерности, когда максимальное число типоразмеров ряда функция спроса задана в явном виде. С увеличением k резко возрастает машинное время, необходимое для получения результатов. Так, например, для расчета оптимальных рядов типажа, результаты которого представлены в табл. 6, было затрачено более 40 ч машинного времени на ЭВМ Наири . Адаптивный алгоритм оптимизации [5] более производителен, однако он и более сложен для программирования. Кроме того, для сокращения времени расчетов он требует предварительной подготовки Исходных даипых. Целесообразная область применения — задачи с большим числом типоразмеров ( тах и случай,когда функция спроса не может быть получена в явном виде. [c.178]

Технологические схемы теплоэнергетических установок с оптимальными свойствами могут быть синтезированы путем последовательного применения методов нелинейного программирования для множества технологических графов, отображающих различные структурные состояния технологической схемы теплоэнергетической установки. Эта наиболее общая задача оптимизации теплоэнергетической установки должна решаться с учетом как иерархической взаимосвязи между подзадачами оптимизации параметров узлов, элементов, агрегатов и установки в целом, так и алгоритмических особенностей оптимизации непрерывно и дискретно изменяющихся параметров. Соответственно в методике решения задачи синтеза оптимальных схем теплоэнергетических установок должны быть итерационно взаимосвязаны алгоритм нелинейного математического программирования, принятый для оптимизации непрерывно изменяющихся термодинамических и расходных параметров установки алгоритм дискретного нелинейного программирования, с помощью которого осуществляется оптимизация дискретно изменяющихся конструктивно-ком-поновочных параметров элементов, узлов и агрегатов установки алгоритм оптимизации вида тепловой (технологической) схемы установки с учетом технических и структурных ограничений. Конструктивные приемы решения этой очень сложной задачи находятся в стадии разработки. [c.11]

Процесс вычислений по методу, примененному для оптимизации непрерывно изменяющихся параметров, разделен на пять частей — блоков программы (рис. 2.7). Вычислительная работа алгоритма оптимизации дискретных параметров представлена на рис. 2.8, а алгоритма поиска допустимого решения — на рис. 2.9. Вычислительные схемы задач поиска допустимого реиенпя и оптимизации непрерывных переменных имеют много общих операторов. Это в значительной степени упрощает вычислительный процесс. [c.33]

Математические модели исследуемых ПГУ представлены в виде системы программ для ЭЦВМ БЭСМ-4. Эта система состоит из двух частей программы расчета тепловой схемы установки и программы определения суммарных расчетных затрат по установке. Алгоритм удовлетворения ограничений на технологические характеристики включен во вторую часть, а на независимые и зависимые параметры — в первую часть. Алгоритм оптимизации параметров ПГУ, основанный на применении градиентного метода, реализован в виде отдельной программы, не содержащей никаких вычислений, кроме подсчета величины шага. Эта программа в значительной степени универсальна и может быть использована для оптимизации большого класса теплоэнергетических установок [75, 88]. [c.135]

Согласно исследованиям ВНИИГС предложен алгоритм оптимизации распределения нагрузки между котлами, когда все они работают в регулировочном режиме в зоне оптимальных нагрузок (см. такж 4.1) [45]. [c.140]

Первыми предложили использовать расходы Qe в градиентном методе в качестве независимых перемеиных Фукуда, Умезу и Секина в 1964 г. [Л. 11]. В отечественной литературе такие же независимые переменные в градиентном методе начали применяться в [Л. 45], а затем в [Л. 56, 84], однако во всех этих работах применены разные алгоритмы оптимизации, связанные с расчетами по Qb. [c.43]

Для получения направления, близкого к проекции вектора-антигра-диента целевой функции на поверхность ограничений наиболее часто используется аппарат линейного программирования (метод возможных направлений Зойтендейка [Л. 29]). В нашей задаче проектирование указанного вектора на поверхность ограничений сводится к минимизации линейной формы (2-29) при учете всех режимных ограничений, причем нелинейные ограничения должны быть предварительно линеаризированы в окрестности рассматриваемой точки. Проверка показала, что применять в этом случае хорошо разработанный аппарат линейного программирования (например, симплекс-метод) нецелесообразно, так как решение только этой линейной вспомогательной задачи потребует весьма больших затрат машинного времени. Выходом из положения является разработка специализированных алгоритмов я программ решения линейной вспомогательной задачи, требующих небольших затрат машинного времени. Оказалось возможным разработать такой сравнительно простой алгоритм проекционного метода лишь для ограничений по W я Qb- Для учета же ограничений по расходам воды в нижние бьефы ГЭС и мощностям ГЭС рекомендуется использовать штрафные функции. Таким образом, предлагаемый алгоритм оптимизации долгосрочных режимов ГЭС является комбинированным он базируется на сочетании проекционного метода и метода штрафных функций. [c.49]

Алгоритм оптимизации в программе NASTRAN принадлежит к семейству методов, называемых градиентными. Эти методы в ходе численного поиска оптимальной конструкции используют кроме значений функции еще и ее градиент. Процесс численного поиска может быть кратко описан следующим образом для дайной точки в пространстве переменных определяются градиенты целевой функции и ограничений, а затем эта информация используется для определения направления поиска, В этом направлении мы двигаемся так далеко, как это возможно, после чего проверяем, найдена ли оптимальная точка. Если точка не найдена, то этот процесс повторяем до тех пор, пока не окажемся в ситуации, когда нельзя добиться улучшения без нарушения какого-либо ограничения. [c.480]

mash-xxl.info

Программы и алгоритмы оптимизации. Алгоритмы оптимизации

6. Оптимизация алгоритмов. Оценка сложности алгоритмов

Похожие главы из других работ:

1.1 Что такое оптимизация

5. Оптимизация

Оптимизация программы

4.1 Оптимизация инвестиций

1.2.5 Оптимизация

2.2 Оптимизация

3 Параметрическая оптимизация

1.3 Оптимизация

2.5 Оптимизация схемы

4.4 Оптимизация раскроя

6. Оптимизация модели

1.3 Однокритериальная оптимизация

3. Оптимизация

Оптимизация

2.5 Оптимизация