Виды выборок в социологическом исследовании и особенности их использования. Релевантность выборки
ЗУБ12-05 / Теория статистики / Теория статистики / Лекции по статистике для заочников / Выборка
Выборочное исследование.
Понятие о выборочном методе.
Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих исследованию единиц совокупности осуществляется случайно, отобранная часть подвергается исследованию, после чего результаты распространяются на всю совокупность.
К использованию выборочного метода прибегают в тех случаях,
1 когда само наблюдение связано с порчей или уничтожением наблюдаемых единиц (пряжа на пряность, электрическая лампочка на продукт горения)
2 большой объем совокупности
3 большие затраты (финансовые и трудовые).
Обычно выборочному обследованию подвергается 5-10% всей совокупности, реже 15-25%.
Целью выборочного наблюдения является определение характеристик генеральной средней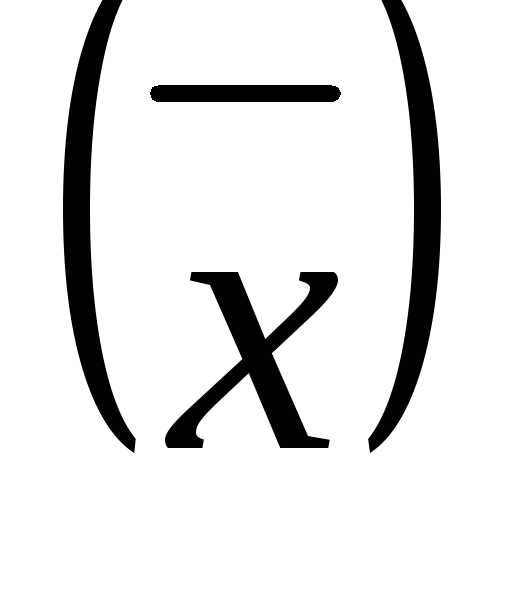 
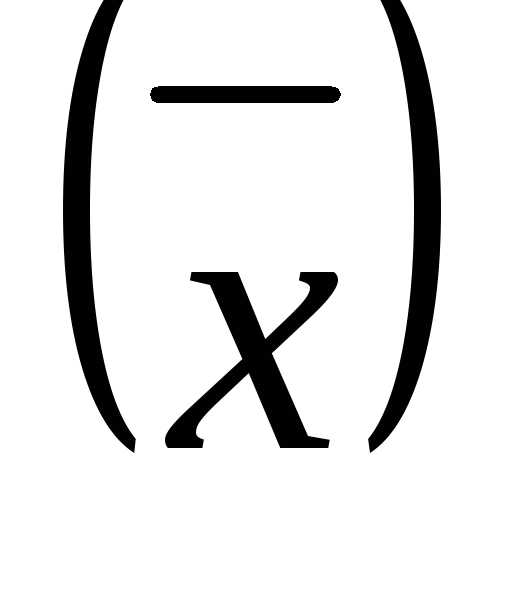и выборочная доля (w) отличаются от генеральных характеристик на величину ошибки выборки (
). Потому необходимо вычислять ошибку выборки или ошибку репрезентативности, которая определяется по формулам, разработанным в теории вероятности для каждого вида выборки и способа отбора.Существуют следующие способы отбора единиц:
1 отбор по схеме возвращенного шара, обычно называемый повторной выборкой.
При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора какой- то единицы, она снова возвращается в совокупность и снова может быть выбранной.
2 отбор по схеме невозвращенного шара, называемый бесповторной выборкой. В этом случае каждая отобранная единица не возвращается обратно, и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастет) (жеребьевка), таблицы случайных чисел например 75 из 780.
Виды выборок.
1 Собственно – случайная.
Это такая, при которой отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности.
При этом количество отобранных единиц обычно определяется исходя из принятой доли выборки.
Для выборки есть отношение числа единиц выборочной совокупности и к численности единиц генеральной совокупности N.
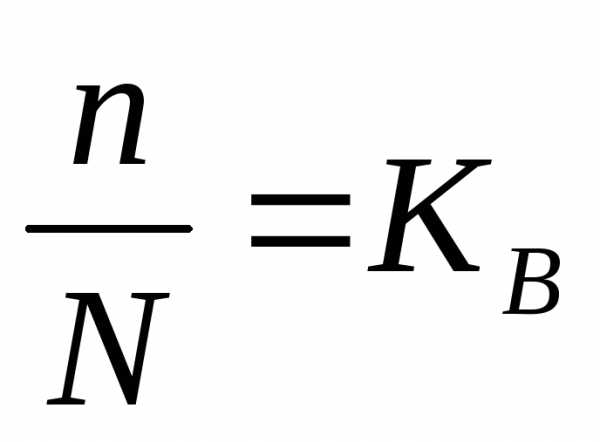
Так при 5% выборке из партии товара в 2000 единиц численность выборки n составляет 100 ед. (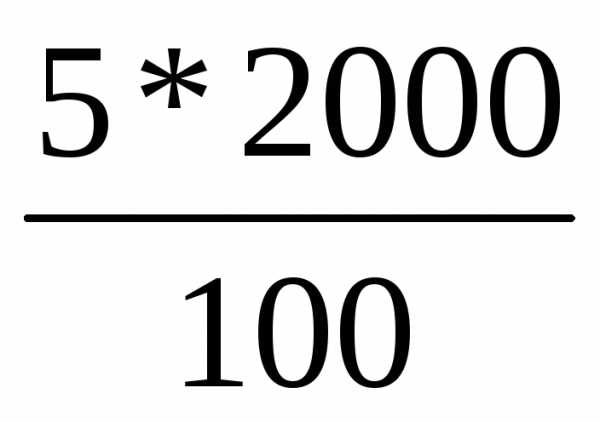
), а при 20% выборке она составит 400 ед.
(
)
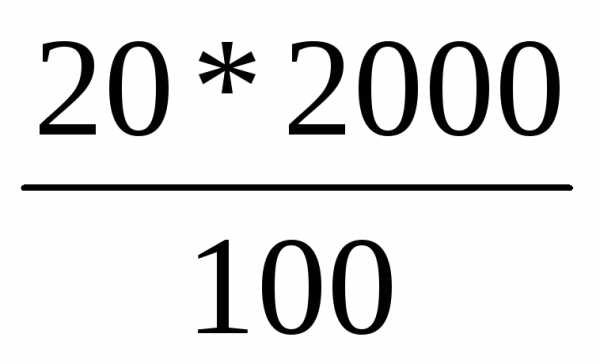Важное условие собственно случайной выборки в том, что каждой единице генеральной совокупности предоставляется равная возможность попасть в выборочную совокупность.
При случайном отборе предельная ошибка выборки для средней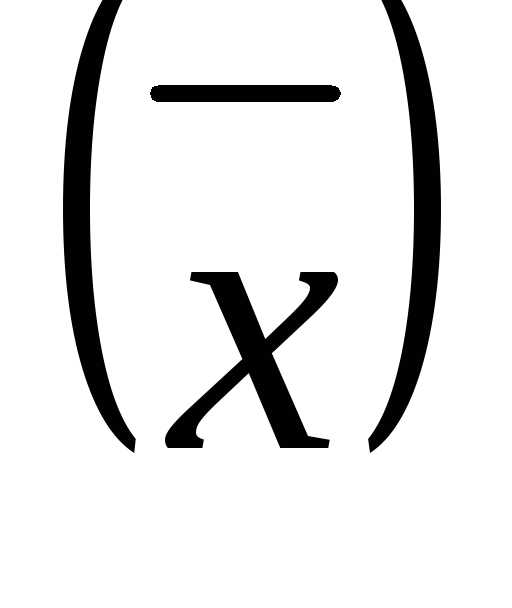 
равна
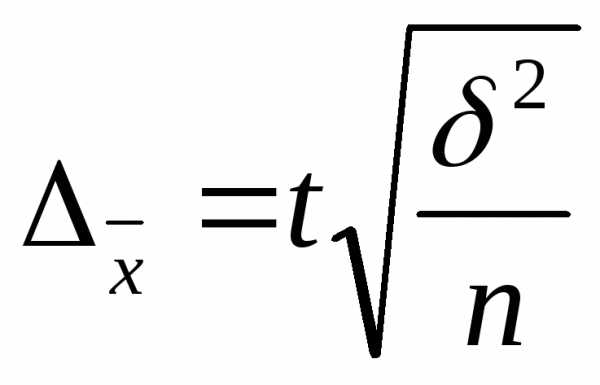
для доли
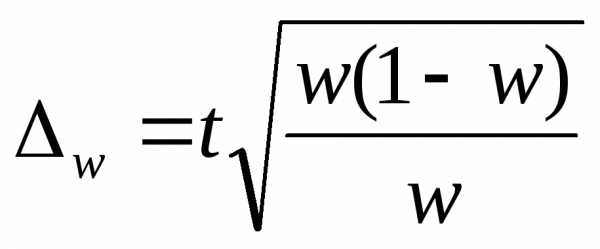
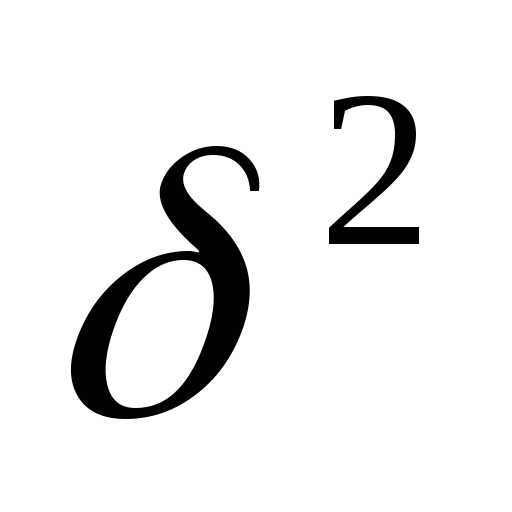
n- численность выборки
t- коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности P.
P=0.683 t=1
P=0.954 t=2
P=0.997 t=3
При бесповторном отборе предельная ошибка выборки определяется по формуле для средней
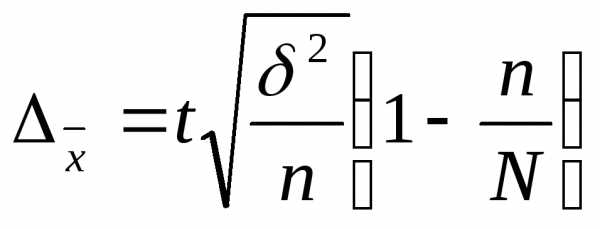
где N –численность генеральной совокупности доли
Пример
Для определения зольности угля в порядке случайной выборке было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке 16%, 
= 5%. В 10-ти пробах зольность угля составила >20% с вероятностью 0,954 определить пределы, в которых будет находиться средняя зольность угля в месторождении и доля угля с зольность >20%
Решение
Средняя зольность
определяем предельную ошибку выборки
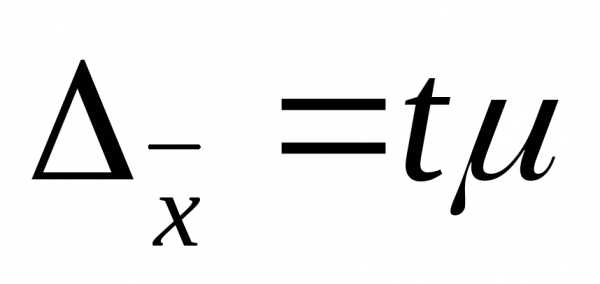2*0.5=1%
при p=0.954 t=2
доля угля с зольностью >20%
выборочная доля определяется
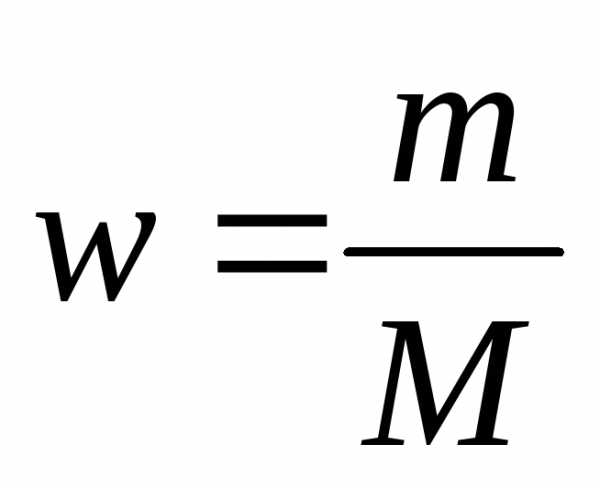
где m- доля единиц, обладающих признаком
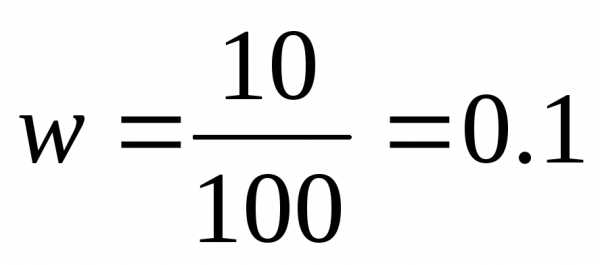
ошибку выборки для доли
С вероятностью 0,954 можно утверждать, что доля угля с зольностью более 20% в месторождении будет находиться в пределах
P= 10%+(-)6% или
Механическая выборка.
Это разновидность собственно – случайной. В этом случае вся генеральная совокупность делится на n равных частей и затем из каждой части отбирается одна единица.
Все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку. При этом из каждой группы должна отбираться та единица, которая находится в середине каждой группы. Это позволяет избежать систематической ошибки выборки.
Применяют: при обследовании покупателей в магазинах, посетителей в поликлиниках, каждый 5,4,3 и т.д
Пример механическая выборка
Для определения среднего срока пользования краткосрочным кредитом в банке будет произведена 5% механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом 30 дней при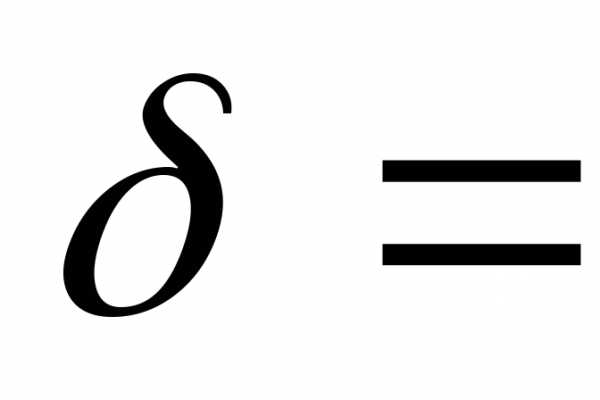 
Решение
Ошибка выборки
т.е. с вероятность 0,954 можно утверждать, что срок пользования кредитом колеблется
1 в пределах 30дн.+(-)2дня, т.е.
2 доли кредитов со сроком > 60дней.
выборочная доля составит
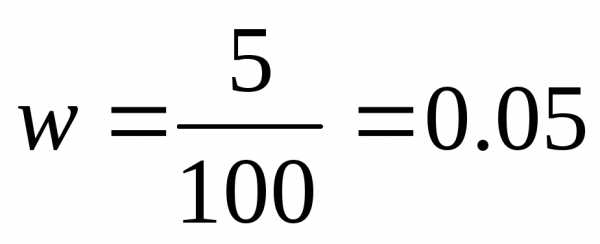
ошибку доли определим
с вероятностью 0,954 можно утверждать, что доля кредитов в банке со сроком пользования >60дней будет находиться в пределах
Типическая выборка.
Генеральная совокупность разделяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность
Например: пр. тр. работников, состоящих из отдельных групп по квалификации.
Важная особенность – дает более точные результаты по сравнению с другими, т.к. в выборке участвует типологическая единица.
Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп.
Объем выборки из типической группы при отборе пропорциональном численности типических групп, определяется по формуле
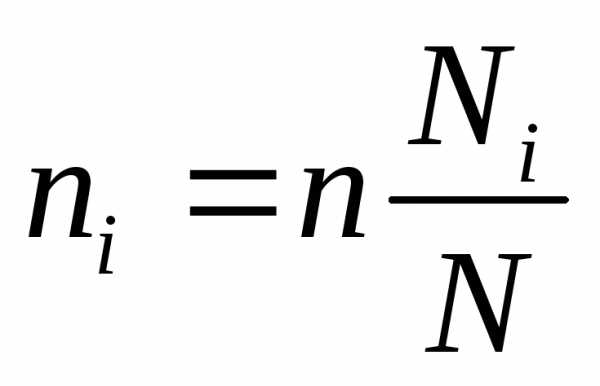
где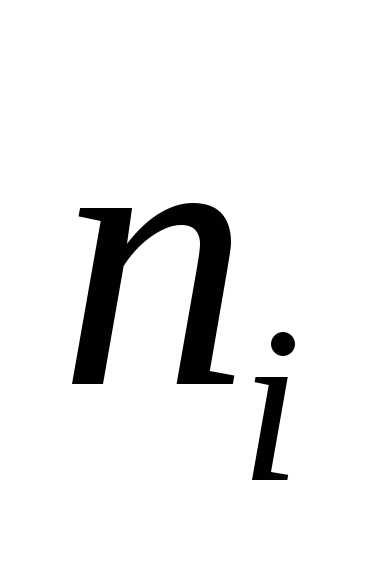 
=V выборки из типической группы
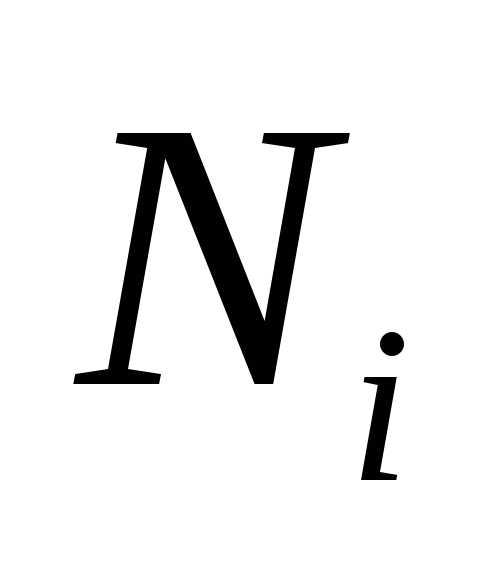= V типической группы.
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам
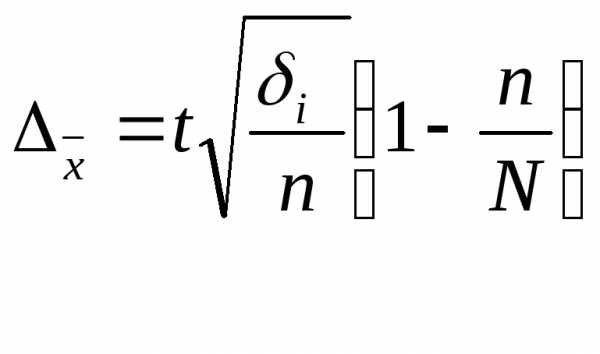
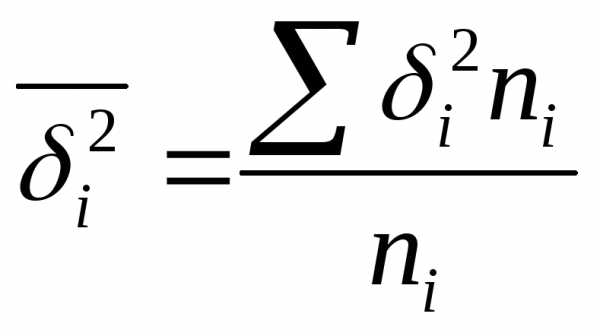
где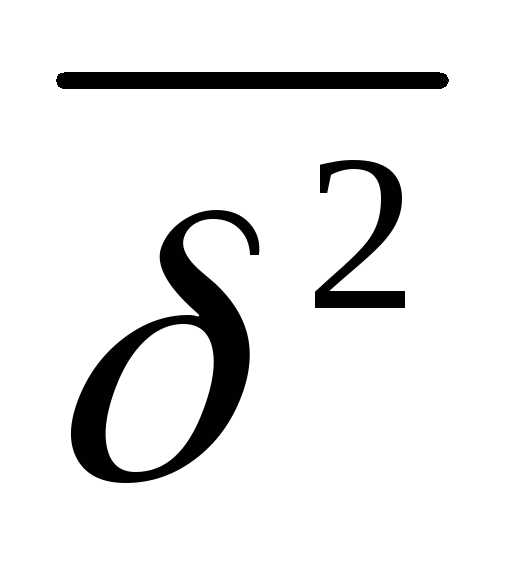 
=дисперсия выборочной совокупности
Пример: типическая выборка
Для определения среднего возраста мужчин, вступающих в брак, в районе была произведена 5% выборка с отбором единиц пропорционально численности типических групп
Внутри групп применялся механический отбор
| Социальная группа | Число мужчин | Средний возраст | Средне квадратическое отклонение | Доля мужчин вступивших во второй брак, % |
| Рабочие | 60 | 24 | 5 | 10 |
| служащие | 40 | 27 | 8 | 20 |
С вероятностью 0,954 определить пределы в которых будут находиться средний возраст мужчин, вступивших в брак, и долю мужчин, вступивших в брак вторично.
Решение
средний возраст вступают в брак мужчины в выборочной совокупности
предельная ошибка выборки
с вероятностью 0,954 можно утверждать, что средний возраст мужчин, вступающих в брак, будет находиться в пределах
для мужчин, вступающих во второй брак находиться в пределах
выборочная доля определяется
выборочная дисперсия альтернативного признака равна
с вероятностью 0,954 можно утверждать, что доля вступающих в брак во второй раз находится в пределах
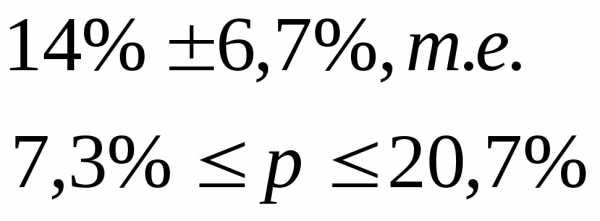
Серийная выборка.
При серийной выборке совокупность делят на одинаковые по объему группы – серии. Выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе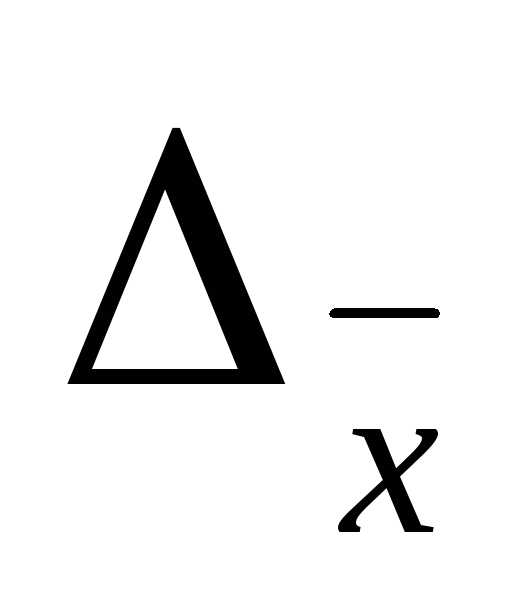 
и
определяют по формуле
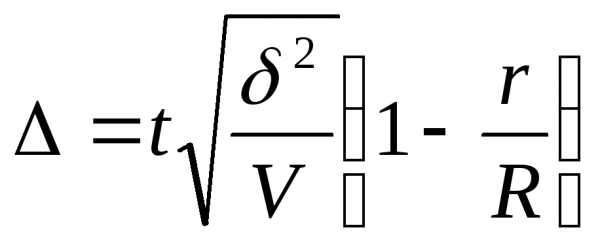
где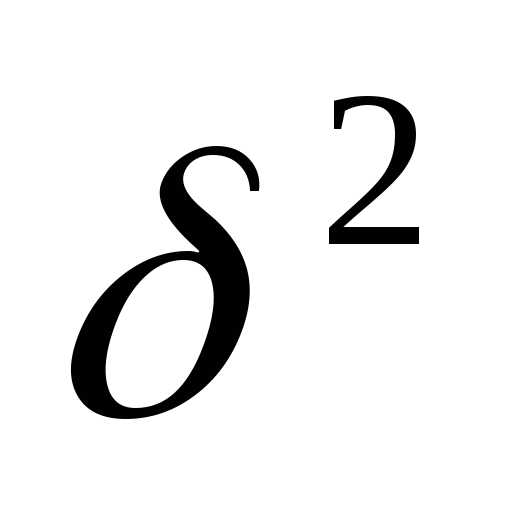 
- межсерийная дисперсия
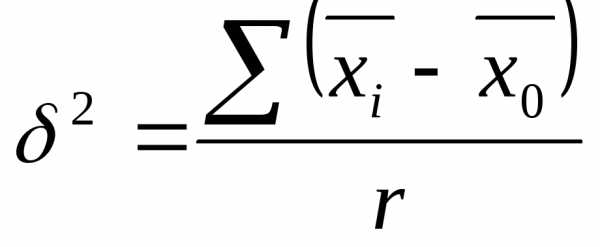
где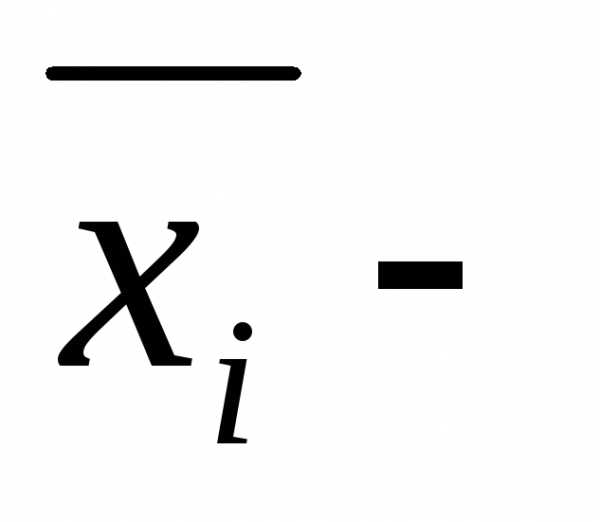 
выборочная средняя серии
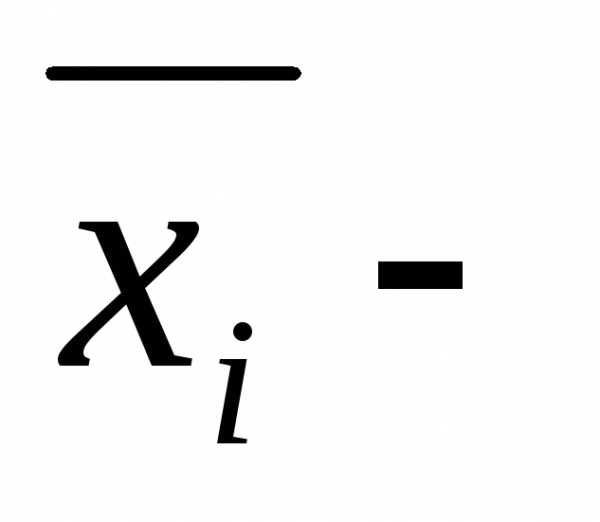выборочная средняя серийной выборки
R- число серий генеральной совокупности
r- число отобранных серий
Пример: в цехе 10 бригад с целью изучения их производительности труда будет осуществлена 20% серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что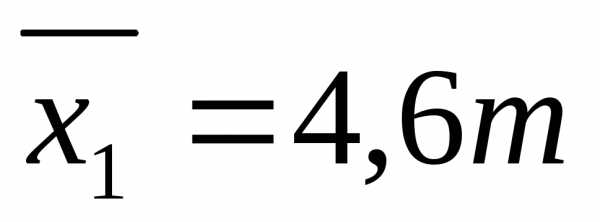 
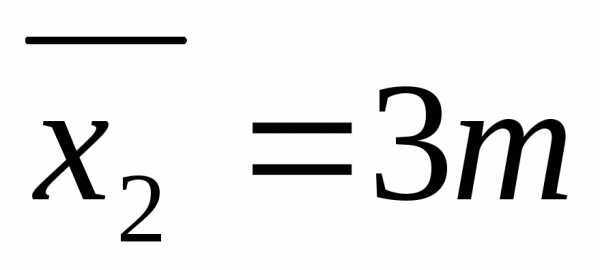с вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.
Решения
выборочная средняя серийной выборки определяется по формуле
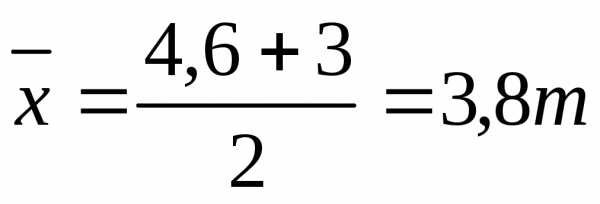
с вероятностью 0,997 можно утверждать, что средняя выработка рабочих цеха находится в пределах
Пример.
На складе готовой продукции цеха находятся 200 ящиков деталей по 40 штук в каждом ящике. Для проверки качества готовой продукции будет произведена 10% серийная выборка. В результате выборки установлено, что для бракованных деталей составляет 15%. Дисперсия серийной выборки равна 0,0049.
С вероятностью 0,997 определить пределы, в которых находится доля бракованной продукции в партии ящиков
Решение
Доля бракованных деталей будет находиться в пределах
определим предельную ошибку выборки для доли по формуле
с вероятностью 0,997 можно утверждать, что доля бракованных деталей
в партии находится в пределах
В практике проектирования выборочного наблюдения возникает потребность нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик - средней и доли.
Предельная ошибка выборки, вероятность ее появления и вариация признака предварительно известны.
При случайном повторном отборе численность выборки определяется по формуле
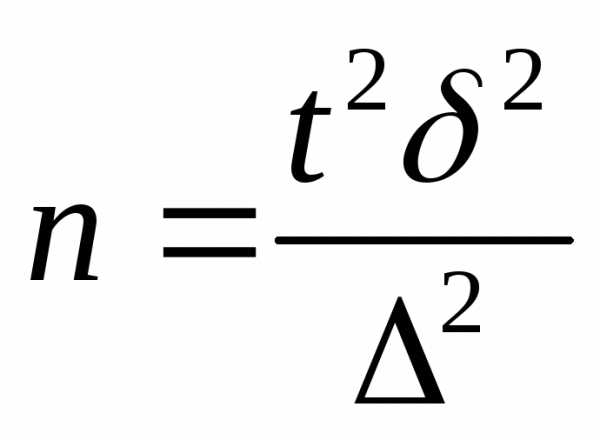
при случайном бесповторном и механическом отборе численность выборки
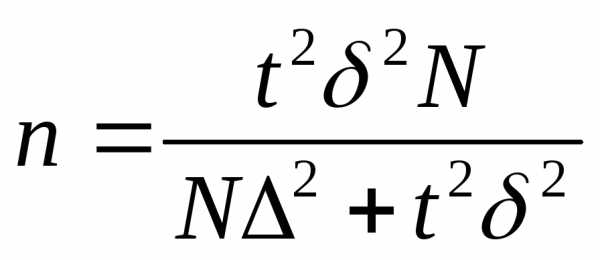
для типической выборки
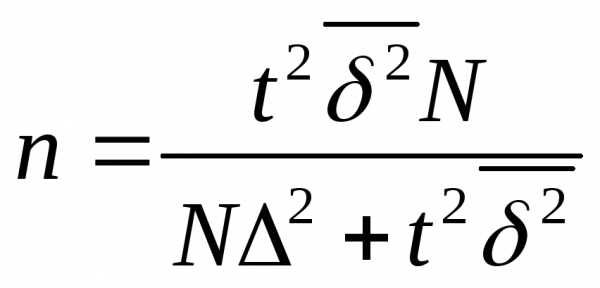
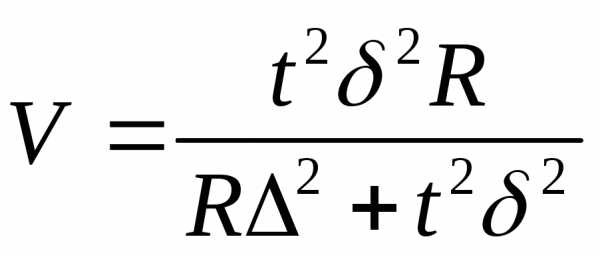
Пример в районе проживает 2000 семей.
Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи.
Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 1 человека при среднем квадратическом отклонении 3 человека.
Решение
Пример.
В городе проживает 10тыс. семей. С помощью механической выборки предлагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью Р=0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,02?
Решение.
studfiles.net
Репрезентативная выборка
Фактически мы начнем не с одного, а с трех вопросов: что такое выборка? когда она является репрезентативной? что она собой представляет?
Совокупность – это любая группа людей, организаций, интересующих нас событий, относительно которых мы хотим сделать выводы, а случай, или объект, – любой элемент такой совокупности1.Выборка – любая подгруппа совокупности случаев (объектов), выделенная для анализа. Если мы захотим изучить деятельность законодателей штата по принятию решений, мы могли бы исследовать такую деятельность в законодательных органах штатов Виргиния, Северная Каролина и Южная Каролина, а не во всех пятидесяти штатах и, исходя из этого, распространить полученные данные на генеральную совокупность, из которой были выбраны эти три штата. Если мы хотим исследовать систему предпочтений избирателей Пенсильвании, мы могли бы сделать это, опросив 50 рабочих компании “Ю. С. Стил” в Питсбурге, и распространить результаты опроса на всех избирателей штата. Аналогично, если мы хотим измерить умственные способности студентов колледжей, мы могли быпротестировать всех игроков защиты, зарегистрированных в штате Огайо в данном футбольном сезоне, и затем распространить полученные результаты на генеральную совокупность, частью которой они являются. В каждом примере мы действуем следующим образом: устанавливаем подгруппу внутри генеральной совокупности, довольно [c.154] подробно изучаем эту подгруппу, или выборку, и распространяем наши результаты на всю совокупность. Это и есть основные этапы формирования выборки.
Однако представляется совершенно очевидным, что каждая из этих выборок имеет существенный недостаток. К примеру, хотя законодательные органы Виргинии, Северной Каролины и Южной Каролины и являются частью совокупности законодательных органов штатов, они в силу исторических, географических и политических причин, скорее всего, будут действовать очень схожим образом и совсем иначе, чем законодательные органы таких отличающихся от них штатов, как Нью-Йорк, Небраска и Аляска. Хотя пятьдесят рабочих-сталелитейщиков в Питсбурге действительно могут быть избирателями штата Пенсильвания, они в силу социально-экономического статуса, образования и жизненного опыта, вполне возможно, будут иметь взгляды, отличные от взглядов многих других людей, точно так же являющихся избирателями. И точно так же, хотя футболисты штата Огайо и являются студентами колледжей, они в силу самых разных причин вполне могут отличаться от других студентов. Иными словами, хотя каждая из этих подгрупп действительно является выборкой, члены каждой из них систематически отличаются от большинства остальных членов совокупности, из которой они выбраны. В качестве отдельной группы ни одна из них не является типичной с точки зрения распределения признаков мнений, мотивов поведения и характеристик в генеральной совокупности, с которой она ассоциируется. Соответственно, политологи сказали бы, что ни одна из этих выборок не является репрезентативной.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности. Таким образом, если 50% всех законодательных органов штатов собираются лишь раз в два года, приблизительно половина состава репрезентативной выборки законодательных органов штатов должна быть такого типа. Если 30% избирателей Пенсильвании принадлежат к “синим воротничкам”, около 30% репрезентативной [c.155] выборки для этих избирателей (а не 100%, как в приведенном выше примере) должны быть из числа “синих воротничков”. И если 2% всех студентов колледжей являются спортсменами, приблизительно та же самая часть репрезентативной выборки студентов колледжей должна приходиться на спортсменов. Инымисловами, репрезентативная выборка представляет собой микрокосм, меньшую по размеру, но точную модель генеральной совокупности, которую она должна отражать. В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выборки, можно без всяких опасений считать применимыми к исходной совокупности. Это распространение результатов и есть то, что мы называем генерализуемостью.
Возможно, пояснить это поможет графическая иллюстрация. Предположим, мы хотим изучать модели членства в политических группах среди взрослого населения США. На рис.5.1 изображено три круга, разделенных на шесть равных секторов. Рис.5.1а представляет всю рассматриваемую совокупность. Члены совокупности расклассифицированы в соответствии с политическими группами (такими, как партии и группы интересов), к которым они относятся. В этом примере каждый взрослый принадлежит по меньшей мере к одной и не более чем к шести политическим группам; и эти шесть уровней членства в одинаковой степени распространены в совокупности (отсюда равные сектора). Предположим, мы хотим исследовать мотивы вступления людей в группу, выбор группы и модели участия, однако из-за ограниченности ресурсов мы в состоянии обследовать только одного из каждых шести членов совокупности. Кого же отобрать для анализа?
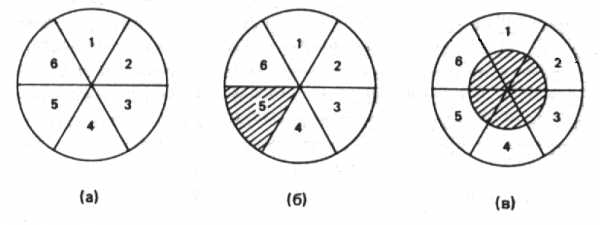
Рис. 5.1. Формирование выборки из генеральной совокупности
Одну из возможных выборок заданного объема иллюстрирует заштрихованная область на рис.5.1б, однако она явно не отражает структуру совокупности. Если бы мы делали обобщения на основе этой выборки, мы пришли бы к выводу: (1) что все взрослые американцы принадлежат к пяти политическим группам и (2) что все групповое поведение американцев совпадает с поведением тех, кто принадлежит именно к пяти группам. Однако мы знаем, что первый вывод не верен, и это может зародить в нас сомнение относительно валидности второго. Таким образом, [c.156] выборка, изображенная на рис.5.1б, нерепрезентативна, поскольку она не отражает распределение данного свойства совокупности (часто называемого параметром) в соответствии с его реальным распространением. Про такую выборку говорят, что она смещена в направлении к членам пяти групп или смещена в направлении от всех остальных моделей членства в группах. Опираясь на такую смещенную выборку, мы обычно приходим к ошибочным выводам относительно генеральной совокупности.
Ярче всего это может быть продемонстрировано на примере катастрофы, постигшей в 30-е годы журнал “Литэрари дайджест”, который организовал опрос общественного мнения относительно результатов выборов. “Литэрари дайджест” представлял собой периодическое издание, в котором перепечатывались редакционные статьи из газет и другие материалы, отражавшие общественноемнение; этот журнал был очень популярен в начале века. Начиная с 1920 г. журнал проводил широкомасштабный общенациональный опрос, в ходе которого более чем миллиону человек по почте рассылались избирательные бюллетени с просьбой отметить, чья кандидатура на предстоящих президентских выборах для них предпочтительнее. В течение ряда лет результаты опроса, проводившиеся журналом, оказывались настолько точными, что опрос, проведенный в сентябре, казалось, делал ноябрьские выборы малосущественными. Да и как притакой большой выборке могла произойти ошибка? Однако в 1936 г. именно это и случилось: с большим перевесом голосов (60:40) победа была предсказана кандидату от республиканской партии Альфу Ландону. На выборах Ландон проиграл инвалиду – [c.157] Франклину Д. Рузвельту – практически с тем же результатом, с которым должен был победить. Доверие к “Литэрари дайджест” было столь сильно подорвано, что вскоре после этого журнал перестал выходить. Что же произошло? Все очень просто: в голосовании, проведенном “Дайджест”, использовалась смещенная выборка. Почтовые открытки рассылались людям, чьи имена были извлечены из двух источников: телефонных справочников и списков регистрации автомобилей. И хотя прежде этот метод отбора не слишком отличался от других методов, совсем по-другому обстояло дело теперь, во время Великой депрессии 1936 г., когда менее состоятельные избиратели, наиболее вероятная опора Рузвельта, не могли позволить себе иметь телефон, не говоря уж об автомобиле. Таким образом, фактически выборка, использовавшаяся в опросе, организованном “Дайджест”, была смещена в сторону тех, кто, скорее всего, должен был выступать за республиканцев, и при этом еще удивительно, что у Рузвельта был такой хороший результат.
Как же решить эту проблему? Возвращаясь к нашему примеру, сравним выборку на рис.5.1б с выборкой на рис.5.1в. В последнем случае для анализа также отобрана шестая часть совокупности, однако каждый из основных типов совокупности представлен в выборке в той пропорции, в которой он представлен во всей совокупности. Такая выборка демонстрирует, что один из каждых шести взрослых американцев принадлежит к одной политической группе, один из шести – к двум и т.д. Такая выборка позволит также выявить другие различия между ее членами, которые могли бы соотноситься с участием в разном числе групп. Таким образом, выборка, представленная на рис.5.1в, является репрезентативной выборкой для рассматриваемой совокупности.
Конечно, данный пример является упрощенным по крайней мере с двух чрезвычайно важных точек зрения. Во-первых, большинство совокупностей, интересующих политологов, более разнообразно, чем та, что приведена в примере. Люди, документы, правительства, организации, решения и т.п. отличаются друг от друга не по одному, а по гораздо большему числу признаков. Таким образом, репрезентативная выборка должна быть такой, чтобы каждая из основных, отличная от других область была [c.158] представлена пропорционально ее доле в совокупности. Во-вторых, ситуация, когда реальное распределение переменных, или признаков, которые мы хотим измерить, заранее неизвестно, встречается гораздо чаще, чем противоположная, – возможно, оно не измерялось в предшествующей переписи населения. Таким образом, репрезентативная выборка должна быть построена так, чтобы она могла точно отражать существующее распределение даже тогда, когда мы не в состоянии прямо оценить ее валидность. Процедура формирования выборки должна иметь внутреннюю логику, способную убедить нас, что, будь мы в состоянии сравнить выборку с переписью, она действительно оказалась бы репрезентативной.
Чтобы обеспечить возможность точного отражения сложной организации данной совокупности и определенную степень уверенности в том, что предлагаемые процедуры способны сделать это, исследователи обращаются к методам статистики. При этом они действуют по двум направлениям. Во-первых, используя определенные правила (внутреннюю логику), исследователи решают вопрос о том, какие именно конкретные объекты им изучать, что именно включать в конкретную выборку. Во-вторых, используя совсем другие правила, они решают, сколько объектов выбрать. Мы не будем подробно изучать эти многочисленные правила, рассмотрим лишь их роль в политологическом исследовании. Начнем рассмотрение со стратегий выбора объектов, образующих репрезентативную выборку. [c.159]
studfiles.net
Выборка. Типы выборок. Расчет ошибки выборки
Калькуляторы
Калькулятор расчета ошибки и размера выборкиКалькулятор расчета статистической значимости различийГенеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени. Примеры генеральных совокупностей
- Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
- Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
- Юридические лица России (2,2 млн. на начало 2005 года)
- Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей. Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население Москвы.
- Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках соответственно. Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки. Пример: Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности. Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже. Пример: Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об ошибке выборки, подразумевают именно статистическую ошибку. Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих результаты исследования в определенную сторону. Пример:
- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни. Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например, дома).
- Проблема респондентов, отказывающихся отвечать на вопросы анкеты (доля «отказников» в Москве, для разных опросов, колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки 1.1 Случайная выборка (простой случайный отбор) Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел. 1.2 Механическая (систематическая) выборка Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k 1.3 Стратифицированная (районированная) Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом. 1.4 Серийная (гнездовая или кластерная) выборка При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.. 2.1. Квотная выборка Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто. 2.2. Метод снежного кома Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.) 2.3 Стихийная выборка Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов. 2.4 Выборка типичных случаев Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.
Курс лекций по теории статистики
Более подробную информацию по выборочным наблюдениям можно получить просмотрев видеокурс по теории статистики:Выборочное наблюдение Способы формирование выборки Специальные виды отбора
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям:Доверительная вероятность Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятностьОшибка выборки (доверительный интервал) Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения.Доля признака Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют, необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Калькулятор расчета статистической значимости различий
Калькулятор позволяет проверить есть ли статистически значимая разница между долями признака, полученными из независимых выборок. Например, если до начала рекламной кампании марку знали 55% респондентов, а по окончании – 60% - есть ли между этими долями статистически значимая разница, или же эта разница укладывается в ошибку выборки? Примечание. Эта процедура может законно использоваться, только если обе выборки удовлетворяют следующему условию: произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, должны быть не меньше 5.
Оставить свои комментарии по затронутой теме Вы можете на наших страницах в Facebook и Вконтакте.
fdfgroup.ru
Репрезентативная выборка. Рассчитать объем выборки
Один из главных компонентов тщательно продуманного исследования – определение выборки и что такое репрезентативная выборка. Это как в примере с тортом. Ведь не обязательно съедать весь десерт, чтобы понять его вкус? Достаточно небольшой части.
Так вот, торт – это генеральная совокупность (то есть все респонденты, которые подходят для опроса). Она может быть выражена территориально, например, лишь жители Московской области. Гендерно – только женщины. Или иметь ограничения по возрасту – россияне старше 65 лет.
Высчитать генеральную совокупность сложно: нужно иметь данные переписи населения или предварительных оценочных опросов. Поэтому обычно генеральную совокупность «прикидывают», а из полученного числа высчитывают выборочную совокупность или выборку.
Что такое репрезентативная выборка?
Выборка – это чётко определенное количество респондентов. Её структура должна максимально совпадать со структурой генеральной совокупности по основным характеристикам отбора.
Например, если потенциальные респонденты – всё население России, где 54% — это женщины, а 46% — мужчины, то выборка должна содержать точно такое же процентное соотношение. Если совпадение параметров происходит, то выборку можно назвать репрезентативной. Это значит, что неточности и ошибки в исследовании сводятся к минимуму.
Объем выборки определяется с учётом требований точности и экономичности. Эти требования обратно пропорциональны друг другу: чем больше объем выборки, тем точнее результат. При этом чем выше точность, тем соответственно больше затрат необходимо на проведение исследования. И наоборот, чем меньше выборка, тем меньше на неё затрат, тем менее точно и более случайно воспроизводятся свойства генеральной совокупности.
Поэтому для вычисления объема выбора социологами была изобретена формула и создан специальный калькулятор:
Доверительная вероятность и доверительная погрешность
Что означают термины «доверительная вероятность» и «доверительная погрешность»? Доверительная вероятность – это показатель точности измерений. А доверительная погрешность – это возможная ошибка результатов исследования. К примеру, при генеральной совокупности более 500 00 человек (допустим, проживающие в Новокузнецке) выборка будет равняться 384 человека при доверительной вероятности 95% и погрешности 5% ИЛИ (при доверительном интервале 95±5%).
Что из этого следует? При проведении 100 исследований с такой выборкой (384 человека) в 95 процентов случаев получаемые ответы по законам статистики будут находиться в пределах ±5% от исходного. И мы получим репрезентативную выборку с минимальной вероятностью статистической ошибки.
После того, как подсчет объема выборки выполнен, можно посмотреть есть ли достаточное число респондентов в демо-версии Панели Анкетолога. А как провести панельный опрос можно подробнее узнать здесь.
Сохранить
Сохранить
Сохранить
blog.anketolog.ru
Виды выборок в социологическом исследовании и особенности их использования.
Признаки-переменные, полученные при эмпирической операционализации и интерпретации объекта выступают основой построения выборочной совокупности (выборки) исследования.
Понятие «выборки» в статистике, социологии, маркетинге рассматривается в 2-х значениях: 1) этосовокупность элементов генеральной совокупности (ее часть), подлежащих изучению, т.е. выборочная совокупность. В некоторых случаях это микромодель объекта исследования; 2) это процесс формирования выборочной совокупности при необходимом условии обеспечения репрезентативности.
Отбор единиц в выборочную совокупность осуществляется в соответствии с типом планируемой выборки. Тип выборки определяется целью и задачами исследования
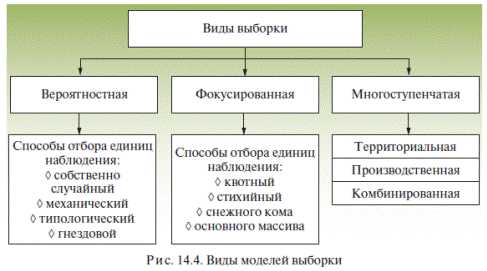
Выборки делятся на 2 большие группы:
СЛУЧАЙНЫЕ (вероятностные)- один из основных отборов, используемых в соц. Исследованиях. Как правило, точные и репрезентативные.Главный принцип – обеспечение возможности каждой единице генеральной совокупности попасть в выборочную. Все элементы ген. совокупности доступны. Используется чаще при относительно небольшой ген. совокупности. Конструируется методом случайного отбора (используются таблицы случайных чисел, лотерейный подбор, систематический (механический) отбор.
Способы отбора:
Собственно случайный. Основан на принципах «урновой модели». Все элементы (респонденты) генеральной совокупности пофамильно и посредством кода (числового номера) заносятся на карточки, после чего последние перемешиваются в ящике, из которого производится отбор одним из двух методов: случайный бесповторный и случайный повторный. При этом очень важно, чтобы карточки были перемешаны тщательно (повышает равную вероятность отбора респондентов).
Систематическая (механическая) выборка. Для больших генеральных совокупностей удобнее применять ее. Общий принцип заключается в том, что все элементы генеральной совокупности сводятся в единый список и из него через равные интервалы отбирается соответствующее число респондентов (выбор каждого n-ого элемента).
Метод стратифицированной выборкидовольно удобный и точный. Если имеется возможность «разбить» генеральную совокупность на однородные непересекающиеся части (страты) по заданному признаку, то отбор респондентов может быть осуществлен из каждой страты отдельно. При этом число респондентов, отбираемых из страты, пропорционально общему числу элементов в ней. А затем производится случайный отбор нужного числа респондентов в рамках страты.
Метод кластерной (гнездовой) выборки – объединение людей в группы (кластеры) (пр. по территориальному признаку). Для получения выборки надо сначала отобрать нужное число кластеров, а затем в каждом из отобранных кластеров отобрать нужное число респондентов, т. е. отбор надо проводить в два этапа (бывает многоступенчатой, т.к. сегментируют на более мелкие кластеры). При этом сохраняется случайный механизм отбора на всех этапах. Кластеры должны отбираться с вероятностью, пропорциональной числу элементов в нем. При этом увеличивается статистическая погрешность. При изучении общественного мнения больших масс населения, проживающих на обширной территории, это единственный способ создать случайную выборку.
!!!Страты должны содержать как можно более однородные элементы, кластеры – как можно более разнородные.
НЕСЛУЧАЙНЫЕ (фокусированные)– используются принципы отбора, отличные от случайного. Неприменимы правила теории вероятности. Ее виды: стихийная выборка, метод квот и целевая.
Стихийная выборка (пр.почтовый опрос читателей журнала или газеты). В данном случае нельзя заранее определить структуру массива респондентов. Затрудняет оценку репрезентативности. Выводы исследования, как правило, распространяются лишь на опрошенную совокупность. Метод снежного кома – разновидность стихийной выборки; когда один респондент определяет другого, другой – третьего и т.д. Используется также в целевой выборке. Метод основного массива применяется в разведывательных исследованиях для проверки какого-нибудь контрольного вопроса. Изучению подвергают только те части совокупности, в которых сосредоточено большинство единиц наблюдения.
Квотная выборка – условная микромодель объекта; сложная, самая репрезентативная для разнородного объекта. До начала исследования имеются статистические данные о контрольных признаках элементов генеральной совокупности. Все данные о том или ином контрольном признаке выступают в качестве квот. Число признаков в качестве квот, как правило, не превышает 4-х.
В пределах заданных ограничений интервьюер сам решает, кого ему опросить. !!! В этом отличие квотной выборки от случайной стратифицированной, при которой интервьюер должен опросить определенных, заранее отобранных людей.
Целевая (экспертная) выборка – отбор по принципу наличия «целевого» признака. Для изучения специфических и труднодоступных объектов; в исследованиях экспериментального плана. Не репрезентативна.
Поиск представителей малочисленных целевых групп в местах скопления («типичных гнездах», пр. целевая гнездовая выборка)
Доступная выборка - опрашиваются только те представители совокупности, которые легко доступны для исследования. В тех случаях, когда отсутствует четкое описание изучаемой совокупности и исследователь не озабочен вопросом, кого именно представляют опрошенные им люди.
Выборка типичных единиц (пр. типичный город каждого региона, типичные представители разных социальных групп и т. д. ) Выбор типичных представителей проводится на основе экспертных оценок или с применением специальных математических методов.
Чистые «идеальные» типы выборок встречаются редко, зачастую носят комбинированный характер.
МНОГОСТУПЕНЧАТАЯвыборка – выборка, основанная на поэтапном многократном использовании одной или нескольких моделей. Используется при большой генеральной совокупности. Формируется в несколько этапов. Носит комбинированный характер.
Территориальная выборка предполагает поэтапный отбор административных объединений и поселений до отбора собственно респондентов. Эта процедура называется районированием. В основе районирования могут лежать географические, урбанистические, этнические, экономические, социальные и другие признаки.
Производственная выборка используется в исследованиях проблем, связанных с трудовыми ресурсами или иными институционально объединенными группами населения.
Комбинированная многоступенчатая выборка предполагает сочетание территориального и производственного принципов районирования.
36. Репрезентативность и валидность социологических исследований.
Репрезентативность- свойство выборочной совокупности воспроизводить параметры генеральной совокупности. Чем точнее состав выборки представляет совокупность по изучаемым вопросам, тем выше ее репрезентативность. Репрезентативность выборки обеспечивается рядом процедур, в том числе правильным определением генеральной совокупности, техникой отбора лиц для наблюдения, типом выборки и др. Повышенная надежность (репрезентативность) выборки допускает ошибку до 3 процентов, обыкновенная - от 3 до 10 процентов, приближенная - от 10 до 20 процентов, ориентировочная - от 20 до 40 процентов и прикидочная - более 40 процентов.
Подробно проблемы обеспечения репрезентативности рассматриваются
статистикой. Они достаточно сложны, поскольку речь идет, с одной стороны, об обеспечении количественной репрезентации генеральной совокупности, с другой - качественной. Качественная репрезентация предполагает обеспечение в выборочной совокупности представительства всех элементов генеральной (к примеру, не может быть и речи о репрезентативности, если опрашиваются только мужчины или только женщины, только молодые люди или только старики; в выборке должны быть представлены все существующие группы). Что же касается количественной репрезентации, то здесь речь идет о том, что все эти группы должны быть представлены в выборочной совокупности в оптимальном (достаточном для нормального представительства) количестве.
Валидность — основной показатель качества измерения в социологическом исследовании, отражающий степень соответствия данных измерения объекту измерения. Валидность измерения, в самом общем смысле, характеризует соответствие измерения его цели. Эмпирический показатель валиден (обоснован, правилен) в той мере, в какой он действительно отражает значение той теоретической переменной, которую предполагалось измерить. Очевидно, что нет смысла говорить о валидности какого-то индикатора самого по себе. Валидность инструмента измерения состоит в однозначностш и правильности получаемых результатов относительно измеряемого свойства объектов, т. е. относительно предмета измерения. Можно сказать, что валидность определяет “чистоту” измерения теоретического конструкта.
Виды валидности по Батыгину:
1.Предикативная валидность — корреляции между результатами измерения и внешними критериями.
2.Конструктная валидность связывает измерительный инструмент со структурой теории.
Виды по Девятко:
1.Валидностъ по содержанию показывает, в какой мере избранные исследователем индикаторы отражают различные аспекты теоретического понятия.
2. Критериальная валидность (или валидность по критерию) показывает, насколько хорошо результаты по данному тесту или индикатору согласуются с результатами измерения другого показателя, называемого критерием.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Объем выборки опроса: расчет генеральной совокупности респондентов
Когда Вы задаете вопрос «Сколько мне потребуется респондентов для опроса?», Вы на самом деле спрашиваете: «Насколько большой должна быть моя выборка, чтобы точно оценить мою совокупность?» Принимая во внимание сложность этих понятий, мы разбили процесс на 5 шагов, давая Вам возможность легко рассчитать идеальный объем выборки и обеспечить точность результатов опроса.
Шаг 1
Что представляет собой Ваша генеральная совокупность?
Под термином «генеральная совокупность» мы понимаем целую группу людей, мнение которой Вы собираетесь выяснить (выборка будет состоять из членов этой совокупности, которые фактически примут участие в опросе).
К примеру, если Вы хотите понять, как найти рынок сбыта для зубной пасты во Франции, Вашей совокупностью будут жители Франции. А если Вы пытаетесь определить, сколько дней отпуска предпочли бы иметь люди, работающие на компанию по производству зубной пасты, то Ваша генеральная совокупность — сотрудники этой компании.
Независимо от того, страна это или компания, установление генеральной совокупности — это важный первый шаг. После того как Вы определились с генеральной совокупностью, установите (приблизительно) ее численность. Например, во Франции живут около 65 миллионов человек, а в компании-производителе зубной пасты работает, скорее всего, гораздо меньше сотрудников.
Получили нужную цифру? Хорошо, тогда идем дальше…
Шаг 2
Какова требуемая точность?
Этот шаг является своего рода оценкой того, на какой риск Вы готовы пойти в отношении возможной неточности ответов на опрос в связи тем фактом, что Вы не опрашиваете всю генеральную совокупность. Поэтому Вам следует ответить на два вопроса:
- Насколько уверенными Вы должны быть в том, что полученные ответы отображают мнения генеральной совокупности?Это Ваш предел погрешности. Итак, допустим, 90% членов выборки любят жевательную резинку со вкусом винограда. Предел погрешности в 5% добавляет по 5% с каждой стороны этого числа, что означает, что фактически 85-95% участников выборки любят жевательную резинку со вкусом винограда. 5% — наиболее часто используемый предел погрешности, но Вы можете устанавливать его значение от 1% до 10% в зависимости от опроса. Не рекомендуется поднимать этот показатель выше 10%.
- Насколько уверенными Вы должны быть в том, что выборка в точности представляет генеральную совокупность?Это Ваш уровень доверия. Уровень доверия — это вероятность того, что выборка является значимой для полученных результатов. Расчет, как правило, производится следующим образом. Если бы Вы в случайном порядке определили еще 30 выборок из данной совокупности, то как часто полученный Вами результат для одной выборки существенно отличался бы от результатов для других 30 выборок? Уровень доверия в 95% означает, что в 95% случаев результаты совпадали бы. 95% — наиболее часто используемое значение, но Вы можете установить его на уровне 90% или 99% в зависимости от опроса. Опускать значение уровня доверия ниже 90% не рекомендуется.
Шаг 3
Какого размера выборка мне нужна?
В таблице, размещенной ниже, выберите приблизительный размер целевой совокупности и предел погрешности для определения количества требуемых завершенных опросов.
Теперь, когда у Вас есть значения шага 1 и шага 2, по удобной таблице ниже определите размер требуемой выборки…
| 100 | 50 | 80 | 99 | 74 | 80 | 88 |
| 500 | 81 | 218 | 476 | 176 | 218 | 286 |
| 1000 | 88 | 278 | 906 | 215 | 278 | 400 |
| 10 000 | 96 | 370 | 4900 | 264 | 370 | 623 |
| 100 000 | 96 | 383 | 8763 | 270 | 383 | 660 |
| 1 000 000+ | 97 | 384 | 9513 | 271 | 384 | 664 |
Примечание. Данные приведены только в качестве ориентировочных инструкций. Кроме того, для генеральной совокупности свыше 1 млн. цифры можно округлять до сотен.
Шаг 4
Насколько отзывчивыми окажутся люди?
К сожалению, не все, кому Вы отправите опрос, дадут на него ответ.
Процент людей, заполнивших бланк полученного опроса, называют «процентной долей ответивших». Определение процентной доли ответивших на Ваш опрос поможет установить общее число экземпляров опроса, которое необходимо разослать для получения требуемого числа ответов.
Процентная доля ответивших прямым образом зависит от ряда факторов, таких как отношения с целевой аудиторией, продолжительность и сложность опроса, предлагаемые поощрения и тема опроса. Для онлайн-опросов, в которых с получателями предварительно не были установлены отношения, процентная доля ответивших в 20-30% считается очень высокой. Более консервативным и вероятным является значение 10-14%, если Вы до этого не проводили опрос в данной совокупности.
Шаг 5
Так скольким же людям отсылать опрос?
Это легкий этап!
Просто разделите число, полученное на шаге 3, на число, полученное на шаге 4. Это и есть Ваше волшебное число.
К примеру, если Вам нужно, чтобы опрос заполнили 100 женщин, пользующихся шампунем, и Вы считаете, что 10% женщин, которым Вы отправили опрос, его заполнят, требуется отослать опрос 1000 женщин (100/10%)!
www.surveymonkey.ru
