Проверка гипотезы об однородности двух ГС по критерию Манна-Уитни. Ранжирование выборки

§ 7. Ранжирование. Способы задания выборки

Пусть каждый объект в выборке изучается относительно некоторого количественного или качественного признака Х.

Примеры:

X – успеваемость по предмету,

Y – познавательная активность школьника по предмету,

Z – объем оперативной памяти.

Качественные признаки во многих случаях можно условно превратить в количественные с помощью ранжирования, т.е. выделения уровней (рангов) качества. При этом обычно лучшему качеству приписывается меньшее числовое значение.

Для признака Х используются 4 ранга – х1, х2, х3, х4:

х1 = «2», х2 = «3», х3 = «4», х4 = «5».

Для признака Y используются обычно 5 рангов:

y1 = «1» – постоянная увлеченность предметом,

y2 = «2» – постоянный интерес к предмету,

y3 = «3» – периодический интерес к предмету,

y5 = «4» – отсутствие интереса к предмету,

y5 = «5» – отказ учиться, неприязнь к предмету.

Для признака Z можно использовать два ранга z1, z2:

z1 = «1» – относительно большой объем оперативной памяти,

z2 = «2» – относительно маленький объем оперативной памяти.

Выборки по одному признаку можно задавать тремя способами:

а) с помощью простого перечисления значений признака,

б) с помощью вариант и частот,

в) с помощью вариант и относительных частот.

Для того чтобы задать выборку с помощью простого перечисления значений признака, нужно записать значения признака для каждого объекта выборки в порядке появления.

Пример. Пусть Х – успеваемость по предмету (в баллах). (2; 3; 4; 5; 2; 3; 2; 5; 5; 5) – выборка объема n = 10.

При задании выборки с помощью вариант и частот предварительно нужно указать варианты – различные значения признака. Для каждой варианты хi определяют ее частоту ni: ni = число появлений варианты хi в выборке. ( ni= n).

В этом случае, для того чтобы задать выборку, достаточно указать лишь варианты и их частоты. Выборку в последнем примере зададим с помощью вариант и частот:

Хi	2	3	4	5	 ni =10.
ni	3	2	1	4	 ni =10.

Если вместо niуказывать относительные частоты wi= ni/n, то выборку можно задать с помощью вариант и относительных частот:

хi	2	3	4	5	 wi =1.
wi	0,3	0,2	0,1	0,4	 wi =1.

§ 8. Выборочные числовые характеристики

По выборке по признаку Х можно найти выборочные числовые характеристики:

Хв – выборочная средняя,

Дв (Х) – выборочная дисперсия,

в (Х) – выборочное среднее квадратическое отклонение.

Выборочную среднюю Хв можно найти по выборке по формулам:

Хв = (х1+ х2+ х3+…+хn)

в случае задания выборки с помощью простого перечисления значений признака;

Хв = ( х1n1+ х2n2+ х3n3+…+хknk)

в случае задания выборки с помощью вариант и частот;

Хв = ( х1w1+ х2w2+ х3w3+…+хkwk)

в случае задания выборки с помощью вариант и относительных частот.

В нашем примере

Хв = (2+3+4+5+2+3+2+5+5+5)= 3,6

Хв = (23+32+41+54)= 3,6

Хв = 20,3+30,2+40,1+50,4= 3,6

Хв характеризует среднее значение признака Х во всей генеральной совокупности. Таким образом, в нашем примере Хв= 3,6 балла – средняя успеваемость ученика по предмету.

Для нахождения дисперсии Д(Х) также могут использоваться различные формулы в зависимости от способа задания выборки. Обычно используют следующую формулу:

Д(Х) = Хв2 – (Хв)2.

Здесь Хв – выборочная средняя признака Х;

Хв2 – выборочная средняя квадрата признака Х;

Хв2 = (х12 + х22 + х32 + … + хn2) – в случае если выборки заданы с помощью перечисления значений признака;

Хв2 = (х12n1 + х22n2+ х32n3+ … + хк2nк) – в случае, когда выборки заданы с помощью вариант и частот.

Найдем Дв(Х), в(Х) в нашем примере.

Имеем:

Хв2 = (223 + 322 + 421 + 524) = 146 = 14,6 ;

Дв(Х) = Хв2 - Хв2 = 14,6 – 3,62 = 14,6 – 12,96 = 1,64 ;

в(Х) = = 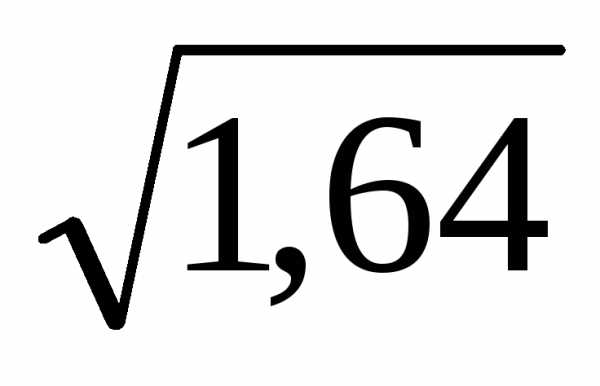≈ 1,28 (балла).

Выборочные числовые характеристики Дв(Х), в(Х) характеризуют разброс значений признака Х во всей генеральной совокупности: чем больше Дв(Х) (или в(Х)) , тем больше разброс.

При малых объемах выборки (n  30) выборочные Дв(Х), в(Х) «исправляют», т.е. берут исправленные характеристики:

Дв испр.(Х) = Дв(Х) ,

в испр(Х) = .

В нашем примере n < 30, поэтому

Дв испр.(Х) = Дв(Х) = 1,64  1,82,

в испр(Х) =  1,35 (балла).

studfiles.net

Систематизация и ранжирование выборки - ЭЛЕМЕНТЫ СТАТИСТИКИ АЛГЕБРА И НАЧАЛА АНАЛИЗА

АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, НАЧАЛА ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ СТАТИСТИКИ

§3. ЭЛЕМЕНТЫ СТАТИСТИКИ.

2. Систематизация и ранжирование выборки.

Важным этапом исследования является систематизация полученных данных (выборки), то есть представление выборки в удобном для дальнейших действий виде.

Пример 1. Все одиннадцатиклассники некоторого района писали одну и ту гамму проверочную контрольную работу по математике по текстам районного управления образования. Выборку составили 30 наугад выбранных работ этих одиннадцатиклассников. Пусть выбранные одиннадцатиклассники получили следующие оценки.

Данные этой выборки можно систематизировать в таблицу по количеству набранных баллов.

Полученный балл за контрольную работу	1	2	3	4	5	6	7	8	9	10	11	12
Количество учащихся	1	2	2	3	2	3	4	4	3	3	2	1

Также данные выборки можно систематизировать по уровням учебных достижений.

Уровень учебных достижений	Начальный уровень	Средний уровень	Достаточный уровень	Высокий уровень
Количество учащихся	5	8	11	6

Операцию расположение случайных величин выборки по принципу неспадання называют ранжированием выборки. При ранжировании выборки каждое следующее число выборки не меньше прежнего.

Пример 2. В результате ранжирования выборки, рассмотренной в примере 1 этого пункта, получим 1; 2; 2; 3; 3; 4; 4; 4; 5; 5; 6; 6; 6; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 9; 10; 10; 10; 11; 11; 12.

na-uroke.in.ua

Математическая статистика

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Математическая статистика - это раздел прикладной математики, в котором рассматриваются методы отыскания законов и характеристик случайных величин по результатам наблюдений и экспериментов.

----------------------------------------------------------------------

Основные задачи математической статистики.

1. Создание методов сбора и группировки обрабатываемого статистического материала, полученного в результате наблюдений за случайными процессами.

2. Разработка методов анализа полученных статистических данных.

3. Получение выводов по данным наблюдений.

----------------------------------------------------------------

Анализ статистических данных включает оценку вероятностей события, функции распределения вероятностей или плотности вероятностей, оценку параметров известного распределения, оценку связей между случайными величинами.

Математическая статистика опирается на теорию вероятностей и в свою очередь служит основой для разработки методов обработки и анализа статистических результатов в конкретных областях человеческой деятельности

----------------------------------------------------------------------

§ 1. ВЫБОРКА И ЕЕ РАСПРЕДЕЛЕНИЕ

1.1. Генеральная совокупность и выборка

Основными понятиями математической статистики являются генеральная совокупность и выборка.

Определение. Генеральная совокупность это совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины.

----------------------------------------------------------------

Генеральная совокупность может быть конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность составляющих ее объектов.

Определение. Выборкой (выборочной совокупностью) называется совокупность случайно отобранных объектов из генеральной совокупности.

Выборка должна быть репрезентативной (представительной), то есть ее объекты должны достаточно хорошо отражать свойства генеральной совокупности.

----------------------------------------------------------------

Выборка может быть повторной, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность, и бесповторной, при которой отобранный объект не возвращается в генеральную совокупность.

Применяют различные способы получения выборки.

1) Простой отбор случайное извлечение объектов из генеральной совокупности с возвратом или без возврата.

2) Типический отбор, когда объекты отбираются не из всей генеральной совокупности, а из ее «типической» части.

----------------------------------------------------------------

3) Серийный отбор объекты отбираются из генеральной совокупности не по одному, а сериями.

4) Механический отбор - генеральная совокупность «механически» делится на столько частей, сколько объектов должно войти в выборку и из каждой части выбирается один объект.

Число объектов генеральной совокупности и число объектов выборки называют объемами генеральной и выборочной совокупностей соответственно. При этом предполагают, что 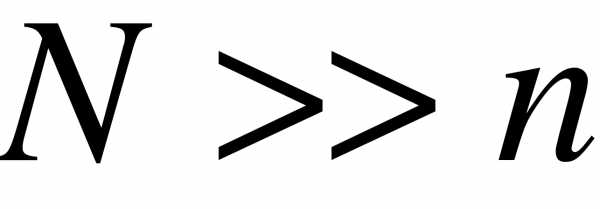(значительно больше).

----------------------------------------------------------------

1.2. Вариационные ряды

Полученные различными способами отбора данные образуют выборку, обычно это множество чисел, расположенных в беспорядке. По такой выборке трудно выявить какую-либо закономерность их изменения (варьирования).

Для обработки данных используют операцию ранжирования, которая заключается в том, что результаты наблюдений над случайной величиной, то есть наблюдаемые значения случайной величины располагают в порядке возрастания.

----------------------------------------------------------------------

Пример 1. Дана выборка :

Проведем ранжирование выборки :

После проведения операции ранжирования значения случайной величины объединяют в группы, то есть группируют так, что в каждой отдельной группе значения случайной величины одинаковы. Каждое такое значение называется вариантом. Варианты обозначаются строчными буквами латинского алфавита с индексами, соответствующими порядковому номеру группы .

----------------------------------------------------------------------

Изменение значения варианта называется варьированием.

Определение. Последовательность вариантов, записанных в возрастающем порядке, называется вариационным рядом.

Число, которое показывает, сколько раз встречаются соответствующие значения вариантов в ряде наблюдений, называется частотой или весом варианта и обозначается 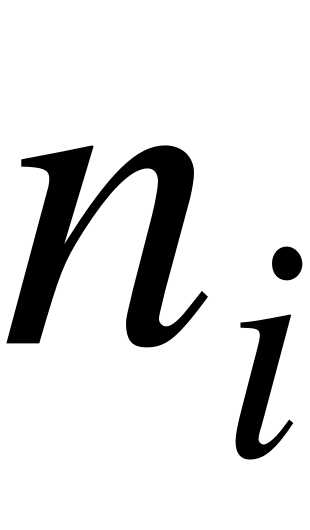, где - номер варианта.

----------------------------------------------------------------

Отношение частоты данного варианта к общей сумме частот называется относительной частотой или частостью (долей) соответствующего варианта и обозначается или , где - число вариантов. Частость является статистической вероятностью появления варианта 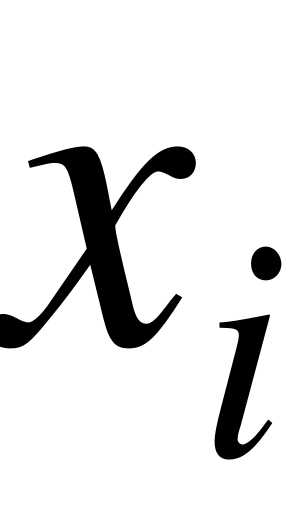. Естественно считать частость аналогом вероятности 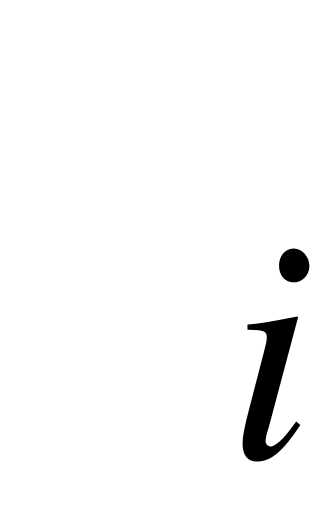появления значения случайной величины .

----------------------------------------------------------------

Определение. Дискретным статистическим рядом называется ранжированная совокупность вариантов 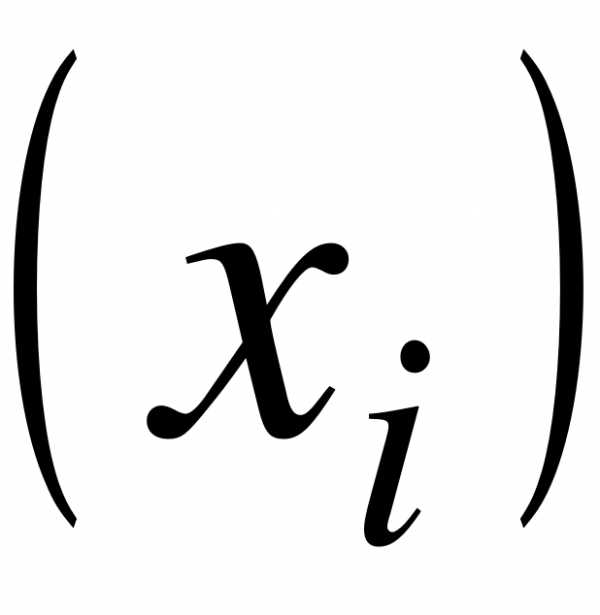с соответствующими им частотами или частостями .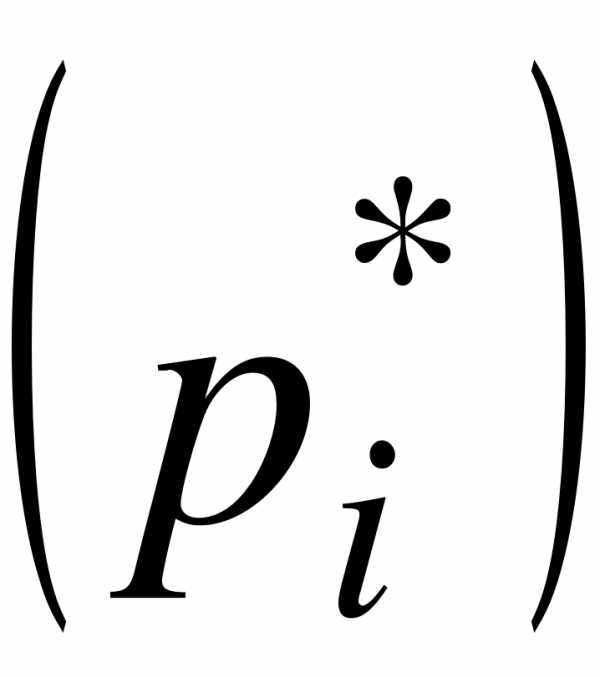

Дискретный статистический ряд удобно записывать в виде табл.1.

Таблица 1 (для примера 1)

----------------------------------------------------------------------

Характеристики дискретного статистического ряда:

1. Размах варьирования .

2. Мода 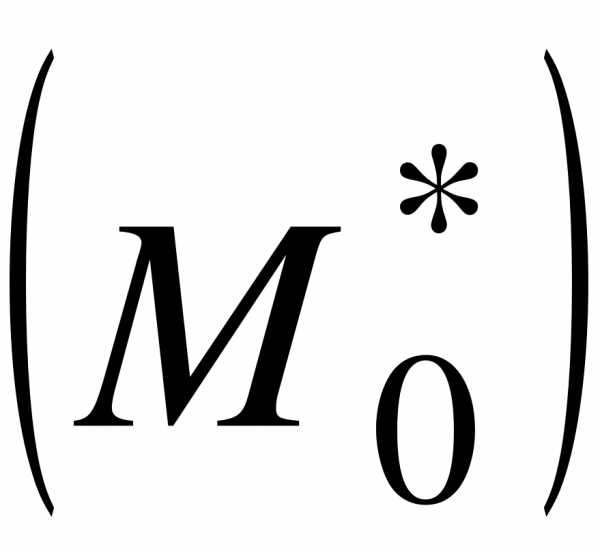- вариант, имеющий наибольшую частоту

( в примере 1. ).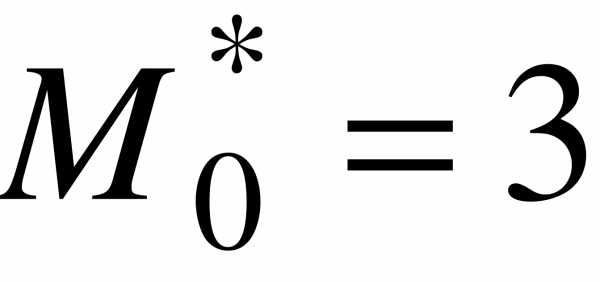

3. Медиана 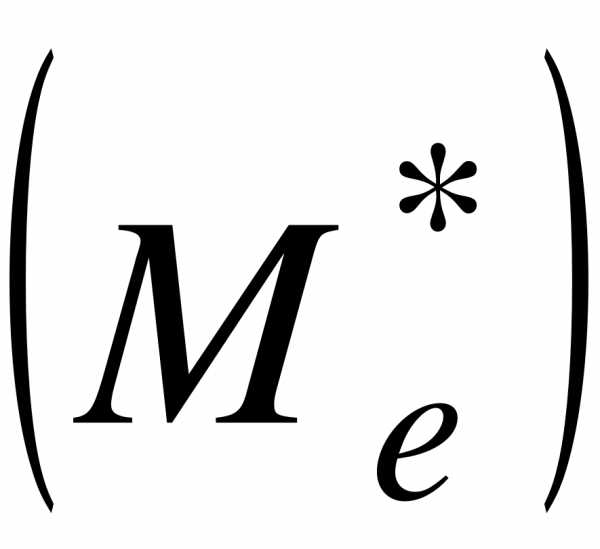- значение случайной величины, приходящееся на середину ряда.

----------------------------------------------------------------------

Пусть - объем выборки.

Если 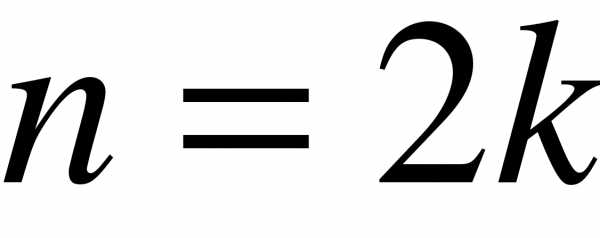, то есть ряд имеет четное число членов, то . Если , то есть ряд имеет нечетное число членов, то .

( в примере 1. ).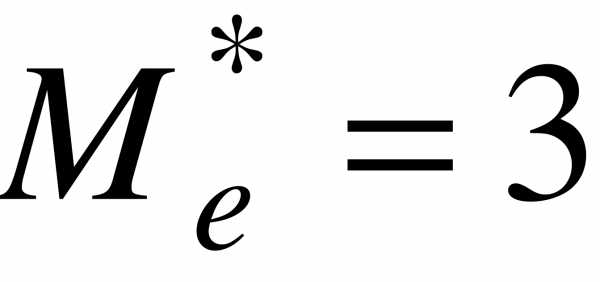

----------------------------------------------------------------------

Если изучаемая случайная величина является непрерывной или число значений ее велико, то составляют интервальный статистический ряд.

Сначала определяют число интервалов , в зависимости от объема выборки, с помощью табл.2.

Таблица 2.

Объем выборки	25-40	40-60	60-100	100-200	более 200
Число интервалов	5-6	6-8	7-10	8-12	10-15

----------------------------------------------------------------------

Затем определяют длину частичного интервала :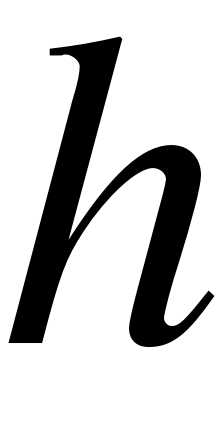

, где - шаг ; 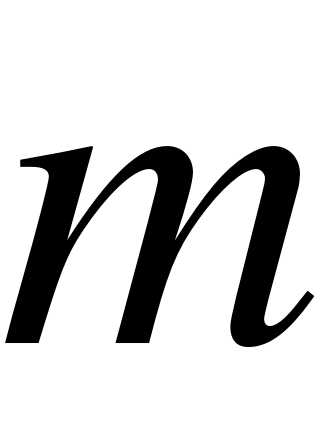- число интервалов .

Более точно шаг можно рассчитать с помощью формулы Стерджеса:

, число интервалов .

Если шаг окажется дробным, то за длину интервала берут ближайшее целое число или ближайшую простую дробь (обычно берут интервалы одинаковые по длине, но могут быть интервалы и разной длины).

----------------------------------------------------------------

За начало первого интервала рекомендуется брать величину , а конец последнего должен удовлетворять условию . Промежуточные интервалы получают, прибавляя к концу предыдущего интервала шаг.

Просматривая результаты наблюдений, определяют сколько значений случайной величины попало в каждый конкретный интервал. При этом в интервал включают значения, большие или равные нижней границе интервала, и меньшие верхней границы.

----------------------------------------------------------------

В первую строку таблицы статистического распределения вписывают частичные промежутки .

Во второю строку статистического ряда вписывают количество наблюдений 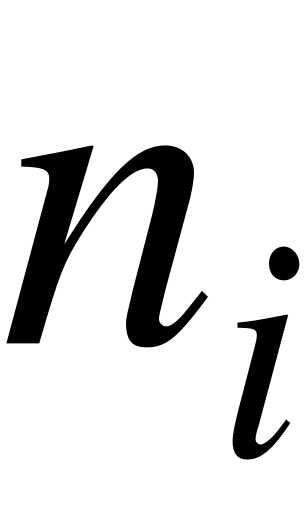(где ) попавших в каждый интервал; то есть частоты соответствующих интервалов.

Иногда интервальный статистический ряд, для простоты исследований, условно заменяют дискретным. В этом случае серединное значение -го интервала принимают за вариант , а соответствующую интервальную частоту - за частоту этого варианта.

1.3. Эмпирическая функция распределения

Пусть получено статистическое распределение выборки и каждому варианту из этой выборки поставлена в соответствие его частость.

Определение. Эмпирической функцией (функцией распределения выборки) называется функция , определяющая для каждого значения частость события ,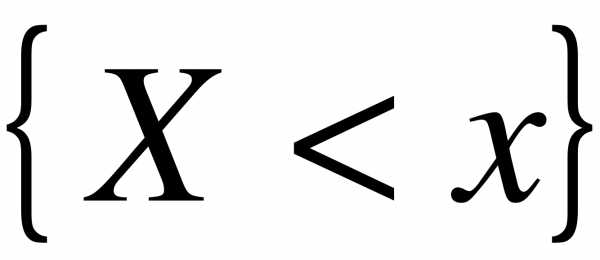

- где - объем выборки, - число наблюдений, меньших .

----------------------------------------------------------------------

При увеличении объема выборки частость события приближается к вероятности этого события. Эмпирическая функция 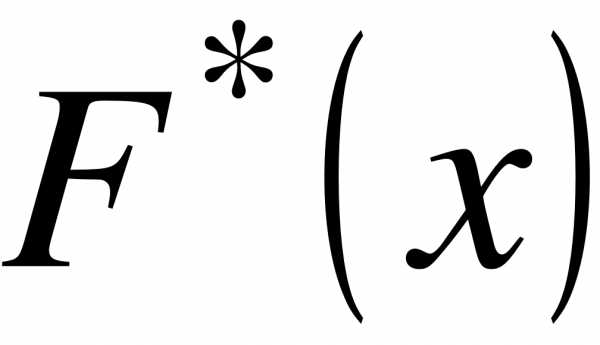является оценкой интегральной функции 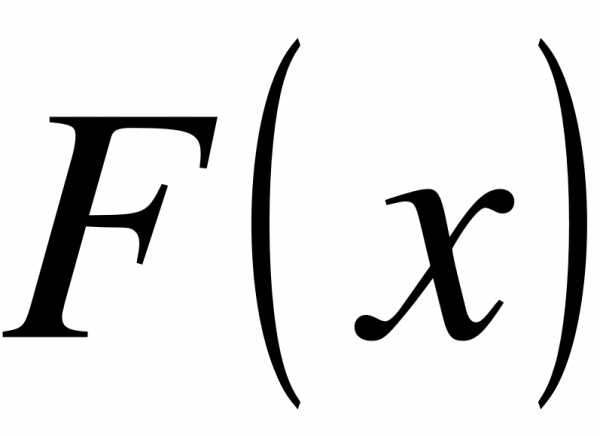в теории вероятностей.

Функция обладает теми же свойствами, что и функция :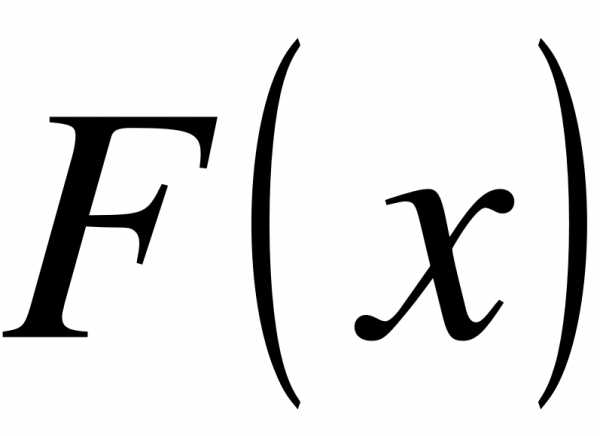

1. ;

2. 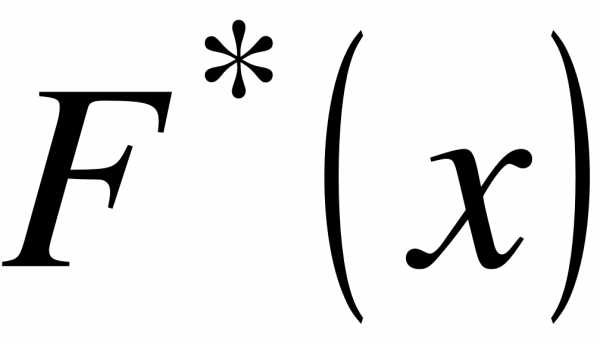-неубывающая функция;

3. , .

----------------------------------------------------------------------

1.5. Графическое изображение статистических данных

Статистическое распределение изображается графически с помощью полигона и гистограммы.

Определение. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами 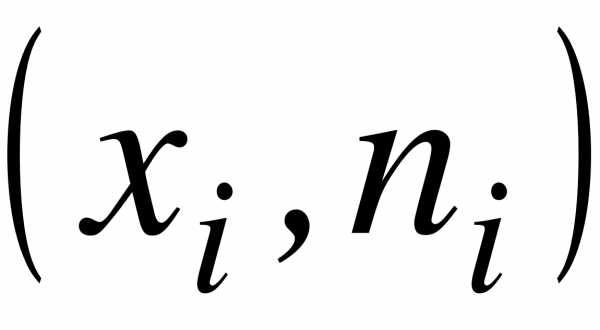; полигоном частостей с координатами , где , .

Полигон служит для изображения дискретного статистического ряда.

----------------------------------------------------------------------

Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей.

Определение. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси 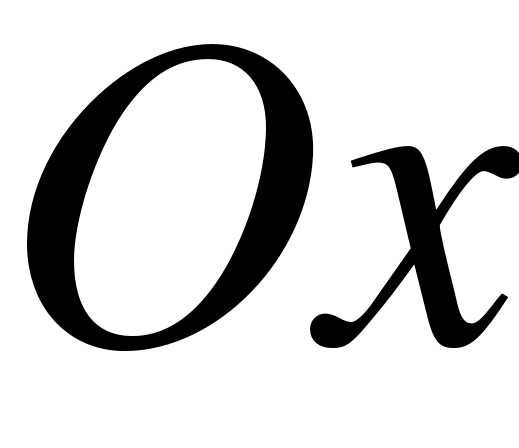и длины их равны длинам частичных интервалов 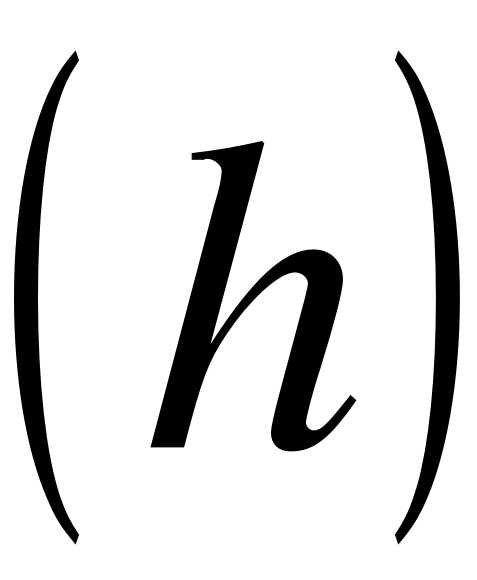, а высоты равны отношению:

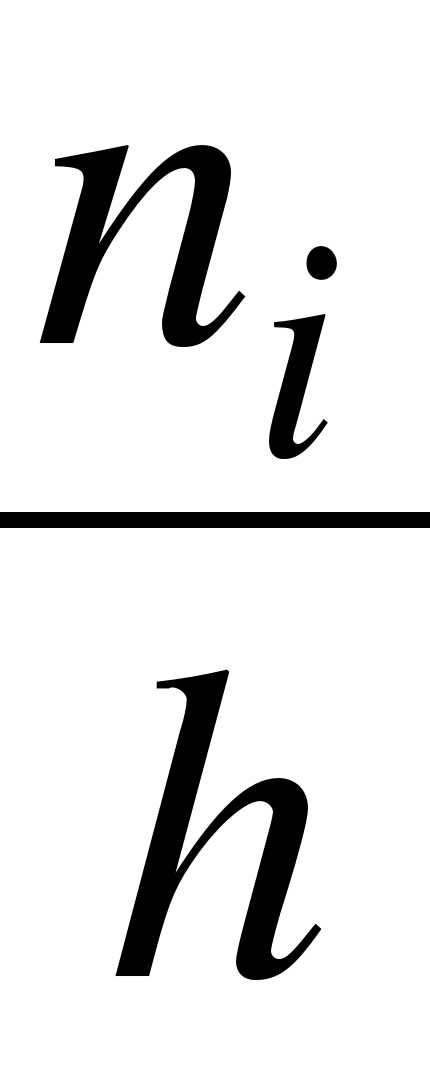- для гистограммы частот; - для гистограммы частостей.

----------------------------------------------------------------------

Гистограмма является графическим изображением интервального ряда.

Площадь гистограммы частот равна , а гистограммы частостей равна 1.

Можно построить полигон для интервального ряда, если его преобразовать в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости). Полигон получим, соединив отрезками середины верхних оснований прямоугольников гистограммы.

----------------------------------------------------------------

1.6. Числовые характеристики выборки

1.6.1. Выборочное среднее. Выборочная дисперсия.

Выборочное среднее квадратическое отклонение

В теории вероятностей определили числовые характеристики для случайных величин, с помощью которых можно сравнивать однотипные случайные величины. Аналогично можно определить ряд числовых характеристик и для выборки. Поскольку эти характеристики вычисляются по статистическим данным (по данным, полученным в результате наблюдений), их называют статистическими характеристиками.

----------------------------------------------------------------------

Пусть дано статистическое распределение выборки объема :

где 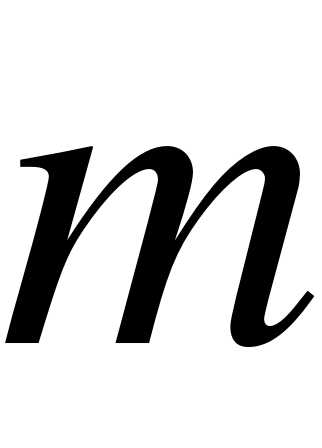- число вариантов.

----------------------------------------------------------------------

Определение. Выборочным средним 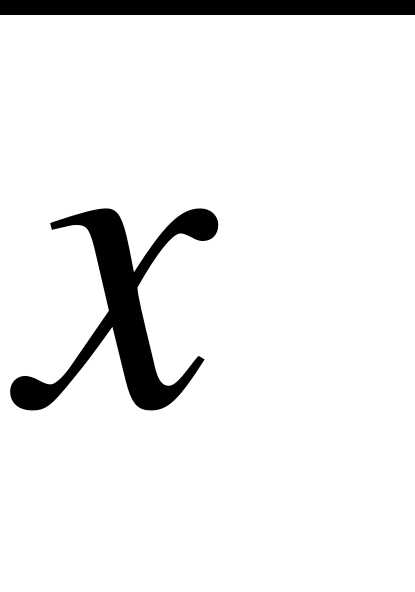называется среднее арифметическое всех значений выборки:

Выборочное среднее можно записать и так: ,

где - частость.

В случае интервального статистического ряда в качестве 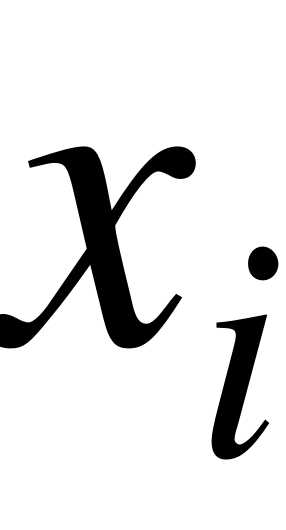берут середины интервалов, а - соответствующие им частоты.

----------------------------------------------------------------

Определение. Выборочной дисперсией 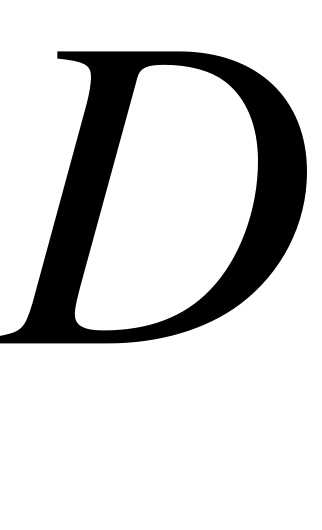называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего :

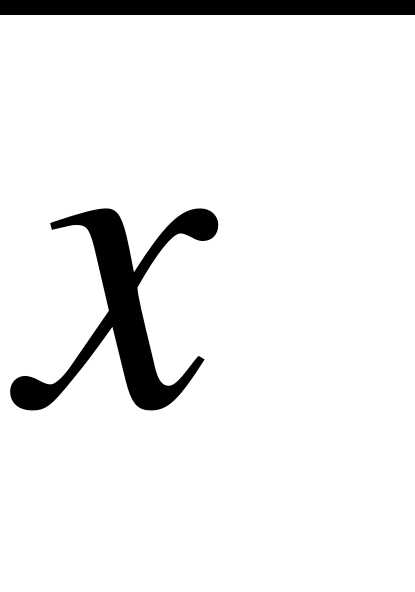или .

----------------------------------------------------------------

Выборочное среднее квадратическое выборки определяется формулой:

Особенность состоит в том, что оно измеряется в тех же единицах, что и данные выборки.

Если объем выборки мал (), то пользуются исправленной выборочной дисперсией:

Величина 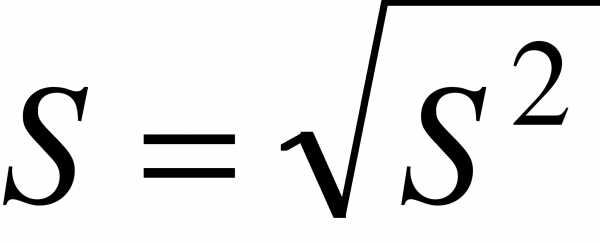называется исправленным средним квадратическим отклонением.

----------------------------------------------------------------

1.6.2. Выборочные начальные и центральные моменты.

Асимметрия. Эксцесс.

Приведем краткий обзор характеристик, которые наряду с уже рассмотренными применяются для анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.

Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия момента статистического ряда.

----------------------------------------------------------------------

Определение. Начальным выборочным моментом порядка называется среднее арифметическое - х степеней всех значений выборки:

или .

Из определения следует, что начальный выборочный момент первого порядка: .

----------------------------------------------------------------

Определение. Центральным выборочным моментом порядка называется среднее арифметическое - х степеней отклонений наблюдаемых значений выборки от выборочного среднего :

или .

Из определения следует, что центральный выборочный момент второго порядка :

----------------------------------------------------------------

Определение. Выборочным коэффициентом асимметрии называется число , определяемое формулой: .

Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.

Если 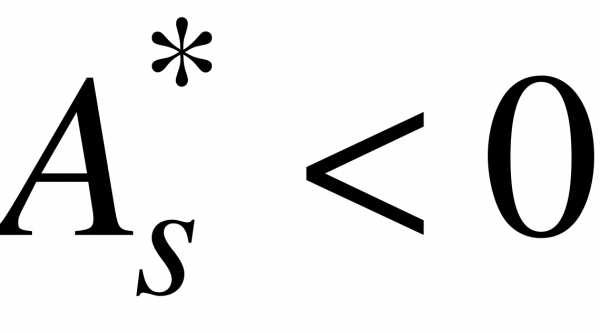, то более пологий «спуск» полигона наблюдается слева; если 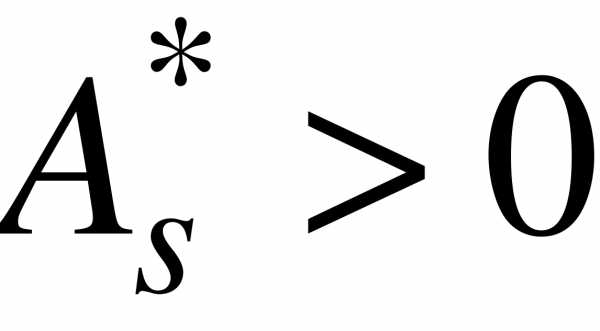- справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.

----------------------------------------------------------------

Определение. Выборочным коэффициентом эксцесса или коэффициентом крутости называется число , определяемое формулой :

Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением.

Коэффициент эксцесса для случайной величины, распределенной по нормальному закону, равен нулю.

----------------------------------------------------------------

Поэтому за стандартное значение выборочного коэффициента эксцесса принимают .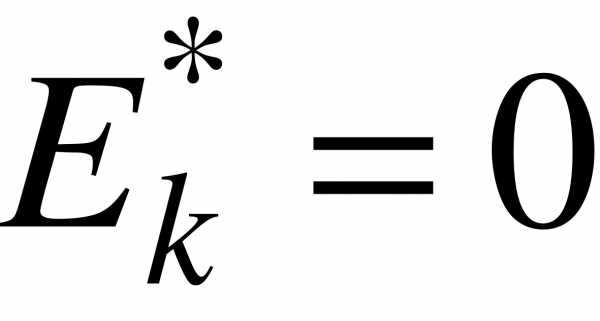

Если 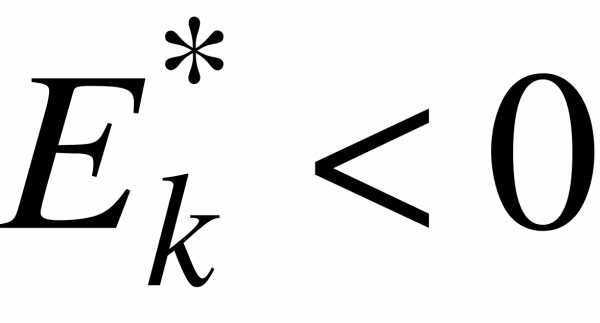, то полигон имеет более пологую вершину по сравнению с нормальной кривой; если 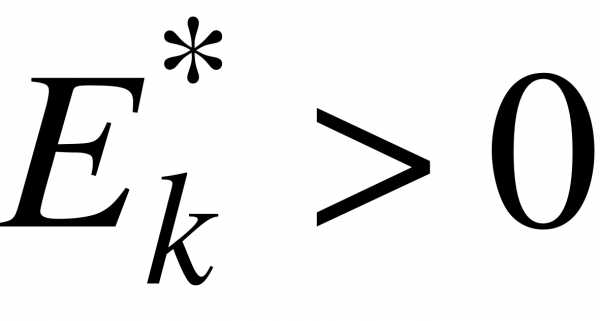, то полигон более крутой по сравнению с нормальной кривой.

1.7. Вычисление числовых характеристик выборки

Таблица 6

- середины интервалов; 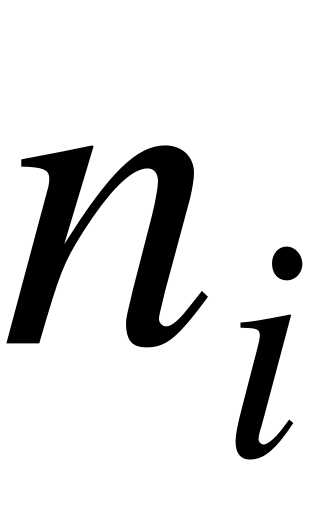- частоты; - объем выборки;

----------------------------------------------------------------------

с помощью суммы находим ;

с помощью суммы находим и ;

с помощью суммы находим ;

с помощью суммы находим .

----------------------------------------------------------------------

refleader.ru

Понятие выборки. Способы первоначальной обработки материала. Ранжирование.

⇐ ПредыдущаяСтр 4 из 10Следующая ⇒

Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Характеристики выборки:

§ Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

§ Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Необходимость выборки

§ Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.

§ Существует необходимость в сборе первичной информации.

Выборка

Править

Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённойпроцедуры выбранных из генеральной совокупности для участия в исследовании.

Содержание [показать]

Объём выборки Править

Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.

Зависимые и независимые выборки Править

При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X сооветствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:

§ пары близнецов,

§ два измерения какого-либо признака до и после экспериментального воздействия,

§ мужья и жёны

§ и т. п.

В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаютсянезависимыми, например:

§ мужчины и женщины,

§ психологи и математики.

Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.

Сравнение выборок производится с помощью различных статистических критериев:

§ t-критерий Стьюдента

§ T-критерий Вилкоксона

§ U-критерий Манна-Уитни

§ Критерий знаков

§ и др.

Репрезентативность Править

Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.

Пример нерепрезентативной выборки Править

В США одним из наиболее известных исторических примеров нерепрезентативной выборки считается случай, происшедший во время президентских выборов в 1936 году[1]. Журнал «Литрери Дайджест», успешно прогнозировавший события нескольких предшествующих выборов, ошибся в своих предсказаниях, разослав десять миллионов пробных бюллетеней своим подписчикам, людям, выбранным по телефонным книгам всей страны, и людям из регистрационных списков автомобилей. В 25 % вернувшихся бюллетеней (почти 2,5 миллиона) голоса были распределены следующим образом:

§ 57 % отдавали предпочтение кандидату-республиканцу Альфу Лэндону

§ 40 % выбрали действующего в то время президента-демократа Франклина Рузвельта

На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднегои верхнего класса (то есть большинство республиканцев, а не демократов).

Виды плана построения групп из выборок Править

Выделяют несколько основных видов плана построения групп[2]:

1. Исследование с экспериментальной и контрольной группами, которые ставятся в разные условия.

§ Исследование с экспериментальной и контрольной группами с привлечением стратегии попарного отбора

2. Исследование с использованием только одной группы — экспериментальной.

3. Исследование с использованием смешанного (факторного) плана — все группы ставятся в разные условия.

Стратегии построения групп Править

Отбор групп для их участия в психологическом эксперименте осуществляется с помощью различных стратегий, которые нужны для того, чтобы обеспечить максимально возможное соблюдение внутренней и внешней валидности[3].

§ Рандомизация (случайный отбор)

§ Попарный отбор

§ Стратометрический отбор

§ Приближённое моделирование

mykonspekts.ru

Проверка гипотезы об однородности двух ГС по критерию Манна-Уитни

(по критерию числа инверсий)

1. Обработка выборок.

Пусть - выборка из ГС I,

- выборка из ГС II, допустимо m ≠ n .

Условие 1. Выборки должны быть независимыми.

Условие 2. Среди чисел нет совпадающих.

Это выполнено с вероятностью 1, если Х - непрерывная случайная величина.

Проводится подсчёт числа инверсий в упорядоченных парах из элементов данных выборок: Число таких упорядоченных пар равно

Определение. Пара даёт одну инверсию, если . Если , то в паре инверсии нет. Случай пока исключается.

Вернёмся к примеру 1. Пусть получены выборки:

физики: 111, 104, 107, 90, 115, 106 m = 6,

психологи: 113, 108, 123, 122, 117, 112, 105 n = 7,

Число инверсий

Для другого порядка выборок

Проверка. (см. свойства статистики критерия).

2. Статистика критерия Манна-Уитни

= число инверсий в выборках

Свойства статистики.

2) ,

так как одна и только одна из пар обязательно даёт одну инверсию, а число пар равно

Основа статистики

1) Если гипотеза верна (законы распределения ГСI и ГСII совпадают), то для любых i, j

, (*)

поэтому, в среднем, Таким образом, при верной

2) Возьмём для простоты m = n. При верной , так как репрезентативные выборки достаточно хорошо отражают свойства генеральных совокупностей, общий вариационный ряд сделанных выборок имеет вид

При неверной (*) нарушается, например и тогда в общем вариационном ряду большая часть элементов расположится в левой половине вариационного ряда, из-за чего станет значительно меньше, чем При самой большой неоднородности распределений ГС I и ГС II общий вариационный ряд имеет вид

Следовательно, статистика критерия оценивает близость распределений ГСI и ГСII по близости её выборочного значения к mn/2.

3. По данному УЗ α при использовании двустороннего критерия Манна-Уитни по таблицам его критических значений находят левое и правое критические значения. Допустимая для принятия m и n область имеет вид

4. По выборкам находят выборочное значение статистики критерия. Если , то принимается и вероятность ошибки в принятии в точности равна α . В противном случае отклоняется.

Замечания

1. Часто в таблицах приводится только левое или правое критическое значение. Тогда недостающее критическое значение находят из равенства .

2. При больших m и n (≥ 50) критические значения статистики критерия приближённо находятся по таблицам квантилей стандартного нормального распределения. Известно, что при больших m и n

Поэтому, если - квантиль стандартного нормального распределения, то отклоняется.

3. Важно. Если в выборках имеется l совпадений, то статистику критерия считают по поправочной формуле

Если число совпадений превышает число инверсий, то пользоваться критерием Манна-Уитни не рекомендуется.

Окончание примера 1.

Возьмём α = 0,05, тогда α/2 = 0,025.

По таблицам (0,025; 6; 7) = 6, тогда (0,025; 6; 7) =36. Так как ,

принимается.

Лучше применить левосторонний критерий, так как = 8 ближе к 0 (к левому краю), чем к 21 (к середине). По таблицам (0,05; 6; 7) = 8, , поэтому принимается.

Общее правило. Если выборочное значение статистики критерия близко к середине (mn/2), то применяют двусторонний критерий, а если к краю (к 0 или к mn) – то соответствующий односторонний критерий.

Ранжирование выборки

Рассматривается ГС со случайным признаком Х , измеренным в порядковой шкале. Вариационный ряд выборки объёма n из этой ГС в идеальном случае имеет вид (например, в случае непрерывной случайной величины Х , когда вероятность совпадения двух значений в выборке равна 0). Но на практике в выборке могут быть одинаковые значения, тогда вариационный ряд имеет вид .

Ранжированные выборки - это приписывание каждому члену вариационного ряда его порядкового номера – ранга в вариационном ряду выборки.

Пример 1. Выборка 2, 5, 19, 8, 1, 4.

Вариационный ряд 1, 2 4, 5, 8, 19.

Ранги членов 1, 2, 3, 4, 5, 6.

Сложности в ранжировании возникают, когда среди элементов выборки встречаются совпадения, Тогда используют средние ранги , которые могут быть дробными.

Пример 2.

Вариационный ряд 1 1 2 2 2 4 5 19,

Ранги членов 1,5 1,5 4 4 4 6 7 8,

так как 1,5 = (1 + 2) / 2 , 4 = (3 + 4 + 5) / 3.

При большом числе совпадающих значений в выборке следует либо повысить точность измерения признака Х , либо перейти к номинативной шкале.

Проверка гипотезы об однородности двух ГС по критерию Уилкоксона (по критерию суммы рангов)

Этот критерий эквивалентен критерию Манна-Уитни.

Постановка задачи – как в критерии Манна-Уитни.

Проверка гипотезы по критерию Уилкоксона

1. Предварительная обработка выборок.

Записывается вариационный ряд для выборок из ГС I и ГС II. Затем общий вариационный ряд ранжируется.

2. Статистика критерия Уилкоксона (статистика суммы рангов)

W(m, n) = сумма рангов элементов выборки из ГС I в общем вариационном ряду. Аналогично можно определить статистику W(n, m).

Существует связь статистик Уилкоксона и Манна-Уитни:

Поэтому применение критерия Уилкоксона даёт тот же результат, что и критерий Манна-Уитни.

3. По данному УЗ α при использовании правостороннего критерия по таблицам находят

Для левостороннего критерия

. (*)

При двустороннем критерии по таблицам находят и по формуле (*) - .

3. По выборкам находят выборочное значение статистики критерия. Если попадает в допустимую область, то принимается. В противном случае отвергается.

studopedya.ru

Методы вероятностной (случайной) выборки

Случайная (вероятностная) выборка — это выборка, для которой каждый элемент генеральной совокупности имеет определенную, заранее заданную вероятность быть отобранным. Это позволяет исследователю рассчитать, насколько правильно выборка отражает генеральную совокупность, из которой она выделена (спроектирована). Такую выборку иногда называют еще случайной.

Вероятностные методы включают:♦ простой случайный отбор,♦ систематический отбор,♦ кластерный отбор,♦ стратифицированный отбор.

Реализовать случайную выборку можно двумя приемами: лотерейным методом и с помощью таблицы случайных чисел. С помощью случайной выборки строится подавляющее большинство телефонных опросов и опросов на основе избирательных списков. Для построения такой выборки необходимо иметь полный список всех элементов генеральной совокупности.

Простой случайный отборПростой случайный отбор предполагает, что вероятность быть включенным в выборку известна и является одинаковой для всех единиц совокупности. Он реализуется двумя методами:♦ отбор вслепую (другое название — метод лотереи или жребия),♦ отбор не вслепую (происходит с помощью таблицы случайных чисел).

Итак, в одном случае вы осуществляете свой выбор не глядя, в другом — все осознавая, но для того, чтобы самому не вмешаться и ничего не испортить, обращаетесь к специальным таблицам.

Кроме того, простой случайный отбор подразделяется на две разновидности уже по другому критерию, а именно — возвращению или невозвращению лотерейного шара (вместо него может быть фамилия респондента) обратно в корзину. В этом случае выделяют:♦ случайный повторный (с возвращением) отбор,♦ случайный бесповторный (без возвращения) отбор.

В чем сходство и различие двух классификаций? В первом случае — вслепую/не вслепую — ученый мог смотреть на то, как осуществляется отбор, хотя никак не мог ему помешать (если отбор проводился вслепую), или выбор осуществляли не его руки, вынимающие из корзины шар, а таблица случайных чисел. Во втором случае — повторный/бесповторный — дело заключается не в исследователе (если отбор проводился не вслепую), а в лотерейном шаре: его либо возвращают для нового выбора, либо не возвращают и продолжают процесс без него.

Соединив оба членения простого случайного метода в декартову систему координат, получим четыре модальности.

Сразу оговоримся, что получившаяся схема не является в строгом смысле изображением логического квадрата, с помощью которого принято показывать отношения совместимости, эквивалентности, противоположности (контрарности), частичной совместимости (субконтрарности), подчинения и противоречивости суждений. В нашей схеме лишь некоторые квадраты дают новый тип случайного отбора или свидетельствуют о том, что данная комбинация действий осуществима. При использовании метода выборки вслепую единицы генеральной совокупности (фамилии, названия или просто номера из списка) можно вносить в карточки, а карточки в перемешанном виде поместить в какую-то непрозрачную емкость (ящик, коробку). Из этой емкости кто-то случайным образом вы-тягивает число карточек, определяемое объемом выборки. После каждого вытягивания и регистрации карточки ее можно возвращать, а можно не возвращать назад. В первом случае говорят о повторном, во втором — о бесповторном отборе. Их комбинация дает два квадрата, имеющих реальное содержание: можно вслепую выбирать из корзины шары и возвращать их для нового выбора, а можно их откладывать в сторону. Однако выборка не вслепую предполагает использование таблицы случайных чисел. Возвращать в нее выбранный номер невозможно, стало быть, образуемые вдоль этой оси квадраты не являются реальными.

Предлагаемая схема выполняет скорее мнемоническую функцию, помогая лучше запомнить материал. Можно также считать, что она имеет демонстративный смысл, но никак не логический. Она придумана для того, чтобы внести какую-то ясность в типологию разновидностей простого случайного отбора.

Вероятностную выборку целесообразно применять только при наличии соответствующих условий. Первое условие осуществления вероятностной выборки — наличие полного списка всех элементов генеральной совокупности (отсутствие или недоступность которого чаще всего и препятствует ее реализации) от 1 до N, где N — общее число всех элементов. Если же он имеется, то производится нумерация, после чего можно использовать вышеописанные методики. При использовании лотерейного метода (или метода жребия) жетоны с номерами всех элементов помещают в урну, тщательно перемешивают и извлекают последовательно п жетонов, где n — число элементов выборочной совокупности. Элементы генеральной совокупности, имеющие номера, оказавшиеся на извлеченных жетонах, будут составлять выборочную совокупность. Это довольно трудоемкая и продолжительная (при больших размерах выборки) операция, к тому же достаточно трудоемкая, поскольку «для обеспечения равного шанса выбора требуется тщательное перемешивание жетонов» после каждой выемки очередного номера.

Второе условие вероятностной выборки — хорошая перемешанность элементов генеральной совокупности. Если выборка элементов производится из ящика, то его содержимое следует тщательно перемешать и уже после этого брать карточки случайным образом. Только при таких условиях все они имеют одинаковую вероятность попасть в выборку. Часто для образования случайной выборки элементы генеральной совокупности предварительно нумеруются, а каждый номер записывается на отдельной карточке. В результате получается пачка карточек, число которых совпадает с объемом генеральной совокупности. После тщательного перемешивания из этой пачки берут по одной карточке. Объект (респондент), имеющий одинаковый номер с карточкой, считается попавшим в выборку. При этом возможны два принципиально различных способа образования выборочной совокупности.

Первый — вынутая карточка после фиксации ее номера возвращается в пачку, после чего карточки снова тщательно перемешиваются. Повторяя такие выборки по одной карточке, можно образовать выборочную совокупность любого объема. Выборочная совокупность, образованная по такой схеме, получила название случайной возвратной выборки.

Второй— каждая вынутая карточка после ее записи обратно не возвращается. Повторяя по такой схеме выборки по одной карточ-ке, можно получить выборочную совокупность любого заданного объема. Выборочную совокупность, образованную по данной схеме называют случайной безвозвратной выборкой. Она возможна лишь в том случае, если из тщательно перемешанной пачки сразу берут нужное число карточек.

Заметим, что различие между случайными выборками с возвра-том и без возврата стирается, если они составляют незначитель-ную часть большой генеральной совокупности.

Однако при большом объеме генеральной совокупности этот метод оказывается очень трудоемким, и поэтому гораздо удобнее пользоваться таблицей случайных чисел. Она доказала свою эф-фективность при формировании равновероятностной выборки из больших совокупностей.

Систематический отбор является вторым по научной значимости, но первым по популярности употребления видом простого случайного отбора. Его называют еще механическим отбором и считают упрощенным вариантом простого случайного отбора.

Примером служат разного рода квартирные выборки: выбираются улицы, на которых интервьюер проводит квартирный опрос. Квартиры выбираются по определенной схеме (крайняя квартира справа от лестницы на последнем этаже первого подъезда и т.д.).

Если под рукой таблицы случайных чисел нет, а генсовокупность относительно невелика14, то можно воспользоваться алфавитным списком, например, персонала предприятия (картотека всегда есть в отделе кадров) или избирательного участка (при опросе по месту жительства). Процедура систематического отбора проста: количество единиц генеральной совокупности, предположим 2000 работников предприятия, делится на количество анкет, скажем 200, и определяется шаг выборки. Он предполагает, что, начиная с любого номера из списка, опрашивается каждый десятый (2000:200 = 10). В формализованном виде данная процедура выглядит так. Из пронумерованного списка через равные интервалы £ отбирается заданное число респондентов. При этом шаг выборки к рассчитывается по простой формуле:

K = N / n

где N — численность генеральной совокупности, n — численность выборочной совокупности.

Таким образом, шаг выборки, а его еще называют «интервалом скачка» или просто «интервалом», — это математический показатель, рассчитанный как отношение объема генеральной совокупности к объему выборки. Он показывает, сколько номеров в списке фамилий людей, вошедших в генеральную совокупность, надо пропустить (через сколько перешагнуть), чтобы в итоге получить список выборочной совокупности. Буквально шаг выборки озная чает расстояние между соседними фамилиями респондентов, из меренное количеством отбракованных фамилий из списка генеральной совокупности.

Другой пример. Предположим, что нам нужно спроектировать выборку численностью 100 из списка 5000 студентов какого-то вуза. Если мы намерены использовать систематическую выборку, то должны вначале рассчитать интервал выборки делением числа элементов в списке на размер выборки. В данном случае, разделив 5000 имен на требуемый размер выборки 100 ед., мы получим интервал (шаг) выборки 50. Так что мы будем систематически двигаться по списку и отбирать каждого пятидесятого студента (отобрав таким образом 100 имен). Определение того места в списке, с которого мы начнем, проводится случайным образом, по таблице случайных чисел (это называется случайным стартом). Таким образом, если случайно выбрана точка старта под номером 31, то в выборку будут включены студенты, стоящие под номерами 31, 81, 131, 181 и т.д.

Итак, в основу систематической выборки положены не вероятностные процедуры, а алфавитные списки, картотеки, схемы, которые обеспечивают равновероятное попадание в выборку всех единиц генеральной совокупности.

Несмотря на свои преимущества, систематическая выборка может иногда иметь своим результатом предубежденную выборку. Такая ситуация возникает, например, когда элементы размещены в списке, ранжированном по каким-то характеристикам. В этой ситуации определение места начала случайного отбора будет влиять на средние характеристики всей выборки. Например, если студенты расставлены в списке в соответствии со средним оценочным баллом от высшего к низшему, систематическая выборка, включающая студентов, стоящих в списке под номерами 1,51,101, будет иметь более низкий средний балл, чем выборка, включающая студентов под номерами 50, 100 и 150. Каждая новая выборка будет давать другой средний балл, который представляет собой предубежденную картину студенческой популяции.

Районированная и стратифицированная выборкиЕсли генеральная совокупность велика, а такое в эмпирическом исследовании случается очень часто, то приходится разделять обследуемую совокупность на более или менее однородные части, а затем осуществлять отбор единиц внутри этих частей. Такую раздробленную на части выборку правильнее всего было бы называть расслоенной. Однако в русском языке подобный термин не утвердился, видимо, как не соответствующий нормам правильного произношения.

Поскольку в отечественной социологии очень много иностранных слов — и это правильно с точки зрения унификации научной терминологии, приведения ее к международным стандартам, — то слову «расслоенная» попытались найти эквивалент. В числе претендентов оказались две наилучшие кандидатуры, а именно термины «районированная» и «стратифицированная».

В русском языке первое слово явно тяготеет к географическому языковому ареалу и обозначает территориальную зону. Поскольку генеральную совокупность, особенно очень большую, например население всей страны, можно разбивать в том числе и по региональному признаку, в отечественной литературе утвердился термин «районированная выборка». Но наряду с тем генеральную совокупность можно расслаивать и по стратам (полу, возрасту, доходам и т.д.), получая в качестве критерия уже не географический район, а социальную группу.

В итоге сложилась практика различения двух разновидностей расслоенной выборки. Если деление происходит по стратам (социальным группам), то выборку именуют стратифицированной, если по экономико-географическим районам, то районированной.

В литературе (да и в маркетинговой практике) два термина — районированная и стратифицированная выборки — нередко считаются эквивалентными. Происходит это потому, что в основе той и другой лежит одна и та же процедура расслоения, а расслаивать в социологии можно двояко: либо по социальным группам (тогда речь идет о социальной структуре и стратификации как ее частном виде), либо по географическим районам. Когда объединяют оба понятия в одно, как правило, дают обобщающее определение подобной выборки, например, такое:Районированная выборка — вид выборки, при котором отбору предшествует процедура районирования (расслоения, стратификации), т.е. разделения исходной совокупности на статистически или качественно однородные подсовокупности, называемые слоями, стратами или типичными группами. Отбор единиц, который может носить как случайный, так и направленный характер, производится независимо из каждого слоя, поэтому районированная выборка равносильна ряду выборок, извлеченных из меньших совокупностей-страт.

В этом определении исходное понятие «районированная выборка» без ущерба для дела можно заменить на «стратифицированную выборку». Таким образом, одинаково правильно будет как разделять одну выборку на две самостоятельные разновидности, районированную и стратифицированную, так и подавать их как единое целое. За единство двух приемов выступает практика социологических исследований. Оказывается, в крупномасштабных проектах социологи начинают с районированной выборки, а затем переходят на стратифицированную. Так, например, в обследованиях Центра «Социо-Экспресс» Института социологии РАН в основе построения районированной выборки лежат десять экономико-географических зон, в каждой из которых выделяются крупные города (численностью свыше 500 тыс. населения), средние города (50-500 тыс.), малые города (до 50 тыс.) или поселки городского типа, а также сельские населенные пункты. Внутри отобранных городов респондентов отбирают случайным методом. Репрезентативность контролируется по региональным пропорциям численности населения, пропорциям между городским и сельским населением, пропорциям между населением указанных типов населенных пунктов.

В международной практике не используется русское слово «район» как географическая зона (ареал, регион, часть территории), поэтому здесь не встретишь и термина «районированная выборка». Вместо него употребляют термин «стратифицированная выборка», подразумевая, что, разбивая единое целое на части, не обязательно точно указывать, что они собой представляют — группы или районы.

В таком случае стратифицированная выборка (stratified sampling) — вероятностная выборка, обеспечивающая равномерное представительство в выборочной совокупности различных частей, типов, групп и слоев населения.

В английском языке слово «стратификация» мало чем отличается от слов «расслоение», «разделение», «разбиение». Это социологи придали стратификации социальный смысл, а в геологии, откуда мы позаимствовали термин, стратификация означает вертикальное расслоение земли на однородные пласты. Ни классов, ни доходов, ни социальных групп здесь нет.

Надо учитывать и другой нюанс. Дело в том, что в зарубежных словарях, прежде всего американских и главным образом ведущих, все, что связано с территориальным признаком, в том числе и расслоение по районам, относится к квотной выборке. К примеру, в знаменитом Оксфордском словаре социологии на термин «stratified sampling» стоит отсылка: см. sampling. Открываем с. 576—577 и читаем о том, что в случае стратифицированной вероятностной {random) выборки речь идет о разбиении совокупности на подгруппы, т.е. страты, например мужчин и женщин, а о районированной выборке в нашем понимании не говорится ни слова. Близкий к районам термин «local areas» употребляется Гордоном Маршаллом (а он считается знатоком в этом деле) только в связи: 1) с первой стадией многоступенчатого отбора, 2) с квотной выборкой.

Возвращаясь от лингвистических тонкостей к методическим, подчеркнем вот еще что: отбор единиц, который может носить как случайный, так и направленный характер, производится независимо из каждого слоя или района, поэтому районированно-стратифицированная выборка (если можно так выразиться) равносильна ряду выборок, извлеченных из меньших совокупностей-страт (районов).

Стратифицированная случайная выборка (в узком значении) основана на выборке по каждой страте отдельно. Это повышает точность результатов либо уменьшает время, силы и стоимость исследования, допуская меньшие размеры выборки при заданном уровне точности. Например, известно, что бедность наиболее часто встречается среди пожилых, безработных и в монородительских семьях. Исследуя проблемы бедности, можно с равным успехом выбрать в качестве объекта любую из трех страт. В отобранных районах или стратах выбор единиц обследования проводится по вероятностному методу.

Основная цель всякого расслоения — повышение точности выборочных оценок. Слои выделяются таким образом, чтобы дисперсия изучаемых переменных внутри слоев была значительно меньше, чем между ними. При расслоении вариация между слоями не входит в среднюю ошибку выборки, а компенсируется самой процедурой выделения слоев. Поэтому расслоение позволяет добиться более высокой степени точности оценок по сравнению с простым случайным отбором. Если каждый слой представляет собой статистически однородную группу, то для любого из них даже выборка малого объема позволит получить достаточно точные оценки, которые, будучи объединены, дадут хорошую оценку для всей совокупности.

Различают стратификацию одномерную и многомерную в зависимости от того, один или несколько признаков положены в основу разделения совокупности. Эти признаки должны иметь тесную связь с изучаемыми переменными, от их выбора в высокой степени зависит эффективность расслоения.

Гнездовая выборкаПротивоположность районированной и стратифицированной выборке составляет гнездовая выборка.

Гнездовая выборка — вид выборки, при котором отбираемые объекты представляют собой группы или гнезда (кластеры) более мелких единиц. Гнездом называют единицу отбора высшей ступени, состоящую из более мелких единиц низшей ступени. В выборку могут быть включены как все единицы низшего уровня, так и их часть. Число единиц, образующих гнездо, называют его размером.

В качестве гнезд выступают населенные пункты, районы, дома, подъезды, предприятия, цехи, бригады.

Гнездовой отбор обладает большими организационными преимуществами — проще осуществлять отбор и обследование нескольких компактных групп, чем десятков или сотен отдельных единиц. Технические преимущества гнездового отбора особенно ощутимы при построении территориальной выборки. Отбор небольшого числа территориальных сегментов (населенных пунктов, районов, жилых кварталов и т.п.), затем выборочный или сплошной опрос проживающего в них населения существенно уменьшают стоимость исследования и сроки проведения.

Процедурно такой метод применить легче, чем вероятностный либо районированный. Проблемы, которые возникают здесь, связаны с определением величины гнезда, количеством гнезд, которые надо обследовать, их размещением в генеральной совокупности.

Основные рекомендации при выборе гнезд сводятся к тому, чтобы различия между гнездами были бы по возможности более неоднородными. Это правило прямо противоположно основному принципу расслоения, в соответствии с которым выигрыш в точности тем больше, чем более однородными будут выделенные слои. Другая рекомендация касается выбора размера гнезд: большое число малых гнезд предпочтительнее малого числа крупных.

psyera.ru

Генеральная совокупность и выборка.

⇐ ПредыдущаяСтр 8 из 27Следующая ⇒

Генеральная совокупность – совокупность элементов, удовлетворяющих неким заданным условиям; именуется также изучаемой совокупностью. Генеральная совокупность (Universe) - все множество объектов (субъектов) исследования, из которого выбираются (могут выбираться) объекты (субъекты) для обследования (опроса).

ВЫБОРКА или выборочная совокупность (Sample) — это множество объектов (субъектов), отобранных специальным образом для обследования (опроса). Любые данные, полученные на основании выборочного обследования (опроса), имеют вероятностный характер. На практике это означает, что в ходе исследования определяется не конкретное значение, а интервал, в котором определяемое значение находится.

Характеристики выборки:

- Качественная характеристика выборки – что именно мы выбираем и какие способы построения выборки мы для этого используем.

- Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Необходимость выборки:

- Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.

- Существует необходимость в сборе первичной информации.

Объём выборки — число случаев, включённых в выборочную совокупность.

Зависимые и независимые выборки.

При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми.

В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми.

Типы выборки.

Выборки делятся на два типа:

- вероятностные;

- не вероятностные;

Репрезентативная выборка — выборочная совокупность, в которой основные характеристики совпадают с характеристиками генеральной совокупности. Только для этого типа выборки результаты обследования части единиц (объектов) можно распространять на всю генеральную совокупность. Необходимое условие для построения репрезентативной выборки — наличие информации о генеральной совокупности, т.е. либо полный список единиц (субъектов) генеральной совокупности, либо информация о структуре по характеристикам, существенно влияющим на отношение к предмету исследования.

17. Дискретный вариационный ряд, ранжирование, частота, частность.

Вариационным рядом (статистическим рядом) – называется последовательность вариант, записанных в порядке возрастания и соответствующих им весов.

Вариационный ряд может быть дискретным (выборка значений дискретной случайной величины) и непрерывным (интервальным) (выборка значений непрерывной случайной величины).

Дискретный вариационный ряд имеет вид:Наблюдаемые значения случайной величины х1, х2, …, хk называются вариантами, а изменение этих значений называются варьированием.

Выборка (выборочная совокупность) – совокупность наблюдений, отобранных случайным образом из генеральной совокупности.

Число наблюдений в совокупности называется ее объемом.

N – объем генеральной совокупности.

n– объем выборки(сумма всех частот ряда).

Частотой варианты хi называется число ni (i=1,…,k), показывающее, сколько раз эта варианта встречается в выборке.

Частостью (относительной частотой, долей) варианты хi (i=1,…,k) называется отношение ее частоты ni к объему выборки n.wi=ni/n

Ранжирование опытных данных - операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания.

Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов хi с соответствующими им частотами или частностями.

mykonspekts.ru