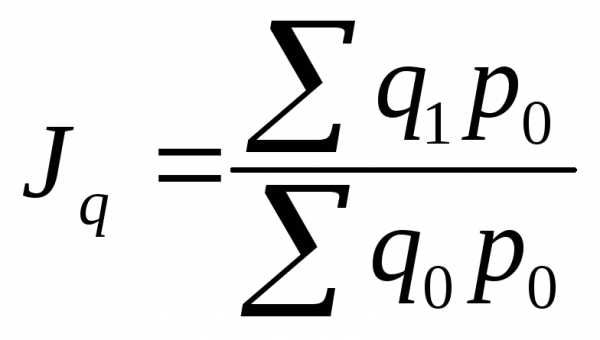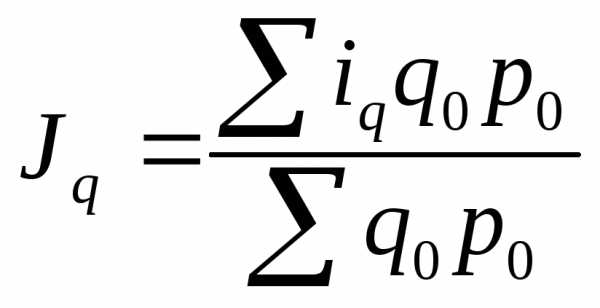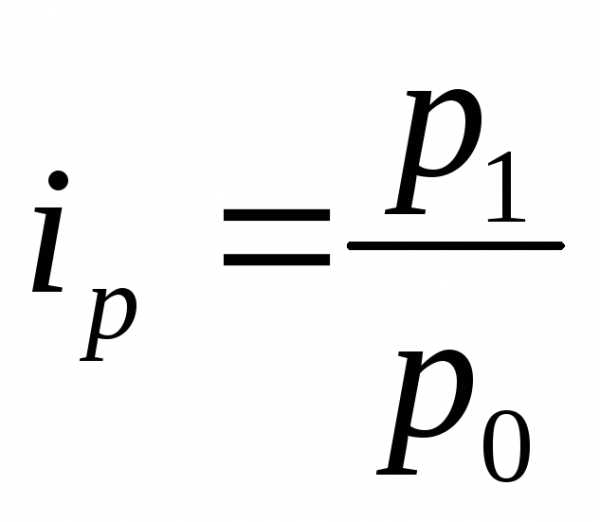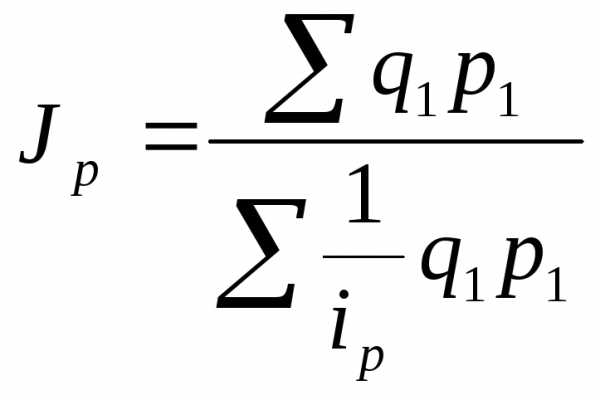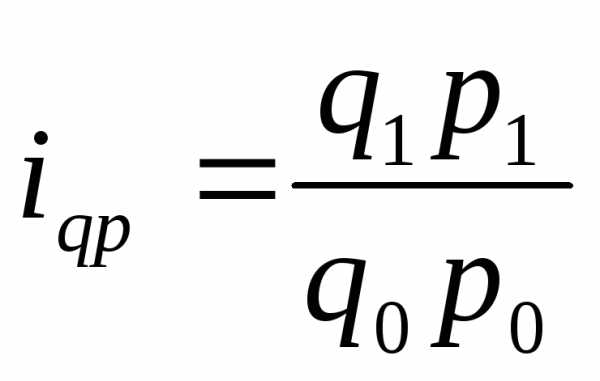ГлавнаяРанжированиеДетерминированный индекс ранжирования

7.4. Скорректированный индекс множественной детерминации. Детерминированный индекс ранжирования


7.4. Скорректированный индекс множественной детерминации

Скорректированный (исправленный, adjustable) коэффициент множественной детерминации 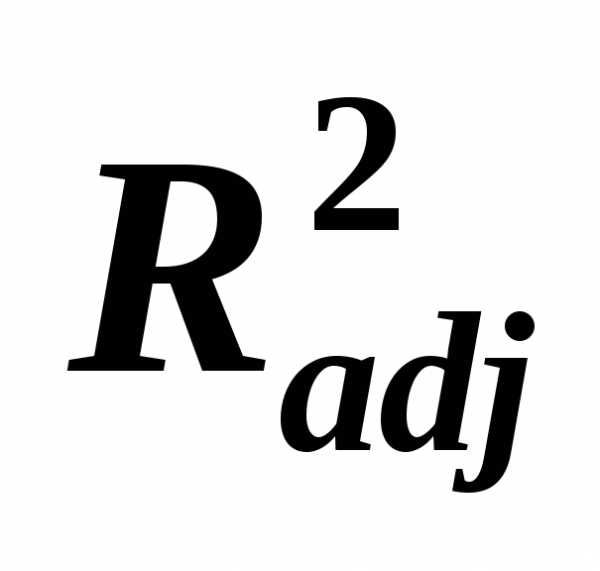содержит поправку на число степеней свободы и рассчитывается по формуле :

(7.23)

Скорректированный коэффициент множественной детерминации используется для сопоставления моделей содержащих различное количество факторов.

Чем больше p, тем больше различие междуи . Чем больше объем выборкиn, тем меньше это различие.

Существенно различным может быть изменение 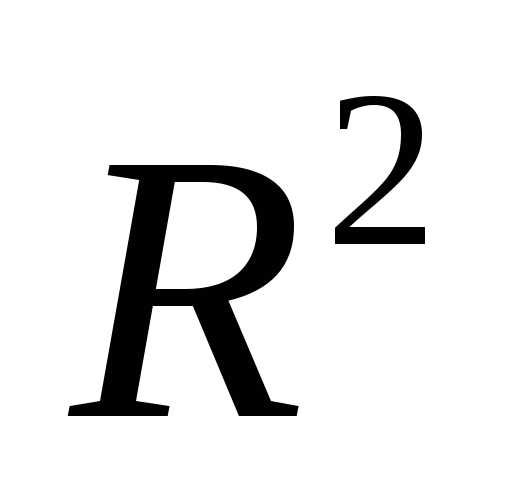и

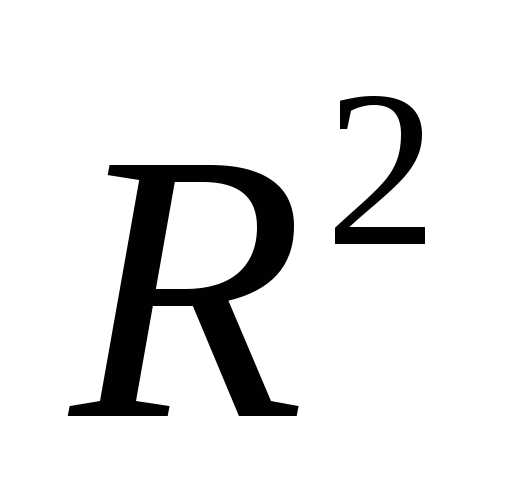при включении дополнительного фактора в уравнение регрессии. Если этот фактор существенно влияет на отклик, то увеличатся значения как так и 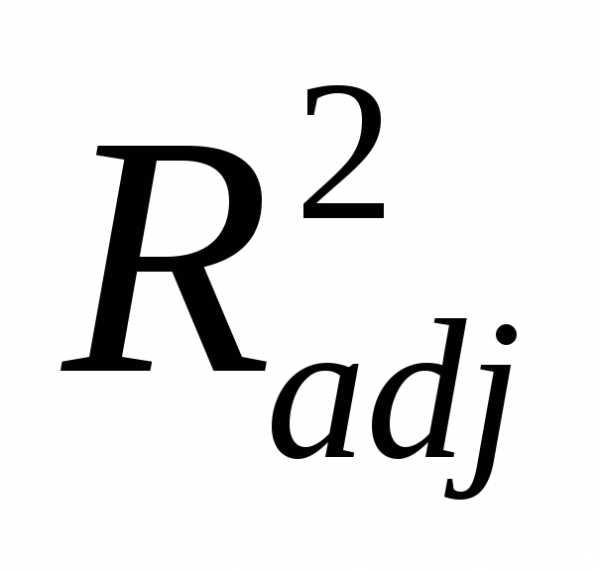. Если вновь добавленный фактор несущественно влияет на отклик, то значение , как правило, увеличивается (может быть незначительно), а значение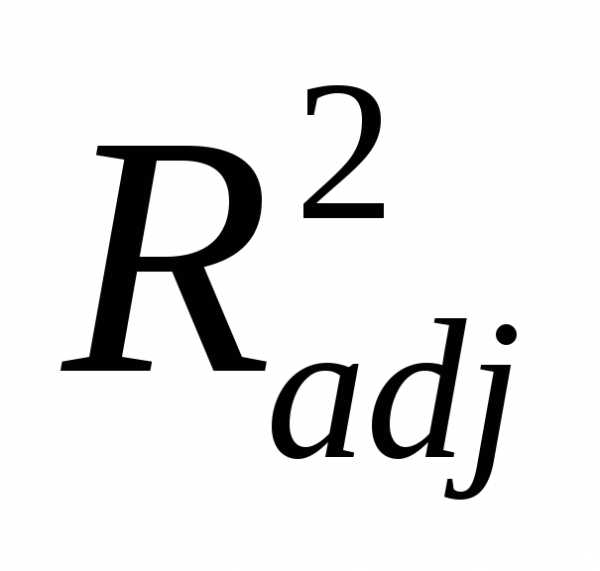- уменьшается. Очевидно, что в этом случае такой фактор в уравнение включать не целесообразно.

7.5. Частная корреляция

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на фактора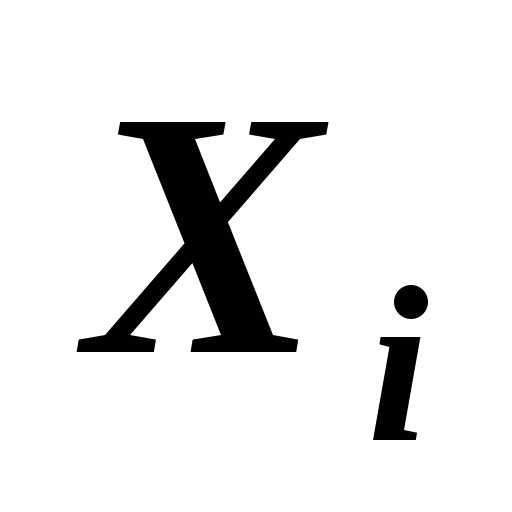при устранении влияния других факторов, включенных в уравнение регрессии, можно определить по формуле:

, (7.24)

где 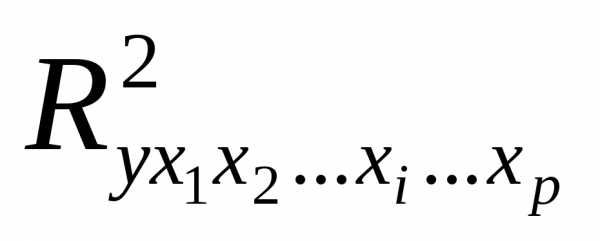- коэффициент детерминированности для уравнения регрессии, в которое включены факторы;- коэффициент детерминированности для уравнения регрессии, в которое включены факторы, т.е. фактор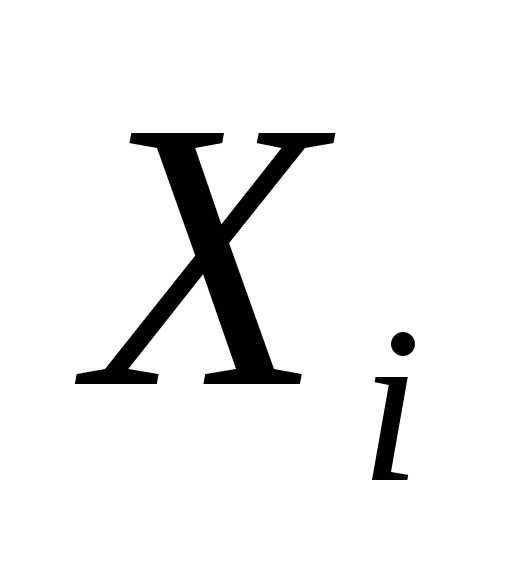

исключен из уравнения. Частные коэффициенты корреляции изменяются в пределах от0до1.

Нетрудно показать, что величина, стоящая под радикалом в правой части равенства (7.24) может быть преобразована к следующему виду:

Правая часть последнего равенства представляет собой отношение приращения объясненной часть вариации отклика за счет включения фактора 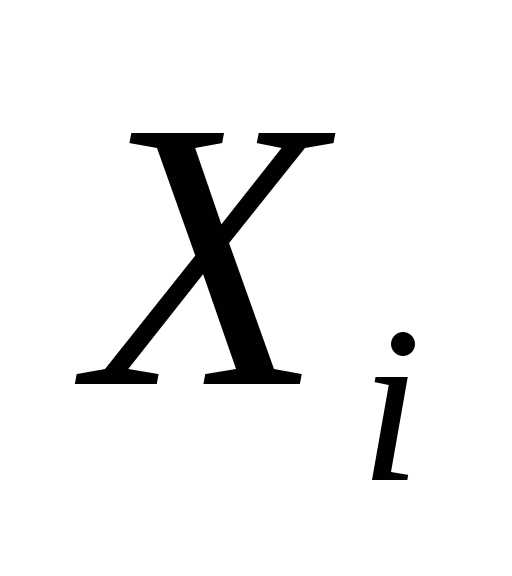в уравнение регрессии к необъясненной доле вариации отклика, имевшей место до введения фактора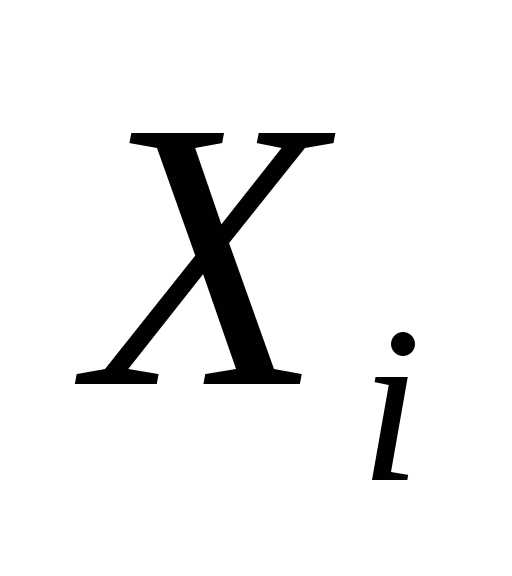в уравнение регрессии.

Таким образом, величина характеризует возрастание коэффициента детерминации за счет введения в уравнение регрессии фактора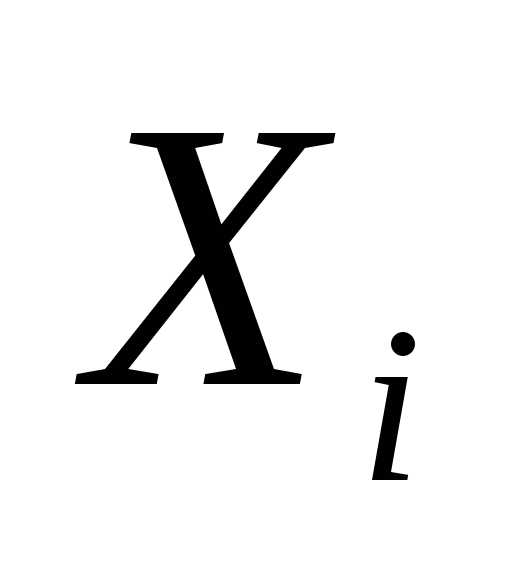. Благодаря этому частные коэффициенты корреляции могут быть использованы для ранжирования влияния факторов на результат.

Так, при двух факторах и i=1 частный коэффициент корреляции

может быть вычислен по формуле

(7.25)

Коэффициент 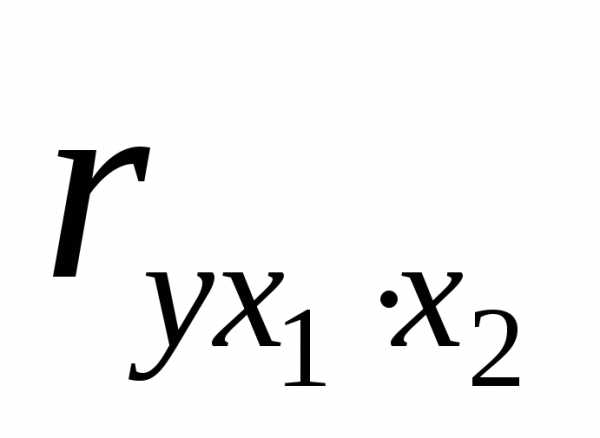показывает тесноту связи междуипри неизменном уровне фактора, включенного в уравнение регрессии.

Аналогично 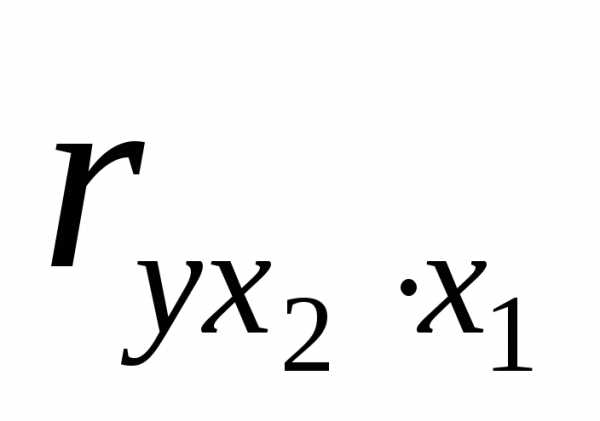можно определить по формуле

(7.26)

Коэффициенты частной корреляции используют для оценки целесообразности включения фактора в уравнение регрессии.

7.6. Геометрическая интерпретация

В основном совпадает с геометрической интерпретацией регрессионного уравнения с одной переменной, приведенной в ЛР №5 [1]. Столбцы значений представим как векторы вp+1-мерном векторном пространствоRp+1.

Векторы порождаютp+1–мерное подпространствоπ(рис.7.1). Рассмотрим векторы

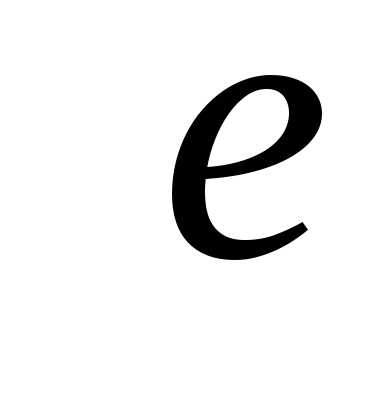и, определяемые следующими соотношениями

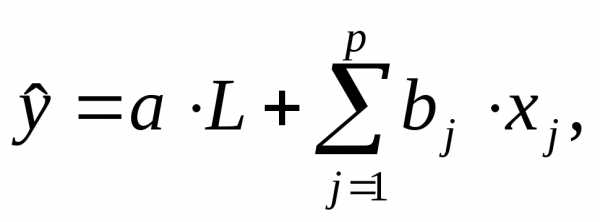(7.27)

Очевидно, что вектор лежит в гиперплоскости (подпространстве)π.

Поставим задачу: найти такие 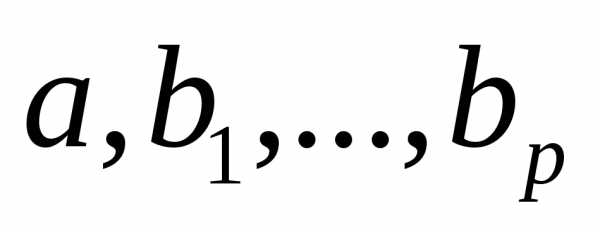, чтобы векторeимел наименьшую длину. Другими словами мы хотим наилучшим образом аппроксимировать векторy вектором, лежащим в гиперплоскостиπ. Очевидно, что решением является такой вектор, для которого векторeортогонален (перпендикулярен) плоскостиπ. Для этого необходимо и достаточно, чтобы векторeбыл ортогонален векторам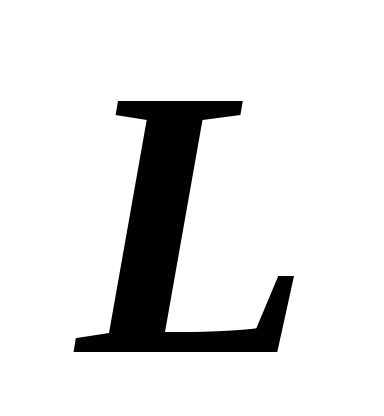и, порождающим плоскостьπ (рис. 5.3). Т.е. векторявляется ортогональной проекцией вектора

на плоскостьπ. Вектор остатковортогоналенπ.

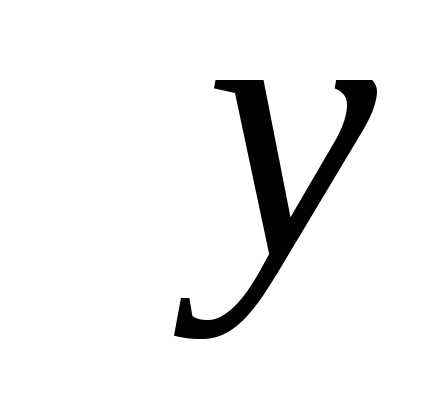
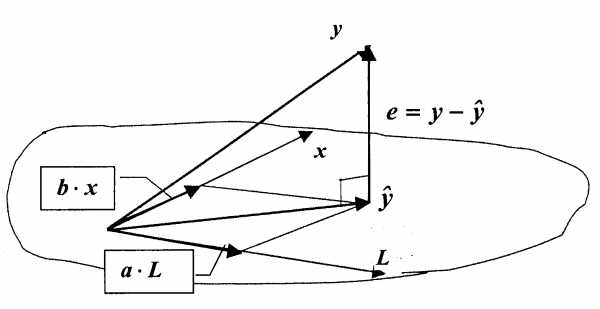
Рис. 7.1Геометрическая интерпретация построения уравнения регрессии

Т.е. фактически актуален рис.5.3 ЛР №5 [1]с заменой векторов, порождающих гиперплоскость π.

studfiles.net

Индекс детерминации - Энциклопедия по экономике

Если коэффициент корреляции возвести в квадрат, то получим коэффициент (индекс) детерминации, который показывает, чему равна доля влияния изучаемого фактора на совокупный показатель.  [c.51] При значениях тесноты связи меньше 0,7 величина индекса детерминации d всегда будет меньше 50%. Это означает, что на долю вариации факторного признака х приходится меньшая доля по сравнению с другими признаками, влияющими на изменение результативного показателя. Синтезированные при таких условиях математические модели связи практического значения не имеют.  [c.51]

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.  [c.6]

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R  [c.7]

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции  [c.52]

Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину Л2 для нелинейных связей называют индексом детерминации.  [c.85]

Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера  [c.85]

Индекс детерминации R2n можно сравнивать с коэффициентом детерминации г2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации г2 меньше индекса детерминации R2 , Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина (Л2 — г2 ) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия R2 , вычисленных по одним и тем же исходным данным, через /-критерий Стьюдента  [c.86]

Оценив параметры этого уравнения по МНК, можно найти теоретические значения объема продукции г и соответственно остаточную сумму квадратов (/ — Р)2, которая используется в расчете индекса детерминации (корреляции)  [c.118]

Поскольку Х0> —у) I (у —у) = 1 — R2, то величину скорректированного индекса детерминации можно представить в виде  [c.119]

Как было показано выше, ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии (/ -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.  [c.121]

Индекс детерминации для данной модели составит  [c.152]

Коэффициент (индекс) детерминации га (т. е. квадрат коэффициента корреляции) определяется как доля общей дисперсии, объясняемой регрессией, т. е.  [c.82]

Относительные показатели, характеризующие взаимосвязь признаков в совокупности явлений, а также взаимосвязь результативных признаков-следствий с факторными признаками-причинами, например, связь уровня душевого дохода с размером потребления мяса или фруктов на одного человека связь дозы удобрений с урожайностью картофеля и т.п. К таким показателям относятся рассматриваемые в главе 8 коэффициенты корреляции, эластичности, детерминации, а также в главе 10 аналитические индексы. Относительные показатели взаимосвязи могут быть как отвлеченными, так и именованными числами.  [c.48]

Метод регрессии предполагает анализ взаимосвязи случайных величин (признаков), среди которых выделяется один результативный признак, зависящий от прочих независимых между собой факторов. Оценка связи выполняется с помощью коэффициента детерминации (индекса корреляции).  [c.467]

Коэффициент детерминации — R2 вычисляется как отношение факторной дисперсии к общей дисперсии, индекс корреляции — R является корнем квадратным из коэффициента детерминации. Для оценки значимости индекса R рассчитывается показатель  [c.468]

Коэффициент детерминации - квадрат коэффициента или индекса корреляции.  [c.7]

Тот же результат даст и индекс множественной детерминации, определенный через соотношение остаточной и общей дисперсии результативного признака.  [c.117]

Формула скорректированного индекса множественной детерминации имеет вид  [c.119]

В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент (индекс) множественной корреляции (детерминации). Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели. Низкое значение коэффициента (индекса) множественной корреляции означает, что в регрессионную модель не включены существенные факторы — с одной стороны, а с другой стороны — рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. Требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.  [c.120]

Индекс множественной детерминации R2 = 0,966  [c.19]

Оцените тесноту связи при помощи коэффициента корреляции, индекса корреляции, коэффициента детерминации.  [c.8]

Рассчитайте коэффициент детерминации и скорректированный индекс множественной корреляции. Охарактеризуйте тесноту связи рассматриваемого набора факторов с исследуемым результативным признаком.  [c.11]

По своему аналитическому выражению коэффициент надежности (или надежность) является квадратом коэффициента корреляции (т.е. коэффициентом детерминации) результатов измерения с истинными результатами, а его квадратный корень (т.е. коэффициент корреляции R) принято называть индексом надежности.  [c.79]

Портфельные менеджеры используют как традиционный подход, так и подход современной портфельной теории, каждый из которых акцентирует внимание на преимуществах снижения риска за счет диверсификации. Традиционный подход основан на подборе акций и облигаций хорошо известных компаний различных отраслей экономики. Современная портфельная теория (СПТ) использует такие статистические понятия, как дисперсия, корреляция и коэффициент детерминации, для измерения риска и потенциала диверсификации альтернативных инвестиционных инструментов. Отрицательно коррелированные вложения обеспечивают максимальный эффект диверсификации. Недиверсифицируемый риск ценной бумаги или портфеля измеряется с помощью фактора "бета", описанного в главе 5. Фактор "бета" измеряет реакцию ценной бумаги или портфеля на изменения рыночного индекса, например "Стэндард энд пур з 500". Чем выше коэффициент детерминации, который измеряет объясняющую способность регрессионного уравнения, тем надежнее оценки фактора "бета". Коэффициент детерминации фактора "бета" выше для портфелей, чем для отдельных ценных бумаг, в результате чего портфельные менеджеры больше доверяют портфельным пока-  [c.178]

Приступая к статистическому исследованию зависимостей между анализируемыми переменными, исследователь должен в первую очередь установить сам факт наличия статистических связей и попытаться измерить степень их тесноты. В качестве основных измерителей степени-тесноты связей между количественными переменными в практике статистических исследований используются индекс корреляции, корреляционное отношение, парные, частные и множественные коэффициенты корреляции, коэффициент детерминации.  [c.97]

Пусть исследуется вопрос о среднем спросе на кофе AQ (в граммах на одного человека). В качестве объясняющих переменных предполагается использовать следующие переменные P - индекс цен на кофе, In YD - логарифм от реального среднедушевого дохода, POP - численность населения, РТ -индекс цен на чай. Можно ли априори предвидеть, будут ли в этом случае значимыми все t-статистики и будет ли высоким коэффициент детерминации R Какими будут ваши предложения по уточнению состава объясняющих переменных.  [c.256]

Индекс детерминации для нелинейных по оцениваемым параметрам функций в некоторых работах по эконометрике принято называть квази-/ 2 . Для его определения по функциям, использующим логарифмические преобразования (степенная, экс понента), необходимо сначала найти теоретические значения пу (в нашем примере In/ ), затем трансформировать их через антилогарифмы антилогарифм (1пу ) = у, т. е. найти теоретические значения результативного признака и далее определять индекс детерминации как квази- R , пользуясь формулой  [c.118]

Коэффициент детерминации ( oeffi ient of determination) представляет собой пропорцию, в которой изменение доходности акций компании WM связано с изменением доходности рыночного индекса. Другими словами, он показывает, в какой степени колебания доходности WM можно отнести за счет колебаний доходности рыночного индекса.  [c.512]

Так как коэффициент неопределенности ( oeffi ient of nondetermination) равен I минус коэффициент детерминации, то он представляет собой пропорцию, в которой изменение доходности акций компании WM не связано с изменением доходности рыночного индекса. Так, 73% величины колебания доходности акций компании WM нельзя приписать колебаниям доходности рыночного индекса.  [c.513]

Значение Л-квадрат (R-squared) аналогично равно коэффициенту детерминации, приведенному в табл. 17.228. Так, 37% величины колебаний цен акций компании Ask omputer может быть отнесено за счет колебаний рыночного индекса, рассматриваемого за 60-месячный период.  [c.514]

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитьгоается по  [c.53]

Следовательно, оценка МНК есть такая, при которой коэффициенты уравнения регрессии равны В = (XTXJ 1XTY (индекс —1 означает обратную матрицу). Коэффициент детерминации (скорректированный) равен  [c.81]

Коэффициент детерминации будет принимать значения от нуля, когда X не влияет на Y, до единицы, когда изменение Y объясняется изменением X. Значение Л2 для рефессии данных по индексам FTSE 100 и S P 500 из табл. 6.1 составляет 0,8548. Обычная интерпретация коэффициента детерминации такова число (значение), скажем Л2 = 0,8548, умножается на 100 и выражается как процентная доля вариации Y, которая объясняется вариацией X. Таким образом, в этом примере 85,48% изменения Y (индекс FTSE 100) объясняются изменением X (индекс S P 500). Доверяете вы или нет тому, что рынок акций США имеет сильное определяющее влияние на рынок Великобритании, будет зависеть от того, насколько основательно вы исследовали конкурирующие теории. Вспомните, что данная регрессионная модель — это только математическое выражение той одной гипотезы. которая проверялась.  [c.279]

Таким образом, введенный с помощью (1.6) индекс корреляции /л. между результи-рующим показателем г и объясняющими переменными формально определен для любой двумерной системы наблюдений. Квадрат его величины (I -i) показывает, какая доля дисперсии исследуемого результирующего показателя rj определяется (детерминируется) изменчивостью (дисперсией) соответствующей функции регрессии / от аргумента , поэтому часто называется коэффициентом детерминации. Соответственно оставшаяся доля дисперсии к (т. е. 1 — n-l) объясняется воздействием неконтролируемой случайной остаточной компоненты ( помехи ), а следовательно, определяет ту верхнюю границу точности, с которой мы сможем восстанавливать (предсказывать) значения rj по заданным значениям объясняющих переменных .  [c.61]

economy-ru.info

013_индексный_метод

Тема 13. Индексный метод

Обычно термин «индекс» используется для некоей обобщающей характеристики изменений. Например, уже знакомый вам индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т. д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.

Индекс представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических показателей:

Например, изменения среднедушевого времени просмотра телевизионных передач в России в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого времени просмотра телевизионных передач в России и развитых странах Запада, Востока, а также провести сравнение с нормативной величиной, отвечающей нормам рекомендуемого просмотра телевизора без вреда для зрения.

Индексы, характеризующие относительное изменение отдельного единичного элемента сложной совокупности называются индивидуальными индексами-i.

Общие (сводные) индексы–J- характеризуют относительное изменение индексируемой величины в целом по сложной совокупности, отдельные элементы которой несоизмеримы в натуральных единицах.

Сущность проблемы, возникающей при построении сводных индексов, заключается в том, что необходимо в одной величине отразить изменения явлений, различных по своей вещественной природе и изменяющихся различным образом.

Индексируемой называется величина, изменение которой характеризуется с помощью индекса, а величина показателя, принимаемая за вес индекса, используется для соизмерения непосредственно несоизмеримых величин.

Наименование

Индиви­дуальные

Агрегатные

Средние

Индекс

физического

объема продукции

Индекс цен

Индекс товарооборота

p– цена единицы товара; q – количество продукции

Формулы индексов

Например, ИПЦ – индекс потребительских цен. Общее изменение образуется под влиянием изменений цен на отдельные товары. Таким образом, мы имеем ряд отношений:

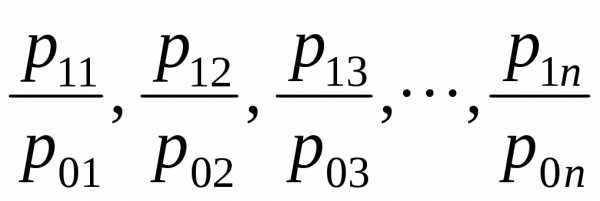и т.д.

Эти отношения есть не что иное, как индивидуальные индексы, и сводный индекс представляет собой средний из них: , где j - номер товара.

Сводные индексы, так же как и индивидуальные, при расчете за несколько периодов могут быть получены и как цепные, и как базисные.

Агрегатные базисные индексырассчитываются по отношению к постоянной базе (индексы с постоянными весами), аагрегатные цепные индексы- по отношению к меняющейся базе (индексы с переменными весами).

Индексам количественных показателей, как правило, соответствуют постоянные веса,индексам качественных показателей-переменные веса.

Если однородная (соизмеримая) продукция производится (продается) на предприятиях (фирмах) с различными условиями, могут быть рассчитаны индексы качественных показателей:

Индекс переменного состава

Индекс переменного состава представляет соотношение двух средних величин изучаемого качественного признака, определяемых как взвешенные величины

, где-доля

Он характеризует общее изменение среднего показателя как вследствие изменения уровня индексируемого показателя, так и изменения структуры в рассматриваемой совокупности.

Индекс фиксированного состава качественных показателей

Индекс фиксированного состава показывает изменение в среднем только одного исследуемого качественного показателя при постоянной структуре, т.е.

Индекс структурных сдвигов

При сопоставлении индексов переменного состава и фиксированного состава определяется индекс структурных сдвигов, который показывает, какое влияние на изменение величины индексируемого показателя оказало изменение в текущем периоде по сравнению с базисным изменение структуры совокупности.

Формулы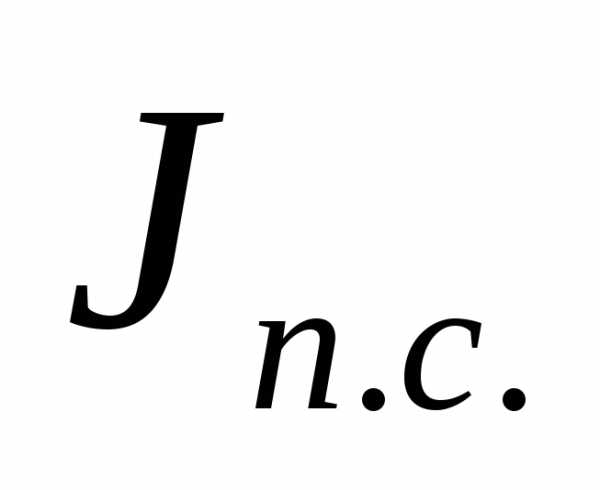, 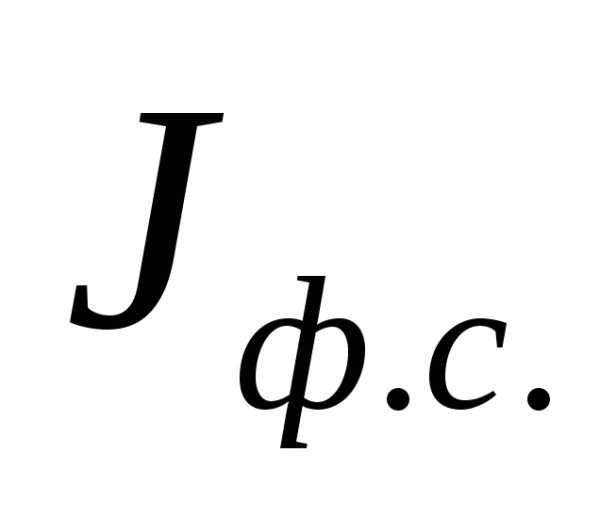и позволяют определить абсолютные характеристика:

  1. абсолютный прирост средней величины и ее разложение на факторы

  1. абсолютный прирост суммарной абсолютной величины и ее разложение на факторы

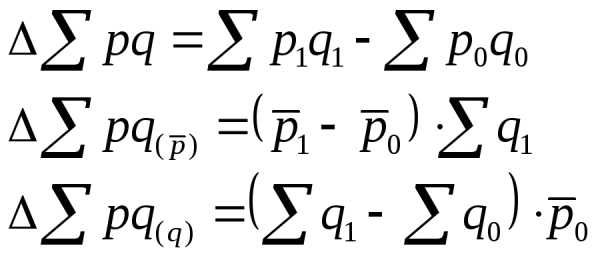
Индексы цен

Индексы цен могут быть рассчитаны по двум вариантам весов - текущим и базисным:

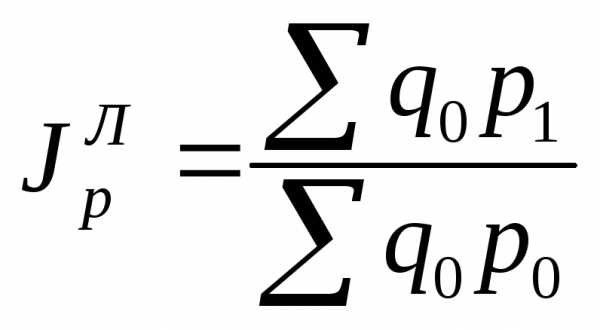
Различия между 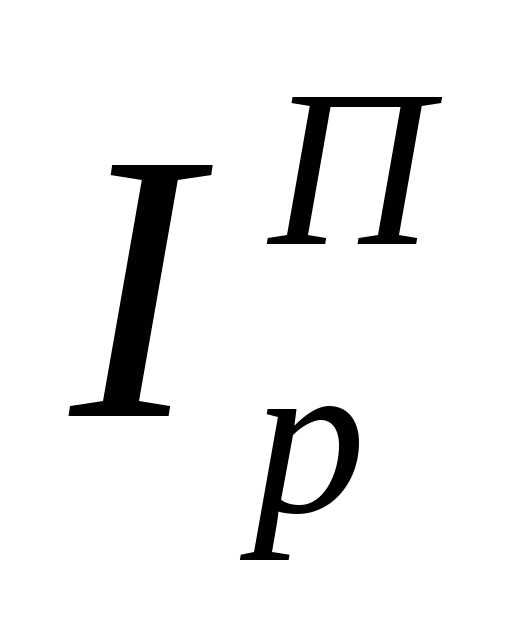и

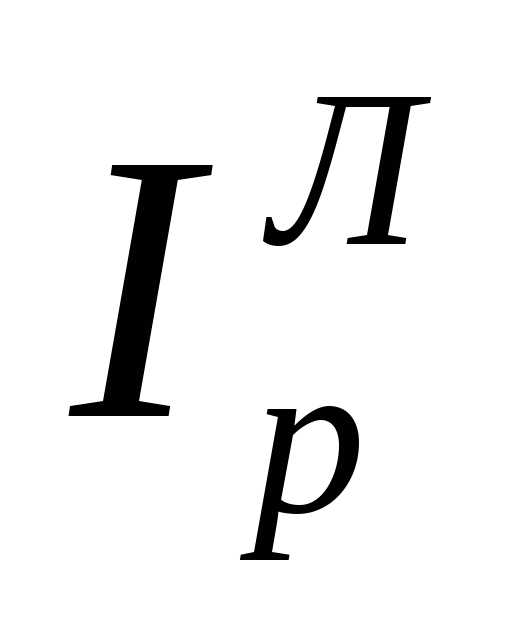
можно определить по формуле, выведенной В.И. Борткевичем (1868-1931 г.г.):

где 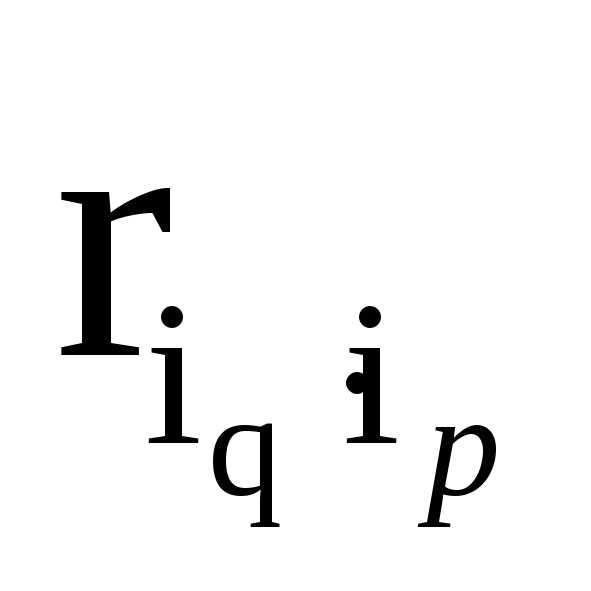- коэффициент корреляции,

- коэффициенты вариации индивидуальных темпов изменения объема и цен

Индекс ассортиментных сдвигов

Используется для характеристики влияния ассортиментных сдвигов на выпуск продукции. Представляет собой соотношение индексов цен Пааше и Ласпейреса.

Факторный индексный анализ

Применяется в случае необходимости выявления влияния факторов на прирост результативного признака при жестко детерминированной связи.

Взаимосвязь признаков представлена произведением результативного признака и фактора.

Разложение общего абсолютного прироста результативного признака методом цепных подстановок:

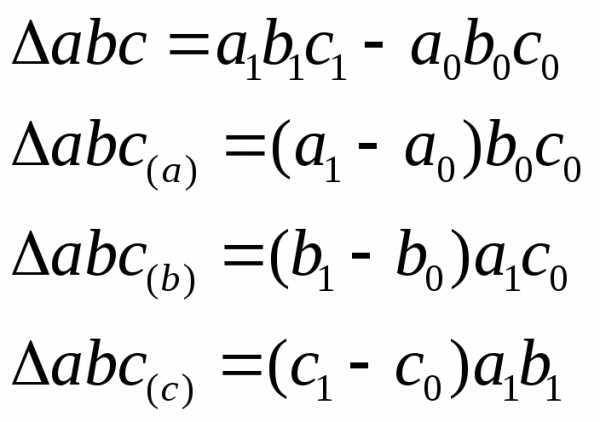
Г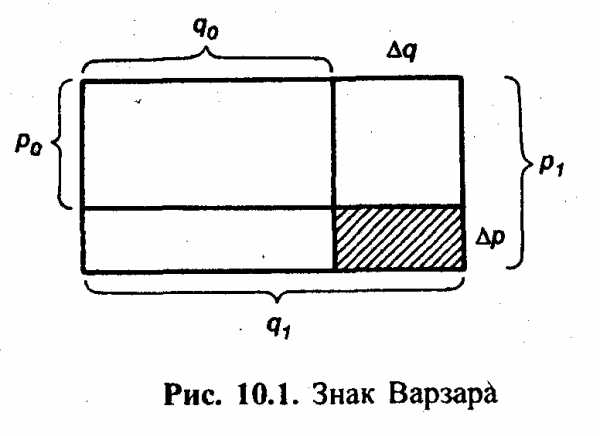рафик Варзара

Изолированная оценка изменения каждого фактора при неизменности другого приводит к недоучету эффекта совместного изменения факторов. Наглядно это можно показать с помощью особого вида плоскостной диаграммы, известной в отечественной статистике как «график Варзара»

Результативное явление представлено здесь в виде прямоугольника, площадь которого в базисном периоде 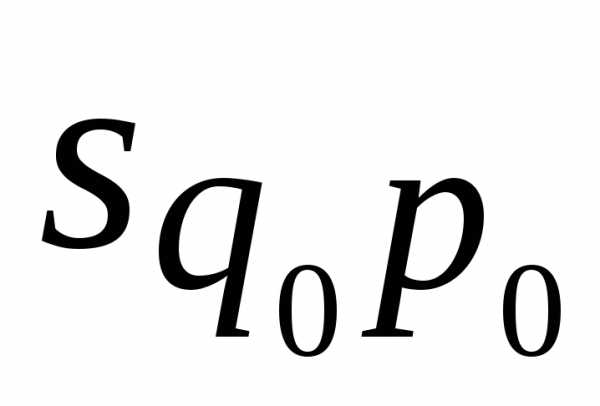,в отчетном -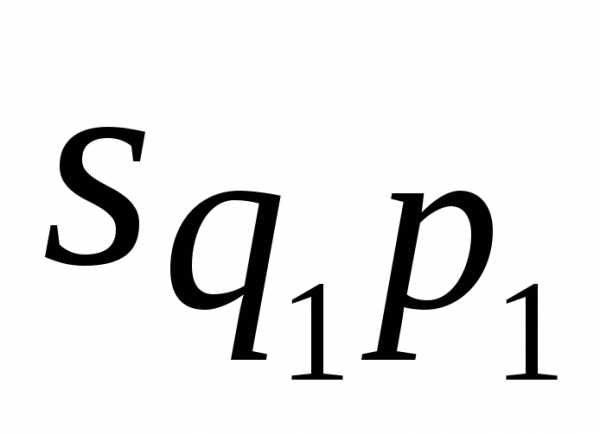. Переход от базисного состояния к отчетному формируется за счет изменения фактора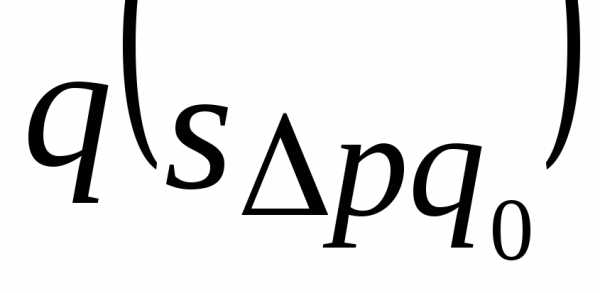, изменения фактора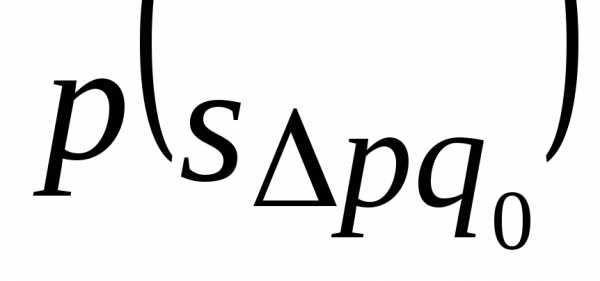и совместного изменения обоих факторов:

Располагая рядом несколько прямоугольников, относящихся к разным показателям, можно сравнивать не только размеры показателя — произведения, но и значения показателей — сомножителей.

Например, с помощью графика Варзара можно графически изображать стоимость продажи отдельных товаров с отображением их цены и количества реализации

Территориальные индексы

При сравнении двух районов А и Б за «базу сравнения» берется один из них, причем важно правильно выбрать район для сравнения.

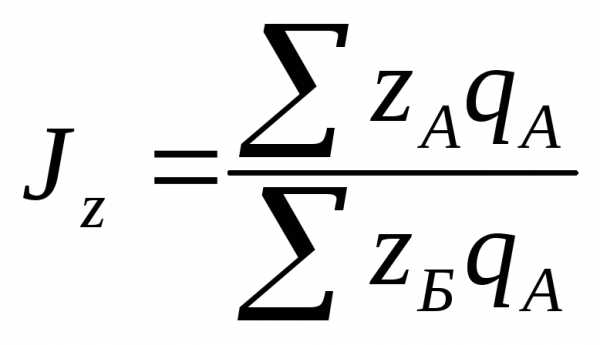или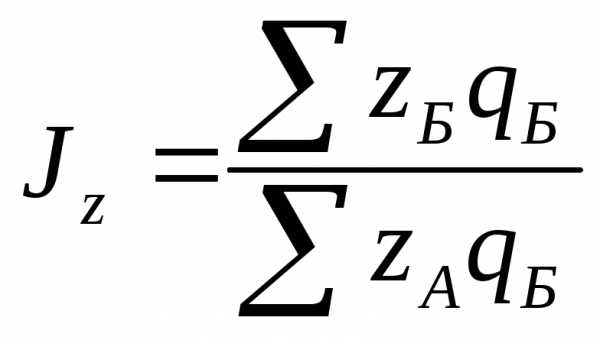

При сопоставлении показателя каждого районас общероссийской (или региональной) средней величиной этого показателя, индексы себестоимости для районов А и Б будут соответственно равны:

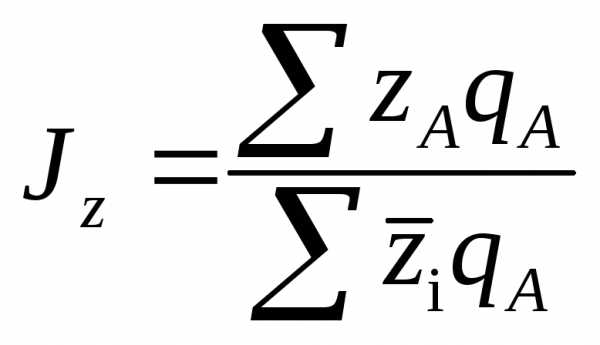или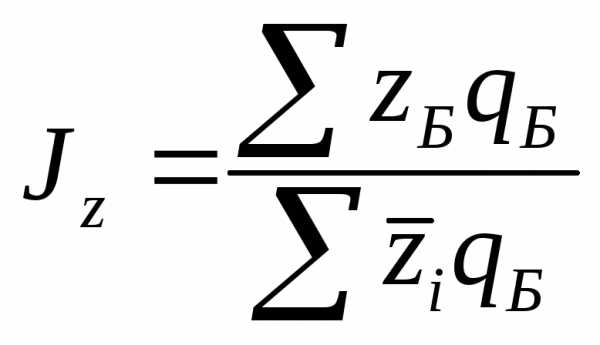

Метод стандартных весов построения территориальных индексов

Используется для получения индекса, дающего возможность непосредственно сопоставлять районы и свободного от влияния различий в структуре. При этом способе значения показателя по видам продукции умножаются на количество продукции, произведенной во всей области, республике или стране. Тогда индексы себестоимости для районов А и Б соответственно равны

или

Данный способ построения территориальных индексов _ применения только для продукции, сопоставимой по районам.

studfiles.net

Примеры двух ранжированных рядов

Из этой таблицы видим, что политологи в первом ряду имеют ранг 2, а во втором ¾ ранг 3, а историки в первом ряду ¾ ранг 1, во втором ¾ ранг 5. Для того чтобы оценить степень согласованности наших, грубо говоря, «ранжировок», можно применить тот же прием, который был применен при вычислении меры качественной ва­риации. Образуем из наших шести объектов различные пары. Таких пар будет 6x5/2=15. Возьмем отдельную пару объектов. Ранги, соот­ветствующие первому объекту, обозначим (i1, j1), а второму ¾ (i2, j2). Эти ранги могут находиться в различных отношениях. Возмож­на одна из двух ситуаций, каждая из которых включает два возможных соотношения между рангами (1а, 16, 2а, 26).

В первой ситуации ранги как бы согласованы, а во втором не согласованы. Подсчитаем, для скольких пар из 15-ти наблюдается согласованность, и обозначим число таких пар через S. Затем под­считаем, для скольких пар наблюдается несогласованность, и обо­значим число таких пар через D. В числителе всех приведенных выше мер стоит как раз разница между числом согласованных и несогласованных пар объектов. Для примера наших ранжирован­ных рядов величина (S-D) равна:

S-D = (3-2) + (2-2) + (2-1) + (0-2) + (1-0) = 1.

Здесь первая скобка ¾ результат анализа согласованности / несогласованности рангов в парах, образованных первым объектом с остальными пятью, т. е. в парах (1 и 2), (1 и З), (1 и 4), (1 и 5), (1 и 6). Среди них согласованность (случай 1а) — в трех парах, а несогласо­ванность (случай 26) — в двух парах. Вторая скобка ¾ результат ана­лиза пар, образованных вторым объектом, т. е. пар (2 и 3), (2 и 4), (2 и 5), (2 и 6). Среди них в двух парах согласованность, а в двух ¾ не­согласованность. Последняя скобка ¾ результат анализа пары (5 и 6).

Мы рассматривали случай отсутствия связанных рангов, поэто­му для определения степени согласованности можно использовать первый из трех коэффициентов, приведенных выше. Знаменатель для его вычисления равен:

S+D = (3+2) + (2+2) + (2+1) + (0+2) + (1+0) = 15

или просто числу различных возможных пар, т. е. 6x5/2=15

Тогда   0,07. В самом деле степень согласованности в наших ранжированных рядах очень мала. Второй из трех коэффициентов учитывает наличие связанных рангов. Кроме соотношений (1а; 1б;

Число пар, соответствующих третьей ситуации (есть связанные ранги во втором ряду ), обозначим через Ту. Число пар, соответ­ствующих четвертой ситуации (есть связанные ранга в первом ряду), обозначим через Тх. Второй коэффициент учитывает число связан­ных рангов в том и другом ранжированных рядах.

И наконец, обратите внимание на коэффициент dy/x. Мер Сомерса всего три по аналогии с мерами «лямбда» Гуттмана и «гамма» Гудмена и Краскала, т. е. ранговые коэффициенты связи бывают и на­правленные. Мы привели только одну из трех мер Сомерса. В случае ее использования вопрос о степени согласованности в ранжированных рядах звучит несколько иначе, а именно: влияет ли «уверенность» на «удовлетворенность» и, наоборот, влияет ли ранжирование по «удов­летворенности» на ранжирование по «уверенности». Разумеется, только в смысле того, что ранжирование объектов по степени убывания «удов­летворенности» (признак У) зависит от ранжирования по степени убы­вания «уверенности» (признак X). Поэтому в знаменателе учитыва­ются связанные ранги только для признака У.

А теперь представим себе, что речь идет об анализе связи по таблице сопряженности (корреляционная таблица) двух признаков, имеющих порядковый уровень измерения. Допустим, что у каждо­го нашего студента-гуманитария есть оценка не только удовлетво­ренности учебой, но и удовлетворенности собой. Оба признака имеют порядковый уровень измерения. Для изучения связи между ними используются те же ранговые меры связи. Их значения рассчитыва­ются по тем же формулам, ибо можно всех наших студентов (объекты ранжирования) упорядочить и получить два ранжированных ряда. Первый  по степени убывания (возрастания) удовлетворенности учебой, а второй ¾ по убыванию (возрастанию) удовлетворенности собой. Естественно, у нас будут сплошь связанные ранги. Напом­ним, что число рангов равно числу объектов, т. е. 1000. Реально никто такое ранжирование не проводит, а просто вычисляются по таблице сопряженности число согласованных пар, число несогла­сованных и число связанных рангов. Существуют коэффициенты ранговой корреляции для быстрого счета (коэффициент Спирмена), но в век компьютеров они уже утратили свою актуальность.

Мы рассмотрели все коэффициенты, необходимые для первоначального понимания того, что они из себя представляют, и почему их так много. В завершение этого раздела книги несколько слов о том, что все эти коэффициенты являются статистиками, т.е. для них можно построить доверительный интервал. Тот интервал, в котором находится истинное значение коэффициента, т. е. для изучаемой генеральной совокупности. Доверительные интервалы есть для «лямбда» [1, с. 34], «may» [1, с. 36], для коэффициентов ранго­вой корреляции [9, с. 185—187].

В рамках книги не ставилась цель привести все меры или дать их классификацию, ибо для этого необходимы серьезные знания в области науки под названием теория вероятности и математическая статистика. Более того, мы намеренно не рассматривали меры для изучения связи между признаками, измеренными по «метрическим» шкалам (по всем, по которым уровень измерения выше порядкового). Такая позиция обусловлена сочетанием двух факторов процесса обучения студентов. Во-первых, в эмпирической социологии такого рода шкалы встречаются реже других. Во-вторых, в читаемом сту­дентам курсе «Теория вероятности и математическая статистика» понятие «связь» вводится именно с такого рода мер связи.

Задание на семинар или для самостоятельного выполнения

Задание выполняется индивидуально. Каждый студент работает с той же матрицей данных (см. первое задание в начале этой гла­вы), с той же таблицей сопряженности.

1. Вычислить значения направленных мер связи Гуттмана, т. е. вычислить два значения. Сравнить результаты с аналогичными ре­зультатами других студентов.

2. Вычислить значения двух направленных коэффициентов Гудмена и Краскала. Сравнить со значениями, полученными в преды­дущем задании.

3. Получить два ранжированных ряда. Объектами ранжирова­ния будут группы, полученные при различных значениях первого признака (номинальный уровень измерения). В каждой группе под­считать среднее арифметическое значение третьего признака (мет­рический уровень измерения) и упорядочить эти группы в порядке убывания / возрастания этих значений. Тем самым получается пер­вый ряд. Для получения второго ряда в тех же группах подсчитать групповой индекс (см. раздел «Логические и аналитические индек­сы») по второму признаку. По значениям этого индекса получить второй ранжированный ряд.

4. Подсчитать необходимый для вашего случая коэффициент ранговой корреляции. Обосновать, почему выбран именно такой, а не другой коэффициент. Проанализировать полученное значение коэффициента.

studfiles.net

Методология индекса | Готовность регионов России к информационному обществу

Структура Индекса

Методология построения Индекса основана на концептуальной схеме оценки «электронной готовности». Индекс российских регионов строится на показателях, характеризующих три ключевых фактора электронного развития (человеческий капитал, экономическая среда, ИКТ-инфраструктура) и показателях доступа и использования ИКТ в шести сферах деятельности – в государственном и муниципальном управлении, бизнесе, образовании, здравоохранении, культуре, а также использование ИКТ домохозяйствами и населением (см. рисунок 1).

Индекс строится на основе агрегирования значений показателей, причем агрегирование происходит на нескольких уровнях, позволяя строить рейтинги регионов по отдельным направлениям и факторам развития информационного общества с различной степенью детализации.

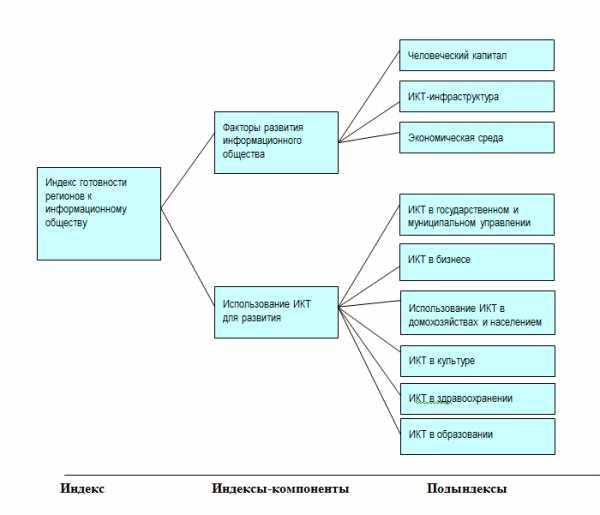
Рисунок 1. Структура индекса готовности регионов к информационному обществу

Для получения оценки предметных областей (подындексов) использовались наборы показателей, объединенные по параметрам оценки данной области. На рисунке 2 для примера приведена структура подындекса «ИКТ в культуре», для подсчета которого использовались 7 показателей.

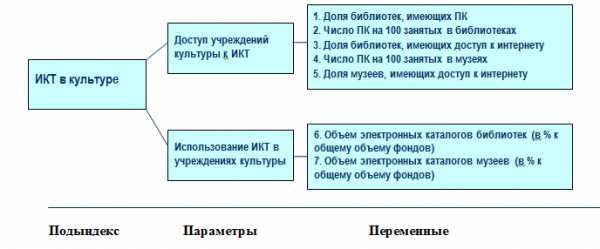
Рисунок 2. Структура подындекса «ИКТ в культуре»

По ряду направлений (ИКТ-инфраструктура, Экономическая среда, Использование ИКТ в домохозяйствах и частными лицами, ИКТ в образовании) подындексы рассчитывались напрямую, на основе составляющих их показателей без введения и расчета промежуточных параметров (как в случае подындекса «ИКТ в культуре» и др.).

Методика подсчета Индекса

Для подсчета Индексов все использованные показатели нормализовались (переводились в безразмерную величину в интервале от 0 до 1). Используемая начиная с Индекса 2008-2009 процедура нормализации отличается от аналогичной процедуры в предыдущих выпусках Индекса. Нормализация основана на расчете (путем деления) отношения текущего значения показателя для субъекта РФ к «эталонному» (нормализующему) его значению – обычно максимально возможному по данному показателю. Нормализованное значение показателя региона х рассчитывается по следующей формуле: Nх = Rx/Rn, где Rx – значение показателя для региона х, а Rn – нормализующее, «эталонное» значение.

Для оценки показателей, увеличение значения которых имеет негативный характер (например, «доля продуктов питания в структуре расходов домохозяйств») использовалась другая формула: Nх = Rn / Rx.

Таким образом, если регион имеет «эталонное» значение показателя, то его оценка по данному показателю равна 1, если значение меньше «эталонного», то его нормализованное значение будет в диапазоне от 0 до 1, и по величине нормализованного значению можно определить насколько регион отстает от «эталонного» значения.

Разрыв между субъектами РФ по отдельным и интегральным показателям рассчитывается путем деления друг на друга значений показателей для этих регионов (т.е. определяется во сколько раз одно значение больше другого), а информационное неравенство – делением максимального по России значения показателя у субъектов РФ на минимальное. При такой процедуре нормализации само значение индекса, изменение его значений и отношение значений для разных субъектов РФ имеет смысл и легко интерпретируется.

В качестве нормализующих («эталонных») значений показателей в случае долевых показателей (их большинство) бралось максимально возможное 100% значение. В других случаях нормализующее значение выбиралось исходя из желаемого, достаточного и достижимого для регионов-лидеров значения показателей на десятилетнем горизонте планирования, с учетом прогнозов значений показателей регионов-лидеров, России в целом и их значений в наиболее развитых странах.

В случае отсутствия значения показателя для отдельного региона его значение определялось с использованием статистических методов (корреляционный анализ и др.).

Значения подындексов подсчитывались как средневзвешенное оценок параметров, характеризующих соответствующую предметную область (если вводились параметры). Значение параметров и ряда подындексов (если для их параметров) рассчитывалось как средневзвешенное нормализованных значений показателей, характеризующих данное направление информационного развития – каждый показатель входит с определенным весовым коэффициентом (в большинстве случаев используются равные веса). Оценка индексов-компонентов («Факторы развития информационного общества» и «Использование ИКТ для развития») строится как среднее арифметическое от оценок подындексов. Общий Индекс готовности регионов к информационному обществу получается как средневзвешенное индексов-компонентов (с весами 1/3 и 2/3 соответственно), что эквивалентно среднему арифметическому от оценок всех входящих в Индекс подындексов. На основе общего Индекса, индексов-компонентов, подыдексов и оценок отдельных показателей строятся рейтинги регионов – ранжированные по значению индексов и отдельных показателей списки регионов.

В выпусках 2004-2005, 2005-2006 и 2007-2008 использовалась другая процедура нормализации показателей. Нормализованное значение показателя региона х рассчитывалось по формуле Nx=6*(Px-Pmin)/(Pmax-Pmin)+1, где Px, Pmax и Pmin – значение показателя региона х, а также максимальное и минимальное значения этого показателя у регионов России. Для оценки показателей, увеличение значения которых имеет негативный характер использовалась другая формула: Nx=6*(Pmax-Px))/(Pmax-Pmin)+1. В этих выпусках индекса веса индексов-компонентов, составляющих Индекс были одинаковые (по ½).

Источники информации

При расчете показателей и подындексов использовались два типа данных:

Расчет показателей и подындекса «ИКТ-инфраструктура» основывался на данных Министерства связи и массовых коммуникаций РФ и данных Росстата.

Расчет числа компьютеров на 100 человек населения осуществлялся с использованием данных о наличии ПК в организациях (форма государственного статистического наблюдения №3-информ) и данных Росстата о наличии компьютеров в домохозяйствах.

Оценка предметной области «Человеческий капитал» основывалась на опубликованных статистических данных Росстата.

Показатели экономической среды рассчитывались на основе опубликованных данных  Росстата.

Составление рейтингов по показателям использования ИКТ домохозяйствами и населением базируется на результатах обследования бюджетов домохозяйств, проводимых Росстатом, и данных опросов населения в регионах, осуществляемых Фондом «Общественное мнение» (проект «Георейтинг»).

Показатели использования ИКТ в органах власти рассчитывались на основе результатов государственного статистического наблюдения по форме № 3-информ (данные по органам государственной власти и местного самоуправления), полученных из базы данных Главного межрегионального центра обработки и распространения статистической информации Федеральной службы государственной статистики (ГМЦ Росстата), а также на основе результатов оценки веб-сайтов региональных органов власти, проводимой Институтом развития информационного общества для каждого выпуска Индекса.

Для оценки использования ИКТ в бизнесе также применялись показатели, полученные на основе баз данных ГМЦ Росстата (результаты обследования предприятий по форме № 3-информ, отобранных по видам экономической деятельности в соответствии с рекомендациями ОЭСР и Евростата для аналогичных обследований).

Оценка использования ИКТ в культуре осуществлялась на основе данных, опубликованных Министерством культуры РФ.

Рейтинг регионов по показателям использования ИКТ в медицине был составлен исходя из результатов обследования организаций здравоохранения по форме № 3-информ из баз данных ГМЦ Росстата.

Рейтинг регионов по показателям использования ИКТ в образовании первый раз он был рассчитан на основе данных единовременного обследования использования ИКТ в общеобразовательных учреждениях, проведенного Россвязьнадзором в начале 2006 г. в рамках подготовки проекта подключения школ к интернету. Начиная с Индекса 2007 – 2008 гг., для построения подындекса «ИКТ в образовании» используются данные Минобрнауки, полученные в рамках государственного статистического наблюдения по форме № Д-4.

Недостающие данные по некоторым регионам были, как отмечалось, восстановлены с помощью статистических методов для получения полных рядов данных, поскольку отсутствие подобных данных сделало бы невозможными расчет композитного индекса и подындексов и межрегиональные сопоставления.

Таким образом, при составлении рейтингов все регионы ранжировались на основе композитных индексов, построенных на основе полного набора данных по всем показателям. Значения композитных подындексов и самого индекса для субъектов РФ округлены до трех знаков после запятой. Тот факт, что некоторые регионы, имеющие в приведенных таблицах одинаковые значения индекса и подындексов, получили разные места в рейтинге, объясняется тем, что при ранжировании использовались неокругленные значения переменных и композитных индексов.

Интерпретация результатов

Ранжирование по индексам-компонентам, подындексам и отдельным показателям позволяет определить зоны отставания региона в использовании ИКТ и оценить сложившиеся на данный момент условия для развития информационного общества. Анализ может проводиться на разных уровнях агрегирования показателей.

Использованная начиная с 2008-2009 гг. процедура нормализации показателей расширяет интерпретационные возможности Индекса готовности регионов России к информационному обществу по следующим направлениям:

 

  1. Нормализованные значения показателей и композитных индексов могут быть интерпретированы как расстояния (в долях) от «эталонных» значений. Например, значение подындекса 0,250 означает, что регион по данному направлению информационного развития отстает в 4 раза (его уровень составляет четвертую часть) от «эталонного» уровня.
  2. Нормализованные значения показателей и композитных индексов позволяют измерять различия между субъектами РФ по уровню информационного развития и тем самым, отслеживать значения соответствующего контрольного показателя Стратегии развития информационного общества в Российской Федерации. Максимальные значения этих различий по интегральным показателям (подындексам, индексам-компонентам и индексу готовности) рассчитываются делением максимального значения композитного индекса у субъектов РФ на его минимальное значение, что позволяет в разах определить уровень информационного неравенства регионов. Аналогично, при желании, можно измерять «расстояние» субъекта РФ от любого другого выбранного для сравнения  региона.
  3. При сохранении набора показателей и фиксированных «эталонных» (нормализующих) их значений становится возможным слежение за изменением композитных индексов субъектов РФ во времени. При избранной процедуре нормализации изменение значений Индекса и его составляющих в разные годы легко интерпретируется и становится значимым, в отличие от предыдущей версии нормализации, в которой нормализованные значения показателей определяются в отношении к максимальному и минимальному значению показателя в текущем году и их сравнение в разные годы ни о чем не говорило.

Вместе с тем при интерпретации данных об относительном уровне использования ИКТ и об имеющихся условиях для развития информационного общества важно понимать, что существует несколько ограничений в аналитическом использовании Индекса и его компонентов, которые необходимо учитывать:

  1. Есть регионы с очень близким значением Индекса готовности, и их различия в уровне готовности находятся вне пределов статистической значимости. Особенно характерно это для регионов, где отсутствующие данные восстанавливались с использованием статистических методов.
  2. Целый ряд регионов, прежде всего Ненецкий и Чукотский автономные округа, отличаются относительно небольшим числом жителей и небольшим числом организаций и предприятий, заполнивших форму государственного статистического наблюдения №3-информ, которая является один из основных источников информации об использовании ИКТ в экономике, государственном управлении и медицине (по ней не опрашиваются предприятия малого бизнеса, и собираемость этой формы далеко не 100%). В этой ситуации статистическая погрешность показателей по этим регионам возрастает и может сказываться на результатах построения индекса.
  3. Использование композитных индексов для характеристики относительного уровня развития информационного общества и отдельных направлений использования ИКТ в регионах России сглаживает определенные проблемы с качеством государственной и ведомственной статистики, однако имеющиеся дефекты официальных данных могут оказывать влияние на результаты рейтинга (особенно на уровне отдельных показателей).

 

Для получения последнего издания Индекса готовности регионов России к информационному обществу 2009-2010 (бумажная версия) обращайтесь в Институт развития информационного общества: тел./факс +7(495)625-42-03, e-mail: [email protected]

Полный отчет

eregion.ru

Как улучшить индекс Хирша? | Хаос. Нелинейная динамика

Традиционно результативность ученого оценивали по числу статей. Потом появилась цитируемость. Наконец, в 2005 г. был придуман индекс Хирша, h.

Это очень показательная величина. Индекс равен h, если у человека есть h статей с цитируемостью выше h. То есть если h=12 (что считается неплохим результатом), то у человека есть 12 статей, каждая из которых имеет цитируемость выше 12. Хирш-индекс хорош тем, что выделяет стабильных ученых, выдающих много хороших работ. На мой взгляд, он является удачным дополнением к интегральным параметрам типа полной цитируемости.

Всем очевидно, что продуктивность ученого нельзя свести к одному числу. Но вот хороший набор параметров уже может давать (хотя бы в среднем) довольно адекватную картину. Хорошую экспертную оценку это никогда не заменит, но не всегда ее можно получить. Поэтому деятельность по придумыванию новых индексов и модернизации существующих весьма осмысленна и востребована. Существует большое количество модификаций индекса Хирша. Разные варианты стремятся учесть само-цитируемость, отсеять так называемые «братские могилы», разделить обзорные и оригинальные статьи, учесть фактор времени, дать больший вес статьям с высокой цитируемостью и т.п. В Архиве (arXiv.org) регулярно появляются статьи по этой тематике. В недавней работе (arXiv:1005.5227) Микаэль Шрейбер (Michael Schreiber) анализирует разные варианты индекса Хирша, используя данные по 26 физикам из одного европейского института. Посмотрим, что получилось.

Шрейбер вначале рассматривает шесть величин. Это полное число публикаций n, число публикаций с ненулевой цитируемостью n1, индекс Хирша h, а также индексы w, h3, hrИндекс w определяется так: 10w<c (w), но c (w+1)<10 (w+1), где c(w) — цитируемость статьи с номером w (статьи упорядочены по цитируемости, номер 1 имеет самая цитируемая). То есть w=3 соответствует тому, что у человека три статьи с цитирумостью выше 30, но четвертая уже имеет менее 40. Далее, индекс h3определяется как h32<c(h3), но c(h3+1)<(h3+1)2. То есть если у человека h3=5, то у него пять статей с цитируемостью выше 25, но шестая имеет цитируемость менее 36. Чтобы ранжировать людей с одинаковым индексом Хирша, вводят интерполяционный индекс hi. Он находится в интервале h<hi<h+1 и определяется линейным интерполированием cI(x)=c (h)+(x-h) (c (h+1) -c (h)), hi=c/hi).

Очевидно, w и h3придают больший вес статьям с высокой цитируемостью (выделяя, как говорят, более компактное «ядро» в наборе публикаций), чем простой или интерполированный индекс Хирша, а n и n1 — напротив. При этом w и h3 оказываются совпадающими у большого числа людей, особенно w. Среди рассмотренных 26 списков «выпало» всего 7 разных значений w, причем значение w=4 соответствует сразу десятку ученых.

Стоит отметить, что ранжирование по h, hI, w и h3, разумеется, совпадает, с единственной оговоркой об одинаковых значениях w и h3, а иногда и h, у разных ученых. А вот лидер (среди 26 рассмотренных ученых) по числу публикаций и числу публикаций с ненулевой цитируемостью оказался лишь четвертым в таком списке.

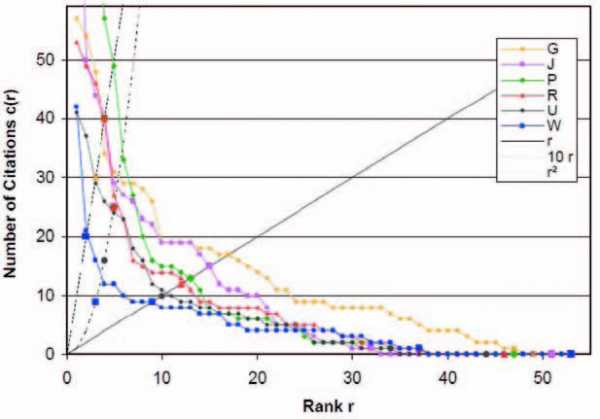
Рисунок 1. Из статьи arXiv:1005.5227 Микаэля Шрейбера (Michael Schreiber)

На рисунке 1 цветом показаны данные по 6 ученым (число 26 было выбрано неслучайно, оно просто соответствует числу букв в латинском алфавите, т.е. имена ученых, чьи списки публикаций использованы в исследовании, в статье не фигурируют.) Три линии, выходящие из начала координат, соответствуют трем индексам: сплошная — обычному Хиршу, длинные штрихи — индексу w, короткие штрихи — индексу h3.

У всех рассмотренных индексов есть важный недостаток: если статья уже вошла в «ядро цитирования», то не важно, насколько велико полное число ссылок на нее. Это вообще недостаток всех «хиршеподобных» индексов. Два человека с одинаковыми индексами могут иметь полную цитируемость, отличающуюся в разы или десятки раз. Поэтому любят вводить коэффициенты так или иначе связанные со средним числом ссылок на статью. Будем обозначать усредненное число ссылок cN. Аргументом этой величины может стоять номер статьи в рейтинге. Кроме банального деления полного числа ссылок на полное число статей вводят модификации. Например, индекс A=cN(h)=s (h)/h. Здесь s — сумма числа цитирований от самой цитируемой статьи до статьи с номером h. То есть среднее число ссылок определяется только по «ядру», соответствующему индексу Хирша. Другие модификации так или иначе связаны с выделением этого «ядра». Например, предлагается брать корень из полного числа статей, т.е. если у человека 150 статей, то усреднение пойдет по 12 наиболее цитируемым.

Если посмотреть на 26 выбранных списков публикаций, то ранжирование не сильно отличается от описанного выше, только поднимаются в списке люди с небольшим числом очень высокоцитируемых статей и проседают те, у кого очень длинный список публикаций при той же полной цитируемости и таких же h.

При этом, считает Шрейбер, плохо базироваться на полном числе публикаций, так как это сама по себе плохо определенная величина, если не вводить жестких критериев селекции. Автоматически базы данных (а все рассуждения обычно применяют к тем данным, которые легко доступны в базе без дополнительной обработки, поэтому, например, все индексы считаются без выбрасывания самоцитирования, что досадно) включают в списки всякую «мелочевку», от которой часто трудно избавиться выставлением флагов и тэгов. Поэтому хочется какого-то самосогласованного выделения «ядра» публикаций, альтернативного хиршевскому.

Рисунок 2. Из статьи arXiv:1005.5227 Микаэля Шрейбера (Michael Schreiber)

Альтернатива оказывается очень похожа на сам индекс Хирша. Это индекс g: g=cN(g). То есть у человека имеется g статей со средней цитируемостью, больше или равной g. То есть это почти то же самое, что индекс Хирша, но уже не просто для цитируемости и статей, расставленных по ней, а для усредненной цитируемости и ранжирования по этой величине. На рисунке 2 показан соответствующий график. Пересечение прямой линии из начала координат с цветной соответствует показателю g для данного ученого. Аналогично hIможно ввести gI, что и делается.

Предельным случаем является цитируемость самой цитируемой статьи («ядро» состоит из одной статьи). Из анализа видно, что ранжирование по этой величине сильно отличается от других, более сглаженных и усредненных подходов. Шрейбер делает вывод, что по самой цитируемой статье плохо судить об интегральном вкладе ученого. Хотя, заметим, речь тут идет не об отдельных случаях особой гениальности, а о показателях вполне средних (в хорошем смысле) ученых. Для них, разумеется, строить какое-то ранжирование исходя из того, что у одного самая цитируемая статья имеет 53 ссылок, а у другого 47, — плохо.

Двигаемся дальше. Среднее можно брать по-разному. Например, можно брать медианное. И, конечно, есть такие индексы. Например, берем «ядро», определенное по Хиршу, и смотрим в нем медианную цитируемость. Получаем индекс т. Можно брать гармоническое или геометрическое среднее. И такие индексы есть. Шрей-бер показывает, что хотя все это и неплохо, но при большей сложности в определении не дает никакого выигрыша в итоге.

Люди играют и с другими вариантами. Например, с квадратным корнем из суммарного числа цитирований по «ядру». К примеру, есть хороший вариант определения индекса g как квадратного корня из s (g). Шрейбер выделяет интерполированный g (т.е. индекс gI) как один из лучших параметров.

Далее, есть весьма сложные индексы. Например, можно определять «энтропию» списка цитирования (максимальную энтропию имеет список, где все статьи имеют одинаковое число ссылок). Здесь опять же анализ выборки из 26 списков цитирования показывает, что увеличение сложности расчета коэффициента не ведет к новым положительным свойствам.

Интересные (но сложные) индексы возникают, если после выделения «ядра по Хиршу» пытаются учесть, насколько «хвост» может вскоре войти в «ядро». В таком случае чем ближе статья в ранге к границе ядра, тем больший вес получает ее цитируемость. То есть если у двух ученых абсолютно одинаковые «ядра по Хиршу», но у одного за «ядром» почти пусто, а у другого есть много статей, которые вот-вот войдут в «ядро» (т.е. возрастет индекс Хирша), то второй будет иметь лучший показатель.

Наконец, есть интересный индекс maxprod. Он определяется как максимум (по r) произведения r c®. Здесь r — номер (ранг) статьи в списке, упорядоченном по цитируемости, а c®, как и выше, — цитируемость статьи с номером r. Обычно этот индекс выше h3, что связано, как правило, с высокой цитируемостью статей внутри «ядра по Хиршу» (скажем, у меня при h=12, по данным NASA, ADS maxprod равен 240 за счет того, что восьмая статья в списке имеет цитируемость 30, но могло бы быть и иначе, если бы тянулся длинный хвост и, скажем, статья с номером 50 имела бы цитируемость 5).

Разумеется, стоит смотреть, как разные индексы коррелируют друг с другом. Хуже всего коррелируют с другими индексами полное число публикаций (n) и число публикаций с ненулевой цитируемостью (n1). Затем из числа описанных выше идут индексы w и A. После — т. А вот, скажем, индекс Хирша, индекс g и maprod неплохо коррелируют друг с другом, т.е. плохо коррелируют или индексы, основанные на большом числе статей (например, на всех), или, наоборот, индексы, основанные на очень маленьком «ядре». Как наилучший Шрейбер выделяет интерполированный g-индекс. По его мнению, стоит добавить его автоматическое определение в ведущих базах данных.

В заключение повторим слова Шрейбера о том, что важнее не качество индекса, а качество базы. Поэтому лучше уж использовать самый примитивный, но по подходящей базе, чем самый наилучший, но по плохой.

Сергей Попов, "Троицкий вариант" № 56, c. 3, "Бытие науки"

chaos.in.ua

Определение индекса технического состояния силовых трансформаторов в процессе их эксплуатации

 

Состояние вопроса: В настоящее время в отечественной электроэнергетике продолжается процесс реформирования, одной из тенденций которого является переход к техническому обслуживанию оборудования по его техническому состоянию, что, наряду с другими мерами, должно способствовать более эффективному управлению производственными активами электроэнергетических предприятий и повышению их конкурентоспособности. Для новой формы обслуживания  необходим динамичный способ  количественной оценки технического состояния оборудования, в качестве которого предлагается некоторый интегральный показатель, получивший название индекса состояния.  

Материалы и методы: Предложенная формализация оценки состояния трансформаторов в виде набора правил-продукций реализована в экспертной системе оценки состояния оборудования «Диагностика+», которая в настоящее время используется на предприятиях МРСК (Россия), KEGOC (Казахстан) и др. в интеграции с системой ТОРО на базе SAP ERP.

Результаты: Для расчета индекса состояния трансформатор рассматривается как сложная техническая система. По результатам эксплуатационных испытаний посредством разработанной системы экспертных оценок определяется состояние каждой подсистемы, а затем сверткой полученных значений с соответствующими весовыми коэффициентами определяется индекс состояния самого объекта. Кроме того, чтобы не пропустить быстроразвивающийся дефект, вводится понятие маркеров инициирующих обслуживающий персонал на оперативные действия.

Выводы: Рассмотренный подход к формализации нечеткой эксплуатационной информации позволяет  выстроить детерминированную схему принятия решений по обслуживанию стареющего  электрооборудования, в  которой процедуры ранжирования, вывода в ремонт и замены конкретных объектов реализуются на основе объективных критериев.

Ключевые слова: электрооборудование, техническое состояние, дефекты, ранжирование, ремонт, замена, индекс технического состояния.

vestnik.ispu.ru

Prostoy-Site | Все права защищены © 2018 | Карта сайта