Решение задач оптимизации в среде ms excel. Задачи оптимизации excel
Решение задач оптимизации в среде ms excel
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Для студентов и слушателей
строительных специальностей, изучающих дисциплины
«Информатика» и «Информационные технологии в строительстве»
Одобрено
редакционно-издательским советом
Саратовского государственного
Технического университета
Саратов 2010
Введение
В методических указаниях рассматриваются задачи оптимизации для инженерных задач и решение их в среде MS Excel для строительных специальностей.
Интерес к этим задачам обусловлен спецификой их формализации и прикладной значимостью.
Функции MS Excel обладают развитым аппаратом численного анализа данных, позволяющим решать сложные задачи линейного и нелинейного программирования со многими неизвестными и ограничениями, что делает его очень удобным инструментом решения задач оптимизации.
В MS Excel для решения различных задач оптимизации есть средство Поиск решения. Эта команда находится в меню Сервис. Если команда не обнаруживается, это значит, надстройка Поиск решения не загружена. Для загрузки надо выбрать Надстройки из меню Сервис. Из списка диалогового окна выбирается Поиск решения и в квадратике устанавливается флажок. В случае отсутствия в списке надстройки Поиск решения, запускается программа установки MS Excel
Данные методические указания рассчитаны на читателей, знакомых с основами работы в Excel, и предназначены для студентов и слушателей курса информатики и информационных технологий в строительстве.
Методические указания содержат примеры решения задач оптимизации в среде MS Excel, а также задания для студентов строительных специальностей.
Задачи оптимизации
Часто возникает ситуация, когда необходимо выбрать из предложенных вариантов один, удовлетворяющий каким-то определенным требованиям. Очевидно, что этот вариант является оптимальным, т.е. наилучшим решением поставленной задачи. Введение нескольких характеристик (требований) для оценки наилучшего варианта приводит к задачам оптимизации.
Задачи оптимизации разделяются на классические и неклассические. В классических задачах требуется найти значения одной или нескольких переменных.. При этом ищется максимум или минимум значения некоторой непрерывной функции. В неклассических задачах имеются дополнительные ограничения, формирующие в совокупности множество допустимых альтернатив.
Задачи оптимизации на сегодняшний день разнообразны по своему характеру. Универсальных методов для их решения практически нет, но существуют типовые классы задач оптимизации, которые могут быть успешно решены с помощью программы электронных таблиц MS Excel. Некоторые из них рассмотрим в данных методических указаниях.
Задача о строительстве объекта относится к классу задач нелинейного программирования и является примером задачи многомерной нелинейной оптимизации.
В математической модели этой задачи используется две независимые переменные, каждая из которых представляет отдельную координату точки на плоскости.
ПОСТАНОВКА ЗАДАЧИ О РАЗМЕЩЕНИИ
СТРОЯЩЕГОСЯ ОБЪЕКТА
Задача может иметь несколько возможных вариантов постановки, отличающихся друг от друга количеством жилых домов и их расположением на координатной плоскости.
Рассмотрим конкретно один из вариантов этой задачи.
Имеются четыре жилых дома, расположенных в некотором микрорайоне города.
Определить местоположение объекта для строительства. Для примера объектом строительства выберем школу.
Требуется построить школу в удобном для всех жителей микрорайона месте, предполагая, что сумма расстояний от построенного объекта до всех жилых домов будет минимальным значением (рис. 1). Это значение и является целевой функцией, которое необходимо определить, используя функции среды MS Excel.
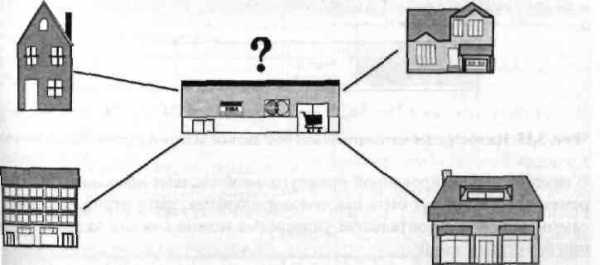
Рис. 1
Другие варианты задачи о строительстве объектов могут быть сформулированы как для различных значений количества домов, местоположения этих домов, так и для различных видов целевой функции.
studfiles.net
Решение задач по оптимизации с использованием MS Excel
Лабораторная работа № 1
Решение задач по оптимизации с использованием MS Excel
Задание 1 «Линейная оптимизационная задача»
Контрольный пример
Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
| Ресурсы | Нормы затрат ресурсов на одно изделие | Общее количество ресурсов | |
| стол | шкаф | ||
| Древесина: | |||
| 1 вида | 0,2 | 0,1 | |
| 2 вида | 0,1 | 0,3 | |
| Трудоемкость (человеко-часов) | 1,2 | 1,5 | 371,4 |
| Прибыль от реализации одного изделия (руб.) |
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.
Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:
1. Для определения каких величин строится модель?
2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
3. Каким ограничениям должны удовлетворять неизвестные?
В данном случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: х1 - количество столов, х2 - количество шкафов
Суммарная прибыль от производства столов и шкафов равна z=6*x1+8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z
Ограничения, которые налагаются на х1 и х2:
· объем производства шкафов и столов не может быть отрицательным, следовательно: х1, х2 ³ 0.
· нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:
0.2x1+ 0.1x2 £40
0.1x1 +0.3x2 £60
Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов
1.2x1+ 1.5х2 £ 371.4
Таким образом, математическая модель данной задачи имеет следующий вид:
Максимизировать
z = 6х1 + 8х2
при следующих ограничениях:
0.2x1+ 0.1x2 £40
0.1x1 +0.3x2 £60
1.2x1+ 1.5х2 £ 371.4
Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
Решение задачи с помощью MS Excel.
1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис. 1).
Рис. 1. Диапазоны, отведенные под переменные, целевую функцию и ограничения
2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:
=0,2*А3+0,1*ВЗ
=0,1*А3+0,3*ВЗ
= 1,2*АЗ+1,5*ВЗ,
а в ячейки В7:В9 - правые части ограничений. (рис.1.)
3. Выбрать команды Сервис/Поиск решения и заполнить открывшееся диалоговое окно Поиск решения как показано на рис 2. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/ Надстройки/ Поиск решения.
Для ввода ограничений нажмите кнопку Добавить.
Внимание! В диалоговом окне Параметры поиска решениянеобходимо установить флажок Линейная модель (Рис.3.).
Рис. 2. Диалоговое окно Поиск решения задачи о максимизации прибыли на фабрике
Рис 3. Параметры поиска решения
4. После нажатия кнопки Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).
Рис. 4. Результаты поиска решения
5. Результаты расчета задачи представлены на рис. 5, из которого видно, что оптимальным является производство 102 столов и 166 шкафов Этот объем производства принесет фабрике 1940 руб. прибыли.
Рис. 5. Результаты расчета
Индивидуальное задание
1. Построить математическую модель задачи, согласно Вашего варианта.
2. Решить задачу с помощью средства MS Exсel Поиск решения.
Лабораторная работа № 2
Решение задач по оптимизации с использованием MS Excel
Задание 2 «Транспортная задача»
Контрольный пример
Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице "Транспортные расходы":
Таблица "Транспортные расходы"
| Лос-Анджелес | Даллас | Сен-Луис | Вашин- гтон | Атланта | ||
| Денвер | 1,50 | 2,00 | 1,75 | 2,25 | 2,25 | |
| Бостон | 2,50 | 2,00 | 1,75 | 1,00 | 1,50 | |
| Новый Орлеан | 2,00 | 1,50 | 1,50 | 1,75 | 1,75 | |
| Даллас | 2,00 | 0,50 | 1,75 | 1,75 | 1,75 |
Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.
· Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции.
Для решения данной задачи построим ее математическую модель.
Неизвестными в данной задаче являются объемы перевозок. Пусть xij - объем перевозок с i-ой фабрики в j-й центр распределения. Функция цели - это суммарные транспортные расходы, т. е. где сij – стоимость перевозки единицы продукции с i-и фабрики j-й центр распределения.
Неизвестные в данной задаче должны удовлетворять следующим ограничениям:
· Объемы перевозок не могут быть отрицательными.
· Так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.
В результате имеем следующую модель: Минимизировать:
при ограничениях:
, j Î [1,5]
xij ³ 0, iÎ [1,4], jÎ [1,5
, iÎ [1,4],
где aij - объем производства на i-й фабрике, bj — спрос в j-м центре распределения.
stydopedia.ru
Решение задач оптимизации в excel`е
Решение задач оптимизации в EXCEL`еВведение. Для решения задач поиска корней уравнения или где требуется отыскать оптимальное решение (например, дающее минимальное или максимальное значения), удовлетворяющее при этом целому ряду дополнительных условий на значения используемых параметров. Для решения таких задач, требующих применения методов, нелинейного программирования (управления), является имеющаяся в MS Excel Надстройка "Поиск решения". Задачи линейного программирования возникают, например, при планировании перевозок, распределения производственных ресурсов, оптимизации структуры производства и т.п.
Активация и использование надстроек
Надстройки – это компоненты Microsoft Excel, предоставляющие доступ к дополнительным функциям и командам. Двумя из наиболее популярных надстроек являются "Пакет анализа" и "Поиск решения", которые реализуют функции расширенного анализа данных. Чтобы использовать эти надстройки, их необходимо установить и активировать.
Ниже описан порядок установки и активации надстроек "Пакет анализа" и "Поиск решения", а также даны инструкции, позволяющие приступить к анализу данных с их помощью. Тот же порядок действий применим к установке и активации многих других надстроек. У некоторых других надстроек (например, продуктов сторонних производителей) могут быть собственные программы установки.
Установка и активация надстроек "Пакет анализа" и "Поиск решения"
Установка и активация надстроек "Пакет анализа" и "Поиск решения"
Рис. 1а. Окно Настройки Примечание. Поскольку в этом случае устанавливаются две надстройки, приглашение установить надстройку будет показано дважды: первый раз для пакета анализа и второй для надстройки "Поиск решения". Обратите внимание, что на вкладку Данные добавлена группа Анализ, которая находится справа. Она содержит кнопки команд для надстроек Анализ данных и Поиск решения (см. рис. 1б и 1в). Рис. 1б. Группа Анализ на вкладке Данные Теперь можно приступить к работе с этими надстройками. |
Рис. 1в. Вкладка "Анализ данных", после установки
надстроек "Анализ данных" и "Поиск решения" Начало работы с надстройкой "Поиск решения"
|
От пользователя требуется умение с помощью серии диалоговых окон правильно сформулировать условия задачи, и если решение существует, то "Поиск решения" отыщет его.
Укажем некоторые возможности надстройки "Поиск решения":
Надстройка "Поиск решения" позволяет использовать одновременно большое количество изменяемых ячеек (в общей сложности до 200 ячеек).
Надстройка "Поиск решения" позволяет задавать ограничения для изменяемых ячеек. Например, при поиске решения, обеспечивающего максимальную прибыль, вы можете задать дополнительные условия (ограничения), например, на общий доход, который находился бы в диапазоне от 20 до 30%, или чтобы расходы не превышали заданной суммы. Подобного рода условия называются ограничениями для решаемой задачи.
Надстройка "Поиск решения" позволяет отыскать оптимальные (минимальные или максимальные) решения, т.е. наилучшие из возможных решений.
Задачи, для решения которых можно воспользоваться надстройкой "Поиск решения", имеют ряд общих свойств:
Имеется единственная ячейка, содержащая формулу, значение которой нужно оптимизировать или же сделать равным конкретному значению. Это значение (минимум, максимум или равно) является конечной целью решения, поэтому эта ячейка называется целевой ячейкой.
Формула в этой целевой ячейке содержит ссылки на ряд изменяемых ячеек (содержащие неизвестные, или переменные, решаемой задачи).
Поиск решения заключается в том, чтобы побрать такие значения этих переменных, которые бы давали оптимальные значения для формулы в целевой ячейке.
Кроме того, может быть задано некоторое количество ограничений – условий или соотношений, которым должны удовлетворять некоторые из изменяемых ячеек (переменных).
Рассмотрим использование надстройки "Поиск решения" на примере задач.
Задача. Найдём минимум функции y=(x-2)2.
Аналитическое решение. Сразу отметим, что эта задача на минимизацию функции. Находим производную и приравниваем её к нулю. Получим уравнение y'=2(x-2)=0. Решаем это уравнение. Ответ: xopt=2, ymin=0.
При численном решении задачи требуется сначала задать начальное приближение x0 (нулевое приближение). Для этого определяют интервал, где находится точка минимума, т.е. на этом интервале функция является унимодальной. Протабулируем функцию на данном интервале и построим её график (см. рис. 2).
Рис. 2. Таблица значений и график y=(x-2)2
Можно, например, взять отрезок [1,5; 2.5] и точку из этого отрезка равную 1,5. И заполняем ячейки согласно рис. 3. В ячейку B2 вводим начальное приближение аргумента, в ячейку B3 (целевая ячейка) нашу функцию, т.е. =(B3-2)^2. На рис. 3. мы видим значение этой функции в точке 1,5.
Рис.3. Ввод исходных данных
Выделяем ячейку B3 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения (см. рис. 4). В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B3. Программа автоматически установила нужные параметры: Минимум, ячейку, где будет находится решение B2, метод решения (окно Выберите метод решения). Щелкаем по кнопке Найти решение. В ячейке B2 мы видим xopt=2 и минимальное значение функции равное нулю (см. рис 5).
Рис. 4. Установка параметров оптимизации
После нажатия кнопки Найти решение, появится окно Результаты поиска решения (см. рис. 5),
Рис. 5. Окно Результаты поиска решения
и в ячейках B2 и B3 мы видим решение нашей задачи (см. рис. 6).
Рис. 6. Решение задачи
Следовательно, xopt=2, а ymin=0.
Условная оптимизация
Как правило, задачи на оптимум решаются при ограничениях (условная оптимизация).
Задача. Найдём минимум функции y=(x-2)2, при ограничении x≥2,5.
Рис. 7. Таблица данных и график функции при x>=2,5
В ячейку B2 вводим начальное приближение аргумента, например, равно 3 (см. рис. 8).
Рис. 8. Ввод исходных данных
Для ввода ограничений в окне Параметры поиска решения есть кнопка Добавить. Также как и в предыдущем примере Выделяем ячейку B3 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения. В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B3. Программа автоматически установила нужные параметры: Минимум, ячейку, где будет находится решение B2, метод решения. Теперь щелкаем мышкой по кнопке Добавить, после чего в открывшемся окне Добавление ограничения в поле Ссылка на ячейку указать ячейку (аргумент), на которую накладывается ограничение. Далее необходимо выбрать тип ограничения из раскрывающегося списка в центре диалогового окна, а затем в поле указать накладываемое ограничение (в данном случае число 2,5) (см. рис. 9).
Рис. 9. На ячейку B2 накладывается ограничение
Для подтверждения выполненных действий следует щелкнуть по кнопке ОК. Щелчок по кнопке Добавить также будет подтверждением, однако при этом диалоговое окно Добавление ограничения не будет закрыто и появится возможность ввести ещё одно ограничение. Так следует поступать в случаях, когда вводимых ограничений несколько.
Система вернёт нас обратно к окну Параметры поиска решения, где в поле В соответствии с ограничением, мы видим введённое ограничение на аргумент (см. рис. 10).
Рис. 10. Поиск решения с ограничением на ячейку B2
В ячейке B2 мы видим xopt=2,5 и минимальное значение функции равное 0,25 (см. рис 11).
Рис. 11. Окно Результаты поиска решения
Рис. 12. Решение
Естественно было ожидать, что минимальное значение будет достигнуто на границе (см. рис. 2).
Многомерная оптимизация
Задача. Найти минимум функции f(x,y)=(x-2)2+(y-3)2.
В ячейку B18 вводим начальное приближение аргумента x0, например x=1, в ячейку B19 вводим начальное приближение аргумента y0, например, y=1, а в ячейку B20 (целевая ячейка) нашу функцию, т.е. =(B18-2)2+(B19-3)2. На рис. 13. мы видим значение этой функции в точке (1,1).
Рис. 13. Ввод исходных данных
Выделяем ячейку B20 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения (см. рис. 14). В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B20. Установим нужные параметры: Минимум, ячейки, где будет находится решение B18, B19 метод решения (окно Выберите метод решения).
Рис. 14. Установка параметров оптимизации
Щелкаем по кнопке Найти решение. В ячейках B18 и B19 мы видим решение: xopt=2, yopt=3 и минимальное значение функции равное нулю, которое находится в ячейке B20 (см. рис 15).
Рис. 15. Окно Результаты поиска решения
Условная оптимизация
Задача. Найти минимум функции f(x,y)=(x-2)2+(y-3)2 при ограничении x+y=7. На лекции мы рассматривали этот пример. Эту задачу мы свели задаче обычного минимума, когда из уравнения, задающего ограничение на переменные, выразили одну из переменных и затем подставили это выражение в целевую функцию. Теперь решим данную задачу в Excel.
Как и прежде заносим в таблицу начальные значения для аргументов функции x и y (ячейки B18 и B19), формулу (целевую функцию) в ячейку B20 и формулу =B18+B19 (т.е. x+y) в ячейку B21 (это ограничение без правой части).
Рис. 16. Ввод исходных данных
Далее по аналогии с предыдущими примерами. Выбираем команду Данные/Поиск решения. Вводим параметры оптимизации (см. рис. 17 и 18).
Рис. 17. Установка ограничения x+y=7
Рис. 18. Результат установки ограничения
Рис. 19. Окно Результаты поиска решения
Следовательно, xopt=3, yopt=4, fmin=2 при ограничении x+y=7.
Поделитесь с Вашими друзьями:
www.psihdocs.ru