Конечно-элементное решение задач топологической оптимизации (2007 г.). Топологическая оптимизация конструкций

Топологическая оптимизация силовых конструкций на основе модели переменной плотности Текст научной статьи по специальности «Механика»

НАДЕЖНОСТЬ ИЗДЕЛИЙ

МАШИНОСТРОЕНИЯ

УДК 629.7

ТОПОЛОГИЧЕСКАЯ ОПТИМИЗАЦИЯ СИЛОВЫХ КОНСТРУКЦИЙ НА ОСНОВЕ МОДЕЛИ ПЕРЕМЕННОЙ ПЛОТНОСТИ

Самарский государственный аэрокосмический университет

Поступила в редакцию 18.03.2011

Дается обзор методов топологической оптимизации конструкций на основе специальных моделей метода конечных элементов (МКЭ). Предлагается стратегия выбора рациональной силовой схемы пространственных тонкостенных конструкций с использованием наглядно представляемых результатов оптимизации континуальной модели переменной плотности.

Ключевые слова: континуальная модель, интерпретация, потоки главных усилий, главные касательные силы

Известно, что выбор параметров силовой схемы существенно влияет на характеристики создаваемой конструкции [1]. Одними из первых возможность алгоритмического подхода к топологической (структурной) оптимизации конструкций, моделируемых по МКЭ, исследовали Hemp W.S. и Topping B.H. В работах, рассмотренных в обзорной статье [2]: пространство, в котором может располагаться конструкция, покрывается сеткой узлов. В этих узлах прикладываются нагрузки и задаются закрепления. Исходная структура получается путем генерации ферменной конструкции, в которой стержневые элементы соединяют каждый узел со всеми остальными узлами. В процессе оптимизации конструкции слабо нагруженные «лишние» элементы удаляются автоматически, когда площадь их поперечного сечения оказывается менее некоторого заданного значения. В результате в силовой схеме фермы должны остаться только стержни, наиболее эффективно передающие приложенные нагрузки к закреплениям. Однако замечено [2], что после удаления в конструкции некоторых элементов может появиться плохая обусловленность матрицы жесткости упругой системы. Также выявлена зависимость получаемых решений от начальной плотности сетки конечных элементов. Kohn R.V. и Strang G.

Болдырев Андрей Вячеславович, кандидат технических наук, доцент кафедры конструкции и проектирования летательных аппаратов. E-mail: [email protected]

[3] объяснили эти особенности тем, что в любой точке допустимой геометрической области с учетом дискретности используемых математических моделей реализуется одно из двух возможных «крайних» состояний: конструкционный материал либо содержится, либо отсутствует. Для устранения указанных недостатков в постановке задачи структурной оптимизации силовых конструкций предложено использовать специфические пористые материалы. При этом в геометрические ограничения, внутри которых может размещаться конструкция, вписывается непрерывная упругая среда (континуальная модель), включающая в себя все возможные силовые схемы. Результаты оптимизации параметров континуальной модели могут дать информацию о наилучшей силовой схеме разрабатываемого объекта. Такой подход, использующий твердое деформируемое тело с переменными по объему характеристиками материала, допускает возможность появления в модели конструкции «переходных» зон между «крайними» вариантами состояния упругой среды.

Отметим, что ранее в работе Комарова А. А. [4] высказана и использована идея применения в процессе проектирования конструкций гипотетического материала с переменным по объему модулем упругости при оптимизации плоских конструкций. В дальнейшем эта идея получила развитие в исследованиях [1, 3, 5-8] в виде тела переменной плотности с соответствующими прочностными и упругими

характеристиками. Bendsoe M.P. и Kikuchi N. [5] решили задачу оптимизации распределения материала в континуальной модели относительно степени пористости материала. В этом исследовании упругая среда, вписанная в допустимую геометрическую область, делится на конечные элементы. За целевую функцию принимается податливость упругой среды, а ограничением является масса материала. Материал упругой среды считается пористым, для чего ему сопоставляется определенная микроструктура. Элементарная ячейка такой микроструктуры для пластины показана на рис. 1. В ячейке имеется полость прямоугольной формы с длинами сторон a и b. Размеры полости внутри ячейки определяют общую пористость материала или долю незаполненного в нем объема. Каждый конечный элемент имеет фиксированное значение пористости. Размеры полостей ai и b и ориентация ячеек Qi рассматриваются как переменные проектирования, где i - номер элемента. Изменение размеров полости и угла ее ориентации влечет за собой изменение свойств материала упругой среды, определяемых методом усреднения (homogenization method) [5, 6]. Свойства материала упругой среды в случае проектирования пространственной конструкции определяются пятью проектными переменными в каждом элементе [6, 7].

Рис. 1. Размеры и ориентация элементарной ячейки

В монографии [6] отмечается, что при проектировании тонкостенных конструкций топологическая оптимизация по методу усреднения обычно приводит к получению стержневых конструкций типа ферм Мичелла [9]. В то же время, например, большинство авиационных конструкций по своей природе являются тонкостенными упругими системами, состоящими из элементов, обладающих различными свойствами. Так, лонжероны, нервюры и шпангоуты обычно состоят из поясов, адекватно моделируемых стержневыми элементами, и

стенки, работающей в плоском (мембранном) напряженном состоянии. Обшивка часто подкрепляется стрингерным набором для увеличения критических усилий потери устойчивости. Следовательно, для эффективного проектирования силовых схем авиационных конструкций решения, получаемые на континуальной модели, должны обосновывать выбор не только стержневых, но и оболочечных элементов.

Для целей топологической оптимизации авиационных конструкций Комаровым В. А. [1] введен в рассмотрение изотропный материал с переменной плотностью р, модуль упругости и прочностные характеристики которого пропорциональны плотности

E = р E а = р а

(1) (2)

где У - допускаемое напряжение материала;

Е и У - модуль упругости и допускаемое напряжение при единичной плотности.

Допустимое геометрическое пространство конструкции разбивается сеткой трехмерных конечных элементов, моделирующих объемное напряженное состояние, и плотности материала в элементах принимаются за переменные проектирования. Особо отметим, что в каждом элементе упругой среды (1) - (2) используется только одна проектная переменная. Эта особенность, с одной стороны, позволяет строить более эффективные алгоритмы оптимизации распределения материала в континуальной модели по сравнению с подходом [5], с другой стороны, предъявляет повышенные требования к процедурам интерпретации получаемых результатов, в том числе к анализу силовой работы среды переменной плотности.

В работе [1] обоснован выбор приближенного алгоритма с использованием концепции полнонапряженности. В [8] этот подход обобщен на случай одновременного учета ограничений на эквивалентные напряжения, обобщенные перемещения и критические усилия потери устойчивости. Вариации проектных переменных в соответствии с алгоритмами [1, 8] вырождают элементы, передача усилий через которые нерациональна, и, наоборот, выделяют из конструкции элементы, обеспечивающие рациональные пути передачи сил. В результате определяется теоретически оптимальная конструкция (ТОК). В [1] разработана методика выбора рациональных силовых схем конструкций типа крыла с использованием картин потоков главных усилий (ЛГУ) главных

Известия Самарского научного центра Российской академии наук, т. 13, №1(3), 2011

касательных сил (ГКС) с учетом конструктивных и технологических требований.

Идеи, высказанные в [1], могут быть использованы и развиты для проектирования произвольных пространственных тонкостенных конструкций. Стратегия выбора рациональной силовой схемы конструкции на основе интерпретации силовой работы тела со свойствами материала (1) - (2) заключается в следующем:

1. Для удобства анализа силовой работы континуальная модель делится на ряд слоев объемных конечных элементов.

2. Первое приближение к выбору рациональной структуры синтезируемого объекта может дать информация о расположении в ТОК сгустков плотности и зон с «разреженной» плотностью (а, следовательно, и с незначительной жесткостью). Граница между вырожденными и невырожденными элементами определит контур силовой части проектируемой упругой системы. Если эта граница не является чётко выраженной, то далее целесообразно прорабатывать несколько вариантов структуры конструкции.

3. Принимая во внимание достаточно малые размеры конечных элементов континуальной модели, полагаем, что компоненты тензора напряжений внутри элементов изменяются незначительно. Поэтому для идентификации основных путей передачи усилий в ТОК анализируются значения напряжений и усилий в центре элементов.

4. Послойная визуализация распределения материала и ПГУ позволяет выявить зоны ТОК, в которых материал работает в существенно одноосном или двухосном напряженном состоянии [1]. В силовой схеме разрабатываемой конструкции в этих зонах целесообразно использовать, соответственно, стержни и оболочки.

5. Для уточнения формы и расположения оболочек можно использовать картины ГКС в различных проекциях ТОК.

6. Элементы, предназначенные для подкрепления оболочек, целесообразно располагать в соответствии с картинами ПГУ, стремясь к тому, чтобы направления стержней были близкими к направлению одного из главных усилий на соответствующем участке.

Рассмотрим особенности анализа ГКС в случае пространственных конструкций. В произвольном элементе серединного слоя ТОК вырежем кубический элемент с гранями единичной длины, параллельными координатным осям (рис. 2).

Со стороны рассматриваемого элемента на единичную площадку смежного элемента, нормальную оси x, действуют касательные силы Тху, и т^, равные касательным напряжениям. Заменим силы ТхУ и тХ2 равнодействующей тх. ГКС Тх можно изображать как векторы без стрелок в центре элементов на схеме соответствующего слоя модели в перпендикулярной оси x проекции. Траектории ГКС в ТОК позволяют выявить рациональные сечения предполагаемых оболочек. Аналогичные картины ГКС ту и т2 можно построить в проекциях, перпендикулярных осям у и г.

Рис. 2. Единичный кубический элемент континуальной модели произвольной пространственной конструкции

В качестве примера визуализации ГКС рассмотрим призматический стержень с квадратным поперечным сечением,

защемленный по одному торцу и нагруженный крутящим моментом по свободному торцу. Для стержня, заполненного материалом переменной плотности, по алгоритму [1] получена ТОК. На рис. 3 показано распределение материала и траектории ГКС в продольном и поперечном сечениях ТОК.

а)

—3

6 )

■ '

1 • -

1 i

)

1 - i

■

' 1

_ _

в)

V-

—]

—s

/ J

г)

Рис. 3. Распределение материала и траектории ГКС в продольном и поперечном сечениях ТОК

Выводы: картины распределения плотности, 111 У и ГКС в континуальной модели объекта, составленной из ряда слоев объемных конечных элементов, позволяют наглядно визуализировать и интерпретировать особенности силовой работы пространственных тонкостенных конструкций с учетом их геометрических форм и граничных условий.

СПИСОК ЛИТЕРАТУРЫ:

1. Комаров, В.А. Проектирование силовых схем авиационных конструкций / В.А. Комаров // Актуальные проблемы авиационной науки и техники -М.: Машиностроение, 1984. С. 114-129.

2. Topping, B.H. Shape Optimization of Skeletal Structures: A Review / B.H. Topping // J. Struct. Engr. 1983. V. 109, №8. P. 1933-1951.

3. Kohn, R.V. Optimal Design and Relaxation of Variational Problems / R.V. Kohn, G. Strang // Communic. Pure and Appl. Math. 1986. V. 39. P. 113-137 (part 1), P. 139-182 (part 2), P. 333-350 (part 3).

4. Комаров, А.А. Основы проектирования силовых конструкций. - Куйбышев: Куйбышевск. книж. изд-во, 1965. 82 с.

5. Bendsoe, M.P. Generating Optimal Topologies in Structural Design Using a Homogenization Method / M.P. Bendsoe, N. Kikuchi // Computer Methods in Applied Mechanics and Engineering. 1988. V. 7. P. 197-224.

6. Bendsoe, M.P. Optimization of Structural Topology, Shape, and Material. - Berlin: Springer, 1995. 271 p.

7. Eschenauer, H.A. Topology optimization of continuum structures: A review / H.A. Eschenauer, N. Ol-hoff // Appl. Mech. Rev. 2001. V. 54, № 4. P. 331389.

8. Болдырев, А.В. Развитие технологии проектирования авиационных конструкций на основе модели переменной плотности / А.В. Болдырев // Общероссийский научно-технический журнал "Полет". 2009. №11. С. 23-28.

9. Michell, A.G.M. The limits of economy of material in frame structures / A.G.M. Michell // Philos. Mag. Series. 1904. V.8, №47. P. 589-597.

TOPOLOGICAL OPTIMIZATION OF LOAD-BEARING CONSTRUCTIONS ON THE BASIS OF VARIABLE DENSITY MODEL

The review of constructions topological optimization methods on the basis of final elements special models is given. Strategy of choice the rational power scheme of spatial thin-walled constructions with the use of visually represented results of optimization by continuum model of variable density is offered.

Key words: continuum model, interpretation, streams of main forces, main tangential forces

Andrey Boldyrev, Candidate of Technical Sciences,

Associate Professor at the Construction and Design

of Aircrafts Department. E-mail: [email protected]

cyberleninka.ru

Как использовать топологическую оптимизацию при моделировании в области акустики

Сегодня Рене Кристенсен (René Christensen) из компании GN Hearing расскажет нам о важности топологической оптимизации для задач акустики и продемонстрирует ее использование с помощью COMSOL Multiphysics.

Топологическая оптимизация — мощный инструмент для поиска оптимальных решений инженерных проблем. В этой статье мы подробно изучим оптимизацию топологии применительно к акустике и ответим на вопрос, как найти оптимальное распределение акустической среды для получения желаемой характеристики или отклика. Возможности этого метода оптимизации будут продемонстрированы на нескольких примерах.

Целевые функции для топологической оптимизации

Многие инженерные задачи включают оптимизацию имеющейся конструкции или проектирование новой конструкции для конкретной прикладной задачи. При этом огромную важность имеет многолетний опыт работы в конкретной отрасли промышленности и знание практических приемов. Однако задачи оптимизации часто бывают настолько сложными, что не всегда можно понять, ведут ли поэтапные изменения конструкции к улучшению. В таких случаях прибегают к оптимизации в математическом смысле.

Прежде чем идти дальше, давайте вспомним некоторые важные термины. В любой задаче оптимизации — параметров, формы или, в нашем случае, топологии — всегда имеется по меньшей мере одна целевая функция. Как правило, нам требуется минимизировать эту функцию. В задачах акустики мы можем минимизировать давление звука в заданной области, а в задачах механики конструкций — напряжения в заданной части конструкции. Мы формулируем эту задачу как

\min_{\chi} F (\chi)

где F — целевая функция. В ходе оптимизации переменная проектирования \chi изменяется так, чтобы получить оптимальное решение. Переменная проектирования задана на области проектирования, которую обозначают Ωd и которая обычно занимает только часть конечно-элементного пространства Ω, как показано на рисунке ниже.

Область проектирования обычно является подмножеством всей области конечных элементов.

Поскольку переменная проектирования представляет собой функцию координат в дискретной области конечных элементов, используемой при проектировании, она фактически является вектором. В нашем случае, для простоты, мы будем говорить о ней как о переменной.

Если задаче оптимизации есть несколько целевых функций, то инженер самостоятельно должен решить, с какими весовыми коэффициентами учитываются эти целевые функции. Поскольку в ходе оптимизации различные цели могут препятствовать друг другу, необходимо обратить особое внимание на постановку задачи.

Кроме целевой функции (функций) обычно в задаче оптимизации есть некоторые ограничения. Они характеризуют предельные значения габаритов и (или) массы, применимые для рассматриваемой задачи. В интерфейсе Optimization (Оптимизация) программного пакета COMSOL Multiphysics можно систематическим образом задавать переменные проектирования, одну или несколько целевых функций и ограничения.

Пример статической задачи механики конструкций

В процессе топологической оптимизации на каждой итерации изменяются значения переменной проектирования, заданной на области проектирования. Переменная проектирования непрерывна во всей области и принимает значения от 0 до 1:

0 < \chi \leq 1\forall (x,y) \in \Omega_d

Мы бы хотели добиться того, чтобы значения переменной проектирования оказались близки к 0 или 1. Тогда мы получим близкую к дискретной конструкцию, область проектирования которой будет охвачена двумя дискретными (бинарными) состояниями. Что это за состояния, зависит от физического смысла нашей задачи оптимизации. Поскольку в литературе топологическая оптимизация широко применяется в задачах механики конструкций, мы сначала изучим её применительно к данной области физики, а в следующем разделе рассмотрим её аналог из акустики.

Мы уже обсуждали оптимизацию топологии для задач механики конструкций с помощью COMSOL Multiphysics в блоге COMSOL. Кратко изложим содержание той статьи. В ней изучалась так называемая MBB-балка (Messerschmitt-Bölkow-Blohm) с целью максимизировать жесткость, минимизируя полную энергию деформации при заданной нагрузке и заданных граничных условиях. Область проектирования занимала всю область конечных элементов. К полной массе конструкции применялось ограничение. В области проектирования модуль Юнга задавался переменной проектирования \chi как

E(\chi) = \left\{ \begin{array}{ll}E_0\ \textrm{for}\ \chi=1\\ \textrm{for}\ \chi=0 \end{array} \right..

Чтобы перейти к бинарному значению переменной проектирования, мы использовали так называемую интерполяцию твердого изотропного материала со штрафом (SINP),

E (\chi) = \chi^p E_0,

где p– множитель штрафа, обычно принимающий значения от 3 до 5. Используя эту интерполяцию и неявную линейную интерполяцию плотности материала, решатель избегал промежуточных значений \chi, так как они давали менее выгодные соотношения жесткости и веса. На рисунке ниже показана полученная топология MBB-балки, полученная в предыдущей статье.

Оптимизированная топология MBB-балки.

На этом рисунке черным отмечен материал с заданным пользователем модулем Юнга E0. Белый цвет соответствует нулевой жесткости, указывая на области, остающиеся пустыми.

Проведение топологической оптимизации в акустических задачах с помощью COMSOL Multiphysics®

Теперь рассмотрим топологическую оптимизацию в акустике. В задачах акустики мы сталкиваемся с зависящими от частоты решениями, которые описывают распространение волн в акустических средах. Переменная проектирования теперь связана с физикой звуковых волн. Вместо бинарного распределения «пустота — материал» мы хотим получить бинарное распределение «воздух — твердое тело», где под "твердым телом" подразумевается текучая среда с высокой плотностью и высоким модулем объемной деформации.

Мы зададим четыре параметра, которые описывают свойства обычной и «твердой» среды в состоянии покоя и при сжатии: Воздуху припишем плотность \rho_1 и модуль объемной деформации K1, а «твердой» среде — более высокую плотность \rho_2 и более высокий модуль объемной деформации K2. Изменяя переменную проектирования, мы меняем плотность \rho и модуль объемной деформации K в области проектирования так же, как мы меняли модуль Юнга в примере, относящемся к механике конструкций. Однако при этом требуется другая интерполяция, чтобы значения материальных свойств не обращались в ноль при нулевом значении переменной проектирования, а принимали значения, характерные для воздуха и твердого тела:

\rho(\chi) = \left\{ \begin{array}{ll}\rho_2\ \textrm{for}\ \chi=1 \\ \rho_1\ \textrm{for} \ \chi=0 \end{array} \right.

K(\chi) = \left\{ \begin{array}{ll}K_2\ \textrm{for}\ \chi=1\\K_1\ \textrm{for}\ \chi=0 \end{array} \right.

Самый простой вариант — линейная интерполяция, задаваемая двумя крайними значениями. Это не лучший подход, поскольку он не предусматривает штрафа за промежуточные значения \chi, и оптимальная конструкция может оказаться не бинарной. Следовательно, такая конструкция будет физически неосуществима. В литературе также известны другие схемы интерполяции. В описываемых в данном блоге случаях будет использоваться так называемое рациональное приближение материальных свойств (RAMP), см. [1].

Как и в случае оптимизации для механики конструкций, мы задаем область проектирования, в которой ищем распределение материала, отвечающее ограничениям. Ограничения на площадь или объем можно задать через переменные проектирования. Например, ограничение на площадь в области проектирования можно задать в виде неравенства

\int^{}_{\Omega_d} \chi d \Omega_d \leq S_r,

где Sr — отношение площади области, которой приписаны свойства твердого тела, к площади всей области проектирования.

Пример: одна целевая функция, одна частота

Рассмотрим пример глушителя (звукопоглощающего устройства). Для простоты ограничимся двухмерной областью. Обычная характеристика глушителя — так называемый коэффициент затухания (снижения шума) TL, который задается отношением входной мощности к выходной мощности:

TL = 10 \log_{10} \left(\frac{W_i}{W_o} \right).

Коэффициент снижения шума вычисляется по так называемой трехточечной схеме, предложенной в [2]. Его мы и выберем в качестве целевой функции, стремясь максимизировать этот коэффициент для одной частоты (в данном случае 420 Гц):

\max_{\chi} TL (420 \text {Hz}).

Определены две области проектирования: над трубчатой секцией и под ней. Область проектирования ограничена следующим образом: не более 5% площади области должно быть заполнено твердым телом, то есть 95% должно быть заполнено воздухом:

\int^{}_{\Omega_d} \chi d \Omega_d \leq 0.05.

Начальное состояние области проектирования — полностью заполненная воздухом область, в которой \chi = 0. На анимации ниже показан переход от начального состояния к итоговой топологии.

Анимация, показывающая переход от начального состояния к оптимизированной топологии глушителя.

Оптимизированная конструкция глушителя имеет топологию «камеры двойного расширения», см. [3]. Коэффициент снижения шума на целевой частоте вырос примерно на 14 дБ, как показано на графике ниже. Однако на частотах, отличных от целевой, коэффициент снижения шума также изменился, что может оказаться важным в конкретной прикладной задаче. Поэтому оптимизации на одной частоте, как правило, может оказаться недостаточно.

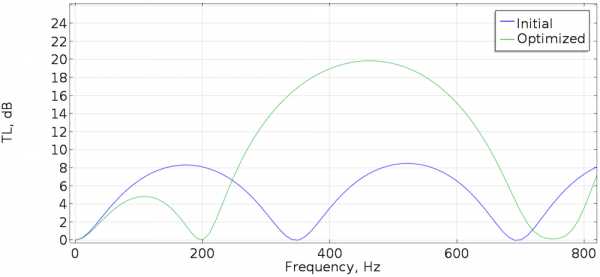Коэффициент снижения шума для начального состояния и оптимизированной конструкции глушителя.

Пример: две целевые функции, две частоты

Давайте перейдем к задаче оптимизации двух целевых функций для двух разных частот. Снова рассмотрим двухмерную комнату с тремя жесткими стенами и заданным давлением, приложенным к левой стене комнаты. В комнате также выделены две целевые области Ω1 и Ω2 в правом верхнем и правом нижнем углу комнаты. Две цели формулируются следующим образом:

Минимизировать уровень звукового давления на частоте f1 и
Минимизировать уровень звукового давления на частоте f2 = 1,5 f1

при заданной круглой области проектирования Ωd и ограничении площади занимаемой "твердым телом", которая не должна превышать 10%. Начальное состояние — \chi = 0, то есть вся область проектирования заполнена воздухом.

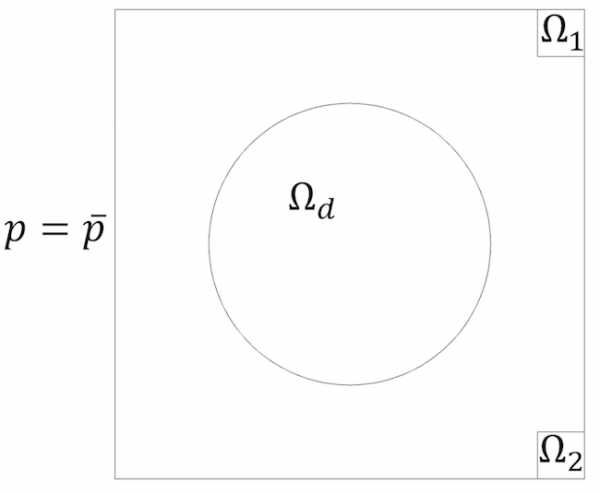Квадратная двухмерная комната с круглой областью проектирования и двумя целевыми областями.

Мы должны решить, с какими весовыми коэффициентами мы учитываем две наши целевые функции или какую важность мы им придаем. В нашем случае обе функции одинаково важны, поэтому задача формулируется как задача минимакса:

\begin{align} \min_{\chi} \max_{f_1 f_2} SPL_i (\chi, f_i) \\ \text {subject to} \int^{}_{\Omega_d} \chi d\Omega_d \leq 0.1. \end{align}

На рисунках ниже синим цветом показана оптимизированная топология и давление звука на обеих частотах в одном масштабе. Обратите внимание, как оптимизация топологии приводит к появлению области низкого давления в правом верхнем углу на первой частоте. В то же время эта же самая топология обеспечивает появление зоны низкого давления в правом нижнем углу на второй частоте. Такого результата было бы сложно добиться методом проб и ошибок.

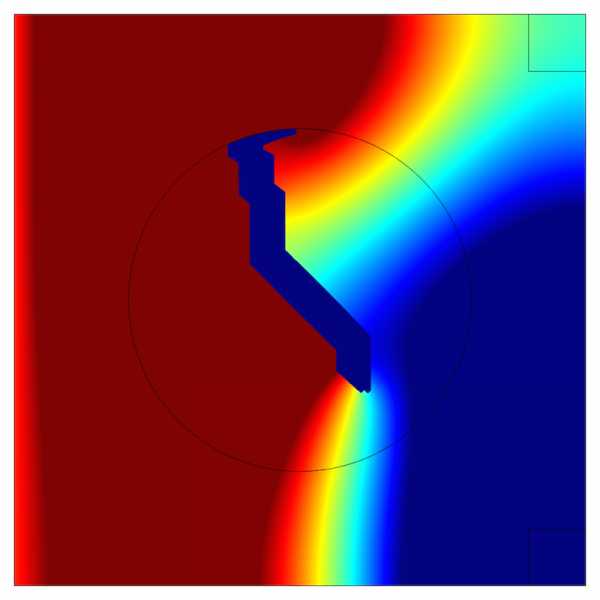
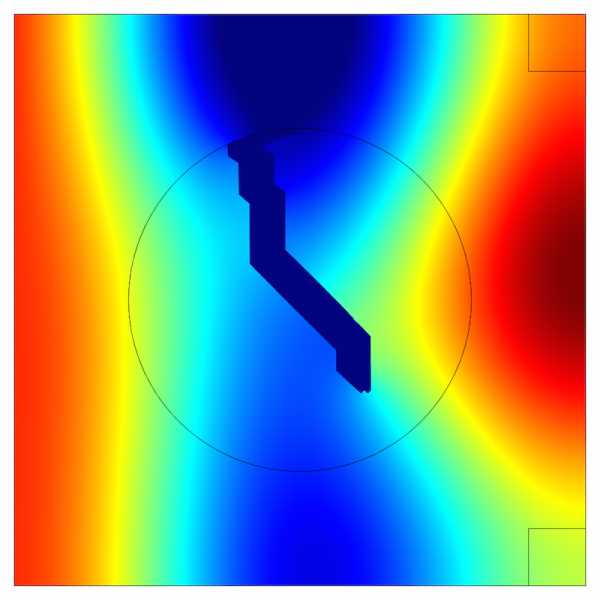
Давление звука на частоте f1(слева) и на частоте f2(справа). Оптимизированная топология показана синим цветом.

Пример: одна целевая функция, несколько частот

В качестве третьего и последнего примера мы оптимизируем одну целевую функцию для диапазона частот. Источник звука излучает звуковые волны в двухмерную область, в которой изначально существует цилиндрическое звуковое поле. В задаче присутствуют две квадратные области проектирования, но мы воспользуемся симметрией задачи и смоделируем лишь половину геометрии. В этом случае нам нужно, чтобы величина звукового давления \overline{p}_{obj} в точке на расстоянии 0,4 м перед источником звука по центральной оси симметрии была постоянной. Оптимизация выполняется в диапазоне частот от 4000 до 4200 Гц (на пяти частотах с шагом 50 Гц). Для этого мы можем использовать функционал Global Least-Squares Objective (Глобальная целевая функция метода наименьших квадратов) в COMSOL Multiphysics со следующей постановкой задачи:

\begin{align} \min_{\chi} \sum_{i=1}^{5} (\mid p_i (\chi, f_i, 0, 0.4) \mid -\overline{p}_{obj})^2 \\ \text {subject to} \int^{}_{\Omega_d} \chi d\Omega_d \leq 0.1. \end{align}

Начальное состояние по-прежнему \chi = 0. Оптимизированная топология и звуковое поле для начального и оптимизированного состояния показаны на рисунке ниже.

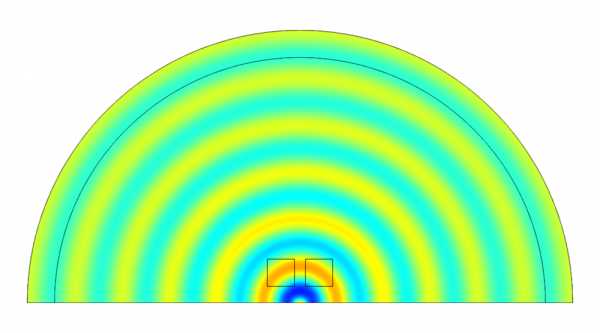
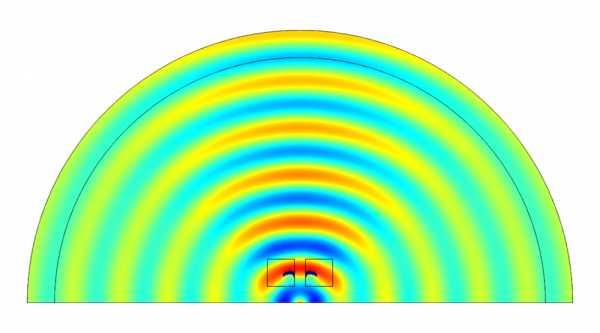
Давление звука в начальном состоянии (слева) и оптимизированном состоянии (справа) на частоте 4 кГц. Оптимальная топология показана синим цветом внутри квадратных областей проектирования.

Так как величина давления звука в точке наблюдения в начальном состоянии ниже целевого давления, оптимизация топологии ведет к появлению отражателя, фокусирующего звук на центральной оси. Величины давления звука до и после оптимизации показаны на графике ниже. После оптимизации величина давления оказалась близка к требуемому целевому значению во всем диапазоне частот.

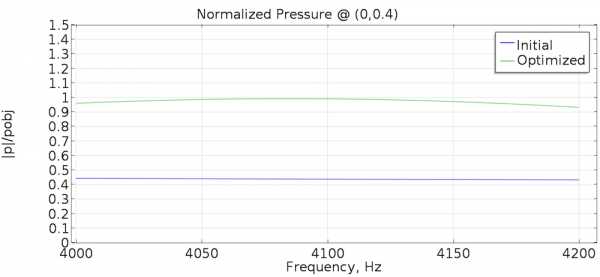Отношение величины давления к \overline{p}_{obj} для начальной и оптимизированной топологии.

Возможности топологической оптимизации для задач акустики

Топологическая оптимизация — весьма перспективный метод создания новых конструкций для инженеров, занимающихся прикладной акустикой. Как было показано в этой статье, этот метод можно успешно применять в COMSOL Multiphysics. Корректно определяя целевые функции и ограничения, можно решать прикладные задачи с помощью новых и необычных топологий, которые сложно было бы обнаружить традиционными методами.

Я хотел бы особо поблагодарить доцента Датского технического университета Нильса Оге (Niels Aage) за плодотворное обсуждение методов оптимизации.

Чтобы узнать больше об оптимизации топологии для задач акустики в COMSOL Multiphysics, вы можете загрузить следующий пример из Галереи приложений: Topology Optimization of Acoustic Modes in a 2D Room (Топологическая оптимизация при распространении акустических мод в двухмерной комнате).

Литература

M.P. Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer 2003.
T.W. Wu, G.C. Wan "Muffler Performance studies and using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss", Trans. ASME: J. Vib. Acoust. 118 (1996) 479-484.
Z. Tao, A.F. Seybert, "A review of current techniques for measuring muffler transmission loss", SAE International, 2003.

О приглашенном авторе

Рене Кристенсен занимается задачами виброакустики больше десяти лет как консультант (компания iCapture ApS) и как инженер-проектировщик слуховых аппаратов (компании Oticon A/S и GN Hearing A/S). Сферой его специализации является моделирование термовязких эффектов в микроакустике, и его докторская диссертация была посвящена этой теме. Рене работает старшим инженером-акустиком в исследовательской группе по технологической акустике компании GN Hearing с 2015 года, занимаясь проектированием и оптимизацией конструкций слуховых аппаратов.

www.comsol.ru

Технологии аддитивного производства и топологической оптимизации

Аддитивное производство (АП), топологическая оптимизация и трехмерная печать оказали заметное влияние на промышленное производство. В отличие от традиционных технологий производства, они позволяют изготавливать детали со сложной геометрией.

Аддитивные технологии предусматривают ряд дополнительных этапов, значительно усложняющих процесс разработки продукции. После создания проекта идеальной детали необходимо выбрать способ ее изготовления с учетом ориентации и конструкции опор. Это далеко не единственный фактор, определяющий возможность печати отдельных компонентов и скорость построения детали. Процесс печати имеет еще больше нюансов: возможно возникновение остаточных напряжений и несоответствие полученной формы заданным критериям. Проектирование с учетом всех факторов позволит в полной мере раскрыть потенциал аддитивного производства.

Процесс проектирования деталей, изготовленных методами аддитивного производства, выходит на новый уровень благодаря таким подходам, как топологическая оптимизация, которая играет важную роль в создании облегченных конструкций и эффективном использовании материала. Оптимизация конструкции также способствует более равномерному распределению напряжений.

Топологическая оптимизация

Без топологической оптимизации вес каждой детали в сборке будет выше, чем он мог бы быть. Лишний вес – это нерациональное использование материала, увеличение нагрузки на подвижные детали, снижение эффективности потребления электроэнергии и повышение расходов на транспортировку. Теперь благодаря топологической оптимизации с использованием таких инструментов как ANSYS Mechanical можно создавать прочные, но облегченные конструкции для разных областей применения. Этот подход обеспечивает простую постановку задач, а также позволяет контролировать соблюдение технологических требований, задавать минимальную толщину материала и удалять участки геометрии.

Традиционные методы проектирования не используют преимущества таких новых технологий, как аддитивное производство, а ведь они позволяют снять конструктивные ограничения и открывают новые возможности. Как правило, оптимальная конструкция детали предусматривает сложную, «органическую» геометрию, для создания которой требуется альтернативный подход. С помощью инструментов топологической оптимизации можно задавать расположение опор и распределение нагрузок по материалу для обеспечения оптимальной формы детали. Данный алгоритм также позволяет уменьшать вес конструкции, импортировать CAD-геометрию и выполнять поверочные расчеты оптимизированной конструкции. Повышается точность пространственного моделирования деталей из композиционных материалов, деталей, напечатанных на 3D-принтере, а также костей и тканей.

Сложности аддитивного производства

Аддитивное производство – довольно молодая технология, возможность широкого применения которой определяет ряд факторов:

Объем печати (габариты, доступные для изготовления детали). Маленькая деталь сложной формы представляет интерес – крупногабаритная деталь сложной формы приносит прибыль.
Скорость печати. Даже если установить 100 новейших DMLS-принтеров (использующих технологию прямого лазерного спекания металлов) и печатать один вид детали в режиме 24/7, производство все равно будет отставать от спроса.
Сбои печати. Они возникают из-за температурных деформаций, неправильной калибровки станка, неисправности механизма распыления порошков и других факторов.
Надежность материалов. Как убедиться в том, что все части детали, изготовленной с помощью аддитивных технологий, обладают одинаковыми механическими свойствами?

Аддитивное производство и объем печати

Использование аддитивных технологий главным образом связано с изготовлением деталей небольшого размера, но с невероятно высоким разрешением и детализацией, которую не обеспечит никакой другой способ производства, будь то литье или обработка деталей. Системы управления и обработки материалов постоянно увеличиваются в габаритах без потери точности, свойственной аддитивному производству. Например, принтеры ExOne печатают не сами детали, а формы для традиционного литья размером с грузовую платформу пикапа. DMLS-принтеры, которые нашли широкое применение в аэрокосмической отрасли, также увеличиваются в габаритах. Это позволяет выполнять синхронную печать нескольких вариантов одной детали без потери точности, а значит, без ущерба для качества поверхности, свойств материала и т.д. Очевидно, что проблема масштабирования находит весьма эффективное инженерное решение.

Аддитивное производство и скорость печати

Прецизионные детали (особенно из металла), создаваемые на современных 3D-принтерах – настоящие шедевры, которые можно подержать в руках, покрутить, установить в автомобиле. Но на сам процесс печати может уйти до восьми часов. Скорость печати зависит от двух главных факторов: толщины слоя и скорости передвижения лазерного луча. Высокотехнологичные компании используют разные подходы к решению этого вопроса. Так, эффективный способ увеличения производительности – использование в принтере нескольких лазеров с разными механизмами управления. По мере увеличения темпов аддитивного производства растет и количество напечатанных деталей, которые используются наравне с заводскими.

Аддитивное производство и сбои печати

Рассмотрим процесс АП с точки зрения физики и материаловедения. Слой металлического порошка поэтапно нагревается и охлаждается. После распыления нового слоя предыдущий подвергается повторному нагреву, в результате чего происходит сплавление двух слоев в единое целое. К моменту окончания печати каждый слой подвергается многократному циклическому изменению температуры, приводящему к возникновению в детали остаточных деформаций. Неравномерное распределение порошка, а также циклическое тепловое расширение и сжатие может спровоцировать образование небольшого дефекта микроструктуры. На уровне макроструктуры возможно появление дополнительных деформаций, обусловленных сложной формой детали или конструкцией опор. Эти и многие другие сценарии могут стать причиной сбоев печати: деформации и, как следствие, выхода детали за пределы допусков, растрескивания или разлома детали либо серьезного повреждения дорогостоящего 3D-принтера.

Компьютерное моделирование

Компьютерное моделирование позволяет прогнозировать исход 3D-печати и рассчитывать выходные параметры готовой детали, тем самым предупреждая возникновение подобных проблем. Последующее изменение трехмерной конструкции с учетом обнаруженных недостатков обеспечит успешное построение безупречной детали.

В конце 2017 г. ведущие компании ANSYS и 3DSIM объединили свои усилия в разработке уникального комплексного решения для моделирования процессов аддитивного производства. Мощные инструменты exaSIM и FLEX от 3DSIM и рабочая среда ANSYS Workbench в сочетании с полной линейкой решателей ANSYS открывают инженерам, проектировщикам и операторам беспрецедентные возможности для моделирования всех этапов аддитивного производства – от проектирования до 3D-печати.

ANSYS exaSIM (разработка компании 3DSIM) позволяет операторам и проектировщикам деталей для аддитивного производства обнаруживать и устранять остаточные напряжения и деформации и, как следствие, не допускать выхода за пределы допусков и предотвращать сбои печати без проведения натурного эксперимента.

С помощью ANSYS FLEX (другого продукта 3DSIM) операторы могут рассчитывать оптимальные рабочие характеристики принтера и параметры подачи материала, а также предсказывать поведение материала во время печати и оптимизировать его свойства на уровне микро- и макроструктуры.

Более того, решатели ANSYS для параллельного выполнения прочностных, гидродинамических и тепловых многодисциплинарных расчетов в единой рабочей среде Workbench помогают предотвратить любой сбой в процессе аддитивного производства.

Новые решения ANSYS для моделирования процессов аддитивного производства применение у следующих специалистов:

Операторы, которым для успешной 3D-печати необходим инструмент настройки рабочих параметров принтера, опор и ориентации детали.
Проектировщики и инженеры, которые проверяет возможность изготовления детали на конкретном принтере и из конкретного материала.
Технологи, которые с помощью предварительного компьютерного моделирования проверяют проектные решения и определяют условия успешного аддитивного производства.
Ученые и инженеры-исследователи, которые занимаются оценкой, описанием и оптимизацией свойств материала на уровне микроструктуры.
Разработчики оборудования для аддитивного производства и поставщики аддитивных технологий.

multiphysics.ru

Конечно-элементное решение задач топологической оптимизации (2007 г.) - FEA.RU | CompMechLab

На сегодняшний день применение всего инструментария конечно-элементной (КЭ) оптимизации конструкций позволяет существенно упростить конструкторскую работу. Целью данной работы является исследование возможностей КЭ оптимизации топологии и формы деталей, а также изучение вопросов оптимизации тонкостенных конструкций с целью снижения массы и улучшения жесткостных характеристик. Как основной инструмент топологической оптимизации используется программная система FE-DESIGN Tosca. Исследования проведены в рамках тестовой академической лицензии, предоставленной компанией Mechanical Engineering Service.

В программной системе Tosca в качестве алгоритма топологической оптимизации получил применение метод критерия оптимальности (Optimality Criterion, OC), а также контроллерный алгоритм оптимизации Tosca (Tosca controller-based algorithm). Разработчиками заявлена, а в данной работе продемонстрирована возможность использования адаптивного перестроения сетки, создания групп симметрии, предопределения псевдоплотности выбранной области, контроль членов и толщины получаемой конструкции, управление радиусом фильтрации, учет возможности изготовления конструкции.

Для иллюстрации работы алгоритмов выбрана тестовая задача топологической оптимизации консольной балки. На изображениях ниже можно видеть постановку задачи и ход оптимизации.


Рис. 1. Постановка задачи	Рис. 2. Процесс топологической оптимизации

Для этой же модели проведено исследование работы групп симметрии. Их использование при решении сложных промышленных задач с большим числом степеней свободы может помочь сократить объем вычислений.


Рис. 3. Циклическая симметрия	Рис. 4. Симметрия относительно линии

Рис. 5. Симметрия относительно точки	Рис. 6. Симметрия вращения

На примере задачи о пластине с U-образным вырезом рассмотрена работа контроля размера членов.


Рис. 7. Постановка задачи	Рис. 8. Без контроля размера членов

Рис. 9. Минимальный размер членов	Рис. 10. Максимальный размер членов

Как пример MIN-MAX задачи рассмотрена оптимизация искривленной плоскости с тремя условиями нагружения:


Рис. 11.	Рис. 12. Ход топологической оптимизации

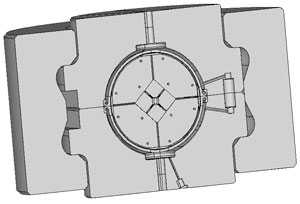
В качестве реальной промышленной задачи большой размерности рассмотрена задача топологической оптимизации затвора установки высокого давления «Кристалл», применяемой для изготовления искусственных алмазов.


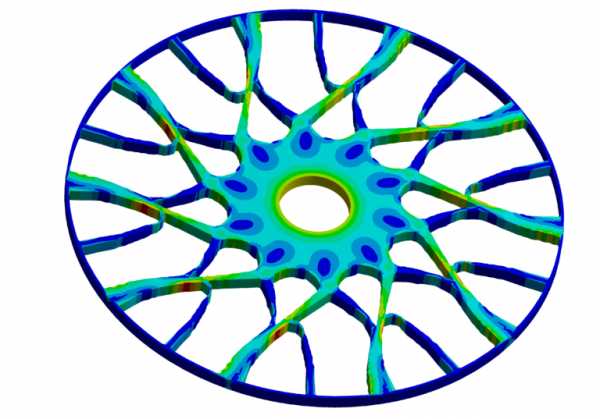
Рис. 13. Вид установки «Кристалл» в сборе	Рис. 14. Итог оптимизации затвора (с учетом симметрии)

При проведении исследований для получения итогового результата оптимизации использовались возможности модуля Tosca.Smooth, позволяющей выполнять обработку и сглаживание результатов оптимизации формы и экспорта результата в CAD-форматах.

Рис. 15. Топологическая оптимизация затвора сосуда высокого давления

Таким образом, на примере тестовых задач, показано, каким образом топологическая оптимизация позволяет снижать массу конструкций. В процесс оптимизации легко могут быть добавлены условия на симметрию, контроль возможности изготовления путем литья или фрезеровки независимо от количества условий нагружения.

fea.ru

Обзор софта для топологической оптимизации и бионического дизайна / Блог компании Top 3D Shop / Хабр

Биодизайн, или бионический метод проектирования предполагает использование в разрабатываемых конструкциях эффективных решений позаимствованных в природе. В целом, это плавные линии, распределенная структура тонких сплошных или трубчатых конструкций. Биодизайн — частный случай топологической оптимизации, средства достижения оптимального сочетания механической прочности и легкости, путем хорошо просчитанного распределения материала в детали, как правило — с усложнением ее структуры.

В этой статье мы рассматриваем ПО, которое способно справиться с этими задачами.

Как это работает

Современные средства проектирования позволяют не только прогнозировать степень деформации детали, но и оптимизировать ее, в соответствии с заданными рамками массы и прочности. В общем случае, подготавливается модель-заготовка, из которой в дальнейшем удаляется лишний материал. Этот процесс носит название топологической оптимизации. Еще один термин, часто употребляемый в данном контексте — “генеративный дизайн”, он обозначает проектирование, частично выполняемое программными алгоритмами. Результатом топологической оптимизации является сложная структура, на основе которой формируется модель детали для производства. Такая деталь обладает требуемой прочностью при минимальной массе, но сложна в изготовлении традиционными способами, оптимальным будет аддитивное производство.

Примеры реализации

Изделия, выполненные с помощью генеративного дизайна, имеют непривычный футуристический вид и часто служат для демонстрации возможностей аддитивных технологий.

BMW S1000RR

Вот, например, BMW, для демонстрации перспектив технологии, сделала концепт-байк на основе S1000RR, но с легкой 3D-печатной металлической рамой. Если говорить о более утилитарных применениях — BMW уже использует 3D-печать в производстве “Роллс-Ройсов” и родстеров i8.

Мост MX3D

Голландцы из MX3D закончили производство несущей основы моста, который планируется установить в Амстердаме в 2019 году. При изготовлении моста использовалось ПО Autodesk и технология WAAM — наплавление металлического прутка промышленным роботом-манипулятором.

Российская промышленность

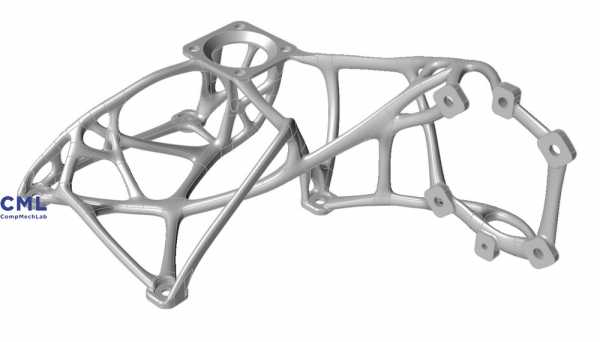
Мосты мы пока не печатаем, но в утилитарных областях топологическая оптимизация успешно применятся. Например, работает в этом направлении «Центр компьютерного инжиниринга» СПбПУ, используя ПО собственной разработки. Подробнее о решаемых задачах можно прочитать на сайте центра, здесь отметим, что речь идет в основном об аэрокосмической отрасли.

Программное обеспечение — комплексные системы

На рынке присутствует значительное количество программных продуктов, посредством которых можно производить расчеты по топологической оптимизации. Как правило, эту функциональность предоставляют пакеты, производящие моделирование деформаций и прочностные расчеты. Начнем с “больших” комплексов, применяемых для проектирования и расчетов в машиностроении.

Siemens NX

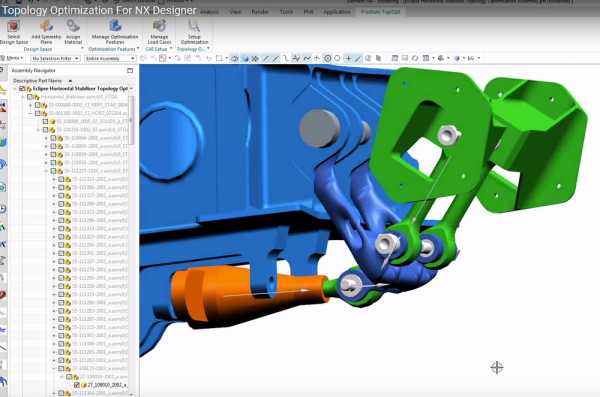
NX — универсальная комплексная система для проектирования, инженерных расчетов и подготовки управляющего кода для станков с ЧПУ — CAD, CAE и CAM. Топологическая оптимизация в рамках модуля NX CAE ориентирована на взаимодействие деталей в CAD-сборке.

В рабочее пространство помещается деталь подлежащая оптимизации, к ней присоединяются другие, которые не будут затронуты процессом, но участвуют во взаимодействии. Указание креплений и приложенных нагрузок производится именно в рамках сборки.

Siemens Solid Edge

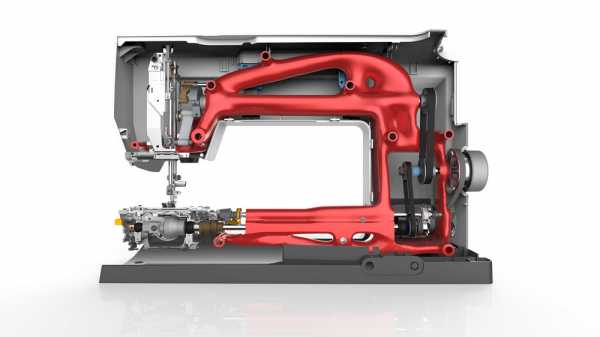
Solid Edge — CAD-система твердотельного и поверхностного моделирования, прежде всего предназначенная для работы с деталями и сборками, но обладающая встроенным модулем инженерного анализа. Разработчик позиционирует Solid Edge как средство быстрого проектирования и прототипирования, «заточенное» под аддитивное производство.

Оптимизация производится в несколько шагов, без необходимости тонких настроек: загрузить «болванку», указать отверстия и места приложения нагрузки, задать требуемую долю снижения массы и запас прочности. Полученная деталь может быть напрямую отправлена в печать или доработана штатными средствами Solid Edge.

CATIA 3DEXPERIENCE

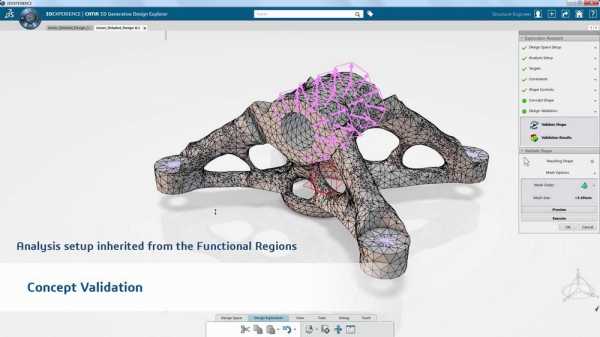
Платформа 3DEXPERIENCE, по состоянию на начало 2018 года, состоит из 104 модулей, которые называются ролями. Это решения для различных задач проектирования, управления процессом разработки, симуляции, визуализации. Одна из этих ролей — Function Driven Generative Designer.

Эта роль не только позволяет произвести оптимизацию топологии детали в соответствии с указанными требованиями, но и доработать полученный объект — упростить, убрать неровности.

SOLIDWORKS

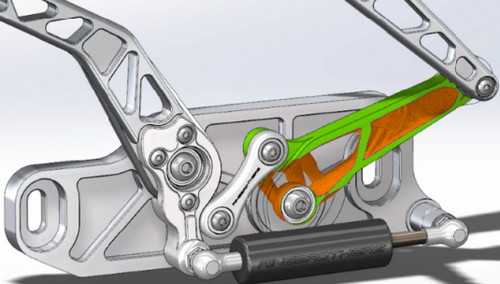
Оптимизация топологии была добавлена в SOLIDWORKS 2018. Она доступна в модуле SOLIDWORKS Simulation редакций Professional и Premium. Инженер указывает нагрузки, условия оптимизации — например, наилучшее отношение жесткости к массе, и запускает исследование топологии. По завершении процесса, для подготовки к производству, выполняется сглаживание сетки оптимизированной детали.

Autodesk Fusion 360

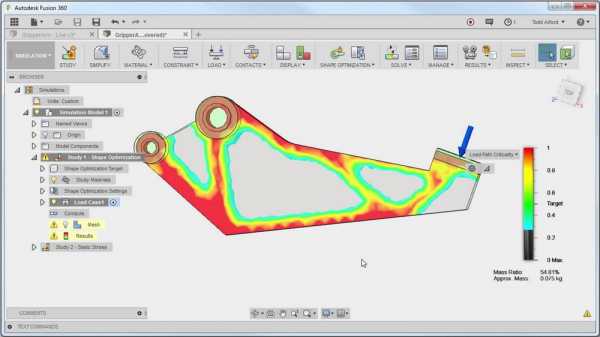
Облачная платформа для проектирования, инженерных расчетов и подготовки к производству на станках с ЧПУ — CAD/CAE/CAM. В максимальной подписке, которая называется Ultimate, доступен модуль Advanced Simulation. Он отвечает за моделирование деформаций, работу с анизотропными материалами и оптимизацию топологии — Shape optimization.

Возможности для настройки оптимизации не очень широки, но для основной задачи — создания детали с минимальной массой и необходимой прочностью — достаточны.

ANSYS Mechanical

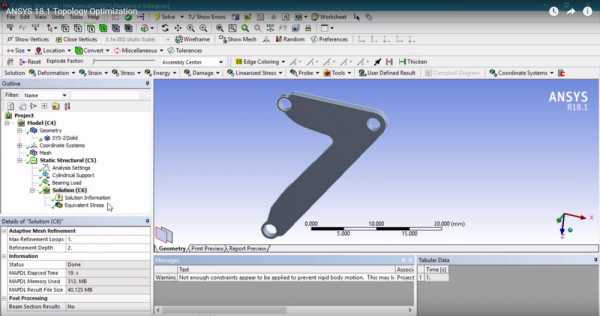
Основные функции этого программного продукта:

— статические расчеты; — динамический анализ; — тепловые расчеты; — акустические расчеты.

ANSYS Mechanical позволяет моделировать деформацию конструкций под нагрузкой, рассчитывать влияние вибраций и возникновение резонансов. Для проведения автоматизированной топологической оптимизации необходимо импортировать модель-заготовку детали, указать точки крепления и приложения нагрузок, задать граничные условия, такие как минимальная толщина. Возможно моделирование как традиционных материалов, так и анизотропных — композиты, 3D-печатные детали.

Более простое и доступное программное обеспечение

Перейдем от «тяжелого» промышленного ПО к решениям, отличающимся меньшей функциональностью, более низким порогом вхождения и сравнительно доступной стоимостью.

solidThinking Inspire

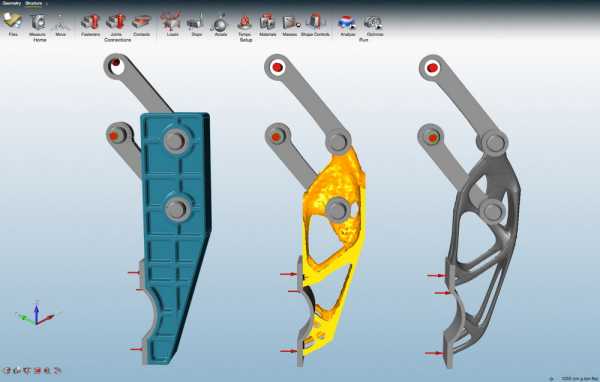
В сравнении, например, с Ansys Mechanical — это более дружелюбное ПО, рассчитанное на решение нескольких узких задач — моделирования взаимодействия деталей в сборках, простого эскизного проектирования, топологической оптимизации. Объекты, с которыми необходимо работать, могут быть как созданы в Inspire, так и импортированы из других CAD-систем.

После «отрезания лишнего» оптимизированная деталь упрощается и сглаживается, что значительно улучшает внешний вид и позволяет сразу отправить ее в производство.

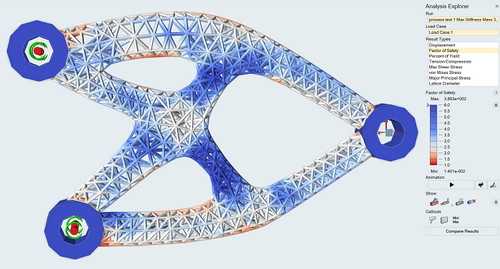
Помимо топологической оптимизации, Inspire способна формировать сетчатое заполнение вместо сплошного, эта функция пригодится при необходимости еще больше снизить массу детали.

Autodesk Netfabb Ultimate

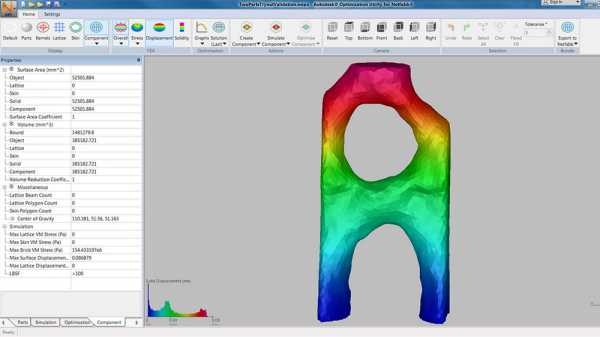
Эта программа известна многим пользователям 3D-принтеров, как удобное средство «ремонта» сетки и разделения модели на части. Функциональность Netfabb 2018 значительно шире — там, например, есть создание ветвистых поддерживающих структур для FDM-печати, моделирование деформации металлических деталей для SLS и SLM, а в редакции Ultimate добавлены топологическая оптимизация и генерация сетчатого заполнения.

Для чего и для кого

Сейчас средства топологической оптимизации, в основном — компоненты больших CAD/CAM/CAE пакетов разработки Siemens, Dassault Systèmes, Autodesk. И применяется эта технология, если не говорить о чисто демонстрационных целях, в основном при 3D-печати металлическими сплавами. Генеративный дизайн, в сочетании с прочностным анализом, решает задачу уменьшения массы изделия при сохранении прочности, что актуально не только в аэрокосмической отрасли. В любом производстве экономия материала приведет к меньшим затратам, особенно когда речь идет о дорогостоящих металлических порошках.

Назвать простыми для освоения и финансово доступными большинство описанных программных продуктов сложно. Но есть и более простые решения, например — solidThinking Inspire. Можно предположить, что, со снижением стоимости оборудования и расходных материалов для печати металлами и инженерными пластиками, сравнительно несложные средства топологической оптимизации получат более широкое распространение.

Чтобы получить консультацию по выбору софта и приобрести ПО для CAD/CAM/CAE, обращайтесь в Top 3D Shop. Мы поможем с выбором программных продуктов и оборудования для решения любых задач прототипирования и производства.

Хотите больше интересных новостей из мира 3D-технологий?

Подписывайтесь на нас в соц. сетях:

habr.com

АЛГОРИТМ ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ МЕМБРАННЫХ КОНСТРУКЦИЙ | Опубликовать статью РИНЦ

Морозова Н.Е.1, Аль-Згуль С.Х.2

1 ORCID: 0000-0002-3063-7550, Кандидат технических наук,

Южный федеральный университет

2ORCID: 0000-0001-6182-786X, Студент 4-го курса

МГТУ им. Н.Э.Баумана,

АЛГОРИТМ ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ МЕМБРАННЫХ КОНСТРУКЦИЙ

Аннотация

В статье изложен алгоритм оптимизации топологии мембранных конструкций. Использован метод последовательных нагружений в сочетании с методом конечных элементов. В качестве стандартного выбран треугольный конечный элемент с девятью степенями свободы. Рассмотрен алгоритм реализации МКЭ с использованием вариационного уравнения Лагранжа в итерационном методе адаптивной эволюции, позволяющий оптимизировать топологию мембраны. В качестве варьируемого параметра топологии мембраны рассмотрена ее толщина.

Ключевые слова: мембрана, абсолютно гибкая пластина, самоорганизация, адаптивная эволюция, метод конечных элементов, топологическая оптимизация.

Morozova N. E.1, Al-Zgul S.H. 2

1 ORCID: 0000-0002-3063-7550, PhD in Engineering,

Southern Federal University

2ORCID: 0000-0001-6182-786X, Student of the 4th course

Bauman Moscow State technical university,

TOPOLOGICAL OPTIMIZATION ALGORITHM OF MEMBRANE SRUCTURES

Abstract

The article describes an algorithm for optimizing the topology of membrane structures. The method of successive loading in combination with the finite element method was used in the research. We have chosen a triangular finite element with nine degrees of freedom as a standard. The paper considers an algorithm for the implementation of the finite element method in combination with Euler–Lagrange equation in the iterative method of adaptive evolution. It enables the optimization of the membrane topology. The thickness of the membrane is considered as a variable parameter of the membrane topology.

Keywords: membrane, absolutely flexible plate, self-organization, adaptive evolution, finite element method, topological optimization.

Широкое распространение мембранных покрытий вызвано тем, что эти конструкции широко используются и в новом строительстве зданий и сооружений различного назначения, и при реконструкции. Приоритетной задачей проектирования мембранных конструкций, является оптимизация геометрических характеристик, при соблюдении требований прочности, жесткости и устойчивости на всех этапах жизненного цикла. В статье [7] приводится подробный обзор истории развития направления оптимизационной топологии, рассматриваются способы решения задач оптимизации.

Целью данного исследования является разработка алгоритма реализации МКЭ с использованием вариационного уравнения Лагранжа в итерационном методе адаптивной эволюции, позволяющего оптимизировать топологию мембраны. В качестве варьируемого параметра топологии мембраны будем рассматривать ее толщину. Оптимальной будет являться энергетически равнопрочная мембранная конструкция с учетом ограничения на нормируемую плотность энергии деформации.

Основные зависимости, описывающие поведение абсолютно гибких пластин, построены на гипотезах технической теории пластин о недеформируемости плоских нормалей и пренебрежимой малости поперечных нормальных напряжений. В соответствии с принятыми гипотезами о поведении абсолютно гибких пластин в процессе деформирования, вектор напряжений и деформаций имеют следующий вид:

Компоненты тензора конечных деформаций выражаются через перемещения срединной поверхности мембраны [1]:

(1)

Для получения более точной картины напряженно-деформированного состояния мембраны, исследование работы конструкции в физически линейной стадии работы недостаточно. Поэтому на втором этапе должна быть учтена физическая нелинейность, предполагающая упругопластический характер работы с использованием уравнения деформационной теории пластичности.

В первом приближении расчетной схемы будем предполагать, что физические зависимости принимаются в виде обобщенного закона Гука:

Эффективным прямым методом для построения процедур по отысканию числовых полей неизвестных функций на основе вариационных принципов механики, является метод конечных элементов. Связь полных деформаций с полными перемещениями осуществляется через матрицу В1 и матрицу операций дифференцирования А : .

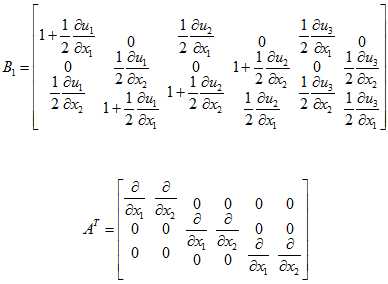
Геометрические зависимости в инкрементальной постановке имеют следующий вид:

– вектор приращений деформаций

Физические зависимости в инкрементальной форме:

Система уравнений для физически линейного расчета имеет вид:

(2)

При получении основных конечноэлементных соотношений расчета мембран используется вариационный принцип Лагранжа [6].

(3)

где

– удельная потенциальная энергия; – вектор поверхностных сил; – заданный вектор поверхностных сил; – деформированная элементарная площадь; – элементарная площадь до деформации; – перемещения срединной поверхности мембраны; – вектор объемных сил; – деформированный элементарный объем; – элементарный объем до деформации; – заданный вектор объемных сил;

Условие стационарности функционала П1 определяется следующим уравнением

δП1=0, (4)

где

Выделяя правую часть, получаем следующую запись вариационного уравнения Лагранжа:

(5)

В качестве типового используется треугольный конечный элемент с девятью степенями свободы, позволяющий аппроксимировать плоскую поверхность практически любой формы.

Для получения конечноэлементных зависимостей функцию перемещений представляем в виде:

(6)

При построении локальных интерполяционных функций используем естественные координаты. Введя обозначение, перепишем вариационное уравнение (5) в следующем виде:

(7)

Из (7) в силу произвольности вариаций следует:

(8)

В результате получаем основное матричное соотношение для расчета мембран в физически линейной постановке:

(9)

где

– касательная матрица жесткости треугольного конечного элемента;

– вектор узловых сил, порожденный внешней нагрузкой;

– вектор неуравновешенных сил

(10)

где – секущая матрица жесткости.

Пренебрегая при малом шаге по нагрузке величиной , переходим к итерационным уравнениям метода последовательных нагружений:

(11)

Для получения на 1-м шаге не вырожденной матрицы жесткости может быть использована процедура нахождения начальных перемещений с использованием известных решений Феппля [1], либо любых других решений, удовлетворяющих граничным условиям. Также для решения этой проблемы можно использовать возможность получения статического решения динамическим методом [3].

С целью оптимизации геометрических и физических параметров рассматриваемой абсолютно гибкой пластины, используем законы сохранения самоорганизующихся механических систем, изложенные в [5, C. 94-112].

Для построения уравнения адаптивной эволюции, оптимизирующего топологию мембран принимаем гипотезу о возникновении структурообразующей интервальной константы – нормируемой плотности энергии деформации. Эта интервальная константа зависит от механических характеристик материала – модуля упругости, допускаемого напряжения и т.д.

В процессе топологической оптимизации мембранной конструкции, возникающие самоорганизующиеся системы, имеющие зоны разрушения не рассматриваются.

В частности будем считать, что для элементарного объема самоорганизующейся системы разность потенциальной энергии деформации текущего состояния и идеального изоэнергетического стремится к нулю: – соответственно объем материала в текущем и изоэнергетическом состоянии.

Последовательность операций итерационного алгоритма, моделирующего эволюционный процесс, имеет следующий вид:

(12)

s1 – число итераций внутреннего цикла, равное числу приращений нагрузки, s2 – число итераций внешнего цикла, необходимых для стабилизации решения, s3 – общее число элементов.

На первом шаге внешнего цикла полагаем заданной толщину мембраны h=h(1). После определения узловых перемещений qm во внутреннем цикле, для каждого конечного элемента вычисляется средняя плотность энергии деформации и уточненная толщина конечного элемента пластины h:

(13)

(14)

– площадь r-го конечного элемента

Количество итераций внешнего цикла s2 определяется условием достижения объемом материала заданной погрешности. В процессе топологической оптимизации мембранной конструкции необходимо задавать диапазон изменения толщины, исходя из конструктивных соображений.

Изложенный в данной статье алгоритм топологической оптимизации мембранных конструкций на основе метода адаптивной эволюции самоорганизующихся механических систем, может быть реализован в виде дополнительного оптимизационного модуля к программному комплексу ЛИРА-САПР, с целью использования удобной графической среды для ввода исходной расчетной схемы и визуализации полученных результатов.

Список литературы / References

Kirchhoff G. Vorlesungen über mathematische Physik. Mechanik./ G.Kirchhoff— Leipzig: B. G. Teubner, 1876. —466 P.
Трофимов В.И., Еремеев П.Г. Мембранные конструкции зданий и сооружений / В.И. Трофимов, П.Г. Еремеев– М.: Стройиздат, 1990. – 213 с.
Васильков Г.В., Морозова Н.Е. Статический расчет мембранных покрытий в физически нелинейной постановке // Рост. инж.-строит. ин-т. – Ростов н/Д, 1991. – C. 19.- Деп в ВИНИТИ 2.04.1991. №1405-В-91
Васильков Г.В. Теория адаптивной эволюции механических систем/ Г.В. Васильков. – Ростов н/Д.: Терра-Принт, 2007. – 248 c.
Вольмир А.С. Гибкие пластинки и оболочки / А.С. Вольмир. – М.: Гостехиздат, 1956. – 420 с.
Сысоева В.В., Чедрик В.В. Алгоритмы оптимизации топологии силовых конструкций / В.В. Сысоева, В.В. Чедрик // Ученые записки ЦАГИб. – – Т. XLII–C. 91-102.

Список литературы на английском языке /References in English

Kirchhoff G. Vorlesungen über mathematische Physik. Mechanik. [Lectures on mathematical physics. Mechanics.] / G.Kirchhoff— Leipzig: B. G. Teubner, 1876. — 466 p.
Trofimov V.I., Eremeev P.G. Membrannye konstrukcii zdanij i sooruzhenij [Design of membranes for buildings and structures.] / V.A. Trofimov – M.: Strojizdat, 1990. – 213 р. [in Russian]
Vasil’kov G.V., Morozova N.E. Staticheskij raschet membrannyh pokrytij v fizicheski nelinejnoj postanovke [Static analysis of membrane coating in physically nonlinear statement] / G.V.Vasil’kov, N.E. Morozova // Rost inzh -stroit in-t [Rostov civil engineering Institute].– Rostov, 1991. – P. 19. – deposited in VINITI 2.04.1991. №1405-V-91. [in Russian]
Vasil’kov G.V. Teorija adaptivnoj jevoljucii mehanicheskih system [Theory of adaptive evolution of mechanical systems] / G.V.Vasil’kov – Rostov: Terra-Print, 2007. –248 p.[in Russian]
Vol’mir A.S. Gibkie plastinki i obolochki [Flexible plates and shells] A.S. Vol’mir – M.: Gostehizdat, 1956. –420 p. [in Russian]
Sysoeva V.V., Chedrik V.V. Algoritmy optimizacii topologii silovyh konstrukcij [Algorithms topology optimization of the power structures] V.V.Sysoeva, V.V.Chedrik // Uchenye zapiski TSAGIb [Scientific notes of SAHIb]. – 2011. – T. XLII–P. 91-102. [in Russian]

research-journal.org

Топологическая оптимизация силовых конструкций методом выпуклой линеаризации | Кишов

Топологическая оптимизация силовых конструкций методом выпуклой линеаризации

Е. А. Кишов, В. А. Комаров

Аннотация

Предложен аппарат топологической оптимизации, основанный на методе выпуклой линеаризации. Формулировка задачи подразумевает минимизацию энергии деформации конструкции при ограничении на объём материала. Решение основано на использовании явной, выпуклой и сепарабельной аппроксимации Лагранжиана с привлечением теории двойственности. Для связи проектных переменных (плотности) с упругими характеристиками материала (модулем упругости) использована нелинейная степенная модель. Проведён анализ чувствительности целевой функции и функции ограничений. Получены основные расчётные формулы итерационного алгоритма оптимизации. Рассмотрен ряд тестовых задач топологической оптимизации, соответствующих передаче усилий элементарными способами: растяжением, сдвигом и кручением. Для всех случаев вычислена величина силового фактора: аналитически и при помощи конечно-элементной модели. Показано полное соответствие полученных силовых схем инженерным представлениям о теоретически оптимальных конструкциях для данных примеров.

Ключ. слова

Топологическая оптимизация; SIMP-модель; силовая конструкция; метод выпуклой линеаризации; нелинейное программирование; метод конечных элементов

1. Комаров В.А. Проектирование силовых аддитивных конструкций: теоретические основы // Онтология проектирования. 2017. Т. 7, № 2 (24). C. 191-206. DOI: 10.18287/2223-9537-2017-7-2-191-206

2. Niu M.C.Y. Airframe structural design: Practical Design Information and Data on Aircraft Structures. Hong Kong: Conmilit Press Ltd, 1988. 612 p.

3. Ендогур А.И. Проектирование авиационных конструкций. М.: МАИ-ПРИНТ, 2009. 537 с.

4. Комаров А.А. Основы проектирования силовых конструкций. Куйбышев: Куйбышевское книжное издательство, 1965. 88 с.

5. Комаров В.А. Проектирование силовых схем авиационных конструкций // Сб. статей «Актуальные проблемы авиационной науки и техники». М.: Машиностроение, 1984. C. 114-129.

6. Bendsoe M.P., Sigmund O. Topology Optimization: Theory, Methods and Applications. Springer, 2003. 271 p.

7. Christensen P.W., Klarbring А. An introduction to structural optimization. Springer, 2003. 214 p.

8. Лазарев И.Б. Математические методы оптимального проектирования конструкций. Новосибирск: Новосибирский институт инженеров железнодорожного транспорта, 1974. 192 с.

9. Bendsoe M.P. Optimal shape design as a material destribution problem // Structural Optimization. 1989. V. 1, Iss. 4. P. 193-202. DOI: 10.1007/bf01650949

10. Fleury C., Braibant V. Structural optimization: a new dual method using mixed variables // International Journal for Numerical Methods in Engineering. 1986. V. 23, Iss. 3. P. 409-428. DOI: 10.1002/nme.1620230307

11. Conn A.R., Gould N.I.M., Toint Ph.L. Trust Region Methods. SIAM, 2000. 959 p.

12. Комаров В.А. Повышение жёсткости конструкций топологическими средствами // Вестник Самарского государственного аэрокосмического университета имени академика С. П. Королёва. 2003. № 1 (3). C. 24-37.

13. Комаров В.А. К доказательству теорем об изменении жёсткости конструкций // Вестник Самарского государственного аэрокосмического университета имени академика С.П. Королёва. 2004. № 1 (5). С. 49-51.

14. Wasiutinski Z. On the congruency of the forming according to the minimum potential energy with that according to the equal strength // Bull. Acad. Polon. Sci. 1960. No. 6. P. 344-365.

15. Козлов Д.М., Майнсков В.Н., Резниченко Г.А. Проектирование детали: учебное пособие. Самара: Самарский государственный аэрокосмический университет, 2012. 88 с.

16. Lewinski T., Zhou M., Rozvany G.I. N. Extended exact solutions for least-weight truss-layouts – Part I: Cantilever with horizontal axis of symmetry // International Journal of Mechanical Sciences. 1994. V. 36, Iss. 5. P. 375-398. DOI: 10.1016/0020-7403(94)90043-4

17. Sigmung O., Aage N., Andreassen E. On the (non-)optimality of Michell structures // Structural and Multidisciplinary Optimization. 2016. V. 54, Iss. 2. P. 361-373. DOI: 10.1007/s00158-016-1420-7

journals.ssau.ru