Оптимизация режима энергосистемы с учетом потери активной мощности при передаче. Оптимизация режима энергосистемы

1. Оптимизация режимов энергосистем

Режимом энергосистемы называют некоторое состояние ее, определяемое значениями температуры – t, давления – p, частоты – f, напряжения – U, тока – I, активной мощности – P, реактивной мощности – Q и других физических величин, называемых параметрами режима, которые характеризуют процесс производства, преобразования, передачи и распределения энергии.

Режимы делятся на стационарные и переходные. Оптимизируются только стационарные режимы.

Оптимизация обеспечивается на всех этапах:

Оптимально должно работать все оборудование (с максимальным КПД). Это определяется в основном его техническим состоянием;
Распределение нагрузки между параллельно работающими агрегатами;
Распределение нагрузки между объектами ЭС. Здесь экономический эффект достигается не только за счет экономии топлива в процессе генерации, но и за счет снижения потерь в сети.

1.1. Параметры режима эс

Математическая модель режима – это система нелинейных алгебраических уравнений, как правило, узловых.

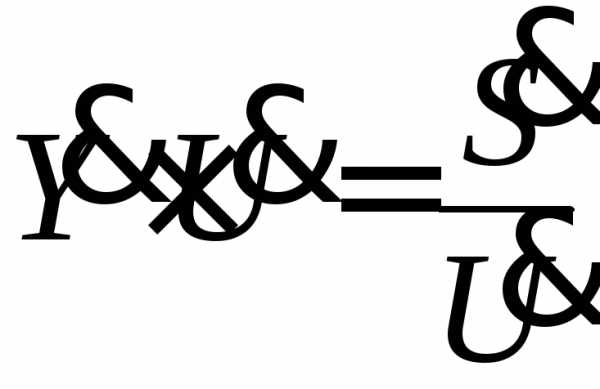
где 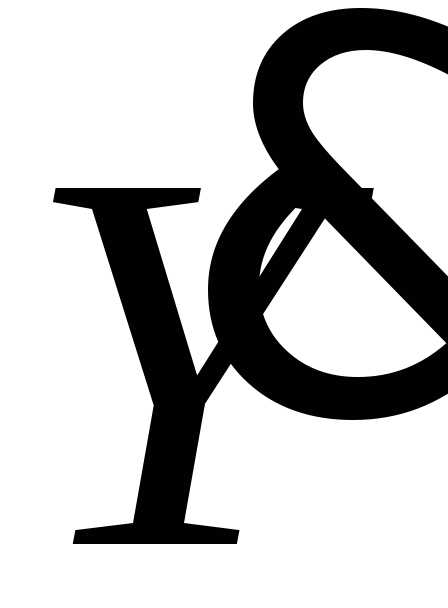- матрица узловых проводимостей, имеет порядокn;

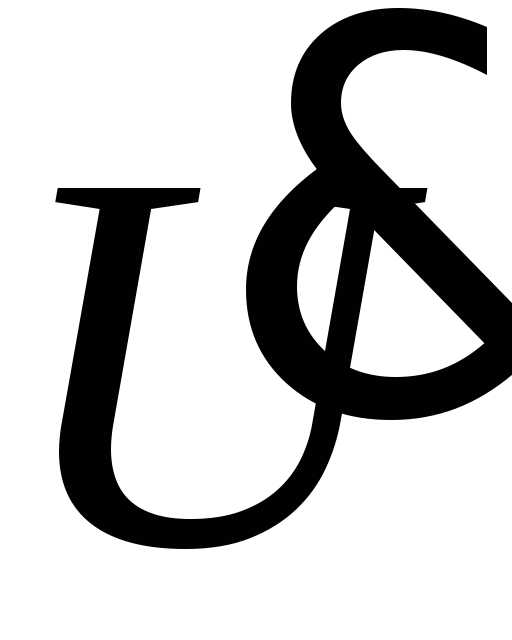- вектор напряжений в узлах;

- вектор узловых мощностей;

n – количество независимых узлов.

Для решения системы должны задаваться независимые параметры, к числу которых относятся узловые мощности и напряжения в балансирующем узле. Имея эти параметры можно однозначно определить режим (если он существует) путем решения системы (1).

Все остальные параметры режима, получаемые на основе расчета: напряжения в узлах ЭС – US, потоки по линиям – Pl, Ql, токи в ветвях – Il, потери – P и др., называют зависимыми параметрами режима.

Часть независимых параметров (узловые мощности) в нормальных условиях не подчиняются диспетчеру (нагрузки в узлах). Остальные (мощности источников) должны оптимизироваться. К числу независимых параметров относятся и коэффициенты трансформации автотрансформаторов связи сетей разных напряжений (КТ), которые могут регулироваться с помощью РПН.

Своеобразным независимым параметром является и состав включенного в работу оборудования, который характеризуется графом G.

Независимые параметры режима, оптимизация которых должна проводиться при диспетчерском управлении, можно рассматривать как вектор X = { Pi, Qi, KT, G, }, где индекс i определяет источники.

По аналогии вектор зависимых параметров объединяет все остальные параметры режима, однозначно определяемые при фиксированных допустимых значениях всех независимых параметров:

Y = {US, Pl, Ql, Il, , P,… }

Для определения Y при заданных X используются различные методы и программы расчета стационарных режимов.

1.2. Формулировка задачи оптимизации

В общем случае оптимизация заключается в поиске такого состава оборудования и параметров его работы, при которых потребности в энергии за период T обеспечиваются при минимальных затратах. Решение этой сложной задачи обычно проводится в два этапа. На первом выбирается состав включенного в работу оборудования при упрощенной оптимизации режима.

На втором этапе для принятого состава оборудования .проводится оптимизация режима его работы. При этом должны учитываться затраты не только в энергосистеме, но и у потребителей. В состав затрат в энергосистеме входят амортизация, зарплата, стоимость топлива и различные налоговые отчисления. От режима в основном зависит расход топлива, который и является определяющим целевую функцию.

У потребителей затраты возникают из-за низкого качества электроэнергии, определяемого в первую очередь уровнем напряжения на их шинах. Наличие на потребительских подстанциях трансформаторов с РПН позволяет поддерживать оптимальное напряжение в пределах регулировочного диапазона. В связи с этим затраты у потребителей можно в общем случае не учитывать.

Таким образом, в качестве целевой функции можно принять:

где 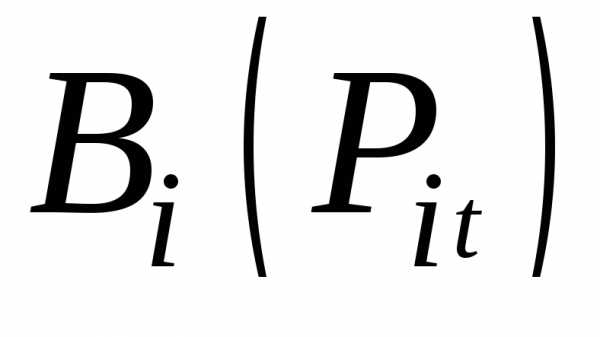- расходная характеристика топливаi-ой ТЭС;

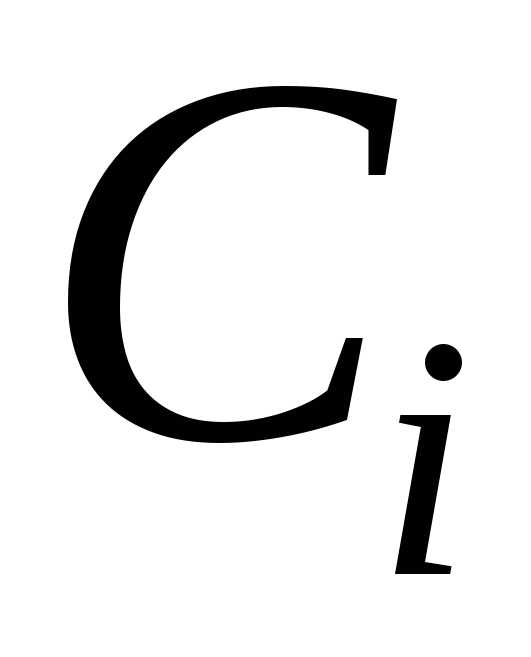- цена топлива;

T – расчетный период.

Оптимизацию за период T проводят там, где имеются в системе электростанции с ограниченным запасом первичного ресурса топлива на ТЭС или воды на ГЭС

При нормированных запасах топлива можно проводить оптимизацию для каждой ступени графика отдельно и независимо

Оптимизация должна проводиться с учетом ограничений, накладываемых на независимые параметры, например на мощности электростанций, а также на зависимые параметры режима, например на напряжения в узлах.

Расходная характеристика топлива 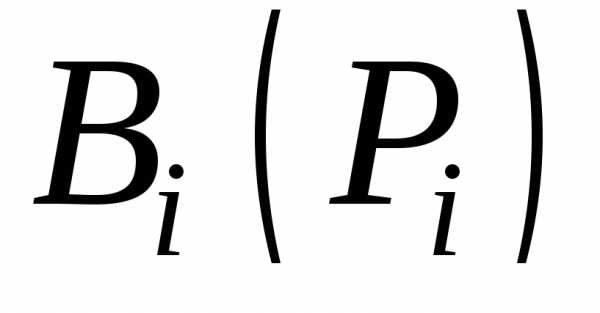является нелинейной зависимостью. Ограничения на зависимые параметры также являются нелинейными, поэтому задача оптимизации относится к нелинейному программированию, которая в общем виде записывается так:

F(Х)  min ,

G(x) >= 0.

Здесь Х = {x1,…,xn} – вектор неизвестных, G(X) = {g1(x),…,gm(x)} – вектор-функция, состоящая из m элементов.

Если F(Х) или g(Х) или оба нелинейные, то задача относится к нелинейному программированию.

studfiles.net

Оптимизация распределения активной нагрузки энергосистемы между ТЭС и ГЭС с использованием программа MATLAB

В работе исследованы оптимальное распределение активной нагрузки энергосистемы между гидравлическими и тепловыми электростанциями с использованием программного комплекса Маtlab. Рассмотрен пример оптимального покрытия графика нагрузки энергосистемы всех суточных интервалов, обеспечивающих минимальный расход топлива.

Ключевые слова: энергосистема, электростанция, оптимизация, расход топлива, расход воды, график нагрузки, программирование.

В задаче краткосрочного оптимального планирования режимов гидротепловых энергосистем вместе с тепловыми электростанциями (ТЭС) расчетными станциями являются также гидроэлектростанции (ГЭС), имеющие водохранилища с регулированием расхода воды и, соответственно, мощности в рассматриваемом периоде. ГЭС, работающие на бытовом расходе рек, мощности которых определяются текущими притоками воды, заменяются соответствующими отрицательными нагрузками и не участвуют в оптимизационном процессе [1–3].

В тех случаях, когда режимы работы энергосистемы в отдельные моменты времени независимы друг от друга, задача оптимизации ее режима за цикл регулирования сводится к последовательной оптимизации режима для коротких интервалов (моментов) времени, например, для каждого часа суточного цикла регулирования, в отдельности. Задача оптимизации значительно усложняется в тех случаях, когда необходимо вводить условия, определяющие связь между режимами в отдельных интервалах времени. Такая связь возникает при наличии в энергосистеме электростанций с ограниченными запасами энергоресурсов, в частности ГЭС с водохранилищами и заданными расходами воды за цикл регулирования [2].

Условие баланса мощностей в энергосистеме без учёта потерь активной мощности в сети запишется как

W = PT + PГ — РС,

где PT, PГ, РС — соответственно активные мощности ТЭС, ГЭС и нагрузки ЭЭС.

Для ГЭС с суточным циклом регулирования сумма часовых расходов воды Q(t) за сутки должна быть равна заданному суточному притоку воды Qсут.прит. к водохранилищу.

Для определения минимума расхода условного топлива на генерируемые ТЭС и ГЭС при условии соблюдения баланса активных мощностей в сети и притока воды на ГЭС составляется функция Лагранжа в виде:

и, берутся частные производные от неё, приравняя их к нулю:

где

Отсюда

Тогда критерием оптимального распределения активной нагрузки энергосистемы между ТЭС и ГЭС является:

Величина  носит название коэффициента Лагранжа и показывает какому количеству сэкономленного топлива ΔВ соответствует увеличение на 1 м3 пропускаемого через турбину ГЭС объёма воды. Таким образом, ГЭС сводится к разряду ТЭС. Значение  остаётся постоянным для всех расчётных часов.

Для определения значения  можно воспользоваться методом подбора.

Задавшись некоторым достоверным значением  и умножив его на характеристику относительных приростов (ХОП) расхода воды ГЭС, осуществляется распределение графика нагрузки энергосистемы между ТЭС и ГЭС. Затем, опираясь на полученные мощности ГЭС, определяются часовые расходы воды Q(t), сумма которых даёт суточный расход Qсут.

Если при этом заданный суточный расход воды ГЭС Qзад равен расчетному Qсутсдостаточной точностью , то дальнейшая коррекция не производится. В противном случае значение  изменяется последовательно в большую сторону, если Qсут. > Qзад, и в меньшую сторону, если Qсут.Qзад.

На основе полученного вывода разработан программный комплекс на базе Маtlab. Программа составлена для оптимального распределения графиков суммарных активных нагрузок энергосистемы между тепловыми и гидроэлектростанциями. Она позволяет определить оптимальные графики нагрузок всех электростанций, участвующих в оптимизации, с учетом технологических ограничений. Программа предусматривает выполнения оптимизации в условиях наличия в энергосистеме множества тепловых и гидроэлектростанций. Она дает возможность определить оптимальные режимы электростанций и энергосистемы с высокой точностью и надежностью [4].

Эффективность алгоритма, данного предложенного программного комплекса исследован на примере в оптимальном покрытии суммарного графика нагрузки энергосистемы (табл. 1) за цикл регулирования, состоящий из четырёх интервалов, одним ТЭС и ГЭС со следующими исходными данными:

Расходные характеристики эквивалентных ТЭС и ГЭС, заданные в виде полиномов второй степени:

;

Суточный расход воды на ГЭС .
Регулировочный диапазон электростанций:

Таблица 1

Суммарный график нагрузки энергосистемы.

Время суток, ч	0–6	6–12	12–18	18–24
Суммарная нагрузка PН, МВт	430	650	820	490

Ниже приводится результаты данного исследования, полученные в программном комплексе Маtlab.

Суточный график нагрузки энергосистемы:

Рн= [430,000 650,000 820,000 490,000]

Оптимальные значения относительных приростов для каждого интервала нагрузки:

bopt = [1,880 2,750 3,420 2,120]

Оптимальное значение выработки мощности ГЭС для каждого часа нагрузки:

Рoпт = [149,492 225,613 284,235 170,491]

Оптимальное значение выработки мощности ТЭС для каждого часа нагрузки:

Рoпт = [280,000 425,000 536,667 320,000]

Значения расхода топлива на ТЭС для каждого часа интервала:

Bрасх = [391,200 726,875 1071,367 471,200]

Значения расхода воды на ГЭС для каждого часа интервала:

Qрасх = [274,163 428,348 586,583 310,909]

Заданное значение расхода воды для ГЭС [м3]:

Qзад = 9600,000

Расчетное значение расхода воды для ГЭС [м3]:

Qрасчет = 9600,003

Значение λ удовлетворяющее условию заданного расхода воды:

λ = 1,143.

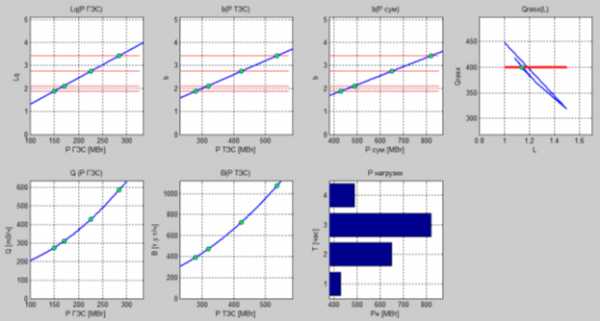
Рис. 1. Результаты расчета в программе Маtlab.

Полученные результаты с высокой точностью совпадают с результатами, полученными методом равенства относительных приростов расхода топлива (ОПРТ) (табл. 2).

Таблица 2

Результаты равенств ОПРТ.

Интервал времени	PС	PГ	PТ	Qчас, часовой расход воды	Qинт, расход воды за каждый интервал
часы	МВт	МВт	МВт	м³/ч	м³
0–6	430	149,781	280,219	274,639	1647,831
6–12	650	225,569	424,431	428,241	2569,447
12–18	820	284,132	535,868	586,274	3517,645
18–24	490	170,450	319,5	310,834	1865,004
Суточный расход воды, Qсут					9599,927

Окончательное значение

Максимальный небаланс воды

Расход топлива на ТЭС за сутки

Вывод:

Данная программа может быть использована диспетчерскими пунктами энергосистем для оптимального управления их режимами, также при проведении лабораторных и практических занятий по курсам «Электрические сети и системы», «АСУ и оптимизация режимов электрических станций и систем».

Литература:

Фазылов Х. Ф., Насыров Т. Х. Установившиеся режимы электроэнергетических систем и их оптимизация. –Т.: Молия, 1999.
Гайибов Т. Ш. Алгоритм оптимизации краткосрочных режимов гидротепловых энергосистем кусочно-линейной аппроксимацией нелинейных зависимостей. Электрика, 2009, № 4, с. 26–30.
Автоматизация диспетчерского управления в электроэнергетике/ Под общей ред. Ю. Н. Руденко и В. А. Семенова. — М.: Изд-во МЭИ, 2000.-648 с.
Гайибов Т. Ш., Реймов К. М. Программа «TESGES» для оптимального покрытия графиков нагрузок энергосистемы тепловыми и гидравлическими электрическими станциями. /Программа для ЭВМ/ № DGU 03033. 10.02.2015 г. Агентство по интеллектуальной собственности Республики Узбекистан.

Основные термины (генерируются автоматически): ГЭС, программный комплекс, активная нагрузка энергосистемы, цикл регулирования, ТЭС, суточный расход воды, суммарный график нагрузки энергосистемы, оптимальное распределение, высокая точность, суточный цикл регулирования.

moluch.ru

Оптимизация - режим - энергосистема

Cтраница 1

Оптимизация режима энергосистем по Р тепловых электростанций, или распределение активных мощностей между тепловыми станциями, позволяет найти активные мощности станций, соответствующие минимуму суммарного расхода условного топлива ( стоимости) на тепловых электрических станциях с приближенным учетом потерь в сети при заданных нагрузках потребителей. [1]

Общую задачу оптимизации режимов энергосистем методически удобно разделить на две частные: оптимизацию активных нагрузок и оптимизацию реактивных нагрузок. Условия наивыгоднейшего распределения активных и реактивных нагрузок внешне не связаны между собой. [2]

В результате всего этого задачу оптимизации нормального краткосрочного режима энергосистемы следует отнести к векторным целочисленным, многоэкстремальным задачам нелинейного программирования. [3]

Предложен стохастический подход к решению задачи оптимизации режимов энергосистем, учитывающий стохастический характер нагрузки и обеспечивающий минимум потерь активной и реактивной мощностей в электроэнергетической системе. Показано, что задача оперативного управления режимами электроэнергетических систем может быть представлена в виде двухэтапной задачи стохастического программирования. Приведена формулировка данной задачи и намечены пути ее решения. [4]

В энергетических задачах динамическое программирование может использоваться при оптимизации режимов энергосистем, каскада гидростанций и режима развития. [5]

В книге рассмотрены задачи оптимального регулирования речного стока водохранилищами ГЭС как при однозначно заданных гидрографах, так и при вероятностном прогнозе речного стока. Рассматриваются вопросы учета краткосрочной ( суточной и недельной) оптимизации режимов энергосистем при расчетах долгосрочных режимов водохранилищ ГЭС и, наоборот, учет результатов долгосрочной оптимизаций режимов водохранилищ ГЭС при оперативной ( краткосрочной) оптимизации режимов энергосистем. [6]

Автоматизированная система диспетчерского управления высших уровней осуществляет координацию работы локальных систем регулирования и оптимизацию режима энергосистемы в целом ( см. гл. [7]

Но эта идея - - деление времени на конечные малые интервалы - может быть введена в решение задачи не после получения соответствующих уравнений оптимального режима, а до этой операции. Это и приводит к модели с дискретным временем, когда рассматриваются только средние за интервалы зна-чения расходов естественного притока к водохранилищу и зарегулированных расходов. Такая модель была использована: в задаче оптимизации режимов энергосистем значительно раньше, чем модель с непрерывным временем, в работе [26] которая была первой работой по вероятностной теории сезонных режимов. [9]

К таким станциям могут быть отнесены некоторые мелкие ТЭС и ГЭС, переменный режим которых практически не влияет на экономичность режима системы. Отнесем к этой же категории и АЭС, работа которых в переменном режиме крайне нежелательна. Это положение можно принять лишь в известной мере условно, так как в принципе регулировочный диапазон мощностей на АЭС имеется и в некоторых пределах он практически используется. Однако вследствие того, что ядерное топливо и издержки на его сжигание принципиально отличаются от органического топлива и соответствующих издержек на его использование, то оптимизация режима энергосистемы при наличии в ней атомных электростанций в вычислительном отношении несколько усложнится. [10]

Страницы: 1

www.ngpedia.ru

Содержание.

Министерство образования и науки Российской Федерации

Южно-Уральский государственный университет

Кафедра «Электрические станции, сети и системы»

Б. Г. Булатов

АСУ И ОПТИМИЗАЦИЯ

Конспект лекций

Челябинск

2003

Булатов Б.Г. АСУ и оптимизация: Конспект лекций. – Челябинск: ЮУрГУ, 2003 - 72с.

Содержание. 3

Введение 5

1. Оптимизация режимов энергосистем 6

1.1. Параметры режима ЭС 6

1.2. Формулировка задачи оптимизации 7

1.3. Особенности задачи нелинейного программирования 8

1.4. Методы безусловной оптимизации 9

1.4.1. Метод покоординатного спуска 11

1.4.2. Градиентный метод 11

1.4.3. Метод случайного поиска 12

1.4.4. Метод деформированного многогранника 13

1.5. Оптимизация с учетом ограничений в форме равенств 13

1.5.1. Метод прямой оптимизации 14

1.5.2. Метод приведенного градиента 14

1.5.3. Метод неопределенных множителей Лагранжа 15

1.6. Оптимизация с учетом ограничений в форме неравенств 16

1.7. Условия оптимального распределения нагрузки между параллельно работающими блоками 18

1.8. Характеристики основного оборудования ТЭС 20

1.9. Характеристики блоков 23

1.10. Маневренные свойства блока 24

1.11. Методы распределения нагрузки между блоками на КЭС 25

1.11.1. Графический метод. 25

1.11.2. Распределение с помощью ЭВМ. 25

1.12. Влияние погрешностей в определении  на пережог топлива 26

1.13. Условие оптимального распределения в системе с ТЭС 27

1.14. Условия распределения мощности и энергии с учетом рынка перетоков 29

1.15. Определение удельных приростов потерь 29

1.16. Мероприятия по снижению потерь в сети 32

1.17. Распределение нагрузки в системе с ГЭС 32

1.18. Определение характеристик ГЭС 34

1.19. Распределение нагрузки в системе с ГЭС 35

1.19.1. Применение динамического программирования для выбора графика сработки водохранилища для ГЭС 36

1.20. Оптимизация реактивной мощности в системе 38

1.21. Комплексная оптимизация режима 39

1.22. Выбор состава включенного в работу оборудования. 40

1.23. Применение ЭВМ для оптимизации 42

1.24. Оптимизация надежности 43

1.24.1. Выбор оптимального аварийного резерва 44

1.24.2. Определение дискретных рядов аварийного выхода и снижения нагрузки 46

1.25. Оптимизация качества электроэнергии. 48

1.26. Интегральный критерий качества. 49

1.27. Определение оптимального напряжения для осветительной нагрузки. 51

2. Автоматизированные системы управления (асу). 53

2.1. Энергосистема как объект управления. 54

2.2. Подсистемы АСУ ТП. 54

2.3. Подсистемы технического обеспечения. 55

2.3.1. Датчики электрических параметров. 56

2.3.2. Счетчики. 57

2.3.3. Устройства преобразования информации. 57

2.3.4. Средства связи в АСУ и телемеханика. 59

2.3.5. Регистраторы событий. 61

2.3.6. Автоматизированные системы контроля и учета электроэнергии (АСКУЭ). 62

2.3.7. Средства отображения информации. 62

2.3.8. Информационное обеспечение. 63

2.4. Подсистемы программного обеспечения АСУ. 64

2.5. АСУ ТП ТЭС. 68

2.6. АСУ ПЭС 71

2.7. АСУ ТП подстанций. 71

2.8. Контроль за работой ПЭ энергосистемы. 72

Введение

Эксплуатация энергосистем связана с большими затратами и, в первую очередь, с затратами на топливо. Запасы органического топлива на Земле сокращаются, поэтому растут цены на топливо и обостряется проблема повышения эффективности процессов производства, передачи и распределения энергии. Завершившаяся реструктуризация Единой Энергосистемы России и разделение ее на компании создают условия для развития конкуренции в сферах генерации и сбыта. Но с технической точки зрения и с позиций управления энергосистема остается единой.

Сложности управления энергетикой сегодня связаны с тем, что существенно сокращены инвестиции и изношено основное оборудование.

Все это требует дальнейшего развития и совершенствования современных способов управления, использующих математические методы и ЭВМ. Упрощенная схема управления показана на рис. 1.1.

X – вектор внешних воздействий на систему;

Y – вектор параметров режима ;

Z – критерий управления, формализующий основные цели функционирования энергосистемы;

U – вектор управления.

Функциональные зависимости Y(X,U), Z(X,Y,U).

Рис. 1.1. Цель управления Zextr.

ЭВМ используется здесь как средство для автоматизации человеческой деятельности по управлению. Поэтому такие системы называются автоматизированными системами управления (АСУ).

Введение и эксплуатация АСУ требует больших капиталовложений. Окупаются эти вложения за счет снижения эксплуатационных расходов путем снижения расходов топлива, повышения надежности и улучшения качества поставляемой энергии.

И хотя относительная экономия затрат на топливо составляет обычно не более 1,5 – 2 %, в абсолютном исчислении она дает вполне ощутимые результаты.

Значительный эффект в системах достигается за счет постоянного контроля состояния и снижения аварийности.

studfiles.net

ОПТИМИЗАЦИЯ ЭНЕРГОСИСТЕМ - PDF

Стандарт организации

ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО «СИСТЕМНЫЙ ОПЕРАТОР ЕДИНОЙ ЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ» СТО 59012820.. -2015 (обозначение)..2015 (дата введения) Стандарт организации ПОРЯДОК ПОДГОТОВКИ ЗАКЛЮЧЕНИЙ О ВОЗМОЖНОСТИ

Подробнее

Стандарт организации

Приложение к приказу ОАО «СО ЕЭС» от 29.05.2015 146 ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО «СИСТЕМНЫЙ ОПЕРАТОР ЕДИНОЙ ЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ» СТО 59012820.27.100.001-2015 Регистрационный номер (обозначение) 29.05.2015

Подробнее

ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПРАВИТЕЛЬСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ П О С Т А Н О В Л Е Н И Е от 10 мая 2017 г. 543 МОСКВА О порядке оценки готовности субъектов электроэнергетики к работе в отопительный сезон В соответствии с Федеральным

Подробнее

п.п. Действующая редакция Новая редакция

рынка техническим требованиям в связи с уточнением порядка формировании параметров вращающийся и холодный резерв. п.п. Действующая редакция Новая редакция п.5.3.1 Для ГЭС на период проведения неотложных

Подробнее

Стандарт организации

Приложение 6 к приказу 475 от 05.12.2012 в редакции приказов 142 от 15.03.2013 225 от 14.07.2015 200 от 18.04.2013 385 от 25.11.2015 208 от 25.04.2013 418 от 24.12.2015 245 от 04.06.2013 21 от 08.02.2016

Подробнее

docplayer.ru

Оптимизация режима энергосистемы с учетом потери активной мощности при передаче.

Один из методов, применяемы для определения потерь активной мощности при передаче электроэнергии, является линейный метод коэффициентов токораспределения.

Суть заключается в следующем: ток каждой ветви в рассматриваемом режиме может быть получен как сумма токов частных режимов.

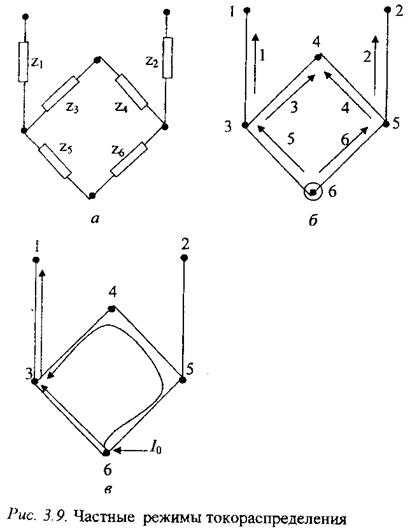Присутствуют только в 1 из независимых узлов. Таким образом число таких частных режимов равно n – числу независимых узлов.

Например схема замещения на рис. 3.9 а содержит 6 узлов 6 ветвей. Необходимо пронумеровать ветви и узлы, 1 из них выбрать в качестве балансирующего. Далее следует произвольно задать условно положительные направления ветвей.

Частный режим токораспре-деления представлен на рис 3.9.в.

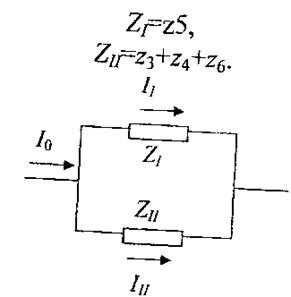В данном случае схему замещения можно представить так

Далее расчет ведем методом линейных коэффициентов токораспределения.

Для данной схемы справедливы ур-я:

для тока 5-ой ветви

Если предположить что сопротиления всех линий равны то для тока 3 –ей ветви

Знак ”-” возникает поскольку направление тока противоположно условно-положительным направлениям. Аналогичным образом вычисляются а41 а61.

Как следует из рисунка ток в ветви 2 отсутствует т.е. а21=0 следовательно а11=0.

Коэффициенты токораспределения вычисляются аналогичным образом для частных режимов и могут быть представлены в виде матрицы коэффициентов:

В соответветствии с методом наложения ток каждой из ветвей определяется как сумма токов, протекающая по этой ветви во всех частных схемах

При равенстве всех узловых напряжений для n+1, где n+1 – число узлов, комплексная мощность протекающая по i-ой линии:

Тогда потери при передаче мощности по i-ой линии:

В том числе акт. составляющая потерь:

И суммарные по энергосистеме потери:

Знание зависимости суммарных потерь позволяет определить относительные приросты суммарных потерь передаваемой мощности. при изменении мощности какой либо электростанции.

Условие оптимального распределения активной мощности между электростанциями с учетом потерь.

Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования.

Основные определения: линия поверхности равного уровня целевой функции, допустимая и результирующая области, абсолютный и условный экстремум целевой

Основные определенияОбщая задача отыскание экстремума целевой функции задании ограничения в виде равенств и неравенств, является задачей нелинейного программирования. Выражение целевой функции через зависимые и независимые переменные. Целевую функцию можно рассматривать как функции независимых X и зависимых Y переменных F=ФИ ||X||,||Y||), где Х=(x1…xn) и Y=(y1…yn) - вектора, соответственно независимых и зависимых переменных, n - число независимых переменных, т - число зависимых переменных. Если целевой функции является суммарный расход топливной энергосистеме, то в качестве независимых переменных может рассматриваться активные и реактивные мощности генераторных узлов ||X|| - PГ i , QГ I где i=1…n - номер электростанции, а в качестве зависимых переменных ||Y|| - напряжение генераторных Uh2…Um нагрузочных UГ1…Un узлов и мощность балансирующего узла P. Таким образом, оптимальное значение целевой функции: BOРТ = minB(||X||,||Y||) с учетом связи между и зависимыми и независимыми переменными ФИ(||X||,||Y||). Уравнения связи.В качестве уравнений связи можем использовать уравнения узловых напяжений, записанные в форме баланса токов для каждого узла

Si*/Ui* - YiБUБ – YijUj = 0 где i=1…n, n – число независимых узлов или же в матричном виде. ||S*\||U*||-||YБ|| UБ = ||Y||x||U||

Мощность уравнений связи целевую функцию можно выразить через независимые переменные F=F(Х). Длялюбых векторов РГ, QГ можно найти узловые токи ||I||, из узловых уравнений в форме баланса токов Ii=Si*\Ui* - YБiUБ напряжения U=||Y||-1||I|| мощность балансирующего узла целевая функция представляется как функция только с независимыми переменных F=F(||Х||) частности для оптимизации режима электростанций B=B1||P1||+B2||P2||+…Bn||Pn|| + BБ||PБ(||P||)||, где Bi||Pi|| - расходные характеристики электростанций. Оптимальный режим должен удовлетворять режимным йниям, в общем случае в виде системы неравенств , xiMIN <xi<xiMAX, i=1…n; yjMIN <xj<xjMAX, j=1…m; zSMIN <zS(||X||,||Y||)< zSMAX, s=1…S

S - некий контролируемый параметр, являющийся функцией от векторов зависимых и независимых переменных, которые не входят в целевую функцию. Например, если вектор независимых параметров – мощности электростанций независимых узлов и зависимый параметр - мощность балансирующего узла входят в целевую функцию, то в качестве вектора. Z могут быть выбраны узловые напряжения, которые (если пренебречь потерями активной мощности при передаче электроэнергии) не оказывают влияния] суммарный расход топлива в энергосистеме (на целевую функцию но зависят от оптимизируемых параметров. Расчет узловых напряжений позволило в каждом итерационном шаге контролировать допустимые оптимизируемого режима, Линия поверхности равного уровня целевой функции Линия (поверхность) равного уровня целевой функции геометрическое место точек в пространстве независимых переменных, в которых целевая функция имеет одно и тоже значение F=(X)=const. На рис. линии равного уровня целевой функции отчечены как замкнутые кривые, образующие элленпсы вокруг которой соответствует экстремум целевой функции. Допустимая и результирующая области DХ - допустимая область по параметрам X, поскольку для области выполняется система неравенств x1 MIN <x1<x1MAX и x2 MIN <x2<x2MAX. В общем случае, при наличии n независимых переменых область n - мерный параллелограмм, в данном случае для визуальной наглядности число независимых переменных выбрано равным. На допустимую область DХ накладываются границы допустимых областей DY и DZ. Здесь X - вектор оптимизируемых параметров, в координатах, которых ищется экстремум целевой функциям, Y, Z – контролируемые параметры, которые зависят от параметров оптимизируемые ограничения на которые могут нарушаться в процессе оптимизации. Границы допустимых областей для Y, Z в коор, оптимизируемых параметров - это геометрическое место (значений оптимизируемых параметров), которым соответствуют граничные значения контролируемых параметров. Область D - выпуклая, если для любой пары точек, прямая, соединяющая эти две точки, также целиком принадлежат области D. Абсолютный и условный экстремум целевой функции Абсолютный экстремум X* - точка в координатах независимых переменных, которой соответствует предельное значение целевой функции. Условный или относительный экстремум X'* - это то границе области D, в которой целевая функция имеет предельное, значение внутри данной области. Значения независимых параметров в точке X’*соответствующее им значение целевой функции F=(X’*) решение задачи оптимизации.Целевая функция может быть мультимодальной и унимодальной. В первом случае найденное решение может быть локальным, во втором случае оно всегда глобально. Активные и пассивные ограниченияОграничения параметров могут быть активные придающие параметрам в точке условного экстремума граничное значение, как, например, параметрам Z или же пассивные.

21-25Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике. Возможные направления. Градиент и антиградиент целевой функции. Способы задания длинны шага. Метод оптимизации при постоянной длине шага.

studopedia.net

Оптимизация режимов энергосистем - Контрольная работа

Оптимизация режимов энергосистем

Учебная программа

дисциплины для специальности 1-43 01 02 “Электроэнергетические системы и сети”

специализации 1-43 01 02 01 “Проектирование и эксплуатация электроэнергетических систем”

1. Цель дисциплины

Приобретение знаний в области оптимизации режимов электроэнергетических систем и основных электрических сетей на основе специальных математических методов и вычислительных средств.

К основным задачам дисциплины относится обучение принципам наивыгоднейшего распределения мощностей между генерирующими источниками, определения суммарных потерь и относительных приростов потерь через узловые мощности, оптимизации режимов сложно-замкнутых неоднородных сетей.

В результате изучения дисциплины студент должен

знать:

- общие сведения об электроэнергетических системах и их режимах, рациональном управлении энергосистемой;

- критерии и методы оптимального распределения мощностей в электроэнергетической системе;

- методы оптимизации режимов сложно-замкнутых неоднородных электрических сетей.

уметь:

- определить оптимальное распределение активных мощностей по методу относительных приростов;

- определять потери и относительные приросты потерь в сетях;

- выполнять распределение мощностей в энергосистеме на основе аналитических методов оптимизации;

- выполнять расчет экономического распределения мощностей в замкнутой сети;

- выбирать инновационные способы оптимизации режимов работы электрических сетей.

2. Виды занятий и формы контроля

Виды занятий и формы контроля	Дневное отделение	Заочное отделение
Курс	4	6
Семестр	8	11
Лекции, час	28	8
Лабораторные занятия, час	14	10
Контрольная работа (семестр)	-	11
Экзамен (семестр)	8	11
Самостоятельная работа, час	56	80
Аудиторных часов	42	18
Всего часов изучения дисциплины	98	98

3 Содержание учебной дисциплины

3.1. Темы и их содержание

Тема 1. Общие сведения об электроэнергетических системах и их режимах

Цели и задачи курса, литература, методика проведения лекционных, лабораторных и самостоятельных занятий. Общая постановка задачи об оптимизации. Основные понятия и определения. Графики нагрузки. Балансы мощности и энергии. Резервы мощности.

Тема 2. Наивыгоднейшее распределение нагрузки энергосистемы

О рациональном управлении энергосистемой. Постановка задачи оптимизации режима энергосистемы и основные этапы ее решения. Упрощенный алгоритм комплексной оптимизации режима энергосистемы.

Тема 3. Критерии и методы оптимального распределения мощностей в электроэнергетической системе

Математическая формулировка задачи оптимизации. Прямой метод оптимизации. Метод неопределенных множителей Лагранжа. Учет потерь в сетях при распределении активных мощностей. Достаточные условия существования уелевой функции (приведенных затрат).

Тема 4. Практические способы распределения активной нагрузки по расходным характеристикам

Оптимальное распределение активных мощностей методом относительных приростов. Табличный способ распределения нагрузки. Экономичное распределение активной нагрузки между станциями с учетом потерь мощности (графоаналитическое решение).

Тема 5. Потери в сетях Определение суммарных потерь активной мощности через узловые мощности. Собственные и взаимные сопротивления узлов и их определение. Относительные приросты потерь в сетях. Тема 6. Аналитические методы распределения активных мощностей в энергосистеме

Метод основанный на аппроксимации расходных характеристик полиномами второй степени. Метод последовательных приближений. Метод динамического программирования. Градиентный метод оптимизации. Учет ограничений в виде неравенств. Метод штрафных функций.

Тема 7. Оптимальные условия работы энергосистем

Оптимальное распределение реактивных мощностей. Взаимосвязь оптимального распределения активной и реактивной мощности. Охрана окружающей среды и оптимальные режимы нагрузки. Оптимизация уровня надежности работы энергосистемы. Резерв мощности в энергосистеме. Оптимизация качественных показателей электроэнергии. Оптимальные значения частоты и напряжений.

Тема 8. Оптимизация режимов работы основных электрических сетей энергосистем

Понятие об экономическом, естественном и принудительном распределении мощностей. Распределение мощностей в замкнутой сети, обеспечивающее минимальные потери мощности. Оптимизация режимов замкнутых электрических сетей при помощи вольтодобавочных трансформаторов. Обобщенный метод контурных уравнений. Оптимизация режимов работы замкнутых сетей с помощью установок и продольной компенсации. Оптимизация оперативного управления режимами сложно-замкнутых неоднородных сетей. Экономические режимы работы подстанций. Оптимизация режимов работы электрических сетей на основе инновационных способов уменьшения потерь мощности и энергии. Оптимизация основных сетей энергосистем по напряжению и реактивной мощности.

3.2. Примерный перечень лабораторных занятий

1. Оптимальное распределение активных мощностей между агрегатами электростанций методом относительных приростов

2. Оптимальное распределение активных мощностей между агрегатами электростанций методом динамического программирования

3. Оптимальное распределение активных мощностей градиентным методом

4. Определение относительных приростов потерь мощности в электрической сети

5. Оптимизация режимов основных сетей энергосистем по напряжению и реактивной мощности за счет изменения коэффициентов трансформации трансформаторов и автотрансформаторов связи

6. Оптимизация режимов основных сетей энергосистем по напряжению и реактивной мощности за счет изменения генерирующих мощностей источников реактивной мощности

7. Оптимизация режимов работы замкнутых электрических сетей с помощью вольтодобавочных трансформаторов

Резервные занятия

8. Оптимизация режимов работы замкнутых электрических сетей с помощью установок продольной компенсации

9. Исследование целесообразности регулирования напряжения в сетях сверхвысокого напряжения с учетом потерь на корону

10. Изучение экономических режимов работы подстанций

11. Определение оптимальных мест размыкания распределительных электрических сетей 35 – 110 кВ

4. Информационно-методическое обеспечение

4.1. Основная литература

1. Веников В.А. и др. Оптимизация режимов электростанций и энергосистем: Учебник для вузов/ В.А.Веников, В.Г.Журавлев, Т.А. Филлипова - М.: Энергоатомиздат, 1990 - 352 с., илл.

4.2. Дополнительная литература

2. Арзамасцев Д.А. и др. АСУ и оптимизация режимов энергосистем. Учебн. пособ. для студентов вузов./ Арзамасцев Д.А., Бартоломей П.И., Холян А.М. Под ред. Арзамасцева Д.А. - М.: Высш.шк.,1983 – 208 с., илл.

3. Электрические системы. Электрические расчеты, программирование и оптимизация режимов. Под ред. В.А.Веникова. Учебное пособие для электроэнерг. вузов. - М.: Высшая школа, 1973 - 320 с. илл.

4. Электрические системы. Кибернетика электрических систем. Под ред. В.А.Веникова. Учебн. пособие для электроэнергетических вузов. - М.: Высшая школа, 1974 - 328с. илл.

5. С.К. Гурский, Г.Е. Поспелов, В.Т. Федин Оптимизация режимов энергосистем. Учебное пособие по разделу курса "АСУ и оптимизация режимов энергосистем" для студентов дневного, вечернего и заочного отделения специальности "Электрические системы" (0302). Минск: БГПА, 1977 - 139 с.

6. Оптимизация режимов энергетических систем / Синьков В.М., Богословский А.В., Григоренко В.Г., Калиновский Л.А., Огородников А.А., Мозговая Э.А. Издательское объединение "Вища школа". 1976, 308 с.

7. Прокопенко В.Г., Фурсанов М.И. Лабораторный практикум по дисциплинам “Оптимизация режимов энергосистем и сетей” и “Оптимизация электроэнергетических систем”. – Минск: БНТУ, 70 с

8. Маркович И.М. Режимы энергетических систем. - М.: Энергия, - 1969, 352 с.

9. Методы оптимизации режимов энергосистем / В.М. Горнштейн, Б.П. Мирошниченко, А.В. Пономарев и др. Под ред. В.М. Горнштейна. - М.: Энергия, - 1981, - 336 с., илл.

10. С.К. Гурский, С.В. Домников, О.И. Александров. Лабораторный практикум по курсу "АСУ и оптимизация режимов энергосистемы" для студентов электроэнергетических специальностей. Часть 2. Оптимальное распределение нагрузок в энергосистеме. Минск: БПИ, 1984,-56 с.

11. Электроэнергетические системы в примерах и иллюстрациях. Учебное пособие для вузов. Ю.Н. Астахов, В.В. Ежков и др. Под ред. В.А. Веникова - М.: Энергоатомиздат, 1982 - 504 с., илл.

12. Совалов С.А. Режимы единой энергосистемы. - М.: Энергоатомиздат, 1983, - 384 с., илл.

13. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию. – Мн.: Вышэйшая школа, 1978. – 256 с.

4.3. Компьютерные программы и другие научно-методические материалы

1. Программа RASTR расчета и анализа режимов сложнозамкнутых электрических сетей.

2. Программы по распределению активных мощностей в энергосистеме – разработки кафедры “Электрические системы” БНТУ.

3. Программы по оптимизации режимов электрических сетей энергосистем разработки кафедры “Электрические системы” БНТУ.

textarchive.ru