ГлавнаяОптимизацияПостановка задачи оптимизации функции одной переменной

13. Приведите и объясните постановку задачи оптимизации функций одной переменной. Постановка задачи оптимизации функции одной переменной


Общие сведения

        1. Постановка задачи безусловной оптимизации функции многих переменных

Постановка задачи поиска минимума функции содержит:

  1. целевую функцию 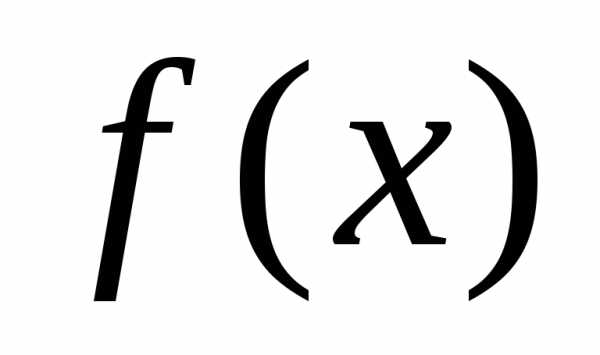где, определенную наn-мерном евклидовом пространстве.

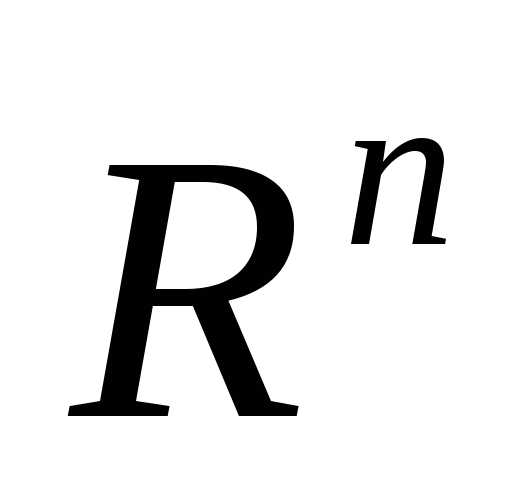  2. множество допустимых решений 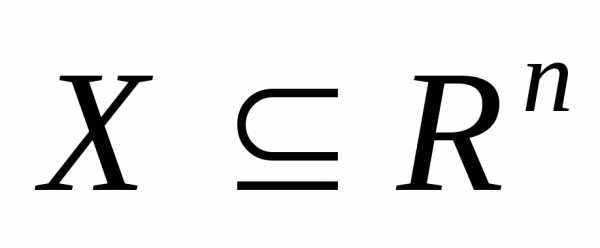, среди элементов которого осуществляется поиск.

Требуется найти такой вектор из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве:

Если множество допустимых решений 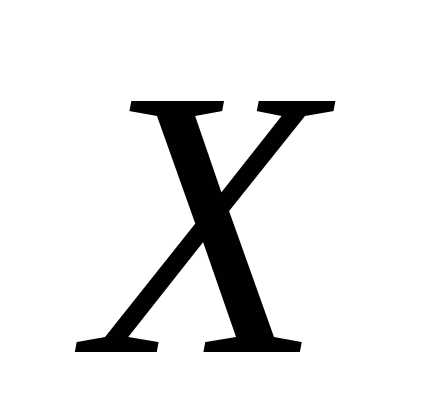задается ограничениями, накладываемыми на вектор, то решается задач условного экстремума. Если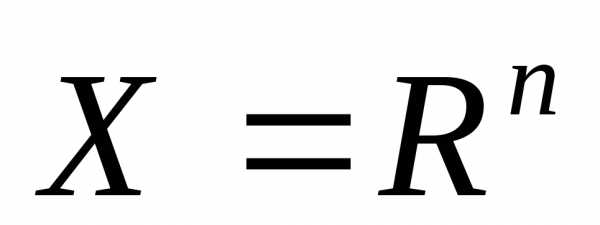, т.е. ограничения на вектор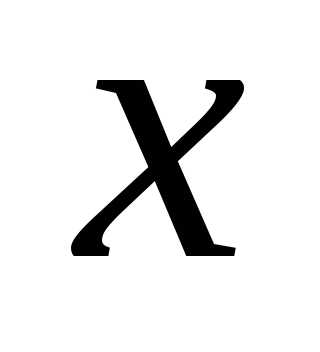отсутствуют, то решается задача поиска безусловного экстремума.

Введем обозначения:

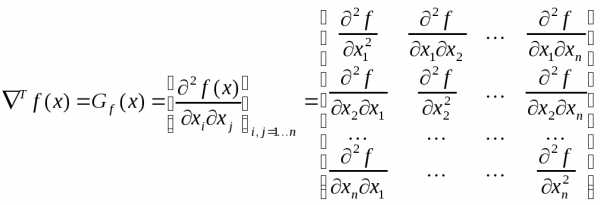
              1. Глобальный оптимум функции

      Точка 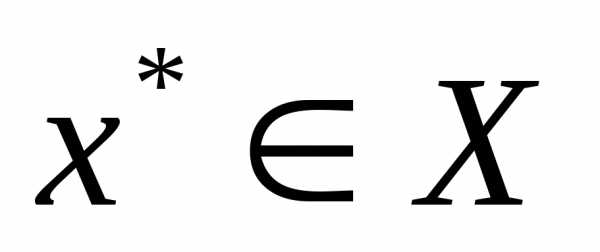называется точкой глобального минимума функции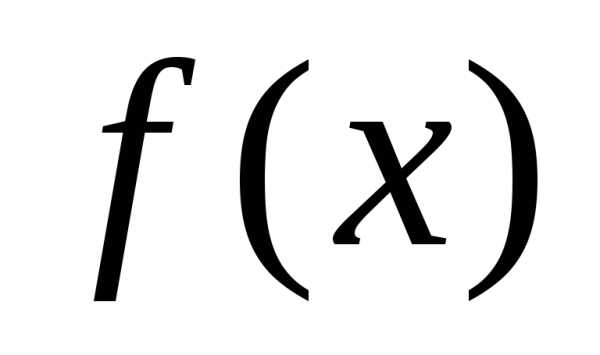на множестве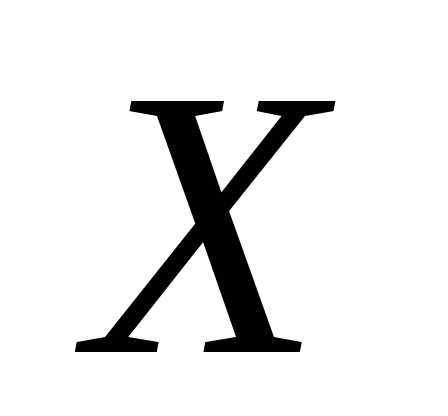, если функция достигает в этой точке своего наименьшего значения, т.е.:

      ,

              1. Локальный оптимум функции

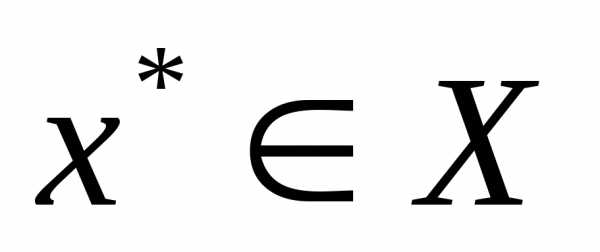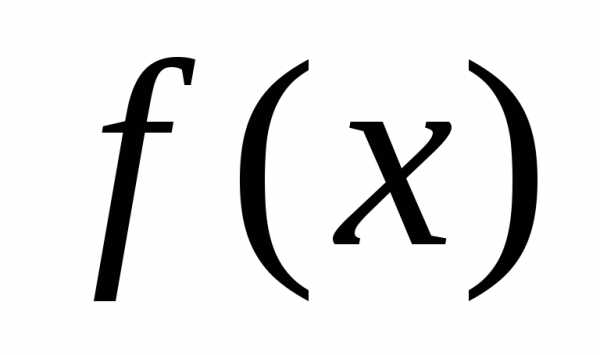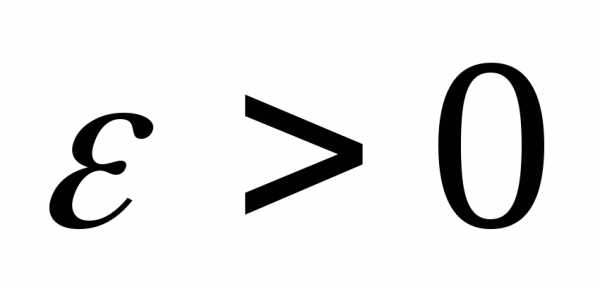      Точка называется точкой локального минимума функциина множестве, если существует, такое, что если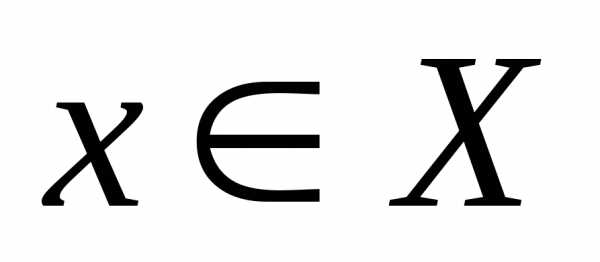и, то.

              1. Выпуклость множеств и функций

      Множество 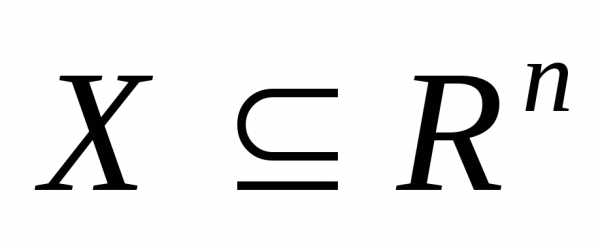называется выпуклым, если оно содержит всякий отрезок, концы которого принадлежат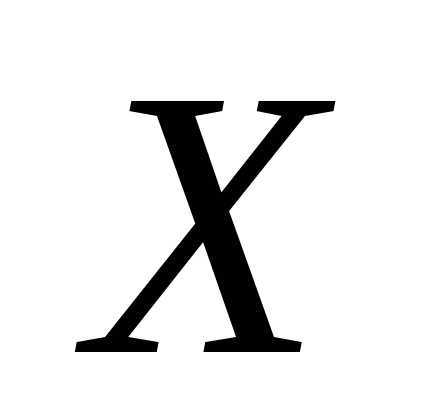, т.е. если для любых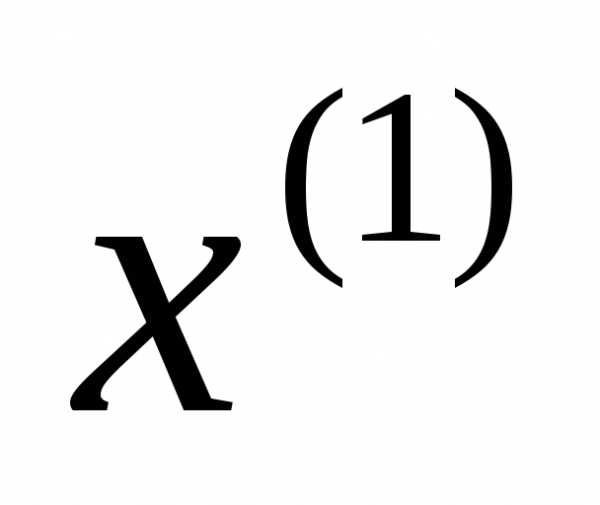

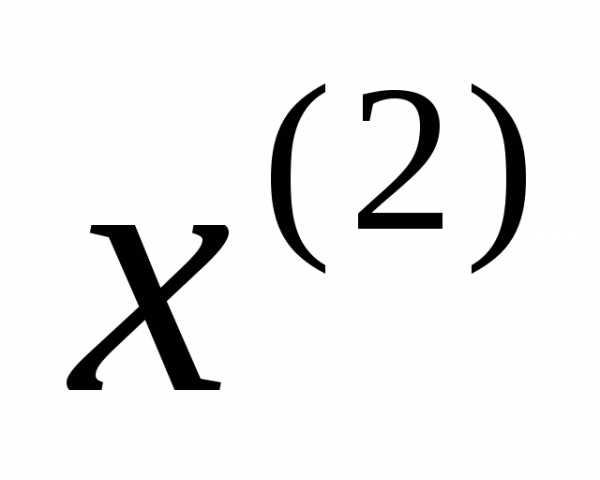
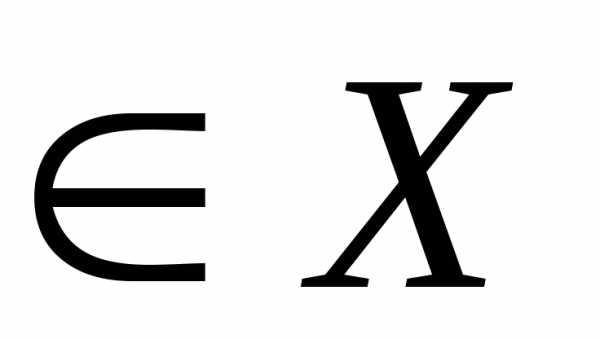      ,исправедливо.

      Функция 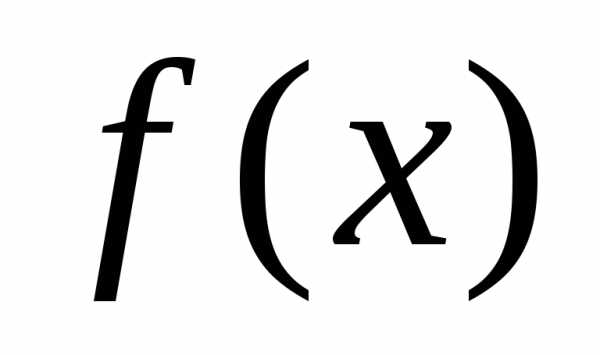, определенная на выпуклом множестве, называется выпуклой, если,,.

      Функция , определенная на выпуклом множестве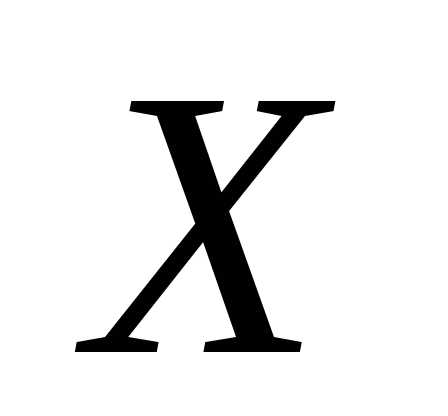, называется строго выпуклой, если,,.

      Функцию 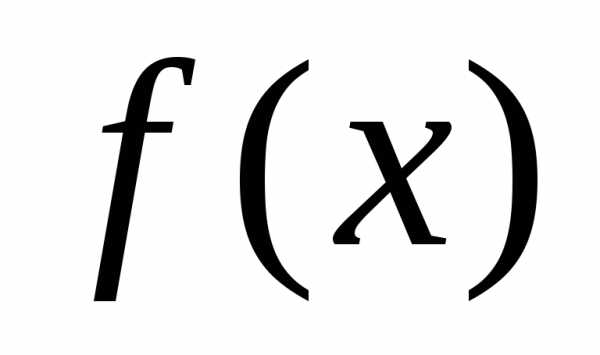называют выпуклой (строго выпуклой), если она целиком лежит не выше (ниже) отрезка, соединяющего две ее произвольные точки.

      Если 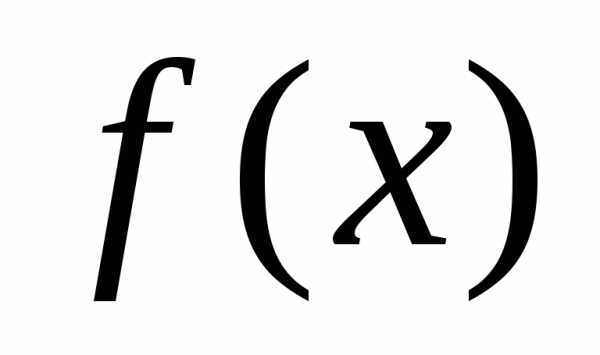выпуклая функция на выпуклом множестве, то всякая точка локального минимума является точкой ее глобального минимума на

      . Если выпуклая функция достигает своего минимума в двух различных точках, то она достигает минимума во всех точках отрезка, соединяющего эти две точки.

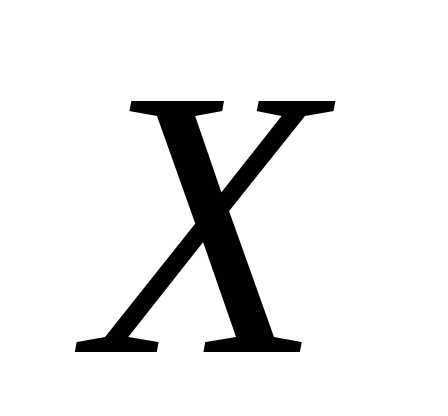
          1. Методы прямого поиска безусловного оптимума функции многих переменных

      Методы прямого поиска являются методами, в которых используются только значения функции.

      Методы прямого поиска наиболее эффективно используются если функция 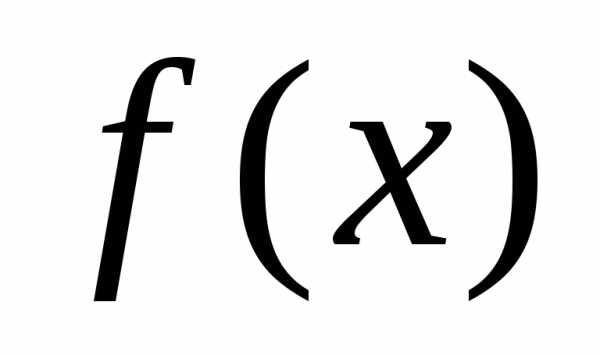и/или ее градиент разрывны в точке оптимума, аналитическое выражение градиента невозможно или затруднено, а численное дифференцирование требует больших вычислительных ресурсов.

      С общих позиций их можно разделить на эвристические (метод покоординатного спуска, метод Нелдера-Мида) и теоретические (метод сопряженных направлений). Эвристические методы реализуют процедуру поиска с помощью интуитивных геометрических представлений. Теоретические методы – с помощью фундаментальных математических теорем.

            1. Эвристические методы

              1. Метод Хука-Дживса (метод прямого поиска)

      Хук и Дживс предложили логически простую стратегию поиска, использующую априорные сведения и в то же время отвергающую устаревшую информацию относительно характера топологии целевой функции в . Этот алгоритм включает два основных этапа: «исследующий поиск» вокруг базисной точки и «поиск по образцу», т.е. в направлении, выбранном для минимизации. На рис. 1 представлена упрощенная информационная блок-схема этого алгоритма.

      Рассматриваемый алгоритм состоит из следующих операций. Прежде всего задаются начальные значения элементов x, а также начальное приращение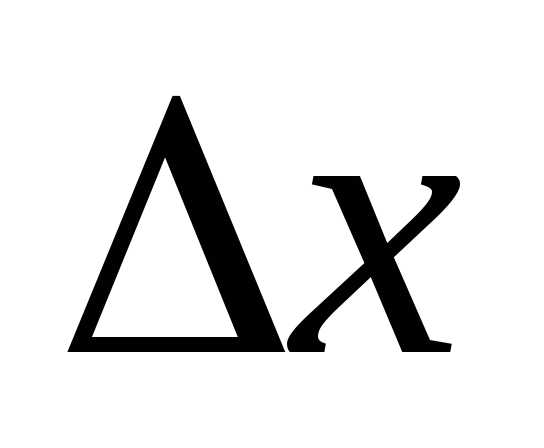. Чтобы начать «исследующий поиск», следует вычислить значение функции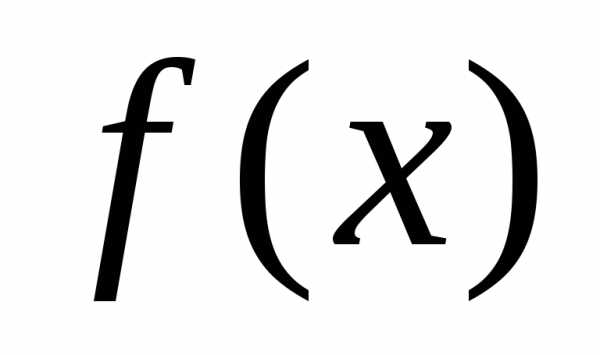в базисной точке (базисная точка представляет собой начальный вектор предполагаемых искомых значений независимых переменных на первом цикле). Затем в циклическом порядке изменяется каждая переменная (каждый раз только одна) на выбранные величины приращений, пока все параметры не будут таким образом изменены. В частности,

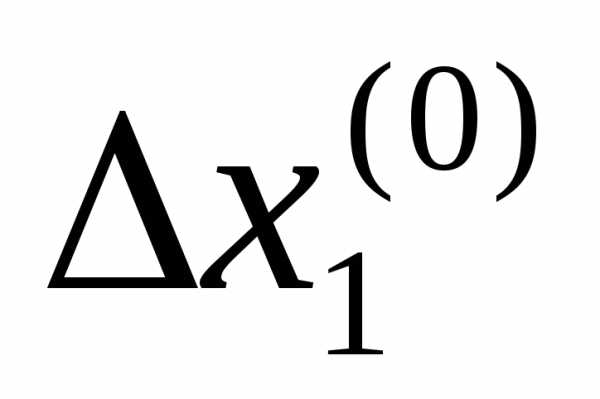      изменяется на величину, так что. Если приращение не улучшает целевую функцию,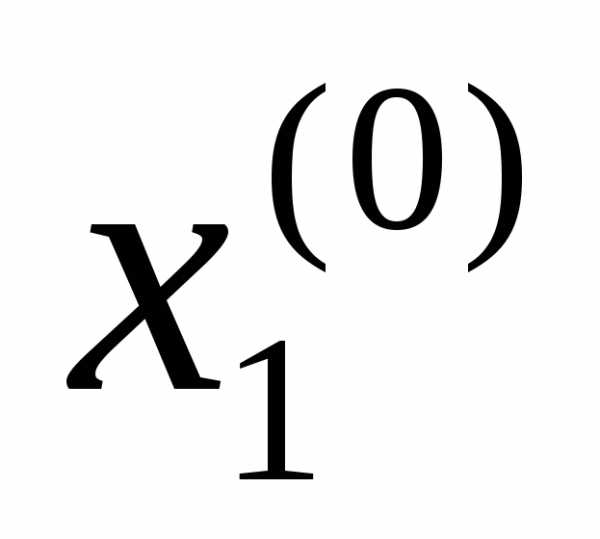изменяется на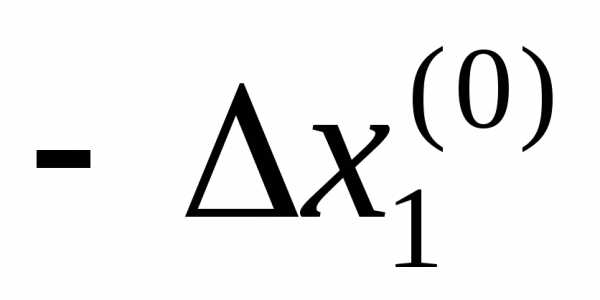и значение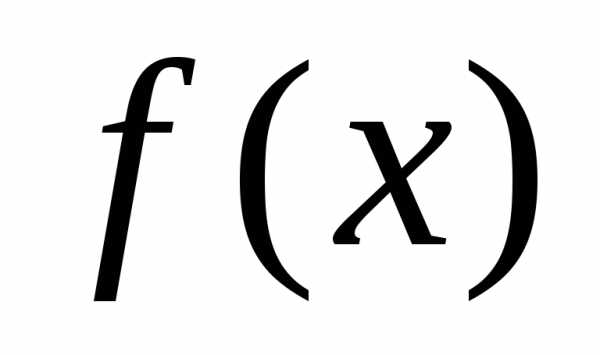проверяется как и ранее. Если значение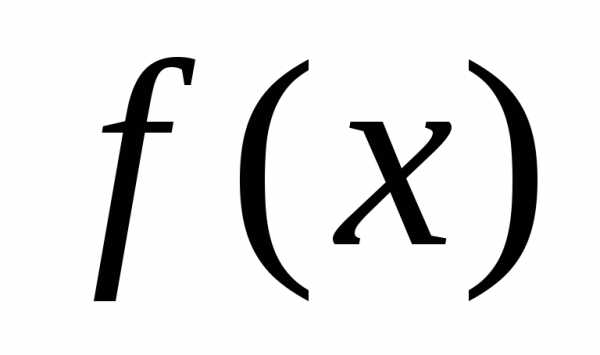не улучшают ни, ни, тооставляют без изменений. Затемизменяют на величину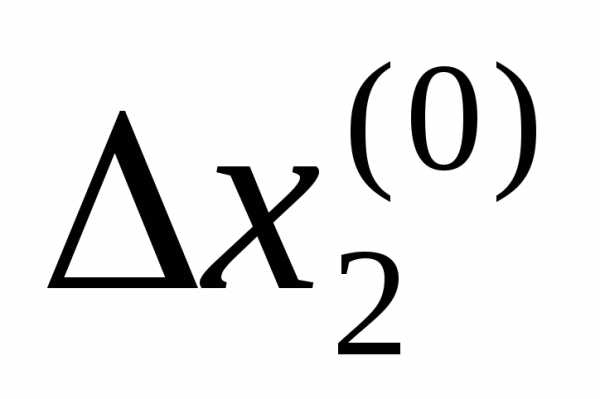и т.д., пока не будут изменены все независимые переменные, что завершает один исследующий поиск. На каждом шаге или сдвиге по независимой переменной значение целевой функции сравнивается с ее значением в предыдущей точке. Если целевая функция улучшается на данном шаге, то ее старое значение заменяется на новое при последующих сравнениях. Однако если произведенное возмущение поxнеудачно, то сохраняется прежнее значение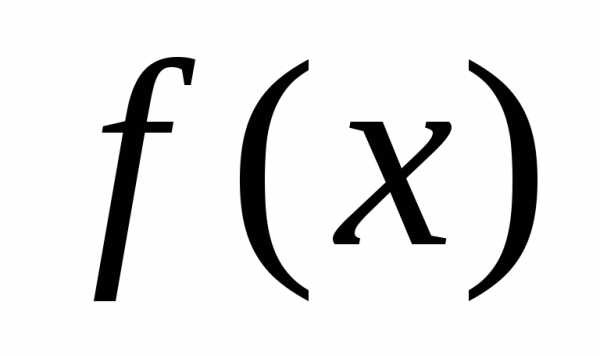
      .

      После проведения одного (или более) исследующего поиска применяется стратегия поиска по образцу. Удачные изменения переменных в исследующим поиске (т.е. те изменения переменных, которые уменьшили 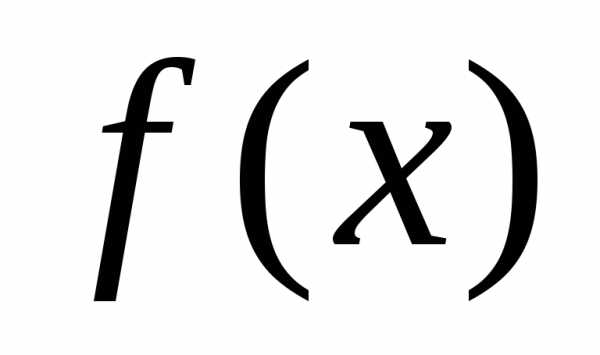) определяют вектор, указывающий некоторое направление минимизации, которое может привести к успеху. Серия ускоряющихся шагов, или поиск по образцу, проводится вдоль этого вектора до тех пор, пока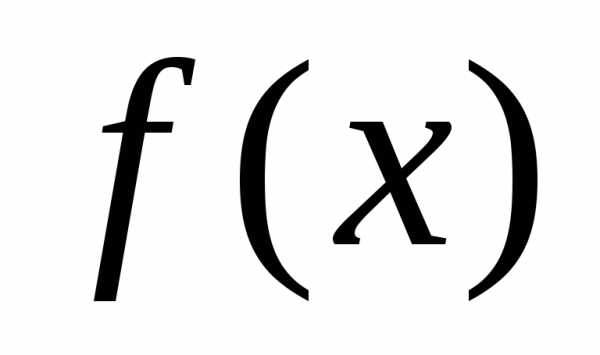уменьшается при каждом таком поиске. Длина шага при поиске по образцу в данном координатном направлении приблизительно пропорциональна числу удачных шагов, имевших место ранее в этом координатном направлении во время исследующих поисков за несколько предыдущих циклов. Для ускорения процесса оптимизации изменение размера шага

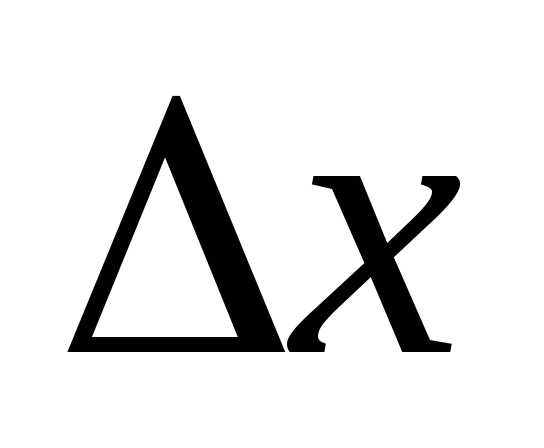      в поиске по образцу осуществляется путем введения некоторого множителя при величине, используемой в исследующих поисках. Исследующий поиск, проводимый после поиска по образцу, называется исследующим поиском типа II; успех или неудачу по данному образцу нельзя установить до завершения исследующего поиска типаII.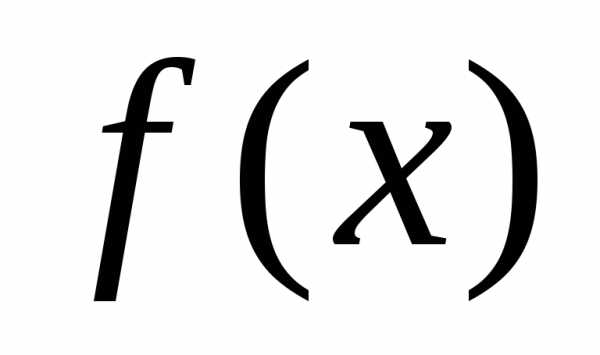

      Если 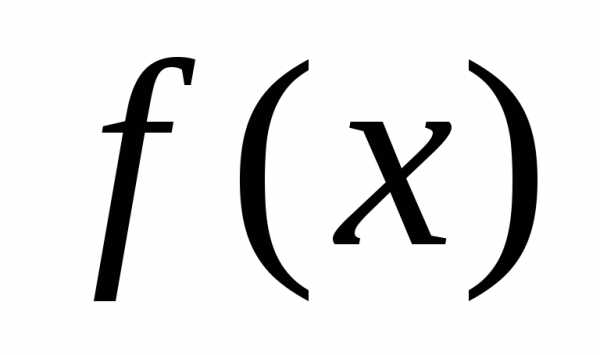не уменьшается в процессе исследующего поиска типаII, то говорят, что данный поиск по образцу неудачен, и проводится новый исследующий поиск типаIдля определения нового удачного направления. Если исследующий поиск типаIне дает нового удачного направления, то последовательно уменьшают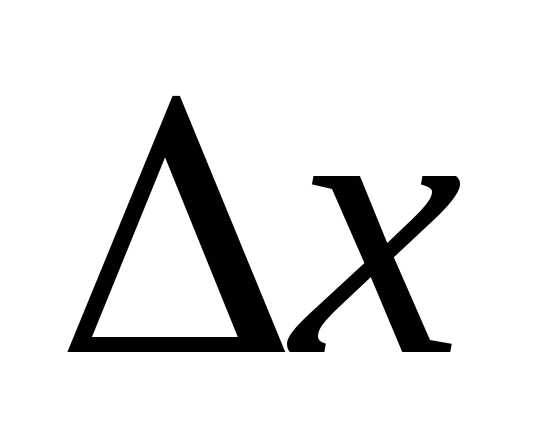, пока либо можно будет определить новое удачное направление, либо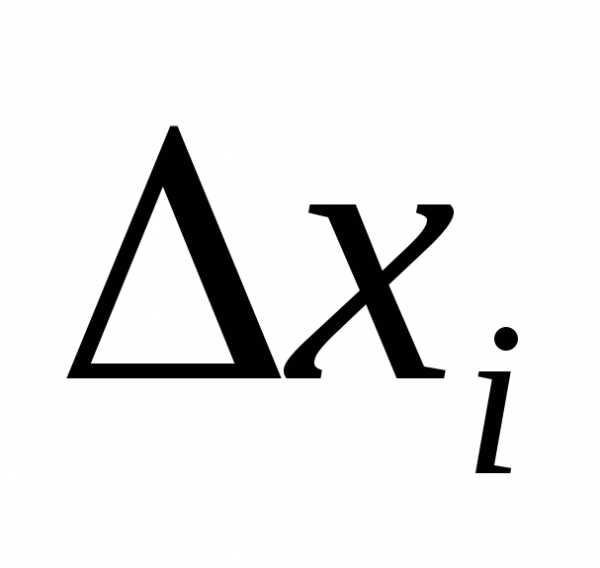

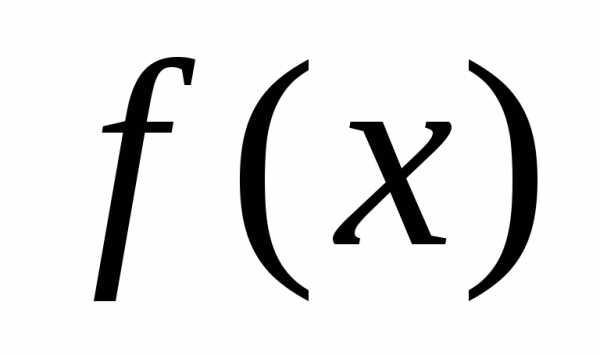      не станет меньше, чем некоторая заранее заданная величина. Невозможность уменьшить, когда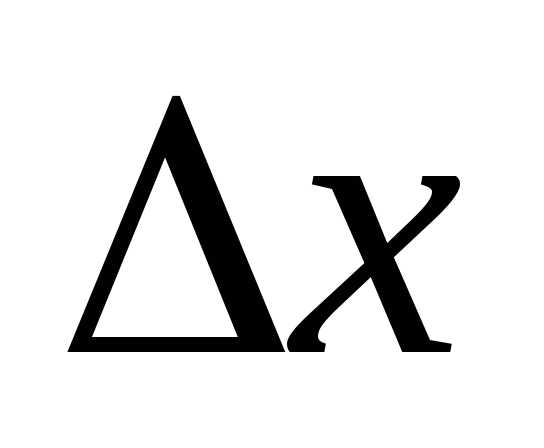достаточно мала, указывает на то, что достигнут локальный оптимум. Описанная последовательность поисков заканчивается, если оказываются удовлетворенными условия трех основных тестов. Первый тест проводится после каждого исследующего поиска и поиска по образцу: изменение целевой функции сравнивается с заранее малой величиной. Если значение целевой функции не отличается на величину, большую, чем это число, от предыдущего основного значения целевой функции, исследующий поиск или поиск по образцу считается неудачным. В противном случае проводится тест для определения, увеличилась ли целевая функция (неудача) или уменьшилась (удачный поиск) этот второй тест нужен для того, чтобы быть уверенным, что значение целевой функции все время улучшается. Третий тест проводится после неудачи в исследующем поиске на стадии уменьшения изменения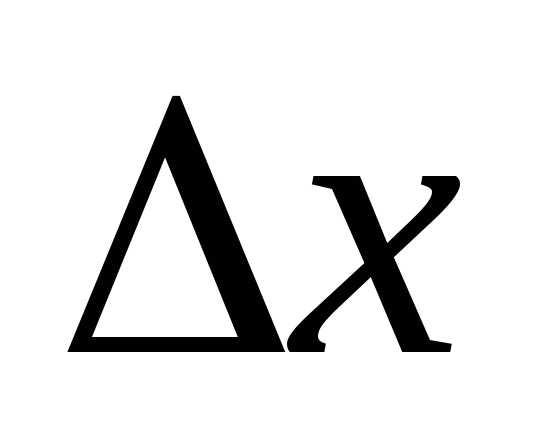
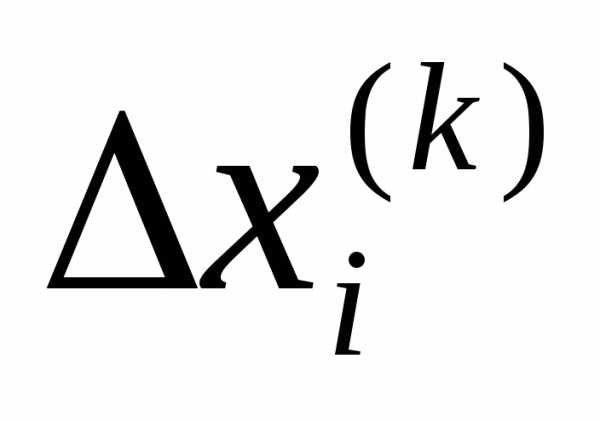      . Поиск может быть закончен, если на данном шаге изменение каждой переменнойоказывается меньше, чем некоторое заранее определенное число.

      Рис. 1. Информационная блок-схема минимизации прямым поиском

      studfiles.net

      Методы оптимизации функции многих переменных

            1. Схема безусловной оптимизации функции многих переменных

              1. Общие критерии останова численных методов оптимизации функции многих переменных

      1. Достигнута заданная норма градиента:

      2. Достигнуто предельное количество итераций:

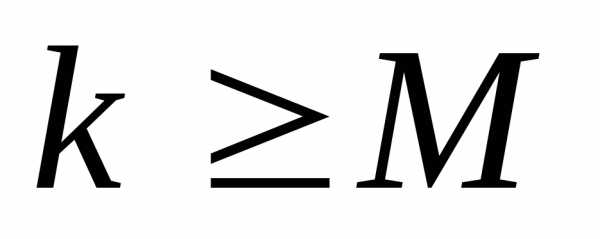
      3. Изменение значения функции и текущего приближения к точке оптимума меньше заданных величин: и

              1. Модельная схема применения методов оптимизации функции многих переменных

      Методы оптимизации функции носят итерационный характер и имеют единую модельную схему. Имея текущее приближениетекущей точкина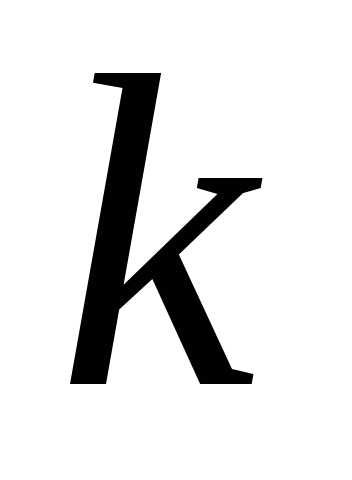-ой итерации выполняется следующая последовательность шагов:

      Шаг 1:Проверка соблюдения условия останова.

        Шаг 2:Расчет направления поиска. Вычислить не нулевой вектор S(k)- направление поиска.

        Шаг 3:Расчет длины шага. Вычислить положительное число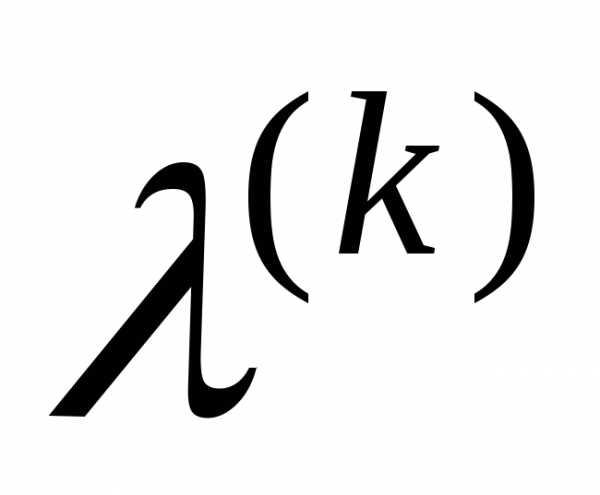, обеспечивающее выполнение неравенства:

        Шаг 4:Пересчет оценки решения.

        Переход на шаг 1.

        Эффективность алгоритмов выполненных по модельной схеме зависит от двух параметров:

          Способы определения достаточно хорошо отработаны и гарантируют убывание функции.

          Главной частью алгоритмов оптимизации, определяющих их "лицо и название", является расчет .

                1. Градиентные методы

                  1. Аффинная (линейная) модель функции многих переменных

          Аффинная модель функции 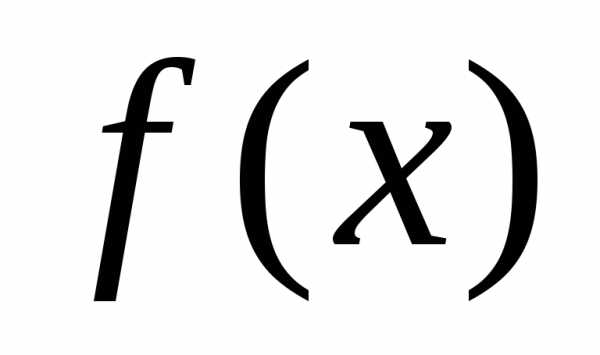имеет вид:

          ,

          тогда

          .

          Для того чтобы вектор S(k)был направлением минимизации, обычно контролируется выполнение условия:

          .

                  1. Метод Коши

          Направление вектора градиента функции является направлением возрастания функции, тогда антиградиент является направлением убывания функции в точке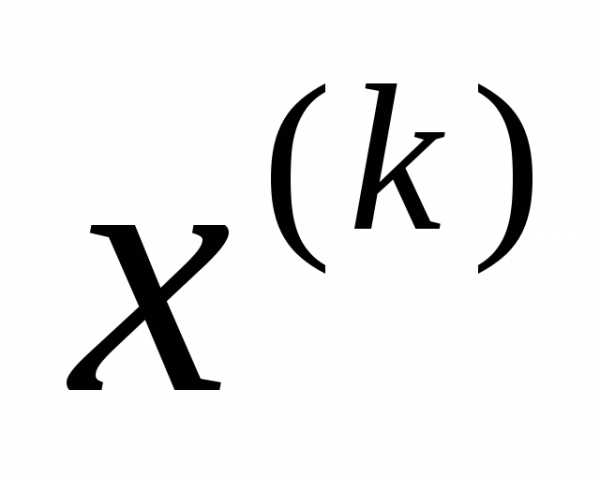. Такое направление называется направлением наискорейшего спуска. Метод, использующий такой способ расчета направления, называется метод наискорейшего спуска (метод Коши).

          Итерационная формула метода выглядит следующим образом:

          Метод Коши гарантирует сходимость для сильно выпуклых функций. Для таких функций скорость сходимости метода – линейная.

          Эффективность алгоритма зависит от вида минимизируемой функции. Алгоритм наискорейшего спуска сойдется за одну итерацию при любом начальном приближении для функции , но схо­димость будет очень медленной, например, в случае функции вида. В тех ситуациях, когда линии уровня минимизируемой функции представляет собой прямолинейный или, хуже того, криволинейный "овраг" эффективность алгоритма оказывается очень низкой. Очевидно, что хорошие результаты может давать пред­варительное масштаби­рование функций.

          Процесс наискорейшего спуска обычно быстро сходится вдали от точки экстремума и медленно в районе экстремума. Поэтому метод наискорейшего спуска нередко используют в комбинации с другими алгоритмами.

                  1. Расчет направления поиска методами сопряженных градиентов

          Другой способ расчета направления поиска S(k)учитывает информацию об изменении градиента при переходе отx(k-1)кx(k):

          В этом случае градиенты будут сопряженными.

          Методы, базирующиеся на этой формуле, называются методами сопряженных градиентов:

                    1. Метод Флетчера-Ривса

            В методе Флетчера-Ривса вычисляется по следующей формуле:

            , .

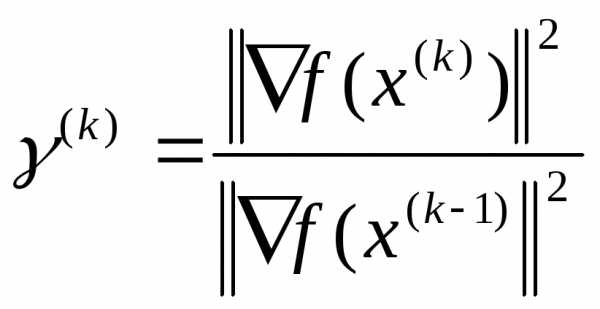            Такое вычисление обеспечивает для квадратичной функции видапостроение последовательности-сопряженных направлений(). Для квадратичных функций с матрицей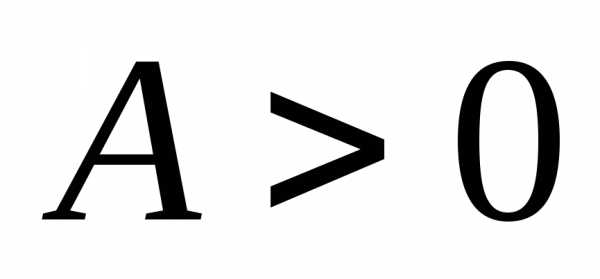метод Флетчера-Ривса является конечным и сходится за число шагов не превышающее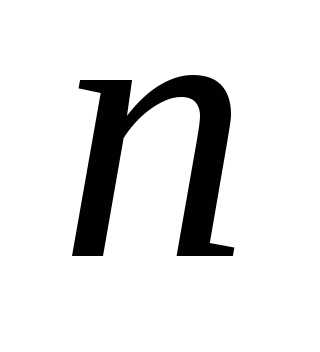. При минимизации неквадратичных функций метод не является конечным. Скорость сходимости метода:.

                    1. Метод Полака-Рибьера

            Для неквадратичных функций, как правило, используется метод Полака-Рибьера, в котором величина 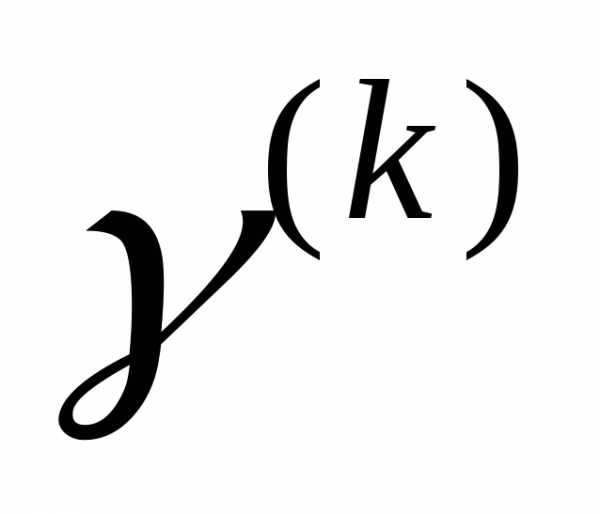вычисляется следующим образом:

            ,.

            Часто при практических реализациях метода предусматривается использование итерации наискорейшего градиентного спуска, тогда:

            ,

            Метод Полака-Рибьера гарантирует сходимость для сильно выпуклых функций со сверхлинейной скоростью сходимости.

                  1. Методы второго порядка

                    1. Квадратичная модель функции многих переменных

            Методы второго порядка основаны на использовании квадратичной модели функции в окрестности точки :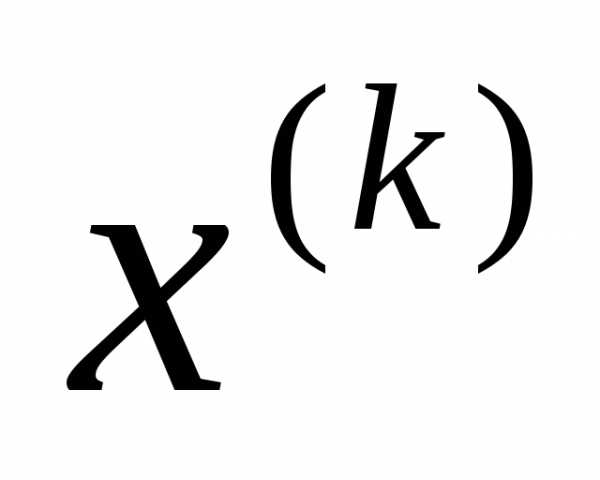

            .

            Квадратичная модель приводит к линейной модели для градиента f(x):

            Тогда направление может быть найдено из соотношения:

            ,

            .

                    1. Метод Ньютона

            Т.к. матрица Гессе является симметричной и в окрестностях точки оптимума положительно определенной.

            Вычисленное таким образом направление называется ньютоновским направлением, а метод – метод Ньютона.

            Итерационная формула метода Ньютона имеет вид:

            .

            В случае, если матрица не является положительно определенной используется вычисление точки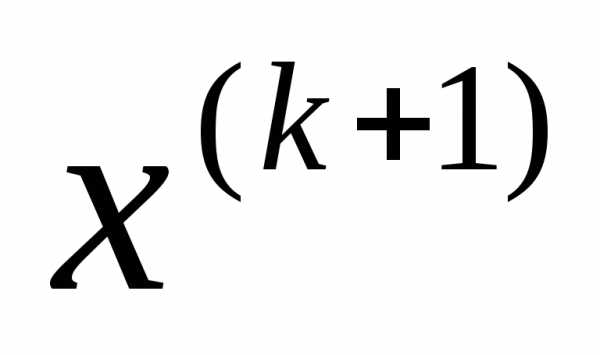по методу наискорейшего спуска:

            .

            Сходимость метода Ньютона доказана только для сильно выпуклых функций и для достаточно хорошего начального приближения. В этом случае метод имеет квадратичную скорость сходимости.

            studfiles.net

            4. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ. УСЛОВИЯ ОПТИМАЛЬНОСТИ

            4.1. Целевая функция. Локальный и глобальный оптимумы

            Оптимизационная задача в евклидовом пространстве Rn представляет собой отыскание наименьшего или наибольшего значения некоторой скалярной функции

            u = f(x), xΩ Rn,

            на заданном множестве G Ω.

            Эта задача записывается следующим образом

            f (x)→min (max),x G,

            (4.1)

            при этом функцию f называют целевой функцией или критерием оптимальности, множествоG – множеством возможных (допустимых) решений задачи (4.1), а точких G – ее допустимыми точками.

            Задача (4.1) называется задачей без ограничений или задачей безусловной оптимизации, если G=Rn и задачей с ограничениями или задачей условной оптимизации, еслиG≠Rn.

            Решить задачу (4.1) означает найти точку х* (а также соответствующее значениеf (х*)) такую, что

            f (x* ) ≤ f(x) ( f(x*) ≥ f(x)) x G

            или установить неразрешимость этой задачи. Решение х* называют оптимальным (или точкой экстремума), а значениеf (х*) – оптимумом (или экстремумом) функцииf на множествеG.

            Задачи

            f (х) → min,х G иf (х) → max,х G,

            называют соответственно задачей минимизации и максимизации функции f на множествеG.

            Оптимальное решение х* доставляет на множествеG минимум

            30

            (наименьшее значение) в задаче минимизации и максимум (наибольшее значение) – в задаче максимизации.

            Тот факт, что решение х =х* оптимально, записывают в виде

            f (x*) = min f (x) − в задачах минимизации

            x G

            и

            f(x*) = max f (x) − в задачах максимизации.

            xG

            Заметим, что задачу максимизации функции f (x) можно свести к задаче минимизации, заменивf (x) на противоположную по знаку функциюG(х) =–f (x). Это означает, что оптимальные решения задачf (x)→max иG(x)→min совпадают, а экстремальные значения функций равны по модулю (|f (x0)| = |G(x0)|). Поэтому далее, в основном, будут рассматриваться задачи минимизации. Все результаты, полученные для задач минимизации легко переформулировать применительно к задачам максимизации.

            Теория оптимизации предусматривает рассмотрение двух видов оптимумов: локальный и глобальный.

            Говорят, что точка х0 доставляет функцииf локальный (строгий локальный) минимум на множествеG, если существуетε-окрестностьU(х0,ε) точких0 такая, что

            f (x0 ) ≤ f(x) ( f(x0 ) < f(x)) x G∩U(x0 ,ε) .

            (4.2)

            Глобальный (строгий глобальный) минимум функции f на множествеG доставляет точках*, если

            f (x*) ≤ f(x) ( f(x* ) < f(x)) x G.

            (4.3)

            В соответствии с приведенными определениями точку х0 называют точкой локального минимума, аx* – точкой глобального минимума.

            Точка локального минимума не всегда является точкой глобального минимума.

            Например, функция одной переменной y=f (x),x [a,b], график которой изображен на рисунке 4, имеет две точки локального минимумах'

            31

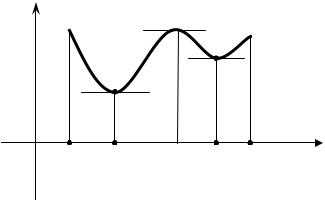
            и х" и одну глобального минимумах'.

            y

            x

            Рис.4. График функции одной переменной y=f (x),x [a,b]

            Все определения для максимума функции получаются заменой в выражениях (4.2) и (4.3) знака неравенства на противоположный.

            4.2. Разрешимость задачи оптимизации

            Вопрос о существовании решения является одним из основных при рассмотрении задач оптимизации. Если допустимое множество G конечно, то решение задачи (4.1) существует, – достаточно перебрать все точки изG и выбрать среди них точкух*, удовлетворяющую условию (4.3). В случае, когда множествоG бесконечно, задача минимизации функцииf наG может не иметь решения. Например, функция одной переменной

            1,

            x = 0

            f (x) =

            x [−1,0) (0,1]

            x2,

            не достигает наименьшего значения ни в одной точке отрезка [-1,1].Теорема Вейерштрасса (4.1), определяет широкий класс задач оп-

            тимизации, для которых решение существует:

            32

            Теорема 4.1:

            Если функция u=f (x) определена и непрерывна на замкнутом ограниченном множествеG Rn, тоx',x''G такие, что

            f (x')= minf (x)

            и

            f (x")= maxf (x)

            x G

            x G

            В теории оптимизации иногда удобно рассматривать более общую задачу оптимизации, в которой понятие решения определяется таким образом, что оно существует всегда. Для того чтобы сформулировать эту обобщенную задачу, понадобится определение точной нижней грани и точной верхней грани функции.

            Число f 0 (или символ−∞) называют точной нижней гранью илиинфинумом (от латинскогоinfinum – наименьшее) функцииf на множествеG, если неравенствоf 0 < f (x) справедливо дляx G, кроме того, для любого числаλ >f 0 найдется точках'G такая, что дляf (x')<λ.

            Тот факт, что f 0 – точная нижняя грань функцииf на множествеG, записывают в виде

            f 0 = inff (x).

            x G

            Число f * (или символ +∞) называют точной верхней гранью илисупремумом (от латинскогоsupremum – наибольшее) функцииf на множествеG, если неравенствоf * > f (x) справедливо дляx G, и для любого числаλ <f * найдется точках'G такая, чтоf (x') >λ. Для точной верхней грани используют обозначение:

            f * = supf (x).

             

            x G

             

            В рассмотренном выше примере:

             

            f 0 = inff (x)= 0

            ,

            x G

             

            но нельзя указать точку, в которой точная нижняя грань достигается. В таких случаях, задача оптимизации записывается в виде

            f (x) → inf, (f (x) →sup),x G.

            33

            studfiles.net

            13. Приведите и объясните постановку задачи оптимизации функций одной переменной

            Задача оптимизации, функция цели которой зависит от одной переменной, относится к самому простому типу оптимизационных задач и имеет вид

            Анализ задач такого типа занимает центральное место в оптимизационных исследованиях, как теоретической, так и практической направленности. Прежде всего это связано с тем, что методы оптимизации функций одной переменной используются для решения промежуточных подзадач во время поиска экстремума функций многих переменных. Важность оптимизационных задач с одной управляемой переменной обусловила разработку большого количества алгоритмов их решения.

            14. Какая функция называется унимодальной?

            15. Сформулируйте правило исключения интервалов (метод исключения интервалов)

            Методы поиска, которые позволяют определить оптимум функции одной переменной путем уменьшения интервала поиска, носят название методов исключения интервалов.

            Все методы одномерной оптимизации основаны на предположении, что исследуемая целевая функция в допустимой области по крайней мере обладает свойством унимодальности, так как для унимодальной функции W(x) сравнение значений W(t) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точки оптимума отсутствуют.

            Правило исключения интервалов. Пусть W(x) унимодальна на отрезке [a,b], а ее минимум достигается в точке x*. Рассмотрим x1 и x2, расположенные a<x1<x2<b.

            Если W(x1)>W(x2), то точка минимума W(x) не лежит в интервале (a,x1), т.е. x*Є (x1,b).

            Если W(x1)<W(x2), то точка минимума W(x) не лежит в интервале (x2,b), т.е. x*Є (a,x2).

            Это правило позволяет реализовать процедуру поиска путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается тогда, когда оставшийся подынтервал уменьшается до достаточно малых размеров.

            Главное достоинство поисковых методов - основаны на вычислении только значений функции и, следовательно, не требуют выполнения условия дифференцируемости и записи в аналитическом виде. Последнее свойство особенно ценно при имитационном моделировании.

            Процесс применения методов поиска на основе исключения интервалов включает два этапа:

            этап установления границ интервала;

            этап уменьшения интервала.

            Этап установления границ интервала

            Выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно используется эвристический метод, например, Свенна, в котором (k+1) пробная точка определяется по рекуррентной формуле

            xk+1 = xk + 2kD , k=0,1,2... (3.1)

            где

            xo - произвольно выбранная начальная точка;

            D - подбираемая величина шага.

            Знак D определяется путем сравнения значений W(x), W(xo + |D | ), W(xo -|D | ):

            если W(xo -|D| ) W(x) W(xo + |D| ), то D имеет положительное значение;

            если W(xo -|D| ) W(x) W(xo + |D| ), то D имеет отрицательное значение;

            если W(xo -|D| ) W(x) W(xo + |D| ), то точка минимума лежит между xo - |D| и xo + |D| и поиск граничных точек завершен;

            если W(xo -|D| ) W(x) W(xo + |D| ), то имеем противоречие предположению об унимодальности.

            Пример 3.

            W(x)=(100-x)2, xo=30, |D| =5.

            Определим знак D :

            W(30)=4900;

            W(30+5)=4225;

            W(30-5)=5625.

            Выполняется условие W(xo -|D| ) W(x) W(xo + |D| ), следовательно, D имеет положительное значение; x*=30.

            x1=xo+20D = 35;

            x2=x1+21D = 45, W(45)=3025 < W(x1) ® x*>35;

            x3=x2+22D = 65, W(65)=1225 < W(x2) ® x*>45;

            x4=x3+23D = 105, W(105)=25 < W(x3) ® x*>65;

            x5=x4+24D = 185, W(185)=7225 > W(x4) ® x*<185.

            Искомый интервал 65<x*<185.

            studfiles.net

            Лекция №1 Постановка задачи оптимизации

            Оптимизация САПР

            Лекция №1

            Постановка задачи оптимизации

            1. Модель оптимизируемого объекта.

            1) Анализ модели: определ. вект. вых. хар-к.

            2) Изменение модели: → структурные: кол-во переменных, кас. Ф (измен.)

            → параметрические: изм. пар-ров

            – обычно фиксирован.

            В обычно выделяют: подмножество коэф. наз-ся вектор варьируемого коэф.

            Будем считать, что . Обычно на значения коэф. накладываются ограничения, определ. услов. их физ. реализуемости.

            Скорее всего в этой последовательности наилучший вариант.

            Задача. Найти такое значение обеспеч. наилучшие вых. хар-ки (чаще всего встреч.)

            Свойства модели (влияющие на нахождение наилучш. вых. хар-ки.):

            1. Аналит. зависимость, анал. выр. исп. теорет. зн.
            Алгорит. завис-ть, вычисл. задача (система ур-й), 99%
            1. Дискрет. или непрерыв. хар-р зависимость вых. хар-к от варьир. параметров.
            Если хар-р зав. непр., то ф-ии бывают гладкие или нет (это можно оценить) и порядок гладкости.
            1. Наклад. ограничения на вар. парам. или нет? Можно ли их классифицировать, если есть?
            2. Трудоемкость процесса анализа, вычисл. производных.
            Эти свойства модели очень важны.

            Пример:

            Смысл ур-й менять нельзя, но можно менять коэффициент.

            Будем рассматривать параметр. изменения.

            1. Постановка задач оптимизации.
            Дано:
            1. Мат. модель.
            2. D – это ограничение на , вытекающее из специфики решения задачи.
            3. - то, к чему должны стремиться
            4. - целевая функция, критерий качества, функционал качества (разница между желаемым и действительным).
            Замечание. Построению F будет посвящена отдельная тема.

            Функционал отображает вектор в скаляр.

            Не всегда функционал отображает разницу между жел. и действит., но иногда и занимается поиском max и min и т.д.

            Смысл F:

            А) «как можно больше» (обратная задача)

            Б) «как можно меньше»

            В) «как можно ближе» (min разности между желаемым и действительным)

            Во всех трех случаях речь идет о поиске min.

            Найти:

            1. Обсуждение основных подходов к решению задач.
            Если сотни параметров, то этот подход не подходит.

            Нас интересует время решения этой задачи

            Нам нужно уменьшить Т.

            Типовой алгоритм:

            Начало

            Синтез структ. мод.

            Задание N, i=0

            Анализ мод.

            Вычисл.

            конец

            Задача математического программирования

            Если целевая функция или ограничения не линейны, то это задача нелинейного математического программирования.

            Если целевая функция или ограничения линейны, то это задача линейного математического программирования.

            В течение ближайших 6 тем не обращаем внимания на F.

            В зависимости от вида целевой функции и ограничений задачу можно классифицировать.

            Если ограничения заданы, то задача условной оптимизации, иначе безусловной оптимизации.

            Лекция №2

            {Если нелинейная целевая функция и нелин. }

            Дальнейшая классификация будет производиться последовательно.

            Задача нелинейного программирования.

            Условие существования экстремума целевой функции

            (задача безусловной оптимизации)

            Формулировка задачи:

            – n-мерное Евклид. пространство

            Все точки допустимы.

            I
            1. Обоснование необходимости изучения темы.
              1. Задача проще, лучше начинать с нее.
              2. Такие задачи редко, но на практике.
              3. переход от задачи условной оптимизации к безусловной.
            2. Зачем нужны условия экстремума.
              1. Для оценки задачи ( или нет min)
              2. Нужны критерии как для построения методов решения задач, так и для остановки процесса поиска.
            Основное внимание на теоремы, док-ва которых имеют конструктивный характер.

            II. Определение min целевой функции

            Определение: Скалярная функция n переменных : , т.е. вектор в скаляр наз-ся нормой вектора, если она удовлетворяет следующим трем условиям:

            Нормированное пространство.

            В рамках данного определения переход от вектора к скаляру определяется не единственным образом.

            Евклидова норма вектора

            ;

            Определение.

            Т. х наз. точка локации min ф-ии, если справедливо следующее:

            Если в определении поменять знак на противоположный, то это будет определение лок. max.

            Т. min и max называются экстремальными точками.

            Для использования в алгоритмах это определение не годится по очевидным причинам. Поэтому такое определение будет использоваться только в теоретических выкладках.

            Определение. Функция наз-ся унимодальной, если она в области определения имеет единственный min.

            Если много экстремумов, то мультимодальной.

            Min наз-ся глобальным, если внем ф-ия принимает наименьшее значение.

            В унимодальной ф-ии локальные и глобальные min совпадают.

            Поиску глобального min будет посвящена отдельная тема.

            III.  экстремума.

            Теорема Вейерштрасса.

            Если ф-ия непрерывна и ограничена на , то она там имеет глобальный min.

            Результат имеет слишком общий характер, практически ничего не дает для построения методов.

            1) Условие  экстремума гладкой функции одной переменной.

            Потребуем, чтобы функция была гладкой, чем выше порядок гладкости, тем лучше.

            Гладкая в некоторой окрестности, если есть производная в этой окрестности.

            Если первый порядок гладкости.

            Мы считаем, что - т. min в необход. Все зависит от .

            Пусть ф-ия имеет 2-й порядок гладкости.

            Необходимое условие 1-го пор. формул в виде след. теоремы (Th. Ферма):

            Пусть т. min и ф-ия диф. в этой точке ( хотя бы 1-я производная), тогда 1-я производная в т. min =0.

            Док-во Th:

            Получено противоречие, заключающееся в том, что в окрестности т.  т. с меньшим значением ф-ии, чем в т. min. Это противоречие устраняется, если производная равна 0.

            Теорема доказана.

            Обратим внимание на конструктивный характер доказательства Th.

            В док-ве показан способ перехода из текущей точки в точку с меньшим значением ф-ии.

            Производная в т. , не равна 0.

            , р надо выбирать очень маленьким.

            Это лежит в основе построения градиентных методов оптимизации.

            Основные задачи при нахождении min:

            1. Выбрать направление.
            2. Выбрать шаг.

            Необходимое условие 2-го порядка:

            Пусть т. min и в этой т. ф-ия 2 раза диф., тогда 2-я произв. ф-ии неотрицательна.

            Определение. Т. наз-ся стационарной, если произв. ф-ии в этой точке равна 0.

            Задача док-ть (на след. лекции)

            Теорема достаточное условие экстремума.

            Пусть стационарная точка и 2-я производная положительна в т. , тогда т. лок. min.

            Док-во:

            Геометрическая иллюстрация этих теорем.

            Лекция №3
            2) Условие экстремума гладкой ф-ии многих переменных.

            Док-во (необх. 2-го порядка):

            Это и док. необ. усл. 2-го порядка.

            Th. доказана.

            Далее идет обощение полученных результатов одном. ф-и на многом. случай.

            Теорема Ферма.

            Пусть - т. min и дифференцируема в окрестности этой точки.

            Тогда градиент в = 0.

            Если градиент в какой-либо точке равен 0, то эта точка наз-ся стационарной.

            Док-во:

            А это противоречит 1). Значит предположение о том, что не верно.

            Th. доказана.

            Определение:

            Матрица А наз-ся положительно определенной, если

            квадратичная форма

            Такое определение для вычислительной практики не подходит.

            Теорема (необходимое условие 2-го порядка).

            Пусть - т. min и градиент в ней не равен 0, тогда Гессиан ф-ии явл-ся не отрицательно определенной матрицей.

            Док-во:

            Отсюда вытекает, что , что и доказывает теорему.

            Определение.

            Т. будет наз-ся седловой, если

            Теорема (дост. усл-е экстремума)

            max или min седл. т.

            Линии постоянного уровня в седловой т. не замкнуты.

            Пусть

            Тогда т. явл-ся т. локального min.

            Док-во:

            Всегда можно выбрать , когда второе слагаемое будет > третьего.

            Что и доказывает теорему.

            Условие экстремума и количественные оценки положительной определенности Гессиана

            Th. Ферма имеет конструктивный характер.

            Пусть G – Гессиан.

            Если все соб. значения >0, то G полож. определено.

            Можно рассмотреть следующие случаи соб. значений:

            1. . Матрица положительно определена. Если рассматривать стационарные точки, то это точки min (локальн.).
            2. . Матрица отрицательно определена. Если стац. т. – т. max (локальный).
            3. - знаконеопределенная матрица. Т. седловая.
            4. . Матрица неотриц. определен. (полуопределенная матрица). Недостаток информации. Т. стационарна.

            Обусловленность экстремума

            Замечание. Вывод числа обусл. Матрицы смотри в дисциплине алгоритмизация вычислений.

            1. Норма матрицы.
            ставит в соответствие матрице скаляр.

            Замечание.  много способов определения нормы матрицы. Большинство из них будут рассматриваться в АВ.

            Покажем как организуется вычисление нормы матрицы на практике.

            1. Спектральная норма матрицы
            Утверждение. Значение отношения Релея на всех ненулевых векторах совпадает со значением квадратичной формы.

            (определенных на мн-ве векторов единичной длины)

            Доказать самостоятельно!

            Максимальное значение квадрата нормы матрицы равно собственному значению матрицы В.

            Лекция №4

            Задача. Показать, что

            число обусловленности

            Чем оно больше, тем хуже, тем сложнее решение задачи.

            Частный случай:

            Числа обусловленности – мера искажения окружности.

            В целевых ф-ях имеют место гребни и овраги.

            Если есть узкий и извилистый овраг, резко увеличивается кол-во шагов поиска.

            Хорошо обусловленная матрица – число обусловленности не велико.

            Плохо обусловленная матрица – число обусловленности велико.

            Выводы:

            1. Получены необх. и дост. условия экстремума гладкой ф-ии.
            2. Отмечен подход к построению(нахождению) т. min ф-ии . Док-во Th. Ферма.
            3. Услов. экстремума легко проверяется.
            4. Отмечена важная характеристика экстрем., определяемая через число обуслов.
            Условие существования экстремума гладкой функции многих переменных

            (условная оптимизация с ограничениями типа равенств)

            1. Формулировка задачи.

            функциональные ограничения

            прямые

            ограничения равенства неравенства

            n-мерная зад. гиперпараллелепипед.

            Обычно эти ограничения формируются физическими параметрами.

            Прямые ограничения будут рассмотрены в отдельной теме.

            - ограничения типа равенств

            - ограничения типа неравенств

            - ограничение типа равенств

            В нашем случае:

            Такая система имеет бесчисленное мн-во решений.

            1. Обоснование необходимости изучения этой темы

            I.Основные подходы к решению задач

            Метод замены переменных

            Из системы уравнений необходимо определить:

            Пример:

            Характеристики метода:

            1. Для использования этого метода нужна аналитическая зависимость от х услов. функции и огранич. (скорее всего будет алгоритм. зав.)
            2. если будет такое ограничение, то нельзя разделить на зависимые и независимые переменные.
            3. Даже если можно разделить на зависимые и независимые переменные, то нужна квалификация для решения системы.

            Вывод: для практики такой подход не применим, а только для решения учебных задач.

            Метод множителей Лагранжа

            Позволяет:

            1. Сформулировать необходимые условия  экстремума целевой функции при ограничениях типа равенств.
            2. Свести задачу услов. оптим. к задаче безуслов. оптимизации.

            Ф-я Лагранжа зависит от переменных.

            Пусть при некотором найдено значение целевой ф-ии для такое, что ф-я Лагранжа принимает min значение.

            =0

            Если т.  обл. огранич., видим, что min ф-ии Лагранжа будет совпадать с min ф-ии .

            Аналитический метод

            - буквы

            1. Найти
            2. Подставить найденное значение в ограничения и найти числовое значение для всех 
            3. Подставить найденные в и найти числовые значения .
            Пример:

            Теоретически можно построить численный метод:

            построить ф-ию Лагранжа. используя  методы (Ньютона), найти все стационарные точки. Провести исследование всех стационарных точек, в том числе и седловых (седло может быть разделено по перем.  и х, из всех min по х выбрать наименьший.

            Теорема (необходимое условие экстремума)

            1. Пусть
            Матрица якобы не вырождена.

            Для того чтобы была т. min, необходимо, чтобы было решением следующей системы уравнений:

            Лекция №5

            Док-во:

            Считаем, что - т. min должны получить .

            В производной огранич. исп. правило дифференцирования сложной функции.

            A

            Если матрица не вырожд., то имеет одно решение.

            Из  что могут быть определены однозначно.

            1. Суммируем все ограничения при этом i-е ограничение умножаем на .

            Изменим порядок суммирования в последнем выражении. Вынесем эл-ты типа

            Прибавим к последнему выражению необх. условие экстремума из формулы .

            Подставим , определяемые из системы .

            = 0

            Утверждение доказано (Th.)

            Интерпретация множителей Лагранжа

            Выводы по теме:

            1. Отмечены 2 подхода к решению задач (зам. пер. и мн-ли Лагранжа).
            2. Получены необх. условия экстремума для зад. услов. min с огран. типа равенства.
            3. Приведена интерпрет. мн-й Лагранжа.
            Лекция №6

            Минимизация однопараметрической унимодальной функции

                            1. Формулировка задачи

            Обоснование необходимости изучения темы.

            а) такие задачи имеют место;

            б) минимиз. многопараметр. ф-и сводится к решению последовательности задач минимиз. однопарам. ф-и.

            Лекция №7

            Особенности этой задачи:

            1) Высокая вероятность того, что унимодальна.

            1. Высокая трудоемкость, а иногда и не возможность вычисления производной:
            а) может быть не диф.

            б) если диф., то трудоемкость вычисл. производной очень высока (диф. по всем парам.)

            Вывод: эта задача очень часто решается на практике. Надо изучать специфические методы (без использования производных) отыскания min.

            Постановка задачи

            Необходимо за конечное число шагов m или с точностью, локализовать т. min.

            Можно установить связь между .

            Основа рассматриваемого метода

            Предполагая, что функция унимодальна, можно отбросить одну из частей (заведомо не содержащую т. min).

            Общая характеристика метода

            Методы делятся на 2 группы:

            1. пассивная стратегия поиска min.
            2. последовательная стратегия поиска:
            выбираются порциями в процессе min ф-и. Выбор зависит от результата min на предыдущем шаге. Основная опер. выбор и вычисление . Облад. лучшей гибкостью и дают лучшие результаты.

            Общее для 2-ой группы методов:

            Отличие: в правилах генерации точек, трудоемкостью вычисления .

            Можно классифицировать по исп. :

            1 группа: нужны качественные оценки .

            - узел интерполяции

            Метод последовательного дихотомического поиска

            На каждом шаге генерируются две точки, и в этих точках вычисляется значение функций. Наиболее трудоемкая операция – вычисление значения ф-й.

            Точки генерируются по специальному правилу:

             - малое число, сравнимое с компьютерной погрешностью, генерируются близко к середине.

            Если считать, что функция на каждом шаге вычисляется два раза, то

            Если целевая функция вычисляется очень быстро, то можно применять этот метод.

            Алгоритм:

            Основная цель: обеспечить наиболее быстрое убывание отрезка неопредел. при min количестве вычислений целевой функции. Для достижения этой цели предлагается: на 1-ом шаге вычислить 2 значения целевой функции, на всех остальных – только 1 раз. Эта идея реализуется в методе Фибоначчи и в методе золотого сечения.

            Методы Фибоначчи и золотого сечения

            Общая часть

            Будем задавать точки параметрически.

            Завис. от пар. на котор.

            При таком выборе точек справедливо следующее

            Лекция №8

            Утверждение:

            Для того, чтобы или , необходимо

            Док-во:

            Рассмотрим первый случай:

            Что и требовалось доказать.

            Рассмотрим другую ситуацию:

            Утверждение доказано.

            Эта задача решается по разному при методе Фибоначчи и методе золотого сечения.

            Метод Фибоначчи

            Основные этапы:

            Задача.

            1. Выражаем все через
            В результате получим:

            1. Подставляем в ограничение для
            Оказывается, что в этой системе неравенств  одно наиболее жесткое, которое гарантирует выполнение всех неравенств одновременно.

            1. записывается через числа Фибоначчи в целевой функции:

            Оптимальное решение имеет следующий вид:

            Наиболее быстрый метод.

            Получим аналитическое выражение для вычисления n-го числа Фибоначчи.

            1. Используется для вычисления n-го числа Фибоначчи.
            2. Используется для оценки скорости работы метода Фибоначчи.
            Предположим , то

            Замечание. при больших N метод Фибоначчи может оказаться численно неустойчивым (найденный отрезок не будет содержать т. min). Это будет происходить всегда, рано или поздно. Но нужно сделать много шагов. Тем позже будет проявляться численная неустойчивость, чем точнее .

            Метод Золотого Сечения

            Говорят, что х провод. зол. сеч. отрезка, если выполняется следующее условие:

            Имеется две точки, проводящие зол. сеч. и . и симметричны относительно центра.

            проводит золотое сечение отрезка .

            edu.znate.ru

            Постановка задачи многомерной оптимизации

            Изобретательство Постановка задачи многомерной оптимизации

            просмотров - 150

            МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

            Исследование задач многомерной оптимизации сводится к поиску точек минимума функции многих переменных на всœем пространстве соответствующей размерности. Такая задача сложнее задачи минимизации функции одной переменной, так как с ростом размерности пространства переменных возрастают объем вычислений и сложность алгоритмов, затрудняется анализ поведения целœевой функции

            Будем рассматривать функции многих переменных как функции, заданные в точках -мерного евклидова пространства . Точки представляются векторами-столбцами координат: , где символ «» - знак транспонирования. В дальнейшем, там где это не приводит к недоразумениям, символ «Т», будем опускать.

            1. Точка принято называть точкой глобального минимума функции , если для всœех выполняется неравенство . Значение принято называть минимумом функции. Множество всœех точек глобального минимума функции будем обозначать через .

            Замечание. В случае если , то вместо минимума функции иногда рассматривают ее точную нижнюю грань .

            2. Точка принято называть точкой локального минимума функции , если существует -окрестность точки :такая, что для всœех выполняется неравенство .

            Теперь сформулируем постановку задачи безусловной оптимизации.

            Дана целœевая функция переменных , определœенная не всœем пространстве . Требуется определить минимум этой функции на и точки в которых он достигается.

            Условимся для обозначения данной задачи использовать следующую краткую стандартную запись:

            (4.1)

            или ей эквивалентную , .

            Классический метод решения задачи безусловной оптимизации

            Под классическим методом решения поставленной задачи (4.1) принято понимать подход к поиску минимума функции, который основан на дифференциальном исчислении функций многих переменных.

            Напомним некоторые понятия и факты, известные из курса математического анализа.

            1. В случае если функция дифференцируема в точке , то ее приращение можно записать в виде

            ,

            где - первый дифференциал в точке .

            2. Вектор принято называть градиентом функции в точке . В малой окрестности точки градиент указывает направление наискорейшего возрастания функции , а его норма характеризует скорость этого возрастания. Градиент в точке перпендикулярен линии (поверхности) уровня , проходящей через эту точку. Очевидно, , в связи с этим

            (4.2)

            3. В случае если функция дважды дифференцируема в точке , то

            ,

            где - второй дифференциал в точке .

            Используя матрицу вторых производных (матрицу Гессе, гессиан) , второй дифференциал можно записать так: , в связи с этим

            . (4.3)

            4. Из формул (4.2) и (4.3) следует, что для малых

            (4.4)

            или

            (4.5)

            ᴛ.ᴇ. в малой окрестности точки поведение дифференцируемой функции приближенно описывается формулой (4.4), а дважды дифференцируемой - формулой (4.5), причем представление (4.5) является более точным.

            5. В случае если в точке функция дифференцируема и достигает локального минимума, то

            или (4.6)

            (крайне важное условие минимума). Точки, в которых выполнено условие (4.6), называются стационарными точками дифференцируемой функции .

            6. В случае если в стационарной точке функция дважды дифференцируема и матрица ее вторых производных положительно определœена, то есть точка локального минимума (достаточное условие минимума).

            Условия 5 и 6 лежат в основе классического метода минимизации функций, дифференцируемых во всœем пространстве . Приведем алгоритм этого метода.

            Шаг 1. Решив систему уравнений (4.6), найти всœе стационарные точки функции .

            Шаг 2. Используя достаточные условия минимума, среди стационарных точек функции найти точки локального минимума и, сравнивая значения функции в них, определить точки глобального минимума.

            Пример 4.1. Классическим методом решить задачу

            .

            Шаг 1. Запишем систему (3.12): ; ; . Решив ее, получим стационарную точку .

            Шаг 2. Находим гессиан . Так как, согласно критерию Сильвестра, эта матрица положительно определœена, заключаем, что является точкой минимума функции . Минимальное значение .

            Замечание. Классический метод минимизации функций многих переменных имеет ограниченное практическое применение в основном из-за трудностей в аналитическом решении системы уравнений (4.6). Вместе с тем, на практике часто аналитическое задание функции неизвестно, а ее значения получаются в результате измерений. Все это вынуждает заняться разработкой других методов решения задачи (4.1) более удобных для компьютерной реализации.

            Читайте также

          1. - Постановка задачи многомерной оптимизации

            МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ Исследование задач многомерной оптимизации сводится к поиску точек минимума функции многих переменных на всем пространстве соответствующей размерности. Такая задача сложнее задачи минимизации функции одной переменной, так как с... [читать подробенее]

            2. oplib.ru

            Prostoy-Site | Все права защищены © 2018 | Карта сайта