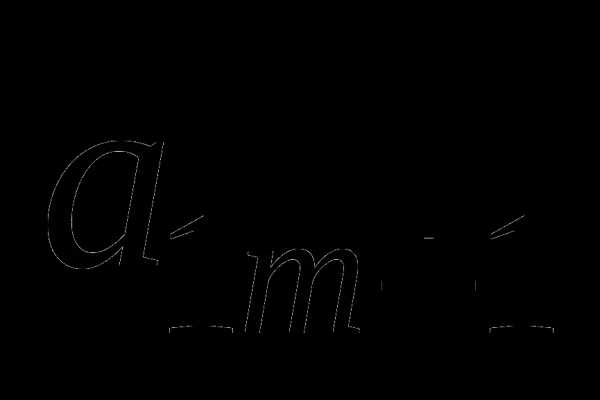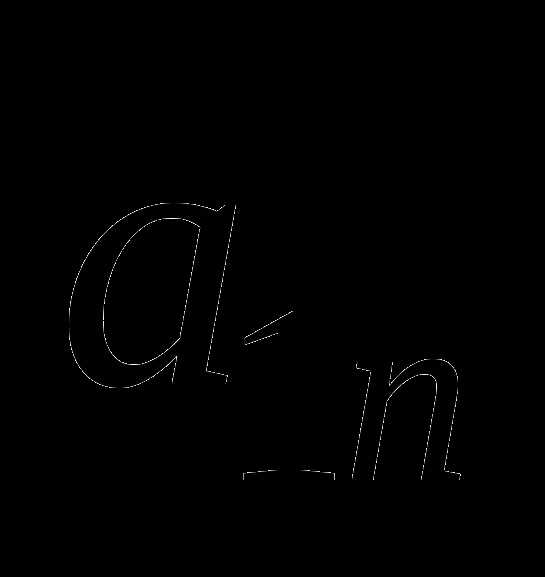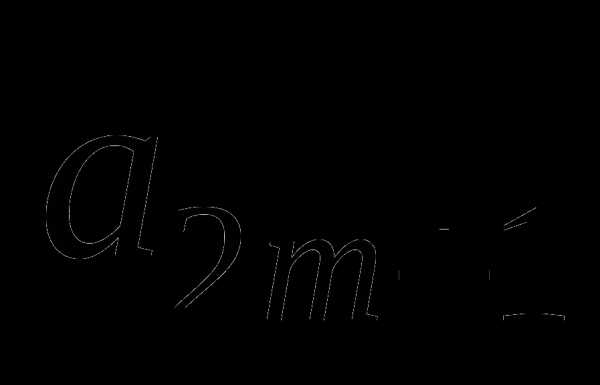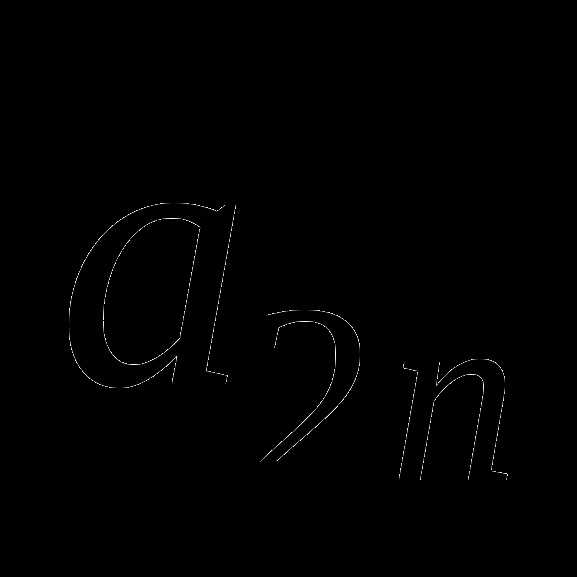Урок по теме: "Решение задач оптимизации в MS Excel". Решение задач оптимизации в microsoft excel

Решение задач оптимизации в среде Microsoft Excel

8.1. Цель лабораторной работы

Целью лабораторной работы является изучение средств Excel для нахождения оптимальных решений (значений управляемых параметров) при заданных критерии эффективности и ограничениях.

8.2. Задания к выполнению лабораторной работы

Решить предложенную преподавателем задачу оптимизации средствами Microsoft Excel 2013.

8.3. Подготовка к работе

Для выполнения работы следует ознакомиться с примером действий для выполнения заданий, рассмотренным в разделе 8.4

8.4. Примеры действий по выполнению заданий к лабораторной работе.

В качестве примера рассмотрим решение следующей задачи оптимизации.

Задача: завод производит электронные приборы трех видов (прибор А, прибор В, прибор С).

Для сборки используются микросхемы трех типов (тип1, тип2, тип3)

Стоимость изготовления приборов одинакова. Ежедневно на склад завода завозят по 500 микросхем типа1 и по 400 типа2 и типа3.

Дано (см. таблицу ниже) количество деталей каждого типа, требуемое для создания одного прибора класса A, класса B и класса C:

	Прибор А	Прибор В	Прибор С
Тип1
Тип 2
Тип 3

Найти максимальное суммарное количество приборов различного вида (А, В и С), которое может произвести завод в день, если производственная мощность завода позволяет использовать запас поступающих микросхем полностью.

В этой задаче оптимизации независимыми (управляемыми) переменными (параметрами) от которых зависит критерий эффективности (целевая функция) и ограничения, являются количество приборов типа А, типа В и типа С, производимые в день. Целевой функцией (критерием эффективности) максимум которой ищется в задаче, является суммарное количество приборов трех типов, производимое в день. Ограничения связаны с необходимостью не превышать количество микросхем разных типов, поставляемых ежедневно.

Для решения задачи оптимизации необходимо ввести данные задачи в табличном виде, задать формулы ограничений, которые должны удовлетворять решению задачи, и задать формулу для целевой функции (критерия эффективности)

Примером решения этой задачи может быть приведенная ниже последовательность действий.

1. Запустите программу Excel (Пуск -> Все программы ->Microsoft Office->Microsoft Excel 2013) и откройте книгу examples, созданную ранее.

2. Создайте новый лист, дважды щелкните на его ярлычке и присвойте ему имя «Решение задачи оптимизации».

3. В ячейки А2, A3 и А4 занесите дневной запас комплектующих — числа 500,400 и 400, соответственно.

4. В ячейки С1, D1 и Е1 занесите нули — в дальнейшем значения этих ячеек будут подобраны автоматически. В ячейках С1, D1, E1 будут находиться значения, равные количеству приборов соответственно типов А, В, С, производимых в день.

5. В ячейках диапазона С2:Е4 разместите таблицу расхода комплектующих.

	Прибор А	Прибор В	Прибор С
Тип1
Тип 2
Тип 3

6. В ячейках В2:В4 нужно указать формулы для расчета расхода комплектующих по типам. В ячейке В2 формула будет иметь вид =$C$1*C2+$D$1*D2+$E$1*E2, а остальные формулы можно получить методом автозаполнения (обратите внимание на использование абсолютных и относительных ссылок).

7. В ячейку F1 занесите формулу, вычисляющую общее число произведенных приборов: для этого выделите диапазон С1:Е1 и щелкните на кнопке «Автосумма» (Формулы ->Автосумма).

Для последующих действий нам потребуется команда «Поиск решения», но по умолчанию она отключена. Чтобы включить эту команду, необходимо проделать следующие действия:

àНа главной панели инструментов щелкнуть правой кнопкой мыши -> настройка панели быстрого доступа -> надстройки -> поиск решения (нажмите “Перейти”) ->(поставьте галочку напротив “поиск решения”) ->OK.

8. Выберите команду: Данные ->Поиск решения — откроется диалоговое окно Поиск решения.

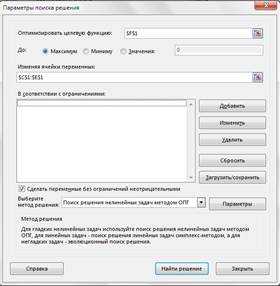
9. В поле «Установить целевую ячейку» укажите ячейку, содержащую оптимизируемое значение (F1). Установите переключатель Равной максимальному значению (требуется максимальный объем производства).

10. В поле Изменяя ячейки задайте диапазон подбираемых параметров — С1 :Е1.

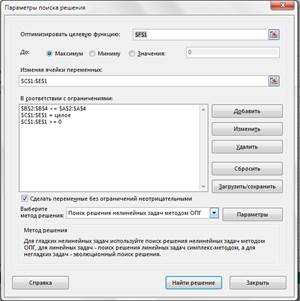
11. Чтобы определить набор ограничений, щелкните на кнопке «Добавить». В диалоговом окне «Добавление ограничения» в поле «Ссылка на ячейку» укажите диапазон В2:В4. В качестве условия задайте «<=». В поле «Ограничение» задайте диапазон А2:А4. Это условие указывает, что дневной расход комплектующих не должен превосходить запасов. Щелкните на кнопке «ОК».

12. Снова щелкните на кнопке «Добавить». В поле «Ссылка на ячейку» укажите диапазон С1:Е1. В качестве условия задайте >=. В поле «Ограничение» задайте число 0. Это условие указывает, что число производимых приборов неотрицательно. Щелкните на кнопке «ОК».

13. Снова щелкните на кнопке «Добавить». В поле «Ссылка» на ячейку укажите диапазон «С1:Е1». В качестве условия выберите пункт «цел». Это условие не позволяет производить доли приборов. Щелкните на кнопке «ОК».

14. Щелкните на кнопке «Найти решение». По завершении оптимизации откроется диалоговое окно «Результаты поиска решения».

15. Установите переключатель «Сохранить найденное решение», после чего щелкните «ОК».

16. Сохраните рабочую книгу examples.

8.3. Контрольные вопросы.

1. Как формулируется задача оптимизации в табличном виде?

2. Как формулируются критерий эффективности и ограничения, которым должно удовлетворять решение?

3. Какие программы Excel используются для нахождения оптимальных значений независимых(управляемых) переменных и соответствующего значения целевой функции?

Литература

1. «Информатика. Базовый курс» под ред. Симоновича С.В. Питер, 2010 г.

2. «Понятный самоучитель Excel 2013» Лебедев А.Н, Питер, 2014г.

student2.ru

Решение задач оптимизации в среде MS Excel - 28 Августа 2014

Содержание:

Предисловие Структура книги Рекомендации по изучению книги Благодарности Часть I. Задачи оптимизации и их основные свойства Глава 1. Общая характеристика задач оптимизации 1.1. Природа и особенности задач оптимизации 1.2. Примеры типовых задач оптимизации 1.2.1. Задача о коробке максимального объема 1.2.2. Задача о пожарном ведре 1.2.3. Задача об оптимальной диете 1.2.4. Транспортная задача 1.2.5. Задача о минимальном пути в графе 1.2.6. Задача коммивояжера 1.2.7. Задача о рюкзаке 1.2.8. Задача о назначении 1.2.9. Задача о минимальном покрывающем дереве в графе 1.2.10. Задача о максимальном потоке в сети 1.2.11. Задача водопроводчика 1.3. Методология системного моделирования 1.4. Процесс постановки и решения задач оптимизации 1.4.1. Анализ проблемной ситуации 1.4.2. Построение математической модели 1.4.3. Анализ модели 1.4.4. Выбор метода и средства решения 1.4.5. Выполнение численных расчетов 1.4.6. Анализ результатов расчетов 1.4.7. Применение результатов расчетов 1.4.8. Коррекция и доработка модели 1.5. Математическая модель задач оптимизации 1.5.1. Понятие математической модели и ее основные элементы 1.5.2. Характеристика переменных 1.5.3. Характеристика ограничений 1.5.4. Характеристика целевой функции 1.5.5. Общая классификация задач оптимизации 1.6. Основные подходы к решению задач оптимизации 1.6.1. Понятие оптимального решения задачи оптимизации 1.6.2. Проблема существования и единственности решения задач оптимизации 1.6.3. Понятие о методах и алгоритмах решения задач оптимизации 1.6.4. Структура описания задач оптимизации Глава 2. Основные приемы практической работы в среде MS Excel 2.1. Общая характеристика программы электронных таблиц MS Office Excel 2003 2.2. Основные элементы рабочего интерфейса MS Office Excel 2003 2.2.1. Главное меню 2.2.2. Стандартная панель инструментов 2.2.3. Панель инструментов Форматирование 2.2.4. Строка ввода и редактирования формул 2.2.5. Область рабочего листа 2.2.6. Область задач 2.3. Основные приемы работы с электронной таблицей 2.3.1. Ввод и форматирование данных 2.3.2. Копирование и перенос данных ячеек и рабочих листов 2.3.3. Ввод, редактирование и копирование формул 2.4. Основные виды диаграмм в программе MS Excel и приемы их построения 2.4.1. Построение графика функции одной переменной 2.4.2. Построение графика функции двух переменных Часть II. Задачи непрерывной оптимизации Глава 3. Задачи нелинейного программирования 3.1. Общая характеристика задачи нелинейного программирования 3.1.1. Математическая постановка задачи нелинейного программирования 3.1.2. Основные методы решения задач нелинейного программирования 3.2. Задача о коробке максимального объема 3.2.1. Математическая постановка задачи о коробке максимального объема 3.2.2. Решение задачи о коробке максимального объема с помощью программы MS Excel 3.2.3. Аналитическое решение задачи о коробке максимального объема 3.3. Задача о пожарном ведре 3.3.1. Математическая постановка задачи о пожарном ведре 3.3.2. Решение задачи о пожарном ведре максимального объема с помощью программы MS Excel 3.3.3. Аналитическое решение задачи о пожарном ведре 3.4. Задача о строительстве универсама 3.4.1. Содержательная постановка задачи о строительстве универсама 3.4.2. Математическая постановка задачи о строительстве универсама 3.4.3. Решение задачи о строительстве универсама с помощью программы MS Excel 3.5. Тестовые задачи нелинейного программирования 3.5.1. Задача оптимизации с целевой функцией Розенброка и ее решение с помощью программы MS Excel 3.5.2. Задача оптимизации с целевой функцией Пауэлла и ее решение с помощью программы MS Excel 3.5.3. Задача оптимизации с двумерной экспоненциальной целевой функцией и ее решение с помощью программы MS Excel 3.6. Упражнения 3.6.1. Задача Тартальи 3.6.2. Задача Ферма 3.6.3. Задача Кеплера 3.6.4. Обобщенная задача Кеплера 3.6.5. Задача Евклида 3.6.6. Обобщенная задача Евклида 3.6.7. Задача Зенодора 3.6.8. Задача Архимеда 3.6.9. Задача Еерона 3.6.10. Задача Аполлония для эллипса 3.6.11. Задача Аполлония для параболы 3.6.12. Задача Аполлония для гиперболы 3.6.13. Задача о вписанном прямоугольнике 3.6.14. Задача о вписанном треугольнике 3.6.15. Задача о вписанном конусе 3.6.16. Задача о вписанном тетраэдре 3.6.17. Задача о треугольнике 3.6.18. Задача об угле и точке 3.6.19. Задача о трех точках 3.6.20. Обобщенная задача о точках Глава 4. Задачи линейного программирования 4.1. Общая характеристика задачи линейного программирования 4.1.1. Математическая постановка задачи линейного программирования 4.1.2. Основные методы решения задач линейного программирования 4.2. Задача об оптимальной диете 4.2.1. Математическая постановка задачи об оптимальной диете 4.2.2. Решение задачи об оптимальной диете с помощью программы MS Excel 4.3. Задача о производстве красок 4.3.1. Общая постановка задачи производственного планирования 4.3.2. Математическая постановка задачи о производстве красок 4.3.3. Графическое решение задачи о производстве красок 4.3.4. Решение задачи о производстве красок с помощью симплекс-метода 4.4. Двойственная задача линейного программирования 4.4.1. Математическая формулировка двойственной задачи линейного программирования 4.4.2. Математическая постановка двойственной задачи о красках 4.4.3. Решение двойственной задачи о красках с помощью программы MS Excel 4.5. Транспортная задача линейного программирования 4.5.1. Математическая постановка транспортной задачи 4.5.2. Решение транспортной задачи с помощью программы MS Excel 4.5.3. Решение транспортной задачи с помощью метода потенциалов 4.6. Упражнения 4.6.1. Задача о производстве клея 4.6.2. Задача об оптимальной диете 4.6.3. Транспортная задача Часть III. Задачи дискретной и комбинаторной оптимизации Глава 5. Задачи целочисленного линейного программирования 5.1. Общая постановка задачи целочисленного линейного программирования 5.1.1. Математическая постановка задачи целочисленного линейного программирования 5.1.2. Основные методы решения задач целочисленного линейного программирования 5.2. Задача о рюкзаке 5.2.1. Математическая постановка одномерной задачи о рюкзаке 5.2.2. Решение одномерной задачи о рюкзаке с помощью программы MS Excel 5.2.3. Аналитическое решение одномерной задачи о рюкзаке 5.3. Задача об изготовлении часов 5.3.1. Математическая постановка задачи об изготовлении часов 5.3.2. Графическое решение задачи об изготовлении часов 5.4. Задача о планировании перевозок пассажиров 5.4.1. Математическая постановка задачи о планировании перевозок пассажиров 5.4.2. Решение задачи о планировании перевозок пассажиров с помощью программы MS Excel 5.5. Задача об изготовлении стержней 5.5.1. Содержательная постановка задачи 5.5.2. Математическая постановка задачи об изготовлении стержней 5.5.3. Решение задачи об изготовлении стержней с помощью программы MS Excel 5.6. Транспортная задача целочисленного линейного программирования 5.6.1. Математическая постановка транспортной задачи 5.6.2. Решение многопродуктовой целочисленной транспортной задачи с помощью программы MS Excel 5.7. Упражнения 5.7.1. Задача о погрузке автомобиля 5.7.2. Задача об изготовлении обуви 5.7.3. Задача об изготовлении мебели 5.7.4. Многопродуктовая транспортная задача Глава 6. Задачи оптимизации с булевыми переменными 6.1. Общая постановка задачи оптимизации с булевыми переменными 6.1.1. Математическая постановка задачи оптимизации с булевыми переменными 6.1.2. Основные методы решения задач оптимизации с булевыми переменными 6.2. Задача о рюкзаке с булевыми переменными 6.2.1. Математическая постановка одномерной задачи о рюкзаке с булевыми переменными 6.2.2. Решение одномерной задачи о рюкзаке с булевыми переменными с помощью программы MS Excel 6.2.3. Решение задачи о рюкзаке с помощью метода динамического программирования 6.3. Задача водопроводчика 6.3.1. Математическая постановка задачи водопроводчика 6.3.2. Решение задачи водопроводчика с помощью программы MS Excel 6.3.3. Аналитическое решение задачи водопроводчика 6.4. Задача о назначении 6.4.1. Математическая постановка задачи о назначении 6.4.2. Решение задачи о назначении с помощью программы MS Excel 6.4.3. Решение задачи о назначении с помощью венгерского метода 6.5. Упражнения 6.5.1. Двумерная задача о рюкзаке 6.5.2. Задача водопроводчика 6.5.3. Задача о назначении Глава 7. Задачи оптимизации на графах 7.1. Общая характеристика задач оптимизации на графах 7.1.1. Математическая постановка задачи оптимизации на графах 7.1.2. Основные методы решения задач оптимизации на графах 7.2. Задача о минимальном покрывающем дереве в графе 7.2.1. Математическая постановка задачи 7.2.2. Решение задач о минимальном и максимальном покрывающем дереве в графе с помощью программы MS Excel 7.2.3. Решение задачи о максимальном покрывающем дереве в графе с помощью программы MS Excel 7.2.4. Решение задач о максимальном и минимальном покрывающем дереве с помощью жадного алгоритма 7.3. Задача о минимальном пути в графе 7.3.1. Математическая постановка задачи 7.3.2. Решение задачи о минимальном пути в ориентированном графе с помощью программы MS Excel 7.3.3. Решение задачи о минимальном пути в графе с помощью алгоритма пометок Дейкстры 7.4. Задача нахождения максимального пути в ориентированном графе 7.4.1. Содержательная постановка задачи нахождения критического пути выполнения бизнес-процесса 7.4.2. Математическая постановка задачи 7.4.3. Решение задачи нахождения критического пути в сетевом графе с помощью программы MS Excel 7.4.4. Решение задачи нахождения критического пути в сетевом графе с помощью алгоритма расстановки постоянных пометок 7.5. Задача о максимальном потоке в сети 7.5.1. Математическая постановка задачи 7.5.2. Решение задачи о максимальном потоке в сети с помощью программы MS Excel 7.5.3. Решение задачи о максимальном потоке в сети с помощью алгоритма пометок Форда - Фалкерсона 7.6. Упражнения 7.6.1. Задача о минимальном и максимальном покрывающем дереве в графе 7.6.2. Задача о минимальном и максимальном пути в ориентированном графе 7.6.3. Задача о максимальном потоке в сети Глава 8. Задачи комбинаторной оптимизации 8.1. Общая характеристика задач комбинаторной оптимизации 8.1.1. Математическая постановка задачи комбинаторной оптимизации 8.1.2. Основные методы решения задач комбинаторной оптимизации 8.2. Задача коммивояжера 8.2.1. Математическая постановка задачи 8.2.2. Решение задачи коммивояжера с помощью программы MS Excel 8.2.3. Решение задачи коммивояжера с помощью алгоритма динамического программирования 8.3. Задача о разбиении 8.3.1. Содержательная постановка задачи 8.3.2. Математическая постановка задачи 8.3.3. Решение задачи о разбиении с помощью программы MS Excel 8.3.4. Решение задачи о разбиении с помощью алгоритма динамического программирования 8.4. Упражнения 8.4.1. Задача коммивояжера 8.4.2. Задача о разбиении Часть IV. Задачи многокритериальной оптимизации Г лава 9. Задачи многокритериального линейного и целочисленного программирования 9.1. Общая характеристика задач многокритериальной оптимизации 9.1.1. Математическая постановка задачи многокритериальной оптимизации 9.1.2. Основные подходы и методы решения задач многокритериальной оптимизации 9.1.3. Метод уступок для решения задач многокритериальной оптимизации 9.1.4. Метод минимального отклонения от идеальной точки 9.2. Задача об оптимальной диете с двумя целевыми функциями 9.2.1. Математическая постановка задачи и подходы к ее решению 9.2.2. Решение многокритериальной задачи об оптимальной диете с помощью программы MS Excel методом уступок 9.2.3. Решение двухкритериальной задачи о диете с помощью программы MS Excel методом минимального отклонения 9.2.4. Решение двухкритериальной задачи о диете с помощью программы MS Excel методом аддитивной свертки 9.3. Задача о производстве красок с двумя целевыми функциями 9.3.1. Математическая постановка двухкритериальной задачи о производстве красок 9.3.2. Графический способ построения множества Парето для двухкритериальной задачи о производстве красок 9.4. Двухкритериальная задача о рюкзаке 9.4.1. Математическая постановка двухкритериальной задачи о рюкзаке 9.4.2. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом уступок 9.4.3. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом минимального отклонения 9.4.4. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом аддитивной свертки 9.5. Упражнения 9.5.1. Двухкритериальная задача о производстве клея 9.5.2. Двухкритериальная задача о погрузке автомобиля 9.5.3. Двухкритериальная задача об изготовлении обуви Глава 10. Задачи многокритериальной булевой оптимизации 10.1. Общая характеристика задач многокритериальной оптимизации с булевыми переменными 10.2. Задача водопроводчика с двумя целевыми функциями 10.2.1. Математическая постановка двухкритериальной задачи водопроводчика 10.2.2. Решение двухкритериальной задачи водопроводчика с помощью программы MS Excel методом уступок 10.2.3. Решение двухкритериальной задачи водопроводчика с помощью программы MS Excel методом минимального отклонения 10.2.4. Решение двухкритериальной задачи водопроводчика с помощью программы MS Excel методом аддитивной свертки 10.3. Двухкритериальная задача о назначении 10.3.1. Математическая постановка двухкритериальной задачи о назначении 10.3.2. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом уступок 10.3.3. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом минимального отклонения 10.3.4. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом аддитивной свертки 10.4. Двухкритериальная задача о наборе высоты и скорости 10.4.1. Содержательная постановка индивидуальной задачи о наборе высоты и скорости летательным аппаратом 10.4.2. Математическая постановка двухкритериальной задачи о наборе высоты и скорости 10.4.3. Решение двухкритериальной задачи о наборе высоты и скорости с помощью программы MS Excel методом уступок 10.4.4. Решение двухкритериальной задачи о наборе высоты и скорости с помощью программы MS Excel методом минимального отклонения 10.4.5. Решение двухкритериальной задачи о наборе высоты и скорости с помощью программы MS Excel методом аддитивной свертки 10.5. Упражнения 10.5.1. Двухкритериальная задача о рюкзаке 10.5.2. Двухкритериальная задача водопроводчика 10.5.3. Двухкритериальная задача о назначении Часть V. Программирование задач оптимизации в среде Excel Глава 11. Алгоритмы и программы решения задач оптимизации на графах 11.1. Особенности разработки пользовательских программ в среде MS Excel 11.1.1. Среда и язык программирования Visual Basic For Applications 11.1.2. Создание пользовательской функции для вычисления двумерной экспоненциальной функции 11.1.3. Построение графика функции двух переменных 11.1.4. Программа изображения структуры неориентированного графа 11.2. Минимальное покрывающее дерево графа и его графическое изображение 11.2.1. Программа нахождения минимального покрывающего дерева графа 11.2.2. Программа изображения минимального покрывающего дерева графа 11.3. Максимальное покрывающее дерево графа и его графическое изображение 11.3.1. Программа нахождения максимального покрывающего дерева графа 11.3.2. Программа изображения максимального покрывающего дерева графа 11.4. Путь минимальной длины и его графическое изображение 11.4.1. Программа нахождения минимального пути в ориентированном графе 11.4.2. Программа изображения минимального пути в ориентированном графе 11.5. Путь максимальной длины и его графическое изображение 11.5.1. Программа нахождения критического пути в сетевом графе 11.5.2. Программа изображения критического пути в сетевом графе 11.6. Упражнения 11.6.1. Максимальный поток в сети 11.6.2. Графическое изображение максимального потока в сети Глава 12. Алгоритмы и программы решения задач комбинаторной оптимизации 12.1. Задача коммивояжера и ее решение с помощью VBA 12.1.1. Алгоритм приближенного решения задачи коммивояжера 12.1.2. Программа приближенного решения задачи коммивояжера 12.1.3. Программа изображения полного замкнутого пути в ориентированном графе 12.2. Задача о разбиении и ее решение с помощью VBA 12.2.1. Алгоритм приближенного решения задачи о разбиении 12.2.2. Программа приближенного решения задачи о разбиении 12.3. Использование программ на языке VBA в книгах MS Excel 12.3.1. Экспорт и импорт модулей с текстами программ на VBA 12.3.2. Использование шаблонов с текстами программ на VBA 12.3.3. Создание и использование надстроек пользователя с текстами программ на VBA 12.4. Внешние программы и их использование в среде MS Excel 12.4.1. Разработка внешней функции в среде Borland Delphi и ее использование в среде MS Excel 12.4.2. Разработка внешней функции в среде MS Visual Studio .NET и ее использование в среде MS Excel 12.4.3. Разработка функции нахождения минимального пути в среде Borland Delphi и ее использование в среде MS Excel 12.5. Упражнения 12.5.1. Модификация программы приближенного решения задачи коммивояжера 12.5.2. Модификация программы приближенного решения задачи о разбиении 12.5.3. Разработка программы нахождения максимального покрывающего дерева 12.5.4. Разработка программы нахождения критического пути Приложения Приложение 1. Основные понятия теории множеств, теории графов и комбинаторного анализа Множество и способы его задания Основные теоретико-множественные операции Булеан или множество всех подмножеств Отношения и способы их задания Операции над бинарными отношениями Отображение Свойства бинарных отношений, заданных на одном базисном множестве Некоторые специальные виды бинарных отношений, заданных на одном базисном множестве Отношение строгого частичного порядка Отношение толерантности Отношение эквивалентности Перестановка Сочетание Размещение Приложение 2. Назначение операций главного меню программы электронных таблиц MS Office Excel 2003 Приложение 3. Назначение операций главного меню редактора Visual Basic пакета MS Office System 2003 Список литературы Предметный указатель

radiosit.ru

"Решение задач оптимизации в MS Excel"

Здесь Вы можете скачать Урок по теме: "Решение задач оптимизации в MS Excel" для предмета : Информатика. Данный документ поможет вам подготовить хороший и качественный материал для урока.

Нестеренко Олеся Викторовна

Учитель математики и информатики

МАОУ СОШ №45 г. Калининграда

Решение задач оптимизации в MS Excel

Задача 2.4. Решить симплексным методом задачу о составлении рациона питания животных, условия которой приведены в задаче 1.2.

Задача 1.2. Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 ден. ед. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов, 2 ед. нитратов. Один килограмм корма II стоит 10 ден. ед. и содержит 3 ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов.

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 16 ед.

Решение:

Представим данные, содержащиеся в условии задачи, в табличном виде.

Питательное вещество

Число единиц питательных веществ на 1 кг корма		Необходимый минимум питательных веществ
I	II	Необходимый минимум питательных веществ
Белки	3	1	9
Жиры	1	3	6
Углеводы	1	8	8
Нитраты	2	4	16 (max)
Цена 1 кг корма, р	80	10

Составим экономико-математическую модель задачи. Обозначим x1, x2 − количество кормов видов I и II, входящих в рацион питания. Тогда общая стоимость рациона (целевая функция) запишется в виде Z = 80 x1 + 10 x2 .

C учетом того, что количество единиц питательных веществ, входящих в

рацион кормления, не должно быть меньше (больше) указанного минимума

(максимума), ограничения запишутся в виде следующих неравенств:

3 x1 +x 2 ≥ 9 − для белков,

x1 + 3 x 2 ≥ 6 − для жиров,

x1 + 8 x 2 ≥ 8 − для углеводов,

2 x1 + 4 x 2 ≤ 16 − для нитратов.

Кроме того, по смыслу задачи должно выполняться условие

x1 ≥ 0, x2 ≥ 0.

Таким образом, экономико-математическая модель задачи примет следующий вид: составить рацион питания, при котором достигается минимум

целевой функции:

Z ( X ) = 80 x1 + 10 x2 → min

при ограничениях:

(1.1)

Приводим систему линейных неравенств (1.1) к каноническому виду, вводя в каждое неравенство дополнительную неотрицательную переменную. Получим систему линейных уравнений:

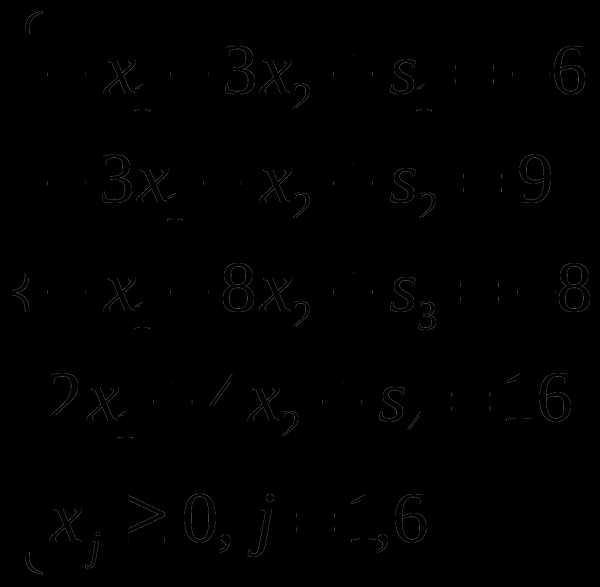(1.2)

Целевая функция будет иметь вид

Векторный анализ системы ограничений:

Расширенная целевая функция:

Вектора:

P1(x1)	P2(x2)	P3(x3)	P4(x4)	P5(x5)	P6(x6)
-6	-1	-3	1	0	0	0
-9	-3	-1	0	1	0	0
-8	-1	-8	0	0	1	0
16	2	4	0	0	0	1

Базис:Базисный вектор №1: x3Базисный вектор №2: x4Базисный вектор №3: x5Базисный вектор №4: x6

Расширенная целевая функция:

При заполнении таблицы воспользуемся следующим алгоритмом:

Алгоритм симплекс-метода

Задача должна быть приведена к каноническому виду. Система ограничений приведена к единичному базису, т.е. разрешена относительно некоторых базисных переменных (не умоляя общности, будем считать, что относительно первых m переменных) с помощью метода Жордана – Гаусса. Получено соответствующее исходное опорное решение .
Для удобства ведения вычислений записываем все в симплекс-таблицу (табл.). Столбец «Базис» содержит список базисных переменных; следующий столбец «cj базиса» содержит коэффициенты целевой функции при базисных переменных; следующие столбцы содержат коэффициенты системы ограничений при соответствующих переменных; столбец «bi» - столбец свободных членов системы ограничений. Последняя строка содержит симплекс – разности, рассчитанные по формуле и последняя ячейка содержит значение целевой функции =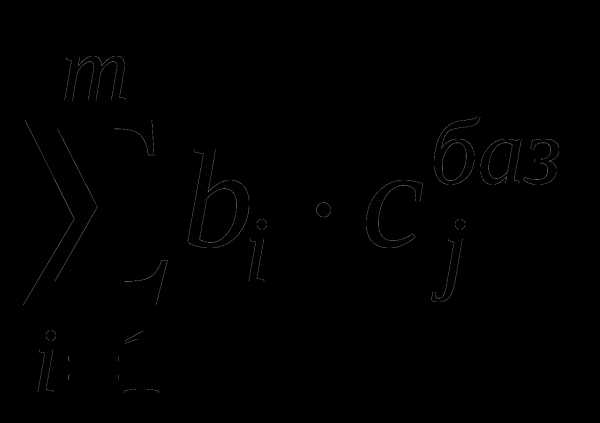. Отметим, что симплекс – разности базисных переменных всегда равны нулю.

Таблица

№

Базис	cj базиса	с1	с2	…	сm	cm+1	…	cn	bi
Базис	cj базиса	x1	x2	...	xm	xm+1	…	xn	bi
1	x1	с1	1	0		0
2	x2	с2	0	1		0
…	…	…	…	…	…	…	…	…	…	…	…
m	xm	сm	0	0		1
					…			…

Если все симплекс – разности неотрицательны, т.е. 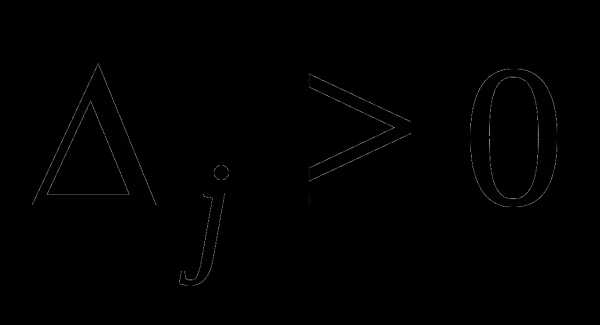, то опорный план оптимален.
Если хотя бы одна симплекс – разность отрицательна, , и в соответствующем столбце нет положительных элементов, то задача не имеет оптимального решения, т.е. .
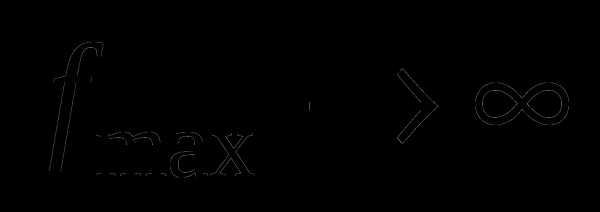Если хотя бы одна симплекс – разность отрицательна, , и в каждом столбце, имеющем отрицательную оценку, есть хотя бы один положительный элемент, то полученный опорный план можно улучшить.
Выбираем разрешающий столбец «р», которому соответствует наименьшая отрицательная оценка.
Выбираем разрешающую строку «к», которой соответствует наименьшее из отношений правых частей к соответствующим положительным элементам разрешающего столбца . Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом.
Переходим к новой симплекс – таблице, в которой будет новый базис: базисная переменная на «к» - ом месте в старом базисе меняется на новую переменную . Соответствующий вектор новой базисной переменной нужно превратить в единичный. Для этого разрешающую строку делим на , чтобы на месте разрешающего элемента появилась единица. Умножая разрешающую строку на подходящие числа и складывая её с остальными строками получаем нули в разрешающем столбце. После этого выписываем новый опорный план и пересчитываем строчку оценок. Переходим к пункту 3.

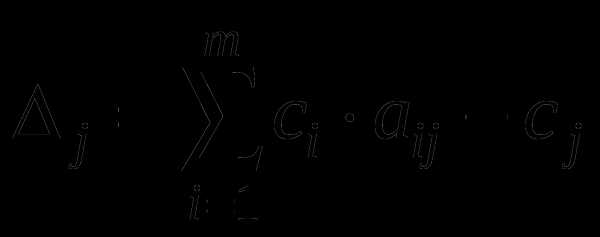
называется симплекс – разностью или оценкой.

Составляем симплекс – таблицу:

Таблица №1

№

Базис	cj базиса	с1=80	с2=10	c3=0	с4=0	c5=0	c6=0	P0(bi)
Базис	cj базиса	P1	P2	P3	P4	P5	P6	P0(bi)
1	P3	0	-1	-3	1	0	0	0	-6	6
2	P4	0	-3	-1	0	1	0	0	-9	3
3	P5	0	-1	8	0	0	1	0	-8	8
4	P6	0	2	4	0	0	0	1	16	8
			-80	-10	0	0	0	0	S min=0

Невозможно выбрать столбец замещения, так как нет положительных dj! Выберем столбец таким образом. Чтобы избавиться от недопустимого решения, т.е. от отрицательных значений в столбце свободных членов (Р0). Замещаемый базисный вектор: P3 (1-я строка) Новый базисный вектор: P1 (1-й столбец) Заменяем базисный вектор P3 на P1. Таблица №2

№

Базис	cj базиса	P0	80	10	0	0	0	0
Базис	cj базиса	P0	P1	P2	P3	P4	P5	P6
1	P1	80	6	1	3	-1	0	0	0
2	P4	0	9	0	8	-3	1	0	0
3	P5	0	-2	0	-5	-1	0	1	0
4	P6	0	4	0	-2	2	0	0	1
S min =			480	0	230	-80	0	0	0
S min =

Замещаемый базисный вектор: P5 (3-я строка) Новый базисный вектор: P2 (2-й столбец) Заменяем базисный вектор P5 на P2. Таблица №3

№

Базис	cj базиса	P0	80	10	0	0	0	0
Базис	cj базиса	P0	P1	P2	P3	P4	P5	P6
1	P1	80	4,8	1	0	-1,6	0	0,6	0
2	P4	0	5,8	0	0	-4,6	1	1,6	0
3	P2	10	0,4	0	1	0,2	0	-0,2	0
4	P6	0	4,8	0	0	2,4	0	-0,4	1
S min =			388	0	0	-126	0	46	0
S min =

Замещаемый базисный вектор: P4 (2-я строка) Новый базисный вектор: P5 (5-й столбец) Заменяем базисный вектор P4 на P5.

Таблица №4

№

Базис	cj базиса	P0	80	10	0	0	0	0
Базис	cj базиса	P0	P1	P2	P3	P4	P5	P6
1	P1	80	2,625	1	0	0,125	-0,375	0	0
2	P5	0	3,625	0	0	-2,875	0,625	1	0
3	P2	10	1,125	0	1	-0,375	0,125	0	0
4	P6	0	6,25	0	0	1,25	0,25	0	1
S min =			221,25	0	0	6,25	-28,75	0	0
S min =

Замещаемый базисный вектор: P6 (4-я строка) Новый базисный вектор: P3 (3-й столбец) Заменяем базисный вектор P6 на P3. Таблица №5

№

Базис	cj базиса	P0	80	10	0	0	0	0
Базис	cj базиса	P0	P1	P2	P3	P4	P5	P6
1	P1	80	2	1	0	0	-0,4	0	-0,1
2	P5	0	18	0	0	0	1,2	1	2,3
3	P2	10	3	0	1	0	0,2	0	0,3
4	P3	0	5	0	0	1	0,2	0	0,8
S min =			190	0	0	0	-30	0	-5
S min =

Невозможно выбрать столбец замещения, так как нет положительных dj! Получено оптимальное решение.

x2	x3	x4	x5	x6
2	3	5	0	18	0

Из таблицы получим значения переменных целевой функции:

Целевая функция: S min = 80·2+10·3 И в результате: S min = 190; Ответ: x1=2; х2=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.

Решение задачи с помощью MS EXCEL

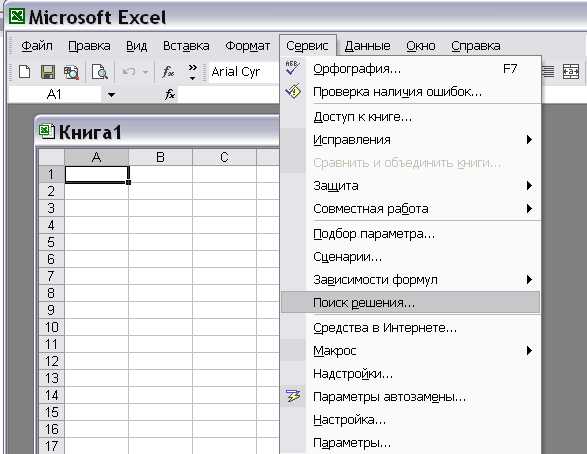
Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис» (рис. 1).

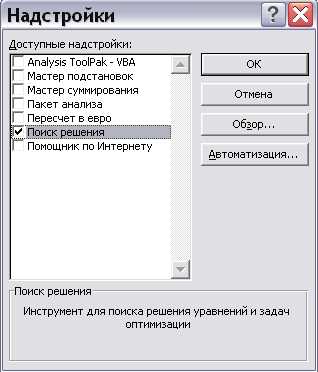
Если в версии Excel, установленной на Вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения» (рис. 2).

Рис. 1

Рис. 2

Рассмотрим использование данной надстройки на примере. Решим с её помощью задачу, математическая модель которой строилась. Математическая модель задачи имеет вид:

целевой функции:

Z ( X ) = 80 x1 + 10 x2 → min

при ограничениях:

Составим шаблон в редакторе Excel, как показано на рис. 3

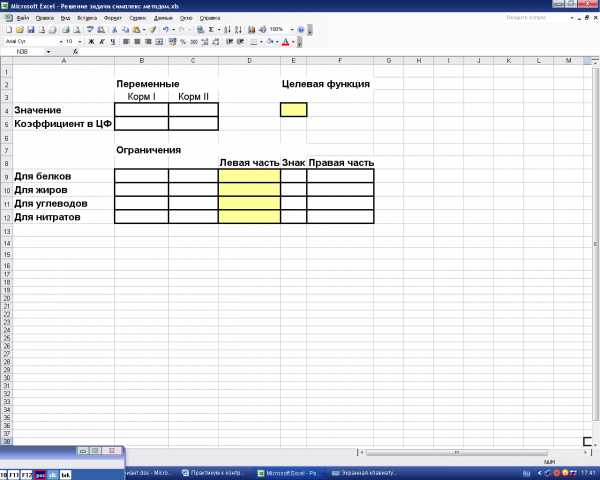
Рис.3. Шаблон оформления задачи

Теперь занесём данную в задаче числовую информацию (рис. 4).

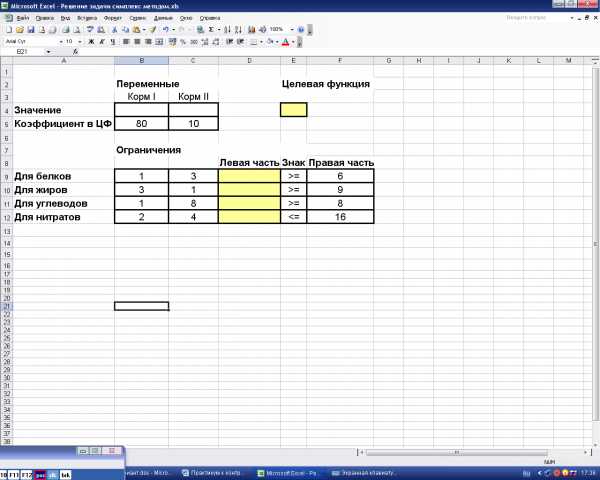
Рис.4. Исходные данные задачи

В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем листе.

Ячейки B4 – С4 называются в Excel изменяемыми (в нашей модели это неизвестные переменные), т.е., изменяя их Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).

Теперь необходимо ввести формулы. В нашей математической модели, целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение можно рассматривать как произведение вектора (80,10) на вектор (Х1,Х2).

В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. В ячейку Е4 необходимо вызвать данную функцию, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном случае, это В5:С5) и ячеек, в которые в результате решения будут помещены значения Х1 и Х2 (ячейки В4:С4) (рис. 5).

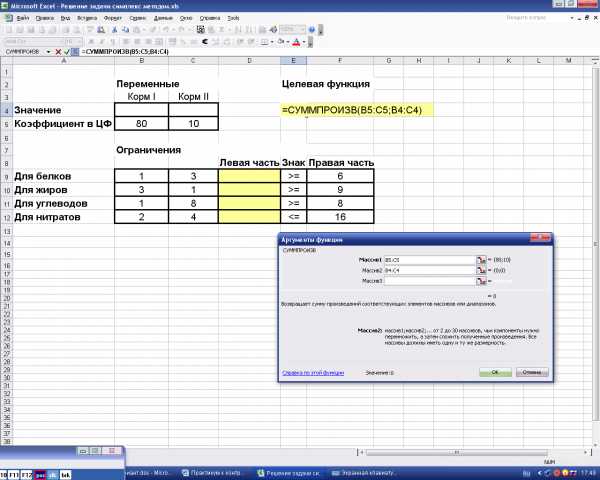
Рис.5. Вызов функции СУММПРОИЗВ.

Каждая левая часть ограничения тоже представляет собой произведение двух векторов: соответствующей строки матрицы затрат и вектора неизвестных. То есть, выражение Х1+3Х2 (для первого ограничения Х1 + 3Х2 6) будем рассматривать как произведение вектора коэффициентов (1,3) и вектора переменных (Х1,Х2).

В ячейке, отведенной для формулы левой части первого ограничения (D9), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов В9:С9 и адрес значений переменных В4:С4 (рис. 6).

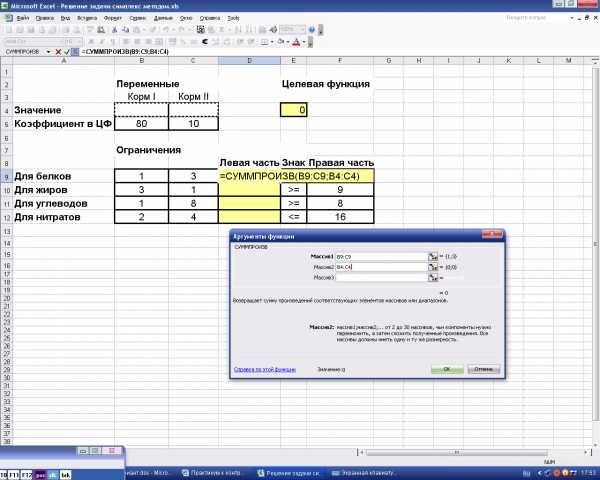
Рис.6

В четыре оставшиеся ячейки графы «Левая часть» вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введёнными формулами показан на рис.7.

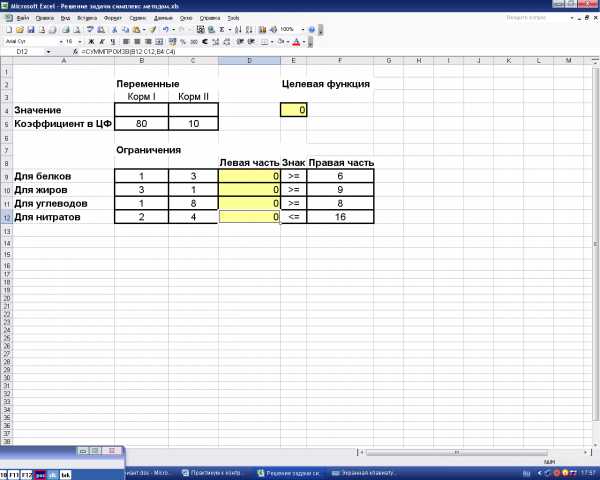
Рис.7

Важно, чтоб к моменту вызова сервиса «Поиск решения» на рабочем листе с задачей должны быть занесены формулы для левых частей ограничений и формула для значения целевой функции.

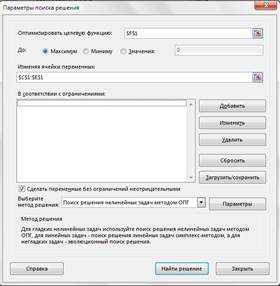
В меню Сервис выбираем Поиск решения. В появившемся окне задаём следующую информацию:

в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Е4;
«флажок» устанавливаем на вариант «максимальному значению», т.к. в данном случае, целевая функция дохода подлежит максимизации;
в качестве изменяемых ячеек заносится адрес строки значений переменных В4:С4;
справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 8)

Рис.8 Форма для занесения одного ограничения ЗЛП

Рис.9 Занесение первого ограничения задачи

в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения D9, выбирается требуемый знак неравенства (в нашем случае, F9 (рис. 9).
аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК».

Таким образом, окно «Поиск решения» с занесенной информацией выглядит следующим образом (рис.10):

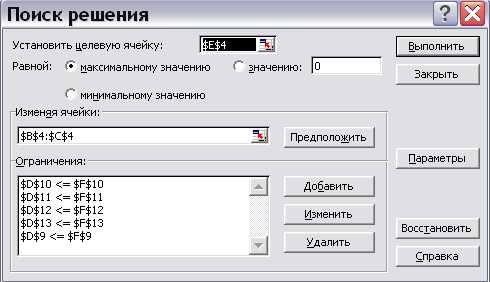
Рис.10.

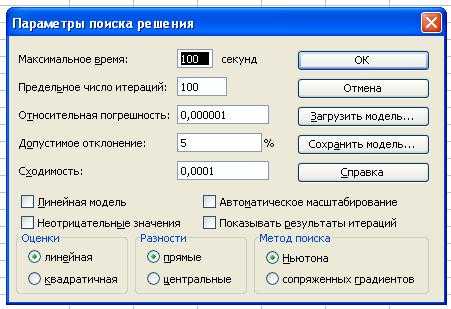
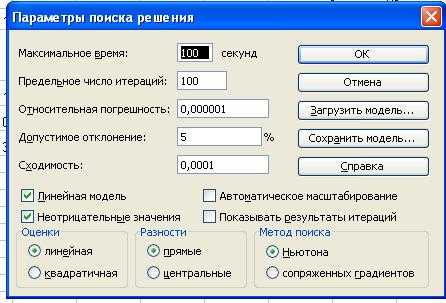
Далее необходимо нажать кнопку Параметры, установить «флажки» «Линейная модель» и «Неотрицательные значения», поскольку в данном случае задача является ЗЛП, а ограничение 6) требует неотрицательности значений (рис.11).

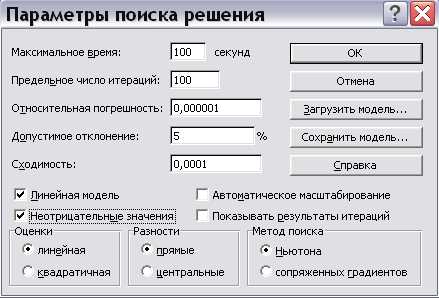
Рис.11 Установка параметров

Затем следует нажать «ОК», «Выполнить», после чего появляется окно результата решения (рис.12).

Рис.12. Окно результата решения

Если в результате всех действий получено окно с сообщением «Решение найдено», то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав «ОК». В результате получено решение задачи из примера 1. (рис.13).

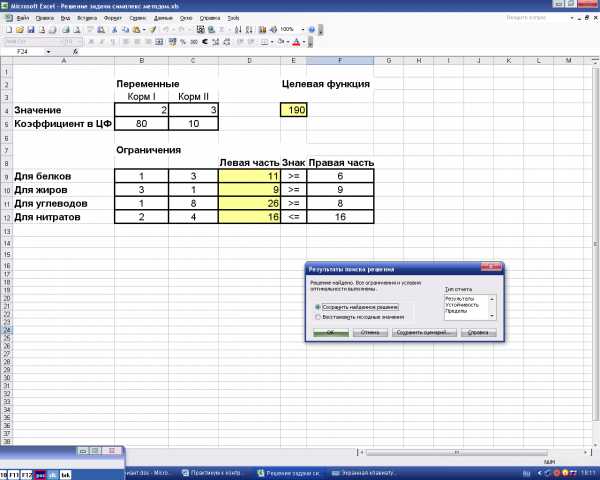
Рис.13 Результат применения «Поиска решения»

Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рис.14), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).

Рис.14. Сообщение об ошибке

В данном разделе рассмотрен общий формат решения задач оптимизации в Excel. В зависимости от экономических моделей, выполняют его соответствующие модификации.

Ответ: x1=2; х2=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Высшая математика для экономистов / Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
Горчаков А.А., Орлова И.В. Компьютерные экономико - математические модели. – М.: Компьютер, ЮНИТИ, 1995.
Ерохин Н.М., Орехов Н.А., Сидоренко А.В. Статистические модели и планирование экспериментов в экономике: Методическое пособие. – Калуга: КФ МГТУ, 1994.
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М., 1997.
Исследование операций / Под ред. М.А. Войтенко и Н.Ш. Кремера. – М.: Экономическое образование, 1992.
Исследование операций в экономике: Учебное пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М., И.М. Тришин, М.Н. Фридман; под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2004.
Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. – Минск: Вышэйшая школа, 1994.
Математическое программирование / Под ред. Н.Ш. Кремера. – М.: Финстатинформ, 1995.
Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике: Учебное пособие для вузов / Под ред. проф. Н.А. Орехова. – М.: ЮНИТИ-ДАНА, 2004.
Орехов Н.А., Сахаров Г.В., Карпушин А.А. Введение в моделирование экономических процессов и явлений. – Калуга: КФ МГЭИ, 1997.
Сборник задач и упражнений по высшей математике: математическое программирование / Под ред. А.В. Кузнецова. – Минск: Высшая школа, 1995.
Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.

docbase.org

Решение задач оптимизации в среде Microsoft Excel

приобрестиРешение задач оптимизации в среде Microsoft Excelскачать (533 kb.)Доступные файлы (1):

n1.docx

Вариант 20:

На мебельной фабрике требуется раскроить 5000 прямоугольных листов фанеры размером 4х5 м каждый, с тем чтобы получить два вида прямоугольных деталей: деталь А должна иметь размер 2х2 м; деталь Б- размер 1х3 м. необходимо чтобы деталей А оказалось не меньше чем деталей Б. Каким образом следует производить раскрой, чтобы получить минимальное (по площади) количество отходов?

Вариант 55:

Фирма по прокату автомобилей «Золотое кольцо России» собирает заявки на аренду во всех городах России. Клиент имеет возможность получить автомобиль в любом удобном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своем родном городе. Работники фирмы забирают оставленные автомобили и перегоняют их для передачи новым клиентам. Сейчас 4 автомобиля компании оставлены в Клину, 3 – в Ростове Великом, 6 – в Ярославе и 1 – в Серпухове. Имеются заказы на 5 автомобилей во Владимире, на 3 в Санкт-Петербурге и на 6 в Москве.

Расстояние между городами (в км) приведены в следующей таблице:

	Владимир	Санкт-Петербург	Москва
Клин	300	550	100
Ростов Великий	200	620	200
Ярославль	350	570	250
Серпухов	250	700	150

Составьте план, по которому следует перегонять автомобили новым клиентам. Ориентируйтесь на минимизацию расстояния, которое пройдут все перегоняемые автомобили.

Вопросы:

Чему равно минимальное расстояние, которое должны пройти все автомобили?

Сколько автомобилей следует перегнать в Москву из Ярослава?

Насколько увеличится минимальное расстояние, которое должны пройти все автомобили, если дополнительно стало известно, что еще один автомобиль оставлен в Серпухове и еще один клиент появился в Москве?

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧ.ВАРИАНТ 20

Константы
1. Обозначим через mij– количество листов вида i, полученных при раскрое листа фанеры j-способом.

i=1, 2 j=1, 2, 3

mij=

Пусть сj- количество отходов полученных при раскрое j-м способом.

С1-1 с2-2 с3-0

Обозначим через N количество листов. N=5000

Переменные
1. Обозначим через хj- количество единиц материала, раскраиваемых по j-му способу.
2. Обозначим через Fk фактическое количество заготовок k.
3. Обозначим через S количество отходов, которые останутся после раскроя.
Решение
1. Зададим математическую модель нахождения фактического количества заготовок k.
2. Зададим математическую модель нахождения общего количества отходов . Его минимизация является целью решения задачи:

3.3. Ограничения

3.3.1. Необходимо чтобы деталей А оказалось не меньше чем деталей Б. F1>=F2

3.3.2. Количество раскроенных листов должно быть равно N.

3.3.3. Количество должно быть целым числом.

3.3.4 Так как х количество деталей, то они не могут быть отрицательным т.е. Хj>=0.

ВАРИАНТ 55

Константы

1.1. Обозначим через mij- расстояние между i-м городом, в котором оставлены машины, и j-м городом, куда нужно перевезти.

300	550	100
200	620	200
350	570	250
250	700	150

I=1, 2, 3, 4 J=1,2,3

mij=

1.2. Сi- количество автомобилей оставленных в i-м городе.

C1 - 4 C2– 3 C3 - 6 C4 - 1

1.3. Nj- количество автомобилей в j-м городом, куда нужно перевезти.

N1– 5 N2– 3 N3– 6

2. Переменные

2.1. Обозначим через хij– число перевозок из i-ого города в j-ый город.

2.2. S- Суммарное пройденное расстояние.

3. Решение

3.1. Математическая модель количества увезенных машин из i-го города

Математическая модель количества перевозок в j-ый город

3.2. Функцией цели является суммарное пройденное расстояние

3.3. Ограничения.

3.3.1. Число перевозок должно быть целым.

3.3.2. хij >=0

3.3.3. 3.3.4 РЕШЕНИЕ ЗАДАЧ СРЕДСТВАМИ ЭЛЕКТРОННЫХ ТАБЛИЦ

Вариант 20

АНАЛИЗ НАЙДЕННОГО РЕШЕНИЯ

Количество листов раскроенных первым способом – 2000, вторым – 0, третьим – 3000. Число полученных деталей А- 14000, деталей Б – 14000.

Вариант 55

АНАЛИЗ НАЙДЕННОГО РЕШЕНИЯ

Минимальное суммарное пройденное расстояние равно 3810 км, минимальное расстояние, которое прошли все автомобили – 100 км. Из Ярославля в Москву перегнали 2 автомобиля. Если еще один автомобиль оставлен в Серпухове и еще один клиент появился в Москве, то минимальное расстояние увеличится на 150 км (станет равным 3960 км).

nashaucheba.ru

Решение задач оптимизации в среде Microsoft Excel

8.1. Цель лабораторной работы

8.2. Задания к выполнению лабораторной работы

Решить предложенную преподавателем задачу оптимизации средствами Microsoft Excel 2013.

8.3. Подготовка к работе

8.4. Примеры действий по выполнению заданий к лабораторной работе.

В качестве примера рассмотрим решение следующей задачи оптимизации.

Задача:завод производит электронные приборы трех видов (прибор А, прибор В, прибор С).

Для сборки используются микросхемы трех типов (тип1, тип2, тип3)

	Прибор А	Прибор В	Прибор С
Тип1
Тип 2
Тип 3

Примером решения этой задачи может быть приведенная ниже последовательность действий.

1. Запустите программу Excel (Пуск -> Все программы ->Microsoft Office->Microsoft Excel 2013) и откройте книгу examples, созданную ранее.

2. Создайте новый лист, дважды щелкните на его ярлычке и присвойте ему имя «Решение задачи оптимизации».

3. В ячейки А2, A3 и А4 занесите дневной запас комплектующих — числа 500,400 и 400, соответственно.

5. В ячейках диапазона С2:Е4 разместите таблицу расхода комплектующих.

	Прибор А	Прибор В	Прибор С
Тип1
Тип 2
Тип 3

8. Выберите команду: Данные ->Поиск решения — откроется диалоговое окно Поиск решения.

10. В поле Изменяя ячейки задайте диапазон подбираемых параметров — С1 :Е1.

15. Установите переключатель «Сохранить найденное решение», после чего щелкните «ОК».

16. Сохраните рабочую книгу examples.

8.3. Контрольные вопросы.

1. Как формулируется задача оптимизации в табличном виде?

2. Как формулируются критерий эффективности и ограничения, которым должно удовлетворять решение?

Литература

1. «Информатика. Базовый курс» под ред. Симоновича С.В. Питер, 2010 г.

2. «Понятный самоучитель Excel 2013» Лебедев А.Н, Питер, 2014г.

studlib.info

РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MS EXCEL

Транскрипт

1 Министерство образования и науки Российской Федерации Федеральное агентство по образованию Саратовский государственный технический университет РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MS EXCEL Методические указания к изучению дисциплины «Информатика» для студентов и слушателей строительных специальностей Одобрено редакционно-издательским советом Саратовского государственного технического университета Саратов 2007

2 ВВЕДЕНИЕ В методических указаниях приводятся задания и рассматриваются задачи оптимизации инженерных задач и решение их в среде MS Excel. Функции MS Excel обладают развитым аппаратом численного анализа данных, позволяющим решать сложные задачи линейного и нелинейного программирования со многими неизвестными и ограничениями, что делает его очень удобным инструментом решения задач оптимизации. В MS Excel для решения различных задач оптимизации есть средство Поиск решения. Эта команда находится в меню Сервис. Если команда не обнаруживается, это значит, надстройка Поиск решения не загружена. Для загрузки надо выбрать Надстройки из меню Сервис. Из списка диалогового окна выбирается Поиск решения и в квадратике устанавливается флажок. В случае отсутствия в списке надстройки Поиск решения, запускается программа установки MS Excel. Данные методические указания предназначены для студентов и слушателей курса информатики и информационных технологий в строительстве, знакомых с основами работы в Excel. 3

3 1. ЗАДАЧИ ОПТИМИЗАЦИИ Часто возникает ситуация, когда необходимо выбрать из предложенных вариантов один, удовлетворяющий каким-то определенным требованиям. Очевидно, что этот вариант является оптимальным, т.е. наилучшим решением поставленной задачи. Введение нескольких характеристик (требований) для оценки наилучшего варианта приводит к задачам оптимизации. Задачи оптимизации разделяются на классические и неклассические. В классических задачах требуется найти значения одной или нескольких переменных. При этом ищется максимум или минимум значения некоторой непрерывной функции. В неклассических задачах имеются дополнительные ограничения, формирующие в совокупности множество допустимых альтернатив. Задачи оптимизации на сегодняшний день разнообразны по своему характеру. Универсальных методов для их решения практически нет, но существуют типовые классы задач оптимизации, которые могут быть успешно решены с помощью программы электронных таблиц MS Excel. Некоторые из них рассмотрим в данных методических указаниях. Задача о строительстве объекта относится к классу задач нелинейного программирования и является примером задачи многомерной нелинейной оптимизации. В математической модели этой задачи используются две независимые переменные, каждая из которых представляет отдельную координату точки на плоскости ПОСТАНОВКА ЗАДАЧИ О РАЗМЕЩЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА Задача может иметь несколько возможных вариантов постановки, отличающихся друг от друга количеством жилых домов и их расположением на координатной плоскости. Рассмотрим конкретно один из вариантов этой задачи. Имеются четыре жилых дома, расположенных в некотором микрорайоне города. Определить местоположение объекта для строительства. Для примера объектом строительства выберем школу. Требуется построить школу в удобном для всех жителей микрорайона месте, предполагая, что сумма расстояний от 4

4 построенного объекта до всех жилых домов будет минимальным значением (рис. 1). Это значение и является целевой функцией, которую необходимо определить, используя функции среды MS Excel. Рис. 1 Другие варианты задачи о строительстве объектов могут быть сформулированы как для различных значений количества домов, местоположения этих домов, так и для различных видов целевой функции. 5

5 1.2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ О МЕСТОПОЛОЖЕНИИ ВНОВЬ СТРОЯЩЕГОСЯ ОБЪЕКТА Для математической постановки задачи следует ввести обозначения четырех координат, используя прямоугольную систему координат, в которой исходные дома и школа будут представлять отдельные точки на плоскости (рис. 2). x 1 x 2 x x 3 x 4 Рис. 2 Координаты исходных домов могут быть записаны как координаты соответствующих точек в виде (х i,у i ), где i Є {1, 2, 3, 4}. Координаты для школы, которую предполагается построить, можно положить равными (х, у). Очевидно, они служат переменными рассматриваемой задачи оптимизации, каждая из которых по своему характеру может принимать действительные значения. В некоторой фиксированной прямоугольной системе координат значения переменных х,у могут быть как положительными, так и отрицательными. Задачу о строительстве школы можно считать задачей оптимизации без ограничений. В качестве целевой функции данной задачи будем рассматривать сумму расстояний от искомой точки (х, у) до каждой из заданных точек (х i,у i ), где i Є {1, 2, 3, 4}. 6

6 Расстояние от i-го дома до школы определим по формуле: r 2 2 ( x x ) ( y y ) i i i, где i ª. Общее расстояние от всех четырех домов до школы будет определяться выражением: r r 1 r2 r3 r 4. Таким образом, математическая постановка задачи о строительстве школы может быть записана в следующем виде: 4 f ( x, y) i ( x x ) i 2 ( y y 1 x, y R i ) 2 min, где R область значений для х и у. Поскольку целевая функция данной задачи является нелинейной, задача о строительстве школы относится к классу задач нелинейного программирования без ограничений РЕШЕНИЕ ЗАДАЧИ О МЕСТОПОЛОЖЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА С ПОМОЩЬЮ MS EXCEL Для решения данной задачи с помощью программы МS Ехсеl создадим новый лист. Переименуем его, например, «Задача о строительстве школы». Выполним подготовительный этап для решения, т.е. создадим макет листа (рис. 3). Для этого применим знания, приобретенные при выполнении второй контрольной работе по освоению МS Ехсеl, например, такие как объединение ячеек, обрамление ячеек, автозаполнение ячеек, написание формул с использованием Мастера формул, знание функций математических категорий и т.д. Покажем умение пользоваться процедурой поиска решения, которая позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, связанных с формулой в целевой ячейке. 7

7 Рис. 3 В ячейке G12 будет помещено значение целевой функции. Формула для ее вычисления: =СУММ(B7:B10). В ячейку B7 будет введена формула: =КОРЕНЬ(($B$12-B2)^2+($D$12-D2)^2). Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню Сервис Поиск решения (рис. 4). 8

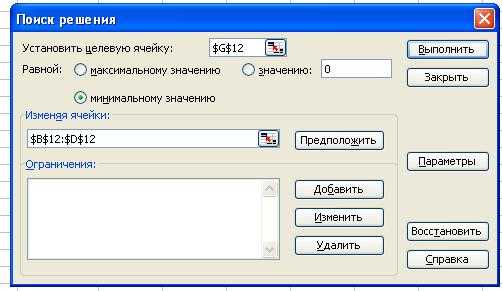
8 Рис. 4 В поле с именем Установить целевую ячейку ввести абсолютный адрес ячейки $G$12 значение целевой функции, а в поле с именем Изменяя ячейки ввести абсолютный адрес ячеек $B$12:$D$12 (рис. 4). Поля с ограничениями можно оставить пустыми, поскольку целевая функция является выпуклой на всем множестве допустимых значений. Параметры поиска решения можно оставить без изменения (рис. 5). Параметры поиска решения задаются в каждом случае отдельно. Рис. 5 9

9 Результат выполнения задачи о строительстве школы вместе с графическим представлением показан на рис. 6. Рис. 6 Замечание. Графическое представление размещения домов и школы выполнено с применением Мастера диаграмм (рис. 7). Для этого выделяют предварительно массив данных, т.е. ячейки B14:C19. Затем выбирают тип диаграммы Стандартные Точечная, заполняют последовательно четыре шага Мастера диаграмм и получают рис.6. Тема применения и использования Мастер диаграмм была изучена ранее при выполнении второй контрольной работы ([2], [3]). 10

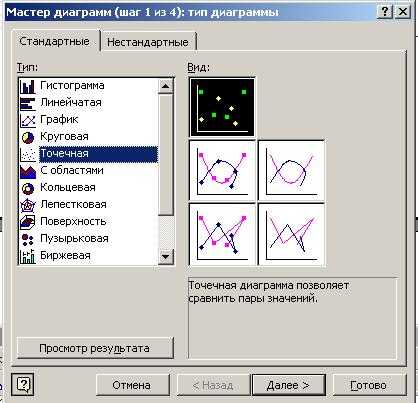
10 Рис. 7 Достоинство использования MS Excel для решения поставленной задачи наглядно продемонстрировано в данном примере. 2. ЗАДАЧА ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ Задача об изготовлении стержней является разновидностью типовой задачи планирования производства и по своему характеру относится к классу задач геометрического программирования. Задачи этого класса после предварительных преобразований могут быть эффективно решены с помощью модели целочисленного линейного программирования ПОСТАНОВКА ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ Изготовление стержней заключается в разрезании исходной заготовки на отрезки заданной длины. Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить нужный комплект стержней требуемых длин наиболее эффективным способом разрезания исходного материала, при 11

11 котором на изготовление необходимого количества комплектов стержней потребуется наименьшее количество исходных заготовок. Аналогичные задачи встречаются часто на практике. В качестве исходных заготовок могут выбираться самые различные материалы, поступающие на строительство объектов в виде целых единиц, например, труб, досок, бревен, арматуры и т.д. Для их использования в строительстве приходится разрезать эти единицы заготовок на нужные отрезки. Длины этих отрезков должны соответствовать требуемым размерам. При неправильном выборе разрезания заготовок теряется часть материала, остатки выбрасываются. Для более эффективного и экономичного способа разрезания предлагается применить математический метод оптимизации, причем он должен быть применен для всей партии заготовок. При использовании метода должны быть рассмотрены все возможные способы разрезания исходных заготовок. На этой основе попытаемся разработать математическую модель задачи об изготовлении стержней МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ Сущность задачи об изготовлении стержней заключается в следующем. Производственное предприятие изготавливает металлические стержни трех видов фиксированной длины: 2,9 м, 2,1 м и 1,5 м соответственно. Для изготовления этих стержней поступает партия заготовок исходного материала, который также представляет собой металлические стержни длиной 7,4 м. Способ изготовления стержней заключается в разрезании исходной заготовки на отрезки заданной длины. Длины отрезков задаются, исходя из нужд производства. Рассмотрим шесть способов разрезания указанных отрезков, например, как показано в табл. 1. В последней, седьмой, строке указаны остатки, полученные при разрезании стержня длиной 7,4 м на отрезки требуемых длин, размеры которых указаны во 2-й, 3-й, 4-й и 5-й строках табл

12 Таблица 1 Способы 1-й 2-й 3-й 4-й 5-й 6-й разрезания Длина 1 2,9 2,9 2,1 2,9 2,1 2,9 Длина 2 1,5 2,9 2,1 2,1 1,5 2,1 Длина 3 1,5 1,5 1,5 2,1 1,5 1,5 Длина 4 1,5 0 1,5 0 1,5 0 Сумма отрезков 7,4 7,3 7,2 7,1 6,6 6,5 Остаток 0 0,1 0,2 0,3 0,8 0,9 Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить 100 комплектов стержней требуемых длин наиболее эффективным способом разрезания исходного материала. При этом учесть, чтобы на изготовление необходимого количества комплектов стержней потребовалось наименьшее количество исходных заготовок. Из стержня длиной 7,4 м можно, например, изготовить один комплект деталей, длины отрезков которых соответственно равны 2,9; 2,1; 1,5 м. Остаток после разрезания стержня будет равен 0,9 м. Следовательно, если нужно получить 100 таких комплектов потребуется 100 стержней заготовок и оставшийся отход будет в сумме составлять 90 м. В случае других предложенных методов, например, первого способа разрезания, остатков материала совсем не будет, но не будет и длины отрезка, равной 2,1 м, а такой стержень необходим. Исходная задача преобразуется в задачу определения оптимального числа различных способов разрезания исходных заготовок. При этом будет изготовлено заданное число стержней требуемой длины, а общее число исходных заготовок должно быть минимальным. Исходными переменными математической модели задачи об изготовлении стержней являются x i количество исходных заготовок, разрезанных i-м способом для изготовления отдельных деталей. Математическая постановка данной задачи может быть записана в виде: x x x x x x min , x 13

13 где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств: x 2x x x x3 2x4 x5 x x1 x2 2x3 3x5 x6 100 x1, x2, x3, x4, x5, x6 0 x1, x2, x3, x4, x5, x6 целые числа, (1) т.к. из табл. 1 видно, что размер 2,9 м для х 1 встречается один раз, для х 2 два раза, для х 3 и х 5 не выбираются, х 4 и х 6 один раз. Отрезков длиной 2,9 м выбирают не меньше 100 штук. Получаем первое неравенство системы. Точно также рассматриваем отрезки длиной 2,2 м и 1,5 м. Получаем следующие два неравенства. Значения не могут быть отрицательными числами, поэтому четвертое неравенство системы показывает, что каждое значение x i больше или равно нулю. Предлагается коэффициенты при x i первоначально выбрать равными единице и полагать x i целыми. Математическая модель (1) относится к классу задач целочисленного линейного программирования, которая может быть решена с помощь MS Excel РЕШЕНИЕ ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ С ПОМОЩЬЮ MS EXCEL Для решения данной задачи с помощью программы МS Ехсеl создадим новый лист. Переименуем его, например, «Изготовление стержней». Выполним подготовительный этап для решения, т.е. создадим макет листа для исходных данных (рис. 8). Для удобства и наглядности в ячейки А10:A16, B10:G10, h20, I10, h23 вносим необходимый текст, ячейки В13 и G13 объединяем и также вносим текст в полученную ячейку. Текст не влияет на решение рассматриваемой задачи. В ячейки B12:G12 вводим единицы значения целевой функции. В ячейку h21 размещаем формулу для целевой функции: =СУММПРОИЗВ(B11:G11;B11:G11). 14

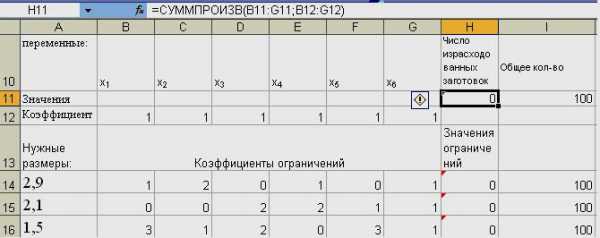
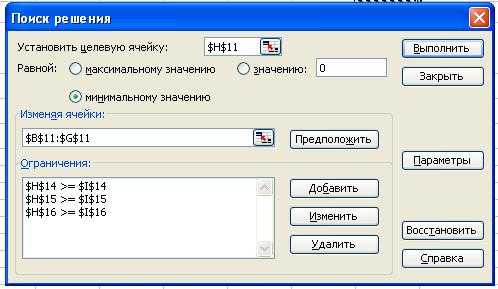
14 Рис. 8 Ячейки B11:G11 оставляем незаполненными, в них будут размещены значения, являющиеся результатом решения задачи. В ячейку Н14, используя Мастер функций, вводим формулу: =СУММПРОИЗВ($B$11:$G$11;B14:G14). Эту формулу копируем в ячейки Н15: Н16. Вызвав мастер поиска решения из меню Сервис Поиск решения, устанавливаем в появившемся диалоговом окне целевую функцию, указываем изменяемые ячейки и ограничения (рис. 9), заполняем необходимые данные в параметрах поиска решения, указывая Линейная модель Неотрицательные значения (рис. 10). Рис. 9 15

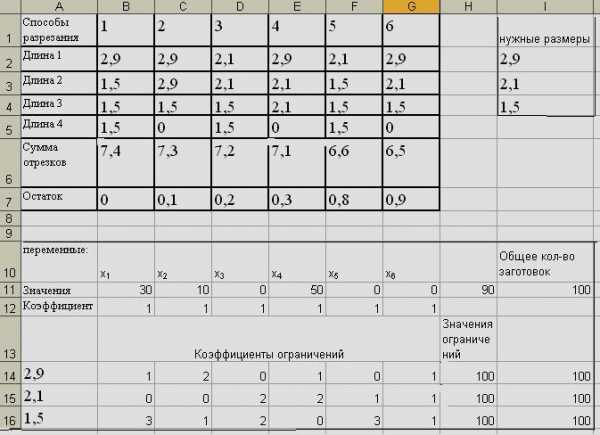
15 Рис. 10 Выполнив Поиск решения, нажав предварительно ОК в окне Параметры поиска решения, получаем найденное решение (рис. 11). Рис

16 Результатом решения задачи об изготовлении стержней являются найденные оптимальные значения переменных: х 1 = 30, х 2 = 10, х 3 = 0, х 4 = 50, х 5 = 0, х 6 = 0, которым соответствует значение целевой функции f орт = 90. Вывод. Из имеющихся заготовок для изготовления 100 комплектов деталей требуемых длин следует первым способом разрезать 30 стержней, вторым способом 10 стержней и четвертым способом 50 стержней. Общее число израсходованных заготовок будет равно 90, что является минимальным из всех возможных вариантов разрезания исходных заготовок. 17

17 3. ЗАДАНИЯ ЗАДАНИЕ 1. ОПРЕДЕЛЕНИЕ МЕСТОПОЛОЖЕНИЯ СТРОЯЩЕГОСЯ ОБЪЕКТА 1. По последней цифре номера зачетной книжки (студенческого билета) выбрать номер варианта. 2. По номеру варианта в табл. 2 выбрать соответственно количество домов микрорайона, координаты каждого дома и строящегося объекта. Таблица 2 варианта Количество домов Координаты домов Строящийся объект (3,-4), (6,-8), (18,20) почта 1 4 (3,-6), (7,-10), (15,18), (26,-5) универсам 2 5 (4,-6), (8,-12), (16,11), (12,-24), (24,-48) поликлиника 3 6 (5,-5), (10,-10), (1,-20), (15,-15), (20,-7), (30,-2) аптека 4 7 (0,-5), (5,-10), (10,-20), (15,-15), (19,-7), (28,-2), (30, 10) школа 5 8 (-10,-5), (10,-1), (1,-20), (15,-15), (20,-17), (30,-2), (25,-30), (5,-10) библиотека 6 4 (11,-5), (20,-10), (30,-20), (15,-15) аптека 18

18 Окончание табл (5,-6), (10,-11), (1,-22), (15,-17), (20,-20), (30,-2), (0,1) стадион 8 6 (8,-5), (11,-14), (1,-25), (15,1), (20,-9), (30,-25) школа 9 5 (7,-5), (10,-10), (1,-20), (15,-15), (-4,10) магазин Замечание. Значения координат объектов могут быть как положительными числами, так и отрицательными. 3. Создать на листе MS Excel макет задачи строящегося объекта, подписать ячейки с входными и выходными данными. 4. Внести нужные формулы. 5. Показать графическое расположение домов и строящегося объекта микрорайона 6. Выделить на графике имеющиеся дома и строящийся объект в виде черных квадратиков. 7. Получить решение задачи и сделать соответствующие выводы. ЗАДАНИЕ 2. ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ ОПРЕДЕЛЕННЫХ РАЗМЕРОВ ИЗ ЦЕЛЫХ ЗАГОТОВОК Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить n комплектов требуемых длин стержней наиболее эффективным способом разрезания исходного материала, при котором на изготовление необходимого количества комплектов стержней потребуется наименьшее количество исходных заготовок. 1. По последней цифре номера зачетной книжки выбрать номер варианта из табл Продумать метод разрезания заготовки из материала. 19

19 варианта Количество способов разрезания заготовки Количество комплектов деталей требуемой длины, шт Материал Заготовки Длина, м Детали Требуемые длины, м Таблица арматура 8,0 1,5 1,6 1, доски 6,0 2,1 2,4 2, трубы 7,0 1,4 1,9 0, бревна 4,5 3,1 2,1 0, уголок 12,4 2,4 2,6 2, швеллер 8,4 1,8 1,5 2, доски 6,4 2,4 1,5 0, арматура 6,5 1,7 1,4 1, трубы 5,5 2,1 2,7 3, двутавр 7,2 1,9 2,1 2,4 3. Построить математическую модель. 4. Заполнить пустые ячейки табл. 4. Размер таблицы зависит от номера варианта. Количество столбцов этой таблицы соответствует указанному количеству способов разрезания заготовки. Таблица 4 Способы разрезания Длина 1 Длина 2 Длина 3 Длина 4 Длина n Сумма отрезков Остаток Замечание. Метод указан в [1]. заполнения таблицы и решение задачи 20

20 5. Построить макет на листе MS Excel, при этом подписывая все исходные данные, т.е. поясняя, в какой ячейке находится то или иное значение. 6. Вписать в ячейки нужные формулы для расчета суммы отрезков, подсчета остатка. 7. Написать формулу для целевой функции. 8. Получить решение задачи и сделать соответствующие выводы. Указание. Требования к оформлению заданий такие же, как и для второй контрольной работы, т.е. составить пояснительную записку в MS Word, создать рабочий файл в MS Excel, работу разместить на дискете или на диске СD-RW, напечатать пояснительную записку на листах формата А4 и сдать работу до начала сессии в ауд. 1/

21 ЛИТЕРАТУРА 1. Леоненков А. В. Решение задач оптимизации в среде MS Excel / А. В.Леоненков. СПб.: БХВ Петербург, Лавренов С. М. Excel. Сборник примеров и задач / С. М. Лавренов. М.: Финансы и статистика, Уэллс Э. Microsoft Excel 97: Разработка приложений / Э. Уэллс, С. Хешбаргер, пер. с англ. М.: Microsoft Press,

22 СОДЕРЖАНИЕ ВВЕДЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ...4 Постановка задачи о размещении строящегося объекта...4 Математическая постановка задачи о местоположении вновь строящегося объекта...6 Решение задачи о местоположении строящегося объекта с помощью MS Excel ЗАДАЧА ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ...11 Постановка задачи об изготовлении стержней...11 Математическая постановка задачи об изготовлении стержней...12 Решение задачи об изготовлении стержней с помощью MS Excel ЗАДАНИЯ Задание 1. Определение местоположения строящегося объекта Задание 2. Изготовление деталей определенных размеров из целых заготовок...19 ЛИТЕРАТУРА

23 РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MS EXCEL Методические указания к изучению дисциплины «Информатика» Составили: МОЖАЕВА Надежда Алексеевна КОЗЛОВ Вячеслав Викторович ЗУЕВА Наталья Геннадьевна Рецензент Ф.С. Селиванов Редактор О.А. Луконина Подписано в печать Формат 60 х 84 1/16 Бум. тип. Усл.печ.л 1,39 (1,5) Уч.изд.л. 1,3 Тираж 100 экз Заказ Бесплатно Саратовский государственный технический университет , Саратов, Политехническая ул., 77 Отпечатано в РИЦ СГТУ , Саратов, Политехническая ул., 77 24

docplayer.ru