Оптимальное проектирование системы, анализ компромиссов и выбор окончательного варианта модели в Simulink. Оптимизация в симулинк 2014
Оптимальное проектирование системы, анализ компромиссов и выбор окончательного варианта модели в Simulink - Video
"В данном вебинаре будут рассмотрены возможности MATLAB и Simulink для оптимального проектирования систем, анализа компромиссов различных вариантов и выбора наилучшего исполнения модели по заданному критерию.
Многие задачи проектирования включают компромиссы между производительностью, качеством системы и ее стоимостью. При этом стоимость может быть выражена в денежном эквиваленте или измерена физическими характеристиками, как например, вес тела, его объем, вырабатываемая температура или площадь опорной поверхности. Используя в качестве примера модель управления скоростью двигателя, мы рассмотрим Simulink Design Optimization для анализа и решения задач подобного рода, когда необходим компромисс между различными вариантами реализации. В частности, мы решим задачу выбора точности датчика, времени срабатывания приводной системы и шага дискретизации регулятора.
На примерах мы познакомимся и узнаем:
- как использовать моделирование для выбора компромиссного варианта проекта при одновременной оптимизации технических характеристик системы;
- как в Simulink Design Optimization выбрать параметры оптимизации и задавать многокритериальные целевые функции;
- как настраивать переменные в модели, чтобы удовлетворять требованиям к системе и повышать ее производительность
Simulink Design Optimization помогает настраивать параметры модели Simulink за счет оптимизации на основе полученных в процессе симуляции сигналов и заданных пользовательских требований и ограничений. Возможна оптимизация переменных скалярного, векторного и матричного типа, а также задание множества ограничений на любом уровне модели. В данном инструменте поддерживаются непрерывные, дискретные и многоскоростные модели, а также возможен учет неопределенностей этих моделей путем применения метода Монте-Карло.
Вебинар предназначен для инженеров и разработчиков технических систем."
Оптимальное проектирование системы, анализ компромиссов и выбор окончательного варианта модели в Simulink - Video
"В данном вебинаре будут рассмотрены возможности MATLAB и Simulink для оптимального проектирования систем, анализа компромиссов различных вариантов и выбора наилучшего исполнения модели по заданному критерию.
Многие задачи проектирования включают компромиссы между производительностью, качеством системы и ее стоимостью. При этом стоимость может быть выражена в денежном эквиваленте или измерена физическими характеристиками, как например, вес тела, его объем, вырабатываемая температура или площадь опорной поверхности. Используя в качестве примера модель управления скоростью двигателя, мы рассмотрим Simulink Design Optimization для анализа и решения задач подобного рода, когда необходим компромисс между различными вариантами реализации. В частности, мы решим задачу выбора точности датчика, времени срабатывания приводной системы и шага дискретизации регулятора.
На примерах мы познакомимся и узнаем:
- как в Simulink Design Optimization выбрать параметры оптимизации и задавать многокритериальные целевые функции;
- как настраивать переменные в модели, чтобы удовлетворять требованиям к системе и повышать ее производительность
Simulink Design Optimization помогает настраивать параметры модели Simulink за счет оптимизации на основе полученных в процессе симуляции сигналов и заданных пользовательских требований и ограничений. Возможна оптимизация переменных скалярного, векторного и матричного типа, а также задание множества ограничений на любом уровне модели. В данном инструменте поддерживаются непрерывные, дискретные и многоскоростные модели, а также возможен учет неопределенностей этих моделей путем применения метода Монте-Карло.
Вебинар предназначен для инженеров и разработчиков технических систем."
fr.mathworks.com
Семинар "Введение в MATLAB и Simulink для разработки систем управления" 26 Марта 2014
26 марта 2014
09:30
Мероприятие бесплатноеРегистрация обязательнаи заканчивается за сутки до начала мероприятия

Александр Словак
Специализация Александра в ЦИТМ Экспонента - физическое моделирование и системы управления. До прихода в ЦИТМ Экспонента занимался моделированием электромеханических систем в транспорте и энергетике. Имеет пятилетний опыт работы с продуктами MathWorks. Образование - Днепропетровский национальный университет железнодорожного транспорта (Магистр электротехники). В ходе семинара инженер департамента MathWorks расскажет о модельно-ориентированном проектировании в среде MATLAB и Simulink. Будут затронуты вопросы, касающиеся разработки систем управления, интеграции существующего кода в модель, разработки модели объекта управления в Simulink. Кроме того, будет показано, каким образом осуществляется программно-аппаратное тестирование на системе реального времени xPC Target Turnkey и реализация системы управления на встраиваемых платформах путем автоматической генерации кода.Основные вопросы семинара:
• Введение в концепцию МОП для разработки систем управления • MATLAB и Simulink для моделирования и симуляции • Проектирование систем с управляющей логикой и конечных автоматов • Интеграция существующего кода (C, C++, Fortran) в Simulink • Настройка параметров регулятора и оптимизация параметров модели • Обзор доступных методов моделирования объектов управления • Аппаратная реализация и тестирование в реальном времени
На семинар приглашаются: инженеры, системные инженеры, конструкторы, программисты, разработчики высокотехнологичных изделий, в том числе систем реального времени, технические руководители, исследователи и ученые, специалисты отделов систем управления (АСУ), отделов электроники, разработки и тестирования.
Участие бесплатное. Пожалуйста, предварительно зарегистрируйтесь до 25 марта включительно.
Контакты организаторов:
Артем Голубев
Телефон: +7(495)2320023 (+1601) e-mail: [email protected]
Подробная программа семинара
09:30 – 10:00 |
Регистрация участников | |
|
10:00 – 10:15 |
Модельно-ориентированное проектирование•Введение в концепцию МОП для разработки больших систем |
Александр Словак, инженер департамента MathWorks |
|
10:15 – 11:15 |
Продукты MathWorks для разработки сложных систем•MATLAB и Simulink для моделирования и симуляции•Проектирование систем с управляющей логикой и конечных автоматов•Интеграция существующего кода (C, C++, Fortran) в Simulink |
Александр Словак, инженер департамента MathWorks |
|
11:15 – 11:30 |
Перерыв | |
|
11:30 – 11:50 |
Методы оптимизации для уточнения параметров модели•Настройка параметров регулятора и оптимизация параметров модели |
Александр Словак, инженер департамента MathWorks |
|
11:50 – 12:15 |
Обзор доступных методов моделирования объектов управления•Моделирование по фундаментальным принципам•Физическое моделирование•Моделирование по экспериментальным данным |
Александр Словак, инженер департамента MathWorks |
|
12:15 – 12:30 |
Перерыв | |
|
12:30 – 13:45 |
Аппаратная реализация и тестирование в реальном времени•Программно-аппаратное тестирование в реальном времени•Реализация системы управления на встраиваемых платформах |
Александр Словак, инженер департамента MathWorks |
|
13:45 – 14:00 |
Обзор доступных тренингов по затронутым тематикам, ответы на вопросы |
-
Связанные продукты:
-
26 марта 2014
09:30
Москва, ул. Дубосековская, д.4а, ДК МАИ, малый зал
- Мероприятиебесплатное
- Регистрация закрыта
matlab.ru
Вебинар "Оптимальное проектирование системы, анализ компромиссов и выбор окончательного варианта модели в Simulink" 29 Сентября 2014
29 сентября 2014
11:00 и 17:00
Мероприятие бесплатноеРегистрация обязательна
Иван Мелешин, инженер ЦИТМ Экспонента
Иван специализируется на системах управления и физическом моделировании. Образование – МИИТ, инженер по специальности «Управление и информатика в технических системах», к.т.н. «Автоматизация и управление технологическими процессами и производствами (на транспорте)». Профессионал в работе с MATLAB с более чем 7 летним стажем. Так же на счету Ивана работа в научно-исследовательской лаборатории автоматического управления движением поездов, создание алгоритмов и моделей в задачах управления движением поездов метрополитена, повышение энергоэффективности на транспорте.Многие задачи проектирования включают компромиссы между производительностью, качеством системы и ее стоимостью. При этом стоимость может быть выражена в денежном эквиваленте или измерена физическими характеристиками, как например, вес тела, его объем, вырабатываемая температура или площадь опорной поверхности. Используя в качестве примера модель управления скоростью двигателя, мы рассмотрим Simulink Design Optimization для анализа и решения задач подобного рода, когда необходим компромисс между различными вариантами реализации. В частности, мы решим задачу выбора точности датчика, времени срабатывания приводной системы и шага дискретизации регулятора.
На примерах мы познакомимся и узнаем: • как использовать моделирование для выбора компромиссного варианта проекта при одновременной оптимизации технических характеристик системы; •как в Simulink Design Optimization выбрать параметры оптимизации и задавать многокритериальные целевые функции; • как настраивать переменные в модели, чтобы удовлетворять требованиям к системе и повышать ее производительность
Simulink Design Optimization помогает настраивать параметры модели Simulink за счет оптимизации на основе полученных в процессе симуляции сигналов и заданных пользовательских требований и ограничений. Возможна оптимизация переменных скалярного, векторного и матричного типа, а также задание множества ограничений на любом уровне модели. В данном инструменте поддерживаются непрерывные, дискретные и многоскоростные модели, а также возможен учет неопределенностей этих моделей путем применения метода Монте-Карло.
Вебинар предназначен для инженеров и разработчиков технических систем.
Пожалуйста, выберите удобное для участия время и зарегистрируйтесь.
Технические требования
Связанные материалы
Связанные вебинары
matlab.ru
Семинар "Введение в MATLAB и Simulink для разработки систем управления" 25 Апреля 2014
25 апреля 2014
09:30
Мероприятие бесплатноеРегистрация обязательнаи заканчивается за сутки до начала мероприятия

Николай Филаретов, инженер ЦИТМ Экспонента
Специализируется на разработке встраиваемого ПО и верификации систем. Закончил С-Пб НИУ ИТМО в 2011 году по специальности «Управление и информатика в технических системах». Имеет опыт работы в MATLAB свыше 7 лет. Основные направления деятельности – разработка встраиваемых систем, верификация систем, верификация исходного кода согласно отраслевым стандартам. До перехода в ЦИТМ Экспонента работал на предприятиях авиапромышленного комплекса. В ходе семинара инженер департамента MathWorks расскажет о модельно-ориентированном проектировании в среде MATLAB и Simulink. Будут затронуты вопросы, касающиеся разработки систем управления, интеграции существующего кода в модель, разработки модели объекта управления в Simulink. Кроме того, будет показано, каким образом осуществляется программно-аппаратное тестирование на системе реального времени xPC Target Turnkey и реализация системы управления на встраиваемых платформах путем автоматической генерации кода.Основные вопросы семинара:
• Введение в концепцию МОП для разработки систем управления • MATLAB и Simulink для моделирования и симуляции • Проектирование систем с управляющей логикой и конечных автоматов • Интеграция существующего кода (C, C++, Fortran) в Simulink • Настройка параметров регулятора и оптимизация параметров модели • Обзор доступных методов моделирования объектов управления • Аппаратная реализация и тестирование в реальном времени
На семинар приглашаются: инженеры, системные инженеры, конструкторы, программисты, разработчики высокотехнологичных изделий, в том числе систем реального времени, технические руководители, исследователи и ученые, специалисты отделов систем управления (АСУ), отделов электроники, разработки и тестирования.
Участие бесплатное. Пожалуйста, предварительно зарегистрируйтесь.
Подробная программа семинара
|
09:30 – 10:00 |
Регистрация участников | |
|
10:00 – 10:15 |
Модельно-ориентированное проектирование |
Николай Филаретов, инженер департамента MathWorks |
|
10:15 – 11:15 |
Продукты MathWorks для разработки сложных систем |
Николай Филаретов, инженер департамента MathWorks |
|
11:15 – 11:30 |
Перерыв | |
|
11:30 – 11:50 |
Методы оптимизации для уточнения параметров модели |
Николай Филаретов, инженер департамента MathWorks |
|
11:50 – 12:15 |
Обзор доступных методов моделирования объектов управления |
Николай Филаретов, инженер департамента MathWorks |
|
12:15 – 12:30 |
Перерыв | |
|
12:30 – 13:45 |
Аппаратная реализация и тестирование в реальном времени |
Николай Филаретов, инженер департамента MathWorks |
|
13:45 – 14:00 |
Обзор доступных тренингов по затронутым тематикам, ответы на вопросы |
-
Связанные продукты:
-
25 апреля 2014
09:30
Санкт-Петербург, ул. Профессора Попова, дом 5, «ЛЭТИ» им. В.И. Ульянова (корпус 5), малый конференц-зал
- Мероприятиебесплатное
- Регистрация закрыта
matlab.ru
Содержание

| Лист | |
| Введение | 2 |
| 1 Оптимизация системы | 4 |
| 2 Характеристики скорректированной системы | 6 |
| 3. Модель системы в пространстве состояний | 9 |
| 4. Исследование системы на управляемость и наблюдаемость | 10 |
| 5. Цифровая модель САУ | 12 |
| 6. Корреляционная функция между входом и выходом объекта | 14 |
| 7. Корреляционная функция между ошибкой управления и выходной координатой системы | 16 |
| Заключение | 18 |
| Список использованных источников | 19 |

Введение
Моделирование [4] – это замена объекта (оригинала) и фиксация и изучение его свойств путем исследования модели.
Процесс моделирования [4] может быть разбит на следующие этапы:
Формулировка цели моделирования;
Разработка концептуальной модели;
Подготовка исходных данных;
Разработка математической модели;
Выбор метода моделирования;
Выбор средств моделирования;
Разработка программной модели;
Проверка адекватности и корректировка модели;
Планирование машинных экспериментов;
Моделирование;
Анализ результатов моделирования.
В ходе курсовой работы необходимо смоделировать систему управления приводом робота-манипулятора. Целью моделирования является создание эффективной, адекватной модели. При первом рассмотрении системы можно заметить следующее:
На вход системы поступает угол поворота, который, скорее всего, создается механическим усилием;
Этот сигнал с учетом ошибки преобразуется в электрическое напряжение;
Сигнал усиливается, корректируется и направляется на двигатель;
Выходной сигнал двигателя поступает на объект – робот-манипулятор.
В качестве средства моделирования будем использовать среду Matlab 7.0.1. Matlab обладает мощным встроенным языком и прочими средствами для создания эффективной модели системы.
1 Оптимизация системы
Необходимо подобрать параметры корректирующих устройств и коэффициент усиления электронного усилителя такими, чтобы выходной сигнал удовлетворял следующим показателям качества:
максимальное перерегулирование – не более 10%;
время нарастания – не более 3-5с;
длительность переходного процесса – не более 5-7с.
Модель системы, созданная при помощи Simulink, представлена на рис. 1.
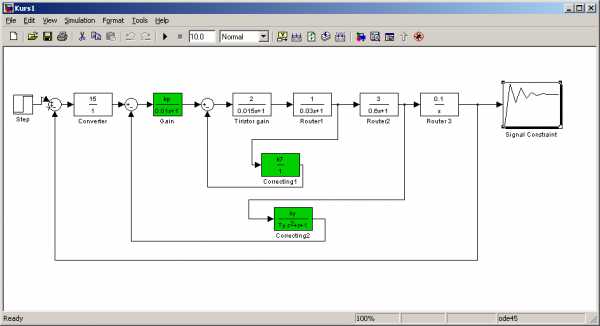
Рис. 1. Модель САУ
Для определения параметров проведем оптимизацию системы средствами Simulink, используем блок Signal Constraint. В качестве начальных значений параметров примем 1. Процесс настройки параметров представлен на рис. 2.
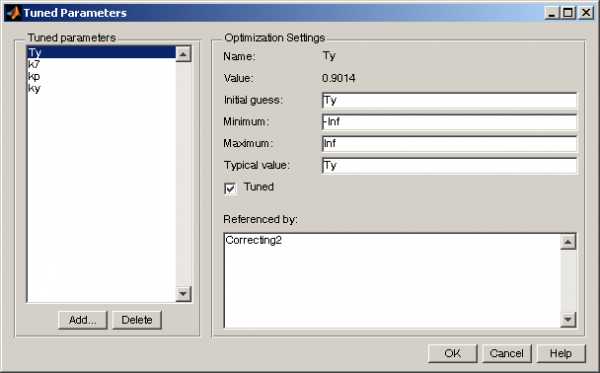
Рис. 2. Настраиваемые параметры
Перед проведением оптимизации необходимо выбрать метод, по которому она будет осуществляться, задать параметры хода оптимизации и желаемые характеристики переходного процесса(рис. 3).
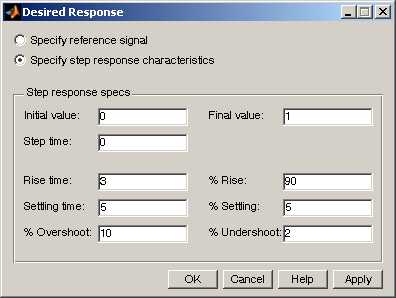
Рис. 3. Настройка характеристик переходного процесса
Ход оптимизации в графическом представлении изображен на рис.4.
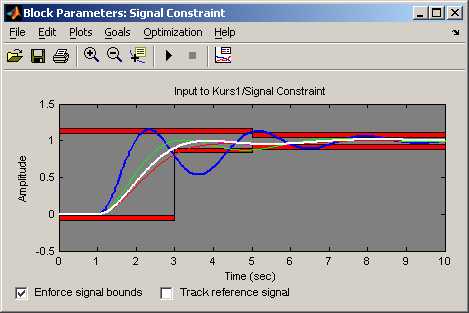
Рис. 4. Ход процесса оптимизации
В итоге, получены следующие значения настраиваемых параметров
Ty =0.9014, k7 =1.3835, kp =0.4197, ky =0.3546.
studfiles.net
Dr. Bob Davidov Автоматическая оптимизация Simulink моделей и регуляторов
Транскрипт
1 Dr. Bob Davidov Автоматическая оптимизация Simulink моделей и регуляторов Цель работы: Ознакомиться с основными методами пакета Simulink Response Optimization для автоматической оптимизации параметров моделей и регуляторов систем управления. Задача работы: Освоить последовательность оптимизации систем управления в среде Simulink Response Optimization MATLAB. Приборы и принадлежности: Персональный компьютер, интегрированная среда Матлаб R2012a с пакетом Simulink Design Optimization. ВВЕДЕНИЕ Для синтеза нелинейных системы управления трудно переоценить значение алгоритма поиска значений параметров обеспечивающих требуемое поведение систем. Такой алгоритм поддерживается модулем Response Optimization входящем в состав пакета Simulink Design Optimization среды МатЛАБ. Модуль оптимизирует линейные и нелинейные системы управления автоматической подстройкой заданных параметров модели по ее реакции. Автоматическая оптимизация повышает точность и быстродействие систем, сокращает время проектирования систем управления. В этой работе на примере оптимизации модели показаны основные этапы работы с пакетом Simulink Response Optimization. ОБЩИЕ СВЕДЕНИЯ Simulink Response Optimization работает с линейными и нелинейными, дискретными и непрерывными моделями. Пакет выполняет оптимизацию модели в циклической последовательности. На каждом шаге он запускает модель, сравнивает переходный процесс выбранной переменной состояния модели с заданными ограничениями, показывает промежуточные результаты оптимизации, подстраивает параметры модели в соответствии с выбранным алгоритмом численной оптимизации и вновь запускает модель с уточненными параметрами и так до достижения заданной формы переменной состояния модели. Перед началом оптимизации пользователь выбирает параметры модели которые необходимо подстраивать в процессе оптимизации, задает диапазон изменения параметров, выбирает метод оптимизации (градиентный метод, Монте Карло), назначает критерии оптимизации (например, величину перерегулирования или время переходного процесса) и их величины в виде коридора ограничений переходного процесса (например, см. Рис. 6). Для оптимизации во временной области можно расставить на графике отклика уровни границы коридора в который должен попадать оптимизированный сигнал. В библиотеке Simulink > Signal Design Optimization > Signal Constraints имеются три блока задания коридоров:
2 В блоке Check Custom Bounds верхние (upper) и нижние (lower) границы (bounds) задаются матрицами амплитуд горизонтальных линий (например, [ ; ]) и соответствующих временных (в секундах) точек начала и концов линий (например, [0 8.5; ]). В блоке Check Against Reference коридор задается интервалом времени (например, linspace(0,10)), функцией эталонного переходного процесса (например, 1-exp(- linspace(0,10)/2)), абсолютным и относительным отклонениями соответственно от оси и от графика функции. В блоке Check Step Response Characteristics коридор рассчитывается после вода в закладке Bounds основных показателей качества переходного процесса при типовом (ступенчатом) воздействии (Рис. 1.) Перерегулирование (Overshot), % Зона установления, % (Setting) Установившееся значение (Final Value) Рост, % (Rise) Спад, % (Undershoot) Начальное значение (Initial Value) Время роста (Rise Time) Время регулирования (Setting Time) Время Рис. 1. Основные показатели качества переходного процесса при типовом (ступенчатом) воздействии задаваемые в блоке Check Step Response Characteristics для расчета коридора отклика системы. Во всех блоках Signal Constraints кнопкой Show Plot окна Bound открывается график с заданными границами коридора отклика модели. С помощью меню, мыши или горячих клавиш границы коридора можно перемещать, разворачивать, разбивать, укорачивать и
3 удлинять до требуемого размера. После установки приемлемых границ, кнопкой Update block необходимо зафиксировать новые границы в статусе исходных границ для поиска оптимального переходного процесса. При этом, ранее введенные значения границ на закладке Bound будут пересчитаны. ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ОПТИМИЗАЦИИ ПАРАМЕТРОВ МОДЕЛИ Для поиска оптимальных параметров модели при помощи модуля Response Optimization пакета Simulink Design Optimization следует. 1. В рабочей области (workspace) MATLAB задать начальные, наилучшие по предварительной оценке значения параметров модели которые необходимо оптимизировать. 2. Заменить соответствующие значения оптимизируемых параметров модели названиями переменных workspace 3. Подсоединить блок(и) Constraint ко всем откликам (переменным состояния) модели формы которых должны соответствовать заданным ограничениям. 4. Задать ограничения - коридоры откликов. 5. Ввести в окно Design Optimisation > параметры модели, которые необходимо оптимизировать и указать диапазон поиска параметров. 6. При необходимости ввести (Неточно определенные параметры). 7. Подать на вход модели воздействие (ступенчатое, импульсное, др.), для которого требуется получить желаемый переходной процесс в точках с Constraint блоками. 8. Командой Evaluate Requirements построить переходные процессы для начальных значений параметров относительно коридора ограничений. 7. В меню > Optimization Options выбрать метод и алгоритм оптимизации, задать допустимые отклонения параметров и функции оптимизации задать максимальное количество итераций 8. Нажать кнопку для запуска процесса оптимизации. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задание 1. Построение модели системы управления. 1. Рассчитайте передаточную функцию системы управления стабилизацией маятника в верхнем положении.
4 В качестве примера оптимизации параметров рассмотрим модель стабилизации маятника в верхнем положении равновесия [1, стр. 141]. Пусть масса маятника (Рис. 2) сосредоточена в точке, трение и сопротивление среды отсутствуют, длина маятника L численно равна значению g ускорения свободного падения. Малые отклонения маятника от верхнего положения равновесия описываются дифференциальным уравнением второго порядка где u(t) управляющее воздействие. (p 2-1)y(t) = u(t), Рис. 2. Маятник. Верхнее положение маятника является примером неустойчивого состояния. Нижнее положение маятника нейтрально в смысле устойчивости это так называемая колебательная граница устойчивости. Поскольку порядок объекта равняется двум. То для решения уравнений системы необходим регулятор первого порядка с тремя коэффициентами. (p + a 0R ) u(t) = - (b 1R p + b 0R )y(t) (1) Передаточная функция разомкнутого контура стабилизации с расчетными коэффициентами регулятора имеет следующий вид. 1 15( s + 1) Wp ( s) = W ( s) WR 1( s) = (2) 2 s 1 s Постройте модель контура (2) стабилизации маятника в Simulink. Рис. 3. Модель стабилизации маятника в верхнем положении.
5 3. Постройте график переходного процесса маятника в верхнее положение с начальной позиции 0.9. Рис. 4. Переходный процесс маятника y(t), начальное положение y0 = Замените числовые значения блоков параметров регулятора модели следующими переменными: a0r = 7; b0r = 15; b1r = 15; 5. Откройте Explorer модели и введите начальные значения переменных регулятора в поле InitFcn. Или разместите переменные a0r, b0r, b1r с начальными значениями через командную строку в workspace. Примечание. Команды поля InitFcn выполняются перед запуском модели. Выражения a0r = 7; b0r = 15; b1r = 15 позволяют присвоить значения переменным и разместить их в области workspace. 6. Добавьте в модель блок, например, Check Custom Bounds из библиотеки Simulink > Signal Design Optimization > Signal Constraints и подключите его к выходу системы.
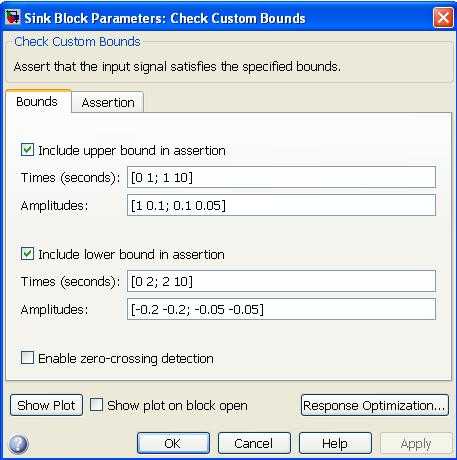
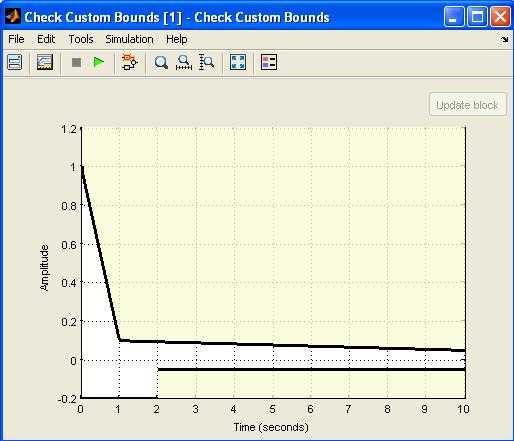
6 Рис. 5. Модель с Constraint блоком задания допустимого коридора движения переменной. 7. Используя расчетные данные стабилизации маятника (Рис. 4) задайте допустимые границы коридора движения переменной. Постройте границы коридора введя команду Show Plot закладки Bounds. Рис. 6. Границы коридора для оптимального отклика системы. 8. Нажмите клавишу Response Optimization закладки Bounds. 9. Добавьте переменные регулятора в список Design Variable Set и задайте зону поиска переменных.
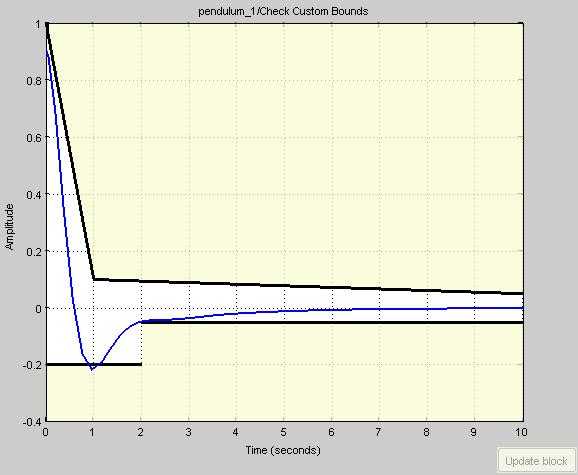
7 10. Командой Add Plot постройте отклик модели при начальных параметрах. На графике видно расположение границ коридора относительно переходного процесса модели с расчетными параметрами. 11. Выберите, в каком формате будете наблюдать прогресс оптимизации: в виде табличных данных или в виде изменяющегося графика переходного процесса (отклика системы). 12. Запустите процесс оптимизации параметров модели по реакции системы. 13. Наблюдайте значения переменных a0r; b0r; b1r после окончания оптимизации в окне Design Optimization > MATLAB workspace или непосредственно в workspace.
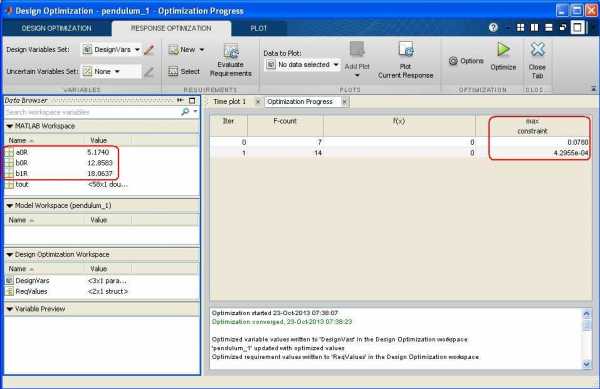
8 14. Для сравнения исходного переходного процесса (Рис. 4) и переходного процесса с оптимизированными параметрами постройте следующую модель. Примечание. Поле InitFcn модели (см. П. 5) должно быть пустым.
9 Рис. 7. Модель для сравнения исходного переходного процесса (реакции системы) и процесса после оптимизации. 15. Запустите модель. Сравните исходный процесс и процесс после процедуры оптимизации. 16. Постройте табличную зависимость оптимизации системы управления стабилизацией маятника в верхнем положении от метода оптимизации (Design Optimization > Options > Optimization method).
10 Метод Значения параметров Переходный процесс Расчет [1, стр. 141] Gradient descent (Градиентного спуска) a0r = 7; b0r = 15; b1r = 15; График расчетного процесса показан на рисунках таблицы бирюзовым цветом. Pattern Search Розовый график Розовый график
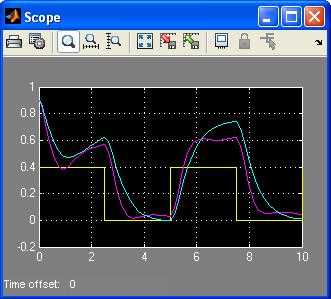
11 Simplex Search Розовый график 17. Сравните время расчета регулятора и реакцию исходного процесса с соответствующими результатами оптимизации пакета Simulink Response Optimization. 18. Для полученных наборов параметров регулятора постройте траектории движения маятника при переменном заданном воздействии в зоне верхней точки равновесия. Метод Значения параметров Переходный процесс Pattern Search Бирюзовый график расчетные параметры Розовый график оптимизированные параметры
12 Желтый график заданные координаты Simplex Search 19. Убедитесь в том, что модель оптимальная при одном варианте изменения заданного воздействия, не всегда оптимальна при других вариантах заданного воздействия при одних и тех же значениях параметров модели..
13 Задание 2. Оптимизация параметров PID регулятора. 1. Постройте модель стабилизации маятника в верхнем положении с Constraint блоком и PID регулятором библиотеки Simulink > Continuous > PID controller. 2. Введите нулевые значения усиления пропорциональной Kp, дифференциальной Kd и интегральной Ki составляющих регулятора. 3. Запустите движение маятника из положения Убедитесь, что движение неустойчиво. 5. Задайте диапазон изменения параметров регулятора с границами коридора для оптимального отклика системы (см. Рис. 6).
14 6. Запустите процесс поиска оптимальных параметров. 7. Убедитесь в сходимости процесса оптимизации. Запишите значения параметров регулятора по окончании процесса. 8. Запустите модель. Рассмотрите переходный процесс движения к положению равновесия. Рис. 8. Движение маятника при оптимизированных параметрах PID регулятора. После выхода в заданное нулевое положение без перерегулирования наблюдается уход маятника из положения равновесия. 9. Уберите интегральную составляющую регулятора и повторите оптимизацию параметров и постройте переходный процесс.
15 10. Поверьте будет ли устойчив процесс стабилизации маятника с оптимизированными Kp и Kd параметрами при изменении заданных координат. Рис. 9. Движение маятника при изменении заданного положения. Положение маятника (розовый график), заданное положение (желтый график).
16 КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие преимущества можно получить при использовании Simulink Response Optimization в разработке систем автоматического управления? 2. Как задается целевая функция в пакете Response Optimization? 3. Почему следует рассматривать поведение модели с оптимизированными параметрами при разных входных воздействиях? 4. Как можно настроить параметры PID регулятора Simulink модели? БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. А.А. Алексеев, Д.Х. Имаев, Н.Н. Кузьмин, В.Б. Яковлев. Теория управления: Учеб./ СПб.: Изд-во СПбГЭТУ ЛЭТИ, Институт цветных металлов и материаловедения СФУ. 0%B0%D1%86%D0%B8%D1%8F+%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%8 0%D0%BE%D0%B2+%D0%B2+simulink&source=web&cd=3&ved=0CCkQFjAC&url=http%3A%2F%2Fwww.i cm.institute.sfu-kras.ru%2fsites%2ficm.institute.sfukras.ru%2ffiles%2flab_rab_3_response_optimization.doc&ei=stxetom3osln4qs_2ygdbw&usg=afqjcnep OeU_2xnqm913ve6uE1Uo9b9ItQ&cad=rjt
docplayer.ru