Математическая формулировка основной задачи оптимизации параметров и допусков. Формулировка задач оптимизации
Формулировка - задача - оптимизация
Формулировка - задача - оптимизация
Cтраница 1
Формулировка задачи оптимизации в способе 6 оказывается достаточно общей. Важно отметить, что общность критерия здесь не сопровождается уменьшением эффективности поиска, затраты машинного времени в способе 6 могут быть сведены до уровня, не превышающего затраты ранее рассмотренных способов. [1]
Как правило, формулировка задачи оптимизации включает выбор критерия оптимальности, установление ограничений, выбор оптимизирующих факторов и запись целевой функции. [2]
Перечислим несколько примеров возможных формулировок задачи оптимизации теплообменника. [3]
В приведенной выше формулировке задач оптимизации нефтедобычи отражается комплексность постановок задачи проектирования и анализа разработки нефтяных месторождений, где во взаимосвязи рассматриваются физико-геологические и гидродинамические ограничения, технологические и экономические условия, входящие в систему технологических и экономических ограничений в функцию цели. [4]
Следует отметить, что формулировка задачи оптимизации с. [5]
В некоторых случаях для формулировки задачи оптимизации приходится рассматривать более абстрактные математические понятия - функциональные, или бесконечномерные, пространства ( точками таких пространств являются функции, а не наборы чисел) и в качестве критерия оптимизации - функционалы, заданные на подмножествах этих пространств. Каждую такую бесконечномерную задачу оптимизации можно аппроксимировать с любой наперед заданной точностью конечномерной задачей, рассмотренной выше, и с точки зрения непосредственно практических приложений достаточно было бы ограничиться именно конечномерными задачами. Однако теоретическая ценность перехода к бесконечномерным пространствам для целого ряда случаев не вызывает сомнений. [6]
С учетом изложенного основные понятия и формулировку задачи оптимизации ЭМУ целесообразно рассмотреть на примере параметрической оптимизации, а особенности решения этой задачи на других этапах проектирования будут рассмотрены в следующей главе. [7]
В главе 13 подробно рассматривается оптимизация, начиная с формулировки задачи оптимизации. Собственно оптимизация и является основой процесса проектирования конструкции. Мощные средства анализа конструкций программы NASTRAN являются лишь ядром средств оптимизации. Интерфейс FEMAP открывает доступ не ко всем возможностям аппарата оптимизации NASTRAN, однако приведенные примеры построения моделей анализа и оптимизационных моделей тонкостенных конструкций позволяют читателю изучить эту важную область. [8]
Применение детерминированных зависимостей (4.5.5) на базе случайных процессов стока ( и, возможно, потребностей в воде) служит основой для формулировки задачи оптимизации в детерминированном виде. [9]
На более крупных территориях и участках рек при обосновании водоохранной деятельности приходится оперировать не отдельными сооружениями или мероприятиями, а некоторыми агрегированными сооружениями или способами очистки сбросных вод. При этом формулировки задач оптимизации мало меняются при переходе к объектам большей крупности. [10]
На более крупных территориях и участках рек при обосновании водоохранной деятельности приходится оперировать не отдельными сооружениями или мероприятиями, а некоторыми агрегированными сооружениями или способами очистки сбросных вод. При этом формулировки задач оптимизации мало меняются при переходе к объектам большей крупности. [11]
Если выполняются эти условия, необходимо правильно сформулировать задачу оптимизации. При формулировке задачи оптимизации должны быть выявлены: 1) параметры, характеризующие состояние каждой стадии; 2) управляющие параметры на каждой стадии; 3) ограничения, которые накладываются на параметры состояния процесса и управляющие параметры. Кроме того, должно быть составлено математическое описание для каждой стадии и определен критерий оптимальности. [12]
Пусть LI ( iQn m h) inlLI ( S ( Qn m h)), где нижняя грань берется по всем схемам, реализующим оператор Qn m k - Величина L ( Qn m k) характеризует индивидуальный оператор 0к тд. Именно эта величина, как было видно из формулировки задачи оптимизации в § 1, есть искомое значение показателя качества в общей поста-нов ке задачи структурного синтеза. [13]
Простота перехода от (4.5.6) к (4.5.5) основана на монотонности А / 3 ( Р) при всех а. Применение детерминированных зависимостей (4.5.5) на базе случайных процессов стока ( и, возможно, потребностей в воде) служит основой для формулировки задачи оптимизации в детерминированном виде. [14]
Любой технологический процесс характеризуется рядом показателей - таких как производительность G, вектор К, определяющий качество выходного продукта, показатель, надежности процесса Р, капиталовложения М, затраты на обслуживание So. Каждый такой показатель определенным образом характеризует процесс. При формулировке задачи оптимизации часть этих показателей может быть введена в критерий оптимальности, а остальные должны учитываться при формировании ограничений, определяющих множество допустимых решений. [15]
Страницы: 1
www.ngpedia.ru
Формулировка задачи оптимизации процесса - Справочник химика 21
Соотношение (VI,23) по существу является математической формулировкой задачи оптимизации /V-стадийного процесса и еще не содержит указаний, как именно нужно максимизировать критерий Rfj, чтобы получить оптимальную стратегию (VI,22). [c.253]Если выполняются эти условия, необходимо правильно сформулировать задачу оптимизации. При формулировке задачи оптимизации должны быть выявлены 1) параметры, характеризующие состояние каждой стадии 2) управляющие параметры на каждой стадии 3) ограничения, которые накладываются на параметры состояния процесса и управляющие параметры. Кроме того, должны быть составлены 1) математическое описание для каждой стадии 2) критерий оптимальности. [c.213]
Формулировка задачи оптимизации. В качестве критерия оптимизации процесса окисления этилена принята себестоимость с единицы продукта — окиси этилена (при заданной производительности установки) [c.118]Обобщая положения предыдущего раздела, дадим следующую формулировку задачи оптимизации квазистатического блока. Пусть процесс описывается системой дифференциальных уравнений в частных производных первого порядка [c.209]
Простота перехода от (4.5.6) к (4.5.5) основана на монотонности A P) при всех а. Применение детерминированных зависимостей (4.5.5) на базе случайных процессов стока (и, возможно, потребностей в воде) служит основой для формулировки задачи оптимизации в детерминированном виде. [c.158]
Повышение уровня знаний о природе элементарных процессов в аппарате и их взаимном влиянии вносят коррективы и в формулировку задачи расчета аппарата. В этой формулировке появляются уже вопросы оптимизации, т. е. выбора наилучших форм организации процесса. Однако совмещение задач расчета и оптимизации продолжается лишь до того момента, когда наши знания и возможности достигают определенного уровня. [c.21]
Выделение исследуемой адсорбционной системы из общей химико-технологической схемы с целью формулировки в общем виде задачи оптимизации адсорбционно-десорбционного процесса и его конкретных критериев оптимизации. [c.9]
Понятие сопряженного процесса является обобщением понятия сопряженной системы, применяемой в вариационном исчислении для формулировки необходимых условий оптимальности [37] (в принципе максимума Понтрягина сопряженную систему использовали применительно к задаче оптимального управления [19]). С появлением вычислительной техники и началом бурного развития методов численного решения задач оптимизации было обращено внимание на другой аспект возможного использования сопряженной системы, а именно, на удобство получения с ее помощью градиента оптимизируемой величины. [c.139]
Отмеченные структурные и процессные особенности многопродуктовых химико-технологических систем налагают определенные условия на формулировку задач их структурной и параметрической оптимизации. В частности, структура системы претерпевает многократные изменения в процессе ее работы. Поэтому требуются специа)п.ные алгоритмы, позволяющие определять оптимальную последовательность вариантов аппаратурной структуры, для которой затем определяются размеры, производительность и количество единиц технологического оборудования [12,13]. [c.143]
В связи со сказанным выше представляется целесообразным находить оптимальные условия проведения ионообменных процессов, используя математические модели. Это расширяет возможности решения задачи оптимизации, так как варьирование параметров проводится не экспериментально, а на математической модели, записанной в виде программы для ЭВМ [2, 3]. В этом случае варьируются все параметры опыта в широком диапазоне их изменения с любой заданной точностью. В настоящей статье излагаются принцип и результат оптимизации некоторых типичных ионообменных процессов, которые реализуются в следующем порядке 1) формулировка критерия оптимальности 2) выбор параметров оптимизации и обоснование ограничений 3) выбор метода оптимизации 4) обоснование математической модели процесса. [c.169]
Задача 3. Одним из вариантов задачи проектирования совмещенных схем является случай, когда на оборудовании схемы предполагается выпускать только один продукт, то есть если придерживаться введенных ранее определений, то совмещенная схема вырождается в индивидуальную. Индивидуальные схемы используются в многоассортиментных произ водствах в тех случаях, когда по той или иной причине совмещение технологических процессов оказывается невозможным. Модель задачи проектирования индивидуальной схемы и управления ею формально совпадает с моделью (3.3) — (3.16), но множество I теперь состоит из одного элемента и, следовательно, во всех формулах индекс i может быть опущен. Известны немногочисленные публикации, касающиеся различных упрощенных задач синтеза ХТС периодического действия. Одной из первых работ этого цикла была статья [59], опубликованная в 1960 году, в которой описана задача синтеза оптимальной ХТС, ориентированной на производство единственного продукта. Следующим этапом явилась формулировка аналогичной задачи для индивидуальной ХТС, содержащей оборудование периодического и полунепрерывного действия, [60]. Задача оптимизации ХТС формулируется как задача выбора полунепрерывного оборудования опти- [c.48]
При правильной постановке задачи экономической оптимизации химико-технологических процессов возможна такая формулировка ( получить максимальный выход продукции при заданном расходе сырья или для заданного выхода продукции обеспечить минимальный расход сырья ), в которой соблюдается требование нахождения оптимального значения только одного тех-нико-экономического показателя. [c.44]
Поэтому при формулировке задач оптимизации в терминах динамического программирования всегда следует стремиться к тому, чтобы размерность стадии оптимизируемого процесса была по возможности невысокой, так как современные вьгчисли-тельные машины допускают решение указанным методом задач, размерность которых не превышает 4 — 5. [c.280]
Этап 5. Математическое описание процесса состоит из математического описания отдельных блоков. Задачей математического описания яв.ляются установление в математической форме связи критерия оптимизации с управляемыми переменными, а такн е математическая трактовка всех имеющихся ограничений. Иными словами, цель этого этапа — получение математической формулировки задачи оптимизации. Математические модели блоков могут быть основаны на физико-химических закономерностях и чисто эмпириче-скими (основаны на полииомпнальном представлении зависимости выходных переменных блоков от входных). В задачах оптимального проектирования обычно используются модели первого типа, так как только они позволяют осуществлять достаточно широкую экстраполяцию данных при изменении масштабов аппаратов. Существенное место на этом этапе принадлежит задаче нахождения констант I, составленных математических моделях и вопросам их проверки. В 5 0делях, основанных на физико-химических закономерностях, как правило, значительно меньшее количество неизвестных констант подлежит уточнению до данным опыта, чем в эмпирических, однако п для них число определяемых констант может быть весьма большим (например, модель химического реактора для сложной реакции). [c.18]
Формулировка задачи оптимизации в данном случае такая же, как ж в дредудущем (см. стр. 175). Отличие будет состоять лишь в том, что добавятся ограничения типа неравенств (VII,616). Для решения этой задачи может применяться метод проектирования градиента (см. стр. 60), использование которого потребует вычисление производных выходных переменных схемы до всем управлениям, а также от переменных (fe = 1 ,. . ., 1 i = р ,. . р ) по управлениям в предшествующих блоках. Для расчета этих производных может быть использован сопряженный процесс, описанный выше (см. стр. 178). [c.197]
Таким образом, использование СКДИ ADAR в качестве инструмента исследования позволяет существенно упростить и ускорить процесс подготовки информации и анализа промежуточных результатов. Работа в режиме активного диалога в сочетании с интеллектуальными возможностями СКДИ ( досчет необходимых данных, пересылка информации по потокам агрегата, автоматизированный анализ данных при вводе и обработке информации и т. д.) позволяет избежать множества ошибок на этапе формулировки задачи и в процессе ее решения. Так, при решении данной задачи уже на начальном этапе исследований было выяснено, что трехслойная схема теряет работоспособность при наличии флюктуаций параметров оптимизации попытка размещения исходной области неопределенности в допустимой области поиска оказалась неудачной. При этом 87% рассмотренных в процессе размещения вариантов ведения технологического процесса оказались нереализуемы. Этот факт может служить подтверждением вывода о трудности (а иногда, и в данном случае в частности, иринципиальной невозможности) практической реализации решений, получаемых методами традиционной оптимизации. [c.276]
Принятие решений на базе зкономико-математических моделей оптимизации основного производства НПП представляет собой итеративный процесс, отдельными этапами которого являются решение исходной задачи с использованием оптимизационных методов, анализ конкретных результатов, уточнение данных, а иногда и самой формулировки задачи, и переход к новому решению. [c.76]
Формулировка и решение задач проектирования, а также оптимизации расписания работы многоассортиментных производств следуют за этапом анализа и оптимизации технологических структур этих производств, который предназначен для определения оптимального качественного содержания будущего производства. Качественное содержание проектируемого производства дает ответ на вопросы, какие виды продукции целесообразно выпускать и из каких видов сырья , какие группы видов продукции следует образовать для формирования соответствующих технологических схем (как базовых единиц обобщенной структуры будущего производства) , какие процессы и какие типы оборудования следует применять в каждой из схем В Ыпуока продукции . В связи с этим оптимизация структуры МАХП, являясь многоэтапной и итерационной (т. е. повторяемой) относительно некоторого периода времени, выбран- [c.20]
chem21.info
Математическая формулировка основной задачи оптимизации параметров и допусков
Большинство задач параметрического синтеза элементов сводится к решению задачматематического программирования.
Задача математического программированияформулируется следующим образом:
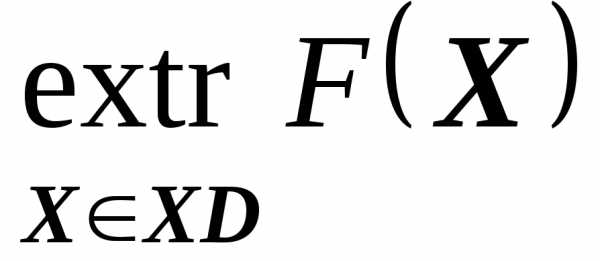, (5.4)
т. е. нужно найти экстремум(максимум или минимум)целевой функцииF(X), иначе называемойфункцией качества, в пределах допустимой областиХДизменения управляемых параметровX. ОбластьХДможет задаваться совокупностью ограничений типа неравенств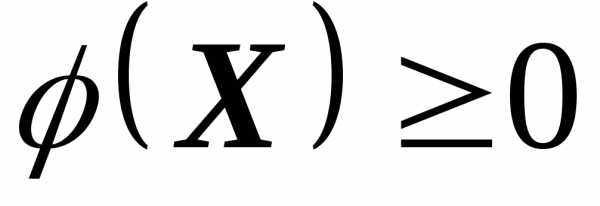 
и типа равенств 
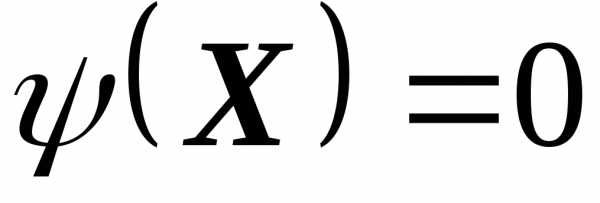, т. е.
. (5.5)
где φ(Х) иψ(Х) — вектор-функции.
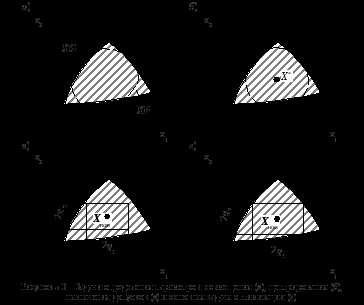
Основная задача оптимизации параметров и допусков— двухэтапная.
Этап 1— решениезадачи предварительной оптимизации параметров элементов. Цель решения этой задачи — определение некоторой опорной точки (точки экстремума)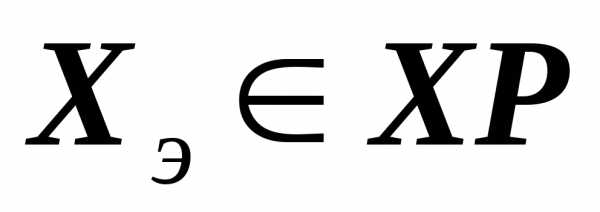 
, рис.5.4а.
Возможны случаи, когда вектор ТТзадан достаточно жестко и областьХРоказываетсяпустой. В этих случаях результатом решения является фиксация данного факта с указанием тех выходных параметров, требования к которым не могут быть одновременно удовлетворены. На основании этих данных инженер принимает решение либо об изменении структуры объекта, либо об изменении технических требований.
Основными вопросами, решаемыми при сведении предварительной задачи оптимизации к задаче математического программирования (5.4), являютсявыбор критерия оптимальности, количественно выражаемогоцелевой функцией,ограниченийиспособа нормирования параметров.
Целевая функция и ограничения обычно формируются на основе заданных условий работоспособности. Наиболее популярны частныйимаксиминныйкритерии оптимальности.
В частном критерии оптимальностив качествецелевой функциивыбирается один из выходных параметров, напримерyk. Условия работоспособности всех остальных выходных параметроввходят вограничения.Система ограниченийдополняется прямыми ограничениями (5.2).
Чаще используют максиминный критерий оптимальности, при котором точкаХэразмещается внутри областиХРнамаксимальном расстоянииот ближайшей границы области. Постановка задачи обычно производится при выборе в качествецелевой функциинаименьшего из запасов работоспособности выходных параметров
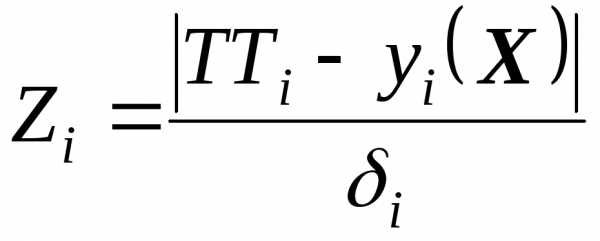, (5.6)
а в качестве ограничений— прямых ограничений (5.2).
Этап 2— решениезадачи вписывания допусковой области. Задача сводится к взаимному расположению заданной области работоспособностиХРи некоторой допусковой областиXGв пространствеХП.
Задача может быть представлена как задача математического программирования, в которой в качестве управляемых параметровфигурируют параметры, задающиеформугиперфигурыXGи ееположениев пространствеХП, в качествецелевой функции— некоторая оценка размеров области пересеченияХРиXG, а в качествеограничений— условия малости рассогласования положений областейХРиXG. При определении допусков вписываемой фигурой является гиперпараллелепипед, рис.5.4б.
Разновидности постановок задач параметрического синтеза
Постановки остальных задач параметрического синтеза как задач математического программирования являются теми или иными разновидностями рассмотренных постановок предварительной оптимизации и вписывания гиперфигур.
Для решения задач оптимизации параметровдостаточно выполнить этап предварительной оптимизации с использованием максиминного критерия и с нормированием пространства выходных параметров с помощью запасов работоспособности (5.6).
Задачи назначения допусковсводятся к выполнению только этапа вписываниягиперфигурыв область работоспособности. Упрощающим отличием этих задач является задание положенияцентравписываемогогиперкуба.
Задачи совмещения и центрирования— двухэтапные: этап 1 —предварительная оптимизация, а этап 2 —центрирование. Последнее отличается тем, что здесь допуски заданы и нужно только совместить центр области работоспособности с центром допусковой области. Такое совмещение может выполняться аналогично вписыванию гиперкуба в основной задаче, но возможны и другие способы, например центрирование путем вписываниягиперсферымаксимального радиуса.
Задачи назначения технических требований на промежуточных иерархических уровнях нисходящего проектированияпо своему характеру, способам постановки и решения близки к основной задаче оптимизации параметров и допусков. Но в задачах назначения ТТ результатом решения являются условия работоспособности при проектировании объекта на следующем иерархическом уровне, а не допуски, используемые при дальнейшем изготовлении деталей.
Задачи назначения технических требований ТТ на основе мнений экспертоврешаются в процессевнешнего проектирования, когда структура будущего объекта отличается большой неопределенностью. Поэтому первой особенностью этих задач является использованиеприближенных математических моделей, отражающих представления идеологов разрабатываемой сложной системы о соотношениях между достижимыми параметрами объектов, сроками проектирования, затратами на разработку и изготовление, т. е. учитываются технико-экономические соображения, относящиеся ко всему жизненному циклу объекта.
В процессе внешнего проектирования разработчик должен иметь возможность оперативного внесения изменений в используемые математические модели, изменений целевых функций, ограничений и управляемых параметров. Такая оперативность — вторая особенность реализации задач назначения ТТ при внешнем проектировании.
Задачи идентификации параметров разрабатываемых математических моделейформулируются как задачи математического программирования, в которыхцелевая функция— оценка степени совпадения выходных параметров, получаемых с помощью испытуемой и эталонной моделей, ауправляемые параметры — параметры испытуемой математической модели.
Задачи определения областей адекватности математических моделейотличаются от задач назначения допусков при заданном векторе номинальных значений тем, что вписывание производится не в пространстве параметров элементов, а в пространстве внешних параметров, так как область адекватности должна характеризовать диапазоны изменения внешних переменных, в которых математическая модель адекватна.
Решение задач параметрического синтеза в САПР выполняется методами поисковой оптимизации, основанной на последовательных приближениях к оптимальному решению. Каждая итерация представляет собой шаг в пространстве управляемых параметров.
Основными характеристиками метода оптимизации являются способы определения направления, в котором производится шаг в пространстве ХП, величины шага и момента окончания поиска. Эти характеристики и формулировки задач математического программирования определяют показатели эффективности поиска — надежность отыскания экстремальной точки, точность попадания в окрестности этой точки, затраты вычислительных ресурсов на поиск.
studfiles.net
Общая формулировка задачи оптимизации - Справочник химика 21
Общая формулировка задачи оптимизации [c.24]Общая формулировка задачи оптимизации и характеристика методов ее решения [c.14]
В отличие от случая системы 1-1, анализ общего случая 1 Л системы, стадии которой образованы неодинаковыми аппара- а-ми с различными скоростями загрузки и выгрузки, не дает э-отношений для прямого определения объема промежуточной ( и-кости. Математическая формулировка задачи оптимизации объема емкости в общем случае представляет собой проблему дискретной минимаксной оптимизации, для решения которой рекомендуется применять численные методы. [c.204]
Выделение исследуемой адсорбционной системы из общей химико-технологической схемы с целью формулировки в общем виде задачи оптимизации адсорбционно-десорбционного процесса и его конкретных критериев оптимизации. [c.9]Следует отметить, что формулировка задачи оптимизации с. х.-т. с. в виде задачи (1,1), (1,2), (1,3) и два аспекта методов спуска, о которых говорилось выше, являются общими для любых конечномерных задач оптимизации, а вся специфика задач оптимизации с. х.-т. с. связана с первым аспектом методов спуска — методом вычисления минимизируемой функции и ее первых производных. [c.14]
При формулировке задач в терминах динамического программирования часто возникают затруднения. Как и в других разделах математики, здесь весьма существенна формулировка задачи. Часто неудачная формулировка влечет за собой путаницу или вообще неблагоприятный исход. В отличие от линейного программирования, где симплекс-метод является универсальным методом, в динамическом программировании отсутствует общий алгоритм, пригодный для всех задач. Каждая задача имеет свои собственные трудности, и в каждом случае требуется уметь найти наиболее подходящую методику оптимизации. [c.23]
Для проектируемой или эксплуатируемой системы названные выше критерии должны быть выражены в заданной степени. Это общее требование обуславливает либо проблема решения многокритериальной задачи векторной оптимизации, либо проблема формулировки глобального (обобщенного или компромиссного) критерия. [c.36]
Пример VI-3. Графически проанализировать процедуру оптимизации каскада реакторов для реакции произвольного порядка. Формулировка оптимальной задачи такая же,, как и в примере VI-1, т. е. для заданной степени превращения исходного вещества А в каскаде (для заданной концентрации определить время. пребывания Ti для всех реакторов так, чтобы общее время пребывания реагентов в каскаде было минимальным. [c.293]
В предыдущем параграфе рассмотрена общая формулировка задачи проектирования простейшего варианта оптимальной совмещенной химико-технологической системы периодического типа. Напомним, что простейший вариант совмещенной схемы обозначает отсутствие байпассных и рециклических потоков, что значительно упрощает формулировку задачи оптимизации. [c.45]
Математическая постановка задачи создания как отдельного химико-технологического аппарата (ХТА), так и химико-технологической системы (ХТС) в целом является общей для них и состоит в формулировке задачи многокритериальной оптимизации с заданным набором целевых функций Р, определяющих требования проектировщика к создаваемому объекту, и вектором ограничений двух типов ограничений типа равенств Р(2) = О, соответствуюгцих полной математической модели конструируемого объекта, и ограничений типа неравенств соответствующих [c.44]
Чаще всего используются диспетчерские правила управления. Основы методики управления по таким правилам для изолированных водохранилищ сезонного, годового и многолетнего регулирования были заложены еще в классической работе [Крицкий и Менкель, 1952. В дальнейшем эта методология была обобщена для учета случайных колебаний водопотребности [Плешков, 1975], для построения диспетчерских графиков гидроузлов специального (прежде всего энергетического) назначения [Резниковский и Рубинштейн, 1974 1984] и т. п. Постепенно формулировка общей проблемы построения диспетчерских правил приняла форму задачи оптимизации (что характерно и для зарубежных исследований). Делались также попытки формализовать ее для систем водохранилищ [Чабан, 1986]. Исследования, проводившиеся в начале 80-х годов, продемонстрировали высокую сложность решения возникающих задач даже при принятии целого ряда упрощаю- [c.382]
В области теплоснабжения фундаментальные исследования этого периода принадлежат Б Л. Шифринсону [269], который в общем виде рассмотрел задачи технико-экономического расчета разветвленных тепловых сетей произвольной конфигуращ и (но с одним источником) и дал их формулировку как задач на условный экстремум. В отличие от А.М. Занфирова он, используя аналогию с расчетом электрических сетей, берет в качестве основных переменных не диаметры, а потери напора на участках сети, что позволяет существенно упростить вид необходимых условий минимума общих расчетных затрат по сети в целом. В результате им впервые с методической и аналитической точек зрения был обоснован для практического применения метод равномерной потери напора вдоль главной (наиболее протяженной) магистрали тепловой сети. Данный метод и до сего времени остается одним из основных проектных методов, причем оптимизация удельной потери напора для каждого объекта заменена нормированием этой величины, что в условиях ручного счета было вполне оправданным из-за большого объема проектных работ. [c.169]
chem21.info
Формулирование задачи оптимизации - Справочник химика 21
Формулирование задачи оптимизации. Для каждого из объектов, входящих в систему, представляющую собой технологический процесс, следует установить показатель качества, подлежащий максимизации [c.486]Формулирование задачи оптимизации [c.245]
Некоторые проблемы, возникающие при формулировании задач оптимизации, проиллюстрируем примерами. [c.245]
Пример 23.1. Проблемы формулирования задач оптимизации. [c.245]
С точки зрения формулирования задачи оптимизации (если за критерий оптимальности принять выход), нижний предел — ограничение независимо от того, как снижение температуры влияет на выход, охлаждать смесь нельзя вследствие роста вязкости. А вот верхний предел не стоит считать ограничением. Исследователи забраковали высокотемпературный режим не потому, что не могли его достичь, а вследствие неблагоприятного влияния режима на выход. Здесь нет необходимости в понятии ограничения забраковать высокотемпературные режимы можно непосредственно по величине критерия оптимальности. [c.249]Формулирование задачи оптимизации сводится к следующему [c.182]
Для формулирования задачи оптимизации выражение (5) необходимо дополнить уравнением фильтрации газоконденсатной смеси [50] [c.53]
Проблема корректности постановки собственно задачи оптимизации ХТС, рассмотренная ранее (см. стр. 65), связана с формулированием целевой функции, которая характеризует качество функционирования системы, а также с правильным составлением ее полной математической модели и удачным выбором регламентированных и оптимизирующих информационных переменных на основе глубокого [c.301]
Формулирование состава задач с целью распределения по уровням иерархии всего многообразия конкретных задач оптимизации. [c.9]
Формулирование задач управления относится к самым сложным вопросам при проектировании АСУ ТП. Рассмотрим сначала проблемы автоматизированной оптимизации и стабилизации ХТС. [c.346]
Важнейшее значение при постановке задачи оптимизации каждого аппарата (например, реактора) приобретает формирование критериев оптимизации. Здесь в первую очередь надо считаться с проблемой взаимовлияния аппаратов и при формулировании критериев оптимизации для отдельных аппаратов стремиться к тому, чтобы они по возможности не противоречили друг другу. Строго говоря, с одной стороны, в большинстве случаев сформулировать критерий оптимизации для отдельного реактора, который бы полностью учитывал влияние его на работу всех аппаратов, нельзя. [c.17]
Поскольку выбор той или иной задачи связан с выбором поисковых (независимых) переменных, поставленный вопрос фактически сводится к выбору наилучшей совокупности поисковых переменных. Проблема близка к проблеме выбора множества разрываемых потоков в задаче расчета стационарного режима схемы [3, с. 33] и в том и в другом случае речь идет о выборе наилучшей совокупности итерируемых переменных. Задача выбора оптимальной совокупности поисковых переменных при оптимизации ХТС чрезвычайно сложна. Сложность ее связана с трудностью формулирования критерия, который позволял бы оценивать тот или иной набор поисковых переменных без решения задачи оптимизации ХТС. Наилучшим критерием, конечно, является время, затраченное на решение задачи, но его можно определить только, решив задачу оптимизации. Поэтому цель состоит в том, чтобы косвенным путем оценить это время. Строго поставить и сформулировать эту задачу трудно. Придется пользоваться некоторыми эвристическими правилами, экспериментальными фактами, которые помогут сформулировать эту задачу хотя бы и не очень строго. [c.134]
При формализации задачи оптимизации возникает важное диалектическое противоречие. Задача распадается на три основных этапа 1) формулирование задачи, приведение ее к одной из стандартных форм 2) нахождение оптимальных условий на основе алгоритма оптимизации 3) реализация оптимальных условий на практике. Так вот, методы решения на первом и втором этапах взаимно противоположны второй этап, как правило, целиком формализован на основе алгоритма решения, а первый этап неформален. Здесь не поможет никакая математика. Первый этап решения задачи связывает конкретные особенности объекта с общим методом решения. [c.245]
При формализации задачи оптимизации возникает важное диалектическое противоречие. Задача распадается на три основных этапа. Первый — формулирование задачи, приведение ее к одной из стандартных форм. Второй — нахождение оптимальных условий на основе алгоритма оптимизации. Третий — реализация оптимальных условий на практике. Так вот, методы решения на первом и втором этапах противоположны друг другу второй этап, как правило, целиком формализован на основе алгоритма решения, а первый этап неформален, и никакая математика не поможет ликвидировать это противоречие, потому что первый этап решения Задачи связывает конкретные особенности объекта с общим методом решения. Поэтому именно при формулировании задачи часто возникают большие трудности. Как это ни парадоксально, но иногда именно неформальный этап оказывается ключевым, определяющим успех решения задачи в целом. [c.177]
В такой постановке задача оптимизации требует решения следующих вопросов 1) формулирования целевых функций для установки выделения сырого стирола и отдельных ректификационных агрегатов [c.284]
Качество функционирования ХТС определяют при помощи показателей эффективности, под которыми понимают числовые характеристики системы, оценивающие степень приспособления системы к выполнению поставленных перед ней задач. Выбор показателя эффективности (или критерия оптимизации) является заключительной стадией формулирования целей функционирования ХТС. Для того, чтобы показатель эффективности достаточно полно характеризовал качество функционирования ХТС, он должен учитывать все особенности и свойства системы, а также условия ее функционирования, взаимодействие внутри ХТС и взаимодействие с внешней средой. [c.182]
I, " Таким образом, на основе анализа функций чувствительности удалось разработать методику для формулирования простых задач управления, исходя из глобальной задачи автоматизированной оптимизации. [c.350]
В конечном итоге в результате таких операций находят оптимальную конструкцию или, возможно, несколько таких конструкций, которые можно представить на рассмотрение заказчику. Иногда полученный конечный результат используется для формулирования новых исходных условий задачи при исследовании влияния отдельных параметров для оптимизации всей системы в целом, а не только для выявления оптимальной конструкции теплообменника, основанной до некоторой степени на произвольном выборе начальных требований. [c.21]
В решении дискретной задачи частными алгоритмами число математических моделей составных частей аппаратов бесконечно. Сложные расчетные схемы можно представить как комбинации последовательных систем, которые сходятся, расходятся или замыкаются. Разницы в математическом формулировании граничных уравнений для сходящихся и расходящихся систем нет, так как они не зависят от типа конструкции, что важно для упрощения. Введение упрощений составляет ценное свойство частных алгоритмов, если учесть, что другие методы оптимизации этого не допускают из-за связи с характером системы. Определение допусков по сложным расчетным схемам поясним примером 3. [c.79]
При формулировании задачи оптимизации существенно, яв-ля ется ли рассматриваемая ситуация детерминированной или сто-хастичной т. е. принимается ли во внимание существование случайных возмущений. [c.486]
Пример формулирования задачи для оЬъекта. Рассмотрим в качестве объекта управления реактор, представленный на рис. Х-16. Так как реактор проточный, задачу оптимизации будем формулировать в расчете на установившийся режим его работы. Можно, например, поставить такую задачу достичь при установившемся режиме работы [c.487]
Для моделирования необходимо иметь моделирующую программу и задачу. Моделирующая программа (PA ER) подробно описана в гл. 3. Рассмотрим теперь реальную задачу усовершенствование контактного способа производства серной кислоты. В настоящей главе и последующих семи главах описано применение моделирующей программы PA ER для моделирования производства серной кислоты контактным способом фирмы Канадиэн индастриз ЛТД. (Гамильтон, Канада). Завод описан в разд. 4.1. Общая стратегия, использованная при формулировании задачи моделирования, описана в разд. 4.2 и используется в разд. 4.3 и других разделах всех последующих глав вплоть до гл. 11. В гл. 12 для иллюстрации возможностей применения моделирования с целью усовершенствования производства приведены результаты оптимизации некоторых отделений производства серной кислоты. При этом предполагается, что на вычислительной машине моделирование до сих пор не проводилось и что массив данных о физических параметрах и библиотека вычислительных блоков отсутствуют, [c.82]
Таким образом, введение ряда ограничений и использование несксльких эмпирических зависимостей позволило получить для оптимальных условий не очень сложные аналитические зависимости (32.30) и (32.31). При этом оптимизация проводилась лишь по одному воздействию (скорость газа), которое было принято за основное. Остальные факторы, влияющие на процесс, были учтены при формулировании условий. Такая постановка вопроса несомненно, является упрощенной, но к ней прибегают довольно часто, так как в противном случае задача слишком усложняется. [c.192]
chem21.info
Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
Методы оптимизации (базовый курс)
Содержание
1.1. Область допустимых значений вектора управляемых параметров Х
Тест: Область допустимых значений. Тест 1
Тест: Область допустимых значений. Тест 2
Тест: Область допустимых значений. Тест 3
Тест: Область допустимых значений. Тест 4
1.2. Выпуклое множество допустимых значений вектора варьируемых параметров
1.3. Постановка детерминированной задачи оптимизации
1.4. Классификация критериев оптимальности
1.5. Свойства выпуклых критериев оптимальности
1.6. Классификация детерминированных задач оптимизации.
Глава 2. Условия существования минимума в детерминированных задачах оптимизации
2.1. Одномерная задача оптимизации
2.2. Многомерная задача безусловной оптимизации
2.3. Задача выпуклого программирования
2.4. Задача нелинейного программирования с ограничениями типа равенств
2.5. Теорема Куна-Таккера для задачи нелинейного программирования с ограничениями типа неравенств
2.6. Теорема Куна-Таккера для общей задачи нелинейного программирования
2.7. Аналитическое решение многомерных задач нелинейного программирования
Тест: Аналитическое решение задачи НП. Тест 1
Тест: Аналитическое решение задачи НП. Тест 2
Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
3.1. Классификация методов решения детерминированных задач оптимизации
Тест: Итерационная формула метода решения детерминированной задачи НП. Тест 1
Тест: Итерационная формула метода решения детерминированной задачи НП. Тест 2
3.2. Наилучшие алгоритмы оптимизации
3.3. Экспериментальное тестирование алгоритмов оптимизации
3.4. Классы тестовых функций
Тест: Генерация тестовых функций. Тест 1
Тест: Генерация тестовых функций. Тест 2
Глава 4. Методы поиска минимума одномерных унимодальных функций
4.1. Алгоритм равномерного поиска
4.2. Алгоритм деления пополам
4.3. Алгоритм Фибоначчи
Тест: Алгоритм Фибоначчи. Тест 1
4.4. Алгоритм золотого сечения
4.5. Сравнение эффективности алгоритмов одномерной условной оптимизации
4.6. Метод квадратичной аппроксимации
4.7. Метод Пауэлла
4.8. Методы на основе поиска стационарной точки критерия оптимальности
4.9. Повышение эффективности поиска на основе дополнительной информации о свойствах критерия оптимальности
Глава 5. Методы поиска глобального минимума одномерных многоэкстремальных функций
5.1. Метод перебора. Одномерный метод Монте-Карло
5.2. Метод выделения интервалов унимодальности
5.3. Метод аппроксимирующих моделей
Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы
6.1. Метод Гаусса-Зейделя
Тест: Метод Гаусса-Зейделя. Тест 1
6.2. Метод Хука-Дживса
6.3. Метод Розенброка
6.4. Метод сопряженных направлений
6.5. Симплекс-метод
6.6. Метод деформируемого многогранника (Нелдера-Мида)
Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков
7.1. Метод наискорейшего спуска. Метод дробления шага
Тест: Градиентный метод с дроблением шага. Тест 1
7.2. Метод оптимизации Ньютона
Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска
8.1. Метод с возвратом при неудачном шаге. Метод наилучшей пробы
8.2. Метод комплексов
8.3. Метод повторяющегося случайного поиска
8.4. Метод случайного поиска с постоянным радиусом поиска и случайными направлениями
Глава 9. Многомерная локальная условная оптимизация
9.1. Методы последовательной безусловной оптимизации
9.2. Метод скользящего допуска
9.3. Модифицированный метод комплексов
9.4. Метод линейной аппроксимации
9.5. Метод проекции градиента
Тест: Проектирование точки на множество. Тест 1
Тест: Проектирование точки на множество. Тест 2
Тест: Проектирование точки на множество. Тест 3
Глава 10. Многомерная глобальная условная оптимизация
10.1. Метод сведения к совокупности вложенных задач глобальной одномерной минимизации
10.2. Метод сведения к задаче одномерной глобальной оптимизации с помощью развертки Пеано
10.3. Метод Монте-Карло
Глава 11. Задачи многокритериальной оптимизации и методы их решения
11.1. Постановка задачи многокритериальной оптимизацию. Множество Парето
Тест: Множество Парето. Тест 1
11.2. Метод весовых множителей решения задачи многокритериальной оптимизации
11.3. Метод эпсилон-ограничений решения задачи многокритериальной оптимизации
11.4. Метод справедливого компромисса для решения задач многокритериальной оптимизации
11.5. Метод приближения к идеальному решению для решения задач многокритериальной оптимизации
11.6. Метод последовательных уступок для решения задач многокритериальной оптимизации
studfiles.net
knigechka: Формулировка задачи многомерной оптимизации.
Решение многих теоретических и практических задач сводится к отысканию экстремума скалярной функции n-мерного векторного аргумента x [7].
Оптимизируемую функцию в практических задачах называют также целевой функцией, критерием эффективности, функцией качества. Широкое применение для решения задачи поиска безусловного минимума функции находят релаксационные методы, которые часто называют методами спуска (подъема). Процесс приближенного численного решения задачи оптимизации заключается в построении по определенным правилам последовательности точек , которая при неограниченном увеличении должна сходиться к точке глобального или локального экстремума. При достижении определенной точности вычислений процесс построения последовательности на некотором шаге обрывается, и очередная точка этой последовательности объявляется приближенным решением задачи оптимизации.
Определение. Методом подъема для решения задачи безусловной максимизации функции называют численный метод, который заключается в построении последовательности точек , обладающей свойством
(43)
При этом называют начальной точкой или начальным приближением, а - k-ым приближением.
Часто точки указанной последовательности строят по формуле
, где (44)
- называют величиной шага, а n-мерный вектор - направлением подъема(спуска) на k-том шаге. Различные методы подъема (спуска), использующие в своей основе формулу (44), отличаются друг от друга лишь способом выбора величины шага и направлением.
Алгоритмы безусловной оптимизации делят на классы, в зависимости от максимального порядка производных минимизируемой функции, вычисление которых предполагается. Методы, использующие только значения целевой функции, называют методами нулевого порядка. Если, кроме того, требуется вычисление первых производных минимизируемой функции, то имеют место методы первого порядка, при необходимости вычисления вторых производных – методы второго порядка.
Предлагаю ознакомиться с аналогичными статьями:
knigechka.blogspot.com
