Оптимизация раскроя. Оптимизация раскроя по длине

Решение задач оптимального раскроя средствами MS Excel

Библиографическое описание:

Каюгина С. М. Решение задач оптимального раскроя средствами MS Excel // Молодой ученый. 2016. №23. С. 54-57. URL https://moluch.ru/archive/127/35159/ (дата обращения: 01.11.2018).

В статье рассматривается методика решения задачи оптимального раскроя материалов на заготовки средствами MSExcel.

Ключевые слова: математическая модель, критерий оптимальности, рациональный способ раскроя

Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала.

Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. В качестве критерия выбора оптимальных способов раскроя могут быть использованы минимум отходов, минимальный расход материалов, максимум комплектов, включающих заготовки различных видов.

Задачи такого типа возникают в строительстве, машиностроении, лесной, деревообрабатывающей и лёгкой промышленности. От успешности их решения зависят экономия материалов и снижение отходов.

Рассмотрим методику решения задачи раскроя листовых материалов средствами MSExcel.

Пример. На предприятии имеются древесностружечные плиты (ДСтП) нескольких форматов, приведенные в таблице 1. Спецификация заготовок приведена в таблице 2. Требуется составить оптимальный план раскроя плит ДСтП на заготовки по критерию минимума отходов, при условии выполнения заданной спецификации заготовок.

Таблица 1

Спецификация плит ДСтП

№п/п	Формат плиты, ммхмм	Количество плит, шт.
1	2440x1220	6000
2	1525x1525	8000

Таблица 2

Спецификация заготовок

№п/п	Формат плиты, ммхмм	Количество заготовок на годовую программу, шт.
1	1000x600	12000
2	800x600	12000
3	600x600	18000
4	300x450	12000
5	300x300	24000

На первом этапе решения задачи определяются рациональные способы раскроя материала. Разрабатываются карты раскроя, представляющие собой графическое расположение заготовок на стандартном формате раскраиваемого материала.

При разработке карт раскроя требуется соблюдать следующие условия:

− максимальный выход деталей;

− минимальное количество типоразмеров деталей при раскрое одного формата любого материала;

− минимальное повторение одних и тех же деталей в разных картах раскроя;

− обеспечение минимума отходов [2, c. 49].

В нашем примере использовано шесть карт раскроя, по три для каждого размера древесностружечных плит. В таблице 3 приведён выход заготовок и площадь отходов.

Таблица 3

Расчет количества заготовок

Размер заготовки	Количество заготовок, получаемых по карте раскроя, шт.
	Плита 2440x1220			Плита 1525x1525
	1	2	3	4	5	6
1000x600	4	-	-	-	2	-
800x600	-	4	-	-	-	2
600x600	-	-	8	-	-	2
300x450	-	5	-	6	5	-
300x300	-	-	-	15	-	-
Площадь отходов, м2	0,577	0,382	0,097	0,166	0,586	0,646

На втором этапе решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.

Составим математическую модель оптимизации.

В качестве неизвестных примем Хj— количество плит раскраиваемых j-м способом.

Целевая функция (минимум отходов):

F=0,577Х1+0,382Х2+0,097Х3+0,166Х4+0,586Х5+0,646Х6min

Система ограничений:

по выпуску заготовок:

4Х1+2Х5=12000

4Х2+2Х6=12000

8Х3+2Х6=18000

5Х2+6Х4+5X5=12000

15Х4=24000

по запасам сырья:

Х1+Х2+Х3

Х4+Х5+Х6

по неотрицательности переменных:

Х1,…, Х6>=0

Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века. Надстройка MS Excel «Поиск решения» (Solver) использует этот алгоритм. Именно с помощью симплекс-метода и MS Excel мы будем решать задачу оптимального раскроя [3].

Оформим в MSExcel таблицу с исходными данными и введём формулы (рис.1):

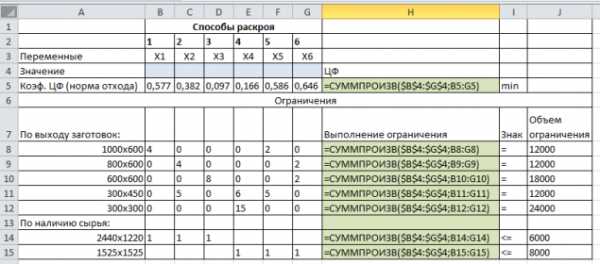
Рис. 1. Оформление таблицы с исходными данными в MSExcel

На вкладке «Данные» нажимаем кнопку «Поиск решения». Откроется диалоговое окно «Поиск решения», в котором указываем ячейку целевой функции, её направление, изменяемые ячейки и задаём ограничения задачи (рис. 2).

Рис. 2. Диалоговое окно «Поиск решения»

Щелчком по кнопке «Параметры» заходим в диалоговое окно «Параметры поиска решения» и устанавливаем флажок «Линейная модель». Нажимаем ОК. Выполняем поиск решения.

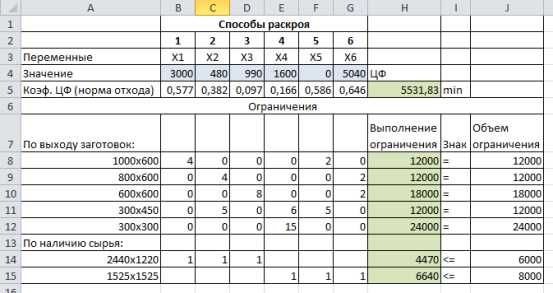
Рис. 3. Результат решения

На рисунке 3 показан оптимальный план раскроя. Следует раскроить древесностружечные плиты размера 2440х1220 первым способом 3000 шт., вторым способом 480 шт. и третьим способом 990 шт. Всего плит данного размера потребуется 4470 шт.

Древесностружечные плиты размера 1525х1525 следует раскроить четвертым способом 1600 шт. и шестым способом 5040 шт. Пятую карту раскроя использовать нерационально. Всего плит этого размера потребуется 6640 шт.

Полученный в оптимальном решении вариант использования карт раскроя плит обеспечит выполнение плана по выходу заготовок всех размеров. Отходы будут минимальными и составят 5531,83 м2.

Литература:

Пижурин А. А. Основы моделирования и оптимизации процессов деревообработки / А. А. Пижурин. — М.: Лесная промышленность, 2004.
Яцун И. В., Чернышев О. Н. Моделирование и оптимизация процессов деревообработки. Часть 1. — Екатеринбург: Редакционно-издательский отдел УГЛТУ, 2011.
Линейный раскрой в Excel [Электронный ресурс] — Режим доступа: http://al-vo.ru/spravochnik-excel/linejnyj-raskroj-v-excel.html

Основные термины (генерируются автоматически): карт раскроя, рациональный способ раскроя, минимум отходов, площадь отходов, спецификация заготовок, формат плиты, заготовка, плита, таблица.

moluch.ru

Программа оптимизации раскроя пиловочника рапира. Раскрой бревна: индивидуальный и групповой способ

Доброго времени суток уважаемые читатели Блога Андрея Ноака. Среди деревообработчиков имеется множество секретов и хитростей повышающих выход пиломатериала из круглого леса, увеличивающих выход первосортных досок и в конечном итоге все приводит к увеличению доходов. Сегодня я, технолог по призванию, расскажу как пилить лес, фишки и хитрости в этом деле.

Но по разным причинам не каждый станет делиться своими методами работы, своими разработками.

Понятие раскрой леса может как бы быть двухзначным. С одной стороны его можно понимать как распиловка леса на станке и получение доски. С другой стороны можно сказать раскрой леса, это распиловка хлыста на сортименты и получение бревен. При этом оба этих значения правильны, просто необходимо указывать какой именно раскрой имеется ввиду. Специально для своих читателей блог Андрея Ноака сделал подборку мероприятий увеличивающих эффективность раскроя леса.

Увеличение эффективности раскроя леса

Для эффективного раскроя круглого леса расчет поставов производить только в специальных программах.
Предварительная подготовка пиловочника к раскрою, а это учет и анализ имеющихся дефектов на древесине и правильная работа лесной биржи.
Программа раскроя круглого леса более эффективна будет только с наличием высокого ассортимента готовой доски по размерам. Особенно актуальным становится наличие тонкого и узкого ассортимента в сочетании с толстым и широким ассортиментом. Толстый и широкий пиломатериал выпиливается из середины, тонкий пиломатериал выпиливается с заболонной части бревна. Но имеется недостаток, можно в огромном количестве пиломатериала запутаться, особенно если сортировка производится вручную. Это может привести к дополнительным рабочим местам. Выходом из такой ситуации может послужить монтаж автоматических сортировок пиломатериала, где программа по заданным критериям рассортировываем пиломатериал.

Стоит помнить, что при установке в середину тонкой и узкой доски идет колоссальное увеличение коэффициента выхода.
Для увеличения прибыли при равных прочих условиях предприятию нужно стремиться производить распил леса так, чтобы больше доски можно было реализовывать и производить толстого и широкого, тонкий и узкий пиломатериал должен производиться как сопутствующий основной (широкой и толстой) доски.
К предыдущему пункту можно добавить еще и то, что каждый пропил снижает отдачу от раскроя круглого леса. Поэтому для некоторых при равных условиях лучше пилить брус.
Каждый деревообработчик знает, чем короче бревно круглого леса, тем эффективней его пилить.
Тщат

studio-firing.ru

Оптимизация раскроя — курсовая работа

Табл. 4

Решая задачу, получаем следующий результат:

	X1	X2	X3	Х4	X5
Minimize	1	1	1	1	1
Заготовка 120 см	1	1	0	0	0	>=	80	-0,5
Заготовка 100 см	1	0	2	1	0	>=	120	-0,5
Заготовка 70 см	0	1	0	1	3	>=	102	-0,33
Solution	80	0	20	0	34		134

Табл. 5

Ответы: 1. Пять способов. 2.134 единицы материала.

3. Три из пяти рациональных способов раскроя.

Описание алгоритма

1. Определяется текущее значение длины раскроя L от минимальной длины детали до длины материала.

2. Вычисляется максимальный индекс (номер) детали, добавление которой возможно.

3. Если нет деталей, которые можно добавить в раскрой, то проверяется не достигнут ли максимум цены раскроя для текущего значения длины раскроя L.

Если максимум достигнут, то он запоминается. Последняя добавленная деталь удаляется из раскроя и добавляется следующая (п. 4). Если нет деталей которые можно добавить в раскрой, происходит выход из цикла.

4. Запоминается текущий раскрой. Длина раскроя уменьшается на длину детали. Цена раскроя увеличивается на цену детали. Определяются детали, добавление которых в раскрой возможно (п. 2).

5. Берется начальная длина раскроя, равная длине материала. Берется деталь, на которой был достигнут максимум для данной длины материала. Из длины материала вычитается длина детали, к стоимости раскроя прибавляется цена детали. П.5 повторяется, пока есть детали, добавление которых к раскрою не превысит длины материала.

6. Зная количество деталей для каждого их вида, составляющих рациональный раскрой, формируется искомый вектор х.

Описание программы

Вид главного окна программы приведено на рисунке:

Рис. 1

После запуска программы пользователю предлагается ввести длину материала и количество типов деталей, затем нужно заполнить поля таблицы с длиной и стоимостью каждой детали.

После ввода данных для решения нужно нажать кнопку "OK", программа выдаст результат в виде таблицы с оптимальными значениями количества типов деталей. Также выводится общая оценка раскроя и остаток материала.

Рис. 2

Для просмотра всех рациональных способов раскроя необходимо нажать на кнопку "Раскрои".

Рис. 3

Для введения новых данных, необходимо удалить старые с помощью нажатия кнопки "Обновить".

Контрольный пример

Работу программы опишем на конкретном примере.

Пусть в задаче генерирования линейного раскроя заданы следующие параметры: длина проката L = 40, количество типов деталей m = 4, а значения длин li и стоимости ci каждой детали приведены в таблице:

i	1	2	3	4
li	7	11	13	17
ci	9	14	16	22

Табл. 6

Выбираем начальное значение длины раскроя, равное минимальной длине детали: l0 = min li = 7 и последовательно «шагаем» до конца проката, т.е. 40.

Чтобы найти максимальную стоимость на каждом шаге, мы перебираем все детали, которые могут поместиться в текущий раскрой, начиная с минимальной по длине. Для подсчета стоимости раскроя на текущем шаге мы вычитаем длину очередной выбранной детали из текущего раскроя и по таблице находим раскрой с длиной, равной полученному остатку и суммируем его оценку с оценкой выбранной детали. Из вычисленных оценок выбираем максимальную и заносим её в таблицу, вместе с номером детали, при которой эта оценка была получена.

Далее в таблице приведены результаты первого этапа (прямого хода) процесса:

l	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
f(l)	9	9	9	9	14	14	16	18	18	18	22	23	23	25	27	28	28
i(l)	1	1	1	1	2	2	3	1	1	1	4	1	1	1	1	2	2

l	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
f(l)	31	32	32	34	36	37	38	40	41	42	44	45	46	47	49	50	51
i(l)	1	1	1	1	1	1	3	1	1	2	4	1	1	1	1	1	1

Табл. 7

Здесь и далее i(l) – номер детали, которой соответствует максимальная оценка раскроя (сумма стоимости всех деталей, входящих в раскрой) f(l) на шаге l.

Рассмотрим более подробно последовательное заполнение таблицы на примере шагов

l = 7…14, 22.

l = 7

Выбираем первую деталь: i = 1. Длина детали 7, оценка 9.

Вычисляем остаток от раскроя: 7 – 7 = 0. Поскольку остаток нулевой, то деталей, которые можно добавить в раскрой, нет. Следовательно, максимальная оценка текущего раскроя равна f = 9. Заносим в таблицу значения i(7) = 1, f(7) = 9 и переходим к следующему шагу раскроя.

2) l = 8

Снова берём первую деталь: i = 1. Длина детали 7, оценка 9.

Остаток: 8 – 7 = 1. Так как деталей с такой длиной нет, максимальная оценка раскроя f = 9. Заносим в таблицу i(8) = 1, f(8) = 9.

3) l = 9

i = 1, остаток 9 – 7 = 2, f = 9.

Заносим в таблицу i(9) = 1, f(9) = 9.

4) l = 10

i = 1, остаток 10 – 7 = 3, f = 9.

Заносим в таблицу i(10) = 1, f(10) = 9.

5) l = 11

i = 1, остаток 11 – 7 = 4, f = 9.

Учитывая, что в текущий раскрой также уместится деталь i = 2 c длиной 11, получим: i = 2, остаток 11 – 11 = 0, f = 14.

Сравним оценки раскроев. Выберем максимальную оценку (f = 14) и соответствующую ей деталь (i = 2).

Заносим в таблицу i(11) = 2, f(11) = 14.

6) l = 12

i = 1, остаток 12 – 7 = 5, f = 9.

I = 2, остаток 12 – 11 = 1, f = 14 (максимум)

Заносим в таблицу i(12) = 2, f(12) = 14.

7) l = 13

i = 1, остаток 13 – 7 = 6, f = 9.

I = 2, остаток 13 – 11 = 2, f = 14.

I = 3, остаток 13 – 13 = 0, f = 16 (максимум)

Заносим в таблицу i(13) = 3, f(13) = 16.

8) l = 14

i = 1, остаток 14 – 7 = 7.

Если мы видим, что длина остатка раскроя больше или равна начальному значению длины раскроя (l0 = 7), т.е. в остаток может поместиться какая-либо деталь (в данном случае с индексом i = 1), из таблицы считываем значение оценки раскроя f(i) при i, равном значению остатка: f (7) = 9, тогда суммарная оценка раскроя f = f(7) + 9 = 9 + 9 = 18 (максимум)

i = 2, остаток 14 – 11 = 3, f = 14.

I = 3, остаток 14 – 13 = 1, f = 16.

Заносим в таблицу i(14) = 1, f(14) = 18.

…16) l = 22

i = 1, остаток 22 – 7 = 15, f (15) = 18, f = 18 + 9 = 27.

I = 2, остаток 22 – 11 = 11, f(11) = 14, f = 14 + 14 = 28 (максимум)

i = 3, остаток 22 – 13 = 9, f(9) = 9, f = 9 + 16 = 25.

I = 4, остаток 22 – 17 = 5, f = 22.

Заносим в таблицу i(22) = 2, f(22) = 28. И т.д., пока не достигнут конец проката.

Выполняем обратный ход (начинаем двигаться с конца таблицы):

l = 40

Из таблицы получаем индекс детали, добавленной в текущий раскрой: i(40) = 1.

Находим длину детали с полученным индексом: l1 = 7.

Вычисляем остаток раскроя: 40 – 7 = 33. Этот остаток используем для следующего шага обратного хода.

2) l = 33

Индекс детали: i(33) = 2.

Длина детали: l2 = 11.

Остаток раскроя: 33 – 11 = 22.

3) l = 22

Индекс детали: i(22) = 2.

Длина детали: l2 = 11.

Остаток раскроя: 22 – 11 = 11.

4) l = 11

Индекс детали: i(11) = 2.

Длина детали: l2 = 11.

Остаток раскроя: 11 – 11 = 0. Обратный ход закончен.

Теперь подсчитываем количество деталей каждого типа, которые мы получили при обратном ходе. Деталь с индексом i = 1 встретилась 1 раз, деталь с индексом i = 2 встретилась 3 раза.

Таким образом, искомый оптимальный раскрой характеризуется следующим четырёхмерным вектором x = (1; 3; 0; 0).

В вышеприведённой таблице с результатами прямого хода выделены номера заготовок, которые при обратном ходе последовательно включались в оптимальный раскрой.

Результат работы программы (проверка алгоритма):

Исходные данные

Длина проката: 40

Количество типов деталей: 4

Длина детали №1….: 7 Цена детали №1….: 9

Длина детали №2….: 11 Цена детали №2….: 14

Длина детали №3….: 13 Цена детали №3….: 16

Длина детали №4….: 17 Цена детали №4….: 22

Результат

Рис. 4

Рис.5

Оптимальное количество деталей каждого типа:

Деталь №1….: 1 шт.

Деталь №2….: 3 шт.

Деталь №3….: 0 шт.

Деталь №4….: 0 шт.

Оценка раскроя: 51 денежных единиц

Остаток материала: 0

Результаты ручного и машинного вычислений совпадают, что говорит о работоспособности разработанного алгоритма.

Заключение

Задача оптимального раскроя материалов является одной из самых важных в ресурсосберегающих технологиях для заготовительного производства, поскольку напрямую ведет к экономии материалов и снижению отходов.

Одним из вариантов такой задачи является задача оптимального линейного раскроя материалов, в рассматриваемом случае − раскрой стержня. Специфика исследуемой задачи требует рассмотрения большого числа возможных компоновок заготовок.

В работе были рассмотрены основные понятия раскроя стандартных форм, показано практическое приложение к решению возникающих задач. Для оптимизации расчетов по таким задачам была разработана программа на языке Delphi, позволяющая реализовать целенаправленный перебор всех способов рационального раскроя за конечное число шагов, в результате чего находится рациональный раскрой с максимумом прибыли.

В данной работе поставленная задача была решена с помощью сеточного метода. Как показала проделанная работа, этот метод эффективен и прост для программной реализации на ЭВМ. Результат, полученный с помощью этого метода, является оптимальным.

В курсовой работе были произведены ручные вычисления и по ним проверена работа запрограммированного алгоритма на ЭВМ. Программа может применяться в различных отраслях промышленности при массовом производстве, при этом в алгоритм следует вносить коррективы, связанные с учетом технологии производства и применяемого оборудования.

referat911.ru