4.9. Оптимизация портфеля ценных бумаг предприятия. Оптимизация портфеля ценных бумаг

4.9. Оптимизация портфеля ценных бумаг предприятия

Данный раздел посвящен выбору оптимизации структуры портфеля ценных бумаг предприятия. Последовательно рассмотрены три модели оптимизации фондового портфеля: Марковица, Шарпа и "Квази-Шарп". Если две первые модели являются классическими, то последняя специально разработана для условий фондового рынка Украины, который находится в стадии становления.

4.9.1. Понятие оптимизации портфеля ценных бумаг предприятия

Основными характеристиками любой ценной бумаги являются – ее доходность и показатель риска. Под риском понимается возможность не получения ожидаемого дохода или утраты (полной или частичной) средств, размещенных в данную ценную бумагу. Как правило, ценные бумаги, обладающие низким показателем риска, дают небольшую доходность, а ценные бумаги, которые могут дать большой доход, имеют значительные показатели риска. Риск принято разделять на рыночный – единый для всех ценных бумаг, которого невозможно избежать, и индивидуальный – присущий конкретной ценной бумаге. Размещая денежные средства в различные ценные бумаги, т.е. формируя портфель ценных бумаг, можно снизить индивидуальный риск: если по одним ценным бумагам будет низкий доход или убыток, то другие это компенсируют своей более высокой доходностью. Чем больше ценных бумаг содержится в портфеле, т. е. чем более он диверсифицирован, тем меньше индивидуальный риск.

Каждое предприятие, желающее разместить свободные средства на фондовом рынке, имеет свою шкалу оценки риска и доходности. Высокая доходность для одного предприятия может показаться низкой для другого. Одни предпочитают низкий риск с низкой доходностью, а другие – согласны на больший риск с большей ожидаемой доходностью.

Целью оптимизации портфеля ценных бумаг является формирования такого портфеля ценных бумаг, который бы соответствовал требованиям предприятия, как по доходности, так и по рискованности, что достигается путем увеличения количества ценных бумаг в портфеле.

Сформулируем задачу оптимизации. Пусть доходность портфеля из N ценных бумаг и его показатель рискаопределяются следующими функциями:

;

где — процентная доля ценной бумаги в портфеле;

—некоторая характеристика риска данной ценной бумаги, обычно это среднее квадратичное отклонение доходности ценной бумаги;

—доходность ценной бумаги.

Содержание каждой функции определяется в дальнейшем при построении модели доходности и риска.

При решении задачи необходимо учесть следующие естественные ограничения:

— сумма долей всех акций (в процентах) составляет 100%:

;

— количество акций не может быть отрицательным:

Решением задачи является некоторая целевая структура портфеля, представленная набором значений (). Идеальная постановка задачи оптимизации портфеля — получить максимальную доходность при минимальном риске:

Но такая задача некорректна, т. е. не имеет однозначного решения. Идеальный результат не достижим, как и все идеальное.

Выходом из положения является введение критериальных ограничений.

Первый вариант — задаться некоторой максимально допустимой величиной риска . Тогда задача оптимизации сводится к выбору такой структуры портфеля, при которой риск портфеля не превышает заданного значения, а доходность портфеля является максимальной. Такая задача будет в дальнейшем называться прямой задачей:

Второй вариант — задаться некоторой минимально приемлемой величиной доходности . В этом случае задача оптимизации сводится к выбору такой структуры портфеля, доходность которого выше либо равна заданному значению, а риск минимален:

Решив прямую и обратную задачи по оптимизации портфеля из N ценных бумаг, предприятие получит данные о том, сколько и каких ценных бумаг необходимо приобрести, чтобы сформировать портфель, имеющий (по меркам предприятия) достаточно высокую доходность при приемлемом риске.

При попытке решения прямой либо обратной задач возникает вопрос, каким образом определяются характеристики портфеля (доходность и риск)? На сегодняшний день наиболее распространены две модели определения характеристик портфеля: модель Марковица и модель Шарпа. Обе модели созданы и успешно работают в условиях уже сложившихся относительно стабильных западных фондовых рынков. К сожалению, украинский фондовый рынок назвать стабильным пока еще нельзя. Поэтому была предпринята попытка, создать модель, способную успешно функционировать в условиях формирующегося, развивающегося и реорганизовывающегося фондового рынка, каковым на сегодняшний день и является фондовый рынок Украины. Предложенная модель получила название "Квази-Шарп" (в следствие схожести в общих чертах с моделью Шарпа) и будет приведена ниже. В дальнейшем каждая модель рассмотрена отдельно.

studfiles.net

Глава 3. Оптимизация портфеля ценных бумаг. Метод Марковица — Мегаобучалка

Задачей оптимизации портфеля будет являться снижение риска.

По итогам расчетов второй главы сформируем ковариационно-дисперсионную матрицу следующего вида:

Составим ковариационно-дисперсионную матрицу ценных бумаг, входящих в состав оптимизируемого портфеля:

Задача оптимизации выглядит следующим образом:

Далее необходимо сформировать функцию Лагранжа:

Теперь продифференцируем полученное уравнение по 5 неизвестным величинам. Получим систему 5 уравнений с 5 неизвестными.

Решив данную систему уравнений, применяя метод Гаусса, получаем неизвестные доли акций в портфеле: ХА=0,69%; ХB=14,44%; ХC=32,04%; ХD=52,84%.

Рассчитаем доходность нового портфеля:

Рассчитаем дисперсию нового портфеля:

Таблица 12

Расчет дисперсии оптимизированного портфеля

		Дисперсия
А	0,69	1,7653	0,000082
В	0,1444	0,0847	0,001766
С	0,3204	0,0386	0,003963
D	0,5284	0,0234	0,006536
		Ковариация
AB	0,000982	0,0003041	0,000001
AC	0,002179	0,0003933	0,000002
AD	0,003593	-0,0000165	0,000000
BC	0,046266	-0,0000324	-0,000003
BD	0,076301	0,0001438	0,000022
CD	0,169299	-0,0000199	-0,000007
Сумма			0,012362

Рассчитаем риск портфеля как корень квадратный из дисперсии:

Таким образом, чтобы получить доходность портфеля -0,02% при минимальном уровне риска, который составит 11,12%, ценные бумаги в портфеле следует распределить следующим образом: «Автоваз» 0,69%; «Башнефть» 14,44%; ОАО «РусГидро» 32,04%; ОАО «Роснефть» 52,84%.

Сравним два портфеля: первый, составленный по результатам фундаментального и технического анализа и второй, составленный по результатам оптимизации (Таблица 13).

Таблица 13

Сравнительная характеристика двух портфелей

№ п/п	Риск портфеля	Доходность портфеля
1.	16,88%	-0,31%
2.	11,12%	-0,02%

Исходя из данных таблицы, следует, что второй портфель является более эффективным по сравнению с первым, так как при увеличении доходности до -0,02% (на 0,29%), уровень риска при этом благодаря оптимизации портфеля уменьшился до 11,12%.

Заключение

Целью курсовой работы являлось расширение, углубление и систематизация знаний теоретических аспектов оптимизации портфеля ценных бумаг, а также применение их для оптимизации конкретного портфеля.

Рассмотрев основные методы оптимизации портфеля ценных бумаг, можно сделать следующие выводы:

· Подход Марковица заключается в том, что он предложил рассматривать доходности активов (и составленных из них портфелей) как случайные величины. В теории Марковица математическое ожидание рассматривается как понятие ожидаемой доходности, а дисперсия (или стандартное отклонение) служит мерой риска. При этом принимается важное соглашение, состоящее в том, что инвестор при принятии инвестиционных решений основывается лишь на двух характеристиках: ожидаемой доходности и риске.

· В модели Шарпа рассматривается взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом. При этом считается, что используемые при расчете доходности и риска портфеля, данные о составе портфеля в прошлые периоды полностью отражают будущие значения доходности. Под риском ценной бумаги Шарп понимал степень зависимости изменения доходности ценной бумаги от изменения доходности рынка в целом.

· В модели Тобина одним из условий является наличие безрисковых ценных бумаг, риск такой ценной бумаги всегда минимален по сравнению с другими ценными бумагами. Задача оптимизации портфеля в этом случае значительно упрощается

Во второй части курсовой работы на основании фундаментального и технического анализа ценных бумаг был сформирован портфель, рассчитаны его риск и доходность.

Портфель состоял из четырех активов: ОАО «Автоваз», ОАО «Башнефть», ОАО «РусГидро и ОАО «Роснефть». Удельные веса активов в портфеле составили: 10, 20, 20 и 50% соответственно.

Доходность сформированного портфеля составила –0,31%. а риск портфеля 16,88%.

В третьей главе с помощью метода оптимизации Марквица, описанного в первой части курсовой работы, был сформирован новый портфель. Рассчитан риск и доходность нового портфеля.

Задачей оптимизации была минимизации риска. Удельные веса ценных бумаг, рассчитанные при решении задачи оптимизации, составили: ОАО «Автоваз» – 0,69%, ОАО «Башнефть» –14,44%, ОАО «РусГидро –32,04% и ОАО «Роснефть» – 52,84%. Риск портфеля при этом составил 11,12%

Таким образом, цель оптимизации портфеля ценных бумаг достигнута.

Список использованной литературы

1) Егорова С.Е., Волкова О.А. Анализ финансовой отчетности. – Псков: Издательство ППИ, 2011, – 224 с.

2) Синицына Н.М. Рынок ценных бумаг. – Н. Новгород: «Полиграфторгсервис», 2004, – 112 с.;

3) Максимова В.Ф.. Инвестиционный менеджмент. – М.: Изд. центр ЕАОИ. 2007, –214 с.;

4) Шапкин А.С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. – М.: «Дашков и Ко», 2006, -544 с.;

5) Шапкин А.С., Шапкин В.А. Управление портфелем инвестиций ценных бумаг. – М.: «Дашков и Ко», 2006, -512 с.;

6) Шаповал А.Б. Инвестиции: математические методы. - М.: Форум-ИНФРА-М, 2005.

7) Абудзин И.С. «К вопросу о проблеме выбора оптимального портфеля ценных бумаг» // Финансовый менеджмент, №4, 2007;

8) Золотых К.И., Хайрулина Л.С. «Оптимизационная модель формирования инвестиционного портфеля» // Финансовый менеджмент, №5,2005;

9) Кох И.А. «Практические подходы к формированию портфеля ценных бумаг» // Финансы и кредит, №41, 2008;

10) Рязанов Б. Теории портфельного инвестирования и их применение в условиях российского рынка // Рынок ценных бумаг – 2011. – №2. – С. – 59-63.

11) Ханин Д.Г. «Возможности применения теории эффективных портфелей на российском фондовом рынке» // Экономический анализ: теория и практика, №5, 2012;

12) Модель Марковица [Электронный ресурс] // http://www.riskstatistic.ru/index/model_markovica/0-43

13) Модель Шарпа [Электронный ресурс] // http://www.riskstatistic.ru/index/model_sharpa/0-44

megaobuchalka.ru

Оптимизация портфеля ценных бумаг средствами Python / Хабр

Введение

На финансовом рынке обращается, как правило, несколько типов ценных бумаг: государственные ценные бумаги, муниципальные облигации, корпоративные акции и т.п.

Если у участника рынка есть свободные деньги, то их можно отнести в банк и получать проценты или купить на них ценные бумаги и получать дополнительный доход. Но в какой банк отнести? Какие ценные бумаги купить?

Ценные бумаги с низкими рисками, как правило, малодоходны, а высокодоходные, как правило, более рискованны. Экономическая наука может дать некоторые рекомендации для решения этого вопроса, но для этого необходимо иметь соответствующие программные средства, желательно с простым интерфейсом и бесплатные.

Программные средства для анализа портфелей ценных бумах должны работать с матрицами доходности и решать задачи нелинейного программирования с ограничениями в виде строгих и нестрогих неравенств. Символьное решение на Python некоторых типов задач нелинейного программирования мною уже рассматривалось в публикации [1]. Однако, применить предложенные в указанной публикации методы для анализа портфеля ценных бумаг нельзя из-за ограничений в виде строгих неравенств.

Целью настоящей публикации является разработка методов оптимизации портфелей ценных бумаг с использованием библиотеки scipy.optimize. Пришлось исследовать и применить при программировании такие мало известные возможности указанной библиотеки, как введение дополнительных ограничений в функцию цели [2].

Постановка задачи об оптимальном портфеле Марковица

Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на приобретение ценных бумаг. Цель инвестора – вложить деньги так, чтобы сохранить свой капитал, а при возможности и нарастить его.

Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Стоимость портфеля – это суммарная стоимость всех составляющих его бумаг. Если сегодня его стоимость есть Р, а через год она окажется равной Р', то (Р'- Р)/Р естественно назвать доходностью портфеля в процентах годовых. Доходность портфеля – это доходность на единицу его стоимости.

Пусть xi – доля капитала, потраченная на покупку ценных бумаг i-го вида. Весь выделенный капитал принимается за единицу. Пусть di – доходность в процентах годовых бумаг i-го вида в расчете на одну денежную единицу.

Доходность колеблется во времени, так что будем считать ее случайной величиной. Пусть mi, ri – средняя ожидаемая доходность и среднее квадратическое отклонение, называемое риском. Через CVij обозначим ковариацию доходностей ценных бумаг i – го и j – го видов.

Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность больше, а риск меньше. Однако, поскольку “нельзя поймать двух зайцев сразу”, необходимо сделать определенный выбор между эффективностью и риском.

Модель оптимального портфеля Марковица, которая обеспечивает минимальный риск и заданную доходность

Такая модель в виде системы из уравнений и неравенств имеет вид [3]:

Необходимо определить: x1,x2…xn.

Исходными данными для расчета является матрица доходности ценных бумаг следующей формы (заполненный пример матрицы в листинге программы):

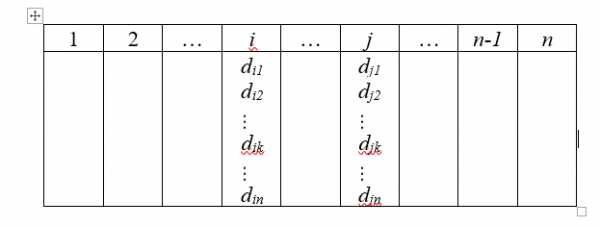
Для реализации модели минимального риска на Python нужно выполнить следующие этапы разработки: 1.Определение средней доходности акций 1-6:

from sympy import * import numpy as np from scipy.optimize import minimize from sympy import * import numpy as np from scipy.optimize import minimize "D- матрица доходности (обычно загружается из файла)" D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102], [12.517, 13.25,12.947,12.596,12.853,13.036], [12.786, 12.822,15.447,14.452,15.143,16.247], [11.863, 12.114,13.359,13.437,11.913,15.300], [11.444, 13.292,13.703,11.504,13.406,15.255], [14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64) d= np.zeros([6,1])# столбец для средней доходности m,n= D.shape#размерность матрицы for j in np.arange(0,n): for i in np.arange(0,m): d[j,0]=d[j,0]+D[i,j] d=d/n print("Средняя доходность акций 1-6 : \n %s"%d)Получим:

Средняя доходность акций 1-6:

[[ 12.19916667] [ 13.17116667] [ 13.98283333] [ 13.73466667] [ 13.46983333] [ 14.84666667]]

2. Построение ковариационной матрицы (m=n=6).

CV= np.zeros([m,n]) for i in np.arange(0,m): for j in np.arange(0,n): x=np.array(D[0:m,j]).T y=np.array(D[0:m,i]).T X = np.vstack((x,y)) CV[i,j]=round(np.cov(x,y,ddof=0)[1,0],3) print(«Ковариационная матрица CV: \n %s»%CV)

Получим:

Ковариационная матрица CV:

[[ 2.117 1.773 2.256 2.347 2.077 1.975] [ 1.773 1.903 1.941 2.049 1.888 1.601] [ 2.256 1.941 2.901 2.787 2.701 2.761] [ 2.347 2.049 2.787 3.935 2.464 2.315] [ 2.077 1.888 2.701 2.464 2.723 2.364] [ 1.975 1.601 2.761 2.315 2.364 3.067]]

3. Символьное определение функции для определения дисперсии доходности портфеля (функции риска).

x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 p q w' , float= True) v1=Matrix([x1,x2,x3,x4,x5,x6]) v2=v1.T w=0 for i in np.arange(0,m): for j in np.arange(0,n): w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})] print("Дисперсия доходности портфеля (функция риска):\n%s"%w) Получим:

Дисперсия доходности портфеля (функция риска):

2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2

4. Определение оптимального портфеля акций для минимального риска и доходности mp=13.25

def objective(x):#функция риска x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):#условие для суммы долей -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def constraint2(x): # задание доходности return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25 x0=[1,1,0,0,0,1]#начальное значение переменных для поиска минимума функции риска b=(0.0,1.0)# условие для x от нуля до единицы включая пределы bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка) con1={'type':'ineq','fun':constraint1} #передача условий в функцию риска(подготовка) con2={'type':'eq','fun':constraint2} #передача условий в функцию риска(подготовка) cons=[con1,con2]#передача условий в функцию риска(подготовка) sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# поиск минимума функции риска print("Минимум функции риска -%s"%str(round(sol.fun,3))) print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3))) Получим:

Минимум функции риска -1.846 Акция 1 доля- 0.141, доходность- 1.721 Акция 2 доля- 0.73, доходность- 9.616 Акция 3 доля- 0.0, доходность- 0.0 Акция 4 доля- 0.0, доходность- 0.0 Акция 5 доля- 0.0, доходность- 0.0 Акция 6 доля- 0.129, доходность- 1.914

Вывод:

Доходными являются 1,2,6 акции. Это и есть часть ответа на вопросы, поставленные в начале публикации.

Полный листинг программы для минимизации риска по методу Марковица при заданной доходностиfrom sympy import * import numpy as np from scipy.optimize import minimize "D- матрица доходности(обычно загружается из файла)" D=np.array([[9.889, 11.603,11.612, 12.721,11.453,12.102], [12.517, 13.25,12.947,12.596,12.853,13.036], [12.786, 12.822,15.447,14.452,15.143,16.247], [11.863, 12.114,13.359,13.437,11.913,15.300], [11.444, 13.292,13.703,11.504,13.406,15.255], [14.696, 15.946,16.829,17.698,16.051,17.140]],np.float64) d= np.zeros([6,1])# столбец для средней доходности m,n= D.shape#размерность матрицы for j in np.arange(0,n): for i in np.arange(0,m): d[j,0]=d[j,0]+D[i,j] d=d/n print("Средняя доходность по столбцам : \n %s"%d) CV= np.zeros([m,n]) for i in np.arange(0,m): for j in np.arange(0,n): x=np.array(D[0:m,j]).T y=np.array(D[0:m,i]).T X = np.vstack((x,y)) CV[i,j]=round(np.cov(x,y,ddof=0)[1,0],3) print("Ковариационная матрица CV: \n %s"%CV) x1,x2,x3,x4,x5,x6,x7,x8,p,q,w=symbols(' x1 x2 x3 x4 x5 x6 x7 x8 p q w' , float= True) v1=Matrix([x1,x2,x3,x4,x5,x6]) v2=v1.T w=0 for i in np.arange(0,m): for j in np.arange(0,n): w=w+v1[p.subs({p:i}),q.subs({q:0})]*v2[p.subs({p:0}),q.subs({q:j})]*CV[p.subs({p:i}),q.subs({q:j})] print("Дисперсия доходности портфеля (функция риска):\n%s"%w) def objective(x):#функция риска x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):#условие для суммы долей -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def constraint2(x): # задание доходности return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - 13.25 x0=[1,1,0,0,0,1]#начальное значение переменных для поиска минимума функции риска b=(0.0,1.0)# условие для x от нуля до единицы включая пределы bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка) con1={'type':'ineq','fun’: constraint1} #передача условий в функцию риска(подготовка) con2={'type':'eq','fun’: constraint2} #передача условий в функцию риска(подготовка) cons=[con1,con2]#передача условий в функцию риска(подготовка) sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# поиск минимума функции риска print("Минимум функции риска -%s"%str(round(sol.fun,3))) print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3)))

Оптимальный портфель Марковица максимальной доходности и заданного, (приемлемого) риска

Система уравнений и неравенств имеет вид:

Оптимизация портфеля максимальной доходности при заданном риске на Pythonimport numpy as np from scipy.optimize import minimize d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) def constraint2(x): x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 \ + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 \ + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 \ + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-2 def constraint1(x): return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0 def objective(x): return -(12.199*x[0] + 13.171*x[1] + 13.983*x[2] + 13.735*x[3] + 13.47*x[4]+ 14.847*x[5] ) x0=[1,1,1,1,1,1] b=(0.0,1.0) bnds=(b,b,b,b,b,b) con1={'type':'ineq','fun':constraint1} con2={'type':'eq','fun':constraint2} cons=[con1,con2] sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons) print("Максимум функции доходности -%s"%str(round(sol.fun,3))) print("Акция 1 доля- %s, доходность- %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print("Акция 2 доля- %s, доходность- %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print("Акция 3 доля- %s, доходность- %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print("Акция 4 доля- %s, доходность- %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print("Акция 5 доля- %s, доходность- %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3))) Часть приведенного листинга не требует пояснений, поскольку всё подробно изложено в предыдущем примере. Однако есть отличия. Столбец средней доходности d и функция условия def constraint2(x) взяты из предыдущего примера, причем в предыдущем примере это была функция минимального риска. Кроме того, для определения максимума перед выводом значения новой функции цели – def objective(x), поставлен знак минус.

Результат:

Максимум функции доходности --14.1 Акция 1 доля- 0.0, доходность- 0.0 Акция 2 доля- 0.72, доходность- 9.489 Акция 3 доля- 0.0, доходность- 0.0 Акция 4 доля- 0.0, доходность- 0.0 Акция 5 доля- 0.0, доходность- 0.0 Акция 6 доля- 0.311, доходность- 4.611

Акции 2,6 доходны. Но это не единственный результат оптимизации средствами scipy optimize minimize. Я решил сравнить результаты с решением той же задачи средствами Mathcad и вот что получил:

Mathcad указывает на те же номера 2,6 доходных акций, но доли другие. В Python 0.720,0.311 в Mathcad 0.539, 0.461, при этом разные значения максимальной доходности соответственно 14.1 и 13.9. Для того чтобы окончательно убедиться какая программа вычисляет оптимум правильно, подставим полученные в Python значения долей в Mathcad, получим:

Вывод: на Python оптимум функции, а следовательно доли и доходность вычисляется более точно, чем при использовании Mathcad.

Формирование оптимального портфеля ценных бумаг по модели Тобина

Портфель Тобина минимального риска:

где d0 – эффективность без рисковых бумаг; x0 – доля капитала вложенная в без рисковые бумаги; xi,xj — доля капитала вложенная в ценные бумаги i-го и j–го видов; di – математическое ожидание (среднее арифметическое) доходности i — й ценной бумаги; vij – корреляционный момент между эффективностью бумаг i-го и j –го видов.

Подбираем долю капитала заданной доходности, задаём общую доходность, приняв для примера следующие числовые значения x0=0.3, d0 =10, dp=12.7.

Реализация портфеля Тобина минимального риска на Pythonimport numpy as np from scipy.optimize import minimize d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) x00=0.3;d0=10;dp=12.7 def objective(x):#функция риска x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 + 3.95*x1*x6\ + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 + 2.901*x3**2 \ + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 + 4.63*x4*x6 \ + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2 def constraint1(x):#условие для суммы долей -1 return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x00 def constraint2(x): # задание доходности return d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5] - dp+x00*d0 x0=[1,1,1,1,1,1]#начальное значение переменных для поиска минимума функции риска b=(-1.0,100.0)# условие для x от нуля до единицы включая пределы bnds=(b,b,b,b,b,b)#передача условий в функцию риска(подготовка) con1={'type':'ineq','fun':constraint1} #передача условий в функцию риска(подготовка) con2={'type':'eq','fun':constraint2} #передача условий в функцию риска(подготовка) cons=[con1,con2]#передача условий в функцию риска(подготовка) sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons)# поиск минимума функции риска print("Минимум функции риска : %s"%str(round(sol.fun,3))) print("Акция 1 доля- %s, доходность: %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print("Акция 2 доля- %s, доходность: %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print("Акция 3 доля- %s, доходность: %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print("Акция 4 доля- %s, доходность: %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print("Акция 5 доля- %s, доходность: %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print("Акция 6 доля- %s, доходность: %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3))) Получим:

Минимум функции риска: 0.728 Акция 1 доля- -0.023, доходность: -0.286 Акция 2 доля- 0.666, доходность: 8.778 Акция 3 доля- -1.0, доходность: -13.983 Акция 4 доля- 0.079, доходность: 1.089 Акция 5 доля- 0.3, доходность: 4.048 Акция 6 доля- 0.677, доходность: 10.054

Доходными являются акции 2,4,5,6.

Портфель Тобина максимальной эффективности

где rp – риск портфеля.

Реализация портфеля Тобина максимальной эффективности на Pythonimport numpy as np from scipy.optimize import minimize x00=0.8;d0=10;rp=0.07 d=np.array( [[ 12.19916667], [ 13.17116667], [ 13.98283333], [ 13.73466667], [ 13.46983333], [ 14.84666667]]) def constraint2(x): x1=x[0];x2=x[1];x3=x[2]; x4=x[3]; x5=x[4]; x6=x[5] return 2.117*x1**2 + 3.546*x1*x2 + 4.512*x1*x3 + 4.694*x1*x4 + 4.154*x1*x5 \ + 3.95*x1*x6 + 1.903*x2**2 + 3.882*x2*x3 + 4.098*x2*x4 + 3.776*x2*x5 + 3.202*x2*x6 \ + 2.901*x3**2 + 5.574*x3*x4 + 5.402*x3*x5 + 5.522*x3*x6 + 3.935*x4**2 + 4.928*x4*x5 \ + 4.63*x4*x6 + 2.723*x5**2 + 4.728*x5*x6 + 3.067*x6**2-rp def constraint1(x): return x[0]+x[1]+x[2]+x[3]+x[4]+x[5]-1.0+x0 def objective(x): return -(d[0,0]*x[0] + d[1,0]*x[1] + d[2,0]*x[2] + d[3,0]*x[3] + d[4,0]*x[4]+ d[5,0]*x[5]+x00*d0) x0=[1,1,1,1,1,1] b=(-1.0,100.0) bnds=(b,b,b,b,b,b) con1={'type':'ineq','fun':constraint1} con2={'type':'eq','fun':constraint2} cons=[con1,con2] sol=minimize(objective,x0,method='SLSQP',\ bounds=bnds,constraints=cons) print("Максимум функции доходности : %s"%str(round(sol.fun,3))) print("Акция 1 доля- %s, доходность: %s"%(round(sol.x[0],3),round(d[0,0]*sol.x[0],3))) print("Акция 2 доля- %s, доходность: %s"%(round(sol.x[1],3),round(d[1,0]*sol.x[1],3))) print("Акция 3 доля- %s, доходность: %s"%(round(sol.x[2],3),round(d[2,0]*sol.x[2],3))) print("Акция 4 доля- %s, доходность: %s"%(round(sol.x[3],3),round(d[3,0]*sol.x[3],3))) print("Акция 5 доля- %s, доходность: %s"%(round(sol.x[4],3),round(d[4,0]*sol.x[4],3))) print("Акция 6 доля- %s, доходность- %s"%(round(sol.x[5],3),round(d[5,0]*sol.x[5],3))) Получим:

Максимум функции доходности: -11.657 Акция 1 доля- 0.09, доходность: 1.096 Акция 2 доля- 0.196, доходность: 2.583 Акция 3 доля- -1.0, доходность: -13.983 Акция 4 доля- 0.113, доходность: 1.552 Акция 5 доля- 0.411, доходность: 5.538 Акция 6 доля- 0.463, доходность- 6.872

Доходными являются акции 1,2,4,5.

Выводы:

Впервые средствами Python решена задача оптимизации портфеля ценных бумаг по моделям Марковица и Тобина. На сравнительном примере c математическим пакетом Mathcad показаны преимущества библиотеки scipy optimize minimize.

Ссылки:

Символьное решение задач нелинейного программирования
scipy.optimize.minimize
Постановка задачи об оптимальном портфеле

habr.com

Оптимизация портфеля ценных бумаг

Главный принцип формирования оптимального портфеля состоит в диверсификации ценных бумаг по видам с учетом ликвидности, доходности и риска. Поэтому рассмотрим методику наилучшего выбора структуры портфеля, то есть способы определения доли капитала для вложения в каждый из образующихся на рынке видов ценных бумаг.

На финансовом рынке имеется возможность приобретения любого из видов различных ценных бумаг, каждая из которых имеет свою цену приобретения Рр_лри этом ожидаемая доходность бумаги вида г составляет с,, г = 1, п. Для осуществления инвестиций инвестор располагает некоторой суммой В. Необходимость соблюдения требований диверсификации независимо от доходности ценной бумаги влияет на его решение не вкладывать в ценные бумаги вида г больше, чем Вг(г = 1, п) единиц средств. Очевидно, что

Построим математическую модель для этой ситуации.

Пусть хг(г = 1, п) — количество ценных бумаг вида г, приобретаемых инвестором. Тогда общий доход инвестора V от приобретения всех видов ценных бумаг составит

Методы решения данной задачи широко известны и здесь не обсуждаются.

Однако в реальной практике ситуация значительно сложнее. Это обусловлено тем, что многие параметры (такие, например, как ожидаемая доходность, вероятность ее получения и т.д.) инвестору заранее не известны. Поэтому рассмотрим более общую задачу формирования оптимального портфеля, связанную с влиянием случайных факторов.

Очевидно, что построение любой модели возможно лишь при упрощении реальной ситуации. В основе современной теории портфельных инвестиций лежат предположения:

1. Инвесторы оценивают активы только по двум параметрам:

а) ожидаемой доходности;

б) среднеквадратическому отклонению доходности от ожидаемой величины.

2. Все инвесторы имеют свободный доступ к финансовым активам.

3. Отсутствуют операционные издержки и налоги.

4. Нет ограничений на короткие продажи.

5. Существует безрисковая ставка процента, по которой инвесторы могут как инвестировать, так и брать кредит.

6. Активы бесконечно делимы. \Данные предположения могут показаться достаточно жесткими, но они вполне приемлемы для получения практическихрешений.

Основной математический постулат, на котором будет строиться последующая теория, — это то, что доходность ценной бумаги является случайной величиной, а конкретное значение доходности — реализацией этой случайной величины.

Для построения математической модели стоимости портфеля введем обозначения.

Дисперсия или вариация доходности г-й ценной бумаги будет равна

Здесь и далее используется операция вычисления математического ожидания £"[•], применяемого к случайной величине, стоящей в скобках. Ожидаемое значение случайной величины обычно понимается как среднее по всем значениям (реализациям), вычисленное с учетом частоты их возможного появления.

Среднеквадратическое отклонение доходности г'-й ценной бумаги (г = 1, п) от ее математического ожидания является мерой риска ценной бумаги. Если вариация равна нулю, то есть У£= 0, а следовательно и a t = 0, то в этом случае неопределенность отсутствует, а значит и риск тоже. Чем больше вариация, тем больше Среднеквадратическое отклонение, тем больше доходность отклоняется от своего ожидаемого значения, тем выше неопределенность, тем выше риск.

В чем интерес инвестора? С одной стороны, для него важно получить максимальную эффективность от вложения своего капитала в ценные бумаги. С другой стороны, он заинтересован в получении гарантий, что его ожидания сбудутся, поэтому важно уменьшить риск.

Очевидно, что ценная бумага, представленная точкой 1, является более предпочтительной по сравнению с ценными бумагами, представленными точками 2 и 3. Также бумага, представленная точкой 4, является более предпочтительной по сравнению с бумагой, представленной точкой 2. И только склонность к риску даст возможность выбора между бумагами, представленными точками 1, 4 или 5.

Рис. 6.1. Представление характеристик различных ценных бумаг

Для дальнейшего рассмотрения вопроса введем понятие ковари-ации двух случайных величин (VtJ):

Ковариация характеризует зависимость двух случайных величин: если Vl} > О, то увеличение одной случайной величины ведет к увеличению другой случайной величины, то есть имеет место прямая зависимость величин; если Vtj < О, то увеличение одной величины ведет к уменьшению другой величины — имеет место обратная зависимость; в случае независимости двух случайных величин

у„ = о.

Ковариация связана с коэффициентом корреляции формулой

Для того чтобы получить ту или другую характеристику, используются соответствующие статистические данные.

Пусть Rlt — доходность г-й (г = 1, п) ценной бумаги в периоде £, где t = 1, Г; Т — число наблюдаемых периодов. Тогда статистические оценки ценной бумаги будут вычисляться следующим образом:

6) статистическая оценка вариации:

а) статистическая оценка математического ожидания:

Перейдем к рассмотрению характеристик портфеля ценных бумаг. Для этого важно знать его структуру, то есть соотношение долей капитала, вложенного в ценные бумаги различных видов.

Переходя к математическому ожиданию, на основании (6.10) получаем

Дисперсия, или вариация эффективности портфеля рассчитывается следующим образом:

Как и в случае с мерой риска для отдельной ценной бумаги, для портфеля такой же мерой риска будет являться среднеквадрати-ческое отклонение, то есть

Рассмотрим следующую ситуацию, когда инвестиционные ресурсы разделены между всеми видами ценных бумаг поровну, то есть

Подставим (6.14) в (6.13), в результате получим инвестиционный риск, равный

На основании чего можно сделать вывод: при до( пншючн шом числе ценных бумаг, включенных в портфепъ, /ни л ограничен и стремится к нулю при п -> ос.

Этот результат известен в теории вероятностей как закон больших чисел, а в теории финансовых рисков — как эффект диверсификации.

Отсюда вытекает основное практическое правило работы на финансовом рынке: для повышения надежности эффекта от вклада в рискованные ценные бумаги целесообразно сделать вложения не в один вид, а сформировать портфель, содержащий возможно большее разнообразие ценных бумаг, эффект от которых случаен, но случайные отклонения независимы.

где р —коэффициент корреляции.

Полученные выводы сделаны на основании гипотезы о независимости эффектов. Рассмотрим случай, когда доходности ценных бумаг являются зависимыми случайными величинами. Подставим выражение (6.6) в (6.12) и получим'

Таким образом, при полной прямой корреляции диверсификация не дает положительного эффекта, то есть риск портфеля не зависит от числа ценных бумаг и не стремится к нулю при увеличении числа видов ценных бумаг. В результате проведенного анализа сле-

дует: чем меньше корреляция между доходностями ценных f)t/*ui/t тем больше возможности снижения риска путем диверсификации портфеля.

Естественно, что ожидаемая эффективность и риск портфеля будут зависеть от его структуры, то есть доли исходного каптала, вложенного в каждый из видов ценных бумаг. Инвестор всегда сталкивается с дилеммой — желанием сформировать портфель с возможно большей ожидаемой эффективностью и в то же время возможно меньшим риском. Поскольку нельзя поймать двух зайцев сразу, необходимо сделать выбор. Он зависит от характера самого инвестора и от его склонности к риску. Портфели, имеющие наименьший риск для заданной ожидаемой или наибольшую ожидаемую доходность при заданном уровне риска, называются эффективными портфелями.

Сформировать эффективный портфель — значит найти доли капитала х\, г = 1, п, которые следует вложить в ценные бумаги г-го вида, чтобы получить наименьший риск при заданной ожидаемой эффективности или наибольшую ожидаемую эффективность при заданном уровне риска. То есть необходимо решить соответствующие задачи математического программирования:

Математическая формализация vo.lo; впервые оыла предложена Г.Марковичем в 1951 г., за что позднее он был удостоен Нобелевской премии в области экономики.

Проведем анализ решения данной задачи. ^ __

Пусть в результате решения найдены доли капитала х\ (i = 1, и) эффективного портфеля .в Ее ли х\ > О, то это означает, что инвестор должен вложить долю х\ своего капитала в i-и вид ценных бумаг. Если же х\ < О, то инвестору следует взять в долг с обязателъп ном последующего возврата ценные бумаги г -го вида на сумму, ранную х\ долей своего капитала. Такое взятие в долг называется короткой

HJ5

продажей {short sale). Инвестор в таком случае рассчитывает на понижение курса ценных бумаг. Если взятие в долг невозможно, то в соответствии с формулами (6.18), (6.19) следует ввести дополнительное ограничение неотрицательности переменных, то есть

х, > i = 1, п.

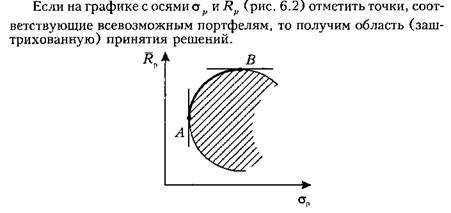
Рис. 6.2. Область принятия решений по формированию портфеля

Эффективным портфелям соответствуют точки, расположенные на части АВ кривой, ограничивающей эту область. Эта часть кривой называется множеством Парето, или эффективной границей.

Через несколько лет после опубликования знаменитой статьи Г. Марковица другой американский мономист Д. Тобин (также впоследствии лауреат Нобелевской премии) исследовал вопрос о влиянии безрисковых ценных бумаг с фиксированным доходом на формирование портфеля и доказал, что одной из важнейших задач является задача правильного распределения капитала между безрисковыми и рисковыми вложениями.

Однако при использовании изложенного выше метода возникает единственная проблема — получение достоверной статистической информации, необходимой для расчета эффективного портфеля. Эта проблема весьма актуальна для стран с развивающейся рыночной экономикой, то есть для стран, появившихся на постсоветском пространстве, где рынок ценных бумаг только начинает зарождаться и речь пока не идет об эффективной статистике. Но даже в странах с высокоразвитым рынком ценных бумаг статистика дает информацию о периодах, предшествующих моменту принятия решения по формированию портфеля.

При формировании портфеля всегда хотелось бы иметь информацию о будущих периодах инвестирования и о состоянии и перспективах развития заемщиков. Для получения такой информации наряду с известными аналитическими методами прогнозирования, основанными на использовании временных рядов, широко применяются методы экспертных оценок и основанные на них методы анализа, базирующиеся на использовании нечетких множеств.

stydopedia.ru

Управление и оптимизация портфеля ценных бумаг

Характерная для России политическая неопределенность и напряженность макроэкономических показателей делают рынок ГКО-ОФЗ спекулятивным и слабопредсказуемым даже в краткосрочной перспективе. В таких условиях возрастает значение выработки оптимальной стратегии управления портфелем государственных ценных бумаг, основанной на сложившихся закономерностях динамики рынка. Под управлением портфеля ценных бумаг понимается сохранение или изменение его структуры для достижения целей инвестора на основе анализа конъюнктуры рынка.

В настоящий момент на российском фондовом рынке наименее безопасным средством инвестирования являются государственные ценные бумаги. К преимуществу данного вида инвестиций помимо относительно высокой доходности и минимального (по российским меркам) риска следует отнести и высокую ликвидность этого финансового инструмента. Льготная ставка налогообложения доходов по государственным ценным бумагам делает вложение средств в них достаточно привлекательным для инвестора. Для придания устойчивости любому портфелю доля государственных ценных бумаг должна составлять значительную часть его стоимости.

Наряду с портфелями сформированными из ценных бумаг, привлеченных с разных сегментов финансового рынка (государственных, муниципальных, корпоративных ценных бумаг, а также фьючерсов и опционов), в российской практике существуют портфели сформированные только из государственных ценных бумаг (например, ГКО/ОФЗ). Сочетание в этих ценных бумагах доходности, высокой ликвидности и надежности позволяют формировать из них практически любые виды портфеля.

Портфель роста формируется из наиболее динамично растущих государственных облигаций преимущественно с коротким сроком до погашения. Задача управления таким портфелем заключается в получении дохода в кратчайшие сроки. Как правило, портфель такого рода формируется для клиентов, инвестирующих свои денежные средства до 21-30 дней.

Портфель ликвидности формируется из государственных облигаций с коротким или средним сроком до погашения, обладающих относительно стабильными (не снижающимися) ценами. Задача управления в этом случае сводится к формированию портфеля, реализация которого в минимальные сроки (1-2 дня) была бы, по крайней мере, безубыточной для клиента.

Портфель дохода формируется из государственных облигаций дальних выпусков. Стратегия управления такими портфелями заключается в покупке на аукционе или вторичных торгах облигаций с приемлемой доходностью, а затем их погашения. Портфель дохода обычно формируется для клиентов - физических лиц.

Для оптимизации управления портфелем ГКО-ОФЗ специалисты инвестиционного банка «Восток-Запад» предлагают весь портфель разделить на инвестиционную часть, в которой облигации, как правило, держаться до погашения и управляемую, призванную поддерживать высокую ликвидность вложений и получать дополнительную доходность.

Инвестиционный портфель (консервативный) формируется банком для страховки выплат по обязательствам на заданном инвестиционном периоде. Сроки и объемы погашения облигаций в портфеле должны приблизительно совпадать со сроками и объемами обязательств банка. Таким образом, доля консервативной части диктуется потребностью в обеспечении обязательств банка.

В условиях отсутствия в настоящее время у банков денежных пассивов (более 12 месяцев) специалисты рекомендуют использовать для инвестиционного портфеля короткие ценные бумаги, последний купон по которым известен (это касается ОФЗ-ПК). Кроме того, портфель, составленный из дальних выпусков, очень чувствителен к возможному повышению уровня процентных ставок, что может привести к снижению его текущей стоимости.

В управляемый портфель рекомендуется покупать недооцененные выпуски с высоким потенциалом роста (или ОФЗ-ПК с высоким купоном). Высокий потенциал роста на вторичном рынке имеют более длинные выпуски (со сроком до погашения более 60 дней). Основные методы получения дохода: процентный и ценовой арбитраж.

Защита от процентного риска в управляемом портфеле государственных ценных бумаг подразумевает его диверсификацию по критерию срочности выпусков отдельных займов. Управляемый портфель условно разбивается на две части:

- ликвидную, ориентированную на поддержание требуемого уровня текущей ликвидности. В этом случае размещение средств должно подразумевать возможность их изъятие для покрытия экстренных платежей;

- доходную, ориентированную на получение повышенной доходности к концу инвестиционного периода.

Целесообразность продажи или перевода облигаций из консервативной части в управляемую определяется на основании исследования конъюнктуры рынка, содержащего вывод о том, что их реализация по текущей доходности более выгодна, чем получение фиксированной доходности при погашении. Этот способ управления портфелем государственных ценных бумаг, представляется рациональным и может быть рекомендован институциональным инвесторам для работы на фондовом рынке.

Одним из крупнейших держателей российских ГКО-ОФЗ является ПКБ «Кредитимпекс Банк». Накопленный банком с 1993 г. опыт работы с этими активами, позволяет ему дать ряд практических рекомендаций по формированию и управлению портфелем ГКО-ОФЗ.

В ПКБ «Кредитимпекс Банк» создана двухуровневая система управления портфелями ГКО-ОФЗ. Непосредственное управление ими осуществляется финансовыми менеджерами. В зависимости от содержания, сложности и объема определенного портфеля, каждый менеджер управляет частью собственного портфеля банка и 3-5 клиентскими портфелями. Главный менеджер осуществляет перераспределение между отдельными менеджерами клиентских портфелей и долей собственного портфеля ГКО-ОФЗ.

При формировании портфелей менеджеры банка руководствуются принципом получения доходности на 10-15% выше средней по рынку, условием достижения которой служит оптимальная диверсификация портфеля в зависимости от сроков погашения обращающихся на рынке выпусков ГКО-ОФЗ. При включении в портфель бумаг с различными сроками погашения и доходностями риск инвестора недополучить прогнозируемый на расчетный срок доход снижается. Чем больше срок размещения, тем больше используется форм диверсификации портфеля.

Работа по управлению портфелем начинается после размещения средств и составления сбалансированного (по срокам и доходностям) портфеля ГКО-ОФЗ. По каждому из выпусков ГКО-ОФЗ, обращающимся на рынке, менеджер строит кривые роста цен и изменения доходностей к погашению и к аукциону, а также кривые изменения средневзвешенной доходности рынка. Сравнивая полученные зависимости с динамикой изменения доходности по данной серии (находящейся в портфеле банка и рассчитанной с учетом комиссионных при покупке и продаже облигаций), менеджер принимает решение о переформировании портфеля.

Как правило, на финансовом рынке доходность инвестиций прямо пропорциональна сроку вложений, и, следовательно, задача поддержания оптимального портфеля ГКО-ОФЗ сводится к постоянному решению одновременно двух, по сути, обратных, задач: достижению максимальной средневзвешенной доходности к погашению портфеля и минимального средневзвешенного срока до погашения.

В зависимости от текущих целей банка и состояния рынка в целом задача оптимизации портфеля ГКО-ОФЗ формируется следующим образом: при заданной средневзвешенной доходности к погашению портфеля выбрать те серии ГКО (ОФЗ), которые обеспечат минимальный срок до погашения портфеля в целом, или при заданном средневзвешенном сроке до погашения портфеля выбрать те серии ГКО, которые обеспечат максимальную доходность к погашению портфеля в целом.

Для расчета средневзвешенного срока до погашения портфеля А. Чернавин и А. Рогожин предлагают воспользоваться следующей формулой

где Vi - объем ГКО i-й серии в портфеле по текущим ценам; Yi - доходность к погашению ГКО i-й серии; ti - срок до погашения ГКО i-й серии.

Средневзвешенная доходность к погашению находится по формуле

Следует отметить, что при наличии на рынке некоторого числа серий ГКО/ОФЗ, различных по срокам и доходностям к погашению однозначного решения данной задачи не существует. Специалисты «Кредитимпекс Банка» считают, что при управлении портфелями ГКО/ОФЗ в каждый конкретный момент можно говорить лишь об оптимальном по срокам и доходности портфеле.

Каждый менеджер банка самостоятельно принимает решение о перевложениях средств и выборе новой серии для включения в портфель, основываясь на собственном опыте и прогнозе движения рынка. Для снижения субъективной составляющей рискованности общего портфеля банка, на этапе формирования портфеля ГКО-ОФЗ средства равномерно распределяются между менеджерами, а затем доли каждого менеджера варьируются.

В результате некоторого уменьшения влияния на рынок ГКО волюнтаристских решений властей и крупных операторов появилась возможность применения научных методов к его исследованию и подготовки решений по управлению портфелями конкретных инвесторов.

Как мы уже отмечали, на российском фондовом рынке классические методы управления портфелем ценных бумаг практически не применимы. При формировании портфеля максимизация доходности является главной целевой функцией (по сравнению с минимизацией риска), поскольку отражает основной смысл деятельности рационального портфельного инвестора на отечественном рынке ценных бумаг. Очевидно, что успех управления портфелем зависит от удачного сочетания научных методов с эрудицией экспертов, непосредственно работающих на данном сегменте фондового рынка.

Для достижения наилучшего для инвестора соотношения между прибылью и риском ставится задача поиска оптимального портфеля. В зависимости от выбора критерия оптимальности существуют разные подходы к формированию оптимального портфеля. Критерий оптимальности это некоторая функция, зависящая от структуры инвестиций. Максимальное (или минимальное) значение этой функции будет соответствовать структуре оптимального портфеля.

Для управления портфелем государственных ценных бумаг, в частности ГКО, российские менеджеры используют модель поиска оптимальной структуры портфеля по прогнозу динамики цен на отдельные выпуски ГКО.Целью управления такого портфеля является максимизация стоимости портфеля в конечный момент времени. Математически это можно выразить следующим образом

где t - конечный срок инвестирования; i - выпуск ГКО; Хit - количество ценных бумаг i-го выпуска в день Т; Cit - цена i-ro выпуска в день t.

Эта модель, основываясь на прогнозе цен, рекомендует вкладывать средства в тот выпуск, у которого темп роста цен Cit +1/ Cit максимален.

При таком вложении денег переоценка за период до ближайших торгов окажется максимальной, а если она максимальна каждый день, то максимальной будет и стоимость портфеля в конце планового периода.

Из анализа оптимального решения вытекает, что средства следует вкладывать в один выпуск, а именно, в тот, цены на который будут расти наиболее быстро. Такой вывод противоречит общепринятому понятию оптимального портфеля, который должен быть диверсифицирован. Однако подобный подход к формированию оптимальной структуры портфеля обычно аргументируется тем, что диверсификация оправдана лишь в случае вложения средств в существенно различные финансовые инструменты (а в данном случае речь идет только о ГКО).

www.jourclub.ru

Оптимизация портфеля ценных бумаг - страница 3

Рассмотрев и разобрав основные понятия рынка ценных бумаг, его основные компоненты перейдем непосредственно к теме Диплома. Итак, что же такое управление портфелем ценных бумаг? II Управление портфелем ценных бумаг Портфельные инвестиции связаны с формированием портфеля и представляют собой диверсифицированную совокупность вложений в различные виды финансовых активов. Портфель ценных бумаг– собранные воедино различные инвестиционные финансовые ценности, служащие инструментом для достижения конкретной инвестиционной цели вкладчика. Формируя портфель, инвестор исходит из своих "портфельных соображений". "Портфельные соображения" – это желание владельца средств иметь их в такой форме и в таком месте, чтобы они были безопасными, ликвидными и высокодоходными. Принципами формирования инвестиционного портфеля являются безопасность и доходность вложений, их стабильный рост, высокая ликвидность. Под безопасностью понимаются неуязвимость инвестиций от потрясений на рынке инвестиционного капитала и стабильность получения дохода. Ликвидность инвестиционных ценностей – это их способность быстро и без потерь в цене превращаться в наличные деньги. Ни одна из инвестиционных ценностей не обладает всеми перечисленными выше свойствами. Поэтому неизбежен компромисс. Если ценная бумага надежна, то доходность будет низкой, так как те, кто предлагает надежность, будут предлагать высокую цену. Главная цель при формировании портфеля состоит в достижении наиболее оптимального сочетания между риском и доходом для инвестора. Иными словами, соответствующий набор инвестиционных инструментов призван снизить риск потерь вкладчика до минимума и одновременно увеличить его доход до максимума. Управление инвестиционным портфелем включает, как и управление любым сложным объектом с переменным составом, планирование, анализ и регулирование состава портфеля. Кроме того, управление любым портфелем включает в себя осуществление деятельности по его формированию и поддержанию с целью достижения поставленных инвестором перед портфелем целей при сохранении необходимого уровня его ликвидности и минимизации расходов, связанных с ним. Ликвидность- это степень легкости, с которой можно покупать и продавать активы или обменивать их на денежные средства. Чем выше общий интерес инвесторов к ценной бумаге, тем больше вероятный объем операций по этой ценной бумаге, и это должно создавать у инвесторов большую уверенность в том, что они смогут найти соответствующих контрагентов, желающих заключить сделку в противоположном направлении по разумной цене. Если же акции прочно связаны в контрольных пакетах, для публичных торгов может остаться только небольшое количество акций в свободном обращении. В таком случае ликвидность будет низкой и, следовательно, будет сложно покупать или продавать ценные бумаги в более или менее достаточных объемах. Соответственно именно по этой причине биржи допускают к торгам только те акции, количество которых в свободном обращении составляет не менее двадцати пяти процентов выпуска. Рассматривая вопрос о формировании портфеля, инвестор должен определить для себя значения основных параметров, которыми он будет руководствоваться. К основным параметрам инвестиционного портфеля относятся: тип портфеля; сочетание риска и доходности портфеля; состав портфеля; стиль управления портфелем. Существует два типа портфелей: а) портфель, ориентированный на преимущественное получение дохода за счет высокого уровня прибыли от инвестиционных проектов, а также процентов и дивидендов по ценным бумагам; б) портфель, направленный на преимущественный прирост курсовой стоимости входящих в него ценных бумаг. В портфель обязательно должны входить различные по риску и доходности элементы. Причем, в зависимости от намерений инвестора, доли разнодоходных элементов могут варьироваться. Эта задача вытекает из общего принципа, который действует на инвестиционном рынке: чем более высокий потенциальный риск несет инструмент, тем более высокий потенциальный доход он должен иметь, и, наоборот, чем ниже риск, тем ниже ставка дохода. Первоначальный состав портфеля определяется в зависимости от инвестиционных целей вкладчика – возможно формирование портфеля, предлагающего больший или меньший риск. Исходя из этого инвестор может быть агрессивным или консервативным. Агрессивный инвестор – инвестор, склонный к высокой степени риска. В своей инвестиционной деятельности он делает акцент на вложение в рискованные бумаги и проекты. Консервативный инвестор – инвестор, склонный к меньшей степени риска. Он вкладывает средства преимущественно в облигации и краткосрочные ценные бумаги.

Цели формирования портфеля

Сохранение капитала

Развитие производства

Получение процента

Рис. 1. Цели портфеля инвестиционных проектов Существуют несколько стилей управления портфелем активов. Рассмотрим принципы основных из них. Технический и фундаментальный анализы. В техническом используется графический и математический подход к анализу изменения цен в прошлом. Этот подход основывается на базовом предположении, что модели изменения цены повторяются и различимы. Здесь требуется сбор и изучение огромного объема данных. Затем цены изображаются графически с использованием графика с осями х и у для характеристик цены и времени. По сути, технические аналитики занимаются поиском тенденций (“трендов”) и поворотных моментах в этих трендах. Также важно изучить степень изменчивости (крайние значения изменения цены за определенные промежутки времени) и то, что известно под названием “среднее скользящее значение” (т.е. придание более поздним ценам большего веса по сравнению с более ранними). В фундаментальном анализе используются доступные финансовые показатели для расчета широкого спектра коэффициентов. Исходя из этих коэффициентов аналитик определяет ряд норм прибыли и роста и может оценить в цифрах будущую доходность компании. Существенные различия в этих двух подходах заключаются в следующем: технический анализ исходит из того, что история цен имеет важнейшее значение для определения вероятностных цен в будущем, в то время как фундаментальный анализ основывается на расчете будущей стоимости (и её дисконтировании до текущей стоимости), исходя из убеждения, что то, что происходило раньше, не оказывает влияния на вероятные будущие цены. И хотя эти подходы диаметрально противоположны, в практике торговли фундаментальный анализ, как правило, используется для принятия долгосрочных инвестиционных решений, а технический- для определения времени осуществления инвестиции (покупки или продажи). Использование технического анализа имеет несколько преимуществ. Во-первых, этот метод неэмоционален в том смысле, что аналитик (или инвестор) отслеживает только изменение цен на ценную бумагу. Его личные ожидания не влияют на его решения, т. е. решения принимаются только на основании графиков и цифр. Второе крупное преимущество в том, что этот метод ориентирован во времени в том смысле, что он показывает аналитику, когда нужно покупать или продавать, а выбор времени является важнейшим фактором в искусстве консультирования по инвестициям. Один из недостатков заключается в том, что у этого метода нет теоретической базы. За “моделями” технического анализа не стоит никакой экономической или статистической теории. Другими словами, нет рационального обоснования данного метода. Неудивительно, что критики этого метода часто сравнивают технический анализ с колдовством или алхимией. Источником одного из вариантов этого спора стала статистическая теория. На Западе в значительном числе исследовательских работ изучалось движение цен на ценные бумаги. В исследованиях использовались самые передовые статистические методы и изучались цены на ценные бумаги практически всех стран. Результаты просто поразительны. В половине исследований сделан вывод о том, что цены на ценные бумаги меняются как случайные числа. Учитывая тренд изменения цены, существует 50% математической вероятности того, что на следующий день она повысится и 50% того, что она упадет, независимо от предшествующей конфигурации графика цены. Из этого можно сделать вывод, что в изменении цен на ценные бумаги нет определенных моделей. Другая половина исследователей пришла к иному выводу, т.е. что изменения цен не случайны и что такие модели существуют. Исследовательские работы не дают однозначного результата. Но тот факт, что существуют значительные сомнения в существовании упорядоченных моделей в изменении цен на ценные бумаги, является серьезной проблемой для достоверности метода технического анализа. И последнее, возможно, самое важное замечание, состоит в том, что метод технического анализа опирается на распознавание определенных конфигураций. Два специалиста по техническому анализу, изучающих один и тот же график изменен цен, могут вполне сделать разные выводы из этого материала. Фундаментальный анализ во многом основывается на субъективных мнениях, хотя эти мнения и опираются на очень информированные источники и данные по качеству. Эти два метода анализа, фундаментальный и технический, очень разные, но необязательно считать их конкурирующими. Они могут дополнять друг друга. Стратегия использования обоих методов заключается в том, чтобы пользоваться преимуществами каждого из них, а именно: 1. Использовать фундаментальный анализ для отбора ценных бумаг 2. Использовать технический анализ для выбора момента проведения операции. Пассивное управление. Пассивное управление акциями. Теоретическая состоятельность пассивного метода опирается на ряд идей, выдвинутых за последние 50 лет, получивших общее название современная теория портфеля. Те, кто разработал эту теорию, действовали в ответ на классический стиль активного управления, при котором управляющий портфелем использует финансовый и коммерческий анализ, опыт и инстинкт для определения того, стоит ли купить какую-либо акцию или продать ее – такие действия основываются на вере в то, что в случае принятия ряда правильных решений их портфель сможет превзойти своих соперников и среднерыночные показатели. Теоретики и практики современной теории портфеля придерживаются более количественного подхода. Они построили и проверили свою теорию на основе данных о рыночных ценах более чем за полвека. Предварительный вывод заключался в том, что цены на отдельные ценные бумаги меняются случайным образом, причем их изменение не связано с событиями, происходящими в компании или предшествующими изменениями цен. Причина случайного изменения цен в том, что общая сумма знаний о деятельности компании (в случае радикальных сторонников теории сюда входят знания о предсказуемых будущих событиях) уже отражена в цене и что новые события заставляют эту цену реагировать так быстро, что не остается времени для получения выгодны от особых знаний. В центре современной теории портфеля также лежит показатель под названием “бета”. По сути это мера изменчивости цены определенной ценной бумаги (или группы ценных бумаг, например, из одной отрасли) по отношению к другим ценным бумагам или другому показателю (например, индексу). Он служит мерой эластичности процентного изменения цены акции по отношению к одновременному процентному изменению рынка или индекса. Величину коэффициента “бета” можно рассчитать только путем оценки зарегистрированных изменений стоимости во времени по сравнению с изменениями рынка за тот же период. Очевидно, что чем больше для этого данных, тем надежнее результат. Коэффициент “бета” рынка или индекса принимается за 1 (или 100), поскольку он используется как базовый показатель. Соответственно если бета акции выше 1, это означает, что при 10%-ном повышении (или снижении) цен на рынке цена на акцию с бетой от 0 до 1 поднимется (или упадет) меньше, чем на 10%. Отрицательные значения “беты” встречаются очень редко, т.е. это “беты” ценных бумаг, цена которых меняется в направлении, обратном общему изменению рынка. Возможность измерить изменчивость ценной бумаги не меняет концепции эффективного рынка; она всего лишь описывает характеристики небольшой части рынка. Рассчитав “бету” для каждой акции, можно определить, будет ли портфель или определенная акция более или менее изменчивой, чем в среднем по рынку (по отношению к соответствующему индексу) или по отношению к любой другой акции, и специально сформировать портфель так, чтобы его изменчивость была выше, ниже или равна средней и определить точно, насколько выше или ниже будет его изменчивость. Чем больше число имеющихся в портфеле акций, тем меньше влияют отдельные акции на его изменчивость, вплоть до момента, когда входящие в портфель акции те же, что и входят в выбранный индекс всех акций – тогда изменчивость портфеля соответствует изменчивости самого индекса. В действительности для достижения такой точки нужно гораздо меньшее число акций, чем входит в большинство индексов, и поэтому необязательно иметь все входящие в индекс акции для того, чтобы довольно точно повторить поведение индекса. Строгое применение методов современной теории портфеля требует, чтобы портфель точно соответствовал индексу и впоследствии не менялся, если не изменится индекс. Приверженцы пассивного управления указывают, что это экономит большие суммы комиссионных, которые возникают при активном управлении портфелем, что уменьшает доход от портфеля; более того, плата за управление пассивным портфелем гораздо ниже, поскольку не нужно нанимать высокооплачиваемых исследователей, аналитиков и управляющих, нужна всего лишь простая компьютерная программа, что должно дать дополнительные преимущества. Однако при попытке достичь такой утопии и возникают практические проблемы. Вот некоторые из них. Индексы не статичны, их составляющие могут измениться по ряду причин: ° снижение значения конкретной составляющей части; ° появление нового составляющего; банкротство; ° слияние или поглощение. Каждым индексом управляет руководящий комитет, который контролирует соответствие портфеля структуре выбранного индекса, обсуждает и предлагает изменения к нему. Это означает, что в пассивные портфели должны вноситься поправки для отражения новой ситуации и, как следствие, необходимо нести затраты, поскольку надо будет продать одни ценные бумаги и купить другие, иногда в небольших количествах, что может означать уплату комиссионных выше среднего размера. Также следует учитывать спред между рыночными ценами покупки и продажи. По этой причине, как правило, неэкономично управлять пассивным портфелем, кроме случаев, когда его размер достаточен для преодоления этой проблемы. Другой фактор, который необходимо учитывать – это то, что индексированные фонды могут привлекать новых подписчиков или что существующим инвесторам может потребоваться изъять деньги из фонда. Это опять же приводит к покупкам и продажам; теоретически каждая новая подписка на акции или изъятие средств может потребовать купли-продажи небольших количеств каждого элемента индекса. Как было показано выше, управлять индексированным фондом, который точно повторяет индекс путем включения в портфель входящих в индекс акций в той же пропорции (или с тем же весом), как и в самом индексе, относительно сложнее и дороже. Учитывая, что в индекс может входить 500 – 1000 составляющих, и потребность постоянно корректировать портфель в соответствии с вышеупомянутыми событиями, связанные с такими операциями затраты делают невозможным точное копирование поведения индекса в пассивном фонде. Поскольку с самим индексом не связано никаких затрат, так как это теоретическая конструкция, доход от пассивного портфеля неизбежно будет ниже. Варианты пассивного управления направлены на то, чтобы свести к минимуму величину отставания. Существует возможность при помощи компьютерных моделей показать, что количество ценных бумаг меньшее, чем число бумаг, входящих в индекс, может дать приемлемую копию индекса, вполне достаточную для достижения желаемого результата. Естественно, что это приветствуется, поскольку в результате скорее всего сократится число необходимых поправок и соответственно объем расходов. Есть несколько вариантов такого метода; все они направлены на сведение к минимуму количества входящих в портфель акций при одновременной оптимизации соотношения с выбранным индексом. На многих рынках можно заключать сделки по фьючерсам на индексы. Используя сочетание денежных депозитов для получения дохода, который может быть больше неполученного от акций дохода, и покупки фьючерса, можно приблизиться к доходу от индексного фонда, вложенного в физические ценные бумаги. Риск состоит в том, что цена фьючерсного контракта может быть выше или ниже его справедливой стоимости в зависимости от совокупного мнения рынка (т. е. эта цена меняется не в точном математическом соотношении с базовым индексом). Это может привести к отклонениям в поведении самого индекса, но по мнению сторонников этого метода, более высокая доходность, часто доступная по денежным депозитам, в совокупности с более низкими затратами на операции создает противовес этому риску. продолжение