Методы оптимизации группового принятия решений. Новые методы оптимизации

«Методы оптимизации» - часть 3

9) Если F 0 оказывается хуже S (значение целевой функции в наихудшей точке D предыдущего комплекса), т.е. новая точка находится дальше от экстремума, чем вершина с номером D , то новая вершина находится смещением x i 0 на половину расстояния к лучшей из вершин комплекса G : .

Затем вновь вычисляют значение целевой функции F 0 и сравнивают его с S . Смещением к лучшей вершине по формуле (15) продолжают до тех пор, пока F 0 не станет лучше S .

За счет этой процедуры происходит последовательное сжатие комплекса к лучшей вершине.

10) Если вычисленное в новой точке х 0 значение F 0 лучше S , то в Комплексе на месте наихудшей точки х D фиксируется точка х 0 и значение S заменяется на F 0 .

Затем вычисления повторяются, начиная с п. 3, и продолжаются до тех пор пока не будет выполнено условие остановки, т.е. не будет найден с заданной точностью экстремум целевой функции.

Метод Хука-Дживса (конфигураций)

Эффективность прямого поиска точки минимума можно повысить, если на каждом k-м шаге поиска соответствующим образом выбирать направление спуска. Для этого на каждом k-м шаге выделяют предварительный этап исследующего поиска. Целью этого этапа является выбор направления спуска путем исследования поведения целевой функции f(x) в окрестности точки xk-1, найденной на предыдущем шаге. В результате выполнения этапа исследующего поиска находится точка xk, для которой f(xk ) < f(xk-1 ). Направление спуска, завершающего k-w. шаг поиска, определяется вектором xk - xk-1 . Такая стратегия поиска, получила название метода Хука - Дживса.

Исследующий поиск 1

Вдоль координатных орт выполняют малые шаги. Т.е. локальное обследование точки х1 , для поиска лучшей чем х1 точки. Если шаг удачный то точку фиксируют и продолжают шаги из неё, если не удачный то делают шаг в противоположную сторону, если полученная точка снова хуже, то по этой оси шаг не делается.

Ускоряющий поиск

Выполняем единичный шаг вдоль направления

, . Затем производим исследующий поиск в окрестности x3 , в надежде найти точку лучшую чем x2 .

Начальный этап

β = 10, ε = 10-4 – 10-8 , k = 1, х1 , h2 = … =hn =0.1;

Основной этап

Шаг 1.

Выполнить ИП1 и отыскать т. х2 для которой

Шаг 2.

Если ИП1 удачен т.е. найдена х2 , то перейти на шаг 3, иначе, но в то же время h<ε необходимо уменьшить шаг в β раз и вернуться на шаг 1. При h<ε остановиться х* = х1 .

Шаг 3.

Выполнить УП в пробную точку

Обозначить

В окрестности х3 попытаться ИП2 найти т. х4 «лучшую» чем х1 .

Шаг 4.

Если ИП2 удачен, то положить

и вернуться на шаг 1.

Иначе: уменьшить шаг в β раз и вернуться на шаг 1.

Метод Хука-Дживса с одномерной минимизацией

Данный метод является аналогом метода циклического покооординатного спуска (ЦПС) с ускоряющим шагом. Начиная со второй итерации, устанавливается новый способ построения направления ускоряющего поиска. Организацию итерационной процедуры и отличие метода Хука-Дживса с одномерной минимизацией от метода ЦПС раскрывает представленное ниже пошаговое описание алгоритма.

Начальный этап

(1) Исходные данные - базовая точка x , погрешность вычисления минимума e, матрица координатных направлений p = {pi }, i = 1,2,...,n , где pi = ei - i-ый единичный орт в Rn , т.е. ei = 1 и eji = 0 при всех i ¹ j .

(2) Начальную точку x1 принять равной базовой точке: x1 = x .

Основнй этап

Шаг 1.

Выполнить ЦПС из начальной точки x1 в конечную точку xn+1 , последовательно решая n-задач одномерной минимизации вдоль координатных направлений p .

комментарии

скачать[зарегистрируйтесь]

ДОБАВИТЬ КОММЕНТАРИЙ [можно без регистрации]перед публикацией все комментарии рассматриваются модератором сайта - спам опубликован не будет

Хотите опубликовать свою статью или создать цикл из статей и лекций?Это очень просто – нужна только регистрация на сайте.

mirznanii.com

4.5.5. Прямые методы условной оптимизации

1. В качестве первой вершины начального комплекса выбирают некоторую допустимую точку X[1,0]. Координаты остальных

q–1вершин комплекса:хi [j,0]=аi +ξi (bi –ai ),I=1,2,...,n;j=2,...,q. Здесьаi ,bi – соответственно нижнее и верхнее ограни-

чения на переменную хi ,ξi – псевдослучайные числа, равномерно распределенные на интервале [0;1]. Полученные таким образом

точки удовлетворяют ограничениям аi ≤хi ≤ bi , однако ограниче-

ния zj (X)≤0 могут быть нарушены. В этом случае недопустимая точка заменяется новой, лежащей в середине отрезка, соединяющего недопустимую точку с центром тяжести выбранных допустимых вершин. Данная операция повторяется до тех пор, пока не будут выполнены все ограничения задачи.

2.Далее, как и в методе деформируемого многогранника, на каждой итерации заменяется вершина X[h,k], в которой значение целевой функции имеет наибольшую величину. Для этого она отражается относительно центра тяжестиX[n+2,k] остальных вершин комплекса. ТочкаX[n+3,k], заменяющая вершинуX[h,k], определяется по формулеX[n+3,k]=(a+1)X[n+2,k]+aX[h,k], гдеа>0

–некоторая константа, называемая коэффициентом отражения. Наиболее удовлетворительные результаты дает значение а=1,3. При этом новые вершины комплекса отыскиваются за небольшое количество шагов, а значения целевой функции уменьшаются достаточно быстро.

3.Если f(X[n+3,k])≥f(X[h,k]), то новая вершина оказывается худшей вершиной комплекса. В этом случае коэффициента уменьшается в два раза. Аналогично поступают, если при отраже-

нии нарушаются ограничения zj (X)≤0, до тех пор, пока точкаX[n+3,k] не станет допустимой.

Вычисления заканчиваются, если значения целевой функции в центре тяжести комплекса мало меняются в течение пяти после-

довательных итераций: | f(X[n+2,k+1])–f(X[n+2,k])|≤ε,k=1,2....,5,

где ε – заданная константа. В этом случае центр тяжести комплекса считают решением задачи.

Достоинства комплексного метода Бокса: его простота, удобство для программирования, надежность в работе. Метод на каждом шаге использует информацию только о значениях целевой функции и функций ограничений задачи. Все это обусловливает успешное применение его для решения различных задач нелинейного программирования.

studfiles.net

ПРИМЕНЕНИЕ МЕТОДОВ ОПТИМИЗАЦИИ В ИНЖЕНЕРНОЙ ПРАКТИКЕ — КиберПедия

Теория оптимизации находит эффективное применение во- всех направлениях инженерной деятельности, и в первую очередь в следующих четырех ее областях:

1) проектирование систем и их составных частей;

2) планирование и анализ функционирования существующихсистем;

3) инженерный анализ и обработка информации;

4) управление динамическими системами.

При рассмотрении приложений методов оптимизации при проектировании и анализе функционирования систем следует иметь в виду, что оптимизация — всего лишь один этап в процессе формирования оптимального проекта или условий эффективного функционирования системы. Процесс инженерного проектирования (рисунок 2.1), является циклическим и включает синтез (определение) структуры системы, построение модели, оптимизацию параметров модели и анализ полученного решения. При этом оптимальный проект или новый план функционирования системы строится на основе решения серии оптимизационных задач, способствующего дальнейшему совершенствованию структуры системы.

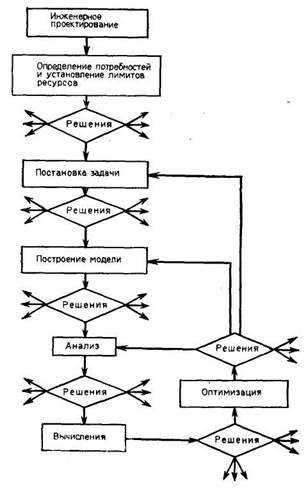
Рисунок 2.1 - Этапы процесса инженерного проектирования

ОПТИМИЗАЦИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

В данной работе приводятся фундаментальные понятия и конкретные методы, используемые при поиске безусловных минимумов функций нескольких переменных.

Методы прямого поиска

Многомерные методы, реализующие процедуру поиска оптимума на основе вычисления значений функции, с общих позиций можно разделить на эвристические и теоретические. Эвристические методы, как это следует из названия, реализуют процедуры поиска с помощью интуитивных геометрических представлений и обеспечивают получение частных эмпирических результатов. С другой стороны, теоретические методы основаны на фундаментальных математических теоремах и обладают такими операционными свойствами, как сходимость (по крайней мере при выполнении некоторых определенных условий). Ниже рассматриваются три метода прямого поиска:

1) поиск по симплексу, или S2-метод;

2) метод поиска Хука — Дживса;

3) метод сопряженных направлений Пауэлла.

Первые два из перечисленных методов относятся к категории эвристических и реализуют принципиально различающиеся стратегии поиска. В процессе поиска по S2-методу последовательно оперируют регулярными симплексами в пространстве управляемых переменных, тогда как при реализации метода Хука— Дживса используется фиксированное множество (координатных) направлений, выбираемых рекурсивным способом. Метод Пауэлла основан на теоретических результатах и ориентирован на решение задач с квадратичными целевыми функциями; для таких задач метод сходится за конечное число итераций. К числу общих особенностей всех трех методов следует отнести относительную простоту соответствующих вычислительных процедур, которые легко реализуются и быстро корректируются.

Критерий оптимальности

Сначала рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условия, которые (в достаточно общих возможных ситуациях) позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли эти точки точками минимума, максимума или седловыми точками. При этом задача выбора указанных точек остаётся вне рамок проводимого анализа; основное внимание уделяется решению вопроса о том, соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется

минимизировать f(х), xÎRN, (3.1)

при отсутствии ограничений на х, где х — вектор управляемых переменных размерности N, f — скалярная целевая функция. Обычно предполагается, что xi(для всех значений i = 1, 2, 3,…, N)могут принимать любые значения, хотя в ряде практических приложений область значений х выбирается в виде дискретного множества. Кроме того, часто оказывается удобным предполагать, что функция f и ее производные существуют и непрерывны всюду, хотя известно, что оптимумы могут достигаться в точках разрыва f или ее градиента

(3.2)

Функция f может принимать минимальное значение в точке , в которой f или f претерпевают разрыв. Кроме того, в этой точке f может не существовать. Для того чтобы построить систему конструктивных критериев оптимальности, необходимо (по крайней мере на первой стадии исследования) исключить из рассмотрения подобные ситуации, которые весьма усложняют анализ. Наконец, в ряде случаев приходится ограничиваться лишь идентификацией локальных оптимумов, поскольку нелинейная целевая функция f не всегда обладает свойством выпуклости и, следовательно, может оказаться мультимодальной.

Далее перейдем к вопросу анализа «в динамике», который формулируется следующим образом: если точка х(0)не удовлетворяет условиям, налагаемым упомянутыми выше критериями оптимальности, то как получить «хорошее» новое приближение x(1)к решению х*? Попытка дать ответ на этот вопрос приводит к необходимости рассмотрения ряда методов, описание которых составляет значительную часть данной главы. Рассматриваемые методы классифицируются в соответствии с тем, используется ли информация о производных исследуемых функций.

Рассматрим условия, которые позволяют характеризовать (т. е. классифицировать) точки пространства управляемых переменных. Критерии оптимальности необходимы для распознавания решений и, кроме того, составляют основу большинства используемых методов поиска решений. Рассмотрим разложение Тейлора для функции нескольких переменных:

f(x)=f( )+ f( ) ∆x+½∆x f( )∆x+O (∆x), (3.3)

где — точка разложения из пространства RN; ∆х = х - — величина изменения х; f(x) — N-мерный вектор-столбец первых производных f(х), вычисленных в точке ; f( ) = H ( ) — симметрическая матрица порядка N×N вторых частных производных f(x), вычисленных в точке . (Эту матрицу часто называют матрицей Гессе. Ее элемент, расположенный на пересечении i-й строки и j-го столбца, равен f / dx x .) O (∆x) — сумма всех членов разложения, имеющих порядок по ∆x выше второго. Пренебрегая членами высших порядков (т. е. исключая O (∆x)), определим величину изменения целевой функции f(х), соответствующего произвольному изменению х:

∆ f(x)= f(x) - f( ) = f( ) ∆x+½∆x f( )∆x (3.4)

Напомним, что по определению во всех точках из окрестности точки минимума целевая функция принимает значения, которые превышают минимальное, т. е. имеет место неравенство

∆f = f(x) - f( ) ≥0. (3.5)

Точка является точкой глобального минимума, если неравенство (3.5) выполняется для всех хÎ RN; такие точки будем обозначать через х**. Когда формула (3.5) справедлива лишь в некоторой δ-окрестности точки , т. е. для всех х, таких, что ||х – || < δ при заданном δ > 0, то есть точка локального минимума, или х*. Если же

∆ f = f(x) – f( ) ≤0. (3.6)

то есть точка максимума (локального или глобального в соответствии с данными выше определениями). Исключение знака равенства из формул (3.5) и (3.6) позволяет определить точку строгого минимума или максимума. В случае когда ∆f принимает как положительные и отрицательные, так и нулевые значения в зависимости от выбора точек из δ-окрестности, точка представляет собой седловую точку.

Вернемся к равенству (3.4) и вспомним о выдвинутом ранее предположении о том, что f(х), f(x) и f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент f( ) должен быть равен нулю, т. е. должна быть стационарной точкой. В противном случае разность ∆f может принимать положительные или отрицательные значения в зависимости от знаков f( ) и ∆х. Таким образом, точка должна удовлетворять условию стационарности

f( ) = 0, (3.7)

и формула (3.4) принимает следующий вид:

∆f(x) = +½∆x f( )∆x. (3.8)

Очевидно, что знак ∆f(x) определяется квадратичной формой

Q(х) = ∆x f( )∆x (3.9)

или Q(z)=zTAz.

Из линейной алгебры известно, что

А — положительно определенная матрица, если Q(z)>0 для любых z;

А — положительно полуопределенная матрица, если Q (z)≥0 для любых z;

А — отрицательно определенная матрица, если Q(z)<0 для любых z; (3.10)

А — отрицательно полуопределенная матрица, если Q(z)≤0 для любых z;

А — неопределенная матрица, если Q (z)>0 для некоторых z и Q(z)<0 для остальных z.

Из (3.10) следует, что стационарная точка есть

точка минимума, если 2f( ) — положительно полуопределенная матрица;

точка максимума, если 2f( ) — отрицательно полуопределенная матрица; (3.11)

cедловая точка, если 2f(x) 0 — неопределенная матрица.

3.3 Метод поиска по симплексу (S2-метод)

Первые попытки решения оптимизационных задач без ограничений на основе прямого поиска связаны с использованием одномерных методов оптимизации. Как правило, при реализации таких методов допустимая область определения показателя качества функционирования системы (целевой функции) заменяется дискретным множеством (решеткой) точек пространства управляемых переменных, а затем используются различные стратегии уменьшения области, которая содержит решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах решетки и, следовательно, непригодной для решения задач с числом переменных, превышающим 2. Более полезная идея заключается в выборе базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с двумя переменными можно воспользоваться квадратным образцом, изображенным на рис. 3.1. Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится, аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Рисунок 3.1 - Квадратный образец (частный случай кубического образца)

Этот тип эволюционной оптимизации был использован Боксом и другими исследователями для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба, т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно N, то поиск по кубическому образцу требует 2 +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.

Одна из вызывающих особый интерес стратегий поиска положена в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер. Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в N-мерном пространстве представляет собой многогранник, образованный N+1 равностоящими друг от друга точками-вершинами.

Например, в случае двух переменных симплексом является равносторонний треугольник; в трехмерном пространстве симплекс представляет собой тетраэдр. В алгоритме симплексного поиска используется важное свойство симплексов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается. Нетрудно видеть, что при переходе к новому симплексу требуется одно вычисление значения целевой функции. Рис. 3.2 иллюстрирует процесс построения нового симплекса на плоскости.

a — начальный симплекс; x(1), x(2), x(3); б — новый симплекс; x(2),x(3), x(4)

Рисунок 3.2 - Построение нового симплекса

Алгоритм симплекс-метода

Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом определяется вершина, которой соответствует наибольшее значение целевой функции. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка минимума, либо не начнется циклическое движение по двум или более симплексам. В таких ситуациях можно воспользоваться следующими тремя правилами.

cyberpedia.su

Методы оптимизации управленческих решений

Поиск Лекций

Оптимизация управленческих решений может выполняться следующими методами:

1. Экoнoмикo-мaтeмaтичecкиe методы (математическое моделирование)

Применяют в тех случаях, когда управленческое решение принимается на основе обширной цифровой информации, которая может быть легко формализована. Широкое использование математических моделей позволяет дать количественную характеристику проблемы и найти оптимальный вариант ее решения.

Заключается в нахождение максимума или минимума целевой функции при заданных ограничениях. Тaкoйвыбopнaзывaютoптимизaциoнным. Необходимое условие использования оптимального подхода к планированию и управлению (принципа оптимальности) — гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Пpимepaмиoптимизaциoнныxкpитepиeвявляютcя: мaкcимyмпpибыли, дoxoдoв, пpoизвoдитeльнocти; минимyмзaтpaт, пoтepьoтбpaкa.

2. Теория игр

Теоретико-игровые методы служат для принятия решения в условиях неопределенности, когда принимающий решение субъект (игрок) располагает информацией лишь о множестве возможных ситуаций, в одной из которых он в действительности находится, о множестве решений (стратегий), которое он может принять, и о количественной мере того «выигрыша», который он мог бы получить, выбрав данную стратегию. Игровые задачи управления предполагают участие в активном воздействии на объект управления двух игроков с противоположными интересами.

3. Методы экспертной оценки

Построение экспертом рациональной процедуры интуитивно-логического анализа в сочетании с количественной оценкой и обработкой результатов. Применяются для широкого круга неформализуемых проблем, которые не всегда могут быть оценены в количественном измерении, а также для решения проблем социально-экономического характера или в условиях отсутствия информации из внешних источников. Существуют высокие требования к компетентности экспертов.

4. Метод мозгового штурма (мозговая атака)

Применяется в тех случаях, когда имеется минимум информации о решаемой проблеме и установлены сжатые сроки для ее решения. Тогда приглашаются специалисты, имеющие отношение к данной проблеме, им предлагается участвовать в форсированном обсуждении ее решения. При этом строго соблюдаются следующие правила:

все высказываются по очереди;

говорят лишь тогда, когда могут предложить новую идею;

высказывания не критикуются и не осуждаются;

все предложения фиксируются.

Обычно этот способ позволяет быстро и правильно решить возникшую проблему.

Разновидностью метода мозгового штурма является мнение жюри. Суть этого метода состоит в том, что к обсуждению проблемы привлекаются специалисты различных сфер деятельности, взаимодействующие между собой. Например, к решению о выпуске нового товара привлекаются менеджеры производственного, коммерческого и финансового подразделений фирмы. Применение данного метода способствует генерированию новых идей и альтернативных вариантов.

5. Метод свободных ассоциаций

Учёными отмечено что на этапе генерирования идей при использовании новых ассоциаций повышается результативность творческой деятельности за счет возникновения новых идей. В процессе зарождения ассоциаций устанавливаются неординарные связи между элементами решаемой проблемы и прежним опытом лиц, привлеченных к коллективной работе. Данный метод и технология его исполнения учитывает особенности деятельности мозга человека, вырабатывающего новые идеи при возникновении новых ассоциативных связей. Так, если члены группы предлагают слово, понятие, то оно может стать базисом для установления ассоциативных связей.

6. Метод инверсии

При поиске идеи решение проблемы часто можно найти, изменив направление поиска на противоположное, противоречащее сложившимся традиционным взглядам, продиктованным логикой и здравым смыслом. Нередко в ситуациях, в которых логические приемы, процедуры мышления оказываются бесплодными, оптимальна противоположная альтернатива решения.

7. Метод синектики

Дает возможность получить наиболее оригинальные идеи за счет «обучения» участников использованию в процессе «мозговой атаки» методов аналогии, интуиции, абстрагирования, свободного размышления, применения неожиданных метафор, элементов игры, что позволяет привычную проблему в непривычной ситуации решить неожиданно и оригинально.

8. Метод 635

Группа из шести участников анализирует и формулирует заданную (проблемную) ситуацию. Каждый участник заносит в формуляр три предложения по решению задачи (в течение 5 мин) и передает формуляр соседу. Заполняющий формуляр принимает к сведению предложения своего предшественника, а под ними в трех полях вносит еще три собственных предложения. Эти предложения могут использоваться в дальнейшей разработке записанных решений, но могут выдвигаться новые. Процесс заканчивается, когда участники обработали все формуляры.

Условия: рекомендуемое количество участников — 6. Время на ротационную фазу может увеличиваться на последующих фазах. Технология позволяет получить до 108 (6 х 3 х 6) предложений.

9. Метод Дельфи

Внешне метод реализуется как многоуровневая процедура анкетирования с обработкой и сообщением результатов каждого тура экспертам, работающим изолированно друг от друга. Им предлагаются вопросы и формулировки ответов без аргументации. Например, в ответах могут быть числовые оценки параметров. Полученные оценки обрабатываются с целью получения средней и крайних оценок. Экспертам сообщаются результаты обработки первого тура опроса с указанием расположения оценок каждого. При отклонении оценки от среднего значения эксперт ее аргументирует.

В дальнейшем (во втором туре) эксперты изменяют свою оценку, объясняя причины корректировки. Результаты обрабатываются и сообщаются экспертам. При отклонениях оценок от среднего значения эксперты комментируют их. Туры повторяются, пока оценки не станут стабильными

poisk-ru.ru

Методы оптимизации группового принятия решений.

Если прогностический проект предполагает коллективную работу над проблемой, то в этом случае могут применяться разные виды эвристических методов решения задач на стадиях «планирование» - для генерирования и отбора нестандартных идей и проблем исследования, на стадии «оценка результатов» - для обсуждения и дискуссии относительно достоверности и качества прогноза, на стадии «презентации» – защите проекта, для оценки прогностической ценности проекта. В основе применения всех этих методов лежат общие принципы творческого производства идей. Во-первых, творчество легко блокируется оценкой и критикой. Процесс генерации идей должен быть отделен от процесса их оценки и выбора лучшей идеи. Во-вторых, творчеству препятствует переизбыток опыта, знаний или экспертной квалификации. В группах, где происходит создание идей, должны обеспечиваться разнохарактерность и присутствие различных дисциплин. В-третьих, в этих группах не должны участвовать агрессивные, склонные к доминированию, навязыванию своего мнения люди. В-четвертых, маленькие группы очень сильно зависят от модератора, а в больших блокируется спонтанность. Оптимальный размер инновационной группы - порядка двенадцати человек. Наконец, результаты деятельности группы зависят от рабочих условий. Требуется тихая, приятная и расслабляющая атмосфера, без внешних воздействий и наблюдателей. Метод «мозгового штурма». В обычных условиях творческая активность человека часто сдерживается явно и не явно существующими барьерами (психологическими, социальными, педагогическими и т. д). Диалог в условиях "мозговой атаки" выступает в роли средства, позволяющего высвободить творческую энергию участников решения творческой задачи. Прямая "мозговая атака" явл. методом коллек-го генерирования идей решения творческой задачи. Цель этого метода заключается в сборе как можно большего количества идей, освобождении от инерции мышления, преодолении привычного хода мысли в решении творческой задачи. Массовая "мозговая атака", предложенная Дж. Дональдом Филипсом, позволяет существенно увеличить эффективность генерирования новых идей в большой аудитории. Особенность этой модификации метода заключается в том, что присутствующих делят на малые группы численностью 5–6 человек. После разделения аудитории на малые группы последние проводят самостоятельную сессию прямой "мозговой атаки". "Мозговой штурм" - этот метод был предложен советским исследователем Е. А. Александровым и модифицирован Г. Я. Бушем. Наиболее эффективные результаты достигаются в случаях, когда все участники "мозговой атаки" рационально распределяются на группы: 1) генерирование идей: 2) группа анализа проблемной ситуации и оценки идей; 3) группа генерирования контр-идей. Метод эвристических вопросов (Д. Пойя). Этот метод известен также как метод "ключевых вопросов". Метод эвристических вопросов целесообразно применять для сбора дополнительной информации в условиях проблемной ситуации или упорядочения уже имеющейся информации в самом процессе решения творческой задачи. Эвристические вопросы служат дополнительным стимулом, формируют новые стратегии и тактики решения творческой задачи. Достоинство метода эвристических вопросов заключается в его простоте и эффективности для решения любых задач. Эвристические вопросы особенно развивают интуицию мышления, такую логическую схему решения творческих задач. Недостатки и ограничения этого метода заключаются в том, что он не дает особо оригинальных идей и решений и, как другие эвристические методы, не гарантирует абсолютного успеха в решении творческих задач. Метод многомерных матриц. Этот метод среди исследователей и изобретателей также известен как метод "морфологического ящика" или метод "морфологического анализа". Исходная идея метода многомерных матриц в решении творческих задач заключается в следующем. Поскольку новое очень часто представляет собой иную комбинацию известных элементов или комбинацию известного с неизвестным, то матричный метод позволяет это сделать не путем проб и ошибок, а целенаправленно и системно. Таким образом, метод многомерных матриц базируется на принципе системного анализа новых связей и отношений, которые проявляются в процессе матричного анализа исследуемой проблемы. Достоинством метода многомерных матриц является то, что он позволяет решить сложные творческие задачи и найти много новых, неожиданных, оригинальных идей. Недостатками и ограничениями метода многомерных матриц может быть то, что даже при решении задач средней трудности в матрице могут оказаться сотни вариантов решений, выбор из которых оптимального оказывается затруднительным. Данный метод не гарантирует, что будут учтены все параметры исследуемой системы. Применение метода требует определенного навыка и мастерства. Метод свободных ассоциаций. Замечено, что результативность творческой деятельности, особенно на этапе генерирования новых идей, существенно повышается, если широко использовать все новые и новые ассоциации, которые в итоге порождают по-настоящему продуктивные идеи решения проблемы. В процессе зарождения ассоциаций устанавливаются неординарные взаимосвязи между компонентами решаемой проблемы и элементами внешнего мира, включая компоненты прежнего опыта творческой деятельности лиц, участвующих в коллективном решении проблемы, творческой задачи. В результате процесса зарождения новых ассоциативных связей и возникают творческие идеи решения проблемы. Метод инверсии. Метод инверсии (в психологии его иногда называют методом обращения) представляет собой один из эвристических методов творческой деятельности, ориентированный на поиск идей решения творческой задачи в новых, неожиданных направлениях, чаще всего противоположных традиционным взглядам и убеждениям, которые диктуются формальной логикой и здравым смыслом. Изобретатели давно обратили внимание на то, что часто в ситуациях, когда логические приемы, процедуры мышления оказываются бесплодными и заходят в тупик, естественно предположить, что оптимальной является принципиально противоположная альтернатива решения. Метод эмпатии (метод личной аналогии). Процесс применения аналогии является как бы промежуточным звеном между интуитивными и логическими процедурами мышления. В решении творческих задач используют различные аналогии: конкретные и абстрактные; ведутся поиски аналогии живой природы с неживой, например в области техники. В этих последних аналогиях могут быть, в свою очередь, установлены аналогии по форме, структуре, функциям, процессам и т. д. В ситуациях мысленного построения аналога иногда хорошие эвристические результаты дает такой прием, как гиперболизация, например значительное увеличение или, наоборот, уменьшение масштабов объекта или его отдельных частей. Чаще всего эмпатия означает отождествление личности одного человека с личностью другого, когда пытаются мысленно поставить себя в положение другого. Не случайно эмпатия, или личная аналогия, в решении творческой задачи понимается как отождествление человека с объектом, процессом, некоторой системой. Когда применяется метод эмпатии, то объекту приписывают чувства, эмоции самого человека: человек идентифицирует цели, функции, возможности, плюсы и минусы, например машины, со своими собственными. Метод синектики (Дж. Гордон). Суть метода синектики заключается в следующем. На первых этапах его применения идет процесс обучения "механизмам творчества". Часть этих механизмов авторы методики предлагают развивать обучением, развитие других не гарантируется. Первые называют "операционными механизмами". К ним причисляют прямую, личную и символическую аналогии. Такие явления, как интуиция, вдохновение, абстрагирование, свободное размышление, использование не относящихся к делу возможностей, применение неожиданных метафор и элементов игры, считают "неоперационными механизмами", развитие которых не гарантируется обучением, хотя может оказать на их активизацию положительное влияние. В процессе применения метода синектики большое внимание уделяется использованию метода аналогий. Аналогия используется в самых различных видах: как личная (эмпатия), прямая, фантастическая и символическая. Символическая аналогия, например, приняла форму конкретного приема определенного поиска названия, характеризующего в парадоксальной форме определенное понятие. Метод организованных стратегий. Одним из главных психологических барьеров в решении творческих задач является инерция мышления и неспособность решающего уйти, отказаться от наиболее очевидного способа и найти новый подход, новое направление в поисках идей решения. И даже если мы выбираем правильные направления (стратегии) поиска идеи решения, то возникают опасения, что мы упустили что-то главное, возможно, более оригинальную стратегию, идею.

students-library.com