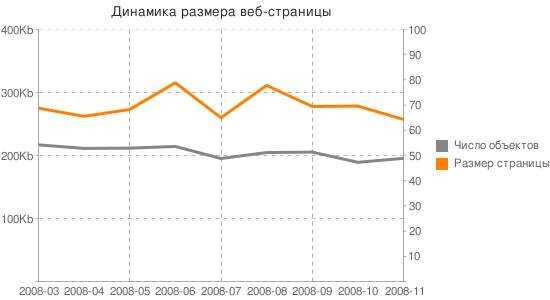
РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ С ПОМОЩЬЮ НЕЙРОННОЙ СЕТИ ХОПФИЛДА SOLVING OPTIMIZATION PROBLEMS USING HOPFIELD NEURAL NETWORK. Нейронные сети для оптимизации

АНАЛИЗ МЕТОДОВ ОПТИМИЗАЦИИ ПАРАМЕТРОВ НЕЙРОННЫХ СЕТЕЙ НА ПРИМЕРЕ ЗАДАЧИ КЛАССИФИКАЦИИ ИЗОБРАЖЕНИЙ

Аннотация. В статье приведён обзор популярных методов оптимизации параметров нейронных сетей, а также представлены результаты сравнения этих методов на примере обучения свёрточной нейронной сети для решения задачи классификации символов.

Ключевые слова: нейронные сети, свёрточные нейронные сети, методы оптимизации.

 

Процесс обучения нейронной сети заключается в подстройке весов её нейронов. Целью обучения нейронных сетей является поиск такого состояния их весов, которое минимизирует некоторую целевую функцию на обучающей и тестирующей выборках. Задача обучения нейронных сетей достаточно сложна и это связано со следующими причинами:

- нейронная сеть может содержать очень большое количество связей, поэтому пространство возможных состояний нейронной сети огромно и рассмотреть их все практически невозможно;

- нейронные сети, которые содержат более чем один нейрон в скрытом слое, имеют не одно, а несколько оптимальных состояний, обусловленных наличием у функции ошибки нескольких минимумов, однако истинно оптимальным состоянием является только одно, где обеспечивается глобальный минимум;

- наличие множества локальных минимумов существенно затрудняет поиск глобального оптимума.

В настоящее время для решения задачи оптимизации параметров нейронных сетей разработано большое количество различных методов. В основном эти методы являются методами первого порядка и, в частности, вариациями градиентного спуска. Обновление весов нейронной сети происходит посредством применения итерационного метода обратного распространения ошибки [2]. Далее будут рассмотрены популярные методы оптимизации.

Градиентный спуск. Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом [1]. Тогда выражение изменения весов  на i-ой итерации имеет следующий вид:

(1)

где:  – коэффициент скорости обучения на -ой итерации;

        – градиент целевой функции  относительно весов , обновлённых на итерации .

Метод градиентного спуска может застревать в локальных минимумах целевой функции . Для преодоления этого используется так называемый метод моментов или инерции, который состоит в добавлении в формулу (1) терма «инерции»:

(2)

где:  – коэффициент инерции, может принимать как фиксированное значение, так и изменятся в зависимости от , например ;

        – изменение весов на предыдущей итерации.

AdaGrad. Этот метод был представлен в 2011 году [4]. Суть AdaGrad состоит в масштабировании коэффициента скорости обучения для каждого параметра в соответствии с историей градиентов этого параметра. Такое масштабирование делается путём деления текущего градиента на сумму квадратов предыдущих градиентов. Формула изменения весов методом AdaGrad следующая:

 

	(3)

где:  – сумма квадратов градиентов;

        – коэффициент сглаживания, .

Adam. Метод Adam [5] можно рассматривать как обобщение AdaGrad. Он сочетает в себе и идею накопления движения, и идею более слабого обновления весов для типичных признаков. Метод Adam преобразует градиент следующим образом:

где:  – оценка математического ожидания;

        – оценка средней нецентрированной дисперсии;

        и  – окна накопления,  и ;

        и  – скорректированные значения оценок математического ожидания и средней нецентрированной дисперсии, влияет на первых шагах обучения;

        – коэффициент сглаживания, .

Выбор эффективного метода проводился на основе результатов тестирования нескольких методов оптимизации по критерию скорости сходимости. Тестирование проводилось на LeNet-подобных свёрточных нейронных сетях.

 

В качестве тестовой задачи была выбрана задача классификации рукописных цифр и для обучения использовалась база MNIST [7]. Эта база состоит из бинарных изображений рукописных цифр размером  пикселей. Количество изображений в обучающей и в тестирующей выборках составило 60000 и 10000 соответственно. Предварительной обработки изображений не проводилось. Пример изображений базы MNIST приведён на рисунке 1.

В эксперименте использовалось четыре сети, описание структур которых приведено в таблице 1. В таблице используется следующая нотация описания структуры свёрточных нейронных сетей:

-  обозначает операцию свёртки, где  – число выходных каналов,  и  – высота и ширина ядра фильтра свёртки;

-  обозначает операцию объединения с размером окна и шагом по осям равными  соответственно, где  – функция, применяемая к окну объединения;

- запись вида  обозначает операцию матричного умножения на веса соответствующего полносвязного слоя с  нейронами;

- функции активации записываются одном словом их названия (например , ) и к аргументу этих функций в обязательном порядке прибавляется вес смещения поканально, в случае если предыдущей операцией была свёртка, или понейронно – если предыдущей операцией было матричное умножение на веса полносвязного слоя; число параметров смещения соответственно равно числу каналов или нейронов предыдущей операции.

Таблица 1.

Структуры сетей используемых в проводимом эксперименте

Уровень глубины

CNN-3

CNN-4

9226 параметров	79296 параметров
1
2
3
Классификатор

 

Шаг обучения  задавался для всех методов равным . Коэффициент инерции для градиентного спуска с инерцией вычислялся по следующей формуле: . Для метода Adam параметры  и  устанавливались равными  и  соответственно. В качестве целевой функции использовалась средняя категориальная перекрёстная энтропия [3]. Параметры сетей инициализировались посредством метода описанного Яном ЛеКуном [6]. Значения весов смещения инициализировались константным значением равным . Последний слой сетей, расположенный непосредственно перед функцией SoftMax полностью инициализировался константным значением . Всего было проведено  эпох обучения для каждой сети. За одну эпоху по всей обучающей выборке формировались мини пакеты по 5000 примеров.

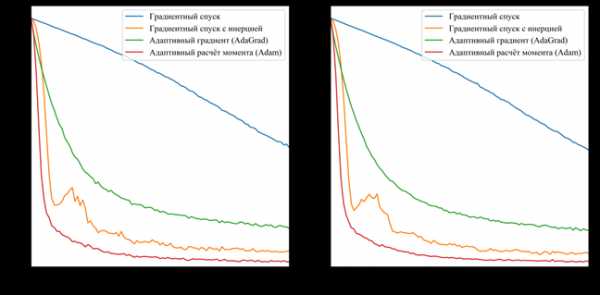
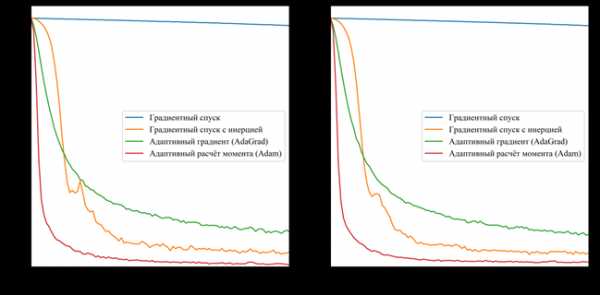
На рисунках 2 и 3 приведены графики изменения значения целевой функции в процессе обучения сетей с шифрами CNN-3 и CNN-4. В таблицу 2 сведены значения целевой функции на обучающей и тестирующей выборках обученных разными методами оптимизации свёрточных нейронных сетей.

Таблица 2.

Значения целевой функции обученных сетей

Структура сети

Градиентный спуск

Градиентный спуск с инерцией

AdaGrad

Adam

обуч.	тест.	обуч.	тест.	обуч.	обуч.	тест.	обуч.
CNN-3	1,136	1,108	0,140	0,130	0,370	0,343	0,050	0,049
CNN-4	2,240	2,234	0,128	0,126	0,324	0,301	0,025	0,044

 

а)                                                                  б)

а – графики изменения целевой функции на обучающей выборке;

б – графики изменения целевой функции на тестирующей выборке;

Рисунок 2. Графики изменения целевой функции сети с шифром CNN-3.

 

a)                                                         б)

а – графики изменения целевой функции на обучающей выборке;

б – графики изменения целевой функции на тестирующей выборке;

Рисунок 3. Графики изменения целевой функции сети с шифром CNN-4.

 

Основываясь на полученных результатах, очевидно, что наиболее эффективным методом оптимизации является метод Adam. Он показал наибольшую скорость сходимости для обоих вариантов сетей по сравнению с другими методами. Второе место принадлежит методу градиентного спуска с инерцией. Однако, несмотря на хорошую скорость сходимости, на такой простой задаче он имеет нестабильную траекторию схождения (исходя из выбросов на приведённых графиках), поэтому вместо него следует использовать AdaGrad. Простой градиентный спуск за указанное число итераций не сумел сойтись. Это связано в первую очередь с маленьким коэффициентом шага обучения, однако исходя из опыта, этот метод эффективен только на начальных итерациях и часто застревает в локальных минимумах.

 

Список литературы:

1. Градиентный спуск // Википедия : свободная энциклопедия. – 2017. [электронный ресурс] – Режим доступа. – URL: https://ru.wikipedia.org/wiki/Градиентный_спуск (дата обращения 12.05.2017).
2. Метод обратного распространения ошибки // Википедия : свободная энциклопедия. – 2017. [электронный ресурс] – Режим доступа. – URL: https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки (дата обращения 12.05.2017).
3. Cross entropy // Википедия : свободная энциклопедия. – 2017. [электронный ресурс] – Режим доступа. – URL: https://en.wikipedia.org/wiki/Cross_entropy (дата обращения 12.05.2017).
4. Duch, J. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization / J. Duch, E. Hazan, Y. Singer // Journal of Machine Learning Research. – 2011. – P.2121-2159.
5. Kingma, D.P. Adam: A Method for Stochastic Optimization / D.P. Kingma, J.L. Ba. – 2014. – 15 p. – (Preprint / arXiv.org; № 1412.6980).
6. LeCun, Y. Efficient BackProp / Y. LeCun [et al.]. // Neural Netowriks: ticks of the trade. – UK Springer, 1998. – P.9-50.
7. LeCun, Y. Gradient-based learning applied to document recognition / Y. LeCun [et al.]. // Proceedings of the IEEE. – 1998. – P.2278-2324.

sibac.info

РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ С ПОМОЩЬЮ НЕЙРОННОЙ СЕТИ ХОПФИЛДА SOLVING OPTIMIZATION PROBLEMS USING HOPFIELD NEURAL NETWORK

4886

FUNDAMENTAL RESEARCH № 2, 2015

TECHNICAL SCIENCES

УДК 517.977.56

РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ

С ПОМОЩЬЮ НЕЙРОННОЙ СЕТИ ХОПФИЛДА

Хассанин Хатем Мохамед Абдель Максуд

Национальный исследовательский Томский политехнический университет,

Томск, е-mail: [email protected]

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. Большее ко-

личество задач сводятся к задачам оптимизации: безусловная оптимизация нелинейных функций; метод

наименьших квадратов; решение нелинейных уравнений; линейное программирование; квадратичное про-

граммирование; условная минимизация нелинейных функций; минимакский метод; многокритериальная оп-

тимизация. В свете этих положений актуальность данной работы очевидна и заключается в необходимости

рассмотрения решения задач оптимизации с помощью нейронной сети. Реализация численных алгоритмов

осуществлялась посредством программ Matlab. Нейронная сеть представляет собой систему «нейронов»,

взаимодействующих между собой наподобие настоящей нейронной сети мозга. «Нейрон» в данном случае

представляется неким обладающим состоянием вычислительным процессом, так что сеть может работать

параллельно. Искусственная сеть «обучается» решению некоторой задачи, что, по сути, сводится к вычисле-

ниям весовых коэффициентов матрицы, без всякой «магии». С помощью нейронных сетей пытаются решать

различные задачи. Целью написания данной работы явилось изучение решения задач оптимизации с помо-

щью нейронной сети Хопфилда.

Ключевые слова: оптимизация, полусфера, устойчивая точка, бассейн аттрактора, нейронная сеть Хопфилда

SOLVING OPTIMIZATION PROBLEMS USING HOPFIELD NEURAL NETWORK

Hassanin Hatem Mohamed Abdel Maksoud

National research Tomsk polytechnic university, Tomsk, е-mail: [email protected]

The optimization is the process of selecting the best option of all. A large number of tasks reduced to optimization

problems: the unconstrained optimization of nonlinear functions; method of least squares; solution of nonlinear

equations; linear programming; quadratic programming; conditional minimization of nonlinear functions; mini max

methods; multi-objective optimization. In the light of these provisions, the relevance of this work is evident for the

need to address solving optimization problems using neural network. The implementation of numerical algorithms

implemented by software Matlab. A neural network is a system of «neurons», interacting with each other like this

neural network of the brain. «Neuron» in this case, it is a kind of having state of the computational process, so that

the network can operate in parallel. Artifi cial network «learns» the solution of certain problems that, in fact, reduced

to the computation of the weight coeffi cients of the matrix, without any «magic». With the help of neural networks,

we try to solve various problems. The purpose of writing this paper is to study the solution of optimization problems

using the Hopfi eld neural network.

Keywords: optimization, hemispherical, stable point, the basin of attraction, Hopfi eld neural network

Нейронная сеть представляет собой

систему «нейронов», взаимодействую-

щих между собой наподобие настоящей

нейронной сети мозга. «Нейрон» в дан-

ном случае представляется неким обла-

дающим состоянием вычислительным

процессом, так что сеть может работать

параллельно. Искусственная сеть «обу-

чается» решению некоторой задачи, что,

по сути, сводится к вычислениям весо-

вых коэффициентов матрицы. С помощью

нейронных сетей искусственная сеть пы-

тается решать различные задачи.

Целью данной работы явилось ре-

шение задачи оптимизации с помощью

нейронной сети программы Matlab [2]. До-

стижение поставленной цели может быть

реализовано посредством решения следую-

щих задач:

1. Формирование основ работы ней-

ронных сетей.

2. Выделение проблем, возникающих

при решении задач оптимизации с помо-

щью нейронной сети Хопфилда.

Выбор оптимального решения прово-

дится, как правило, с помощью некоторой

функции, называемой целевой функцией.

Целевую функцию можно записать в виде

u = f(x), x  G,

где G – некоторая область ограничений.

Джон Хопфилд в 1982 году привлек

к анализу нейронных сетей мощный аппа-

рат статистической физики (на основе ана-

логий между нейронными сетями и особ

www.researchgate.net

Редукция нейронных сетей при помощи вариационной оптимизации / Хабр

Привет, Хабр. Сегодня я бы хотел развить тему вариационной оптимизации и рассказать, как применить её к задаче обрезки малоинформативных каналов в нейронных сетях (pruning). При помощи неё можно сравнительно просто увеличить «скорострельность» нейронной сети, не перелопачивая её архитектуру. Идея редукции лишних элементов в алгоритмах машинного обучения совсем не нова. На самом деле, она старее чем понятие deep learning: только раньше резали ветви решающих деревьев, а сейчас веса в нейронной сети.

Основная мысль проста: мы находим в сети подмножество бесполезных весов и обнуляем их. Без полного перебора сложно сказать, какие веса по-настоящему участвуют в предсказании, а какие только притворяются, но это и не требуется. Недурно работают различные методы регуляризации, Optimal Brain Damage и другие алгоритмы. Зачем же вообще удалять какие-либо веса? Оказывается, что это улучшает обобщающую способность сети: как правило, малозначимые веса либо просто вносят шум в предсказание, либо специально заточены на признаки тренировочного датасета (т.е. артефакт переобучения). В этом смысле редукцию связей можно сравнить с методом отключения случайных нейронов (dropout) во время тренировки сети. Кроме того, если в сети много нулей, она занимает меньше места в архиве и способна быстрее считаться на некоторых архитектурах.

Звучит неплохо, но гораздо интереснее выкидывать не отдельные веса, а нейроны из полносвязных слоёв или каналы из свёрток целиком. В этом случае эффект сжатия сети и ускорения предсказаний наблюдается намного более явно. Но это сложнее, чем уничтожение отдельных весов: если попытаться провести Optimal Brain Damage, взяв вместо одной связи всю пачку, результаты скорее всего окажутся не очень впечатляющими. Чтобы можно было безболезненно удалить нейрон, нужно специально сделать так, чтобы у него не было ни одной полезной связи. Для этого нужно как-то побудить «сильные» нейроны становиться сильнее, а «слабые» — слабее. Эта задача нам уже знакома: по сути мы заставляем сеть быть разреженной (sparsity inducing) с некоторыми ограничениями на группировку весов.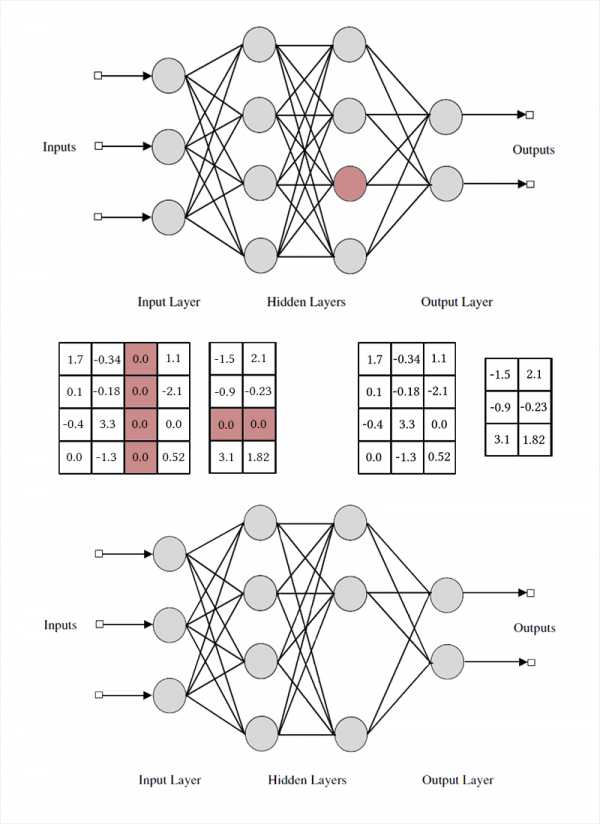 Обратите внимание, что для удаления одного нейрона или свёрточного канала, нужно модифицировать две матрицы весов. Я не буду делать различий между свёрточными каналами и нейронами: работа с ними одинакова, отличаются лишь конкретные удаляемые веса и способ транспонирования.

Простой способ: групповая L1-регуляризация

Для начала расскажу про наиболее простой и эффективный способ изъятия лишних нейронов из сети — групповую LASSO-регуляризацию. Чаще всего именно её применяют, чтобы держать бесполезные веса в сетях близко к нулю; она тривиально обобщается на поканальный случай. В отличие от обычной регуляризации, мы не регуляризируем веса или активации слоя напрямую, идея чуть-чуть хитрее. [Channel Pruning for Accelerating Very Deep Neural Networks; Yihui He et al; 2017]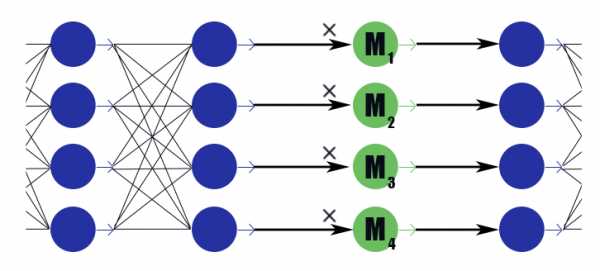 Рассмотрим специальный маскирующий слой с вектором весов . Его вывод — просто поэлементное произведение на выводы предыдущего слоя, активационной функции у него нет. Поместим по маскирующему слою после каждого слоя, каналы в котором хотим отбрасывать, и подвергнем веса в этих слоях L1-регуляризации. Таким образом вес маски , умножающийся на i-тый вывод слоя неявно налагает ограничение на все веса, от которых зависит этот вывод. Если среди этих весов, скажем половина полезных, то будет держаться ближе к единице, и этот вывод сможет хорошо передавать информацию. Но если только один или вовсе ни одного, упадёт до нуля, что обнулит вывод нейрона и, по сути, обнулит все веса, от которых зависит этот вывод (в случае активационной функции равной нулю в нуле). Обратите внимание, что таким образом сеть получает меньше негативного подкрепления в случае законно больших весов, или законно сильного отклика. Имеет значение полезность нейрона в целом.

Получается вот такая формула:

Где — константа взвешивания loss'a сети и loss'a разреженности. Похоже на обычную формулу L1-регуляризации, только во втором члене содержатся вектора маскирующих слоёв, а не веса сети.

После окончания обучения сети мы пробегаемся по нейронам и маскирующим их значениям. Если больше определённого порога, то веса нейрона умножаются на , если меньше, то из матриц входящих и исходящих весов удаляются соответствующие нейрону элементы (как на картинке немного выше). После этого маски можно отбросить и доучить сеть.

В применении групповой LASSO есть несколько тонкостей:

1. Обычная регуляризация. Вкупе с регуляризацией маскирующих весов следует применять L1/L2 регуляризацию и ко всем остальным весам сети. Без этого уменьшение маскирующего веса в случае ненасыщаемых активационных функций (ReLu, ELu) будет запросто компенсировано увеличением весов, и обнуляющего эффекта не выйдет. Да и для обычных сигмоид это позволяет лучше запустить процесс с положительной обратной связью: малоинформативного вывода становится меньше, из-за чего оптимизатору приходится сильнее задуматься над каждым конкретным весом, из-за чего вывод становится ещё более малоинформативным, из-за чего уменьшается ещё больше и так далее.
2. Авторы статьи также советуют накладывать сферическое ограничение на веса слоёв . Вероятно, это должно поспособствовать «перетеканию» весов от слабых нейронов к сильным, но я не заметил особой разницы.
3. Двухтактное обучение. Авторы статьи предлагают попеременно обучать обычные веса нейронной сети и маскирующие веса. Это дольше, чем обучать всё за раз, но как будто бы результаты чуть лучше?
4. Не забывайте про длительную точную подстройку сети (fine-tuning) после фиксации маски, это очень важно.
5. Внимательно следите, как у вас стоят маски: до или после функции активации. У вас могут быть проблемы с активациями, которые не равняются нулю при аргументе равном нулю (например, сигмоида).
6. Pruning не дружит с batchnorm примерно по той же причине, по которой с ним не дружит dropout: с точки зрения нормализации, когда в пачке 32 значения из которых 12 нулевые, и когда в пачке 20 значений — это очень разные ситуации. После выдирания обнулённых весов распределение, выученное batchnorm слоем перестаёт быть валидным. Нужно либо вставлять pruning-слои после всех batchnorm-слоёв, либо как-то модифицировать последние.
7. Также есть сложности с применением редукции каналов к «ветвистым» архитектурам и residual-сетям (ResNet). После обрезки лишних нейронов во время слияния ветвей могут не совпасть размерности. Это легко решается введением буферных слоёв, нейроны в которых мы не отбраковываем. Кроме того, если ветви сети несут разное количество информации, имеет смысл установить для них разный , чтобы не оказалось, что Pruning просто порезал все нейроны в наименее информативной ветви. Впрочем, если все нейроны порезались, то не так уж ветвь и важна?
8. В оригинальной постановке задачи указано жёсткое ограничение на количество ненулевых каналов, но на мой взгляд тут достаточно менять лишь параметра взвешивания изначального loss'а и L1-loss'а маскирующих весов, а дальше пусть сам оптимизатор решает, сколько каналов оставлять.
9. Маски захвата. Этого нет в оригинальной статье, но на мой взгляд, это хороший практический механизм для улучшения сходимости. Когда значение маски достигает некоторого заранее заданного низкого значения, мы обнуляем его и запрещаем менять эту часть маски. Таким образом слабые веса полностью перестают вносить вклад в предсказание уже во время тренировки модели, а не вносят в соответствующие суммы какие-то паразитные значения. Теоретически это может помешать потенциально полезному каналу вернуться в строй, но не думаю, что такое происходит на практике.

Сложный способ: L0-регуляризация

Но мы же не ищем лёгких путей, правда?

Отбраковка каналов при помощи L1-регуляризации не совсем честна. Она позволяет каналу перемещаться по шкале «сильный отклик» — «слабый отклик» — «нулевой отклик». Только когда маскирующий вес оказывается достаточно близок к нулю, мы отбрасываем канал при помощи маски захвата. Такое перемещение здорово искажает картину и вносит изменения в другие каналы во время тренировки: прежде чем они смогут выучить, что делать, когда предыдущий нейрон полностью отключён, они должны выучить, что делать, когда он систематически даёт слабый отклик.

Напомню, что в идеале нам бы хотелось жадным образом выбрать наименее информативный канал из сети, продолжить учить сеть без него, удалить следующий наименее информативный канал, снова подстроить сеть и так далее. Увы, в такой постановке задача вычислительно неподъёмна даже для сравнительно простых сетей. К тому же такой подход не оставляет каналам второго шанса — единожды удалённый нейрон не снова может вернуться в строй. Немного изменим задачу: будем иногда удалять нейрон, а иногда оставлять. Притом, если нейрон в целом полезный, чаще оставлять, а если бесполезный — наоборот. Для этого будем использовать такие же маскирующие слои, как в случае L1-регуляризации (не зря же их вводили!). Только их веса будут не перемещаться по всей действительной оси с аттрактором в нуле, а будут сконцентрированы вокруг 0 и 1. Не то чтобы стало сильно проще, но по крайней мере разобрались с проблемой категоричности удаления нейронов.

Инстинкт обучатора сетей подсказывает, что не стоит решать задачу перебором, а нужно добавить количество активных нейронов в слоях на текущем прогоне в функцию потерь. Однако такой член в loss'е будет ступенчато-постоянным, и градиентный спуск не сможет с ним работать. Нужно как-то научить алгоритм обучения периодически исключать некоторые нейроны, несмотря на отсутствие градиента.

У нас есть способ временно удалять нейроны: мы можем применить dropout к маскирующему слою. Пусть во время обучения с вероятностью и с вероятностью . Теперь в функцию потерь можно поместить сумму , которая является действительным число. Здесь мы сталкиваемся с очередным препятствием: распределение-то дискретно, непонятно, как с ним работать backpropagation'у. Вообще существуют специальные алгоритмы оптимизации, которые могут нам здесь помочь (см. REINFORCE), но мы предпримем другой подход.

Тут-то и настал момент, где в дело вступает вариацонная оптимизация: мы можем приблизить дискретное распределение нулей и единиц в маскирующем слое непрерывным и оптимизировать параметры последнего при помощи обычного алгоритма обратного распространения. В этом и состоит идея работы [Learning Sparse Neural Networks Through L0 Regularization; Christos Louizos et al; 2017].

Роль непрерывного распределения будет исполнять hard concrete distribution [The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables; Chris Maddison; 2017], вот такая хитрая штука из логарифмов, приближающая распределение Бернулли:

— смещение распределение относительно центра, а — температура. При распределение всё больше начинает приближать истинное распределение Бернулли, но теряет дифференцируемость. При плотность распределения вогнута (это интересующий нас случай), при — выпукла. Мы пропускаем это распределение через жёсткую сигмоиду, чтобы оно с конечной ненулевоей вероятностью умело выдавать и , а на интервале (0, 1) обладало непрерывной дифференцируемой плотностью. После окончания pruning'a мы смотрим в какую сторону сместилось распределение и заменяем случайную переменную на конкретное значение маски и доводим до кондиции уже детерминированную модель.

Чтобы чуть лучше почувствовать распределение, приведу несколько примеров его плотности для разных параметров:

Плотность распределения По сути у нас получился «умный» dropout-слой, который выучивает, какие выводы нужно чаще выбрасывать. Но что же конкретно мы оптимизируем? В loss следует поместить интеграл от плотности распределения в ненулевой области (вероятность, что маска окажется равной не нулю во время тренировки проще говоря): К двухтактному обучению, обычной регуляризации и прочим подробностям имплементации упомянутым в главе про L1-регуляризацию добавляются следующие особенности:

• Ещё раз: наш «умны»й dropout-слой с некоторой заметной вероятностью обнуляет выход, с некоторой — оставляет как есть, и плюс, есть небольшой шанс, зависящий от , что вывод будет умножен на случайное число от 0 до 1. Последняя часть скорее паразитная чем полезная для нашей конечной цели, но без неё никак — она нужна для обратного прохода backpropagation'a.
• Вообще и и — тренируемые параметры, но в своих экспериментах я почувствовал, что если просто задать маленькую (0.05) и в процессе обучения её ещё линейно уменьшать, то алгоритм сходится лучше, чем если её честно выучивать. лучше задать достаточно большую , чтобы изначально нейроны чаще сохранялись, чем отбрасывались, но недостаточно большую, чтобы насытилась сигмоида в loss'e.
• Если заменить в формулах на просто как будто бы сеть лучше сходится и меньше шансов нарваться на NaN во время тренировки. При таком манёвре нужно не забыть изменить член в функции потерь и инициализацию.
• Также если сжульничать и заменить обычную сигмоиду в loss'e на жёсткую с ограничениями по , регуляризация будет лучше сходиться и действовать сильнее.
• К и можно дополнительно применить регуляризацию, чтобы ещё больше увеличить разреженность.
• После окончания тренировки следует бинаризировать полученные результаты и упорно дообучать сеть с детерминированной маской до выхода val accuracy на константу. В статье приводится более точная формула, по которой вывод нейрона можно сделать детерминированным во время валидации или для выпуска сети в релиз, но кажется, что к концу обучения оказываются достаточно поляризованными, чтобы сработала и простая эвристика: — маска 0, — маска 1 (но это не точно). После перехода к детерминированным маскам вы увидите скачок качества. Не забывайте, что мы сюда обнулять веса пришли, и ниже определённого порога веса всё равно нужно заменять маскирующие веса на нули.
• Дополнительный плюс L0-подхода — маскирующие слои начинают работать как dropout, что вносит в сеть мощный регуляризирующий эффект. Но это палка о двух концах: если начинать обучение со слишком маленьким , есть риск порушить предварительно обученную структуру сети.

Эксперименты

Для эксперимента возьмём датасет CIFAR-10 и сравнительно простую сеть в четыре свёрточных слоя, за которыми следуют два полносвязных: Conv2D, Mask, Conv2D, Mask, Pool2D, Conv2D, Mask, Conv2D, Mask, Pool2D, Flatten, Dropout (p=0.5), Dense, Mask, Dense (logits). Считается, что алгоритмы pruning'а лучше работают на более «толстых» сетях, но тут я столкнулся с чисто технической проблемой недостатка вычислительных мощностей. В качестве оптимизатора использовался Adam с learning rate = 0.0015 и batch size = 32. Дополнительно использовались обычные L1 (0.00005) и L2 (0.00025) регуляризации. Image augmentation не применялся. Сеть обучалась 200 эпох до схождения, после чего сохранялась, и к ней применялись алгоритмы редукции нейронов.

Кроме применения для pruning'a алгоритмов, описанных выше, установим тривиальную отсчётная точку, чтобы убедиться, что алгоритмы вообще что-то делают. Попробуем попеременно выкидывать из каждого слоя первых нейронов и доучивать получившуюся сеть.

На графике представлены результаты сравнения L1 и L0 алгоритмов редукции каналов после серии экспериментов с разными константами мощности регуляризации. По оси X отложено уменьшение количества весов в процентах после применения алгоритма. По оси Y — точность порезаной сети на валидационной выборке. Синяя полоса посередине — примерное качество сети, ещё не подвергнутой вырезанию нейронов. Зелёная линия представляет простой алгоритм L1-обучения масок. Красная линия — L0-pruning. Фиолетовая линия — удаление первых каналов. Чёрные треугольники — обучение сети, у которой изначально было меньшее количество весов.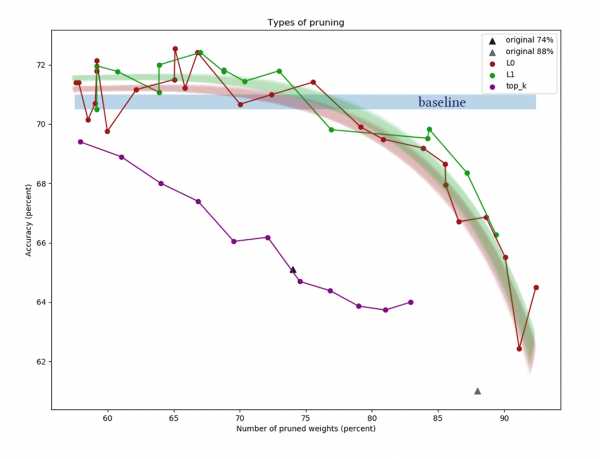 Ещё один пример для CIFAR-100 и чуть более длинной и широкой сети примерно такой же архитектуры и с похожими параметрами обучения: 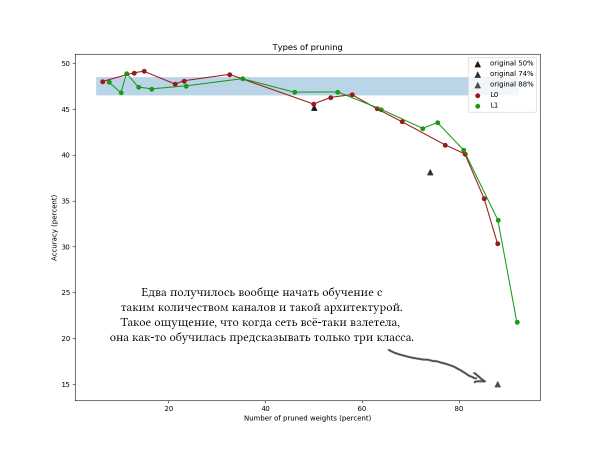Ииии на графиках хорошо видно, что простой L1-алгоритм справляется ничуть не хуже хитрой вариационной оптимизации, и как будто бы даже чуть больше улучшает качество сети при малых значениях компрессии. Результаты также подтверждаются разовыми экспериментами с другими датасетами и архитектурами сетей. Это абсолютно ожидаемый результат, на который я и рассчитывал, когда начинал эксперименты над редукцией сетей. Честно. Sigh.

Ну ладно, если честно, я был слегка удивлён, и пробовал играться с алгоритмом и сетью: разные архитектуры, гиперпараметры сети, точные формулы hard concrete distribution, начальные значения и , количество эпох промежуточной подстройки. Выглядит L0-регуляризация в теории круто, но на практике для неё сложнее подобрать гиперпараметры, и считается она дольше, так что я бы не советовал применять её без дополнительных экспериментов и обработки напильником. Пожалуйста, не считайте потраченным время на чтение статьи: L0-pruning выглядит действительно очень правдоподобно, и я бы сказал, что скорее я где-то неправильно применил алгоритм, что не получил обещанного прироста. Плюс, вариационная оптимизация является основой для ещё более продвинутых алгоритмов редукции [например, Compressing Neural Networks using the Variational Information Bottleneck, 2018].

В целом можно сделать следующие выводы:

1. Многие каналы в обученной сети явно избыточны. Даже при установке малой константы регуляризации маски легко достичь сокращения 30-50% весов. Но если изначально тренировать слишком «тонкую» сетку, сложно достичь хороших результатов. Это говорит в пользу благотворного влияния широких слоёв на целевую функцию сети и в пользу теории лотерейных билетов [The Lottery Ticket Hypothesis: Training Pruned Neural Networks, J. Frankle and M. Carbin, 2018] (чем больше нейронов, тем больше шансов, что хотя бы один из них инициализируется так, что сформирует хорошее правило).
2. Если начать с широкой сети и понемногу выкидывать каналы с доучиванием, то сеть держится весьма неплохо. Но если выкинуть сразу слишком много весов без доучивания точность сети непоправимо ухудшится. Пластичность нейронов лучше себя проявляет, когда сеть близко к оптимальному состоянию?
3. Хоть и нельзя уменьшать количество весов сколь угодно долго, в этом деле можно зайти на удивление далеко. Судя по научным статьям и моим экспериментам спад обычно начинается в районе 60-90% компрессии по весам. Хоть в моих экспериментах разрыв между кривыми алгоритмов редукции нейронов и кривыми выбрасывания первых нейронов составил <7%, многие научные статьи рапортуют о гораздо большем превосходстве.
4. Обратите внимание, что в случае несильной компрессии (<60%) алгоритмы редкции нейронов работают как регуляризаторы: точность на валидационной выборке после работы алгоритмы даже выше, чем изначальная!
5. Кроме L1 и L0 были испробованы алгоритмы обрезки каналов по величине весов и среднему количеству нулей функции активации (APoZ), но они не представлены на графике, т.к. показали себя едва лучше, чем просто обнуление верхних каналов.
6. В статьях обычно тренируют сеть до упора, и только потом применяют к ней алгоритмы отсекания лишних нейронов. Делается это, я так понимаю, для чистоты эксперимента, и чтобы было видно, что качество сети несильно ухудшилось относительно точки отсчёта. Но если вы уже знаете архитектуру и базовую точность, с которой соревнуетесь, то предварительное обучение до выхода на планку как будто бы необязательно. Всё равно после начала работы алгоритма pruning'а веса очень здорово переколбашиваются, и изначально точность заметно падает. Можно натренировать сеть до более-менее вменяемого состояния, после чего одновременно обучать и очищать сеть.

Пару слов о технической стороне вопроса

Помните, как я в начале поста написал, что после завершения алгоритма прунинга можно «просто вырезать лишние куски сети целиком»? Так вот, вырезать лишние куски сети совсем не просто. Tensorflow и прочие библиотеки строят вычислительный граф, и его нельзя так просто изменить, когда он уже в работе. Приходится сохранять сеть с вычисленными масками, выдирать из неё список нужных весов, транспонировать веса нужным образом, удалять обнулённые группы, транспонировать обратно, и создавать новую сеть на основе выходного набора тензоров. Получившаяся сеть должна обладать такой же планировкой, как и исходная, но в ней будет меньше нейронов. Ожидайте головную боль с поддерживанием одинаковой схемы сети в функции создания изначальной и финальной сети, особенно, если они не линейные, а ветвистые.

Вероятно для удобного маскирования придётся создавать свои слои. Это несложно, но будьте внимательны, в какие коллекции вы добавляете параметры маскрирования. Тут несложно ошибиться и случайно тренировать параметры редукции каналов вместе со всеми остальными весами.

Следует заметить, что заметная часть весов сетей с не очень глубокими архитектурами обычно сконцентрирована на переходе из свёрточной части в полносвязную. Так происходит из-за того что последний свёрточный слой делается плоским, вследствие чего в нём как бы образуется (количество каналов)*(ширина)*(высота) нейронов, и следующая матрица весов получается очень широкой. Эти веса вряд ли получится порезать; более того этого не надо делать, иначе последние слои сети окажутся «слепы» к фичам, найденным в некоторых местах. Старайтесь в таких случаях делать финальное количество каналов меньшим и пользоваться maxpool'ингом или вовсе использовать полностью свёрточные или полностью полносвязные архитектуры.

Всем спасибо за внимание, если кому-то интересно повторить эксперименты над CIFAR-10 и CIFAR-100, код можно взять на гитхабе. Хорошего рабочего дня!

habr.com

Нейронные сети для начинающих. Часть 1 / Хабр

Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.

Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат. Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:

a b c

0	0	0
0	1	1
1	0	1
1	1	0

Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.

Что такое нейронная сеть?

Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.

Какие бывают нейронные сети?

Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.

Для чего нужны нейронные сети?

Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:

Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.

Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.

Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.

Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.

Что такое нейрон?

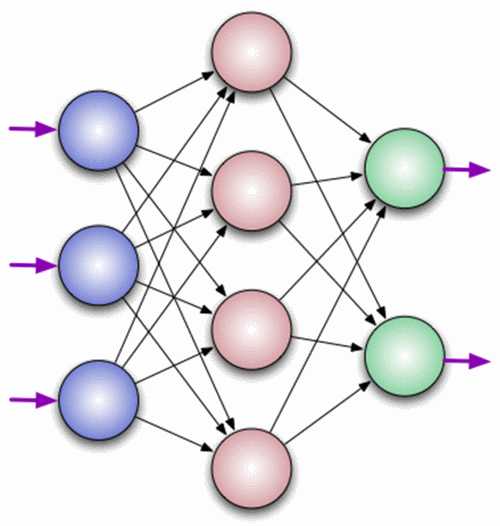Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.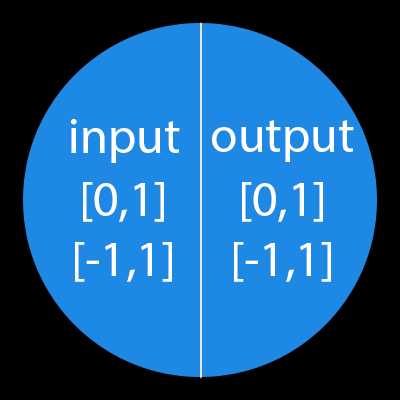Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.

Что такое синапс?

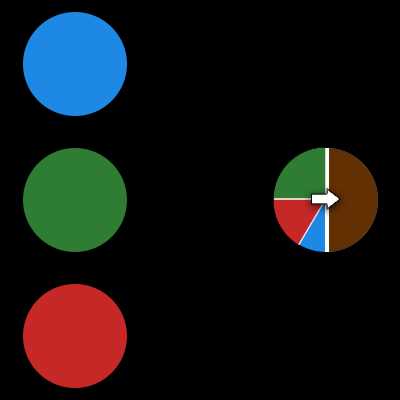Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.

Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.

Как работает нейронная сеть?

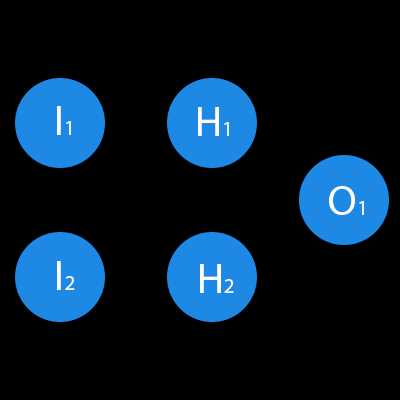
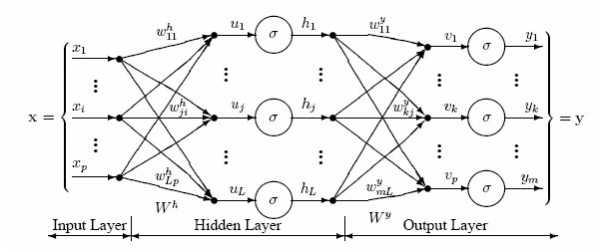
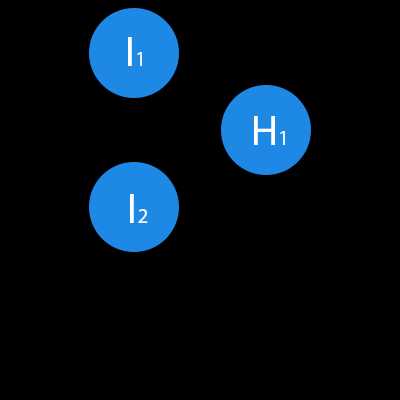В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.

Функция активации

Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.

Линейная функция

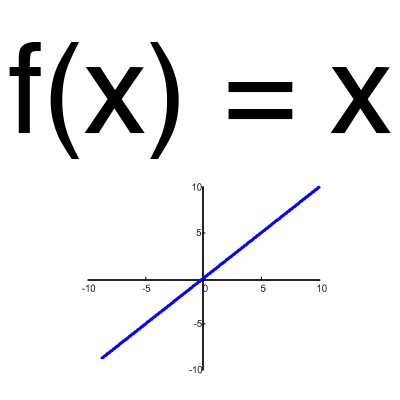Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.

Сигмоид

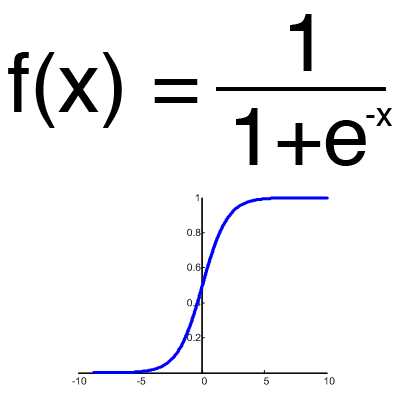Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.

Гиперболический тангенс

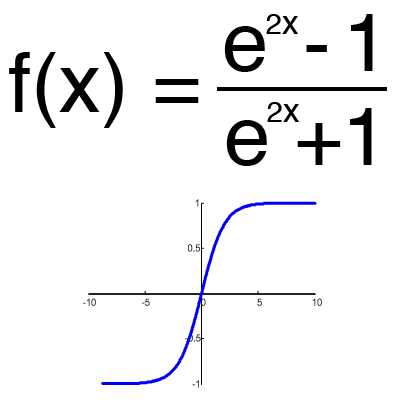Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.

Тренировочный сет

Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.

Итерация

Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.

Эпоха

При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.

Ошибка

Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.

MSE

Root MSEArctan Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.

Задача

Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.

Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.

Решениеh2input = 1*0.45+0*-0.12=0.45 h2output = sigmoid(0.45)=0.61

h3input = 1*0.78+0*0.13=0.78 h3output = sigmoid(0.78)=0.69

O1input = 0.61*1.5+0.69*-2.3=-0.672 O1output = sigmoid(-0.672)=0.33

O1ideal = 1 (0xor1=1)

Error = ((1-0.33)^2)/1=0.45

Результат — 0.33, ошибка — 45%.

Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.

Использованные ресурсы: — Раз — Два — Три

habr.com

Постановка задачи оптимизации при обучении нейронной сети

Пусть имеется нейронная сеть, выполняющая преобразование F:XY векторов X из признакового пространства входов X в вектора Y выходного пространства Y. Сеть находится в состоянии W из пространства состояний W. Пусть далее имеется обучающая выборка (X,Y),  = 1..p. Рассмотрим полную ошибку E, делаемую сетью в состоянии W.

Отметим два свойства полной ошибки. Во-первых, ошибка E=E(W) является функцией состояния W, определенной на пространстве состояний. По определению, она принимает неотрицательные значения. Во-вторых, в некотором обученном состоянии W*, в котором сеть не делает ошибок на обучающей выборке, данная функция принимает нулевое значение. Следовательно, обученные состояния являются точками минимума введенной функции E(W).

Таким образом, задача обучения нейронной сети является задачей поиска минимума функции ошибки в пространстве состояний, и, следовательно, для ее решения могут применяться стандартные методы теории оптимизации. Эта задача относится к классу многофакторных задач, так, например, для однослойного персептрона с N входами и M выходами речь идет о поиске минимума в NxM-мерном пространстве.

На практике могут использоваться нейронные сети в состояниях с некоторым малым значением ошибки, не являющихся в точности минимумами функции ошибки. Другими словами, в качестве решения принимается некоторое состояние из окрестности обученного состояния W*. При этом допустимый уровень ошибки определяется особенностями конкретной прикладной задачи, а также приемлемым для пользователя объемом затрат на обучение.

Модель Хопфилда

Модель Хопфилда (J.J.Hopfield, 1982) занимает особое место в ряду нейросетевых моделей. В ней впервые удалось установить связь между нелинейными динамическими системами и нейронными сетями. Образы памяти сети соответствуют устойчивым предельным точкам (аттракторам) динамической системы. Особенно важной оказалась возможность переноса математического аппарата теории нелинейных динамических систем (и статистической физики вообще) на нейронные сети. При этом появилась возможность теоретически оценить объем памяти сети Хопфилда, определить область параметров сети, в которой достигается наилучшее функционирование.

В этой лекции мы последовательно начнем рассмотрение с общих свойств сетей с обратными связями, установим правило обучения для сети Хопфилда (правило Хебба), и затем перейдем к обсуждению ассоциативных свойств памяти этой нейронной сети при решении задачи распознавания образов.

Сети с обратными связями

Рассмотренный нами ранее ПЕРСЕПТРОН относится к классу сетей с направленным потоком распространения информации и не содержит обратных связей. На этапе функционирования каждый нейрон выполняет свою функцию - передачу возбуждения другим нейронам - ровно один раз. Динамика состояний нейронов является безитерационной.

Несколько более сложной является динамика в сети Кохонена. Конкурентное соревнование нейронов достигается путем итераций, в процессе которых информация многократно передается между нейронами.

В общем случае может быть рассмотрена нейронная сеть (см. Рис. 8.1), содержащая произвольные обратные связи, по которым переданное возбуждение возвращается к данному нейрону, и он повторно выполняет свою функцию. Наблюдения за биологическими локальными нейросетями указывают на наличие множественных обратных связей. Нейродинамика в таких системах становится итерационной. Это свойство существенно расширяет множество типов нейросетевых архитектур, но одновременно приводит к появлению новых проблем.

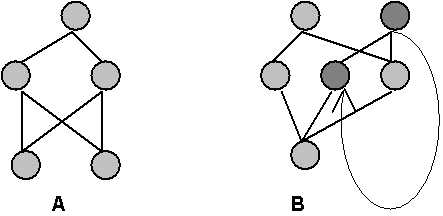
Рис. 8.1. Фрагменты сетей с прямым рапространением (A) и с наличием обратных связей (B)

Безитерационная динамика состояний нейронов является, очевидно, всегда устойчивой. Обратные связи могут приводить к возникновению неустойчивостей, подобно тем, которые возникают в усилительных радиотехнических системах при положительной обратной связи. В нейронных сетях неустойчивость проявляется в блуждающей смене состояний нейронов, не приводящей к возникновению стационарных состояний. В общем случае ответ на вопрос об устойчивости динамики произвольной системы с обратными связями крайне сложен и до настоящего времени является открытым.

Ниже мы остановимся на важном частном случае нейросетевой архитектуры, для которой свойства устойчивости подробно исследованы.

studfiles.net

Заблуждения о нейронных сетях | Школа по созданию торговых роботов

3 Апрель 2017      Дмитрий Высоцкий      Главная страница » Блог      Просмотров:  

Stuart Reid

Нейронные сети – один из самых популярных классов алгоритмов для машинного обучения. В финансовом анализе они чаще всего применяются для прогнозирования, создания собственных индикаторов, алгоритмического трейдинга и моделирования рисков. Несмотря на все это, репутация у нейронных сетей подпорчена, поскольку результаты их применения можно назвать нестабильными.

Количественный аналитик хедж-фонда NMRQL Стюарт Рид в статье на сайте TuringFinance попытался объяснить, что это означает, и доказать, что все проблемы кроются в неадекватном понимании того, как такие системы работают. Мы представляем вашему вниманию адаптированный перевод его статьи.

1. Нейронная сеть – это не модель человеческого мозга

Человеческий мозг – одна из самых больших загадок, над которой бьются ученые не одно столетие. До сих пор нет единого понимания, как все это функционирует. Есть две основные теории: теория о «клетке бабушки» и теория дистрибутивного представительства. Первая утверждает, что отдельные нейроны имеют высокую информационную вместимость и способны формировать сложные концепты. Например, образ вашей бабушки или Дженнифер Энистон. Вторая говорит о том, что нейроны намного проще в своем устройстве и представляют комплексные объекты лишь в группе. Искусственную нейронную сеть можно в общих чертах представить как развитие идей второй модели.

Огромная разница ИНС от человеческого мозга, помимо очевидной сложности самих нейронов, в размерах и организации. Нейронов и синапсов в мозгу несоизмеримо больше, они самостоятельно организуются и способны к адаптации. ИНС конструируют как архитектуру. Ни о какой самоорганизации в обычном понимании не может быть речи.

Что из этого следует? ИНС создаются по архетипу человеческого мозга в том же смысле, как олимпийский стадион в Пекине был собран по модели птичьего гнезда. Это ведь не означает, что стадион – это гнездо. Это значит, что в нем есть некоторые элементы его конструкции. Лучше говорить о сходстве, а не совпадении структуры и дизайна.

Нейронные сети, скорее, имеют отношение к статистическим методам – соответствия кривой и регрессии. В контексте количественных методов в финансовой сфере заявка на то, что нечто работает по принципам человеческого мозга, может ввести в заблуждение. А в неподготовленных умах вызвать страх угрозы вторжения роботов и прочую фантастику.

Пример кривой, также известной как функция приближения. Нейронные сети очень часто используют для аппроксимации сложных математических функций

2. Нейронная сеть – не упрощенная форма статистики

Нейронные сети состоят из слоев соединенных между собой узлов. Отдельные узлы называются перцептронами и напоминают множественную линейную регрессию. Разница в том, что перцептроны упаковывают сигнал, произведенный множественной линейной регрессией, в функцию активации, которая может быть как линейной, так и нелинейной. В системе со множеством слоев перцептронов (MLP) перцептроны организованы в слои, которые в свою очередь соединены друг с другом. Есть три типа слоев: слои входных данных и выходных сигналов, скрытые слои. Первый слой получает паттерны входных данных, второй может поддерживать список классификации или сигналы вывода в соответствии со схемой. Скрытые слои регулируют веса входных данных, пока риски ошибки не сводятся к минимуму.

Картирование инпутов/аутпутов

Перцепторы получают векторы входных данных — z=(z1,z2,…,zn) из n атрибутов. Вектор называется входным паттерном (input pattern). Вес такого «инпута» определяется весом вектора, принадлежащего к этому перцептрону — v=(v1,v2,…,vn). В контексте множественной линейной регрессии это можно представить как коэффициент регрессии. Сигнал перцептрона в сети, net, обычно складывается из входного паттерна и его веса.

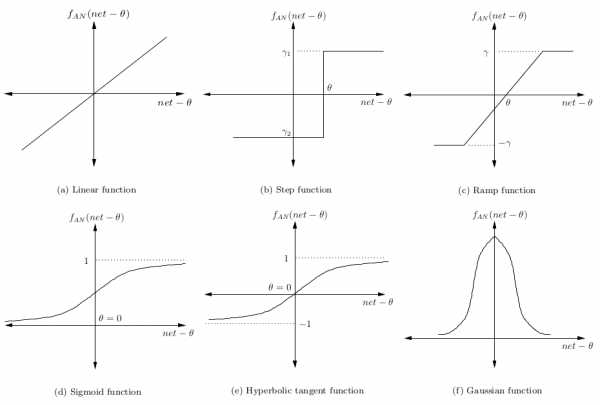
Сигнал минус смещение θ затем преобразуется в некую активационную функцию. Обычно это монотонно возрастающая функция с границами (0,1) или (-1,1). Некоторые наиболее популярные функции представлены на картинке:

Простейшая нейронная сеть – так, которая имеет лишь один нейрон, картирующий входные сигналы в выходные.

Создание слоев

Как видно из рисунка, перцептроны организованы в слои. Первый слой, который позже получит название входного, получает паттерн p в процессе обучения – Pt. Последний слой привязан к ожидаемым выходным сигналам для этих паттернов. Паттерны могут быть величинами разных технических индикаторов, а потенциальные выходные сигналы могут быть категориями {BUY,HOLD,SELL}.

Скрытый слой – тот, который получает инпуты и аутпуты от другого слоя и формирует аутпуты для следующего. По одной из версий, скрытые слои извлекают выступающие элементы из входящих данных, которые имеют значение для предсказания результата. В статистике такая техника зовется первичным компонентным анализом.

Глубокая нейронная сеть имеет большое количество скрытых слоев и способна извлекать больше подходящих элементов данных. Недавно их с успехом использовали для решения проблем распознавания образов.

В задачах трейдинга при использовании глубоких сетей есть одна проблема: данные на входе уже подготовлены и может быть сразу несколько элементов, которые необходимо извлечь.

Правила обучения

Задача нейронной сети минимизировать степень ошибки ϵ. Обычно этот показатель рассчитывается как сумма квадратов ошибок. Хотя такой вариант может быть чувствителен к постороннему шуму.

Для наших целей мы можем использовать алгоритм оптимизации, чтобы приспособить показатели веса к сети. Чаще всего для обучения сети применяют алгоритм градиентного спуска. Он работает через калькуляцию частичных дериватов ошибок с учетом их веса для каждого слоя и затем двигается в обратном направлении по уклону. Минимизируя ошибку, мы увеличиваем производительность сети в выборке.

Математически это правило обновления можно выразить в следующей формуле:

η – частота обучения, отвечающая за то, как быстро или медленно сеть конвергируется. Выбор частоты обучения имеет серьезные последствия в плане производительности нейронной сети. Маленькое значение приведет к медленной конвергенции, большое может привести к отклонениям в обучении.

Итак, нейронная сеть – это не есть упрощенная форма статистики для ленивых аналитиков. Это некая выдержка серьезных статистических методов, применяемых уже сотни лет.

3. Нейронная сеть может быть исполнена в разной архитектуре

До этого момента мы рассуждали о самой примитивной архитектуре нейронной сети – системе многоуровневых перцептронов. Есть еще множество вариантов, от которых зависит производительность. Современные достижения в изучении машинного обучения связаны не только с тем, как работают оптимизационные алгоритмы, но как они взаимодействуют с перцептронами. Автор предлагает рассмотреть наиболее интересные, с его точки зрения, модели.

Рекуррентная нейронная сеть: у нее некоторые или все соединения отыгрывают назад. По сути, это принцип технологии Feed Back Loop (уведомление провайдера сервису рассылки при наборе критического числа жалоб на спам). Считается, что такая сеть лучше работает на серийных данных. Если так, то этот вариант вполне уместен в отношении финансовых рынков. Для более подробного ознакомления нам предлагают почитать вот эту статью.

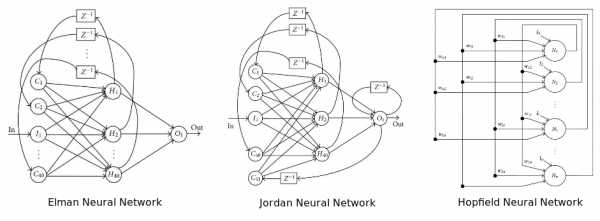
На диаграмме изображены три популярных архитектуры нейронных сетей

Последний из придуманных вариантов архитектуры рекуррентной нейронной сети – нейронная машина Тьюринга. Она объединяет архитектуру стандартной сети с памятью.

Нейронная сеть Больцмана – одна из первых полностью связанных нейронных сетей. Она одной из первых была способна обучаться внутренним представлениям и решать сложные задачи по комбинаторике. Про нее говорят, что это версия Монте-Карло рекуррентной нейронной сети Хопфилда. Ее сложнее обучать, но если поставлены ограничения, то она эффективней традиционной сети. Самое распространенное ограничение в отношении сети Больцмана – запрет на соединения между скрытыми нейронами. Собственно, еще один вариант архитектуры.

Глубокая нейронная сеть – сеть со множеством скрытых слоев. Такие сети стали крайне популярны в последние годы, из-за их способности с блеском решать проблемы по распознаванию голоса и изображения. Число архитектур в данном варианте растет небывалыми темпами. Самые популярные: глубокие сети доверия, сверточные нейронные сети, автокодировщики стэка и прочее. Самая главная проблема с глубокими сетями, особенно в случае с финансовым анализом, — переобучение.

Адаптивная нейронная сеть одновременно адаптирует и оптимизирует архитектуру в процессе обучения. Она может наращивать архитектуру (добавлять нейроны) или сжимать ее, убирая ненужные скрытые нейроны. По мнению автора, эта сеть лучше всего подходит для работы на финансовых рынках, потому что сами эти рынки не стационарны. То есть сеть способна подстраиваться под динамику рынка. Все, что было здорово вчера, не факт, что будет оптимально работать завтра.

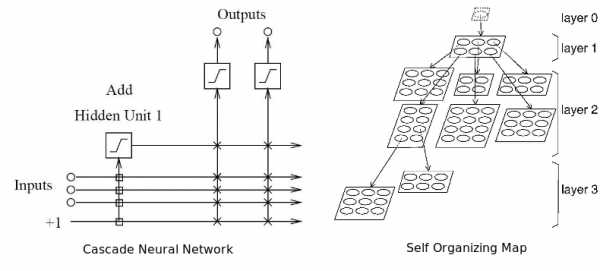
Два типа адаптивных нейронных сетей: каскадная и самоорганизующаяся карта

Радиально-базисная сеть – не то чтобы отдельный тип архитектуры в плане размещения соединений и перцептронов. Здесь в качестве активирующей функции используется радиально-базисная функция, чьи аутпуты зависят от расстояния от конкретной точки. Самое распространенное применение этой функции – гауссовское распределение. Она также используется как ядро в векторной машине поддержки.

Проще всего – попробовать несколько вариантов на практике и выбрать наиболее подходящий под конкретные задачи.

4. Размер имеет значение, но больше – не всегда значит лучше

После выбора архитектуры возникает вопрос, насколько большой или насколько небольшой должна быть нейронная сеть? Сколько должно быть «инпутов»? Сколько нужно использовать скрытых нейронов? Скрытых слоев (в случае с глубокой сетью)? Сколько «аутпутов» нужно нейронам? Если мы промахнемся с размером, сеть может пострадать от переобучения или недообучения. То есть не будет способна грамотно обобщать.

Сколько и какие инпуты нужно использовать?

Число входных сигналов зависит от решаемой проблемы, количества и качества доступной информации и, возможно, некоторой доли креатива. Выходные сигналы – это простые переменные, на которые мы возлагаем некие предсказательные способности. Если входные данные к проблеме не ясны, можно определять переменные для включения через систематический поиск корреляций и кросс-корреляций между потенциальными независимыми переменными и зависимыми переменными. Этот подход детально рассматривается в этой статье.

С использованием корреляций есть две основные проблемы. Во-первых, если вы используете метрику линейной корреляции, вы можете непреднамеренно исключить нужные переменные. Во-вторых, две относительно не коррелированных переменных могут быть потенциально объединены для получения одной хорошо коррелированной переменной. Когда вы смотрите на переменные изолировано, вы можете упустить эту возможность. Здесь можно использовать основной компонентный анализ для извлечения полезный векторов в качестве входных сигналов.

Другая проблема при выборе переменных – мультиколлинеарность. Это когда две или более переменных, загруженных в модель, имеют высокую корреляцию. В контексте регрессивных моделей это может вызвать хаотичные изменения регрессивного коэффициента в ответ на незначительные изменения в модели или в данных. Учитывая то, что нейронные сети и регрессионные модели схожи, можно предположить, что та же проблема распространяется на нейронные сети.

Еще один момент связан с тем, что за выбранные переменные принимают пропущенные отклонения в переменных. Они появляются, когда модель уже сформирована, а за бортом осталась парочка важных каузальных переменных. Отклонения проявляют себя, когда модель получает неверное возмещение отсутствующим переменным через переоценку или недооценку других переменных.

Сколько необходимо скрытых нейронов?

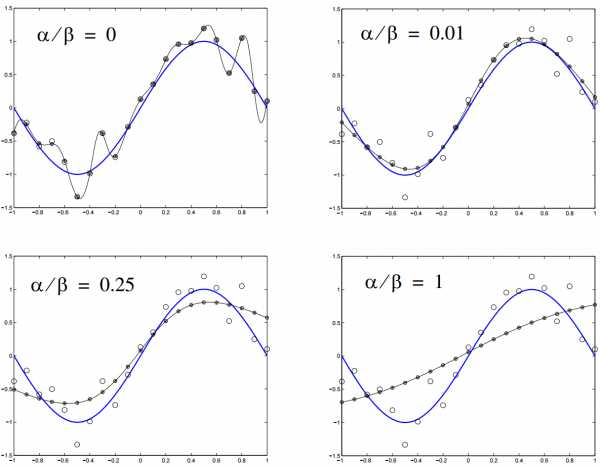
Оптимальное число скрытых элементов – специфическая проблема, решаемая опытным путем. Но общее правило: чем больше скрытых нейронов – тем выше риск переобучения. В этом случае система не изучает возможности данных, а как бы запоминает сами паттерны и любой содержащийся в них шум. Такая сеть отлично работает на выборке и плохо за пределами выборки. Как можно избежать переобучения? Есть два популярных метода: ранняя остановка и регуляризация. Автор предпочитает свой, связанный с глобальным поиском.

Ранняя остановка предполагает разделение процесса обучения на этапы самого обучения и валидации результатов. Вместо того чтобы обучать сеть на ограниченном числе итераций, вы обучаете ее пока производительность сети на этапе подтверждения не начинает падать. По-существу, это не дает сети использовать все доступные параметры и ограничивает способности к простому запоминанию паттернов. Ниже показаны две возможные точки остановки:

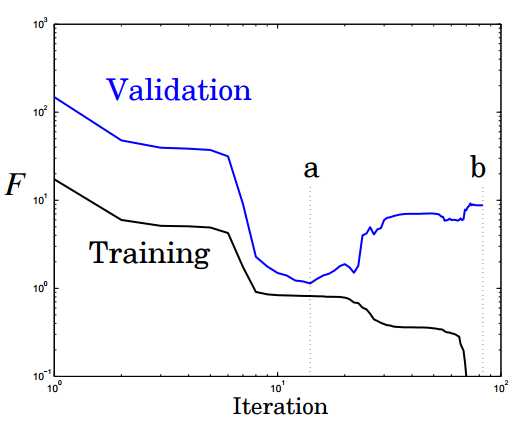
Еще одна картинка показывает производительность и степень переобучение сети при остановке в этих точках a и b:

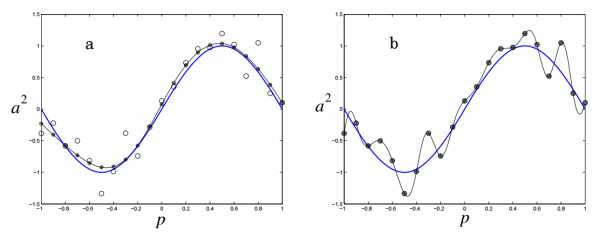
Регуляризация штрафует нейронную сеть за использования усложненной архитектуры. Сложность в данном случае измеряется размером и весом сети. Она устанавливается через добавление интервала к функции ошибки, который привязан к весу и размеру. Это то же самое, что добавление приоритета, который заставляет поверить нейронную сеть функцию на однородность.

n- это число нагрузок (весов) в нейронной сети. Параметры α и β контролируют уровень, после которого наступает недообучение или переобучение сети. Подходящие значения для них можно подобрать через Байесовский анализ и оптимизацию.

Другая техника, довольно дорогостоящая в плане вычислений, — глобальный поиск. Здесь алгоритм поиска используется для дифференциации архитектуры сети и нахождения ее оптимального варианта. Обычно для этого берут алгоритм генерации, о котором будет сказано ниже.

Что такое «аутпуты»?

Нейронную сеть можно использовать для регрессии или классификации. В первой модели мы работаем с единичным значением на выходе. То есть нужен всего один нейрон выхода. Во второй модели нейрон выхода нужен для каждого класса, к которому может принадлежать паттерн, в отдельности. Если классы не известны – используются самоорганизующиеся карты.

Подытожим эту часть рассказа. Лучший подход для определения размера сети – следовать принципу Оккама. То есть для двух моделей с одинаковой производительностью, модель с меньшим количеством параметров будет генерализировать успешней. Это не значит, что нужно обязательно выбирать простую модель в целях повысить производительность. Верно обратное утверждение: множество скрытых нейронов и слоев не гарантирует превосходство. Слишком много внимание сегодня уделяется большим сетям, и слишком мало самим принципам их разработки. Больше – не всегда лучше.

5. К нейронной сети применимо множество обучающих алгоритмов

Обучающий алгоритм призван оптимизировать вес нейронной сети, пока не наткнется на некое условие остановки. Это может быть связано с появлением ошибки в тренировочном сете на приемлемом уровне точности (например, когда работа сети на этапе валидации начинает ухудшаться). Это может быть точка, когда израсходован некий вычислительный бюджет сети. Самый популярный вариант алгоритма – метод обратного распространения с использованием градиентного стохастического спуска. Обратное распространение состоит из двух шагов:

— Прямое прохождение: обучающие данные проходят через сеть, записывается выходной сигнал и подсчитываются ошибки.— Обратное распространение: сигнал ошибки протаскивается обратно через сеть, вес сети оптимизируется с использованием градиентного спуска.

С этим подходом может возникнуть несколько проблем. Подгонка всех весов одновременно может привести к чрезмерному перемещению сети в весовом пространстве. Алгоритм градиентного спуска довольно медленный и восприимчив к локальному минимуму. Локальный минимум – специфическая проблема для определенных нейронных сетей. Первая проблема решаема через использования разных вариантов градиентного спуска: (QuickProp), Nesterov’s Accelerated Momentum (NAG), Adaptive Gradient Algorithm (AdaGrad), Resilient Propagation (RProp) или Root Mean Squared Propagation (RMSProp).

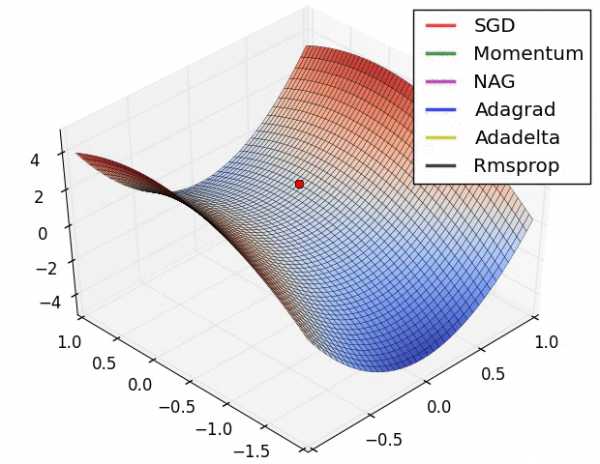
Но все эти алгоритмы не могут преодолеть локальный минимум, и менее полезны, когда пытаются одновременно оптимизировать архитектуру и нагрузку сети. Нужен алгоритм глобальной оптимизации. Это может быть метод роя частиц (Particle Swarm Optimization) или генетический алгоритм. Вот, как это работает.

Векторное представление нейронной сети кодирует нейронную сеть по вектору нагрузки, каждый из векторов представляет вес соединения в сети. Мы можем обучать сеть, используя мета-эвристический поисковой алгоритм. На слишком больших сетях метод работает плохо, потому что сами векторы становятся слишком большими.

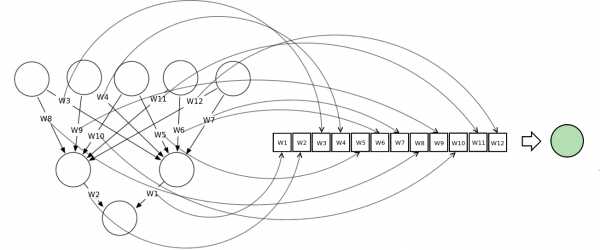
На диаграмме показано, как нейронная сеть может быть представлена в векторной нотации

Метод роя частиц обучает сеть через построение популяции/роя. Каждая нейронная сеть здесь представлена как вектор нагрузки и скорректирована по отношению к позиции глобальной лучшей частицы и ее собственной лучшей позиции.

Эта функция приспособления просчитывается как сумма квадратов ошибок реконструированной нейронной сети после завершения одного прямого прохождения. Выгоду получаем на оптимизации скорости обновления весов связей. Если весы будут регулироваться слишком быстро, сумма квадратов ошибок стагнирует, обучение не происходит.

Генетический алгоритм строит популяцию вектора, представляющего нейронную сеть. Далее с ней проводятся три последовательные операции для улучшения работы сети:

— Выборка: после каждого прямого прохождения подсчитывается сумма квадратов ошибок, популяция нейронной сети ранжируется. Верхний процент популяции выбирается для выживания и используется для кроссовера.— Кроссовер: верхний x% генов популяции соревнуется между собой, получаем некое новое потомство, каждое потомство представляет, по сути, новую нейронную сеть.— Мутация: этот оператор требует поддержки генетического разнообразия в популяции, небольшой процент ее отбирается для прохождения мутации, то есть некоторые весы сети будут регулироваться случайно.

6. Нейронным сетям не всегда нужен большой объем данных

Нейронные сети могут использовать три основных обучающих стратегии: контролируемое обучение, неконтролируемое и усиленное обучение. Для первой, нужны, по крайней мере, два обучающих сета данных. Один из них будет состоять из входных с ожидаемыми выходными сигналами, второй с входными без ожидаемых выходных. Оба должны включать маркированные данные, то есть паттерны с изначально неизвестным предназначением.

Неконтролируемая стратегия обычно используется для выявления скрытых структур в немаркированных данных (например, скрытых цепей Маркова). Принцип работы тот же, что и у кластерных алгоритмов. Усиленное обучение основано на простом допущении о наличие выигрышных сетей и помещении их в плохие условия. Два последних варианта не подразумевают использование маркированных данных, поэтому правильный выходной сигнал здесь неизвестен.

Неконтролируемое обучение

Одна из самых популярных архитектур для такого типа сети – самоорганизующаяся карта. По сути, это техника масштабирования в нескольких измерениях, которая конструирует приближение функции плотности вероятности какого-либо основного цикла данных. Z – сохраняет топологическую структуру сета данных, картируя векторы входных сигналов – zi. Она взвешивает векторы — vj, в будущей карте V. Сохранение топологической структуры означает, что, если два вектора стоят близко друг к другу в Z, нейроны, к которым они относятся, также будут расположены в V. Более подробно можно почитать здесь.

Усиленное обучение

Эта стратегия состоит из трех компонентов: установки на то, как нейронная сеть будет принимать решения, используя технические и фундаментальные индикаторы, функции достижения цели, которая отделяет зерна от плевел, и функции значения, нацеленной на перспективу.

7. Нейронную сеть нельзя обучить на любых данных

Одна из главных проблем, почему нейронная сеть может не работать, заключается в том, что нередко данные плохо готовят перед загрузкой в систему. Нормализация, удаление избыточной информации, резко отклоняющихся значений должны проводиться перед началом работы с сетью, чтобы улучшить ее производственные возможности.

Мы знаем, что у нас есть слои перцептронов, соединенных по весу. Каждый перцептрон содержит функцию активации, который, в свою очередь, разделены по рангу. Входные сигналы должны быть масштабированы, исходя из этого ранга, чтобы сеть могла различать входные паттерны. Это предпосылки для нормализации данных.

Резко выделяющиеся значения или намного больше или намного меньше большинства других значений в наборе данных для сета. Такие вещи могут вызвать проблемы в применении статистических методов – регрессии и подгонки кривой. Потому что система постарается приспособить эти значения, производительность ухудшится. Выявить такие значения самостоятельно может быть проблематично. Здесь можно посмотреть инструкцию по техникам работы с резко отклоняющимися значениями.

Внесение двух или более независимых переменных, которые близко коррелируют друг с другом также может вызвать снижение способности к обучению. Удаление избыточных переменных, ко всему прочему, ускоряет время обучения. Для удаления избыточных соединений и перцептронов можно использовать адаптивные нейронные сети.

8. Нейронные сети иногда требуется обучать заново

Даже если вы настроили должным образом нейронную сеть, и она торгует успешно в выборке и за ее пределами, еще не значит, что через некоторое время она не перестанет работать. Дело не в ней, дело в том, как ведет себя финансовый рынок. Финансовые рынки – комплексные адаптивные системы. То, что работает сегодня, может не работать завтра. Эту их характеристику называют нестационарностью или динамической оптимизацией. Нейронные сети пока не умеют с этим справляться.

Динамическая среда финансовых рынков очень сложная штука для моделирования нейронной сетью. Есть два выхода из ситуации: время от времени переобучать сеть или использовать динамическую нейронную сеть. Она призвана отслеживать изменения в среде по времени и приспосабливать их к архитектуре и нагрузке системы. Для решения динамических проблем можно использовать многосторонние мета-эвристические алгоритмы оптимизации. Они будут отслеживать изменения к локальному опыту по времени. Один из вариантов – оптимизация множественного роя, производная от метода роя частиц. Генетические алгоритмы с улучшенной диверсификацией и памятью также могут быть полезны в динамичной среде.

9. Нейронная сеть – это не черный ящик

Сама по себе нейронная сеть – это «черный ящик». Это создает определенные проблемы для людей, которые работают или планируют с ней работать. Например, фондовые управляющие не понимают, как система принимает решения по финансовым операциям. Отсюда получается, что нельзя рассчитать риск трейдинговой стратегии, которой обучилась сеть. Опять же банки, использующие нейронную сеть для просчетов кредитных рисков, не могут верифицировать ее позиции по кредитному рейтингу для тех или иных клиентов. Для этих целей были придуманы алгоритмы извлечения правил работы сети. Знания могут быть вытащены из сети в виде математических формул, символической логики, нечеткой логики, дерева решений.

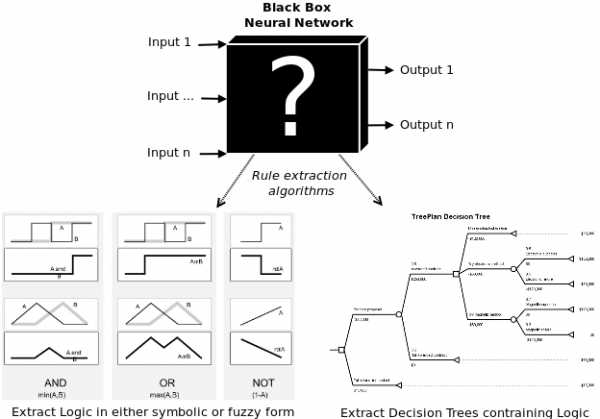
Математические правила: некоторые алгоритмы позволяют извлекать множественные строки линейной регрессии. Проблема в том, что зачастую они понятны только в контексте работы «черного ящика».

Пропозициональная логика: раздел математической логики, который имеет дело с дискретными значениями переменных. Эти переменные A и B чаще всего имеют значения «верно» — «неверно», но также могут иметь значения дискретного уровня – «покупать, «удерживать», «продавать».

К ним применимы логические операции: OR, AND и XOR. Результаты этих операция называются предикатами, количественные значения которых также можно рассчитать. Между предикатами и пропозициональной логикой есть различие. Если у нас простая нейронная сеть с ценой (P), простым скользящим средним (SMA), экспоненциальным скользящим средним (EMA) в качестве входных сигналов, и мы хотим извлечь тренд стратегии в пропозициональной логике, мы действуем по следующим правилам:

Нечеткая логика (fuzzy logic) – это то место, где встречается вероятность и пропозициональная логика. Последняя имеет дело с абсолютами – «купить», «продать», «верно», «неверно», 0 или 1. Трейдер никак не может подтвердить подлинность этих результатов. Нечеткая логика преодолевает это ограничение, вводя функцию членства, обозначающую принадлежность переменной к определенной области, домену. Например, компания (GOOG) имеет значение 0,7 в домене BUY и 0,3 в домене SELL. Комбинация такой логики и нейронной сети называется нейро-нечеткая система.

Дерево решений показывает, как принимаются решения при загрузке определенной информации. В этой статье можно почитать, как построить анализ безопасности дерева решения, используя генетическое программирование.

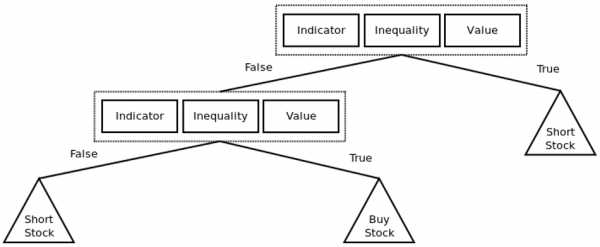
Пример простой стратегии онлайн-трейдинга, представленной в виде дерева решений. Треугольники представляют узлы решений (например, BUY, HOLD или SELL для покупки, удержания или продажи акций). Каждый элемент представляет собой пару

10. Нейронную сеть создать и применить нетрудно

Если говорить о практике, создать нейронную сеть с нуля довольно проблематично. К счастью, сейчас существуют сотни пакетов с открытым доступом, которые делают работу с нейронными сетями немного проще. Ниже приведен список таких пакетов, которые можно пользовать в количественном анализе в финансовой сфере. Список далеко не полный, инструменты даны в алфавитном порядке.

Caffe Сайт — http://caffe.berkeleyvision.org/ Репозиторий на GitHub — https://github.com/BVLC/caffe

EncogСайт — http://www.heatonresearch.com/encog/Репозиторий на GitHub — https://github.com/encog

h3OСайт — http://h3o.ai/Репозиторий на GitHub — https://github.com/h3oai

Google TensorFlowСайт — http://www.tensorflow.org/Репозиторий на GitHub — https://github.com/tensorflow/tensorflow

Microsoft Distributed Machine Learning TookitСайт — http://www.dmtk.io/Репозиторий на GitHub — https://github.com/Microsoft/DMTK

Microsoft Azure Machine LearningСайт — https://azure.microsoft.com/en-us/services/machine-learningРепозиторий на GitHub — github.com/Azure?utf8=%E2%9C%93&query=MachineLearning

MXNetСайт — http://mxnet.readthedocs.org/en/latest/Репозиторий на GitHub — https://github.com/dmlc/mxnet

NeonСайт — http://neon.nervanasys.com/docs/latest/index.htmlРепозиторий на GitHub — https://github.com/nervanasystems/neon

TheanoСайт — http://deeplearning.net/software/theano/Репозиторий на GitHub — https://github.com/Theano/Theano

TorchСайт — http://torch.ch/Репозиторий на GitHub — https://github.com/torch/torch7

SciKit LearnСайт — http://scikit-learn.org/stable/Репозиторий на GitHub — https://github.com/scikit-learn/scikit-learn

Заключение

Нейронные сети – это класс мощных алгоритмов машинного обучения. В их основе лежат статистические методы анализа. Вот уже много лет их с успехом применяют к разработке стратегий трейдинга и финансовых моделей. Несмотря на это, у нейронных сетей не очень хорошая репутация, основанная на неудачах практического применения. В большинстве случаев причины неудач лежат в неадекватных конструкторских решениях и общем непонимании того, как они работают. В этой статье автор попытался артикулировать лишь некоторые из самых распространенных заблуждений в надежде, что кому-нибудь эта информация пригодится в реальной практике.

     Вы уже сейчас можете записаться на Видео курс и научиться самому делать абсолютно любых зарабатывающих торговых роботов!   Можно записаться на следующий поток ОнЛайн курса, информацию по которому можно посмотреть тут:   Если же вам не хочется тратить время на обучение, то вы просто можете выбрать уже готовые роботы из тех, что представлены у нас!   Также можете посмотреть совершенно бесплатные наработки для МТ4, Квика, МТ5. Данный раздел также постоянно пополняется.

 Не откладывайте свой шанс заработать на бирже уже сегодня!       Договор-оферта

Читайте также:

    

daytradingschool.ru

от одного нейрона до глубоких архитектур / Хабр

Многие материалы по нейронным сетям сразу начинаются с демонстрации довольно сложных архитектур. При этом самые базовые вещи, касающиеся функций активаций, инициализации весов, выбора количества слоёв в сети и т.д. если и рассматриваются, то вскользь. Получается начинающему практику нейронных сетей приходится брать типовые конфигурации и работать с ними фактически вслепую.

В статье мы пойдём по другому пути. Начнём с самой простой конфигурации — одного нейрона с одним входом и одним выходом, без активации. Далее будем маленькими итерациями усложнять конфигурацию сети и попробуем выжать из каждой из них разумный максимум. Это позволит подёргать сети за ниточки и наработать практическую интуицию в построении архитектур нейросетей, которая на практике оказывается очень ценным активом.

Иллюстративный материал

Популярные приложения нейросетей, такие как классификация или регрессия, представляют собой надстройку над самой сетью, включающей два дополнительных этапа — подготовку входных данных (выделение признаков, преобразование данных в вектор) и интерпретацию результатов. Для наших целей эти дополнительные стадии оказываются лишними, т.к. мы смотрим не на работу сети в чистом виде, а на некую конструкцию, где нейросеть является лишь составной частью.

Давайте вспомним, что нейросеть является ничем иным, как подходом к приближению многомерной функции Rn -> Rn. Принимая во внимания ограничения человеческого восприятия, будем в нашей статье приближать функцию на плоскости. Несколько нестандартное применение нейросетей, но оно отлично подходит для цели иллюстрации их работы.

Фреймворк

Для демонстрации конфигураций и результатов предлагаю взять популярный фреймворк Keras, написанный на Python. Хотя вы можете использовать любой другой инструмент для работы с нейросетями — чаще всего различия будут только в наименованиях.

Самая простая нейросеть

Самой простой из возможных конфигураций нейросетей является один нейрон с одним входом и одним выходом без активации (или можно сказать с линейной активацией f(x) = x):N.B. Как видите, на вход сети подаются два значения — x и единица. Последняя необходима для того, чтобы ввести смещение b. Во всех популярных фреймворках входная единица уже неявно присутствует и не задаётся пользователем отдельно. Поэтому здесь и далее будем считать, что на вход подаётся одно значение.

Несмотря на свою простоту эта архитектура уже позволяет делать линейную регрессию, т.е. приближать функцию прямой линией (часто с минимизацией среднеквадратического отклонения). Пример очень важный, поэтому предлагаю разобрать его максимально подробно.

import matplotlib.pyplot as plt import numpy as np # накидываем тысячу точек от -3 до 3 x = np.linspace(-3, 3, 1000).reshape(-1, 1) # задаём линейную функцию, которую попробуем приблизить нашей нейронной сетью def f(x): return 2 * x + 5 f = np.vectorize(f) # вычисляем вектор значений функции y = f(x) # создаём модель нейросети, используя Keras from keras.models import Sequential from keras.layers import Dense def baseline_model(): model = Sequential() model.add(Dense(1, input_dim=1, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model # тренируем сеть model = baseline_model() model.fit(x, y, nb_epoch=100, verbose = 0) # отрисовываем результат приближения нейросетью поверх исходной функции plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True) plt.show() # выводим веса на экран for layer in model.layers: weights = layer.get_weights() print(weights) Как видите, наша простейшая сеть справилась с задачей приближения линейной функции линейной же функцией на ура. Попробуем теперь усложнить задачу, взяв более сложную функцию:def f(x): return 2 * np.sin(x) + 5 Опять же, результат вполне достойный. Давайте посмотрим на веса нашей модели после обучения:[array([[ 0.69066334]], dtype=float32), array([ 4.99893045], dtype=float32)] Первое число — это вес w, второе — смещение b. Чтобы убедиться в этом, давайте нарисуем прямую f(x) = w * x + b:def line(x): w = model.layers[0].get_weights()[0][0][0] b = model.layers[0].get_weights()[1][0] return w * x + b # отрисовываем результат приближения нейросетью поверх исходной функции plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=3, antialiased=True) plt.plot(x, line(x), color='yellow', linewidth=1, antialiased=True) plt.show() Всё сходится.

Усложняем пример

Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала. Как же захватить нейросетью нелинейность аппроксимируемой функции?

Давайте попробуем накидать побольше нейронов, скажем пять штук. Т.к. на выходе ожидается одно значение, придётся добавить ещё один слой к сети, который просто будет суммировать все выходные значения с каждого из пяти нейронов:

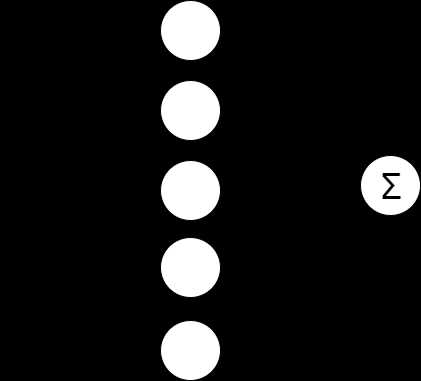def baseline_model(): model = Sequential() model.add(Dense(5, input_dim=1, activation='linear')) model.add(Dense(1, input_dim=5, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model Запускаем: И… ничего не вышло. Всё та же прямая, хотя матрица весов немного разрослась. Всё дело в том, что архитектура нашей сети сводится к линейной комбинации линейных функций:

f(x) = w1' * (w1 * x + b1) +… + w5' (w5 * x + b5) + b

Т.е. опять же является линейной функцией. Чтобы сделать поведение нашей сети более интересным, добавим нейронам внутреннего слоя функцию активации ReLU (выпрямитель, f(x) = max(0, x)), которая позволяет сети ломать прямую на сегменты:

def baseline_model(): model = Sequential() model.add(Dense(5, input_dim=1, activation='relu')) model.add(Dense(1, input_dim=5, activation='linear')) model.compile(loss='mean_squared_error', optimizer='sgd') return model Максимальное количество сегментов совпадает с количеством нейронов на внутреннем слое. Добавив больше нейронов можно получить более точное приближение: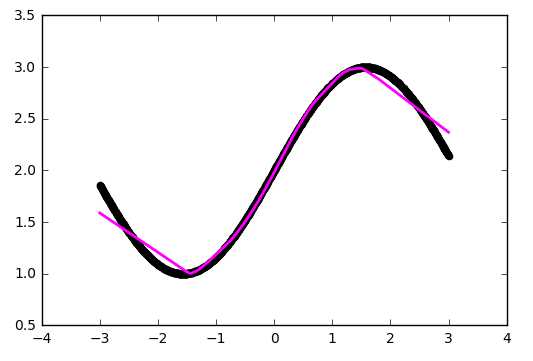

Дайте больше точности!

Уже лучше, но огрехи видны на глаз — на изгибах, где исходная функция наименее похожа на прямую линию, приближение отстаёт.

В качестве стратегии оптимизации мы взяли довольно популярный метод — SGD (стохастический градиентный спуск). На практике часто используется его улучшенная версия с инерцией (SGDm, m — momentum). Это позволяет более плавно поворачивать на резких изгибах и приближение становится лучше на глаз:

# создаём модель нейросети, используя Keras from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD def baseline_model(): model = Sequential() model.add(Dense(100, input_dim=1, activation='relu')) model.add(Dense(1, input_dim=100, activation='linear')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model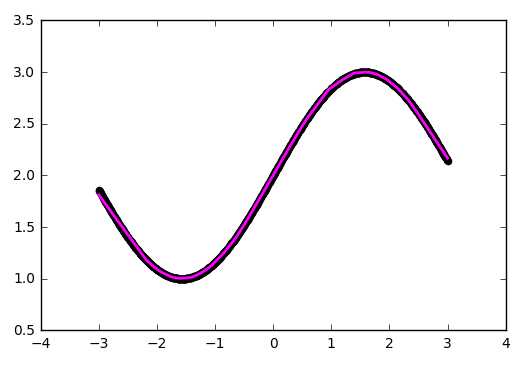

Усложняем дальше

Синус — довольно удачная функция для оптимизации. Главным образом потому, что у него нет широких плато — т.е. областей, где функция изменяется очень медленно. К тому же сама функция изменяется довольно равномерно. Чтобы проверить нашу конфигурацию на прочность, возьмём функцию посложнее:def f(x): return x * np.sin(x * 2 * np.pi) if x < 0 else -x * np.sin(x * np.pi) + np.exp(x / 2) - np.exp(0)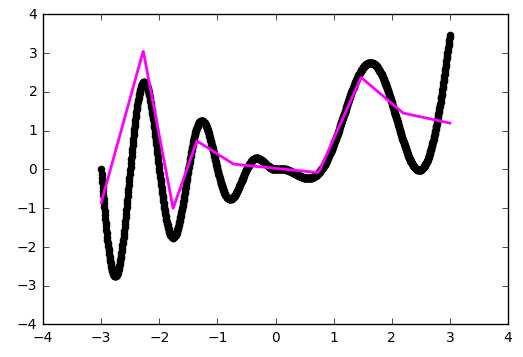 Увы и ах, здесь мы уже упираемся в потолок нашей архитектуры.

Дайте больше нелинейности!

Давайте попробуем заменить служивший нам в предыдущих примерах верой и правдой ReLU (выпрямитель) на более нелинейный гиперболический тангенс:def baseline_model(): model = Sequential() model.add(Dense(20, input_dim=1, activation='tanh')) model.add(Dense(1, input_dim=20, activation='linear')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model # тренируем сеть model = baseline_model() model.fit(x, y, nb_epoch=400, verbose = 0)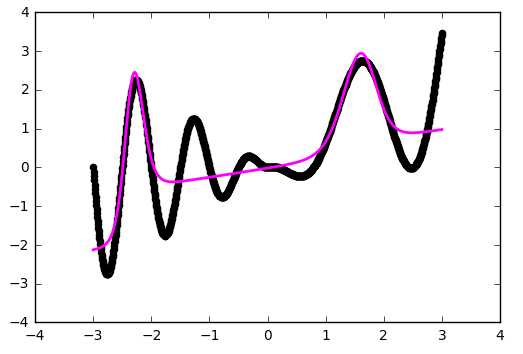

Инициализация весов — это важно!

Приближение стало лучше на сгибах, но часть функции наша сеть не увидела. Давайте попробуем поиграться с ещё одним параметром — начальным распределением весов. Используем популярное на практике значение 'glorot_normal' (по имени исследователя Xavier Glorot, в некоторых фреймворках называется XAVIER):def baseline_model(): model = Sequential() model.add(Dense(20, input_dim=1, activation='tanh', init='glorot_normal')) model.add(Dense(1, input_dim=20, activation='linear', init='glorot_normal')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model Уже лучше. Но использование 'he_normal' (по имени исследователя Kaiming He) даёт ещё более приятный результат:

Как это работает?

Давайте сделаем небольшую паузу и разберёмся, каким образом работает наша текущая конфигурация. Сеть представляет из себя линейную комбинацию гиперболических тангенсов:

f(x) = w1' * tanh(w1 * x + b1) +… + w5' * tanh(w5 * x + b5) + b

# с помощью матрицы весом моделируем выход каждого отдельного нейрона перед суммацией def tanh(x, i): w0 = model.layers[0].get_weights() w1 = model.layers[1].get_weights() return w1[0][i][0] * np.tanh(w0[0][0][i] * x + w0[1][i]) + w1[1][0] # рисуем функцию и приближение plt.scatter(x, y, color='black', antialiased=True) plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True) # рисуем разложение for i in range(0, 10, 1): plt.plot(x, tanh(x, i), color='blue', linewidth=1) plt.show() На иллюстрации хорошо видно, что каждый гиперболический тангенс захватил небольшую зону ответственности и работает над приближением функции в своём небольшом диапазоне. За пределами своей области тангенс сваливается в ноль или единицу и просто даёт смещение по оси ординат.

За границей области обучения

Давайте посмотрим, что происходит за границей области обучения сети, в нашем случае это [-3, 3]: Как и было понятно из предыдущих примеров, за границами области обучения все гиперболические тангенсы превращаются в константы (строго говоря близкие к нулю или единице значения). Нейронная сеть не способна видеть за пределами области обучения: в зависимости от выбранных активаторов она будет очень грубо оценивать значение оптимизируемой функции. Об этом стоит помнить при конструировании признаков и входных данный для нейросети.

Идём в глубину

До сих пор наша конфигурация не являлась примером глубокой нейронной сети, т.к. в ней был всего один внутренний слой. Добавим ещё один:def baseline_model(): model = Sequential() model.add(Dense(50, input_dim=1, activation='tanh', init='he_normal')) model.add(Dense(50, input_dim=50, activation='tanh', init='he_normal')) model.add(Dense(1, input_dim=50, activation='linear', init='he_normal')) sgd = SGD(lr=0.01, momentum=0.9, nesterov=True) model.compile(loss='mean_squared_error', optimizer=sgd) return model Можете сами убедиться, что сеть лучше отработала проблемные участки в центре и около нижней границы по оси абсцисс:Пример работы с одним внутренним слоемN.B. Слепое добавление слоёв не даёт автоматического улучшения, что называется из коробки. Для большинства практических применений двух внутренних слоёв вполне достаточно, при этом вам не придётся разбираться со спецэффектами слишком глубоких сетей, как например проблема исчезающего градиента. Если вы всё-таки решили идти в глубину, будьте готовы много экспериментировать с обучением сети.

Количество нейронов на внутренних слоях

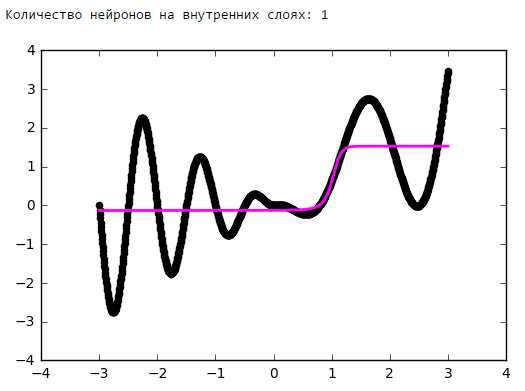
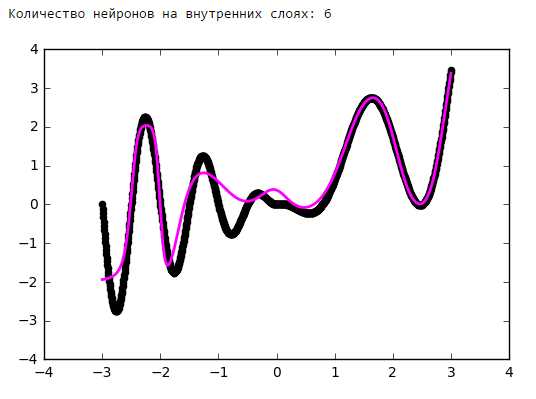
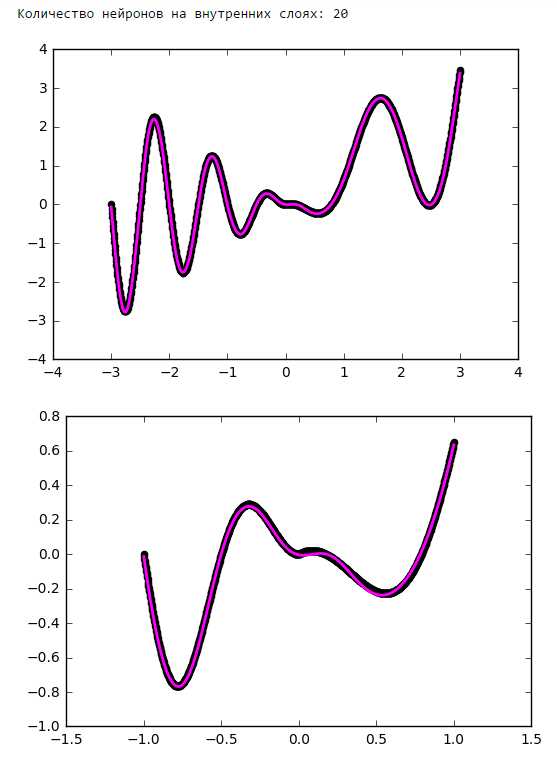
Просто поставим небольшой эксперимент: 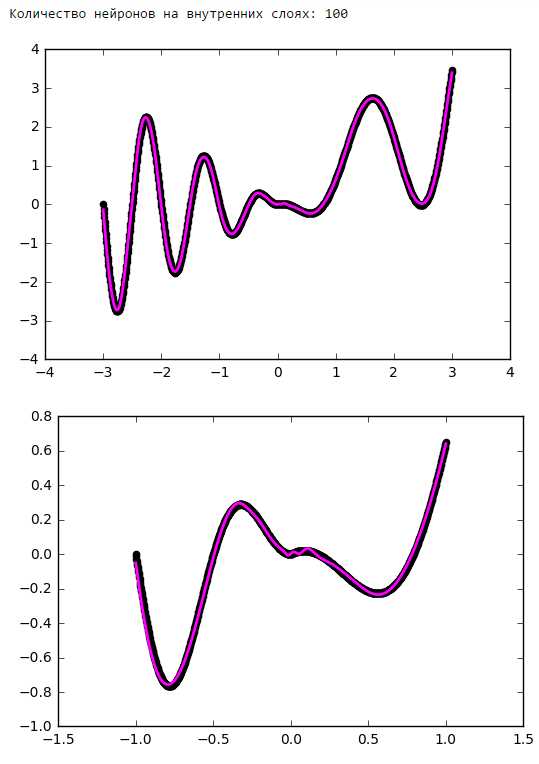Начиная с определённого момента добавление нейронов на внутренние слои не даёт выигрыша в оптимизации. Неплохое практическое правило — брать среднее между количеством входов и выходов сети.

Количество эпох

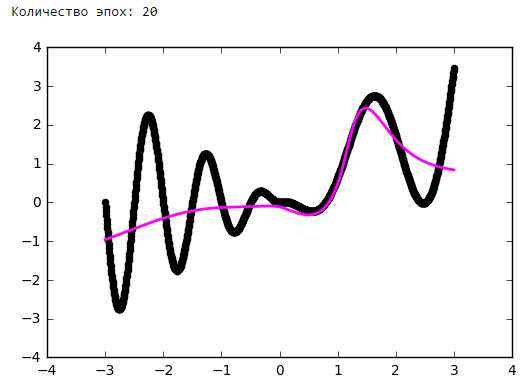
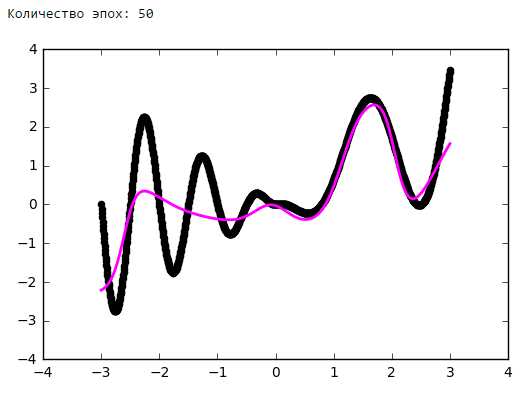
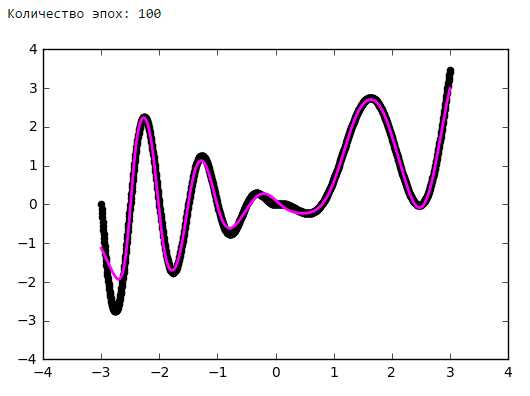
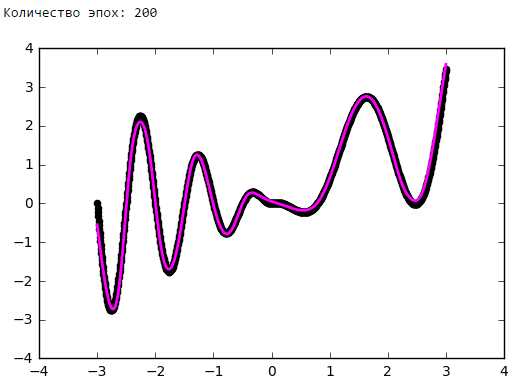
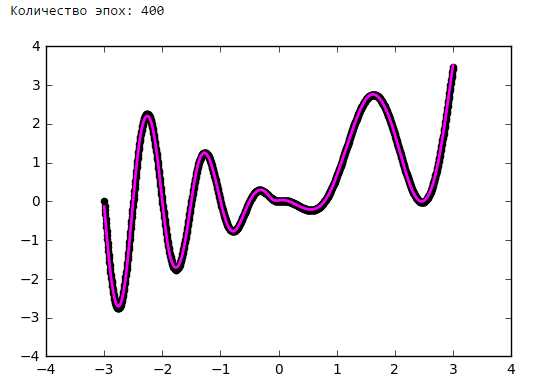
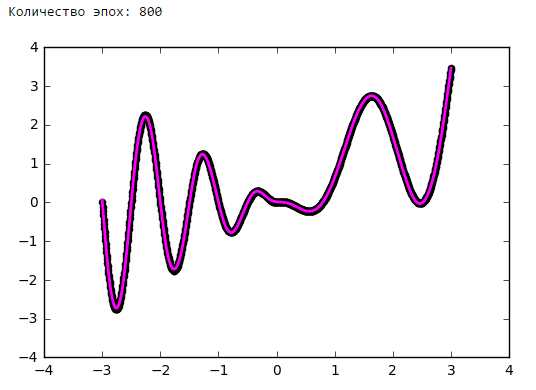
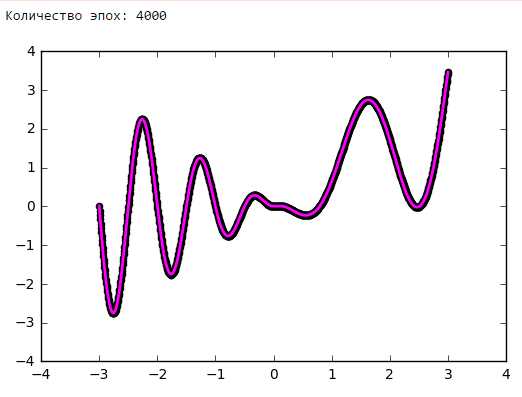
Выводы

Нейронные сети — это мощный, но при этом нетривиальный прикладной инструмент. Лучший способ научиться строить рабочие нейросетевые конфигурации — начинать с более простых моделей и много экспериментировать, нарабатывая опыт и интуицию практика нейронных сетей. И, конечно, делиться результатами удачных экспериментов с сообществом.

habr.com

---

• 
  Методы черной оптимизации сайтов
• 
  Оптимизации сайтов список работ
• 
  Оптимизация и поддержка сайтов
• 
  Что такое клиентская оптимизация
• 
  Яндекс директ оптимизация кампании
• 
  Инструменты для оптимизации сайтов
• 
  Оптимизация структуры капитала предприятия
• 
  Дефрагментация диска и оптимизация
• 
  Советы по оптимизация сайта
• 
  В целях оптимизации работы
• 
  Оптимизация сайт своими руками

Prostoy-Site | Все права защищены © 2018 | Карта сайта