Методы оптимизации управления для менеджеров - Зайцев М.Г.. Методы оптимизации управления для менеджеров компьютерноориентированный подход. Методы оптимизации управления для менеджеров зайцев

Методы оптимизации управления для менеджеров - Зайцев М.Г

которое, если сократить обе части на 100, приводится к виду

2Х1 + Х2=100

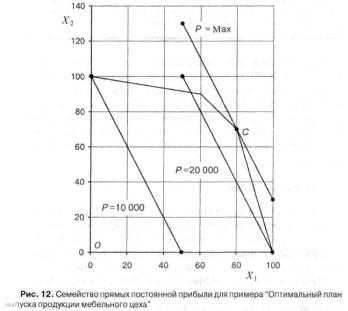
График этой линии внутри области допустимых планов показан на рис. 12. На этом же рисунке показан участок линии, содержащий планы, для которых достигается ежедневная прибыль Р=20000:

(20000 = 200Х1 + 100Х2 →2Х1 + Х2=200).

Видно, что эти линии параллельны. Таким образом, становится ясно, что графическим изображением уравнения для прибыли является семейство параллельных прямых (две из которых показаны на рис. 12). Причем, чем больше прибыль Р, тем правее расположена линия, содержащая планы, отвечающие этой прибыли.

Очевидно, что максимум прибыли достигается в угловой точке С области допустимых планов. Прямая, проходящая через эту точку, - последняя из семейства прямых прибыли, которая имеет хотя бы одну общую точку с областью допустимых планов. Все прямые, лежащие правее ее (отвечающие большим значениям прибыли), целиком находятся вне области допустимых планов.

В данном случае оптимальный план (точка С) лежит на пересечении границ ресурсов "труд" и "ДСП". Ресурс "стекло" при этом расходуется не полностью. Это означает, что координаты точки, соответствующей оптимальному плану, одновременно удовлетворяют уравнениям двух линий, изображающих предельные расходы ресурсов "труд" и "ДСП":

3,5Х1 + Х2=350

Х1 + Х2=150

Решив эту систему уравнений (например, выразив Х1 из второго уравнения и подставив его в первое), нетрудно получить значения Х1=80, Х2 = 70, которые и были получены при решении этой задачи с помощьюMS-Excel.

Следует заметить, что подобное графическое решение очень трудно провести для задач с тремя переменными решения. В этом случае область допустимых планов представляет собой многогранник сложной формы в 3-мерномпространстве. Что же касается задач с числом переменных более трех, то графически изобразить область допустимых планов вообще нельзя, поскольку это многогранник в многомерном пространстве.

Таким образом, графическое решение никоим образом нельзя рассматривать как практический метод решения задач линейного программирования. Однако проведенный графический анализ дает очень важное интуитивное представление о том, где находится оптимальный план-решениезадачи линейной оптимизации.

Оптимум (максимум или минимум) целевой функции достигается в одной из угловых точек области допустимых планов. Эта точка является пересечением границ тех ресурсов, которые при оптимальном плане расходуются полностью.

Исключение из этого правила составляют случаи, когда линии постоянной прибыли параллельны границе области допустимых планов, соответствующей предельному расходу одного из ресурсов (см. рис. 12). В таких случаях существует бесконечно много планов, отвечающих оптимальному значению целевой функции. (В многомерном случае говорят, что "гиперплоскость" постоянной прибыли параллельна гиперплоскости — границе одного из ресурсов.)

Симплекс-метод

Сделанный вывод на первый взгляд позволяет предложить простой метод решения задач линейного программирования: надо просто "перебрать" все угловые точки области допустимых планов, в каждой из них вычислить значение целевой функции и выбрать ту угловую точку, где целевая функция оптимальна.

Однако количество угловых точек области допустимых планов растет очень резко с ростом числа переменных и особенно числа ограничений. Так, для небольшой задачи линейного программирования с 20 переменными и 10 ограничениями число угловых точек составляет около 30 млн., а для задачи с 100 переменными и 20 ограничениями это число может достигать 47 трлн. (47х1012). Чтобы сосчитать значения целевой функции во всех этих точках, компьютеру, выполняющему миллион арифметических операций в секунду, потребуется около года непрерывной работы. Вместе с тем ваш персональный компьютер, используя надстройку "Поиск решения"MS-Excel,решит такую задачу за доли секунды. Дело, разумеется, в том, чтоMS-Excelиспользует эффективные алгоритмы решения задач. Эти алгоритмы не перебирают все угловые точки подряд, а, начав с любой из них, выбирают каждую последующую так, чтобы значение целевой функции и ней было гарантированно ближе к оптимальному.

Первый такой алгоритм, называемый симплекс-методом,был предложен американским математиком Джорджем Данцигом в 1947 г. С тех пор появились различные модификации этого алгоритма, ускоряющие сходимость алгоритма к оптимальному решению. Кстати, симплекс (лат. simplex) означает замкнутую область и многомерном пространстве (область допустимых планов).

Как меняется оптимальное решение при изменении целевых коэффициентов?

На рис. 13 показано, как меняется наклон семейства прямых постоянной прибыли, если уменьшать прибыль от продажи одно-iо шкафа от 200 до 150 и далее до 50 у.е.

Очевидно, что изменение наклона прямых постоянной прибыли от 200 до 150 у.е. (и даже до 100 у.е.) не приведет к изменению оптимального решения. По-прежнемупоследней точкой области допустимых планов, которой коснется прямая максимальной прибыли, будет точкаС. Отсюда следует важный вывод:

Существует определенный интервал устойчивости, в котором изменение целевых коэффициентов не приводит к изменению оптимального решения.

Разумеется, значение максимума прибыли при изменении целевого коэффициента меняется, но оптимальный план остается абсолютно тем же.

Однако при дальнейшем уменьшении прибыли от продажи одного шкафа (до 50 у.е.) последней точкой, которой касается прямая постоянной прибыли при ее движении в сторону больших значений прибыли, станет точка В. При этом резко изменится оптимальный план и соответствующее значение максимальной прибыли.

Таким образом, если значение целевого коэффициента выходит за пределы интервала устойчивости, оптимальное решение резко изменяется, переходя в совершенно другую угловую точку области допустимых планов. Предсказать, в какую именно, невозможно. Для этого нужно заново решить задачу линейного программирования с новыми параметрами.

Отчет об устойчивости

В процессе поиска оптимального решения MS-Excelформирует так называемы отчет об устойчивости, в котором, в частности, выдает интервал изменений коэффициентов целевой функции, внутри которого их изменение не приводит к изменению оптимального решения. Для получения этого отчета, после того как "Поиск решения" нашел оптимальное решение, нужно в окне "Результаты поиска решения", перед тем как нажать на кнопку Ok, щелкнуть мышкой по строке "Устойчивость" в списке "Тип отчета" (см. рис. 6). Тогда после нажатия на кнопку OkMS-Excelсоздаст дополнительный лист "Отчет об устойчивости". Распечатку такого отчета для задачи об оптимальном плане выпуска продукции мебельного цеха дана на рис 14.

Первая таблица отчета об устойчивости "Изменяемые ячейки содержит столбцы "Целевой коэффициент", "Допустимое увеличение" и "Допустимое уменьшение". В первом из них даны исходные значения целевых коэффициентов: прибыль от продажи одного шкафа (200 у.е.) и одной тумбы (100 ух.). Второй и третий столбцы содержат информацию об интервале устойчивости найденного оптимального решения. При увеличении прибыли от продажи шкафа до 350 у.е. (на 150 у.е.

больше исходного значения) и при ее уменьшении до 100 у.е. оптимальное решение не изменяется. Аналогично второй целевой коэффициент может изменяться в пределах от 57,14 у.е. (уменьшение на 42,86 у.е. относительно исходного значения) до 200 у.е.

Смысл столбца "Нормированная стоимость" мы прокомментируем позже.

Во второй таблице отчета об устойчивости - "Ограничения" аналогичные интервалы устойчивости установлены для запасов ресурсов "ДСП", "стекло", "труд" (столбцы "Ограничения, правая часть", "Допустимое увеличение" и "Допустимое уменьшение"). Однако смысл этих интервалов несколько иной. При изменении запасов ресурсов оптимальное решение будет изменяться непрерывно (как можно увидеть, анализируя рис. 11), При движении границ ресурсов координаты угловой точки, очевидно, будут непрерывно меняться, но до тех пор, пока решение будет оставаться в той же угловой точке области допустимых планов, будет оставаться неизменной так называемая теневая цена ресурса - важнейшая характеристика оптимального решения. Для того чтобы понять, что это такое, необходимо рассмотреть так называемую двойственную задачу к задаче об оптимальном плане выпуска продукции мебельного цеха.

Упражнение по использованию отчета об устойчивости: влияние изменений в ценовых коэффициентах

В этом упражнении вы имеете возможность проверить правильность данных, приведенных в отчете об устойчивости к задаче об оптимальном плане выпуска продукции мебельного цеха.

I. Решите задачу об оптимальном плане выпуска продукции мебельного цеха (рис. 1) и получите отчет об устойчивости. II. Измените коэффициенты целевой функции (в ячейках С9, D9) и с помощью надстройки "Поиск решения" найдите,

как изменится решение (Х1,Х2) и значение целевой функции.

Результаты впишите в пустые рамки (см. ниже). 1. Увеличить норму прибыли при производстве шкафа на 100 у.е.

2.Увеличить норму прибыли при производстве шкафа на 160 у.е.

3.Уменьшить норму прибыли при производстве тумбы на 40 у.е.

4.Уменьшить норму прибыли при производстве тумбы на 50 у.е.

В некоторых случаях решение (Х1,Х2) не меняется, в других-изменяется.

Как это объяснить с помощью данных таблицы "Изменяемые ячейки" отчета Excel об устойчивости?

III. Для последнего случая (п. 1.4) сделайте новый отчет об устойчивости. Обратите внимание, что в колонке "Нормированная стоимость" таблицы "Изменяемые ячейки" для тумбы появилось отрицательное число.

Попробуйте выяснить, что оно означает.

Для этого увеличьте прибыль от продажи тумбы на величину, слегка превышающую по модулю это отрицательное число, и решите задачу еще раз. Что произошло? Каков смысл данных в колонке "Нормированная стоимость" таблицы "Изменяемые ячейки" отчета Excel об устойчивости?

Если продукт входит в оптимальный план, в колонке "Нормированная стоимость" отчета об устойчивости для этого продукта стоит 0. Если продукт не входит в оптимальный план, в этой колонке стоит отрицательное число, показывающее, на сколько (по абсолютной величине) нужно увеличить прибыль от производства единицы этого продукта, чтобы он вошел в оптимальный план.

3.2. Двойственная задача. Теневые цены

Для любой задачи линейного программирования можно сформулировать задачу-двойник,или, иначе, двойственную задачу. Этазадача-двойникявляется своеобразным ''зеркальным отражением‖ исходной задачи, поскольку ее формулировка использует те же параметры, что и исходная задача, а ее решение может быть получено одновременно с решением исходной задачи. Фактически при решении исходной задачисимплекс-методомодновременно решается и двойственная задача, и наоборот. Следует также отметить, что исходная и двойственная задачи совершенно симметричны. Если двойственную задачу рассматривать как исходную, то исходная будет для нее двойственной.

Одной из важнейших "зеркальных" связей между исходной и двойственной задачами является связь "переменные решения - теневые цены ресурсов". Для того чтобы уловить эту связь, сформулируем содержательно двойственную задачу к знакомой нам задаче об оптимальном плане выпуска продукции мебельного цеха.

Постановка двойственной задачи к задаче об оптимальном плане выпуска продукции мебельного цеха

Пусть имеется покупатель на все ресурсы, используемые для выпуска продукции мебельного цеха (ДСП, стекло и труд). Таблица параметров та же, что и для исходной задачи (табл. 5).

Какие цены на эти ресурсы нужно назначить, чтобы продать их было выгоднее, чем производить продукцию? Какую минимальную сумму можно выручить от продажи ресурсов при этом условии?

Таблица 5 Параметры задачи

	Ресурсы	Запасы	Продукты
			Шкаф	Тумба
	ДСП	350	3,5	1

Стекло	240	1	2
Труд	150	1	1
Прибыль		200	100

Поскольку в этой задаче три вида ресурсов, то переменных решения, очевидно, должно быть тоже три. Это цены, которые назначает производитель при продаже,

1	м ДСП	Y1,
1	м стекла	Y2,

1 дня труда рабочего цеха - Y3.

Сразу заметим, что эти цены называются теневыми. Они, разумеется, не могут иметь никакого отношения к рыночным ценам на данные ресурсы, поскольку, как будет видно из решения, никаких рыночных (или внерыночных) механизмов формирования цен на данные ресурсы в решении не рассматривается.

Теневые цены характеризуют ценность ресурсов для производителя.

Целевая функция - это, очевидно, прибыль, которую получит производитель - продавец ресурсов, если продаст по этим ценам все имеющиеся ресурсы. Таким образом, целевая функция, записанная в таблице элементов модели, - это сумма произведений искомых цен Y1, Y2, Y3 на запасы имеющихся ресурсов, приведенных в соответствующем столбце таблицы параметров задачи. Разумеется, интерес продавца ресурсов состоит в том, чтобы продать их подороже. Однако интерес покупателя в том, чтобы купить подешевле.

Решение данной задачи позволит продавцу определить нижние границы цен на ресурсы, которые он может назначить, чтобы прибыль от их продажи была не ниже, чем прибыль от производства товаров на основе этих ресурсов. Целевую функцию данной задачи можно также рассматривать как издержки покупателя ресурсов, которые необходимо минимизировать, приняв во внимание интересы производителя - продавца ресурсов.

Цель производителя - продавца ресурсов - найти минимальное значение суммарной выручки от продажи всех ресурсов при условии, что продать их было бы не менее выгодно, чем производить из них продукцию.

Соответственно при записи ограничений в таблице элементов модели (табл. 6) использован тот же принцип. Если производить (продавец ресурсов) хочет продать 3,5 м ДСП, 1 м стекла и I день труда рабочего, то он должен получить не меньше, чем прибыль от производства одного шкафа (на который, согласно данным таблицы параметров, и идут все эти ресурсы). Аналогично если он хочет продать 1 м ДСП, 2 м стекла и 1 день труда рабочего он должен получить не меньше, чем прибыль от производства одной тумбы.

Таблица 6 Элементы модели

Переменные решения	Целевая функция
Y1 – цена 1 м ДСП
Y2 – цена 1 м стекла	C=350Y1 +240Y2+150Y3

Y2 – цена 1дня труда рабочего цеха

Ограничения

3,5Y1 +1Y2+1Y3 ≥200

1Y1 +2Y2+1Y3 ≥200 Y1, Y2, Y3 ≥0

Симметрия исходной и двойственной задач хорошо видна из исходной таблицы параметров и элементов решения этих двух задач (табл. 7). Как видно из этой таблицы, в исходной задаче две переменные и три ограничения; в двойственной – наоборот: три переменные и два ограничения. Исходная задача – это задача на максимум прибыли производителя продуктов; двойственная – на минимум издержек покупателя ресурсов.

Целевая функция исходная задача формируется как сумма произведений строки переменных (количеств продуктов разного типа Х1,Х2) на строку прибылей от производства единицы каждого продута; целевая функция двойственной задачи – как сумма произведений столбца переменных (теневых цен ресурсов Y1, Y2, Y3) на столбец запасов этих ресурсов.

Аналогично ограничение на расходы каждого из используемых ресурсов в исходной задаче формируется как сумма произведений строки переменных (X1, X2) на расход данного ресурса при производстве единиц каждого продукта. Ограничение на выручку от продажи ресурсов, идущих на производство данного продукта в двойственной задаче, формируется как сумма произведений столбца переменных решений (Y1, Y2, Y3) на столбец расходов каждого из используемых ресурсов на производство единицы данного продукта.

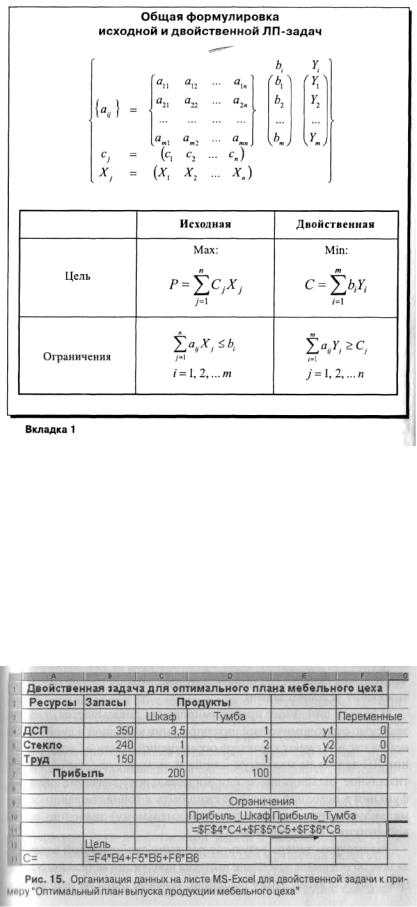
Эта симметрия проявляется и при сопоставлении более общих формулировок исходной и двойственной задач, когда n продуктов может быть произведено из m ресурсов (вкладка 1).

Здесь матрица {aij} может быть интерпретирована как расход каждогоi-горесурса на единицуj-гопродукта.

Строка целевых коэффициентов cj тогда представляет собой величину прибыли на единицуj-гопродукта. Строка переменных Xj – количество производимых единицj-гопродукта.

Решение двойственной задачи об оптимальном плане выпуска продукции мебельного цеха с помощью

MS-Excel

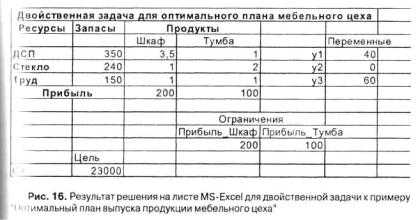
I. Организуйте данные так, как показано на рис. 15 "Двойственная задача к задаче об оптимальном плане выпуска продукции мебельного цеха".

1.Формула в ячейке В13 для целевой функции означает:

С = 350Y1+240Y2+150Y3.

2.Формула в ячейке D11 - это выражение для левой части первого ограничения 3,5Y1 +1Y2+1Y3. He забудьте сделать адреса ячеек, в которых содержатся переменные, абсолютными ($ перед буквенным обозначением столбца и номером ряда можно получить, нажав на функциональную клавишу F4 на клавиатуре компьютера).

3.Протяните формулу в ячейке D11 на ячейку Е11.

II. Вызовите "Поиск решения":

1.Целевая ячейка: В13 -Мин.

2.Изменяя ячейки: F4:F7.

3. Ограничения:

D11≥C7 (т.е. 3,5Y1 +Y2+Y3 ≥200)

E11≥D7 (т.е. Y1 +2Y2+Y3 ≥200) F4:F7 (т.е. Y1, Y2, Y3 ≥0)

4. He забудьте отметить в параметрах минимизации, что это линейная модель.

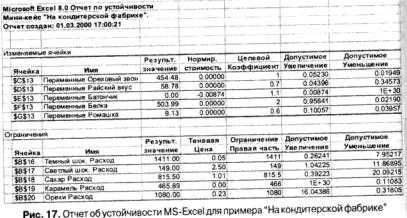
III. Решение двойственной задачи представлено на рис. 16.

Обратите внимание, что цена ресурса "стекло" Y2 = 0. Подумайте почему.

Анализ решения двойственной задачи

Прежде всего обратим внимание на то, что значение минимальной выручки при продаже ресурсов Cmin в точности совпадает со значением максимальной прибыли при производстве Рmах. ЭТОТ результат следует из содержательной постановки нашей двойственной задачи. Действительно, если бы получилось, что эта выручка меньше, чем прибыль от производства, то это значило бы, что продавать ресурсы менее выгодно, чем производить из них продукцию. А если бы выручка от продажи ресурсов оказалась больше, чем прибыль от производства, то это значило бы, что теневые цены на ресурсы не минимальны. И то и другое противоречит условию задачи.

В теории линейного программирования доказывается, что независимо от экономической интерпретации исходной и двойственной задач, а также от характера ограничений (< или >), если решение ЛП-задачина максимум или на минимум существует, то оптимальное (максимальное или минимальное) значение целевой функции в исходной задаче должно быть в точности равно оптимальному (минимальному или максимальному) значению целевой функции двойственной задачи.

Рассмотрим теперь результат решения двойственной задачи к задаче об оптимальном плане выпуска продукции мебельного цеха (рис. 16). Согласно этому решению, теневые цены на используемые ресурсы "ДСП", "стекло" и "труд" равны соответственно Y1=40; Y2=0; Y3=60.

Бросается в глаза нулевая цена второго ресурса - "стекло". Что это значит? Разумеется, рыночная цена на товар не может равняться нулю. Разумеется, если производитель - продавец ресурсов и отдаст стекло по цене ниже рыночной, он никогда не отдаст это задаром. Однако, как уже отмечалось выше, при решении двойственной задачи мы получаем не рыночные, а особые, теневые цены, которые характеризуют ценность данного ресурса для данного производителя в конкретной производственной ситуации.

С этой точки зрения нетрудно понять, что нулевое значение и теневой цены стекла обусловлено тем обстоятельством, что при минимальном плане выпуска продукции мебельного цеха ежедневные запасы стекла избыточны (см. рис. 7,12). Каждый день из 240 м стекла производитель использует только 220 м. Если предположить себе, что производитель ежедневно складирует эти излишки, то получается, что стекло ему просто некуда девать.

Предложенную выше экономическую интерпретацию (продавец производственных ресурсов) было удобно использовать на старой формулировки двойственной задачи о мебельном цехе. Для практического использования теневых цен в решении задач оптимального управления необходимо связать ценность ресурсов (теневые цены) и прибыль от производства. Это нетрудно сделать.

Допустим, что величины запасов одного из ресурсов b1 = 350, b2= 240 и b3= 150 (например, ДСП) увеличились на малую величину b1=1. Коэффициенты b1, b2 и b3 – это целевые коэффициенты в двойственной задаче. Согласно анализу, который мы провели выше для исходнойЛП-задачи,при изменении целевых коэффициентов существует некоторый интервал устойчивости. Если значение изменяемого целевого коэффициента остается внутри этого интервала устойчивости, то оптимальное решение не изменяется.

Допустим, что интервал устойчивости в нашей двойственной задаче достаточно большой, так что увеличение запасов всех ресурсов на единицу не приводит к изменению теневых цен Y1,Y2, Y3 (которые для двойственной задачи как раз и представляют собой оптимальное решение). Мы проверим позже, что это так и есть для нашей задачи.

Тогда очевидно, что минимальное значение выручки от продажи всех ресурсов увеличится (поскольку теперь продается

не 350 м ДСП, а 351 м) и составит C'minc= Cmin+ b1Y1, где C'minc - новое значение выручки, a Cmin - старое значение. Поскольку, согласно общему соотношению между прямой и двойственнойЛП-задачами,минимальное значение целевой

функции в двойственной задаче (в нашем случае Cmin) всегда равно максимальному значению целевой функции в исходной задаче (в нашем случае - прибыли от производстваРтах), то это означает, что увеличение запаса ДСП на величину b1 приведет к увеличению прибыли от производства Рmах.

Таким образом, можно записать, что если увеличить какой-либоi-йресурс, используемый для производства продукции, на величину bi (не выходя за пределы интервала устойчивости), то это приведет к увеличению прибыли Pmax= bi Yi.

Полученная простая формула, связывающая изменение максимальной прибыли (в исходной задаче) с изменением одного из ресурсов и теневой ценой ресурса (из двойственной задачи), является важнейшим соотношением двойственности и демонстрирует основную ценность теневых цен для менеджера.

Теневая цена ресурса показывает, насколько увеличится прибыль от производства при увеличении данного ресурса на единицу.

Ясно, что если запасы ресурса избыточны (т.е. не полностью используются при оптимальном плане производства), то теневая цена такого ресурса должна быть равна нулю, поскольку увеличение запасов такого ресурса не приведет к увеличению прибыли, а только увеличит неиспользованный остаток.

Следует подчеркнуть, что теневые цены ресурсов будут изменяться, если изменение любого параметра ЛП-задачивыйдет за пределы интервала устойчивости. Понятно, например, что если уменьшить ежедневный запас стекла b2 до

величины, меньшей, чем 220 м (см. рис. 7, 12), то дальнейшее его уменьшение скажется на прибыли, т.е. теневая цена стекла Y2 перестанет быть равной нулю.

Как уже отмечалось, при решении симплекс-методомисходной задачи сразу же решается и двойственная. Если "Поиск решения"MS-Excelполучил решение задачи об оптимальном плане продукции, то он нашел и теневые цены ресурсов. Никаких дополнительных операций по решению двойственной задачи на Практике делать не нужно. Полученные нами значения двойственных цен ресурсов мебельного цеха Y1=40; Y2=0; Y3=60 можно найти в колонке ―Теневые цены‖ таблицы "Ограничения" отчета об устойчивости для прямой задачи об оптимальном плане выпуска продукции (рис. 14).

Приведенная в этой таблице информация - теневые цены и интервал устойчивости изменения запасов каждого из ресурсов, в котором значения теневых цен сохраняются, - помогает менеджеру не решая задачи заново, оценить, запасы какого ресурса нужно увеличивать, чтобы максимально увеличить прибыль, и какое будет увеличение прибыли при заданном изменении данного запаса.

Упражнение по использованию отчета об устойчивости: влияние изменений в правых частях ограничений

Для того чтобы освоиться с новым понятием теневых цен и научиться их правильно использовать для управленческого анализа организации производства, проделайте следующее упражнение.

I. Решите задачу об оптимальном плане выпуска продукции мебельного цеха (рис. 1) и получите отчет об устойчивости. II. Переключитесь на вновь созданный лист отчета об устойчивости. Найдите в таблице "Ограничения" колонку

"Теневые цены", рассчитайте изменение целевой функции при изменении ресурса bi по формуле P= bi Yi и занесите результат в третью колонку данной таблицы для перечисленных случаев изменения запаса ресурсов:

III.Вновь переключитесь на лист, содержащий прямую задачу о продукции мебельного цеха. Изменяя лимиты ресурсов (в ячейках В6:В8) в соответствии с п. И, каждый раз вызывая "Поиск решения" и заново решая оптимизационную задачу, прямым рас четом найдите изменение целевой функции и переменные решения в случаях 1-5п. II и запишите эти изменения

вчетвертую колонку таблицы.

Водних случаях результаты вашего предварительного расчета (третья колонка) совпадают с решением с помощью ни стройки "Поиск решения" (четвертая колонка), а в других нет. Почему?

Вкачестве справочного материала приведем комментарии к отчету об устойчивости MS-Excel,а также перечислим основные отношения двойственности. Пункты I, II.1, II.2, III соотношения двойственности могут быть проверены на примере задачи о мебельном цехе. Пункты II.3, II.4 удобнее проверить позднее, при анализемини-кейса"На кондитерской фабрике".

Комментарии к отчету об устойчивости MS-Excel

I. Влияние изменения запаса ресурсов (правых частей ограничений - bi)

1. Отчет Excel об устойчивости включает таблицу "Ограничения" и в ней колонку "Теневая цена" (Shadow Price). Теневые цены -этооценки двойственной задачи. Они показывают, как меняется целевая функция при малом изменении bi:

P= bi Yi.

2.Эти оценки верны только в пределах устойчивости решения, т.е. пока изменение bi;. не изменяет угловую точку области допустимых решений, в которой достигается максимум целевой функции (при этом численные значения переменных решениях, конечно, изменяются). При выходе bi за пределы устойчивости все теневые цены изменятся.

3Пределы изменения bi, в которых оптимальное решение соответствует той же самой угловой точке, также даны в таблице "Ограничения" ("Допустимое увеличение" и "Допустимое уменьшение").

a) Причем если ресурс используется полностью (дефицитный), существует как верхний, так и нижний предел.

b) Если же ресурс используется не полностью, верхний предел устойчивости равен бесконечности (Excel пишет 1Е+30, что означает 10+30, максимально известное программе число).

4Следует понимать, что пределы устойчивости для изменения bi даются при условии, что все остальные значения правых частей bк (при k≠i) остаются неизменными. Одновременное изменение двух и более коэффициентов(bi и bк)} каждого внутри своего интервала устойчивости, может привести к изменению теневых цен.

5.Для оценки влияния одновременного изменения нескольких значений bi следует вычислить относительные изменения bi/max bi, где max bi - это предел либо увеличения, либо уменьшения bi (в зависимости от знака ЛЬ), и вычислить сумму

этих относительных изменений. При этом, если эта сумма больше 1, теневые цены изменятся, если меньше - нет.

II. Влияние изменений в коэффициентах целевой функции

1.Изменение коэффициентов целевой функции сj не изменяет вида области допустимых решений. Оно изменяет наклон семейства прямых, изображающих целевую функцию.

2.До тех пор пока изменение наклона не превышает некоторых пределов, оптимальное решение {Xj} вообще не меняется (максимальное значение целевой функции при этом, конечно, меняется).

3.При выходе значений коэффициента сj за эти пределы решение скачком перемещается в другую угловую точку области допустимых решений (при этом решение {Хj} может измениться очень сильно).

4."Допустимое увеличение" и "Допустимое уменьшение" для каждого коэффициента целевой функции сj, при которых оптимальное решение не изменяется, приведены в таблице "Изменяемые ячейки" отчета Excel об устойчивости.

a) Причем если Xj > 0 (продукт входит в оптимальный план), то имеется как верхний, так и нижний предел для изменения соответствующегоj-гокоэффициента целевой функции.

b) Если же Хj=0, то "Допустимое уменьшение" может быть как угодно велико - продукт все равно не войдет в оптимальный план. Верхний предел "Допустимое увеличение" показывает, насколько нужно увеличить соответствующий целевой коэффициент, чтобыj-йпродукт вошел в оптимальный план.

c) Величина, противоположная этому увеличению, называется Нормированная стоимость (Reduced Cost) и показывает, на сколько нынешняя цена продукта ниже минимальной цены (или издержки выше максимальных), при которойj-йпродукт может войти в оптимальный план.

5.Следует понимать, что пределы устойчивости для изменения сj даются при условии, что значения всех остальных целевых коэффициентов ck (при k≠i) остаются неизменными. Одновременное изменение двух и более коэффициентов (cj и ck), каждого внутри своего интервала устойчивости, может привести к изменению оптимального решения.

6.Для оценки влияния одновременного изменения нескольких значений cj следует вычислить относительные изменения

cj/max cj, где max cj - это предел либо увеличения, либо уменьшения cj (в зависимости от знака cj), и вычислить сумму этих относительных изменений. При этом, если эта сумма больше 1, оптимальное решение {Хj} изменится, если меньше - нет.

Основные соотношения двойственности

I. Если решения исходной задачи на максимум существует, то решение двойственной задачи на минимум точно ему равно:

Pmax=Cmin

Теневые цены для двойственной задачи – это оптимальное решение Xj для прямойЛП-задачи

II.Для оптимальных планов исходной и двойственной задачи:

1.Если т.е.i-йресурс использован полностью при производстве продукции по оптимальному плану, то его теневая цена больше нуля Yi>0

2.Если же т.е.i-йресурс не использован полностью при производстве продукции по оптимальному плану, то его теневая цена равна нуля Yi=0.

3.Если Xj>0, т.е. еслиj-йпродукт вошел в оптимальный план, то в соответствующем ограничении двойственной задачи реализует знак равенство, т.е. выручка от продажи ресурсов, идущих на производство

единицы этого продукта, равна прибыли от его производства:

4. Если же Xj=0, т.е. еслиj-йпродукт не входит в оптимальный план, то в соответствующем ограничении двойственной задачи реализует знак ―больше‖, т.е. выручка от продажи ресурсов, идущих на

производство единицы этого продукта, больше равна прибыли от его производства:

III. Теневые цены Yi показывают, на сколько увеличится значение Pmax, если запасы ресурса увеличить на единицу:

Pmax= biYi

3.3. Мини-кейс"На кондитерской фабрике". Акт 2 (Жаль... ведь мы все так любим "Батончик"!)

После решения задачи об оптимальном плане для родной кондитерской фабрики юноша (сын владельца фабрики) испытал двойственное чувство. С одной стороны, прибыль, соответствующая найденному им производственному плану, почти на 430 у.е. больше, чем по плану мастера, т.е. он заработал более 400 баксов. Это здорово!

С другой стороны, почему компьютер отказался от выпуска "Батончика" (эту конфету юноша с детства любил больше всех остальных)? Юноша был уверен, что "Батончик" - один из лучших продуктов, которые выпускает фабрика его отца. Если его не окажется на прилавках, может пострадать имидж фабрики. Ведь не только он сам, но и все соседи в округе обожают эту конфету!

Кроме того, он вспомнил, что на занятиях по количественным методам в менеджменте преподаватель все время твердил об анализе полученного оптимального решения на устойчивость: малые изменения величины запасов могут привести к радикальному изменению решения! А вдруг этот вредный старый мастер не только план производства определяет на глазок, но и запасы сырья взвешивает кое-как?А что, есликаких-тозапасов не хватит для его оптимального плана? Он не доберет прибыли! Может быть, тогда более прибыльным станет иной план? Какой?

И еще одна мысль. У него есть в кармане около 50 баксов. Может, пустить их в дело? Докупить у знакомого оптовика какого-нибудьсырья, потихоньку подложить на склад (чтобы мастер не заметил), как будто так и было. Тогда можно получить дополнительную прибыль (и премию от отца). Только вот какого сырья докупать? И сколько? И на сколько от этого возрастет прибыль?

Итак, ответьте на следующие вопросы

1.Как надо изменить норму прибыли для любимого продукта сына хозяина фабрики ("Батончика"), чтобы он вошел в оптимальный план? (Ответьте, не решая задачу, анализируя лишь отчет об устойчивости.)

2.Введите это изменение в данные и решите задачу заново. Как изменился оптимальный план?

3.Какой ресурс является наиболее дефицитным (т.е. максимально влияет на прибыль)?

4.Можете ли вы сказать (не решая задачу снова), как изменится прибыль от производства, если количество этого ресурса оценено: а) с избытком в 10 весовых единиц; б) с недостатком в 5 единиц?

5.Есть ли другой способ добиться производства "Батончика" (кроме изменения нормы прибыли)?

Комментарии к мини-кейсу

Вопросы 1-2

Согласно отчету об устойчивости (рис. 17), нормированная стоимость конфеты "Батончик", не вошедшей в оптимальный план, составляет 0,00874 у.е. Абсолютная величина этого числа показывает, на сколько нужно увеличить прибыль от производства одного пакетика этих конфет, чтобы "Батончик" вошел в оптимальный план.

Добавим к цене "Батончика" 0,01 у.е. В этом случае прибыль на единицу этого продукта станет равной 1,11 у.е. Решение задами с этим новым значением параметра показано на рис. 18. Для сравнения внизу листа MS-Excelприведены суммарная прибыль от производства и оптимальный план производства для старого значения параметра 1,1 у.е.

Видно, сколь драматически отличаются решения в этих двух случаях, хотя значения прибыли практически одинаковы! В таких случаях обычно говорят, что решение задачи неустойчиво.

Решение называется неустойчивым, если малые изменения параметров приводят к огромным изменениям решения. Чаще всего о неустойчивости говорят в негативном смысле, подразумевая даже, что неустойчивость ограничивает

возможности аналитика использовать количественные методы для принятия управленческих решений. Действительно, поскольку в реальной ситуации параметры модели всегда известны с определенной неточностью (ошибкой), а малые изменения параметров приводят к катастрофическим изменениям решения, то найденное оптимальное решение бесполезно! Оно рассчитано для строго определенных значений параметров, при других значениях параметров оно будет совершенно другим, а каковы реальные значения интересующих нас параметров, мы точно не знаем.

Если мы попытаемся выбрать между несколькими альтернативами, каждая из которых может стать оптимальной при незначительном изменении параметров, то не сможем сделать правильный выбор. В этом случае действительно уместно говорить о "деструктивной" роли неустойчивости и пытаться найти методы борьбы с ней. В курсе "Количественные методы в менеджменте" можно столкнуться с примером такой "дурной" неустойчивости при рассмотрении методов выбора альтернатив в условиях риска.

Однако в случае с данным мини-кейсомнеустойчивость решения не кажется очень страшной, ведьприбыль-тов обоих случаях почти одинакова! Попробуйте вернуть прежнее значение прибыли для "Батончика" (1,1 у.е.) - прибыль уменьшится до 1498,5 у.е. Это менее чем на 1% ниже оптимальной. Попробуйте ввести целочисленные ограничения на количество пакетиков каждого из продуктов или просто потребовать, чтобы количество произведенных пакетиков "Батончика" было не менее 100, 300, 500. Во всех чих случаях вы получите другие оптимальные решения, а прибыль будет отличаться от оптимальной (для исходного варианта постановки задачи) не более чем на 1%.

Таким образом, в вашем распоряжении окажется множество альтернативных решений, сильно различающихся по значениям переменных, но очень близких по прибыли. Это не плохо. Это очень хорошо!

Наличие многих, пусть не вполне оптимальных, но "хороших" альтернативных решений позволяет менеджеру выбрать такое, которое в наилучшей степени отвечает тем или иным неформализуемым требованиям и условиям, которые всегда присутствуют при принятии решений.

В данном случае таким неформализуемым условием является любовь лица, принимающего решение, к "Батончику", который, к несчастью, не вошел в оптимальный план при исходной постановке задачи. За эту любовь приходится платить либо повышением цены на данный продукт, либо снижением валовой прибыли. Что предпочесть?

-Смириться с отсутствием "Батончика" в оптимальном плане?

-Повысить цену?

-Ввести ограничение на минимальное количество пакетиков "Батончика"?

На эти вопросы модель ответа не даст. Модели не принимают решений! Это задача менеджера. Наличие множества альтернативных решений поможет ему выбрать решение, "приятное во всех отношениях". При этом оно необязательно должно быть оптимальным в строго математическом смысле слова.

studfiles.net

Методы оптимизации управления для менеджеров. Компьютерно-ориентированный подход. Зайцев М.Г.

Методы оптимизации управления для менеджеров. Компьютерно-ориентированный подход. Зайцев М.Г.

Содержание Вместо предисловия 3ВВЕДЕНИЕ 41.1. Курс "Количественные методы в менеджменте" в программе MB A 4Какие вопросы рассматриваются в курсе "Количественные методы в менеджменте"? 4Количественные модели и методы в бизнесе и управлении 4Роль менеджера в эффективном использовании количественных методов 5Миссия курса "Количественные методы в менеджменте" 5Место курса "Количественные методы в менеджменте" в программе MB A 5Методика изложения материала курса 6Компьютерная поддержка курса 6Основное содержание курса "Количественные методы в менеджменте" 6Как работать с этой книгой? 71.2. Принятие решений в условиях определенности 7Примеры ситуаций принятия решений в условиях полной определенности 8Целевая функция 9Переменные решения 9Параметры модели 9Ограничения 9Контрольные вопросы к разделу 1 92 МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 102.1. Оптимальный план выпуска продукции мебельного цеха (Product Mix) 11Формализация примера и основные соотношения 11Решение задачи об оптимальном плане выпуска продукции с помощью Excel 122.2. Мини-кейс "На кондитерской фабрике" 14Формализация мини-кейса и основные соотношения 14Решение мини-кейса "На кондитерской фабрике" с помощью Excel 15Предубеждение о целочисленном ограничении 17Заключение к разделу 2 17Контрольные вопросы к разделу 2 17Примеры для самостоятельного анализа к разделу 2 183 АНАЛИЗ ОПТИМАЛЬНОГО РЕШЕНИЯ ЛП-ЗАДАЧ 193.1. Графическое решение задачи об оптимальном плане выпуска продукции мебельного цеха 20Упражнение по использованию отчета об устойчивости: влияние изменений в ценовых коэффициентах 233.2. Двойственная задача. Теневые цены 23Решение двойственной задачи об оптимальном плане выпуска продукции мебельного цеха с помощью MS-Excel 26Анализ решения двойственной задачи 27Упражнение по использованию отчета об устойчивости: влияние изменений в правых частяхограничений 283.3. Мини-кейс "На кондитерской фабрике". Акт 2 (Жаль... ведь мы все так любим "Батончик"!) 29Комментарии к мини-кейсу 30Заключение к разделу 3 31Контрольные вопросы к разделу 3 32Примеры для самостоятельного анализа к разделу 3 324 ИСПОЛЬЗОВАНИЕ ЦЕЛОЧИСЛЕННЫХ ПЕРЕМЕННЫХ В ЛП-ЗАДАЧАХ 35Условие целочисленности 35Проблемы типа "брать/не брать". Логические переменные 364.1. Проблема постоянных издержек в линейном программировании. Мини-кейс "На кондитерскойфабрике". Акт 3 (Проблема учета постоянных издержек) 36Анализ 3-го акта мини-кейса "На кондитерской фабрике" 37Организация данных для анализа 3-го акта мини-кейса на листе MS-Excel 384.2. Оптимальный план размещения предприятий 38Анализ примера 38Организация данных на листе MS-Excel 39Заключение к разделу 4 40Контрольные вопросы к разделу 4 40Примеры для самостоятельного анализа к разделу 4 405 ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ 425.1. Организация оптимального снабжения 42Переменные, целевая функция и ограничения модели 42Опорный план 43Метод "северо-западного угла". Циклы 44Общая формулировка транспортной задачи 45Решение транспортной задачи с помощью MS-Excel 465.2. Осложнения транспортной задачи 46Несбалансированность: излишек запасов 46Несбалансированность: дефицит запасов 47Запрещенный маршрут 475.3. Задача о назначениях 48Постановка задачи: Расстановка рабочих по операциям 48Пример для решения с помощью MS-Excel: Построение команд 48Решение 49Анализ решения. Расчеты типа "что, если..." 49Заключение к разделу 5 52Контрольные вопросы к разделу 5 53Примеры для самостоятельного анализа к разделу 5 53Применение методов линейного и целочисленного программирования в реальном бизнесе 556 УПРАВЛЕНИЕ ЗАПАСАМИ (в пренебрежении случайными вариациями спроса) 56Важность проблемы управления запасами 56Фундаментальный вопрос управления запасами 57Незавершенная работа (Work-in-process) 57Функции запасов 576.1. Издержки по формированию и содержанию запасов 586.2. Модель экономичного размера заказа 60Основные допущения и параметры модели 60Выражения для издержек хранения и оформления заказа 60Формула для оптимального (экономичного) размера заказа 61Проблемы применения оптимального решения на практике 62Анализ устойчивости оптимального решения 63Модификации модели экономичного размера заказа 646.3. Модель производства оптимальной партии продукции 64Пример: План работы универсальной производственной линии 64Формула для оптимального размера партии 65Анализ примера об универсальной производственной линии 656.4. Модель планирования дефицита 66Формулы для оптимального размера заказа и оптимальной величины дефицита 67Пример: Продажа автомашин со стоянки 68Анализ примера о продаже машин со стоянки 686.5. Учет оптовых скидок в модели экономичного размера заказа 70Пример: Выбор поставщика для оптовых закупок 71Анализ примера о выборе поставщика с помощью MS-Excel 716.7. Оптимальное управление запасами в условиях переменного (неслучайного) спроса 74Пример: Планирование производства детали на универсальной линии "с горизонтом" 8 недель 74Анализ примера о плане производства детали с помощью MS-Excel 74Заключение к разделу 6 76Контрольные вопросы к разделу 6 76Примеры для самостоятельного анализа к разделу 6 77Применение методов управления запасами в реальном бизнесе 787 КОЛИЧЕСТВЕННЫЕ МЕТОДЫ УПРАВЛЕНИЯ ПРОЕКТАМИ (в пренебрежении случайнымивариациями длительностей отдельных стадий проекта) 797.1. Пример: Проект "Снеси-построй" 79Диаграмма Гантта 80Сетевые диаграммы 817.2. Критический путь (СРМ) 83Расчет ранних и поздних стартов и финишей для каждой стадии проекта 83Определение временных резервов для каждой стадии проекта "Снеси-построй" с помощью MS-Excel 85Упражнение: Влияние изменения длительности отдельных стадий на длительность проекта 86Выводы по упражнению 877.3. Сокращение длительности проекта. Соотношение длительность/издержки (CPMICost) 87Стоимость сокращения отдельных стадий проекта 87Расчет соотношения длительность/издержки для проекта "Снеси-построй" 88Оптимизация длительности проекта 907.4. Распределение финансовых ресурсов по времени в процессе выполнения проекта 91Ограничение ежедневного расхода ресурсов 91Таблица MS-Excel для расчета ежедневных расходов по проекту "Снеси-построй" 927.5. Использование программы MS-Project 2000 для планирования и анализа проектов 94Ввод информации о проекте в MS-Project 2000. Определение критического пути 94Информация о стоимости ресурсов и исследование соотношения длительность/издержки в MS-Project 96Заключение к разделу 7 100Контрольные вопросы к разделу 7 100Примеры для самостоятельного анализа к разделу 7 100Применение количественных методов управления проектами в реальном бизнесе 102Ответы на контрольные вопросы 103Ответы к примерам для самостоятельного анализа 107Литература 114Глоссарий 114Список рисунков 298Список таблиц 301Список вкладок с формулами 302  < Предыдущая Следующая >

www.1variant.ru

Методы оптимизации управления для менеджеров - Зайцев М.Г

Разумеется, это не единственный (и необязательно оптимальный) вариант. Целевая функция при этом равна 899. Чтобы превратить данную задачу в задачу о назначениях, нужно определить время для подготовки каждого

индивидуального (а не "усредненного") аудитора для аудита каждого клиента. При этом придется заполнить таблицу размером 75х90 (75 мест в командах для работы с разными клиентами и 90 аудиторов). При этом получится несбалансированная задача о назначениях. Каждый столбик этой таблицы это ―запрос‖ работы аудитором (сумма единичек в столбике должна быть равна 1), а каждая строчка - "запрос" клиентом аудитора на некоторое место в команде (сумма единичек в строчке тоже должна быть равна 1). К этой таблице нужно добавить один столбец (плановая учеба), который поглотит 15 "лишних" аудиторов, чтобы сбалансировать задачу.

Пример 2

Значение целевой функции равно 537. План перевозок представлен в таблице.

Пример 3

А. Значение целевой функции равно 248. План перевозок представлен в таблице.

Потребители D7 и D9 не получат соответственно 6 и 4 контейнера.

В. Значение целевой функции равно 204. План перевозок представлен в таблице.

На складах S1, S3 иSA останется соответственно 3,10 и 7 контейнеров.

Пример 4

План назначений представлен в таблице. Рабочие S4 иS8 не включены в "бригаду".

Для времени выполнения фиктивной операции Dfikt всем рабочим следует приписать одинаковое время. Оптимальный план назначений не зависит от того, каково конкретное значение этого времени. Однако нелепая функция будет правильно отражать суммарные затраты времени "бригады" на выполнение всех 10 реальных работ, если это время равно 0. в этом случае значение целевой функции равно

157.

Раздел 6 Пример 1

Если D - годовой спрос, aQ - величина единичного заказа, тоTR 2QD .

Таким образом, этот показатель стимулирует менеджера, ответственного за склад, использовать минимально возможный размер единичного заказа (так как спрос D вряд ли может контролироваться ЭТИМ менеджером). При этом, разумеется, издержки оформления, размещения и доставки заказа могут стать недопустимо высокими.

Если менеджер использует экономичный размер заказа (минимизирующий полные издержки управления складом), то

	значение TR будет выражаться следующей формулой:TR	2DCh%	, где С- стоимость единицы запаса, h% - удельная
		S

издержка хранения, выраженная как процент от стоимости единицы запаса, S - издержка оформления и размещения заказа. От менеджера, ответственного за склад, реально зависит лишь издержкаS, Если она уменьшается (более эффективно

работают менеджеры склада), TR растет.

При прочих равных условиях TR будет тем выше, чем дороже хранимый товар, чем выше спрос и внутренняя норма доходности фирмы.

Пример 2

Удельная издержка хранения составляет 150*24%=36 руб. в год на одно кресло. Стоимость демонтажа и монтажа выплачивается равномерно по мере замены кресел и никак не входит в издержки хранения (лишнее данное).

Годовую потребность можно оценить как сумму замененных кресел за предшествующие 12 месяцев: D=13 086.

Тогда при существующей системе управления складами, когда заказывают 15 тыс. кресел 1 раз в год, суммарные издержки (исключай собственно затраты на покупку кресел, на демонтаж старых и монтаж новых кресел) составят 280 тыс. руб. в год.

Экономичный размер заказа 2696 и соответствующие ему суммарные издержки – 97 066,6 руб. Если делать заказ 5 раз в год (при этом Q=2617 кресел), суммарные издержки 97 106,9 руб. (что практически не отличается от минимально возможных).

Таким образом, исходя из анализа суммарных издержек управления запасом, можно рекомендовать заказывать 2617 кресел 5 раз в год.

Поскольку ―спрос‖ на ежемесячную замену кресел случаен, при рекомендуемой стратегии может возникнуть дефицит кресел на складе. Оценка риска возникновения дефицита и величины резервного запаса (и соответствующие увеличения затрат) дается статистической теорией управления запасами, которая в дайной книге не рассматривалась.

Однако поскольку фирма до сих пор заказывала 15 тыс. кресел в год и "затоваривания" склада не произошло, можно принять, что 1914 кресел (15 000 – 13 086) и есть резервный запас на год. Это значит, что во всех формулах вместо D следует использовать15 000.

Тогда суммарные издержки при экономичном размере запаса (который теперь равен 2887 кресел) составят 103 923 руб. в год., а при удобном размере заказа 3000 (5 раз в год) - 104 000 руб.

Видно, что новая стратегия в 2,8 раза дешевле.

Не исключено, однако, что годовая потребность реально ниже, чем 15 000 и часть кресел просто регулярно разворовывается. Это, однако, не меняет принципиального вывода о необходимости изменения стратегии управления складом.

Пример 3

При заданных параметрах экономичный размер заказа у внешнего поставщика равен EOQ = 392 при суммарных издержках управления запасом 612,37 долл. в год.

В зависимости от издержек запуска линии на производство данных деталей экономичный размер партии продукции и суммарные годовые издержки даны в таблице.

Таким образом, при существующем положении дел выгоднее заказывать деталь у внешнего поставщика. Чтобы издержки управления запасом при собственном изготовлении детали стали меньше, чем при закупке у внешнего поставщика, следует добиться уменьшения издержек запуска линии до величины ниже 27 долл. (ее можно найти подбором этого параметра в MS-Excel).

Пример 4

Следует покупать у первого поставщика но цене 780 руб. за штуку 3000 штук 3,3333 раза в год.

Пример 5

Годовая потребность компании в агентах D = 27.

Стоимость (суммарные издержки) программы независимо от числа обучаемых аналогично издержке оформления, размещения и доставки заказа S = 12 тыс. долл.

Издержка "хранения" специалиста в течение одного месяца 1500. Это значит, что H=18 тыс. в год. Тогда оптимальный набор EOQ = 6 агентов.

Набирать группу нужно 4,5 раза в год.

Интервал между наборами t = 8/3 месяца. После окончания программы до начала новой, таким образом, проходит ⅔ месяца.

Спрос на агентов 27 в год, или 2,25 в месяц. Таким образом, после окончания программы и до начала новой программы потребуется 3,75 человека. Останутся невостребованными 2,25 человека.

Пример 6

Результаты расчета полных издержек управления складом представлены в таблице.

Как видно в этом примере, стратегия "Все сразу" хуже, чем стратегия "Лот равен заказу". Использование эвристической методики, представленной в примере раздела 6.7, дает минимум издержек в случае трех лотов: 80на первой неделе, 110 на четвертой и 110 на седьмой неделе.

Однако в данном случае более эффективным будет, как не трудно проверить, произвести три других лота: 80 на первой неделе, 130 на четвертой и 90 – на восьмой неделе.

Этот результат может быть получен автоматически при применении так называемого алгоритма Baгнера-Уитина(WW), основанного на методе динамического программирования. Однако при внимательном взгляде на результат нашей эвристической стратегии"Оптим-3‖также можно легко заметить, что такое изменение привело к уменьшению издержек.

Дело в том, что отнесение требования седьмой недели (20 изделии) к лоту на четвертой неделе снижает максимальный остаток на складе (и значит, складские издержки) с 90 (на седьмой неделе) до 80 (на четвертой неделе).

Раздел 7

Пример 1

Рассуждение управляющего проектом абсолютно неверно.

Вариант 1 означает отсрочку проекта на 2 недели (так как временной резерв стадии H – 4 недели). Следовательно, суммарные издержки от выполнения и задержки начала работ по этой стадии будут 18 тыс. долл.

При выборе варианта 2 задержки окончания проекта не произойдет и суммарные издержки будут равны цене, запрашиваемой другим субподрядчиком, - 15 тыс. долл.

При выборе варианта 3 задержки окончания проекта не произойдет, а суммарные издержки равны 14 тыс. долл. Таким образом, выбрать нужно вариант 3.

Пример 2

Критический путь ADEG. Соотношение "длительность - издержки" представлено в таблице.

После сокращения проекта на 6 недель появляется новый критический путь, проходящий через стадию F. Однако поскольку предшественником (дальним)F, так же как иG, являетсяА, то при сокращенииА на 1 день оба критических пути сокращаются на 1 день.

Поскольку нормальная стоимость проекта составляет 74 у.е., то в случае ограничения бюджета 80 у.е. проект можно сократить только на 2 недели.

Пример 3

Срок выполнения проекта30 дней. Критический путь ABEFI.

Еженедельные расходы меняются от 4 у.е. до 35,6 у.е. как для расписания "начинать так рано, как только возможно", так и для расписания "заканчивать так поздно, как только возможно". В первом случае предел 35,6 у.е. достигается с 11-йпо13-юнеделю и с23-йпо28-юпеделю, а во втором - с18-йпо20-юи с25-йпо30-юнеделю.

Для того чтобы удовлетворить требование финансового департамента, необходимо сдвинуть на 6 недель начало стадии D (это не приведет к удлинению проекта, так как временной резерв стадииD равен 7 неделям), а стадию I сдвинуть на 6 недель, что удлинит проект на 6 недель.

Другой способ удовлетворить ограничение по еженедельному расходу средств - снизить, если это возможно, вдвое еженедельное финансирование стадии G с соответствующим удлинением ее в два раза. В этом случае длительность проекта составит 34 недели.

Литература

1.Эддоус М., Степфилд Р. Методы принятия решений. М :ЮНИТИ-Аудит1997.

2.Томас Р. Количественные методы анализа хозяйственной деятельности. М.: Дело и Сервис, 1999,

3.Вснтцель Е.С. Исследование операций. М: Наука, 1988.

4.Исследование операций в экономике / Под ред. Н.Ш. Кремера. М: ЮНИТИ, 1997.

5.Фомин Г.П. Математические методы и модели и коммерческой деятель кости, м.: Финансы и статистика, 2001.

6.Красс М.С., Чупрынов Б.П Основы математики и ее приложений в экономическом образовании. Разд. II "Основы оптимального управления". М.: Депо 2001.

7.Вагнер Г. Основы исследования операций: В 3 т. М.: Мир, 1972.

8.Таха X. Введение и исследование операций. М.: Мир, 1985.

9.Чейз Р.Б., Эквилайн И.Дж., Якобс Р.Ф. Производственный и операционный менеджмент. М; СПб.; Киев: Изд. Дом

"Вильяме", 2001.

10.Козловский В.А. Маркина Т.Н., Макаров В.М. Производственный и операционный менеджмент: Учебник и практикум "Специальная литература", СПб., 1998.

11.Austin I.M . Ghamlforoiish Г Management Science for Decision Markers West Publishing Company, 1993.

12.Lawrence J.A.. Pasternack HA. Applied Management Science (Computer Integrated Approach for Decision Making). J Willey& Sons, 1999

Глоссарий

Анализ			устойчивости		Необходимый этап применения количественных методов в менеджменте. Отвечает на вопрос, как
решения (Sensitivity analysis)					изменения параметров модели (считавшихся постоянными и "не зависящими" от менеджера в процессе
					поиска решения) влияют на полученное оптимальное решение.
Булевы			(логические)		Переменные, которые могут принимать только два значения 0 и 1. Эти значения можно сопоставить с
переменные				(Binary	ответом на некоторый вопрос типа "да-нет","брать-небрать" и т. п.
variables)					Используются, когда требуется решить, какие из большого набора элементов нужно выбрать, чтобы
					оптимизировать целевую функцию и удовлетворить заданным ограничениям, а какие отбросить.
Вершинная				сетевая	Сетевая диаграмма, в которой каждая стадия соответствует узлу, а стрелки используются только для
диаграмма			(Activity-on-		обозначения связей и последовательности стадий. Представление о фиктивных стадиях (работах) в этом
nodes diagram)					случае излишне.
Временной		резерв		(Slack	Допустимый временной интервал, в котором можно изменять длительность или моменты начала работ
time)					некритических стадий без изменения длительности проекта. Временной резервкритических стадий равен
					нулю. Они не могут быть отсрочены или удлинены без соответствующего удлинения проекта в целом.
Время поставки (Lead Time)					Время от подачи заявки до поступления запаса на склад.
Двойственная			задача ЛП		Для любой ЛП-задачиможно сформулироватьдвойственную задачу, тесно связанную с исходной ЛП-
(Dual problem)					задачей. При решении исходной задачи одновременно может быть получено и решение ее двойственной
					задачи. Решением двойственной задачи являются теневые цены для ресурсов исходной задачи.
Диаграмма		Гантта		(Gantt	Диаграмма, в которой стадии проекта изображаются прямоугольниками, длины которых пропорциональны
chart)					длительности стадий, причем прямоугольник, отвечающий стадии, последовательно откладывают в момент
					окончания самого позднего предшественника. Позволяет определить длительность проекта.
Допустимое решение (план)					Набор значений переменных решения, удовлетворяющий всем наложенным на процесс управления
(Feasible solution)					ограничениям.
Задача	о		назначениях		Частный случай ЛП-задачи.Наиболее распространенный вариант задачи состоит в выборе такого
(Assignment Problem)					распределения работ между исполнителями, который минимизирует суммарные временные затраты на
					выполнение работ или другие характеристики эффективности работ.
Издержки			размещения		Второй обязательный параметр в моделях управления запасами. Представляет собой издержки, связанные
заказа (Ordering Costs, Setup					с подачей заказа, оформлением заявки, расходами на связь, получением и размещением заказа на складе.
Costs)					Не зависит от размера заказа.
Издержки		хранения		запаса	Первый обязательный параметр в моделях управления запасами. Обычно выражается в % от стоимости
(Holding Costs)					запаса, поскольку включает неполученные проценты на инвестированный в запас каптал. Также могут
					включать прямые издержки на страховку, содержание склада, охрану и т.д. Обычно относятся к храпению
					единицы запаса в течение года.
Интервал			устойчивости		Интервал, в котором изменение коэффициентов целевой функции не приводит к изменениюоптимального
оптимального			решения		решения, или интервал, в котором изменение правых частейограничений не приводит к изменению
(Range	of	optimality,		Range	теневых цен.

of feasibility)
Критическая стадия (Criticial					Стадия, для которой изменение моментов начала и конца работ обязательно приведет к изменению
activity)					длительности всего проекта. Для некритических стадии существует некоторый временной резерв, в
					котором моменты начала и конца работ можно изменять без изменения длительности проекта.
Критический		путь	(Critical		Непрерывная последовательность критических стадий от начала к концу проекта.
path)					На сетевой диаграмме критический путь имеет наибольшую длительность, равную продолжительности
					проекта.
Линейное					Другой возможный перевод с английского – линейная оптимизация.
программирование			(Linear		Методы нахождения оптимального решениядля моделей, у которых целевая функцияи ограничения
Programming)					являются линейными, т.е. все функции представляют собой суммы произведений переменных решения (в
					первой степени) на постоянные коэффициенты.
Метод	"северо-западного				Метод формирования опорного плана транспортной задачи.
угла"	(Northwest			coner
method)
Метод критического				пути	Определяет последовательность стадий на сетевой диаграмме с максимальной суммарной длительностью
(СРМ Critical Path Method)					(критический путь).
					Позволяет также определить временные резервы некритических стадий. Используется для оценки
					соотношения "длительность проекта – издержки" и для оптимизации длительности проекта.
					Основан на предположении о том, что длительность каждой стадии проекта строго определена и не
					подвержена случайным изменениям.
Нормированная					Величина, выдаваемая отчетом по устойчивости MS-Excel,показывает, насколько нужно увеличить
(редуцированная) стоимость					прибыль на единицу данного продукта, чтобы он вошел в оптимальный план. Для продукта, входящего в
(Reduced Cost)					оптимальный план, редуцированная стоимость равна 0.
Ограничения (Constraints)					Математически выражаются в виде неравенств или равенств для переменных решения, включающих
					параметры, которые отражают реальные пределы использования доступных ресурсов в процессе
					управления или внешние ограничения на изменения переменных решения.
Опорный	план			(Initial	Допустимый план перевозок для транспортной задачи, в котором число ненулевых перевозок равно сумме
Feasible Solution)					числа поставщиков и потребителей минус 1. Оптимальный план перевозок нужно искать только среди
					множества опорных планов.
Оптимальное			решение		Набор значений переменных решения, удовлетворяющий всем наложенным на процесс управления
(план) (Optimal solution)					ограничениям и обращающийцелевую функцию в максимум или минимум.
Отчет	по	устойчивости			Один из отчетов, выдаваемый надстройкой "Поиск решения", содержащий информацию обинтервалах
(Sensitivity Report)					устойчивости при изменении коэффициентовцелевой функции и правых частей ограничений, а также
					информацию о теневых ценах.
Параметры			модели		Величины, количественно характеризующие условия функционирования управляемой системы,
(Parameters)					организации или процесса, которые при поиске оптимального решения менеджер должен считать
					неизменными.
Переменные			решения		Величины, количественно характеризующие управляемую систему, организацию или процесс, которые
(Decision variables)					менеджер может непосредственно изменять с целью добиться максимально эффективного управления
					(получить оптимальное значение целевой функции).
Поиск решения (Solver)					Надстройка MS-Excel,позволяющая осуществить поиск оптимального решения для задачлинейной (и
					нелинейной) оптимизации с ограничениями.Число переменных решенияне может превышать 200. Для
					каждой изменяемой ячейки (переменной) может быть задано по 2 ограничения (снизу и сверху). Кроме
					того, можно задать 100 дополнительных ограничений.
Проблема		постоянных			Если оптимизируется строго линейная модель, то можно учесть
издержек		(Fixed-Charge			лишь переменные издержки, т.е. те, которые пропорциональны количеству произведенной продукции.
Problem)					Для учета постоянных операционных издержек необходимо введениебулевой (логической) переменной в
					ЛП-задачу.
Сетевая диаграмма (Network					Графическое отображение стадий проекта и связей между ними с помощью стрелок и узлов.
diagram, PERT chart)					Наиболее наглядно изображает соотношения "предшественник - последователь" для стадий проекта.
Сетевое		планирование			Количественный метод планирования и анализа сложных проектов. Включает разбиение проекта на
(Project Scheduling)					отдельные стадии (работы), установление связей между ними, графическое отображение этих связей с
					помощью сетевых диаграмм (графов) и анализ сетевых диаграмм с целью определения средней
					длительности и распределения вероятностей для времени выполнения проекта, допустимого временного
					интервала выполнения каждой стадии, возможных результатов и стоимости удлинения или сокращения
					отдельных стадий проекта.
Симплекс (Simplex)					Геометрическая область в многомерном пространстве, каждая точка которой является образом
					допустимого решения ЛП-задачи.
Симплекс-метод			(Simplex		Эффективный метод перебора угловых точек области допустимых решений с целью нахождения
algorithm)					оптимального решения ЛП-задачи.Предложен Дж. Данцигом в 1947 г. Метод (или его последующие
					модификации) лежит в основе всех компьютерных алгоритмов для решения ЛП-задач.
Стрелочная			сетевая		Сетевая диаграмма, в которой каждая стадия изображается стрелкой, а узлы отображают начало и конец
диаграмма		(Activity-on-			стадии. С целью недопущения ситуации, когда несколько стадий-стрелоксоединяют одну и ту же пару
arrows diagram)					узлов, вводится представление о фиктивных стадиях (работах), изображаемых пунктирной стрелкой.
Теневая цена (Shadow price)					Показывает, как изменится целевая функция ЛП-задачи,если количество соответствующего дефицитного
					ресурса увеличить на единицу. Для недефицитного ресурса теневая цена равна нулю.
Транспортная				задача	Частный случай ЛП-задачи.Состоит в выборе такого плана перевозок однотипных грузов от нескольких
(Transportation Problem)					поставщиков к нескольким потребителям, который минимизирует транспортные издержки с учетом
					реальных запасов каждого из поставщиков и при удовлетворении заказов каждого из потребителей.
Фиктивный		поставщик			В правильно поставленной транспортной задаче сумма запасов поставщиков должна быть равна сумме
(потребитель)			(Dummy		заказов потребителей (условие сбалансированности), Если в реальности это не так, следует добавить
source, destination)					фиктивного поставщика (или потребителя), запас (или заказ) которого восстанавливает баланс, а стоимость
					перевозок запасов от него (к нему) нулевая. То, что "получают" реальные потребители от фиктивного
					поставщика, - это их дефицит. То, что "отправляют" реальные поставщики фиктивному потребителю, - это

	запасы, оставшиеся на их складах.
Целевая функция (Objective	Количественный показатель эффективности управления, зависящий от переменных решения и от
function)	параметров. При оптимальном выборепеременных решения достигает максимального или минимального
	значения (в зависимости от целей управления).
Целочисленное	Методы решения ЛП-задачс дополнительным ограничением: все или часть переменных могут принимать
программирование (Integer	только целые значения.
Programming)	По форме ЛП-задачии ЦЛП очень похожи. Однако задачи ЦЛП гораздо более сложны, их решение требует
	использования гораздо более сложных алгоритмов и больших временных затрат.
Циклические перестановки	Метод оптимизации плана перевозок транспортной задачи посредством преобразования опорных планов.
(Stepping-stonemethod)
экономичный размер заказа	Размер заказа, при котором суммарные годовые издержки, включающие издержки хранения и издержки
(Economic Order Quantity)	подачи заказа, минимальны.

studfiles.net

Организация оптимального снабжения - Методы оптимизации управления для менеджеров

5.1. Организация оптимального снабженияВ районе имеется 2 песчаных карьера, с которых песок вывозится на 5-тонных грузовиках. Предприятия-поставщики S1и S2 разрабатывающие карьеры, могут поставлять соответственно 100 и 200 грузовиков с песком в день. В этом районе имеется 3 завода железобетонных конструкций - потребители песка D1 D2и D3, которым требуется соответственно 80, 90 и 130 грузовиков с песком в день. Стоимости перевозки песка одним грузовиком от карьера- поставщика Siк заводу-потребителю Di(в условных единицах) приведены в таблице параметров. Составить план перевозок, минимизирующий затраты. Переменные, целевая функция и ограничения моделиТребуемый план перевозок должен определить, какое количество грузовиков Хijследует направить с карьера Siна завод Dj. Поскольку, очевидно, существуют 6 различных маршрутов, то в этой простой задаче имеется 6 переменных, что и отражено в таблице элементов модели. Целевая функция в данной задаче - суммарные транспортные издержки - равна сумме произведений переменных решения Хij на стоимости перевозки единицы груза cijприведенные в таблице параметров. В стандартной транспортной задаче считается, что необходимо, безусловно, удовлетворить все требования потребителей (привезти именно то количество грузов, которое они запрашивали) и вывезти от поставщиков все грузы, которые они имеют на складах. При этом, очевидно, предполагается, что спрос и предложение строго сбалансированы. Если обозначить запасы i-го поставщика Si, а заказы j-го потребителя Dj, то для данной задачи нетрудно проверить, что S1+S2=D1+D2+D3В общем случае, если имеется т поставщиков и п потребителей, условие сбалансированности означает, что Если это условие не выполняется, т.е. транспортная задача не сбалансирована, упоминавшиеся выше специальные высокоэффективные алгоритмы ее решения не могут быть применены. Чтобы обеспечить их применение, в формулировку задачи вносят искусственные изменения, восстанавливающие баланс спроса и предложения. Как это делается, мы рассмотрим ниже, в разделе "Осложненные случаи транспортной задачи". Итак, выполнение требования вывезти все, что производят поставщики песка за день, означает, что сумма перевозок Х11+Х12+Х13 из первого карьера на 1, 2 и 3-й заводы-потребители должна равняться производительности первого карьера (100 грузовиков с песком), а сумма перевозок Х21+Х22+Х23из второго карьера на 1, 2 и 3-й заводы-потребители - производительности второго карьера (200 грузовиков). Это первые два ограничения на перевозки, приведенные в таблице элементов модели в столбце "Поставщики". Аналогично необходимо потребовать, чтобы сумма перевозок на каждый из трех заводов - потребителей песка с двух карьеров была точно равна ежедневному заказу на песок от данного завода. Эти требования выражаются тремя равенствами в столбце "Потребители". Обратим внимание, что в отличие от рассмотренных ранее примеров ЛП-задач, где ограничения выражались нестрогими неравенствами (типа "меньше или равно" или "больше или равно"), в транспортной задаче ограничения задаются строгими равенствами. В других ЛП-моделях также вполне могут встретиться ограничения в виде равенств (особенно в тех случаях, когда переменные решения представляют собой доли какой-то заданной суммы или компоненты какой-то смеси и т.п.), однако в транспортной задаче это абсолютное правило. Заметим также, что структура ограничений транспортной задачи исключительно проста: все коэффициенты при переменных решения в ограничениях равны единице. Именно эти особенности и позволяют применять упомянутые выше специальные эффективные алгоритмы решения таких задач. Опорный планПодсчитаем количество ограничений-равенств в нашей транспортной задаче. На первый взгляд их пять. Однако если сложить первые два, то получится такое же равенство, как и при сложении последних трех ограничений: В таких случаях математики говорят, что записанные пять ограничений не являются независимыми. Поскольку первые два ограничения в сумме означают то же самое, что и последние три, фактически ограничений, влияющих на значения переменных решения, не пять, а четыре. Поскольку ограничения в этой задаче образуют систему уравнений относительно переменных решения, можно было бы попытаться решить эту систему, чтобы найти значения переменных. Но переменных решения в нашей задаче 6, а независимых уравнений для их решения только 4. Можно произвольно положить значение двух каких-нибудь переменных решения равными 0 (например, X11=0 и Х]2=0), тогда остальные переменные решения могут быть однозначно определены из системы уравнений, образованной ограничениями. Получившийся план перевозок, разумеется, необязательно будет оптимальным, но он обязательно является допустимым, поскольку удовлетворяет всем ограничениям. Такой план называется опорным. От множества других допустимых планов он отличается тем, что число ненулевых переменных решения (ненулевых перевозок) точно равно количеству независимых ограничений в транспортной задаче или, иначе, сумме числа поставщиков и потребителей минус 1. В нашей задаче число ненулевых перевозок в опорном плане равно 2 (количество поставщиков) + 3 (количество потребителей) -1=4. В общем случае если имеется т поставщиков и п потребителей, то количество ненулевых перевозок в опорном плане будет т + п - 1. Если, например, т = 10, а п = 20, то количество переменных будет 200, а количество ненулевых переменных в опорном плане - только 29. В теории линейного программирования доказывается, что оптимальный план обязательно является опорным. Иными словами, искать оптимальный план перевозок нужно только среди опорных планов. В этом и состоит основное значение опорного плана. Разумеется, опорных планов может быть много. В нашем примере нетрудно пересчитать, что существует 15 различных способов присвоить нули двум переменным из шести (т.е. имеется 15 опорных планов). В случае когда т = 10, п = 20, число различных опорных планов будет выражаться огромным числом 7,18*10 34. Таким образом, о том, чтобы перебрать все возможные опорные планы и выбрать среди них оптимальный, в общем случае транспортной задачи, разумеется, не может быть и речи. Однако возможность осуществлять поиск только среди опорных планов все равносильно упрощает задачу по сравнению с общей задачей линейного программирования. Опорным называется такой план, в котором количество ненулевых перевозок равно сумме количеств поставщиков и потребителей минус единица. Оптимальный план перевозок следует искать только среди множества опорных планов. Метод "северо-западного угла". ЦиклыХотя в настоящем учебном пособии мы не ставили целью рассмотрение технических аспектов оптимизационных алгоритмов, все же, чтобы продемонстрировать роль введенного понятия опорного плана и дать представление об упоминавшихся выше специальных эффективных алгоритмах решения транспортных задач, представляет интерес получить решение нашей "игрушечной" транспортной задачи без помощи компьютера. Для начала необходимо просто написать какой-нибудь опорный план. Это легко сделать с помощью так называемого метода "северо-западного угла". В правом верхнем углу каждой клетки таблицы перевозок укажем стоимость перевозки единицы груза и будем стремиться последовательно удовлетворять требования каждого потребителя и каждого поставщика. Начнем заполнение таблицы перевозок с левого верхнего ("северо-западного") угла. Потребителю D1требуется 80 единиц груза. Эти 80 единиц груза могут быть доставлены от первого поставщика S1. Поэтому запишем в клетку S1D1количество перевозок 80. Поставщик S1 требует, чтобы с его предприятия было вывезено 100 единиц груза, а пока вывезено только 80. Увезем оставшийся груз к потребителю D2. Запишем в клетку S1D2остающиеся у поставщика S120 единиц груза. Займемся теперь потребителем D2. Ему требуется 90 единиц груза, а пока доставлено от S1только 20. Недостающие 70 единиц доставим от поставщика S2. Продолжая заполнять таблицу, позаботимся об удовлетворении поставщика S2. От него вывезено 70 единиц груза, в то время как требуется вывезти 200. Увезем оставшийся груз к потребителю S3, и, поскольку наша транспортная задача сбалансирована, именно эти оставшиеся у поставщика S2 130 единиц груза и нужны потребителю D3В результате такой методики заполнения таблицы перевозок мы удовлетворили требования всех поставщиков и потребителей (т.е. все ограничения задачи). При этом видно, что из шести клеток таблицы перевозок мы заполнили четыре. Две клетки остались пустыми. Таким образом, мы получили опорный план. Легко видеть, что полученный план можно улучшить (уменьшить суммарные транспортные издержки). Маршрут S1D3имеет цену перевозки единицы груза меньше, чем S1D2. Понятно поэтому, что было бы дешевле вывезти 20 единиц груза от поставщика .S2 не к потребителю D2, а к потребителю D3. Но в таком случае, чтобы не нарушить выполнение требований потребителей D2и D3 необходимо увеличить количество грузов, перевезенных от поставщика S2к потребителю D2, за счет уменьшения числа единиц грузов, перевезенных от S2 к D3Тогда таблица перевозок приобретет следующий вид.

Полученный нами план также является опорным. Легко видеть, что в результате этого преобразования 20 единиц грузов были как бы перенесены по круговому пути, или, как говорят, по "циклу", S1D2 → S1D3 → S2D3→S2D2. При переносе каждой единицы груза из S1D2в S1D3выигрыш в цене составляет 3 у.е.. Аналогично при переносе единицы груза из S2D3в S2D2происходит выигрыш в 1 у.е.. Итак, при переносе 20 единиц груза по этому циклу выигрыш в издержках составил 4 у.е. * 20 = 80 у.е. Говорят, что найденный нами цикл имеет "отрицательную цену" (- 4 у.е.). Процесс оптимизации плана перевозок, таким образом, состоит в отыскании циклов с отрицательной ценой и переносе наименьшего в этом цикле количества грузов вдоль этого цикла. В процессе такого преобразования план остается опорным и суммарная стоимость перевозок шаг за шагом уменьшается. Процесс следует продолжать до тех пор, пока не останется циклов с отрицательной ценой. Получившийся в результате план, очевидно, будет оптимальным. В нашей "игрушечной" задаче таких циклов, как легко убедиться, нет уже после первого циклического переноса. Таким образом, таблица перевозок (2) представляет собой оптимальный план перевозок для нашей задачи. В теории линейного программирования разработаны простые методы, позволяющие автоматически находить циклы с отрицательной ценой. Мы не будем на них останавливаться. Заметим только, что описанная методика выделения циклов с отрицательной ценой и преобразования одного опорного плана в другой посредством циклических перестановок приводит к очень эффективным алгоритмам решения транспортных задач. Заметим также, что если "Запасы" поставщиков и "Заказы" потребителей выражены целыми числами, то и все перевозки в оптимальном плане, как очевидно из самого метода решения задачи, будут целыми. Напомним, что общие алгоритмы решения ЛП-задач (например, симплекс-метод) отнюдь не гарантируют получения целочисленных решений, даже если во всех ограничениях фигурируют целые числа. Общая формулировка транспортной задачиПрежде чем перейти к решению более или менее значительных транспортных задач на компьютере с помощью MS-Excel, остановимся на описании общей формулировки транспортной задачи, тем более что она полностью соответствует организации данных на листе MS-Excel. Итак, при постановке транспортной задачи необходимо прежде всего задать таблицу транспортных издержек для перевозок единицы груза cijот i-го поставщика к j-му потребителю. Эта таблица имеет т строк (по числу поставщиков) и п столбцов (по числу потребителей). Таблица перевозок Xij имеет те же размеры (m*n) и содержит переменные решения. Необходимо также задать запасы поставщиков, готовые к вывозу (на рисунке это столбец Si) и величины заказов потребителей (на рисунке это строка Dj). Требования вывезти запасы каждого i-го поставщика и удовлетворить заказ каждого j-го потребителя означают соответственно, что сумма переменных решения вдоль каждой i-й строки должна быть равна запасу этого поставщика Si, а сумма переменных решения вдоль каждого j-го столбца должна быть равна заказу соответствующего потребителя DjНаконец, чтобы получить целевую функцию (суммарные издержки), необходимо рассмотреть суммы произведений каждой строки таблицы транспортных издержек на соответствующую строку таблицы перевозок и сложить их, суммируя по i от 1 до т. Это и даст двойную сумму, показанную на вкладке 2.

Решение транспортной задачи с помощью MS-Excel Для практического решения транспортной задачи с помощью MS-Excel рассмотрим чуть более сложный пример. Пусть имеются 4 поставщика и 5 потребителей. Издержки перевозки единицы груза от i-го поставщика в j-й пункт назначения, запасы поставщиков и заказа потребителей даны в таблице. Оптимизировать план перевозок. D1 D2 D3 D4 D5 Запасы S1 13 7 14 7 5 30 S2 11 8 12 6 8 48 S3 6 10 10 8 11 20 S4 14 8 10 10 15 30 Заказы 18 27 42 26 15 Организуйте данные так, как показано на рис. 22. 1. В ячейках I4-I7 - суммы произведения цены перевозки единицы груза на объем перевозки от i-го поставщика к любому потребителю. В ячейке 18 сумма этих сумм (т.е. двойная сумма) - целевая функция, которую нужно минимизировать. a) В ячейках I11:I14 — ограничения на количества груза, которые нужно увезти от каждого поставщика. b) В ячейках B16:F16 - ограничения на количества груза, которые нужно привезти к каждому потребителю. 2. Вызовите "Поиск решения": a) Целевая ячейка: I8, - Мин b) Изменяя ячейки: B11:F14 c) Ограничения: B11:F14 ≥ 0 (перевозки неотрицательны) 111:114 = 0 (ограничения на количества груза от каждого поставщика) B16:F16 = 0 (ограничения на количества груза каждому потребителю) При такой организации данных все перевозки окажутся целыми числами (если целыми являются числа в колонках "Запасы" и строке "Заказы"). Однако не следует требовать явно, чтобы переменные В11-F14 были целыми!3. Проверьте, что в полученном решении ровно т + п - 1 ненулевых перевозок. 4. Повторите расчет, максимизируя транспортные издержки, чтобы оценить отличие наилучшего варианта от наихудшего. 5.2. Осложнения транспортной задачи Как уже отмечалось выше, эффективные методы решения транспортной задачи применимы только при условии, что она сбалансированная, т.е. если сумма запасов, которые поставщики хотят вывезти, равна сумме заказов потребителей. На практике нередко встречаются случаи, когда сумма запасов превышает сумму заказов (излишек запасов) или, наоборот, сумма запасов меньше, чем сумма заказов (дефицит запасов). В первом случае часть запасов, очевидно, должна остаться на складах поставщиков, и дополнительный вопрос при этом состоит в том, сколько грузов не вывозить (оставить на складе) у каждого поставщика, чтобы сумма транспортных издержек при выполнении заказов потребителей была бы минимальной. Во втором случае дополнительный вопрос состоит в том, как распределить дефицит между потребителями. Разумеется, в реальности этот случай сложнее для менеджера, отвечающего за доставку заказов потребителям. Решение проблемы будет, по-видимому, определяться ценностью каждого из потребителей для поставщика и исходом переговоров. Однако если предположить, что все потребители одинаково ценны (или, точнее, одинаково безразличны) для поставщика дефицитного груза и проблема состоит только в том, чтобы подешевле развезти весь имеющийся на складах поставщика товар, то этот второй случай с точки зрения оптимизации издержек мало чем отличается от первого. Несбалансированность: излишек запасовВ случае излишка запасов, т.е. когда добавим в таблицу транспортных издержек и в таблицу перевозок по одному лишнему столбцу. Это можно трактовать так, как если бы появился еще один, фиктивный, потребитель. Потребуем, чтобы заказ этого "потребителя" в точности равнялся разности между суммой всех запасов и суммой всех заказов а издержки перевозок грузов к нему от любого поставщика были равны нулю. Например, допустим, что в нашей первой задаче о перевозке песка с двух карьеров на 3 завода производительность первого карьера не 100, а 150 грузовиков в день. Тогда задача становится несбалансированной: потребность заводов — 300 грузовиков с песком в день, а карьеры могут добывать 350. В этом случае нужно снизить добычу песка на каждом из карьеров. Но сколько грузовиков нужно ежедневно не загружать на первом карьере и сколько - на втором? В соответствии со сформулированным рецептом добавим 4-й столбец, представляющий фиктивного потребителя с нулевыми ценами перевозок и с заказом, равным 50 (разница между запасами (150 + 200) и заказами от реальных заводов (80 + 90 + 130)). Тогда переменные Х14и Х24покажут, сколько грузовиков песка нужно оставить (т.е. не отправлять на заводы, не добывать, хотя это и позволяют производственные мощности карьеров) соответственно на первом и на втором карьерах.

topuch.ru

Методы оптимизации управления для менеджеров

МЕТОДЫ ОПТИМИЗАЦИИ УПРАВЛЕНИЯ для МЕНЕДЖЕРОВ Компьютерно-ориентированный подход Содержание Вместо предисловия ............................................................................................................................................. 3 ВВЕДЕНИЕ ........................................................................................................................................................... 4 1.1. Курс "Количественные методы в менеджменте" в программе МВА ....................................................... 4 Какие вопросы рассматриваются в курсе "Количественные методы в менеджменте"? ........................... 4 Количественные модели и методы в бизнесе и управлении ........................................................................ 4 Роль менеджера в эффективном использовании количественных методов ............................................... 5 Миссия курса "Количественные методы в менеджменте" ........................................................................... 5 Место курса "Количественные методы в менеджменте" в программе МВА ............................................. 5 Методика изложения материала курса ........................................................................................................... 6 Компьютерная поддержка курса ..................................................................................................................... 6 Основное содержание курса "Количественные методы в менеджменте" .................................................. 6 Как работать с этой книгой? ............................................................................................................................ 7 1.2. Принятие решений в условиях определенности ........................................................................................ 7 Примеры ситуаций принятия решений в условиях полной определенности ............................................. 8 Целевая функция .............................................................................................................................................. 9 Переменные решения ....................................................................................................................................... 9 Параметры модели ........................................................................................................................................... 9 Ограничения ...................................................................................................................................................... 9 Контрольные вопросы к разделу 1 ................................................................................................................. 9 2 МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.................................................................................. 10 2.1. Оптимальный план выпуска продукции мебельного цеха (Product Mix) ........................................... 11 Формализация примера и основные соотношения ..................................................................................... 11 Решение задачи об оптимальном плане выпуска продукции с помощью Excel ...................................... 12 2.2. Мини-кейс "На кондитерской фабрике". .................................................................................................. 14 Формализация мини-кейса и основные соотношения ................................................................................ 14 Решение мини-кейса "На кондитерской фабрике" с помощью Excel ....................................................... 15 Предубеждение о целочисленном ограничении .......................................................................................... 17 Заключение к разделу 2 ................................................................................................................................. 17 Контрольные вопросы к разделу 2 ............................................................................................................... 17 Примеры для самостоятельного анализа к разделу 2 ................................................................................. 18 3 АНАЛИЗ ОПТИМАЛЬНОГО РЕШЕНИЯ ЛП-ЗАДАЧ ............................................................................... 19 3.1. Графическое решение задачи об оптимальном плане выпуска продукции мебельного цеха ............. 20 Упражнение по использованию отчета об устойчивости: влияние изменений в ценовых коэффициентах ............................................................................................................................................... 23 3.2. Двойственная задача. Теневые цены ......................................................................................................... 23 Решение двойственной задачи об оптимальном плане выпуска продукции мебельного цеха с помощью MS-Excel ........................................................................................................................................ 26 Анализ решения двойственной задачи ......................................................................................................... 27 Упражнение по использованию отчета об устойчивости: влияние изменений в правых частях ограничений .................................................................................................................................................... 28 3.3. Мини-кейс "На кондитерской фабрике". Акт 2 (Жаль... ведь мы все так любим "Батончик"!) .......... 29 Комментарии к мини-кейсу ........................................................................................................................... 30 Заключение к разделу 3 ................................................................................................................................. 31 Контрольные вопросы к разделу 3 ............................................................................................................... 32 Примеры для самостоятельного анализа к разделу 3 ................................................................................. 32 4 ИСПОЛЬЗОВАНИЕ ЦЕЛОЧИСЛЕННЫХ ПЕРЕМЕННЫХ В ЛП-ЗАДАЧАХ ....................................... 35 Условие целочисленности ............................................................................................................................. 35 Проблемы типа "брать/не брать". Логические переменные ....................................................................... 36 4.1. Проблема постоянных издержек в линейном программировании. Мини-кейс "На кондитерской фабрике". Акт 3 (Проблема учета постоянных издержек) ............................................................................. 36 Анализ 3-го акта мини-кейса ―На кондитерской фабрике‖........................................................................ 37 Организация данных для анализа 3-го акта мини-кейса на листе MS-Excel ............................................ 38

4.2. Оптимальный план размещения предприятий ......................................................................................... 38 Анализ примера .............................................................................................................................................. 38 Организация данных на листе MS-Excel ...................................................................................................... 39 Заключение к разделу 4 ................................................................................................................................. 40 Контрольные вопросы к разделу 4 ............................................................................................................... 40 Примеры для самостоятельного анализа к разделу 4 ................................................................................. 40 5 ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ .................................................................. 42 5.1. Организация оптимального снабжения ..................................................................................................... 42 Переменные, целевая функция и ограничения модели .............................................................................. 42 Опорный план ................................................................................................................................................. 43 Метод "северо-западного угла". Циклы ....................................................................................................... 44 Общая формулировка транспортной задачи ................................................................................................ 45 Решение транспортной задачи с помощью MS-Excel ................................................................................. 46 5.2. Осложнения транспортной задачи ............................................................................................................. 46 Несбалансированность: излишек запасов .................................................................................................... 46 Несбалансированность: дефицит запасов .................................................................................................... 47 Запрещенный маршрут .................................................................................................................................. 47 5.3. Задача о назначениях .................................................................................................................................. 48 Постановка задачи: Расстановка рабочих по операциям ........................................................................... 48 Пример для решения с помощью MS-Excel: Построение команд ............................................................. 48 Решение ........................................................................................................................................................... 49 Анализ решения. Расчеты типа "что, если..." .............................................................................................. 49 Заключение к разделу 5 ................................................................................................................................. 52 Контрольные вопросы к разделу 5 ............................................................................................................... 53 Примеры для самостоятельного анализа к разделу 5 ................................................................................. 53 Применение методов линейного и целочисленного программирования в реальном бизнесе ................... 55 6 УПРАВЛЕНИЕ ЗАПАСАМИ (в пренебрежении случайными вариациями спроса) ............................... 56 Важность проблемы управления запасами .................................................................................................. 56 Фундаментальный вопрос управления запасами ........................................................................................ 57 Незавершенная работа (Work-in-process) ..................................................................................................... 57 Функции запасов ............................................................................................................................................ 57 6.1. Издержки по формированию и содержанию запасов .............................................................................. 58 6.2. Модель экономичного размера заказа ....................................................................................................... 60 Основные допущения и параметры модели ................................................................................................. 60 Выражения для издержек хранения и оформления заказа ......................................................................... 60 Формула для оптимального (экономичного) размера заказа ..................................................................... 61 Проблемы применения оптимального решения на практике .................................................................... 62 Анализ устойчивости оптимального решения............................................................................................. 63 Модификации модели экономичного размера заказа ................................................................................. 64 6.3. Модель производства оптимальной партии продукции .......................................................................... 64 Пример: План работы универсальной производственной линии .............................................................. 64 Формула для оптимального размера партии ............................................................................................... 65 Анализ примера об универсальной производственной линии ................................................................... 65 6.4. Модель планирования дефицита ................................................................................................................ 66 Формулы для оптимального размера заказа и оптимальной величины дефицита .................................. 67 Пример: Продажа автомашин со стоянки .................................................................................................... 68 Анализ примера о продаже машин со стоянки ............................................................................................ 68 6.5. Учет оптовых скидок в модели экономичного размера заказа ............................................................... 70 Пример: Выбор поставщика для оптовых закупок ..................................................................................... 71 Анализ примера о выборе поставщика с помощью MS-Excel ................................................................... 71 6.7. Оптимальное управление запасами в условиях переменного (неслучайного) спроса ......................... 74 Пример: Планирование производства детали на универсальной линии "с горизонтом" 8 недель ........ 74 Анализ примера о плане производства детали с помощью MS-Excel ...................................................... 74 Заключение к разделу 6 ................................................................................................................................. 76 Контрольные вопросы к разделу 6 ............................................................................................................... 76 Примеры для самостоятельного анализа к разделу 6 ................................................................................. 77

Применение методов управления запасами в реальном бизнесе .................................................................. 78 7 КОЛИЧЕСТВЕННЫЕ МЕТОДЫ УПРАВЛЕНИЯ ПРОЕКТАМИ (в пренебрежении случайными вариациями длительностей отдельных стадий проекта) ................................................................................ 79 7.1. Пример: Проект "Снеси-построй" ............................................................................................................. 79 Диаграмма Гантта ........................................................................................................................................... 80 Сетевые диаграммы ........................................................................................................................................ 81 7.2. Критический путь (СРМ) ............................................................................................................................ 83 Расчет ранних и поздних стартов и финишей для каждой стадии проекта .............................................. 83 Определение временных резервов для каждой стадии проекта "Снеси-построй" с помощью MS-Excel.......................................................................................................................................................................... 85 Упражнение: Влияние изменения длительности отдельных стадий на длительность проекта ............. 86 Выводы по упражнению ................................................................................................................................ 87 7.3. Сокращение длительности проекта. Соотношение длительность/издержки (CPMICost) ................... 87 Стоимость сокращения отдельных стадий проекта .................................................................................... 87 Расчет соотношения длительность/издержки для проекта ―Снеси-построй‖ .......................................... 88 Оптимизация длительности проекта ............................................................................................................ 90 7.4. Распределение финансовых ресурсов по времени в процессе выполнения проекта ............................ 91 Ограничение ежедневного расхода ресурсов .............................................................................................. 91 Таблица MS-Excel для расчета ежедневных расходов по проекту "Снеси-построй" .............................. 92 7.5. Использование программы MS-Project 2000 для планирования и анализа проектов ........................... 94 Ввод информации о проекте в MS-Project 2000. Определение критического пути ................................. 94 Информация о стоимости ресурсов и исследование соотношения длительность/издержки в MS-Project.......................................................................................................................................................................... 96 Заключение к разделу 7 ............................................................................................................................... 100 Контрольные вопросы к разделу 7 ............................................................................................................. 100 Примеры для самостоятельного анализа к разделу 7 ............................................................................... 100 Применение количественных методов управления проектами в реальном бизнесе ................................. 102 Ответы на контрольные вопросы .................................................................................................................... 103 Ответы к примерам для самостоятельного анализа ...................................................................................... 107 Литература ........................................................................................................................................................ 114 Глоссарий .......................................................................................................................................................... 114

topuch.ru

Методы оптимизации управления для менеджеров - Зайцев М.Г

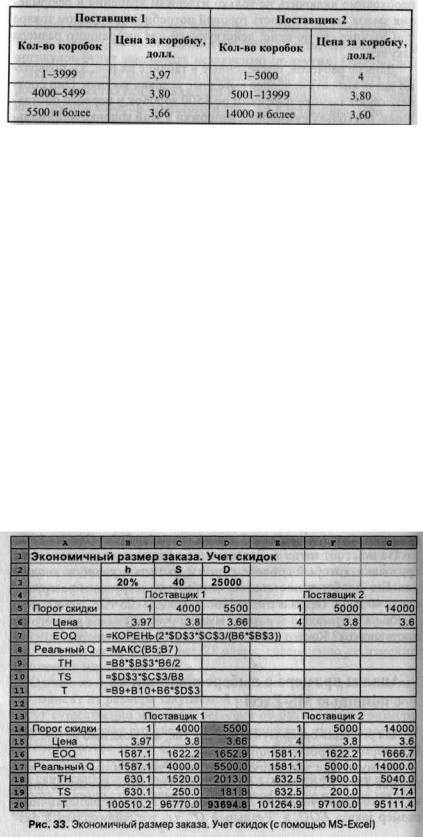
Баланс выигрышей от оптовых скидок и потерь от роста складских издержек при росте размера заказа удобно анализировать с помощью MS-Excel.

Пример: Выбор поставщика для оптовых закупок

Рассмотрим конкретный пример такого анализа. Автомобильный завод может закупать коробки с мелкой деталью у одного из двух поставщиков на следующих условиях.

Для оценки издержек хранения менеджмент использует внутреннюю норму доходности завода, равную 20%. Оформление заказа не стоит ничего. Доставка осуществляется на заводском грузовике, который способен увезти до 30 тыс. коробок за один раз. Его пробег к поставщику и обратно, загрузка и разгрузка стоят 40 долл. Годовая потребность завода - 25 тыс. коробок.

Каков оптимальный размер заказа с учетом скидок каждого из поставщиков? Какого поставщика следует предпочесть?

Анализ примера о выборе поставщика с помощью MS-Excel

Для решения организуйте данные так, как показано на рис. 33. Все формулы протягиваются вправо. Формулы для экономичного размера заказа и двух видов издержек 77/и 71Уне требуют пояснений. Обратите

внимание лишь на то, что для вычисления ТН иTS используется не экономичный размер заказаEOQ, а "РеальныйQ\ т.е. тот минимальный размер, который поставщик разрешит купить по данной цене. Например, если мы собираемся купить товар по цене 3,8 долл. за коробку у первого поставщика, то, хотя с точки зрения минимизации складских издержек нам выгоднее купить 1622 коробки, поставщик не позволит этого сделать, так как порог, начиная с которого действует эта цена, - 4 тыс. коробок. Таким образом, реальный объем закупки, который мы можем сделать по цене 3,8 долл., - 4 тыс. коробок. В этом смысл данной строки и формулы в ней (максимум между экономичным размером заказа 1622 и порогом, начиная с которого действует данная цена, - 4 тыс.).

При расчете последней строки - суммарных издержек в сумму необходимо включить не только издержки хранения и оформления заказа, но и стоимость годовой потребности в данном товаре при закупке его по цене, действующей для выбранного размера закупки.

Данные расчетов, приведенные в таблице на рис. 33, позволяют легко выбрать наиболее выгодные условия закупки. Они соответствуют закупке партиями по 5500 коробок у первого поставщика, поскольку суммарные издержки в этой колонке минимальны.

Характерно, что, хотя минимальная оптовая цена меньше у второго поставщика (3,6 долл. против 3,66 долл. у первого поставщика), порог, начиная с которого действует эта цена, слишком высок (14 тыс. против 5500 у первого поставщика). Поэтому выигрыш от использования такой скидки полностью "съедается" слишком высокими издержками хранения (5040 долл. против 2013 долл. у первого поставщика).

6.6. Оптимальный размер заказа для группы товаров

Если на складе торговой компании хранятся тысячи наименований товаров, вряд ли можно себе представить, что каждый из артикулов будут заказывать независимо от других. Обычно под "заказом" в такой компании понимают выбор ассортимента товаров и количества единиц каждого артикула для достаточно большой группы товаров от одного и того же поставщика. При этом затраты S на составление, оформление, размещение и доставку такого заказа для группы товаров лишь условно можно было бы распределить между отдельными его артикулами. В этом случае, хотя конкретные формулы для экономичного размера каждого артикула в заказе и для частоты, с которой нужно делать подобный заказ, отличаются от приведенных выше выражений дляEOQ и n, общая формулировка модели может быть полностью сохранена.

Пример: Одновременный заказ группы товаров

Фирма заказывает у одного и того же поставщика K=10 наименований товаров. Закупочные цены и оценки годового спроса на каждое наименование даны в таблице. Стоимость оформления, размещения и доставки каждого заказа для этой группы ТО варов составляет 60 долл. Издержки хранения для каждого наименования фирма оценивает в 10% в год от закупочной цены единицы товара.

-Сколько раз в год нужно делать заказ для этой группы товаров?

-Каковы будут при этом полные складские издержки фирмы за год для работы с этой группой товаров?

-Если распределить затраты S на оформление и размещение заказа равномерно между всеми артикулами так, что Si = 6 долл. для каждого, каковы будут оптимальные размеры и частота заказа для каждого из артикулов?

-Как сильно будут различаться издержки в случае независимого заказа каждого артикула и в случае заказа для группы товаров?

-Насколько реалистично предположение о затратах на независимый заказ каждого из артикулов?

Анализ примера о группе товаров с помощью MS-Excel

Эта задача легко может быть решена аналитически. Однако мы начнем с "эвристического", численного решения с помощью MS-Excelи надстройки "Поиск решения".

Сначала найдем размеры "экономичных размеров заказов" для каждого наименования в предположении, что издержки заказа для каждого наименования равны Si=6 долл.

На листе MS-Excel"Оптимальный заказ для группы товаров" (рис. 34) произведен расчет по формулам для экономичного размера заказа для каждого наименования и просуммированы издержки для всех товаров, если бы они заказывались независимо. Годовые издержки в этом случае составили бы 3042 долл., а частота заказов варьировала бы от 61 раза в год для товара №1 до 10 раз в год для товара №10 (заметим, что наименования товаров упорядочены по стоимости годовых запасов).

Если товары всех наименований заказываются одновременно, то следует задать число заказов в год для группы товаров п (это сделано в ячейке F27 рис. 34) и вычислять величину каждого заказа (в ячейках Е30:Е39) по формулеDi/n. Годовые издержки хранения для каждого наименования вычисляются так же, как раньше, а годовые издержки "оформления" заказа - это простопхS. Суммарные годовые издержки представлены в ячейке Н40.

Для того чтобы получить цифры, представленные на этом листе MS-Excel(рис. 34),

-задайте сначала п = 10 в ячейке F27,

-вызовите "Поиск решения" и задайте целевую ячейку Н40, а изменяемую ячейку - F27.

"Поиск решения" (в результате решения нелинейной оптимизационной задачи) найдет оптимальное значение

п= 30 и значение целевой функции (суммарных годовых издержек), равное 3612 долл.

Вслучае нелинейной оптимизации следует иметь в виду, что любой алгоритм ищет лишь локальный минимум. Минимумов может быть много, и алгоритм в зависимости от начальных условий может "сойтись" к различным минимумам. Поэтому в случае нелинейной оптимизации необходимо попробовать различные начальные условия поиска, чтобы увеличить уверенность в получении действительно минимально (или максимально) возможного результата для целевой функции. В данном случае можно повторить поиск, стартовав со значения n = 61.

К счастью, в данной задаче получается тот же самый результат.

Видно, что размеры и частоты в случае независимых для каждого наименования "оптимальных" заказов и в случае общего заказа для группы товаров разнятся очень сильно. Однако суммарные годовые издержки отличаются в этих случаях примерно лишь на 20%.

При этом нужно понимать, что в данном случае "размазывание" издержек заказа S по отдельным артикулам вряд ли реалистично. Представим себе, что для доставки товаров от поставщика компания использует грузовик. Стоимость аренды грузовика не зависит от количества перевозимого груза (если его объем и вес не превышают некоторых предельных значений). Если стоимость доставки груза составляет основную часть издержек заказаS=60 долл., то при вычислении "экономичного размера заказа" для каждого наименования, независимо от других,

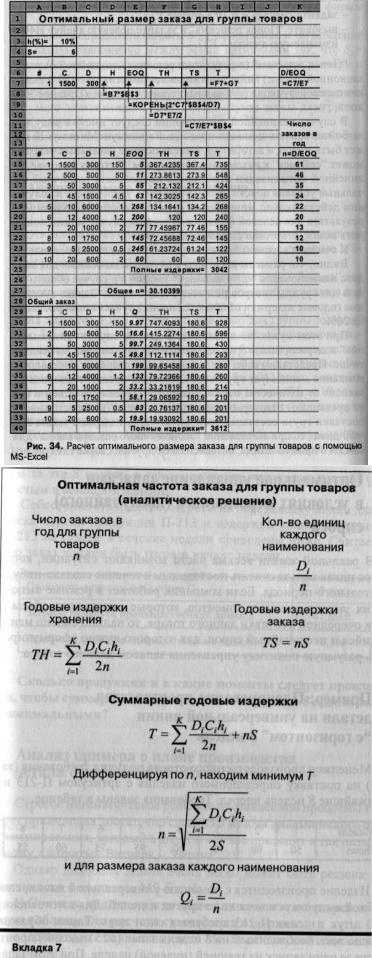
скорее следует использовать St= 60 долл., чемSt= 6 долл. Излишне говорить, что в этом случае годовые складские издержки будут намного выше (нетрудно проверить, что получится 9620 долл.), чем в случае оптимального заказа для группы товаров.

В заключение приведем аналитическое решение этой задачи для группы из К товаров.

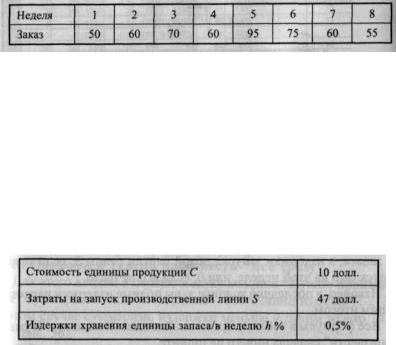
6.7.Оптимальное управление запасами в условиях переменного (неслучайного) спроса

Вреальной жизни весьма часто возникают ситуации, когда спрос никак нельзя считать постоянным в течение сколько-нибудьдлительного периода. Если компания работает в режиме выполнения заказов внешних клиентов, которые определяют объем и срок очередной поставки данного товара, то налицо сильно меняющийся и неслучайный спрос, для которого нужно сформулировать разумную политику управления запасом данного товара.

Пример: Планирование производства детали на универсальной линии "с горизонтом" 8 недель

Менеджер производственного отдела получил требования (заказ) на поставку определенного изделия с артикулом П-213на ближайшие 8 недель вперед. Требования заданы в таблице.

Изделие производится с помощью универсальной линии, способной выпускать и несколько других изделий. Для изготовления 100 штук изделия П-213требуется один день. Таким образом, можно весь необходимый на 8 недель запас (525 изделий) произвести за один запуск на текущей (нулевой) неделе. При этом запас будет храниться на складе в течение 8 недель, постепенно уменьшаясь.

Можно производить накануне очередной недели ровно столько, сколько нужно клиенту. Тогда склад будет пустовать, а количество запусков линии будет равно количеству недель.

Возможно и множество других вариантов, и менеджеру нужно выбрать тот, который соответствует минимальным полным издержкам за эти 8 недель, в предположении, что склад должен быть пустым в конце 8-йнедели.

Себестоимость изделия, затраты на переналадку линии для запуска партии продукции П-213и издержки хранения единицыП-213на складе в течение недели приведены ниже. Считается, что заказ должен быть готов в начале недели.

Сколько продукции и в какие моменты следует произвести, чтобы суммарные издержки за планируемые 8 недель были минимальными?

Анализ примера о плане производства детали с помощью MS-Excel

Строгое математическое решение поставленной проблемы требует применения достаточно сложною метода динамического программирования, который в данном случае приводит к так называемому алгоритму Вагнера - Уитина.

Однако подобная задача очень легко может быть решена эвристически с помощью MS-Excel.

1)Сначала подготовим данные для анализа и построим общую таблицу для расчета суммарных издержек.

• Организуйте данные на листе MS-Excclтак, как показано на рис. 35.

• Рассчитайте величину годового спроса и издержек хранения единицы продукции за год (формулы в ячейках D3 и D4). Рассчитайте размер EOQ (по формуле в ячейке F3). ВеличинаEOQ не имеет прямого отношения к данной задаче, но ее интересно использовать как одну из пробных стратегий для лучшего понимания особенностей данной проблемы.• Формулы основной таблицы имеют совершенно прозрачный смысл.

Запас на складе на текущей неделе, очевидно, равен запасу, оставшемуся с прошлой недели, плюс партия произведенной продукции, минус заказ, отправленный клиенту.

Издержки хранения - это h% от стоимости хранимого на складе запаса, а издержки запуска новой партии равны S, если такой запуск был на этой неделе, или 0, если его не было.

Наконец, в последней колонке даны полные издержки нарастающим итогом.

Все формулы в таблице протягивайте вниз. В колонку "Нужно произвести" сначала ничего не пишите.

2)Попробуем простую методику "Размер партии равен заказу (Lot-for-Lot)".

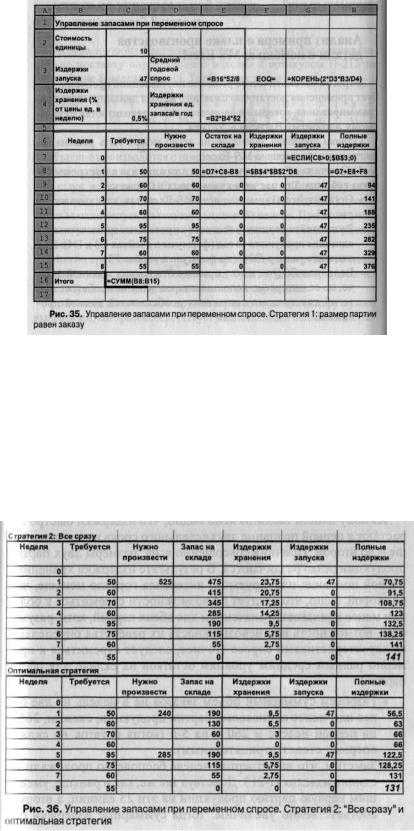
•Введите в колонку "Нужно произвести" значения, равные значениям в колонке"Требуется".

•Прочтите значения суммарных издержек и остатка на складе в конце планируемого периода в соответствующих колонках в нижней строке таблицы.

Суммарные издержки равны 376 у.е. (рис. 35).

3) Попробуем теперь произвести "Все сразу".

Для этого введем в первую ячейку колонки "Нужно произвести" суммарный заказ на 8 недель - 525 единиц

изделия П-213.И этом случае суммарные издержки меньше и равны только141 v.e. (рис. 36).

4) Рассмотрим теперь методику, включающую экономичный размер заказа EOQ.

•Введите в первую ячейку колонки "Нужно произвести" рассчитанное вами значениеEOQ.

•Найдите в колонке "Запас на складе" строчку с первым отрицательным значением и введите в колонке"Нужно произвести" на этой строчке значениеEOQ.

•Прочтите значения суммарных издержек и остатка на складе в конце планируемого периода.

•Подумайте, не лучше ли было бы в эту строчку ввести не EOQ, акакое-нибудьдругое число? Какое? Конечно, нетрудно догадаться, что произвести нужно неEOQ, а именно такое количество изделий, которого

не хватает для выполнения всех оставшихся заказов (чтобы остаток на складе в конце восьминедельного периода равнялся нулю).

Это, однако, еще не все. Приглядевшись, можно заметить, что на неделе непосредственно перед запуском новой партии остаток на складе составляет 16 единиц. Понятно, что лежать им без дела целую неделю ни к чему.

Поэтому можно партию, произведенную на первой неделе, уменьшить на эти 16 единиц (335 единиц), что, несомненно, снизит издержки хранения. Понятно, что вторую партию нужно на эти 16 единиц увеличить (190 единиц).

В результате суммарные издержки оказываются чуть меньше, чем при стратегии "Все сразу", - 140,5 у.е.

5) Оптимальная стратегия.

Из полученной таблицы ясно видно, что издержки быстро нарастают в первой половине двухнедельного срока и гораздо меньше - во второй. Причина совершенно ясна: размеры двух партий продукции резко различаются. В результате издержки хранения в первой половине планируемого интервала гораздо меньше, чем во второй. Ясно, что следует по возможности стремиться к более или менее одинаковым значениям для обеих партий, хотя, разумеется, возможность или невозможность их равенства определяется характеристиками спроса (точнее, следует стремиться к примерно равным средним уровням остатков на складе для обеих партий).

•Разобьем суммарный объем заказов на 8 недель на две более или менее одинаковые партии продукции, скажем, 265 -напервой неделе и 260 - на5-й(когда остаток на складе впервые станет отрицательным).

•Заметим, что на четвертой неделе бесполезно пролежали 25 единиц изделия П-213.Действуя так же, как и раньше, уменьшим первую партию продукции на эти 25 единиц, а вторую соответственно увеличим. Тогда суммарные издержки составят 131 у.е., что на 10 единиц меньше, чем в стратегии "Все сразу" (рис. 36).

Можно в принципе попробовать разбить суммарный заказ в 525 единиц на 3 примерно одинаковые партии продукции. Однако ясно, что вряд ли уменьшение размеров партий продукции в этом случае приведет к большему снижению издержек хранения, чем при переходе от одной партии ("Все сразу") к двум (240 и 285), а увеличение издержек запуска по-прежнемусоставит 47 у.е. Проверка действительно показывает, что наилучшее разбиение на 3 партии (180, 155 и 190) дает суммарные издержки 164,25 у.е, что существенно больше, чем при разбиении на 2 партии.

Итак, хотя в данном случае модель экономичного размера заказа не является оптимальной стратегией управления запасами, лежащая в ее основе концепция баланса переменных издержек хранения и постоянных издержек заказа (или запуска новой партии продукции) остается весьма плодотворной и позволяет на основе несложной игры с электронной таблицей быстро определить оптимальную стратегию.

Заключение к разделу 6

Основной вопрос, рассматриваемый в различных моделях и примерах этого раздела: Какова должна быть величина товарного

запаса на складе, величина оптового заказа или величина выпускаемой партии продукции, чтобы минимизировать складские издержки при заданном постоянном или непостоянном, но известном спросе?

При ответе на этот вопрос необходимо прежде всего выделить и правильно оценить два типа издержек:

•издержки хранения, пропорциональные количеству хранимых единиц запаса, стоимости единицы запаса и времени хранения. Коэффициент пропорциональности есть удельные издержки храненияН в расчете на единицу запаса в год. Это переменные издержки;

•издержки по запуску новой партии продукции (в производстве) или затраты на формирование, оформление и доставку заказа (в торговле). Это постоянные издержки. Они не зависят от величины предполагаемой партии продукции или величины заказа.

Простейшие модели управления запасами - модель экономичного размера заказа и модель оптимальной партии продукции - минимизируют сумму этих двух типов издержек в условиях заданного и постоянного спроса.

Модель с планированием дефицита исследует (в тех же предположениях) дополнительную возможность уменьшения суммарных складских издержек за счет сознательного допущения дефицита и введения системы предварительных заказов. Эта система требует учета еще одного типа издержек, связанного с поддержанием системы предварительных заказов и компенсацией частичной потери "доброго отношения" клиентов из-запостоянного дефицита. Модель эффективна при работе с весьма дорогостоящими запасами.

Все рассмотренные в разделе модели дают надежные оценки оптимальных размеров заказов (партий продукции), устойчивые к ошибкам в данных об издержках и других необходимых параметрах. Последнее весьма важно, так как используемые в моделях данные всегда носят характер статистических оценок и не могут быть "точно измерены". В связи с этим рекомендации, данные в моделях, следует использовать не как догму, а как полезный ориентир при выборе оптимальной тактики управления запасами.

Применение идеи о минимизации суммы двух основных типов издержек (переменных издержек хранения и постоянных издержек формирования, оформления и доставки заказа или издержек по запуску новой партии продукции) оказывается плодотворным и в тех случаях, когда предположения простых перечисленных выше моделей не выполняются, а именно:

- при учете оптовых скидок, когда стоимость единицы запаса, а значит, и издержки хранения зависят от размера заказа; - при оптимизации заказа для партии различных типов запасов;

- при рассмотрении вопроса о количестве запусков производственной линии и об оптимальных величинах партий продукции, когда речь идет об удовлетворении переменного во времени спроса.

Аналитический поиск минимума суммарных издержек в этих случаях может оказаться весьма сложным. Однако реализация эвристических методик поиска минимума издержек с помощью MS-Excelпозволяет быстро получить если не всегда оптимальное, то по крайней мере "очень хорошее" решение.

Контрольные вопросы к разделу 6

1.Перечислите основные функции запасов. Содержит ли ваша фирма какие-либозапасы? Какова их функция в работе вашей фирмы?

2.Что называется издержками хранения? Объясните, почему это переменные издержки. Можно ли назвать издержки хранения фактическими затратами или это всегда упущенные возможности?

3.Перечислите возможные составляющие издержек хранения. Оцените издержки хранения основных запасов вашей фирмы.

4.Почему можно говорить лишь об оценке, а не о точном определении (расчете) издержек хранения?

5.Из чего складываются издержки оформления заказа для фирмы оптовой торговли?

6.В какой вид издержек нужно включать фактические затраты на содержание склада (аренда помещения, оплата коммунальных услуг, I труда кладовщиков и грузчиков)? Влияют ли эти затраты на выбор оптимального размера заказа конкретного запаса? Почему?

7.Каковы основные допущения модели экономичного размера заказа? Насколько они реалистичны?

8.Объясните вид зависимости полных складских издержек от величины заказа (рис. 28). Почему всегда существует оптимальный размер заказа, минимизирующий издержки?

9.Насколько важны неточности в определении издержек хранения I и издержек оформления заказа при оценке величины экономичного размера заказа EOQ?

10.Если по практическим соображениям вам удобно увеличить I (уменьшить) размер заказа на 40% по сравнению с EOQ, на сколько j примерно возрастут полные складские издержки?

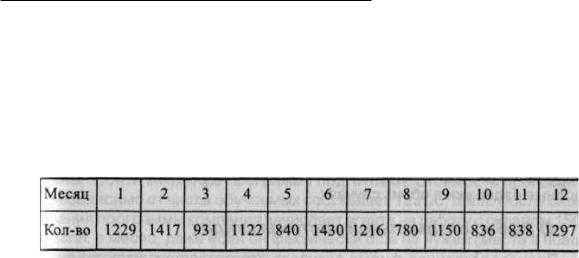
Средняя стоимость запасов на складе в ттеченигода

11.Допустим, что фирма может либо произвести партию продукции на собственной производственной линии с издержкой запуска линии S, либо закупить эту партию у внешнего поставщика с затратами на оформление заказа, так же равными S. Что придется делать чаще: запускать собственную линию или делать внешний заказ? Что выгоднее?

12.Объясните, в чем состоит отличие модели с планированием дефицита от модели экономичного размера заказа. Почему оптимальный размер заказа в этой модели всегда выше, чем EOQ?

13.В модели с планированием дефицита полные издержки всегда ниже, чем в модели EOQ. Докажите это. Если это так, то какие сомнения могут возникать относительно ее практического применения?

14.Объясните, каким образом учет оптовых скидок может изменить оптимальный размер заказа по сравнению с определенным в модели EOQ?

Примеры для самостоятельного анализа к разделу 6

1) Критерий скорости "оборачиваемости" склада

Эффективность работы склада часто измеряют с помощью отношения, характеризующего скорость оборачиваемости финансовых средств, вложенных в запасы (turnover ratio -TR):

TR Стоимсть ттоваро проданных со склада в ттеченигода.

Означает ли высокое значение TR эффективность работы склада на самом деле?

Определите величину TR в зависимости от D,Н и S. К какой стратегии подталкивает менеджера склада этот критерий (особенно если не он отвечает за эффективность продаж)?

Рассчитайте TR, если на складе используется модель экономичного размера запаса. Как изменитсяTR при увеличенииD, И илиS в этом случае?

Указание

Обозначьте стоимость единицы товара через С. Стоимость товаров, проданных со склада за год, определяется годовой потребностью D, а средняя стоимость запасов на складе - средним уровнем запаса (Q/2, где Q - размер единичного заказа).

2) Оптимальное управление запасами на стадионе

Большой крытый стадион на 100 тыс. зрителей вынужден из-заестественного износа и варварского поведения болельщиков постоянно заменять часть пластиковых кресел. В последние 12 месяцев меняли следующее число кресел (см. таблицу).

Кресла заказывают у постоянного поставщика по цене 150 руб./шт. Гак как склады стадиона очень большие, администрация заказывает один раз в год по 15 тыс. кресел (как рекомендовали специалисты4 года назад). Стоимость заказа составляет 10 тыс. руб.,

так как для стадиона делают фирменные кресла с соответствующей символикой и это требует переналадки оборудования на фабрике. Демонтаж сломанного и монтаж нового кресла стоят 30 руб./шт. Хранение кресел на складе формально ничего не стоит.

Как вы полагаете, является ли существующий план заказов оптимальным? Почему? Если средний доход по рублевым вложениям в регионе составляет не менее 24% в год, то можно ли изменить план заказов так, чтобы снизить издержки? Приведите план заказов, обеспечивающий минимальные издержки.

Указание

Подумайте, какие данные вам необходимы для определения издержек хранения (а какие - нет). Найдите годовой спрос по данным последних 12 месяцев. Рассчитайте EOQ. Рассчитайте полные издержки при варианте режима заказов, принятого на стадионе и в моделиEOQ.

Предложите удобную систему заказов и оцените ее издержки.

3) "Произвести товар у себя или закупить у внешнего поставщика?"

Производственная компания имеет универсальную линию для производства 10 различных видов деталей. Мощность линии для производства детали с артикулом Ф-413составляет 8 тыс. деталей в год. Потребность в этой детали на сборочном конвейере - 3 тыс. деталей в год. Стоимость переналадки линии для выпуска этой детали составляет 50 долл., а издержки хранения деталиФ-413на складе - 10% стоимости детали. Себестоимость деталиФ-413равна 23 долл.

Деталь Ф-413можно закупить у другого производителя по цене 25 долл. При этом расходы на оформление, размещение и доставку заказа составляют S = 40 долл. за заказ.

Какая из двух возможностей экономичнее?

Как изменится ответ, если S = 35 долл., 20 долл.?

Указание

Используйте формулы для EOQ иEBQ, вычислите и сопоставьте полные издержки в обоих случаях.

4) Выбор оптимальной системы скидок

Производственная фирма закупает ответственную электронную схему у внешнего поставщика. Отдел закупок рассматривает троих претендентов на поставку этой схемы. Первый поставщик предлагает следующую систему скидок:

до 3000 шт.	~	794 руб.
от 3000 до 5000 шт.	~	780 руб.
свыше 5000 шт.	~	770 руб.

Второй, более крупный поставщик предлагает более существенные скидки:

до 10 000 шт.	~	800 руб.
от 10 000 до 20 000 шт. ~		760 руб. свыше
20 000 шт.	~ 720 руб.

Третья, мелкая фирма не дает существенных скидок и готова поставлять продукцию небольшими партиями:

до 1500 шт.	~	800 руб.
от 1500 до 2500 шт.	~	790 руб.

свыше 2500 шт.

~ 782 руб.

Внутренняя норма доходности фирмы составляет около 30%, издержки, связанные с оформлением, доставкой и размещением заказа этих электронных схем, оцениваются в 90 000 руб. за заказ. Годовая потребность предприятия - 10 000 схем. Однако площадь складов позволяет хранить запас, в несколько раз превышающий годовую потребность.

У какого поставщика и какой величины нужно сделать заказ, чтобы минимизировать полные складские издержки для этого запаса?

Указание

Используйте методику расчета полных издержек, реализованную в разделе 6.5 "Учет оптовых скидок в модели экономичного размера заказа" (пример "Выбор поставщика для оптовых закупок").

5^ Частота набора и тренинга новых сотрудников

Быстро развивающейся компьютерной компании каждый год требуются 27 агентов для новых торговых представительств. Агенты должны пройти месячную программу подготовки. Стоимость программы независимо от числа обучаемых составляет 12 тыс. долл. После окончания программы компания зачисляет агента на работу с окладом 1500 долл. в месяц, даже если он фактически еще не нужен (места в новом представительстве еще нет).

Сколько раз в год следует производить набор новых групп для обучения на подготовительной программе, чтобы минимизировать затраты компании на подготовку новых агентов? Сколько обучаемых будет в каждой группе? Сколько "готовых"

агентов будут еще не определены на работу в момент начала работы новой программы?

Указание

Хотя описанная ситуация на первый взгляд не имеет ничего общего с задачами управления запасами, по форме она полностью подпадает под модель экономичного размера заказа. Установите, какие затраты фирмы соответствуют здесь "издержкам хранения", а какие -"издержкамоформления заказа" и примените формулу дляEOQ, чтобы определить размер группы для обучения на программе.

6^ План производственного отдела

Менеджер производственного отдела получил заказ на определенный вид продукции на следующие 10 недель. Для производства партии данной продукции необходимо настроить оборудование цеха, что влечет постоянную издержку в 100 у.е. Издержка хранения 1 единицы продукции на складе составляет 1 у.е. в неделю. Как спланировать выпуск данного вида продукции, чтобы минимизировать суммарные издержки запуска партии и хранения?

Указание

Используйте методику анализа данных в MS-Excel,предложенную в разделе 6.7 "Оптимальное управление запасами в условиях переменного (неслучайного) спроса", и "оптимальную стратегию", рассмотренную для примера "Планирование производства детали на универсальной линии "с горизонтом" 8 недель".

В данном случае, однако, решение, полученное вами по предложенной в разделе 6.7 методике, не будет самым хорошим. Попробуйте его улучшить, обратив внимание на столбец "Остаток на складе".

Применение методов управления запасами в реальном бизнесе

Blue Bell trims its inventory Jerry R. Edwards, Harvey M. Wagner and William P. Wood, Interfaces 15,#1,1985

Компания "Blue Bell" резко снижает объем запасов

Втечение 21 месяца компания "Blue Bell" уменьшила размеры своих запасов более чем на 31 %: с 371 до 256 млн. долл. без уменьшения объема продаж или снижения уровня обслуживания благодаря использованию количественных моделей и методов управления запасами. Успех обеспечили удачная комбинация инновационных подходов и энтузиазм менеджеров. Многие из этих моделей абсолютно стандартные, однако использование специфической системы маркировки сделало возможным их удачное практическое применение. Менеджмент уделил серьезное внимание развитию системы и обеспечению ресурсов, способствующих успеху проекта,

Development and implementation of an integrated inventory management program at Pfizer Pharmaceuticals P. P. Kleutghen and J. С McGce , INTERFACES 15, #1 1985

Развитие и применение интегральной программы управления запасами в компании "Pfizer Pharmaceuticals"

Вкомпании "Пфайзер" разработана и внедрена целостная система управления запасами для операций в масштабе США. Использована серия моделей оптимизации и количественных методов управления запасами, покрывающая всю сложную цепочку поставок компании. Реализация программы позволила снизить уровень складских запасов на 23,9 млн., а также уменьшить количество отсрочек в выполнении заявок на 95% за 3 года.

7 КОЛИЧЕСТВЕННЫЕ МЕТОДЫ УПРАВЛЕНИЯ ПРОЕКТАМИ (в пренебрежении случайными вариациями длительностей отдельных стадий проекта)

В этом разделе рассматриваются широко используемые на практике методики планирования и анализа проекта: метод критического пути (СРМ), соотношение "длительность - издержки" проекта{СРМ/ Cost), а также распределение ресурсов по времени выполнения проекта при заданных ограничениях.

Изучив материал раздела и реализовав описанные процедуры решения приведенных примеров на компьютере, вы

•познакомитесь с графическими способами представления проекта: диаграммами Гантта и сетевыми диаграммами;

•освоите методику нахождения критических стадий и временного резерва некритических стадий и научитесь оценивать влияние изменений длительности отдельных стадий проекта на сроки завершения проекта в целом;

•зная цену ускорения работ и сокращения длительности стадии на заданное время, сможете решить, какие стадии и на сколько требуется сократить, чтобы выполнить проект к заданному сроку с минимальными дополнительными издержками;

•научитесь использовать MS-ExcelиMS-Projectдля определения критического пути, временного резерва отдельных стадий и соотношения "длительность - издержки" проекта;

•научитесь использовать эвристический подход для пересмотра расписания проекта с целью удовлетворить дополнительные ограничения по расходованию ресурсов с помощью MS-Excel.

Управление проектами всегда рассматривалось как важная составляющая менеджмента. Сейчас, в условиях постоянных и быстрых изменений внешней среды бизнеса, все больше компаний перестраивают управление по типу матричной структуры с формированием рабочих групп по управлению отдельными проектами и все больше менеджеров оказываются вовлеченными в эту работу. Если вам придется выполнять работу по управлению проектом, полученные в этом разделе знания и навыки анализа проекта с помощью MS-ExcelиMS-Project,несомненно, окажутся востребованными.

Под проектом понимают совокупность операций (заданий, работ), которые нужно выполнить для достижения поставленной цели в ограниченное время, при ограниченных материальных, людских и финансовых ресурсах:

-строительство нового предприятия или жилого дома;

-ликвидация последствий стихийного бедствия;

-разработка нового продукта и технологии для его производства;

-проведение маркетинговой кампании;

-организация конференции;

-проведение аудита большой компании -

вот лишь некоторые примеры многочисленных деловых проектов.

Сложные проекты могут содержать тысячи операций, требующих различных затрат времени и ресурсов. Одни операции должны следовать в строгой очередности, другие могут выполняться независимо и параллельно. Отсрочка начала работ или задержка их завершения для некоторых операций может и не привести к удлинению проекта в целом, в то время как для других операций такие задержки критически влияют на срок выполнения проекта. Поэтому планирование, мониторинг и управление сложным проектом, правильное распределение ресурсов, выявление и концентрация внимания менеджера на ―критических‖ операциях, определяющих срок завершения проекта в целом, очень затруднительны без специальных методик и инструментов количественного анализа, рассмотрению которых и посвящен настоящий раздел.

Два наиболее широко распространенных в настоящее время метода - СРМ (английская аббревиатура

Critical Path Method, т.е. метод критического пути) и PERT (Program Evaluation and Review Technique,т.е. метод анализа и обзора проекта) - были развиты в 50-х годах двумя независимыми группами аналитиков.

Метод СРМ был разработан Дж. Келли и М. Уолкером в связи с планированием и координацией проектов реконструкции химических заводов корпорации "Дюпон". Этот метод предполагает планирование, анализ и управление проектом в условиях полной определенности, когда длительность всех операций, необходимых для выполнения проекта, хорошо определена.Метод PERT был создан в результате совместных усилий авиационной корпорации "Локхид", проектного бюровоенно-морскоговедомства США и консалтинговой фирмы "Буз, Ален & Гамильтон" в связи с необходимостью ускорить выполнение грандиозного проекта установки ядерных ракет на подводных лодках "Поларис". После успешного испытания советской ядерной бомбы в 1949 г. правительство США стремилось любой ценой опередить СССР в начавшейся гонке вооружений, и министерство обороны США придавало проекту "Поларис" первостепенное значение. В этом проекте принимало участие более 3 тыс. субподрядчиков. Он включал значительный объемнаучно-исследовательскихи проектных работ, длительность которых невозможно было определить точно. Вследствие этого разработчики методаPERT явно учли вероятностный разброс длительностей отдельных стадий проекта и особое внимание уделили оценкам вероятности завершения проекта к определенному сроку.

Оба метода дополняют друг друга и в настоящее время используются совместно. Однако, поскольку СРМ предполагает анализ проекта в условиях полной определенности, мы рассмотрим его в настоящем разделе, а рассмотрение методаPERT, включающего в анализ вероятностные аспекты, перенесем во вторую часть курса.

7.1. Пример: Проект "Снеси-построй"

Для иллюстрации основных этапов планирования и анализа проекта рассмотрим упрощенный пример проекта сноса старого здания в центре большого города и построения на его месте многоэтажного гаража.

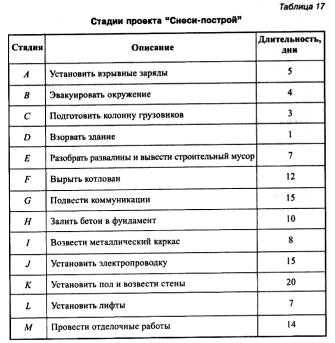
Проект содержит следующие крупные мероприятия по сносу дома:

• технические:

-установить взрывные заряды,

-взорвать здание,

-разобрать развалины и вывезти строительный мусор;

• организационные:

-эвакуировать окружение,

-подготовить колонну грузовиков;

• крупные строительные мероприятия по возведению многоэтажного гаража:

-вырыть котлован,

-подвести коммуникации,

-залить бетон в фундамент,

-возвести металлический каркас,

-установить электропроводку,

-установить пол и возвести стены,

-установить лифты,

-провести отделочные работы.

Каждое из перечисленных мероприятий может рассматриваться как независимая стадия проекта (или работа), требующая собственных материальных, финансовых и людских ресурсов. Для каждой стадии должна быть оценена длительность проведения работ, исходя из имеющихся ресурсов. В настоящем разделе мы будем считать, что эти длительности не подвержены случайным вариациям (условие "полной определенности"), но могут быть уменьшены путем вложения дополнительных финансовых средств.

Первый вопрос, возникающий при беглом взгляде на таблицу с описанием: сколько времени требуется для выполнения всего проекта? Искушение ответить на этот вопрос, просто просуммировав длительности отдельных стадий, очевидно, дает сильно завышенную длительность проекта (121 день). Поскольку разные стадии требуют использования различных трудовых ресурсов, понятно, что некоторые из них могут выполняться независимо друг от друга и параллельно. Вместе с тем некоторые стадии не могут быть начаты до того, как завершены будут другие стадии.

Например, невозможно взорвать здание, не установив взрывные заряды и не проведя эвакуацию окружения. В то же время подготовка колонны грузовиков (стадия С) может проводиться параллельно стадиям А, В иD, но должна быть закончена до начала стадииЕ (разбор развалин и вывоз мусора).

Таким образом, с самого начала планирования и анализа проекта необходимо четко представить себе взаимосвязи между отдельными стадиями и установить соотношения "предшественник - последователь" для всех стадий проекта.

Диаграмма Гантта

Допустим, что менеджер проекта, основываясь на знании современных строительных технологий и на здравом смысле, установил такие соотношения "предшественник - последователь" для стадий проекта.

Далее, наиболее простым инструментом, позволяющим получить некое наглядное представление о проекте и определить его длительность, является диаграмма Гантта. Такие диаграммы Генри Гантт впервые применил в начале века для минимизации времени выполнения последовательности машинных операций.

studfiles.net

Использование программы - Методы оптимизации управления для менеджеров

7.5. Использование программы MS-Project 2000 для планирования и анализа проектовРассмотренные выше в разделе 7 приемы и алгоритмы нахождения критического пути и расчета соотношения "длительность/издержки" (CPMICost) с помощью MS-Excel помогают ясно понять принципы, лежащие в основе этих методов планирования и управления проектами, однако требуют слишком много времени и интеллектуальных усилий для своей реализации, чтобы быть использованными в практическом менеджменте. При этом совершенно ясно, что эти алгоритмы вполне могут быть поручены компьютеру.В настоящее время на рынке программного обеспечения можно найти несколько программ, предназначенных для автоматизации процесса планирования, анализа и мониторинга проектов. Среди них Microsoft Project, Time Line, Primavera Project Planner, Spider Project. Мы не будем анализировать все эти программы, а приведем лишь краткое описание использования Microsoft Project для нахождения критического пути, получения диаграммы Гантта и сетевой диаграммы, а также расчета стоимости проекта и соотношения "длительность/издержки".Заметим, что MS-Project имеет прекрасный обучающий блок (Tutorial) и справочную систему (on-line Help), однако все это на английском языке (программа не русифицирована). Поэтому автор надеется, что повторение решения уже решенных выше (с помощью MS-Excel) задач анализа проекта "Снеси-построй" будет небесполезно.Ввод информации о проекте в MS-Project 2000. Определение критического пути1. Вызовите MS-Project 2000. Используя пункт меню Project _ Project Information, введите дату начала проекта, например на месяц вперед от сегодняшней даты (поскольку речь идет о планировании проекта).2. В колонку Task Name введите инициалы этапов (А, В,... М), а в колонку Duration - и их длительности.На этой стадии ввода информации MS-Project, на диаграмме Гантта, вес стадии изображены в виде прямоугольников, построенных от базовой линии - даты начала проекта(рис. 46).3. Следующий этап - задание соотношений "предшественник-последователь" между стадиями проекта. Стадии А, В и С не имеют предшественников. Поэтому начнем со стадии D. - Сделайте двойной щелчок в поле Task Name задачи D. - В Появившейся форме Task Information выберите вкладку Predecessors. - В ноле Task Name (имеется в виду имя предшественника) введите последовательно имена предшественников стадии D - А и B, по одному в каждой строке (рис. 47). Обратите внимание на вкладку Notes в том же окне. В нем вы можете ввести Ваши пометки относительно данной стадии (например, содержание задачи "Взорвать здание").Начальный этап ввода информации в MS-Project (названия и длительности стадий) соотношения "предшественник - последователь" еще не задан. - Введите предшественников для всех стадий проекта.

После этого MS-Project изобразит полную диаграмму Гантта (со связями между задачами, изображенными стрелками, но без указания критических стадий), вычислит длительность проекта, определит критический путь (хотя пока и не показывает его) и будет способна изобразить сетевую диаграмму проекта.4. Определите вычисленную длительность проекта. Для этого - выберите пункт меню Project_Project Information. - в появившемся окне Project Information нажмите кнопку Statistics и прочтите даты старта и финиша и длительность проекта {Duration).5. Вид изображенной диаграммы Гаи па можно изменить так, чтобы критические стадии были различимы.

- Выберите пункт меню Format_GanttChartWizard. Это вызовет мастер диаграммы Гантта, который шаг за шагом проведет вас через процесс преобразования вида диаграммы.- "Нажмите" кнопку Next. В появившемся окне Step 2 установите переключатель на отметке "Critical Path" ("Критический путь").- "Нажмите" кнопку Next. Мастер доставит вас сразу на 9-й шаг (Step 9). Мастер просит вас решить, какую еще информацию вы хотите видеть на диаграмме Гантта (ресурсы, даты). Для наших нынешних целей дополнительная информация не нужна. Поэтому поставьте переключатель в положение "No, thanks".- "Нажмите" кнопку Next. На следующем шаге (Step 13) вы можете выключить или оставить изображение связей между задачами в виде стрелочек (на ваше усмотрение).- "Нажмите" последовательно кнопку Next, в появившемся окне - кнопку Format it и затем - кнопку Exit Wizard.- Теперь критические стадии помечены красным цветом (рис. 49).6. Посмотрите сетевую диаграмму проекта. Для этого- "Нажмите" кнопку-иконку Network diagram на экране (слева от колонки номеров стадий).- Получившаяся сетевая диаграмма слишком крупная, так как содержит много деталей относительно каждой стадии. Уменьшите ее, исключив эти детали. Выберите пункт Format_Layout и установите флажок в квадратик "Hide all fields except ID" в правом нижнем углу окна Layout (рис. 50).- Чтобы вернуться вновь к описанию стадий и диаграмме Гантта, нажмите кнопку-иконку Gantt chart, расположенную на экране в той же колонке иконок, что и кнопка-иконка Network diagram, прямо над ней.7. MS-Project может также предоставить информацию о раннем и позднем старте и о временном резерве для каждой стадии. Для получения этой информации- выберите пункт меню View_Table и- в открывшемся подменю выберите пункт Schedule,- отодвиньте вертикальную границу диаграммы Гантта влево и прочтите искомую информацию.Диаграмма Гантта с изображением критических стадий (введены названия, длительности стадий и соотношения "предшественник - последователь"):a) Start, Finish - даты ранних старта и финиша,b) Late Start, Late Finish даты поздних старта и финиша,c) Free Slack и Total Slack. Последний - это временной резерв, рассчитанный в MS-Excel в разделе 7.2.Free Slack показывает, насколько можно сдвинуть данную стадию, не отодвигая стар г последователя, независимо оттого, является последователь критической стадией или нет.Если последователь - критическая стадия, то Free Slack равен Total Slack. Если последователь - некритическая стадия, то, даже если данная стадия сама некритическая, Free Slack равен нулю. Пример такой стадии в проекте "Снеси-построй" - стадия F. Это связано с тем, что, как указывалось в выводах к упражнению после раздела 7.2, последовательные некритические стадии фактически имеют общий временной резерв.8. Поэкспериментируйте с длительностью критических и некритических стадий. Повторите упражнение "Влияние изменения длительности отдельных стадий на длительность проекта", приведенное после раздела Информация о стоимости ресурсов и исследование соотношения длительность/издержки в MS-Project Рассмотрение с помощью MS-Project задачи о соотношении между величиной сокращения стадий проекта и его стоимостью, решенной в разделе 7.3, можно провести, комбинируя MS-Project и MS-Excel (или калькулятор). В MS-Project нужно уменьшать длительность отдельных стадий, следить за тем, что при этом уменьшается

длительность проекта (не появляется новых критических стадий), а стоимость сокращения проекта вычислять отдельно в MS-Excel (при этом понадобится нижняя часть таблицы с рис. 43) или просто на калькуляторе. Понятно, что с точки зрения практического использования это не более чем примитивный паллиатив.Разумеется, MS-Project должна сама рассчитывать стоимость проекта и ее изменение при сокращении длительности проекта. Однако в отличие от рассмотренной в разделе 7.2 задачи в MS-Project задается не стоимость той или иной стадии проекта и ее возрастание при сокращении стадии, а стоимость использования ресурсов (материальных и трудовых) для выполнения работ по этой стадии. Расписание работ по проекту и его бюджет в MS-Project полностью определяются наличием тех или иных ресурсов, стоимостью их использования в рабочее время и в сверхурочные часы. По терминологии разработчиков, весь проект является "Efforts driven" или "Resources driven" ("Движимый ресурсами").Поэтому вместо цены сокращения стадии на 1 день и максимально возможного сокращения стадии, заданных в табл. 17 и использованных при анализе соотношения "длительность/издержки‖ в разделе 7.2, сейчас необходимо:- приписать каждой стадии свой ресурс;- рассчитать по данным табл. 17 стандартный и сверхурочный тарифы использования ресурсов для выполнения работ по каждой стадии;- ввести эту информацию в MS-Project.

Стандартный почасовой тариф (Std. Rate) легко рассчитать, зная нормальную длительность и нормальную стоимость стадии:Std. Rate = Нормальная стоимость/Нормальная длительность.Например, для стадии A: Std. Rate = 6 у.е./5 дней = 1,2 у.е./ день.Сокращение стадии на 2 дня будем трактовать как результат использования сверхурочной работы. Вместо 5 дней по 8 рабочих часов (всего 40 ч за 5 дней) рабочие отработают три дня: 8 ч по стандартному тарифу и 16/3 сверхурочных часов каждый день (всего 40 ч за 3 дня). Поскольку удорожание стадии при ее сокращении на 2 дня составляет 2 у.е. (ее полная стоимость после сокращения 8 у.е. вместо 6 у.е.) и поскольку это удорожание произошло за счет использования 16 сверхурочных часов (двух дней работы по сверхурочному тарифу), найдем, что сверхурочный тариф (Ovt. Rate) равенOvt. Rate = Std. Rate + Удорожание стадии / Кол-во сокращенных дней.Для стадии АOvt.Ratc=I,2+ 2/2-2,2 у.е./день.Таким образом, рассчитаны две последние колонки в табл. 22. В тех случаях, когда сокращение стадии невозможно, сверхурочному тарифу можно приписать очень большое число (так, чтобы ее сокращение было экономически невыгодно). Именно это сделано в табл. 22 для стадий В,D и L.Теперь можно автоматизировать процесс вычисления изменения стоимости Проекта при его сокращении, введя в MS-Project информацию о ресурсах и почасовую стоимость их использования в Стандартные рабочие часы (Std. Rate) и сверхурочно (Ovt. Rate).Проведем последовательной сокращение проекта на максимально возможное количество дней и найдем соответствующие стоимости этих сокращений, используя MS-Project, сокращая на каждом шаге выбранную стадию на 1 день и записывая результатысокращения в таблицу. День сокращения Стадия Суммарные издержки (Так же, как это делалось в разделе 7.2 с помощью MS-Excel.) Ввод информации о ресурсах в MS-Project1. Выберите пункт меню Window_Split. При этом экран разобьется на две части: в верхней части по- прежнему будет описание стадий проекта и диаграмма Гантта, а в нижней появятся формы для ввода информации (о ресурсах, предшественниках или последователях - в зависимости от текущих установок MS-Project).2. Вам необходимо установить в нижней части экрана форму с информацией о занятости ресурсов - Resource Work. Для этого- выделите нижнюю форму, щелкнув где-нибудь на ней, - выберите пункт меню Format Details,- в появившемся подменю выберите пункт Resource Work (рис. 51).3. Введите информацию об именах и почасовых стоимостях ресурсов, действуя следующим образом.- Выделите поле Task Name стадии в верхней части экрана, для которой собираетесь определять ресурс (начните со стадии A). Имя выделенной задачи появится в поле Name нижней формы (Resource Work).- Щелкните на поле Resource Name в нижней форме и введите имя ресурса, обозначив его так же, как и задачу (но строчной буквой). Нажмите кнопку Ok на нижней форме.- Дважды щелкните на имени вновь введенного ресурса. Появится форма Resorce Information.-Выделите вкладку Costs (Издержки). Появится форма (рис. 52), в которую нужно ввести стандартный и сверхурочный тарифы для данного ресурса, рассчитанные в таблице (см. выше). Не забудьте отметить, что это тариф за день (например, 1,2/d). После ввода этой информации нажмите кнопку Ok и форма исчезнет.- Щелкните по кнопке Next в нижней форме (Resource Work). В поле Name нижней формы (Resource Work) появится имя следующей стадии проекта. Повторите ввод информации о ресурсе для этой стадии и для всех последующих стадий проекта.- После введения информации о почасовых тарифах каждого из ресурсов MS-Project сосчитает стоимость проекта. Узнать величину этой стоимости можно, обратившись в пункт меню Project_Project Information и в появившемся окне Project Information нажав на клавишу Statistics.4. Примем, что для сокращения времени выполнения работ по данной стадии у нас есть только один путь - использование сверхурочного труда. В этом случае сокращение времени работ неизбежно приведет к удорожанию стадии. Для введения количества сверхурочных часов- щелкните в поле Ovt. Work нижней формы (Resource Work).- введите в это поле 8h сверхурочных часов, если вы хотите сократить длительность стадии на 1 день, 16h- для сокращения на 2 дня и т.д.,- проверьте, что стоимость проекта действительно увеличилась при введении сверхурочных часов, обращаясь в пункт меню Project_Projectlnformation_Statistics.5. Проверьте, что другие "способы" сокращения длительности стадии не приводят к увеличению длительности.- Если просто уменьшить продолжительность стадии в верхнем списке стадий, то MS-Project воспримет это как уменьшение объема работ по данной стадии и снизит стоимость проекта.- Если привлечь дополнительные ресурсы при выполнении этой стадии, увеличив процент использования ресурса в нижней форме Resource Work (например, со 100 до 200%), длительность стадии сократится вдвое, но стоимость проекта не изменится (вдвое больше рабочих сделают ту же работу за вдвое меньшее время, но при почасовой оплате это тс же самые издержки).6. Подумайте, какие стадии надо сокращать в первую очередь, а какие не надо (или нельзя) сокращать совсем. Используя MS-Project, сокращайте длительность проекта маленькими шагами: на каждом шаге только на один день. Следите внимательно, не изменился ли критический путь!- Сокращайте длительность тех стадий, которые вы считаете необходимым сократить для сокращения длительности проекта, с помощью увеличения Ovt.Work.- Проверяйте, как увеличилась стоимость проекта, обращаясь в пункт меню Project_Project Information_Statistics.7. Постройте таблицу ―Длительность/издержки‖В результате вы получите ту же табл. 19, но используя только MS-Project. Заключение к разделу 7Все стадии проекта делятся на два различных типа: критическиеи некритические. Увеличение длительности критических стадий или отсрочка их выполнения неизбежно ведут кудлинению проекта, вто время как некритические стадии имеют некоторыйвременнойрезерв, так что отсрочка их окончания врамках этого временного резерва не ведет кувеличению длительности проектаПри необходимости сокращения проекта совершенно бесполезно сокращать некритические стадии, так как это приведет только кувеличению их временного резерва, но никак не изменит длительности проектаСокращать следует только критические стадииСуществуют два основных способа графического представления проекта: диаграммаГантта исетевые диаграммыСпомощью диаграммыГантта легко определить длительность проектаОднако она не всегда позволяет отличить критические стадии от некритических, особенно всложных проектахСетевые диаграммы более наглядно передают временные соотношения "предшественник - последователь " между стадиями проекта и позволяют ввести понятие пути как непрерывной последовательности стадий проекта, идущей от его начала кконцуПуть на сетевой диаграмме, характеризуемый максимальной суммарной длительностью составляющих его стадий, называетсякритическими определяет продолжительность проекта вцеломВсе стадии, составляющие критический путь, являютсякритическими. Количество критических путей для данного проекта может быть больше одногоСетевые диаграммы позволяют наглядно отобразить критический путь (или несколько критических путей) ипроанализировать возможности возникновения дополнительных критических путей впроцессе сокращения длительности стадийОпределение критического пути (путей) сводится красчету ранних и поздних стартов ифинишей для каждой стадии проекта сучетом соотношений "предшественник - последователь ". Наглядно этот расчет может быть представлен как нахождение моментов старта (и финиша) каждой стадии спомощью построения двух диаграммГанттаОдну нужно строить, откладывая последовательно от начала проекта кконцу, длительность каждой стадии от момента окончания ее последнего(самого длительного) предшественника, те начиная стадию "так рано, как только возможно ". Другую диаграмму нужно строить, откладывая последовательно от конца проекта кначалу длительность каждой ста- дии от момента начала ее самого раннего последователя, те начиная стадию "так поздно, как только возможно ", чтобы не изменить момент окончания проектаРазность между поздними иранними стартами (или финишами) стадий даст временной резерв каждой стадииЕсли этот временной резерв равен нулю, то стадия критическаяПри необходимости сокращения длительности проекта на заданную величину при минимальных дополнительных издержках следует сокращать только критические стадии сшагом в 1 временную единицу (день, неделя ит д.). На каждом шаге следует выбирать те критические стадии, стоимость сокращения которых на 1 временную единицу наименьшая (самые "дешевые "). При каждом очередном сокращении необходимо следить, не появился ли дополнительный критический путьЕсли такой путь появляется, дальнейшее сокращение выбранной критической стадии обычно блокируется вновь появившейся критической стадией на "параллельной " ветви проектаНередко при этом требуется сокращать сразу две "параллельные " критические стадии для сокращения проекта на единицу времени

topuch.ru

---

• 
  Договор на услуги по оптимизации сайта
• 
  Что такое дефрагментация диска и оптимизация
• 
  Оптимизация видео для сайта что это
• 
  Оптимизация товарных запасов в розничной торговле
• 
  Методы оптимизации и разработки финансовых планов
• 
  План оптимизации расходов бюджетного учреждения образец
• 
  Это раскрутка сайта или поисковая оптимизация
• 
  Что такое дефрагментация и оптимизация диска
• 
  Плагины для оптимизация сайта на wordpress
• 
  Оптимизация работы склада и складских технологий
• 
  Методы оптимизации и исследование операций лекции

Prostoy-Site | Все права защищены © 2018 | Карта сайта