Оптимизация грузопотоков для однородного груза (бензина). Методы оптимизации грузопотоков

Оптимизация грузопотоков — курсовая работа

Таким образом, получаем улучшенный план перевозок (табл. 13):

Пункт отправления	Строка Столбец	Пункт назначения					Наличие груза, т
		Б1	Б2	Б3	Б4	Б5
		V1=6	V2=8	V3=5	V4=4	V5=8
А1	U1=0	6 10	14	5 10	11	8	20
А2	U2=-2	6	6 5	3 5	2 10	6 20	40
Потребность в грузе, т		10	5	15	10	20	-

3.1.6. Производим расчет индексов U и V для занятых клеток, используя правила, указанные в пункте 3.1.3., а затем сравниваем во всех незанятых клетках расстояния lij с суммой соответствующих ей индексов по критерию Ui + Vj ≤ lij (смотри пункт 3.1.4.). Сумма индексов во всех незанятых клетках соответствует данному критерию, т.е. оптимальные размеры и направления грузопотоков определены для краски эмалевой белой.

3.4. Составляем сводный план грузопотоков (табл. 14), т.е. объединяем оптимальные планы по перевозке краски разной номенклатура в единый план перевозок.

Сводный план грузопотоков по перевозке краски эмалевой белой, голубой, бежевой

Пункт отправления	Строка Столбец	Пункт назначения					Наличие груза, т
		Б1	Б2	Б3	Б4	Б5
		V1	V2	V3	V4	V5
А1	U1	6 10	14	5 45	11	8 15	70
А2	U2	6	6 5	3 5	2 10	6 30	50
А3	U3	3 10	8 15	7 0	5 30	10 15	70
Потребность в грузе, т		20	20	50	40	60	-

РАЗРАБОТКА ПЛАНА РАЦИОНАЛЬНЫХ МАРШРУТОВ ПЕРЕВОЗОК

Разработка рациональных маршрутов движения АТС при перевозке грузов – это организация транспортного процесса (выполнение заданного объема транспортной работы при минимуме затрат) таким образом, чтобы был определен оптимальный вариант плана работы ПС. Планирование рациональных маршрутов движения ПС иначе называется маршрутизацией. Маршрутизация перевозок – это составление маршрутов движения подвижного состава или его порядка следования между корреспондирующими точками.

По одному маршруту могут перевозиться различные грузы, которые должны удовлетворять следующему условию: их можно транспортировать одним и тем же подвижным составом. Следовательно, маршрутизацию перевозок можно осуществлять только при наличии групп грузов, требующих для перевозки однотипного подвижного состава. В связи с этим первый шаг по осуществлению маршрутизации перевозок заключается в классификации грузов, предъявляемых к перевозке, на группы, однородные с точки зрения возможности их транспортировки на одном и том же подвижном составе. Маршруты составляются отдельно по каждой группе грузов.

При перевозке массовых грузов помашинными отправками задача маршрутизации перевозок может быть решена с помощью метода совмещенных планов (совмещенных матриц). Суть этого метода заключается в том, что сводный план перевозки грузов и оптимальный план подачи порожнего подвижного состава заносят в единую матрицу, т.е. эти планы совмещают (отсюда и название метода).

Решение задачи маршрутизации перевозок с использованием метода совмещенных планов включает в себя пять этапов: составление матрицы подачи порожнего подвижного состава под погрузку, составление матрицы совмещенных планов перевозки грузов, составление маятниковых маршрутов, составление кольцевых маршрутов и выбор начальных пунктов маршрутов.

Минимизация холостых пробегов автомобилей и нахождение оптимального плана возврата порожних автомобилей под погрузку после их выгрузки

Составляем матрицу условий (табл.15). В соответствии с алгоритмом метода потенциалов находим допустимый план холостых пробегов.

Пункт отправления	Строка Столбец	Пункт назначения					Наличие груза, т
		Б1	Б2	Б3	Б4	Б5
		V1=6	V2=11	V3=5	V4=9	V5=13
А1	U1=0	6 4	14	5 10	11	8	14
А2	U2=-7	6	6	3	2 8	6 2	10
А3	U3=-3	3 0	8 4	7	5	10 10	14
Потребность в грузе, т		4	4	10	8	12	-

Аналогично пунктам 3.1.2.-3.1.6. получаем оптимальный план возврата порожняка под погрузку (табл. 16).

Оптимальный план возврата порожняка под погрузку

Пункт отправления	Строка Столбец	Пункт назначения					Наличие груза, т
		Б1	Б2	Б3	Б4	Б5
		V1=2	V2=7	V3=5	V4=4	V5=8
А1	U1=0	6	14	5 10	11	8 4	14
А2	U2=-2	6	6	3	2 2	6 8	10
А3	U3=1	3 4	8 4	7	5 6	10	14
Потребность в грузе, т		4	4	10	8	12	-

freepapers.ru

Оптимизация грузопотоков

Простои самосвалов в очередях и экскаваторов в ожидании самосвалов

Длительное пребывание карьерных самосвалов в очереди в местах погрузки и выгрузки приводит к снижению производительности и увеличению расхода топлива. В свою очередь, каждая минута простоя экскаватора без погрузки на грузовики – потеря времени и денег. Система DISPATCH обеспечивает проверенную в отрасли оптимизацию назначения грузовиков в режиме реального времени, сводя к минимуму их пребывание в очереди и простой экскаваторов.

Модуль Optimization системы DISPATCH использует модель программирования дорожных систем и лучшего пути (BP) вместе с модулем слежения за перевозками Haulage Tracking для определения производительности источников горного материала (например, экскаваторов и погрузчиков) и его приемников (отвалов и дробилок). Этот расчет основывается на определении объема доступного горного материала источника, вместимости районов сброса горного материала и времени в пути между ними.

Система применяет алгоритм линейного программирования (LP), чтобы определить максимально возможную скорость потока между источниками горного материала и его приемниками. Она также принимает во внимание эксплуатационные показатели парка средств перевозки, например размер оборудования, соответствие экскаватора и грузовика, а также закрепление экскаватора за районом. На основании этих факторов рассчитывается оптимальная скорость потока материала. Затем для приведения доступных ресурсов перевозки в соответствие с оптимальным потоком материала используется алгоритм динамического программирования (DP).

Низкое качество шихтовки

Неверное содержание полезного ископаемого может привести к снижению уровня производительности фабрики или даже к повреждению стационарного оборудования. Клиенты с повышенными требованиями в этом вопросе, могут максимально увеличить производительность, с использованием ограничения по усреднению материала.

Модуль отслеживания сорта Grade Tracking позволяет отслеживать качество полезного ископаемого для каждого участка и типа материала в отдельности. Полученная информация позволяет выполнять мелкомодульные измерения исходного содержания полезного компонента, которая служит основой для алгоритма усреднения DISPATCH.

Модуль Blending системы DISPATCH автоматизирует процесс усреднения на дробилках и складах, обеспечивая предприятие точным контролем качества добываемого материала. Он оптимизирует назначение карьерных самосвалов для перевозки материала, с учетом усреднения, и не нарушает его целевых показателей, несмотря на незапланированные перерывы в работе экскаватора. В некоторых случаях необходимо удерживать несколько различных характеристик материала в заданных пределах, чтобы отвечать требованиям дробилки или заказчика. Модуль Blending учитывает все эти факторы для выполнения плана предприятия по уровню качества.

Заправки и пересменка

Когда у автосамосвалов заканчивается топливо, это вызывает нарушение процесса добычи на любом руднике, в то время как ненужные заправки снижают коэффициент использования оборудования и его производительность. Модуль заправок Fuelling системы DISPATCH позволяет автоматизированно контролировать топливо и другие жидкости, которые заливаются в автосамосвалы, экскаваторы, и вспомогательное оборудование. Когда уровень топлива самосвала достигает предварительно установленного минимального значения, он автоматически отправляется на дозаправку. Это позволяет, минимизировать пробег и простои на заправке. Кроме того, система постоянно отслеживает резкие изменения в количестве топлива, и сигнализирует диспетчеру или другим заинтересованным лицам о возможных случаях несанкционированного слива топлива в режиме реального времени.

Модуль управления пересменой Shiftchange системы DISPATCH позволяет существенно повысить производительность техники в конце и начале смены за счет того, что система автоматически осуществляет решение о назначении транспорта на площадку пересмены. Диспетчер задает в системе определенное время начала и окончания пересмены, и система Dispatch при запросе самосвала следующего назначения на месте разгрузки рассчитывает, успеет ли самосвал сделать еще один рейс к какому-либо экскаватору, учитывая при этом время движения, очереди под экскаваторами, скорости погрузок каждого экскаватора, потребность в самосвалах каждой погрузочной единицы, время движения от предполагаемого в следующем рейсе месте разгрузки до площадки пересмены и др. Если самосвал теоретически может успеть сделать еще один рейс, он будет назначен на экскаватор, если нет, то система назначит его на ту площадку, на которой ему назначено произвести пересмену. Модуль Shiftchange обеспечивает эффективное и своевременное принятие решений по распределению персонала и доведения производительности до максимума.

Задержки и черезмерная длительность рейсов

Когда производственный процесс не соответствует принятой процедуре, могут быстро накапливаться технологические простои. Система DISPATCH оперативно управляет оборудованием и работниками, а также создает графики работы, таким образом обеспечивается высокая эффективность управления многоэтапными операциями.

Модуль управления персоналом Lineup Management автоматически определяет квалифицированный персонал для работы с оборудованием перед началом смены, отображая задания для операторов оборудования на экране с прокручивающимися составами бригад. Вы можете настроить список работников и поддерживать текущий уровень квалификации каждого сотрудника. Доступны следующие типы квалификации: Неквалифицированный, Стажер, Квалифицированный и Опытный. Есть возможность закреплять операторов за оборудованием до пересмены либо на основании их постоянного назначения, или на основании готовности к работе с оборудованием.

Ошибочные рейсы и выбор неправильного пути приводит к ненужному расходу топлива и потере времени, что в свою очередь является причиной преждевременного износа оборудования. Вычисляя лучший путь между начальной и конечной точкой, и сигнализируя операторам о неправильных маршрутах, система DISPATCH обеспечивает максимально эффективное движение.

Неверно направленные грузы

Отправка руды в отвал – это буквально выброшенные на ветер деньги. С другой стороны, если пустую породу отправить на фабрику, могут возникнуть дорогостоящие простои и ухудшится качество усредненного продукта. Система управления машинами ProVision непрерывно сопоставляет содержание полезного ископаемого с заданными местами выгрузки.

ProVision интегрируется с имеющимся в распоряжении ПО для планирования горных работ, обеспечивая операторов обновлениями о границах залегания руды в режиме реального времени. Все решения системы ProVision легко интегрируются с системой DISPATCH и выдают предупреждения о возможной отправке груза в неправильную точку.

Неровные уступы и некачественное проектирование взрывов

Неровные уступы требуют значительной доработки при помощи вспомогательного оборудования с целью избежания повреждений технологического оборудования. Система ProVision Shovel обеспечивает индикацию границ залегания руды и отметки высот экскаватора в реальном времени в сравнении с планом. Если значение отметки высот превышает или находится ниже требуемого уровня, установленного проектом горных работ, или когда выбор материала не соответствует плану, операторы немедленно получают предупреждение об этом.

Благодаря более точной отработке уступов сокращается время на постановку под погрузку из-за более ровной погрузочной площадки. Ровный уровень уступа также уменьшает время подготовки под бурение, а также увеличивает производительность экскаваторов за счет общего сокращения обслуживания уступа.

Проектирование взрывов должно соответствовать крепости пород, чтобы избежать повышенного расхода взрывчатых веществ и неправильного дробления. Модуль Stratification системы ProVision создает сечение породы для каждой скважины, что позволяет оптимизировать проектирование взрывов. Управление машинами в режиме реального времени помогает операторам бурить в соответствии с планом.

www.modularmining.com

Оптимизация и безопасность перевозочного процесса

1 Оптимизация грузопотоков

В решении задач, направленных на дальнейшее совершенствование работы автомобильного транспорта и повышение эффективности использования транспортных средств, экономное использование трудовых, финансовых и материальных ресурсов, рост производительности труда и снижение себестоимости перевозок, важная роль отводится применению современных экономико-математических методов и электронно-вычислительной техники (ЭВМ).

Одним из основных резервов снижения транспортных издержек является достижение наименьшего расстояния перевозок грузов путем рационального закрепления получателей за поставщиками (оптимизация грузопотоков).

Цель работы - освоить методику решения заданной транспортной задачи с помощью экономико-математических методов.

Задача оптимизации грузопотоков - это определение плана перевозок однородных (взаимозаменяемых) грузов от m поставщиков Аi к n потребителям Bj с учетом ограничений на ресурсы и потребности, обеспечивающие минимальную транспортную работу.

Если обозначить объем вывоза груза от поставщиков Аi через Qi , требуемый объем завоза груза потребителю Bj через Qj, перевозимое количество груза от i-го поставщика j-му потребителю Qij, кратчайшее расстояние перевозки от i -го поставщика до j -го потребителя через lij, то задачу оптимизации грузопотоков можно выразить в следующей математической форме:

во все j-e пункты получения груза из i-ro пункта отправления может быть вывезено только Qj единиц груза

=Qi, i = 1,2…,m ; (1.1)

из всех i - х пунктов отправления j-му пункту получения должно быть доставлено только Qj единиц груза

=Qj, j = 1,2…,n. (1.2)

При этом общий объем транспортной работы перевозок должен быть минимальным, что соответствует достижению наименьшего среднего расстояния перевозок

min , (1.3)

а искомые переменные не могут быть отрицательными числами, т.е.

Если общий объем вывоза грузов от поставщиков равен общему объему их завоза потребителям, то имеет место условие

= . (1.5)

Ограничения (1.1),(1.2),(1.4),(1.5) и целевая функция (1.3) являются закрытой моделью классической задачи линейного программирования.

Для оценки первоначального базисного и отыскания оптимального плана закрепления потребителей груза за поставщиками как задачи линейного протраммирования используются следующие методы: квадратов, опорных элементов, распределительные (Хичкока, Креко, модифицированный, распределительный метод — МОДИ), с разрешающими элементами.

Широкое применение получил метод МОДИ, который называют еще методом потенциалов.

Для решения поставленной транспортной задачи предлагается использовать данный метод.

Рассмотрим решение транспортной задачи этим методом на примере.

Условия задачи. Имеется несколько поставщиков и получателей однородной или взаимозаменяемой продукции. Известны наличие груза у каждого поставщика и потребность в нем у каждого получателя, а также расстояния между ними (таблицы 1.1,1.2,1.3).

Таблица 1.1 - Наличие груза у поставщиков

Индекс поставщика	Наличие груза, т
А1	1106
А2	504
А3	504
Итого:	2114

Таблица 1.2 - Потребность в грузе у получателей

Индекс получателя	Потребность в грузе, т
Б1	714
Б2	504
Б3	504
Б4	392
Итого:	2114

Необходимо составить оптимальный план закрепления получателей за поставщиками, при котором общая стоимость доставки груза была бы минимальной.

В соответствии с «Прейскурантом № 13-01-02 единых тарифов на перевозку грузов автомобильным транспортом» стоимость перевозки зависит от класса груза и расстояния доставки. Согласно условию, груз является однотипным, т. е. имеет одинаковый класс, и поэтому стоимость перевозки будет зависеть только от расстояния.

Следовательно, задача на отыскание оптимального варианта закрепления получателей за поставщиками сводится к отысканию минимального среднего расстояния перевозки грузов.

Для получения оптимального плана закрепления получателей за поставщиками задачу решаем методом последовательного улучшения вариантов.

Таблица 1.3 - Расстояние от поставщиков до получателей, км

Получатели	Поставщики
Получатели	А1	А2	А3
Б1	16	8	26
Б2	24	30	6
Б3	12	26	16
Б4	20	36	26

Исходные данные задачи сводим в матрицу №1, представляющую собой таблицу, в которой по строкам располагаем сведения о потребителях груза, а по столбцам - о поставщиках. В верхнем правом углу каждой клетки матрицы - в квадрате - проставляем расстояние от поставщиков к потребителям.

Получатели	Вспомогательные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3

Б1			16		8		26	714

Б2			24		30		6	504

Б3			12		26		16	504

Б4			20		36		26	392

Наличие груза, т		1106		504		504		2114

Рисунок 1.1 - Матрица №1. Исходный план перевозок

Матрица с проставленными в ней исходными данными показана на рисунке 1.1 и называется исходным планом перевозок.

Математически транспортная задача линейного программирования формулируется следующим образом. Обозначим количество груза буквой х с двумя индексами: первый показывает, откуда везут, а второй - куда доставляют груз.

Первая группа уравнений - по поставщикам

Вторая группа показывает ограничение количества груза по получателям

Общее уравнение для отыскания минимального среднего расстояния перевозки

Cmin =16x11+8x21+26x31+24x12+30x22+6x32 +12x13+26x23+16x33+ +20x14+36x24+26x34. (1.8)

Приведенное уравнение является линейным, так как содержит неизвестные только в первой степени. Согласно условию и смыслу, значение может быть только положительным.

Решение задачи с таким количеством неизвестных представляет значительные трудности, поскольку дает большое число их возможных значений. Подобные задачи лучше всего решать методом последовательного улучшения вариантов закрепления получателей за поставщиками.

Согласно заданию составляем первичный план закрепления получателей за поставщиками

Получа- тели	Вспомогательные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3

1	2	3		4		5		6
Б1		714	16		8		26	714

Б2			24	504	30		6	504

1	2	3		4		5		6
Б3			12		26	504	16	504

Б4		392	20		36		26	392

Наличие груза, т		1106		504		504		2114

Рисунок 1.2 - Матрица №2. Первичный план закрепления получателей за поставщиками

Клетки матрицы, в которых поставлены цифры загрузки, называются загруженными (клетки А1Б4, А1Б1,АЗБ3, А2Б2). Остальные клетки, не имеющие загрузки, называются незагруженными.

Решение задачи возможно при соблюдении некоторых правил.

Правило 1. Число загруженных клеток в матрице должно быть равно m+n-1 (m, n - число строк и столбцов).

В нашем примере m = 4, n = 3, следовательно, m+n -1=4+3 - 1=6. На матрице число загруженных клеток равно 4.

Если число загруженных клеток больше m+n - 1, то план закрепления получателей за поставщиками составлен неверно, и задачу решить нельзя. Нужно составить новый план закрепления, соблюдая приведенное выше правило. Если число загруженных клеток меньше m+n - 1, то задачу решить можно, загружая недостающее число клеток нулевой загрузкой (фиктивная загрузка). Для этого в одну или несколько клеток проставляют ноль.

Правило 2. Нулевую загрузку проставляют в клетках столбца с наименьшим количеством груза и с минимальным расстоянием.

Матрица с нулевой загрузкой (№3) приведена на рисунке 1.3.

Получа- тели	Вспомогательные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3

Б1		714	16	0	8		26	714

Б2			24	504	30	0	6	504

Б3			12		26	504	16	504

Б4		392	20		36		26	392

Наличие груза, т		1106		504		504		2114

stud24.ru

Оптимизация грузопотоков для однородного груза (бензина)

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Новосибирский Государственный Технический Университет

Кафедра технологии машиностроения

Расчетно-графическая работа

по дисциплине: «Организация перевозочных услуг и безопасность транспортного процесса»

Факультет: МТФ

Группа: ТА-602

Выполнил: Полонник Э.А.

Вариант: 10

Проверил: Рахимянов К.Х.

Новосибирск, 2010

Содержание

Содержание. 1

1. Разработка модели транспортной сети. 2

2. Выбор модели подвижного состава. 3

3. Маршрутизация перевозок. 4

4. Оптимизация грузопотоков. 5

Список литературы.. 6

1. Разработка модели транспортной сети

В табл. 1.1 представлены исходные данные, которые содержат информацию о виде грузов и объёме перевозок между пунктами транспортной сети.

Таблица 1.1.

Исходные данные

Откуда	Куда	Вид груза	Объем перевозок, т/месяц
ЖД Склад №2	Мебельная фабрика	Пиломатериалы	750,00
Склад речпорта	Металлургический комбинат	Руда	4200,00
Склад речпорта	Завод строительных материалов	Мрамор	800,00
Металлургический комбинат	Завод ЖБИ №2	Металлопрокат	800,00
Металлургический комбинат	Склад речпорта	Металлопрокат	500,00
Металлургический комбинат	ЖД Склад №3	Металлопрокат	1000,00

На основании исходных данных составляю таблицу грузопотоков между грузообразующими и грузополучающими пунктами (табл. 1.2).

Таблица 1.2.

Грузопотоки между пунктами транспортной сети

Пункты отправления	Пункты назначения
Пункты отправления	Мебельная фабрика	Металлург. комбинат	З-д строит. материалов	Завод ЖБИ №2	Склад речпорта	ЖД Склад №3	Всего
ЖД Склад №2	750,0	-	-	-	-	-	750,0
Склад речпорта	-	4200,0	800,0	-	-	-	5000,0
Металлургический комбинат	-	-	-	800,0	500,0	1000,0	2300,0
Всего	750,0	4200,0	800,0	800,0	500,0	1000,0	8050,0

На основании табл. 1.2 и схемы транспортных магистралей и расположения объектов транспортной сети (прил. 1) рассчитываю общие характеристики транспортных перевозок: коэффициент неравномерности объема перевозок () и коэффициент неравномерности грузооборота (). Данные коэффициенты определяются отношением размаха варьирования соответствующего показателя к его средней величине.

Коэффициент неравномерности объема перевозок определится как:

где Qmax – максимальная величина объема перевозок, т; Qmix – минимальная величина объема перевозок, т; Qср – средняя величина объема перевозок, т.

Максимальная и минимальная величины объема перевозок определяются из исходный данных (табл. 1.1) и составляют соответственно 4200 т и 500 т

Средняя величина объема перевозок определяется как среднее арифметическое от всех объемов перевозок:

Таким образом, неравномерность объема перевозок:

Коэффициент неравномерности грузооборота определится как:

где Pmax – максимальная величина грузооборота; Pmix – минимальная величина грузооборота; Pср – средняя величина грузооборота.

Грузооборот и объем перевозок имеют между собой следующую зависимость:

где l – расстояние перевозки 1 т груза, км.

Расстояния по данным перевозкам определяются согласно схеме (прил. 1) и представлены в табл. 1.3.

На основании имеющихся данных определяю значения максимального, минимального и среднего грузооборота:

Таблица 1.3.

Расстояния перевозок

Откуда	Куда	Расстояние, км
ЖД Склад №2	Мебельная фабрика	14,00
Склад речпорта	Металлургический комбинат	35,00
Склад речпорта	Завод строительных материалов	28,00
Металлургический комбинат	Завод ЖБИ №2	21,00
Металлургический комбинат	Склад речпорта	35,00
Металлургический комбинат	ЖД Склад №3	21,00

Таким образом, неравномерность грузооборота:

2. Оптимизация грузопотоков

Исходные данные представлены в табл. 2.1, табл. 2.2 и в прил. 1, которые содержат информацию о поставщиках и потребителях грузов, расстоянии между ними и количестве перевозимого груза.

Таблица 2.1.

Исходные данные по поставщикам

Поставщики	ЖД Станция "Западная"	ЖД Станция "Восточная"
Объем поставок	1100,00	560,00

Примечание: груз однородный - бензин, т

Таблица 2.2.

Исходные данные по потребителям

Получатели груза	АЗС №2	АЗС №4	АЗС №5	АЗС №8	АЗС №9
Объем потребления, т	200,00	400,00	560,00	320,00	180,00

Оптимизация грузопотоков выполняется по отдельным маршрутам. Классическая задача оптимизации возникает при организации перевозок однородных грузов в большом объеме от n поставщиков m потребителям. В данном случае, имеется две железнодорожные станции и пять автозаправочных станций, куда поставляется бензин. Такая задача решается универсальным методом линейного программирования.

Рекомендуемая ниже методика предусматривает решение транспортной задачи линейного программирования (T3ЛП) методом потенциалов. Условия задачи задаются в виде распределительной таблицы. Дадим содержательную постановку ТЗЛП.

Имеется два пункта поставки однородного груза А1, A2 и пять пунктов потребления груза В1, В2, В3, В4, B5. В пунктах А1, A2 находится груз в количестве соответственно 1100 и 560 т. В пункты В1, В2, В3, В4, B5 требуется доставить соответственно 200, 400, 560, 320, 180 т груза. Затраты на перевозку 1т груза между пунктами поставки и пунктами потребления приведены в матрице С (в тыс. руб.).

где Сij – стоимость перевозки 1 т груза от поставщика с номером i (i = 1, 2) к потребителю с номером j (j = 1, 2, 3, 4, 5).

Необходимо найти такой план закрепления потребителей за поставщиками, чтобы общие затраты по перевозкам груза были минимальными.

Представим данную задачу в виде матрицы перевозок (табл. 2.3).

Таблица 2.3.

Матрица перевозок

Базы	Потребители										Запасы
	АЗС №2		АЗС №4		АЗС №5		АЗС №8		АЗС №9
ЖД станция "Западная"		130		170		200		200		130	1100

ЖД станция "Восточная"		180		130		50		100		190	560

Потребности	200		400		560		320		180		1660

Обозначим Xij (т) – величину поставки от базы поставщика

vunivere.ru

3. ОПТИМИЗАЦИЯ ГРУЗОПОТОКОВ. Организация процесса перевозок

Основы оптимизации перевозочного процесса Методы маршрутизации перевозок грузов

Определение кратчайших расстояний между пунктами транспортной сети Транспортная сеть образуется вершинами и звеньями сети. l Вершинами транспортной сети являются точки на местности наиболее важные для определения расстояний или маршрутов движения автомобилей. Связь между вершинами с указанием расстояния между ними образуется звеньями сети. l Транспортная сеть считается заданной, если определены ее вершины, звенья и их длина. l

Определение кратчайших расстояний между пунктами транспортной сети При определении кратчайших расстояний «методом потенциалов» используется следующий алгоритм: начальной точке сети, за которую может быть принята любая из точек, присваивается потенциал, равный нулю i=0. определяются потенциалы соседних с начальной точкой вершин сети l где i - потенциал предшествующей вершины; ℓij -длина звена, соединяющего вершины i и j.

Определение кратчайших расстояний между пунктами транспортной сети из всех полученных потенциалов выбирается наименьший, который проставляется у соответствующей вершины, а звено (i – j) отмечается стрелкой; решение продолжается до тех пор, пока всем вершинам сети не будут присвоены потенциалы. Величина потенциалов у соответствующих вершин показывает кратчайшее расстояние от выбранного начального пункта до данного пункта. Звенья со стрелками образуют кратчайший маршрут движения от начального пункта до всех остальных.

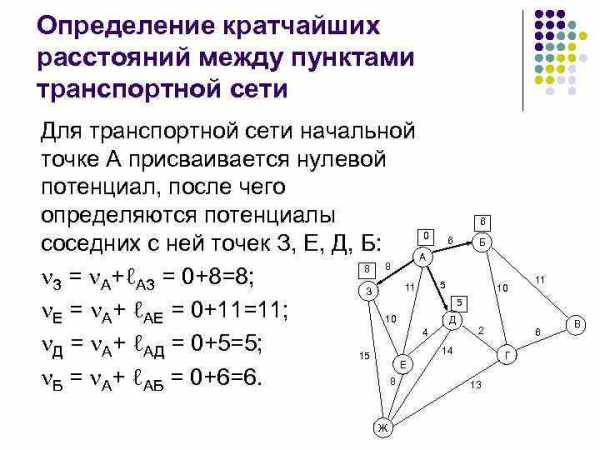Определение кратчайших расстояний между пунктами транспортной сети Для транспортной сети начальной точке А присваивается нулевой потенциал, после чего определяются потенциалы 0 соседних с ней точек З, Е, Д, Б: А 8 8 З = А+ℓАЗ = 0+8=8; 11 З Е = А+ ℓАЕ = 0+11=11; 10 4 Д = А+ ℓАД = 0+5=5; 15 Е Б = А+ ℓАБ = 0+6=6. 8 Ж 6 6 Б 5 10 11 5 Д 2 14 6 Г 13 В

Определение кратчайших расстояний между пунктами транспортной сети Из вычисленных потенциалов наименьший имеет точка Д, поэтому ей присваивается потенциал 5, который проставляется около вершины в квадрате, а ветвь АД отмечается стрелкой. Вершина Д из дальнейшего рассмотрения исключается, поэтому соответствующие потенциалы зачеркиваются. На следующем этапе определяются потенциалы вершин, соседних с вершиной Д: Е = Д+ℓДЕ = 5+8=13; Ж = Д+ℓДЖ = 0+11=11; Г = Д+ℓДГ = 0+8=8. Из всех рассчитанных потенциалов наименьший имеет вершина Б; ей присваивается потенциал 6 и стрелкой отмечается наименьшее расстояния от вершины А. Вершина Б из дальнейшего рассмотрения исключается, поэтому соответствующие потенциалы зачеркиваются.

Транспортная задача и методы ее решения В пунктах А 1, А 2, Аn имеется однородный груз в объемах аi единиц. Этот груз необходимо доставить в пункты потребления В 1, В 2, Вm в количестве bj единиц. Известны расстояния (стоимость) перевозок сij между всеми пунктами отправления и получения груза. Требуется построить такой план перевозок, при котором потребность в грузе всех пунктов потребления будет удовлетворена, весь груз из пунктов отправления будет вывезен и при этом будет обеспечен минимум транспортной работы, что соответствует достижению наименьшего среднего расстояния перевозок груза. l

Транспортная задача и методы ее решения l Экономико-математическая модель транспортной задачи i - количество поставщиков; j - количество потребителей; ai - ограничения по предложению;

Транспортная задача и методы ее решения где bj - ограничения по спросу; cij - элементы целевой матрицы; xij - объем корреспонденции между пунктами i и j. При решении транспортной задачи распределительным методом используется следующая методика: на основании исходных данных составляется матрица распределительного метода;

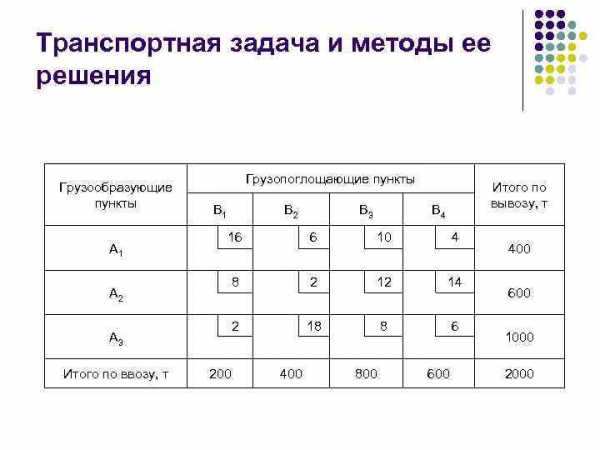Транспортная задача и методы ее решения Грузообразующие пункты А 1 Грузопоглощающие пункты В 1 В 2 В 4 16 6 10 4 8 2 12 14 2 18 8 6 А 2 А 3 Итого по ввозу, т В 3 Итого по вывозу, т 200 400 800 600 400 600 1000 2000

Транспортная задача и методы ее решения составляется первый допустимый план перевозок. Ячейки содержащие объем перевозок называются загруженными. Количество загруженных клеток всегда должно равняться величине i+j-1. Если количество загруженных клеток менее чем i+j 1, то недостающее количество клеток получается путем загрузки соответствующего количества свободных клеток нулями (нулевые загрузки). Клетка, в которой проставлена нулевая загрузка, считается загруженной.

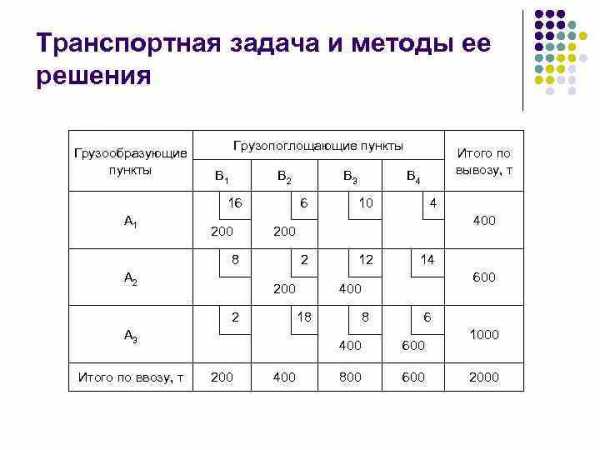Транспортная задача и методы ее решения Грузообразующие пункты Грузопоглощающие пункты В 1 В 2 16 А 1 200 6 10 4 400 2 200 2 12 14 600 400 18 А 3 Итого по ввозу, т В 4 200 8 А 2 В 3 Итого по вывозу, т 8 6 400 200 400 600 800 600 1000 2000

Транспортная задача и методы ее решения определяются специальные цифровые индексы (потенциалы) Потенциалы загруженных ячеек Потенциалы незагруженных ячеек

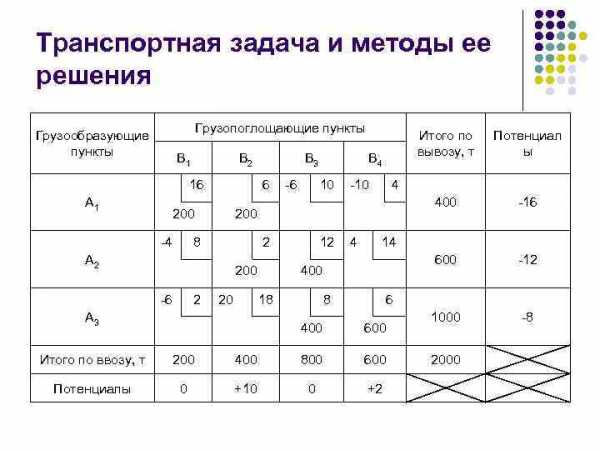Транспортная задача и методы ее решения Грузопоглощающие пункты Грузообразующие пункты В 1 16 А 1 6 200 -4 2 А 2 200 2 10 -10 20 12 1000 -8 14 400 18 А 3 4 -12 4 200 8 -6 -6 В 4 -16 600 В 3 Потенциал ы 400 В 2 Итого по вывозу, т 8 6 400 600 Итого по ввозу, т 200 400 800 600 Потенциалы 0 +10 0 +2 2000

Транспортная задача и методы ее решения полученное решение (план перевозок) проверяется на оптимальность; При решении задачи на минимум оптимальный вариант получается в том случае, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются положительными величинами. Наличие свободных клеток с отрицательными значениями потенциалов говорит об имеющихся резервах, использовав которые можно получить лучший вариант решения.

Транспортная задача и методы ее решения Если решается задача на максимум, то оптимальный вариант получается в случае, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются отрицательными величинами. В случае, если оптимальное решение не достигнуто, производится перераспределение грузопотоков;

Транспортная задача и методы ее решения Перераспределение загрузок клеток начинается с определения наиболее потенциальной незагруженной ячейки. Для этой клетки строится контур замкнутая ломаная линия, состоящая из прямых горизонтальных и вертикальных отрезков, пересекающихся под прямым углом, соединяющих эту клетку с другими загруженными клетками. После этого всем узлам контура попеременно, начиная с выбранной незагруженной ячейки, присваивается положительный (+) и отрицательный ( ) знаки.

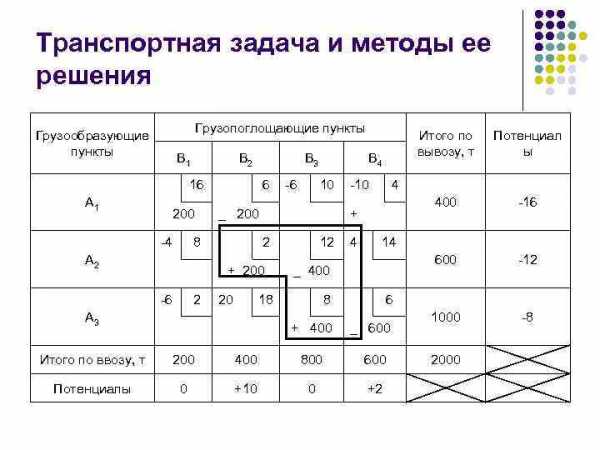Транспортная задача и методы ее решения Грузопоглощающие пункты Грузообразующие пункты В 1 В 2 16 А 1 200 -4 6 2 2 20 400 -10 12 4 8 1000 -8 6 + 400 А 3 -12 14 _ 400 18 -16 4 + + 200 -6 10 _ 200 8 А 2 -6 В 4 Потенциал ы 600 В 3 Итого по вывозу, т _ 600 Итого по ввозу, т 200 400 800 600 Потенциалы 0 +10 0 +2 2000

Транспортная задача и методы ее решения Количество перераспределяемого груза определяет наименьший объем груза, стоящий в углах контура с отрицательным знаком. Количество груза, указанное в этой ячейке, отнимается из всех клеток со знаком минус и прибавляется во все клетки со знаком плюс. При этом общая сумма в столбцах остается прежней, а изменяется лишь перераспределение груза среди потребителей.

Транспортная задача и методы ее решения полученное новое решение проверяется на оптимальность. Если решение улучшить нельзя, оно считается оптимальным.

Транспортная задача с дополнительными условиями l В случае, когда у грузоотправителей имеются излишки груза, которые никому не ввозится (спрос меньше предложения) решается транспортная задача с распределением резерва: в матрицу распределительного метода вводится фиктивный столбец с ограничением по спросу равным разности между суммами фактических величин спроса и предложения.

Транспортная задача с дополнительными условиями l поскольку излишек груза никуда не вывозится, то в углах клеток столбца ставятся нули; дальше задача решается обычным путем по алгоритму распределительного метода, рассматривая фиктивный столбец, как еще один потребитель груза. Аналогично решается задача, в случае когда спрос превышает предложение. Для недостающего объема груза вводится фиктивная строка.

Транспортная задача с дополнительными условиями l l В случае, когда в силу каких-то причин невозможно удовлетворить спрос потребителя Вj поставками из Аi, то есть на корреспонденцию из Аi в Вj налагается запрет – запрещение корреспонденции. Чтобы решить задачу, достаточно вместо реального элемента целевой матрицы, стоящего в клетке Аi. Вj, поставить очень большую величину М, которая больше любого элемента целевой матрицы, имеющегося в данной задаче.

Транспортная задача с дополнительными условиями l l Обязательная, или директивная, корреспонденция означает обязательность поставки из точки Аi в точку Вj части или всего объема материалов, имеющихся в Аi. В этом случае величина обязательной поставки вычитается из суммы спроса Вj и суммы ограничения Аi и при решении задачи не учитывается. При подсчете окончательного значения грузооборота обязательный объем прибавляется к полученному оптимальному объему грузооборота.

Транспортная задача с дополнительными условиями l При распределении грузопотоков взаимозаменяемых ресурсов планирование грузопотоков производится после, того как их объем с помощью переводных коэффициентов будет выражен в условных единицах, которые будут выражать ограничения по спросу и предложению. После этого задача решается обычным способом

present5.com

Стратегия управления доставкой груза на транспорте — курсовая работа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «Управление грузовой и коммерческой работой»

Курсовая работа

по дисциплине

«Менеджмент в отрасли»

на тему:

«Стратегия управления доставкой груза на транспорте»

Выполнил:	Проверил:
студент гр. ГК-42	преподаватель
Исаченко К.С.	Настаченко Е.В.

Гомель 2008 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «Управление грузовой и коммерческой работой»

Пояснительная записка

к курсовой работе

по дисциплине «Менеджмент в отрасли»

Курсовая работа сдана _________________

Курсовая работа выполнена на __________

Курсовая работа защищена на ___________

2008 г. СОДЕРЖАНИЕ

Введение………………………………………………………………………….3

1 Оптимизация грузопотоков для заданного региона транспортной сети…...5

1.1 Общее положение……………………………………………………………5

1.2 Постановка и решение задачи оптимизации грузопотоков……………….6

2 Определение оптимального замкнутого маршрута……………………........15

2.1 Общие теоретические положения……………………………………….....15

2.2 Расчет оптимального замкнутого маршрута………………………………19

3 Выбор и расчет загрузки транспортных средств для доставки грузов потребителю……………………………………………………………………………24

3.1 Определение транспортных характеристик заданных грузов……………24

3.2 Транспортные тарифы и правила их применения………………………...28

3.3 Выбор наиболее производительного транспортного средства……….......31

4 Расчет оптимальной интенсивности поступления вагонов………………....37

4.1 Общие положения теории очередей……………………………………......37

4.2 Характеристика трехканальной модели очереди………………………….39

4.3 Расчет оптимальной интенсивности поступления вагонов в транспортно-грузовую систему………………………………………………………………..40

Заключение………………………………………………………………………43

Список использованной литературы……………………………………….…..45

ВВЕДЕНИЕ

Для любой отрасли народного хозяйства необходимо тщательно спланированное управление, что способствует эффективному введению хозяйственной деятельности. Увеличение затрат на единицу продукции, уменьшение конкурентоспособности и, следовательно, уменьшение прибыли могут быть вызваны ошибками в планировании производства, оказании услуг. Для составления оптимального плана необходимо детальное изучение рынка, на котором функционирует предприятие, а именно спроса, уже существующие предложения, определяющие факторы конкурентоспособности. При анализе ситуации, сложившейся на рынке широко используются моделирование и экономико-математические методы.

Применительно к транспортной сфере планирование процесса перевозок выражается в определении сложившихся грузо- и пассажиропотоков, зон производства и зон потребления, в расчете оптимальных, конкурентоспособных тарифов. В данной курсовой работе рассматриваются основные разделы управления процессом перевозки. В первой главе на основании данных об избытке и недостатке грузов на станциях планируются направления вагонопотоков. Определяющим фактором при осуществлении перевозки является стоимость и время транспортировки груза, которые напрямую зависят от расстояния. Во второй главе, основываясь на данных о расстоянии между пунктами, был спланирован оптимальный маршрут коммивояжера. Планирование пути производилось с использованием метода линейного программирования. В третьей главе рассматривается зависимость между свойствами груза и видом транспорта, используемого для его транспортировки, так как вследствие большой номенклатуры грузов необходимо правильно подобрать соответствующий подвижной состав и погрузочно-разгрузочные механизмы. Для принятия правильного решения по оптимизации грузопотоков необходимо установить критерий и сравнить возможные варианты по этому критерию. В качестве критерия оптимизации (целевой функции) нужно выбрать минимальные транспортные издержки, т.е. необходимо минимизировать транспортную работу (вагоно-километры). В данной курсовой работе необходимо разработать модель-аналог, которая будет наглядно иллюстрировать размер, направление и характеристику грузопотоков на полигоне транспортной сети. Одним из методов решения задач оптимизации является линейное программирование. В нем учитывается большое число переменных, подчиненных определенным ограничениям. При решении таких задач необходимо получить оптимальное (экстремальное) значение определенного критерия эффективности, например, затрат, прибыли, количества произведенных продуктов или других показателей при условии, что удовлетворяются поставленные ограничения. При помощи метода линейного программирования были рассчитаны издержки, возникающие из-за разницы во времени прибытия вагонов для разгрузки.

1 Оптимизация грузопотоков для заданного региона

транспортной сети

1.1 Общие положения

Для того чтобы менеджер принял правильные оптимальные решения по распределению грузопотоков на заданном направлении, необходимо разработать и решить модель оптимизации. Модель – это отображение некоторых реальных явлений (в данном случае грузопотоков), используемых в целях управления. В данной курсовой работе необходимо разработать модель-аналог, которая будет наглядно иллюстрировать размер, направление и характеристику грузопотоков на полигоне транспортной сети.

Разработка модели оптимизации грузопотоков условно включает 5 взаимосвязанных этапов:

постановка или формулировка задачи;
разработка математической модели изучаемой системы;
отыскание решения с помощью этой модели;
проверка данной модели и получаемого решения;
уточнение принятого решения на практике.

Для принятия правильного решения по оптимизации грузопотоков необходимо установить критерий и сравнить возможные варианты по этому критерию.

В качестве критерия оптимизации (целевой функции) нужно выбрать минимальные транспортные издержки, т.е. необходимо минимизировать транспортную работу (ваг-км).

Одним из методов решения задач транспортной оптимизации является линейное программирование.

В нем учитывается большое число переменных, подчиненных определенным ограничениям. При решении таких задач необходимо получить оптимальное (экстремальное) значение определенного критерия эффективности, например, затрат, прибыли, количества произведенной продукции или других показателей, при условии, что удовлетворяются поставленные ограничения. Эти ограничения в свою очередь носят различный характер и объясняются условиями производства, управления, сбыта, хранения, наличия сырья или законодательными положениями.

1.2 Постановка и решение задачи оптимизации грузопотоков

Для решения задач оптимизации используют линейное программирование. При этом задачи должны иметь следующие условия:

необходимо наличие линейной функции цели (например, прибыли, затраты или количество перевезенных грузов), экстремум которой необходимо отыскать.
необходимо указать ограничение, в пределах которого может достигаться экстремум функции цели. Это ограничение следует задавать в виде системы линейных равенств или неравенств (расстояние между всеми транспортными узлами планируемого объема перевозок заданных грузов).

Сущность задачи заключается в определении такого плана регулировки порожних вагонов из пунктов отправления (избыток вагонов) в пункты назначения (недостаток вагонов), чтобы суммарные затраты на пробег порожних вагонов были минимальными при условии, что выполняются все имеющиеся ограничения.

Математическая модель этой задачи такова:

; , ;

, ; , ;

Условие данной задачи составлено таким образом, что избыток порожних вагонов равен недостатку (задача является сбалансированной). Если задача не сбалансирована, то добавляется мнимый поставщик или потребитель.

Определим оптимальное распределение порожних грузовых вагонов при перевозке каменного угля.

В таблице 1.1 и 1.2 приведены условия задачи и удельный (на 1 грузовой вагон) затраты на порожний пробег.

Таблица 1.1 – Условие задачи

Пункты отправления	Пункты назначения
Пункты отправления	D1	D2	D3	D4	D5	Избыток вагонов
S1	X11	X12	X13	X14	X15	230
S2	X21	X22	X23	X24	X25	200
S3	X31	X32	X33	X34	X35	100
Недостаток вагонов	100	50	110	180	90	530

Таблица 1.2 – Расстояние между пунктами отправления и назначения

Пункты отправления	Пункты назначения
Пункты отправления	D1(Г)	D2(В)	D3(Е)	D4(З)	D5(И)	Избыток вагонов
S1(А)	310	250	335	170	80	230
S2(Б)	110	570	210	310	400	200
S3(Д)	150	310	250	230	140	100
Недостаток вагонов	100	50	110	180	90	530

В таблице 1.1 указано, что в пунктах S1, S2 и S3 имеется избыток порожних вагонов в количествах 230, 200 и 100 вагонов. Соответственно в пунктах D1, D2, D3, D4 и D5 не хватает 100, 50, 110, 180 и 90 порожних вагонов.

В таблице 2.2 приведены расстояния Lij на порожний пробег одного вагона из пункта отправления i в пункт назначения j.Таким образом, определим такие значения Xij (i=1, 2, 3; j = 1, 2, 3, 4, 5) таблицы 1.1, чтобы удовлетворить поставленным ограничениям и минимизировать суммарные затраты:

min L = 310X11 + 250X12 + 335X13 + 170X14 + 80X15 + 110X21 + 570X22 + + 210X23 + 310X24 + 400X25 + 150X31 + 310X32 + 250X33 + 230X34 + 140X35;

X11 + X12 +X13 +X14 +X15 = 230;

X21 + X22 + X23 + X24 + X25 = 200;

X31 + X32 + X33 + X34 + X35 = 100;

X11 + X21 + X31 = 100;

X12 + X22 + X32 = 50;

X13 + X23 + X33 = 110;

X14 + X24 + X34 = 180;

X15 + X25 + X35 = 90.

Получение исходного опорного плана. Первым шагом при решении транспортной задачи является получение допустимого плана, т. е. возможного решения, которое удовлетворяет поставленным ограничениям. Если при этом получены минимальные суммарные затраты, то такой план называется оптимальным планом или решением, в данном случае это минимальный план. Исходный план можно легко построить, используя разработанный алгоритм, называемый «правилом северо-западного угла».

«Правило северо-западного угла» формулируется следующим образом:

1. Начать с северо-западного угла исходной таблицы (таблица 1.1) и сравнить количество вагонов, имеющихся в пункте отправления Si с количеством вагонов, потребных в пункте назначения Dj.

Если D1 < S1, т. е. если количество вагонов, потребных в пункте D1 меньше количества вагонов, имеющихся в пункте S1, то принять X11 = D1 и перейти к переменной Х12 (т. е. к следующей переменной по горизонтали).

Если D1 = S1,то принять X11 = D1 и перейти к переменной Х22 (т. е. по диагонали).

Если D1 > S1, то принять X11 = S1 и перейти к переменной Х21 (т. е. по вертикали).

2. Продолжать этот процесс шаг за шагом (от северо-западного до юго-восточного угла таблицы).

Таблица 1.3 – Первый опорный план

Пункты отправления	Пункты назначения
Пункты отправления	Г (410)	В (350)	Е (435)	З (535)	И (445)	Избыток вагонов
А (100)	100	50	80			230
Б (225)			30	170		200
Д (305)				10	90	100
Недостаток вагонов	100	50	110	180	90	530

myunivercity.ru