Методы оптимизации. Особенности исследуемых экспериментальных областей и их ограничения. Методы экспериментальной оптимизации
Метод экспериментальной оптимизации - Энциклопедия по экономике
| Рис.3.5.4. Метод экспериментальной оптимизации с использованием имитационной модели |  |
Сущность метода экспериментальной оптимизации [c.99]
Если исследуемый объект настолько сложен, что его математическая модель непригодна для применения аналитических или численных методов, то для его исследования применяют метод экспериментальной оптимизации. При этом методе как целевая функция, так и система [c.99]
При использовании метода экспериментальной оптимизации с использование имитационной модели объекта перед исследователем помимо создания моделирующего алгоритма возникают проблемы разработки алгоритма оптимизации, включающего моделирующий алгоритм в качестве одного из элементов — этапа расчета значения целевой функции для определения значений переменных. Для этого должна быть продумана алгоритмическая и программная реализация решения оптимизационной задачи. [c.103]
Решить ее можно с помощью численных методов оптимизации (так называемой экспериментальной оптимизации). [c.44]
В учебном пособии рассмотрены основные разделы курса Имитационное моделирование место имитационного моделирования (ИМ) в составе экономико-математических методов, общая характеристика имитационного моделирования, структура имитационных моделей, основные этапы процесса имитации, модели глобальных систем и экономических систем масштаба предприятия, использование ИМ в управлении предприятием, статистическое ИМ и экспериментальная оптимизация, управленческие имитационные игры и организационные аспекты ИМ. [c.2]
Анализ причин технологических потерь способствует их сокращению. Подлежат систематической проверке и герметизации все точки, где возможны испарение и утечки нефти и нефтепродуктов через неплотности должны быть пересмотрены схемы технологических связей между установками с целью сокращения числа промежуточных хранилищ и исключения излишних перекачек необходимо широко применять метод дифференциации карт технологического режима, чтобы обеспечить оптимальный режим во всех процессах и таким путем сокращать потери при проведении производственного инструктажа особо важна требовательность к строгому соблюдению технологического режима при устойчивых потерях эффективна экспериментальная проверка технологического режима для его оптимизации. [c.103]
В условиях конструкторской подготовки производства весьма трудно обеспечить равномерную по календарным срокам сдачу технической документации на опытные образцы. Выявленные в процессе проектирования недочеты конструкции, необходимость конструкторских доработок и изменений, естественно, вызывает многочисленные отклонения от плановых сроков и, как следствие, неравномерное поступление заказов в экспериментальные цехи. В таких условиях большую роль играет применение математических приемов, позволяющих оперативно маневрировать ресурсами и обеспечить выравнивание загрузки производственных участков. В частности, оптимизация загрузки опытного производства, маневрирование ресурсами могут выполняться методами математического моделирования. [c.130]
Значительный научный задел имеется и в области экономико-математического моделирования. Теоретически обоснованы и экспериментально проверены методы и модели, позволяющие решать важные планово-экономические задачи, связанные с планированием межотраслевых связей в народном хозяйстве, оптимизацией развития и размещения отдельных отраслей и производств, рационализацией транспортных связей, прогнозированием спроса населения на различные предметы потребления и др. При этом необходимо иметь в виду, что для этих и ряда других плановых задач наукой разработаны эффективные экономико-математические методы решения, основанные на использовании ЭВМ. Без ЭВМ невозможно не только решение указанных задач, но и накопление, хранение и обновление таких огромных массивов данных, какие, например, необходимы для создания комплексной системы плановых норм и нормативов. [c.25]
При изучении и/или оптимизации сложных систем непосредственные экспериментальные воздействия на них по различным причинам -ограниченные временные рамки, высокая стоимость и др. - невозможны или нежелательны, поэтому основным методом изучения и прогнозирования поведения производственного процесса при изменениях его структуры, параметров и внешних условий служит моделирование [237]. [c.79]
Другой подход к разработке бюджета основан на планировании на основе оптимизации прибыли. Прежде всего определяется функция реагирования сбыта, представляющая собой прогнозные оценки вероятного объема сбыта в течение определенного отрезка времени, на разные затраты на один или несколько элементов комплекса маркетинга. Эта функция оценивается на основе статистических, экспериментальных и экспертных методов (рис. 15.5). [c.509]
При этом возможны ситуации, когда каждый из параметров влияет не па один технико-экономический показатель, а на целую группу, причем это влияние может быть разнонаправленным. Это еще более усложняет определение потерь. Оптимизация точности в таких условиях является сложной многопараметрической задачей, решать которую целесообразно как расчетными, так и экспериментальными методами. [c.170]
Метод эволюционных операций — это процедура оптимизации качества выпуска продукции путем экспериментального варьирования факторов и оценки результатов непосредственно в производственном потоке. Этот метод был предложен Боксом и Уилсоном и показал себя весьма хорошо в химической промышленности с точки зрения улучшения качества выхода процессов. Типичная ситуация состоит в том, что осуществляется некоторый процесс, в котором регулируются такие факторы, как температура, время, вес и состав загрузки. На первой стадии факторы циклически варьируются, причем так, чтобы обнаружить улучшение или ухудшение качества. На этой стадии могут возникнуть убытки, которые, однако, обычно окупаются на второй стадии, когда в результате полученной информации регулируемые факторы устанавливаются на соответствующих уровнях. Процедура повторяется вплоть до выявления оптимальных условий. [c.193]
На стадии опытно-конструкторских работ проводится конкретное воплощение результатов НИР в конструкторскую документацию. На этой стадии с использованием различных методов прогнозирования и экспериментальных технологий оптимизируются кинематическая схема и принцип действия объекта, показатели его качества, решаются вопросы сертификации. Отличительные черты ПКО, СКВ очень высокие фондовооруженность и информационная обеспеченность труда конструкторов наличие современных методов конструирования и оптимизации высокий технический уровень экспериментальной и испытательной базы использование системы автоматизированного проектирования (САПР) создание для конструкторов благоприятных условий труда и отдыха высокая заработная плата конструкторов развитие международного сотрудничества [c.81]
Место имитационного моделирования в составе экономико-математических методов. 2.Мысленные и машинные модели социально экономических систем. 3.Социально-экономические процессы как объекты моделирования. 4. Структура и классификация имитационных моделей. 5.Основные этапы процесса имитации. 6.Определение системы, постановка задачи, формулирование модели и оценка ее адекватности. 7.Экспериментирование с использованием ИМ, механизм регламентации, интерпретация и реализация результатов. 8.Организационные аспекты имитационного моделирования. 9.Основные компоненты динамической мировой модели Форрестера. 10.Концепция петля обратной связи . И.Структура модели мировой системы. 12. Каноническая модель предприятия. 13.Моделирование затрат предприятия. 14.Моделирование налогообложения. 15.Использование имитационного моделирования для планирования. 16.Содержание процессов стратегического и тактического планирования. 17.Основные модули системы поддержки принятия решений. 18.Сущность статистического ИМ. 19.Метод Монте-Карло. 20.Идентификация закона распределения. 21.Классификация систем МО. 22.Сущность метода экспериментальной оптимизации. 23.Формирование концептуальной модели. 24.Принципы выбора критерия оптимальности, разработка алгоритма оптимизации. 25.Эвристические алгоритмы поиска решений. 26.Управленческие имитационные игры, их природа и сущность. 27. Структура и порядок разработки управленческих имитационных игр. [c.121]
Последовательные методы экспериментального поиска чаще всего основаны на принципах построения численных методов, среди которых можно выделить симплекс-метод, метод покоординатной оптимизации, градиентный метод и его модификации. [c.104]
Плодотворность обоих методов была установлена экспериментально. Интересное свойство схемы заключается в таком изменении стандартной процедуры ( поиска образа в терминологии Хука и Дживса [13]), применяемой для оптимизации функции с численными значениями, чтобы стала возможна оптимизация GT4 путем рекурсивного обращения его к самому [c.390]
Во ми. случаях ситуации повторяются, и унравленч. решение может быть принято на основе предыдущего опыта. Это относится в основном к формализованным решениям. Если же ситуация является специфической, требуется выработка решения применительно к сложившимся условиям. Строится модель решения задачи, собирается необходимая информация и проводится расчёт вариантов решения. Важнейшая проблема П. у, р. т. — оптимизация управленч. решений, выбор критерия оптимальности. При этом широко применяются методы линейного и динамич. программирования, статистич, решений, теория игр, корреляционные модели. Математич. модели решений дают возможность получить необходимые и достоверные знания об исследуемом объекте, моделировать и изучать явления, к-рые не поддаются экспериментальной проверке (см. Математические методы в экономических исследованиях). [c.341]
economy-ru.info
Многомерные методы экспериментальной оптимизации.
Для поиска экстремума функции многих переменных применяется ряд методов, среди которых отметим:
метод покоординатной оптимизации; метод Бокса − Уилсона; последовательный симплексный метод.
Метод покоординатной оптимизации Метод покоординатной оптимизации, называемый также методом Гаусса–Зейделя, сводит многомерную оптимизацию к последовательному применению одномерной к сечениям функции. Для этого фиксируют значения всех переменных, кроме одной, к которой применяется один из методов одномерной оптимизации. Затем начинают поиск по второй переменной, фиксируя первую на значении, обеспечившем экстремум, и т. д. После того как список переменных исчерпался, возвращаются к первой переменной, и так до тех пор, пока значение отклика возрастает (убывает). Метод отличается простотой, однако для функций овражистого типа, для которых линии равного уровня сильно вытянуты в направлении, не параллельном осям координат, поиск может продолжаться довольно долго. Метод Бокса−Уилсона На основе малой серии опытов строится линейное описание поверхности отклика в окрестности начальной точки. В центре этой локальной области определяется значение градиента, после чего начинаются опыты в направлении градиента. Бокс и Уилсон предложили использовать дробные факторные планы для поиска линейной модели. Метод состоит из последовательности циклов, каждый из которых содержит два шага.
1. Построение линейной модели в окрестности некоторой начальной точки с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьирования по отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели бы одинаковый порядок. В случае адекватности линейной модели коэффициенты регрессии совпадают с компонентами градиента, т.е. , где i, j,…,k – направляющие векторы осей координат. Обычно переходят к нормированному градиенту делением его компонент на норму либо просто на . Компоненты нормированного градиента обозначим .
2. Пошаговое увеличение величины целевой функции (движение в направлении градиента). Координаты точки наблюдения на -м шаге при движении в направлении градиента определяются по формуле:, где ≥1 – параметр, позволяющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной области, тем меньше . Движение в направлении градиента продолжается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план, находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям.
Геометрическая интерпретация метода приведена на рис.4. Здесь поверхность отклика задается линиями уровня.
Рис. 4. Схема метода Бокса–Уилсона
Рассмотрим в качестве примера использование метода Бокса−Уилсона для поиска максимума функции
. (6.11)
Допустимая область изменения переменных: 0£х1£20, 0£х2£10, 1£х3£15. Начальная точка поиска х0==(3,2,4). Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями: , i=1,2,3. Значения Di желательно подбирать такими, чтобы приращения функции по каждому из аргументов были сопоставимы, то есть
. Примем D1=1, D2=2, D3=3. В соответствии с (6.1) стандартизованная переменная , если , и при .
Линейная модель требует для своей оценки не менее четырех экспериментов. Воспользуемся ДФЭ 23-1 с ГС: (табл. 16).
Таблица 16
|
i |
х1ст |
х1 |
х2ст |
х2 |
х3ст |
х3 |
y |
|
1 |
1 |
4 |
1 |
4 |
1 |
7 |
40,8 |
|
2 |
-1 |
2 |
1 |
4 |
-1 |
1 |
26,2 |
|
3 |
1 |
4 |
-1 |
0 |
-1 |
1 |
24,4 |
|
4 |
-1 |
2 |
-1 |
0 |
1 |
7 |
25,4 |
В последнем столбце табл.16 содержатся значения функции (6.11) для исходных переменных, то есть 40,8=у(4,4,7) и так далее.
МНК-оценки коэффициентов линейной модели составят:
;;.
Отнормируем полученные компоненты градиента, поделив их на максимальное значение : b1=3,4/4,3=0,79, b2=1, b3=0,91. Движение в направлении градиента представлено в табл.17.
Таблица 17
|
Формулы для вычисления компонент вектора |
Номера компонент вектора |
у |
||
|
1-я |
2-я |
3-я |
||
|
х0 |
3 |
2 |
4 |
31,3 |
|
Di |
1 |
2 |
3 |
|
|
bi |
0,79 |
1 |
0,91 |
|
|
bi´Di |
0,79 |
2 |
2,73 |
|
|
x0+1´bi´Di |
3,79 |
4 |
6,73 |
39,9 |
|
x0+2´bi´Di |
4,58 |
6 |
9,46 |
46,4 |
|
x0+3´bi´Di |
5,37 |
8 |
12,19 |
50,6 |
|
x0+4´bi´Di |
6,16 |
10 |
14,91 |
52,6 |
Движение в направлении градиента после четвертого шага невозможно из-за ограничения на х3. Теперь следует определить градиент в точке x0+3´bi´Di. Поскольку темп роста функции замедлился на последних шагах, область линейного описания следует сузить, уменьшив значения Di.
students-library.com
Симплекс-метод экспериментальной оптимизации.
Последовательный симплексный метод Этот метод требует проведения минимально возможного числа опытов при определении направления движения.
Симплексом в n-мерном пространстве называют многогранник с (n+1)-й вершиной. Если расстояния между вершинами симплекса одинаковы, такой симплекс называют регулярным. Симплексный метод включает в себя следующие основные процедуры:
1. Линейное преобразование входных переменных с таким расчетом, чтобы изменение каждой из них на единицу одинаково сказывалось бы на изменении выходной переменной.
2. Построение регулярного симплекса и реализация опытов в вершинах симплекса.
3. Отбрасывание вершины с минимальным значением целевой величины и построение нового симплекса, который образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой зеркальным отображением отброшенной вершины относительно противоположной ей -мерной грани исходного симплекса. Координаты этой новой вершины рассчитываются по формуле: ,
где − номер отброшенной вершины.
4. Проведение эксперимента в вершине и возврат к п. 3. Если оказывается, что выходная переменная в новой вершине приняла значение меньшее, чем в остальных вершинах симплекса, то следует возвратиться к предыдущему симплексу. Во избежание зацикливания в качестве отбрасываемой выбирают вершину, в которой выходная переменная имеет величину, следующую по порядку за наихудшей вершиной симплекса. Аналогично следует поступать, если новая вершина выходит за пределы симплекса.
5. Если при перемещении симплекса за шагов некоторая вершина сохраняет свое положение, то симплекс совершит оборот относительно этой вершины. Это означает достижение области оптимума. Другим условием достижения оптимума является выполнение неравенства:, где e – малая величина (порог), – среднее значение выходной величины в вершинах симплекса.
К числу достоинств симплексного метода наряду с экономичностью по числу опытов и простотой вычислений следует отнести также возрастание эффективности метода с ростом числа входных переменных, устойчивость выделения направления движения, поскольку оно определяется только соотношением целевых величин, а не их абсолютными значениями.
Графическая иллюстрация симплексного метода при двух входных переменных приведена на рис.5. Здесь поверхность отклика задается линиями уровня.
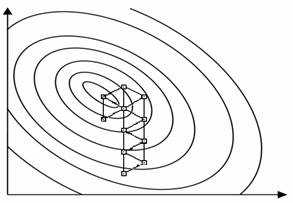
Рис. 5. Схема последовательного симплексного метода
students-library.com
4.2 Планирование эксперимента и методы оптимизации параметров процесса
Основной целью проведения современного эксперимента с позиций производителя продукции является разработка математической модели, адекватно описывающей процесс и позволяющий, в конечном результате, осуществлять его управление. Именно с помощью такой модели можно эффективно управлять производством, оперативно изменяя его параметры в соответствии с запросами потребителя и обеспечивая выпуск высококачественной продукции.
При этом исследователь должен:
1) обеспечить высокую надежность и четкость интерпретации результатов экспериментальных исследований;
2) составить четкую и последовательную логическую схему построения всего процесса исследования: что, когда и как нужно делать;
3) максимально формализовать процесс разработки модели и сопоставления экспериментальных данных различных опытов одного и того же объекта исследований с целью широкого применения электронно-вычислительных средств.
Всем перечисленным требованиям отвечают статистические методы планирования эксперимента, являющиеся одним из эмпирических способов математического описания и оптимизации сложных процессов. Начало математическому планированию экспериментов положено в 30-40-х годах.
При планировании эксперимента рассматриваются только такие объекты, для которых выполняются требования воспроизводимости и управляемости. Первое требование означает, что при повторении эксперимента при одних и тех же значениях входных параметров результаты эксперимента имеют разброс, не превышающий некоторой заранее заданной величины (т. е. требований к точности эксперимента). Второе требование означает, что объект исследования должен быть управляемым, т.е. эксперимент - активным.
Планирование эксперимента состоит в процедуре выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом обеспечивается следующее:
• одновременное варьирование всеми переменными по специальным правилам;
• использование математического аппарата, формализующего многие действия экспериментатора;
• выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов;
• минимизация общего числа опытов.
Наиболее часто требуется установить количественную связь между значением выходного параметра и факторами, от которых он зависит. Такой эксперимент называется интерполяционным.
В этом случае для описания объекта исследования удобно пользоваться кибернетической схематизацией, представляющей объект исследования в виде «черного ящика» (рис. 14.1). Стрелки справа, обозначенные уь изображают функции, результаты процесса характеристики целей исследования, т.е. «параметров оптимизации». Встречаются и другие названия: «критерий оптимизации», «целевая функция», «выход черного ящика», «функция отклика» или просто «отклик» и т.д. Все способы такого воздействия на объект исследования (входы «черного ящика») обозначены хi, и называются «факторами», «независимыми переменными». Совокупность возможных значений всех факторов можно рассматривать как k-мерное «факторное пространство» с координатами (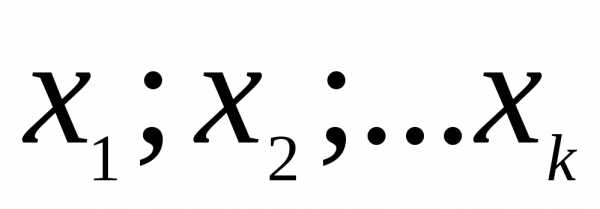
).
Для решения задачи необходимо создать математическое описание процесса, то есть математические модели, связывающие параметр оптимизации с факторами обычно представляется в виде полинома, где У - функция отклика, а Х1, Х2,Хз,..., Хн - факторы исследуемого процесса. Процесс проверки степени соответствия математической модели описываемому процессу называют «проверкой адекватности», а полученную модель - «адекватной».
Каждый фактор может принимать в опыте одно из нескольких значений. Эти значения называют «уровнями». Всякий фактор имеет определенное число дискретных уровней. Фиксированный набор уровней факторов (т.е. установление каждого фактора на некоторый уровень) определяет одно из возможных состояний «черного ящика». Одновременно это есть условия проведения одного из возможных опытов. Перебор всех возможных наборов состояний дает полное множество различных состояний данного «ящика», т. е. число возможных различных опытов. Число различных состояний получается путем возведения числа уровней факторов в степень числа факторов k.
Выбор параметра оптимизации определяется тем аспектом, который в конкретном случае представляет наибольший интерес.
Параметры оптимизации могут быть весьма разнообразными:
- экономические: прибыль, себестоимость, рентабельность и т.п.;
- технико-экономические: производительность, эффективность, долговечность, надежность и т.п.;
- статистические: характеристика распределения, дисперсия, стандартное отклонение;
- чисто технические: размер, характеристика механических свойств и т.п. При механической обработке могут выбираться такие параметры оптимизации, как стойкость режущего инструмента, точность базирования, точность обработанных поверхностей, шероховатость поверхности детали и т. п.
Параметр оптимизации должен удовлетворять следующим требованиям.
1. Быть количественным, т. е. всегда задаваться числом. То множество значений, которые может принимать параметр оптимизации, называется областью определения. Если нет способа измерения параметра оптимизации или он не может быть количественно зафиксирован, необходимо провести его ранжирование, то есть присвоение рангов по заранее выбранной шкале.
2. Быть однозначным в статистическом смысле, т. е. заданному набору значений факторов должно соответствовать с точностью до ошибки эксперимента определенное значение параметра оптимизации.
3. Быть простым, иметь физический смысл, легко вычисляться и выражаться одним числом.
4. Оценивать действительную эффективность функционирования системы или качество объекта, т.е. задача эксперимента должна ставиться корректно.
5. Обладать по возможности универсальностью и полнотой, то есть всесторонне характеризовать объект исследования, что выполняется далеко не всегда. Например, часто характеристики качества вступают в противоречие с экономическими аспектами.
Выбор факторов играет важнейшую роль в построении математической модели, см. § 3.4
Если какой-либо существенный фактор окажется не включенным в совокупность управляемых исследователем условий проведения экспериментов, и при этом его уровень не будет контролироваться, то это может привести к значительным погрешностям результатов. Если неучтенный фактор произвольно принимал случайные значения, а информация об этом не была зафиксирована, это также значительно увеличит ошибку опыта. При поддержании фактора на некотором фиксированном уровне (не задействован в эксперименте) может быть получено ложное представление об оптимуме, так как при другом фиксированном уровне этого фактора оптимум параметра оптимизации может сместиться.
При планировании эксперимента факторы должны быть управляемыми (активный эксперимент). Нужно знать последовательность действий (операций), с помощью которых устанавливаются конкретные значения (уровни) фактора («операциональный» фактор).
Дополнительные требования предъявляются к совокупности факторов:
1. Требование совместности: все комбинации факторов должны быть осуществимы и безопасны. Если это требование не выполняется, необходимо разбить область определения факторов на диапазоны, «блоки».
2. Требование независимости, «некоррелированности», «ортогональности» факторов. При существенной связи между рассматриваемыми факторами (явление «мультиколлинеарности») не удаётся получить достоверной математической модели
studfiles.net
12. Симплекс-метод экспериментальной оптимизации. Последовательный симплексный метод Этот метод требует проведения минимально возможного числа опытов при определении направления движения.
Симплексом в n-мерном пространстве называют многогранник с (n+1)-й вершиной. Если расстояния между вершинами симплекса одинаковы, такой симплекс называют регулярным. Симплексный метод включает в себя следующие основные процедуры:
1. Линейное преобразование входных переменных с таким расчетом, чтобы изменение каждой из них на единицу одинаково сказывалось бы на изменении выходной переменной.
2. Построение регулярного симплекса и реализация опытов в вершинах симплекса.
3. Отбрасывание вершины с минимальным значением целевой величины и построение нового симплекса, который образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой зеркальным отображением отброшенной вершины относительно противоположной ей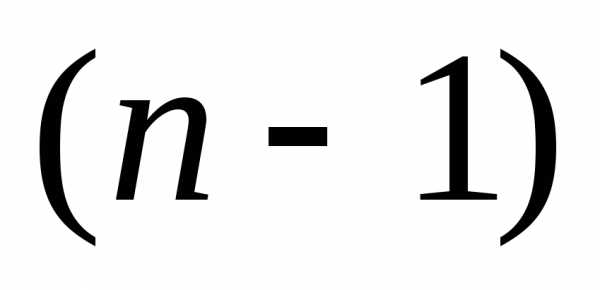 
-мерной грани исходного симплекса. Координаты этой новой вершины рассчитываются по формуле:,
где 
− номер отброшенной вершины.
4. Проведение эксперимента в вершине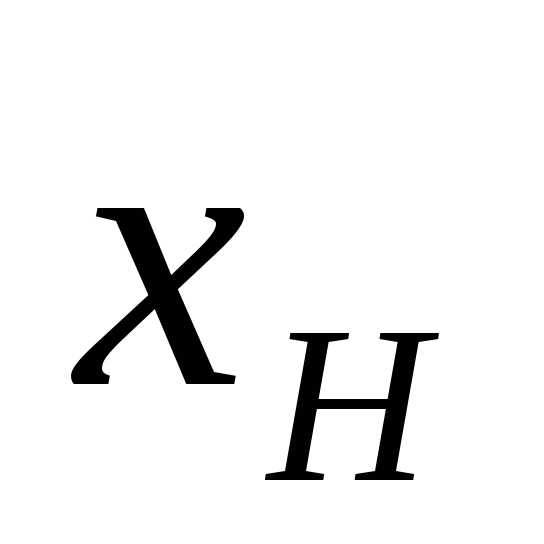 
и возврат к п. 3. Если оказывается, что выходная переменная в новой вершине приняла значение меньшее, чем в остальных вершинах симплекса, то следует возвратиться к предыдущему симплексу. Во избежание зацикливания в качестве отбрасываемой выбирают вершину, в которой выходная переменная имеет величину, следующую по порядку за наихудшей вершиной симплекса. Аналогично следует поступать, если новая вершина выходит за пределы симплекса.
5. Если при перемещении симплекса за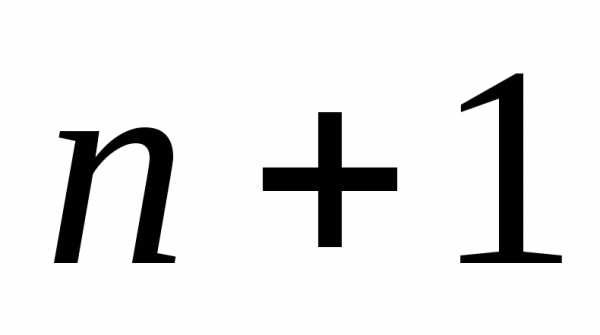 
шагов некоторая вершина сохраняет свое положение, то симплекс совершит оборот относительно этой вершины. Это означает достижение области оптимума. Другим условием достижения оптимума является выполнение неравенства:
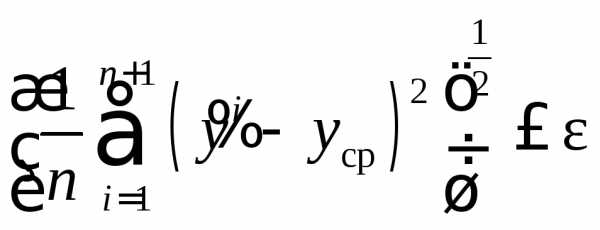, где – малая величина (порог), 
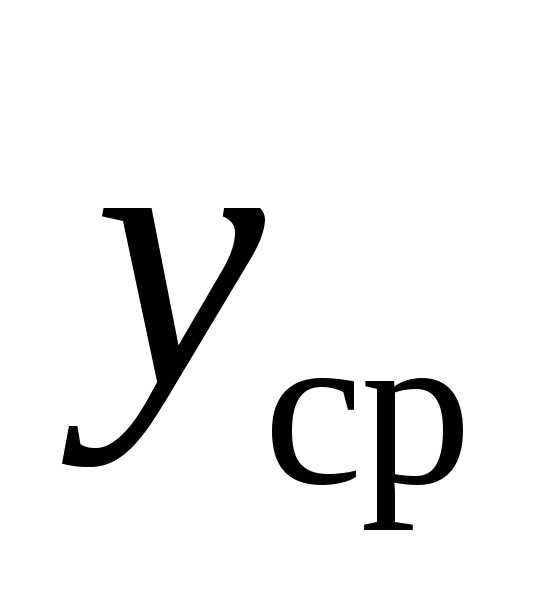– среднее значение выходной величины в вершинах симплекса.
К числу достоинств симплексного метода наряду с экономичностью по числу опытов и простотой вычислений следует отнести также возрастание эффективности метода с ростом числа входных переменных, устойчивость выделения направления движения, поскольку оно определяется только соотношением целевых величин, а не их абсолютными значениями.
Графическая иллюстрация симплексного метода при двух входных переменных приведена на рис.5. Здесь поверхность отклика задается линиями уровня.
x2
x1
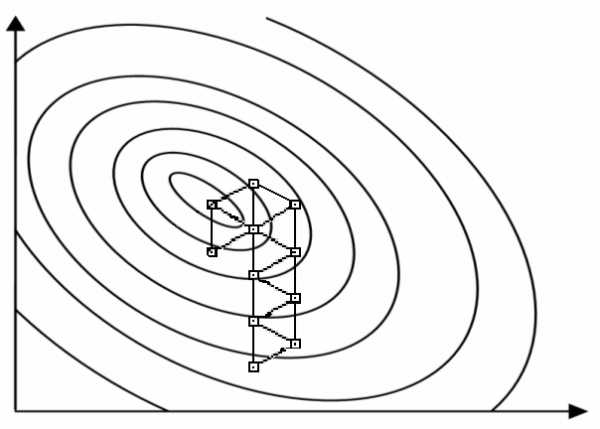
Рис. 5. Схема последовательного симплексного метода
13. Метод Бокса-Уилсона.
На основе малой серии опытов строится линейное описание поверхности отклика в окрестности начальной точки. В центре этой локальной области определяется значение градиента, после чего начинаются опыты в направлении градиента. Бокс и Уилсон предложили использовать дробные факторные планы для поиска линейной модели. Метод состоит из последовательности циклов, каждый из которых содержит два шага.
1. Построение линейной модели в окрестности некоторой начальной точки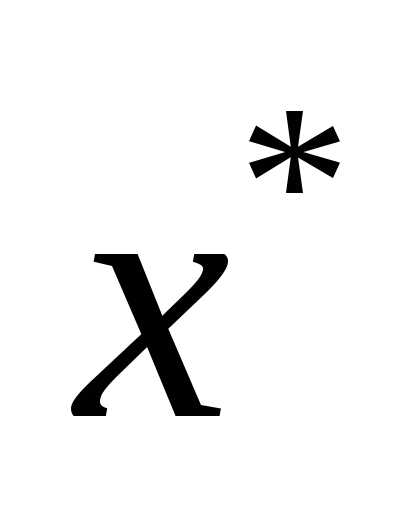 
с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьированияпо отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели бы одинаковый порядок. В случае адекватности линейной модели коэффициенты регрессии совпадают с компонентами градиента, т.е. 
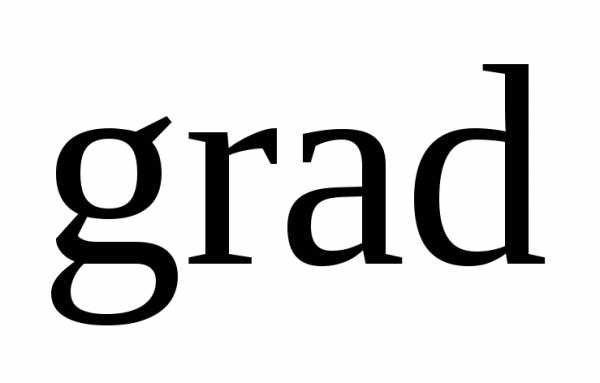, где i, j,…,k – направляющие векторы осей координат. Обычно переходят к нормированному градиенту делением его компонент на норму 
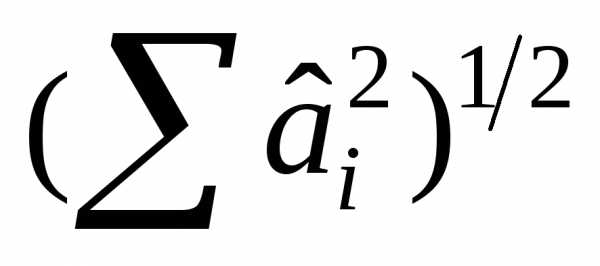либо просто на
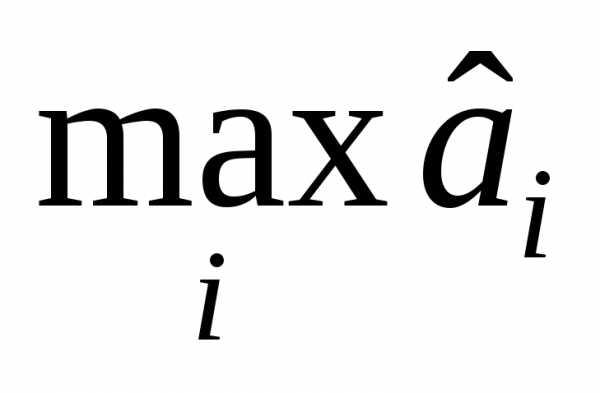. Компоненты нормированного градиента обозначим.
2. Пошаговое увеличение величины целевой функции (движение в направлении градиента). Координаты точки наблюдения на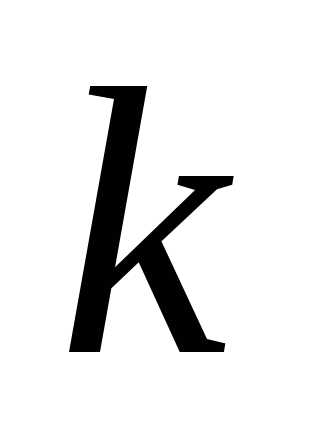 
-м шаге при движении в направлении градиента определяются по формуле:, где
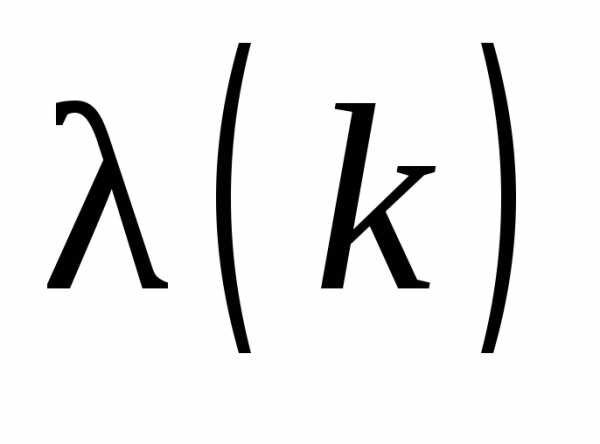≥1 – параметр, позволяющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной области, тем меньше 
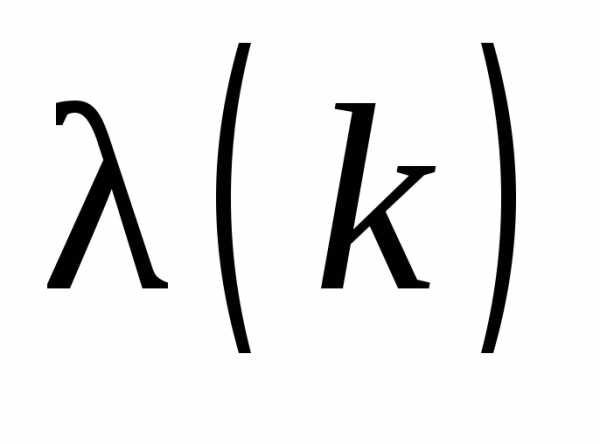. Движение в направлении градиента продолжается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план, находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям.
Геометрическая интерпретация метода приведена на рис.4. Здесь поверхность отклика задается линиями уровня.
x2
x1
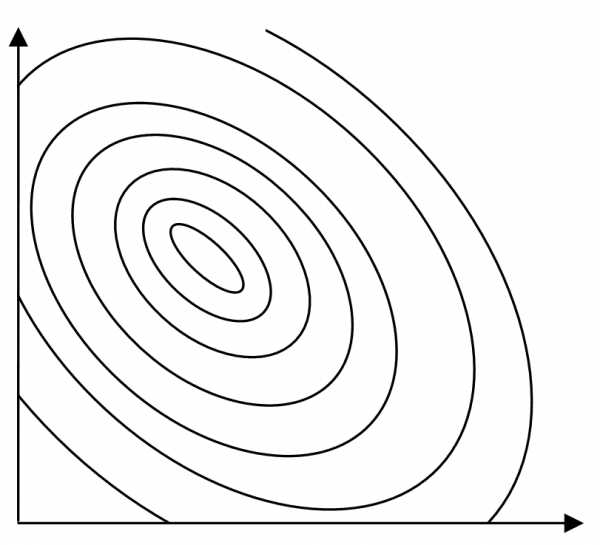
Рис. 4. Схема метода Бокса–Уилсона
Рассмотрим в качестве примера использование метода Бокса−Уилсона для поиска максимума функции
. (6.11)
Допустимая область изменения переменных: 0х120, 0х210, 1х315. Начальная точка поисках0=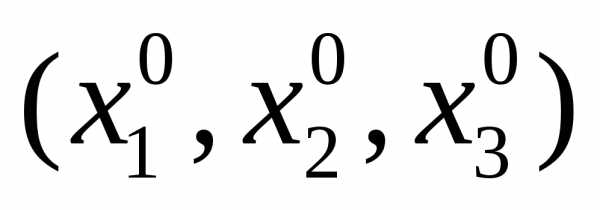
=(3,2,4). Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями:,i=1,2,3. Значенияi желательно подбирать такими, чтобы приращения функции по каждому из аргументов были сопоставимы, то есть
. Примем 1=1,2=2,3=3. В соответствии с (6.1) стандартизованная переменная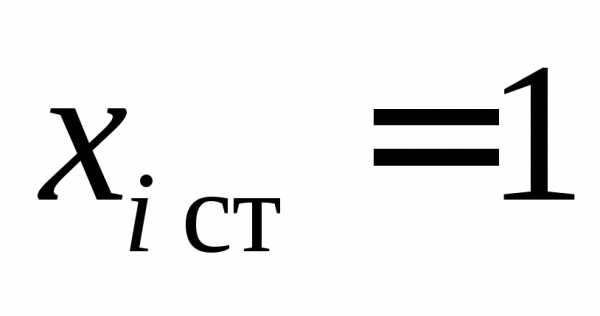
, если, и
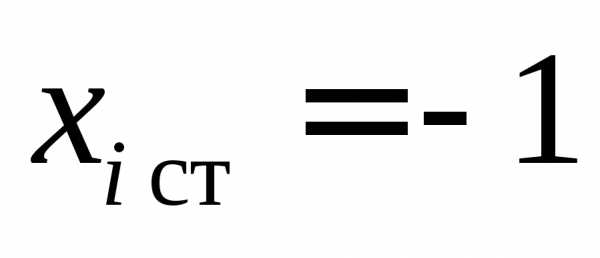при.
Линейная модель требует для своей оценки не менее четырех экспериментов. Воспользуемся ДФЭ 23-1с ГС: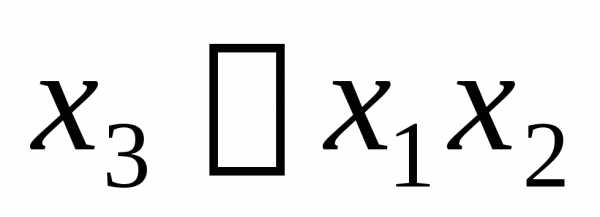
(табл. 16).
Таблица 16
| i | х1ст | х1 | х2ст | х2 | х3ст | х3 | y |
| 1 | 1 | 4 | 1 | 4 | 1 | 7 | 40,8 |
| 2 | -1 | 2 | 1 | 4 | -1 | 1 | 26,2 |
| 3 | 1 | 4 | -1 | 0 | -1 | 1 | 24,4 |
| 4 | -1 | 2 | -1 | 0 | 1 | 7 | 25,4 |
В последнем столбце табл.16 содержатся значения функции (6.11) для исходных переменных, то есть 40,8=у(4,4,7)и так далее.
МНК-оценки коэффициентов линейной модели составят:
; ; .
Отнормируем полученные компоненты градиента, поделив их на максимальное значение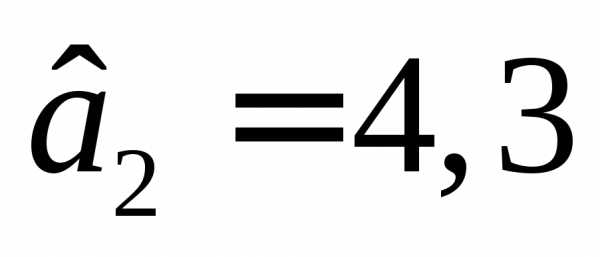 
:
b1=3,4/4,3=0,79,b2=1,b3=0,91. Движение в направлении градиента представлено в табл.17.
Таблица 17
| Формулы для вычисления компонент вектора | Номера компонент вектора | у | ||
| 1-я | 2-я | 3-я | ||
| х0 | 3 | 2 | 4 | 31,3 |
| i | 1 | 2 | 3 | |
| bi | 0,79 | 1 | 0,91 | |
| bii | 0,79 | 2 | 2,73 | |
| x0+1bii | 3,79 | 4 | 6,73 | 39,9 |
| x0+2bii | 4,58 | 6 | 9,46 | 46,4 |
| x0+3bii | 5,37 | 8 | 12,19 | 50,6 |
| x0+4bii | 6,16 | 10 | 14,91 | 52,6 |
Движение в направлении градиента после четвертого шага невозможно из-за ограничения на х3. Теперь следует определить градиент в точкеx0+3bii. Поскольку темп роста функции замедлился на последних шагах, область линейного описания следует сузить, уменьшив значенияi.
studfiles.net
Исследование и экспериментальная оптимизация систем управления
Постановка задачи
Решение многих задач управления, проектирования, планирования в той или иной мере связано с оптимизацией, т.е. с нахождением наилучших в определенном смысле значений различных параметров. Для химического реактора, например, оптимизация означает выбор таких значений температуры, давления, расходов и концентраций компонентов реакции, при которых реакция будет протекать с максимальным выходом целевого продукта, либо продукция будет соответствовать определенным требованиям к качеству, либо, наконец, реакция будет протекать за минимальное время. Обычно задается некоторый критерий оптимизации (целевая функция) Y, зависящий от ряда управляемых факторов: .Тогда задача оптимизации сводится к отысканию таких значений компонентов вектора управляемых факторов , при которых целевая функция достигает экстремума. Функция
образует некоторую поверхность в n+1-мерном пространстве управляемых факторов и целевой функции Y. Эту поверхность обычно называют поверхностью отклика, а отдельные значения Y, соответствующие некоторой комбинации компонентов вектора , — просто откликом.
Целевые функции, такие, как производительность, прибыль, часто связаны с величинами, характеризующими качество продукции. Например, необходимо найти такой режим работы некоторого аппарата, при котором производительность его будет максимальной, а качество продукции — соответствовать требованиям стандартов. Здесь одна целевая функция, а именно: характеристика качества продукции выступает в роли ограничения. Такого вида ограничения называются функциональными, так как характеристика качества продукции, так же как и целевая функция (производительность), являются некоторыми функциями от вектора управляемых факторов . Кроме функциональных ограничений могут быть также и факторные, т. е. ограничения, накладываемые да одну, несколько или все составляющие вектора . Учитывая все вышесказанное, задачу оптимизации в самом общем виде можно записать следующим образом:
Yjmin≤Yj≤Yjmax, j=1(1)m;
ximin≤xi≤ximax, i=1(1)k, k≤n.
В тех случаях, когда зависимость задана в аналитической форме , координаты оптимальной точки ( ) в факторном пространстве можно найти, решив систему дифференциальных уравнений вида
Такое решение задачи оптимизации возможно в том случае, если отсутствуют факторные и функциональные ограничения. Если решается задача отыскания оптимума при ограничениях, то используются методы математического программирования, либо задача поиска условного экстремума с помощью множителей Лагранжа сводится к задаче поиска безусловного экстремума.
Однако в большинстве практических случаев аналитическая зависимость Y(X) неизвестна, и исследователь располагает только возможностью наблюдать значения отклика при различных комбинациях управляемых факторов . При этом процедура измерения наблюдаемого значения отклика предоставляет собой сумму истинного значения отклика и случайной ошибки опыта ε.
У=М{У}+ε.
Для решения задачи оптимизации используют два принципиально различных подхода:
1 Оптимальные условия определяют с помощью математической модели объекта. Для этого вначале каким-либо образом находят математическую модель, а затем аналитическим или численным методом решают задачу оптимизации.
2. Экспериментальный поиск оптимальных условий осуществляют непосредственно на объекте без использования модели объекта.
Поисковые методы, или методы экспериментальной оптимизации, в отличие от аналитических требуют вначале локального изучения поверхности отклика по результатам ряда экспериментов, специально спланированных вблизи исходной точки. Точка спектра плана в этом случае выбирается, таким образом, который позволит организовать движение в направлении экстремума функции отклика. Экстремальное значение функции отклика достигается с помощью многократной последовательной процедуры изучения поверхности отклика и продвижения в факторном пространстве. Рассмотрим методы поиска максимума функции отклика (поиск минимума функции отклика ничем принципиально не отличается).
Все поисковые методы позволяют найти экстремум функции отклика в результате поэтапного движения. На каждом этапе реализуются две операции. Первая операция — исследование поверхности отклика в окрестности некоторой точки факторного пространства в целях определения направления движения к экстремуму функции отклика. Вторая операция — организация движения к экстремуму в выбранном направлении. Все методы поиска экстремума отличаются характером первой или второй операции.
Метод Гаусса—Зайделя
Метод Гаусса — Зайделя, или метод покоординатного поиска, является классическим методом поиска экстремума функции. Последовательное движение к экстремуму осуществляют путем поочередного варьирования каждым трактором до достижения частного экстремума функции отклика. При этом все остальные факторы стабилизируют на некоторых уровнях. Достигнув частного экстремума по последнему фактору Хп, переходят к варьированию первым Х1. Направление движения по каждой из координат факторного пространства определяют путем постановки в окрестности исходной точки двух пробных опытов с координатами (Хi - дельта Хi) и (Хi + дельта Хi). Движение осуществляется в том направлении, в котором наблюдается большое значение отклика. Идея метода Гаусса — Зайделя может быть показана на примере двухфакторной задачи (рис. 7.1).
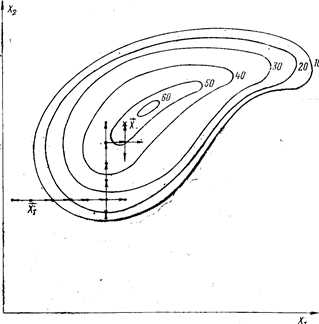
Рис. 7.1. Движение к оптимуму методом Гаусса—Зайделя (цифрами обозначены линии равного уровня поверхности отклика в некоторых относительных единицах)
При использовании метода Гаусса — Зайделя для оптимизации двухфакторного процесса последовательность операций следующая:
1. Определяется начальная точка Х1 движения к экстремуму функции отклика. В качестве начальной точки выбирается наилучшая из известных рабочих точек.
2. Задается шаг варьирования дельта Хi , по каждому управляемому фактору Хi (i = 1,2).
3. Для определения направления движения первого рабочего цикла (по координате Х1 совершается два пробных опыта с центром в начальной точке, т. е. совершаются два пробных шага в точки в которых производится по одному измерению отклика у.
4. Сравниваются значения отклика в пробных точках и формируется функция Sign(Y1 - Y2).
5. Осуществляется первый цикл рабочего движения (с тем же или большим шагом) в направлении возрастания уровня выхода Y(Х).
6. После каждого рабочего шага производится измерение значения отклика Y(Х).
7. Первый цикл рабочего движения прекращается по достижении в некоторой точке Хh частного экстремума функции отклика по соответствующей переменной. Движение к экстремуму в данном направлении прекращается, если выполняется неравенство
Уh+1 < Уh
8. Точка Хh является исходной для следующего цикла рабочего движения (по координате Х2). Из данной точки делаются два пробных шага в точки X1 = const
9. Движение вдоль координаты Х2 производится аналогично описанному выше.
10. По окончании второго цикла рабочего движения переходят к третьему (по координате Х1) и т. д.
Критерием окончания поиска оптимума методом Гаусса — Зайделя является неудачная попытка организовать движение из некоторой точки Хk, любое движение из которой приводит к уменьшению значения функции отклика. Данная точка принимается за точку максимума целевой функции, определенную с точностью до максимального шага варьирования дельта Хi .
Эффективность метода Гаусса — Зайделя существенно зависит от вида поверхности отклика и от выбора начальной точки поиска. Данный метод является классическим. Он позволяет, постепенно переходя от одной переменной к другой, при нахождении локального оптимума решать задачу экспериментальной оптимизации.
Однако с ростом числа переменных Хi эффективность метода снижается из-за роста числа опытов на поиск оптимума.
Метод градиента
При поиске оптимума (максимума) методом градиента движение осуществляется в направлении наиболее быстрого возрастания значения отклика, т. е. в направлении градиента функции отклика (целевой функции). Движение по градиенту производится на один шаг, пропорциональный вектору градиента. Направление движения корректируют после каждого рабочего шага, т. е. после каждого шага заново вычисляют значение вектора grad Y(Х) по результатам специально спланированных пробных экспериментов.
Так как компоненты вектора градиента есть не что иное, как коэффициенты при линейных членах разложения функции Y(Х) в ряд Тэйлора то степеням Xi (i = 1- n), то их можно получить как линейные коэффициенты регрессии
Grad Y(X) =b1*i1 + b2*i2 + … + bn*in
Для получения оценок линейных коэффициентов регрессии можно воспользоваться любым из известных методов экспериментального получения математической модели объекта. Например, можно реализовать ПФЭ и ДФЭ с центром в начальной точке поиска.
Поиск оптимума методом градиента выполняется по следующей схеме:
1. Задаются шаги варьирования дельта Xi, для всех управляемых факторов. Величина шага то каждому фактору выбирается из тех же соображений, что и при ПФЭ или ДФЭ.
2. Задается параметр рабочего шага лямбда. Рабочий шаг должен быть пропорционален вектору градиента.
3. В начальной точке поиска Х1, которая выбирается так же, как и в методе Гаусса — Зайделя, реализуется пробный эксперимент для определения направления первого рабочего шага.
4. По результатам пробного эксперимента вычисляется оценка вектора
Grad Y(X) =b1*i1 + b2*i2 + … + bn*in
5. Совершается рабочий шаг в направлении Grad Y(X) .
6. В точке Х2 процедура определения направления дальнейшего движения к оптимуму полностью повторяется.
7. Поиск прекращается, когда модуль градиента у становится малой величиной, т. е. когда оценки коэффициентов регрессии становятся незначимыми.
Достигнутая точка принимается за абсолютный экстремум с точностью до величины последнего рабочего шага. Метод градиента более оптимален, чем метод Гаусса — Зайделя в смысле пути движения к оптимуму и в том смысле, что конечный шаг меньше начального (в методе Гаусса—Зайделя—постоянный).
Конечный шаг определяет точность нахождения оптимума.
Характер движения к оптимуму при использовании метода градиента показан на рис. 7.3.
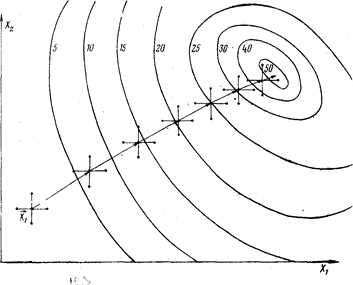
Рис. 7.3. Движение к оптимуму методом градиента
Для выбора параметра рабочего шага лямбда необходимо ориентироваться на физические и технологические ограничения, накладываемые на факторы. Параметр лямбда выбирают таким образом, чтобы до границы было сделано несколько шагов.
Эффективность метода снижается при работе исследователя в условиях больших погрешностях измерений факторов и с ростом числа самих факторов (более трёх).
Метод случайного поиска
Существует множество модификаций случайного поиска. Характерной особенностью случайного поиска является случайный выбор направления движения к экстремуму. Имеются алгоритмы случайного поиска, в которых информация, полученная на предыдущих этапах, используется для адаптации процедуры поиска, что позволяет повысить его эффективность. Рассмотрим один из наиболее простых методов случайного поиска. В этом методе рабочий шаг из некоторой точки Хh совершается после пробного эксперимента в точке
Хh+1 = Хh + p
гдеp - случайный вектор фиксированной длины
Отклики, полученные в точках Хh+1 и Хh, сравниваются, после чего совершается рабочий шаг в точку Хh+1 по направлению вектора p в сторону возрастания отклика. Длина рабочего шага лямбда выбирается большей или равной длине пробного шага р.
Алгоритм метода случайного поиска следующий:
1. Определяется начальная точка поиска Х1 которая выбирается на основе априорной информации и соответствует максимальному из известных значений отклика.
2. Определяются длины соответственно пробного р и рабочего лямбда шагов, причем р больше или равно лямбда.
3. Вычисляются компоненты лямбда1, лямбда2, … лямбда п случайного вектора p, определяющего направление пробного шага из начальной точки
Х1. Вектор лямбда представляет собой случайный вектор длиной р, равномерно распределенный на n-мерной сфере.
Указанный способ формирования случайного вектора не обеспечивает строго равномерного распределения его по окружности радиуса р, однако для практических задач такое приближение вполне достаточно.
4. Производится два пробных эксперимента в точках Х1 и Х1+ лямбда
5. Совершается рабочий шаг в направлении возрастания отклика
6. В точке Х2 повторяется процедура формирования случайного вектора p и совершается рабочий шаг в следующую точку.
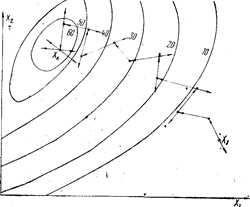
Рис. 7.6. Движение к оптимуму методом случайного поиска
7. Критерием окончания поиска является возрастание числа неудачных шагов, т. е. многократное повторение ситуации без улучшения результатов исследований.
Траектория движения к экстремуму методом случайного поиска для двухфакторной задачи показана на рис. 7.6.
Достоинством метода случайного поиска является возможность решения задачи оптимизации с большим числом исследуемых факторов (сто и более), при этом движение к оптимуму начинается уже после проведения первых двух опытов.
Симплексный метод
Симплексный метод поиска оптимума можно для оптимизации одновременно по нескольким выходным параметрам оптимизации. Его применение требует проведения минимального числа опытов для определения направления движения.
Прежде чем перейти к описанию алгоритма симплексного метода дадим несколько определений. N-мерным симплексом называется многогранник, образованный в N-мерном пространстве N+1 вер шинами, которые не лежат ни в одном пространстве меньшей размерности. Например, для n = 1 симплексом является отрезок прямой, для n = 2—треугольник, для n = 3—пирамида.
Симплекс называется правильным, если расстояние между всеми соседними вершинами одинаково. Если отбросить любую вершину симплекса и построить новую точку, зеркальную относительно оставшейся грани, то оставшаяся грань и зеркальная точка образуют симплекс той же размерности. Правильный симплекс всегда можно получить из произвольного путем преобразования системы координат (в дальнейшем будем рассматривать только правильные симплексы). В симплексном методе поиска оптимума все опыты проводят в точках факторного пространства, являющихся вершинами правильного симплекса.
Алгоритм поиска следующий:
1. Выбирается исходная точка поиска из тех же соображений, что
и в ранее рассмотренных методах, В окрестности исходной точки Х^ необходимо построить начальный симплекс. Для построения симплекса необходимо прежде всего задать его размер. Размер симплекса выбирается так же, как и шаг варьирования. Необходимо также задать первоначальное положение симплекса в пространстве. Существует несколько способов построения исходного симплекса. Рассмотрим один из них.
Рис. 7.6. Симплекс с вершиной (а) и центром (б) в начале координат
Длина ребра симплекса / (размер симплекса) здесь принята за единицу. Центр симплекса помещается в начале координат, а h+1 вершина - на оси Хп (рис. 7.6.). Остальные вершины располагаются симметрично относительно координатных осей. Координаты вершины определяются матрицей
| № вершины | Координаты | |||||
| X1 | X2 | X3 | … | Xn-1 | Xn | |
| - r1 | - r2 | r3 | … | rn-1 | - rn | |
| R1 | - r2 | r3 | … | rn-1 | - rn | |
| R2 | … | … | … | … | ||
| … | … | … | … | … | ||
| n | … | … | Rn-1 | - rn | ||
| n+1 | … | Rn |
При длине ребра симплекса L = 1 величины Ri и ri определяются выражениями
ri = 1/sq{2*i*(i+1)} i = 1,n
Ri = 1/sq{2*(i+1)} i = 1,n
где sq – квадратный корень.
2. В каждой вершине, координаты которых рассчитываются проводится по одному опыту. Наблюдаемые значения отклика в вершинах симплекса обозначим через Yhi, где h—номер симплекса, i —номер вершины h-го симплекса.
3. Движение к экстремуму осуществляется путем перехода от старого симплекса к новому. В старом симплексе отбрасывается вершина с наименьшим откликом и строится новая вершина, «зеркальная» отброшенной относительно оставшейся грани. Оставшаяся грань и зеркальная точка образуют новый симплекс. Координаты зеркальной точки Xi (i =1, п) вычисляются по формуле
Xh+1,j,i = 2/n * { Xh,1,i + Xh,2, i + … + Xh,j-1,i + Xh,j+1, i + … + Xh,h+1, i} - Xh,j,i
Для того чтобы найти i-ю координату зеркальной точки, необходимо i-е координаты оставшихся точек старого симплекса сложить, умножить на величину 2/п и из полученного результата отбросить i-ю координату отброшенной точки.
4. Если наименьшее значение отклика наблюдается в нескольких вершинах одновременно, то вопрос об отбрасывании той или иной вершины решается случайным образом с равной вероятностью.
5. При движении к оптимуму может возникуть ситуация, когда наименьшее значение отклика наблюдается в зеркальной точке нового симплекса. В этом случае необходимо вернуться к предыдущему симплексу и отбросить в нем вершину со следующим по малости откликом.
6. Преобразование поступательного движения симплекса во вращательное вокруг некоторой точки X* факторного пространства может свидетельствовать о выходе симплекса в область оптимума. Однако может оказаться, что в этой точке неправильно определено значение отклика. В точке вращения необходимо поставить несколько параллельных опытов. Если в результате такого уточнения наибольшее значение отклика подтверждается, то это означает, что достигнута оптимальная область. Если наибольшее значение отклика в точке вращения не подтверждается, то поступают так же, как в п. 5, т. е. возвращаются к предыдущему симплексу и отбрасывают вершину со следующим по малости откликом.
7. При достижении области оптимума размер симплекса уменьшается в 2 раза и движение продолжается по тому же алгоритму.
8. Оптимум считается достигнутым, если выполняется условие: разброс результатов в вершинах симплекса примерно равна ошибке измерения выходного (оптимизируемого) параметра.
9. В условиях большой ошибки эксперимента рекомендуется в каждой вершине симплекса проводить несколько параллельных опытов и использовать усредненное значение отклика.
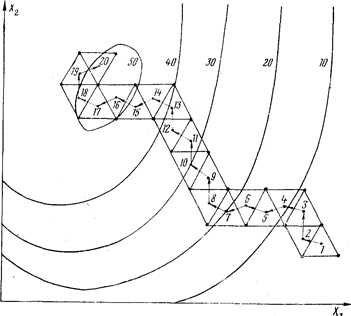
Рис. 7.7. Движение к оптимуму симплекс-методом
Вопросы для самоконтроля:
1. Нужна ли математическая модель объекта исследования при решении задач экспериментальной оптимизации?
2. Назовите условия целесообразного применения каждого из методов оптимизации.
3. Какой метод работает в условиях больших ошибок измерения факторов?
4. Какой метод успешно работает при большом количестве исследуемых факторов?
5. Как будет двигаться симплекс в условиях ограничений на управляемые факторы?
6. В каком случае Вы выберете градиентный метод оптимизации?
7. Как будет вести себя симплекс в условиях дрейфа области оптимума?
Читайте также:
lektsia.info
Методы оптимизации. Особенности исследуемых экспериментальных областей и их ограничения.
Методы оптимизации позволяют достигать локальной оптимизации, но НЕ глобальной.
Исследуемая область:
Монотонность (нет точек перегиба, нет производных, равных нулю, экстремумов).
Время оптимизации (на выбор варианта).
Ограничения:
Выпуклые области– области, в которых нельзя найти такого отрезка, концы которого принадлежат области, а сам он пресекает ее границы;
Вогнутые области– те, в которых можно найти отрезок, концы которого принадлежат области, а сам он пересекает ее границы.
Понятие особых точек.
На экспериментальной поверхности могут существовать особые точки, в которых либо производные (градиенты) могут равняться нулю или отсутствовать, либо иметь бесчисленное множество решений, приводящих к тому, что алгоритмы вычислительных программ требуют дополнительных критериев к оптимизации.
Метод Гаусса-Зейделя.
При оптимизации по методу Гаусса-Зейделя последовательное продвижение к экстремуму осуществляется путем поочередного варьирования каждого фактора до достижения частного экстремума выходной величины.
Таким образом, точка перемещается попеременно вдоль каждой из координатных осей xi факторного пространства.
При достижении целевой функции по предыдущей координате -
После достижения частного экстремума по последней переменной xk , переходят снова к варьированию первой и т.д. Поиск экстремума прекращается в точке, движения из которой в любом направлении не приводят к уменьшению выходного параметра.
Метод случайного поиска (МСП).
Характерной чертой данного метода является случайный выбор направления движения на каждом шаге. Если точка после i-го шага занимает - положение в векторном пространстве, то следующий рабочий шаг будет совершен лишь после выполнения пробного эксперимента, которому будет соответствовать, где- случайный вектор определенной длины.
Значение исравниваются и производитсяi+1 рабочий шаг вдоль вектора .
Критерий выхода целевой функции является увеличение неудачных шагов.
Основным недостатком метода является большая трудоемкость и длительность поиска экстремума.
Метод градиента.
При оптимизации градиентным методом движение совершается в направлении наибольшего критерия градиента оптимизации, т.е. в направлении градиента целевой функции.
При этом направление движения корректируется после каждого рабочего шага, т.е. заново определяется значение градиента по результатам:
.
Поскольку координатами вектора градиента служат коэффициенты при линейных членах разложения функции в ряд Тейлора, то соответствующие компоненты вектора градиента могут быть получены как коэффициентылинейной аппроксимации поверхности отклика в близи исходной точки поверхности.
Линейные коэффициенты обычно оцениваются экспериментально. Наиболее просто каждый из коэффициентов определяется по результатам двух пробных экспериментов в окрестности исходной точки.
В этом случае, приращение целевой функции Δxi можно считать пропорциональным значению величины частной производной
.
После нахождения соответствующего градиента, выполняется рабочий шаг по направлению к экстремуму.
Т.е. из вектора , где- параметр рабочего шага, показателем выхода к экстремуму является критерий.
studfiles.net
