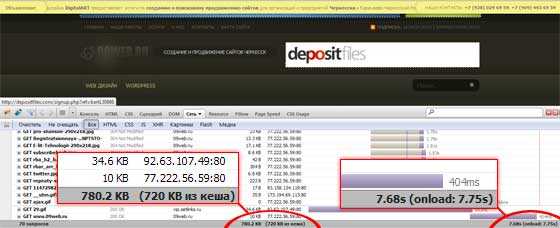
Оптимизация функций одной и нескольких переменных в PTC MathCAD. Mathcad оптимизация

Оптимизация функций одной и нескольких переменных в PTC MathCAD

1. Поиск экстремума функции

Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.

Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.

2. Экстремум функции одной переменной

Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис.2 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).

В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

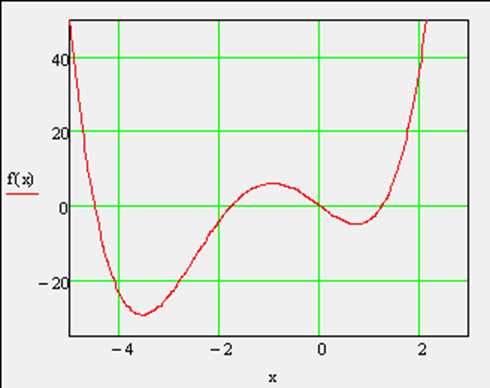Рис. 1. График функции f(х)=х4+5х3-10х

Построим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.

Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.

· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;

· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;

f (x1, … , хм,…) — функция;
x1, … , xм — аргументы, по которым производится минимизация (максимизация).

Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис.1) без дополнительных условий показаны в листинге на рис.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.

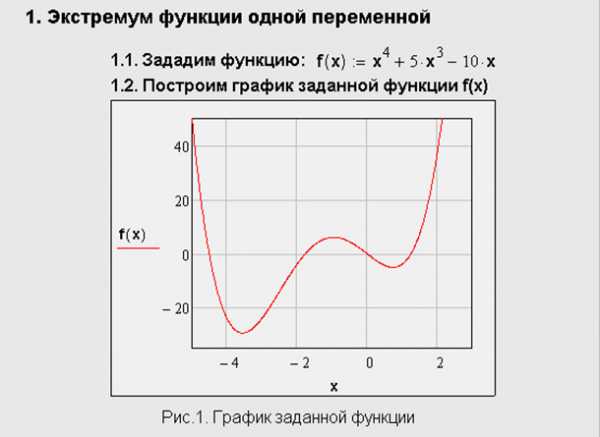
Рис.2. Поиск локальных экстремумов функции одной переменной

Как видно из листинга, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются локальные различные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).

3. Условный экстремум

В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. На рис.3 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.

Рис. 3. Три примера поиска условного экстремума функции

Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия — 3<х<0 в последнем примере листинга задать -5<х<0, то при том же самом начальном х=-10 будет найден максимум Maximize(f,x) =-0.944, что неверно, поскольку максимальное значение достигается функцией f (х) на левой границе интервала при х=-5. Выбор начального приближения х=-4 решает задачу правильно, выдавая в качестве результата Maximize (f ,x) =-5.

4. Экстремум функции многих переменных

Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером (рис.4) нахождения минимума функции, показанной в виде графика трехмерной поверхности (рис. 4).

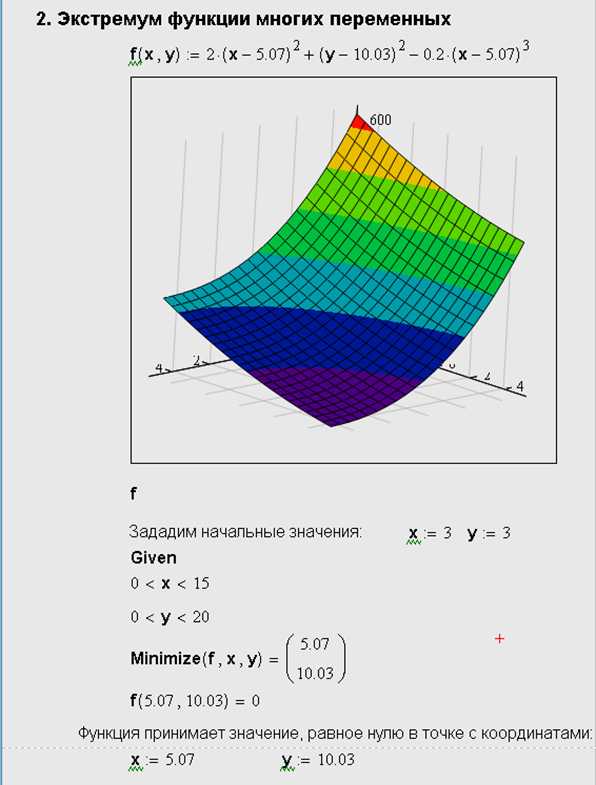
Рис. 4. Минимум функции двух переменных

Поиск минимума можно организовать и с помощью функции Minerr. Для этого в листинге (рис.4) надо поменять имя функции Minimize на Minerr, а после ключевого слова Given добавить выражение, приравнивающее функцию f (х,у) значение, заведомо меньшее минимального, например f (х,у) =0.

Скачать пример

cadregion.ru

Оптимизация функций одной и нескольких переменных в PTC MathCAD — Cadregion.ru

Оптимизация функций одной и нескольких переменных в PTC MathCAD

1. Поиск экстремума функции

2. Экстремум функции одной переменной

Рис. 1. График функции f(х)=х4+5х3-10х

Построим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.

· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;

· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;

f (x1, … , хм,…) — функция;
x1, … , xм — аргументы, по которым производится минимизация (максимизация).

Рис.2. Поиск локальных экстремумов функции одной переменной

3. Условный экстремум

Рис. 3. Три примера поиска условного экстремума функции

4. Экстремум функции многих переменных

Рис. 4. Минимум функции двух переменных

Скачать пример

new.cadregion.ru

Иллюстрированный самоучитель по MathCAD 12 › Оптимизация [страница - 111] | Самоучители по математическим пакетам

В этой главе рассматриваются задачи на поиск экстремума функций и близкие к ним задачи приближенного решения алгебраических нелинейных уравнений и систем. Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов.

Для численного решения задач поиска локального максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Принцип их действия очень близок к принципу расчетов, заложенных во встроенной функции Find, предназначенной для решения алгебраических уравнений (см. главу 5).

В задачах на условный экстремум встроенные функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции.

Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером нахождения максимума и минимума функции, показанной в виде графиков трехмерной поверхности и линий уровня (листинг 6.5).

Задачи поиска условного экстремума функции многих переменных часто встречаются в экономических расчетах для минимизации издержек, финансовых рисков, максимизации прибыли и т. п. Целый класс экономических задач оптимизации описывается системами линейных уравнений и неравенств.

Несмотря на то, что, как уже говорилось, разработчиками Mathcad символьное решение задач оптимизации не предусмотрено, пользователь все-таки имеет возможность аналитического исследования экстремумов функций, опираясь на базовые сведения математического анализа.

Градиентные численные методы решения задач отделения корней уравнений и поиска экстремума функций очень близки. Поэтому, в частности, пользователь может тем же самым образом, с помощью контекстного меню, выбирать конкретный метод приближенного решения для функций Minimize и Maximize.

Еще один широко распространенный круг задач на решение систем уравнений, называемых обратными, наиболее типичен для современной экспериментальной физики. Значительную часть обратных задач относят к классу некорректно поставленных (или просто некорректных), которые, благодаря своей принципиальной неустойчивости, требуют специального подхода.

Одним из наиболее простых методов решения некорректных обратных задач является концепция поиска их квазирешения. Рассмотрим обратную задачу AY=B, где неизвестный вектор Y подлежит определению, а оператор (в линейном случае, матрица) А и вектор правых частей уравнений в известны.

Говоря о некорректных задачах, нельзя не отметить, что для их решения советским математиком Тихоновым был предложен чрезвычайно эффективный метод, называемый регуляризацией и основанный на привлечении дополнительной априорной информации о решении, которая может быть как качественной, так и количественной. Например, можно искать решение, максимально близкое к некоторому профилю, т. е.

samoychiteli.ru

Pers.narod.ru. Обучение. Безусловная и условная оптимизация в MathCAD

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

Для решения оптимизационных задач без ограничений (безусловной оптимизации) в MathCAD используются две функции:

Maximize(f,список_параметров) – вычисляет точку максимума;
Minimize(f,список_параметров) – вычисляет точку минимума.

Здесь f – имя минимизируемого функционала, определенного до обращения к функции, а список_параметров содержит перечисление через запятую имен переменных, относительно которых решается задача минимизации или максимизации. Перед обращением к функциям Maximize, Minimize (имена которых начинаются прописными буквами) обязательно задать начальные значения всем параметрам оптимизации. Следует также понимать, что, если решение не единственно, будет найден максимум или минимум, ближайший к начальным значениям.

Для решения оптимизационных задач с ограничениями (условной оптимизации) применяются те же функции Maximize и Minimize, но они входят в блок решения Given и перед ними размещаются ограничения в виде равенств или неравенств, определяющие допустимую область значений параметров оптимизации.

В частности, легко решить задачу как линейного, так и нелинейного программирования. Подробнее тема описана в этой лекции, а здесь приведём пример документа, решающего все 4 задачи - безусловной минимизации и максимизации и условной минимизации и максимизации.

Безусловная и условная оптимизация в MathCAD, документ .xmcd (55 Кб)

pers.narod.ru

Применение программирования в системе Mathcad для целочисленной многокритериальной оптимизации

Mathcad является математическим пакетом, в котором легко осуществлять расчёты на естественном математическом языке. Однако в него также встроены средства программирования, позволяющие писать функции для разнообразных вычислений, как в обычных языках структурного программирования, но с некоторыми особенностями: в Mathcad есть богатые диалоговые возможности и средства упрощённой работы с матрицами, в том числе с векторами.

При помощи Mathcad можно построить систему функций, которые будут автоматически проделывать всю работу при различных начальных условиях. При этом можно проследить весь процесс нахождения решения, что в обычных языках программирования не так просто осуществимо, как в Mathcad.

Задача такова: имеется система обработки данных, состоящая из коммутаторов, процессоров и устройств памяти. Блок данных поступает в коммутатор, откуда направляется к одному из процессоров, где проходит обработку. Оттуда снова через коммутатор идёт в одно из устройств памяти, где остаётся на хранение. Пример структуры такой системы показан на рисунке (здесь К – коммутатор, Р – процессор, М – память):

Требуется найти оптимальное число элементов каждого типа, при котором система будет удовлетворять заданным ограничениям. В качестве критериев оптимальности рассматривается надёжность (P), среднее время пребывания заявки в системе (U), максимальная интенсивность входного потока заявок (Λ), стоимость системы (С). В качестве исходных данных даётся время обслуживания в узле каждого типа, надёжность работы элементов (коэффициент готовности), стоимость элементов, а также ограничения: максимальное значение стоимости системы, максимальное время пребывания заявки в системе, минимальная надёжность (коэффициент готовности).

Так как оптимизация целочисленная, число допустимых решений ограничено (хотя и велико), и применение компьютера позволяет рассмотреть их все. Значит, можно перебрать все возможные конфигурации системы, сравнить их характеристики и определить лучшую систему. Поскольку критериев оптимальности несколько (то есть стоит задача многокритериальной оптимизации), требуется провести выбор по какому-либо обобщённому критерию.

Для этого в Mathcad мы сначала задаём начальные условия (в виде векторов).

Затем определяем функции для нахождения значений характеристик системы, которые являются критериями оптимальности, и функцию, определяющую, удовлетворяет ли система заданным ограничениям на значения своих характеристик.

Далее создаём функцию, формирующую множество систем, удовлетворяющих ограничениям. Для каждой возможной системы вычисляются и проверяются значения критериев. В итоге формируется матрица критериев систем, входящих в область допустимых решений.

Определяется функция для нормализации, которая приводит значения каждого критерия к виду «чем больше, тем лучше» (от 0 до 1).

Формируется функция нахождения области Парето (выделяющая из множества допустимых решений множество эффективных решений для сокращения перебора).

Наконец, реализуются функции для проведения многокритериальной оптимизации. Они выбирают единственное решение по матрице критериев. В данной работе для нахождения оптимального решения были использованы: минимаксный критерий, аддитивный критерий, мультипликативный критерий, метод отклонения от идеала, метод главного критерия, метод последовательных уступок, метод STEM.

Теперь, когда есть все необходимые функции для проведения оптимизации, можно получить решение. Вот как выглядит в Mathcad вывод ответа:

Имя системы – это строка-список: число коммутаторов, процессоров и устройств памяти в ней.

Таким образом, в Mathcad можно не только вести расчёты ad hoc, но и создавать сложные вычислительные программы многократного использования. Благодаря привычной математической записи и наглядности процесса вычислений не требуется специальная подготовка или большие усилия при разработке, отладке, сопровождении и использовании таких программ.

Полные версии исходных кодов можно загрузить по адресу: /tpr-mathcad.zip.

gigabaza.ru

Иллюстрированный самоучитель по MathCAD 7 › Управление вычислительными процессами › Вычисления в автоматическом режиме (Automatic Calculation). Оптимизация вычислений (Optimization). [страница - 122] | Самоучители по математическим пакетам

Вычисления в автоматическом режиме (Automatic Calculation). Оптимизация вычислений (Optimization).

Операция Automatic Calculation (Автоматические вычисления) в подменю Math обеспечивает переключение между ручным и автоматическим режимами вычислений. Если против названия этой операции мышью установить "птичку", то будет работать автоматический режим вычислений, в противном случае, когда "птички" нет, – ручной.

Как правило, автоматический режим вычислений намного удобнее ручного, поэтому он установлен по умолчанию.

Оптимизация вычислений (Optimization)

Оптимизация вычислений достигается заменой сложной функции или математического выражения их аналитическим представлением (если оно, конечно, есть). Для иллюстрации техники оптимизации рассмотрим рис. 7.5.

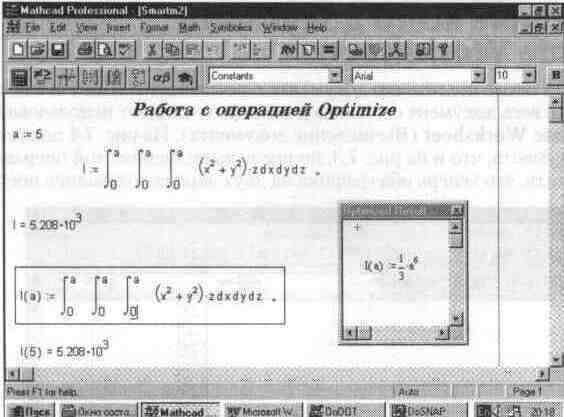Рис. 7.5. Пример на оптимизацию вычислений

На рисунке вначале показано вычисление тройного интеграла обычным способом. Поскольку вычисления производятся численным методом, то они достаточно трудоемки и задержка выдачи результата заметна даже на скоростных ПК с процессором Pentium.

Во втором случае использовалась техника оптимизации. Выражение для интеграла, оформленное как функция 1(n), было выделено, а затем исполнена операция Optimize (Оптимизация), после чего скорость вычислений увеличилась в несколько раз.

Признаком оптимизации выражения является появление после него красной звездочки – знака *. Кроме того, установив в оптимизированное выражение курсор мыши и щелкнув ее левой клавишей, можно наблюдать появление окна с оптимизированным выражением; на рис. 7.5 это окно также показано. Нетрудно заметить, что в нашем примере довольно сложный интеграл оказался замененным достаточно простым аналитическим выражением.

Разумеется, вычисление по такому выражению намного проще, чем по полному интегралу. Особенно большой выигрыш оптимизация может дать при многократном вычислении сложных функций, содержащих интегралы, производные, суммы, произведения и ряды. Бывают, впрочем, случаи, когда исходное выражение превращается в не менее сложное оптимизированное выражение. Тогда оптимизация оказывается бесполезной. Оптимизацию можно задать в тексте документа специальными словами – директивами, но эта возможность будет рассмотрена позже.

samoychiteli.ru

Оптимизация функций одной и нескольких переменных в PTC MathCAD. Mathcad оптимизация