Математические методы оптимизации (стр. 1 из 4). Математические методы оптимизации

Методы математической оптимизации - Энциклопедия по экономике

Критерии и способы оценки сравнительной экономической эффективности проектов детально излагаются в главе 5. Однако вопросы, рассматриваемые на стадии ТЭО, настолько широки и разноплановы, что одних экономических критериев здесь явно недостаточно. Формальные методы математической оптимизации здесь играют подчиненную роль. А главное внимание обращено на творческую проработку ft анализ имеющихся альтернатив. Оценку их эффективности дают с помощью целой группы экономических, социальных, экологических, технико-технологических, а нередко - и международных аспектов. Наиболее удачный вариант проектных решений принимают к осуществлению и утверждают в виде "Технического задания на разработку проекта строительства предприятия" (ТЗ).  [c.55] Например, отыскание оптимального/для одной рыночной системы или одного сценарного спектра является задачей математической оптимизации. В этих случаях методы математической оптимизации могут быть достаточно грубыми, вроде перебора всех значений / от 0 до 1,0 с шагом 0,01. В качестве целевой функции для отыскания среднего геометрического HPR при различных условиях и заданном значении/может выступать одна из функций, представленных в главе 1. Роль варьируемого параметра здесь играет то значение / которое тестируется в интервале от 0 до 1.  [c.172]

Теперь, когда у нас есть координаты для отдельной точки (ее широта, долгота и высота), нам нужна некая процедура поиска, метод математической оптимизации, для изменения значений / подставляемых в целевую функцию таким образом, чтобы возможно скорее и проще добраться до вершины поверхности.  [c.173]

В прошлом было разработано множество методов математической оптимизации, многие из которых весьма продуманны и эффективны. У нас есть из чего выбирать. Ключевым вопросом является К какой целевой функции мы будем применять эти методы математической оптимизации в нашей новой методологии инвестирования капитала Целевая функция является ее сердцевиной. Далее мы обсудим этот вопрос и проиллюстрируем на примерах, как работать с целевыми функциями. После этого мы займемся методами оптимизации целевых функций.  [c.173]

Далее, руководствуясь используемым методом математической оптимизации, мы стали бы изменять наши значения/ В итоге мы нашли бы оптимальные значения 0,21, 0,21, 0,21 для / , f2 и fv соответственно. Это дало бы нам  [c.181]

Кроме двух описанных грубых методов математической оптимизации существуют и более совершенные. Это — замечательная ветвь современной математики, и я настоятельно призываю вас познакомиться с ней, просто в надежде, что вы извлечете из этого какую-то долю того удовлетворения, которую получил я от ее изучения.  [c.185]

В целом, различные методы математической оптимизации могут быть классифицированы по принципу используемого аппарата следующим образом  [c.186]

Хотя вы можете использовать любой упомянутый алгоритм многомерной оптимизации, я предпочел генетический алгоритм потому, что он является, возможно, единственным наиболее устойчивым методом математической оптимизации, за исключением весьма грубых приемов перебора всех возможных комбинаций значений переменных.  [c.188]

Методы математической оптимизации, 623  [c.768]

Наиболее важным и перспективным и в то же время наименее разработанным является применение методов математической оптимизации в народнохозяйственном планировании.  [c.93]

Математическое моделирование технологических процессов основывается на теории процесса как результате соответствующих исследований. Однако нередко встречаются процессы столь сложные, что теоретическое изучение их механизма требует весьма длительных сроков, тогда как задачи оптимизации подлежат решению в более короткое время. Поэтому для моделирования технологических процессов используются методы математической статистики, позволяющие на основе эксперимента давать математическое описание очень сложных или малоизученных процессов.  [c.100]

Оптимизация производственной программы предприятия. Для выбора более рациональных вариантов смешения компонентов в товарные нефтепродукты и для расчета оптимальной производственной программы на нефтеперерабатывающих предприятиях применяют методы математического программирования.  [c.73]

Одним из наиболее известных методов является система Аккорд (автоматизация контроля и координации оптимальных режимов деятельности). Оптимизация рабочей силы в этой системе выполняется по программе Дельта . Идея алгоритма этой программы сводится к использованию метода линейного программирования на сети. Можно отметить достаточную строгость применяемого в этом методе математического аппарата. Недостаток этого метода заключается в том, что оптимизация проводится без учета механизации работ (путем добавления или изменения одних рабочих).  [c.47]

В условиях конструкторской подготовки производства весьма трудно обеспечить равномерную по календарным срокам сдачу технической документации на опытные образцы. Выявленные в процессе проектирования недочеты конструкции, необходимость конструкторских доработок и изменений, естественно, вызывает многочисленные отклонения от плановых сроков и, как следствие, неравномерное поступление заказов в экспериментальные цехи. В таких условиях большую роль играет применение математических приемов, позволяющих оперативно маневрировать ресурсами и обеспечить выравнивание загрузки производственных участков. В частности, оптимизация загрузки опытного производства, маневрирование ресурсами могут выполняться методами математического моделирования.  [c.130]

Новые возможности для использования всех рассмотренных выше методов открываются применением в планировании методов экономико-математического моделирования. Так, например, аппарат межотраслевого моделирования позволяет увязать баланс народного хозяйства с системой материальных балансов, с отраслевыми расчетами потребности в продукции и структуры затрат на ее производство, с расчетами по капитальному строительству, уровню жизни населения и др., а в конечном счете — поставить и решить задачу оптимизации межотраслевых связей. Тем самым балансовый метод получает свое дальнейшее развитие за счет применения методов межотраслевого моделирования и оптимального планирования. Методы сетевого планирования, матричной алгебры, оптимизации выступают в качестве инструментов практической реализации программно-целевого подхода, а методы математической статистики находят широкое применение в прогнозировании.  [c.95]

На основе обобщения опыта социалистического планирования и с учетом новейших достижений экономической теории, кибернетики и других наук в эскизном проекте АСПР комплексно и предметно охарактеризованы методология, методика и технология разработки системы перспективных и текущих планов, обеспечивающие реализацию намеченных в решениях партии и правительства направлений совершенствования планирования в условиях широкого использования современных методов и средств обработки информации. В эскизном проекте АСПР дано функциональное описание работы центральных плановых органов и их подразделений на каждой стадии составления долгосрочных, среднесрочных и краткосрочных планов, рассмотрены проектируемые плановые процессы и задачи, реализация которых обеспечит взаимную увязку всех видов государственных планов экономического и социального развития, единство их отраслевого, территориального и программного разрезов, а также определены экономико-математические модели, предназначенные для использования в сводных и отраслевых подсистемах АСПР в различных режимах и на различных стадиях планирования, методы согласования, оптимизации и балансовой увязки отдельных разделов плана. Эти методы и модели ориентированы на использование плановыми работниками при решении задач электронной вычислительной техники, комплекса информационных средств, предполагают перестройку технологических процессов переработки информации при решении плановых задач, требуют внесения уточнений, изменений, дополнения действующих правовых норм планирования, в некоторых случаях — организационной перестройки плановых органов и их взаимодействия в процессе работы над планами, делают необ-  [c.170]

Основной метод исследования операций - изучение математических моделей операций. Сущность оперативного подхода заключается в следующем определение и математическая формулировка цели операции, критерия оптимальности (показателя качества процесса) и ограничений построение математической модели операции, выражающей эффективность исследуемой системы как функцию множества переменных, из которых, по крайней мере, хотя бы одна поддается управлению определение (а в случае необходимости прогнозирование) входной информации выбор метода оптимизации с помощью методов математического программирования нахождение оптимального решения проверка полученной модели путем сравнения с оригиналом операции и в случае необходимости корректировка модели и ее решения.  [c.307]

Поиски оптимальных решений (наилучшего варианта) на базе имеющейся информации производят с применением математических методов". Математическое обеспечение представляет собой комплекс экономико-математических моделей, алгоритмов и алгоритмических языков, программ и методических указаний, с помощью которых решаются задачи автоматизированной обработки информации и оптимизации планово-экономических расчетов.  [c.382]

Математическое программирование — важный раздел современной прикладной математики. Методы математического (прежде всего линейного) программирования служат основным средством решения задач оптимизации производственно-хозяйственной деятельности. По своей сути эти методы есть средство плановых расчетов. Их ценность для экономического анализа выполнения планов состоит в том, что опи позволяют оценивать напряженность плановых заданий, определять лимитирующие группы оборудования, виды сырья и материалов, получать оценки дефицитности произведенных ресурсов и т.п.  [c.268]

Математическое обеспечение (МО) — это совокупность математических методов, моделей и алгоритмов обработки информации, используемых при решении функциональных задач и в процессе автоматизации проектировочных работ АИТ. Математическое обеспечение включает средства моделирования процессов управления, методы и средства решения типовых задач управления, методы оптимизации исследуемых управленческих процессов и принятия решений (методы многокритериальной оптимизации, математического программирования, математической статистики, теории  [c.50]

Это особый вид экономико-математических моделей, описывающих варианты решения определенной проблемы. Нормативные модели оптимизации включают переменные для выбора варианта решения и его оценки. Модели оптимизации содержат уравнения взаимосвязи переменных и критерий для выбора — функционал или целевую функцию. Целевая функция принимает значения в области, ограниченной условиями задачи. В состав целевой функции входят управляемые переменные, параметры задается форма функции. Для решения оптимизационных задач применяются методы математического программирования.  [c.435]

А (существенная доля в общем объеме закупок). Планирование по материалам группы А основывается на концепции точно в срок (оптимизация издержек по заготовлению при условии непрерывного обеспечения производства необходимым количеством материалов) и применении соответствующих методов математического моделирования (модель EOQ).  [c.285]

Принятие решения в рамках указанных моделей в большинстве случаев удается свести к решению одной или нескольких задач математического программирования. В тех случаях, когда существует множество критериев оценки качества решения, как правило, осуществляется свертка векторного критерия в скалярный, используются методы лексикографической оптимизации, методы последовательных уступок или иные эвристические человеко-машинные процедуры.  [c.186]

Можно сказать, что отыскание корней имеет отношение к математической оптимизации, так как первая производная в точке оптимума функции (т. е. на экстремуме) будет равна 0. Следовательно, вы могли бы заключить, что традиционные методы отыскания корней, например метод Ньютона, можно использовать для решения оптимизационных задач (применение собственно методов оптимизации для отыскания корней уравнения, напротив, чревато обилием трудностей).  [c.183]

В учебном пособии рассматриваются основные методы построения математических моделей процессов, явлений и объектов в экологии планирование экспериментов и статистическая обработка их результатов методы их оптимизации.  [c.2]

ОПТИМИЗАЦИЯ ПРОИЗВОДСТВА ПРОДУКЦИИ В АССОРТИМЕНТЕ МЕТОДАМИ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ  [c.112]

Разделение труда и выделение управленческих функций в отдельную сферу деятельности большого числа людей обусловило и дифференциацию решений — выделились управленческие решения (УР). Суть выделения была замечена не сразу, имелись попытки использовать для них методы разработки технических решений с хорошим математическим аппаратом, в том числе законы нормального распределения данных, методы математического программирования и оптимизации. Это хорошо смотрелось на бумаге, однако в практике напряженной управленческой деятельности польза от этих методов для руководителей была  [c.5]

Для оптимизации конструирования и проектирования используются аналитические и графические методы математического и реального моделирования, а также натурные испытания.  [c.184]

Кибернетика экономическая — научная отрасль знаний, применяющая методы математического моделирования и системного анализа для оптимизации и совершенствования экономических систем, управления социалистической экономикой.  [c.72]

Подготовка экономической информации относится к наиболее трудоемким и ответственным этапам при использовании математических методов для оптимизации отраслевых планов. В основном объем исходной экономической информации определяется экономико-математической моделью. Подготовка включает следующие элементы  [c.195]

Как показывает практика использования экономике-математических методов для оптимизации отраслевых планов, в химической промышленности пока еще не достигнуто идентичности между условиями и ограничениями, используемыми в настоящее время при составлении планов традиционными и новейшими методами. Различие определяется не только в номенклатуре рассматриваемых производств (в отраслевом планировании оно значительно шире, чем в оптимизационных расчетах), но и в учете специфических особенностей развития отдельных предприятий. Это делает в значительной степени несопоставимыми варианты планов, составленных различными методами. Поэтому выявленный экономический эффект оптимизации может быть связан и с недоучетом отдельных условий, принятых при составлении планов развития отрасли традиционными методами.  [c.226]

Оценивая рассмотренные возможности использования экономико-математических методов для оптимизации развития и размещения отрасли, можно говорить о целесообразности их использования для задач на всех этапах.  [c.229]

Эта задача относится к типу оптимизационных задач, решаемых методами математического программирования (линейного программирования, если ограничения и целевая функция задачи имеют линейный характер). Причем минимизация необходимых инвестиций при обеспечении хотя бы нулевых (но без убытков) прибылей оказывается задачей, обратной по отношению к рассмотренной в предыдущей главе задаче оптимизации цены, объема выпуска и постоянных текущих затрат для максимизации прибылей предприятия. Дело в том, что в предыдущей задаче оптимизации на основе анализа безубыточности прибыль П максимизировалась при отсутствии жесткого ограничения на привлекаемые инвестиции /. В задаче, которая формулируется ниже, наоборот, максимизируется экономия на инвестициях (минимизируются инвестиции) при отсутствии жесткого ограничения на любые будущие положительные прибыли предприятия. В решении этой задачи они могут быть сколь угодно малыми, лишь бы не превратились в убытки. Иначе говоря, как и в предыдущей задаче, безубыточность предприятия в соответствующие календарные периоды должна быть гарантирована.  [c.151]

Методы математического моделирования процессов позволяют существенно уменьшить объем и продолжительность проектных разработок и могут быть использованы как для решения проектных задач при создании новых промышленных объектов, так и для оптимизации уже осуществленных технологических режимов. Математическое описание содержит необходимые исходные данные для автоматизации управления технологическими процессами описывающие уравнения вводят в ЭЦВМ, которая на их основе выдает команды для постоянного поддержания оптимального технологического режима.  [c.100]

Итак, методы многокритериальной оптимизации позволяют тем или иным образом преодолеть трудности, связанные с неединственностью критерия. При этом, однако, приходится решать задачу, значительно более сложную, чем задача оптимизации. Поэтому задачи многокритериального выбора удается решить в случае относительно простых моделей. Что же следует делать, если модели сложны Ведь достаточно адекватная математическая модель некоторой экономической системы может оказаться настолько сложна, что и обычную оптимизационную задачу решить не удается. В этом случае для исследования экономических систем применяются имитационные эксперименты.  [c.61]

Период 50-х годов. В 50-х годах тенденции управленческих подходов и методы обоснования решений в развитых странах стали меняться. Получили развитие децентрализация управления, привлечение персонала к широкому участию в управлении, повышение роли человеческих отношений в управлении, методы математического программирования, исследование операций, моделирование и оптимизация прибыли в обосновании управленческих решений13.  [c.13]

Необходимость и целесообразность построения такой цепочки обусловливается недостаточной корректностью имеющихся постановок задачи оптимального календарного планирования основного производства НПП, наличием ряда трудноформализуемых и случайных факторов, которые не всегда удается учесть в модели. Анализ оптимальных решений осуществляется специалистами, которые оценивают качество и эффективность разработанного календарного плана. В связи с этим основные требования, предъявляемые к математической модели производства и методу ее оптимизации, определяются фактором оперативности получения допустимого решения и условием достижения приемлемых результатов на первых же итерациях процедуры.  [c.76]

Основной недостаток алгоритма — это большой объем накладных расходов на обработку данных, требуемых для расчета и хранения вариантов решений. Тем не менее, благодаря своей конструктивной устойчивости и эффективности приложений в области оптимизационных проблем, будь то крупные, нелинейные или зашумленные, по убеждению автора, он станет фактически предпочтительным методом оптимизации в будущем (не считая появления лучших алгоритмов, обладающих теми же желательными свойствами). По мере того, как компьютеры становятся все более мощными и дешевыми, проблема вычислительных издержек утрачивает свою остроту. Воистину, если бы скорость обработки была нулевой, если бы скорость не играла роли, то генетический алгоритм стал бы предпочтительным методом решения для почти всех задач математической оптимизации.  [c.191]

Область исследования операций, которая занимается оптимизацией, т.е. нахождением максимума (или минимума) целевой функции при заданных ограничениях, называется математическим программированием. С точки зрения современного русского языка этот термин не вполне удачен, поскольку сейчас под программированием однозначно понимается написание программ для компьютеров (людей, профессионально занимающихся этой работой, называют программистами). В английском языке значение слова programming определено не столь жестко и может означать планирование, выбор программы (плана) действий. Именно в этом контексте следует понимать и термин математическое программирование. Некоторым оправданием этому термину в русском переводе может служить то обстоятельство, что всякая реализация методов математического программирования в практике управления невозможна без использования компьютерных программ. Поэтому все эти методы являются фактически компьютерными алгоритмами.  [c.30]

ОПТИМАЛЬНАЯ (ИЛИ ОПТИМИЗАЦИОННАЯ) ЗАДАЧА [optimization problem] — экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличныхресурсов. (Иногда то же Экстремальная задача.) Решается с помощью оптимальной модели методами математического программирования, т.е. путем поиска максимума или минимума некоторых функций или функционалов при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация).  [c.242]

economy-ru.info

Математическая метода - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Математическая метода - оптимизация

Cтраница 1

Математические методы оптимизации и оптимального управления в задачах как термодинамики, так и микроэкономики имеют свои особенности. Связано это, во-первых, с тем, что в каждой из этих областей важную роль играют циклические процессы, при которых скорость изменения состояния всей или части системы в среднем за цикл равна нулю. Во-вторых, математические модели часто приводят к уравнениям ляпуновского типа, для которых скорость изменения состояния не зависит от самого состояния. Эти особенности позволяют в ряде случаев свести задачи оптимального управления к усредненным задачам нелинейного программирования, определяют метод получения и характер оптимального решения. Последняя глава книги посвящена методам оптимизации и оптимального управления, применяемым для решения задач о предельных возможностях макроуправляемых систем.  [1]

Математические методы оптимизации можно эффективно применять лишь при наличии математического описания оптимизируемого объекта. Если же математическое описание, достаточно точное в качественном и количественном отношении, отсутствует, то единственная возможность оптимизации заключается в исследовании реального объекта, для чего его оборудуют необходимыми измерительными средствами и проводят достаточно большое число экспериментов. Однако такой подход к отысканию оптимальных условий осуществления процесса обладает рядом принципиальных недостатков, к числу которых относится прежде всего сложность изменения аппаратурного оформления. Кроме того, не всегда удается оборудовать объект нужными измерительными средствами без значительного изменения нормального режима его работы. Наконец, достигаемые при оптимизации действующего объекта результаты носят обычно частный характер и почти не поддаются обобщению, что затрудняет накопление опыта, получаемого при оптимизации даже аналогичных производств.  [2]

Математические методы оптимизации электронных схем основаны на исследовании локального поведения целевой функции E ( q) при небольшом регулировании параметров компонентов схем и экстраполировании этих результатов на случай больших по величине изменений параметров.  [4]

Технические средства обработки данных и математические методы оптимизации никак не могут подменить социальное, экономическое и административное руководство.  [5]

Эффективны задачи, использующие математические методы оптимизации и анализа. Но исследование состава задач, функционирующих в АСУ, показывает, что всего несколько процентов ( в лучших случаях не более 7 %) задач решается с использованием методов оптимизации.  [7]

Приведенная классификация задач, использующих математические методы оптимизации, является, конечно, условной. Возможны и другие варианты классификации. На практике при решении какой-либо крупной npo - блемы управления обычно приходится совместно использовать методы решения нескольких из рассмотренных выше задач.  [8]

Приведенная классификация задач, использующих математические методы оптимизации, условна. На практике при решении какой-либо более или менее крупной проблемы управления обычно приходится совместно использовать методы решения нескольких из рассмотренных задач.  [9]

В предлагаемом учебном пособии описаны математические методы оптимизации, получившие за последние годы распространение в химической технологии. Систематизация и прикладная направленность этих методов позволили сформировать курс лекций, читаемый в течение нескольких лет на кафедре кибернетики химико-технологических процессов Московского химико-технологического института им. Содержание книги в основном соответствует принятому изложению лекционного материала, за исключением глав I и II, где приведены краткие сведения, рассматриваемые в других курсах кафедры и нужные для иллюстрации методов решения оптимальных задач. Кроме того, некоторые специальные математические вопросы, не относящиеся непосредственно к методам оптимизации, но необходимые при их изложении, вынесены в Приложение к книге. Такое построение учебного пособия исключает необходимость предварительного знакомства с дисциплинами, выходящими за рамки обычных курсов химико-технологических вузов, и делает его доступным для инженеров-химиков и технологов, занимающихся оптимизацией химических производств и владеющих математической подготовкой в объеме технического вуза. Книга может оказаться также полезной аспирантам химико-технологических специальностей и химических факультетов университетов.  [10]

Рассмотрены общие принципы моделирования и математические методы оптимизации химических процессов, моделирование экзотермических и эндотермических процессов, а также процессов в псевдоожиженном слое.  [11]

Рассмотрены общие принципы моделирования и математические методы оптимизации химических процессов, моделирование экзотермических и эндотермических процессов, а также процессов в псевдоожиженном слое.  [12]

Математические модели процессов позволяют эффективно использовать математические методы оптимизации, определять оптимальные решения на той или иной стадии проектирования. По существу задачи оптимального проектирования эквивалентны задачам отыскания тех параметров математических моделей, которые определяют конструктивное оформление и режим процесса при заданных требованиях к количественным и качественным характеристикам получаемой продукции.  [13]

Вариантй решения данной задачи также Основываются на математических методах оптимизации. В качестве критериев оптимизации могут быть приняты, например: минимум длительности производственного цикла; равномерность загрузки оборудования; минимум издержек производства, связанных с планированием; минимум суммарного времени разницы сроков выпуска деталей по календарным графикам и директивным срокам внутримесячных поставок.  [14]

При решении задач построения систем электроснабжения получили распространение такие математические методы оптимизации, как симплексный, градиентный и другие, которые позволяют решать самые разнообразные задачи, связанные с нахождением оптимальных значений различных параметров.  [15]

Страницы:      1    2    3

www.ngpedia.ru

Математические методы теории оптимизации. — КиберПедия

Задача о рационе.

 

Фермер имеет в своем распоряжении n-видов кормов для кормления домашних животных, каждый из которых содержит m-видов различных питательных веществ. Известно, что единица каждого вида кормов содержит определенное количество единиц каждого вида питательных веществ и имеет конкретную стоимость.

Требуется составить такой рацион, который бы удовлетворял потребность во всех питательных веществах, и имел бы наименьшую стоимость.

 

Транспортная задача.

 

Определить оптимального план перевозок однородного продукта из пунктов отправления в пункты назначения при известных тарифах, запасах в пунктах отправления и потребностях в пунктах назначения.

Раздел 1.

Линейное программирование.

Предметом изучения данного раздела являются линейные экстремальные задачи, в которых целевая функция и функция ограничения линейны.

Определение: общей задачей линейного программирования называется задача, состоящая в нахождении максимального значения целевой функции.

 

1) Z= cjxj max при условии

2) aijxj{ } bi(i= )

3) xj 0 (j n)

 

где aij; bi; cj – заданные постоянные величины,

1. целевая функция задачи (линейная форма)

2. ограничение задачи (типа равенства или неравенства)

3. условие неотрицательности переменной

 

Определение: стандартной (симметричной) задачей ЛП называется задача, в которой целевая функция исследуется на максимум или минимум, ограничение только типа неравенств, причем в одну сторону, а для всех переменных выполняется условие неотрицательности.

 

Определение канонической формы задач.

Канонической (основной) задачей линейного программирования называется задача, в которой:

1) функция цели исследуется на максимум или минимум 2) ограничение задачи только типа неравенства (в одну сторону)

3) все переменные неотрицательны (xj ≥ 0)

4) элементы столбца правых частей положительны (bi>0 i= )

 

Определение: совокупность n-чисел (x1……xn), удовлетворяющих ограничению задачи, назовем допустимым решением или планом задачи. План X*=(X …X ) называется оптимальным, если на нем целевая функция принимает максимальное (минимальное) значение.

 

Элементы выпуклого анализа.

Линейная комбинация векторов (*) R=a1A1+…+anAn называется выпуклой, если выполняется условие:

ai=1 и все ai неотрицательны.

В двухмерном случае выпуклой комбинацией двух векторов (точек двухмерного пространства) есть отрезок, их соединяющий.

Определение: множество называется выпуклым, если вместе с каждой парой своих элементов, оно содержит все их выпуклые комбинации.

 

 

 

выпуклое невыпуклое

множество множество

Система линейных неравенств в ограничениях задачи ЛП стандартной формы определяет некоторое выпуклое возможно неограниченное множество, которое называют многогранником решений.

 

Ограниченный и Неограниченный

многогранники решения.

 

 

Определение: угловая точка многогранника решений – это такая точка многогранника, которая не является выпуклой линейной комбинацией никаких других точек многогранника (не лежит на отрезке, соединяющим две другие точки многогранника).

Если система ограничений содержит конечное число неравенств, то число угловых точек будет конечно и не превосходит С -числа сочетаний.

Теорема № 1.

Целевая функция задач линейного программирования достигает своего максимального значения в одной или нескольких угловых точках многогранника. Если она принимает максимальное значение большие, чем в одной из угловых точек, то она достигает такого же значения и в любой точке, являющаяся выпуклой линейной комбинацией этих угловых точек. Содержательно: это означает, что прямая, соответствующая целевой функции, параллельна одной из граней многогранника.

Опорное и базисное решение.

 

Если система линейных уравнений имеет переменных больше, чем уравнений, то она имеет бесконечное множество решений, в каждом из которых некоторые переменные полагают как базисные, а некоторые как свободные, причем базисных ровно столько, сколько уравнений в системе, а свободных n-m, где n – число переменных, а m – число уравнений. Применительно к задачам линейного программирования при переходе к канонической форме всегда имеем систему, в которой число неизвестных больше числа уравнений. При этом столбец B является линейной комбинацией (см. векторное представление задач) векторов A1+…+An и некоторых дополнительных, которые возникают в результате перехода к канонической форме. Следовательно, в качестве базисных переменных можно выбрать только m-переменных, а остальные все переменные в силу их не отрицательности положить равными нулю. Такое решение называется опорным.

Рассмотрим канонический вид задачи ЛП:

Z=C1X1+…+CnXn max

(*) A1X1+…+AnXn=B

Xj³0 j= .

B>0

Симплексный метод.

 

Основная идея: Симплекс метод – это направленный перебор опорных решений задачи линейного программирования, при котором значения целевой функции на каждом следующем шаге больше (не меньше), чем на предыдущих.

По процедуре метода переход от одной угловой точки к другой осуществляется с помощью преобразований Жордана - Гаусса. Преобразования осуществляются над строками матрицы и состоят в следующем:

1)перемена строк местами

2)умножение строки на число, отличное от нуля

3)сложение двух строк покомпонентно (элементов, стоящих в одном столбце).

Для решения задач симплекс- методом следует выполнить действия:

0) Построить экономико - математическую модель задачи

1) Привести задачу к канонической форме.

2) Составить исходную симплекс таблицу

3) Проверить план на оптимальность.

4) Если план не оптимальный, то переходим к новому опорному плану с помощью преобразований Жордана-Гаусса.

 

Задача № 1.

Предприятие планирует выпуск трех видов изделий и при этом предполагает использовать три вида ресурсов. Известны цена реализации (прибыль) единицы каждого вида изделия C1,C2,C3, запасы ресурсов каждого вида В1, В2, В3, расходы каждого вида ресурсов на производство единицы каждого вида продукции aij. Требуется составить план производства ( указать сколько и какой продукции надо выпускать, чтобы получить максимальную прибыль от ее реализации).

a) Составление экономико-математической модели:

В качестве переменных Х1,Х2,Х3 выбираем количество продукции каждого вида. Следовательно, значение этих переменных неотрицательно.

b) Целевая функция выражает прибыль от реализации и, следовательно, имеет представление Z=C1X1+C2X2+C3X3 и исходя из содержания задачи она должна быть максимальной.

c) Ограничения:

· Не отрицательность переменных из пункта а)

· Ограничение по ресурсам. Расход каждого вида ресурса на производство всех видов продукции не превосходит их заданных объемов:

a1x1+…..+a1nxn≤b1

……………

am1x1+…..+amnxn≤bm

Из содержания задачи b1 и bm должны быть положительны, т.к. это запасы ресурсов.

Дано: C1=5, C2=4, C3=3 , aij

В1=50, В2=60, В3=30.

Целевая функция Z=5x1+4x2+3x3 max выражает собой прибыль от реализации продуктов.

4x1+3x2+x3 40

2x1+5x2+2x3 50

x1+2x2+4x3 60

x1,x2,x3 0

Для решения задачи симплекс-методом приводим ее к канонической форме. В данном случае не выполняется лишь одно условие канонической формы, а именно ограничения должны быть типа равенства. Для перехода к ограничениям типа равенства в левую часть каждого из неравенств вводится своя неотрицательная добавочная переменная (в случае если левая часть меньше или равна правой), и избыточная неотрицательная переменная вычитается (в случае если левая часть больше или равна правой), которые входят в функцию цели с нулевыми коэффициентами.

 

Z=5x1+4x2+3x3+0x4+0x5+0x6 max

x1+3x2+2x3+x4 =40

4x1+x2+x3+x5 =50

2x1+2x2+x3 +x6=60

x1,x2,x3,x4,x5,x6 0

Это есть каноническая форма задачи. Для решения симплекс-методом составляется исходная симплекс-таблица.

 

Т.к. симплекс-метод есть направленный перебор угловых точек (опорных решений), то необходимо определить исходное опорное решение, отправляясь от которого с помощью процедур симплекс-метода определим хотя бы одно оптимальное или установим неразрешимость задачи.

Каждое опорное решение определяется некоторым базисом векторов-условий, и т.к. размерность векторов равна 3, то базис должен содержать ровно 3 вектора. Из канонической формы задачи определяем «явные» базисные вектора размерностью три А1, А2, А3, т.к. это три единичных вектора размерностью три, которые образуют базис. Следовательно, все остальные переменные Х1,Х2,Х3должны быть равны нулю.Из уравнения канонической формы видно, что Х4=50, Х5=60, Х3=30.

Таким образом, получим исходный опорный план Х0=(0,0,0,50,60,30), значение целевой функции на котором равно нулю, что соответствует естественной постановке задачи, а именно если ничего не производится Х1,Х2,Х3=0, то и прибыль отсутствует. В столбец B заносим коэффициенты целевой функции при базисных переменных. В столбец В заносим значения базисных переменных.

m+1 строка называется строкой оценок или индексной (Zj – Cj)

Zj – значение функции цели на j-векторе и равно скалярному произведению двух векторов СБ и Аj: Zj=СБ*Aj

На пересечениях индексной строки и столбца В находятся значения целевой функции на данном опорном плане.

План оптимальный в задаче на максимум (минимум), если все оценки индексной строки не отрицательные (не положительные).

Следствие:

Если среди оценок индексной строки есть отрицательные, то данный план неоптимальный и его можно попытаться улучшить с помощью преобразований Жордана-Гаусса (согласно следующей теореме).

 

Теорема 4.2 «О переходе к новому опорному плану»

Для перехода к новому опорному плану (к новому базису отличного от данного) будем следовать следующим правилам:

1. Правило определения вектора вводимого в базис.

Расширенная задача.

Пусть требуется найти min Z=C1X1+…+CnXn при ограничениях:

a11x1+…+a1nxn=b1

………………… (*)

am1x1+…+amnxn=bm

xj 0 j=

bj>0 i=

 

Определение: Задача, состоящая в нахождении минимума функции

F=C1X1+…+CnXn+MXn+1+…+MXn+m min , при ограничениях

xj 0 j=

a11+…+a1nxn+xn+1 =b1

…………………………

am1x1+amnxn+…+xn+m=bm

 

где М - некоторое достаточно большое положительное число, конкретное значения которого обычно не задается, называется расширенной задачей по отношению к задаче (*).

Содержательно: Если в канонической форме задачи нет вообще единичного базиса (или он частичный), то в левой части ограничений вводится столько искусственных переменных, сколько не хватает векторов до единичного базиса, которые входят в функцию цели с коэффициентом М, конкретное значение которого может быть не задано заранее (или же его значение на 3-4 порядка больше, чем порядок коэффициента целевой функции).

В этом случае всегда существует опорное исходное решение расширенной задачи X0=( b1…bn), которое определяется системой из n искусственных единичных векторов.

Теорема 5.1

Если в оптимальном плане X*=( X … ,X ) расширенной задачи значения всех искусственных переменных равны нулю, то план *=( , …, X ) исходной задачи является оптимальным планом исходной задачи.

Содержательно: если в найденном оптимальном плане расширенной задачи все искусственные переменные равны нулю, то имеем оптимальный план исходной задачи.

Замечание: возможна ситуация, когда в плане расширенной задачи все искусственные переменные равны нулю, но при этом он не будет оптимальным планом исходной задачи, и поэтому его следует довести до оптимального плана исходной задачи без искусственных переменных.

 

Исходная симплекс-таблица расширенной задачи.

 

Пусть X0=(0,…0, b1…bm) исходный опорный план расширенной задачи, тогда значение целевой функции f на данном плане равняется: F(X0)=М , а значения оценок будут равны: Zj-Cj=-M aij-Cj , следовательно значение целевой функции и значения оценок состоит из двух частей, одна из которых содержит M, а другая нет.

Тогда в отличии от классического симплекс-метода таблица содержит две индексные строки (m+1) и (m+2). В (m+2) строку заносят коэффициент при М, а в (m+1) - часть оценки, не содержащую М.

Вычисления (пересчет симплекс-таблиц) проводятся по (m+2) строке до тех пор пока:

1. Либо все искусственные вектора не будут исключены из базиса.

2. Либо не все искусственные вектора будут исключены, но (m+2) строка не содержит больше положительных элементов, соответствующих искусственным векторам.

В первом случае базис соответствует некоторому опорному плану исходной задачи, и определение ее оптимального плана проводим только по (m+1)строке.

Во втором случае, если элемент, стоящий на пересечении (m+1) строк и столбца B отрицателен, то исходная задача не имеет решения (признак неразрешимости), а если же он равен нулю, то найденный опорный план исходной задачи является вырожденным (для данного метода), и базис содержит, по крайней мере, хотя бы один из искусственных векторов.

Если исходная задача содержит несколько единичных векторов (<m), то их следует вводить в искусственный базис; искусственных переменных столько, сколько не хватает векторов до единичного базиса.

 

Экономическая интерпретация

Прямая: сколько и какой продукции необходимо произвести, чтобы при заданных ценах реализации, объемах и заданном способе производства получить максимальную прибыль от реализации произведенной продукции. Z=CX max AX£B X³0

Двойственная: какова должна быть оценка цены единицы каждого вида ресурсов, чтобы при имеющихся их объемах, величин стоимости реализации и заданном способе производства, минимизировать общую оценку стоимости затрат. F=BY min ATY³C Y³0

Лемма 1.

Для любых планов X и Y прямой и двойственной задач соответственно (прямая – максимум, двойственная – минимум) имеет место Z(X*) F(Y*), где Z – целевая функция переменной, F – функция двойственной задачи.

 

Теорема 6.3.

Пусть X*=(X ,…X ) допустимое решение прямой задачи. Вектор X* является оптимальным решением прямой задачи тогда и только тогда, когда среди решений системы уравнений (1) при X 0 содержалось хотя бы одно допустимое решение двойственной задачи, в которой yi=0 при aijxj<bi.

Теорема 8.1

В оптимальном плане двойственной задачи Y* значение переменной y*i численно равно частной производной оптимального значения целевой функции (производная значения целевой функции берется как от функции объема ресурсов) Zmax (b1…bm) по данному аргументу.

Изменение объемов дефицитных ресурсов приводит к изменению значений целевой функции на оптимальном плане. И это изменение определяется величиной y*i и характеризуется лишь в случае, когда данное значение положительно. Эта характеристика скорости изменения (интенсивности) оптимального значения целевой функции в зависимости от интенсивности изменения объемов ресурсов. При расширении производства требуется определить выбор тех видов ресурсов, увеличение объемов которых позволит наиболее эффективно организовать производство данного вида продукции. Для данной задачи расширение возможно только второго вида.

Раздел II.

Специальные задачи ЛП

Пример: «Задача о рюкзаке (задача загрузки корабля)»

Имеется n видов предметов, j-й предмет имеет массу aj и ценность cj. Следует загрузить рюкзак вместимостью В, так что ценность груза была максимальной.

Xj- -количество предметов j-ого вида (неделимых)

Тогда при ограничениях:

Пример: «Задача о распределение инвестиций»

Имеется n проектов и для любого j-ого проекта определен эффект от реализации γj при необходимых объемах инвестиций gj, т.е. γj gj.

Общий объем инвестиций не превышает В. Определить, какие проекты нужно реализовать, чтобы суммарный эффект был максимальным.

Х= 0 если Рj не реализуется

1 если Рj реализуется

 

Тогда при ограничениях

Схема алгоритма

1. Пусть в результате решения ослабленной задачи получен оптимальный план, имеющий хотя бы одну нецелочисленную компоненту.

Замечание: 1-й алгоритм Гомори решает только полностью целочис­ленные задачи, поэтому результатом его решения может быть опти­мальный план только с целочисленными компонентами.

2. В симплекс-таблице оптимального решения выбираем значение базисной переменной задачи Х*j с наибольшей дробной частью. Если таких переменных несколько, то выбираем любую.

Этой переменной соответствует строка симплекс-таблицы, на­зываемая строкой, производящей отсечение (производящей стро­кой).

Выписывается уравнение

(полагая, что первые m перемен­ных базисные для данного оптимального решения).

На основании этой строки, предполагаем, что m первые перемен­ные являются базисными, и т.к. коэффициенты целевой функции - целые числа, то зна­чение целевой функции на целочисленном решении также должно быть целочисленно.

Представим каждый коэффициент данной строки в виде целой и дробной частей.

Тогда 0<qj<1

0≤qj<1

qj - положительная дробь

qij - неотрицательная дробь

Переносим все целые части коэффициентов в одну сторону, ос­тавляя все дробные в другой:

Так как все переменные xm+1,...,xn принимают целочисленные значения и силу их небазисности, то правая часть уравнения является целочисленной. Сле­довательно, в силу неотрицательности дробных частей и переменных зада­чи и левая часть должна быть неотрицательна:

, следовательно,

Так как qj<1, заменяя в правой части qj, получим строгое нера­венство

Так как левая часть неравенства должна принимать целые зна­чения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде:

Вводя остаточную переменную Sj (переменную Гомори), получим

Где Sj – неотрицательная добавочная переменная, которая по определению должна принимать целочисленное значение, что для данной системы ограничений при xj=0 имеет вид:

Следовательно, она принимает отрицательное значение, т.е. является недопустимой, и, таким образом, полученное ранее решение ослабленной задачи не удовлетворяет данному ограничению. В этой ситуации обычно используют двойственный симплекс-метод или М-метод.

Вывод: строится ограничение, которому не удовлетворяет оптимальный нецелочисленный план. Следовательно, надо решить задачу с исходной целевой функцией и расширенной системой ограничений.

 

Метод ветвей и границ.

Идея метода: пусть решена задача без условия целочисленности и х*r – целочисленная переменная, значение которой в оптимальном плане является дробным. Тогда интервал [х*r]< х r<[х*r]+1 не содержит допустимых решений с целочисленной координатой хr. Следовательно, допустимое решение с целочисленной координатой хr удовлетворяет одному из следующих условий : [ х r≤[х*r] или х r≥[х*r]+1.

Введение этих условий в исходную задачу порождает две несвязанных между собой задачи с одной и той же целевой функцией, но не пересекающихся областями допустимых решений. В этом случае говорят, что задача разветвляется.

Осуществляемый в процессе учет необходимых условий целочисленности позволяет исключить часть многогранника решений, не содержащих решений с целочисленной координатой х r.

Геометрическая интерпретация:

Вырезаем «полосу», не содержащую решение с целочисленной координатой х1. Затем решаем каждую из подзадач. Если полученный оптимум окажется допустимым для целочисленной задачи, то значение его фиксируется как наилучшее, и при этом нет необходимости продолжать ветвление данной подзадачи. В противном случае подзадача, в свою очередь, разбивается на две подзадачи при условие целочисленности значений, которые в оптимальном плане не оказались целыми. Как только полученное допустимое целочисленное решение одной из подзадач окажется лучше имеющегося, то одно фиксируется вместо зафиксированного ранее.

Процесс ветвления продолжается до тех пор, пока не приведет к целочисленному решению или пока не будет установлена невозможность сосуществования такого, либо улучшение уже имеющегося.

Эффективность вычислительной схемы существенно повышается с введением понятия «граница», на основе которого делается вывод о необходимости дальнейшего разбиения каждой из подзадач.

Суть: если оптимальное решение подзадачи без условия целочисленности обеспечивает худшее значение целевой функции, чем имеющееся ранее, то подзадача далее не рассматривается, и говорят, что она прозондированна, и ее можно вычеркнуть из списка подзадач, порожденных исходной задачей. Другими словами, как только получено допустимое целочисленное решение, соответствующее значение целевой функции может быть использовано в качестве верхней (в случае минимизации) или нижней (в случае максимизации) границы, наличие которой позволяет формализовать процедуру исключения прозондированных задач. Этот метод позволяет решать как полностью, так и частично целочисленные задачи.

 

Транспортная задача

1. Транспортная задача. Распределительный метод.

2. Метод потенциалов (Канторовича)

3. Задача о назначениях. Венгерский алгоритм.

 

Классическая транспортная задача – это задача о наиболее экономичном плане перевозок однородного (или взаимозаменяемых) продукта из заданных пунктов отправления (пункта производства или хранения) в пункты назначения (пункты потребления данного продукта). Наиболее часто встречается в распределительных экономических задачах.

Эта задача связана с территорией, распределением, назначениями, транспортом и размерами производства. Кроме того, различные варианты этой задачи встречаются в задачах организации производства, принятия решений и организационного управления.

Классическая подстановка: имеется m пунктов производства или складирования однородного продукта, запасы которого равны соответственно A1…Ai….Am. Имеется n пунктов потребления этого же продукта с потребностями В1…Вj….Вn. Известны тарифы (транспортные расходы, связанные с доставкой единицы продукта из заданного пункта отправления в заданный пункт потребления)

Требуется составить план перевозок (указать какое количество из какого пункта отправления и в какой пункт потребления следует перевезти продукт), обеспечивающий наиболее экономичным путем (при суммарных минимальных затратах на перевозку) удовлетворение всех пунктов потребления за счет реализации всего продукта, находящегося в пунктах отправления.

Фактически требуется указать вектор поставок ( ), где xij – количество единиц продукта, направленного из i-го пункта отправления в j-й пункт потребления и удовлетворяющий следующим условиям:

1) Условие полного удовлетворения потребностей всех пунктов потребления.

2) Весь продукт, хранимый на базах, должен быть вывезен.

и дающий минимум целевой функции

Транспортная задача исследуется только на минимум.

 

Определение: Транспортная задача называется закрытой (сбалансированной), если суммарный объем запасов равен суммарному объему потребностей:

В противном случае она называется открытой.

 

Теорема 1 (необходимое условие разрешимости транспортной задачи)

Транспортная задача разрешима тогда и только тогда, когда она сбалансированная.

 

Если задача открытая, то ее всегда можно привести к закрытой, при этом следует произвести следующие преобразования:

а) Случай дефицита (суммарное потребление строго больше суммарных запасов). В этом случае вводят фиктивный пункт отправления с запасами, равными , из которого перевозка во все пункты назначения осуществляется по нулевым тарифам.

б) Случай избытка продукта. Вводится фиктивный пункт потребления с потребностями , перевозки в который со всех пунктов отправления осуществляются по нулевым тарифам.

 

Вторая транспортная теорема

Х – невырожденный опорный план, который не является оптимальным, т.е. среди свободных клеток есть положительные. Тогда:

1) среди положительных оценок свободных клеток выбираем наибольшее, и для этой клетки строим цикл, в котором выставляем чередующие знаки – и +, начиная со свободной клетки.

2) среди всех поставок положительных клеток цикла выбирается наименьшая, которая затем прибавляется к поставкам в отрицательных клетках цикла и вычитается из поставок положительных клеток цикла. В результате такого преобразования получаем новый опорный план, который может быть вырожденным (это возможно если наименьшая «положительная» поставка находится в двух или более клетках цикла). И тогда прежде чем проверять полученный план на оптимальность, его следует сделать не вырожденным.

 

Замечание: если клеток с наибольшей положительной оценкой несколько, то для каждой из них следует построить цикл, расставить знаки и определить величину минимальной положительной поставки. Выбираем клетку для перераспределения, для которой найденная положительная поставка цикла будет наибольшей, и именно по данному циклу осуществляем переход к новому опорному плану.

 

Математические методы теории оптимизации.

Понятие экстремальных задач, примеры. Основные понятия ЛП.

В связи с расширением круга приложений математики к различным направлениям экономики в последнее время применение классических методов оказалось затруднительным в силу возросшей сложности и разнообразия возникших проблем. В первую очередь это относится к задачам управления, различным задачам выбора, разрешения конфликтных ситуаций, задачам обслуживания и т.п.

Такого рода задачи решение достигается, как правило, в граничных точках области изменения исследуемых параметров. В этой связи классических методов недостаточно и исследование экономических задач привело к возникновению нового направления, предметом изучения которого является: формализация, постановка, нахождение методов решения различных классов задач, связанных с теми или иными проблемами оптимизации, и анализ полученных результатов с целью их практического использования. Всякая оптимизация связана с наличием ограничений: на ресурсы, на способы действий, на возможности. В экономических задачах управления и планирования процесс решения обычно сводится к выбору системы функции и системы параметров, которые называются характеристиками экономической системы. В настоящее время главным образом под характеристиками понимают только систему параметров. Таким образом, проблема управления и планирования сводится к экстремальным задачам следующего вида:

(1) требуется определить max (min) f(xi..xn), при условии:

(*) gi(xi…xn) {£;=;³}bi

(**) xj³0 j£n, где

– f(xi…xn) – показатель качества решений (целевая функция) и.

– условия (*) и (**) – ограничения, которые определяют некоторое множество допустимых решений (область определения целевой функции).

Для того, чтобы решить экстремальную задачу (1), достаточно найти ее оптимальное значение (указать значение всех переменных, удовлетворяющих ограничениям задачи, которые доставляют функции f наибольшее или наименьшее значение среди всех значений функции на допустимых множестве переменных или доказать, что таких решений нет).

Процедура нахождения решения экстремальных задач называется процедурой оптимизации.

1. Задача (1) является неразрешимой, если она не имеет решения. Это возможно в случае, когда целевая функция не ограничена на допустимом множестве решений. Решить экстремальную задачу – найти ее оптимальное решение, либо установить ее неразрешимость.

2. Математическая дисциплина, занимающаяся изучением экстремальных задач и разработкой методов их решений при различных допущениях относительно для различных функций fi и gi, называется математическим программированием, или математическими методами оптимизации.

Основная особенность экстремальных задач, в отличие от задач на условный экстремум, состоит в наличии неравенств среди ограничений и, следовательно, классические методы не применимы.

Методы решения задачи (1) во многом зависят от тех или иных свойств множества допустимых значений, и поэтому методы оптимизации рассматриваются как совокупность ряда самостоятельных дисциплин. Все задачи можно условно разделить на два больших класса: линейные и нелинейные.

Для задач первого класса характерна линейность целевой функции и функций, входящих в ограничение. Для этого класса задач существует универсальный метод их решения. Среди задач нелинейного программирования разработаны алгоритмы решения только для задач выпуклого программирования.

Отдельным классом задач являются задачи целочисленного и динамического программирования. И в последнее время особое внимание уделяется методам теории игр для анализа рыночных отношений и сетевого планирования моделирующего процесса реализации проектов во времени, а также задач распределения ресурсов и продуктов.

Историческая справка.

В 1930 году А.Н. Толстым в сборнике «Планирование перево­зок» была изложена методика составления плана перевозок, обеспечивающего наименьший суммарный пробег. По существу, была сформулирована впервые транспортная задача, но при этом не приводилось точных математических формулировок и формальных доказательств. Первая строгая математическая постановка была предложена в 1941 году Ф. Хичкоком, в честь которого эта задача в западной литературе именуется проблемой Хичкока.

В 1931 году венгр Эгервари рассмотрел и решил задачу выбора «Венгерским алгоритмом».

В 1939 году Л.В. Канторович в книге «Математические методы организации и планирования производства» предложил решение задачи по распределению обработки пяти видов материалов между восьмью станками.

Во время второй мировой войны ряд американских ученых и английских математиков был привлечен

cyberpedia.su

Математические методы оптимизации

Задание 1. Графическое решение задачи распределения ресурсов

· Записать стандартную и каноническую формы.

· Найти все базисные и допустимые базисные решения. Определить оптимальное базисное решение.

· Найти графически оптимальное базисное решение.

Фирма выпускает два вида изделий А и В. Каждое изделие проходит обработку на двух технологических линиях.

Известна таблица технологических коэффициентов

- времени обработки (в минутах) каждого изделия на каждой технологической линии. Кроме этого, известны рыночная цена каждого изделия и и общее время каждой линии и .

РЕШЕНИЕ

Запишем стандартную и каноническую формы

Обозначим:

план выпуска изделия А; план выпуска изделия В.

Тогда затраты линии 1 и линии 2, необходимые для производства плана

будут равны соответственно:

План

будет допустимым, если затраты для линии 1 и линии 2 не превосходят общего времени работы каждой из линий, т.е. выполняются неравенства:

Целевой функцией служит выручка от реализации допустимого плана

при ограничениях (1.1)

Для канонической формы эти ограничения нужно преобразовать в равенства. Для этого введём две дополнительные переменные

остаток от производства на линии 1 (остаток времени обработки) остаток от производства на линии 2 (остаток времени обработки).

Тогда получим каноническую форму задачи:

-найти переменные

, которые дают максимум целевой функции при ограничениях (1.2)

· Найдём все базисные решения.

Полученные ограничения образуют систему двух уравнений с четырьмя неизвестными. Среди бесконечного множества решений этой системы базисные решения получаются следующим образом. Две переменных приравняем к 0. Эти переменные назовём свободными. Значения остальных переменных получаем из решения системы. Эти переменные назовём базисными. Базисное решение называется допустимым, если оно неотрицательно.

1) Пусть

свободные переменные. Подставляя значения (1.2), получаем систему уравнений

Следовательно, базисное решение имеет вид

.

Базисное решение означает, что изделия А и изделия В не производятся. Это базисное решение является допустимым. Выручка от реализации этого плана составит

.

2) Пусть

свободные переменные. Подставляя значения (1.2) получаем систему

Следовательно, базисное решение имеет вид

.

Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 60 ед., время изготовления продукции на линии 1 используется полностью, для производства на линии 2 не хватает 1440 минут работы. Это базисное решение не является допустимым.

3) Пусть

свободные переменные. Подставляя значения в (1.2) получаем систему

для базисных переменных

и . Следовательно, базисное решение имеет вид .

Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 36 единиц, время изготовления продукции линии 1 используется не полностью и его остаток составляет 768 минут, а на линии 2 используется полностью. Это базисное решение является допустимым. Выручка от реализации этого плана составит

ден.ед.

4) Пусть

свободные переменные. Подставляя значения в (1.2) получаем систему

для базисных переменных

. Следовательно, базисное решение имеет вид . Базисное решение означает, что изделия А производится в количестве 32 ед., изделие В не производится, время изготовления продукции линии 1 используется полностью, а время изготовления линии 2 не полностью используется, его остаток составляет 1008 минут. Это базисное решение является допустимым. Выручка от реализации этого плана составит ден. ед.

5) Пусть

свободные переменные. Подставляя значения в (1.2) получаем систему

для базисных переменных

. Следовательно, базисное решение имеет вид . Это базисное решение означает, что изделия А производится 60 ед., изделие В не производится, не хватает времени обработки 1680 минут для первой линии, а время обработки второй линии используется полностью. Это базисное решение не является допустимым.

6) Пусть

свободные переменные. Тогда базисные переменные и найдём из системы уравнений

Отсюда следует, что базисное решение имеет вид

. Это решение означает, что изделия А производятся в количестве ед., изделия В производятся в количестве , время обработки на каждой из линий используется полностью. Это базисное решение является допустимым. Выручка от реализации составит ден.ед.

· Определим оптимальное базисное решение.

Из теории линейного программирования следует, что оптимальное решение можно найти среди допустимых базисных решений. Отсюда следует, что для определения оптимального решения нужно вычислить значения целевой функции на всех допустимых базисных решениях. Оптимальным будет базисное решение, на котором значение целевой функции наибольшее.

В таблице 1.1 приведены все допустимые базисные решения и соответствующие им значения выручки

.

двойственный задача равновесный спрос полезность товар

Таблица 1.1

Максимальное значение выручки достигается на четвёртом базисном решении в этой таблице

mirznanii.com

Математические методы оптимизации ресурсов - часть 3

(2.2), то можно утверждать, что задача линейного

программирования представляет собой частный случай задачи

оптимизации в общем виде.

В современных условиях рьшочных отношений при дефиците

материальных и финансовых ресурсов, несбалансированности производственных

планов по номенклатуре, нормам расходов материалов и

сьфья возникают договорные, производственные, финансовые и

прочие нарушения, корректировки планов, приписки и др.

Сбалансированность планов по номенклатуре, заданным показателям

и ресурсам можно оперативно проверить с помощью

моделирования на ЭВМ не спустя какое-то время, когда обнаружатся

ошибки и просчеты и когда изменить что-либо уже

трудно, а сразу же при решении задачи. При этом необходимо

опираться на достоверную нормативную базу, в частности, на

нормы расхода ресурсов на единицу выпускаемой продукции.

Именно математические модели позволяют проанализировать

причины несбалансированности планов и выявлять недостоверность

исходных данных.

Чем же может помочь ЭВМ в анализе несбалансированных задач?

1. Решая задачу распределения ресурсов на ЭВМ, до получения

окончательного результата нам неизвестно, сбалансирована

она или нет. Однако, если существует подозрение, что задача

может оказаться несбалансированной, то имеет смысл сразу же

так составить математическую модель, чтобы она учитывала

возможную недостачу ресурсов.

2. Если нам желательно минимизировать дополнительные

ресурсы у,- при получении прибыли от производства и выпуска

продукции, то целевую функцию следует записать с учетом

этого условия

а условие получения прибыли включить в состав ограничений.

Результаты решения подобных задач на ЭВМ позволяют

промоделировать возможные ситуации и определить, сколько и

какие ресурсы требуются и каким станет план, если полностью

изыскать необходимые дополнительные ресурсы. Конечно, ЭВМ

не может заменить недостающие ресурсы, но она позволяет при

составлении полной и корректно сформулированной математической

модели показать, что необходимо осуществить, чтобы

выполнить несбалансированный план. Польза от такого анализа

несомненна в любых ситуациях.

В общем преодолеть несбалансированность производственного

плана можно или увеличением ресурсов при возможности

их изыскания, а при невозможности добавления дополнительных

ресурсов путем уменьшения нижнего предела выпуска продукции,

или сокращения норм расходов каждого ресурса на выпуск

единицы продукции. Если удастся преодолеть несбалансированность

планов за счет увеличения ресурсов или снижения

выпуска продукции и расхода ресурсов, то план производства

будет обоснованным, и такие планы нужно выполнять.

Определение координат вершин области допустимых решений

(ОДР) в реальных задачах со многими переменными и ограничениями

связано с очень большими объемами вычислений. Поэтому

для аналитического решения задач линейного профамми-

рования разработан специальный алгоритм направленного перебора

вершин, называемый симплекс-методом, с переходом от

одной вершины к другой в направлении, при котором значение

целевой функции от вершины к вершине улучшается. Определе-

йие значения целевой функции и переменных в одной вершине

считается и т е р а ц и е й . Число итераций зависит от числа

искомых переменных и в реальных задачах может измеряться

сотнями. Вручную с помощью симплекс-метода можно решать

задачи, Содержащие не более десяти переменных. В реальных

ситуациях без ЭВМ и прикладных профамм вычислений поиск

оптимального решения практически невозможен.

Так как оптимальное решение задачи линейного профамми-

рования соответствует вершине ОДР, то можно сформулировать

следующие выводы:

,1) если оптимальным решением являются координаты вершин

ОДР, то сколько вершин имеет ОДР, столько оптимальных

решений может иметь задача;

2) чем больше существует офаничений в модели задачи, тем

больше будет число вершин и, следовательно, число оптимальных

решений;

3) введение дополнительных ограничений никогда не улучшает

оптимального решения (этот вывод особенно важен для

практики планирования: если мы хотим улучшить принятую целевую

функцию, т. е. результат работы, мы должны стремиться к

тому, чтобы иметь как можно меньше ограничений).

mirznanii.com

Оптимизация математические методы - Справочник химика 21

    За последние годы литература по научным основам химической технологии значительно обогатилась, особенно в части теории химических реакторов, математических методов моделирования и оптимизации химико-технологических процессов. При этом широко используется метод теоретических обобщений, так хорошо себя оправдавший в общеинженерном курсе процессов и аппаратов химической технологии. [c.5]     При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации. [c.29]

    Для уяснения сущности вопросов оптимизации, и в частности метода оптимального проектирования, следует прежде всего иметь в виду, что в технике под оптимальным решением понимается, как правило, наиболее выгодное решение, т. е. обеспечивающее наибольший доход цеху, заводу и т. п. Для применения математических методов оптимизации необходимо четко сформулировать критерий оптимизации (функцию дохода), который может быть выражен численно и положен в основу всех аналитических и численных решений в процессе оптимального проектирования. [c.68]

    Поэтому особое значение приобретают вопросы подготовки производства, организации технического контроля, научной организации труда и управления, оптимизации плана, обеспечения достоверной систематической, надежной информацией для оперативного планирования и управления производством с использованием экономико-математических методов (ЭММ) и электронно-вычислительных машин (ЭВМ). [c.12]

    Впервые предложен метод построения математических моделей основных и вспомогательных стадий циклических адсорбционных процессов на основе уравнений тепломассообмена для целей их оптимизации. Изложены методы оптимизации непрерывных и дискретных параметров процессов при различных формах задания информации. На основе рассмотренных математических моделей осуществлены оптимизационные расчеты циклических адсорбционных процессов. Дана оценка режимов функционирования аппаратов, работающих в циклическом адсорбционном процессе, рассмотрены некоторые вопросы расчета надежности этих аппаратов. [c.2]

    Математические методы оптимизации можно эффективно применять лишь при наличии математического описания оптимизируемого объекта. Если же математическое описание, достаточно точное в качественном и количественном отношении, отсутствует, то единственная возможность оптимизации заключается в исследовании реального объекта, для чего его оборудуют необходимыми измерительными средствами и проводят достаточно большое число экспериментов. Однако такой подход к отысканию оптимальных условий осуществления процесса обладает рядом принципиальных недостатков, к числу которых относится прежде всего сложность изменения аппаратурного оформления. Кроме того, не всегда удается оборудовать объект нужными измерительными средствами без значительного изменения нормального режима его работы. Наконец, достигаемые при оптимизации действующего объекта результаты носят обычно частный характер и почти не поддаются обобщению, что затрудняет накопление опыта, получаемого при оптимизации даже аналогичных производств. [c.40]

    В третьей главе рассмотрен автоматизированный структурно-параметрический синтез гибких химико-технологических систем. Изложены задачи синтеза систем в условиях полной и неполной определенности информации. Отдельный параграф посвящен математическим методам и вычислительным алгоритмам структурно-параметрического синтеза систем дискретного типа. Изложены методы автоматической классификации технологических процессов, оптимизации технологической структуры и аппаратурного оформления химико-технологических систем периодического действия — алгоритмы эвристического типа, ветвей и границ , случайного поиска, геометрического программирования, комбинированные. [c.6]

    Специальное программно-математическое обеспечение АСП, позволяющее решать задачи технологического и конструкционного проектирования химических производств, может быть создано только под руководством и при участии инженеров химиков-техно-логов на основе использования методов математического моделирования ХТП, методов синтеза, анализа и оптимизации ХТС, методов теории эвристических решений, а также в результате глубокого изучения и формализации богатого опыта высококвалифицированных инженеров-проектировщиков. [c.12]

    Книга включает разделы, посвященные переносу тепла, устойчивости работы реакторов, оптимизации и регулированию, которые помогут читателю получить ясное представление о факторах, влияющих на протекание химической реакции в промышленных реакторах, еще до изучения математических методов, столь важных для точного инженерного расчета реакторов. [c.2]

    Этот метод называется динамической оптимизацией. Математический аппарат для изучения такой системы обычно включает вариационное исчисление, чтобы получить для каждой [c.119]

    Выше весьма подробно была рассмотрена проблема оптимизации обратимой экзотермической реакции, поскольку с математической точки зрения она бесспорно представляет собой простейший случай. Причина заключается в том, что в этом случае общая скорость реакции должна быть максимальной в любых точках реактора. К сожалению, этот принцип не приложим к другим реакциям, и для них приходится применять более сложные математические методы. [c.150]

    При синтезе ХТС с использованием интегрально-гипотетического принципа независимо от конкретно применяемого математического метода для решения задачи оптимизации гипотетической обобщенной технологической структуры исходят из допущения о том, что все переменные дискретного типа (по своей природе) рассматриваются как непрерывные. [c.172]

    Математические модели процессов позволяют эффективно использовать математические методы оптимизации, определять оптимальные решения на той или иной стадии проектирования. По существу задачи оптимального проектирования эквивалентны задачам отыскания тех параметров математических моделей, которые определяют конструктивное оформление и режим процесса при заданных требованиях к количественным и качественным характеристикам получаемой продукции. [c.15]

    Приведенные характеристики технического состояния крупно-тоннажных ироизводств свидетельствуют о том, что эффективность сложных ХТС в значительной степени определяется их надежностью. В связи с этим разработка способов обеспечения надежности, а также математических методов анализа и оптимизации характеристик надежности сложных ХТС на стадиях их проектирования, сооружения и эксплуатации имеют особую актуальность для ускорения темпов научно-технического прогресса [1, 2, 8, 75, 93]. [c.16]

    В. В. Клименко. Алгоритм адаптивного предсказывающего фильтра для нестационарных процессов. — В сб. Применение математических методов для оптимизации технологических процессов производства строительных материалов . Братск, Стройиздат , 1973, с. 80. [c.133]

    Наряду с чисто математическими методами важное значение для решения задач большой размерности будут иметь эвристические приемы. Один из них — метод укрупнения — был использован для получения хорошего начального приближения в задаче оптимизации каскада реакторов (см. с. 52). [c.261]

    Помимо определенных таким образом подмножеств в рамках системы целесообразно выделить подмножество модулей, являющихся общими для различных подсистем, которые составляют библиотеку специальных и стандартных алгоритмов. К ним можно отнести статистические методы обработки данных, методы оптимизации, стандартные методы вычислительной математики и т. п. Выделенные подмножества составляют основу функциональной среды диалоговой системы. Состав прикладного математического обеспечения, необходимого при разработке технологической схемы в соответствии с рис. 4.2, приведен на рис. 4.7. [c.111]

    Внедрение математических методов и применение электронно-вычислительной техники для оптимизации технологических процессов и управления ими, использование достижений кинетики и катали- [c.4]

    Интерактивный режим позволяет пользователю выбрать вариант постановки задачи термоэкономической оптимизации (из заданной пользователем совокупности критериев оптимальности и соответствующих наборов оптимизирующих переменных) выбрать варианты расчета технологических подсистем (по уровню детализации моделей) выбрать вариант расчета каждой из энергетических подсистем (эксергетическая производительность подсистемы, обобщенная термоэкономическая модель подсистемы данного типа, традиционная математическая модель) выбрать метод безусловной оптимизации из имеющихся в библиотеке и задать его параметры выбрать и задать параметры метода условной оптимизации применить метод декомпозиционной релаксации, сократив число оптимизирующих переменных провести выборочное сканирование области поиска по одной или группе переменных выбрать варианты печати результатов моделирования в начальной и конечной точке поиска, промежуточных результатов оптимизации. [c.418]

    Математическая модель любого процесса реализуется на вычислительной машине. Поэтому моделирование резко сокращает объем часто весьма сложных и дорогих натурных экспериментов и дополняет их исследованиями на вычислительной машине. Метод математического моделирования открывает возможности прогнозирования поведения объектов в неизвестных ситуациях, позволяет изучать многие характеристики проектируемых процессов, оценивать различные варианты аппаратурного оформления, а также использовать математические методы оптимизации для отыскания оптимальных режимов эксплуатации и способов управления ими. [c.13]

    Основная цель применения математических методов оптимизации как раз и состоит в том, чтобы осуществить этот вычислительный процесс наиболее эффективным способом. [c.14]

    В предлагаемом учебном пособии описаны математические методы оптимизации, получившие за последние годы распространение в химической технологии. Систематизация и прикладная направленность этих методов позволили сформировать курс лекций, читаемый в течение нескольких лет на кафедре кибернетики химико-техполо-гических процессов Московского химико-технологического института им. Д. И. Менделеева. Со1[ержание книги в основном соответствует принятому изложению лекционного материала, за исключением глав I и II, где приведены краткие сведения, рассматриваемые в других курсах кафедры и нужные для иллюстрации методов решения оптимальных задач. Кроме того, некоторые специальные математические вопросы, не относящиеся непосредственно к методам оптимизации, но необходимые при их изложении, вынесены в Приложение к книге. Такое построение учебного пособия исключает необходимость предварительного знакомства с дисциплинами, выхо-дяилимп за рамки обычных курсов химико-технологических вузов, и делает его доступным для инженеров-химиков и технологов, занимающихся оптимизацией химических производств и владеющих математической подготовкой в объеме технического вуза. Книга может оказаться также полезной аспирантам химико-технологических специальностей и химических факультетов университетов. [c.10]

    В настоящем разделе дается краткий обзор существующих математических методов, которые можно использовать для решения задачи оптимизации непрерывно изменяющихся параметров адсорбционных установок, а также оценка их перспективности с вычислительной точки зрения. Оценка методов делается на основании практического опыта расчетов. В тех случаях, когда опыт применения отдельных методов слишком мал или полностью отсутствует, оценка производится на базе укрупненных проработок применительно к ряду практических задач. В качестве основного критерия сравнения различных методов принят объем вычислений на ЭВМ, требуемый для отыскания решений с заданной точностью. Кроме того, учитываются область сходимости метода, его универсальность по отношению к возможным изменениям описания физико-технических процессов оптимизируемых установок, гибкость и простота многократного применения, трудности и время программирования, наглядность получаемых на ЭВМ результатов. [c.122]

    При разработке технологической схемы завода требуется детально изучить все возможные варианты производства необходимого количества товарных нефтепродуктов при наименьших капитальных и эксплуатационных затратах. Многовариантность и трудоемкость расчетов, связанных с выбором оптимальной технологической схемы, стали основной причиной привлечения к решению этой задачи математических методов оптимизации. В качестве основного метода решения задачи по выбору оптимальной технологической схемы НПЗ используется линейное программирование. Работы по применению ЭВМ при разработке технологи-ческих схем НПЗ были начаты в 1960 годах и продолжаются в настоящее время. [c.61]

    Создание установок большой единичной мощности по производству нефтяного углерода требует широкого внедрения математических методов оптимизации процессов с помощью ЭВМ. [c.262]

    Особенностью современного развития химической технологии является широкое применение методов математического моделирования, используемых для проведения расчетов, при проектировании и усовершенствовании химикотехнологических процессов. Являясь одним из разделов химической кибернетики, математические методы моделирования и оптимизации позволяют подойти к решению проблем создания промышленных реакторов и химических комплексов с экстремальными технико-экономическими показателями. [c.137]

    Использование современных математических методов и ЭВМ для нахождения оптимального варианта трудового процесса открывает широкие перспективы совершенствования организации и нормирования труда, заложенные в оптимизации трудовых процессов. [c.165]

    Основные математические методы оптимизации (классический математический анализ, вариационное исчисление, линейное и динамическое программирование, принцип максимума и др.) описываются в специальной литературе .  [c.20]

    Полученные в данном н. 6 задачи минимизации функционалов, с ограничениями в виде равенств и неравенств относятся к задачам нелинейной оптимизации (математического программирования), и для их решения существуют специальные методы [15]. [c.177]

    Автоматизированными сиситемами управления(АСУ) называют системы управления звеньями народного хозяйства на различных уровнях, в которых передача, хранение и переработка информации о состоянии управляемого объекта выполняется автоматически с помощью экономико-математических методов с использованием компьютеров. В АСУ объединены в своей деятельности люди и технические средства. Поэтому АСУ следует рассматривать как сложную человеко-машинную систему, в которой роль человека состоит в выборе методов и средств обработки данных, функции контроля исправности системы и принятии решения для оптимизации управления. [c.147]

    Пожалуй, нанлучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различи111Х методов оптимизации. В последующих главах будут рассмотрены перечисленные выше математические методы решения оптимальных задач и примеры их использования. Здесь же дана лишь краткая характеристика указанных методов и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для рс-шеиия конкретной оптимальной задачи. [c.29]

    Динамическое программирование, как и все методы, рассмотренные в предыдущих главах, применяется для оптимизации математически описанных процессов. Поэтому в дальнейшем для многостадийного процесса (рис, VI- ) предполагается изгзестиым математическое описание его каждо стадии, которое представляется в об1цем виде системой уравнений [c.246]

    Для достижения таких эффектов необходимо умело сочетать эмпирические исследования с современными математическими методами, позволяющими определить оптимальный вариант технологического процесса в наикратчайшеё время и при разумном риске. В течение последних лет для этой цели разработаны прогрессивные методы, использующие достижения математики и технической кибернетики, — так называемая стратегия разработки систем, или системотехника. Как и при использовании метода масштабирования, в этом случае также составляется математическая модель, но она описывает весь технологический процесс (или наиболее важную его часть) как систему взаимосвязанных элементов. Модель, в которой ряд величин и зависимостей экстраполируется с объекта меньшего масштаба, вносит в проектные расчеты фактор ненадежности. Системотехника включает также способы оценки надежности и принятия оптимальных решений при проектировании в определенных условиях. Важным преимуществом комплексного математического описания процесса является, возможность определения оптимальных рабочих параметров не для отдельных аппаратов, а для всей технологической цепочки как единого целого. Подробное описание математических методов оптимизации, оценки надежности и теории решений выходит за рамки данной книги, поэтому мы вынуждены рекомендовать читателю специальную литературу (см. список в конце книги). Ниже будут рассмотрены основные понятия, применяемые в системотехнике, и принципы разработки систем, а также их моделей. [c.473]

    Глава VI посвящена оптимизации химических реакторов — области, которая в настоящее время быстро расширяется. Мы ограничили анализ эконолгпческими и техническими принципами и описанием нескольких практических результатов. Некоторые математические методы получения оптимума упоминаются в конце главы. [c.12]

    Ниже мы рассмотрим различные математические методы оптимизации — метод динамического программирования, способ множите-.леп Лагран,ка и метод крутого во> хожд9ния. В пастоящеп книге эти м- тоды ирименепы для оптимизации реакторов, гл они являются чрезвычайно общими и люгут быть и пользованы при исследовании самых различных проблем. [c.219]

    Классификация методов. Для решений сформулированной в гл. 1 задачи комплексной оптимизации параметров и профиля адсорбционных установок или отдельных ее частей и элементов при однозначно (детерминированно) заданных значениях влияющих факторов могут быть применены многие из известных математических методов поиска экстремума функции многих переменных [49, 50]. Однако при практической их реализации на ЭВМ возникают серьезные вычислительные трудности. Некоторые простейшие, широко известные методы минимизации обычно совершенно непригодны для решения реальных задач. Поэтому проблема выбора наиболее целесообразного метода решения задачи поиска минимума сложной функции из числа существующих имеет большое значение. [c.121]

    Структура алгоритмического обеспечения ГЭС сформирована исходя из структуры, алгоритма функционирования и МПЗ, принятых в системе, с учетом специфических особешосгей исходной 1шформащш (возможной неполноты и нечеткости). Алгоритмическое обеспечение ГЭС для управления процессами коксования включает следующие группы алгоритмов функционирования ма-шины логического вьшода математической модели (материального, теплового и гидравлического балансов) оптимизации комбинированным методом система управления базой система управления базами знаний и правил сбора и оценки достоверности экспертных знаний блока объяснений интеллектуального интерфейса прогнозирования возникновения нештатной ситуации консультации в режимах ограниченно-естественного языка и советчика оператора внесения управляющих воздействий. [c.61]

    Как показывает практика, инвестиционный проект, который, несомненно, оптима теп по одному критерию экономической эффективности, часто не явмегся наилучшим с точки зрения других. Кроме того, инвестиции - сложный процесс, подверженный влиянию ршличных факторов, которые не могут быть выражены только четкими количественными величинами, Для преодоления данных трудностей необходимо применение математических методов, которые позволят ранжировать инвестиционные проекты по обобщающему показателю экономической эффективности. Успешно решить поставленную задачу возможно с помощью использования аппарата векторной оптимизации и теории нечетких множеств. [c.70]

    Книга посвящена актуальному в настоящее время вопросу применения математических методов для расчета оптимальных (наилучших) режимов технологических процессов. Дана характеристика основных этапов работ по статической, квазистатической и динамической оптимиаации как действующих химических реакторов, так и при их проектировании. Сопоставлены два важнейших метода оптимизации — метод поиска на объекте и метод оптимизации с помощью математической модели. Большое внимание уделено математическим способам оптимизации — нелинейному программированию и Принципу максимума. [c.4]

    Термины оптимизация и оптимальным ассоциируются с экономико-математическими методами (ЭММ) п ЭВМ, т. е. с метоламн и средствами, способствующими наиболее )ффективмому решению задач иланирования и упраплеиия. Вместе с тем и в действующей практике, основанной на традиционных методах, руководитель любого уровня управления на предприятии также заинтересован в оптимальном решении вопроса по увеличению выпуска продукции, снижению затрат на производство, использованию капиталовложений и т. д. Но он пытается этого достичь, пользуясь в основном установившимися принципами общих закономерностей и далеко не совершенными вычислительными средствами. При этом во многих случаях также рассматривается ряд вариантов, хотя и ограниченный, что обусловливается реальными организационными н техническими возможностями. Тем не менее в отдельных случаях не исключено совпадение результатов решения, полученных с использованием ЭММ и ЭВМ и на основе традиционного подхода. [c.377]

    Рациональное размещение новых предприятий и производств существенно влияет на повышение эффективности производства. Выбор оптимального варианта осуществляют с учетом экономических, социальных и экологических факторов с применением экономико-математических методов, основанных на нахождении минимума приведенных затрат на выпуск продукции вновь строящихся предприятий. Для выбора оптимального варианта размещения предприятий широко используют модели транспортной задачи, решаемой методами линейного программирования, Совершенствование организационной структуры управления не4)теперерабатывающими предприятиями возможно путем укрупнения цехов и участков, централизации и специализации работ, концентрации функций управления вспомогательными службами, оптимизации численности инженерно-технических работников и служащих, широкого применения экономико-математических методов, электронно-вычислительной техники, организационной техники и средств связи. Необходим системный подход к проектированию структур управления. [c.328]

chem21.info

Математические методы оптимизации | Экономико-математическое моделирование

Задание 1. Графическое решение задачи распределения ресурсов

– Записать стандартную и каноническую формы.

– Найти все базисные и допустимые базисные решения. Определить оптимальное базисное решение.

– Найти графически оптимальное базисное решение.

Фирма выпускает два вида изделий А и В. Каждое изделие проходит обработку на двух технологических линиях.

Известна таблица технологических коэффициентов – времени обработки (в минутах) каждого изделия на каждой технологической линии. Кроме этого, известны рыночная цена каждого изделия и и общее время каждой линии и .

Изделия А	Изделия В	Общее время работы линии
Линия 1	60	32	1920
Линия 2	36	60	2160
Цена одного изделия	30	25

РЕШЕНИЕ

Запишем стандартную и каноническую формы

Обозначим:

План выпуска изделия А;

План выпуска изделия В.

Тогда затраты линии 1 и линии 2, необходимые для производства плана будут равны соответственно:

План будет допустимым, если затраты для линии 1 и линии 2 не превосходят общего времени работы каждой из линий, т. е. выполняются неравенства:

Целевой функцией служит выручка от реализации допустимого плана при ограничениях

(1.1)

Для канонической формы эти ограничения нужно преобразовать в равенства. Для этого введем две дополнительные переменные

Остаток от производства на линии 1 (остаток времени обработки)

Остаток от производства на линии 2 (остаток времени обработки).

Тогда получим каноническую форму задачи:

-найти переменные , которые дают максимум целевой функции

при ограничениях

(1.2)

– Найдем все базисные решения.

Полученные ограничения образуют систему двух уравнений с четырьмя неизвестными. Среди бесконечного множества решений этой системы базисные решения получаются следующим образом. Две переменных приравняем к 0. Эти переменные назовем свободными. Значения остальных переменных получаем из решения системы. Эти переменные назовем базисными. Базисное решение называется допустимым, если оно неотрицательно.

1) Пусть Свободные переменные. Подставляя значения (1.2), получаем систему уравнений

Следовательно, базисное решение имеет вид

.

Базисное решение означает, что изделия А и изделия В не производятся. Это базисное решение является допустимым. Выручка от реализации этого плана составит

.

2) Пусть Свободные переменные. Подставляя значения (1.2) получаем систему

Следовательно, базисное решение имеет вид

.

Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 60 ед., время изготовления продукции на линии 1 используется полностью, для производства на линии 2 не хватает 1440 минут работы. Это базисное решение не является допустимым.

3) Пусть Свободные переменные. Подставляя значения в (1.2) получаем систему

Для базисных переменных и . Следовательно, базисное решение имеет вид

.

Это базисное решение означает, что изделие А не производится, изделие В производится в количестве 36 единиц, время изготовления продукции линии 1 используется не полностью и его остаток составляет 768 минут, а на линии 2 используется полностью. Это базисное решение является допустимым. Выручка от реализации этого плана составит ден. ед.

4) Пусть Свободные переменные. Подставляя значения в (1.2) получаем систему

Для базисных переменных . Следовательно, базисное решение имеет вид . Базисное решение означает, что изделия А производится в количестве 32 ед., изделие В не производится, время изготовления продукции линии 1 используется полностью, а время изготовления линии 2 не полностью используется, его остаток составляет 1008 минут. Это базисное решение является допустимым. Выручка от реализации этого плана составит

ден. ед.

5) Пусть Свободные переменные. Подставляя значения в (1.2) получаем систему

Для базисных переменных . Следовательно, базисное решение имеет вид . Это базисное решение означает, что изделия А производится 60 ед., изделие В не производится, не хватает времени обработки 1680 минут для первой линии, а время обработки второй линии используется полностью. Это базисное решение не является допустимым.

6) Пусть Свободные переменные. Тогда базисные переменные и найдем из системы уравнений

Отсюда следует, что базисное решение имеет вид . Это решение означает, что изделия А производятся в количестве Ед., изделия В производятся в количестве , время обработки на каждой из линий используется полностью. Это базисное решение является допустимым. Выручка от реализации составит ден. ед.

– Определим оптимальное базисное решение.

Из теории линейного программирования следует, что оптимальное решение можно найти среди допустимых базисных решений. Отсюда следует, что для определения оптимального решения нужно вычислить значения целевой функции на всех допустимых базисных решениях. Оптимальным будет базисное решение, на котором значение целевой функции наибольшее.

В таблице 1.1 приведены все допустимые базисные решения и соответствующие им значения выручки .

Двойственный задача равновесный спрос полезность товар

Таблица 1.1

Максимальное значение выручки достигается на четвертом базисном решении в этой таблице

Следовательно, изделие А производится в количестве ед., изделие В производится в количестве ед., время обработки на каждой из линий используется полностью ().

Графическое решение задачи

Рассмотрим задачу в стандартной форме: найти переменные , которые обеспечивают максимальное значение функции

При ограничениях

На горизонтальной оси прямоугольной системы координат будем откладывать план выпуска продукции , а на вертикальной – план выпуска второй продукции .

Рассмотрим первое ограничение . Множество точек, удовлетворяющих равенству , образует прямую на плоскости. Построим эту прямую по ее точкам пересечения с осями координат. Для определения координат точки А пересечения с осью в уравнение подставим . Из него следует , т. е . Для определения координат точки В пересечения с осью в уравнение подставим . Из него следует , т. е. . Неравенству удовлетворяют все точки одной из полуплоскостей, которые образовала построенная прямая. Для ее определения достаточно проверить справедливость неравенства для одной точки. Для начала координат неравенство выполняется. Следовательно, все точки полуплоскости, содержащей начало координат, будут графическим изображением этого неравенства. Аналогично построим прямую по ее точкам пересечения с осями координат: . Все точки полуплоскости, содержащей начало координат будут графическим изображением неравенства . Учитывая ограничения на знак , множество точек четырехугольника является множеством всех допустимых решений. Все угловые точки (крайние точки) четырехугольника соответствуют допустимым базисным решениям:

Угловая точка соответствует базисному решению

, , ;

Угловая точка соответствует базисному решению

, , , ;

Угловая точка соответствует базисному решению

, , , ;

Угловая точка соответствует базисному решению , , , .

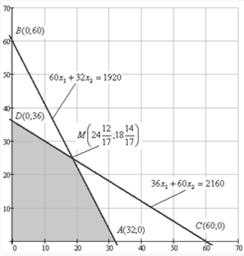
Теперь графически найдем точку четырехугольника , которая определит оптимальное решение.

Из теорем математического анализа следует, что оптимальное решение следует искать только среди точек границы четырехугольника . Для ее определения в начале координат построим вектор , координаты которого являются рыночными ценами. Прямая проходит через начало координат перпендикулярно вектору . Она определяет все планы, в которых выручка равна 0. Вектор указывает направление возрастания выручки. Если прямую нулевой выручки (розовая линия) перемещать параллельно в направлении вектора , то значение выручки будет увеличиваться. Так как среди внутренних точек четырехугольника оптимального решения не может быть, то прямую нужно переместить до границы четырехугольника , т. е. до точки .

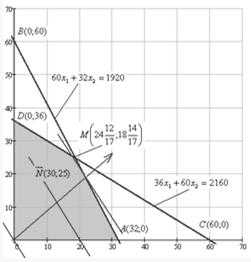
Таким образом, точка определяет оптимальное решение. Соответствующее точке базисное решение

Является оптимальным решением. Максимальная выручка будет равна . Уравнение определяет уравнение максимальной выручки (верхняя розовая линия).

Задание 2. Двойственная задача

– Записать двойственную задачу и дать ее экономический смысл.

– Найти оптимальное решение двойственной задачи.

– Определить целесообразность производства продукции С, для которой на изготовление единицы продукции требуется 60 минут и 50 минут времени изготовления на первой и второй линии соответственно. Рыночная цена составляет 120 ден. ед. за единицу продукции.

РЕШЕНИЕ

Запишем двойственную задачу и дадим ее экономический смысл.

Правило построения двойственной задачи состоит в следующем. Каждому равенству прямой задачи соответствует двойственная переменная

Стрелки показывают, что первому равенству соответствует переменная , а второму – переменная .

Для определения целевой функции двойственной задачи двойственные переменные и умножаются на правые части равенств и складываются:

.

Каждой переменной прямой задачи соответствует ограничение двойственной задачи. Левые части этих ограничений для переменной записываются следующим образом. Двойственные переменные и умножаются на коэффициенты перед переменной и складываются: .

Аналогично, записываются левые части ограничений для переменной . Двойственные переменные и умножаются на коэффициенты перед переменной и складываются: . Левая часть ограничений для переменной равна , а для переменной . Правые части ограничений равны коэффициентам 30, 25, 0, 0 целевой функции

Перед переменными . Левые и правые части ограничений соединяются знаком .

В результате двойственная задача имеет вид:

Найти двойственные переменные и , при которых целевая функция минимальна

При ограничениях

Переменные , называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция достигает минимума.

Экономический смысл двойственной задачи:

Двойственная переменная определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная определяет теневую цену работы 1 минуты оборудования линии 2.

Тогда целевая функция задает стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.

Выражение определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.

Определим величины приведенных стоимостей.

Если величина положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи

Отсюда следует, что при допустимых теневых ценах производство обоих продуктов неприбыльно.

Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам и . Решение двойственной задачи определяет минимальный уровень рыночных цен , при котором производить продукцию неприбыльно.

Найдем оптимальное решение двойственной задачи

Из первого задания следует, что допустимое базисное решение

Является оптимальным решением прямой задачи.

По оптимальному базисному решению прямой задачи найдем оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным нужно заменить равенствами

Из этих равенств найдем оптимальные значения двойственных переменных , минимальное значение целевой функции равно

.

Оптимальная теневая цена работы 1 минуты оборудования линии 1 равна , а оптимальная теневая цена 1 минуты оборудования линии 2 равна .

Стоимость работы технологического оборудования, затраченных на изготовление единицы изделия А равна

,

А стоимость работы технологического оборудования, затраченных на изготовление единицы изделия В равна

.

Приведенные стоимости каждого вида изделия будут раны

Отсюда следует, что производство изделий А и В рентабельно.

Определим целесообразность производства продукции С, для которой на изготовление единицы продукции требуется 60 минут и 50 минут времени изготовления на первой и второй линии соответственно. Рыночная цена составляет 120 ден. ед. за единицу продукции. Для этого вычислим стоимость ресурсов, затраченных на изготовление единицы продукции С:

ден. ед.

Приведенная стоимость этого вида продукции будет равна

.

Отсюда следует, что производство единицы продукции С принесет прибыль ден. ед.

Задание 3. Функция полезности

Пусть функция полезности наборов из двух товаров имеет вид , где

.

– Найти набор товаров, который имеет такую же полезность, как набор и количество второго товара равно 1.

– Для набора найти предельные полезности первого и второго товаров.

– В наборе количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближенное изменение полезности.

РЕШЕНИЕ

1.Функция полезности имеет вид: . Найдем полезность набор :

Кривая безразличия определяет все наборы товаров, которые имеют такую же полезность как набор . Из этого уравнения можно найти набор товаров, в котором количества второго товара равно , подставив это значение в уравнение кривой безразличия , . Таким образом, наборы и безразличны для потребителя.

2. Найдем частные производные функции полезности

Предельная полезность первого товара в наборе равна значению частной производной в точке (3,8):

.

Предельная полезность второго товара в наборе равна значению частной производной в точке (3,8):

Найдем изменение полезности, если количество первого товара увеличивается на 0,1, т. е. , а количество второго товара уменьшается на 0,2, т. е. . Приближенное изменение полезности вычислим по формуле

.

Следовательно, полезность набора , равная , увеличивается на 0,0065. Таким образом, полезность нового набора

Задание 4. Модель Стоуна

Функция полезности потребителя имеет вид

, где

.

1. Найти равновесный спрос и его полезность, если рыночная цена первого товара , рыночная цена второго товара и потребитель выделяет на приобретение товаров сумму денежных единиц.

2. Найти функции спроса на оба вида товаров.

3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

РЕШЕНИЕ

1. Функция полезности потребителя имеет вид

.

Вычислим равновесный спрос при заданных ценах и доходе. Найдем стоимость минимального набора товаров

.

Оставшаяся сумма денег распределяется пропорционально коэффициентам эластичности этих товаров

.

На приобретение первого товара выделяется сумма

.

На приобретение 2-го товара – сумма

.

Поделив выделенные средства на рыночные цены товаров, получаем количество товара, приобретаемое сверх установленных нормативов

Таким образом, оптимальный спрос составит

единиц первого товара и

единиц второго товара.

Полезность равновесного набора будет равна

.

2. Найдем функции спроса, заменяя в формулах спроса

, .

Эти формулы определяют спрос на продукцию при любых ценах и доходах.

3. Оценим влияние на спрос изменения дохода обоих товаров. Найдем реакцию спроса на изменение дохода на 1 денежную единицу. Частные производные по доходу показывают изменение спроса на первый и второй товары соответственно при возрастании дохода на 1 денежную единицу.

Дифференцируя полученные выше функции спроса по М, получаем

.

Вычислим эти частные производные при заданных и :

.

Так как значения частных производных положительные, то оба товара являются ценными: с ростом дохода на 1 денежную единицу спрос на оба товара растет: спрос на первый товар увеличивается на , а второго – на .

При увеличении дохода потребителя на 30 денежных единиц спрос на первый товар увеличится на единицы, а второго на и составит

, .

При уменьшении дохода потребителя на 60 денежных единиц спрос на первый товар снизится на единиц, а спрос на второй товар снизится на единиц и составит соответственно:

, .

belreferatov.net

---

• 
  Методы оптимизации атп
• 
  Оптимизация сайтов сегодня
• 
  Drupal оптимизация seo
• 
  Оптимизация графика сменности
• 
  Оптимизация chrome google
• 
  Planetside 2 оптимизация
• 
  Принципы seo оптимизация
• 
  Seo оптимизация принципы
• 
  Metro 2033 оптимизация
• 
  Оптимизация транспортных потоков
• 
  Оптимизация транспортного налога

Prostoy-Site | Все права защищены © 2018 | Карта сайта