Лабораторная работа 6 Имитационное исследование и оптимизация системы контроля. Лабораторная работа оптимизация

Лабораторная работа № 6Оптимизация технологического процесса.

Методы оптимизации функции 1-ой переменной

Цель работы

Ознакомление с методами одномерной оптимизации (поиска максимума и минимума).

Оптимизация функций одной переменной

Постановка задачи

На практике часто возникает задача нахождения экстремума некоторой целевой функции F(x). Такая функция одного параметра x описывает некоторую кривую на плоскости.

На определённом интервале функция может иметь одно (рис. 1а) или несколько экстремальных значений (рис. 1б).

Функция, изображённая на рис. 1а называется унимодальной.

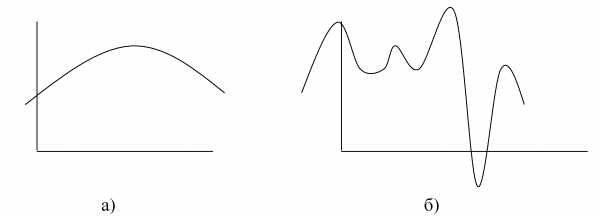
Рис. 1. Функции одного параметра x описывающие некоторую кривую на плоскости.

Функция на рис. 1б имеет несколько экстремумов (максимумов или минимумов). Из них главный (оптимальное решение для рассматриваемого интервала) называется глобальным.

Унимодальная функция не обязательно должна быть гладкой (рис. 2 а), она может быть ломаной (рис. 2б), разрывной (рис. 2в).

Рис. 2. Унимодальные функции

Рассматриваемые методы справедливы для функций на рисунке 2а, а для функций на рисунках 2б, 2в могут использоваться на отдельных интервалах.

Если целевая функция унимодальная, то можно сузить интервал исследования функции на оптимум путём определения значений целевой функции в двух точках интервала задания функций F(x1) и F(x2) и последующего поинтервального сравнения. При этом возможны три случая (рис. 3):

1) если F(x1) > F(x2),то xопт < x2, т.е. оптимум не может находиться правее, интервал [x2 , x] из дальнейшего рассмотрения исключается

2) если F(x1) < F(x2), то хопт > x1

3) если F(x1) = F(x2), то x1 < хопт < x2

Рис. 3. Определение значений целевой функции в двух точках интервала задания функций

Последовательно сужая интервал исследования, в котором находится оптимальное значение функции, можно с достаточной степенью точности найти оптимальное значение переменной.

Задача поиска экстремумов сводится к их локализации и уточнению значений x и F(x) в точке экстремума. В дальнейшем для функций одной переменной под экстремумом будем подразумевать максимум F(x).

Поскольку максимуму функции F(x) соответствует минимум функции - F(x), то, сменив знак у F(x), программами поиска максимума можно пользоваться и для поиска минимума функций. Будем также полагать, что на изменения x (если это особо не оговорено) накладываются ограничения в виде неравенств a < x < b, где a и b – границы интервала поиска. В пределах отрезка [a , b] функцию считаем унимодальной, т.е. содержащей один максимум.

С помощью численных методов мы непосредственно находим максимум (минимум) функции F(x) в некотором интервале, в котором, как предполагается, лежит максимум (минимум). Иногда это единственно возможная стратегия поиска.

На пример, стоимость проведения химического процесса может зависеть от температуры процесса. Инженер знает, что стоимость является функцией от T, хотя может и не знать явного вида функции. Однако он может поставить эксперимент и провести эксперимент при различных температурах и, следовательно, найти стоимость для этих температур и определить минимальную стоимость и температуру проведения процесса, при которой она достигается.

studfiles.net

Лабораторная работа № 9 Оптимизация методом крутого восхождения по поверхности отклика

Цель работы: Приобретение студентом практических навыков работы по методу крутого восхождения (методу Бокса – Уилсона) с помощью специально разработанного тренажера.

Краткое теоретическое содержание работы

Основополагающие принципы рассматриваемого поискового метода экспериментальной оптимизации объектов достаточно подробно изложены в основной рекомендованной литературе [2], [3].

Для реализации данного метода необходимо использовать результаты выполненных ранее лабораторных работ №№5, 6, по материалам которых строятся математические модели исследуемых объектов. Здесь эти материалы используются в качестве подготовительного этапа для собственно оптимизации объекта путем сравнения результатов опытов на линии градиента и поиска экстремума поверхности отклика.

Методические указания к выполнению работы

Сущность и практику применения рассматриваемого метода оптимизации можно наглядно представить с помощью современных компьютерных технологий (см. файл Тренажер1. xls).

Контрольный пример

На экране монитора после запуска этого файла в работу отражены кодированные значения факторов Х1, Х2 (которые для возможности графического отображения взяты в количестве только двух) в матрице плана ПФЭ типа 22 и соответствующие экспериментальные значения отклика Y объекта – см. блок данных Т9:Х12. На границе факторного пространства Х1, 0, Х2 показаны четыре опыта ПФЭ с соответствующими их координатами – точки 1), 2), 3) и 4).

По результатам опытов построена математическая модель (U15:Х15), коэффициенты которой составили b0 = 85; b1 = 4; b2 = 6 в отвлеченных числах.

Вычислены модельные значения отклика

(диапазон Х8:Х12).

Известными из теории вопроса действиями определяем градиент как вектор OG, где координаты точки G соответствуют значениям Х1 = b1 = 4; Х2 = b2 = 6.

Блок S21: АА25 отведен для тренировки в осуществлении поиска искомого max Y. Ось Y из точки Х1 = 0; Х2 = 0 здесь расположена перпендикулярно к плоскости экрана.

Поверхность отклика имитирована моделью второго порядка и от студента скрыта.

Задача заключается в том, чтобы путем пошагового изменения значений факторов Х1 и Х2 найти такое их сочетание на линии градиента, которое обеспечивает max Y.

Перед решением контрольного примера студент должен в ячейку W2 ввести код варианта N = 0.

Обращаясь к блоку данных S21: АА25, видим, что наш мысленный опыт №1 при Х1 = 0,5; Х2 = 0,7 (см. пунктир на графике) дал результат Y = 92,46.

Увеличивая значение Х1 как базового фактора с шагом 0,5, поставим следующий опыт №2 в точке с координатами Х1 = 1,0; Х2 = 1,5. Чтобы получить экспериментальный Y и модельный

результаты опытов, скопируем (например, перетаскиванием табличной ячейкиExcel за малый черный квадрат в правом нижнем углу курсорной рамки) информацию ячейки U24 в ячейку V24, а из ячейки U25 в ячейку V25. Замечаем, что экспериментальное значение отклика объекта Y возросло с 92,46 условных единиц измерения до 96,75. Отсюда можно сделать вывод о том, что мы на правильном пути, и следующий опыт (№3) следует поставить при X1 = 1,5; Х2 = 2,25. В результате копирования ячеек V24 в W24 и V25 в W25 замечаем, что экспериментальное значение Y продолжает возрастать. Следовательно, процесс поиска оптимума следует продолжать в том же направлении.

Следует обратить внимание на то, что экспериментальные значения Y, достигнув экстремума, начинают изменяться в противоположном направлении, в то время как модельные значения продолжают монотонно изменяться в соответствии со своей линейной моделью. В этом проявляется снижение адекватности математической модели по мере удаления от области её определения.

Студенту дается возможность продолжить поиск самостоятельно до получения конечного результата, который нужно представить в отчёте.

В дальнейшем каждый студент выполняет работу по индивидуальному варианту, номер которого определяется как сумма последней и предпоследней цифр студенческого шифра.

Полученные данные представляются в отчёте.

studfiles.net

Лабораторная работа № 6Оптимизация технологического процесса.

Методы оптимизации функции 1-ой переменной

Цель работы

Ознакомление с методами одномерной оптимизации (поиска максимума и минимума).

Оптимизация функций одной переменной

Постановка задачи

На определённом интервале функция может иметь одно (рис. 1а) или несколько экстремальных значений (рис. 1б).

Функция, изображённая на рис. 1а называется унимодальной.

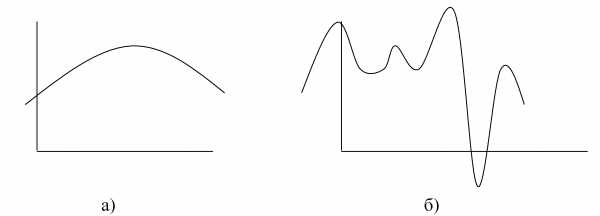
Рис. 1. Функции одного параметра x описывающие некоторую кривую на плоскости.

Рис. 2. Унимодальные функции

2) если F(x1) < F(x2), то хопт > x1

3) если F(x1) = F(x2), то x1 < хопт < x2

Рис. 3. Определение значений целевой функции в двух точках интервала задания функций

studfiles.net

Лабораторная работа № 3 Принятие решений на основе методов оптимизации

Цель работы: знакомство с постановкой и решением задач оптимизации методами линейного программирования, многокритериальной оптимизации и задачами о смене оборудования.

Содержание работы

Изучите по материалам учебного пособия, лекциям и другим источникам методы линейного программирования, решения задач многокритериальной оптимизации, смены оборудования и проделайте следующую работу.

1. Составьте на свой вкус суточное меню из 4–5 продуктов, исходя из следующих условий: суточная потребность человека в белках – 80 г, в жирах – 100г, углеводах – 360г. Общая калорийность меню для юношей 2700 ккал, для девушек – 2300 ккал. Сформулируйте и решите задачу линейного программирования для определения количества продуктов в двух вариантах:

а) Минимальная стоимость при балансе по белкам, жирам и углеводам и общей калорийности.

б) Минимальный вес продуктов при таком же балансе.

в) Сформулируйте двухкритериальную задачу на основе задач а) и б) и решите ее методом линейной свертки критериев, задавшись весом каждого из критериев.

Примечание Калорийность продуктов найдите в Интернете, а их стоимость – в ближайшем магазине. Для решения задачи используйте программу симплекс-метода, которую тоже можно найти в Интернете.

2. Определите для своего варианта оптимальный срок смены автомобиля по методике учебного пособия (п. 2.5.1) при следующих условиях (время рассчитывается в месяцах):

а) начальная цена автомобиля рублей,

б) потеря стоимости определяется формулой ;

в) стоимость обслуживания возрастает по закону

Исходные данные приведены в таблице 3.1.

Таблица 3.1

№ варианта	тыс. руб.	1/мес.	1/мес.
		0,05	0,03
		0,07	0,04
		0,02	0,06
		0,03	0,02
		0,01	0,05
		0,015	0,07
		0,017	0,065
		0,025	0,03
		0,04	0,05
		0,06	0,015
		0,03	0,03
		0,01	0,04
		0,015	0,06
		0,017	0,02
		0,025	0,05
		0,01	0,065
		0,015	0,03
		0,017	0,05
		0,025	0,015
		0,04	0,03
		0,05	0,03
		0,07	0,04
		0,02	0,06
		0,03	0,02
		0,01	0,05
		0,015	0,07
		0,017	0,065
		0,025	0,03
		0,04	0,05
		0,06	0,015
	г00	0,03	0,03
		0,01	0,04
		0,015	0,06
		0,017	0,02
		0,025	0,05

Содержание отчета по работе

Отчет по лабораторной работе должен содержать:

· Титульный лист с указанием номера группы и исполнителей;

· Для задачи 1 выпишите переменные, ограничения и критерии оптимизации, а также полученные решения для каждого из варианта постановки.

· Для задачи 2 постройте график изменения удельной себестоимости и укажите время, когда эта функция достигает минимума.

Лабораторная работа № 4 Вероятностное моделирование динамики систем на основе цепей Маркова с дискретным временем

Цели работы

1. Освоить основные положения теории конечных цепей Маркова (ЦМ) с дискретным временем.

2. Научиться составлять ЦМ для моделирования систем и анализа динамики их функционирования.

3. Научиться вычислять характеристики функционирования ЦМ.

Содержание работы

1) Изучить теоретический материал по ЦМ по учебному пособию (глава 3), по лекциям или другим источникам.

2) Для заданного варианта модели системы составить матрицу переходных вероятностей.

3) Вычислить с помощью пакета MathCad или специально написанной программы векторы вероятностей X(t)пребывания системы в каждом из состояний для 15 шагов при старте из заданного входного состояния и построить соответствующие графики.

4) Структурировать матрицу , выделить множества невозвратных и эргодических состояний и . Выписать матрицы , , .

5) Определить среднее число тактов пребывания процесса в каждом из невозвратных состояний путем вычисления матрицы .

6) На основе матрицы вычислить среднюю трудоемкость процесса .

7) Оценить среднеквадратичное отклонение от среднего числа пребываний процесса в множестве невозвратных состояний , где и соответствующее среднеквадратичное отклонение трудоемкости от среднего .

8) Оценить предельные вероятности пребывания процесса в множестве эргодических состояний:

а) путем прямого возведения матрицы в высокую степень,

б) путем спектрального разложения матрицы.

Содержание отчета по работе

Отчет по лабораторной работе должен содержать:

· титульный лист с указанием исполнителя и номера варианта,

· исходные данные по ЦМ – граф смены состояний, матрицы переходных вероятностей ; , и вектор начальных условий X(0),

· таблицу векторов X(t), t=0,1,…15, полученных по формуле и графики , j=1,…n, t=0,…15;

· матрицу средних значений и оценку средней трудоемкости процесса ,

· матрицу дисперсий и оценку среднеквадратичного отклонения трудоемкости ,

· оценки предельных вероятностей пребывания процесса в состояниях эргодического множества, вычисленные:

а) путем прямого возведения матрицы в высокую степень,

б) путем спектрального разложения матрицы

Исходные данные к работе

Исходные данные представлены в виде таблицы 4.1 и набора схем. По указанному преподавателем номеру варианта в таблице выбирается соответствующая строка. Второй столбец таблицы указывает код схемы и стартовое состояние (например, Г1 – схема Г, старт происходит из состояния S1). Далее указаны вероятности перехода между состояниями в десятых долях (т.е. указанное в таблице значение означает, что ). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов в секундах.

Таблица 4.1

mмах 1/с

0.1

1.2

0.2

0.5

1.2

2.5

10.5

Трудоемкости, С, c

С7

С6

С5

С4

С3

С2

С1

Вероятности переходаРk´10

Р10

Р9

Р8

Р7

Р6

Р5

Р4

Р3

Р2

Р1

Схема, вход

А2

Б1

Б2

В1

В2

Г1

Г2

Д1

Д2

А1

А2

Б1

Б2

В1

В2

Г1

Г2

Д1

Д2

№ вар.

Таблица 4.1(продолжение)

mмах 1/с

0.1

1.2

0.2

Трудоемкости, С, c

С7

С6

С5

С4

С3

С2

С1

Вероятности переходаРk´10

Р10

Р9

Р8

Р7

Р6

Р5

Р4

Р3

Р2

Р1

Схема, вход

А2

Б1

Б2

В1

В2

Г1

Г2

Д1

Д2

А1

А2

Б1

Б2

В1

№ вар.

cyberpedia.su

Лабораторная работа № 1 оптимизация режимов резания

Цель работы — определение подачи и числа оборотов шпинделя, доставлявших экстремум критерию оптимальности.

Основные положения

Решение задач параметрической оптимизации проходит в три этапа:

1) составление математической модели;

2) определение функции цели;

3) выбор метода решения в решение задачи оптимизации.

На 1 этапе составляется математическая модель решаемой задачи, которая определяет область допустимых значений переменных. Переменные — параметры задачи, оптимальное значение которых нужно найти.

Для однорезцовой токарной операции математической моделью является система неравенств или ограничений по точности, технологическим возможностям оборудования и технико-экономическим показателям [2].

Математическая модель включает следующие ограничения.

1. По точности обработки

, (2.1)

где  — допуск на обрабатываемый размер в мм;

СPz, XPz, YPz — коэффициенты сил резания;

t — глубина резания, мм;

KPz — поправочный коэффициент;

KPz=KMKKKrKгр — коэффициенты, учитывающие влияние обрабатываемого материала, главного угла в плане, переднего угла, радиуса при вершине резца, группу обрабатываемости;

—жесткость станка, детали и резца в кг/мм2;

k1; k2 — коэффициенты влияния деформации элементов технологической системы на точность обработки, для продольного точения k1 = 1, k2 = 0,05.

2. По шероховатости поверхности

, (2.2)

где для стальных деталей СН = 0,32; y = 0,8; u = 0,5; x = 0,3; z = 0,35; z1 = 0,335;

Rz — высота микронеровностей в мкм;

r — радиус вершины резца в мм;

, 1 — главный и вспомогательный углы в плане в град.

3. По мощности станка

, (2.3)

где n — число оборотов шпинделя;

N — мощность станка;

D — диаметр обрабатываемой поверхности.

4. По технологическим возможностям станка:

nnmax ; (2.4)

nnmin ; (2.5)

SSmax; (2.6)

SSmin , (2.7)

где nmax, nmin, Smax, Smin — максимальные и минимальные значения чисел оборотов и подач станка по его паспорту.

5. Технико-экономические показатели:

5.1) по стойкости

, (2.8)

где Cv, Yv, Xv, m — коэффициенты стойкости;

Kv — поправочный коэффициент;

Kv= KMдKМи KKKrKо — коэффициенты, учитывающие влияние обрабатываемого материала, материала инструмента, радиуса вершины резца, главного угла в плане, вида обработки;

T — период стойкости резца в мм;

5.2) затраты на режущий инструмент

, (2.9)

—средняя стоимость станкоминуты, для универсальных станков E= 45 руб.;

tсм — время замены инструмента, в среднем tсм 3 мин;

C — стоимость инструмента в руб.;

Q — допускаемые затраты на инструмент в руб.;

lрез — длина резания в мм;

5.3) производительность

, (2.10)

tоб — допускаемое время обработки в мин.

Если одно из ограничений (2.8), (2.9) или (2.10) является критерием оптимальности, то в систему ограничений оно не входит.

На 2 этапе определяется критерий оптимальности и записывается функция цели.

Критериями оптимальности могут быть:

— производительность обработки

функция цели будет иметь вид так какtоб и lрез= const;

— стойкость инструмента

или ;

— затраты на режущий инструмент

или .

На 3 этапе определяется метод решения оптимизационной задачи. Наиболее распространенными методами решения являются геометрический и алгоритмический.

При геометрическом методе решение легко получится, если система неравенств будет линейной. Для этого необходимо неравенства, входящие в систему ограничений, а также функцию цели F прологарифмировать. Тогда в системе координат ln(S) — 0 —ln(n) неравенства системы ограничений дадут прямые линии, а область допустимых значений представит собой многоугольник (рис. 3).

Заштрихованный многоугольник — область допустимых значений S и n. Для нахождения оптимальной точки в этой области необходимо построить линию пересечения плоскости, заданную уравнением функции цели F и плоскости ln(S) — 0 —ln(n). Для этого задаемся каким-нибудь значением F, например F= 0, и строим линию в плоскости ln(S) — 0 —ln(n) (линия 10 на рис. 3). Затем, передвигая линию 10 параллельно самой себе в сторону от начала координат 0 (или к началу координат, если критерий оптимальности T), находим точку многоугольника, которую последней касается линия 10. Эта точка и дает оптимальные для данного критерия значения S0 и n0.

Рис. 3. Геометрический метод

При алгоритмическом методе одним из способов нахождения оптимальных значений S и n является следующий:

1) решаем неравенства (2.1)–(2.10) относительно подачи S, т.е. в левой части остается только подача S;

2) выбираем станок и последовательно от nmin до nmax включаем в неравенства конкретные значения чисел оборотов ni;

3) решая неравенства, находим наименьшее из них значение подачи S;

4) для каждого значения ni определяем Fi;

5) находим значение ni , где Fi будет максимальным или минимальным (в зависимости от критерия оптимальности). Это и даст оптимальные значения n0 и S0.

Блок-схема алгоритма решения на ЭВМ показана на рис. 4

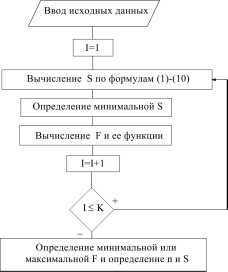
Рис. 4. Блок-схема алгоритма расчета оптимальных режимов

studfiles.net

Лабораторная работа 6 Имитационное исследование и оптимизация системы контроля

Целью данной работы является развитие навыков составления программы имитации элементарной системы массового обслуживания (СМО), ее эксплуатации на примере некоторой системы контроля (СК).

Рекомендуемый порядок выполнения работы:

помощью имитационной модели найти характеристики одноканальной СК;
найти оптимальное число каналов СК, обеспечивающее требуемую вероятность обслуживания изделий;
найти операционные характеристики оптимальной многоканальной СК.

1. Постановка задачи Описание проблемной ситуации

Рассматривается следующий пример.

На выходе поточной линии готовые изделия проходят функциональный контроль на специальных однотипных стендах. Изделия сходят с конвейера в случайные интервалы времени, распределенные равномерно на интервале [a, b] мин.

Если все стенды к моменту поступления изделия на контроль оказываются занятыми, то изделие остается непроверенным и в таком виде может поступить потребителю. При наличии хотя бы одного свободного стенда изделие подвергается контролю. Каждый из стендов одновременно может контролировать только одно изделие. Время контроля на любом стенде случайное и распределено также равномерно на интервале [c, d] мин.

Требуется определить количество контрольных стендов, которые необходимо установить на выходе поточной линии, чтобы обеспечить контроль не менее Р % готовых изделий.

Обсуждение исходной задачи

Анализ любой задачи исследования технической системы целесообразно начинать с классификации данной системы и определения цели исследования.

Рассматриваемая система является дискретной, поскольку в нейсобытия, происходят в некоторые случайные моменты времени. Действительно, изделия, поступающие с поточной линии на контроль, образуют случайныйвходной поток заявок, аконтрольные стенды являютсяканалами обслуживания данных заявок. После обслуживания, изделия не поступают на какую-либо последующую обработку, а образуют случайныйвыходной поток проконтролированных (обслуженных) изделий. Это означает, что СК являетсяразомкнутой и однофазной.

Тот факт, что в случае занятости всех каналов заявка получает отказ, позволяет го-ворить о СК как осистеме обслуживания с отказами, т.е. без очереди (или без ожидания). Источник заявок (поточная линия) может считатьсянеограниченным.

Таким образом, мы классифицировали СК как однофазную, разомкнутую, N-канальную систему массового обслуживания (СМО) с отказами и дисциплиной обслуживания -FIFO.

Цель исследования в этой задаче указана явно:найти такое число каналов N*, которое обеспечит контроль Р % всех изделий. Очевидно, что в терминах теории СМО это требование тождественно требованию обеспечениявероятности обслуживания заявокРобс=Р/100.

Метод решения задачи оптимизации

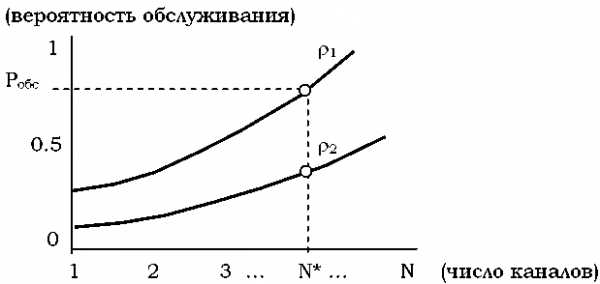
Для того, чтобы найти требуемое (оптимальное) количество каналов, обеспечивающее контроль изделий с вероятностью Робсдостаточно построить зависимости Робс от числа каналовNобслуживания (рис.1).

Рис. 1. Зависимость Робс от числа каналов обслуживания N для разных значений коэффициента нагрузки =Хф.

Такие зависимости называются нагрузочными кривыми. Ясно теперь, что, зная коэффициент загрузки i и требуемую вероятность обслуживания Робс можно всегда определить искомое число каналовN*.

Очевидно, что вся проблема в задачах такого рода заключается в построении нагрузочных характеристик исследуемой СМО. Нагрузочные характеристики для различных СМО имеют разный характер. Они могут быть рассчитаны аналитически либо найдены с помощью имитационных моделей.

Поскольку входной поток рассматриваемой СК не экспоненциальный, то мы не можем использовать уравнения Эрланга, и поэтому единственным способом анализа системы является имитационное моделирование.

Вместо явного построения нагрузочных характеристик в данной работе предлагается программный метод оценки требуемого числа каналовN*.

Для нахождения требуемого числа каналов N* предлагается воспользоваться методом перебора. Это означает, что саму имитационную модель СК включают в определенный внешний цикл программы. В этом цикле осуществляется моделирование и проверка условия обслуживания по вероятности Робсдля последовательного чис-ла каналов N от 1,2, … до N*.

studfiles.net

Overview - Лабораторная работа в Excel. Метод линейной оптимизации

Microsoft Excel 12.0 Отчет по результатам
Рабочий лист: [Книга1.xls]Лист1
Отчет создан: 19.03.2010 20:53:16


Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$F$6	Цена при продаже Объем ресурсов	249,7777777778	249,7777777778


Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$B$3	Переменные Продукт 1	0	0
	$C$3	Переменные Продукт 2	8	8
	$D$3	Переменные Продукт 3	0,8888888889	0,8888888889
	$E$3	Переменные Продукт 4	0	0
	$D$17	Продукт 3	0	0


Ограничения
	Ячейка	Имя	Значение	Формула	Статус	Разница
	$F$7	Сырье, кг Объем ресурсов	41,7777777778	$F$7	не связан.	18,2222222222
	$F$8	Рабочая сила, ч Объем ресурсов	128	$F$8	не связан.	272
	$F$9	Оборудование,ст-ч. Объем ресурсов	128	$F$9	связанное	0
	$B$3	Переменные Продукт 1	0	$B$3	не связан.	5
	$C$3	Переменные Продукт 2	8	$C$3>=$C$4	связанное	0
Microsoft Excel 12.0 Отчет по устойчивости
Рабочий лист: [Книга1.xls]Лист1
Отчет создан: 19.03.2010 20:53:16


Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
	$B$3	Переменные Продукт 1	0	-1,1111111112	30,000000001	1,1111111112	1000000000000000000000000000000
	$C$3	Переменные Продукт 2	8	-18,5555555557	25	18,5555555557	1000000000000000000000000000000
	$D$3	Переменные Продукт 3	0,8888888889	0	56	1000000000000000000000000000000	1,999999997
	$E$3	Переменные Продукт 4	0	-1,777777775	48,000000001	1,777777775	1000000000000000000000000000000
	$D$17	Продукт 3	0	0	0	0	1000000000000000000000000000000

Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
	$F$7	Сырье, кг Объем ресурсов	41,7777777778	0	60	1000000000000000000000000000000	18,2222222222
	$F$8	Рабочая сила, ч Объем ресурсов	128	0	400	1000000000000000000000000000000	272
	$F$9	Оборудование,ст-ч. Объем ресурсов	128	3,1111111111	128	163,9999999985	16

nashaucheba.ru