Примеры задач оптимизации в экономике и финансах. Пример задача оптимизации
Примеры задач оптимизации в экономике и финансах
Теория.
1. Функция полезности с полным взаимозамещением благ:
где коэффициент является числовой оценкой полезности от потребления единицы товара вида i.
2. Функция полезности с полным взаимодополнением благ:
где - количество товара вида i, приходящееся на единицу полезности. Для построения кривых безразличия функции в из уравнения найдем
если (1)
если (2)
если (3)
3.Задача потребительского выбора. Задача потребительского выбора имеет вид: при ограничении и условие .
Решение задачи потребительского выбора: либо графический метод решения задач линейного программирования, либо метод Лагранжа. Решением задачи является набор .
4.Эластичность спроса по цене. Коэффициент ценовой эластичности спроса: процентного изменения количества спрашиваемой продукции к процентному изменению цены, вызвавшему это изменение спроса , где , тогда :
Q1 и Q2 — первоначальный и текущий объем спроса;
P1 и Р2 — первоначальная и текущая цена.
Формула центральной точки:
Пример 1.
Пусть товаром первого вида является кофе, второго – чай, а потребление этих продуктов в количествах и дает полезность, равную с , то есть .
Представим, что потребление кофе уменьшилось на единиц. Тогда полезность упадет до уровня . Чтобы компенсировать эту потерю полезности надо увеличить потребление чая на величину так, чтобы
В результате имеем:
Отсюда найдем .
Таким образом, функция позволяет определить размер замещения одних товаров другими для того, чтобы полезность оставалась на неизменном уровне.
Пример 2.
Приобретается набор из двух товаров: кофе в количестве и сахара в количестве c . Потребление этих товаров дает полезность, равную с, то есть
В случае (1)
и увеличение (уменьшение) потребления кофе влечет увеличения (уменьшения) сахара.
В случае (2) увеличение потребления кофе может привести к нарушению неравенства в (2) и, следовательно, к нарушению уровня полезности, если не увеличиться потребление сахара.
Функция (2) применяется для определения полезности набора взаимодополняющих друг друга товаров.
Пример 3.
Оптимальный набор потребителя составляет 6 ед. продукта х1 и 8 ед. продукта . Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. Функция полезности потребителя имеет вид: u(x1,x2)= .
Решение. Следуя принципу решения, получаем систему уравнений:
,
16p2=240 p2=15 p1=20
Подставив, вместо х1 - 6 ед., вместо х2 - 8 ед., получим: p1=20руб., p2=15руб.
Итак, решение задачи потребительского выбора сводится к решению задач на условный экстремум.
Пример 4.
Цена товара колеблется в интервале от 4 до 5 ден. ед. При Px=4 ден. ед. объем спроса составляет 4000 ед. продукции. При Px = 5 ден. ед. — 2000 ед. Используя первоначальную формулу
рассчитаем значение коэффициента ценовой эластичности для данного ценового интервала:
Однако если в качестве базовой взять другую комбинацию цены и количества продукции, то получим:
И в первом, и во втором случае спрос эластичный, но результаты отражают разную степень эластичности, хотя анализ мы проводим на одном и том же ценовом интервале. Для преодоления этого затруднения экономисты используют в качестве базовых средние величины уровней цены и количеств, т. е.
или
Практика №6
Тема: «Мат.модель транспортной задачи, решение задачи»
Задача №1. (Cдефицитом) Задача №3. (Cдефицитом)
Данные заданы таблицей Данные заданы таблицей
| Стоимость перевозки единицы продукции | Объемы производства | |||
| Объемы потребления |
| Стоимость перевозки единицы продукции | Объемы производства | |||
| Объемы потребления |
Задача №2.(Не сбалансирована) Задача №4.(Не сбалансирована)
Выбрать такое распределение ресурсов по объектам, чтобы минимизировать стоимость назначений.
| Рабочие\Работы | Стоимость выполненных работ | ||||
| I | II | III | IV | V | |
| A | |||||
| B | |||||
| C | |||||
| D |
| Рабочие\Работы | Стоимость выполненных работ | ||||
| I | II | III | IV | V | |
| A | |||||
| B | |||||
| C | |||||
| D |
Задача №5. (Cдефицитом) Задача №5. (Cдефицитом)
| Стоимость перевозки единицы продукции | Объемы производства | |||
| Объемы потребления |
Данные заданы таблицей
| Стоимость перевозки единицы продукции | Объемы производства | |||
| Объемы потребления |
Ответ: №1 212,5 №2 32 №3 598,75 №4 29
№5 №6 №7 №8
mykonspekts.ru
Пример задачи нелинейной оптимизации
Задача. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Пусть xj, j= 1,2,3 – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1)
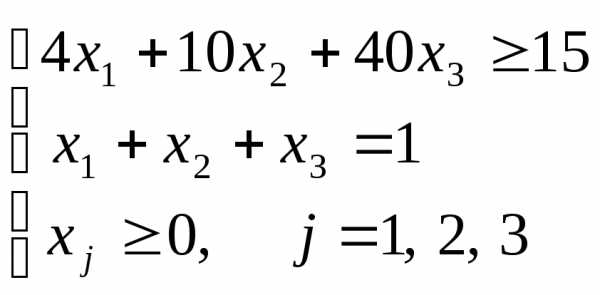
Решение.
Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде:
формулы этого листа приведены в ячейках.
Диалоговое окно Поиск решения с введенными ограничениями, соответствующее приведенному выше рабочему листу:
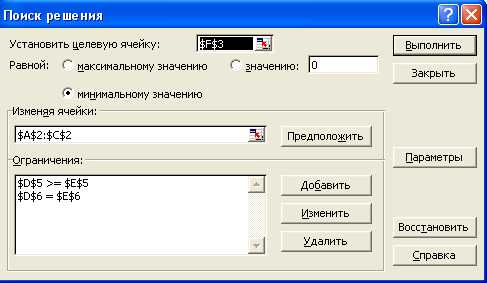
Реализуя приведенную модель средствами MS Excel, будем иметь оптимальный портфель Марковица:
х1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т.е. доли ценных бумаг оказались равными 52,13%; 20,78% и 27,09%. При этом минимальный риск – 23,79, доходность портфеля оказалась равной заданной – 15.
Задачи для самостоятельного решения
1. Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен 100= Х1 + Х2, где Х1 и Х2 – объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:
, .
Необходимо так распределить объем производства между технологическими способами, чтобы минимизировать общие затраты производства.
2. Найти максимальное значение функции 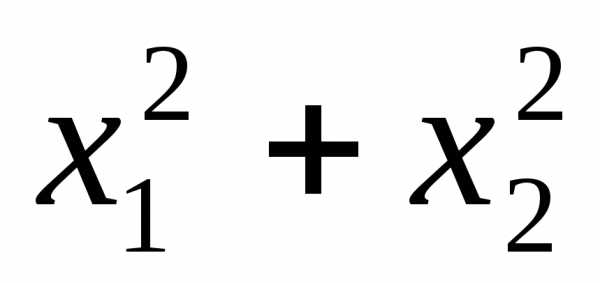 при ограничениях:
при ограничениях:
4. Найти минимум функции при ограничениях:
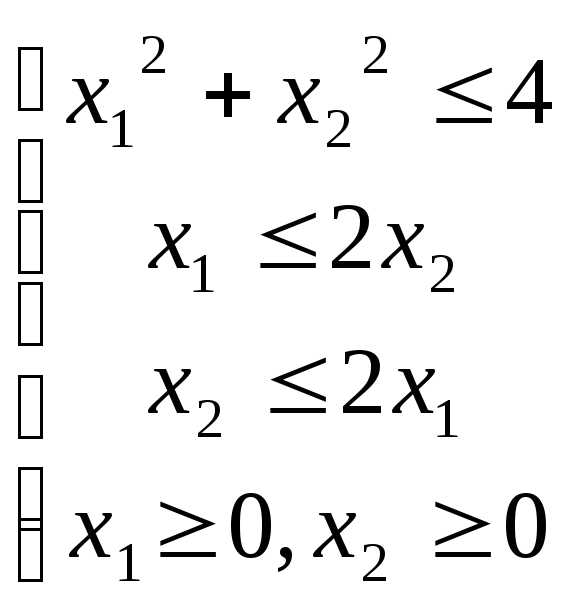
Лабораторная работа №4. Метод кусочно-линейной аппроксимации
Пусть дана система неравенств вида и целевая функция, причем все функции являются выпуклыми, а функцияz выпукла или вогнута на некотором выпуклом множестве М.
являются выпуклыми, а функцияz выпукла или вогнута на некотором выпуклом множестве М.
Рассмотрим приближенное решение задач выпуклого программирования с сепарабельными функциями методом кусочно-линейной аппроксимации.
Функция F(X)=F(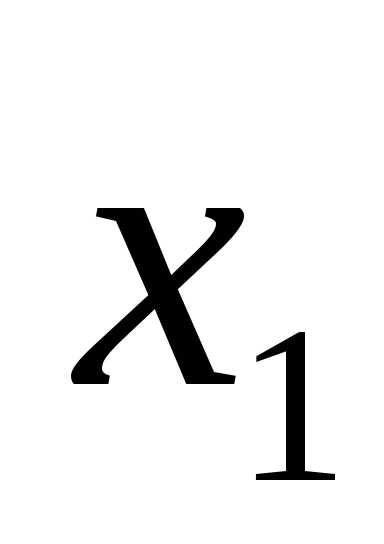 ,…,xn) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т. е. если
,…,xn) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т. е. если
или 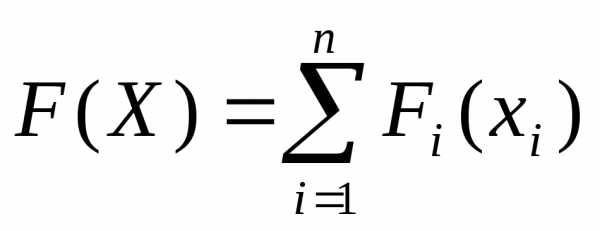
(не исключено, что 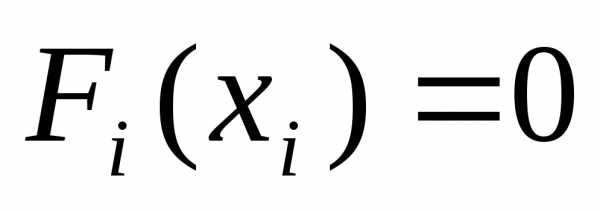
Пусть в задаче ВП и функция цели z, и все ограничения  являются сепарабельными. Тогда задача имеет вид: найти минимум выпуклой (максимум вогнутой) функции
являются сепарабельными. Тогда задача имеет вид: найти минимум выпуклой (максимум вогнутой) функции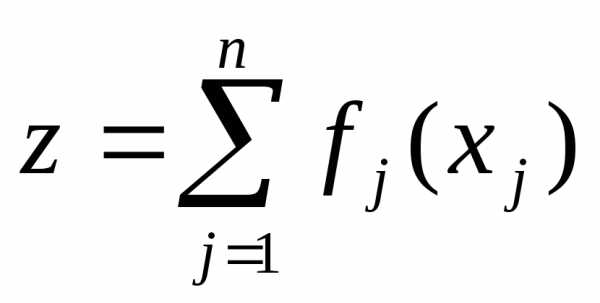 при ограничениях:
при ограничениях:
.
Идея метода кусочно-линейной аппроксимации состоит в том, что все 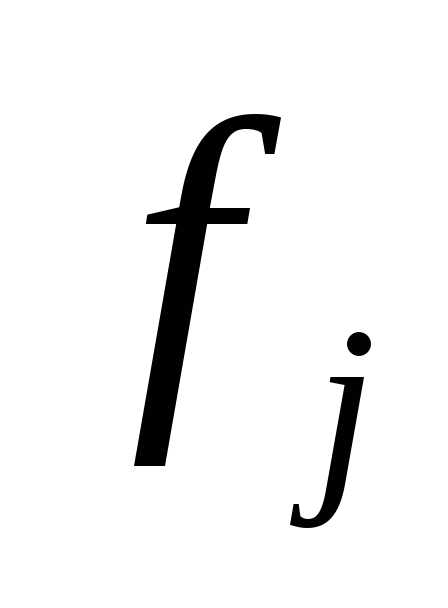 и все
и все заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования. Эта задача решается обычно симплексным методом, и ее решение является приближенным решением исходной задачи ВП.
заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования. Эта задача решается обычно симплексным методом, и ее решение является приближенным решением исходной задачи ВП.
Для построения приближенной задачи рассмотрим кусочно-линейную аппроксимацию функции одной переменной h(x), заданной на отрезке [0,a]. Разобьем этот отрезок на r частей точками x <x<…<xтак, чтобы x
<x<…<xтак, чтобы x =0, x
=0, x
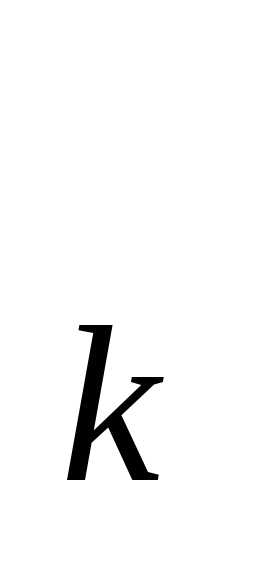 (x) (k=0,…,r) в этих точках. Соединим попарно точки (x
(x) (k=0,…,r) в этих точках. Соединим попарно точки (x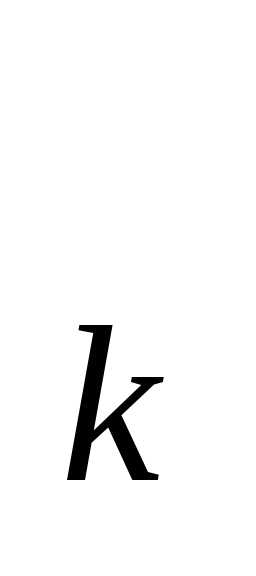 ;h
;h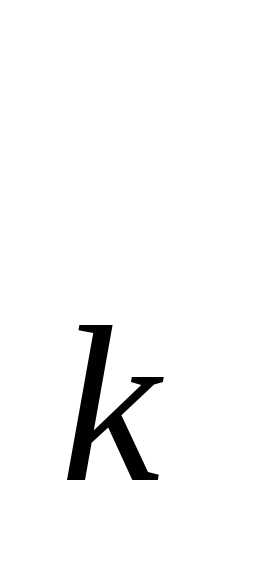 ) и (x
) и (x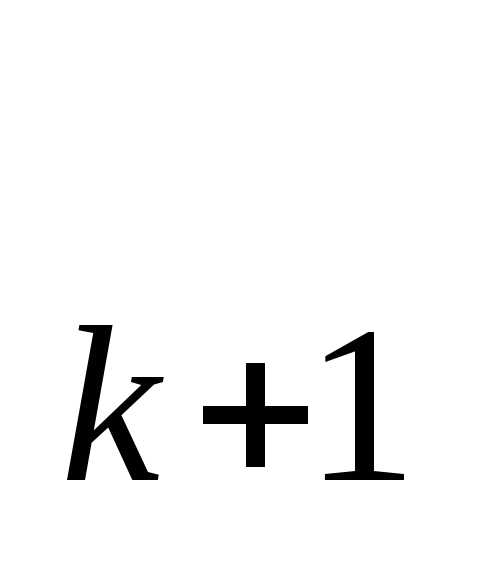 ;h
;h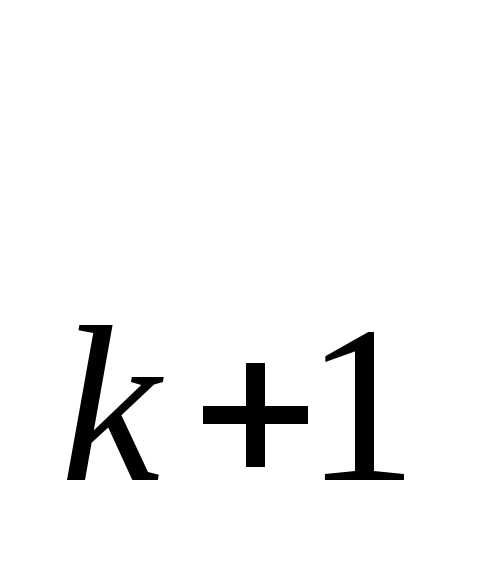 ) отрезками прямых. Состоящая из этих отрезков ломаная
) отрезками прямых. Состоящая из этих отрезков ломаная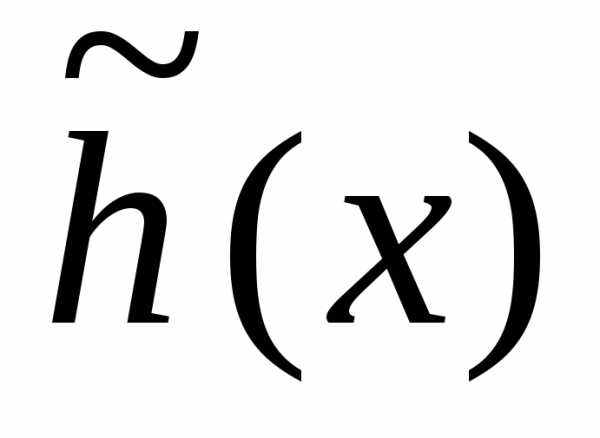 аппроксимирует функциюh(x) на отрезке[0,a].
аппроксимирует функциюh(x) на отрезке[0,a]. Уравнение участка ломаной 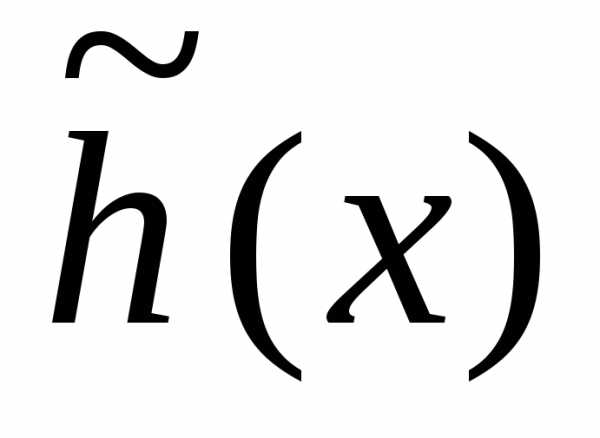 между точками (x
между точками (x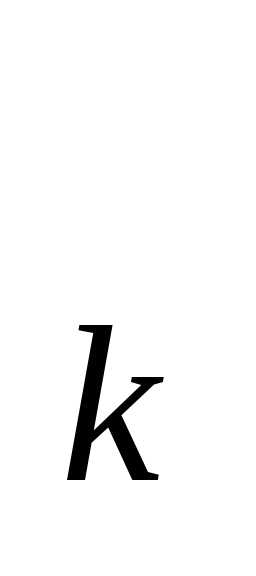 ;h
;h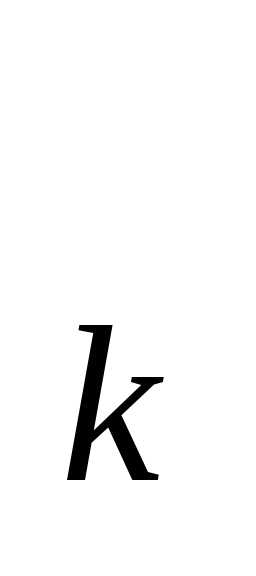 )и (x
)и (x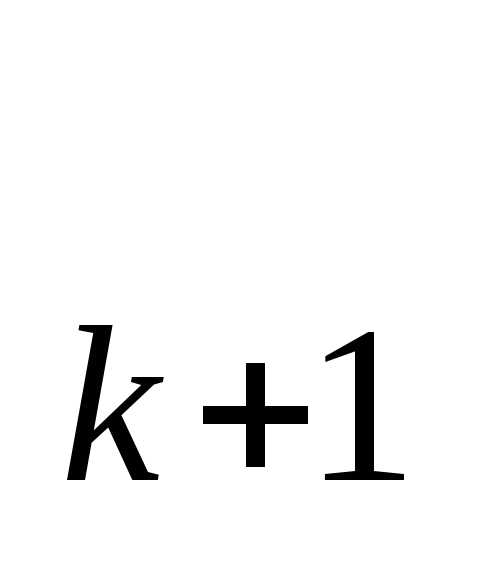 ;h
;h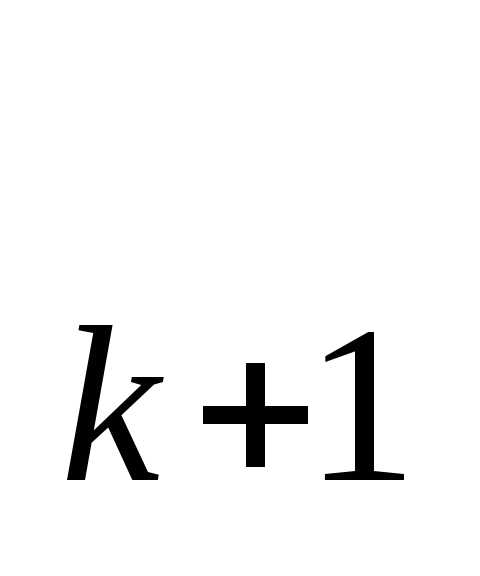 ) имеет вид
) имеет вид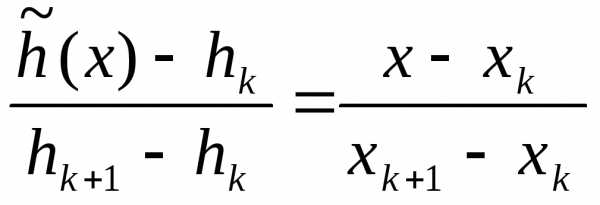 (уравнение прямой, построенной по двум заданным точкам).
(уравнение прямой, построенной по двум заданным точкам).
Если каждое из отношений в этом равенстве обозначить через  , то получим:
, то получим:
и , причем.
Обозначив , можно переписать в виде:
Таким образом, для любого x[0,a] уравнение ломаной можно записать в виде:
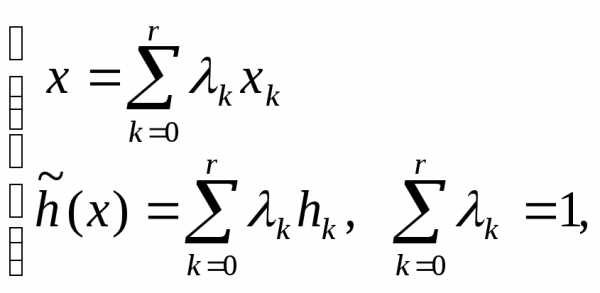 ,
,
причем всегда отличны от нуля только для значения k (если x является внутренней точкой k-го отрезка разбиения), или одно, (если x совпадает с концом отрезка).
Возвращаясь к задаче ВП с сепарабельными функциями, отметим, что, прежде всего (в зависимости от системы ограничений) нужно определить интервал изменения каждой переменной x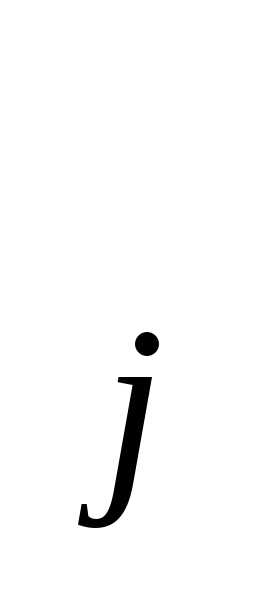 . Затем каждый этот интервал разбивается на части точкамиx
. Затем каждый этот интервал разбивается на части точкамиx и, с использованием полученных формул строится кусочно-линейная аппроксимация для функцийf
и, с использованием полученных формул строится кусочно-линейная аппроксимация для функцийf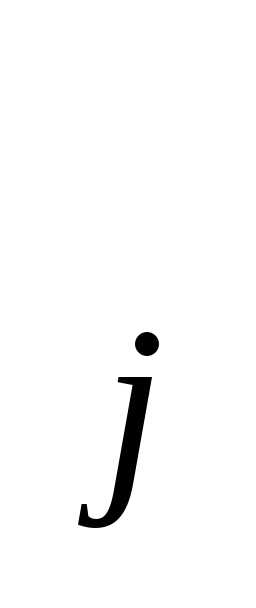 и
и . После этого можно для исходной задачи записать приближенную задачу: найти максимум функции
. После этого можно для исходной задачи записать приближенную задачу: найти максимум функции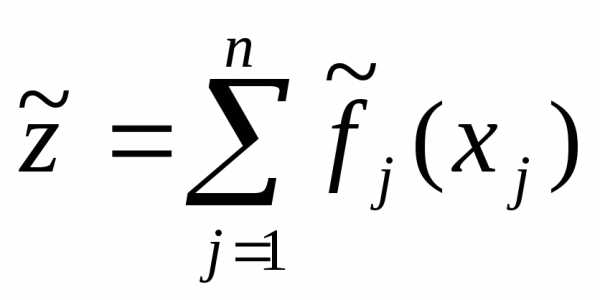 при ограничениях:
при ограничениях:
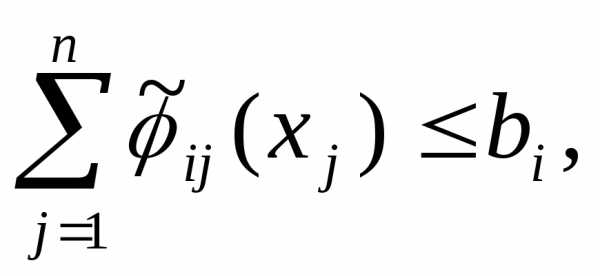
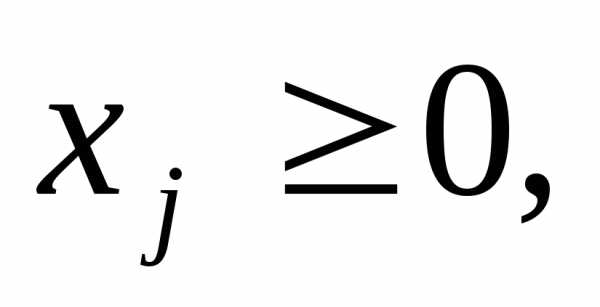
studfiles.net
Разбор примера задачи нелинейной оптимизации — Мегаобучалка
Решим и проанализируем описанную выше ситуацию принятия решения для директора лесозаготовительного комбината.
Анализ будем проводить только с учетом переменных расходов. Как следует из общей теории оптимизации, постоянное слагаемое не оказывает влияние на оптимальный план действий, изменяя только значение целевой функции.
Как видно из данных примера, весь анализ можно провести в терминах количества рабочих. Обозначим через число рабочих на предприятии. Так как мы не можем уволить более 30 человек из имеющихся 70, то переменная ограничена снизу: .
Выпуск продукции пропорционален численности и равен м3 в мес. Доход от продажи в месяц тогда равен:
Если возможную субсидию при учесть в доходной части, то общую функцию месячного дохода можно записать так:
(3)
Если не нанимать новых сотрудников, то будет выполняться условие , а месячные расходы равны:
.
Если нанять новых рабочих, то . Из этого количества рабочих 70 будут «старых», а – «новых». Тогда месячные расходы будут складываться из затрат на «старых» по 80 тыс. руб. на человека и затрат на новых по тыс. руб. на человека. Суммарные затраты составят:
.
В итоге общую функцию месячных затрат можно записать в виде:
(4)
Прибыль комбината (без учета постоянных расходов) равна разнице между доходами (3) и переменными расходами (4) и запишется в виде:
(5)
Таким образом, математически задача формулируется так: найти , при котором функция прибыли (5) имеет максимум.
Очевидно, функция (5) меняется непропорционально искомой переменной и задача является нелинейной.
Пройдем для этой задачи все пункты алгоритма поиска глобального экстремума.
1) Определим градиент функции. В данном случае функции одной переменной градиент совпадает с производной. Если функция задана разными выражениями на разных интервалах, то нужно просто взять производные для каждого интервала. Они будут справедливы при строгом выполнении ограничивающих интервалы неравенств:
(6)
Как видно из выражения (6), производные на втором и третьем интервалах совпадают, но между ними при производная не существует, так как функция терпит разрыв.
2) Определим точки, где производная равна нулю. Для этого определим все , удовлетворяющие равенствам:
Рассмотрим интервал . На нем имеем уравнение:
.
Решая уравнение, находим
.
Однако данное значение не попадает в интервал: . Значит на указанном интервале нулей производной нет.
Рассмотрим интервал . На нем имеем уравнение:
.
Решая уравнение, находим
.
Данное значение принадлежит рассматриваемому интервалу: . Таким образом, является корнем производной.
Рассмотрим интервал . На нем имеем уравнение:
.
Решая уравнение, находим
.
Это значение не принадлежит рассматриваемому интервалу: . Значит на указанном интервале нулей производной нет.
Итак, производная равна нулю только в точке . Определим значение функции в этой точке:
.
То есть наняв 100 рабочих получим прибыль, равную 11400 тыс. руб.
3) Определим точки, где производная не существует. Это все точки границ интервалов. Найдем в них значение функции.
В точке функция имеет излом, но остается непрерывной. Ее значения с обеих сторон совпадают и равны:
.
Если останутся прежние 70 рабочих, то прибыль будет 11133 тыс. руб.
В точке функция имеет скачек. Ее значения разные с двух сторон.
При предел будет равен:
.
При предел будет равен:
.
Таким образом, наняв 150 рабочих получим прибыль, равную 11195 тыс. руб.
Замечание 1. В данной задаче из условия целочисленности числа рабочих можно было не искать значения пределов, а проверить значение прибыли при 150 и 149 рабочих.
Замечание 2. Из экономического смысла задачи очевидно, что предел справа (когда субсидия будет выплачена) будет лучше, чем предел слева (без субсидии).
4) Единственной границей области в данном случае является . При этом значении:
.
То есть при 40 работниках прибыль будет равна 9449 тыс. руб.
5) Поведение функции на бесконечности можно не рассматривать, как в задачах экономики. Однако, если это сделать, то получим:
.
Как и ожидалось, нанимая неограниченное количество рабочих будем получать неограниченные убытки.
6) Из всех найденных значений целевой функции выберем самое большое. Собираем все значения вместе:
,
,
,
,
.
Как видно, наибольшее значение достигается при .
Таким образом, оптимальное управленческое решениебудет таким:
Ø Необходимо привлечь к работе всего 100 человек: 70 уже имеющихся и 30 новых. В этом случае мы получим наибольшую прибыль, равную 11 миллионов 400 тысяч рублей.
Ответить на вопросы, поставленные перед собой новым руководителем, можно так:
Ø Имеющееся количество рабочих не оптимально. Необходимо нанять еще 30 человек. Нанимать рабочих до 150 человек не выгодно, так как получаемая субсидия вместе с ростом доходов не компенсирует полученный рост расходов.
Сделаем еще несколько замечаний.
Ø Если мы сравним суммы прибыли при текущем количестве рабочих (11 млн. 133 тыс. руб.) и оптимальным (11 млн. 400 тыс. руб.), то видно, что прибыль меняется всего на 267 тыс. руб. или менее чем на 3%. Необходимо как следует проанализировать, стоит ли менять сложившийся вариант работы ради таких незначительных изменений. Для анализа необходимо уже будет учесть постоянные издержки. Если они велики, то прибыль с их учетом становится значительно меньше и дополнительные 267 тыс. руб. в месяц являются уже существенным выигрышем.
Ø Принятие на работу всего 150 человек приводит тоже к близкому финансовому результату. Этот случай может быть рассмотрен как вариант расширения предприятия, если есть перспектива поиска лучшего варианта сбыта продукции.
Графическая интерпретация решения.
Построим на одном графике все три функции, описываемые уравнениями (4), (5), (6) (см рис. 1).
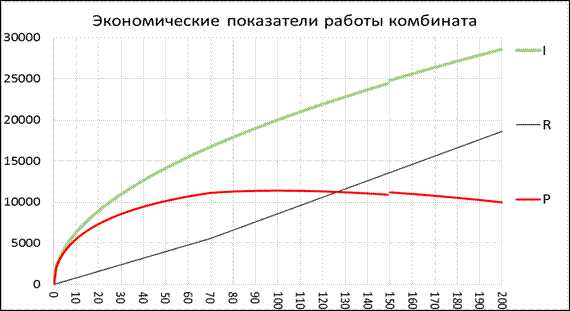
Рис. 1. Графики зависимости экономических показателейот количества рабочих
Из графика видно, что оптимум прибыли достигается примерно при 100 рабочих.
График прибыли ведет себя достаточно плавно в окрестности максимального значения, значит небольшие изменения числа около рабочих 100 человек не сильно влияют на финансовый результат.
Методика и специфика решения задачнелинейной оптимизации в MS Excel
Задачу оптимизации нелинейной функции (6) можно было бы решить не путем анализа с использованием производной, и используя инструмент «Поиск решения» в MS Excel.
Если реализовать вычисления функции (6) по значению переменной в ячейке (см. рис. 2), то можно определить оптимально значение переменной в этой ячейке.
Рис. 2. Реализация вычисления функции прибыли в MS Excel
Для оптимизации используем инструмент «Поиск решения». Настраиваем параметры поиска решения (рис. 3) следующим образом:
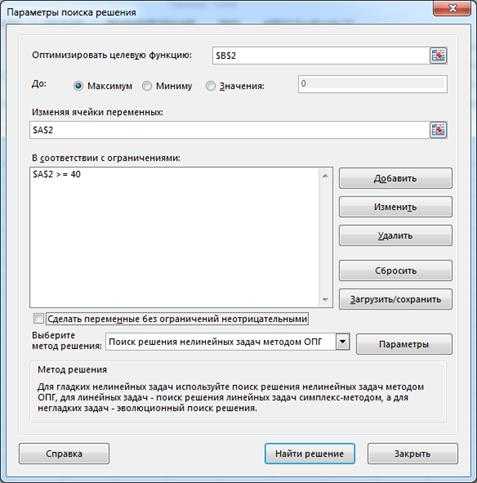
Рис. 3. Настройка инструмента «Поиск решения»
· в поле «Оптимизировать целевую функцию» указываем ячейку, где реализована формула для прибыли;
· в поле «До» указываем «Максимум»;
· в поле «Изменяя ячейки переменных» указываем ячейку, предназначенную для значения переменной ;
· в поле «В соответствии с ограничениями» добавляем ограничение невозможности большого увольнения ;
· состояние поля «Сделать переменные без ограничений неотрицательными» в нашей задаче безразлично, так как единственная переменная ограничена;
· в поле «Выберите метод решения» выбираем «Поиск решения нелинейных задач методом ОПГ» (так как наша задача нелинейная).
Нажав кнопку «Найти решение» получаем форму «Результаты поиска решения» (рис. 4). Убедившись, что в этом окне написано «Решение найдено. Все ограничения и условия выполнены», выбираем «Сохранить найденное решение» и нажимаем кнопку «Ок».
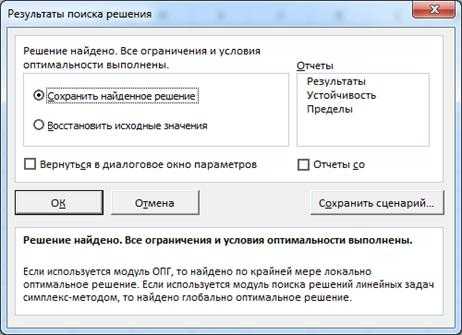
Рис. 4. Форма «Результаты поиска решения»
В ячейке переменной получаем оптимальное решение (рис. 5).
Рис. 5. Значения переменных после оптимизации
Как видим, нам удалось найти правильное решение автоматически.
Замечание: небольшое отличие значения в ячейке для искомой переменной от точного (получилось вместо ) обусловлено численной реализацией метода поиска. Это значение можно смело округлить с заданной точностью.
Важно отметить такую специфику решения нелинейных задач в MS Excel. Поиск решения методом ОПГ ищет значения переменных от начального заданного, обеспечивая постоянное улучшение результата с текущего места. Такая реализация приводит к поиску локального, а не глобального экстремума. Так, «начав» поиск от 70 рабочих мы нашли оптимальное значение 100 человек. Начав же, например, со 160 человек, получим «оптимальное» количество 150 (рис. 6). Выбрав же вначале 200 человек можно снова прийти к оптимальному значению 100.
Рис. 6. Изменение решения при смене начального приближения
Описанное свойство является характерным для большинства алгоритмов численного поиска оптимумов в задачах нелинейной оптимизации. Для того, чтобы получить действительно глобальный максимум необходимо попробовать определить оптимальное решение для нескольких начальных приближений (в задачах экономики они, как правило, выбираются легко из смысла задачи). В задачах с одной и двумя переменными очень помогает построение графиков.
megaobuchalka.ru
3.5. Примеры решения задач оптимизации.
В этом разделе рассмотрено решение типовых экономических задач в электронных таблицах MSExcel. Разумеется, что возможности электронных таблиц не ограничиваются решением задач планирования производства или штатного расписания, транспортной задачи и задачи о назначениях ресурсов. Любая задача, допускающая построение математической модели (см. предыдущий раздел), может быть проанализирована средствамиMSExcel. Заинтересованный читатель найдет дополнительные сведения о решении задач оптимизации в Приложении.
3.5.1. Транспортная задача
Предположим, что ваша фирма занимается производством и продажей продукции. Фирма владеет несколькими заводами, где эта продукция производится, и имеет ряд магазинов. Каждый завод обладает определенными производственными мощностями, а каждый магазин – объемом продаж товара. Для обеспечения высокой эффективности работы фирмы необходимо спланировать перевозки товаров так, чтобы транспортные затраты были как можно меньше. При этом требуется обеспечить вывоз всей продукции с каждого завода и полностью удовлетворить запросы каждого магазина. Для простоты будем полагать, что общий объем производства равен общему объему спроса (сбалансированная задача).
Для решения задачи построим ее математическую модель. Обозначим количество заводов N, а количество магазиновM. Для нумерации заводов и магазинов введем индексыiиj. Индексiпробегает целочисленные значения от 1 доNи указывает номер завода, индексjпринимает значения от 1 доMи соответствует номеру магазина. Объем производстваi-го завода обозначимai, объем спросаj-го магазина -bj. Условие баланса спроса и предложения имеет вид
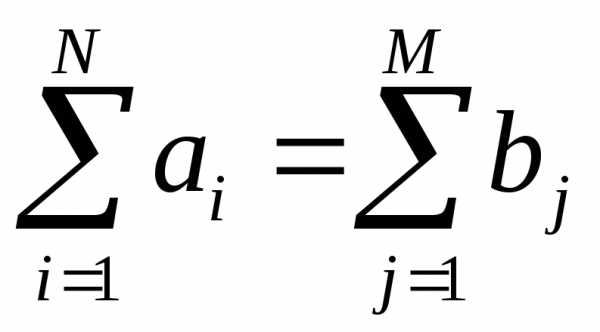 . (3.5.1)
. (3.5.1)
Неизвестными величинами в данной задаче являются объемы перевозок, которые мы обозначим xij. Величинаxij– это объем перевозок сi-го завода вj-й магазин. Затраты на перевозку единицы продукции из пунктаiв пунктjпо аналогии обозначимcij. Очевидно, что величиныxijиcijв нашей задаче могут принимать лишь неотрицательные значения
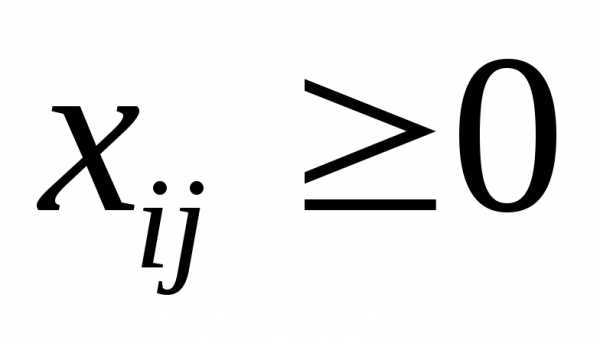 , (3.5.2.)
, (3.5.2.)
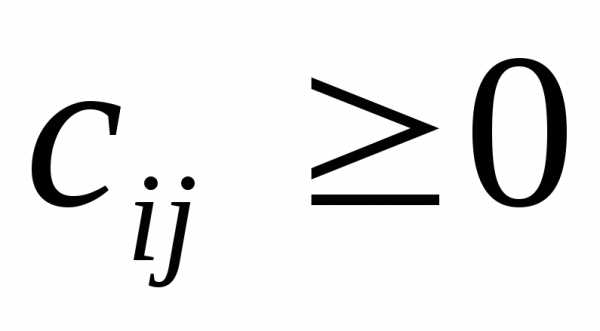 . (3.5.3)
. (3.5.3)
Стоимость одной перевозки составит xijcij, а общие транспортные расходыZбудут складываться из затрат по каждому маршруту:
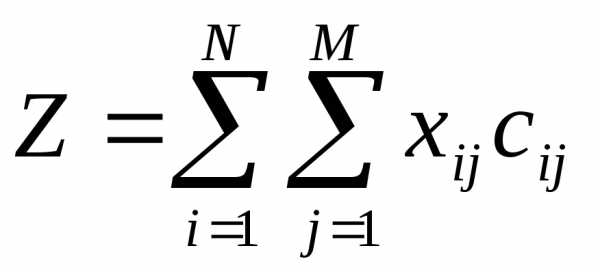 . (3.5.4)
. (3.5.4)
По условию задачи требуется минимизировать совокупные затраты на перевозки. В нашей модели оптимальному графику перевозок соответствует минимальное значение функции Z. Если не накладывать на величиныxijиcijдополнительных условий и попытаться минимизировать целевую функцию (3.5.4), то в результате мы получимZ= 0 иxij= 0. Такой результат, очевидно, не может быть удовлетворительным ответом. Для правильного решения поставленной задачи необходимо ввести ограничения на объемы вывозимой и ввозимой продукции. Объем вывозимой сi-го завода продукции должен быть равен объему производстваai, объем ввозимой продукции должен соответствовать объему спросаbj:
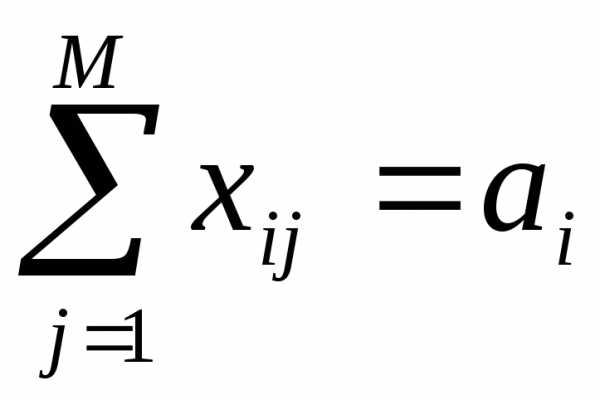 , (3.5.5)
, (3.5.5)
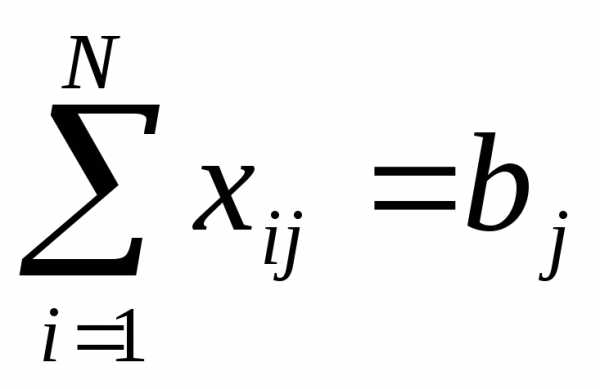 . (3.5.6)
. (3.5.6)
Выражения (3.5.1)-(3.5.6) составляют математическую модель сбалансированной транспортной задачи. Если спрос и предложение не сбалансированы, то в модель нужно ввести фиктивные пункты производства или пункты потребления. В случае дефицита вводится фиктивный завод, стоимость и объем перевозок с которого равны штрафу за недопоставку и объему недопоставки соответственно. В случае перепроизводства продукции вводится фиктивный магазин, стоимость и объем перевозок в который полагается равной стоимости складирования и объему излишней продукции соответственно.
Рассмотрим решение сбалансированной транспортной задачи средствами MSExcel. Пусть имеется 3 завода (N=3) и 4 магазина (M=4). Введем в рабочий лист данные об объемах производства и спроса как показано на рис. 3.15. Для проверки баланса (выражение (3.5.1)) просуммируем значения в диапазонахB4:B6иG4:G7, затем сравним вычисленные суммы в ячейкеC10с помощью формулы
«=ЕСЛИ(B7=G8;"Задача сбалансирована";"Нарушен баланс!")».
Далее в диапазон B14:E16вводим данные о себестоимости перевозок между заводами и магазинами.
Для распределения объемов перевозок между экономическими объектами создадим таблицу «Объемы перевозок» (рис. 3.16). Для проверки условий (3.5.5) и (3.5.6) в ячейках B23:E23иF20:F22вычислим суммы строк и столбцов таблицы «Объемы перевозок». Суммы по столбцам соответствуют объемам ввозимой продукции, а по строкам – объемам вывозимой продукции. Значения объемов перевозок заранее неизвестны, для определенности в качестве начального приближения вводим в ячейкиB20:E22нулевые значения. Для вычисления целевой функции (3.5.4) введем в ячейкуE25формулу
«=СУММПРОИЗВ(B14:E16;B20:E22)».
Теперь рабочий лист содержит всю необходимую информацию для «Поиска решения». Выполним команду «Сервис|Поиск решения» и заполним поля открывшегося диалогового окна (рис. 3.17). Условия (3.5.2), (3.5.5) и (3.5.6) вводим в диалог «Поиск решения» в виде ограничений. Для корректного решения линейной задачи установим флажок «Линейная модель» (кнопка «Параметры»). После нажатия кнопки «Выполнить» «Поиск решения» находит оптимальный план перевозок грузов, показанный на рисунке 3.16.
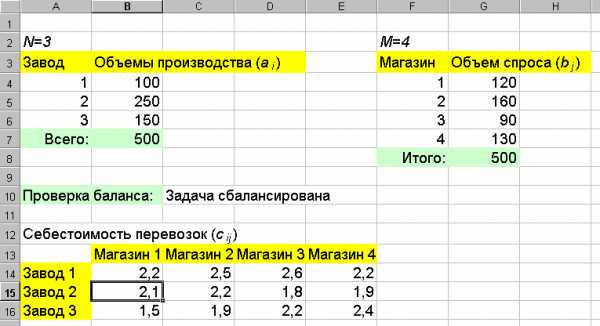
Рис. 3.15. Исходные данные транспортной задачи.
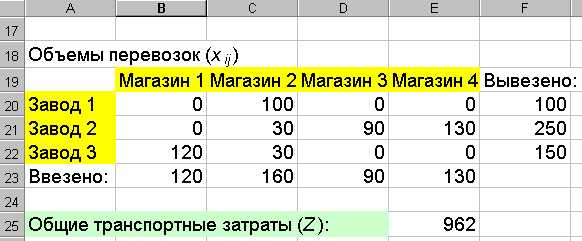
Рис. 3.16. Оптимальное решение транспортной задачи.
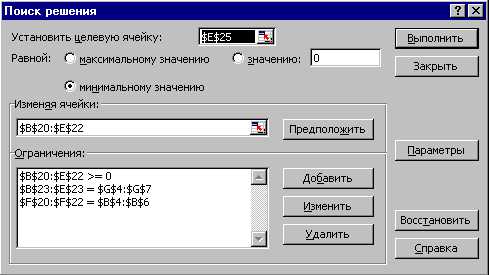
Рис. 3.17. Диалоговое окно «Поиск решения» для транспортной задачи.
studfiles.net
Пример задачи оптимизации - Энциклопедия по машиностроению XXL
В задаче оптимизации структуры сети электросвязи (пример 6,7) матрица [c.329]Для рещения задач частичной оптимизации и конструирования дополнительных расчетных связей типа (4.41) применяются те же методы, которые применимы к полным задачам оптимизации. Более конкретное представление о кибернетическом подходе к математическому моделированию дают два примера, приводимых ниже. [c.102]
С учетом изложенного основные понятия и формулировку задачи оптимизации ЭМУ целесообразно рассмотреть на примере параметрической оптимизации, а особенности решения этой задачи на других этапах проектирования будут рассмотрены в следующей главе. [c.143]
Если число пробных шагов принимается меньшим, чем количество параметров оптимизации и, то при определении направления поиска получается выигрыш по числу обращений к модели объекта проектирования для вычисления значений Q в сравнении с градиентным методом. Однако нужно иметь в виду, что уменьшение числа пробных шагов приводит к соответствующему уменьшению вероятности приближения к направлению градиента, а следовательно, к возможному увеличению количества рабочих шагов по определению экстремума функции цели. Как правило, при решении конкретных задач оптимизации ЭМУ существует оптимальное в заданных условиях количество пробных шагов, позволяющее определить приближение к искомому экстремуму 0 с приемлемыми затратами на поиск. В качестве примера на рис. 5.24 приведены зависимости от числа пробных шагов т колине- [c.159]Вместе с тем методы направленного поиска в силу заложенных в них при создании интеллектуальных возможностей позволяют существенно сократить время решения задач по сравнению с пассивным поиском. В ряде случаев такая экономия времени является существенно важной. Примером здесь может служить массовое решение задач оптимизации в условиях функционирования САПР, где даже небольшая экономия на решении одной задачи дает ощутимую общую выгоду. Поэтому понятно желание найти, способы преодоления недостатков этой группы методов. Рассмотрим некоторые из этих способов. [c.163]
Для получения балки наименьшего объема должна быть сформулирована задача оптимизации, что не является целью настоящего примера. Заметим лишь, что сама постановка задачи оптимизации балки является вариантной и в этой постановке требование равнопрочности не является обязательным. [c.191]
Рассмотренный простой пример примечателен тем, что п нем аналитическое решение удалось довести до конца. К сожалению, ато можно сделать лишь в немногих случаях. Часто задачи оптимизации оказываются аналитически неразрешимыми даже в аналогичных простых постановках. Так, при определении максимальной первой собственной частоты изгибных колебаний стержня заданной массы М,,, заделанного на одном конце и свободного на другом, уравнения движения и оптимальности имеют вид [356] [c.264]
В заключение параграфа укажем на пример акустической оптимизации, описанный в работе [112]. Рассматривалась задача- [c.273]
Оптимизация параметров по нескольким критериям качества. На практике нередко возникают задачи оптимизации когда нужно удовлетворять не одному, а одновременно двум или нескольким критериям качества. Например, во многих случаях желательно, чтобы оборудование АЭС (в том числе и теплообменные аппараты) имело по возможности малую массу (или стоимость) и малые габариты (объем). Если проектировать, к примеру, теплообменный аппарат с оребренными трубками, то может оказаться, что теплообменник минимальной массы (стои- [c.214]
Таким образом, содержащийся в сборнике материал основывается на разнообразных прикладных задачах машиностроения и приборостроения. Их основная цель оптимизировать трудоемкие и дорогостоящие процессы проектирования и расчета машин и механизмов. В связи с широким распространением в промышленности пневматической измерительной аппаратуры контроля и управления актуальной становится и задача оптимизации параметров пневматических регуляторов. Решению этих и других аналогичных задач и посвящается настоящий сборник. Решения иллюстрируются на конкретных примерах. Поэтому следует надеяться, что сборник будет полезен для широкого круга специалистов, работающих в области автоматизации научных исследований. [c.4]
Как следует из рассмотренного примера, при оптимизации решаемой задачи по всем наименованиям номенклатуры запасов в принимаемые решения вносятся значительные коррективы. Периодичность поставок во втором случае значительно меньше периодичности раздельных поставок материалов. При такой системе снабжения материалами значительно сокращаются и суммарные затраты на запасы в первом случае они составляют 92,5 руб/мес, во втором случае — 49,5 руб/мес. К такому выводу можно было прийти, используя формулу (161). [c.326]
Пример 7. Задача оптимизации соотношения толщин слоев металла h и термоизолятора h из условия минимума массы двухслойной стенки (см. рис. 4.10) сохраняет свой смысл и при установившемся температурном состоянии. В этом случае для температуры слоя металла из формулы (4.87) при т -> [c.186]
Важную роль при автоматизации измерений играют алгоритмы построения программных движений исполнительных механизмов КИР. Эффективным методом синтеза таких алгоритмов может служить метод параметрического синтеза и оптимизации, описанных в гл. 2. Проиллюстрируем преимущества этого метода на примере задачи автоматического перемещения каретки-стола из заданного начального состояния х в желаемое конечное состояние Будем искать программное движение в виде [c.299]
Оптимизация динамических режимов относится к наиболее сложны.м задачам из числа реализуемых управляющей подсистемой АСУ ТП. Примерами задач этого класса являются задачи на максимальное быстродействие, когда требуется перевести систему из одного состояния в другое за минимальное время, и задачи на минимальную стоимость, заключающиеся в минимизации стоимости действия системы на заданном интервале времени. Указанные цели соответствуют широкому кругу практических задач оптимизации. [c.461]
Ограничения на случайные величины также могут отсутствовать только при решении относительно простых задач оптимизации параметров узлов и элементов теплоэнергетических установок и неизбежно появляются в той или иной форме в случаях оптимизации более сложных объектов. Практически при решении задач оптимизации параметров и профиля теплоэнергетических установок имеют место все возможные виды ограничений на случайные величины ограничения в виде неравенств непосредственно на случайные величины, линейные и нелинейные относительно случайных величин зависимости в форме равенств и неравенств. Примером нелинейных неравенств могут быть ограничения па значения таких технологических узловых характеристик, как температура стенки труб теплообменника, которая является нелинейной функцией многих случайных величин, характеризующих процесс теплопередачи. [c.175]
Содержание разд. 4 Основные сведения по математике имеет самостоятельное значение для научных работников и специалистов, а также используется в других разделах данной справочной серии. Большое внимание уделено классическим методам математического анализа, теории функций комплексного переменного, уравнениям математической физики и т. д., т. е. именно тем методам, которые в настоящее время наиболее широко используются в исследованиях в теплотехнике. Наряду с традиционным материалом в разделе изложен ряд современных математических результатов. Примерами могут служить параграфы, в которых рассматриваются основы теории обобщенных функций, вычислительные методы, решение задач оптимизации и др., т. е. методы, находящие все большее применение в научных исследованиях, проектировании, планировании и управлении. Дополнительно включены такие сведения, как приближение сплайнами, метод конечных элементов и т. д. особое внимание уделено прикладной интерпретации процессов и результатов математической оптимизации. [c.8]
В качестве примера использования математического моделирования для решения задачи усовершенствования теплоэнергетической системы крупного промышленного предприятия ниже подробно рассмотрена задача оптимизации параметров и вида тепловой схемы ТЭС металлургического комбината полного цикла. [c.242]
Примерами задач такого типа являются определение целесообразных сроков разработки изделия выбор оптимального ряда изделий выбор наилучшего сочетания проектных параметров изделия сравнение вариантов облика создаваемого изделия сравнение двух стратегий поиска неисправностей в схеме выбор из нескольких структурных схем надежности схемы, обеспечивающей работоспособность при наибольшем числе отказов любых из ее элементов. Словом, к этому типу относятся задачи сравнения, упорядочения, оптимизации, причем последние всегда предполагают общую постановку. [c.483]
Общую постановку решения задачи оптимизации тонкостенных оболочек и особенности ее решения рассмотрим на примере трехслойной оболочки. Изложенный подход может быть применен для любой другой системы. [c.27]
Пятая и шестая главы книги носят иллюстративный характер и содержат примеры постановок и решения различных частных задач оптимизации оболочек вращения, работающих на устойчивость, в режиме колебаний или на прочность. [c.7]
ПРИМЕРЫ ПОСТАНОВКИ И РЕШЕНИЯ ВЫПУКЛЫХ ЗАДАЧ ОПТИМИЗАЦИИ ОБОЛОЧЕК ВРАЩЕНИЯ ИЗ КОМПОЗИТОВ [c.218]
Глава 5. Примеры постановки и решения выпуклых задач оптимизации [c.220]
Преимущество методов этой группы — простота и естественность формулировки принципа оптимальности векторной модели оптимизации при сохранении всех возможностей, предоставляемых предыдущей группой методов скаляризации. Недостатком является разрывный характер целевого функционала, что существенно ограничивает (даже в задачах малой размерности) возможности применения быстродействующих регулярных стратегий поиска оптимума. В [16, 107] приведены различные модификации целевых функционалов типа (4.111). Подробное обсуждение методов численной реализации примеров задач оптимизации конструкций вида (4.111) содержится в [107, 108]. [c.208]
Пример задачи оптимизации. Рассмотрим задачу оптимального проектирования элемента корпуса несущей конструкции, представляющего собой многослойную биспирально армированную цилиндрическую ( = 25 см, = 30 см) оболочку из стеклопластика, нагруженную гидростатическим внешним давлением дэ-Оболочка в процессе эксплуатации не должна терять устойчивости и выдерживать в течение конечного промежутка времени действующее давление. Таким образом, несущая способность оболочки определяется реализацией в к01Нструкции при заданных условиях докритического напряженно-дефор.мированного состояния. Критерий эффективности проекта — минимум массы оболочки. [c.259]
Другими интересными примерами задач оптимизации траектории являются задачи вывода спутника на орбиту. Если считать, что основные параметры и летные характеристики ракеты-носителя заданы, то, например, представляет интерес осуществить такой вывод спутника на орбиту, чтобы высота перигея была наибольшей, с целью предотвратить снижение, вызываемое аэродинамическим сопротивлением. В других случаях может потребоваться минимизировать высоту апогея, максимизировать среднее арифметическое апогея и перигея и т. длинейной функцией времени ). Для определения коэффициентов этой линейной функции приходится использовать тот или иной прием приближения, однако здесь, как и в задаче о максимальной дальности полета, главная ценность результата заключается в том, что он подсказыв ает характер функциональной зависимости ij) от [c.43]
Поэтому для решения задач оптимизации при проектировании объектов с дискретными значениями параметров методы оптимизации непрерывных объектов непосредственно неприменимы. Эти задачи относятся к задачам дискретного программирования. Если при оптимизации часть параметров дискретна, а часть имеет непрерывный характер, то задача должна решаться методами частично дискретного программирования. Из-за недифференцируемости выходных параметров в задачах дискретного программирования довольно часто возникают трудности при вычислениях. Рассмотрим пример задачи параметрического синтеза. [c.275]
В зависимости от вида ие.иевой функции, а также от вида ограничений суп1сствуют pa i личные методы оптимизации (методы дифференциального исчислении, методы множителей Лагранжа, методы пжейного и нелиней ного программирования, методы динамического программирования и т. д.). Пример исно, 1ь )ова ния метода множителей Лагранжа для некого рых задач оптимизации конструкций дан в кни ге (23], [c.53]
Весьма эффективно использование ЭВМ в задачах оптимизации параметров режимов сварки, например, по скорости охлаждения в заданном интервале температур (см. п. 7.4). Представленные в п. 7.4 случаи ограничены примерами использования формул для быстродвижущихся источников теплоты. Для уменьшения скоростей охлаждения металла часто специально понижают скорость сварки и в этом случае необходимо использовать формулы типа (6.26). Выразить в явном виде скорость охлаждения dTfdt при определенном значении Т не удается. Подбор оптимальных и и для обеспечения заданной скорости охлаждения в конкретном интервале температур, в особенности если еще ставится задача минимизации длительности пребывания металла выше определенной температуры, без ЭВМ практически невозможен. [c.202]
Методология расчетного проектирования ээлектромеханических преобразователей в САПР изложена в гл. 5. Общность рассмотренных методов и алгоритмов демонстрируется на двух примерах оптимизации расчетных проектов синхронных генераторов и бесконтактных сельсинов. Оба примера детально рассмотрены в [8]. Следует напомнить, что на стадии расчетного проектирования оптимизируются, в основном, конфигурация, обмоточные данные, размеры активной части ЭМП при заданных принципиальных конструктивных вариантах исполнения. Число варьируемых параметров исчисляется десятками, а количество расчетных.связей — сотнями, что делает задачу оптимизации весьма сложной и громоздкой. [c.200]
В качестве важной особенности ЭМУ как объекта оптимизации необходимо отметить большое количество ограничений как основных, так и вспомогательных. Это приводит к сложной конфигурации допустимой области изменения параметров, а также к существенным трудностям попада1ШЯ в нее, что в совокупности значительно усложняет поиск экстремума функции цели. При этом часто лучшим вариантам проекта соответствуют точки в пространстве параметров, лежащие на границе допустимой области. При этом задача оптимизации ЭМУ сводится к отысканию лишь условного зкстремума функции цели. Примеры такой ситуации показаны на рис. 5.15 и 5.16, где представлены области поиска соответственно при минимизации времени разгона асинхронного гиродвигателя с короткозамкнутой беличьей клеткой в пространстве параметров к(кратность максимального момента) и при оптимизации на максимум КПД (р) асинхронного конденсаторного микродвигателя [19] в пространстве параметров к — коэффициента трансформации и Хном номинального скольжения. [c.147]
Часто предварительное исследование практических задач проектирования ЭМУ позволяет упростить поиск оптимального управления и свести его к статической оптимизации. Рассмотрим такую возможность на примере задачи определения оптимального управления асинхронным двигателем (J =780 г M ,d =4,4 см, с =60000об/мин) в процессе разгона. Целью управления является минимизация времени разгона до номинальной частоты вращения П ом- При этом в качестве параметров управления используются значение и частота напряжения питания. Координатами состояния объекта являются частота вращения ротора I2 и ток статора /). При этом накладываются ограничения на значение напряжения ([/ [c.225]
Сопоставление расчетов с экспериментальными результатами разных авторов, относящихся к диффузорам с прямоугольными и криволинейными образующими, показывает удовлетворительную корреляцию, поэтому в одиннадцатой главе на основе описанного метода исследуются конкретные вопросы оптимизации диффузоров. Для поиска оптимальных конфигураций используется оптимальное управление заданного вида (ОУЗВ), в результате чего задача оптимизации сводится к задаче нелинейного математического программирования. Показаны индивидуальные особенности рассматриваемой задачи, а также новые улучшения ОУЗВ. Приводятся характерные формы оптимальных диффузоров и физическая картина движения в них. Показано влияние различных факторов (профиля скорости, габаритов и т.п.) на изменение формы оптимальных диффузоров. Даны конкретные примеры существенного улучшения гидро- и аэродинамического качества диффузоров за счет оптимизации. [c.9]
Оптимизация периодического контроля в одноканальных однофазных системах с непополняемым резервом времени. Задача оптимизации периодического контроля возникает при действии двух факторов возможности, появления в системе или отдельных ее устройствах скрытых (латентных) отказов и частичном или полном обесценивании результатов предыдущей работы, вызванном использованием неисправного оборудования. Обнаружение скрытых отказов производится с помощью периодических сеансов диагностирования. Вероятность обнаружения отказа в каждом сеансе (полнота диагностирования) зависит от длительности сеанса и становится равной единице только при использовании полного теста. Примерами устройств в составе энергосистем, обладающих скрытыми отказами и требующих периодического диагностирования, являются многие устройства системной автоматики автоматические регуляторы частоты (АРЧ), перетока (АРП), автоматические ограничители перетока (АОП), управляющие вычислительные комплексы (УВК), релейные блоки противоаварийной автоматики и др. [11]. [c.310]
Наряду б усовершейСтЁованйем йуЩестйуюЩйх методов утилизации широкие перспективы для эффективного использования ВЭР открываются при энерготехнологическом теплоиспользовании. Уже в настоящее время в ряде отраслей промышленности в технологических процессах производства промышленной продукции созданы н продолжают разрабатываться новые типы энерготехнологических установок, позволяющих осуществить решение задач оптимизации технологических процессов в сочетании с их высокой энергетической эффективностью. Рассмотрим лишь некоторые примеры, иллюстрирующие те основные положения, которые лежат в основе разработок новых конструкций энерготехнологических установок. [c.184]
Примеры. 1. Расчет овтималь-ных рядов силовых узлов, в случае, когда функция спроса задана в явном виде, а число возможных вариантов рядов сравнительно невелико, задача оптимизации параметрических рядов силовых головок может быть решена методом полного перебора всех возможных вариантов тииажа. [c.174]
Таким образом, на каждом этапе решается задача оптимизации по одному постоянному параметру, тогда как все другие уровни кусочнопостоянной аппроксимации коэффициента теплопроводности либо не требуются совсем, либо уже определены на предыдущих этапах решения. Подробности методики расчета, а также иллюстративные примеры приведены в работе [Л. 3-4]. [c.345]
После априорного выбора схемы тока и типа поверхности теплообмена регенератора оптимизацию его режимноконструктивных параметров необходимо вести в рамках общей задачи оптимизации ПТУ. Рассмотрим особенности математического моделирования, а также постановки и решения этих задач на примере регенератора паротурбинной установки, критерием качества которой служит максимум эффективного КПД. Как отмечалось выше, этот критерий, являясь частным случаем критерия минимума приведенных затрат, справедлив для широкого круга наземных стационарных, транспортных, подводных, а также космических установок с радиоизотопным источником теплоты. [c.120]
Рассмотрим применение к задаче оптимизации долгосрочных режимов ГЭС метода динамического программирования, разработанного американским математиком Р. Веллманом [Л. 4]. Практические аспекты метода изложены в [Л. 13], суть его иллюстрируется ниже на примере оптимизации долгосрочных режимов одиночной ГЭС, работающей параллельно с тепловыми станциями. [c.37]
В главе 13 подробно рассматривается оптимизация, начиная с формулировки задачи оптимизации. Собственно оптимизация и является основой процесса проектирования конструкции. Мощные средства анализа конструкций профам-мы NASTRAN являются лишь ядром средств оптимизации. Интерфейс FEMAP открывает доступ не ко всем возможностям аппарата оптимизации NASTRAN, однако приведенные примеры построения моделей анализа и оптимизационных моделей тонкостенных конструкций позволяют читателю изучить эту важную область. [c.17]
Рассмотрим примеры постановки задач оптимизации и структурного синтеза для решения генетическими методами. В каждом из представленных ниже классов задач при использовании НСМ можно получить значительно лучшее приближение к экстремуму по сравнению с альтернативными одноэвристическими методами. [c.190]
Пример 2. Проведем параметрическую оптимизацию линейной системы, рассмотренном в примере I. На основание действует виброускоренне, представляющее собой стационарнып случайный процесс типа белого шума со спектральной плотностью Н- >2л. Задачу оптимизации ставим для условий (4). В качестве ограничиваемого и минимизируемого функционалов выбраны дисперсии (16) и (15) при При расчете дисперсий воспользуемся таблц- [c.316]
Пример 3. Рассмотрим задачу оптимизации нелинейной характеристики демпферов, установленных на всех колесах восьмиколесной машины типа МАЗ-543 с торсионной подвеской. Оптимизация производится для грунтовой дороги с дисперсией 36 см- . Корреляциоц 1ые функции и спектральные плотности возмущений, соответствующие различным скоростям движения по этой дороге, а также принятые при расчетах параметры машины МАЗ-543 приведены в работе [226]. [c.316]
В книге рассматриваются современные модели расчета и методы параметрической оптимизации несущей способности оболочек вращения из композитов двумерной и пространственной структур армирования. Основное внимание при этом уделено оболочкам, работающим на статическую устойчивость или в режиме колебаний, эффективные деформативные характеристики которых определяются методами теории структурного моделирования композита. В задачах, содержащих оценки предельных состояний оболочек по прочности, используется феноменологическая структурная модель прочностных характеристик слоистого композита, параметры которой получены экспериментально. Подробно анализируются особенности постановки задач пара.метрической оптимизации оболочек из композитов. Показана взаимосвязь векторной и скалярной моделей задач оптимизации в случае формализуемых локальных критериев качества проекта. Значительное место отведено изложению и примерам приложения нового метода решения задач оптимизации оболочек из. многослойных композитов — метода обобщенных структурных параметров, применение которого позволяет получить наиболее полную информацию об опти.чальных проектах широкого класса практически важных задач оптимизации. Содержащиеся в книге результаты могут быть использованы для инженерного проектирования оболочек из волокнистых композитов. Табл. 23, ил. 58, библиогр. 181 назв. [c.4]
Дальнейщее изложение вопросов, связанных с постановкой и методами решения задач оптимизации несущих конструкций, будем строить для класса задач оптимизации пространственно илн двумерно армированных слоистых оболочек, работающих на устойчивость (примеры их решения составляют основное содержание заключительных глав монографии). [c.175]
По отношению к задачам оптимизации многослойных оболочек, решаемых в постановке 5 = 0, т. е. с фиксированным набором углов укладки монослоев в пакете, метод ОСП может использоваться как средство диагностики оптимальных решений. Поясним сказанное следующим примером. Пусть некоторая модель оптимизации оболочки Ме определена в классе композитов Пл- , причем углы укладки монослоев в элементарных пакетах могут принимать значения из фиксированного набора, например Фз= 0° гЬ45° 90° . Множество 5е структурных ограничений модели Ме в рассматриваемой постановке задачи оптимизации (5 = 0) определяется системой из трех неравенств [c.198]
Тестовый пример. При расчете оболочек сложных геометрических форм (в частности, тороидальных) наибольшим предпочтением пользуется метод конечных элементов (МКЭ). Специфической особенностью МКЭ в задачах опти.мизации конструкций является необходи.мость предварительной апробации конкретной методики расчета на соответствующем решаемой задаче упрощенном тестовом примере с целью оценки параметров сходимости алгоритма расчета функций предельных состояний конструкции и выбора оптимальной, в смысле объема вычислительных затрат, схемы разбиения оптимизируемой конструкции на конеч1Ные элементы (число элементов А эл, геометрия элементов и т. п.). Поэтому, прежде чем рассматривать постановку и результаты рещения сформулированной задачи оптимизации, коротко остановимся на результатах решения тестовой задачи о потере устойчивости упругой изотропной тороидальной оболочки кругового поперечного сечения, нагруженной гидростатическим внешним давлением (рис. 5.2). Методика решения реализует вариант МКЭ, сформулированный в перемещениях для специального конечного элемента вращения, учитывающего поперечный сдвиг и обжатие нормали в оболочке. [c.225]
mash-xxl.info
Глава 2. Примеры задач оптимизации.
Поиск ЛекцийНаиболее часто встречающиеся типы задач оптимизации – это
1) Производственная задача
2) Внешнеторговая задача
3) Транспортная задача
4) Задача о рациональных смесях (диете)
5) Задача распределения по должностям
Рассмотрим примеры некоторых типов задач оптимизации.
Производственная задача.
Условие задачи:
Мебельная фабрика специализируется на производстве столов, столов, стульев и табуреток. Затраты на производство одного стола составляют 0,08 м3 древесина, и на это потребуется 8 человеко-часов, причём доход от его продажи составит 1500 рублей. Затраты на производство одного стула – 0,02 м3 древесины, на это потребуется 7 человеко-часов, доход от его производства составляет 1200 рублей. Затраты на производство одной табуретки составляет 0,01 м3 древесины, 3 человеко-часа и доход от его продажи составит 500 рублей. Ресурсы ограничены и составляют 10 м3 древесины и 880 человеко-часов. Задача – произвести продукцию в таком объёме, чтобы прибыль оказалась максимальной.
Пусть x – количество столов,
y – количество стульев,
z – количество табуреток.
Допущения в модели оптимизации:
- цены не зависят от объёма производства;
- норма затрат не зависит от объёмов производства.
| Доход (руб) | Расход древесины (м3) | Трудозатраты (чел/час) | |
| Столы | 0,08 | ||
| Стулья | 0,02 | ||
| Табуретки | 0,01 |
Целевая функция:
1500x+1200y+500z → max
Решим систему:
1500x+1200y+500z → max
0,08x+0,02y+0,01z ≤ 10
8x+7y+3z ≤ 880
x, y, z ≥ 0
x, y, z – целые числа
Ответ: x=12, y=0, z=1
Итак, чтобы прибыль мебельной фабрики оказалась максимальной необходимо производить продукцию в следующих объёмах. Надо производить 12 столов и 1 табуретку, а также необходимо отказаться от производства стульев.
Внешнеторговая задача
В моделях оптимизации внешней торговли ограничительные условия отражают специфику отрасли и делятся, как правило, на две группы: условия внешнеторговой деятельности, связанные с внутренними возможностями страны или фирмы, и условия, определяемые внешними рынками. К первой группе можно отнести имеющиеся материальные финансовые средства, выделенные экспортные фонды, мощности по производству экспортных товаров, потребности в импорте. Вторая группа ограничительных факторов учитывает экономико-политические цели и включает ограничения, связанные с международными соглашениями, валютные ограничения, возможности сбыта и закупок товаров на внешних рынках и т.п. В качестве критерия оптимальности решения в задачах оптимизации внешней торговли может быть выбрана, например, цель – максимизация валютной выручки от экспорта или минимизация затрат на производство экспортных товаров и т.п.
Условие задачи.
Страна поставляет товары А, В и С на рынки I, II, III. Причём ёмкость рынка I по товару А составляет 30 тыс. единиц продукции, которая покупается по цене $130. Ёмкость рынка II по товару А составляет 27 тыс. единиц продукции, которая покупается по цене $390 за единицу продукции. На рынке III – неограниченный спрос на товар А, причём его покупают по цене $80 за единицу продукции. Ёмкость рынка I по товару В составляет 22 тыс. единиц продукции, которая покупается по цене $390 за единицу продукции. Ёмкость рынка II по товару В составляет 8 тыс. единиц продукции, которая покупается по цене $250 за единицу продукции. На рынке III продукция В спросом не пользуется. Ёмкость рынка I по товару С составляет 35 тыс. единиц продукции, которая покупается по цене $170 за единицу продукции. Ёмкость рынка II по товару С составляет 30 тыс. единиц продукции, которая покупается по цене $190 за единицу продукции. На рынке III – неограниченный спрос на товар С, который покупается по цене $120 за единицу продукции. Кроме того, страна импортирует товары D, E и F с рынков I, II и III. Максимальное предложение на рынке I по товару D составляет 820 тыс. единиц продукции, которая продаётся по цене $7,3 за единицу продукции. Максимальное предложение на рынке II по товару D составляет 600 тыс. единиц продукции, которая продаётся по цене $10,5 за единицу продукции. Максимальное предложение на рынке III по товару D составляет 930 тыс. единиц продукции, которая продаётся по цене $5,8. Товар Е на рынке I не продаётся. Максимальное предложение на рынке II по товару E составляет 370 тыс. единиц продукции, которая продаётся по цене $12,2 за единицу продукции. Максимальное предложение на рынке III по товару E составляет 120 тыс. единиц продукции, которая продаётся по цене $8,1 за единицу продукции. Товар F на рынке имеет неограниченное предложение, и продаётся по цене $6,1 за единицу продукции. Товар F на рынке II имеет неограниченное предложение, и продаётся по цене $9,3 за единицу продукции. Товар F на рынке III не продаётся. При этом существует договор, по которому страна не имеет права экспортировать товар А более 42 тыс. единиц, товар В – 80 тыс. единиц, товар С – 70 тыс. единиц. Кроме этого, существует ограничение на импорт: количество товара D по всем рынкам не должно превышать 1800 тыс. единиц товара, товар Е должен быть закуплен в количестве не более 250 единиц, а по товару F ограничений нет. Помимо этого, объём продаж на рынке I должен быть не меньше 50 тыс. единиц, объём закупок на рынке II должен быть не больше 1000 тыс. единиц, а на рынке III объём продаж товарами должен равняться объёму закупок. Задача – максимизировать валютную выручку от экспорта.
| Товар А | Товар В | Товар С | Товар D | Товар Е | Товар F | |
| Экспорт | Импорт | |||||
| Цена ($) Ёмкость рынка (тыс ед.) | ||||||
| Рынок I | 7,3 | 6,1 ∞ | ||||
| Рынок II | 10,5 | 12,2 | 9,3 ∞ | |||
| Рынок III | ∞ | ∞ | 5,8 | 8,1 |
Обозначим через хik объем продажи k-ого товара на i- ом рынке.
Пусть x11 – объём продажи товара А на рынке I,
x21 – объём продажи товара А на рынке II
x31 – объём продажи товара А на рынке III
x12 – объём продажи товара B на рынке I
x22 – объём продажи товара B на рынке II
x32 – объём продажи товара B на рынке III
x13 – объём продажи товара C на рынке I
x23 – объём продажи товара C на рынке II
x33 – объём продажи товара C на рынке III
x14 – объём продажи товара D на рынке I
x24 – объём продажи товара D на рынке II
x34 – объём продажи товара D на рынке III
x15 – объём продажи товара E на рынке I
x25 – объём продажи товара E на рынке II
x35 – объём продажи товара E на рынке III
x16 – объём продажи товара F на рынке I
x26 – объём продажи товара F на рынке II
x36 – объём продажи товара F на рынке III
Целевая функция:
130x11+160x21+80x31+390x12+250x22+170x13+190x23+120x33 – 7,3x14 – 10,5x24 –5,8x34 – 12,2 x15 – 8,1 x35 – 6,1x16 – 9,3x26 → max
Ограничения по объему экспортного рынка:
x11 ≤ 30
x21 ≤ 27
x12 ≤ 22
x22 ≤ 8
x13 ≤ 35
x23 ≤ 30
Ограничения по объему импортного рынка:
x14 ≤ 820
x24 ≤ 600
x34 ≤ 930
x25 ≤ 370
x35 ≤ 120
Ограничения по объему экспорта:
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
Ограничения по объему импорта:
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
Ограничения по рынкам:
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Решим систему уровнений:
130x11+160x21+80x31+390x12+250x22+170x13+190x23+120x33 – 7,3x14 – 10,5x24 –5,8x34 – 12,2 x15 – 8,1 x35 – 6,1x16 – 9,3x26 → max
x11 ≤ 30
x21 ≤ 27
x12 ≤ 22
x22 ≤ 8
x13 ≤ 35
x23 ≤ 30
x14 ≤ 820
x24 ≤ 600
x34 ≤ 930
x25 ≤ 370
x35 ≤ 120
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Подготовим задачу к решению на компьютере.
Матрица условий задачи

Ответ:
x11=15, x21=27, x31=0, x12=22, x22=8, x32=0 (по условию задачи), x13=35, x23=30, x33=1,94452, x14=0, x24=0, x34=37,997, x15=0 (по условию задачи), x25=0, x35=1,6, x16=0, x26=0, x36=0 (по условию задачи)
Итак, чтобы максимизировать валютную выручку от экспорта необходимо, чтобы товары экспортировались и импортировались в следующих объёмах. Объём продажи товара А на рынке I должен составлять 15 тыс. единиц продукции; объём продажи товара А на рынке II - 27 тыс. единиц продукции; в то же время, на рынок III поставка товара А не должна осуществляться. Товар В на рынок I должен поставляться в количестве 22 тыс. единиц продукции; на рынок II товар В надо поставлять в количестве 8 тыс. единиц продукции; на рынок III товар В поставляться не будет по условию задачи. Объём продажи товара C на рынке I должен составлять 35 тыс. единиц продукции; объём продажи товара C на рынке II - 30 тыс. единиц продукции; объём продажи товара C на рынке III – 1,94452 тыс. единиц продукции. Товар D не должен импортироваться на I и II рынки, а на рынок III товар D должен импортироваться в объёме 37,997 тыс. Товар Е на рынок I не будет импортироваться по условию задачи; на рынок II товар Е тоже не должен импортироваться; на рынок III товар Е надо импортировать в объёме 1,6 тыс. единиц продукции. Товар F на рынок III не импортируется по условию задачи. На рынки I и II товар F также импортировать не следует.
Заключение
На всех стадиях жизненного цикла предприятия, организации, фирмы приходится принимать множество решений. Любой предприниматель в ходе своей деятельности стоит перед проблемами выборами источников финансирования, задачи подбора помещения, найма работников, выбора стратегии предприятия, партнёров, источников сырья, проблемами сбыта продукции. Все решения этих сложных проблем приходится принимать в условиях недостатка информации и времени. Экономико-математические методы моделирования задач принятия решения помогут найти оптимальные решения. С помощью компьютерной техники, имея определённую модель, которая отражает основные свойства объекта и ситуации, можно рассмотреть различные варианты решений и определить оптимальное решение.
Список литературы:
1. Н.В. Сернова, В.М. Гордуновский, Е.С. Котова Количественные методы принятия решений в бизнесе. М.: Издательский центр «Анкил», 1997.
2. Н.В. Сернова, В.М. Гордуновский, С.Ю. Самохвалов «Балансовые и оптимизационные модели принятия решений». М.: 2003
poisk-ru.ru
29.Задача дискретной оптимизации, пример (постановка задачи и ее эмм).
Целочисленное программирование изучает задачи, в которых на искомые переменные накладываются условия целочисленности, а ОДР конечна.
Задача о ранце.
Постановка: Организация арендует баржу грузоподъемностью 83т на которой предполагает перевозить груз, состоящий из предметов 4 типов. Веса и стоимости предметов равны соответственно 24т,22т,16т,10т и 96у.е.,85у.е.,50у.е.,20у.е. Требуется погрузить на баржу груз максимальной стоимости. ЭММ: Введем обозначения. Пусть Xj, j=1,4 число предметов j-того типа, которое следует погрузить на баржу. С учетом этих обозначений ЭММ задача о подборе для баржи допустимого груза максимальной ценности записывается:
Max f(x1,x2,x3,x4)=96x1+85x2+50x3+20x4
24x1+22x2+16x3+10x4 ≤ 83
xj, j=1,2,3,4 – неотрицательное целое число.
Это модель типа 1а2б3а4а5а – т.е. модель целочисленного (дискретного) линейного программирования. Реализация этой модели средствами EXCEL позволяет получить решение: 1. X1*=3 x2*=0 x3*=0 x4*=1 2.maxf(x)=308y.e.
30.Экономико-математическая модель межотраслевого стоимостного баланса (модель Леонтьева).
ЭММ межотраслевого баланса представляет собой систему уравнений, отражающих функциональную зависимость включенных в его систему элементов:
Х1=Х1,1 + Х1,2 +……+ Х1n + Y1
X2=X2,1 + X2,2 +…….+ X2,n + Y2
Xn = Xn,1 + Xn,2 +……+Xn + Yn
Где Х =(Х1, Х2,…, Хn) – вектор валовой продукции, Y =(Y1, Y2,…,Yn) – вектор конечной продукции (конечное потребление и накопление), Хij – производственные материальные затраты j-й отрасли, с учетом обозначений: Aij = Xij / Xj, Xij =AijXj.
Система уравнений перепишется в виде:
Х1=А1,1*Х1,1 + А1,2*Х1,2 +…..+ А1,n*X1,n + Y1
X2=A2,1*X2,1 + A2,2*X2,2+…..+A2,n*X2,n + Y2
Xn=An,1*Xn,1 + An,2*Xn,2 +…..+An,n*Xn,n +Yn
Или в более компактном виде: Xi = ∑Aij*Xj + Yi, где i=от 1, до n.
Запись в матричной форме: Х = АХ + Y, где А=(Аij) размерностью n*n
Именно в этих двух формах записи и используется ЭММ межотраслевого баланса, которую называют моделью Леонтьева. Элементы Аij матрицы А называют коэффициентами прямых (материальных) затрат. Это – затраты i-й отрасли на единицу (рубль) валовой продукции j-й отрасли. В матричной форме модель Леонтьева записывается Х-АХ=Y или (Е-А)Х=Y.
31.Матрица прямых материальных затрат, ее продуктивность. Признаки продуктивности.
По ЭММ Леонтьева (Е-А)X=Y можно определить объемы валовой продукции отрасли Х1, Х2, …, Хn по заданным объемам конечной продукции: Х = (Е-А)‾¹ Y; X=BY, B=(E-A)‾¹. Элементы Bij обратной матрицы B = (E-A)‾¹ называются коэффициентами полных (материальных) затрат, т.е. это затраты i-й отрасли на каждый рубль конечной продукции отрасли j. Соответственно матрицу В называют матрицей коэффициентов полных затрат, а матрицу А – матрицей коэффициентов прямых затрат. Неотрицательную матрицу А (А≥0) называют продуктивной, если существует хотя бы один такой положительный вектор Х>0, что каждый объект может произвести некоторое количество конечной продукции. Для продуктивности матрицы А необходимо и достаточно, что бы выполнялось одно из перспективных условий: 1) матрица (Е-А) неотрицательно обратима, т.е. существует обратная матрица (Е-А)‾¹ и все ее элементы неотрицательны, 2) положительны все главные миноры матрицы (Е – А), 3) матричный ряд
Е + А + А² + … + =∑А® сходятся, причем ∑А®=(Е-А)‾¹. 4) максимальное собственное число матрицы А меньше 1, т.е. Λ(А) < 1. Собственными значениями (числами) квадратной матрицы А называются корни (решения) характеристического уравнения | А-λЕ |=0.
studfiles.net