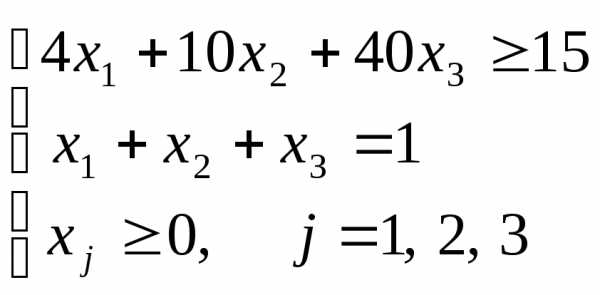Решение задач оптимизации в excel. Оптимизация в excel

Урок №14 Информатика и икт тема: Оптимизация решений в Excel

11 класс Урок №14

Информатика и ИКТ

ТЕМА: Оптимизация решений в Excel.

Цель: --- Познакомить учащихся с понятием оптимизации, сферами применения. Оптимизация решений в Excel.

--- Развитие навыков оптимизации решения в Excel. Использование оптимизации на практике.

--- Воспитывать информационную культуру.

Ход урока:

1. Оргмомент: --- цель урока

--- план урока

--- инструктаж ТБ №68

2. Изучение нового материала:

--- сегодня на уроке мы познакомимся с понятием оптимизации, и рассмотрим оптимизацию решений в Excel. Практическое применение в жизни.

--- свое сообщение нам прочитает Черников Павел. (индивидуальное домашнее задание).

--- итак оптимизация – процесс поиска наиболее оптимального пути решения.

Значение целевого параметра зависит от множества параметров. Такую зависимость описывает целевая фикция

K=F(X1,X2,…….Xn)

K – значение целевого параметра

X1,………Xn – параметры влияющие на развитие системы.

Оптимизация используется в экономическом моделировании, проектировании и многих других отраслях народного хозяйства.

--- В качестве примера рассмотрим задачу поиска вариантов оптимального раскроя листов материала на заготовки определенного размера.

--- В ходе производственного процесса из листов материала получают заготовки деталей двух типов различными способами, при этом количество получаемых заготовок при каждом методе различается.

Способы раскроя заготовок

Тип заготовки	Количество заготовок
Тип заготовки	Способ 1	Способ 2	Способ 3
А	10	3	8
Б	3	6	4

(таблица дается на доске)

--- Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.

--- Формальная модель.

Параметрами, значения которых необходимо определить, являются количества листов материала, которые будут раскроены различными способами:

Х1 – количество листов, раскроенные способом 1;

Х2 – количество листов, раскроенные способом 2;

Х3 – количество листов, раскроенные способом 3;

Тогда целевая функция, значением которой является количество листов материала, примет вид: F=X1+X2+X2

Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количества заготовок, получаемых различными способами, должны выполняться два равенства:

10Х1+3Х2+8Х3=500

3Х1+6Х2+4Х3=800

Кроме того, количества листов не могут быть отрицательными, поэтому должны выполняться неравенства: Х1>=0; Х2>=0; Х3>=0;

Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение.

--- Будем искать решение задачи путем создания и исследования модели в (оптимизации) электронных таблицах.

3. Практическая работа:

--- Создание таблицы в соответствии с параметрами задачи.

(смотреть файл оптимизация пример в папке 11 класс на рабочем столе).

Занести в ячейки формулы:

В4=B2+C2+D2 В7=10*B2+3*C2+8*D2 В8=3*B2+6*C2+4*D2

--- Выполнение гимнастики для глаз.

--- Исследование модели.

Для поиска оптимального набора решений значений параметров, который соответствует минимальному значению целевой функции, воспользуемся надстройкой электронных таблиц Поиск решения.

--- Для активации надстройки ввести команду (Сервис – Надстройки). На диалоговой панели установить флажок перед элементом списка (Поиск решения).

--- Ввести команду (Сервис – Поиск решения). На появившейся диалоговой панели Поиск решения установить:

--- адрес целевой ячейки

--- вариант оптимизации значения (минимизация).

--- адреса ячеек, значения которых изменяются в процессе поиска решения (в которых хранятся значения параметров).

--- ограничения (типа = для ячеек, хранящих количество деталей, и типа >= для параметров количества заготовок).

--- Щелкнуть по кнопке Выполнить. В ячейке целевой функции появиться значение количества листов, а в ячейках параметров значения листов.

--- Таким образом для изготовления 500 деталей А и 300 деталей Б требуется

_____листов материала. При этом _____необходимо раскроить по первому, _____по второму, _____по третьему варианту.

--- В оставшееся время Коваленко, Сингуров, Черников выполняют индивидуальные задания (изменение параметров задачи и анализ результата).

Болдинов, Неупокоев, продолжают выполнение своих проектов. Чесноков работает под руководством учителя.

4. Итог:

--- оптимизация – процесс поиска наиболее оптимального пути решения.

--- применение оптимизации.

--- реализация оптимизации при решении задач в Excel.

5. Домашнее задание:

--- параграф 5.10 учебника

--- Коваленко готовит сообщение на тему «Статистические задачи и использование Excel для их решения.

Оптимизация пример.

Практическое задание

Сообщение оптимизация

Оптимизация. Оптимизационное моделирование в экономике.

В сфере управления сложными системами (например, в экономике, проектировании) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.

Критерием оптимальности могут быть различные параметры; например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.

Развитие сложных систем зависит от множества факторов (параметров), следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция.

K=F(X1,X2,…….Xn) записать на доске

где K – значение целевого параметра

X1,Х2,………Xn – параметры влияющие на развитие системы.

Цель исследования состоит в нахождении экстремума функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами.

Однако часто целевая функция линейна и, соответственно, экстремумов нет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. (Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения).

gigabaza.ru

Решение задач оптимизации в excel

Решение задач оптимизации в EXCEL`е

Введение. Для решения задач поиска корней уравнения или где требуется отыскать оптимальное решение (например, дающее минимальное или максимальное значения), удовлетворяющее при этом целому ряду дополнительных условий на значения используемых параметров. Для решения таких задач, требующих применения методов, нелинейного программирования (управления), является имеющаяся в MS Excel Надстройка "Поиск решения". Задачи линейного программирования возникают, например, при планировании перевозок, распределения производственных ресурсов, оптимизации структуры производства и т.п.

Активация и использование надстроек

Надстройки – это компоненты Microsoft Excel, предоставляющие доступ к дополнительным функциям и командам. Двумя из наиболее популярных надстроек являются "Пакет анализа" и "Поиск решения", которые реализуют функции расширенного анализа данных. Чтобы использовать эти надстройки, их необходимо установить и активировать.

Ниже описан порядок установки и активации надстроек "Пакет анализа" и "Поиск решения", а также даны инструкции, позволяющие приступить к анализу данных с их помощью. Тот же порядок действий применим к установке и активации многих других надстроек. У некоторых других надстроек (например, продуктов сторонних производителей) могут быть собственные программы установки.

Установка и активация надстроек "Пакет анализа" и "Поиск решения"

Откройте вкладку Файл.
Нажмите кнопку Параметры и выберите категорию Надстройки.

Убедитесь, что в нижней части диалогового окна Параметры Excel в поле Управление выбран элемент Надстройки Excel, и нажмите кнопку Переход.
В диалоговом окне Надстройки установите флажки Пакет анализа и Поиск решения и нажмите кнопку ОК (см. рис. 1б).
Если отобразится сообщение о том, что надстройку не удается запустить, и выведется предложение установить ее, нажмите кнопку Да, чтобы установить надстройку.

Рис. 1а. Окно Настройки

Примечание. Поскольку в этом случае устанавливаются две надстройки, приглашение установить надстройку будет показано дважды: первый раз для пакета анализа и второй для надстройки "Поиск решения".

Обратите внимание, что на вкладку Данные добавлена группа Анализ, которая находится справа. Она содержит кнопки команд для надстроек Анализ данных и Поиск решения (см. рис. 1б и 1в).

Рис. 1б. Группа Анализ на вкладке Данные

Теперь можно приступить к работе с этими надстройками.

Рис. 1в. Вкладка "Анализ данных", после установки надстроек "Анализ данных" и "Поиск решения"

Начало работы с надстройкой "Поиск решения"

На листе введите формулу и выделите ячейку с этой формулой.
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
В диалоговом окне Параметры поиска решения выберите вариант Максимум, Минимум или Значение. Если выбран вариант Значение, введите значение в поле.
В поле Изменяя ячейки введите ячейку или диапазон ячеек, для которых необходимо применить поиск решения.
Нажмите кнопку Добавить, чтобы добавить ограничение для ячейки, и введите условие для этой ячейки.
Нажмите кнопку Добавить еще раз, чтобы добавить дополнительные ограничения ячейки (у одной ячейки может быть несколько ограничений), и по завершении нажмите кнопку ОК. Затем нажмите кнопку Решить.

Появится диалоговое окно Результаты поиска решения с сообщением об успешном выполнении операции или об ошибке.

Для того, чтобы использовать надстройку "Поиск решения", не обязательно быть знатоком методов линейного и нелинейного программирования. Нужно знать и понимать какие задачи могут быть решены этими методами.

От пользователя требуется умение с помощью серии диалоговых окон правильно сформулировать условия задачи, и если решение существует, то "Поиск решения" отыщет его.

Укажем некоторые возможности надстройки "Поиск решения":

Надстройка "Поиск решения" позволяет использовать одновременно большое количество изменяемых ячеек (в общей сложности до 200 ячеек).

Надстройка "Поиск решения" позволяет задавать ограничения для изменяемых ячеек. Например, при поиске решения, обеспечивающего максимальную прибыль, вы можете задать дополнительные условия (ограничения), например, на общий доход, который находился бы в диапазоне от 20 до 30%, или чтобы расходы не превышали заданной суммы. Подобного рода условия называются ограничениями для решаемой задачи.

Надстройка "Поиск решения" позволяет отыскать оптимальные (минимальные или максимальные) решения, т.е. наилучшие из возможных решений.

Задачи, для решения которых можно воспользоваться надстройкой "Поиск решения", имеют ряд общих свойств:

Имеется единственная ячейка, содержащая формулу, значение которой нужно оптимизировать или же сделать равным конкретному значению. Это значение (минимум, максимум или равно) является конечной целью решения, поэтому эта ячейка называется целевой ячейкой.

Формула в этой целевой ячейке содержит ссылки на ряд изменяемых ячеек (содержащие неизвестные, или переменные, решаемой задачи).

Поиск решения заключается в том, чтобы побрать такие значения этих переменных, которые бы давали оптимальные значения для формулы в целевой ячейке.

Кроме того, может быть задано некоторое количество ограничений – условий или соотношений, которым должны удовлетворять некоторые из изменяемых ячеек (переменных).

Рассмотрим использование надстройки "Поиск решения" на примере задач.

Задача. Найдём минимум функции y=(x-2)2.

Аналитическое решение. Сразу отметим, что эта задача на минимизацию функции. Находим производную и приравниваем её к нулю. Получим уравнение y'=2(x-2)=0. Решаем это уравнение. Ответ: xopt=2, ymin=0.

При численном решении задачи требуется сначала задать начальное приближение x0 (нулевое приближение). Для этого определяют интервал, где находится точка минимума, т.е. на этом интервале функция является унимодальной. Протабулируем функцию на данном интервале и построим её график (см. рис. 2).

Рис. 2. Таблица значений и график y=(x-2)2

Можно, например, взять отрезок [1,5; 2.5] и точку из этого отрезка равную 1,5. И заполняем ячейки согласно рис. 3. В ячейку B2 вводим начальное приближение аргумента, в ячейку B3 (целевая ячейка) нашу функцию, т.е. =(B3-2)^2. На рис. 3. мы видим значение этой функции в точке 1,5.

Рис.3. Ввод исходных данных

Выделяем ячейку B3 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения (см. рис. 4). В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B3. Программа автоматически установила нужные параметры: Минимум, ячейку, где будет находится решение B2, метод решения (окно Выберите метод решения). Щелкаем по кнопке Найти решение. В ячейке B2 мы видим xopt=2 и минимальное значение функции равное нулю (см. рис 5).

Рис. 4. Установка параметров оптимизации

После нажатия кнопки Найти решение, появится окно Результаты поиска решения (см. рис. 5),

Рис. 5. Окно Результаты поиска решения

и в ячейках B2 и B3 мы видим решение нашей задачи (см. рис. 6).

Рис. 6. Решение задачи

Следовательно, xopt=2, а ymin=0.

Условная оптимизация

Как правило, задачи на оптимум решаются при ограничениях (условная оптимизация).

Задача. Найдём минимум функции y=(x-2)2, при ограничении x≥2,5.

Рис. 7. Таблица данных и график функции при x>=2,5

В ячейку B2 вводим начальное приближение аргумента, например, равно 3 (см. рис. 8).

Рис. 8. Ввод исходных данных

Для ввода ограничений в окне Параметры поиска решения есть кнопка Добавить. Также как и в предыдущем примере Выделяем ячейку B3 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения. В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B3. Программа автоматически установила нужные параметры: Минимум, ячейку, где будет находится решение B2, метод решения. Теперь щелкаем мышкой по кнопке Добавить, после чего в открывшемся окне Добавление ограничения в поле Ссылка на ячейку указать ячейку (аргумент), на которую накладывается ограничение. Далее необходимо выбрать тип ограничения из раскрывающегося списка в центре диалогового окна, а затем в поле указать накладываемое ограничение (в данном случае число 2,5) (см. рис. 9).

Рис. 9. На ячейку B2 накладывается ограничение

Для подтверждения выполненных действий следует щелкнуть по кнопке ОК. Щелчок по кнопке Добавить также будет подтверждением, однако при этом диалоговое окно Добавление ограничения не будет закрыто и появится возможность ввести ещё одно ограничение. Так следует поступать в случаях, когда вводимых ограничений несколько.

Система вернёт нас обратно к окну Параметры поиска решения, где в поле В соответствии с ограничением, мы видим введённое ограничение на аргумент (см. рис. 10).

Рис. 10. Поиск решения с ограничением на ячейку B2

В ячейке B2 мы видим xopt=2,5 и минимальное значение функции равное 0,25 (см. рис 11).

Рис. 11. Окно Результаты поиска решения

Рис. 12. Решение

Естественно было ожидать, что минимальное значение будет достигнуто на границе (см. рис. 2).

Многомерная оптимизация

Задача. Найти минимум функции f(x,y)=(x-2)2+(y-3)2.

В ячейку B18 вводим начальное приближение аргумента x0, например x=1, в ячейку B19 вводим начальное приближение аргумента y0, например, y=1, а в ячейку B20 (целевая ячейка) нашу функцию, т.е. =(B18-2)2+(B19-3)2. На рис. 13. мы видим значение этой функции в точке (1,1).

Рис. 13. Ввод исходных данных

Выделяем ячейку B20 и набираем команду Данные/Поиск решения. Появится окно Параметры поиска решения (см. рис. 14). В поле Оптимизировать целевую функцию мы видим ссылку на ячейку B20. Установим нужные параметры: Минимум, ячейки, где будет находится решение B18, B19 метод решения (окно Выберите метод решения).

Рис. 14. Установка параметров оптимизации

Щелкаем по кнопке Найти решение. В ячейках B18 и B19 мы видим решение: xopt=2, yopt=3 и минимальное значение функции равное нулю, которое находится в ячейке B20 (см. рис 15).

Рис. 15. Окно Результаты поиска решения

Условная оптимизация

Задача. Найти минимум функции f(x,y)=(x-2)2+(y-3)2 при ограничении x+y=7. На лекции мы рассматривали этот пример. Эту задачу мы свели задаче обычного минимума, когда из уравнения, задающего ограничение на переменные, выразили одну из переменных и затем подставили это выражение в целевую функцию. Теперь решим данную задачу в Excel.

Как и прежде заносим в таблицу начальные значения для аргументов функции x и y (ячейки B18 и B19), формулу (целевую функцию) в ячейку B20 и формулу =B18+B19 (т.е. x+y) в ячейку B21 (это ограничение без правой части).

Рис. 16. Ввод исходных данных

Далее по аналогии с предыдущими примерами. Выбираем команду Данные/Поиск решения. Вводим параметры оптимизации (см. рис. 17 и 18).

Рис. 17. Установка ограничения x+y=7

Рис. 18. Результат установки ограничения

Рис. 19. Окно Результаты поиска решения

Следовательно, xopt=3, yopt=4, fmin=2 при ограничении x+y=7.

5-bal.ru

Решение задач оптимизации в excel

Решение задач оптимизации в EXCEL`е

Установка и активация надстроек "Пакет анализа" и "Поиск решения"

Откройте вкладку Файл.
Нажмите кнопку Параметры и выберите категорию Надстройки.
Убедитесь, что в нижней части диалогового окна Параметры Excel в поле Управление выбран элемент Надстройки Excel, и нажмите кнопку Переход.
В диалоговом окне Надстройки установите флажки Пакет анализа и Поиск решения и нажмите кнопку ОК (см. рис. 1б).
Если отобразится сообщение о том, что надстройку не удается запустить, и выведется предложение установить ее, нажмите кнопку Да, чтобы установить надстройку.

Рис. 1а. Окно Настройки

Обратите внимание, что на вкладку ^ добавлена группа Анализ, которая находится справа. Она содержит кнопки команд для надстроек Анализ данных и Поиск решения (см. рис. 1б и 1в).

Рис. 1б. Группа Анализ на вкладке Данные

Теперь можно приступить к работе с этими надстройками.

Рис. 1в. Вкладка "^ , после установки надстроек "Анализ данных" и "Поиск решения"

Начало работы с надстройкой "Поиск решения"

На листе введите формулу и выделите ячейку с этой формулой.
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
В диалоговом окне Параметры поиска решения выберите вариант Максимум, Минимум или Значение. Если выбран вариант Значение, введите значение в поле.
В поле Изменяя ячейки введите ячейку или диапазон ячеек, для которых необходимо применить поиск решения.
Нажмите кнопку Добавить, чтобы добавить ограничение для ячейки, и введите условие для этой ячейки.
Нажмите кнопку Добавить еще раз, чтобы добавить дополнительные ограничения ячейки (у одной ячейки может быть несколько ограничений), и по завершении нажмите кнопку ОК. Затем нажмите кнопку Решить.

Укажем некоторые возможности надстройки "Поиск решения":

Задачи, для решения которых можно воспользоваться надстройкой "Поиск решения", имеют ряд общих свойств:

Рассмотрим использование надстройки "Поиск решения" на примере задач.

Задача. Найдём минимум функции y=(x-2)2.

^ . Сразу отметим, что эта задача на минимизацию функции. Находим производную и приравниваем её к нулю. Получим уравнение y'=2(x-2)=0. Решаем это уравнение. Ответ: xopt=2, ymin=0.

Рис. 2. Таблица значений и график y=(x-2)2

Рис.3. Ввод исходных данных

Рис. 4. Установка параметров оптимизации

После нажатия кнопки Найти решение, появится окно Результаты поиска решения (см. рис. 5),

Рис. 5. Окно Результаты поиска решения

и в ячейках B2 и B3 мы видим решение нашей задачи (см. рис. 6).

Рис. 6. Решение задачи

Следовательно, xopt=2, а ymin=0.

Условная оптимизация

Как правило, задачи на оптимум решаются при ограничениях (условная оптимизация).

Задача. Найдём минимум функции y=(x-2)2, при ограничении x≥2,5.

Рис. 7. Таблица данных и график функции при x>=2,5

В ячейку B2 вводим начальное приближение аргумента, например, равно 3 (см. рис. 8).

Рис. 8. Ввод исходных данных

Рис. 9. На ячейку B2 накладывается ограничение

Для подтверждения выполненных действий следует щелкнуть по кнопке ^ . Щелчок по кнопке Добавить также будет подтверждением, однако при этом диалоговое окно Добавление ограничения не будет закрыто и появится возможность ввести ещё одно ограничение. Так следует поступать в случаях, когда вводимых ограничений несколько.

Система вернёт нас обратно к окну ^ , где в поле В соответствии с ограничением, мы видим введённое ограничение на аргумент (см. рис. 10).

Рис. 10. Поиск решения с ограничением на ячейку B2

В ячейке B2 мы видим xopt=2,5 и минимальное значение функции равное 0,25 (см. рис 11).

Рис. 11. Окно Результаты поиска решения

Рис. 12. Решение

Естественно было ожидать, что минимальное значение будет достигнуто на границе (см. рис. 2).

Задача. Найти минимум функции f(x,y)=(x-2)2+(y-3)2.

Рис. 13. Ввод исходных данных

Рис. 14. Установка параметров оптимизации

Рис. 15. Окно Результаты поиска решения

Условная оптимизация

Рис. 16. Ввод исходных данных

Рис. 17. Установка ограничения x+y=7

Рис. 18. Результат установки ограничения

Рис. 19. Окно Результаты поиска решения

Следовательно, xopt=3, yopt=4, fmin=2 при ограничении x+y=7.

top-bal.ru