Большая Энциклопедия Нефти и Газа. Динамическая оптимизация

Динамическая оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Динамическая оптимизация

Cтраница 1

Динамическая оптимизация - метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и переход из одного режима в другой, осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое сходство со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [2]

Динамическая оптимизация - метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и переход из одного режима в другой осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое сходство со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [4]

Динамическая оптимизация - метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и пер еход из одного режима в другой, осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое сходство со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [5]

Динамическая оптимизация предполагает оптимальное выполнение как установившихся режимов работы установки, так и процессов перехода от одного режима к другому. В этом случае статические зависимости ( 36) и ( 34) заменяют соответствующими динамическими зависимостями, а критерий оптимальности Кэ становится интегральной функцией времени. [6]

Динамическая оптимизация отличается от статической оптимизации еще большей сложностью: процесс не только поддерживается на оптимальном уровне в стационарном режиме, но и переход от одного рабочего положения к другому ведется таким путем, который лучше всего удовлетворяет определенным, чаще всего экономическим, критериям. Этот метод регулирования представляет в настоящее время лишь академический интерес, так как для его осуществления требуются вычислительные устройства большой мощности. Однако практическое его воплощение наверняка окажется возможным в самом недалеком будущем. [7]

Динамическая оптимизация также улучшает процесс, особенно если вход изменяется быстро. Для динамической оптимизации надо довольно много знать об управляемой системе. Если система нелинейная сложного вида, например кусочно-линейная, то необходима аппроксимация. Управление статикой может осуществляться с помощью небольших ЦВМ, не включенных в цепь управления; для динамической оптимизации будут нужны гораздо более крупные машины, особенно для управления в замкнутой цепи. Применение таких машин может быть экономически оправдано только в том случае, если управление с их помощью дает значительный эффект. Увеличение эффективности, полученное выше, не всегда будет наблюдаться для других процессов. [9]

Динамическая оптимизация - метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и переход из одного режима в другой, осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое сходства со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [10]

Динамическая оптимизация - метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и пер еход из одного режима в другой, осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое сходство со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [11]

Динамическая оптимизация особенно выгодна при наличии больших высокочастотных возмущений по качеству сырья. В рассматриваемом случае периодичность возмущений по качеству нефти 9 - Ю ч, а время переходного процесса в атмосферной части установки составляет 20 - 25 мин. При этом решение задачи динамической оптимизации не является обязательным, так как оптимизация связана с большими затратами и выигрыш от нее не окупается. [12]

Задачи динамической оптимизации, рассматриваемые в § 10.3, имеют целевые функции, являющиеся интегралами функции стоимости по времени. [13]

Задачи динамической оптимизации не получили еще распространения в АСУ ТП вследствие сложности их решения; при этом не всегда возможен выигрыш перед простым управлением по возмущению или с помощью обратной связи. При динамическом оптимальном управлении определяется стратегия управления динамическим технологическим объектом, оптимальная с точки зрения выбранного критерия, например среднеквадратической ошибки слежения при наличии неконтролируемого возмущения. Если оптимальная стратегия управления не зависит или слабо зависит от неопределенности, связанной с неизвестными параметрами объекта или неизвестными начальными условиями, то рассматривают адаптивную оптимизацию технологического процесса в динамическом режиме. [14]

Осуществление динамической оптимизации сопряжено с большими трудностями поиска и поддержания оптимальных изменяющихся регулируемых параметров в переходные периоды. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Оптимизация динамическая и статическая - Справочник химика 21

В табл. 1 дана характеристика областей применения различных методов оптимизации, при этом за основу положена сравнительная оценка эффективности использования каждого метода для решения различных типов оптимальных задач. Классификация задач проведена по следующим признакам 1) вид математического описания процесса 2) тип ограничений на переменные процесса и 3) число переменных. Предполагается, что решение оптимальной задачи для процессов, описываемых системами конечных уравнений, определяется как конечный набор значений управляющих воздействий (статическая оптимизация процессов с сосредоточенными параметрами), а для процессов, описываемых системами обыкновенных дифференциальных уравнений, управляющие воздействия характеризуются функциями времени (динамическая оптимизация процессов с сосредоточенными параметрами) или пространственных переменных (статическая оптимизация процессов с распределенными параметрами). [c.34] Системы управления конкретным процессом могут отличаться по своим возможностям и по степени сложности. Нет необходимости повторять, что степень сложности применяемого математического аппарата сильно меняется при переходе от простой системы регулирования к более сложной. Различают следующие уровни автоматизации в порядке возрастания сложности стабилизация входных параметров, динамическое регулирование выходных параметров, статическая оптимизация как основа настройки систем управления, самонастраивающееся управление и, наконец, динамическая оптимизация. [c.110]

Сначала рассматривают вариант IV, поскольку тогда решается принципиальный вопрос об использовании математической модели при автоматической оптимизации. В данном случае могут использоваться как активные, так и пассивные методы поиска оптимума на объекте. Известно, что химико-технологические процессы, — как объекты управления — (в том числе и рассмотренные два реактора синтеза аммиака) обладают такими динамическими свойствами по сравнению со статическими свойствами возмущающих воздействий, что пассивные методы поиска оптимума фактически не применимы. Остаются активные методы поиска (экстремальные системы). Ниже будет показано, что и эти методы прямого поиска на объекте не дают нужного экономического эффекта из-за динамических свойств объекта управления и статических свойств возмущающих воздействий. [c.369]

На этапе макрокинетических исследований решают следующие задачи 1) выбор типа опытного реактора, осуществляемый в соответствии с данными об организации процесса 2) определение модели гидродинамики процесса на основе данных о структуре потоков 3) анализ диффузионных эффектов, процессов массо- и теплопереноса в аппарате и оценка соответствующих тепловых и диффузионных параметров 4) синтез статической математической модели и процесса, установление ее адекватности 5) статическая оптимизация 6) синтез динамической модели процесса и установление ее адекватности анализ параметрической чувствительности 7) анализ устойчивости теплового режима процесса 8) динамическая оптимизация. [c.29]

Методы вариационного исчисления ( см. главу V) обычно используют для решения задач, в которых критерии оптимальности представляются в виде функционалов (I, 27) и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации. [c.32]

Газохроматографические измерения на напористых адсорбентах [27, 40] и даже на кристаллических тонкопористых (например, на цеолитах) [55] при соблюдении необходимых предосторожностей и оптимизации динамических и кинетических факторов работы колонны позволяют получить значения константы Генри, близкие к находимым путем экстраполяции равновесных изотерм адсорбции, определенных статическими методами [166, 167]. Значительным преимуществом элюционного газохроматографического метода является возможность исследования изотермы адсорбции при малых заполнениях поверхности благодаря высокой чувствительности детекторов. Методом фронтальной газовой хроматографии, например с последующей тепловой десорбцией при регулировании концентрации адсорбата в газовой фазе с помощью термостатирования жидкого адсорбата, насыщающего газ-носитель, можно объединить преимущество статического метода (заведомое достижение равновесия) с высокой чувствительностью хроматографического детектирования [161]. Элюционный метод удобнее использовать при более высоких температурах, а метод тепловой десорбции — при обычных и более низких. [c.67]

Основными этапами при разработке реактора и САУ является построение математического описания процессов в реакторе, теоретическая оптимизация, качественный анализ описания, выбор типа реактора и исследование его статических и динамических свойств, определенне основных технологических и конструктивных характеристик реактора, выбор каналов управления, поиск оптимального управления и, наконец, синтез САУ. Значения многих технологических параметров и конструктивных характеристик реактора, как, например, диаметр трубки, размер зерен катализатора, в значительной мере определяющих стоимость, надежность и гидравлическое сопротивление реактора, должны выбираться с учетом реально возможного качества работы САУ. Таким образом, уровень и стоимость системы САУ могут влиять на аппаратурно-технологические решения процесса, а для реакторов, обладающих пониженной стабильностью, целиком определить эти решения. Так, неустойчивость оптимального стационарного режима приводит к частым срывам на высокотемпературный или низкотемпературный режим. Система управления реактором возвращает этот режим в окрестность неустойчивого ста-циоиарного состояния, процесс в целом оказывается нестационарным, рыскающим в окрестности этого состояния. [c.21]

Динамическая оптимизация отличается от статической оптимизации еще большей сложностью процесс не только поддерживается на оптимальном уровне в стационарном режиме, но и переход от одного рабочего положения к другому ведется таким путем, который лучше всего удовлетворяет определенным, чаще всего экономическим, критериям. Этот метод регулирования представляет в настоящее время лишь академический интерес, так как для его осуществления требуются вычислительные устройства большой мощности. Однако практическое его воплощение наверняка окажется возможным в самом недалеком будущем. [c.111]

Первые два аспекта оптимизации, по существующей градации, относятся к статической оптимизации и в принципе должны рассматриваться совместно. Три последние аспекта относятся к динамической оптимизации, и каждый из них имеет самостоятельное значение. [c.22]

Статические модели применяется для расчетного исследования и оптимизации установившихся режимов работы ректификационных колонн. А динамические модели применяются при разработке систем автоматического управления и оптимизации пусковых и переходных режимов установок. [c.63]

Применение теории рециркуляции к каждому из пяти аспектов оптимизации характеризуется своей спецификой. Прежде всего применение теории рециркуляции к вопросам статической и динамической оптимизации промышленных процессов исключает рассмотрение изолированного реактора и требует рассмотрения региона, состоящего либо из отдельной установки, либо из ряда установок с общим аппаратом (например, ректификационная колонна). Это объясняется тем, что по своей сути рециркуляция означает возвращение в процесс выделенных из продуктов реакции компонентов. [c.22]

Задачи оптимизации можно далее классифицировать как статические и динамические. Они существенно отличаются по методам решения. В статических задачах решение находится в виде числовых значений (например, определенных параметров проведения установивщегося процесса). В динамических задачах решение определяется в виде функций времени (например, изменения во времени количества заданного продукта реакции). Последняя задача является более сложной и трудоемкой. Основные принципы стати-, ческой и динамической оптимизации можно найти в работах, посвященных этим вопросам. [c.487]

Книга посвящена теории н практике оптимизации действующих и проектируемых технологических процессов и аппара тов для обезвоживания и обессоливания нефтей. Даны методы построения статических и динамических моделей этих процессов в целом и их отдельных звеньев. Приведены методы оценки резервных возможностей действующих установок и способы выявления их слабых звеньев. Значительное место в книге уделено моделированию кинетики процессов укрупнения эмульсий. [c.2]

Однако наряду с задачами оптимизации стационарных режимов процессов, которые можно охарактеризовать как задачи статической оптимизации, существует целый ряд задач оптимального управления при нестационарных режимах эксплуатации, для решения которых требуется изучение динамики процесса. Эти задачи носят название задач динамической оптимизации. Примером может служить задача оптимального управления периодическим процессом за один рабочий цикл, когда нужно так выбрать закон управления, чтобы получить продукт необходимого качества в течение минимального периода или при заданном времени цикла обеспечить максимальный выход продукции. Сюда же можно отнести задачи пуска процесса и перевода его. с одного режима на другой при минимальных отклонениях качества продукции. [c.23]

Вполне естественно, что представление адсорбционной установки в виде динамической модели более соответствует действительности, чем в виде статической модели. Однако, учитывая особенности адсорбционной установки, приходится на первых порах ограничиваться статической моделью, т. е. искать критерий оптимизации в виде (1.3.2). Вообще говоря, проблему циклических адсорбционных процессов необходимо рассматривать исходя из экономической эффективности всего комплекса. В этом случае охватываются проблемы экологического характера. [c.13]

Система управления, рассмотренная в работе [4], предусматривает наличие двух подсистем подсистемы статической оптимизации , которая, используя полную математическую модель процесса, предсказывает (с учетом ограничений) область локализации оптимума и включается либо при существенном изменении условий протекания процесса, либо при смене критерия управления, и подсистемы динамической оптимизации , которая работает в реальном времени и воспринимает от подсистемы статической оптимизации информацию об изменении рабочей области, а также распознает ситуацию со сменами ограничений. Одновременно на каждом шаге управления подсистема динамической оптимизации, пользуясь упрощенной математической моделью, прогнозирует значение критерия и изменение ограничений, а при необходимости и рассчитывает требующиеся для достижения оптимума управляющие воздействия поскольку и модель процесса и ограничения в этой подсистеме описываются линейными алгебраическими уравнениями, для отыскания экстремума используется линейное программирование. [c.140]

Различают два типа систем оптимального управления с применением вычислительных машин — системы динамического и статического действия. Системы динамического действия возлагают на управляющую машину все функции управления. В этом случае требуется полное математическое описание процесса с учетом динамических свойств объекта. Система статического действия предусматривает сохранение стабилизирующих регуляторов и возлагает на управляющую вычислительную машину лишь коррекцию заданных значений параметров с целью оптимизации режима. Этот тип проще и надежнее, так как при неисправности машины она отключается, а управление процессом сохраняется при помощи стабилизирующих регуляторов на тех же зафиксированных значениях параметров, которые были до повреждения вычислительной машины. [c.365]

Методика экономически обоснованного выбора между системой автоматической стабилизации (САС) системой оптимизации статических режимов (ССО) и системой динамической оптимизации (СДО). [c.168]

Задача оценки переменных состояния химико-технологического процесса, к которым можно отнести температуру, дав.ттение, составы фаз, расходы жидких и газообразных среди т. д., состоит в том, чтобы по показаниям измерительных приборов, функционирующих в условиях случайных помех, восстановить значения переменных состояния системы, наиболее близкие в смысле заданного критерия к истинным значениям. Применительно к химико-технологическим процессам важность решения задач оценки переменных состояния и определения неизвестных параметров модели объекта имеет три аспекта открывается возможность получать непрерывно информацию о тех переменных состояния слонпромежуточных веществ, параметры состояния межфазной поверхности, доля свободных активных мест катализатора и т. п.) реализация непрерывной (в темпе с процессом) оценки переменных состояния и поиска неизвестных параметров модели создает предпосылки для прямого цифрового оптимального управления технологическим процессом решение задач идентификации решает проблему непрерывной оптимальной адаптации нелинейной математической модели к моделируемому процессу в условиях случайных помех и дрейфа технологических характеристик последнего, что необходимо для осуществления статической и динамической оптимизации. [c.283]

Динамическая структура трудовых движений, действий оператора, как правило, чрезвычайно сложна. Нормирование и оптимизация производственной среды только на основании данных статической антропометрии оказываются недостаточными, так как данные о размерах тела и его различных частей не содержат информации о взаимосвязи антропометрических характеристик,, структуры и динамики движений, специфичных для каждого вида выполняемой работы, человеко-машинной системы. [c.115]

Рассмотрев функции и организацию работы системы на каждом уровне, перечислим комплекс задач, которые решаются при взаимодействии всех уровней иерархии. Эти задачи можно разделить на три группы статическая оптимизация для непрерывно действующих ферментационных установок и других подсистем производства, работающих в непрерывном режиме динамическая оптимизация полупериодических и периодических аппаратов и подсистем оценка параметров процессов ферментации и других подсистем для использования их в обратной связи при управлении. [c.252]

Как уже было отмечено, при синтезе алгоритмов стабилизации было применено численное моделирование системы в целом с одновременным применением метода Розенброка для определения оптимальных параметров в алгоритмах стабилизации. Для ограничения времени, необходимого для расчетов на вычислительной машине, математическая модель реактора была упрощена. При упрощении мы исходили из полной метаматической модели реактора в виде системы дифференциальных уравнений в частных производных [215], которая решалась на ЭВМ. Затем численные решения были аппроксимированы в форме последовательного соединения нелинейной статической модели и линейной динамической модели (рис. IX.10). Аппроксимированная модель была использована при оптимизации параметров алгоритмов стабилизации. [c.366]

Книга посвящена актуальному в настоящее время вопросу применения математических методов для расчета оптимальных (наилучших) режимов технологических процессов. Дана характеристика основных этапов работ по статической, квазистатической и динамической оптимиаации как действующих химических реакторов, так и при их проектировании. Сопоставлены два важнейших метода оптимизации — метод поиска на объекте и метод оптимизации с помощью математической модели. Большое внимание уделено математическим способам оптимизации — нелинейному программированию и Принципу максимума. [c.4]

Для автоматически управляемых процессов или систем, различают две стадии оптимизации статическую и динамическую (см. стр. 70). [c.140]

Системы оптимального автоматического управления. При создании систем оптимального автоматического управления ( AO) раз-ч личают статическую и динамическую оптимизацию. [c.70]

Представляют интерес системы статической и динамической оптимизации с применением адаптивных моделей (рис. 1-29). В этих случаях математическое описание получают методами математической статистики, отработав экспериментальные данные, характеризующие зависимость между входными и выходными величинами. Особенность адаптивных моделей заключается [c.73]

Статическая оптимизация решает вопросы создания и реализации оптимальной модели процесса, а динамическая — создания и реализации системы оптимального управления процессом. [c.140]

Для большинства непрерывных каталитических процессов основным является установившийся, или статический, режим. Однако на процесс могут воздействовать разного рода неуправляемые переменные, которые могут меняться либо скачкообразно, но достаточно редко, либо же настолько медленно, что в каждый данный момент процесс можно считать стационарным. Таким образом, под статической оптимизацией будем понимать оптимизацию по заданному критерию статического режима процесса в каждый момент времени, исключая интервалы времени, в течение которых процесс находится в переходном (динамическом) режиме [4, 9]. Такой подход допустим, если среднее время между двумя последовательными возмуш ениями значительно больше постоянной времени объекта. [c.25]

Б связи с тем, что скорость изменения активности катализатора значительно меньше скорости переходных процессов в объекте, можно рассматривать совместно статические уравнения (2) и динамические уравнения (20). Поэтому метод назван квазистатической оптимизацией. [c.34]

Первая из них — задача стабилизации динамических либо статических характеристик системы управления, вторая — задача оптимизации динамических или статических характеристик системы управления в узком смысле. Оптимум функционала можно находить путем поиска. При этом вектрру управления или вектору перестраиваемых параметров регулятора задают пробное движение, затем оценивают отклонение меры качества и в зависимости от этого соответствующим образом изменяют эти векторы. Самонастраивающиеся системы такого типа получили название поисковых систем. [c.187]

Вообще говоря, описанный режим является динамическим. Однако вследствие того, что вредные вещества осаждаются достаточно медленно, удается значительно упростить динамические уравнения объекта. Задачу оптимизации таких режимов будем называть задачей квазистатической оптимизации. В отличие от нее при статической оптимизации стремятся сделать процесс максимально выгодным по принятому критерию в каждый момент времени. При квазистатическом режиме такой подход неприменим из-за возможного интенсивного выделения катализаториых ядов, в результате чего активность катализатора быстро упадет и за цикл работа реактора будет далеко не оптимальной. Поэтому в данном случае приходится ставить задачу оптимизации работы реактора за цикл. В дальнейшем рассматриваются только задачи статической и квазистатической оптимизации каталитических реакторов. [c.18]

Установлено, что усиление шва не снижает статической прочности, однако сильно влияет на вибрационную прочность. Чем больше усиление шва и, следовательно, меньше угол перехода от основного металла к наплавленному, тем сильнее оно снижает предел вьгаосливости. Таким образом, наличие чрезмерного усиления шва может привести к нулю все преимущества, полученные от оптимизации технологического процесса по улучшению качества сварных соединений, работающих при вибрационных, динамических и повторно-статических нагрузках. [c.79]

Динамическая оптимизация — метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся режиме, но и пер"еход из одного режима в другой, осуществляется наилучшим образом. Функция оптимальности становится функцией времени, и задача оптимального управления сводится к максимизации или минимизации определенного критерия во времени. Динамическая оптимизация имеет некоторое xoд твo со статической, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины. [c.71]

chem21.info

Динамическая оптимизация - Справочник химика 21

Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению диф([)еренциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений. [c.32] На этапе макрокинетических исследований решают следующие задачи 1) выбор типа опытного реактора, осуществляемый в соответствии с данными об организации процесса 2) определение модели гидродинамики процесса на основе данных о структуре потоков 3) анализ диффузионных эффектов, процессов массо- и теплопереноса в аппарате и оценка соответствующих тепловых и диффузионных параметров 4) синтез статической математической модели и процесса, установление ее адекватности 5) статическая оптимизация 6) синтез динамической модели процесса и установление ее адекватности анализ параметрической чувствительности 7) анализ устойчивости теплового режима процесса 8) динамическая оптимизация. [c.29]

Если бы реактор работал периодически, следовало бы ставить задачу динамической оптимизации. Можно было бы задать, например, выбор начальных составов реагентов, а также часовую подачу энергии Я, подходящих для этого способа, чтобы получить продукт требуемого качества при экстремальном значении выбранного показателя качества. Например, можно минимизировать время длительности процесса [c.488]

Системы управления конкретным процессом могут отличаться по своим возможностям и по степени сложности. Нет необходимости повторять, что степень сложности применяемого математического аппарата сильно меняется при переходе от простой системы регулирования к более сложной. Различают следующие уровни автоматизации в порядке возрастания сложности стабилизация входных параметров, динамическое регулирование выходных параметров, статическая оптимизация как основа настройки систем управления, самонастраивающееся управление и, наконец, динамическая оптимизация. [c.110]

Так же как и в случае использования эмпирических выражений, результаты изложенных выше исследований нельзя непосредственно экстраполировать на другие виды оборудования или на другие условия. Они также совершенно непригодны для динамической оптимизации, поскольку большие трудности вызывает сильное изменение условий работы, например при пуске. Однако упомянутые методы могут оказаться весьма полезными при стабилизации управления очень крупными колоннами, где вследствие их размеров полные модели были бы практически неприемлемы. [c.116]

Этот метод называется динамической оптимизацией. Математический аппарат для изучения такой системы обычно включает вариационное исчисление, чтобы получить для каждой [c.119]

Вильямс и Отто предложили отличный метод для определения возможности использования динамической оптимизации. Ответы на данный вопрос содержатся в литературе - в работах этих авторов подчеркивается сложность рассмотрения даже весьма простых химических процессов с точки зрения их динамической оптимизации и управления. [c.120]

Для многих сложных процессов периодического типа, а также полунепрерывных процессов в условиях статистической неопределенности информации о процессе, как правило, нелинейном, решается задача динамической оптимизации на конечном интервале времени — задача оптимального перевода объекта из начального состояния в конечное. [c.277]

Вопросы обоснованности использования системы динамической оптимизации чрезвычайно сложны и мало изучены. Однако они настоятельно выдвигаются практикой и связаны с требованием увеличения единичной мощности агрегатов химической и нефтехимической промышленности. Резкое увеличение единичной мощности приводит к значительному вкладу в экономические показатели работы установок динамических режимов (пуск, останов, перевод с режима на режим). [c.195]

В настоящее время только в некоторых частных случаях можно предложить оценку обоснованности применения системы динамической оптимизации. [c.195]

Начиная с 1965 г., многие разделы книги читаются авторами в лекционных курсах Математическое моделирование процессов химической технологии для студентов технологических специальностей, Математическое моделирование и оптимизация процессов химической технологии для студентов, специализирующихся в химической кибернетике в Казанском химико-технологическом институте им. С. М. Кирова, в курсе Автоматизация химических производств , в Московском и Тамбовском институтах химического машиностроения для студентов, специализирующихся в автоматизации химических производств. Учитывая ограниченный объем книги, авторы сознательно не прибегали к детальному изложению всех полученных результатов. Так, не рассматриваются вопросы идентификации математических моделей [60, 72], алгоритмы обработки результатов промышленных экспериментов [53, 72], связь оптимального проектирования (с учетом динамических свойств объектов) и задач управления [73], вопросы динамической оптимизации [68]. [c.8]

На первом этапе ССО сравнивают с идеальной СДО. Идеальной СДО будем называть систему динамической оптимизации, использующую точную модель объекта, т. е. модель, ие-адекватностью которой можно пренебречь. Очевидно, в большинстве случаев такая точная модель динамики процесса пе может быть использована для целей управления из-за большого машинного времени, необходимого для реализации модели, и вследствие того, что в настоящее время методы синтеза систем динамической оптимизации разработаны лишь для сравнительно [c.196]

На втором этапе сравниваются ОПП и переходные процессы в реальной системе динамической оптимизации, сконструированной с использованием приближенной модели и предназначенной для управления рассматриваемым объектом. [c.197]

Система динамической оптимизации может быть применена, если [c.201]

Система динамической оптимизации с данной математической моделью (V. 86) экономически оправдана, если выпол няется неравенство [c.203]

Особенностью задач динамической оптимизации является то, что значение критерия оптимальности оиределяетси не только положением, существующим в рассматриваемый момент времени, но и предысторией процесса, начиная с некоторого начального момента. Поэтому оценка эффективности процесса должна учитывать его поведение в течение всего исследуемого нестационарного периода. Это приводит к необходимости использования в качестве критериев оптимальности интегральных оценок (функционалов) вида [c.23]

Л шожители Лагранжа можно применять для решения задач оптимизации объектов с распределенными параметрами и задач динамической оптимизации (см. главу IV, стр. 176). При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных уравнений. [c.31]

Методы вариационного исчисления (см. главу V) обычно используют для решения задач, в которых критерии 0птнмал1л10стн представляются в виде ((функционалов (1,27) и решениями которых являются неизвестные функции. Такие задачи возникают обычно при статическо оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации. [c.31]

Статьи Гоулда с сотр. затрагивают проблему оптимизации управления реактором как нелинейной системы. В работе Бичера и Гоулда обсуждается возможность динамической оптимизации при помощи цифровых машин. Пользуясь методами вариационного исчисления, они вывели систему уравнений Эйлера— Лагранжа, решаемую для определения оптимального пути, по которому должен следовать процесс в реакторе после внесения возмущения. [c.120]

chem21.info

4.Оптимизация

4.1. Методы оптимизации

Оптимизация - это целенаправленная деятельность, заключающаяся в получении

наилучших результатов при соответствующих условиях.

Выполнение любой задачи оптимизации начинают с определения цели

оптимизации, т.е. формулирования требований, предъявляемых к объекту оптимизации.

От того, насколько правильно выражены эти требования, зависит

возможность реализации поставленной цели.

Для решения задач подобного рода нужно располагать ресурсами оптимизации,

т.е. объект должен обладать определенными степенями свободы -

управляющими действиями, которые позволяют изменить его состояние в соответствии

с заданными требованиями.

Условием правильной постановки оптимальной задачи является наличие

количественной оценки интересующего качества объекта оптимизации, которую

называют критерием оптимальности или целевой функции.

Появление вычислительных машин позволило качественно изменить отношения

исследователя и проектировщика к задачам оптимизации, где от него

теперь требуется предельно точная формулировка задачи и разработка алгоритма

ее решения.

При правильной постановке оптимальной задачи необходимо соблюдение

следующих условий:

1) требование оптимизации только одной величины;

2) наличие степеней свободы у оптимизированного объекта;

3) возможность количественной оценки оптимизированной величины.

4.1.1. Этапы вычислительного процесса при оптимизации.

Перед началом поиска выбирается исходная точка Хiв пределах допустимой

области ХD, заданной прямыми ограничениями управляемых параметров

с определением целевой функции F(Хi). Далее вычислительный процесс состоит

из последовательности шагов. На каждом шаге выбирается направление

движения. Затем производится сам шаг в пространстве управляемых параметров,

в результате из предыдущей точки Хiосуществляется переход в новую

точку Хi+1. В этой точке вычисляется целевая функцияF(Хi+1), благодаря чему

можно судить о достигнутом успехе. Шаг заканчивается проверкой условий

прекращения поиска: если условия выполнены, то поиск заканчивается, иначе

делается переход к новому шагу. Схема вычислений приведена на рис.4.1.

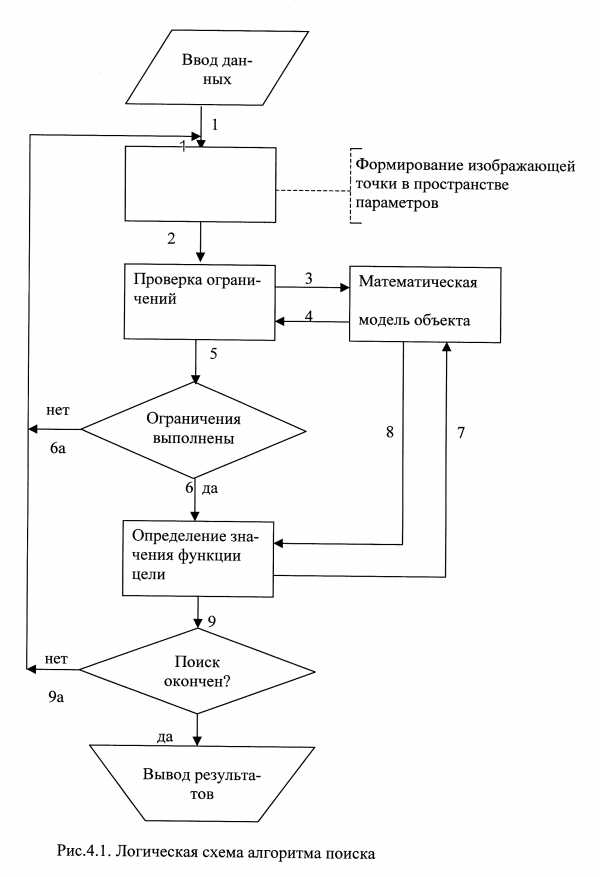
4.1.2. О критериях эффективности алгоритмов

В процессе оптимизации анализ выполняется многократно, что приводит к значитель-ным затратам машинного времени ЭВМ. Если обозначить черезn1- число вариантов анализа работы объекта на этапе вычисления целевой функции, а черезn2- число вариантов на этапе

определения направления поиска и через n3- число шагов поиска, то общее время решения задачи оптимизации на ЭВМ составит

Тм=Тм1(n1∙n2)n3

где Тм1- затраты машинного времени на один вариант анализа работы объекта.

Значения n1,n2,n3– показатели эффективности принятой стратегии поиска с позиций затраты машинного времени, которые, обычно, называют потерями на поиск, относят к кри-териям эффективности алгоритмов.

Кроме потерь на поиск к критериям эффективности относят:

а) точность определения экстремальной точки;

б) надежность поиска, под которой понимают вероятность получения решения задачи с заданной точностью.

4.1.3. Классификация критериев оптимальности

Основная проблема постановки экстремальных задач - формулировка целевой

функции, поскольку все выходные параметры Yявляются функциями вектора внутренних параметров X и, следовательно, не могут изменяться независимо друг от друга. Среди вы-ходных параметров всегда найдутся пары таких параметров, что улучшение одного из них приводит к ухудшению другого. Такие параметры называют конфликтными параметрами. Поэтому при оптимизации невозможно улучшения всех выходных параметров одновременно. Таким образом, многокритериальность задач исследования и обуславливает сложность про-блемы постановки задач оптимизации. Возможны варианты, когда из выходных параметров можно выделить наиболее важный, достаточно полно характеризующий свойства объекта, тогда его можно принять за целевую функцию, в этом случае критерии оптимизации

называют частными критериями.

В большинстве же случаев приходится прибегать к построению комплексного

критерия, при котором целевая функция тем или иным способом объединяет все или большинство выходных параметров. Для установления относительной важности выходных параметров в комплексных критериях, исследователь должен располагать какими-либо ориентирами.

В задачах исследования наилучшим, а часто и единственно корректным, является выбор относительной важности параметров с точки зрения степени выполнения технического задания (ТЗ) на проведения исследований. Ориентация на ТЗ при формулировке комплексно-го критерия - один из важных принципов оптимизации в задачах исследования, поскольку

в ТЗ конкретизируют и количественно оценивают в виде условий работоспособности пред-ставления о целевом назначении и желаемых свойствах исследуемого объекта.

В процессе исследований так подобрать изменяемые параметры объекта, чтобы он был оптимальным относительно целевой функции. При синтезе динамических объектов крите-рием оптимальности может быть одна из оценок качества переходных процессов или их совокупность.

Все критерии качества можно разбить на четыре группы:

- к первой группе относятся критерии точности, использующие для оценки качества величину ошибки в различных типовых режимах;

- вторую группу составляют критерии, определяющие величину запаса устойчивости.

- третья группа критериев качества характеризует быстродействие систем регули-рования.

-к четвертой группе относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстро-действие. Обычно эти критерии базируются на некоторых свойствах кривой переходного

процесса, позволяющие дать оценку быстроты затухания и величины отклонения регу-лируемой величины.

4.1.4. Методы поиска экстремума при исследовании объекта.

Как видно из схемы вычислений при поисковой оптимизации (рис.4.1) движение в пространстве параметров осуществляется шагами. От величины шага зависят многие параметры поиска, такие как потери на поиск, точность определения экстремума, надежность поиска. Оптимальный по величине шаг hнаходится после выбора направления очередного шага путем минимизации целевой функцииF(Х) вдоль избранного направления перемещения в точку такого минимума.

Способ выбора направления очередного шага выражает сущность каждого метода поиска экстремума, об этих методах будет рассказано ниже.

4.1.5. Задачи динамической оптимизации.

Наряду с задачами оптимизации стационарных режимов, которые можно охаракте-ризовать как задачи статистической оптимизации, существует целый ряд задач оптимального управления при нестационарных режимах эксплуатации. Эти задачи носят название задач динамической оптимизации. Особенность их заключается в том, что значение критерия оптимальности определяется не только положением, существующим в рассматриваемый момент времени, но и предысторией процесса, начиная с некоторого начального момента. Это приводит к необходимости использования в качестве критериев оптимальности интегральных оценок (функционалов) вида:

I=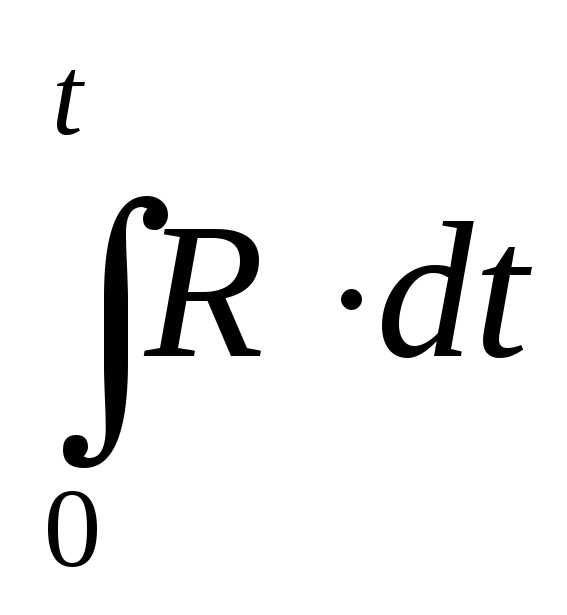(4.1)

гдеR- заданная функция параметров, определяющих состояние процесса в любой момент времени. Критерий оптимальности детерминированного процесса представляется как функция входных Хвх, выходных Хвыхи направляющих параметровU.

R=F(Хвх, Хвых, U) (4.2)

Критерий же оптимальности рассматривается как функция управляющих параметровUi:

R=F1( Хвх,U) 4.3)

Решение задачи оптимизации в этом случае получается в виде зависимости управля-ющих параметров процессаUот входных параметров Хвхи возможно, так же от времениtи пространственных координатZоптимизируемого объекта.

Uопт= U(Хвх, Z,t) (4.4)

Задача определения согласно формуле (4.2) решается лишь тогда, когда известен вид зависимости выходных параметров процесса Хвыхот выходных Хвх, управляющихUпара-метров, т.е. соотношение вида (4.5).

Хвых i = fi(Хвх, U) , i=1..., n, (4.5)

Вид самого критерия оптимальности зависит от конкретного содержания решаемой задачи оптимизации и может оказать существенное влияние и на выбор метода решения.

Большая часть методов решения оптимальных задач основана на предположении,

что математическая модель оптимизируемого объекта известна. Более того, многие методы оптимизации используют конкретные свойства объекта и его математического описания.

В настоящее время для решения оптимальных задач применяют в основном

следующие методы:

- методы исследования функции классического анализа;

- методы, основанные на исследовании неопределенных множителей Лагранжа;

- вариационное исчисление; динамическое программирование;

- принцип максимума;

- линейное программирование;

- нелинейное программирование.

Как правило, нельзя рекомендовать какой-либо один метод для решения всех без исключения задач, возникших на практике. Одни методы в этом отношении являются общими, другие - менее общими. Наконец, целая группа методов (методы исследования функций классического анализа, метод множителей Лагранжа, нелинейное программирова-ние) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами (динамическим программированием, принципом максимума).

4.1.6. Методы исследования функции классического анализа наиболее известны

для решения несложных оптимальных задач. Обычно областью их использование являются задачи с известным аналитическим выражением критерия оптимальности Rи аналитическим выражением, как для производных видаdR/dX, так и частных производных непрерывной функции многих переменныхR=R(х1, х2,... хn). Экстремальные решения оптимальной зада-чи, крайне редко удается лишить аналитическим путем, в связи с чем применяют вычисли-тельные машины.

Решение задачи оптимизации существенно осложняется, когда критерий оптималь-ности является функцией нескольких независимых переменных, даже при известном анали-тическом выражении этой функции. Наибольшее же трудности возникают при отсутствии непрерывности у всех или некоторых производной оптимизируемой функции. В последнем случае для решения оптимальной задачи целесообразно использовать методы нелинейного программирования.

4.1.7. Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и в обычных методах исследования функций, но при наличии ограничений типа равенств на независимые переменные.

Методы можно применять для решения задач оптимизации объектов с распределен-ными параметрами и задач динамической оптимизации. Здесь вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему диф-ференциальных уравнений. Множители Лагранжа используют так же в качестве вспомога-тельного средства при решении задач с ограничением типа равенств в вариационном исчи-слении и динамическом программировании. Следует особо подчеркнуть, что метод множи-теля Лагранжа позволяют найти лишь необходимые условия существования условного экс-тремума для непрерывных функций, имеющих к тому же непрерывные производные.

Полученные в результате решения значения неизвестных Xiдолжны быть проверены на экстремум с помощью анализа производных более высокого порядка или другими методами.

4.1.8. Методы вариационного исчисления

Оптимальные задачи, когда решение представляется не как совокупность значения конечного числа переменных, а как совокупность функции, вид которых заранее не известен, составляют сущность вариационного исчисления. Вариационное исчисление применяется для оптимизации математически описанных процессов.

При статистической оптимизации процессов с распределенными параметрами или в задах динамических оптимизации. Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных уравнений Эйлера.

4.2. Методы детерминированного и случайного поиска

Различие указанных методов (рис.4.2) заключается в определении стратегии поиска направленного движения в n-мерном пространстве к оптимуму.

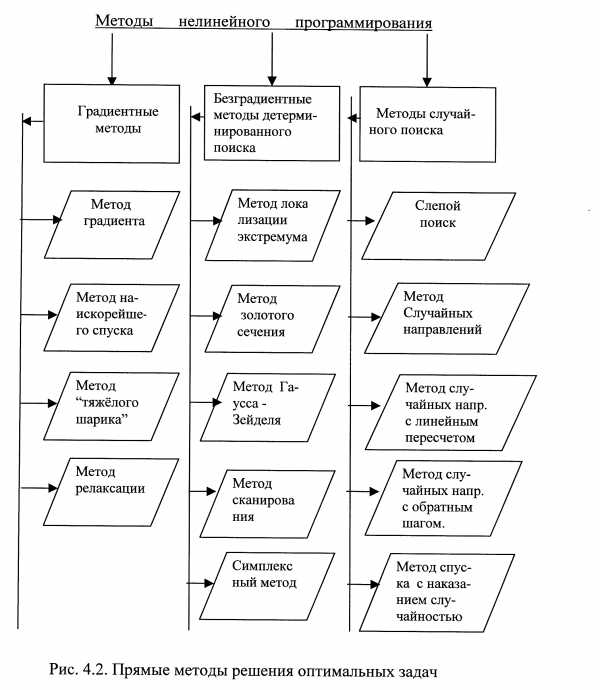
По этому признаку их можно классифицировать на методы и пассивного и направлен-ного поиска.

Последние, в свою очередь, делятся на одноэтапные (градиентные, случайного поиска) и многоэтапные (метод поочерёдного изменения переменных) (рис.4.3).

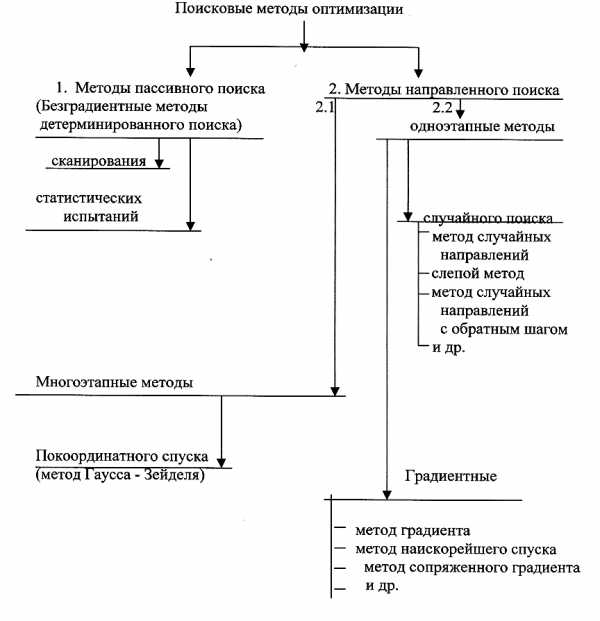
Рис. 4.3. Классификация поисковых методов

4.2.1. В основу градиентных методов поиска положены вычисление и анализ произ-водных целевой функции R(х). Если зависимостьR(х) нельзя записать в явном или анали-тическом виде, то единственным способом определения производныхR(х) является приме-нение численного метода.

В методе градиента используется градиент целевой функции. И поскольку направ-ление градиента в каждой точке совпадает с направлением наибыстрейшего изменения целевой функции, то локально наилучшим является градиентное направление при максими-зации или антиградиентное - при минимизации. Поиск оптимума производится в два этапа.На первом этапенаходятся значения частных производных по всем независимым направ-лениям, которые определяют направление градиента в рассматриваемой точке.На втором этапе осуществляется шаг в выбранном направлении. При выполнении шага одновременно

изменяются значения всех независимых переменных, каждая из них получает приращение, пропорциональное соответствующей градиента по данной оси. В методе градиента важной задачей является выбор стратегии изменения шага. Поскольку после каждого шага прихо-дится находить производные целевой функции по «n» независимым переменным, при слиш-ком малом шаге движение к оптимуму будет долгим из-за необходимости расчета целевой

функции в очень многих точках. Напротив, если шаг выбран слишком большим, то в районе оптимума может возникнуть "рыскание", которое не затухнет, либо затухнет очень медленно. Целесообразно поэтому применять алгоритм градиентного поиска, в котором величина шага меняется автоматически в соответствии с изменением абсолютной величины градиента.

Достоинством этого алгоритма является возможность увеличения и уменьшения в процессе поиска. Момент окончания поиска определяется по выполнению предварительно заданных условий нахождения целевой функции в окрестности экстремальной точки (рис.4.4).

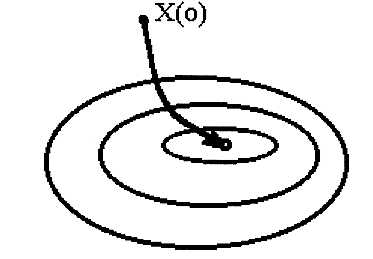
Рис.4.4. Характер движения к оптимуму методом градиента с малым шагом

Метод релаксациизаключаются в отыскании осевого направления, вдоль которого функция цели изменяется наиболее быстро. Осевому направлению соответствует наибольшая по модулю производная. В случае минимизации движение совпадает с направлением оси (знак производной отрицательный) и шаги делаются до тех пор, пока не будет получено минимальное значение по выбранному осевому направлению. После чего вновь определя-ются производные по всем переменным за исключением той, по которой осуществляется

спуск, и снова выбирается осевое направление скорейшего убывания функции цели, по которому производятся дальнейшие шаги. Критерием окончания поиска оптимума является достижение такой точки, из которой по любому осевому направлению дальнейшего убывания функции цели не происходит (рис.4.5). Хотя метод релаксации обладает определенными достоинствами перед методом градиента, поскольку при спуске вдоль выбранного осевого направления не требуется вычисления производных, однако движение происходит все же не в оптимальном направлении, т.к. градиент в данном случае не совпадает с осевым направле-нием.

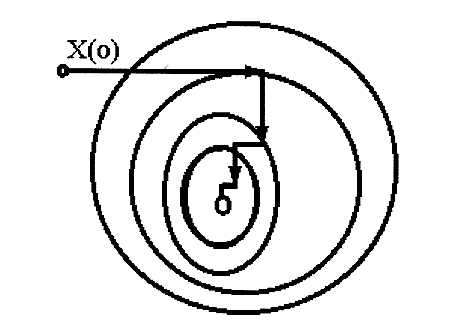
Рис.4.5 Характер движения к оптимуму в методе релаксации

В методе наискорейшего спуска нашло сочетание основных идей и методов релак-сации и градиента. Суть метода заключается в том, что после определения в начальной точке градиента оптимизируемой функцией направление движения поиска сохраняется неизмен-ным до тех пор, пока в этом направлении не будет найден минимум. После чего вычисляется градиент и определяется новое направление поиска. Данный метод является более выгодным из-за сокращения объема вычисления, особенно вдали от оптимума. Вблизи оптимума на-

правление градиента меняется резко, поэтому указанный метод автоматически переходит в метод градиента. Важной особенностью наискорейшего спуска (рис.4.6) является то, что при его применении каждое новое направление движения к оптимуму ортогонально предшест-вующему.

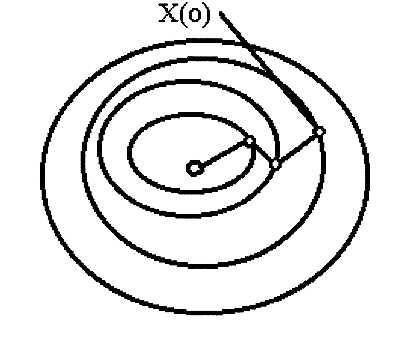
Рис.4.6. Характер движения к оптимуму методом наискорейшего спуска

Это объясняется тем, что движение в одном направлении производится до тех пор, пока оно не окажется касательным к линии постоянного уровня.

Метод "тяжелого шарика"в отличие от ранее рассмотренных может быть исполь-зован в задачах с целевыми функциями, имеющими несколько локальных экстремумов и характеризуется в этом смысле как метод поиска глобального экстремума.

К недостаткам градиентных методовследует отнести то, что для определения

направления движения требуется вычислить значение производной от функции по каждому параметру.

Вычисление производных может быть неточным из-за разнородности параметров, по которым выполняется оптимизация. Поэтому все параметры приводят к безразмерному виду. Поверхность отклика может оказаться такой, что придется часто изменять направление движения, а это приводит к значительным затратам времени при обращении к математиче-ской модели

Безградиентные методы детерминированного поискаиспользуют процесс

поиска информации, получаемую не при анализе производных, а от сравнения величины критерия оптимальности в результате выполнения очередного шага.

Некоторые из этих методов целесообразно применять в сочетании с градиентными

методами, что позволяет иногда довольно эффективные алгоритмы для решения задач нелинейного программирования. Безградиентные методы, кроме того, по характеру наиболее пригодны для оптимизации действующих промышленных и лабораторных установок при отсутствии математического описания объекта оптимизации.

В рассматриваемых методах применяют одномерный и многомерный поиск. Одномер-ный поиск экстремума функции одной переменной часто используют не только как самостоя-ельный метод оптимизации, но и как вспомогательный (например, при спуске по направле-нию) в многомерных методах оптимизации. В число методов одномерного поиска относятся:

1) метод локализации функции одной переменной;

2) метод золотого сечения.

Существо этих методов состоит в определении интервала, где находится экстремум одной переменной. Поскольку точность метода "золотого сечения" (рис.4.7) на порядок выше, то остановимся на нем несколько подробнее. Допустим, что задача состоит в опре-делении положения экстремума функции одной переменной на интервале [А, В]. "Золотым сечением" Zназывают деление отрезка на две части таким образом, чтобы отношение длины меньшего отрезка АС (см. рис.4.7) к длине всего интервала АВ было равно 0,38. При исполь-зовании этого метода имеется возможность с помощью одного вычисления на каждом

этапе локализовать положение экстремума Т2 =1 - Z(0,62 от длины исходного). На рис.4.7 этому соответствует отношение АС/АВ=ВВ/СВ=Т1=0,38.

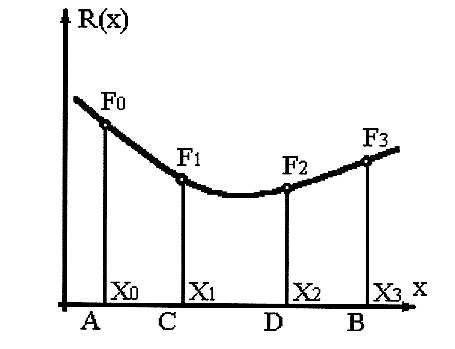
Рис. 4.7. Одномерный поиск методом "золотого сечения"

Метод поочерёдного изменения переменных, называемый такжеметодомГаусса- Зейделя, относится к методам многоэтапного направленного поиска и по существу аналогичен методу релаксации. Отличие в том, что не определяется новое направление с помощью производных, а поочередно изменяются независимые переменные, чтобы по каждой из них достигалось экстремальное значение целевой функции. Стратегия поиска минимума по каждой перемен-ной может быть любая, целесообразно использовать здесь и методы поиска экстремума

функции одной переменной. Простота и сравнительно небольшой объём вычислений, необ-ходимых для его реализации, обусловили его распространение в системах автоматического поиска оптимума функции цели, поэтому рассмотрим некоторые аспекты его практического применения.

Пусть требуется найти минимум функции трех переменных А,В,С. Каждая

переменная определена на интервалах: [А1, А2], [В1, В2], [С1, С2]. Методом "золотого сечения" осуществим поочерёдно минимизацию целевой функции по каждой переменной, которые примут соответственно значения АМ1, ВМ1, СМ1. Получив первый приближённый минимум, повторяют поиск по каждой переменной и, если координаты точки минимума функции цели не изменились, то поиск заканчивают. В качестве критерия минимизация принята улучшенная квадратичная оценка из тех соображений, что в отличие от обычных

интегральных оценок в ней накладываются ограничения не только на величину отклонения х, но также и на скорость отклонения х.

Улучшенная квадратичная интегральная оценка имеет вид

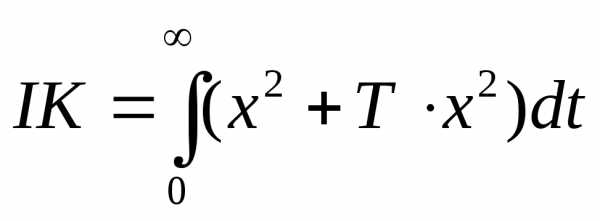(4.6)

где Т - некоторая постоянная времени (экстремаль).

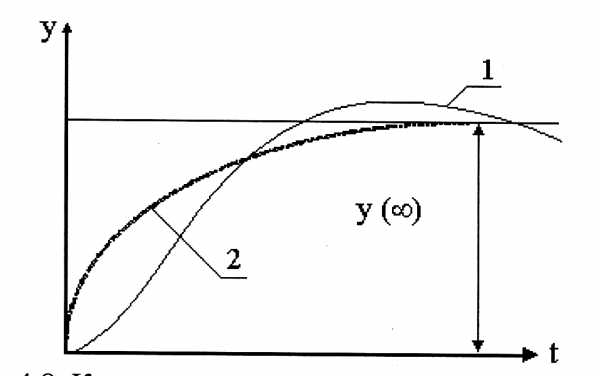
Рис. 4.8. к методу улучшенной квадратичной оценки

1 - реальный переходной процесс; 2 - оптимальный переходной процесс

Минимизация целевой функции по (4.6) позволяет приблизить переходный процесс к экспоненте (рис.4.8) с заданной постоянной времени Т, которая носит название экстремали. Выбор параметров системы по заданной оценке приводит к меньшей колебательности пере-ходных процессов по сравнению с обычной квадратичной интегральной оценкой. При мно-гомерном поиске по методу Гаусса - Зейделя выполняется сравнение координат MINIиMIN2 по каждой переменной. Если это отклонение меньше или равно шагу поиска по каждой пере-менной, то поиск заканчивается с выводом значений координат и целевой функции. В про-тивном случае процесс оптимизации повторяется. Функция цели вычисляется в процессе расчета переходного процесса. За один такт квантования по времени вычисляется ошибка (отклонение) и ее производная. Отклонение находится как разность между установившимся значением, которое определяется путем деления свободных членов числителя и знаменателя передаточной функции, и рассчитанным на данном шаге значением переходного

процесса, как это показано на рис.4.9.

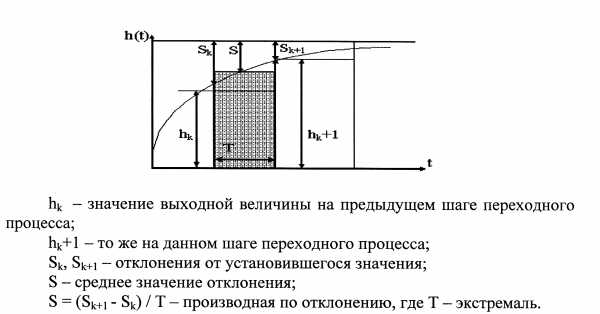
Рис. 4.9. Вычисление улучшенной квадратичной интегральной оценки

Значение интегральной оценки на каждом шаге расчёта определяют по формуле

(4.7)

где τ = 0,618.

Величина интегральной оценки за весь переходный процесса находится как

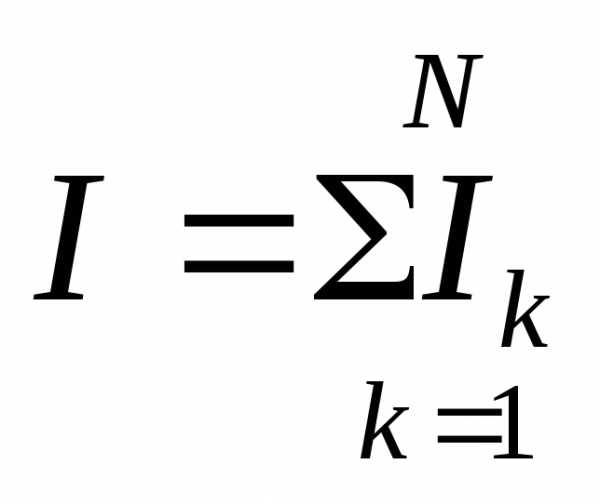(4.8)

где N- количество шагов расчета переходного процесса.

В завершение анализа прямых методов решения оптимальных задач остановимся

на группе методов случайного поиска. Основная идея этих методов, заключается в том, чтобы перебором случайных совокупностей значений независимых переменных найти оптимум целевой функции или направления движения к нему. Общим для всех методом случайного поиска является применение случайных чисел в процессе поиска, и что относятся они к одноэтапным методам направленного поиска.

При использовании слепого поискав допустимой области изменения независимых

переменных случайным образом выбирается точка, в которой вычисляется значение целевой функции. Далее аналогично выбирается другая точка, где также рассчитывается функция цели и сравнивается с полученным ранее. Если новое значение функции цели оказывается меньше (больше) предыдущего, то это значение запоминается вместе с координатами точки, где оно было вычислено. Затем продолжается выборка случайных точек и сравнение значе-ний критерия оптимальности в этих точках с уже найденными точками. Каждый раз, когда получается меньшее значение целевой функции, оно запоминается вместе с соответству-ющими координатами, после чего продолжается поиск лучшего приближения к оптимуму.

В соответствии с методом случайных направлений из некоторой точки Хкв пространстве параметров делается несколько пробных шагов в случайных направлениях

(рис.4.10). Для практических расчётов число шагов в серии часто принимается равным

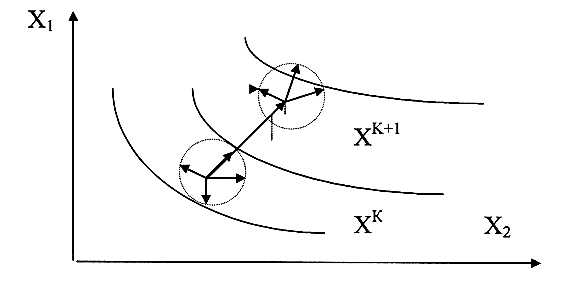
Рис. 4.10. Метод случайных направлений

размерности решаемой задачи mприращения функции цели, сравнивают друг с другом и определяют направления, в котором это улучшение оказалось наибольшим. При этом коор-динаты новой изображающей точки в пространстве параметров определяется по формуле

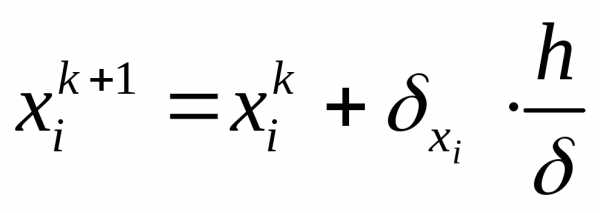(4-9)

где 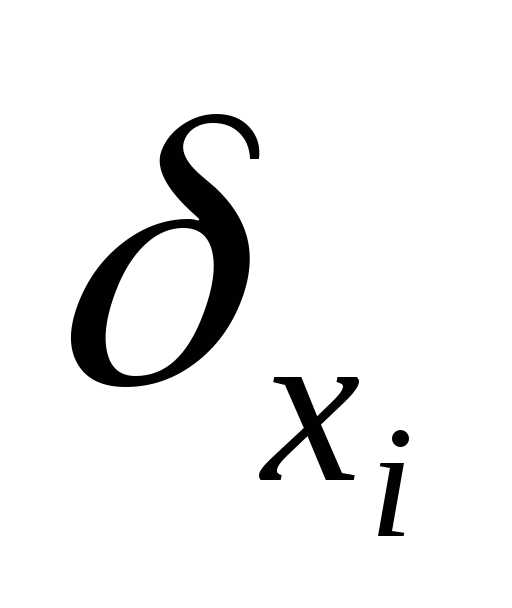- проекция наиболее удачного пробного шага на ось Хi;

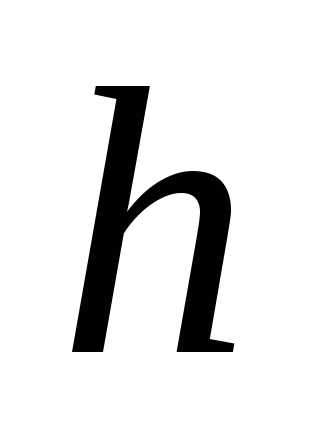- величина рабочего шага;

- значение пробного шага.

Критерием окончания поиска служит минимальный размер шага Нmin, которым и задается точность определения оптимума.

Метод случайных направлений с обратным шагомпредставляет собой улучшение алгоритма, описанного выше. Отличительной его особенностью является то, что при неудач-ном шаге из точки сразу производится шаг в обратном направлении. При достаточном удалении от оптимума такая стратегия оказывается весьма эффективной. Если и обратный шаг оказался неудачным, то можно либо сделать новый случайный шаг из точки Хк, либо перейти к поиску с уменьшенным размером шага из этой точки.

Метод случайных направлений с линейным пересчетомможет использоваться,

если кривизна оптимизируемой функции относительно не высока и в пределах полного шага поиска изменение целевой функции можно аппроксимировать линейной формой.

Метод спуска "с наказанием случайностью" по существу представляет собой аналог метода наискорейшего спуска с той лишь разницей, что направление спуска выби-рается случайным образом. Указанный метод целесообразно использовать тогда, когда для нахождения значений целевой функции не требуется больших вычислительных затрат.

studfiles.net

Задача - динамическая оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Задача - динамическая оптимизация

Cтраница 1

Задачи динамической оптимизации, рассматриваемые в § 10.3, имеют целевые функции, являющиеся интегралами функции стоимости по времени. [1]

Задачу динамической оптимизации рассмотрим для первого реактора, на входе которого сосредоточены все управляющие переменные и на выходе которого управляемые переменные меняются наиболее сильно. [3]

Ставится задача динамической оптимизации по стационарной ( в смысле изменения коэффициентов во времени) модели объекта. Динамика связана с необходимостью учета переходящих запасов полуфабрикатов и готовой продукции на границах шагов дискретности и с наличием интегральных ограничений на весь горизонт планирования. Изменение во времени ограничений по ресурсам учитывается кусочно-постоянной аппроксимацией по шагам дискретности. [4]

Особенностью задач динамической оптимизации является то, что значение критерия оптимальности определяется не только положением, существующим в рассматриваемый момент времени, но и предысторией процесса, начиная с некоторого начального момента. Поэтому оценка эффективности процесса должна учитывать его поведение в течение всего исследуемого нестационарного периода. [6]

Детерминированные модели задач динамической оптимизации непрерывных производств [5, 27, 30] не учитывают вероятностную природу информации о характере протекания технологических процессов в условиях реализации производственной программы предприятия. [7]

В широком классе задач динамической оптимизации региональных ТСВ посредством регулирования речного стока необходим расчет полных динамических характеристик качества воды на выходе водохранилища при интенсивных колебаниях качества воды на входе и нестационарности внутриводоемных процессов. [8]

В книге решен цикл задач динамической оптимизации механизмов с использованием вариационных методов. Рассмотрено два типа задач. К первому типу относятся задачи оптимизации сравнительно несиловых цикловых механизмов, в которых скорость ведущего звена может полагаться известной. Ко второму типу относятся задачи оптимизации силовых механизмов, соединяющих двигатель с рабочим органом машины. [9]

В следующем разделе будет сформулирована задача динамической оптимизации обтекания абсолютно твердых тел и составленных из них механических систем. Для понимания самой постановки такой задачи, ее особенностей, математических трудностей, обусловленных этими особенностями, и способов их преодоления приведены необходимые сведения из теории оптимального управления динамическими процессами. Учебник [31] дает достаточное представление по теории автоматического управления. [10]

Подводя итоги обсуждения путей решения задач динамической оптимизации региональных ТСВ в минимаксной постановке, приведем значения водоохранных и энергетических показателей ( табл. 10 - 2) для различных вариантов управления водохранилищем в маловодный год 95 % - ной обеспеченности при экономически оптимальной очистке сточных вод всех промышленных зон Кузбасса. [12]

Задача 3.1 относится к числу задач динамической оптимизации с ограничениями в виде равенств на фазовые переменные. [13]

Беспоисковые оптимальные адаптивные АСУ ТП решают задачу динамической оптимизации методами беспоисковой адаптации. Они отличаются от аналогичных поисковых систем тем, что адаптация нестационарной системы управления осуществляется под оптимальную эталонную модель. При этом параметры указанной модели вычисляются с помощью поисковых процедур динамической оптимизации заранее, на этапе проектирования. Таким образом, в этих системах задача поиска оптимального управления заменяется более простой в вычислительном отношении задачей подстройки под оптимальную модель системы. [14]

Оптимальное планирование ремонта оборудования относится к классу задач динамической оптимизации. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Динамическая оптимизация с централизованной схемой обнаружения конфликтов

В конвейере с динамическим планированием выполнения команд все команды проходят через ступень выдачи строго в порядке, предписанном программой (упоря-доченная выдача). Однако они могут приостанавливаться и обходить друг друга на второй ступени (ступени чтения операндов) и тем самым поступать на ступени выполнения неупорядочено. Централизованная схема обнаружения конфликтов представляет собой метод, допускающий неупорядоченное выполнение команд при наличии достаточных ресурсов и отсутствии зависимостей по данным. Впервые подобная схема была применена в компьютере CDC 6600.

Прежде чем начать обсуждение возможности применения подобных схем, важно заметить, что конфликты типа WAR, отсутствующие в простых конвейерах, могут появиться при неупорядоченном выполнении команд. В ранее приведенном примере регистром результата для команды SUBD является регистр R8, который одновременно является источником операнда для команды ADDD. Поэтому здесь между командами ADDD и SUBD имеет место антизависимость: если конвейер выполнит команду SUBD раньше команды ADDD, он нарушит эту антизависимость. Этот конфликт WAR можно обойти, если выполнить два правила: (1) читать регистры только во время стадии чтения операндов и (2) поставить в очередь операцию ADDD вместе с копией ее операндов. Чтобы избежать нарушений зависимостей по выходу конфликты типа WAW (например, это могло произойти, если бы регистром результата команды SUBD была бы регистр F10) все еще должны обнаруживаться. Конфликты типа WAW могут быть устранены с помощью приостановки выдачи команды, регистр результата которой совпадает с уже используемым в конвейере.

Задачей централизованной схемы обнаружения конфликтов является поддержание выполнения команд со скоростью одна команда за такт (при отсутствии структурных конфликтов) посредством как можно более раннего начала выполнения команд. Таким образом, когда команда в начале очереди приостанавливается, другие команды могут выдаваться и выполняться, если они не зависят от уже выполняющейся или приостановленной команды. Централизованная схема несет полную ответственность за выдачу и выполнение команд, включая обнаружение конфликтов. Подобное неупорядоченное выполнение команд требует одновременного нахождения нескольких команд на стадии выполнения. Этого можно достигнуть двумя способами: реализацией в процессоре либо множества неконвейерных функциональных устройств, либо путем конвейеризации всех функциональных устройств. Обе эти возможности по сути эквивалентны с точки зрения организации управления. Поэтому предположим, что в машине имеется несколько неконвейерных функциональных устройств.

Машина CDC 6600 имела 16 отдельных функциональных устройств (4 устройства для операций с плавающей точкой, 5 устройств для организации обращений к основной памяти и 7 устройств для целочисленных операций). В нашем случае централизованная схема обнаружения конфликтов имеет смысл только для устройства плавающей точки. Предположим, что имеются два умножителя, один сложитель, одно устройство деления и одно целочисленное устройство для всех операций обращения к памяти, переходов и целочисленных операций. Хотя устройств в этом примере гораздо меньше, чем в CDC 6600, он достаточно мощный для демонстрации основных принципов работы. Поскольку как наша машина, так и CDC 6600 являются машинами с операциями регистр-регистр (операциями загрузки/записи), в обеих машинах методика практически одинаковая. На рис.43 показана подобная машина.

Каждая команда проходит через централизованную схему обнаружения конфликтов, которая определяет зависимости по данным; этот шаг соответствует стадии выдачи команд и заменяет часть стадии ID в нашем конвейере. Эти зависимости определяют затем моменты времени, когда команда может читать свои операнды и начинать выполнение операции. Если централизованная схема решает, что команда не может немедленно выполняться, она следит за всеми изменениями в аппаратуре и решает, когда команда сможет выполняться. Эта же централизованная схема определяет также когда команда может записать результат в свой регистр результата. Таким образом, все схемы обнаружения и разрешения конфликтов здесь выполняются устройством центрального управления.

Каждая команда проходит четыре стадии своего выполнения. (Поскольку в данный момент мы интересуемся операциями плавающей точки, мы не рассматриваем стадию обращения к памяти). Рассмотрим эти стадии сначала неформально, а затем детально рассмотрим как централизованная схема поддерживает необходимую информацию, которая определяет обработку при переходе с одной стадии на другую.

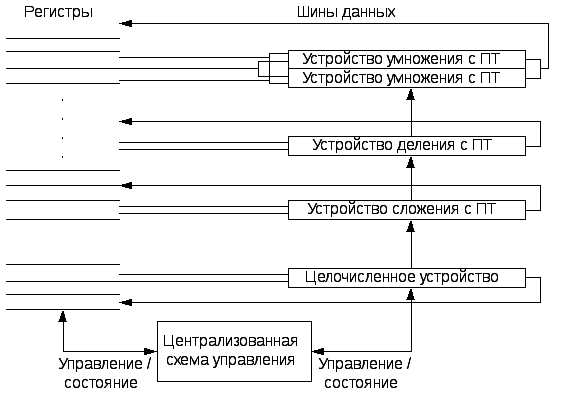
Рис 43 – Централизованная схема управления

Следующие четыре стадии заменяют стадии ID, EX и WB в стандартном конвейере:

Выдача. Если функциональное устройство, необходимое для выполнения команды, свободно и никакая другая выполняющаяся команда не использует тот же самый регистр результата, централизованная схема выдает команду в функциональное устройство и обновляет свою внутреннюю структуру данных. Поскольку никакое другое работающее функциональное устройство не может записать результат в регистр результата нашей команды, мы гарантируем, что конфликты типа WAW не могут появляться. Если существует структурный конфликт или конфликт типа WAW, выдача команды блокируется и никакие следующие команды не будут выдаваться на выполнение до тех пор, пока эти конфликты существуют. Эта стадия заменяет часть стадии ID в нашем конвейере.
Чтение операндов. Централизованная схема следит за возможностью выборки источников операндов для соответствующей команды. Операнд-источник доступен, если отсутствует выполняющаяся команда, которая записывает результат в этот регистр или если в данный момент времени в регистр, содержащий операнд, выполняется запись из работающего функционального устройства. Если операнды-источники доступны, централизованная схема сообщает функциональному устройству о необходимости чтения операндов из регистров и начале выполнения операции. Централизованная схема разрешает конфликты RAW на этой стадии динамически и команды могут посылаться для выполнения не в порядке, предписанном программой. Эта стадия, совместно со стадией выдачи, завершает работу стадии ID простого конвейера.
Выполнение. Функциональное устройство начинает выполнение операции после получения операндов. Когда результат готов оно уведомляет централизованную схему управления о том, что оно завершило выполнение операции. Эта стадия заменяет стадию EX и занимает несколько тактов в рассмотренном ранее конвейере.
Запись результата. Когда централизованная схема управления узнает о том, что функциональное устройство завершило выполнение операции, она проверяет существование конфликта типа WAR.Если этот конфликт типа WAR не существует, централизованная схема управления сообщает функциональному устройству о необходимости записи результата в регистр назначения. Эта стадия заменяет стадию WB в простом конвейере.

Основываясь на своей собственной структуре данных, централизованная схема управления управляет продвижением команды с одной ступени на другую взаимодействуя с функциональными устройствами. Но имеется небольшое усложнение: в регистровом файле имеется только ограниченное число магистралей для операндов-источников и магистралей для записи результата. Централизованная схема управления должна гарантировать, что количество функциональных устройств, которым разрешено продолжать работу на ступенях 2 и 4 не превышает числа доступных шин. Не будем вдаваться в дальнейшие подробности и упомянем лишь, что CDC 6600 решала эту проблему путем объединения 16 функциональных устройств друг с другом в четыре группы и поддержки для каждой группы устройств набора шин, называемых магистралями данных (data trunks). Только одно устройство в группе могло читать операнды или записывать свой результат в течение одного такта.

Общая структура регистров состояния устройства централизованного управления состоит из 3-х частей:

Состояние команды - показывает каждый из четырех этапов выполнения команды.
Состояние функциональных устройств - имеются 9 полей, описывающих состояние каждого функционального устройства:
1. Занятость - показывает, занято устройство или свободно;
2. Op - выполняемая в устройстве операция;
3. Fi - регистр результата;
4. Fj, Fk - регистры-источники операндов;
5. Qj, Qk - функциональные устройства, вырабатывающие результат для записи в регистры;
6. Rj, Rk - признаки готовности операндов в регистрах Fj, Fk
Состояние регистров результата - показывает функциональное устройство, которое будет записывать в каждый из регистров. Это поле устанавливается в ноль, если отсутствуют команды, записывающие результат в данный регистр.

studfiles.net

Оптимизация процессов динамическая - Справочник химика 21

Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению диф([)еренциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений. [c.32] Важной характеристикой любой оптимальной задачи является ее размерность п, равная числу переменных, задание значений которых необходимо для однозначного определения состояния оптимизируемого объекта. Как правило, решение задач высокой размерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программирование и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерности, которые могут быть представлены как многостадийные процессы с относительно невысокой размерностью каждой стадии. [c.34]

Вьиие уже была рассмотрена вычислительная процедура метода динамического программирования при оптимизации процесса, в котором размерность векторов состояния п управления на каждой стадии равна 1. Очевидно, что решение задачи может усложниться, если размерность вектора состояния гп или векторов управления г [c.259]

Более сложная задача возникает при использовании метода динамического программирования для оптимизации процессов с байпасными потоками. Поскольку направление расчета противоположно направлению такого потока, при выборе оптимального управления на стадии, к которой он подводится, состояние этого потока, так же как и состояние выхода предшествующей стадии, необходимо исследовать во всем возможном диапазоне изменения его параметров. Другими словами, размерность задачи выбора оптимального управления изданной стадии увеличивается на размерность состояния байпасного потока. [c.297]

В простейших случаях, когда целевая функция задана аналитически, используют классические методы нахождения экстремума методами дифференциального исчисления. При наличии ограничений типа равенств, наложенных на независимые переменные, используют метод множителей Лагранжа. В более сложных случаях, когда критерий оптимальности представлен в виде функционалов, используют методы вариационного исчисления-, при оптимизации процессов, описываемых системами дифференциальных уравнений, применяют принцип максимума Понтрягина. Используют также динамическое, линейное программирование и другие методы оптимизации. [c.38]

При рассмотрении задачи последовательной оптимизации метод динамического программирования позволяет разбить ее на несколько отдельных задач с меньшим числом переменных, что весьма облегчает вычисления в процессе решения. В частности, если ХТС имеет только последовательные технологические связи, задача совместной максимизации параметров может быть сведена к максимизации [c.309]

Исследование динамических свойств управляемых объектов важно для оптимизации процессов пуска и остановки оборудования, создания систем автоматической защиты, разработки локальных систем автоматического управления и АСУ ТП. В табл. Vni.l приведен перечень объектов, динамическое поведение которых изучено достаточно подробно. Из нее можно сделать следующие выводы [c.294]

Большая часть методов решения оптимальных задач основана на предположении, что математическая модель оптимизируемого объекта известна. Более того, многие методы оптимизации используют конкретные свойства объекта и его математического описа-, ния. Например, для многостадийных процессов эффективным методом оптимизации является динамическое программирование для процессов, описываемых дифференциальными уравнениями, — принцип максимума. [c.27]

Эти затруднения при применении динамического программирования для оптимизации процессов высокой размерности создатель метода Р. Беллман образно назвал проклятием размерности . [c.280]

Выше уже отмечалось, что метод динамического программирования находит весьма широкое применение при решении задач оптимизации процессов химической технологии. Значительное число примеров соответствующих оптимальных задач, сформулированных в терминах указанного метода, можно найти в литературе [2, 3]. В подавляющем большинстве практических задач конечное решение получают только в численной форме. Однако в очень простых случаях оно может быть найдено в аналитическом виде, что видно из приведенных ниже примеров, которые наглядно позволяют проследить основные моменты использования метода динамического программирования при решении задач оптимизации. [c.287]

В предыдущих разделах настоящей главы рассматривались вопросы применения метода динамического программирования для оптимизации дискретных многостадийных процессов. Именно при анализе таких процессов, которые допускают четкое разбиение на стадии, наиболее наглядно проявляются основные достоинства этого метода как способа решения оптимальных задач для процессов с произвольным числом управляемых стадий. Однако метод динамического программирования можно использовать также и для оптимизации процессов с распределенными параметрами и нестационарных процессов с сосредоточенными параметрами, которые изменяются непрерывно. При этом закон их изменения описывается системами дифференциальных уравнений [c.295]

В качестве метода оптимизации процесса управления водным режимом сельскохозяйственных культур выбран метод стохастической поэтапной оптимизации, основанный на принципе динамического программирования. Стохастические задачи динамического программирования решаются ходом назад , так как стохастическая природа процесса не позволяет задать состояние системы в конце планируемого периода. Поэтому оптимальное решение, принимаемое в начале первого периода, находится из заданного условия оптимальности функции цели за весь планируемый промежуток времени. Поскольку величина этой [c.247]

Проблеме оптимизации процессов в химических реакторах посвящен ряд монографий [8—10], поэтому мы ограничимся рассмотрением и обоснованием решения задачи А. Применим для решения этой задачи аппарат динамического программирования при условии соблюдения достаточной общности в постановке задачи. Эти условия сводятся к следующим четырем требованиям 1) управление процессом осуществляется s-вектором 2) процесс описывается системой обыкновенных дифференциальных уравнений 1-го порядка при этом порядок исследуемых реакций может быть произвольным, и, следовательно, система обыкновенных дифференциальных уравнений первого порядка (1) в общем случае не линейна 3) исследуемый процесс является многомерным, т. е. число реагентов может быть произвольным 4) на переменные управления и фазовые переменные наложены ограничения. [c.145]

После проверки адекватности полной математической модели исследуемому объекту (процессу) в цикле с ЭВМ следует провести оптимизацию математической модели любым из известных методов. К методам оптимизации относятся динамическое программирование, нелинейное программирование, принцип максимума и другие. Цель всех этих методов — нахождение оптимальных условий (температуры, давления, соотношения компонентов в реакционной смеси, избирательности, продолжительности и т. д.) проведения процесса в зависимости от общих технико-экономических показателей процесса. Обычно оптимальный режим находят в две ступени. Сначала определяют наилучшие условия процесса теоретически, исходя из его максимальной интенсивности, затем выбирают аппарат, позволяющий наиболее близко подойти к теоретическому оптимуму [91. [c.44]

Поэтому уровень экономичности того или иного химико-технологического аппарата или типового процесса всегда есть величина динамическая. Для объективной оценки этого уровня необходимо выявить и изучить влияние всего многообразия различных факторов на технико-экономические показатели и найти оптимальные условия, а также пределы, обеспечивающие наиболее эффективную совместную работу разной аппаратуры. Последнее условие весьма существенно при оптимизации процессов, поскольку в - связи с непрерывным научно-техническим прогрессом в отраслях промышленности с непрерывной химической технологией, ростом числа взаимосвязанных и взаимообусловленных типовых процессов, расширением диапазона варьирования переменными параметрами значительно возрастают не только связи между совместно работающими аппаратами, но и увеличивается сложность расчетов при экономическом анализе различных вариантов использования техники. [c.19]

Проблемы создания и реализации оптимального стационарного режима процесса решает статическая оптимизация, создания и реализации системы оптимального управления процессом—динамическая оптимизация. [c.202]

В книге Робертса рассматриваются вопросы оптимизации как детерминированных, так и стохастических моделей многостадийных процессов химической технологии методом динамического программирования. Использование этого метода особенно целесообразно при оптимизации процессов химической технологии, осуществляемых через последовательность этапов превращений, таких, как ректификация, абсорбция, экстракция, а также химических процессов, проводимых в цепочке реакторов, в многослойных контактных аппаратах и т. п. Этот метод позволяет определить оптимальную стратегию проведения процессов и, следовательно, может служить основой составления оптимального алгоритма управления процессом. [c.7]

Однако несмотря на отмеченные недостатки, книга Робертса пока остается наиболее доступной для широкого круга специалистов, имеющих дело с вопросами оптимизации процессов химической технологии. Довольно простая форма изложения математических аспектов метода динамического программирования, четкое определение возможностей и границ применимости метода, наглядность и законченность решения приводимых задач делают ее настольным пособием при решении многих вопросов химической технологии и автоматизации химических процессов. [c.9]

Для оптимизации процессов с распределенными параметрами предпочтительнее все же оказывается принцип максимума, которому посвящена следующая глава. Однако всегда нужно учитывать воз-мо кность аппроксимации непрерывного процесса дискретным многостадийным процессом и пользоваться указанной возмо кностью для решения оптимальных задач невысокой размерности. Это обусловлено 1см, что метод динамического программирования представляет в распоряжение исследователя весьма удобную процедуру оптимизации многостадийных процессов, которая сравнительно легко программируется на вычислительных ма1[шнах. [c.319]

Проведены исследования с целью оптимизации процесса сушки трансформаторного масла (ТМ) клиноптилолитом (КП) месторождения Хекордзула (Грузия). Изучено влияние температуры прокаливания КП на глубину осушки ТМ и установлено, что наибольшая глубина осушки ТМ достигается при температуре 235-350°С. Проведена также осушка ТМ измельченным и рассеянным КП при комнатной температуре и установлено, что оптимальные показатели достигаются в области размера частиц адсорбента 3-5 мм повышение осушающей способности КП вызвано увеличением общей площади контакта адсорбента с ТМ и скорости диффузии молекул воды во внутрикристаллическом объеме адсорбента. Дальнейшее увеличение дисперсности КП ухудшает его обезвоживающее действие. Изучена осушка ТМ в динамических условиях при темнературе 25 С осушающая способность оценивалась до проекоковой концентрации 0.002%. [c.184]

Как динамическое программирование, так и принцип максимума применялись для решения различных дискретных и непрерывных задач химической технологии. Принцип максимума, в частности, был использован при оптимизации отдельных реакторов и их каскадов " , перекрестно-поточной экстракционной установки - , а также при оптимизации процесса периодической бщ а рной ректи ф икаци и . [c.130]

Эффективно использование систем динамической оптимизации процесса ККФ [90], а также компьютерной системы оптимизации и управления установкой, которая обеспечивает оптимальное планирование, переход с режима на режим при изменении качества сырья, бопее стабильную и длительную работу 91]. [c.62]

Использование моделей. Идентифицированные и проверенные на адекватность математические модели (в соответствии с правилами теории планирования экспериментов) используются для решения двух классов задач, различающихся критериями и варьируемыми переменными оптимизации проектирования и оптимизации режимов действующих производств. Число реальных полимеризационных процессов, полностью спроектированных с использованием математической модели [12], пока ограничено одним процессом — инициированной полимеризацией стирола. Однако в дальнейшем число таких процессов будет расти, о чем свидетельствует все возрастающий интерес к этой проблеме. Значительно чаще рассматриваются и решаются вопросы оптимизации процессов полимеризации действующих установках. Оптимизация динамических о" в рамках различных систем автоматического регууч к Н.1ИЯ рассматривается обычно применительно к конкретны )лимеризационным процессам например, эмульсионной полу. кизации винилхлорида [130], эмульсионной полиме- [c.229]

Термореактивные пластмассы приобретают все большее значение вследствие возможности их переработки на литьевых мавинах. Оптимизация процессов переработки путем программирования динамического давления дает качественные и экономические преимущества, которые значительно расширяют области применения реакто-пластов. [c.43]

В настоящее время в теории автоматического управления широко развито направление, связанное с оптимизацией систем управления ОРП. Значительные результаты получены А. Г. Бут-ковским [26—28], А. И. Егоровым [61, 62], Т. К. Сиразетдино-вым [101], Ж. Д. Лионсом [80]. Однако достаточно полно решены сейчас лишь вопросы статической оптимизации процессов ректификации. Важные результаты в этом направлении получены И. В. Анисимовым [7, 10—12]. Задачи же динамической оптимизации ректификационных колонн изучены недостаточно, что в значительной степени связано с отсутствием математических методов, позволяющих рассчитывать нестационарные режимы с приемлемой для целен управления скоростью и точностью в широком диапазоне возмущающих воздействий. [c.10]

В книге в доступной форме изложены основы методом оптимизации (классический анализ, вариационное исчисление, принцип максимума, динамическое, линейное и нелинейное программирование) с иллюстрацией их на объектах химической технологии. Сформулированы общие положения, касающиеся выбора критериев о[1ти-мальности химико-технологических процессов, и приведены их математические модели. Рассмотрены задачи, связанные с оптимизацией конкретных процессов. [c.4]

chem21.info