27. Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности. Задачи оптимизации в теории управления

математические основы оптимизации. Многокритериальная оптимизация (особенности оптимизации экономических систем).

Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы.

Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Математическая модель для задачи оптимального управления включает в себя:

-формулировку цели управления, выраженную через критерий качества управления;

-определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления;

-определение ограничений на используемые ресурсы в виде уравнений или неравенств.

Если управляемый объект или процесс является детерминированным, то для его описания используются дифференциальные уравнения. Наиболее часто используются обыкновенные дифференциальные уравнения вида . В более сложных математических моделях (для систем с распределёнными параметрами) для описания объекта используются дифференциальные уравнения в частных производных. Если управляемый объект является стохастическим, то для его описания используются стохастические дифференциальные уравнения.

Реальное поведение объекта или системы всегда отличается от программного вследствие неточности в начальных условиях, неполной информации о внешних возмущениях, действующих на объект, неточности реализации программного управления и т.д. Поэтому для минимизации отклонения поведения объекта от оптимального обычно используется система автоматического регулирования.

Иногда (например, при управлении сложными объектами, такими как доменная печь в металлургии или при анализе экономической информации) в исходных данных и знаниях об управляемом объекте при постановке задачи оптимального управления содержится неопределённая или нечёткая информация, которая не может быть обработана традиционными количественными методами. В таких случаях можно использовать алгоритмы оптимального управления на основе математической теории нечётких множеств (Нечеткое управление). Используемые понятия и знания преобразуются в нечёткую форму, определяются нечёткие правила вывода принимаемых решений, затем производится обратное преобразование нечётких принятых решений в физические управляющие переменные. Задача оптимального управления

Сформулируем задачу оптимального управления:

Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.

здесь — вектор состояния — управление, — начальный и конечный моменты времени.

Задача оптимального управления заключается в нахождении функций состояния и управления для времени , которые минимизируют функционал.

studfiles.net

Методы оптимизации в теории управления Глава 1

Методы оптимизации в теории управления

Глава 1. Задачи конечномерной оптимизации в теории управления 1. 1. Основные понятия теории управления

Обычно в учебных курсах по теории управления рассматриваются некоторые специальные разделы этой теории, такие как теория автоматического управления или математическая теория оптимальных процессов, основанная на принципе максимума Понтрягина или принципе оптимальности Беллмана. В данном же случае нас будет интересовать управляемая система как некая общая концепция кибернетики — науки об управлении.

Под управлением будем понимать процесс такого воздействия на некоторую систему или объект (объект управления), при котором состояние системы или объекта изменяется «в нужную сторону» . Объектами управления, очевидно, могут быть: техническое устройство (например, автомобиль), экономическая ситуация на предприятии или фирме, экосистема региона, процесс разработки программного проекта, сам программный проект и его характеристики и т. п. Предполагается, что мы можем не только оказывать воздействие на объект, но и оценивать результаты этого воздействия по некоторым заданным критериям. Например, критериями качества процесса разработки программного проекта могут служить время завершения проекта и его бюджет (стоимость разработки). Влиять на эти характеристики (управлять ими) мы можем, например, с помощью перераспределения ресурсов между отдельными работами, составляющими данный программный проект.

Общая схема процесса управления приведена на рис. 1. 1. Объект управления рассматривается как сколь угодно сложная система, преобразующая входные управляющие воздействия U(t) в выходные сигналы (траектории) V(t) , характеризующие состояние объекта управления в момент времени t. Очевидно, что реальный объект управления может иметь множество входов и выходов, определяющих его функциональное взаимодействие с внешней средой. Все эти каналы связи со средой на рис. 1. 1 не показаны. Изображены лишь те входы и выходы, которые являются существенными для формулирования задачи управления. Объект управления и воздействующее на него устройство управления образуют систему управления. Предполагается, что на объект управления действуют также возмущения ξ(t), изменяющие, как правило, в непредсказуемом направлении основные характеристики объекта управления.

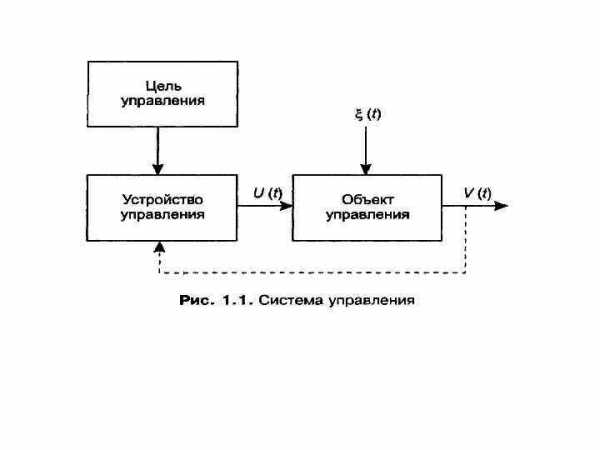
Мы здесь для определенности будем предполагать, что все функции времени, изображенные на рис. 1. 1, являются вектор-функциями с вещественными компонентами и заданными размерностями. Сигнал управления вырабатывается в соответствии с некоторой заданной целью управления, определяемой теми задачами, которые поставлены перед системой управления. Довольно часто в системах управления для выработки управляющих воздействий оказывается необходимой информация о действительном состоянии объекта управления. Эта информация поступает по цепи обратной связи, показанной на рис. 1. 1 пунктирной стрелкой.

В качестве примера объекта управления может выступать некоторый завод, перерабатывающий сырье в готовую продукцию. Здесь под управлением может пониматься вся система мероприятий и нововведений, направленная на достижение определенной цели или целей, связанных, например, с качеством и количеством выпускаемой продукции, а также, возможно, с определенными требованиями к срокам выпуска этой продукции.

Как справедливо указывается в литературе, описание некоторого объекта как объекта управления и выявление каналов воздействия на него может производиться только исходя из заданной цели управления. Так, например, тот же завод с точки зрения служб санэпиднадзора или иных экологических служб является объектом управления, перерабатывающим сырье в промышленные отходы, загрязняющие окружающую среду. В этом случае управление со стороны этих служб будет направлено на снижение влияния вредных техногенных факторов, а вовсе не на интенсификацию производства, как в первом случае.

Основные задачи, решаемые большинством систем управления и отражающие главные цели управления, могут быть отнесены к одному из следующих типов: стабилизация, выполнение программы, слежение, экстремальное управление, оптимизация.

Задача стабилизации заключается в поддержании некоторых выходных (управляемых) характеристик объекта управления на заданных уровнях несмотря на постоянно действующие возмущения ξ(t) : V(t) = const. Задачи стабилизации возникают и решаются в живой природе (поддержание стабильной температуры тела у теплокровных животных), в технических системах (например, стабилизация напряжения и частоты в энергосистемах вне зависимости от нагрузки) и т. д.

Задача выполнения программы, или задача программного управления, возникает, когда необходимо обеспечить наперед заданные траектории V(t). Иначе говоря, необходимо «заставить» объект управления изменять свои управляемые характеристики во времени по заданному закону, по определенной программе V*(t). Например, процесс разработки некоторого технического изделия на заводе должен протекать в соответствии с заранее разработанным временным графиком. Метаморфоза насекомых в живой природе также происходит в соответствии с некоторыми биологическими программами развития. Запускаемый космический аппарат обычно выводится на траекторию в соответствии с заранее заданной расчетной траекторией. Легко видеть, что задача стабилизации является частным случаем задачи программного управления.

В задачах слежения основная проблема сводится к формированию такой выходной траектории V(t). управляемого объекта, которая как можно более точно аппроксимировала бы другую, заранее не известную траекторию V*(t). Например, при управлении пушечной турелью оператор (наводчик орудия) при наводке на цель вращает легкие маховички (задавая траекторию V*(t)), а тяжелая пушечная турель отслеживает движение маховичков, изменяя, ориентацию ствола по углу и по азимуту (реализуя соответствующую траекторию V(t)). Аналогичные задачи слежения возникают, когда антенна радиолокатора отслеживает непредвиденные движения какого-либо летящего объекта. Число подобных примеров легко может быть увеличено.

Задачи экстремального управления, или, как иногда говорят, задачи настройки, возникают довольно часто. Они заключаются в достижении некоторой экстремальной цели, которая к тому же может эволюционировать во времени. Предполагается, что на траекториях объекта управления задан некоторый функционал, отражающий эту цель (обычно его экстремум соответствует некоторому нормальному, благоприятному или наилучшему режиму работы) и зависящий как от управляемых, так и от неуправляемых параметров объекта. Требуется с помощью соответствующих управляющих воздействий добиваться того, чтобы значение целевого функционала в любой момент времени находилось в достаточно малой окрестности экстремума (максимума или минимума — в зависимости от смысловой интерпретации).

Например, при настройке радиоприемника на какую-либо радиостанцию добиваются достижения максимальной громкости. Автоматические системы экстремального управления часто называются системами автоматической оптимизации, или самонастраивающимися системами. Задачи экстремального управления являются в определенном смысле более сложными, чем ранее перечисленные. Действительно, если, например, в задаче стабилизации достаточно одного измерения стабилизируемой величины для определения направления ее корректировки, то в данном случае для синтеза управляющего воздействия необходимо как минимум два поисковых измерения целевого функционала как основного выхода объекта. При настройке путем поиска — специальным образом организованных пробных движений — находится заранее не известное состояние объекта, соответствующее некоторому оптимальному режиму.

Важно отметить, что задачи экстремального управления являются не только более сложными, но и более общими. При необходимости практически любую задачу управления можно сформулировать на языке экстремального управления. Например, задачи стабилизации и программного управления могут быть сформулированы как задачи минимизации невязки (ошибки) между заданными и действительными выходными траекториями объекта. Другое дело — всегда ли оправданы такие формулировки? Это отдельный вопрос, и ответ на него однозначный — не всегда.

Когда мы говорим о задачах оптимизации в теории управления, то подразумеваем задачи реализации некоторых оптимальных (по заданному критерию) выходных траекторий управляемой системы. В частности, может ставиться задача перевода объекта управления из одной точки фазового пространства в другую, например, за минимальное время при соблюдении заданных ограничений, в том числе фазовых. Очевидно, такие задачи непосредственно не могут быть отнесены ни к одному из ранее рассмотренных типов задач (стабилизация, выполнение программы, слежение, настройка).

В качестве примера можно рассмотреть теперь уже ставший классическим пример задачи об оптимальном в смысле расхода горючего режиме набора высоты и скорости летательным аппаратом, например, самолетом [14]. На рис. 1. 2 показано фазовое пространство самолета как объекта управления. Ось абсцисс является осью высот H, а ось ординат — осью скоростей v. Состояние самолета изображается точкой фазового пространства — плоскости v 0 H.

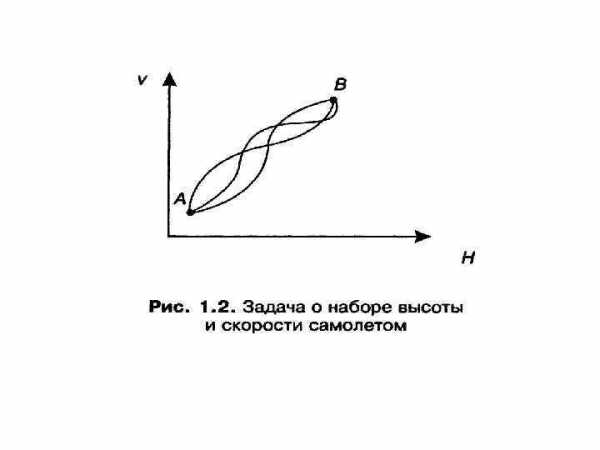
Существует множество траекторий в фазовом пространстве, соединяющих начальную (А) и конечную — целевую — точки (В). Требуется выбрать такое управление самолетом, чтобы набор высоты и скорости проходил в соответствии с некоторой оптимальной траекторией. Под критерием оптимальности в данном примере понимается суммарный расход горючего. Если такая оптимальная траектория рассчитана заранее, то она, в принципе, может выступать в качестве программы при последующем решении задачи программного управления. Однако обычно ситуация оказывается несколько сложнее. Может ставиться задача построения оптимального поведения объекта независимо от того, в какой точке фазового пространства он оказался в процессе реального движения в условиях возмущений. Собственно задача выполнения программы здесь уже не является определяющей.

Нужно ясно понимать, что все перечисленные задачи теории управления могут находиться в определенной иерархической взаимосвязи и присутствовать одновременно при проектировании той или иной системы управления. Например, на одном из иерархических уровней мы можем решать задачу стабилизации, строя соответствующую систему управления. В то же время (на более высоком уровне) может ставиться задача экстремального управления этой системой стабилизации в соответствии с некоторым критерием качества стабилизации и т. д. Число таких «вложений» теоретически не ограничено.

Еще раз отметим, что мы сейчас рассматривали основные задачи теории управления, а не методы их решения. Методы решения сформулированных задач и их реализация в виде конкретных систем управления могут быть различными, и они связаны с основными принципами управления.

Жесткое управление. Принцип жесткого (разомкнутого) управления предполагает отсутствие обратной связи в общей схеме управления (см. рис. 1. 1). Такие системы управления без обратной связи называются разомкнутыми. Чаще всего они применяются для целей программного управления. Принцип жесткого управления проиллюстрирован на рис. 1. 3, где представлена система жесткого управления, решающая задачу программного управления (задачу выполнения заданной программы). Здесь цель управления задает желаемую программу изменения состояния объекта во времени. Эта программа передается управляющему устройству для построения необходимого управления. В результате такого управления состояние объекта должно изменяться по закону. Система управления стремится обеспечить равенство для любого момента времени. Рассмотрим данный процесс жесткого управления подробнее.

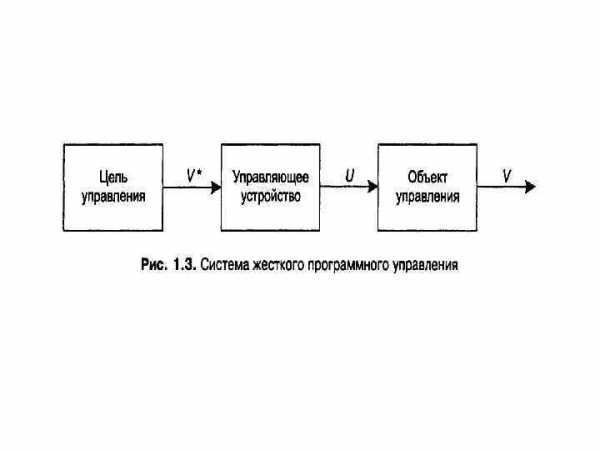
Здесь цель управления V*(t) задает желаемую программу изменения состояния объекта во времени. Эта программа передается управляющему устройству для построения необходимого управления U(t). В результате такого управления состояние объекта должно изменяться по закону V(t). Система управления стремится обеспечить равенство V(t) ≈ V*(t) для любого момента времени. Рассмотрим данный процесс жесткого управления подробнее.

Предположим, что объект управления является безынерционным и описывается оператором F: V(t) = F (U(t)) Предполагаем, что данное равенство справедливо для любого момента времени t. Управляющее устройство вырабатывает управляющее воздействие по закону U(t) = G (G (V*(t)) где G — оператор устройства управления. Очевидно, для достижения равенства V(t) = F (U(t)) = F(G (V*(t))) = V*(t) необходимо обеспечить закон управления G в виде G = F-1 Таким образом, оператор, характеризующий закон управления, является обратным к оператору объекта.

Существенные моменты в процессе жесткого управления сводятся к следующему. Во-первых, для построения закона управления необходимо иметь полную информацию об операторе объекта (математической модели объекта). Во-вторых, предполагается стабильность характеристик объекта, то есть неизменность его оператора. При малейших изменениях в объекте точность жесткого управления может быть нарушена.

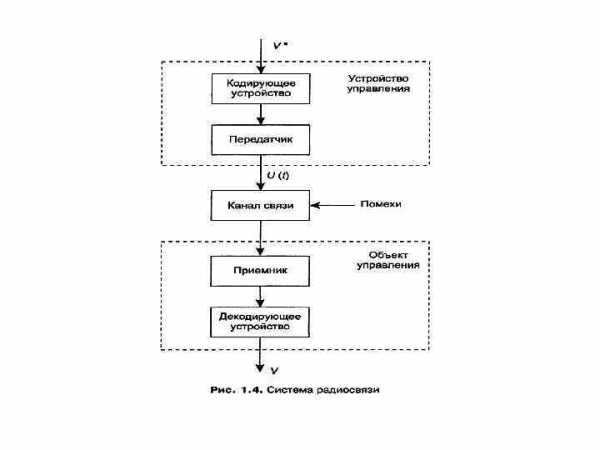
Примером системы жесткого управления является система радиосвязи, когда акустические колебания V*(t) , создаваемые, например, диктором в студии, поступают с микрофона в управляющее устройство, где преобразуются в радиоволны U(t)(рис. 1. 4). После прохождения канала связи радиоволны попадают в приемник, детектируются, усиливаются и при помощи динамика преобразуются снова в акустические колебания. Здесь мы имеем факт управления на расстоянии колебаниями диффузора динамика таким образом, чтобы они копировали колебания в микрофонной цепи передатчика.

Таким образом, в системах жесткого управления управляющему устройству недоступна информация о действительном состоянии объекта управления — какая-либо обратная связь отсутствует. В гораздо большем числе случаев необходимо прибегать к более гибким принципам управления, оказывающимся более эффективными при наличии различных помех, возмущений и изменяющихся параметрах объекта управления.

Регулирование. В системах регулирования, в отличие от жесткого управления, управляющие воздействия строятся в зависимости от фактического текущего состояния объекта управления. Информация о состоянии объекта поступает по специально организованным каналам обратной связи. В этом случае говорят, что реализуется принцип замкнутого управления, а сама система управления называется замкнутой. Здесь так же, как и в предыдущем случае, для эффективного функционирования системы управления часто необходимо иметь модель (оператор) объекта управления. В противном случае построение управляющих воздействий оказывается невозможным или малоэффективным. Основное преимущество замкнутых систем перед разомкнутыми состоит в том, что они оказываются существенно менее зависимыми от неизмеримых возмущений и помех, особенно когда механизм влияния помех на объект управления неизвестен. Пример замкнутой системы программного управления представлен на рис. 1. 5.

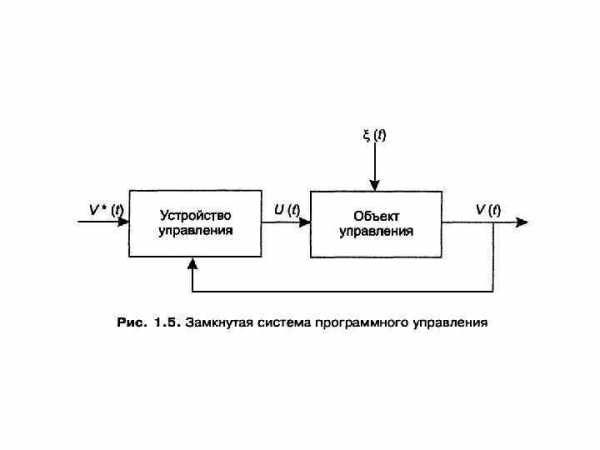
В устройстве управления сравнивается желаемое V*(t) и действительное значения функции V(t). Это позволяет определить, насколько состояние объекта отличается от требуемого (задаваемого программой V*(t) ). В результате управление строится как функция невязки: U(t) = f(V(t) – V*(t) Наличие обратной связи обычно позволяет существенно расширить возможности управления и ослабить требования к знанию структуры и свойств объекта управления.

Другое дело, что даже в этом простом примере нас могут интересовать возникающие при таком управлении колебания температуры. Для уменьшения этих колебаний мы можем начинать интересоваться мощностью нагревательного прибора, его инерционными свойствами, а также свойствами нагреваемой среды — в данном случае воды или воздуха. Например, существенным может оказаться учет нагреваемого объема воздуха или воды и т. д. Таким образом, нас уже интересует модель объекта управления.

Вообще, под сложной системой или объектом часто понимается система с антиинтуитивным поведением, то есть такая система, реакция которой на заданное входное воздействие или сигнал управления не может быть предсказана на основе «здравого смысла» . Мы, следовательно, отличаем сложную систему от большой системы, характеризуемой, например, числовыми массивами или файлами высокой размерности. В этом смысле большая система может быть и простой по поведению. Схема взаимодействия объекта управления с окружающей средой представлена на рис. 1. 6.

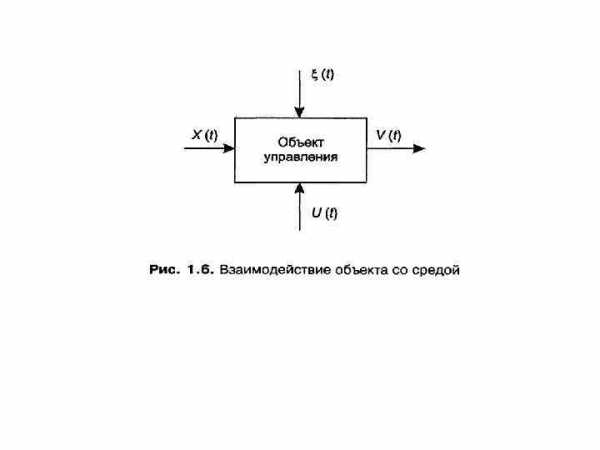
Здесь появился новый канал связи объекта со средой — X(t). Он означает неуправляемое, но наблюдаемое воздействие среды на объект. ξ(t) попрежнему означает вектор неуправляемых и ненаблюдаемых возмущений (как внутренних, так и внешних). Под оператором объекта управления F* будем понимать оператор , связывающий входы объекта с его выходом: V = F*(X, U, ξ )

Перечислим теперь характерные признаки сложности объекта управления. К ним в первую очередь относятся: • Отсутствие описания (в том числе алгоритмического) оператора F *. В то же время, как уже говорилось, для целей управления сложным объектом оно совершенно необходимо. • Неожиданное, антиинтуитивное поведение объекта. Иногда это поведение моделируется и объясняется с помощью введения фактора стохастичности. Поэтому для построения систем управления сложными объектами привлекается аппарат статистической или стохастической теории управления. • Нестационарность оператора F *. (изменчивость во времени)

present5.com

Оптимальные системы автоматического управления Постановка задачи оптимизации управления

В общем случае автоматическая система состоит из объекта управления и совокупности устройств, которые обеспечивают управление этим объектом. Как правило, эта совокупность устройств включает в себя измерительные устройства, усилительные и преобразовательные устройства, а также исполнительные устройства. Если объединить эти устройство в одно звено (управляющее устройство), то структурная схема системы выглядит следующим образом:

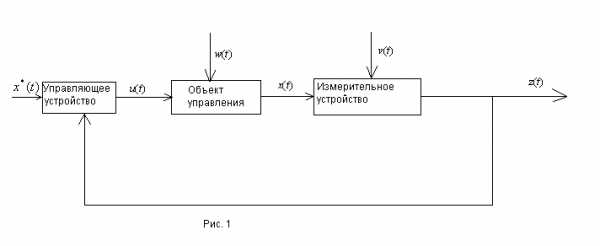
В автоматической системе информация о состоянии объекта управления через измерительное устройство поступает на вход управляющего устройства. Такие системы называются системами с обратной связью или замкнутыми системами. Отсутствие этой информации в алгоритме управления говорит о том, что система разомкнута. Состояние объекта управления в любой момент времени будем описывать 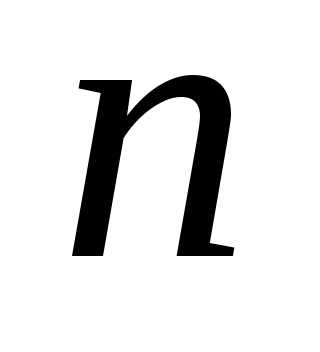переменными, которые называются координатами системы или переменными состояния. Их удобно считать координатами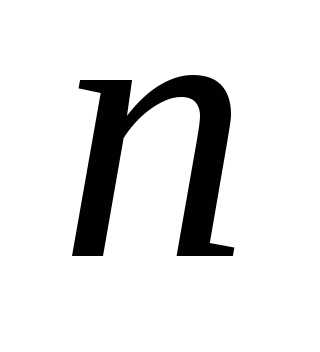- мерного вектора состояния.

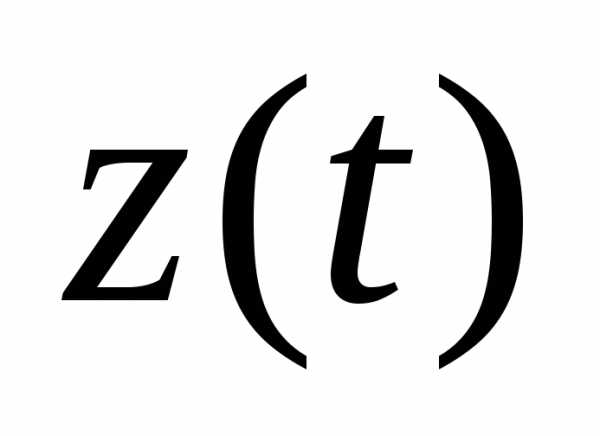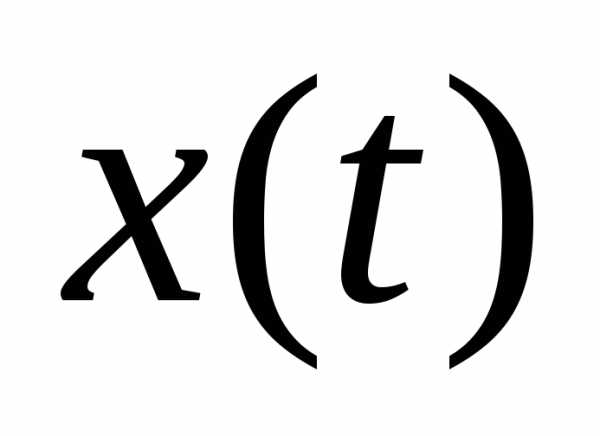Измерительное устройство выдает информацию о состоянии объекта. Если на основании измерения вектора могут быть найдены значения всех координатвектора состояния, то говорят, что система полностью наблюдаема.

Управляющее устройство вырабатывает управляющее воздействие 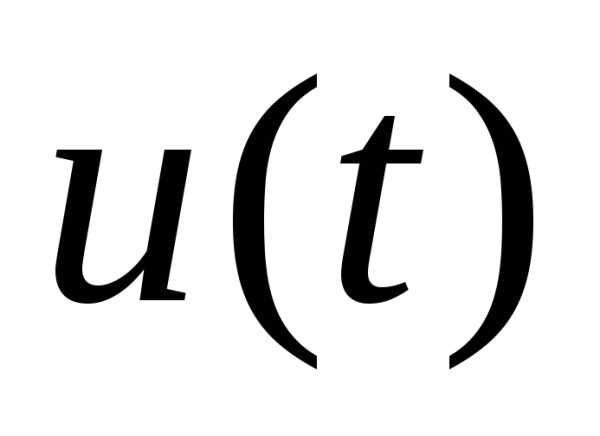. Таких управляющих воздействий может быть несколько, они образуют- мерный управляющий вектор.

На вход управляющего устройства поступает задающее входное воздействие 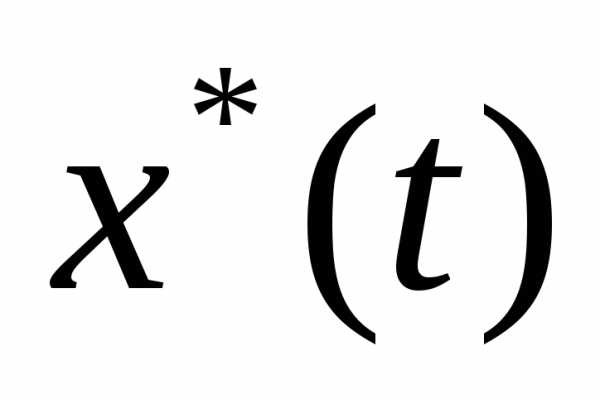. Это входное воздействие несет информацию о том, какое должно быть состояние объекта. На объект управления может действовать возмущающее воздействие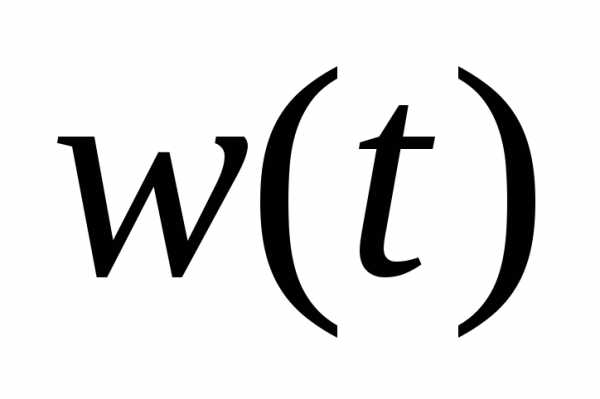, которое представляет собой нагрузку или помеху. Измерение координаты объекта, как правило, осуществляется с некоторыми погрешностями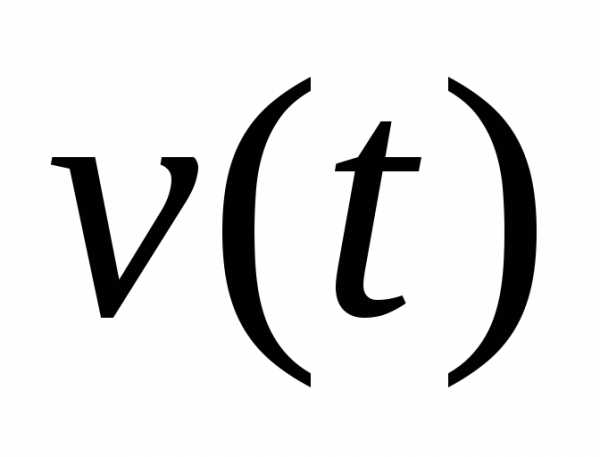, которые тоже носят случайный характер.

Задачей управляющего устройства является выработка такого управляющего воздействия 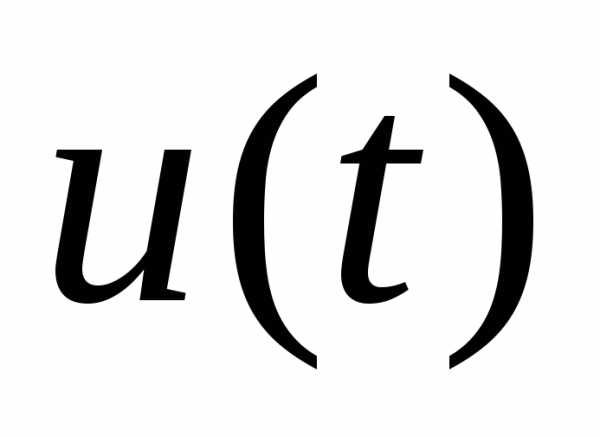, чтобы качество функционирования автоматической системы в целом было бы наилучшим в некотором смысле.

Мы будем рассматривать такие объекты управления, которые являются управляемыми. То есть вектор состояния можно изменять требуемым образом путем соответствующего изменения вектора управления. Будем подразумевать, что объект полностью наблюдаемый.

Так, например, положение летательного аппарата характеризуется шестью координатами состояния. Это 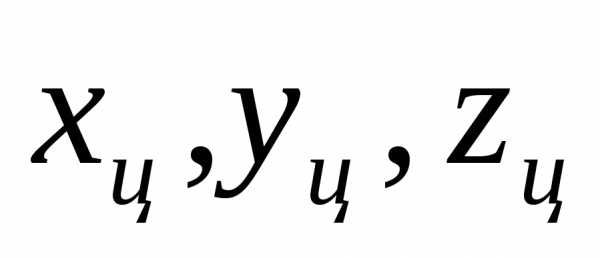- координаты центра масс,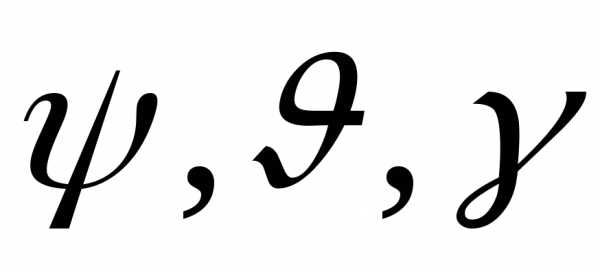- углы Эйлера, определяющие ориентацию летательного аппарата относительно центра масс. Положение летательного аппарата можно изменить с помощью рулей высоты, курса, элерона и с помощью уклонения вектора силы тяги. Таким образом управляющий вектор определен следующим образом:

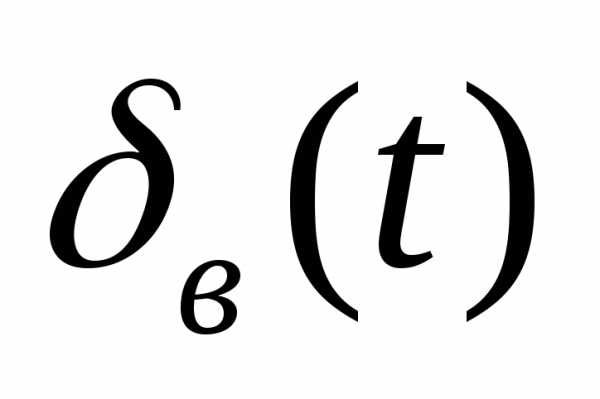- угол отклонения рулей высоты

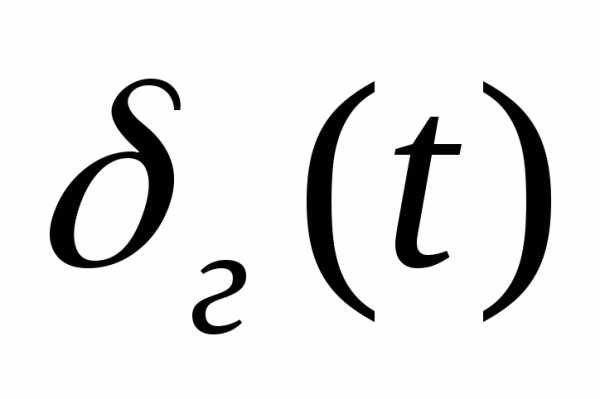- курс

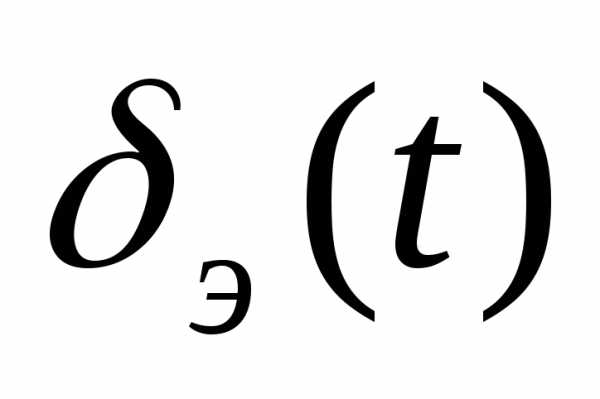- элерон

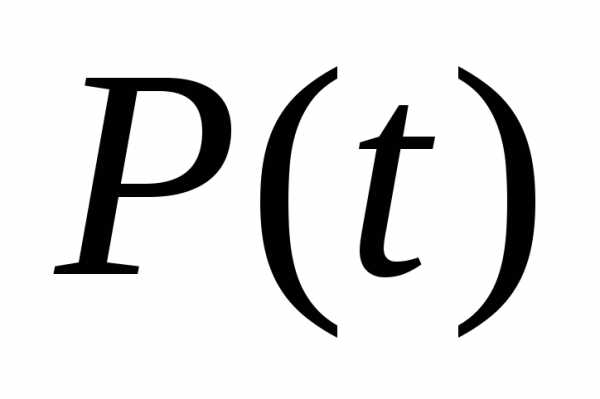- тяга

Вектор состояния 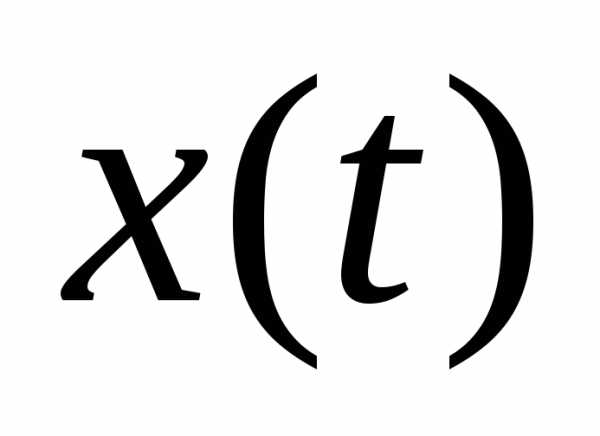в этом случае определяется следующим образом:

Можно поставить задачу выбора управления, с помощью которого летательный аппарат переводится из заданного начального состояния 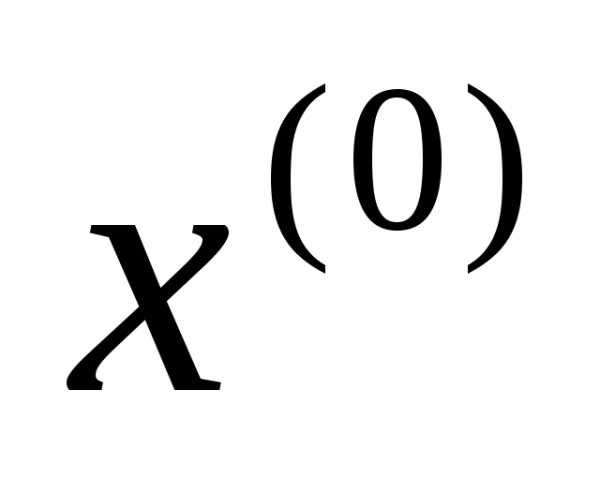в заданное конечное состояние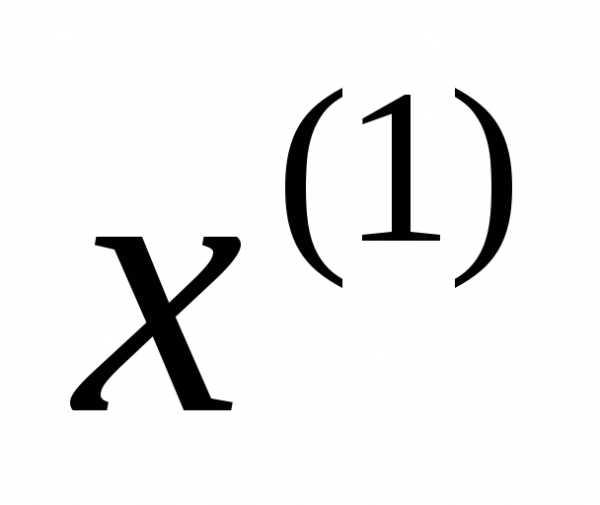с минимальными затратами топлива или за минимальное время.

Дополнительная сложность при решении технических задач возникает в силу того, что на управляющее воздействие и на координаты состояния объекта управления, как правило, накладываются различные ограничения.

На любой угол рулей высоты, курса, элерона существуют ограничения:

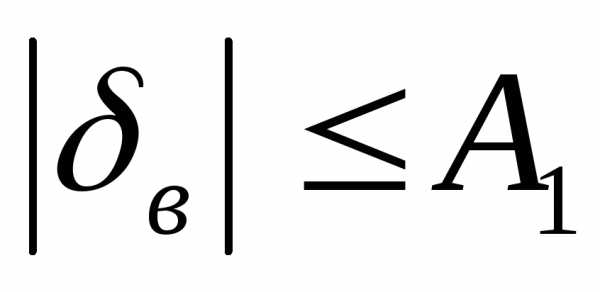
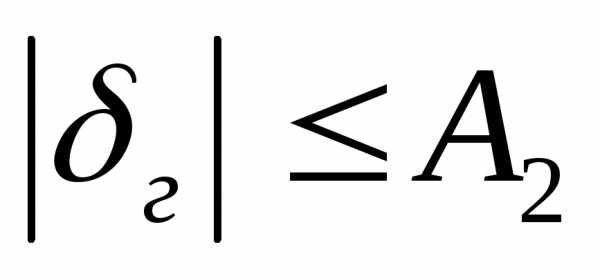
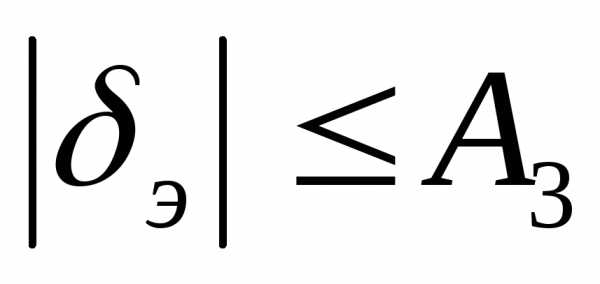
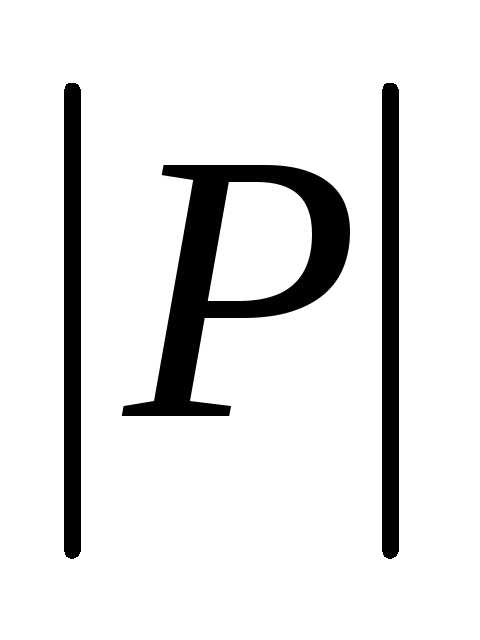- тяга сама по себе ограничена.

На координаты состояния объекта управления и их производные также накладываются ограничения, которые связаны с допустимыми перегрузками.

Мы будем рассматривать объекты управления, которые описываются дифференциальным уравнением:

(1)

Или в векторном виде:

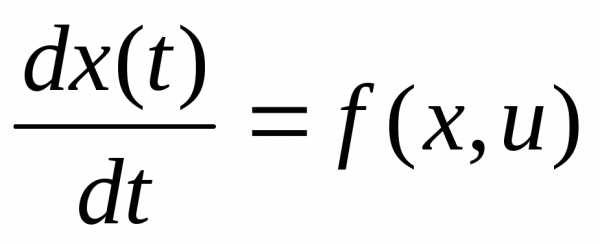
Здесь:

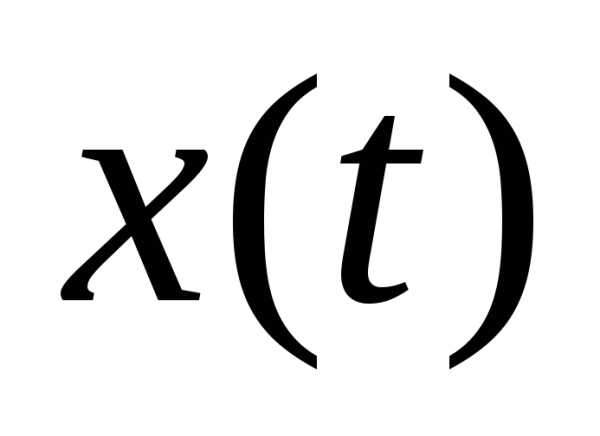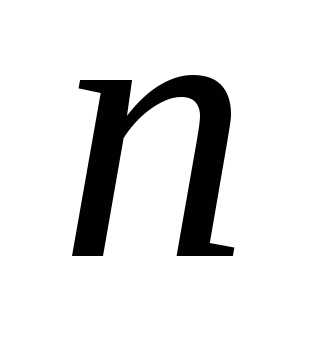--мерный вектор состояния объекта

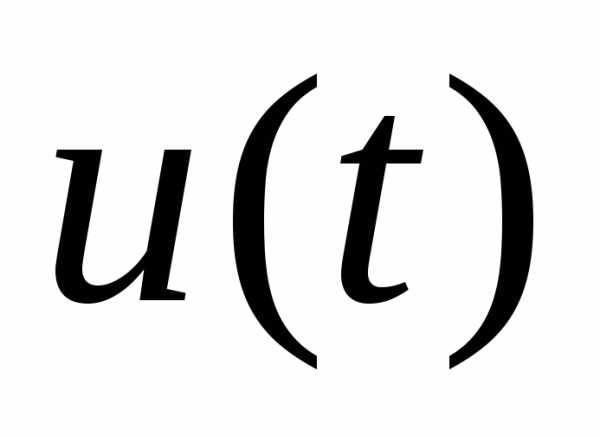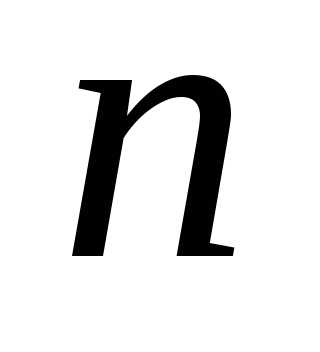--мерный вектор управляющих воздействий

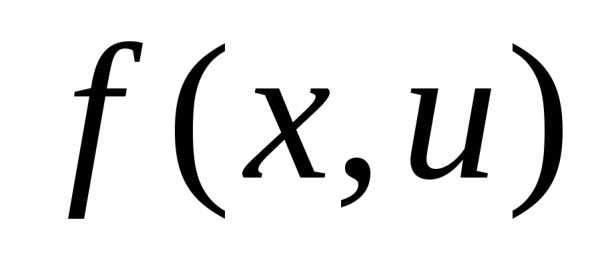- функция правой части уравнения (1)

На вектор управления 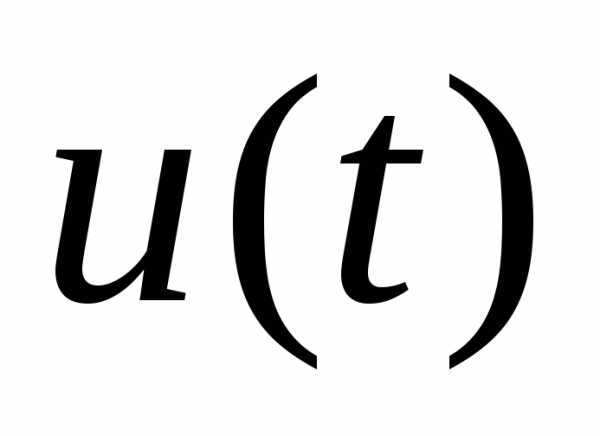накладывается ограничение, мы будем полагать, что его значения принадлежат некоторой замкнутой области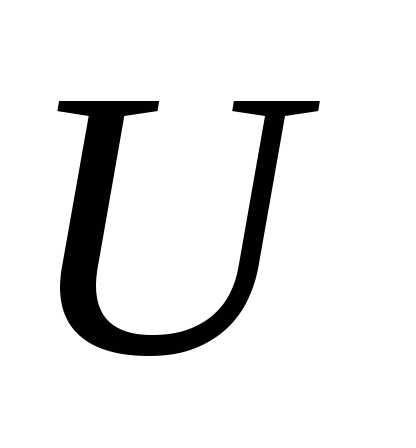некоторого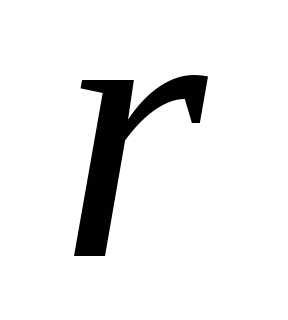-мерного пространства. Это означает, что управляющая функцияв любой момент времени принадлежит области().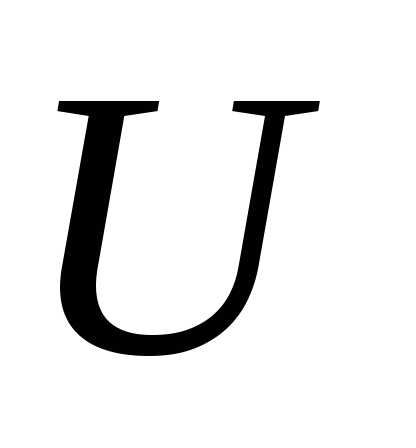

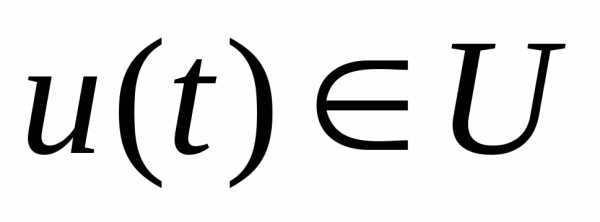Так, например, если координаты управляющей функции удовлетворяет неравенствам:

то область 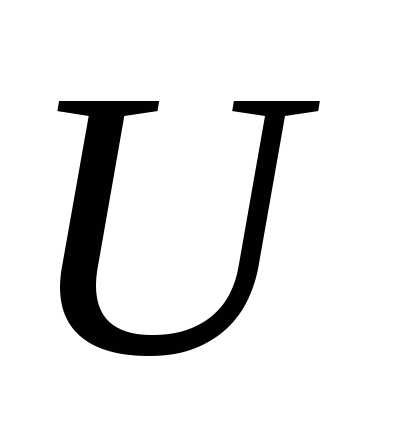является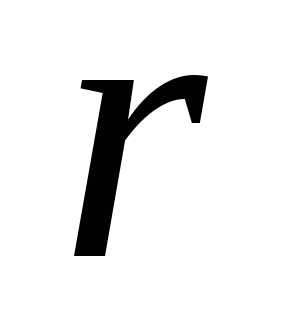-мерным кубом.

Назовем допустимым управлением всякую кусочно-непрерывную функцию 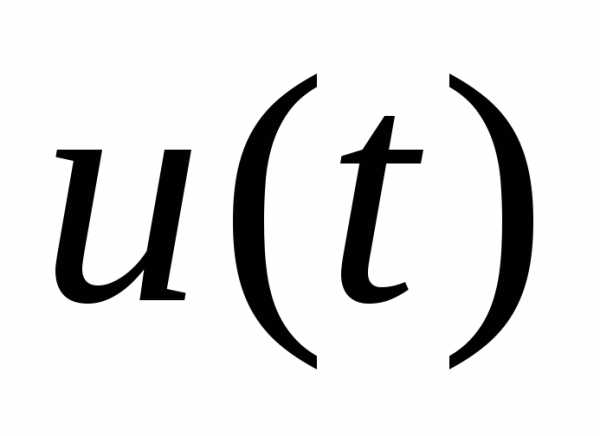, значения которой в каждый момент времени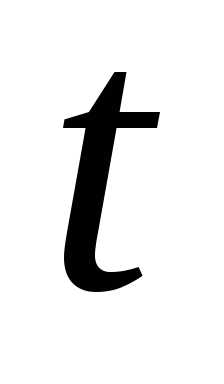принадлежит области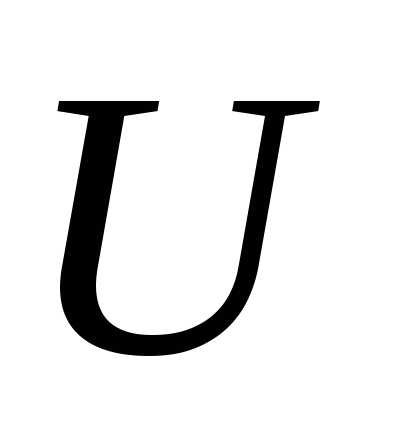, и которая может иметь разрывы первого рода. Оказывается, даже в некоторых задачах оптимального управления решение может быть получено в классе кусочно-непрерывного управления. Для того, чтобы выбрать управление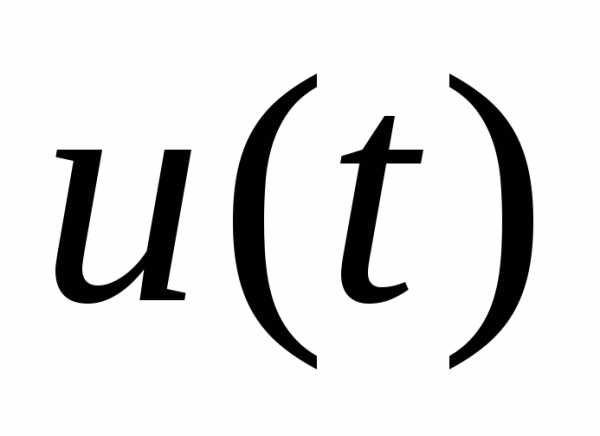как функцию времени и начального состояния системы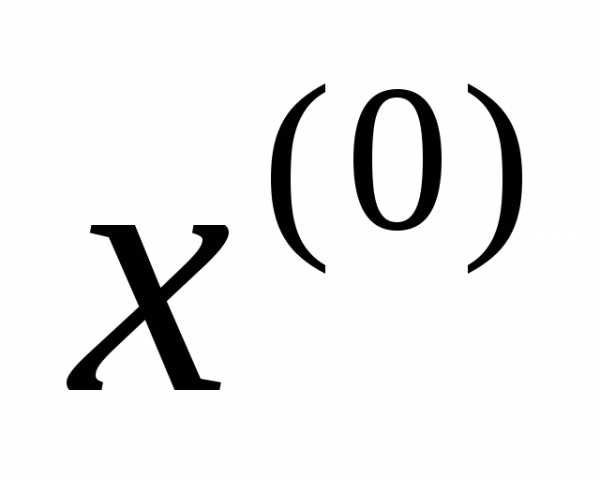, которое однозначно определяет движение объекта управления, требуется, чтобы система уравнений (1) удовлетворяла условиям теоремы существования и единственности решения в области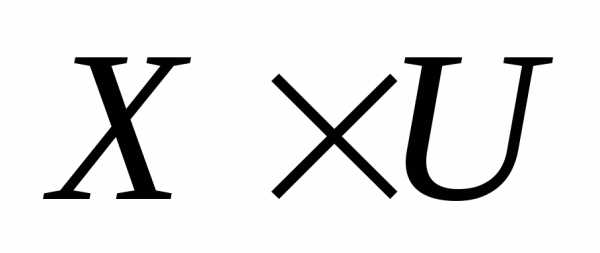. В этой области располагаются возможные траектории движения объекта и возможные управляющие функции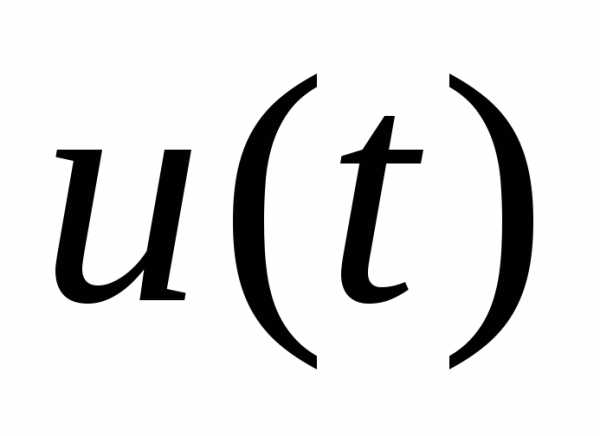. Если область изменения переменных является выпуклой, то для существования и единственности решения достаточно, чтобы функции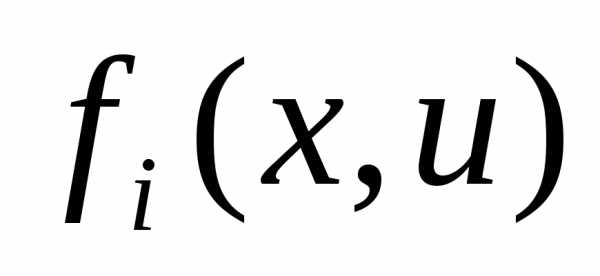. были непрерывны по всем аргументам и имели непрерывные частные производные по переменным.

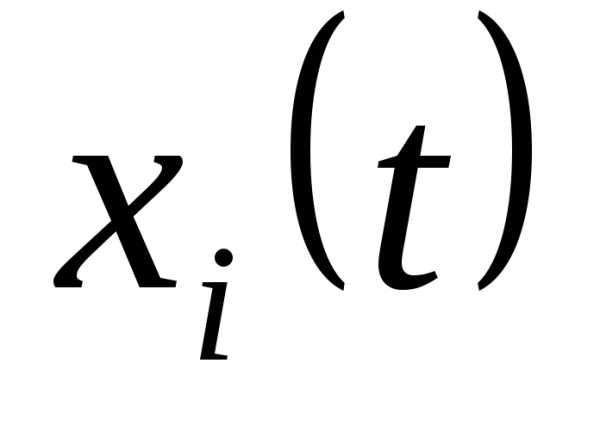В качестве критерия, который характеризует качество работы системы, выбирается функционал вида:

(2)

В качестве функции 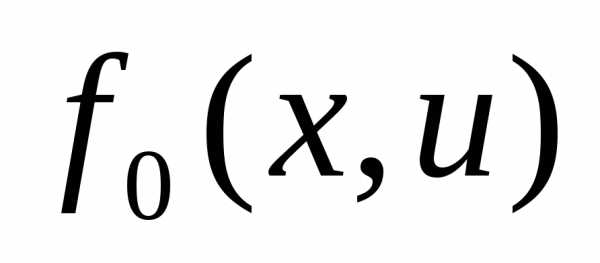будем предполагать, что она непрерывна по всем своим аргументам и имеет непрерывные частные производные по.

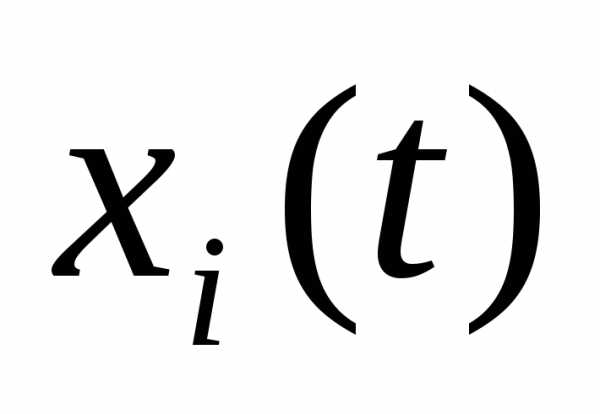studfiles.net

27. Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности.

Под оптимальной САУ понимается наилучшая в некотором смысле система. Критерии оптимальности могут быть различны и зависят от решаемой задачи. Наиболее часто встречаются такие критерии оптимальности:

1) Точность САУ при изменяющемся воздействии,

2) Время переходного процесса,

3) Экономичность;

Производительность;
Интегральные критерии.

К настоящему времени наибольшее развитие получили 2 направления в теории оптимальности систем:

1) Теория оптимального управления движением систем с полной информацией об объекте и возмущениях;

Теории оптимального управления при случайных возмущениях.

Для реализации оптимального управления необходимо:

Определить цель управления. Цель выражается либо целевой функцией, либо критерием оптимизации.

Целевая функция или критерий оптимизации позволяют найти количественный эффект любого решения.

Выбрать модель для анализа и определения эффективности принятого решения.
Изучить все состояния среды функционирования объекта, влияющие на прошлое, настоящее и будущее процесса управления.

При решении задачи оптимального управления используются методы вариационного исчисления, принципы максимума, а также динамическое и математическое программирование.

Задачу оптимального управления в общем случае можно сформировать следующим образом:

Даны:

1)Цель управления, представленная математически в виде некоторого функционала или критерия управления

2)Уравнения системы - они обычно задаются в виде уравнений состояний

3)Система граничных уравнений в начальный и конечный момент времени.

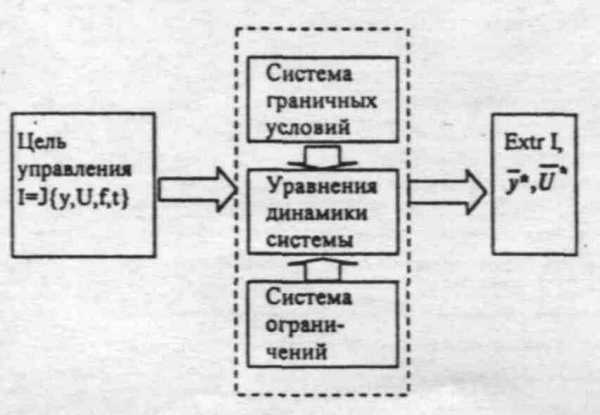
4)Система ограничений, которым должны удовлетворять переменные состояния и уравнения.

Требуется найти:

Вектор управления, при котором критерий цели управления имеет экстремум (max или min).

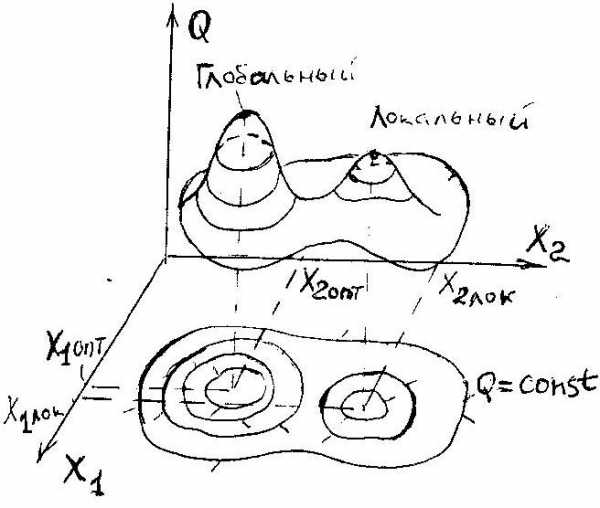
Необходимо отметить, что оптимальное управление в ряде случаев может не существовать, и об этом нельзя судить не решая задачу. Решение задачи нахождения оптимального управления является неоднозначным, т.е. каждое найденное решение дает локальный оптимум. Если найдены все локальные оптимумы, то в этом случае может быть выделен глобальный оптимум. Найденный глобальный оптимум является решением задачи оптимального управления.

Интегральные критерии качества:

Оптимальное Быстродействие

Функционал имеет вид

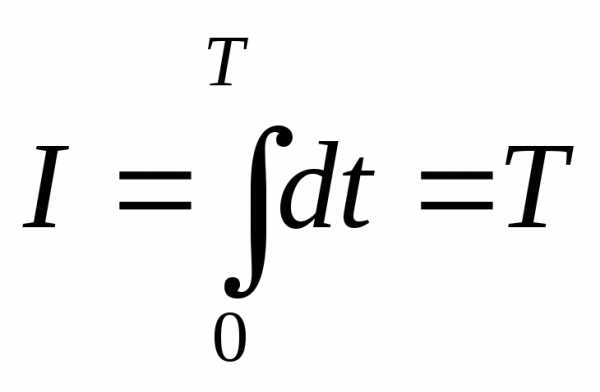
Оптимальная Производительность

Критерием оптимальности явл-ся угол поворота  за определенное время t и функционал имеет вид

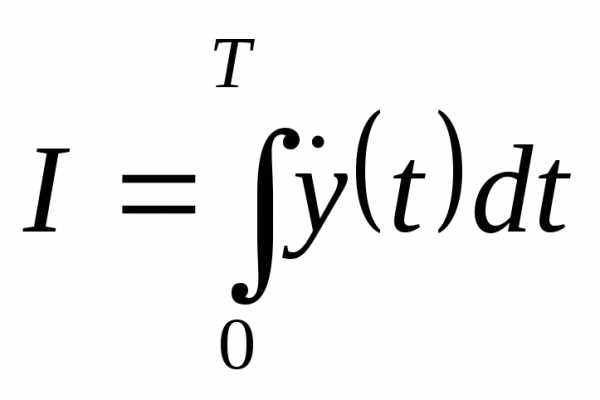
Оптимальная экономичность

Критерием оптимальности явл-ся расход энергии за определенное время и функционал имеет вид

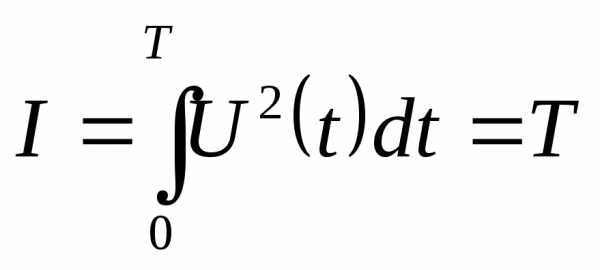
28. Аналитическое конструирование регуляторов. Постановка задачи.

При исследовании качества переходных в линейных САУ вводились разлитые интегральные критерии качества, с помощью которых оценивался переходной процесс на бесконечном интервале времени. При рассмотрении интегральных критериев качества мы убедились в том, что эти критерии позволяют определить параметры регулятора, если задана его структура. Можно поставить более общую задачу: найти закон регулирования - аналитическую функцию, связывающую управляющую координату и управляющее воздействие при этом доставляющее min интегральному критерию качества. Такое оптимальное конструирование дифференциального уравнения регулятора получило название аналитического конструирования регуляторов. По методам решения и постановке задачи эта задача сродни задачам оптимального регулирования.

Это вариационная задача, где в качестве экстремали ищется функция связывающая Х и U.

При аналитическом конструировании задача состоит в том, что бы найти закон регулирования который с учетом уравнений объекта и граничных условий доставлял бы min интегралу, характеризующему квадратичную ошибку системы и гарантирующему ее устойчивость.

Постановка задачи оптимального конструирования регуляторов.

Объект регулирования задан с помощью дифуравнений, что в операторной форме соответствует заданию передаточной функции Wор(S) (или W(S))

Считают что на систему не действуют внешние возмущения, а переходной процесс происходит при изменении начальных условий.

X = y0 – y - рассогласование

Вустойчивой линейной САУ в результате переходного процесса все функции координат должны стремиться к 0. х1() = х2() = … хn() = U() = 0 (2)

В качестве критерия оптимальности выберем интеграл вида

(3), где V- положительно определённая квадратичная форма.

Т.е. если подставитьV в  (3) то это будет квадратичная ошибка системы.

Член U2 в (4) характеризует стоимость процесса управления, т.е. затраты энергии на нагрев. U2 гарантирует отсутствие нереализуемых в линейных регуляторах законов, он гарантирует отсутствие управляющих воздействий, при которых скорость превращается в бесконечность.

Само существование (3) гарантирует устойчивость системы. При аналитическом конструирование задание состоит в том чтобы найти в аналитической форме функцию Ф(U,U,x1…xk) = 0 (5) – который с учётом уравнений объекта и приграничных условий (1) и (2) доставлял бы минимум интегралу (3).

studfiles.net

Оптимизация в системах управления - Задача

Оптимизация в системах управления

Оптимизацией называется процесс улучшения характеристик устройства путем изменения его параметров на основе какого-либо исходного варианта. Методы оптимизации используются широко и являются предметом специального раздела математики. При формализации процесса оптимизации используют следующие определения.

Параметры системы (устройства), которые могут быть изменены в процессе оптимизации, называются параметрами оптимизации.

Функция, которая количественно характеризует соответствие разработанного устройства требованиям технического задания, т. е. характеризует качество разработанного устройства, называется целевой функцией или функционалом качества.

Задача оптимизации - целенаправленный поиск таких параметров системы (элементов устройства), которые обеспечивали бы экстремальное значение целевой функции.

В теории управления методы оптимизации используются в двух аспектах.

Во-первых, методы оптимизации применяются при проектировании систем управления в целях определения оптимальной структуры системы. Во-вторых, алгоритмы работы систем управления строятся на основе методов оптимизации, системы, работающие по таким алгоритмам управления, называются адаптивными или экстремальными регуляторами.

При постановке задачи оптимизации разработчику системы (устройства) необходимо решить 3 проблемы:

Выбор параметров оптимизации и их допустимых значений (ограничений параметров оптимизации).
Выбор целевой функции (критерия оптимальности).
Выбор способа и метода оптимизации.

Все 3 проблемы очень сложные и не всегда решаются однозначно.

В двухмерном случае (то есть, когда параметров оптимизации только 2) целевую функцию - Q можно представить геометрически. Пример такого представления показан на

Рис.1

рис. 1 для сиcтемы с двумя параметрами оптимизацииx1,x2 и целевой функцией Q. Ясно,что такие объемные картины рисовать не удобно. Поэтому часто Q представляют линиями уровня - то есть на плоскости зарисовыва-ют линии, которые являются проекциями линий, в пределах которых Q=const. Если оптимизация – поиск точки максимума, то в нашем случае такая точка - это вершина с координатами (x1ОПТ, x2ОПТ ).

Если на параметры оптимизации не накладываются ограничения, экстремум

называется безусловным. Для примера, рассмотренного на рис. 1, при оптимизации по

максимуму безусловный экстремум соответствует точке максимума функции Q.

Если параметры оптимизации связаны ограничениями, экстремум называется условным. Обычно ограничения задаются из технических, технологических или конструктивных соображений. Эти ограничения записываются в виде неравенств: R  150 Ом; l  l1; l  l2 равенств. Они ограничивают область допустимых значений параметров. Экстремум целевой функции может находится на границе области допустимых параметров. Условный экстремум может не совпадать с безусловным.

Пусть в примере рис.1 задано ограничение типа равенства x1 = a, тогда при поиске максимума можно изменять только один параметр x2 (поиск экстремума может осуществляться только по одной координате) и экстремум, который мы найдем, будет условным. Если задано ограничение типа неравенства, например x1 < a, тогда поиск экстремума может осуществляться только в части плоскости x1,x2 и экстремум будет найден на границе.

Методы оптимизации

Методы поиска положения экстремума целевой функции условно можно разбить на две больших группы.

Аналитические методы.
Алгоритмические или численные методы.

При поиске аналитическим методом - положение экстремума определяется формулой и может быть найдено сразу. Недостатки.

1). Необходимо иметь явное выражение целевой функции

2). Математические трудности

3). При наличии ограничений типа неравенств оптимизация аналитическим методом невозможна.

Алгоритмические методы - указывают способ построения алгоритма отыскания экстремума. Эти методы различаются на следующие:

регулярные;
статистические;
комбинированые методы.

Основные статистические методы:

а) методы случайного поиска,

б) методы случайного поиска с накоплением информации о предшествующем процессе оптимизации, это адаптивные методы.

Рассмотрим подробнее регулярные алгоритмические методы:

Простейший метод - метод прямого перебора.

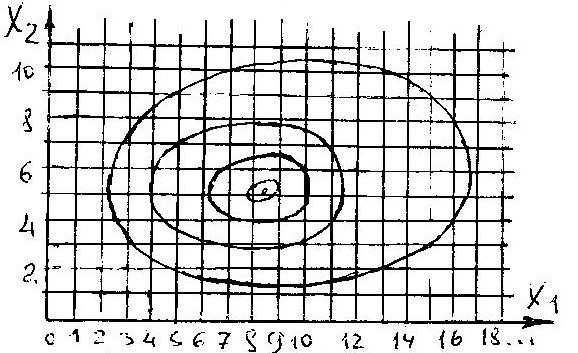
Диапазон изменения каждого параметра оптимизации разбивается на интервалы, целевая

функция рассчитывается поочередно при всех возможных значениях параметров оптимизации. По результатам расчета находят значения параметров, при которых целевая функция имеет экстремум (для двухмерного случая расположение расчетных точек, линии уровня целевой функции и точка экстремума показаны на рис. 2). Недостатком метода является

Рис.2

очень большой объем вычислений. При большом числе параметров оптимизации метод прямого перебора не реализуем.

Метод покоординатного спуска (метод Гаусса – Зейделя)

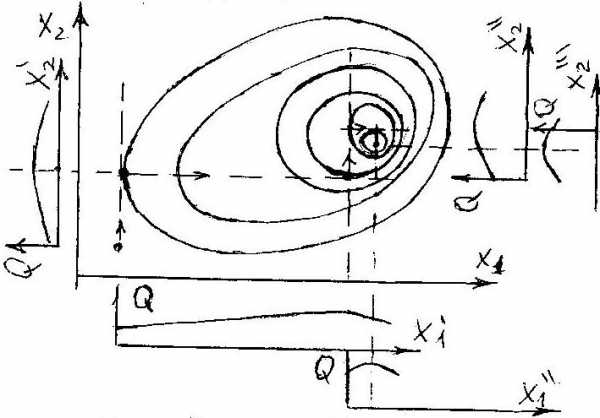
Оптимум ищется поочередно по каждой координате в отдельности. (Сначала ищут

Рис. 3

экстремум по первой координате при фиксированных значениях остальных параметров, затем первой координате присваивают значение, соответствующее экстремуму, и ищут экстремум по по второму параметру и т. д.). Для двухмерного случая линии уровня целевой функции, линии поиска экстремума на плоскости x1,x2 показаны на рис. 3.

Здесь же показаны графики зависимости целевой

функции от одного параметра при поиске экстремума по этому параметру. Достоинство метода - простота реализации. Недостаток – невысокая эффективность.

Градиентные методы.

Градиент функции - вектор, направление которого совпадает с направлением, для которого в данной точке скорость изменения функции максимальна, а длина равна скорости изменения функции в этом направлении. Градиент перпендикулярен линии уровня.

Градиент многомерной функции Q аналитически выражается в виде суммы частных производных по отдельным координатам.

gradQ=Q=(Q/x1)x1+(Q/x2)x2+…+(Q/xn) xn , ( 1 )

где x1 , x2 - единичные орты, направленные вдоль координатных осей. В точке экстремума gradQ=0.

При поиске максимума градиентным методом перемещение точки производится в направлении градиента функции. При этом возникают две задачи:

Определение градиентного направления;
Определение величины рабочего шага.

Для определения длины и направления градиента достаточно найти его проекции на координатные оси, для этого дают приращение последовательно всем входным параметрам и определяют частные производные, затем определяют градиент по формуле ( 1 ).

Шаг - расстояние, на которое перемещается точка оптимизации. В разных методах шаг определяют по-разному.

Например, в методе градиента шаг пропорционален градиенту. То есть: если хp -

вектор входных параметров в точке p, хp+1 - вектор новых значений входных параметров после p-го шага, то:

x p+1= x p+d grad Q( xp ) . ( 2 )

Иногда удобно проводить оптимизацию с заданной длиной шага h, тогда

xp+1= xp+hgrad Q( xp ) / grad Q( xp ).( 3 )

Оптимизация заканчивается, когда grad Q < .

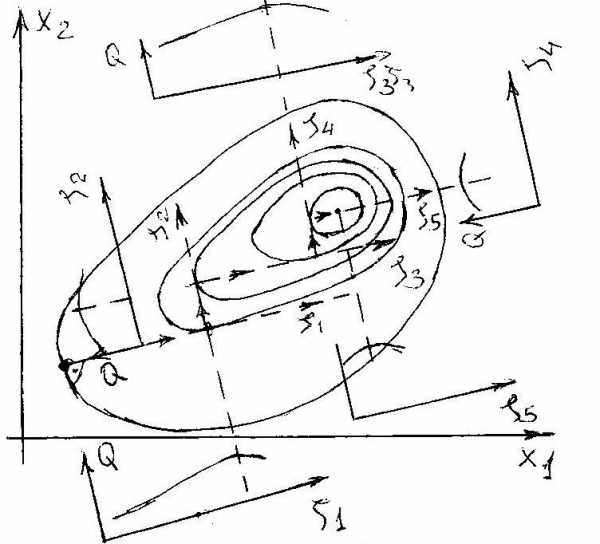
Таким образом в методе градиента есть произвол - выбор шага. На примере видно,

Рис. 4

что при движении в градиентном направлении значение Q изменяется и достигает максимума (минимума), когда вектор касается линии уровня.

Метод оптимизации, при котором новое ( p+1 ) градиентное направление вычисляется лишь после того, как движение в предыдущем направлении

исчерпало себя и приводит к что при движении в градиентном направлении значение Q изменяется и достигает максимума (минимума), когда вектор касается линии уровня. Метод оптимизации, при котором новое ( p+1 )

градиентное направление вычисляется лишь после того, как движение в предыдущем направлении исчерпало себя и приводит к уменьшению целевой функции, называется методом наискорейшего спуска (подъема). Пример для оптимизации по методу наискорейшего спуска показан на рис. 4. Для определения оптимального шага используются методы однопараметрической оптимизации.

Использование градиентных методов позволяет выйти к экстремуму за меньшее число шагов, чем при координатном спуске, то есть градиентные методы являются более эффективными. Существует много разновидностей градиентных методов. При решении конкретной задачи целесообразно подобрать метод наиболее эффективный для этой задачи.

Оптимизация при наличии ограничений

На приведенных примерах не ясно, как использовать градиентные методы при наличии ограничений. Одним из вариантов является метод зигзагообразного движения вдоль границы.

Пусть имеются ограничения типа неравенств:

Ag(x1,x2,…xn)0 , где g=1,2…k - номер ограничения.

В соответствии с этим обозначим  - область допустимых значений x , 2 - область, где ограничения не удовлетворяются. Пусть рабочая точка в процессе поиска экстремума градиентным методом вышла из области 1 в область 2, то есть нарушилось условие Ai(x1,…xn)0. Ясно, что это недопустимо, поэтому необходимо быстрее вернуть поиск в область 1. Ясно, что наиболее быстро это можно сделать двигаясь в

направлении градиента функции нарушенного ограничения . После возвращения в область допустимых значений 1 движение опять организуется в соответствии с

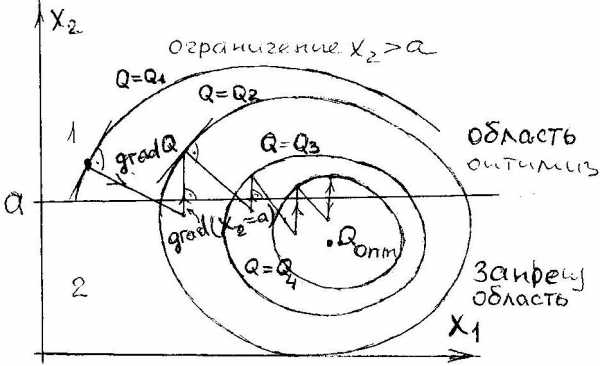
Рис. 5

градиентным методом. Если вновь выйдем из области 1 - еще раз применим тот же прием и так далее. Таким образом, при применении этого способа осуществляется зигзагообразное движение вдоль границы. Поиск прекращается при выполнении одного из следующих условий.

На одном из шагов внутри области 1 выполняется условие gradQ< - малое наперед заданное значение.
Векторы grad Q и  коллинеарные и направлены в противоположные стороны (значит, оптимум на границе и он найден).

Недостаток - медленное движение вдоль границы. В некоторых градиентных методах этот недостаток устраняется.

Общий недостаток градиентных методов – они являются локальными. Кроме того, иногда они не позволяют найти локальный экстремум - например останавливаются в седловинах, на гребнях, в оврагах функций. Однако, градиентные методы просты в реализации, быстро сходятся, поэтому широко применяются при расчетах.

Задача оптимизации - задача нелинейного программирования

Мы познакомились с некоторыми методами поиска оптимальных решений, представили себе, что это такое. Теперь самое время заметить, что сформулированная выше задача минимизации (максимизации) функции при наличии ограничений составляет предмет современного раздела математики, который называется нелинейное программирование.

Есть еще так называемое линейное программирование: задача та же, но целевая функция и ограничения - линейные формулы входных параметров. Некоторые задачи теории антенн и устройств СВЧ сводятся к задаче линейного программирования.

Нелинейное программирование - незаконченный раздел математики. В настоящее время он развивается. Существующие методы решения задачи можно условно разделить на 2 основные группы в соответствии со способом учета ограничений в процессе поиска.

Методы первой группы учитывают ограничения в явном виде (пример - метод зигзагообразного движения вдоль границы ).
Методы второй группы - сводят решение задачи к решению последовательности задач без ограничений.

Одним из них является метод штрафных функций. Выполним обозначение: нам

надо найти вектор x , минимизирующий целевую функцию Q( x ) и удовлетворяющий ограничениям Ai( x )0 i=1,m.

Идея метода штрафных функций: градиентные методы используются к новой функции W( x ), составленной как сума целевой функции Q( x ) и функций ограничений Ai( x ), взятых с некоторыми весовыми коэффициентами Pi.

W( x )=Q( x )+Pi( Ai(x)) .

i=1

Весовые коэффициенты Pi выбирают следующим образом:

 0 , если вектор x удовлетворяет заданному ограничению Ai( x )0

Pi= 

Vi , если не удовлетворяет.

Величину Vi увеличивают при каждом последующем шаге, таким образом W( x ) изменяется в процессе поиска.

Пока поиск идет внутри области допустимых значений Pi=0 и штраф не взимается. Функции Ai( x ) не влияют но поиск и движение происходит по направлению:

gradQ( x ) - поиск максимума ( минимума ).

При попадании в запрещенную область к значению Q( x ) прибавляется штраф величиной

G=Pi*Ai( x ) , причем хотя бы одно значение Pi0 .

i=1

В этом случае минимизация функции происходит в направлении

grad W( x )=grad Q( x )  Pi * grad Ai( x ) .

i=1

Итак ясно, что методов получения оптимальных решений разработано много. Они позволяют решать самые разнообразные задачи и могут быть использованы как при разработке систем автоматического управления, так и при построении алгоритмов работы систем. Многие из них включены в стандартное программное обеспечение современных ЭВМ, так что для их использования достаточно обратиться к соответствующей стандартной программе. Последующий путь конечно проще, чем разработка своей подпрограммы оптимизации. Однако заметим, что подробное описание алгоритма стандартных программ обычно отсутствует. Поэтому на практике оказывается необходимым попробовать программу на тестовых примерах для проверки правильности понимания порядка обращений и возможностей программы.

Выбор целевой функции

Выбор условий функции является одним из важнейших вопросов при оптимизации устройства. Вообще говоря, разрабатываемая система должна удовлетворять целому комплексу требований: должна быть устойчивой, иметь достаточное быстродействие, малую ошибку сопровождения, достаточно монотонный переходный процесс, иметь малую чувствительность к неточности изготовления и влиянию важнейших факторов и так далее. При правильном подходе все эти требования необходимо учитывать при проектировании устройства.

Ясно, что по каждому из этих требований можно построить целевую функцию

Qi, провести оптимизацию и получить соответствующие параметры оптимизации. Требования могут быть противоречивыми и оптимизация по разным требованиям может приводить к разным результатам.

Чтобы удовлетворить всем требованиям в качестве целевой функции Q используют алгебраическую суму Qi с различными весовыми коэффициентами i, которые нормируют и учитывают важность соответствующего требования.

Q=i*Qi .

i=1

При выборе весовых коэффициентов необходимо иметь опыт, так как пренебрежение каким-либо из параметров в пользу другого может дать неверный результат.

textarchive.ru

Задачи оптимизации в теории управления 2, Высшая математика

Пример готового реферата по предмету: Высшая математика

Содержание

Оглавление

Введение 2

1. Линейное программирование 3

2. Динамическое программирование 6

3. Теория графов и оптимизация 11

Заключение 13

Литература 14

Выдержка из текста

Введение

Теория управления — это наука, разрабатывающая и изучающая методы и средства систем управления и закономерности протекающих в них процессах. Предметом теории управления являются не только процессы материального производства, но и сферы деятельности человека: организационно-административное управление, проектирование и конструирование, информационное обслуживание, здравоохранение, научные исследования, образование, и многие другие.

Человек, на протяжении всей своей эволюции, совершая те или иные деяния, старался вести себя таким образом, чтобы результат, достигаемый как следствие некоторого поступка, в определенном смысле оказался наилучшим. Из одного пункта двигаясь в другой, он стремился найти среди возможных кратчайший путь. Занимаясь постройкой кораблей, он пытался придать им такую форму, чтобы вода оказывала бы минимальное сопротивление. Строя жилище, он разыскивал такую его геометрию, которая при минимальном расходе топлива, снабжала приемлемо комфортные условия существования. Можно легко продолжить перечень подобных примеров.

В определенном смысле наилучшие решения задач принято называть оптимальными.

В настоящее время без использования принципов оптимизации не решается ни одна более или менее сложная проблема.

Список использованной литературы

Литература

1. Гасс С.П., Путешествие в страну линейного программирования / Пер. с англ. — М.: Мир, 1973, 176с.

2. Белов В.Б., Теория графов. — М.: Высшая школа, 1976, 392с.

3. Бурков В.Н., Теория графов в управлении организационными системами. — М.: «Синтег», 2010, 124с.

4. Орлов А.И., Задачи оптимизации и нечеткие переменные. — М.:"Знание", 1990., 64с.

5. Орлов А.И., Эконометрика. — М.: «Экзамен», 2002,576с.

6. Карнадская, Н.Л. Принятие управленческого решения — М.: ЮНИТИ, 1999,265с.

7. Кофман А., Фор Р. Займемся исследованием операций / Пер. с франц. — М: Мир, 1976, 280 с.

8. Планкетт Л.Т., Выработка и принятие управленческих решений — М.: ПРИОР, 1998, 300с.

9. Шелобаев С.И., Математические методы и модели в экономике, финансах, бизнесе «ЮНИТИ-ДАНА» 2001, 367

10. Фатхутдинов Р.А., Управленческие решения — М.: ИНФРА-М, 2001, 324с.

11. Эддоус М. П, Методы принятия решений — М.: ИНФРА-М, 1999.

12. Якокка Л.Р., Карьера менеджера — Мн.: Парадокс, 2000, 548с.

referatbooks.ru

Основные принципы организации магистралей МПС, архитектура и построение МПС управления, специализированные процессоры

Под управлением понимается процесс такого воздействия на некоторую систему или объект (объект управления), при котором состояние системы или объекта изменяется «в нужную сторону». Объектами управления, очевидно, могут быть: техническое устройство (например, автомобиль), экономическая ситуация на предприятии или фирме, экосистема региона, процесс разработки программного проекта, сам программный проект и его характеристики и т.п. Предполагается, что мы можем не только оказывать воздействие на объект, но и оценивать результаты этого воздействия по некоторым заданным критериям. Например, критериями качества процесса разработки программного проекта могут служить время завершения проекта и его бюджет (стоимость разработки). Влиять на эти характеристики (управлять ими) мы можем, например, с помощью перераспределения ресурсов между отдельными работами, составляющими данный программный проект.

Общая схема процесса управления приведена на рис. 2.1.

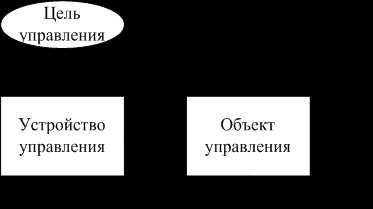
Рис. 2.1. Система управления

Объект управления рассматривается как сколь угодно сложная система, преобразующая входные управляющие воздействия U(t) в выходные сигналы (траектории) V(t), характеризующие состояние объекта управления в момент времени t. Очевидно, что реальный объект управления может иметь множество входов и выходов, определяющих его функциональное взаимодействие с внешней средой. Все эти каналы связи со средой на рис. 2.1 не показаны. Изображены лишь те входы и выходы, которые являются существенными для формулирования задачи управления.

Совокупность объекта управления и воздействующего на него устройства управления называется системой управления. Предполагается, что на объект управления действуют также возмущения x(t), изменяющие, как правило, в непредсказуемом направлении основные характеристики объекта управления. Для определенности будем предполагать, что все функции времени, изображенные на рис. 2.1, являются вектор-функциями с вещественными компонентами и заданными размерностями.

Сигнал управления вырабатывается в соответствии с некоторой заданной целью управления, определяемой теми задачами, которые поставлены перед системой управления. Довольно часто в системах управления для выработки управляющих воздействий оказывается необходимой информация о действительном состоянии объекта управления. Эта информация поступает по цепи обратной связи, показанной на рис. 2.1 пунктирной стрелкой.

Описание некоторого объекта как объекта управления и выявление каналов воздействия на него может производиться только исходя из заданной цели управления. Так, например, тот же завод с точки зрения служб санэпиднадзора или иных экологических служб является объектом управления, перерабатывающим сырье в промышленные отходы, загрязняющие окружающую среду. В этом случае управление со стороны этих служб будет направлено на снижение влияния вредных техногенных факторов, а вовсе не на интенсификацию производства, как в первом случае.

Задача стабилизации – задача,заключающаяся в поддержании некоторых выходных (управляемых) характеристик объекта управления на заданных уровнях, несмотря на постоянно действующие возмущения x(t):

V(t) = const.

Задачи стабилизации возникают и решаются в живой природе (поддержание стабильной температуры тела у теплокровных животных), в технических системах (например, стабилизация напряжения и частоты в энергосистемах вне зависимости от нагрузки) и т.д.

Задача выполнения программы, или задача программного управления – задача обеспечения наперед заданных траекторий V(t), т.е.задача принуждения объекта управления изменять свои управляемые характеристики во времени по заданному закону, по определенной программеV*(t). Например, процесс разработки некоторого технического изделия на заводе должен протекать в соответствии с заранее разработанным временным графиком. Запускаемый космический аппарат обычно выводится на траекторию в соответствии с заранее заданной расчетной траекторией. Легко видеть, что задача стабилизации является частным случаем задачи программного управления.

Задачи слежения – задачи, в которыхосновная проблема сводится к формированию такой выходной траектории V(t) управляемого объекта, которая как можно более точно аппроксимировала бы другую, заранее не известную траекторию V*(t). Например, задачи слежения возникают, когда антенна радиолокатора отслеживает непредвиденные движения какого-либо летящего объекта. Число подобных примеров может быть большим.

Задачи экстремального управления, или, как иногда говорят, задачи настройки, возникают довольно часто. Задачи экстремального управления (задачи настройки) – задачи, заключающиеся в достижении некоторой цели, которая может эволюционировать во времени. Предполагается, что на траекториях объекта управления задан некоторый функционал, отражающий эту цель (обычно его экстремум соответствует некоторому нормальному, благоприятному или наилучшему режиму работы) и зависящий как от управляемых, так и от неуправляемых параметров объекта. Требуется с помощью соответствующих управляющих воздействий добиваться того, чтобы значение целевого функционала в любой момент времени находилось в достаточно малой окрестности экстремума (максимума или минимума – в зависимости от смысловой интерпретации). Например, при настройке радиоприемника на какую-либо радиостанцию добиваются достижения максимальной громкости. Автоматические системы экстремального управления часто называются системами автоматической оптимизации, или самонастраивающимися системами.

Задачи экстремального управления являются в определенном смысле более сложными, чем ранее перечисленные, например, требуется оценивать критерий или его производные. Важно отметить, что задачи экстремального управления являются не только более сложными, но и более общими. При необходимости практически любую задачу управления можно сформулировать на языке экстремального управления. Например, задачи стабилизации и программного управления могут быть сформулированы как задачи минимизации невязки (ошибки) между заданными и действительными выходными траекториями объекта.

Задачи оптимизации в теории управления - задачи реализации некоторых оптимальных (по заданному критерию) выходных траекторий управляемой системы. При этом под критерием оптимальности понимают признак, на основании которого проводятся сравнительная оценка допустимых решений и выбор оптимального решения. В частности, может ставиться задача перевода объекта управления из одной точки фазового пространства в другую, например, за минимальное время при соблюдении заданных ограничений, в том числе фазовых. Очевидно, такие задачи непосредственно не могут быть отнесены ни к одному из ранее рассмотренных типов задач (стабилизация, выполнение программы, слежение, настройка).

В качестве примера можно рассмотреть пример задачи об оптимальном (в смысле расхода горючего) режиме набора высоты и скорости летательным аппаратом, например, самолетом. На рис. 2.2 показано фазовое пространство самолета как объекта управления. Ось абсцисс является осью высот Н, а ось ординат – осью скоростей V. Состояние самолета изображается точкой фазового пространства – плоскости VOH.

Рис. 2.2. Фазовое пространство набора высоты и скорости самолета

Существует множество траекторий в фазовом пространстве, соединяющих начальную (А) и конечную – целевую – точки (B). Требуется выбрать такое управление самолетом, чтобы набор высоты и скорости проходил в соответствии с некоторой оптимальной траекторией. Под критерием оптимальности в данном примере понимается суммарный расход горючего. Если такая оптимальная траектория рассчитана заранее, то она, в принципе, может выступать в качестве программы при последующем решении задачи программного управления. Однако обычно ситуация оказывается несколько сложнее. Может ставиться задача построения оптимального поведения объекта независимо от того, в какой точке фазового пространства он оказался в процессе реального движения в условиях возмущений. Собственно задача выполнения программы здесь уже не является определяющей.

Нужно ясно понимать, что все перечисленные задачи теории управления могут находиться в определенной иерархической взаимосвязи и присутствовать одновременно при проектировании той или иной системы управления. Например, на одном из иерархических уровней мы можем решать задачу стабилизации, строя соответствующую систему управления. В то же время (на более высоком уровне) может ставиться задача экстремального управления этой системой стабилизации в соответствии с некоторым критерием качества стабилизации и т.д. Число таких «вложений» теоретически не ограничено.

Мы сейчас рассматривали основные задачи теории управления, а не методы их решения. Методы решения сформулированных задач и их реализация в виде конкретных систем управления могут быть различными, и они связаны с основными принципами управления.

Жесткое управление. Принцип жесткого (разомкнутого) управления -принцип управления, который предполагает отсутствие обратной связи в общей схеме управления (см. рис. 2.1). Такие системы управления без обратной связи называются разомкнутыми. Чаще всего они применяются для целей программного управления.

Принцип жесткого управления проиллюстрирован на рис. 2.3, где представлена система жесткого управления, решающая задачу программного управления (задачу выполнения заданной программы).

Рис. 2.3. Система жесткого программного управления

Здесь цель управления V*(t) задает желаемую программу изменения состояния объекта во времени. Эта программа передается управляющему устройству для построения необходимого управления U(t). В результате такого управления состояние объекта должно изменяться по закону V(t). Система управления стремится обеспечить равенство V(t)»V*(t) для любого момента времени. Рассмотрим данный процесс жесткого управления подробнее.

Предположим, что:

1) объект управления является безинерционным и описывается оператором F: V(t) = F(U(t));

2) данное равенство справедливо для любого момента времени t;

Управляющее устройство вырабатывает управляющее воздействие по закону где G – оператор устройства управления.

Очевидно, для достижения равенства

необходимо обеспечить закон управления Gв виде G=F-1.

Таким образом, оператор, характеризующий закон управления, является обратным к оператору объекта.

Существенные моменты в процессе жесткого управления сводятся к следующему. Во-первых, для построения закона управления необходимо иметь полную информацию об операторе объекта F(U(t)) (математической модели объекта). Во-вторых, предполагается стабильность характеристик объекта, то есть неизменность его оператора. При малейших изменениях в объекте точность жесткого управления может быть нарушена: G¹F-1.

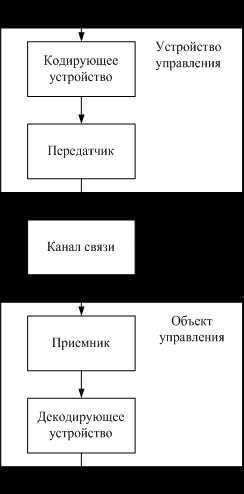
Рис. 2.4. Система радиосвязи

После прохождения канала связи радиоволны попадают в приемник, детектируются, усиливаются и при помощи динамика преобразуются снова в акустические колебания. Здесь мы имеем факт управления на расстоянии колебаниями диффузора динамика таким образом, чтобы они копировали колебания в микрофонной цепи передатчика.

Таким образом, в системах жесткого управления управляющему устройству недоступна информация о действительном состоянии объекта управления – какая-либо обратная связь отсутствует. В гораздо большем числе случаев необходимо прибегать к более гибким принципам управления, оказывающимся более эффективными при наличии различных помех, возмущений и изменяющихся параметрах объекта управления.

Системы регулирования – системы, где управляющие воздействия строятся в зависимости от фактического текущего состояния объекта управления. Информация о состоянии объекта поступает по специально организованным каналам обратной связи. Принцип управления с обратной связью называется принципом замкнутого управления, а сама система управления с обратной связью называется замкнутой системой управления. Здесь так же, как и в предыдущем случае, для эффективного функционирования системы управления часто необходимо иметь модель (оператор) объекта управления. В противном случае построение управляющих воздействий оказывается невозможным или малоэффективным. Основное преимущество замкнутых систем перед разомкнутыми состоит в том, что они оказываются существенно менее зависимыми от неизмеримых возмущений и помех, особенно когда механизм влияния помех на объект управления неизвестен. Пример замкнутой системы программного управления представлен на рис. 2.5.

Рис. 2.5. Замкнутая система программного управления

U(t) = f(V*(t)-V(t)).

Наличие обратной связи обычно позволяет существенно расширить возможности управления и ослабить требования к знанию структуры и свойств объекта управления.

Отметим, что все сложности управления начинаются при попытке управления сложным объектом. Управление простыми объектами обычно не вызывает каких-либо проблем. Например, система управления нагревательными приборами в помещении (или в аквариуме) может быть основана на очень простом принципе: включить подогрев, если температура ниже заданной, и выключить его, если температура выше или равна заданной. В этом случае не нужна никакая модель объекта управления. Другое дело, что даже в этом простом примере нас могут интересовать возникающие при таком управлении колебания температуры. Для уменьшения этих колебаний мы можем начинать интересоваться мощностью нагревательного прибора, его инерционными свойствами, а также свойствами нагреваемой среды – в данном случае воды или воздуха. Например, существенным может оказаться учет нагреваемого объема воздуха или воды и т.д. Таким образом, нас уже интересует модель объекта управления.

Под сложной системойили объектом понимается система с антиинтуитивным поведением, то есть такая система, реакция которой на заданное входное воздействие или сигнал управления не может быть предсказана на основе «здравого смысла». Мы, следовательно, отличаем сложную систему от большой системы, характеризуемой, например, числовыми массивами или файлами высокой размерности. В этом смысле большая система может быть и простой по поведению.

Схема взаимодействия объекта управления с окружающей средой представлена на рис. 2.6.

Рис. 2.6. Взаимодействие объекта со средой

Здесь появился новый канал связи объекта со средой — X(t). Он означает неуправляемое, но наблюдаемое воздействие среды на объект, x(t) по-прежнему означает вектор неуправляемых и ненаблюдаемых возмущений (как внутренних, так и внешних). Под оператором объекта управления понимается оператор F*, связывающий входы объекта с его выходом:

V = F*(X, U, x).

Перечислим теперь характерные признаки сложности объекта управления.

1. Отсутствие описания (в том числе алгоритмического) оператора F*. Для целей управления сложным объектом оно совершенно необходимо.

2. Неожиданное, антиинтуитивное поведение объекта. Иногда это поведение моделируется и объясняется с помощью введения фактора стохастичности. Поэтому для построения систем управления сложными объектами привлекается аппарат стохастической теории управления или теории управления в условиях неопределенности.

3. Нестационарность (изменчивость во времени) оператора F*.

3ys.ru