Нелинейная задача оптимизации производственной деятельности фирмы. Задачи нелинейной оптимизации реферат

Контрольная работа: Контрольная: Методы нелинейной и дискретной оптимизации

Тема: Методы нелинейной и дискретной оптимизации

Раздел: Рефераты по методам оптимальных решений

Содержание.

Введение…………………………………………………………………………...3

1.Теоретическая часть…………………………………………………………….5

1.1.Методы нелинейной и дискретной оптимизации …………………….…….5

2.Практическая часть……………………………………………………………13

2.1.Задание № 1………………………..………………………………………....13

2.2.Задание № 2……………………………………………...…...………………17

2.3.Задание № 3…………………………………………………...…………..….21

2.4.Задание № 4...……..………………………………...…………….………….23

3.Дополнительные задачи………………………………………………………28

Заключение……………………………………………………………………….36

Список использованной литературы…………………………………………...37

Введение.

Задача оптимизации — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Решения задачи оптимизации состоит из нескольких этапов:

– создание модели задачи оптимизации;

– поиск решения задачи оптимизации;

– анализ найденного решения задачи оптимизации.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).

По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

Задачи оптимизации, в которых целевая функция f (x) и ограничения g_i ( x),i=1,…,m являются линейными функциями, разрешаются так называемыми методами линейного программирования.

В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

1) если f (x) и g_i ( x),i=1,…,m — выпуклые функции, то такую задачу называют задачей выпуклого программирования;

2) если X Ϲ Z, то имеют дело с задачей целочисленного (дискретного) программирования.

В данной контрольной работе мы рассмотрим методы нелинейного и целочисленного (дискретного) программирования.

Список использованной литературы.

Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие. – М.: Вузовский учебник, 2012.
Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2е изд., испр. и доп. –М.: Вузовский учебник : ИНФРА-М, 2012.

Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: учебное пособие. –М.: Вузовский учебник, 2012.
Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров. –3 изд., перераб. и доп. – М.: Юрайт, 2012.

Задание № 1.

Решите графическим методом типовую задачу оптимизации. Осуществите проверку правильности решения с помощью средств MS Excel (надстройка Поиск решения).

Фермер планирует засеять кукурузой и соей 400 га земли. Затраты на сев и уборку кукурузы составят 200 ден. ед./га, сои –100 ден. ед./га. На покрытие расходов, связанных с севом и уборкой урожая, фермер получил кредит в размере 60 тыс. ден. ед. Фермер планирует получить: кукурузы – 30 ц/га, сои – 60 ц/га.

Фермер заключил договор на продажу кукурузы по 3 ден. ед./ц и сои по 6 ден. ед./ц. Однако согласно данному договору он обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого – 21 тыс. ц.

Определите, какую площадь нужно засеять фермеру каждой из культур, чтобы получить максимальную прибыль.

Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?

Задание № 2.

Торговая компания собирается приобрести новый товар – комплекты постельного белья. Ожидаемая потребность – 800 единиц в месяц. Товар можно приобрести у поставщика. Стоимость заказа – 150 руб., годовая стоимость хранения единицы товара –6 руб. Доставка товара осуществляется в течение двух дней. Компания работает 300 дней в году.

Рассчитайте объем заказа, минимизирующий общие годовые расходы компании. Определите:

а) оптимальный объём;

б)годовые расходы на хранение запасов;

в) период поставок;

г) точку заказа.

Задание № 3.

В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.) в тот момент, когда оба бухгалтера заняты обслуживанием ранее обратившихся коллег, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно λ=8 , а среднее время, которое затрачивает бухгалтер на оформление документа, – Тср.=7.

Оцените основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени). Определите, сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%.

Задание № 4.

Статистический анализ показал, что случайная величина Х (длительность обслуживания клиента в парикмахерской) следует показательному закону распределения с параметром, а число клиентов, поступающих в единицу времени (случайная величина Y), – закону Пуассона с параметром λ=1,9 и μ=0,6.

Организуйте датчики псевдослучайных чисел для целей статистического моделирования (использования метода Монте–Карло). Получите средствами MS Excel 15 реализаций случайной величины Х и 15 реализаций случайной величины Y.

Дополнительные задачи.

Нелинейная оптимизация, решение задач средствами MS Excel.

Задача № 5.

Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем выпуска продукции равен В = Х1 + Х2, где Х1 и Х2 – объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе производства зависят от объемов нелинейно:

S(X_1) = c_0 + c_1 X_1 +c_2 X_12, c_0, c_1, c_2 > 0,

S(X_2) = p_0 + p_1 X_2 +p_2 X_22, p_0, p_1, p_2 > 0.

Распределите объем производства между технологическими способами таким образом, чтобы общие затраты производства оказались минимальными.

№ задачи

p_0

p_1

p_2

c_0

c_1

c_2

100

Управление запасами.

Задача № 6.

На станке производятся детали в количестве 20 000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 5 000 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 5 руб. в год за одну деталь. Стоимость производства одной детали – 2,5 руб., а стоимость на подготовку производства – 1 000 руб.

Системы массового обслуживания.

Задача № 7.

Поток клиентов, прибывающих в банк, имеет интенсивность девять клиентов в час. Продолжительность обслуживания одного клиента в среднем составляет 8 мин.

Определите, сколько операционистов должно находиться в зале, чтобы среднее число клиентов, ожидающих обслуживания, не превышало трех.

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавить отзыв могут только зарегистрированные пользователи.

studrb.ru

Контрольная работа: Методы нелинейной и дискретной оптимизации (решены 4 задачи)

Тема: Методы нелинейной и дискретной оптимизации (решены 4 задачи)

Раздел: Рефераты по методам оптимальных решений

Содержание

1.4. Методы нелинейной и дискретной оптимизации 3

2.4. Задача 11

3.4. Задача 15

4.4. Задача 18

5.4. Задача 20

Литература 22

1.4. Методы нелинейной и дискретной оптимизации

2.4. Фермер планирует засеять кукурузой и соей 400 га земли. Затраты на сев и уборку кукурузы составят 200 ден. ед./га, сои –100 ден. ед./га. На покрытие расходов, связанных с севом и уборкой урожая, фермер получил кредит в размере 60 тыс. ден. ед. Фермер планирует получить: кукурузы – 30 ц/га, сои – 60 ц/га. Фермер заключил договор на продажу кукурузы по 3 ден. ед./ц и сои по 6 ден. ед./ц. Однако согласно данному договору он обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого – 21 тыс. ц.

Определите, какую площадь нужно засеять фермеру каждой из культур, чтобы получить максимальную прибыль. Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?

3.4. Торговая компания собирается приобрести новый товар – комплекты постельного белья. Ожидаемая потребность – 800 единиц в месяц. Товар можно приобрести у поставщика. Стоимость заказа – 150 руб., годовая стоимость хранения единицы товара –6 руб. Доставка товара осуществляется в течение двух дней. Компания работает 300 дней в году.

Рассчитайте объем заказа, минимизирующий общие годовые расходы компании. Определите:

а) годовые расходы на хранение запасов;

б) период поставок;

в) точку заказа.

4.4. В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.) в тот момент, когда оба бухгалтера заняты обслуживанием ранее обратившихся коллег, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно λ=8 , а среднее время, которое затрачивает бухгалтер на оформление документа, – Тср.=7.

Оцените основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Определите, сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%.

5.4. Статистический анализ показал, что случайная величина Х (длительность обслуживания клиента в парикмахерской) следует показательному закону распределения с параметром, а число клиентов, поступающих в единицу времени (случайная величина Y), – закону Пуассона с параметром λ=1,9 и μ=0,6.

Организуйте датчики псевдослучайных чисел для целей статистического моделирования (использования метода Монте-Карло). Получите средствами MS Excel 15 реализаций случайной величины Х и 15 реализаций случайной величины Y.

Литература

1. Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров. –3-е изд., перераб. и доп. – М.: Юрайт, 2012.

2. Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие. – М.: Вузовский учебник, 2012.

3. Ильина М.А., Копылова Ю.Н., Копылова Н.Т. Методы оптимальных решений. Конспект лекций. Учебно-методичекое пособие. – Барнаул: Изд-во АлтГТУ, 2012.-112 с.

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Добавить отзыв могут только зарегистрированные пользователи.

studrb.ru

Нелинейная задача оптимизации производственной деятельности фирмы

Обратная связь

ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Пусть производственная фирма выпускает один продукт, либо несколько продуктов в заданной пропорции. Тогда ее выпуск за заданный плановый период – это количество единиц продукта одного вида, либо число многономенклатурных агрегатов.

Пусть для выпуска продукции фирмой используются два вида ресурсов. И величина выпуска описывается нелинейной двухфакторной производственной функцией Кобба-Дугласа:

Здесь - это количество используемых в течение планового периода единиц первого ресурса, а - количество единиц второго ресурса. Обычно в качестве первого ресурса рассматривается капитал, а в качестве второго – труд. Положительный коэффициент равен объему выпуска продукции при единичных затратах ресурсов. Эластичность выпуска по первому ресурсу удовлетворяет неравенствам . И эластичность выпуска по второму ресурсу удовлетворяет тем же неравенствам.

По своему содержательному смыслу количества используемых ресурсов – неотрицательны. Это означает выполнение неравенств

Пусть известны цена единицы первого ресурса и цена единицы второго ресурса . Тогда суммарные затраты на использование ресурсов в течение планового периода равны

где и – двумерные векторы, а – их скалярное произведение.

Эти затраты не могут превышать максимально возможного за плановый период общего объема издержек , что означает справедливость неравенства

Пусть известна цена единицы производимого продукта . Тогда прибыль (чистый доход) фирмы за плановый период равна

Эту величину надо максимизировать.

Собирая все вместе, математическую постановку нелинейной задачи оптимизации производственной деятельности фирмы запишем в виде:

при ограничениях

Укажем способ решения этой задачи с помощью инструмента Поиск решения. Для примера рассмотрим задачу, исходные данные которой приведены в таблице 5.1.

Таблица 5.1

q₁	q₂	Q	p	A	α	1-α
				1,745	0,628	0,372

Математическая запись данного примера имеет вид:

при ограничениях

Рассмотрим три этапа решения данного примера с помощью инструмента Поиск решения.

Этап 1. Введем исходные данные нелинейной задачи оптимизации производственной деятельности фирмы. В соответствующие ячейки введем координаты начальной точки, формулы для вычисления суммарных затрат на использование ресурсов , значения производственной функции Кобба-Дугласа и значения прибыли . Для рассматриваемого примера это можно сделать, например, следующим образом.

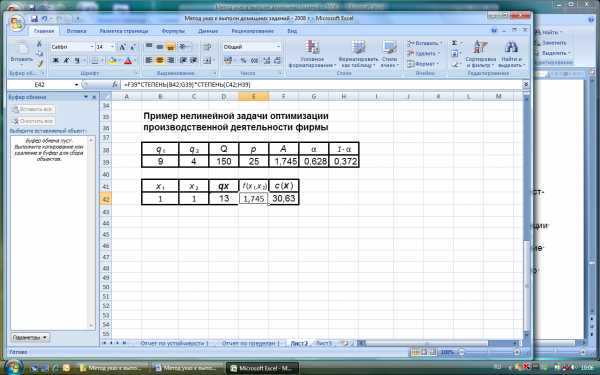
Рисунок 5.1. Входные данные примера нелинейной задачи

оптимизации производственной деятельности фирмы

На рисунке 5.1 видно, что исходные данные примера расположены в горизонтальном массиве, элементы которого введены в ячейки диапазона B39:h49. Непосредственно над каждой ячейкой, расположенной в этом диапазоне, написано обозначение того входного параметра, который содержится в этой ячейке.

Для переменных компонент и вектора , использован горизонтальный массив, состоящий из двух элементов, которые содержатся в ячейках диапазона B42:C42. Экспериментально замечено, что использовать в качестве начальных значений этих компонент нулевые значения нельзя. Инструмент Поиск решения принимает начальную точку (0,0) за оптимальное решение в тех задачах, в которых она не является даже точкой локального максимума. В качестве начальных точек рекомендуется выбирать точки с одинаковыми и положительными компонентами. В данном примере в качестве начальной точки выбрана точка (1,1).

В ячейку D42 введена формула для вычисления суммарных затрат на использование ресурсов . В ней использована встроенная функция суммирования СУММПРОИЗВ из категории Математические функции. Эта функция возвращает сумму произведений соответствующих элементов массивов. Сама формула имеет запись =СУММПРОИЗВ(B39:C39;B42:C42).

В ячейке E42 содержится формула для вычисления значения производственной функции Кобба-Дугласа . Ее запись видна в верхней строке формул рисунка 5.1. Она имеет вид =F39*СТЕПЕНЬ(B42;G39)* СТЕПЕНЬ(C42;h49). В ней использована встроенная функция СТЕПЕНЬ (POWER) из категории Математические функции. Данная функция возвращает результат возведения числа в степень.

В ячейку F42 введена формула для вычисления значения прибыли . Она имеет вид =E39*E42-D42. Ее запись видна в верхней строке формул рисунка 5.4.

Этап 2. Вызовем инструмент Поиск решения и введем условия задачи.

После выполнения указанных выше действий появится диалоговое окно Поиск решения, показанное на рисунке 5.2.

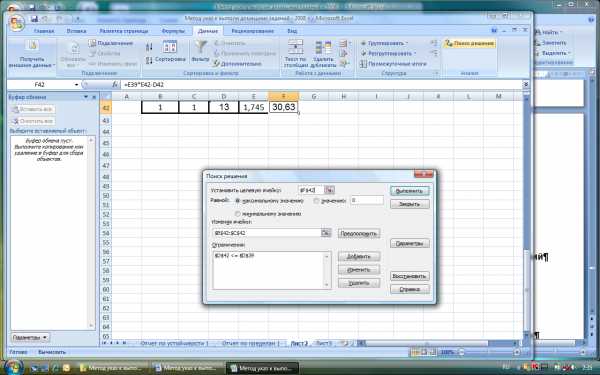
Рисунок 5.2. Диалоговое окно Поиск решения для примера нелинейной

задачи оптимизации производственной деятельности фирмы

В пункте 3 подробно описано, как можно задать условия задачи в диалоговом окне Поиск решения.

Далее, после щелчка по кнопке Параметры, переходим в диалоговое окно Параметры поиска решения. Установим в нем значения параметров, показанные на рисунке 5.3.

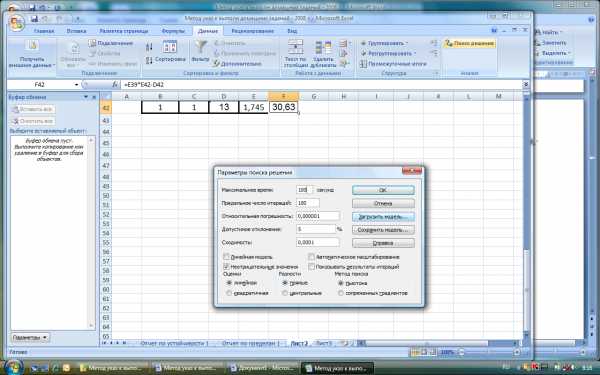
Рисунок 5.3. Диалоговое окно Параметры поиска решения для

примера нелинейной задачи оптимизации производственной

деятельности фирмы

На рисунке 5.3 видно, что флажок установлен только для параметра Неотрицательны значения. Флажок для параметра Линейная модель устанавливать нельзя, потому что решается нелинейная задача.

После окончания введения параметров щелкнем по кнопке OK и вернемся в диалоговое окно Поиск решения.

Этап 3. Решение задачи инструментом Поиск решения.

Для решения нашего примера инструментом Поиск решения, надо в диалоговом окне Поиск решения, показанном на рисунке 5.2, щелкнуть по кнопке Выполнить.

После завершения работы инструмента Поиск решения появится диалоговое окно Результаты поиска решения, изображенное на рисунке 3.5. В этом окне надо поставить флажок на опцию Сохранить найденное решениеи затем щелкнуть кнопку OK.

Результат решения нашего примера приведен на рисунке 5.4.

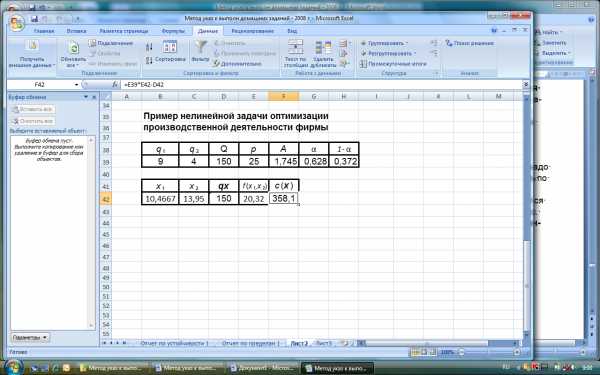
Рисунок 5.4. Результат решения примера нелинейной задачи

оптимизации производственной деятельности фирмы

Этап 4. Анализ полученного решения.

Сравнивая значения ячеек D39 и D42 видим, что суммарные затраты на использование ресурсов в течение планового периода в нашем примере являются максимально возможными.

megapredmet.ru