12. Критерии оптимальности в виде линейной функции от управления. Виды критериев оптимизации

8.Виды критериев оптимальности и их содержание.

Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой - критерием оптимальности.

Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.

На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации. Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность). Однако в частных задачах оптимизации, когда объект является частью технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура). Например, устанавливается оптимальный температурный профиль, длительность цикла "реакция-регенерация".

Рассмотрим более подробно требования, которые должны предъявляться к критерию оптимальности. 1. Критерий оптимальности должен выражаться количественно. 2. Критерий оптимальности должен быть единственным. 3. Критерий оптимальности должен отражать наиболее существенные стороны процесса. 4. Желательно чтобы критерий оптимальности имел ясный физический смысл и легко рассчитывался.

9. Критериальный анализ ситуации: метод базовых шкал, ранжирование и выбор критериев.

При формировании ситуаций, целей, ограничений и вариантов решений лиц принимающих решения и эксперты производят объективные и субъективные измерения характеристик достоверности, важности и предпочтительности. Для осуществления субъективных измерений применяются различные методы, наиболее употребительными из которых являются: ранжирование, парное сравнение, непосредственная оценка и последовательное сравнение.

При описании методов предположим, что имеется конечное число измеряемых объектов X=(x1,…,xm) и сформулирован один или несколько признаков сравнения, по которым осуществляется сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой сравнения объектов. Эта процедура включает построение отношений между объектами эмпирической системы, выбор отображающей функции f и определение типа шкалы измерений.

Ранжирование.На основе знаний и опыта ЛПР или эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения, и приписывает им соответствующие числовые представления. Эти числовые представления могут быть любыми, но должны удовлетворять единственному условию - их последовательность должна быть монотонна. В практике ранжирования чаще всего в качестве числового представления последовательности упорядоченных объектов используется натуральный ряд чисел, называемых рангами и обозначаемых буквой r. При этом наиболее предпочтительному объекту присваивается ранг 1, а по мере убывания предпочтения значение ранга возрастает. Эквивалентным объектам присваиваются одинаковые ранги. Если объекты неразличимы, то вводится понятие связного ранга – среднее арифметическое между соседними рангами. Связные ранги могут быть дробными.

При проведении группового ранжирования для mобъектов с участиемdэкспертов получаем матрицу (таблицу) размеромm*d. Аналогичный вид таблица имеет при проведении ранжирования 1 экспертом дляmобъектов на основании данныхdкритериев.

Достоинством ранжирования как метода субъективного измерения является простота осуществления процедур, не требующая какого-либо трудоемкого обучения экспертов. Недостатком ранжирования является практическая невозможность упорядочения большого числа объектов.

Непосредственная оценка (метод базовых шкал).Непосредственная оценка представляет собой процедуру приписывания объектам числовых значений в шкале интервалов. ЛПР или эксперту необходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом эквивалентным объектам приписываются одинаковые числа.

Переход от размерного показателя к балльной оценке осуществим по формуле:

А – значение размерного показателя;

Min и Max – границы интервала размерного показателя;

x– балльная оценка показателя.

Применяются 5-, 10- и 100-балльные шкалы.

studfiles.net

Основные типы критериев оптимизации.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

1. критерий минимального расхода энергии;

2. критерий быстродействия;

3. критерий минимальной интегральной квадратичной ошибки;

4. критерий минимального расхода топлива;

5. критерий оптимального конечного значения;

6. сложные критерии.

Критерий быстродействия.

В этом случае требуется перевести из состояния Z0 при t0 в сост. Zk за min возможное время. Ограничением является |Ui(t)| ). Критерий формируется в виде j= .

Критерий min расхода энергииj= – используется когда управляющее воздействие определенным количество энергоносителя, потребляется объектом. В этом случае, интеграл от квадрата воздействия, являются мерой расхода

Критерий min расхода топлива.

В этом случае необходимо определить вектор управления и который приведет систему из состояния z0 при t0 в состояниеzк приtк с минимальной затратой топлива. Он формулируется в ивде:

Критерий минимальной интегральной квадратичной ошибки.

Система управления включает в себя объект и регулятор:

х – входное воздействие

u – управляющее воздействие

Е – ошибка.

Согласно критерия необходимо обеспечить минимальное интегрирование квадратичной ошибки. В общем случае он записывается в виде: где z – вектор состояния системы.

Ограничением явл.: , критерий формируется в виде

6. Виды систем управления. Правила оформления ФСА.

Система управления может быть местной и централизованной. В первом случае управляющую систему располагают рядом с объектом управления, во втором- на расстоянии от объекта, в специальном помещении.

При местном управлении работу объекта обычно наряду с автомат устройствами обеспечивает человек проводя вручную часть технических операций. В центральной системе управления всеми техническими опер-ми ведется дистанционно.

Работы системы управления оценивается показателями эффективности, в качестве которого выбирают один или несколько выходных параметров объекта.

Условные графические обозначения на схемах выполняютсплошной толстой основной линией, а горизонтальнуюразделительную черту внутри графического обозначения и линиисвязи – сплошнойтонкой по ГОСТ 2.303–68.

Измеряемые величины и функции, выполняемые приборами исредствами автоматизации, обозначаются прописными буквамилатинского алфавита. При отсутствии необходимых буквенныхобозначений для этой цели используются резервные буквы. Все случаи их применения должнысопровождаться необходимыми пояснениями на схемах. Также используются дополнительные буквенные обозначения, отражающиефункциональные признаки средств автоматизации, в том числеизмерительных преобразователей, преобразователей рода энергиисигналов и вычислительных устройств.

Методика построения условных обозначений заключается вследующем: в верхней части графического обозначения(окружности, овала) наносятся обозначения измеряемой величины и функций, выполняемых прибором. При этом порядок их расположения (слева направо) должен быть следующим:–обозначение измеряемой величины;– обозначение, уточняющее (если это необходимо) основную измеряемую величину;–обозначение (обозначения) функций, выполняемых прибором.

Измерительные устройства уровня. Функциональная схема САК уровня.

Поплавковые уровнемеры

В поплавковых уровнемерах имеется плавающий на поверхности жидкости поплавок, в результате чего измеряемый уровень преобразуется в перемещение поплавка. В таких приборах используется легкий поплавок, изготовленный из коррозионно-стойкого материала. Показывающее устройство прибора соединено с поплавком тросом или с помощью рычагов. Поплавковыми уровнемерами можно измерять уровень жидкости в открытых емкостях.

Гидростатические уровнемеры

Гидростатический способ измерения уровня основан на том, что в жидкости существует гидростатическое давление, пропорциональное глубине, т. е. расстоянию от поверхности жидкости. Поэтому для измерения уровня гидростатическим способом могут быть использованы приборы для измерения давления или перепада давлений. В качестве таких приборов обычно применяют дифманометры. При включении дифманометра перепад давлений на нем будет равен гидростатическому давлению жидкости, которое пропорционально измеряемому уровню.

Радиоизотопные уровнемеры

Такие уровнемеры применяют для измерения уровня жидкостей и сыпучих материалов в закрытых емкостях. Их действие основано на поглощении у-лучей при прохождении через слой вещества. В радиоизотопном уровнемере источник и приемник излучения подвешены на стальных лентах , на которых они могут перемещаться в трубах по всей высоте бака . Ленты намотаны на барабан, приводимый в движение реверсивным электродвигателем.

8. Виды критериев оптимальности и их содержание

Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.

9. Структура компьютерной системы поддержки принятия решений

Компьютерная поддержка процесса принятия решений, так или иначе, основана на формализации:

методов получения объективных (измеряемых) и субъективных (даваемых руководителем или экспертом) исходных и промежуточных оценок;

алгоритмизации самого процесса принятия решений;

анализа ситуации;

выработки решения.

Она заключается в помощи руководителю в процессе принятия решений и включает:

1. помощь руководителю при анализе объективной составляющей, т.е. в понимании и оценке сложившейся ситуации и ограничений, накладываемых складывающейся ситуацией;

2. выявление предпочтений руководителя, т.е. в выявлении и ранжировании приоритетов, учете неопределенности в оценках руководителя и формировании его предпочтений;

3. генерацию возможных решений, т.е. формирование списка альтернатив;

4. оценку возможных альтернатив, исходя из предпочтений руководителя и ограничений, накладываемых внешней средой;

5. анализ последствий (прогноз) результатов принимаемых решений;

6. поддержку переговоров при принятии согласованного группового решения;

7. выбор лучшего, с точки зрения руководителя, варианта.

studfiles.net

12. Критерии оптимальности в виде линейной функции от управления.

R=C0+C1U1+…+CnUn=ΣCiUi, U0=1 (1)

Используется при решении экономических задач, плановых, связанных оптимизированным распределении ресурсов между различными производствами. Если в качестве критерия выступает зависимость к-л показателя технологического процесса от технологических параметров, то критерий такого вида м. использовать при оптимизации технологических режимов. Формирование критерия такого вида м. проследить на следующем примере:

Пусть предприятие производит три вида продукции A, В, С цена каждого вида а, в, с.

Требуется выбрать производительность по каждому виду продукции U1, U2, U3 таким образом, чтобы получить мах стоимость при реализации всей продукции. Критерий будет иметь вид:

A a U1 R=aU1+вU2+cU3 (2)

B в U2 a11U1+a12U2+a13U3≤в1 (3)

C с U3 a21U1+a22U2+a23U3≤в2 (4)

Если продукция А, В, С производится из двух видов в1, в2 сырья, при чем запасы сырья ограниченны, то (2) д.б. дополнен ограничениями (3) и (4), учитывающие запасы сырья. В (3) и (4)

a11-A количество единиц сырья 1 идущее на получение продукции А

a12-B количество единиц сырья 1 идущее на получение продукции В

a13-C количество единиц сырья 1 идущее на получение продукции С

a21-A количество единиц сырья 2 идущее на получение продукции А

a22-B количество единиц сырья 2 идущее на получение продукции В

a23-C количество единиц сырья 2 идущее на получение продукции С

(R=f(U)-max при условии (3) и (4))-U1opt, U2opt,U3opt

Задачи оптимизации в системах (2), (3), (4) формулируется: определить U1, U2, U3 так, чтобы критерий R достигая мах, и удовлетворялись условия (3), (4)

13. Критерии оптимальности в виде функционала.

Функционал – это математический оператор, переводящий функцию в число; например скалярное произведение двух векторов 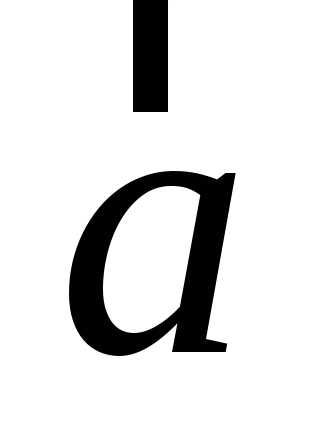и

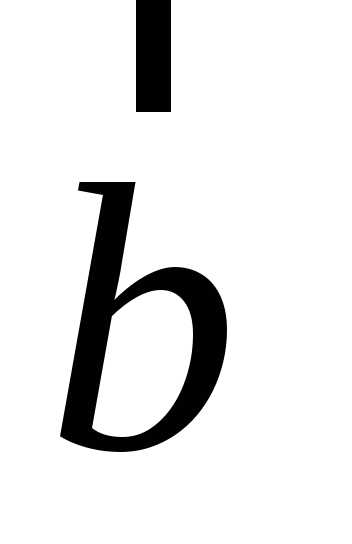
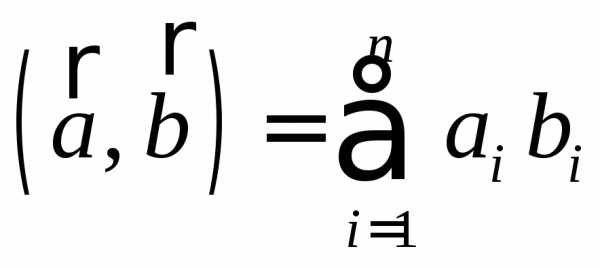, где

Функционал м. имеет вид определенного интеграла 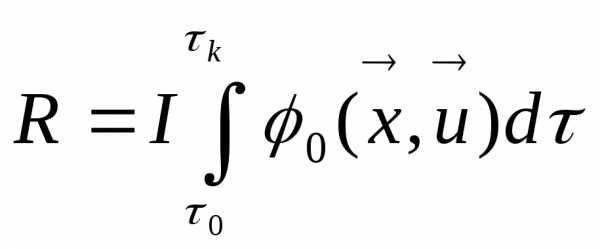(1)

τ – независимая переменная в уравнениях математической модели.

Такая форма критерия присуща процессам с непрерывно-распределенными параметрами, н-р А-Р-S (Р-целевой продукт) Реакция проводится в реакторе периодического действия при постоянном 0t, значение к. д. б. оптимальным с тем чтобы выход целевого продукта был мах.

Математическая модель реактора периодического действия работающего при постоянной 0t, поддержанной заданной точностью АСР :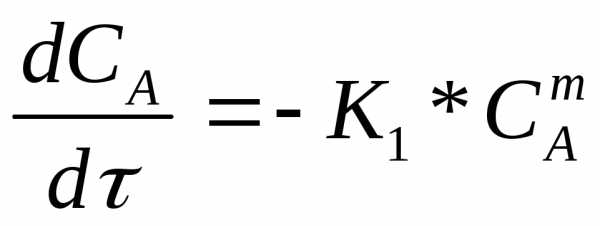

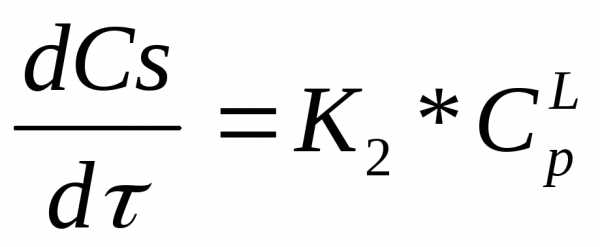
Предположим нас интересует Cр после окончания реакции в момент τк : Ckp= R – критерий

τk-задано, закон Аррениуса: K1=K10-E1/RT, K2=K20-E2/RT

CA,Cp,Cs– параметры состояния

T-управления

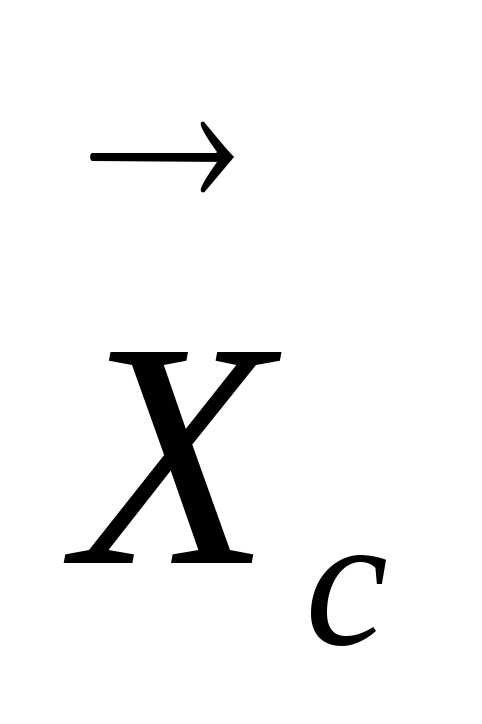–параметры состояния обьекта и его фазовые координаты

14.Линейное программирование. Постановка задачи лп.

Задача, оптимизации с критерием оптимизации в виде линейной функции от управлений решаются методами, которые называются линейным программированием. Примером такой задачи является задача распределения сырья между различными производствами с тем, чтобы получить максимум доход от произведенной продукции. Пусть из 2-х видов сырья изготавливают продукцию 2-х видов, Х1 и Х2- число единиц продукции 1-ого и 2-ого вида соответственно. С1 и С2 –цена видов продукции видов 1 и 2, тогда R=C1X1+C2X2- max(x1x2) пусть В1 и В2-кол-во сырья 1-ого и 2-ого вида имеющихся в наличии на начало пр-ва. Аij-число i-ого вида сырья идущего на получение j-ого вида прод-ии

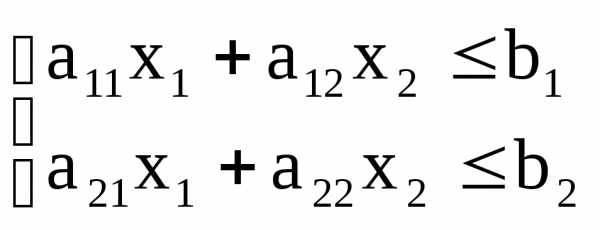Неравенство является ограничением в этой задаче относительно переменных Хj.В данной задаче линейного программирования будет

Xj≥0, при j=1.2…
Xj≠0, при j=1.2…

Т.е. все оптимизирующие положительны, но не достигают бесконечно большого значения.

В таком виде формируют транспортные задачи оптимальной организации доставки сырья из различных складов и нескольких потребителей при минимальных затратах.

studfiles.net

Критерий оптимальности

объективно обусловлено многими факторами: характером общественного строя, экономическими законами, масштабами решений (народное хозяйство, отрасль производства, отдельное предприятие), содержанием целей, на достижение которых направлены действия, и т. д. Принцип оптимальности заимствован из математического программирования и теории управления. Методологической основой теории оптимизации экономики является принцип народно-хозяйственной оптимальности, т. е. изучение экономических явлений с позиций целого, с позиций всего народного хозяйства.

Критерий оптимальности призван помочь обосновать решение. Практические задачи обоснования решения можно условно подразделить на 3 типа. Сущность задач 1-го типа заключается в необходимости выбора наилучшего варианта действий, обеспечивающих достижение вполне определённого, т. е. заданного результата при минимальном расходе ресурсов. В задачах 2-го типа объём имеющихся ресурсов зафиксирован, нужно найти наилучший вариант их использования для получения максимального результата. Задачи, в которых поиск наилучшего варианта ведётся при отсутствии жёстких ограничений как по объёму используемых ресурсов, так и по конечному результату, относятся к 3-му типу. При обосновании решений оперируют понятием степень достижения цели, которую характеризуют определённым показателем.

Ресурсы, имеющиеся в распоряжении общества, отрасли или предприятия, ограничены, поэтому объём ресурсов, выделяемых на одну цель, в какой-то степени зависит от того, сколько их выделено на др. цели. Следовательно, любой вариант распределения ресурсов прямо или косвенно касается одновременно несколько целей и поэтому характеризуется несколькими показателями.

Решение задачи любого типа в принципе сводится к рассмотрению множества альтернатив с последующей их сравнительной оценкой и выбором наилучшей. Примером задачи 1-го типа может служить т. н. транспортная задача. В стране имеется n мест добычи угля, откуда он доставляется т потребителям, расположенным в различных городах страны. Известна стоимость доставки тонны угля из i-го места добычи (i = 1, 2,..., n) в j-й пункт потребления (j = 1, 2,..., m).

Количество угля xj, необходимое каждому потребителю, также известно. Следует определить план доставки потребителям требующегося количества угля при минимуме затрат. Решение такой задачи методологически просто, поскольку значения всех показателей, характеризующих результаты действий, — xj зафиксированы (являются ограничениями в виде равенств). Каждый вариант плана обеспечения потребителей углём оценивается одним переменным показателем — затратами, являющимися Критерий оптимальности Значительно сложнее решать задачи подобного типа, когда, кроме денежных затрат, приходится учитывать расход материальных, трудовых и др. ресурсов, которые иногда не удаётся выразить в денежной форме. Аналогичные трудности возникают в задачах 2-го типа, поскольку результаты распределения ресурсов характеризуются несколькими показателями, имеющими переменное значение. Случай, когда сравниваются различные варианты капиталовложений в развитие отрасли, производственные объединения или отдельные предприятия и соответствующие им конечные результаты работы, является примером задачи 3-го типа. С такими задачами чаще всего приходится встречаться в процессе планирования, когда нужно решить, что лучше — повысить производственные возможности за счёт увеличения капиталовложений или, предположим, оставить те и др. на прежнем уровне. Результаты каждого решения характеризуются сочетанием значений нескольких показателей. Чтобы установить, какое из возможных решений лучше, нужно сравнить их по нескольким показателям. В этом случае может возникнуть необходимость в формировании Критерий оптимальности, который облегчит сравнительную оценку альтернатив. В качестве Критерий оптимальности можно использовать величину, которая, как и отдельные показатели, измеряется в непрерывной или дискретной шкалах. Причём дискретные оценки могут быть порядковыми и метрическими. Порядковая шкала представляет собой последовательность различных сочетаний значений показателей, составленную исходя из соответствия этих сочетаний определённым целям. При использовании подобной шкалы для сравнения вариантов нельзя установить, насколько один результат лучше другого, можно только определить, какой из вариантов лучше других. Метрическая шкала, в отличие от порядковой, допускает оценку «расстояния» между двумя соседними порядками (рангами), т. е. позволяет установить, насколько одна альтернатива лучше другой. Примером порядковой шкалы для одного показателя могут быть словесные (качественные) определения степени достижения намеченной цели: полное удовлетворение какой-либо потребности, частичное удовлетворение потребности и т. п. Показатель, выраженный в метрической шкале, может представлять собой объём продукции определённого назначения. На практике чаще всего приходится сравнивать альтернативы, различающиеся конечными результатами и затратами типа «лучше и дороже», «хуже и дешевле». Причём результаты характеризуются несколькими показателями. Задачи подобного типа иногда называют задачами векторной оптимизации. При этом компонентами вектора являются показатели, характеризующие степень достижения отдельных целей. Среди сравниваемых вариантов обычно выделяют рациональные, к числу которых относятся варианты, обеспечивающие достижение определённого результата при минимуме затрат или достижение максимального результата при определённых затратах. Выбор наилучшего (оптимального) варианта из числа рациональных может производиться с помощью соответствующих Критерий оптимальности Объективная необходимость сравнивать варианты по нескольким несоизмеримым показателям является основной причиной трудностей, которые нужно преодолеть при формировании Критерий оптимальности Нельзя считать лучшим вариант, при котором один показатель невозможно дальше увеличивать, не уменьшая значения хотя бы одного из остальных (т. н. оптимум или максимум по Парето). Критерий оптимальности должен быть таким, чтобы в общем случае можно было сравнивать варианты, когда один из показателей (одна из компонент вектора) возрастает, а другой уменьшается. По-видимому, самое большое, на что можно рассчитывать при сравнении векторов (сочетаний значений нескольких показателей, характеризующих степень достижения различных целей),— это установление предпочтений между ними, т. е. оценка векторов с помощью порядковой шкалы. Следует заметить, что оценки векторов по порядковой шкале вполне достаточно для сравнения вариантов и выбора наилучшего из них.

В условиях социалистического общества все решения, принимаемые на различных уровнях в системе планирования и управления, должны в максимально возможной степени соответствовать высшей цели — наиболее полному удовлетворению потребностей общества. Эта цель может быть достигнута при условии постановки и последующего достижения определённой совокупности социально-экономических целей, предусматривающих удовлетворение всех потребностей общества. Для удовлетворения потребностей общество должно производить различную продукцию. Необходимость в этой продукции зависит от уровня удовлетворения личных и др. непроизводственных потребностей сегодня и в будущем. Т. о., уровень развития производства можно рассматривать как аргумент, функцией которого является степень удовлетворения непроизводственных потребностей общества. Одна из задач планирования — определение наиболее рациональных пропорций в производстве различных продуктов. В процессе планирования должны быть рассмотрены варианты распределения трудовых и др. ресурсов, имеющихся в распоряжении общества, и выбран тот вариант, который в наибольшей степени отвечает потребностям общества. Маркс писал, что «общественная потребность, то есть потребительная стоимость в общественном масштабе, — вот что определяет здесь долю всего общественного рабочего времени, которая приходится на различные особые сферы производства» (Маркс К. и Энгельс Ф., Соч., 2 изд., т. 25, ч. 2, с. 186). Т. о., сравнительная оценка вариантов народно-хозяйственного плана должна производиться по критерию, отражающему степень соответствия плана общественным потребностям. Планы реализуются во времени и пространстве. Следовательно, в общем случае значения отдельных показателей должны характеризовать изменения степени удовлетворения потребностей в разные годы периода планирования и в различных районах страны. Сравнение вариантов плана по большому числу показателей представляет значительные трудности. Чтобы уменьшить число показателей, прибегают к обобщению информации. Чем выше уровень планирующего органа, тем больше степень обобщения. Так, для принятия решения на высшем уровне степень удовлетворения определённой потребности населения, по-видимому, можно представить как отношение планируемого объёма производства продуктов некоторого вида к количеству продуктов (услуг), обеспечивающему данную потребность в соответствии с платёжеспособным спросом населения, а также за счёт общественных фондов. При этом степень удовлетворения потребности будет характеризоваться одним показателем W. Чтобы избежать необходимости оперировать значениями этого показателя в разные годы, можно учитывать его значение на конец планируемого периода. Это допустимо, если предполагается равномерное увеличение значения показателя по годам. Если исходить из необходимости удовлетворения n потребностей общества, то каждый вариант народно-хозяйственного плана будет характеризоваться, как минимум, сочетанием значений n показателей W1, W2,..., Wn.

Сравнительная оценка вариантов плана, разрабатываемого на любом уровне, может производиться либо непосредственно по сочетанию значений показателей, либо по специально сформированному Критерий оптимальности Главным требованием, которому должен отвечать Критерий оптимальности, используемый на любом уровне, является возможность обеспечить оценку вариантов исходя из поставленной цели. Одним из способов отражения соответствия различных сочетаний значений нескольких показателей высшей цели является упорядоченная последовательность этих сочетаний.

Выбор или формирование Критерий оптимальности — главный вопрос сравнительной оценки альтернатив. При этом основным методологическим принципом является системный подход к оценке возможных решений. Сущность системного подхода заключается в том, что целесообразность тех или иных изменений объекта определяется с учётом его взаимосвязей, исходя из интересов системы, составной частью которой является рассматриваемый объект. Нельзя дать заранее какие-либо рекомендации относительно конкретного содержания Критерий оптимальности Они могут быть сделаны только после рассмотрения общих целей и установления степени соответствия различных сочетаний значений показателей, характеризующих объект, целям, которые стоят перед системой.

При обосновании решений особое значение имеет учёт неопределённости, например, характеристик разрабатываемой техники, её стоимости, условий, в которых она будет использоваться, и т. п.

Существует формальная «теория принятия решений», которая рассматривает различные способы формирования критерия оценки альтернатив в условиях неопределённости: критерий максимина, критерий минимаксного сожаления и т. п. Сравнение альтернатив нужно всегда проводить по одному критерию. Однако это не исключает возможности поочерёдной оценки вариантов сначала по одному, а затем по другому критерию.

Вопросам количественного обоснования решений в условиях неопределённости уделено значительное внимание в литературе по анализу систем. Анализ систем представляет собой метод оценки альтернатив в условиях неопределённости при наличии нескольких противоречивых целей. Применение этого метода облегчает обоснование целей действий, а также выявление преимуществ и недостатков альтернативных вариантов действия. Однако окончательный выбор осуществляется руководителем, ответственным за принятие решения.

Лит.: Льюс Р. Д., Райфа Х., Игры и решения, пер. с англ., М., 1961; Пугачев В. Ф., Оптимизация планирования (теоретические проблемы), М., 1968; Федоренко Н. П., О разработке системы оптимального функционирования экономики, М., 1968; Солнышков Ю. С., Как обосновать решение, М., 1972.

Ю. С. Солнышков.

Статья про слово "Критерий оптимальности" в Большой Советской Энциклопедии была прочитана 11265 раз

Интересное

bse.sci-lib.com

Классификация по виду критерия оптимальности и ограничивающих функций

Если критерий оптимальности ( ) – линейная функция, а множество – выпуклый многогранник, то задача (1),(2) называется задачей линейного программирования.

Если критерий оптимальности ( ) – есть отношение двух линейных функций, а множество – выпуклый многогранник, задача (1),(2) называется задачей дробно-линейного программирования.

Пусть область определяется только ограничениями типа неравенств:

(3)

Тогда если функция ( ) и функции ( ), [1, ] являются сепарабельными, то задача (1), (3) называется задачей сепарабельного программирования.

Тогда если функция ( ) и ограничивающие функции ( ), [1, ] являются позиномами, то задача (1), (3) называется задачей геометрического программирования

Если ( ) – квадратичная функция, т.е. ( )= + , а множество есть выпуклое множество, то задача (1),(2) называется задачей квадратичного программирования. Здесь -( * ) симметричная матрица, -( *1) вектор.

Задачи линейного, дробно-линейного, сепарабельного и геометрического программирования редко возникают в САПР и в данном курсе не рассматриваются.

Если множество является конечным множеством, то задача (1), (2) называется задачей дискретного программирования.

Если множество является множеством целых чисел, то задача (1), (2) называется задачей целочисленного программирования.

Задачи дискретного и целочисленного программирования обычно изучаются в курсах исследования операций и в данном курсе не рассматриваются.

Если функция ( ) является выпуклой, то задача (1,2) называется задачей выпуклого программирования. Заметим, что определение выпуклой функции ( ) требует выпуклости области ее определения .

В общем случае задача (1),(2) называется задачей нелинейного программирования. Часто задачи выпуклого программирования также относят к задачам нелинейного программирования.

Классификация по наличию или отсутствию ограничений.

Если ограничения на вектор отсутствуют ( = ), то задача (1),(2) называется задачей оптимизации без ограничений или задачей безусловной оптимизации.

Если имеются ограничения на вектор ( ) то задача (1),(2) называется задачей оптимизации с ограничениями или задачей условной оптимизации.

Классификация характеру ограничений.

Среди задач условной оптимизации выделяют следующие классы задач:

· задачи условной оптимизации с ограничениями типа неравенств, когда

· задачи условной оптимизации с ограничениями типа равенств, когда

· задачи условной оптимизации с ограничениями общего вида, когда имеются как ограничения типа неравенств, так и ограничения типа равенств, т.е. когда

megaobuchalka.ru

Вид - критерий - оптимальность

Cтраница 1

Вид критерия оптимальности ( или целевой функции) определяется конкретным содержанием решаемой задачи оптимизации. [1]

Прибыль в виде критерия оптимальности применяют тогда, когда В У может быть обеспечена необходимым количеством сырья, соответствующим оптимальной по критерию Я производительности. Поясним это более подробно. [2]

При решении задач связанных с нахождением оптимально режима работы объекта выбор вида критерия оптимальности зависит от конкретной задачи. [3]

Таким образом, количество полюсов оптимальной передаточной функции замкнутой системы определяется уравнением объекта и видом критерия оптимальности. [5]

Периодичность, продолжительность, трудоемкость и затраты денежных средств на техническое обслуживание и ремонты могут находиться в различных соотношениях в зависимости от конструктивных особенностей машины, условий ее эксплуатации и вида критерия оптимальности, принятого в системе обслуживания и ремонта. [7]

Количественную оценку оптимизируемого качества объекта, т.е. цель оптимизации, обычно называют критерием оптимальности, или целевой функцией. Вид критерия оптимальности определяется конкретным содержанием решаемой задачи оптимизации и может оказывать существенное влияние на выбор метода решения. В конечном итоге достигаемое значение критерия оптимальности дает количественную оценку эффекта оптимизации. [8]

Все модели, описанные в главе 1, довольно однотипны. Различаясь видом критерия оптимальности, они обладают схожими ограничениями. Это дает возможность обобщить их и построить достаточно универсальную модель. Инструментом этого обобщения и средством придания модели свойства универсальности выступают ингредиенты и технологические способы. [9]

В табл. 2 и 3 собраны основные конструкции, необходимые для составления функции Лагранжа R. В табл. 2 для каждого вида критерия оптимальности / приведено слагаемое Ко в функции R. [10]

Неравенство ( 111 65) представляет собой второе необходимое условие существования экстремума критерия оптимальности. Это условие вытекает из общих свойств рассматриваемого типа реакций, тогда как условие ( 111 64) связано с видом критерия оптимальности, поскольку содержит стоимостные коэффициенты яд и 5у, от величины которых, а точнее от величины их отношения s / jsy, зависит возможность существования оптимума. Jsy, оптимальное значение времени пребывания неограниченно возрастает, что соответствует приближению к оптимальной задаче, в которой требуется найти минимальные потери исходного сырья без учета затрат на реактор. [12]

Одноуровневая одноцелевая система характеризуется наличием одной цели и расположением решающих элементов на одном иерархическом уровне. Она включает в себя класс задач отыскания решения в многомерном пространстве, например отыскание экстремума функций многих переменных на выпуклом множестве. К этому классу задач относится, например, задача оптимизации долгосрочного режима работы каскада ГЭС ц энергосистеме с ограничениями. Действительно, все ГЭС расположены относительно энергосистемы на одном уровне - вес вырабатывают электроэнергию. Цель системы в данном случае формализована в виде критерия оптимальности, например минимума расхода условного топлива на ТЭС энергосистемы. Все прочие цели, имеющиеся у ГЭС, включая и ее обязательство перед водохозяйственным комплексом, игнорируются или фиксируются в виде ограничений. Попытка высвободить входящие в систему ограничений цели приведет лишь к тому, что задача в данной постановке будет неразрешима, если меж / iy этими целями возникнут конфликтные отношения. [13]

Страницы: 1