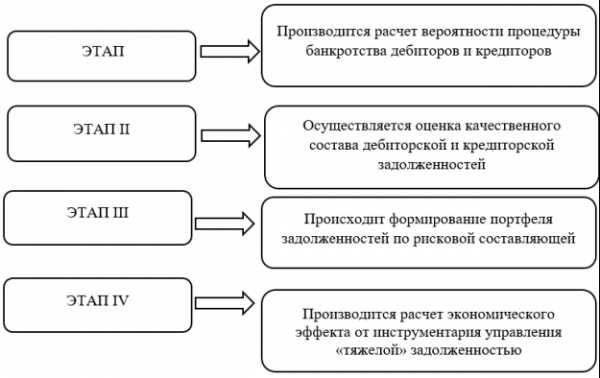
« Стохастические методы оптимизации работы вычислительных систем». Стохастические методы оптимизации
Вопрос 24. Методы стохастической многокритериальной оптимизации — Мегаобучалка
Нужно для управления сложными системами. Особенность именно стохастической оптимизации – все переменные не детерминированные, а случайные (спрос, курсы валют, курсы акций). Детерминированные – запланированные затраты, инвестиции. Разница в том, что здесь мы максимизируем или минимизируем матожидания, квантили, отклонения – смотря что нас интересует. Соотвественно переменные тоже в виде матожиданий и тд представлены. В остальном методы такие же, как для детерминиированных процессов (в последнем вопросе):
Постановка задачи: Пусть имеются критерии . Требуется найти точку , которая оптимизирует все эти критерии. Критерии называют частными критериями. В совокупности они образуют векторный критерий . А именно, рассматривается задача: при условии .
Обычно нет решения, минимизирующего все частные. => нужно искать компромиссное решение. Их стараются найти в классе так называемых эффективных решений (множество Парето).
Метод аналитической иерархии. Общая схема МАИ. Постановка задачи:
1.Задана общая цель (n), назначена соответствующая система, которая должна оптимизироваться.
2. Задано произвольное число альтернатив, из которых нужно выбрать лучшее
3. Задано произвольное число частных критериев, по которым анализируются эти альтернативы.
Требуется найти наилучшую альтернативу. Атрибуты:
1. На первом шаге задача оптимизации структурируется в виде соответствующей иерархии ( цели, критерии и альтернативы).
Сумма показателей равна 1.
Va=8*0,6+5*0,1+9*0,3=8
2. Реализация попарных сравнений для элементов каждого уровня с учетом специфики требований элементов более высокого уровня иерархии. При этом результаты попарных сравнений реализуются в виде матрицы, по которым затем определяется веса важности этих элементов
3. Определяются количественные индикаторы альтернативы, называемые приоритетами.
Шкала сравнений: 1.Эквивалентны (1) 2.Умеренное превосходство (3-1) 3.Существенное превосходство (5-1) 4.….(7-1) 5.….(9-1)
Матрица сравнений сравнивает каждый элемент с каждым:
| А | Б | С | Д | сумма | Нормируем | Итог | |
| А | 1/2 | 1*1/2+2*1/4+3*1/6+6*1/12=2 | |||||
| Б | 1/2 | 3/2 | 12/2 | 1/4 | |||
| С | 1/3 | 2/3 | 12/3 | 1/6 | 4/6 | ||
| Д | 1/6 | 1/3 | 1/2 | 12/6 | 1/12 | 4/12 | |
| сумма |
Свойства матрицы:
· aii=1, для любых i
· aij=1/aji =>aij*1/aji=1 – обратно симметричная матрица
· aik*akj=aij
· vi/vk*vk/vj=vi/vj – согласованная матрица
1. Перед нами несколько функций: одну нужно максимизировать, другую минимизировать и т.п.
Множество Парето – общее у всех. Как его найти?
1. g(1)(x)->max => 1/ g(1)(x)->min (все задачи необходимо сводить на мин.)
2. g(2)(x)->min
3. …
Нужно найти наилучшее решение х1…хn, которое минимизирует все эти функции.
Частный случай: Абсолютное решение. Ситуация, когда все функции можно минимизировать.Решение наз-ся абсолютным, когда оно оптимизирует одновременно все частные критерии.
Решение называется Парето оптимальным, если нельзя улучшить показатель хотя бы одного критерия, при этом чтобы не ухудшились показатели другого критерия. Необходимо использовать прямые методы: задача должна сводиться к однокритериальной.
Опр.Решение называется эффективным или оптимальным по Парето, если нет другого решения такого, что , причем хотя бы для одного “<”.
Бывает несколько парето-опт. Тогда необходим доп. перебор эфф. решений. Приёмы:
o методы сведения задач многокритериальной оптимизации к задачам скалярной оптимизации;
o методы компенсации;
o методы порогов сравнимости.
megaobuchalka.ru
Вопрос 24. Методы стохастической многокритериальной оптимизации — КиберПедия
Нужно для управления сложными системами. Особенность именно стохастической оптимизации – все переменные не детерминированные, а случайные (спрос, курсы валют, курсы акций). Детерминированные – запланированные затраты, инвестиции. Разница в том, что здесь мы максимизируем или минимизируем матожидания, квантили, отклонения – смотря что нас интересует. Соотвественно переменные тоже в виде матожиданий и тд представлены. В остальном методы такие же, как для детерминиированных процессов (в последнем вопросе):
Постановка задачи:
Пусть имеются критерии .
Требуется найти точку , которая в некотором смысле минимизирует все эти критерии. Критерии называют частными критериями.
В совокупности они образуют векторный критерий , который и полежитоптимизации.
задача:
при условии .
Обычно нет решения, минимизирующего все частные. =>нужно искать компромиссное решение.Их стараются найти в классе так называемых эффективных решений (множество Парето).
Множество Парето – общее у всех. Как его найти?
1. g(1)(x)->max => 1/ g(1)(x)->min (все задачи необходимо сводить на мин.)
2. g(2)(x)->min
3. …
Нужно найти наилучшее решение х1…хn, которое минимизирует все эти функции.
Решение называется Парето оптимальным, если нельзя улучшить показатель хотя бы одного критерия, при этом чтобы не ухудшились показатели другого критерия. Необходимо использовать прямые методы: задача должна сводиться к однокритериальной.
Бывает несколько парето-опт. Тогда необходим доп. перебор эфф. решений. Приёмы:
o методы сведения задач многокритериальной оптимизации к задачам скалярной оптимизации;
o методы компенсации;
o методы порогов сравнимости.
Метод аналитической иерархии. Общая схема МАИ. Постановка задачи:
1.Задана общая цель (n), назначена соответствующая система, которая должна оптимизироваться.
2. Задано произвольное число альтернатив, из которых нужно выбрать лучшее
3. Задано произвольное число частных критериев, по которым анализируются эти альтернативы.
Требуется найти наилучшую альтернативу. Атрибуты:
1. На первом шаге задача оптимизации структурируется в виде соответствующей иерархии ( цели, критерии и альтернативы).
2. Реализация попарных сравнений для элементов каждого уровня с учетом специфики требований элементов более высокого уровня иерархии. При этом результаты попарных сравнений реализуются в виде матрицы, по которым затем определяется веса важности этих элементов
3. Определяются количественные индикаторы альтернативы, называемые приоритетами.
Шкала сравнений: 1.Эквивалентны(1) 2.Умеренное превосходство (3-1) 3.Существенное превосходство (5-1) 4.….(7-1) 5.….(9-1)
Матрица сравнений сравнивает каждый элемент с каждым:
| А | Б | С | Д | сумма | Нормируем | Итог | |
| А | 1/2 | 1*1/2+2*1/4+3*1/6+6*1/12=2 | |||||
| Б | 1/2 | 3/2 | 12/2 | ||||
| С | 1/3 | 2/3 | 12/3 | 1/6 | 4/6 | ||
| Д | 1/6 | 1/3 | 1/2 | 12/6 | 1/12 | 4/12 | |
| сумма |
Свойства матрицы:
· aii=1, для любых i
· aij=1/aji =>aij*1/aji=1 – обратно симметричная матрица
· aik*akj=aij
· vi/vk*vk/vj=vi/vj – согласованная матрица
1. Оптимизация основного частного критерия
Среди частных критериев выделяется один, принимается как основной. Для остальных указываются приемлемые значения.
при ограничениях
где — задаваемые допустимые значения для каждого критерия.
cyberpedia.su
« Стохастические методы оптимизации работы вычислительных систем»
- Home
- Documents
- « Стохастические методы оптимизации работы вычислительных систем»
Published on30-Dec-2015
View52
Download0
DESCRIPTION
Санкт-Петербургский государственный университет Математико-механический факультет Кафедра системного программирования. « Стохастические методы оптимизации работы вычислительных систем». лекция профессора Граничина Олега Николаевича для стажеров лаборатории - PowerPoint PPT Presentation
Transcript
- «Стохастические методы оптимизации работы вычислительных систем» лекция профессора Граничина Олега Николаевича для стажеров лаборатории Системного программирования и технологий СПбГУ Санкт-Петербургский государственный университет Математико-механический факультет Кафедра системного программирования Санкт-Петербург 2004
- Кибернетика Н.Винер: «информационно-управленческую связь в разнообразных явлениях и процессах («живых» и машинных) надо рассматривать как неотъемлемую их составную часть». Кибернетика – область науки, техники и биологии
- Разделение кибернетики к 1970-м Роботы, Квантовые компьютеры
- Задачи кибернетики к 2050 Доклад Мюррея www.cds.caltech.edu/~murray/cdspanel Создание команды роботов-футболистов Управление через Интернет Асинхронная теория управления Динамически реконфигурируемое интеллектуальное управление Перепрограммировать систему управления бактерией
- Системное программирование Операционные системы Программирование «ядер» процессоров Системное администрирование Организация работы систем (сложных систем)
- Что такое «система»? Математические модели результат эксперимента - число, множество чисел, кривая и т.п. погрешности статистическая (случайная) систематическая (модели)
- Динамика
- Новые задачи поведение группы людей процессы образования белка в клетках распространение фронта ударной волны внутри вещества, движение в турбулентном потоке или в разреженном газе, течения концентрированных дисперсных смесей, реакция на внешнее нагружение сред со сложной внутренней структурой, пластические течения твердых материалов при интенсивных нагрузках, переходные слои вблизи межфазных границ
- Новый тип моделей
- Уровни описания модели Solid Liquid Gas Macro Mezo Micro
- Невозможно (трудно) исключить систематические ошибки (погрешности модели) Рандомизация модели позволяет: дать обоснованные ответы для задач, в которых пользуются догадками и эвристическими решениями получать решения сложных задач за конечное (полиномиальное) время с определенной степенью достоверности
- Простой пример Y=X+V
- Рандомизированный алгоритм
- Результаты моделирования
- Искусственный интеллект
- Настройка нейронных сетей
- Оптимизация работы сервера
- Панель управления и диаграмма блока выходных данных
- Результат адаптации
- Биоинформатика
- Виртуальный футбол Для апробирования новых методов и демонстрации в широких кругах их преимуществ хотелось бы поддержать команду «студентов» для разработки и развития виртуальной команды роботов, либо играющих в футбол, либо стреляющих танков. www.robocup.org - футбол www.thetech.org/exhibits/online/robotics/robotart/ www.robotbattle.com/home.html www.koth.org
- Заключение Спецкурс+спецсеминар Четверг 9.45-12.50 ауд.1522 (мат.-мех.) [email protected] www.math.spbu.ru/user/gran/oleg_gr.html Граничин О.Н., Поляк Б.Т. «Рандомизированные алгоритмы оценивания и оптимизации при почти произвольных помехах», М. Наука, 2003
- Спасибо за внимание О современном понимании кибернетики Н.Винер писал, что «информационно-управленческую связь в разнообразных («живых» и машинных) явлениях и процессах надо рассматривать как неотъемлемую их составную часть». Исторически, как главное, в этой фразе было воспринято слово – «управление». Часто «кибернетику» называют «наука об управлении» (может быть, точнее говорить о «обратных связях»). Этот взгляд не достаточен с современной точки зрения. Прежде всего, надо осмыслить первое слово – «информация». В задачах «принятия решений» надо понимать, что информация о реальной системе проявляется в двух видах: наблюдаемые значения (традиционное понятие) и сформировавшиеся к текущему моменту структурные связи в системе (структуры). По-моему, наиболее адекватное современное понимание термина «информация» состоит в расширении его понимания до «структур», либо надо слово «структуры» в каком-нибудь виде включить в формулировку основного принципа кибернетики. Информационно-управленческая связь = информация + обратная связь Задачи кибернетики (теории управления) на ближайшие 50 лет Группа ведущих мировых ученых, проработав несколько лет, составила список приоритетных задач кибернетики (теории управления) на ближайшие 50 лет (доклад Мюррея): www.cds.caltech.edu/~murray/cdspanel Среди них Создание команды роботов-футболистов Управление через Интернет Асинхронная теория управления Динамически реконфигурируемое интеллектуальное управление Перепрограммировать систему управления бактерией Необходимо возрождение понятия «Кибернетика» Точное решение любой проблемы возможно при точной постановке задачи, но связи и отношения в реально существующем мире настолько сложны и многообразны, что практически невозможно математически строго описать многие явления. Типичным подходом в теории является выбор близкой к реальным процессам математической модели и включение в нее различных помех, относящихся, с одной стороны, к грубости математической модели и, с другой стороны, характеризующих неконтролируемые внешние возмущения на объект или систему. Для всех математических моделей результатом эксперимента является математический объект - число, множество чисел, кривая и т.п. С математической точки зрения значительный круг прикладных задач имеет своей целью восстановление по экспериментальным данным характеристик (параметров) объекта. При этом реальные системы редко исчерпывающе описываются ограниченными математическими моделями. Выбирая модель для решения реальной задачи, принято говорить о, так называемой, систематической погрешности (погрешности модели), которая может быть количественно выражена расстоянием от реального оператора до выбранной модели. Другой тип погрешностей (ошибок), с которыми может столкнуться экспериментатор, связан с ошибками измерения. Такие ошибки называют статистической погрешностью (случайной погрешностью). Процесс выбора характеристик (параметров) модели из заданного класса для наилучшего описания результатов представляет собой одно из достаточно общих определений понятия оценивания. Hа практике процесс оценивания часто удается связать с какой-нибудь количественной характеристикой качества оценивания и, естественно, при выборе оценок стараться минимизировать отрицательное влияние погрешностей как статистической, так, по возможности, и систематической. Во многих задачах погрешности удобно интерпретировать как помехи (ошибки) наблюдения (измерения результатов эксперимента). При разработке алгоритмов оценивания в большинстве математических исследований последних 50-ти лет помехам в измерениях или ошибкам в описании свойств модели приписываются какие-либо полезные статистические характеристики. На их основе теоретически исследуются свойства оценок. Hаиболее часто предполагается, например, центрированность помех. В инженерной практике широко используются алгоритмы, основанные на идеях обыкновенного метода наименьших квадратов (МНК), представляющего собой усреднение данных наблюдения. Если при этом предположение о центрированности помех было сделано без достаточных обоснований, то практическое использование алгоритмов такого типа нецелесообразно. Так обстоят дела, например, в условиях возможного противодействия "противника". В частности, если помеха определяется детерминированной (неслучайной) неизвестной функцией (противник глушит сигнал) или помехи измерения --- зависимая случайная последовательность, то результат применения к наблюдениям операции усреднения никакой полезной информации в себе не несет. Обычно в такой ситуации последовательность наблюдений называют вырожденной и вопрос о получении "хорошего" решения задачи не рассматривают. Эти трудности в использовании стандартных методов стохастической оптимизации приводят к необходимости исследовать алгоритмы, обеспечивающие высокое качество оценивания при минимальных предположениях о статистических свойствах помех. Другая близкая проблема, с которой сталкиваются при практическом применении алгоритмов оценивания и оптимизации, - недостаточная вариативность последовательности наблюдений. Например, при синтезе адаптивного управления главная цель состоит в минимизации отклонения вектора состояния системы от заданной траектории, что часто приводит к вырожденной последовательности наблюдений. В то время, как для успешного проведения идентификации неизвестных параметров системы должно быть обеспечено "разнообразие" наблюдений.
docslide.net
МЕТОД СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ ЛОГИСТИЧЕСКОЙ ИНФРАСТРУКТУРЫ
Быстров О.Ф. Метод стохастической оптимизации логистической инфраструктуры / О.Ф. Быстров, М.Д. Бокарева, Е.И. Соколова // Экономика и бизнес: теория и практика. – 2016. – №5. – С. 35-38.
МЕТОД СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ ЛОГИСТИЧЕСКОЙ ИНФРАСТРУКТУРЫ
О.Ф. Быстров, д-р экон. наук, профессор
М.Д. Бокарева, студент
Е.И. Соколова, студент
Московский государственный университет путей сообщения Императора Николая II «МИИТ»
(Россия, г. Москва)
Аннотация. Ряд задач экономики сводится к поиску значений управляемых переменных, доставляющих оптимальное значение некоторой целевой функции – стоимости перевозок, грузооборота и т.п. При этом для решения подобных задач наряду с методами математического анализа и математического программирования может успешно использоваться последовательный симплексный метод.
Ключевые слова: последовательный симплексный метод (ПСМ), симплексный поиск, деформация симплекса.
Сущность ПСМ состоит в том, что движение к оптимуму в k-мерном пространстве управляемых переменных xi осуществляется последовательным отражением вершин симплекса. В k-мерном евклидовом пространстве k-мерный симплекс представляет собой фигуру, образованную k+1 точками (вершинами).
В одномерном пространстве симплекс есть отрезок прямой, в двумерном – треугольник, в трехмерном – тетраэдр. В ПСМ используются регулярные симплексы (расстояния между вершинами равны). Алгоритм перемещения симплекса в сторону цели состоит в зеркальном отражении вершины с наихудшим значением целевой функции. Например, при поиске максимума целевой функции целесообразно движение от вершины Vs с наименьшим значением W к противоположной грани симплекса. Важное преимущество симплексного поиска перед другими методами состоит в том, что на каждый шаг требуется всего одно измерение целевой функции W, что значительно повышает эффективность поисковой оптимизации.
Вместе с тем постоянный размер симплекса не обеспечивает одновременно высокую скорость движения симплекса в начале поиска и точность отыскания экстремума на заключительном этапе оптимизации. Поэтому для достижения быстрого и точного решения требуется измерение размеров симплекса в процессе поиска. Деформация симплекса предусматривает сокращение или увеличение расстояния L между его вершинами с сохранением одной из них. В качестве последней можно выбрать вновь полученную вершину, либо вершину с наилучшим значением целевой функции y. При этом размеры ребер симплекса в процессе поиска определяются следующей зависимостью:
Ln=L0 * yn, (1)
где n –номер шага;
yn – числовая последовательность, определяющая закон изменения шага.
Важно помнить о том, что шаги симплекса за пределы факторного пространства и в обратном направлении запрещены.
ПСМ является достаточно эффективной оптимизационной процедурой для широкого класса задач, связанных с поиском минимума/максимума унимодальных функций. В задачах глобальной оптимизации ПСМ приходится использовать многократно, каждый раз изменяя координаты центра начального симплекса. Эффективность глобальной оптимизации в ряде случаев может быть существенно увеличена, если процедуре ПСМ придать свойства так называемого «случайного поиска».
Рассмотрим данный метод на конкретной задаче.
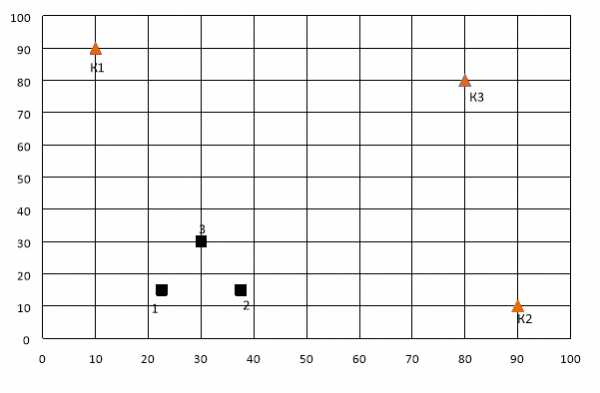
В регионе имеются три карьера природного сырья. Для освоения данных месторождений планируется построить горный обрабатывающий комбинат (ГОК). Координаты карьеров следующие: К1 (10;90), К2 (90;10), К3 (80;80).
Стоимость перевозки 1 тонны сырья на 1 километр составляет: для первого карьера – 500 у.е., для второго – 600 у.е. и для третьего – 700 у.е.
Требуется выбрать оптимальное место для строительства ГОК, обеспечив минимум транспортных издержек.
В качестве целевой функции воспользуемся выражением:
В системе координат XY изобразим исходный симплекс со стороной в 15 км и местосположение карьеров.
|
|
| Рис. 1. Исходные данные для поиска координат ГОК |
Алгоритм метода:
1. Рассчитаем W для трёх вершин начального симплекса.
2. Найдем сумму W1, W2, W3.
3. Найдем р1, р2, р3:
рi = Wi / ∑Wj; j= 1,3. (3)
4. На отрезке числовой оси отметим значения р1 и (р1 + р2) в интервале от 0 до 1.
5. С помощью генератора случайных чисел (ГСЧ) получаем число α є R (0;1), отмечаем его на отрезке числовой оси. В зависимости от того, в какой из трех образовавшихся интервалов 1, 2 и 3 попадет число, ту вершину и отражаем.
Оптимальным месторасположением ГОК является вершина, в которой значение W окажется минимальным в последнем симплексе.
Траектория поисковой оптимизации для n = 4 шагов представлена на рис. 2.
|
|
| Рис. 2. Пример последовательного симплекса метода в режиме стохастической оптимизации |
Таким образом, нами рассмотрена методика стохастической оптимизации логистической инфраструктуры, которая является универсальной и обладает, согласно закону больших чисел, вероятностной сходимостью к правильному результату.
Библиографический список
1. Балдин К.В. Математические методы в экономике. Теория, примеры, варианты контрольных работ: Учеб. пособие / К.В. Балдин, О.Ф. Быстров – М.: Издательство Московского психолого-социального института; Воронеж: Издательство НПО «МОДЭК», 2003. – 112 с.
2. Быстров О.Ф., Мальцев A.B., Охотников Г.Н., Ролдугин В.Д., Торбин В.У. Теоретические основы моделирования военно-технических систем / Учебник под редакцией Быстрова О.Ф. – М: МО СССР РВСН, 1993. – 488 с.
STOCHASTIC METHOD OF OPTIMIZATION OF LOGISTICS INFRASTRUCTURE
O.F. Bystrov, doctor of economic sciences, professor
M.D. Bokareva, student
E.I. Sokolova, student
Moscow state university of railway engineering of emperor Nicholas II «MIIT»
(Russia, Moscow)
Abstract. A number of problems in economics is reduced to finding the values of the controlled variables, delivering optimal value of some objective function — the cost of transport, freight turnover, etc. At the same time to solve these problems, along with the methods of mathematical analysis and mathematical programming sequential simplex method can be used successfully (PSM).
Keywords: serial simpleksnyj methods (PSM), simpleksnyj search, deformation simplex.
economyandbusiness.ru
«Оптимизация решений в условиях стохастической неопределенности».
Условие: в дирекции производственного предприятия принято решение вложить финансы в логистический проект по созданию транспортно-складской системы. Требуется оценить риск потери инвестиций для данного проекта и составить рейтинг проектов по данному показателю.
Факторы риска:
R1-пожар;
R2-криминогенный риск;
R3-банкротство страховщика;
R4-нарушение режима перевозки;
R5-невыполнение технико-технологических требований транспортировки;
R6-природно-климатические катаклизмы;
R7-отказ транспортировать средства и оборудование;
R8-нарушения в работе транспорта;
R9-риск ущерба от непрофессионального персонала;
R10-несвоевременная поставка груза;
R11-появление конкурентов;
R12-нарушение контроля партнеров;
R13-срыв финансового проекта;
R14-изменение цен на товар;
R15-иные виды риска.
Оценим в баллах или % от планированной прибыли max ущерб от каждых выполненных видов риска.
Табл1.,
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 | R12 | R13 | R14 | R15 |
| 34 | 70 | 73 | 99 | 43 | 66 | 99 | 11 | 64 | 35 | 50 | 23 | 71 | 39 | 31 |
-коэффициент ущерба, связанный с данным риском.
С использованием экспертного анализа перепланируем риски с точки зрения возможности(вероятности) их наступления.
Табл2.,
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 | R12 | R13 | R14 | R15 | ||
| 55 | 97 | 40 | 37 | 23 | 98 | 82 | 25 | 87 | 61 | 80 | 65 | 14 | 27 | 57 | ||
| 9 | 2 | 10 | 11 | 14 | 1 | 4 | 13 | 3 | 7 | 5 | 6 | 15 | 12 | 8 | ||
Пересчитаем впо формуле=1-
Табл3
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | B13 | B14 | B15 |
| 0,47 | 0,93 | 0,4 | 0,34 | 0,14 | 1 | 0,8 | 0,2 | 0,87 | 0,6 | 0,74 | 0,67 | 0,07 | 0,27 | 0,54 |
Пронормируем их суммой.
Табл.4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0,058 | 0,115 | 0,05 | 0,042 | 0,017 | 0,124 | 0,099 | 0,024 | 0,108 | 0,075 | 0,092 | 0,083 | 0,009 | 0,033 | 0,067 |
Значение элементов в табл4 можно интерпретировать как субъективные вероятности событий, приводящих к ущербу.
Рассчитаем числовое значение обобщенного показателя риска как математическое ожидание ущерба.
ОПР= =56,87
Таким образом, математическое ожидание ущерба от факторов риска для проекта 1 равно 56,87. Для остальных проектов оно соответственно равно:
Проект 2-57,40; Проект 3-54,51; Проект 4-66,67.
Вывод: по критерию наименьшего результата выбираем лучший проект-это проект 3.
«Методы стохастической оптимизации с использованием последовательно-симплексного поиска».
Исследуем на экстремум функцию
Решение: определим границы факторного пространства:
0≤ ≤1, 0≤≤1
Опр. коорд. центра тяж.исход. симплекса с ребром l=0,2 (0,36;0,66)
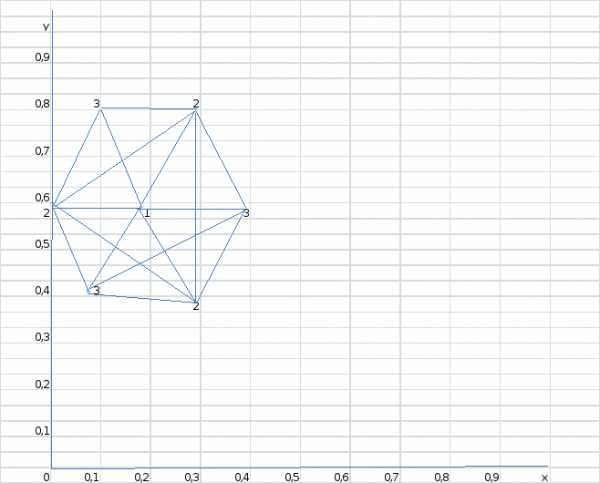
=0,17; =0,58 2.=0,29; ;=0,79 3.=0,39;=0,57
Y1=-1,613,Y2=-1,686, Y3=0,309
Третий наибольший ранг принимается минимальным значением.
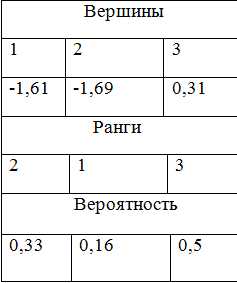 Вер-ти рассч. след.образом: каждый ранг делится на сумму вер-тей.
Вер-ти рассч. след.образом: каждый ранг делится на сумму вер-тей.
Измеряем зне цел. фун. в новом выражении. Представляем их в фун. Записываем необходимые значения, выставляем ранги, вероятности.
2( 0,29;39)
Y2=0,336
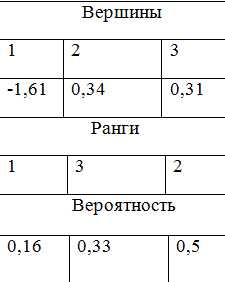
Y3=-1,91
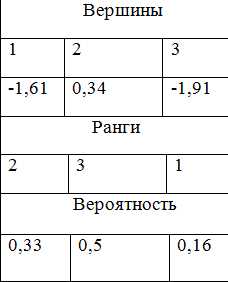
Y2=3,96
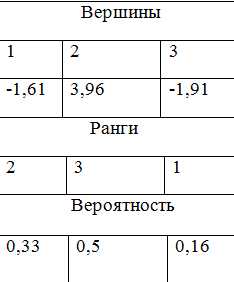
Y3=-3,34
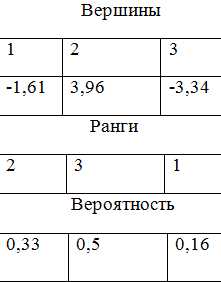
studfiles.net
Стохастическая оптимизация • ru.knowledgr.com
Методы стохастической оптимизации (SO) - методы оптимизации, которые производят и используют случайные переменные. Для стохастических проблем случайные переменные появляются в формулировке самой проблемы оптимизации, которые включают случайные объективные функции или случайные ограничения, например. Стохастические методы оптимизации также включают методы со случайным, повторяет. Некоторые стохастические методы оптимизации используют случайный, повторяет, чтобы решить стохастические проблемы, объединяя оба значения стохастической оптимизации.
Стохастические методы оптимизации обобщают детерминированные методы для детерминированных проблем.
Методы для стохастических функций
Частично случайные входные данные возникают в таких областях как оценка в реальном времени и контроль, основанная на моделировании оптимизация, куда моделированиями Монте-Карло управляют как оценки фактической системы,
и проблемы, где есть экспериментальная (случайная) ошибка в измерениях критерия. В таких случаях знание, что ценности функции загрязнены случайным «шумом», приводит естественно к алгоритмам, которые используют статистические инструменты вывода, чтобы оценить «истинные» ценности функции и/или принять статистически оптимальные решения относительно следующих шагов. Методы этого класса включают
- стохастическое приближение (SA), Роббинсом и Монро (1951)
- стохастический спуск градиента
- конечная разность SA Кифером и Волфовицем (1952)
- одновременное волнение SA Осколком (1992)
- оптимизация сценария
Рандомизированные методы поиска
С другой стороны, даже когда набор данных состоит из точных измерений, некоторые методы вводят хаотичность в процесс поиска, чтобы ускорить прогресс. Такая хаотичность может также сделать метод менее чувствительным к моделированию ошибок. Далее, введенная хаотичность может позволить методу избежать местного оптимума и в конечном счете приблизиться к глобальному оптимуму. Действительно, этот принцип рандомизации, как известно, является простым и эффективным способом получить алгоритмы с почти определенной хорошей работой однородно через многие наборы данных для многих видов проблем. Стохастические методы оптимизации этого вида включают:
- моделируемый отжиг С. Киркпэтриком, К. Д. Джелэттом и М. П. Векки (1983)
- квант, отжигающий
- Коллективы вероятности Д.Х. Уолпертом, С.Р. Биениавским и Д.Г. Рэджнэраяном (2011)
- реактивная оптимизация поиска (RSO) Роберто Баттити, Г. Теккьолли (1994), недавно рассмотренный в справочнике
- метод поперечной энтропии Рубинштайном и Кроезе (2004)
- случайный поиск Анатолием Жиглявским (1991)
- стохастическое туннелирование
- параллель, умеряющая a.k.a. точная копия, обменивает
- стохастическое восхождение на вершину
- алгоритмы роя
- эволюционные алгоритмы
- генетические алгоритмы Голландией (1975)
- стратегии развития
См. также
- Глобальная оптимизация
- Машина, учащаяся
- Оптимизация сценария
- Гауссовский процесс
- Модель в пространстве состояний
- Прогнозирующий контроль модели
- Нелинейное программирование
- Michalewicz, Z. и Fogel, D. B. (2000), как решить его: современная эвристика, Спрингер-Верлэг, Нью-Йорк.
Внешние ссылки
Программное обеспечение
ru.knowledgr.com
Один прямой метод стохастической оптимизации Текст научной статьи по специальности «Математика»
7. Кремлёв А. Г., Гребенникова И. В. Об асимптотике ансамбля траекторий управляемой сингулярно возмущенной системы с запаздыванием // Новости научной мысли - 2006 : материалы науч.-практ. конф. Днепропетровск, 2006. T. 4. С. 65-69.
8. Кремлёв А. Г. Итерационный метод решения задач оптимального управления сингулярно возмущенными системами при квадратичных ограничениях // Журн. вычислительной мат. и мат. физики. 1994. Т. 34, № 11. С. 1597-1616.
УДК 519.6
ОДИН ПРЯМОЙ МЕТОД СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ
В. В. Колбин, М. В. Свищикова
Санкт-Петербургский государственный университет E-mail: [email protected], [email protected]
Предлагается прямой метод стохастического программирования, основанный на пошаговом вычислении линейной аппроксимирующей программы.
Ключевые слова: стохастическое программирование, выпуклость, прямые методы.
9. Рокафеллар Р. Выпуклый анализ. М. : Мир, 1973. 492 с.
10. Васильева А. Б., Бутузов В. Ф. Асимптотические разложения решений сингулярно возмущенных уравнений. М. : Наука, 1973. 192 с.
11. Кириллова Ф. М. Относительная управляемость линейных динамических систем с запаздыванием // Доклады АН СССР. 1967. Т. 174, № 6. С. 1260-1263.
12. Натансон И. П. Теория функций вещественной переменной. М. : Наука, 1974. 468 с.
A Direct Method of Stochastic Optimization V. V. Kolbin, M. V. Svishchikova
A direct method is proposed for stochastic programming. On each step the method uses solving of the linear program which is the linear approximation of input stochastic programs.
Keywords: stochastic programming, convex, direct methods.
ВВЕДЕНИЕ
Целью данной работы является получение эффективного алгоритма решения следующей, часто возникающей в экономических моделях, задачи стохастического программирования.
Требуется минимизировать целевую функцию / общего вида при ограничениях двух типов
f (х, и) ^ min,
д(х,и) < 0, H(и)х - h(u) < 0,
(1)
(2) (3)
где < = (<¿>1,..., <г)т € О С Яг — набор параметров задачи, О — пространство элементарных событий, / : О х Я+ ^ Я1, Я+ = {х | х > 0}, д : О х Я+ ^ Ят,
g =
( gi(x,u)\
\дт(х,и)/
, H =
( hii (и) ... hi n (и)\
\hki (и) ... hkn (и)
, h =
/hi (и)\
\hk (и)/
xi
x=
(4)
xn
Неравенства в (2) и (3) понимаются покомпонентно. Функции / и д предполагаются при любом значении набора < по х € Я+ выпуклыми и непрерывно дифференцируемыми.
В наборе < присутствуют параметры двух типов. В один тип входят такие случайные факторы, как спрос, погода, выход из строя оборудования и т.п. Они относятся к будущему. В другой — величины детерминированные, но известные неточно, такие как численность трудящихся, объем месторождения и т. п. Они относятся к прошлому или настоящему. Так же как и в первом типе, эти величины удобно трактовать как случайные с известными параметрами распределения.
Взаимосвязь между набором < и ограничениями (2) и (3) различна. Ограничения (3) должны выполняться при любой мыслимой реализации параметров (таково, например, ограничение числа пассажиров в такси). Иными словами, необходимо соблюдать при каждой случайной реализации условий задачи общие физические ограничения системы, которых нельзя нарушать вообще. Ограничения (2)
© Колбин В. В., Свищикова М. В., 2012
11
¡^rg^^pgja j^s-,,__Изв. Сарат. ун-та. Нов. сер. 2012. Т. 12. Сер. Математика. Механика. Информатика, вып. 4
должны выполняться в среднем (как, например, требование достаточной заполняемости конкретных авиарейсов, для того чтобы данное направление имело доходность и не было убыточным). Таким образом, необходимо, чтобы средние долговременные договорные обязательства в целом (поставки сырья и производство продукции, прибыль и т. п.) были удовлетворены, хотя при этом допускаются нарушения в кратковременных требованиях.
После введения случайностей в f, g, H, h решение задачи (1)-(4) становится случайным, что делает эту задачу как модель каких-то реальных событий неадекватной. Действительно, полученное решение задачи (1)-(4) xopt = x(u) должно быть принято до реализации настоящих случайных параметров из набора x, а те параметры из набора и, которые были известны неточно, так и остаются известными неточно к моменту принятия решения xopt. Иными словами, возникает порочный замкнутый круг: Природа делает свой ход и после принятия решения xopt, которое выбирается как функция от и.
Поэтому появление случайностей порождает серьезную проблему: формализацию понятия оптимальности параметров управления x в новых условиях, которое позволило бы создать новую задачу — задачу стохастической оптимизации. Известны различные приемы подобной формализации. Один из самых сложных — использование квантилей [1]. Другой способ — расчет управляющих параметров x по наихудшей реализации и [2-4], т. е. поиск argx ш minmaxf (x,u).
' x ш
Тем самым реализуется «правильный» порядок действий: Человек делает первый ход, стараясь добиться минимальности f (x,u), имея ввиду, что Природа после этого выберет и наихудшим образом. Поскольку на самом деле Природа не является сознательным противником Человека, поиск минимакса зачастую дает результат, субъективно воспринимаемый как неудовлетворительный.
Наиболее распространено применение детерминированных эквивалентов, которое обращается с Природой как c противником без интеллекта [2-7].
1. ПОСТРОЕНИЕ ДЕТЕРМИНИРОВАННЫХ ЭКВИВАЛЕНТОВ
При трактовке всех параметров набора и как случайных величин {ut}[=0 ограничение (2) согласно его смыслу естественно заменить на
E[g(x,u)] < 0, (5)
а ограничение (3) практически не меняется
H(u)x - h(u) < 0 V и е О. (6)
Здесь Е — символ математического ожидания.
Наиболее распространенный подход к формированию целевой функции [1-4] аналогичен трансформации (2) в (5) и дает
F(x) = Е [f (x, и)] ^ min, (7)
x^0
т. е. x надо выбрать так, чтобы среднее значение целевой функции было минимальным.
Найдем детерминированный эквивалент ограничениям (6), когда элементы матрицы H и столбца h имеют линейную зависимость от параметров и:
hj (и) = hj + h ¿j и, h¿ (и) = h¿ + h¿ и,
где h ¿j и h¿ — строки длиной r — (hj,..., hijr) и (h¿i,..., hir) соответственно, и все случайные величины из набора и распределены на конечных сегментах c полудлиной <5s > 0 : [и0 — ós,u° + <5s]. Тогда для любых значений переменных x существует максимум по и левых частей системы (6), т. е. величин
n n r
A¿(u) = H¿ (u)x — h¿ (u) = hijxj + h¿juxj — h¿ — h¿u = a¿s (x)ue + 0¿ (x). (8)
j=i j=i s=1
Здесь e¿(x) — скалярная функция, ais(x) = J^j hijsxj — his. Поскольку A¿(и) является сепарабельной функцией, то при сделанных предположениях относительно диапазонов изменения us максимайзер
12
Научный отдел
функции Aj(w) из (8) находится элементарно:
(Z>s(i,x) = <¿>0 + Ss signais(x), s = 1,r (9)
для каждого i-го ограничения из (6). Пусть (D = (Z>i,... ). Подставляя найденные максимай-зеры (9), i = 1,m, в каждую строку i-й функции-ограничения (6), получим детерминированный эквивалент для системы (6)
H(o>(i,x))x — hj(<¿>(i,x)) < 0, i = 1,k.
(10)
Его можно было бы снабдить эпитетом «настоящий», поскольку в отличие от детерминированных эквивалентов (5) и (7) он не требует переосмысления исходной задачи, а является сверткой по < каждого ¿-го ограничения из (6).
2. ИТЕРАТИВНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ (7), (5), (10)
Изложим для задачи (7), (5), (10) прямой итеративный алгоритм.
Шаг 0. Задается е ^ 0, натуральное число К, выбирается начальная точка х0 и назначается
у = х0, г = 0, я = 0.
Шаг 1. Генерируется случайный набор параметров < = < = (<,..., <) и составляется линейная программа
f (x*, о/) + V/(x*, a/)(x — x*)
x>0 '
g(x*,о*) + g'(x*,u/)(x — x*) < 0, Hj(w(i,x*))x — hj(w(i, x*)) < 0, i = l, k.
(11)
Здесь под градиентом понимается строка V/ = матрица Якоби
(dg!
dxi
f
dx1
' dxn
с помощью штриха обозначается
g =
dffm
V dx1
dgi \
dxr
dgm dxn /
Шаг 2. Система (11) решается одним из известных методов (например, симплекс-методом). Обозначим ее решение через Х.
Шаг 3. Положим = xt + pt(x* — xt). (Выбор весов pt обсудим после описания алгоритма.) Шаг 4. Если |xt+1 — y| > е, тогда {y := xt+1; S := 0; перейти на Шаг 5}.
S := S + |xt+1 — x*|.
Если S > Ке, то {вывод xt+1; выход из алгоритма}.
Шаг 5. Полагается t := t + 1. Переход к Шагу 1. (Таким образом, если предыдущее t обозначить через t', то после Шага 5 будет верно x* = x*'+1.)
Пояснения к алгоритму Формирование весов. Веса {pt }f° будем выбирать классическим образом [2-6] согласно аксиомам:
I. pt > 0 для всех t.
II. £ р2 < ГО.
t=1
n
III. £ pt ^ ГО при n ^ ro.
t=1
Такие веса существуют. Например, pt = 1/t. Они обеспечивают, с одной стороны, возможность уйти от «начальной» точки x0 к решению задачи (7), (5), (10), сколь далеко бы от «начальной» точки оно ни находилось (аксиома III). C другой стороны, в асимптотике «колебания» элементов последовательности {x*}f°, если она сходится к решению, относительно решения будут стремиться к
— min
Математика
13
Изв. Сарат. ун-та. Нов. сер. 2012. Т. 12. Сер. Математика. Механика. Информатика, вып. 4
нулю (аксиома II). Естественное требование смещения от текущей итеративной точки в направлении полученного минимума содержится в аксиоме I.
Правило остановки (Шаг 4). Зададимся конечной погрешностью е > 0. После £-й итерации сделаем еще столько шагов, чтобы их суммарная длина превосходила е в К раз. Другими словами,
-1
^ |Х+1 - X | > Ке.
Если при этом все итерации от г-й до (г + N)-й остаются в шаре радиуса е с центром X, т. е. {Х С , то на этом заканчивается итеративный процесс. В качестве ответа можно взять
последнюю итеративную точку из множества {xj .
Теорема. Алгоритм Шаг 1 - Шаг 5 с выбором весов согласно аксиомам I, II, III сходится.
Действительно, поскольку разность Х — X соответствует обобщенному градиенту, то приведенный алгоритм с указанным выбором весов подпадает под действие теоремы Ю. М. Ермольева [3], что обеспечивает сходимость этого алгоритма.
ЗАКЛЮЧЕНИЕ
Предлагаемый итеративный алгоритм вполне адекватен рассматриваемой задаче. Его сходимость имеет и некоторые недостатки, присущие сходимости классических прямых методов стохастического программирования, в частности замедление сходимости с возрастанием индекса шага итерации. Преимущество по сравнению с ними видится в более легком пошаговом решении линейной программы (11), чем вычисление обобщенного градиента с последующим нахождением проекции на допустимое множество [2, 3, 7].
Представляется интересным расширение области применения приводимого алгоритма на задачу более общего вида, а именно на ограничения вида (3) с нелинейностью по x.
Библиографический список
1. Кибзун А. И., Кан Ю. С. Задачи стохастического программирования с вероятностными критериями. М.: Физматлит, 2009. 372 с.
2. Ермольев Ю. М., Ляшко И. И., Михалевич В. С., Тю-пля В. И. Математические методы исследования операций. М. : Наука, 1979. 312 с.
3. Ермольев Ю. М. Методы стохастического программирования. М. : Наука, 1976. 340 с.
4. Поляк Б. Т. Введение в оптимизацию. М. : Наука, 1979. 384 с.
5. Юдин Д. Б. Математические методы управления в условиях неполной информации. М. : Сов. радио, 1974. 400 с.
6. Kolbin V. V. Stochastic programming. Boston, USA : D. Reidel Publ. C., 1977. 325 p.
7. Ермольев Ю. M, Норкин В. И. Методы решения невыпуклых негладких задач стохастической оприми-зации // Кибернетика и системный анализ. 2003. № 5. С. 89-106.
УДК 517.937: 517.983
УСЛОВИЯ ОБРАТИМОСТИ ОДНОГО КЛАССА НЕСАМОСОПРЯЖЕННЫХ ОПЕРАТОРОВ
С. В. Марюшенков
Воронежский государственный университет E-mail: stasint1 @ mail.ru
В данной работе получены условия обратимости одного класса несамосопряженных операторов, являющихся разностью неограниченного антисопряженного и нормального оператора.
Ключевые слова: несамосопряженный оператор, нормальный оператор.
The Conditions of Invertibility of a Class Nonselfadjoint Operators
S. V. Maryushenkov
In this work we obtain the conditions of invertibility of a class of nonselfadjoint operator that are difference between the nonbounded antisymmetric and the normal operator.
Key words: nonselfadjoint operator, normal operator.
© Марюшенков С. В., 2012
cyberleninka.ru