Большая Энциклопедия Нефти и Газа. Теория оптимизации

Тема 15. Основные понятия теории оптимизации.

На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. В подобной ситуации может оказаться и отдельно взятый человек, например, когда он решает вопрос о распределении своих расходов, и целое предприятие или даже отрасль, если необходимо определить, как использовать имеющиеся в их распоряжении ресурсы, чтобы добиться максимального выхода продукции, и, наконец народное хозяйство в целом. Естественно, при большом количестве решений должно быть выбрано наилучшее.

Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. И от того, как будут распределены эти, как правило, ограниченные ресурсы, будет зависеть конечный результат деятельности.

Суть методов оптимизации (оптимального программирования) заключается в том, чтобы, исходя из наличия определенных ресурсов, выбрать такой способ их использования (распределения), при котором будет обеспечен максимум или минимум интересующего показателя. [1]

Необходимым условием использования оптимального подхода к планированию (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Именно такие ситуации, как правило составляют повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей).

Оптимальное программирование, таким образом, обеспечивает успешное решение целого ряда экстремальных задач производственного планирования. В области же макроэкономического анализа, прогнозирования и планирования оптимальное программирование позволяет выбрать вариант народнохозяйственного плана (программы развития), характеризующийся оптимальным соотношением потребления и сбережений (накоплений), оптимальной долей производственных капиталовложений в национальном доходе, оптимальным соотношением коэффициента роста и коэффициента рентабельности национальной экономики и т. д.

Оптимальное программирование обеспечивает получение практически ценных результатов, так как по своей природе оно вполне соответствует характеру исследуемых технико-экономических процессов и явлений. С математической и статистической точек зрения этот метод применим лишь к тем явлениям, которые выражаются положительными величинами и в своей совокупности образуют объединение взаимозависимых, но качественно различных величин. Этим условиям, как правило, отвечают величины, которыми характеризуются экономические явления. Перед исследователем экономики всегда имеется – некоторое множество разного рода положительных величин. Решая задачи оптимизации, экономист всегда имеет дело не с одной, а с несколькими взаимозависимыми величинами или факторами.

Оптимальное программирование можно применять лишь к таким задачам, при решении которых оптимальный результат достигается лишь в виде точно сформулированных целей и при вполне определенных ограничениях, обычно вытекающих из наличных средств (производственных мощностей, сырья, трудовых ресурсов и т. д.). В условия задачи обычно входит некоторая математически сформулированная система взаимозависимых факторов, ресурсы и условия, ограничивающие характер их использования.

Задача становится разрешимой при введении в нее определенных оценок как для взаимозависимых факторов, так и для ожидаемых результатов. Следовательно, оптимальность результата задачи программирования имеет относительный характер. Этот результат оптимален только с точки зрения тех критериев, которыми он оценивается, и ограничений, введенных в задачу.

Отталкиваясь от вышесказанного, для любых задач оптимального программирования характерны три следующих момента: [2]

1) наличие системы взаимозависимых факторов;

2) строго определенный критерий оценки оптимальности;

3) точная формулировка условий, ограничивающих использование наличных ресурсов или факторов.

Из многих возможных вариантов выбирается альтернативная комбинация, отвечающая всем условиям, введенным в задачу, и обеспечивающая минимальное или максимальное значение выбранного критерия оптимальности. Решение задачи достигается применением определенной математической процедуры, которая заключается в последовательном приближении рациональных вариантов, соответствующих выбранной комбинации факторов, к единственному оптимальному плану.

Математически это может быть сведено к нахождению экстремального значения некоторой функции, то есть к задаче типа:

Найти max (min) f(x) при условии, что переменная х (точка х) пробегает некоторое заданное множество Х:

f(x) ® max (min), х I Х (4.1)

Определенная таким образом задача называется задачей оптимизации. Множество Х называется допустимым множеством данной задачи, а функция f(x) – целевой функцией. [3]

Итак, оптимизационной является задача, которая состоит в выборе среди некоторого множества допустимых (т. е. допускаемых обстоятельствами дела) решений (Х) тех решений (х), которые в том или ином смысле можно квалифицировать как оптимальные. При этом допустимость каждого решения понимается в смысле возможности его фактического существования, а оптимальность – в смысле его целесообразности.[4]

Очень многое зависит от того, в каком виде задается допустимое множество Х. Во многих случаях это делается с помощью системы неравенств (равенств): [5]

q1 (х1, х2, … , хn) {? , = , ?} 0,

q2 (х1, х2, … , хn) {? , = , ?} 0, (4.2)

……………………………..

qm (х1, х2, … , хn) {? , = , ?} 0,

где q1, q2, … ,qm – некоторые функции, (х1, х2, … , хn) = х – способ, которым точка х задается набором из нескольких чисел (координат), являясь точкой n-мерного арифметического пространства Rn. Соответственно множество Х есть подмножество в Rn и составляет множество точек (х1, х2, … , хn) I Rn и удовлетворяющих системе неравенств (2.2.2).

Функция f(х) становится функцией n переменных f(х1, х2, … , хn), оптимум (max или min), который требуется найти.

Понятно, что следует найти не только само значение max (min) (х1, х2, … , хn), но и точку или точки, если их больше одной, в которых это значение достигается. Такие точки называются оптимальными решениями. Множество всех оптимальных решений называют оптимальным множеством. [6]

Задача, описанная выше, есть общая задача оптимального (математического) программирования, в основе построения которой лежат принципы оптимальности и системности. Функция f называется целевой функцией, неравенства (равенства) qi (х1, х2, … , хn) {? , = , ?} 0, i = 1, 2, … , m – ограничениями. [7] В большинстве случаев в число ограничений входят условия неотрицательности переменных:

х1 ? 0, х2 ? 0, … , хn ? 0,

или части переменных. Впрочем, это может быть и необязательным.

В зависимости от характера функций-ограничений и целевой функции различают разные виды математического программирования: [8]

1. линейное программирование – функции линейны;

2. нелинейного программирования – хотя бы одна из этих функций нелинейна;

3. квадратичного программирования – f(х) является квадратичной функцией, ограничения линейны;

4. сепарабельное программирование – f(х) представляет собой сумму функций, различных для каждой переменной, условия – ограничения могут быть как линейными, так и нелинейными;

5. целочисленное (линейное или нелинейное) программирование – координаты искомой точки х являются только целыми числами;

6. выпуклое программирование – целевая функция – выпуклая, функции – ограничения – выпуклые, то есть рассматриваются выпуклые функции на выпуклых множествах и т. п.

Наиболее простым и часто встречающимся является случай, когда эти функции линейны и каждая из них имеет вид:

а1х1 + а2х2 + … аnхn + b ,

то есть имеет место задача линейного программирования. Подсчитано, что в настоящее время примерно 80-85% всех решаемых на практике задач оптимизации относятся к задачам линейного программирования.[9]

Сочетая в себе простоту и реалистичность исходных посылок, этот метод вместе с тем обладает огромным потенциалом в области определения наилучших с точки зрения избранного критерия планов.

Первые исследования в области линейного программирования, ставившие своей целью выбор оптимального плана работы в рамках производственного комплекса относятся к концу 30-х годов нашего века и связаны с именем Л.В. Канторовича.[10] В отечественной научной традиции именно его принято считать первым разработчиком этого метода.

В 30-е гг., в период интенсивного экономического и индустриального развития Советского Союза, Канторович был в авангарде математических исследований и стремился применить свои теоретические разработки в практике растущей советской экономики. Такая возможность представилась в 1938 г., когда он был назначен консультантом в лабораторию фанерной фабрики. Перед ним была поставлена задача разработать такой метод распределения ресурсов, который; мог бы максимизировать производительность оборудования, и Канторович, сформулировав проблему с помощью математических терминов, произвел максимизацию линейной функции, подверженной большому количеству ограничителей. Не имея чистого экономического образования, он тем не менее знал, что максимизация при многочисленных ограничениях—это одна из основных экономических проблем и что метод, облегчающий планирование на фанерных фабриках, может быть использован во многих других производствах, будь то определение оптимального использования посевных площадей или наиболее эффективное распределение потоков транспорта.

Говоря о развитии этого метода на Западе, следует сказать о Тьяллинге Купмансе, американском экономисте-математике голландского происхождения.

В миссии торгового флота Купманс пытался так разработать маршруты флотов союзников, чтобы снизить до минимума затраты на доставку грузов. Задача была крайне сложной: тысячи торговых судов везли миллионы тонн грузов по морским путям между сотнями портов, рассеянных по всему миру. Эта работа предоставила возможность Купмансу применить свои математические знания к решению фундаментальной экономической проблемы – оптимальному распределению дефицитных ресурсов между конкурирующими потребителями.

Купманс разработал аналитическую методику, названную анализом деятельности, которая решительно изменила подход экономистов и руководителей к распределению маршрутов. Впервые он описал эту методику в 1942 г., назвав ее «Соотношение между грузами на различных маршрутах» ("Exchange Ratios Between Cargoes on Various Routes"), где показал возможность подхода к проблеме распределения как к математической проблеме максимизации в пределах ограничений. Величина, подлежащая максимальному увеличению, — это стоимость доставленного груза, равная сумме стоимостей грузов, доставленных в каждый из портов. Ограничения были представлены уравнениями, выражающими отношение количества расходуемых факторов производства (например, судов, времени, труда) к количеству груза, доставленному в различные места назначения, где величина любой из затрат не должна превышать имеющуюся в распоряжении сумму.

При работе над проблемой максимизации Купманс разработал математические уравнения, которые нашли широкое применение как в экономической теории, так и в практике управления. Эти уравнения определяли для каждой из затрат на производство коэффициент, равный цене этой затраты в условиях идеальных конкурентных рынков. Таким образом была установлена основополагающая связь между теориями эффективности производства и теориями распределения через конкурентные рынки. Кроме того, уравнения Купманса представляли большую ценность для центральных планирующих органов, которые могли использовать эти уравнения для определения соответствующих цен на различные затраты, оставляя при этом выбор оптимальных маршрутов на усмотрение местных директоров, обязанность которых состояла в максимизации прибыли. Метод анализа деятельности мог широко применяться любыми руководителями при планировании процессов производства.

В 1975 году Л.В. Канторовичу и Тьяллингу Ч. Купмансу была присуждена Нобелевская премия «за вклад в теорию оптимального распределения ресурсов».

Говоря о первых исследованиях в области линейного программирования, нельзя также не упомянуть еще об одном американском ученом – Джордже Д. Данциге. Конкретная формулировка метода линейного программирования восходит к его работе, выполненной им по заказу ВВС США во время Второй Мировой войны, когда возникла проблема координации действий одной большой организации в таких вопросах, как накопление запасов, производство и содержание оборудования и материально-технического снаряжения, причем имелись альтернативы и ограничения. Кроме того, в свое время Дж. Данцинг работал совместно с В.В. Леонтьевым, и симплекс-метод решения линейных оптимизационных задач (наиболее часто применяемый для их решения) появился в связи с одним из первых практических применений метода межотраслевого баланса.

studfiles.net

Тема 1. Основы теории оптимизации

1.Основы теории оптимизации 1.1.Постановка и решение задачи оптимизации

В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение наилучшего варианта из множества возможных альтернатив без их полного перебора и оценивания.

Постановка любой задачи оптимизации включает в себя 4 этапа.

1)Установление границ подлежащей оптимизации системы

Здесь под системой понимается некая изолированная часть реального мира – например, промышленная установка, предприятие и т.д. Чтобы выделить изучаемую систему из внешней среды, важно четко определить ее границы и зафиксировать на некотором заранее выбранном уровне представления ее взаимосвязи с внешней средой. Часто первоначальный

выбор границ системы оказывается слишком жёстким и тогда для получения адекватного решения в систему включают дополнительные подсистемы, оказывающие существенное влияние на ее функционирование. Однако это ведёт к увеличению размерности и сложности системы, значительно затрудняет ее анализ.

2)Выбор характеристического критерия

Характеристический критерий представляет собой скалярную меру “качества” решения. Наилучшему решению задачи оптимизации обязательно отвечает оптимальное, т.е. максимальное или минимальное, значение критерия. В прикладных задачах характеристический критерий часто имеет экономический или технологический характер, например, им может быть величина прибыли предприятия или масса, т.е. задача может состоять в максимизации прибыли или минимизации массы двигателя.

Критериев может быть много и тогда задача становится многокритериальной. Существуют специальные методы решения многокритериальных задач, но можно привести многокритериальную задачу к однокритериальной. Для этого один из критериев выбирается в качестве первичного, а остальные становятся вторичными. Первичный критерий используется как характеристический, а вторичные формируют ограничения задачи. (Многокритериальная оптимизация: Мат. аспекты / Б. А. Березовский, Ю. М. Барышников, В. И. Борзенко, Л. М. Кемпнер; М. Наука 1989)

3)Выбор независимых переменных, используемых для определения характеристик системы и идентификации вариантов решения Необходимо разделить переменные на те, значения которых могут изменяться в достаточно

широком диапазоне и те, значения которых фиксированы и определяются внешними факторами. Первые являются независимыми переменными, а вторые – параметрами задачи.

Далее необходимо провести различие между параметрами задачи, которые могут предполагаться постоянными, и параметрами, которые испытывают флуктуации под воздействием внешней среды.

Важно, что выбор определенного набора независимых переменных в конкретной прикладной задаче почти всегда представляет собой компромисс между стремлением учесть все переменные, которые влияют на функционирование системы, и стремлением выбрать только те из них, чье влияние на выбранный характеристический критерий наиболее существенно.

Последнее стремление продиктовано необходимостью разумного упрощения задачи.

4)Построение математической модели системы

Модель системы описывает взаимосвязь между переменными и отражает степень их влияния на характеристический критерий.

В самом общем представлении структура модели в технике включает основные уравнения материальных и энергетических балансов, соотношения, связанные с проектными решениями, а также уравнения, описывающие физические процессы, протекающие в системе. Эти уравнения обычно дополняются неравенствами, определяющими области допустимых значений переменных.

“Корректная постановка задачи служит ключом к успеху оптимизационного исследования и ассоциируется в большей степени с искусством, нежели с точной наукой.”[3] Решение оптимизационной задачи – это приемлемый набор значений независимых

переменных, которому отвечает оптимальное значение характеристического критерия.

1.3. Структура оптимизационных задач

Несмотря на то, что прикладные задачи оптимизации относятся к различным областям практической деятельности и представляют различные системы, они имеют общую форму. Все эти задачи можно охарактеризовать как задачи минимизации вещественнозначной функции f (x) с ограничениями на ееN -мерныйвекторный аргументx .

Общий вид задачи условной оптимизации


Минимизировать f (x) :R N R1 при ограничениях

hk (x) 0,	k 1...K		(1.1)
g j (x) 0,
g j (x) 0,		j 1...J	(1.2)
xiL xixiR ,
xiL xixiR ,		i 1...I	(1.3)

Здесь f (x) - целевая функция задачи, уравненияhk (x) 0 – называются ограничениями в виде равенств, а неравенстваg j (x) 0 – ограничениями в виде неравенств. Предполагается, что все функции в задаче вещественнозначны, а число ограничений конечно.

Задачи оптимизации можно классифицировать в соответствии с видом функций f (x) ,g(x) иh(x) , а также размерностью вектораx .

Если ограничения (1.1) – (1.3) отсутствуют, то это задача безусловной оптимизации. Такие задачи с N 1 называются задачами одномерной оптимизации, приN 1 – многомерной безусловной оптимизации.

Если в задаче оптимизации функции hk (x) иg j (x) линейны, то это задача с линейными ограничениями. При этом целевая функция может быть как линейной, так и нелинейной. Задача условной оптимизации, в которой все функции линейны, называется задачей

линейного программирования (ЛП). Если при этом координаты вектора x должны принимать только целые значения, то задача называется задачей целочисленного программирования

(ЦЛП).

Задачи с нелинейными целевой функцией и/или ограничениями называются задачами нелинейного программирования (НЛП).

1.3. Практическое применение методов оптимизации

К задачам на поиск оптимума сводятся многие из проблем математики, системного анализа, техники, экономики, медицины и статистики. В частности они возникают при построении математических моделей, когда нужно определить такую структуру и такие параметры модели, которые обеспечивали бы наилучшее согласование с реальностью. Другой традиционная область применения оптимизации – процедуры принятия решений, т.к. большинство из них нацелено именно на “оптимальный” выбор. Помимо оптимизационных задач, представляющих самостоятельный интерес, на практике часто возникают задачи, которые “встроены” в вычислительные процессы, где играют хотя и существенную, но все же вспомогательную роль.

studfiles.net

Теория - оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1

Теория - оптимизация

Cтраница 1

Теория оптимизации широко используется при выполнении процедур проектирования ИЭТ, в том числе в рамках САПР. Теория функциональной организации менее известна, хотя и является важным звеном в раскрытии процессов формирования качества и стоимости функций изделий, определении истоков появления низкого качества и высоких затрат, представления тенденций развития систем. Использование этой теории для решения задач электронной промышленности представляется особенно актуальным. [1]

Теория оптимизации играет важную роль при проектировании механизма взаимодействия подсистем. Принцип совместной оптимизации базируется на соблюдении следующих условий. [2]

Теория оптимизации нестационарных динамических систем получила интенсивное развитие в конце 60 - х годов в результате применения линейного и нелинейного программирования. Подходы, основанные на теории оптимального управления, излагаются в работах [ ПО ] и [187], однако в них не развиваются численные методы и не даны приложения этих методов. [3]

В теории оптимизации, как известно, имеется ряд эффективных процедур решения задач нелинейного программирования, причем в большинстве случаев используют цифровую ЭВМ. [4]

В теории оптимизации встречается ситуация, когда не постоянное ( скажем, периодическое) управление дает в среднем за большое время лучший результат, чем любой фиксированный выбор параметра. [5]

В теории оптимизации такой критерий принято называть целевой функцией. Ее значения выражаются через проектные параметры, которые однозначно определяют решаемую задачу. С математической точки зрения для п проектных параметров S целевая функция / / ( Sn) описывает некоторую ( п 1) - мерную поверхность. [6]

В теории оптимизации доказано, что такой алгоритм обеспечивает сходимость к одному из локальных минимумов функции ошибки, при условии правильного выбора е О на каждой итерации. Такой метод оптимизации называется методом наискорейшего спуска. [7]

Согласно теории оптимизации ( принципу совместной оптимизации), достижение эффективного конечного результата в инвестиционно-строительной сфере возможно при условии взаимного согласия всех участников проекта действовать не в самых выгодных для них условиях. Преследование ими только своих собственных экономически оптимальных целей может нанести ущерб другим участникам и проекту в целом. Незнание или игнорирование положений теории оптимизации служит одной из главных причин недостаточной эффективности большинства инвестиционных проектов и низкой отдачи в целом от инвестиций в основной капитал. [8]

В теории оптимизации важную роль играют некоторые классы вещественнозначных функций, определенных на выпуклых множествах из Rn. [9]

Согласно теории оптимизации процессов, оптимальный температурный профиль в реакторах или их последовательностях соответствует максимуму дифференциальной селективности в каждом из их элементов. [10]

Существует теория оптимизации СВЧ коммутационных устройств [16], согласно которой для любой конструкции выключателя, при любом способе включения диода в волновод с любыми дополнительными реактивными элементами ( штыри, диафрагмы и др.) максимальное отношение Z - запД - пр получается тогда, когда Z - чисто активное коммутируемое сопротивление, равное Rz W - в - состоянии пропускания, r3 W - в состоянии запирания. [11]

Развитие теории оптимизации подчеркивает могущество и большое практическое значение классических методов вариационного исчисления, особенно методов Майера и Больца. [12]

Применение теории оптимизации к конструкциям в последнее время привлекает все большее внимание. [13]

Развитие теории оптимизации ярко подчеркивает могущество и большое практическое значение классических методов вариационного исчисления, особенно методов Майера и Больца. [14]

Применение теории оптимизации к конструкциям в последнее время привлекает все большее внимание. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Модуль 1. Общая теория оптимизации — Мегаобучалка

Модульная единица 1.1Основы теории оптимизации.

Основные понятия теории оптимизации – локальный и глобальный оптимум, пространство оптимизации, допустимая область, целевая функция, ограничения. Классификация моделей и методов оптимизации.

Модульная единица 1.2Методы одномерной и многомерной оптимизации

Экстремумы функций одной и многих переменных.

Модульная единица 1.3Оптимизационные задачи с ограничениями Градиентные алгоритмы оптимизации функций многих переменных. Направление «наискорейшего» спуска, методы наискорейшего спуска, особенности работы методов наискорейшего спуска, метод сопряженного градиента Флетчера-Ривса, партан-метод и модифицированный партан-метод.

Модуль 2.Прикладные задачи оптимизации

Модульная единица 2.1Задачи линейного программирования

Постановка задачи ЛП. Виды задач ЛП: задача общего вида, транспортная задача, задача о назначении. Условия построения моделей ЛП. Каноническая и стандартная формы задач ЛП, переход от одной формы к другой. Графический метод решения задач. ЛП. Характерные черты задач ЛП. Опорный план задачи ЛП, оптимальный план задачи ЛП. Выпуклая линейная комбинация, выпуклый многогранник, граница множества, замкнутое множество. Основные теоремы ЛП: о пересечении выпуклых множеств, о выпуклом многограннике, о выпуклости множества допустимых решений задачи ЛП, об оптимальном решении задачи ЛП, о виде угловой точки допустимого многогранника, о линейной независимости столбцов матрицы задачи ЛП.

Модульная единица 2.2Задачи целочисленного программирования

Выпуклые функции и градиент. Приближенные методы решения задач

Модульная единица 2.3Задачи выпуклого программирования

Метод отсечения Гомори.

Модуль 3.Численные методы оптимизации

Модульная единица 3.1Численные методы оптимизации

Методы прямого поиска для решения задач НЛП. Модификация метода Хука-Дживса, комплексный метод Бокса, штрафные и барьерные функции, метод скользящего допуска

Таблица 4

Содержание лекционного курса

№ п/п	№ модуля и модульной единицы дисциплины	№ и тема лекции	Вид кон- трольного ме- роприятия	Кол-во часов
1.	Модуль 1. Общая теория оптимизации	Тестирование, контрольные работы, зачет
Модульная единица 1.1Основы теории оптимизации	Лекция №1 Начальные сведения о задачах оптимизации	Тестирование
Лекция №2 Понятие о методах оптимизации	Тестирование
Модульная единица 1.2Методы одномерной и многомерной	Лекция №3 Производные и дифференциалы функции многих переменных	Контрольные работы
Лекция №4 Экстремумы функций одной переменных	Тестирование
Лекция №5 Экстремумы функций многих переменных	Тестирование
Модульная единица 1.3Оптимизационные задачи с ограничениями	Лекция №6 Задачи на условный экстремум	Контрольные работы
Лекция №7 Градиентные методы нахождения оптимума	Контрольные работы
Лекция №8 Приближенные методы нахождения экстремума	Тестирование
2.	Модуль 2.Прикладные задачи оптимизации	Тестирование, контрольные работы, зачет
Модульная единица 2.1Задачи линейного программирования	Лекция №9 Симплексный метод ЗЛП	Контрольные работы
Лекция №10Системы объяснений в экспертных системах	Контрольные работы
Лекция №11 Транспортная задача	Тестирование
Модульная единица 2.3Задачи целочисленного программирования	Лекция №12 Выпуклые функции и градиент	Тестирование
Лекция №13 Приближенные методы решения задач	Тестирование
Модульная единица 2.2Задачи выпуклого программирования	Лекция № 15 Метод отсечения Гомори	Контрольные работы
3.	Модуль 3.Численные методы оптимизации	Тестирование, контрольные работы, зачет
Модульная единица 3.1 Численные методы оптимизации	Лекция № 16 Задачи одномерной оптимизации	Контрольные работы
Лекция № 17 Градиентные методы	Контрольные работы
Лекция № 18 Элементы многомерной оптимизации	Тестирование
Итого:	Зачет

Лабораторные/практические/семинарские занятия

Таблица 5

Содержание практических/лабораторных занятий и контрольных мероприятий

megaobuchalka.ru

Теория оптимизации Википедия

У этого термина существуют и другие значения, см. Оптимизация.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Граф параболоида описанного функцией z = f(x, y) = −(x² + y²) + 4. Глобальный максимум от (x, y, z) = (0, 0, 4) обозначен синей точкой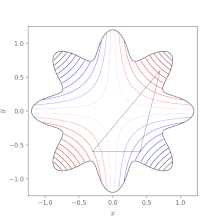

Поиск минимума Нелдера-Мида Функции оптимизации. Симплексные вершины упорядочиваются по их значению, при этом 1 имеет наименьшее (лучшее) значение.

Теорию и методы решения задачи оптимизации изучает математическое программирование.

Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]

Постановка задачи оптимизации[ | код]

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
Критерий поиска (max или min).

Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:

Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
Показать, что целевая функция f(x→){\displaystyle f({\vec {x}})}

ru-wiki.ru

Основные понятия оптимизации

Под оптимизацией понимают процесс выбора наилучшего варианта из множества всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбирать наилучший вариант конструкции, наилучшее распределение ресурсов и т. др.

В процессе решения задач оптимизации, как правило, необходимо найти оптимальное значение некоторых параметров, которые определяют данную задачу. При решении инженерных задач их принято называть проектными параметрами. В качестве проектных параметров могут быть значения линейных размеров о(єкта, массы, температуры и т. др. Число _ проектных параметров _ характеризует размерность (степень сложности) задачи оптимизации.

Выбор оптимального решения или сравнения двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), которая определяется проектными параметрами. Эта величина называется целевой функцией или критерием качества. В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет максимум (или минимум). Таким образом, целевая функция — это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные задачи.

ЛОкальный экстремум ищется в задаче где оптимизация проводится по всему пространству(задача безусловной оптимизации). Условный экстремум ищется в задаче , где определяется область оптимизации каким нибудь множеством (в виде системы неравенств или равенств, это называется задачей условной оптимизации).

Целевая функция

ЦЕЛЕВАЯ ФУНКЦИЯ [target function] в экстремальных задачах — функция, минимум или максимум которой требуется найти. Это ключевое понятие оптимального программирования. Найдя экстремум Ц. ф. и, следовательно, определив значения управляемых переменных, которые к нему приводят, мы тем самым находим оптимальное решение задачи. Таким образом, Ц. ф. выступает как критерий оптимальностирешения задачи.

Различается ряд видов Ц. ф.: линейная, нелинейная, выпуклая, квадратичная и др. — в соответствии с формой математической зависимости, которую они отображают. Следует также выделить термин “целевой функционал”: он применяется обычно, если Ц. ф. задачи является функцией от некоторых функций-ограничений.

Различают прямые и функциональные ограничения.

Прямые ограничения накладываются на управляемые параметры: xt >xni; xt

Область Хд в пространстве управляемых параметров, заданную прямыми ограничениями, называют допустимой областью или областью допустимых значений управляемых параметров X

В качестве примера прямых ограничений можно назвать ограничения на диаметры валов.

Кроме первых ограничений в задачах оптимизации могут быть функциональные ограничения.

Эти ограничения подразделяются на два вида: ограничения-неравенства и ограничения-равенства.

Прямые ограничения (12.

4) можно рассматривать как частный случай функциональный ограничений (12.

Функциональные ограничения устанавливают некоторые зависимости между управляемыми параметрами, нарушение которых недопустимо по условиям обеспечения работоспособности или регламентируемой эффективности функционирования технического объекта.

Наложенные ограничения приводят к тому, что поиск оптимального решения ограничивается некоторой областью Хр в пространстве управляемых параметров.

Задачи проектирования технических объектов характеризуются большим количеством оптимизируемых параметров и наличием ограничений, накладываемых на параметры.

Метод случайного поиска

Random-walk method

Метод экспериментального поиска экстремума функций многих переменных. Основная идея метода заключается в том, что точку каждого пробного опыта для изучения поверхности отклика выбирают случайным образом. Несмотря на произвольность выбора пробной точки, алгоритм случайного поиска позволяет последовательно приближаться к экстремальной области.

Метод половинного деления один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до того времени, пока не будет достигнута заданная точность Е. Метод используется при решении квадртных уравнений и уравнений высших степеней. Достоинство метода половинного деления : более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [а,b] содержится более одного корня, то метод не работает.

Методы поиска экстремума функций многих переменных

Методы поиска экстремумов функций f (х1,…,хn) подразделяются на градиентные и безградиентные по следующему признаку: градиентные основаны на вычислении и анализе частных производных функции f (х1,…,хn), безградиентные не используют значений производных.

Будем рассматривать эти методы как методы поиска min f (x1,x2,…,xn). Вначале рассмотрим некоторые градиентные методы.

.4.1 Метод координатного спуска

Идея метода: Движение от начальной точки по направлению одной из осей координат до момента начала возрастания целевой функции, переход к направлению другой оси и т.д., пока не будет достигнута точка, движение из которой по любой оси координат с минимально возможным шагом приводит

к увеличению значения целевой функции (рисунок 2.9).

Методы градиента Идея методов: Каждая следующая точка поиска min f (x1,x2,…,xn) (каждый новый член минимизирующей последовательности) получается в результате перемещения из предыдущей точки по направлению антиградиента целевой функции.

Метод наискорейшего спуска

Так называют модификацию метода градиента с постоянным шагом, позволяющую сократить общий объем вычислений при некотором увеличении числа членов минимизирующей последовательности за счет меньшего количества вычислений частных производных целевой функции. При использовании этого метода аргументы целевой функции изменяются в соответствии с выражением (2.8), но значения ее производных не пересчитываются до тех пор, пока не сложится ситуация f (х1(k+1),х2(k+1),…,хn(k+1)) f (х1(k),х2(k),…, хn(k)) (рисунок 2.12). Дробление шага поиска производится, когда во вновь выбранном направлении (после пересчета значений частных производных) не удается сделать ни одного результативного шага, останов поиска – при выполнении неравенства (2.6).

sundekor.ru

Теория оптимизации математическая - Справочник химика 21

За последние годы стремительно развивается и совершенствуется теория математического моделирования химико-технологических процессов (ХТП) и химико-технологических систем (ХТС). Значительные успехи в области математического моделирования ХТП, разработки методов синтеза, анализа и оптимизации ХТС, появление мощных быстродействующих ЭВМ третьего и четвертого поколений позволили в настоящее время создать целый ряд автоматизированных систем проектирования (АСП) химических производств. [c.8] За последние годы литература по научным основам химической технологии значительно обогатилась, особенно в части теории химических реакторов, математических методов моделирования и оптимизации химико-технологических процессов. При этом широко используется метод теоретических обобщений, так хорошо себя оправдавший в общеинженерном курсе процессов и аппаратов химической технологии. [c.5]

Специальное программно-математическое обеспечение АСП, позволяющее решать задачи технологического и конструкционного проектирования химических производств, может быть создано только под руководством и при участии инженеров химиков-техно-логов на основе использования методов математического моделирования ХТП, методов синтеза, анализа и оптимизации ХТС, методов теории эвристических решений, а также в результате глубокого изучения и формализации богатого опыта высококвалифицированных инженеров-проектировщиков. [c.12]

Третья задача связана с развитием математической теории нестационарных процессов — качественным и численным анализом математических моделей процессов, а также с постановкой и разработкой теории оптимизации и управления нестационарных процессов. [c.227]

Доступность изложения, сравнительная простота используемого математического аппарата, наглядность приводимых примеров и подробное описание результатов практического решения разнообразных задач исследования, обеспечения, повышения и оптимизации надежности различных объектов дают возможность читателю получить как общее представление, так и активно овладеть основными понятиями, принципами, способами и методами теории надежности, а также применить ее в практической работе. [c.8]

Завершено исследование концентрационной зависимости усиления каучуков и резин дисперсным наполнителем. Предложена усовершенствованная математическая модель структурно-механического поведения ТРТ смесевого типа в условиях одноосного растяжения, прогнозирующая влияние эффективной концентрации поперечных химических связей в пластифицированном полимерном связующем, его температуры структурного стеклования, объемной доли, формы и фракционного состава частиц твердых компонентов с учетом возможного их отслоения от связующего на ход кривой растяжения (сжатия). Существенно развита теория оптимизации рецептур ТРТ с использованием компьютерного моделирования. [c.78]

Для процессов второго типа значительно труднее дать обоснованные рекомендации по выбору наиболее целесообразных мест и времени закалки и вообще по организации оптимального режима процесса. В этом случае в большей мере необходима последовательная математическая теория оптимизации процесса. До тех пор, пока такая теория не построена, можно попытаться найти относительно простые соотношения, позволяющие оценивать скорости закалки в тех или иных конкретных условиях, а также выяснить механизм процессов, способных обеспечивать необходимые скорости охлаждения плазменной струи. [c.181]

Решение этой задачи составляет содержание математической теории оптимизации. Часть математических методов оптимизации — в первую очередь, дифференциальное исчисление и вариационное исчисление — возникли на классическом этапе развития математики. В середине XX века создан целый ряд новых методов линейное программирование, динамическое программирование, нелинейное программирование, принцип максимума. С ними можно познакомиться по работам [23—26]. [c.182]

С появлением электронных вычислительных машин методом количественного анализа процессов химической технологии становится математическое моделирование. Принципы математического моделирования контактно-каталитических реакторов разработаны Боресковым [11 и Слинько [3]. Математическое моделирование процессов химической технологии сводится к математическому описанию всего процесса в целом [4] и по отдельны.м его стадиям [5, 61. Оно включает воспроизведение и анализ моделей на электронных вычислительных машинах как в целом для процесса, так и по стадиям. Таким образом, вместо многоступенчатого воспроизведения самого процесса, как это делается с применением теории подобия при физическом моделировании, при математическом моделировании воспроизводится сама модель, что требует меньших затрат средств и времени. Весьма существенна при этом возможность довольно быстрого воспроизведения оптимальных вариантов модели, т. е. оптимизации математической модели, а следовательно, и самого процесса. [c.6]

Материал книги охватывает важнейшие проблемы современной инженерной химии приложение законов физической химии к решению инженерные задач, явления переноса массы, энергии и количества движения, вопросы теории подобия, теорию химических реакторов, проблемы нестационарные процессов. Специальные главы посвящены методам математической статистики и вопросам оптимизации химико-технологических процессов. [c.5]

Сложная иерархическая организация гетерогенно-каталитических систем затрудняет построение основ теории на строгих законах гетерогенного катализа, выраженных в количественной форме, поскольку обширные накопленные знания в литературе представлены преимущественно в описательной форме. Большой удельный вес информации описательного (качественного) характера о поведении гетерогенно-каталитических систем часто затрудняет строгую математическую постановку и решение задач исследования, моделирования, управления и оптимизации гетерогенно-каталитических процессов, что является существенным тормозом в решении как фундаментальных, так и прикладных задач гетерогенного катализа. [c.107]

Для решения задач оптимизации химико-технологических процессов обычно используют методы нелинейного программирования (поисковые методы) [1, 3] и методы теории оптимального управления вариационного исчисления [4], динамического программирования 15], принципа максимума Понтрягина [6], дискретного принципа максимума 17]. Наибольшее распространение получили поисковые методы как наиболее гибкие и универсальные. Эти методы находят также широкое применение при решении задач идентификации (определение некоторых коэффициентов уравнений, представляющих собой математическую модель исследуемого процесса). Кроме того, поисковые методы могут быть эффективно использованы при синтезе оптимальной структуры химико-технологических систем, который в общем случае представляет собой задачу дискретно-непрерывного программирования в частности, они могут быть использованы при получении нижних оценок в методе ветвей и границ (см. гл. VI). [c.14]

Метод многоуровневой оптимизации может быть гарантированно сведен к глобальному решению полной задачи оптимизации, если удовлетворяются определенные математические условия. Примененные математические доводы основаны на простых понятиях теории множеств и топологии. [c.316]

Совместный труд ученых СССР и ГДР посвящен рациональному выбору и оптимизации химико-технологических систем (ХТС) производств химической и нефтехимической промышленности. Рассмотрена теория математического моделирования систем аппаратов, взаимосвязанных технологическими потоками, приведен расчет отдельных элементов и всей системы в целом. Уделено внимание вопросам надежности, чувствительности и управления ХТС. Каждая глава снабжена примерами решения конкретных задач. [c.2]

Глобальная задача автоматической защиты не формулируется в таком строгом математическом виде, в каком была сформулирована задача оптимизации и стабилизации. Это связано, по-видимому, с тем, что теория автоматической защиты еще разрабатывается. Однако существуют некоторые общие положения, которые можно рассматривать как эвристический вариант глобальной задачи автоматической защиты. [c.347]

При втором методе для математического описания используют эмпирические (формальные) математические зависимости. Было показано что теория подобия не применима к процессам, протекающим в химических реакторах. Отсюда формальные эмпирические соотношения, выведенные для лабораторных установок, нельзя использовать для расчета промышленных реакторов. Таким образом, второй метод мало применим к задаче оптимизации каталитического реактора при проектировании. [c.22]

Сложность и большая размерность задач оптимизации с. х.-т. с., с одной стороны, требует разработки специальных методов, учитывающих специфику данных задач. С другой стороны, необходимо использовать максимум того, что создано в теории математического программирования и теории оптимального управления. [c.11]

К задачам оптимизации [65] в технической диагностике применимы математические методы линейного, нелинейного и динамического программирования, теорий массового обслуживания, сетевого планирования и т.д. Применение сложного математического аппарата для решения задач, связанных с технической диагностикой оправдано, поскольку использование методов оптимизации позволяет в ряде случаев существенно снизить затраты на техническое обслуживание и ремонт аппаратов [33]. [c.38]

ОД структурным анализом будем понимать получение некоторых свойств математической модели схемы исходя только из ее структуры, т. е. исходя лишь из уравнений связи [3, с. 23]. Используя методы структурного анализа, часто удается понизить размерность решаемых задач путем сведения одной задачи большой размерности к ряду взаимосвязанных задач меньшей размерности (если это, конечно, возможно). Структурный анализ вначале возник как средство повышения эффективности алгоритмов расчета с. х.-т. с. Однако методы структурного анализа, как видно из содержания последуюш их глав, имеют значение и для других разделов теории моделирования сложных схем — устойчивости, оптимизации и др. [c.44]

В процедуре построения математической модели оптимизации конструкторской точности (рис. 1.8) основное значение придавалось построению математической модели функционирования по метрическому и механическому свойствам. Разработана процедура построения математической модели функционирования, предусматривающая постановку вычислительного и натурного экспериментов в однородных условиях работы КСП. Для моделей и структур, независимых от функционального свойства, применяли теорию [c.31]

Математическое моделирование технологических процессов основывается на теории процесса как результате соответствующих исследований. Однако нередко встречаются процессы столь сложные, что теоретическое изучение их механизма требует весьма длительных сроков, тогда как задачи оптимизации подлежат решению в более короткое время. Поэтому для моделирования технологических процессов используются методы математической статистики, позволяющие на основе эксперимента давать математическое описание очень сложных или малоизученных процессов. [c.100]

Теория рециркуляции сделала возможным создать наиболее общую математическую модель химического комплекса любой сложности и тем самым обеспечить возможность его оптимизации. Этим объясняется то, что методы оптимизации химических комплексов впервые были начаты и реализованы на основе теории рециркуляции [11,12,61]. [c.20]

Проблемы создания математических моделей для процессов химической технологии несомненно являются наиболее важными при постановке задач оптимизации указанных процессов. Современный уровень теории оптимальных процессов и возможности математики, вооруженной средствами вычислительной техники, позволяют решать большинство возникающих в практике оптимальных задач. Поэтому широкое распространение методов оптимизации по существу немыслимо без детальной проработки вопросов математического моделирования существующих и на этой основе вновь проектируемых процессов. [c.90]

Основу второй ступени иерархии (см. рис. 1-3) химического предприятия составляют производственные цеха и системы автоматического управления цехами. Цех — это взаимосвязанная совокупность отдельных типовых технологических процессов" и аппаратов, при взаимодействии которых возникают статистические распределенные по времени возмущения, т. е. существуют стохастические взаимосвязи между входными и выходными переменными подсистем. Для анализа функционирования подсистем второй ступени иерархии необходимо использовать статистико-вероятностные математические методы. Среди них широкое применение начинают получать сравнительно новые разделы математики, такие, как теория марковских цепей, теория графов, теория массового обслуживания и др. На этой ступени иерархии происходит статистическое обогащение информации, а при управлении подсистемами возникают задачи оптимизации и программирования для оптимальной координации работы аппаратов и оптимального распределения нагрузок между ними. [c.13]

В связи с использованием математической модели при разработке системы управления техническими объектами в области теории управления возникло новое направление, охватывающее методы построения математической модели объекта управления. Это направление, которое менее десяти лет назад было названо теорией идентификации (отождествления объекта моделью), довольно быстро развивалось во многих странах мира. Были получены значимые теоретические и практические результаты. В настоящее время теория идентификации наряду с теорией оптимизации составляет важнейщий раздел в теории управления и интенсивно развивается у нас в стране и за рубежом. При этом следует указать, что результаты теории идентификации нашли широкое применение и в таких областях, как медицина, биология и сельское хозяйство, что свидетельствует об универсальности разрабатываемых методов и их практической значимости. [c.11]

Книга посвящена проблеме оптимизации, имико-технологических процессов, возникающей при проектировании новых процессов и интенсификации действующих производств, а также при разработке автоматизированных систем управления технологическими процессами (АСУ ТП). Б ней рассматриваются основные этапы этой задачи (расчет стационарных режимов химико-технологических систем, методы безусловной минимизации, алгоритмы учета ограничений), приводятся многочисленные примеры использования описанных методов при решении тестовых и реальных задач оптимизации химико-технологиче-ских процессов. Большое внимание уделено проблеме синтеза хнмико-технологических систем — новому и быстро развивающемуся разделу теории математического моделирования. [c.2]

В книге изложены математические п фиапко-хцмнческие основы теории хим11чес1 нх реакторов. Рассмотрены принципы математического описания химических реакций, вопросы термостатики и взaимнoг(J влияния химических и физических стадий ироцессов, а также методы расчета и оптимизации различных типов химических реакторов. Приведено большое количество примеров п задач для самостоятельного решения. [c.4]

Для достижения таких эффектов необходимо умело сочетать эмпирические исследования с современными математическими методами, позволяющими определить оптимальный вариант технологического процесса в наикратчайшеё время и при разумном риске. В течение последних лет для этой цели разработаны прогрессивные методы, использующие достижения математики и технической кибернетики, — так называемая стратегия разработки систем, или системотехника. Как и при использовании метода масштабирования, в этом случае также составляется математическая модель, но она описывает весь технологический процесс (или наиболее важную его часть) как систему взаимосвязанных элементов. Модель, в которой ряд величин и зависимостей экстраполируется с объекта меньшего масштаба, вносит в проектные расчеты фактор ненадежности. Системотехника включает также способы оценки надежности и принятия оптимальных решений при проектировании в определенных условиях. Важным преимуществом комплексного математического описания процесса является, возможность определения оптимальных рабочих параметров не для отдельных аппаратов, а для всей технологической цепочки как единого целого. Подробное описание математических методов оптимизации, оценки надежности и теории решений выходит за рамки данной книги, поэтому мы вынуждены рекомендовать читателю специальную литературу (см. список в конце книги). Ниже будут рассмотрены основные понятия, применяемые в системотехнике, и принципы разработки систем, а также их моделей. [c.473]

И. Следуег развивать исследования путем аппроксимации совершенных, но громоздких комплексных технико-экономичес-ких моделей с привлечением математического аппарата, например теории сплайнов и других методов. Реализация этой задачи позволит подойти вплотную к корректному и простому решению более сложных задач оптимизации технологических, энергетических и транспортных установок на основе простых и надежных технико-экономических аппроксимативных моделей, адекватных их более сложным аналогам — исходным моделям. [c.317]

В книге рассмотрены основные принципы моделирования, анализа и синтеза сложных химико-технологических систем (ХТС). Приведены методы расчета материальноэнергетических балансов и степеней свободы ХТС описаны математические модели технологических операторов (элементов систем), изложены основы матричного, детерминант-ного и топологического методов анализа ХТС. На основе использования топологических моделей (теории графов) ХТС рассмотрены методы разработки оптимальной стратегии (алгоритмов) исследования и декомпозиционные принципы оптимизации ХТС. Даны методы построения специальных программ математического моделпровапия ХТС на ЦВМ. [c.4]

Цирлин A. М., Крылов Ю. М., Матвеев В. В. и др. Оптимизация циклических режимов культивирования микроорганизмов для процессов с разбав-лением//Тезисы докладов 1-й Всематематической теории биологических процессов.— Калининград, 1976.— С. 175—176. [c.7]

Как показывает практика, инвестиционный проект, который, несомненно, оптима теп по одному критерию экономической эффективности, часто не явмегся наилучшим с точки зрения других. Кроме того, инвестиции - сложный процесс, подверженный влиянию ршличных факторов, которые не могут быть выражены только четкими количественными величинами, Для преодоления данных трудностей необходимо применение математических методов, которые позволят ранжировать инвестиционные проекты по обобщающему показателю экономической эффективности. Успешно решить поставленную задачу возможно с помощью использования аппарата векторной оптимизации и теории нечетких множеств. [c.70]

Исходя из основных положений теории рециркуляции в комплексных системах, недостаточно оптимизировать локально отдельные агрегаты или даже целые регионы, состоящие либо из одной, либо из ряда однотипных установок и имеющие общие элементы. Оптимальная работа отдельно взятых составляющих химического комплекса будет коренным образом отличаться от оптимальной работы их в условиях, когда они испытывают влияние сопряженной работы других установок. Поэтому определение условий проведения отдельных процессов должно проводиться в соответствии с лаилучшими результатами работы всего комплекса. Оптимизацию сложных комплексов теория рециркуляции осуществляет на базе математического описания всей совокупности и взаимосвязи химических, физических, физико-химических процессов и их экономики. Такая оптимизация названа глобальной созданы методы ее практического осуществления [55.......58]. [c.272]

Научные интересы теория автоматизированного синтеза высоконадежных ресурсосберегающих химико-технологических систем (ХТС), топологические модели (фафы) сложных ХТС искусственный интеллект и гибридные экспертные системы в химической технологии компьютерные модели представления знаний для поиска рациональных решений математически неформализованных задач химической технологии обеспечение и оптимизация показателей надежности сложных ХТС. [c.14]

Книга посвящена одному из важнейших разделов общей теории математического моделирования химико-технологи-ческих процессов — проблеме их оптимизации. В книге дается характеристика основных задач оптимизации, возни-каюищх при проектировании новых процессов и интенсификации действующих производств, при разработке автоматизированных систем управления химико-технологическими процессами (АСУТП), и излагается ряд поисковых алгоритмов решения этих задач. Приведены решения задач оптимизации конкретных процессов. [c.4]

Определение оптимальных конструкций аппаратов, оптимальных условий проведения ХТП является конечной целью любых работ по их моделированию. Эти задачи решаются как при проектировании новых производств, так и для интенсификации действующих, в том числе при разработке автоматизированных систем управления технологическими процессами (АСУТП). Естественно поэтому, что проблемы оптимизации всегда находились в круге интересов специалистов но моделированию ХТП и в настоящее время стали составной частью общей теории математического моделирования химико-технологических процессов. [c.7]

Интрилигатор М. Математические методы оптимизации и экономическая теория / Пер. с англ. - М. Прогресс, 1975. - 608 с. [c.220]

Перейдем к рассмотрению изменения профилей различных параметров вдоль реактора в системе с рециркуляционной петлей. Необходимое превращение на выходе из реактора может быть получено различными изменениями вдоль реактора параметров системы — температуры, давления, концентрации. Оно связано с количеством рециркулируемых в начало реактора компонентов. Естественно, что для каждой конкретной реакции роль указанных факторов проявляется по-разному. Несомненно, что широкое использование результатов одновременного поиска изменения профилей различных параметров может привести к весьма интересным результатам. Однако для решения этой задачи желательно дальнейшее совершенствование математических методов оптимизации и более детальное изучение химических аспектов процесса. Рассмотрение реакции дегидрирования этана показало, что существует определенный профиль температуры, который отвечает максимальной нроизвоцительности реактора по целевому продукту. При этом расход исходного сырья не является максимальным и соответствует строго определенной селективности и глубине превращения на выходе из реактора. Следовательно оптимальные профили изменения параметров режима эксплуатации действующих реакторов должны определяться одновременным изменением производительности аппарата. В частности, исследования по определению оптимального температурного профиля для консекутивной реакции показали, что в этом случае необ ходимо реакцию начать с самой высокой температуры оптимального профиля. Затем углубление процесса следует проводить по мере снижения температуры также в соответствии с оптимальным профилем, найденным, подчеркиваю, для рециркуляционной системы. Кстати, в этом плане применение увеличенной рециркуляции непрореагпровавшего сырья в адиабатических реакторах (таких, как реактор для каталитического дегидрирования этилбензола в стирол) люжет значительно повысить их мощность по свежему сырью. Прп такой постановке вопроса реакторы должны конструироваться таким образом, чтобы они удовлетворяли требованиям теории. Это противоречит существующему укоренившемуся положению, когда реакция осуществляется в готовой конструкции реактора в зависимости от его возможностей, [c.15]

Таким способом технологическую системы удается описать формулами и уравнениями. Совокупность таких уравнений, не обладая всей широтой охвата, который н])исущ детально разработанной теории процесса, после проверки эмпирическими методами все же может вполне удовлетворительно использоваться для технических целей. Эта совокупность уравнений называется математической моделью. Новые статистические методы, новые вычислительные устройства и повышенный интерес к задачам, связанным с оптимизацией процессов и управлением ими, во многом способствовали совершенствованию методов построения таких моделей. Важнейшие новые методы включают планирование последовательности измерений для выяснения клю- [c.6]

chem21.info