Шпаргалка: Оптимизация выбора потребителя. Оптимизация потребительского выбора

Оптимизация выбора потребителя

Министерство образования

Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

РЕФЕРАТ

на тему: «Оптимизация выбора потребителя»

Выполнили

студенты

Куропатенкова Ю.В.

Кульша М.О.

Ходатович Е.Д.

Минск 2007

Оглавление

Введение

1. Задача оптимизации выбора потребителя

Заключение

Список литературы

Введение

Потребитель, имея доход, желает его потратить и, естественно, с максимальной пользой. Польза понимается в смысле системы его предпочтений или его функции полезности. В нашей работе мы рассмотрели, как можно оптимизировать выбор потребителя.

1. Задача оптимизации выбора потребителя

Суть оптимизации выбора потребителя.

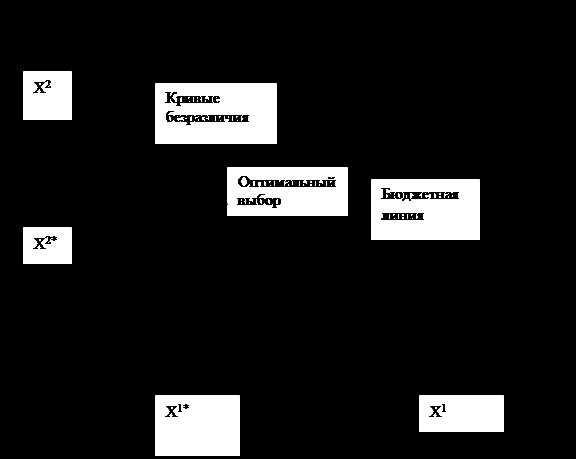
Выбор ( X1* , X2* ) является оптимальным выбором для потребителя. Множество наборов, которые он предпочитает (X1* , X2* ), а именно множество наборов, располагающееся над его кривой безразличия, не пересекает наборы, которые он может себе позволить приобрести, а именно наборы под бюджетной линией. Таким образом, набор (X1* ,X2* ) – это наилучший набор, который потребителю по карману.

Для того чтобы рассмотреть эту задачу следует использовать в качестве приложения нахождения условного экстремума с помощью множителей Лагранжа.

Как отдельные потребители выбирают, какое количество каждого товара им купить, с учетом предпочтений и бюджетных ограничений? Мы предполагаем, что потребители делают этот выбор по рациональным соображениям – они выбирают товары так, чтобы максимизировать получаемое удовлетворение с учетом доступного им ограниченного бюджета.

Отвечающая требованиям рыночная корзина должна удовлетворять двум условиям:

1. Она должна находится на бюджетной линии. Почему? Заметим, что любая рыночная корзина левее и ниже бюджетной линии оставляет неизрасходованной некоторую часть дохода, который, будучи потраченным, мог бы увеличить удовлетворение потребителя. Разумеется, потребители могут – и иногда действительно делают это – сберечь некоторую часть доходов для будущего потребления. Однако пока мы упростим ситуацию, предположив, что весь доход тратится сразу. Также заметим, что любая рыночная корзина правее и выше бюджетной линии не может быть приобретена при имеющемся уровне дохода. Вот почему единственный рациональный и осуществимый выбор – это корзина, лежащая на бюджетной линии.

2. Она должна обеспечивать потребителю наиболее предпочтительную комбинацию товаров и услуг.

Эти два условия сводят проблему максимального удовлетворения потребителя к вопросу выбора подходящей точки на бюджетной линии.

Если проанализировать графически проблему выбора потребителя между продовольствием и одеждой, то можно сделать вывод, что корзина, которая приносит максимальное удовлетворение, должна лежать на самой верхней кривой безразличия, касающейся бюджетной линии. В точке касания бюджетной линии и кривой безразличия, наклон бюджетной линии точно равен наклону кривой безразличия. Поскольку предельная норма замещения (MRS) является отрицательной величиной, обратной углу наклона кривой безразличия, то можно сказать, что удовлетворение достигает максимума (при данном бюджетном ограничении) в точке, где

Задачу оптимизации выбора потребителя можно рассмотреть в качестве приложения метода нахождения условного экстремума множителей Лагранжа.

Будем считать, что каждый товар имеет цену pi, а индивид имеет доход Q – какое-то количество денег, в рамках которого он и действует, покупая нужный ему набор товаров. На покупку набора товаров X=(xi ,…, xn ) надо затратить денег в количестве c(X)=pi xi +…+pn xn =

Таким образом, индивид может купить только такой набор X, при котором PX≤Q. Следовательно, множество наборов товаров, доступных ему при доходе Q. есть B=B(P,Q)={X; X≥0, PX≤Q}. Это множество называется бюджетным множеством. Бюджетное множество ограниченно и замкнуто.

Доказательство. Пусть r=min pi , тогда, как легко видеть, если X

B, то x≤Q/r для i=1,…,n, т.е. множество B ограниченно. Докажем замкнутость. Пусть Хк В для всякого k N и Xk Z. Тогда в силу непрерывности линейной функции

PXk

PZ и, поскольку, PXk ≤Q, то и PZ≤Q. Следовательно, ZB.

Граница бюджетного множества называется множество G = {X

B: PX = Q}. Граница G – это отрезок в случае двух товаров, часть плоскости, ограниченная треугольником, в случае трёх товаров, и в общем случае, есть часть гиперплоскости в пространстве товаров.

Бюджетное множество B (P, Q) зависит от дохода Q и системы цен P, но от каких либо характеристик индивида, например системы его предпочтений, не зависит.

Потребитель, имея доход, желает его потратить и, естественно, с максимальной пользой. Польза понимается в смысле системы его предпочтений или его функции полезности. Это приводит к следующей задаче математического программирования.

Найти набор товаров X=(xi ,…, xn ), максимизирующий функцию полезности u(xi ,…, xn ), при выполнении бюджетного ограничения PX =pi xi +…+pn xn ≤Q; по смыслу задачи все переменные принимают неотрицательное значение, т.е. xi ≥0, i=1,…, n.

Рассматриваемую задачу можно сформулировать более кратко:

Или даже так:

(1)

G, тогда PZ 0. Но тогда YВ, однако u(Z+Y)>u(Z). В силу того, что каждый товар желателен. Получили противоречие с тем, что Z – точка максимума функции c(X) на бюджетном множестве.

Предположение: Если u(X) – строго вогнут, то решение задачи (1) единственно, т.е. существует только одна точка максимума функции полезности на бюджетном множестве.

Напомним, что функция u(X) называется строго вогнутой, если для любых X, Y из того, что 0 <λ<1 следует, что u(λx+(1-λ)Y)> λ u u(X)+(1-λ) u(Y).

Доказательство. Предположим, что А и С – две точки максимума, т.е. u(X)

u(A)=u(C) для любой точки X множества В. Мы уже знаем, что точки А и С лежат на границе бюджетного множества, т.е. РА=РС=Q. Рассмотрим точку Е=А/2 + С/2. Видим, что РЕ = Р(А/2 + С/2)= Q, т.е. ЕВ. В силу строгой вогнутости функции u(X) имеем: u(Е) > u(А)= u(С). Получили противоречие с тем, что А и С – есть точки максимума функции на бюджетном множестве.

Итак, при строгой вогнутости функции полезности существует в бюджетном множестве единственная точка максимума функции полезности. Таким образом, у потребителя даже нет выбора в том, как с наибольшей потратить свои деньги, т.к. существует единственный набор товаров, максимизирующий полезность. Это единственная точка максимума называется точкой спроса, или просто спросом потребителя. Эта точка обозначается Х*.

Изучим точку спроса. Пока установлено только, что она должна лежать на границе бюджетного множества. Таким образом, задача (1) сводиться к следующей:

Или

Эту задачу можно решить с помощью множителей Лагранжа. Составим функцию Лагранжа L(X, λ)=u(X) + λ(Q-PX), найдём частные производные и приравняем их к нулю:

Заключение

Таким образом, существует только одна точка максимума функции полезности на бюджетном множестве.

Следовательно, у потребителя даже нет выбора в том, как с наибольшей выгодой потратить свои деньги, т.к. существует единственный набор товаров, максимизирующий полезность. Это единственная точка максимума называется точкой спроса, или просто спросом потребителя.

mirznanii.com

«Оптимизация выбора потребителя»

Министерство образования

Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

РЕФЕРАТ

на тему: «Оптимизация выбора потребителя»

Выполнили

студенты

Куропатенкова Ю.В.

Кульша М.О.

Ходатович Е.Д.

Минск 2007

Оглавление

Введение

1. Задача оптимизации выбора потребителя

Заключение

Список литературы

Введение

Задача оптимизации выбора потребителя

Суть оптимизации выбора потребителя.

Выбор ( X1*, X2*) является оптимальным выбором для потребителя. Множество наборов, которые он предпочитает (X1*, X2*), а именно множество наборов, располагающееся над его кривой безразличия, не пересекает наборы, которые он может себе позволить приобрести, а именно наборы под бюджетной линией. Таким образом, набор (X1*,X2*) – это наилучший набор, который потребителю по карману.

Отвечающая требованиям рыночная корзина должна удовлетворять двум условиям:

Она должна находится на бюджетной линии. Почему? Заметим, что любая рыночная корзина левее и ниже бюджетной линии оставляет неизрасходованной некоторую часть дохода, который, будучи потраченным, мог бы увеличить удовлетворение потребителя. Разумеется, потребители могут – и иногда действительно делают это – сберечь некоторую часть доходов для будущего потребления. Однако пока мы упростим ситуацию, предположив, что весь доход тратится сразу. Также заметим, что любая рыночная корзина правее и выше бюджетной линии не может быть приобретена при имеющемся уровне дохода. Вот почему единственный рациональный и осуществимый выбор – это корзина, лежащая на бюджетной линии.

Она должна обеспечивать потребителю наиболее предпочтительную комбинацию товаров и услуг.

Будем считать, что каждый товар имеет цену pi, а индивид имеет доход Q – какое-то количество денег, в рамках которого он и действует, покупая нужный ему набор товаров. На покупку набора товаров X=(xi,…, xn) надо затратить денег в количестве c(X)=pixi+…+pnxn=

Доказательство. Пусть r=min pi, тогда, как легко видеть, если XB, то x≤Q/r для i=1,…,n, т.е. множество B ограниченно. Докажем замкнутость. Пусть Хк В для всякого k N и Xk Z. Тогда в силу непрерывности линейной функции

PXk PZ и, поскольку, PXk≤Q, то и PZ≤Q. Следовательно, ZB.

Граница бюджетного множества называется множество G = {XB: PX = Q}. Граница G – это отрезок в случае двух товаров, часть плоскости, ограниченная треугольником, в случае трёх товаров, и в общем случае, есть часть гиперплоскости в пространстве товаров.

Найти набор товаров X=(xi,…, xn), максимизирующий функцию полезности u(xi,…, xn), при выполнении бюджетного ограничения PX =pixi+…+pnxn ≤Q; по смыслу задачи все переменные принимают неотрицательное значение, т.е. xi≥0, i=1,…, n.

Рассматриваемую задачу можно сформулировать более кратко:

Или даже так:

(1)

Поскольку u(X) – непрерывная функция своих аргументов, а бюджетное множество В ограниченно и компактно, то u(X) достигает на множестве В своего максимума, т.е. решение задачи 1 существует. Очевидно, что любая точка Х* максимума функции c(X) лежит на границе G бюджетного множества. Действительно, если предположим противное, то есть что Z – точка максимума, но Z G, тогда PZ 0. Но тогда YВ, однако u(Z+Y)>u(Z). В силу того, что каждый товар желателен. Получили противоречие с тем, что Z – точка максимума функции c(X) на бюджетном множестве.

Напомним, что функция u(X) называется строго вогнутой, если для любых X, Y из того, что 0 λ u u(X)+(1-λ) u(Y).

Доказательство. Предположим, что А и С – две точки максимума, т.е. u(X)u(A)=u(C) для любой точки X множества В. Мы уже знаем, что точки А и С лежат на границе бюджетного множества, т.е. РА=РС=Q. Рассмотрим точку Е=А/2 + С/2. Видим, что РЕ = Р(А/2 + С/2)= Q, т.е. ЕВ. В силу строгой вогнутости функции u(X) имеем: u(Е) > u(А)= u(С). Получили противоречие с тем, что А и С – есть точки максимума функции на бюджетном множестве.

Или

Заключение

Таким образом, существует только одна точка максимума функции полезности на бюджетном множестве.

znakka4estva.ru

Оптимизация выбора потребителя - реферат, курсовая работа, диплом, 2017

- 10 -

Министерство образования

Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

РЕФЕРАТ

на тему: «Оптимизация выбора потребителя»

Выполнили

студенты

Куропатенкова Ю.В.

Кульша М.О.

Ходатович Е.Д.

Минск 2007

Оглавление

ВВЕДЕНИЕ

1. Задача оптимизации выбора потребителя

Заключение

Список литературы

ВВЕДЕНИЕ

1. Задача оптимизации выбора потребителя

Суть оптимизации выбора потребителя.

Выбор ( X1*, X2*) является оптимальным выбором для потребителя. Множество наборов, которые он предпочитает (X1*, X2*), а именно множество наборов, располагающееся над его кривой безразличия, не пересекает наборы, которые он может себе позволить приобрести, а именно наборы под бюджетной линией. Таким образом, набор (X1*,X2*) - это наилучший набор, который потребителю по карману.

Как отдельные потребители выбирают, какое количество каждого товара им купить, с учетом предпочтений и бюджетных ограничений? Мы предполагаем, что потребители делают этот выбор по рациональным соображениям - они выбирают товары так, чтобы максимизировать получаемое удовлетворение с учетом доступного им ограниченного бюджета.

Отвечающая требованиям рыночная корзина должна удовлетворять двум условиям:

1. Она должна находится на бюджетной линии. Почему? Заметим, что любая рыночная корзина левее и ниже бюджетной линии оставляет неизрасходованной некоторую часть дохода, который, будучи потраченным, мог бы увеличить удовлетворение потребителя. Разумеется, потребители могут - и иногда действительно делают это - сберечь некоторую часть доходов для будущего потребления. При этом пока мы упростим ситуацию, предположив, что весь доход тратится сразу. Также заметим, что любая рыночная корзина правее и выше бюджетной линии не может быть приобретена при имеющемся уровне дохода. Вот почему единственный рациональный и осуществимый выбор - это корзина, лежащая на бюджетной линии.

2. Она должна обеспечивать потребителю наиболее предпочтительную комбинацию товаров и услуг.

Будем считать, что каждый товар имеет цену pi, а индивид имеет доход Q - какое-то количество денег, в рамках которого он и действует, покупая нужный ему набор товаров. На покупку набора товаров X=(xi,…, xn) надо затратить денег в количестве c(X)=pixi+…+pnxn=

Таким образом, индивид может купить только такой набор X, при котором PX?Q. Следовательно, множество наборов товаров, доступных ему при доходе Q. есть B=B(P,Q)={X; X?0, PX?Q}. Это множество называется бюджетным множеством. Бюджетное множество ограниченно и замкнуто.

- 10 -

Доказательство. Пусть r=min pi, тогда, как легко видеть, если XB, то x?Q/r для i=1,…,n, т.е. множество B ограниченно. Докажем замкнутость. Пусть Хк В для всякого k N и XkZ. Тогда в силу непрерывности линейной функции

PXk PZ и, поскольку, PXk?Q, то и PZ?Q. Следовательно, ZB.

Граница бюджетного множества называется множество G = {XB: PX = Q}. Граница G - это отрезок в случае двух товаров, часть плоскости, ограниченная треугольником, в случае трёх товаров, и в общем случае, есть часть гиперплоскости в пространстве товаров.

Найти набор товаров X=(xi,…, xn), максимизирующий функцию полезности u(xi,…, xn), при выполнении бюджетного ограничения PX =pixi+…+pnxn?Q; по смыслу задачи все переменные принимают неотрицательное значение, т.е. xi?0, i=1,…, n.

Рассматриваемую задачу можно сформулировать более кратко:

Или даже так:

(1)

Поскольку u(X) - непрерывная функция своих аргументов, а бюджетное множество В ограниченно и компактно, то u(X) достигает на множестве В своего максимума, т.е. решение задачи 1 существует. Очевидно, что любая точка Х* максимума функции c(X) лежит на границе G бюджетного множества. Действительно, если предположим противное, то есть что Z - точка максимума, но Z G, тогда PZ <Q. При этом тогда потребитель имеет неиспользованное количество денег Q - PZ, и на эти деньги он может купить какое-то количество товаров Y, причём можно считать, что Y>0. Но тогда YВ, однако u(Z+Y)>u(Z). В силу того, что каждый товар желателен. Получили противоречие с тем, что Z - точка максимума функции c(X) на бюджетном множестве.

Предположение: Если u(X) - строго вогнут, то решение задачи (1) единственно, т.е. существует только одна точка максимума функции полезности на бюджетном множестве.

Напомним, что функция u(X) называется строго вогнутой, если для любых X, Y из того, что 0 <л<1 следует, что u(лx+(1-л)Y)> л u u(X)+(1-л) u(Y).

Доказательство. Предположим, что А и С - две точки максимума, т.е. u(X)u(A)=u(C) для любой точки X множества В. Мы уже знаем, что точки А и С лежат на границе бюджетного множества, т.е. РА=РС=Q. Рассмотрим точку Е=А/2 + С/2. Видим, что РЕ = Р(А/2 + С/2)= Q, т.е. ЕВ. В силу строгой вогнутости функции u(X) имеем: u(Е) > u(А)= u(С). Получили противоречие с тем, что А и С - есть точки максимума функции на бюджетном множестве.

Или

Эту задачу можно решить с помощью множителей Лагранжа. Составим функцию Лагранжа L(X, л)=u(X) + л(Q-PX), найдём частные производные и приравняем их к нулю:

Заключение

Таким образом, существует только одна точка максимума функции полезности на бюджетном множестве.

referatwork.ru

15.1.1. Межвременной выбор потребителя и его оптимизация. Экономическая теория: учебник

15.1.1. Межвременной выбор потребителя и его оптимизация

Ирвинг Фишер впервые поставил вопрос о возможности оптимизации потребительского выбора путем сопоставления потребления в настоящем и будущем. При этом в модели исследуются те ограничения, с которыми сталкивается потребитель, делая выбор между потреблением и сбережением в различные периоды времени (межвременный выбор).

Уравнение межвременного бюджетного ограничения потребителя, показывающее все возможные сочетания потребления в первом и во втором периодах при данных величинах дохода за весь период жизнедеятельности экономического субъекта (рис. 15.1).

Рис. 15.1. Модель межвременного бюджетного ограничения потребителя

Все потребители стремятся максимизировать функцию полезности двух благ: потребление в первом периоде (C1) и во втором (C2). Предпочтение потребителей между настоящим и будущим потреблением описывается семейством кривых безразличия, каждая из которых иллюстрирует равный уровень полезности для потребления разных наборов потребления сегодня и в будущем, при этом, стремясь максимизировать полезность, экономический субъект пытается достичь наиболее высокой кривой безразличия. Однако стремления субъектов наталкиваются на межвременные бюджетные ограничения.

Вопрос о функции потребления и сбережения определяется двумя моментами:

1. Влиянием роста дохода:

• по мере роста дохода линия бюджетных ограничений сдвигается вправо и «достигает» кривой безразличия с более высоким уровнем потребления;

• если потребитель в двух периодах использует нормальные блага, то в результате роста дохода будет наблюдаться прирост потребления и в первом, и во втором периодах;

• потребление будет определяться текущей стоимостью дохода в данном периоде и дисконтированной стоимостью дохода будущего периода.

2. Изменением процентной ставки.

Согласно модели И. Фишера потребление зависит не только от текущего дохода, но и от того количества доходов, которое потребитель рассчитывает получить в течение всей своей жизни.

Экономический анализ И. Фишера показал, что значения изменения процентной ставки неоднозначно влияют на поведение кредиторов и заемщиков.

Изменение процентной ставки оказывает влияние на изменение и потребления, и сбережения. Иногда полагают, что рост процентной ставки всегда приводит к росту сбережений. Однако это не всегда так, ибо поведение потребителя во многом определяется тем, какую роль он сейчас играет: заемщика или кредитора.

Кроме этого необходимо учитывать действия эффекта замены и эффекта дохода.

• Эффект замены состоит в том, что рост процентной ставки делает потребление во втором периоде более дешевым благом по сравнению с первым периодом, т. е. уменьшение потребления в первом периоде (С1) увеличивает сбережения в этом периоде (S1):

– ?С1 = ?S1.

Это приводит к повышению потребления во втором периоде С2 на величину, равную r? S1. Другими словами, уменьшение потребления на 1 единицу в первом периоде С1 приводит к росту потребления во втором периоде (С2) на величину, большую единицы. Итак, эффект замены действует в строну ?С2 во II периоде и ? С1 в I периоде, что приводит к ?S1 в I периоде.

Эффект дохода отражается в изменении потребления и в первом, и во втором периодах, которые связаны с переходом к новой кривой безразличия, показывающей более высокий уровень потребления.

Однако данный эффект по-разному влияет на состояние экономических субъектов, находящихся в роли кредиторов и заемщиков.

Для кредитора эффект дохода, будучи величиной положительной, увеличивает потребление и С1, и С2. Для заемщиков отрицательный эффект дохода сокращает потребление в обоих периодах. При этом сбережения кредиторов (S1) снижаются, а сбережения заемщиков (S) увеличиваются.

Итак, на агрегированном уровне эффект дохода заемщиков и кредиторов нейтрализуется.

Функция потребления И. Фишера отражает зависимость потребительских расходов от текущей (дисконтированной) стоимости совокупного дохода за все периоды жизнедеятельности:

Поделитесь на страничке

Следующая глава >

econ.wikireading.ru

Шпаргалка - Оптимизация выбора потребителя

Министерство образования

Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

РЕФЕРАТ

на тему: «Оптимизация выбора потребителя»

Выполнили

студенты

Куропатенкова Ю.В.

Кульша М.О.

Ходатович Е.Д.

Минск 2007

Оглавление

Введение

1. Задача оптимизации выбора потребителя

Заключение

Список литературы

Введение

Задача оптимизации выбора потребителя

Суть оптимизации выбора потребителя.

Выбор ( X1*, X2*) является оптимальным выбором для потребителя. Множество наборов, которые он предпочитает (X1*, X2*), а именно множество наборов, располагающееся над его кривой безразличия, не пересекает наборы, которые он может себе позволить приобрести, а именно наборы под бюджетной линией. Таким образом, набор (X1*,X2*) – это наилучший набор, который потребителю по карману.

Отвечающая требованиям рыночная корзина должна удовлетворять двум условиям:

Она должна находится на бюджетной линии. Почему? Заметим, что любая рыночная корзина левее и ниже бюджетной линии оставляет неизрасходованной некоторую часть дохода, который, будучи потраченным, мог бы увеличить удовлетворение потребителя. Разумеется, потребители могут – и иногда действительно делают это – сберечь некоторую часть доходов для будущего потребления. Однако пока мы упростим ситуацию, предположив, что весь доход тратится сразу. Также заметим, что любая рыночная корзина правее и выше бюджетной линии не может быть приобретена при имеющемся уровне дохода. Вот почему единственный рациональный и осуществимый выбор – это корзина, лежащая на бюджетной линии.

Она должна обеспечивать потребителю наиболее предпочтительную комбинацию товаров и услуг.

Будем считать, что каждый товар имеет цену pi, а индивид имеет доход Q – какое-то количество денег, в рамках которого он и действует, покупая нужный ему набор товаров. На покупку набора товаров X=(xi,…, xn) надо затратить денег в количестве c(X)=pixi+…+pnxn=/>

Доказательство. Пусть r=min pi, тогда, как легко видеть, если X/>B, то x≤Q/r для i=1,…,n, т.е. множество B ограниченно. Докажем замкнутость. Пусть Хк/> В для всякого k />N и Xk/>Z. Тогда в силу непрерывности линейной функции

PXk/>PZ и, поскольку, PXk≤Q, то и PZ≤Q. Следовательно, Z/>B.

Граница бюджетного множества называется множество G = {X/>B: PX = Q}. Граница G – это отрезок в случае двух товаров, часть плоскости, ограниченная треугольником, в случае трёх товаров, и в общем случае, есть часть гиперплоскости в пространстве товаров.

Найти набор товаров X=(xi,…, xn), максимизирующий функцию полезности u(xi,…, xn), при выполнении бюджетного ограничения PX =pixi+…+pnxn≤Q; по смыслу задачи все переменные принимают неотрицательное значение, т.е. xi≥0, i=1,…, n.

Рассматриваемую задачу можно сформулировать более кратко:

Или даже так:

/>(1)

Поскольку u(X) – непрерывная функция своих аргументов, а бюджетное множество В ограниченно и компактно, то u(X) достигает на множестве В своего максимума, т.е. решение задачи 1 существует. Очевидно, что любая точка Х* максимума функции c(X) лежит на границе G бюджетного множества. Действительно, если предположим противное, то есть что Z – точка максимума, но Z/>G, тогда PZ <Q. Однако тогда потребитель имеет неиспользованное количество денег Q – PZ, и на эти деньги он может купить какое-то количество товаров Y, причём можно считать, что Y>0. Но тогда Y/>В, однако u(Z+Y)>u(Z). В силу того, что каждый товар желателен. Получили противоречие с тем, что Z – точка максимума функции c(X) на бюджетном множестве.

Доказательство. Предположим, что А и С – две точки максимума, т.е. u(X)/>u(A)=u(C) для любой точки X множества В. Мы уже знаем, что точки А и С лежат на границе бюджетного множества, т.е. РА=РС=Q. Рассмотрим точку Е=А/2 + С/2. Видим, что РЕ = Р(А/2 + С/2)= Q, т.е. Е/>В. В силу строгой вогнутости функции u(X) имеем: u(Е) > u(А)= u(С). Получили противоречие с тем, что А и С – есть точки максимума функции на бюджетном множестве.

Или

/>/>/>

Заключение

Таким образом, существует только одна точка максимума функции полезности на бюджетном множестве.

www.ronl.ru

Потребительский выбор. Оптимальный выбор потребителя

Новые рефераты:

Повышение пенсионного возраста.
Безработица и её социально-экономические последствия.
Основные направления в развитии социологической теории ХХ века.
Колебательные реакции.
Предмет формальной логики.
Роль и значение времени в управлении.
Античная философия.
Социальная поддержка многодетных семей (на примере Архангельской области).
Рыночные структуры.
Причины и типология кризисов в социально-экономических системах.
Этапы реинжиниринга бизнес-процессов. Роль творчества в процессе реинжиниринга.
Главная » Микроэкономика. Курс лекций » Потребительский выбор. Оптимальный выбор потребителя

Потребительский выбор. Оптимальный выбор потребителя
Продолжим рассмотрение примера с покупками пива и пиццы. Потребитель хотел бы добиться наилучшей из возможных комбинаций этих товаров на самой высокой кривой безразличия. Но он должен учитывать бюджетные ограничения, определяющие его финансовые возможности. Оптимум выбора. На рис. 4.5 представлены линия бюджетного ограничения и три кривых безразличия. Наивысшая из доступных потребителю кривых безразличия, кривая 2, соприкасается с бюджетной линией. Точка соприкосновения носит название точки оптимума.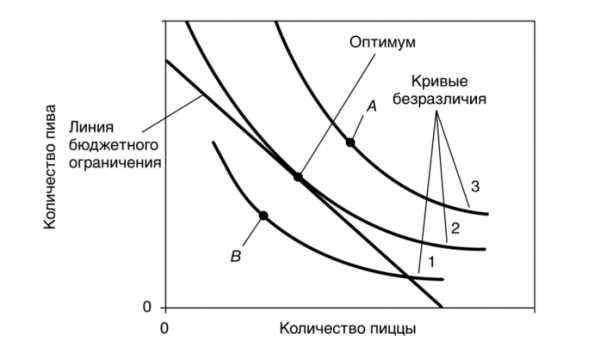 Рис. 4.5. Потребительский оптимум — линия бюджетного ограничения и три кривых безразличия На нашем рисунке кривая безразличия 2 — наивысшая из доступных потребителю. Точка оптимума отражает наилучшую доступную потребителю комбинацию количества пива и пиццы. Он предпочел бы точке оптимума точку Л, принадлежащую расположенной выше, на кривой безразличия 3, но не может позволить себе приобрести определяемый ею набор пива и пиццы в силу бюджетного ограничения. Точка В отвечает его возможностям, но она лежит на кривой безразличия 1, расположенной ниже, чем кривая 2, поэтому потребитель не согласится сделать выбор в ее пользу, поскольку она удовлетворяет его в меньшей степени. Маржинальная норма замещения и относительная цена товара. В точке оптимума наклон кривой безразличия равен наклону линии бюджетного ограничения. Линия бюджетного ограничения является касательной к кривой безразличия. Наклон кривой безразличия равен маржинальной норме замещения между пивом и пиццей, а наклон линии бюджетного ограничения отражает сравнительную стоимость этих товаров. Итак, потребитель выбирает набор товаров таким образом, чтобы их маржинальная норма замещения была равна их относительной цене. Анализ рынков показывает, что рыночные цены отражают маржинальную оценку стоимости товара потребителем. Анализ потребительского выбора подтверждает эту закономерность. Относительная цена определяет пропорцию, в которой рынок готов заменить один товар другим. Маржинальная норма замещения отражает готовность к замене товаров потребителя. Оптимальная оценка товаров потребителем измеряется как маржинальная норма замещения; она соответствует оценке товаров рынком, которая равна их относительной цене. В результате оптимизации потребительского выбора рыночная стоимость товаров отражает их оценку покупателем.Влияние доходов потребителя на его выбор Рассмотрим ситуацию, когда доходы потребителя пива и пиццы увеличиваются. В этом случае он может приобрести большее количество обоих товаров. Увеличение доходов приведет к сдвигу бюджетной линии вправо, как показано на рис. 4.6. Так как относительная цена товаров остается прежней, наклон линии ограничения бюджета не изменяется, и ее новое положение будет параллельно исходному положению.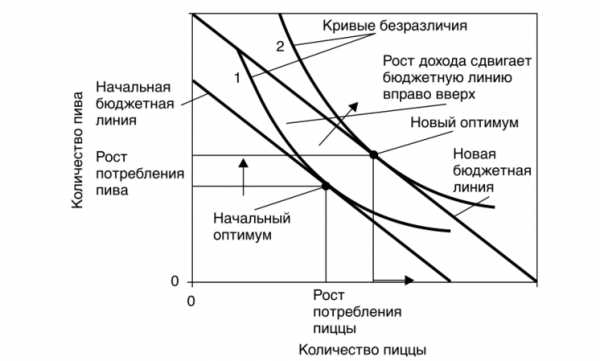 Рис. 4.6. Влияние роста доходов потребителя на его выбор Рост финансовых возможностей потребителя позволит ему выбрать лучшее сочетание количества пива и пиццы. При этом он достигает новой кривой безразличия, расположенной выше прежней. С учетом перехода на новую кривую безразличия и сдвига линии ограничения бюджета точка потребительского оптимума переместится в новое положение. Нормальный товар — это товар, спрос на который по мере увеличения доходов потребителей возрастает. На рис. 4.6 отражено изменение выбора потребителя в сторону увеличения приобретения и пива, и пиццы. Такая ситуация встречается наиболее часто. Потребление нормальных товаров увеличивается вместе с ростом доходов покупателя. Кривые безразличия на рис. 4.6 принадлежат нормальным товарам.Влияние изменения цен на потребительский выбор Предположим, цена литра пива снизилась с 50 до 25 руб. Покупательная способность потребителя возрастает. Уменьшение цены одного из товаров вызывает сдвиг линии ограничения бюджета вправо. Предположим, потребитель тратит весь свой доход — 1000 руб. на пиццу. В этом случае новая цена пива никак не отразится на количестве приобретаемых им товаров. На рис. 4.7 положение точки А не изменится.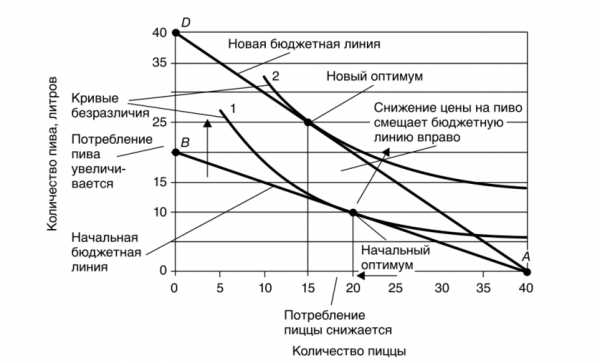 Рис. 4.7. Влияние изменения цены товара на выбор потребителя Пусть потребитель использует весь свой доход на приобретение пива. Он получает возможность увеличить покупки напитка в два раза и приобрести 40, а не 20 литров. В этом случае точка пересечения линии ограничения бюджета с вертикальной осью сместится из положения В в положение D. При сдвиге бюджетной линии вправо изменился ее наклон. Наклон линии ограничения бюджета отражает относительную цену товаров. В нашем примере цена литра пива уменьшилась с 50 до 25 руб., а цена порции пиццы осталась на прежнем уровне в 25 руб. Поэтому у потребителя появилась возможность заменить одну порцию пиццы не !/2 литра, а целым литром пива. Наклон бюджетной линии изменился — увеличился в два раза. Выбор потребителя смещается от начального положения оптимума к новому, который определяет изменение объемов покупки обоих видов товаров. Как изменение положения бюджетной линии повлияет на приобретение того или иного товара — зависит от вкусов потребителя. В нашем примере потребитель предпочел покупать больше пива и меньше пиццы. Это означает: пицца для рассматриваемого потребителя низший товар. Низшие товары. Товары, объем покупок которых по мере роста доходов потребителя сокращается, экономисты называют низшими товарами. В нашем примере к ним относится пицца.Эффект дохода и эффект замещения Влияние изменения цены товара на уровень потребления определяется эффектом дохода и эффектом замещения. Понять смысл каждого из этих эффектов можно на примере реакции потребителя на снижение цены пива. Возможны два следующих варианта: 1. «Цена на пиво снизилась. Это делает меня богаче, можно покупать больше и пива и пиццы». Это эффект дохода. 2. «Цена на пиво снизилась. Могу приобретать больше любимого пива. Поскольку пицца стала относительно более дорогим товаром, пиццы следует покупать меньше». Это эффект замещения. Каждое из этих суждений вполне рационально. Снижение цены на пиво выгодно потребителю. Если пицца и пиво для потребителя нормальные товары, он использует увеличение своей покупательской способности для приобретения большего количества того и другого продукта. Эффект дохода позволяет ему покупать больше пиццы и больше пива. Но пиво становится относительно дешевле пиццы. Поэтому эффект замещения может вынудить потребителя сделать выбор в пользу большего количества пива и меньшего количества пиццы. Таким образом, потребитель будет покупать больше пива, поскольку этому способствует действие обоих эффектов. Но остается неясным, будет ли покупатель приобретать больше пиццы, так как в этом вопросе влияние эффектов дохода и замещения противоположно. Построение кривой спроса Кривая спроса демонстрирует влияние цены товара на уровень спроса. Можно рассматривать кривую спроса как отражение оптимальных решений потребителя, возникающих при анализе взаимного расположения линии бюджетного ограничения и кривых безразличия. График на рис. 4.8 представляет кривую спроса, построенную на основании решений потребителя. На рис. 4.7 анализируется влияние цен на пиво на выбор потребителя.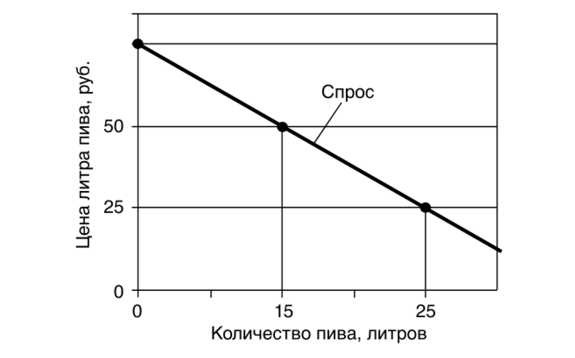 Рис. 4.8. Построение кривой спроса по данным потребительского выбора на рис. 4.6 Цена литра пива в примере уменьшилась с 50 до 25 руб. за литр. Из графика на рис. 4.7 видно: когда цена пива снижается, линия ограничения бюджета сдвигается вправо. В силу влияния эффектов дохода и замещения потребление пива увеличивается с 15 до 25 литров. Так теория потребительского выбора дает теоретическое обоснование кривой спроса. Лекция, реферат. Потребительский выбор. Оптимальный выбор потребителя - понятие и виды. Классификация, сущность и особенности.
Оглавление книги открыть закрыть

referatwork.ru

Оптимизация выбора потребителя - Реферат

Министерство образования

Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

РЕФЕРАТ

на тему: «Оптимизация выбора потребителя»

Выполнили

студенты

Куропатенкова Ю.В.

Кульша М.О.

Ходатович Е.Д.

Минск 2007

Оглавление

Введение

1. Задача оптимизации выбора потребителя

Заключение

Список литературы

Введение

1. Задача оптимизации выбора потребителя

Суть оптимизации выбора потребителя.

Отвечающая требованиям рыночная корзина должна удовлетворять двум условиям:

2. Она должна обеспечивать потребителю наиболее предпочтительную комбинацию товаров и услуг.

Будем считать, что каждый товар имеет цену pi , а индивид имеет доход Q – какое-то количество денег, в рамках которого он и действует, покупая нужный ему набор товаров. На покупку набора товаров X=(xi ,…, xn ) надо затратить денег в количестве c(X)=pi xi +…+pn xn =

Таким образом, индивид может купить только такой набор X, при котором PX≤Q. Следовате

льно, множество наборов товаров, доступных ему при доходе Q. есть B=B(P,Q)={X; X≥0, PX≤Q}. Это множество называется бюджетным множеством. Бюджетное множество ограниченно и замкнуто.

Доказательство. Пусть r=min pi , тогда, как легко видеть, если XB, то x≤Q/r для i=1,…,n, т.е. множество B ограниченно. Докажем замкнутость. Пусть Хк В для всякого k N и Xk Z. Тогда в силу непрерывности линейной функции

PXk PZ и, поскольку, PXk ≤Q, то и PZ≤Q. Следовательно, ZB.

Рассматриваемую задачу можно сформулировать более кратко:

Или даже так:

(1)

Поскольку u(X) – непрерывная функция своих аргументов, а бюджетное множество В ограниченно и компактно, то u(X) достигает на множестве В своего максимума, т.е. решение задачи 1 существует. Очевидно, что любая точка Х* максимума функции c(X) лежит на границе G бюджетного множества. Действительно, если предположим противное, то есть что Z – точка максимума, но Z G, тогда PZ <Q. Однако тогда потребитель имеет неиспользованное количество денег Q – PZ, и на эти деньги он может купить какое-то количество товаров Y, причём можно считать, что Y>0. Но тогда YВ, однако u(Z+Y)>u(Z). В силу того, что каждый товар желателен. Получили противоречие с тем, что Z – точка максимума функции c(X) на бюджетном множестве.

Или

Заключение

Таким образом, существует только одна точка максимума функции полезности на бюджетном множестве.

Шпаргалка: Оптимизация выбора потребителя. Оптимизация потребительского выбора

Оптимизация выбора потребителя

«Оптимизация выбора потребителя»

Оптимизация выбора потребителя - реферат, курсовая работа, диплом, 2017

15.1.1. Межвременной выбор потребителя и его оптимизация. Экономическая теория: учебник

Шпаргалка - Оптимизация выбора потребителя

Потребительский выбор. Оптимальный выбор потребителя

Потребительский выбор. Оптимальный выбор потребителя

Оглавление книги открыть закрыть

Оптимизация выбора потребителя - Реферат