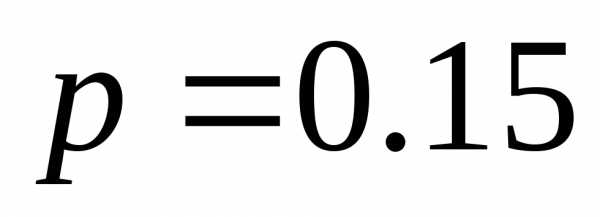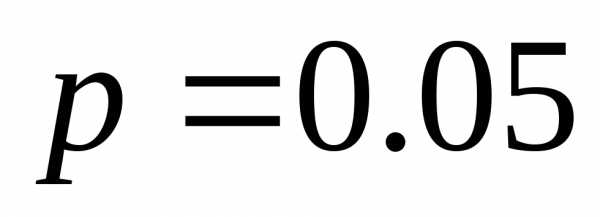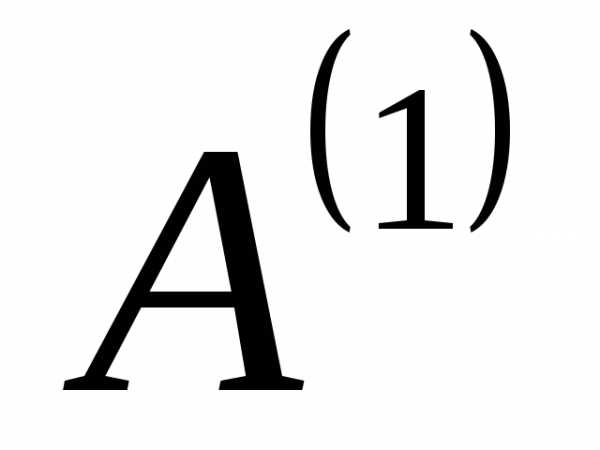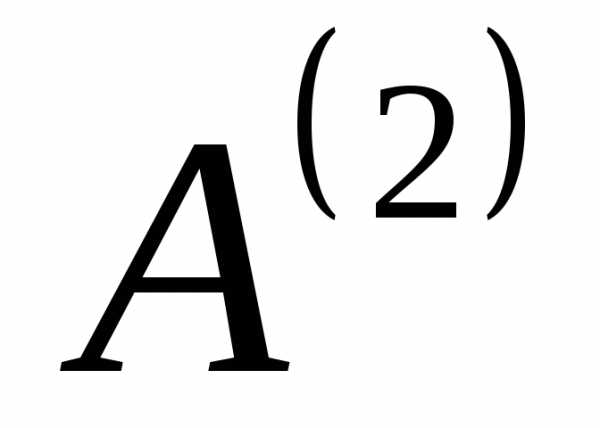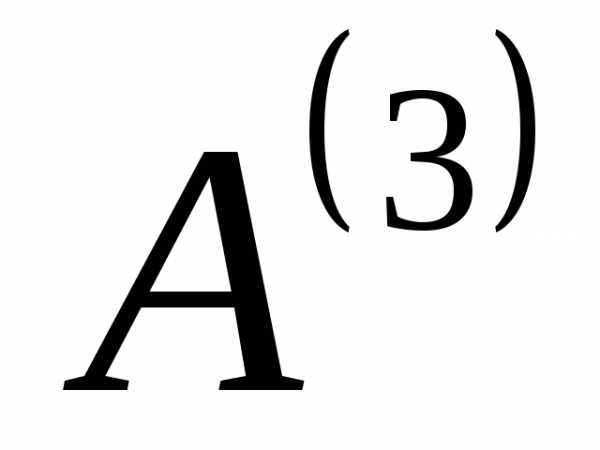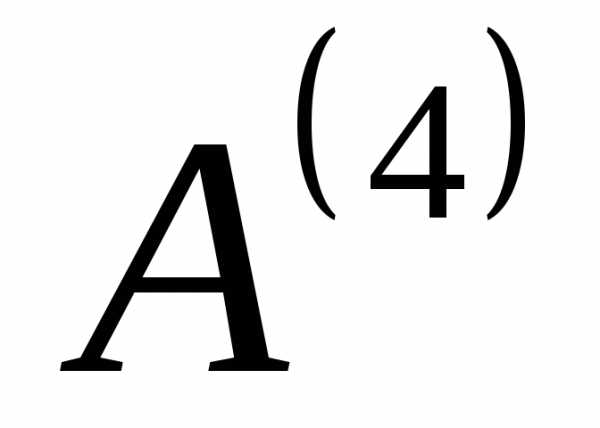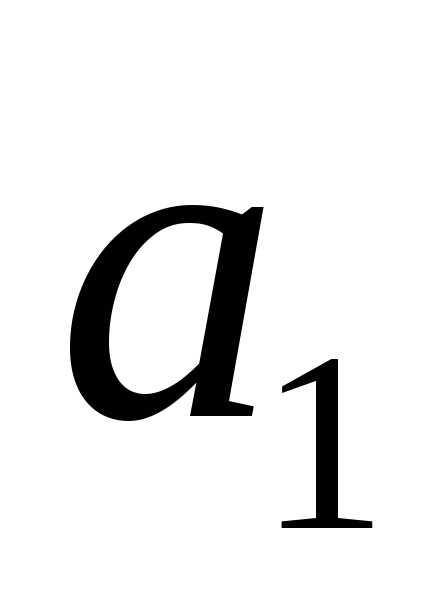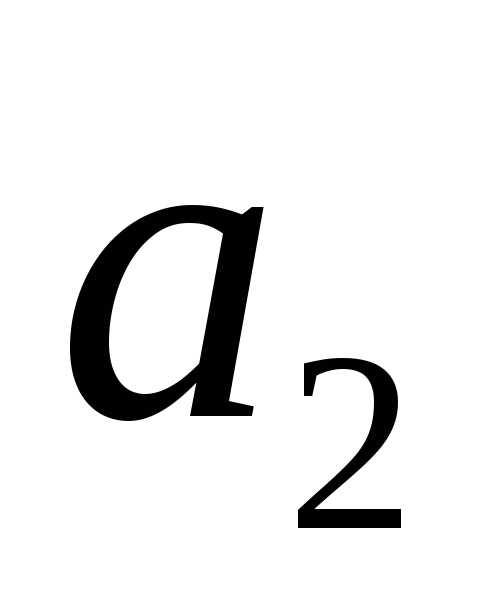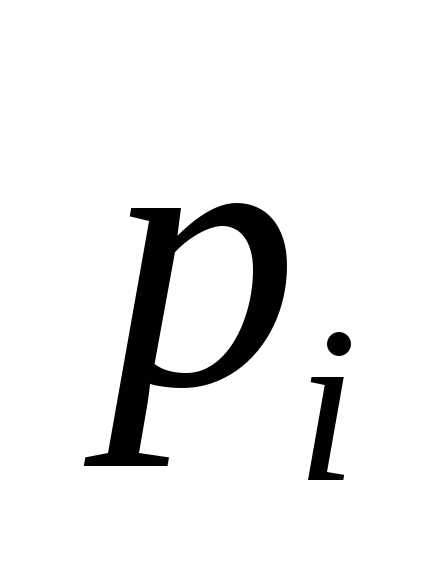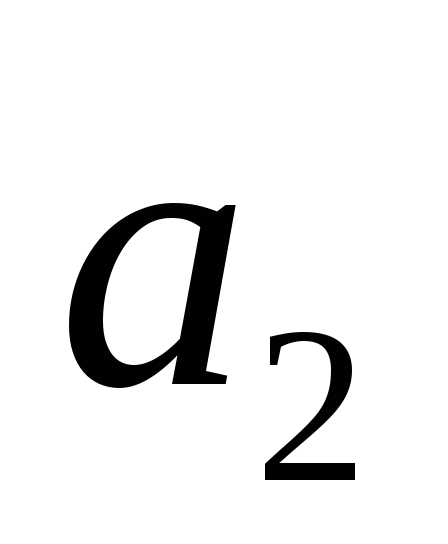Коды Хаффмана: примеры, применение. Оптимизация хаффмана

Алгоритм Хаффмана на пальцах / Хабр

Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.

К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).

Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.

Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.

Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.

Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).

Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.

Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.

Для начала посчитаем частоты всех символов:

Символ Частота

'b'	3
'e'	4
'p'	2
' '	2
'o'	2
'r'	1
'!'	1

После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:

Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь. Повторим те же шаги и получим последовательно: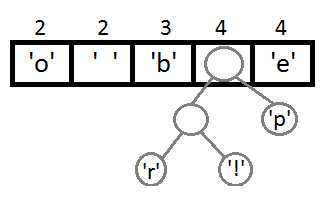

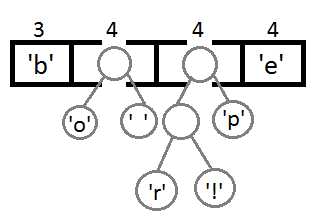
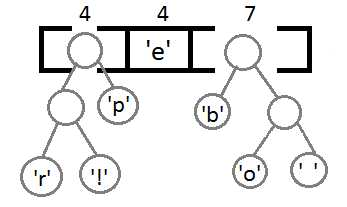
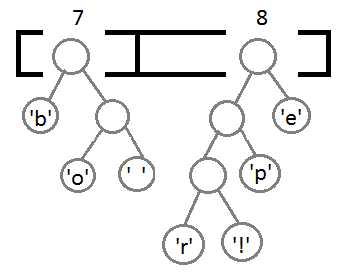
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево: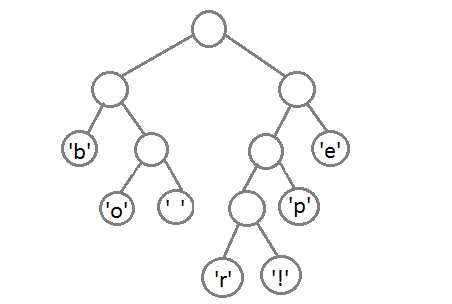

Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо: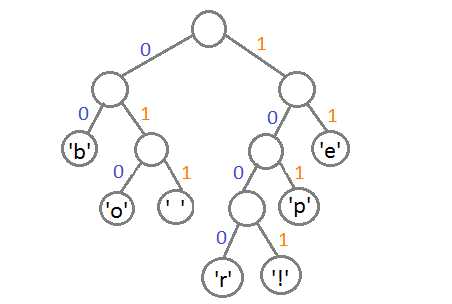

Если мы так сделаем, то получим следующие коды для символов:

Символ Код

'b'	00
'e'	11
'p'	101
' '	011
'o'	010
'r'	1000
'!'	1001

Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».

Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для 'b', то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на 'b'.

На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.

Входная строка: «beep boop beer!» Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000» Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001» Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.

Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.

Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!

Скачать исходный код

Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.

habr.com

Коды Хаффмана: примеры, применение

На данный момент мало кто задумывается над тем, как же работает сжатие файлов. По сравнению с прошлым пользование персональным компьютером стало намного проще. И практически каждый человек, работающий с файловой системой, пользуется архивами. Но мало кто задумывается над тем, как они работают и по какому принципу происходит сжатие файлов. Самым первым вариантом этого процесса стали коды Хаффмана, и их используют по сей день в различных популярных архиваторах. Многие пользователи даже не задумываются, насколько просто происходит сжатие файла и по какой схеме это работает. В данной статье мы рассмотрим, как происходит сжатие, какие нюансы помогают ускорить и упростить процесс кодирования, а также разберемся, в чем принцип построения дерева кодирования.

История алгоритма

Самым первым алгоритмом проведения эффективного кодирования электронной информации стал код, предложенный Хаффманом еще в середине двадцатого века, а именно в 1952 году. Именно он на данный момент является основным базовым элементом большинства программ, созданных для сжатия информации. На данный момент одними из самых популярных источников, использующих этот код, являются архивы ZIP, ARJ, RAR и многие другие.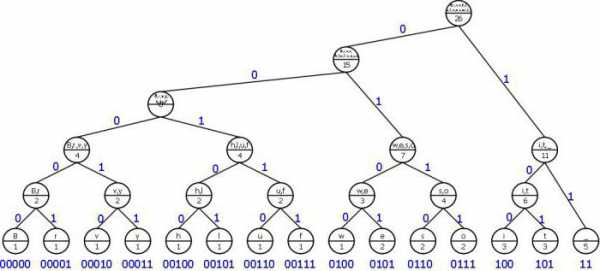

Также данный алгоритм Хаффмана применяется для сжатия JPEG-изображений и других графических объектов. Ну и все современные факсы также используют кодирование, изобретенное в 1952 году. Несмотря на то что со времени создания кода прошло так много времени, по сей день его используют в самых новых оболочках и на оборудовании старого и современного типов.

Принцип эффективного кодирования

В основу алгоритма по Хаффману входит схема, позволяющая заменить самые вероятные, чаще всего встречающиеся символы кодами двоичной системы. А те, которые встречаются реже, заменяются более длинными кодами. Переход на длинные коды Хаффмана происходит только после того, как система использует все минимальные значения. Такая методика позволяет минимизировать длину кода на каждый символ исходного сообщения в целом. 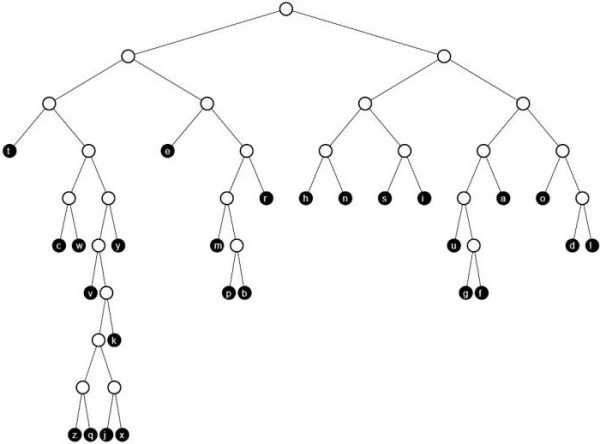Важным моментом является то, что в начале кодирования вероятности появления букв должны быть уже известны. Именно из них и будет составляться конечное сообщение. Исходя из этих данных, осуществляется построение кодового дерева Хаффмана, на основе которого и будет проводиться процесс кодирования букв в архиве.

Код Хаффмана, пример

Чтобы проиллюстрировать алгоритм, возьмем графический вариант построения кодового дерева. Чтобы использование этого способа было эффективным, стоит уточнить определение некоторых значений, необходимых для понятия данного способа. Совокупность множества дуг и узлов, которые направлены от узла к узлу, принято называть графом. Само дерево является графом с набором определенных свойств:

в каждый узел может входить не больше одной из дуг;
один из узлов должен быть корнем дерева, то есть в него не должны входить дуги вообще;
если от корня начать перемещение по дугам, этот процесс должен позволять попасть совершенно в любой из узлов.

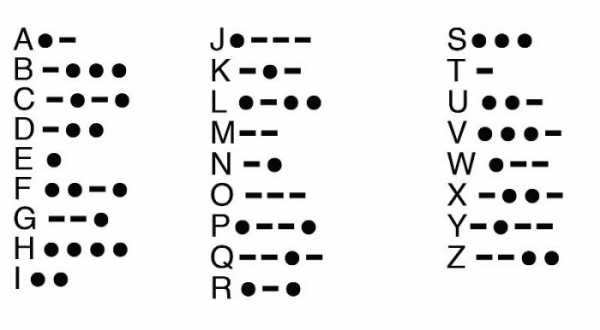Существует также такое понятие, входящее в коды Хаффмана, как лист дерева. Он представляет собой узел, из которого не должно выходить ни одной дуги. Если два узла соединены дугой, то один из них является родителем, другой ребенком, в зависимости от того, из какого узла дуга выходит, и в какой входит. Если два узла имеют один и тот же родительский узел, их принято называть братскими узлами. Если же, кроме листьев, у узлов выходит по несколько дуг, то это дерево называется двоичным. Как раз таким и является дерево Хаффмана. Особенностью узлов данного построения является то, что вес каждого родителя равен сумме веса всех его узловых детей.

Алгоритм построения дерева по Хаффману

Построение кода Хаффмана делается из букв входного алфавита. Образуется список тех узлов, которые свободны в будущем кодовом дереве. Вес каждого узла в этом списке должен быть таким же, как и вероятность возникновения буквы сообщения, соответствующей этому узлу. При этом среди нескольких свободных узлов будущего дерева выбирается тот, который весит меньше всего. При этом если минимальные показатели наблюдаются в нескольких узлах, то можно свободно выбирать любую из пар. 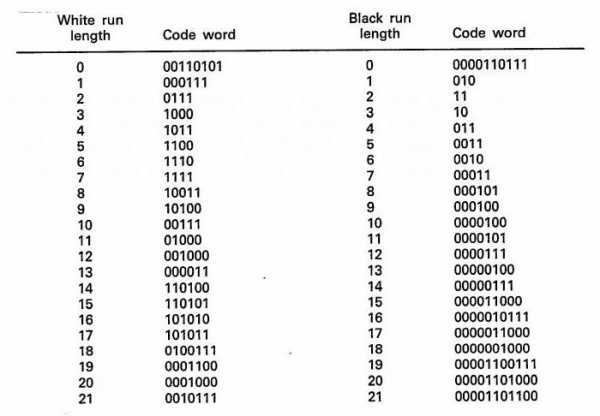После чего происходит создание родительского узла, который должен весить столько же, сколько весит сумма этой пары узлов. После этого родителя отправляют в список со свободными узлами, а дети удаляются. При этом дуги получают соответствующие показатели, единицы и нули. Этот процесс повторяется ровно столько, сколько нужно, чтобы оставить только один узел. После чего выписываются двоичные цифры по направлению сверху вниз.

Повышение эффективности сжатия

Чтобы повысить эффективность сжатия, нужно во время построения дерева кода использовать все данные относительно вероятности появления букв в конкретном файле, прикрепленном к дереву, и не допускать того, чтобы они были раскиданы по большому количеству текстовых документов. Если предварительно пройтись по этому файлу, можно сразу просчитать статистику того, насколько часто встречаются буквы из объекта, подлежащего сжиманию.

Ускорение процесса сжатия

Чтобы ускорить работу алгоритма, определение букв нужно проводить не по показателям вероятности появления той или иной буквы, а по частоте ее встречаемости. Благодаря этому алгоритм становится проще, и работа с ним значительно ускоряется. Также это позволяет избежать операций, связанных с плавающими запятыми и делением. Кроме того, работая в таком режиме, динамический код Хаффмана, а точнее сам алгоритм, не подлежит никаким изменениям. В основном это связанно с тем, что вероятности имеют прямую пропорциональность частотам. Стоит обратить особое внимание на то, что конечный вес файла или так называемого корневого узла будет равен сумме количества букв в объекте, подлежащем обработке.

Заключение

Коды Хаффмана - простой и давно созданный алгоритм, который до сих пор используется многими известными программами и компаниями. Его простота и понятность позволяют добиться эффективных результатов сжатия файлов любых объемов и значительно уменьшить занимаемое ими место на диске хранения. Иными словами, алгоритм Хаффмана – давно изученная и проработанная схема, актуальность которой не уменьшается по сей день. 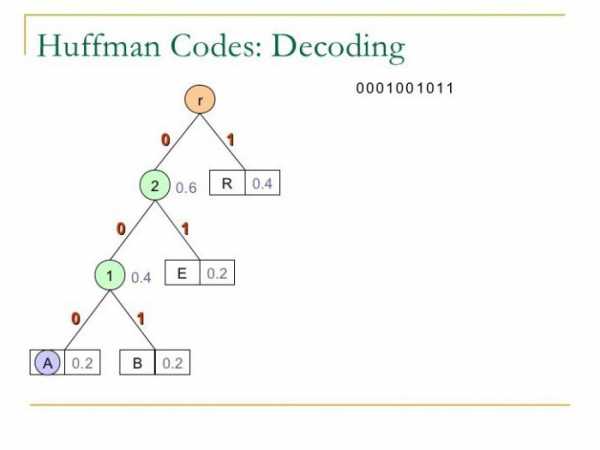А благодаря возможности уменьшить размер файлов, их передача через сеть или другими способами становится более простой, быстрой и удобной. Работая с алгоритмом, можно сжать совершенно любую информацию без вреда для ее структуры и качества, но с максимальным эффектом уменьшения веса файла. Иными словами, кодирование по коду Хаффмана было и остается самым популярным и актуальным методом сжатия размера файла.

fb.ru

Руководство по оптимизации JPG. ~ Eugeneer's Digital Cloud World

Добрый день! Очередное детальное руководство от команды Айри.рф про то как правильно оптимизировать JPEG изображения на сайте без видимых потерь качества, чтобы сократить их размер до 50%. Замечу что первые 5 методов доступны даже новичку, с остальными следует быть особо осторожными.

Формат JPEG в силу DCT-кодирования и таблиц Хаффмана изначально подразумевает потерю качества. И даже сохранение в режиме "100%" не устранит потерь. Но эти потери можно сделать незаметными для глаза или допустимыми в конкретном случае использования. Или использовать некоторые особенности формата, чтобы кодировать JPEG совсем без потерь.

1. Оптимизация для Web

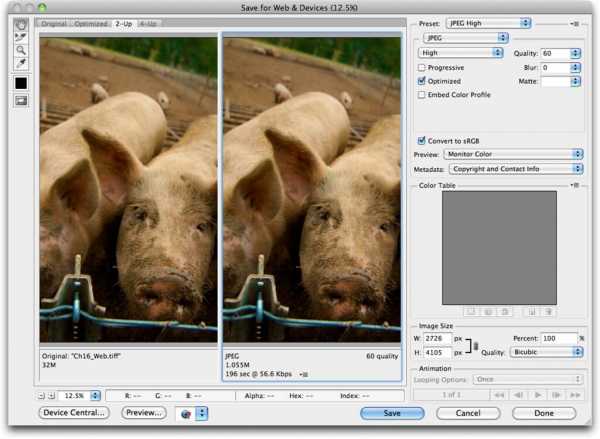Базовый совет: при сохранении в любом редакторе (Photoshop, Gimp и др.) используйте отдельную опцию «Сохранить для Web». Это сделает изображение совместимым по цветовой палитре со всеми браузерами. А также удалит из него некоторую дополнительную информацию (например, превью-изображения), которая необходима обычным редакторам для быстрого просмотра множества изображений, но совершенно не подходит браузерам (которые не используют превью в JPEG-изображениях ни в каком виде).

Естественно, что фактические размеры изображения должны соответствовать максимальным размерам, используемым на сайте. Наиболее частая ошибка в работе с картинками на сайте: взять их в исходном виде, без приведения к нужным размерам. Это многократно увеличивает размер сайта и существенно замедляет его загрузку.

2. Удаление мета-информации

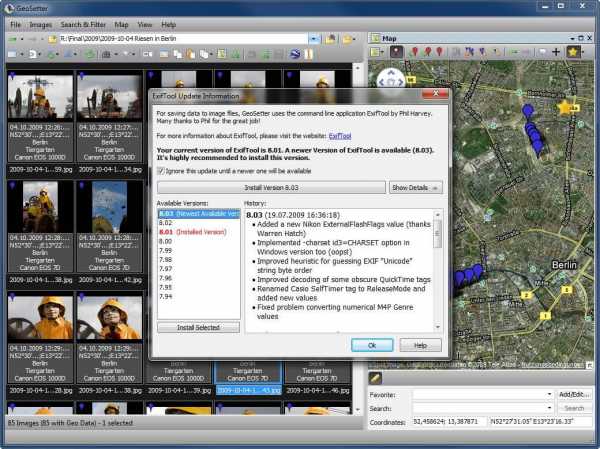В качестве дальнейшей оптимизации JPEG без воздействия на цветовые данные можно и стоит рассмотреть различные утилиты для удаления EXIF-чанков и комментариев.

Лучшей в данном классе утилит будет ExifTool, которая доступна для всех платформ. ExifTool распознает дополнительные теги (EXIF chunks) почти всех устройств и прикладных программ и позволяет безболезненно для качества изображения их убрать (или извлечь или заменить).

Удаление мета-информации и EXIF-chunks производится вне основных данных изображения (DCT-преобразования и таблиц Хаффмана) и гарантирует сохранение качества.

3. «Последовательная» оптимизация

Формат JPEG содержит еще одну интересную особенность — возможность делать несколько кадров изображения, отрисовывая их последовательно (от этого и происходит термин «последовательные» (progressive) JPEG). Есть вероятность, что первоначально эту возможность хотели использовать для JPEG-анимации, но в конкретной реализации она нашла лучшее применение.

«Последовательные» JPEG улучшают пользовательское восприятие при загрузке больших файлов (сначала показывается смазанная копия, затем она улучшается в поступлением данных) и обладают меньшим размером (в среднем, если JPEG изображение больше 10 Кб).

Сейчас «последовательные» JPEG файлы поддерживаются всеми браузерами, и нет никаких причин их не использовать. Не всегда такие файлы будут меньше обычных, но проверку на размер обычной и «последовательной» версии необходимо выполнять при сохранении или оптимизации файлов.

Выигрыш в размере «последовательных» JPEG обычно не больше 20% от исходного размера файла.

4. Сохранение не в 100% качестве

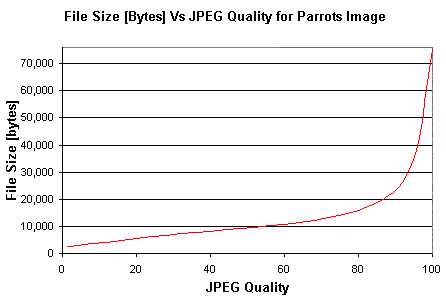100% качество (максимальный уровень качества в графическом редакторе) при сохранении JPEG-файлов не подразумевает отсутствие потерь. В силу ограничений формата каждый JPEG файл представляет информацию с потерями. Но можно уменьшить размер файла и, практически, не увеличить чисто потерь.

Оптимальным будет использование 90-95% максимального качества (в зависимости от вашего редактора или консольной утилиты): это либо 90-95% при максимуме 100%, либо 10-11 при максимуме в 12. В этом случае размер изображения будет меньше при том же визуальном качестве. И из изображения не будут удалены небольшие детали (что может произойти при дополнительных оптимизациях, включаемых в вашем редакторе, по умолчанию, при качестве меньше 90).

Как видно из графика выше, даже использование качества 95 вместо 100 обычно позволяет сократить размер в 1,5-2 раза. Я лично сохраняю в Paint.NET на 80%.

5. Использование другого формата

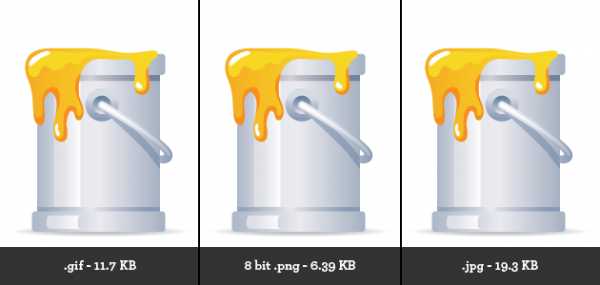Не всегда изображения в JPEG-формате будут занимать меньше места. Иногда правильнее сохранять их в SVG (логотипы), PNG (при небольшой цветовой палитре) или даже в WebP (если все браузеры ваших пользователей это поддерживают). Даже если формат WebP не полностью поддерживается в браузерах (на текущих момент покрытие составляет в районе 70%), можно сохранять изображение в двух форматах — лучшем из стандартных (например, JPEG) и альтернативном (WebP) и отправлять пользователям те изображения, которые поддерживает их web-браузер (определяя это по HTTP заголовку Accept).

Правильное определение формата изображение может сократить размер в 2-3 раза.

6. Оптимизация для Retina-устройств

При использовании изображений двойного разрешения для соответствующих устройств (с Retina) можно применять следующую хитрость. Поскольку физически большее изображение отобразится в меньшую площадь, то исходное изображение можно сохранить с существенно меньшим качеством (при этом потери качества не будут заметны при попиксельном сравнении).

На примере выше более высокая степень сжатия для изображения с двойной плотностью пикселей дало 30% выигрыша в размере без видимой потери качества.

Описанные методики позволяют существенно (иногда в несколько раз) сократить размер JPEG-изображения и применить к ним другие, продвинутые техники оптимизации.

7. Оптимизация для решетки 8×8

Достаточно известный прием (автор метода — Сергей Чикуёнок), использующий особенность JPEG сжимать изображение квадратами 8×8 (из-за DCT преобразования). Для оптимальной четкости изображения (и понижения его качества без видимого ущерба для картинки) нужно выровнять границы элементов изображения по решетке 8×8.

При переводе в формат JPEG изображение нарезается на квадраты 8×8, которые могут быть независимо оптимизированы (с большим числом деталей — с лучшим качеством, однотонные — с меньшем качеством). Если детали изображения не будут совпадать с решеткой 8×8, то на границе решетки будет существенное размытие деталей (которое, конечно, можно нивелировать за счет более высокого качества сжатия — но это приведет к увеличению размера изображения).

Выигрыш от такой техники обычно составляет 5-10%.

Для автоматизации техники возможно настроить смещение границ изображения на 1-4 пикселя по обоим осям с тем же качеством (и сохранение среди результирующих изображений). Изображения меньшего размера будет лучше оптимизировано под решетку 8×8.

8. Селективная оптимизация

Логичным продолжением оптимизации для решетки 8×8 будет выборочное качество изображения (количество деталей) для разных зон изображения. Техника называется Selective optimization и доступна в нескольких инструментах.

В частности, в Adobe Photoshop необходимо создать одну или несколько масок изображений для лучшего качества (остальное изображение будет сжато сильнее) и применить ее при сохранении JPEG изображения (подробная инструкция). В результате — при том же качестве отображения деталей размер изображения будет меньше.

Эта техника дает выигрыш в 3-20% относительно исходного изображения.

9. Оптимизация цвета и яркости

Еще один прием от Сергея позволяет отбросить цветовую информацию для тех частей изображения, которые комбинируют черный и другой цвет в мелких текстурах. За счет уменьшения информации о смене цвета JPEG получается меньше по размеру, но на качестве изображения это не отражается (ведь все равно, какая нулевая яркость у цвета, если он черный).

Прием достаточно сложен в освоении: нужно переключиться в режим Lab Color, затем в Channels выбрать цвета, у которых уменьшить детализацию (смазать фон), затем меняем Levels, чтобы цвет изображения остался прежним. Полная версия руководства доступна здесь.

Выигрыш от таких манипуляций с изображением может достигать еще 10-15%.

10. Оптимизация субвыборки

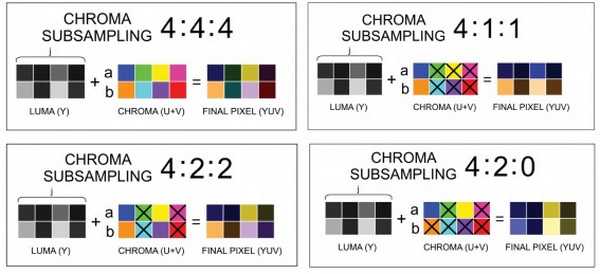В качестве более автоматизируемой альтернативы уменьшению цветовой информации с сохранением яркости изображения можно рассмотреть технику Chroma subsampling (субвыборка яркости). Если кратко, то при сохранении канала яркости в YCbCr-представлении изображения (Y — яркость, Cb — один цвет (синий), Cr — второй цвет (красный)) уменьшаются различия в цветах соседних пикселей. 1×1 subsampling означает отсутствие каких-либо изменений в цвете, 2×1 и 1×2 усредняют информацию только по одному измерению (горизонтали или вертикали, соответственно). 2×2 subsampling усредняет информацию сразу в 4 пикселях.

В другом представлении схемы — J:a:b (например, 4:2:2) — первая цифра означает ширину области усреднения (в данном случае 4 пикселя), вторая цифра — число результирующих значений цветов в первой строке, третья цифра — число результирующих цветов во второй строке. Всего строк 2 (высота области — 4 пикселя). Таким образом, схема 4:2:2 соответствует 2×1 subsampling, 4:4:4 — 1×1 subsampling, 4:2:0 — 2×2 subsampling, 4:4:0 — 1×2 subsampling.

11. Оптимизация таблиц Хаффмана

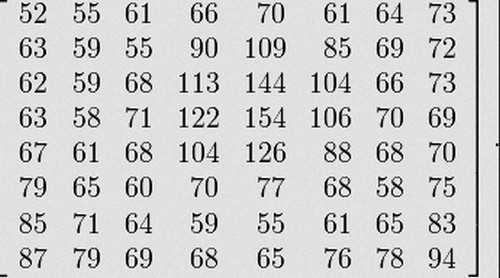Кодирование Хаффмана позволяет представить цветовую информацию (по разным каналам) в качестве сжимаемой таблицы (с потерей информации). JPEG-файлы используют именно эти таблицы. Оптимальный выбор порядка расположения коэффициентов в такой таблице позволяет существенно сократить ее размер. Этим и пользуются различные варианты утилит для оптимизации таблиц Хаффмана.

Наиболее известной является jpegtran, которая входит в набор libjpeg-progs и во множество утилит редактирования и оптимизации изображения. Менее известным вариантом оптимизатора является набор библиотек libjpeg-turbo, который содержит улучшенные инструкции и дополнительную оптимизацию для таблиц Хаффмана.

И совсем малоизвестным будет пакет mozjpeg, который реализует все наработки libjpeg-turbo и некоторые дополнительные улучшения по производительности. Каждая из описанных библиотек обратно совместима с jpegtran (и может использоваться как полноценная замена этой утилите).

Выигрыш от оптимизированных таблиц Хаффмана составляет 5-20% на изображение.

nyukers.blogspot.com

DTP - Настольные издательские системы

Все материалы, находящиеся в этом разделе, являются переводами документов с сайта http://www.prepressure.com.

Сжатие Хаффмана

Алгоритм сжатия Хаффмана назван по имени его изобретателя, Дэвида Хаффмана, бывшего профессором Массачусетского технологического института.

Сжатие Хаффмана - алгоритм компрессии без потерь, которые идеален для сжатия текстов и программных файлов. Это объясняет его широкое распространение во многих многих программах архивации.

Как работает сжатие Хаффмана

Сжатие Хаффмана относится к семейству алгоритмов с переменной длиной кодового слова. Это означает, что отдельные символы (например буквы в текстовом файле) заменяются битовой последовательностью с меньшей длиной. При этом символы, чаще встречающиеся в файле, заменяются более короткой кодовой последовательностью, чем реже встречающиеся символы.

Наглядный пример, который пояснит эти принципы: допустим, мы хотим сжать следующую последовательность данных:

ACDABA

Здесь 6 символов и это 6 байтов или 48 бит. При использовании сжатия Хаффмана, в файле ищется наиболее часто встречающася последовательность символов. (в данном случае буква 'A' встречается 3 раза) и строится кодовая последовательность, которая заменяет символы более короткими последовательностями битов. В этом примере алгоритм построит следующую последовательность: A=0, B=10, C=110, D=111. Сжатый файл тогда будет выглядеть так:

01101110100

Итак, от исходных 48 битов осталось 11, и коэффициент сжатия для этого файла составляет 4 к 1.

Сжатие Хаффмана может быть оптимизировано двумя различными путями:

Адаптивный алгоритм Хаффмана динамически изменяет кодовые последовательности в соответствии и частотой появления символов.
Расширенный алгоритм Хаффмана может кодировать группы символов вместо отдельных символов.

Достоинства и недостатки

Этот алгоритм наиболее эффективен для сжатия текстов или программных файлов. Изображения лучше сжимаются другими алгоритмами сжатия.

Где используется сжатие Хаффмана

Сжатие Хаффмана широко используется в программах архивации, таких как pkZIP, lha, gz, zoo и arj. Также применяется в сжатиях JPEG и MPEG.

mikeudin.net

Прикладные техники оптимизации JPEG / ИТ / Лента.co

Читать оригинал публикации на seonews.ru

Сразу оговорюсь, что формат JPEG (в силу DCT-кодирования и таблиц Хаффмана) изначально подразумевает потерю качества. И даже сохранение в режиме "100%" не устранит потерь. Но эти потери можно сделать незаметными для глаза или допустимыми в конкретном случае использования.

1. Оптимизация цвета

JPEG-формат не подразумевает прозрачности, но в качестве альтернативного канала цветности используется яркость (luminance). На этом основан оптимизационный прием от Сергея Чикуёнка, который позволяет отбросить цветовую информацию для тех частей изображения, которые комбинируют черный и другой цвет в мелких текстурах. За счет уменьшения информации о смене цвета JPEG получается меньше по размеру, но на качестве изображения это не отражается (ведь все равно, какая нулевая яркость у цвета, если он черный).

Выигрыш от таких манипуляций с изображением может достигать еще 10-15%.

2. Оптимизация subsampling

Последнюю схему subsampling поддерживает большое количество оборудования и прикладных программ. В частности, ImageMagick (через опцию -sampling-factor) и GIMP. По результативности схема 4:2:0 позволяет выиграть 17% (это также подтверждается по результатам оптимизации сервиса Айри).

3. Оптимизация для решетки

Достаточно известный прием (автор метода — Сергей Чикуёнок), использующий особенность JPEG сжимать изображение квадратами 8×8 (из-за DCT-преобразования). Для оптимальной четкости изображения (и понижения его качества без видимого ущерба для картинки) нужно выровнять границы элементов изображения по решетке 8×8.

Выигрыш от такой техники обычно составляет 5-10%.

4. Оптимизация по маске

Эта техника дает выигрыш в 3-20% относительно исходного изображения.

5. Оптимизация таблиц Хаффмана

Но для полноты картины нужно упомянуть пакет mozjpeg, который реализует все наработки libjpeg-turbo и некоторые дополнительные улучшения по производительности. Каждая из описанных библиотек обратно совместима с jpegtran (и может использоваться как полноценная замена этой утилите).

Выигрыш от оптимизированных таблиц Хаффмана составляет 5-20% на изображение.

Описанные методики позволяют существенно (до 40%) сократить размер JPEG-изображения, даже если вы уже применили к нему другие, более простые, оптимизационные методы.

lenta.co

Huffman

Веретенников А. Б. 2008. http://cs.usu.edu.ru/home/abv/

Алгоритм Хаффмана основывается на том, что символы в текстах как правило встречаются с различной частотой.

При обычном кодировании мы каждый символ записываем в фиксированном количестве бит, например каждый символ в одном байте, или в двух.

Однако, т. к. некоторые символы встречаются чаще, а некоторые реже − можно записать часто встречающиеся символы в небольшом количестве бит, а для редко встречающихся символов использовать более длинные коды. Тогда суммарная длина закодированного текста может стать меньше.

Закодируем строку "Сжатие Хаффмана"

Вначале нужно подсчитать количество вхождений каждого символа в тексте.

С	ж	а	т	и	е		Х	ф	м	н
1	1	4	1	1	1	1	1	2	1	1

Эта таблица называется "таблица частот".

Теперь будем строить дерево

Узел дерева будет образован набором символов и числом - суммарным количеством вхождений данных символов в тексте. Назовем указанное число - весом узла.

Листьями дерева будут узлы, образованные одним символом:

Теперь будем циклически делать следующее:

1) Ищем среди узлов, не имеющих родителя, два узла, имеющих в сумме наименьший вес.

2) Создаем новый узел, его потомками будут два выбранных узла. Его весом будет сумма весов выбранных улов. Его набор символов будет образован в результате объединения наборов символов выбранных узлов.

Создаем первый узел

Создаем еще один узел

Теперь для каждого узла, имеющего потомков, пометим дуги, идущие вниз, на одной дуге напишем 0, на другой 1.

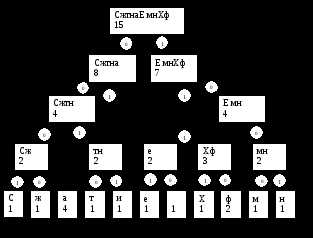
Теперь, чтобы получить код символа, надо, начиная с корня дерева идти вниз до листа соответствующего данному символу. При этом следует записывать те значения, которые написаны на тех дугах, которые мы проходим.

Получаются следующие коды

С	0001
ж	0000
а	01
т	0010
и	0011
е	1011
	1010
Х	111
ф	110
м	1000
н	1001

Заметим, что код является префиксным, т. е. ни один код символа не является префиксом кода другого символа. Также видно, что для часто встречающихся символов коды короче.

Как будет выглядеть закодированная строка:

С	ж	а	т	и	е		Х	а	ф	ф	м	а	н	а
0001	0000	01	0010	0011	1011	1010	111	01	110	110	1000	01	1001	01

Т. е.

0001000001001000111011101011101110110100001100101

Для декодирования можно воспользоваться построенным деревом. Начинаем с корня дерева и в качестве текущего бита берем начало текста.

В цикле делаем следующее

1) Смотрим, какое значение у текущего бита, и идем в низ по дереву по дуге, на которой указано такое же значение.

2) Переходим к следующему биту.

3) Если сейчас находимся в листе дерева: читаем символ находящийся в этом листе и записываем его в результат декодирования, переходим снова в корень дерева.

Примечание: при передаче закодированных данных требуется также передавать дерево или таблицу частот, чтобы можно было восстановить дерево.

В данном примере, дуги помечались случайным образом, учитывалось только то, что на дугах, идущих к потомку узла должны быть разные значения.

Чтобы передавать таблицу частот нужно всегда помечать левую дугу 1, а правую 0 (или наоборот), чтобы можно было восстановить дерево по таблице.

1) статический

2) динамический

3) адаптивный

Рассмотренный пример относится к динамическому алгоритму Хаффмана.

Статический алгоритм отличается от него тем, что таблица частот не вычисляется по тексту, а используется некоторая ранее вычисленная таблица. Соответственно, для динамического алгоритма требуется два прохода по тексту, первый для построения таблицы, второй − для кодирования. Для статического алгоритма требуется только один проход, т. к. таблица уже есть.

Естественно, при использовании статического алгоритма возникает риск того, что алгоритм будет не эффективен из-за несоответствия реальных частот и значений в таблице.

Тем не менее иногда статический алгоритм можно применять, например, известно, что в обычных текстах, например художественная литература, журналы, частоты символов как правило примерно одинаковые для различных текстов.

Адаптивный алгоритм мы не рассматриваем здесь. Вкратце можно сказать, что в этом алгоритме также используется один проход, но при этом дерево постоянно перестраивается, т. е. меняются коды символов.

Замечание: в литературе часто рассматривают только два алгоритма Хаффмана, например

1) статический и динамический.

2) динамический и адаптивный.

При этом, когда рассматривают только динамический и адаптивный алгоритмы, часто называют тот алгоритм, который мы здесь называем динамическим как "Статический", а тот, который мы занимаем адаптивным − "Динамическим". В результате возникает путаница в терминологии − в разной литературе авторы называют одинаково разные алгоритмы.

Вход программы: некоторый текст.

Результаты работы программы:

1) таблица частот.

2) код каждого символа.

3) закодированный текст (без кодирования таблицы частот).

4) декодированный текст (с использованием дерева).

Пример

Вход программы: Сжатие Хаффмана

Результат работы программы:

Таблица частот:

С=1

ж=1

а=4

т=1

и=1

е=1

Х=1

ф=2

м=1

н=1

Коды символов:

С=0001

ж=0000

а=01

т=0010

и=0011

е=1011

=1010

Х=111

ф=110

м=1000

н=1001

Закодированный текст:

0001000001001000111011101011101110110100001100101

Декодированный текст:

Сжатие Хаффмана

В следующем примере показано, как можно создавать дерево на языке Jscriptс помощью объектов.

В примере создается и выводится на экран следующее дерево.

Пример кода:

Node = new Object()

Node.Text = "AB"

Node.Count = 5

Left = new Object()

Left.Text = "A"

Left.Count = 2

Node.Left = Left

Right = new Object()

Right.Text = "B"

Right.Count = 3

Node.Right = Right

function WriteTree(Prefix, N)

{

if (N == undefined)

return

WScript.Echo(Prefix + "text: "+N.Text+", count: "+N.Count)

WriteTree(Prefix+" ",N.Left)

WriteTree(Prefix+" ",N.Right)

}

WriteTree(" ",Node)

Данный пример выводит на экран:

text: AB, count: 5

text: A, count: 2

text: B, count: 3

Еще один пример (делает то же самое):

function TreeNode(Text, Count)

{

this.Text = Text

this.Count = Count

}

TreeNode.prototype.WriteTree = function(Prefix)

{

if (Prefix == undefined)

Prefix = " "

WScript.Echo(Prefix + "text: "+

this.Text+", count: "+this.Count)

if (this.Left != undefined)

this.Left.WriteTree(Prefix+" ")

if (this.Right != undefined)

this.Right.WriteTree(Prefix+" ")

}

Node = new TreeNode("AB",5)

Node.Left = new TreeNode("A",2)

Node.Right = new TreeNode("B",3)

Node.WriteTree()

studfiles.net

5. Префиксный код Хаффмана

Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Схему построения кодов Хаффмана мы рассмотрим на том же примере, на котором рассматривали построение кодов Шеннона–Фано.

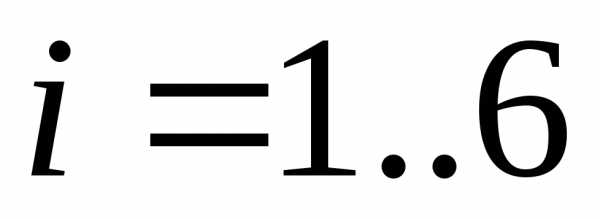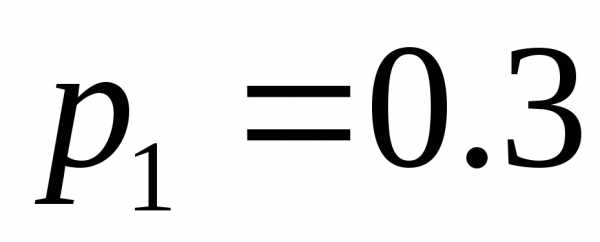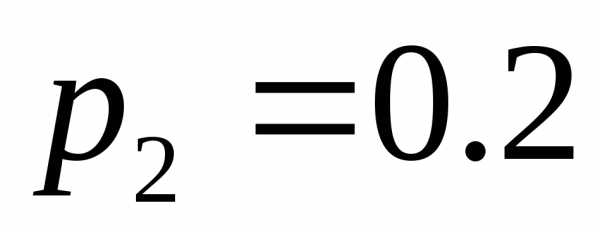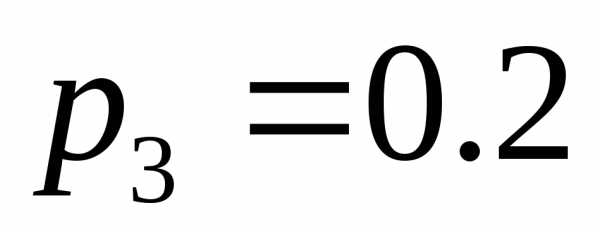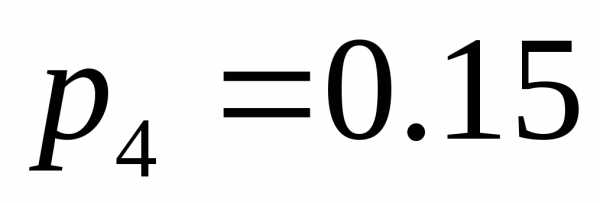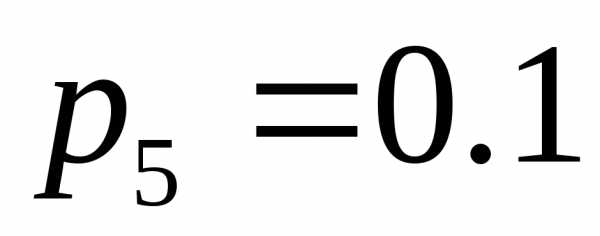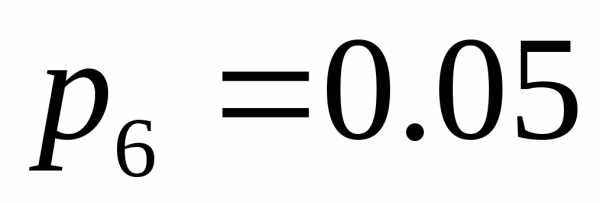Пусть имеется первичный алфавит , состоящий из шести знаков:, где. Пусть вероятности появления этих знаков в сообщениях таковы:,,,,и. Расположим эти знаки в таблице в порядке убывания вероятностей.

Создадим новый вспомогательный алфавит 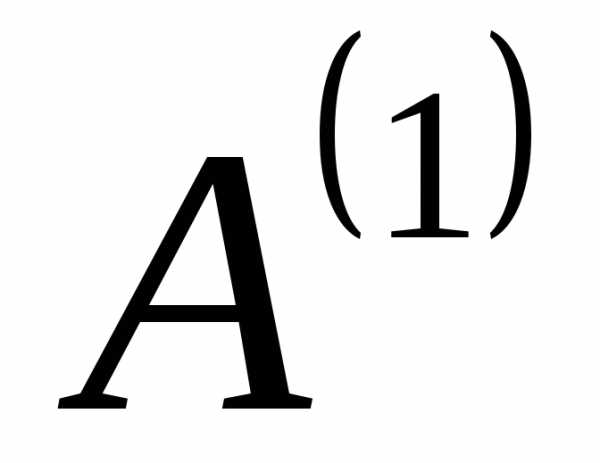, объединив два знака с наименьшими вероятностями и заменив их одним (новым) знаком. Вероятность этого нового знака будет равна сумме вероятностей тех исходных знаков, которые в него вошли. Остальные знаки исходного алфавита включим в новый вспомогательный алфавит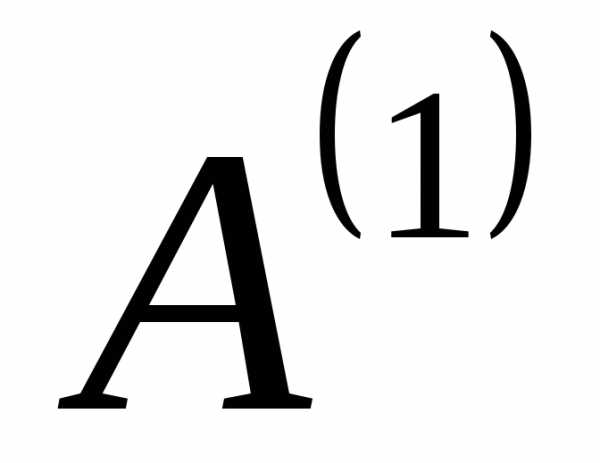без изменений. Расположим знаки полученного алфавита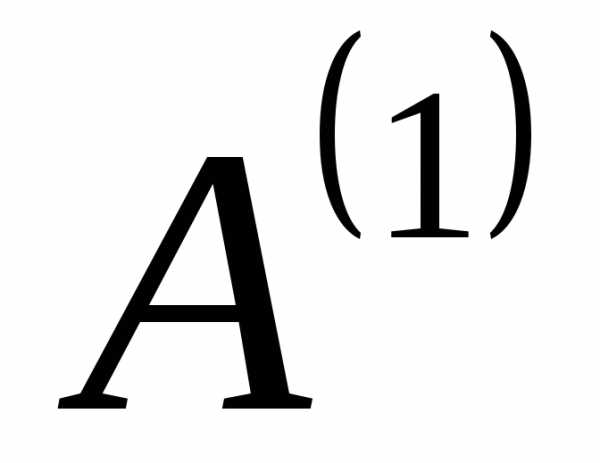для удобства в порядке убывания. В алфавите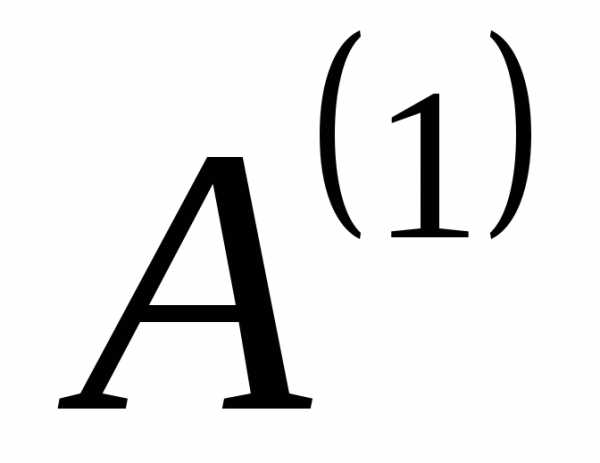на 1 знак меньше, чем в исходном алфавите.

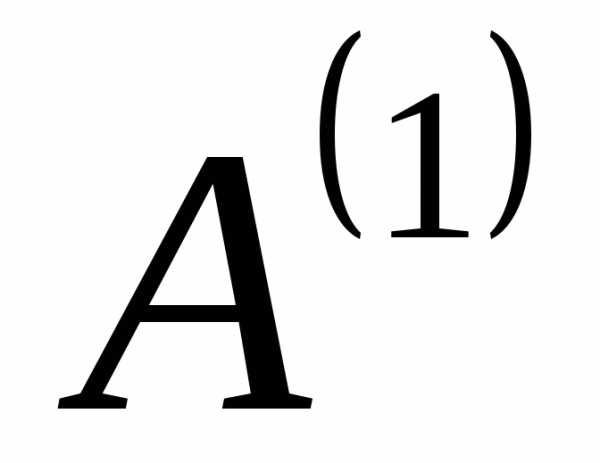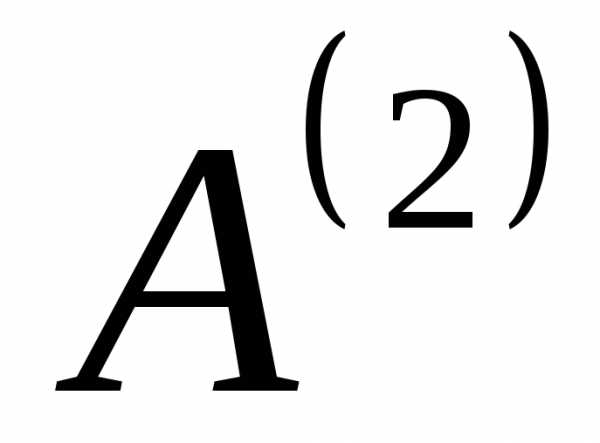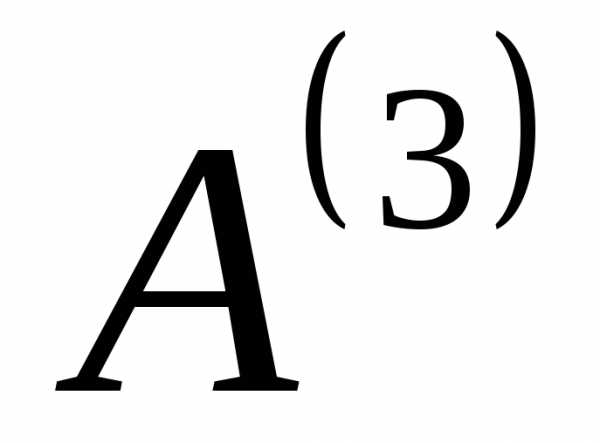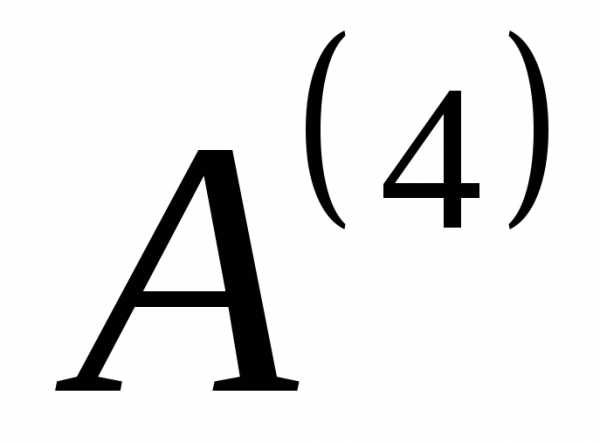Продолжим таким же образом создавать новые алфавиты до тех пор, пока в последнем полученном вспомогательном алфавите не останется два знака. В нашем случае получается 4 (четыре) вспомогательных алфавита: ,,и. Результат действий по созданию вспомогательных алфавитов можно представить в видетабл. 8:

Табл. 8. Вспомогательные алфавиты

, ,

, ,,

, ,

Для удобства можно было работать только с таблицей вероятностей, не обращая внимание на содержание алфавитов (табл. 9):

Табл. 9. Таблица вероятностей

Последовательность предпринятых действий по объединению и упорядочиванию знаков для формирования вспомогательных алфавитов можно показать стрелками (табл. 10).

Табл. 10. Последовательность действий при формировании вспомогательных алфавитов

Теперь эту таблицу продублируем, однако, для простоты (чтобы освободить место для письма) не будем переписывать вероятности, подразумевая, что они остаются на своих местах – в своих клетках. Вместо вероятностей будем писать коды. Приписывать очередной разряд будем справа, как и в случае кодов Шеннона–Фано.

Последовательность действий (в направлении, обратном направлению стрелок) выглядит следующим образом.

Символам алфавита присвоим сверху вниз 0 и 1, то есть символы 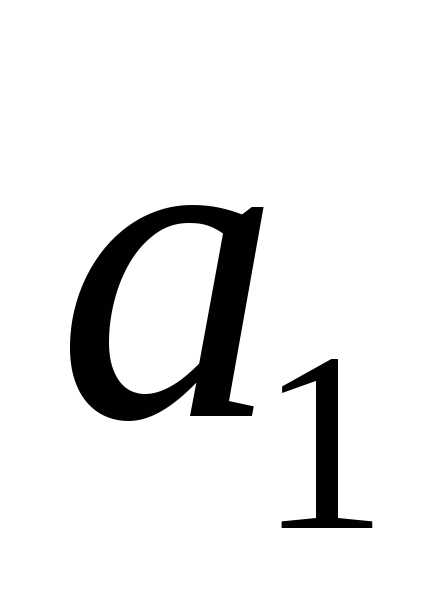и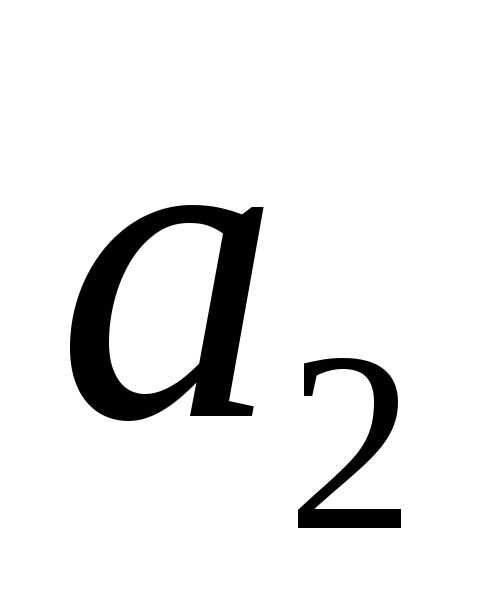из алфавита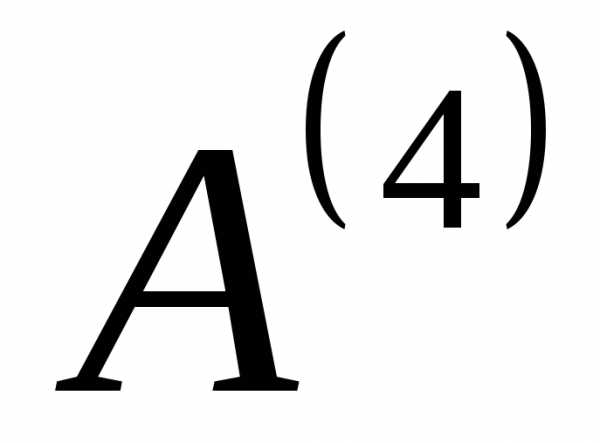получат коды «0» и «1» соответственно (табл. 11):

Табл 11. Построение кода Хаффмана

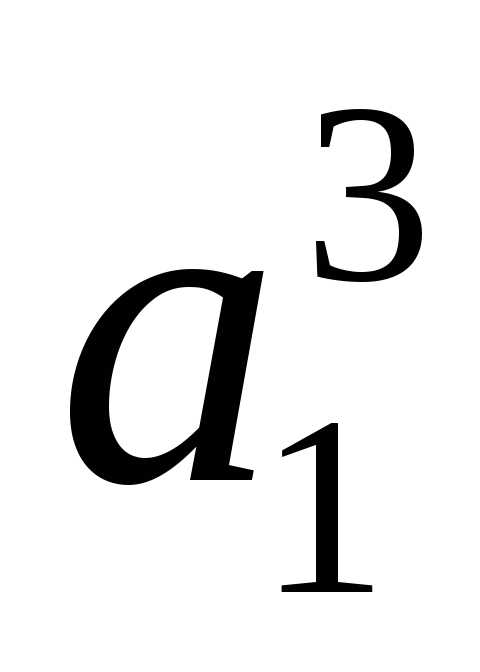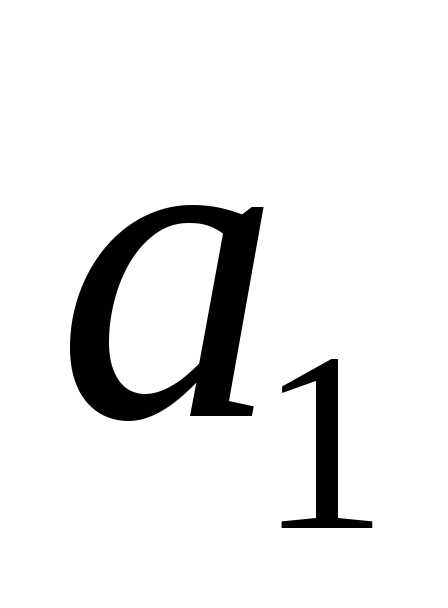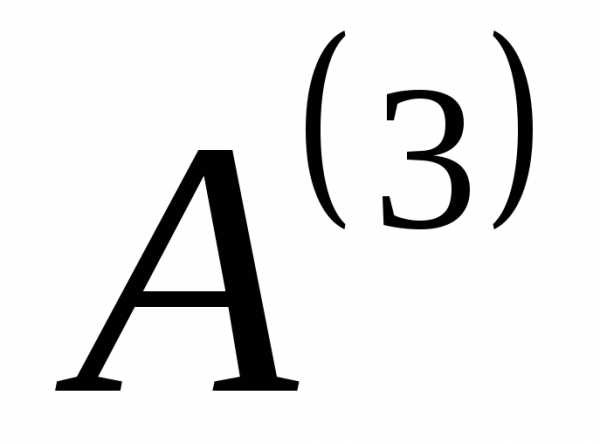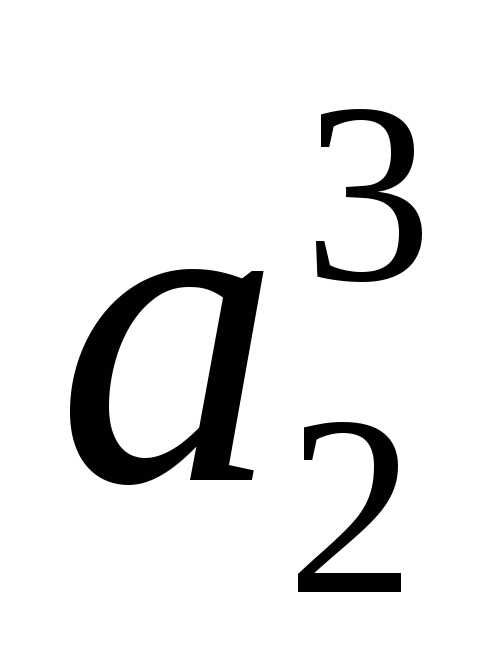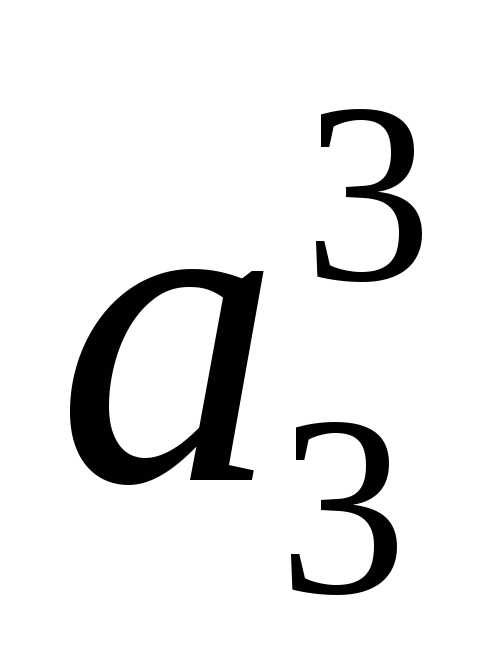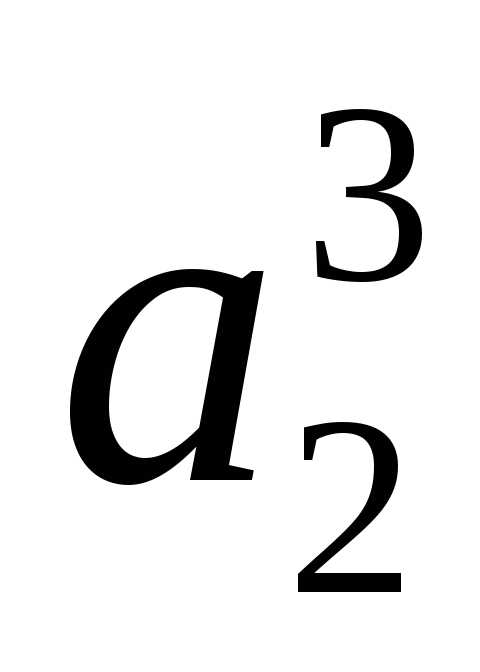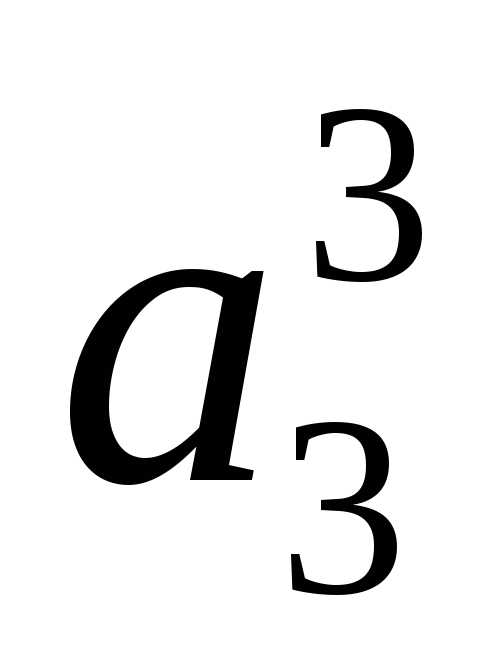Символ (то есть символиз алфавита) наследует по стрелке код «1». Коды дляистроим следующим образом. Первый слева разряд их кода наследуется по стрелке от– то есть «0». Вторые слева их разряды будут «0» и «1» сверху вниз дляисоответственно (табл. 12):

Табл 12. Построение кода Хаффмана (продолжение)

Аналогично строятся коды и далее (табл. 13).

Табл 13. Построение кода Хаффмана (продолжение)


00	00	00	1	0
10	10	01	00	1
11	11	10	01
010	010	11
0110	011
0111

Последовательность действий

Итак, полученные коды выглядят так (табл. 14):

Табл 14. Код Хаффмана

Знак		Код
Знак		Код
	0.30	00
	0.20	10
	0.20	11
	0.15	010
	0.10	0110
	0.05	0111

Полученные коды удовлетворяют условию Фано, то есть являются префиксными и, следовательно, не требуют разделителя.

Найдем среднюю длину полученного кода:

Таким образом, для кодирования одного символа первичного алфавитапотребовалось в среднем 2.45 символов вторичного (двоичного) алфавита, как и в случае кода Шеннона–Фано.

Избыточность полученного двоичного кода равна:

то есть избыточность также около 2.5.

Посмотрим, является ли этот код оптимальным. Нулей в полученных кодах – 8 штук, а единиц – 9 штук. Таким образом, вероятности появления 0 и 1 существенно сблизились (0.47 и 0.53 соответственно). Следовательно, полученный код оптимален.

Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона–Фано становится очевидной, если сравнить избыточности этих кодов для какого-либо естественного языка. При кодировании русского алфавита кодами Хаффмана средняя длина кода оказывается равной , при этом избыточность кода равна, то есть не превышает 1, что заметно меньше избыточности кода Шеннона–Фано.

Код Хаффмана важен в теоретическом отношении, поскольку в теории информации доказано, что он является самым экономичным из всех возможных, то есть ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.

Таким образом, можно заключить, что существует способ построения оптимального неравномерного алфавитного кода.

Код Хаффмана, кроме теоретического, имеет и практическое значение. Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) – широко применяются в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.

studfiles.net
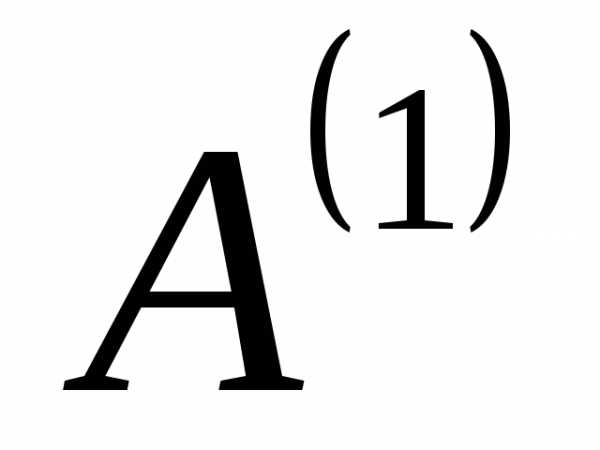
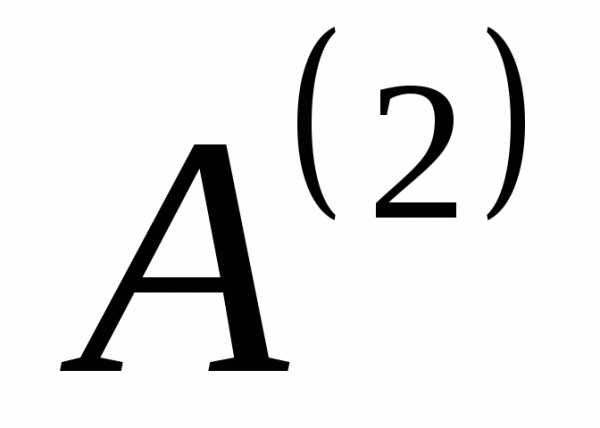
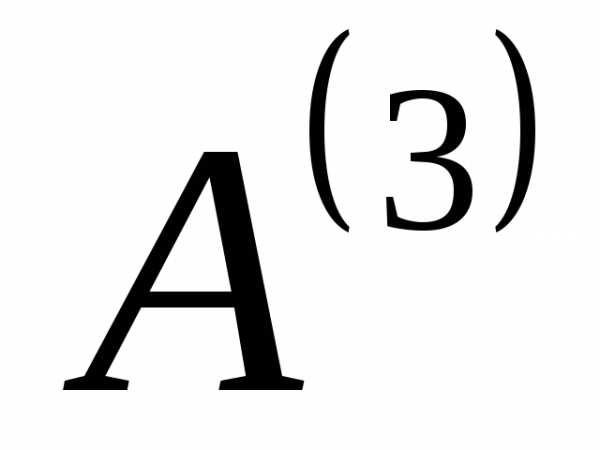
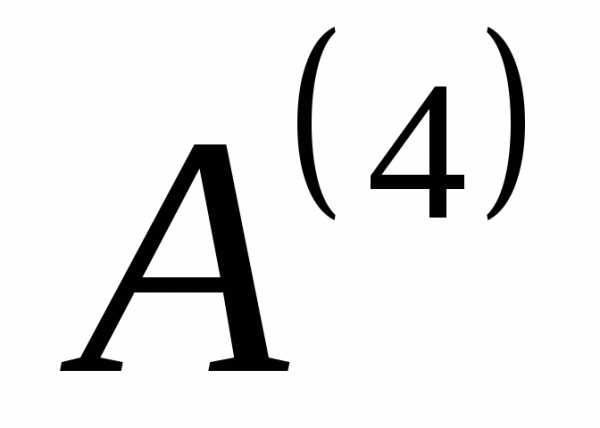
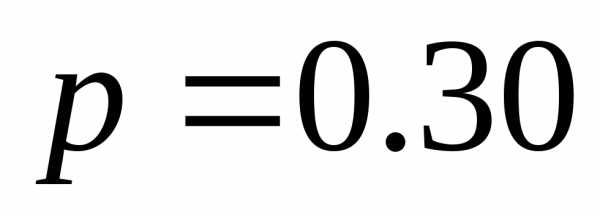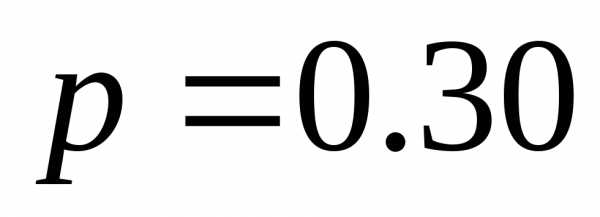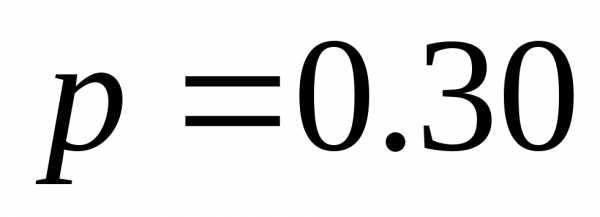
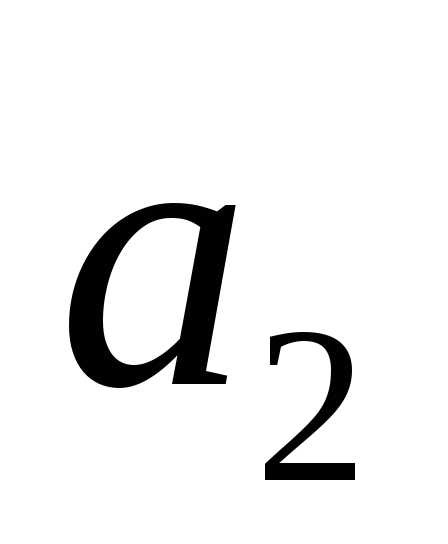
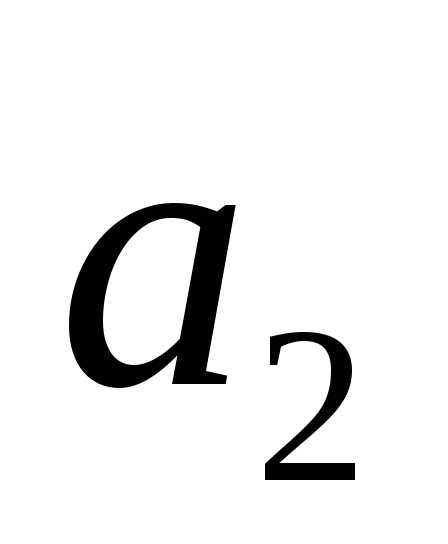
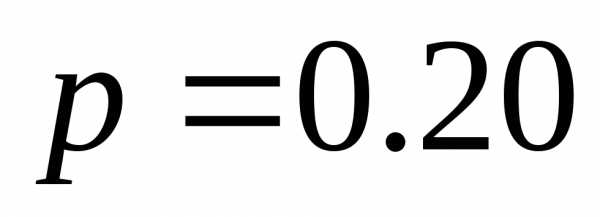
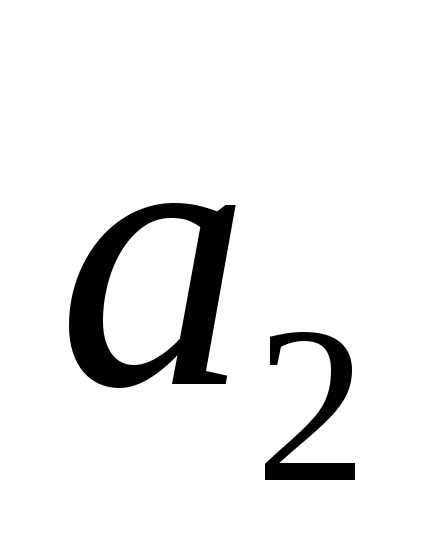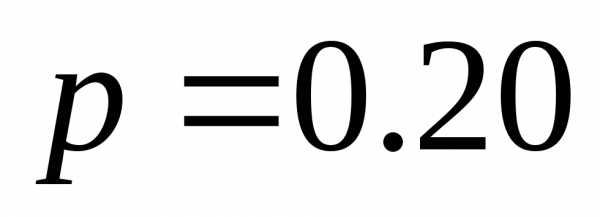
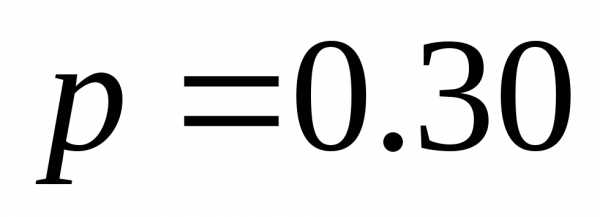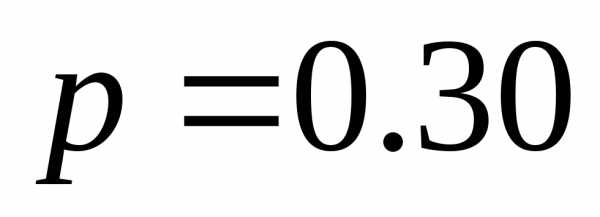
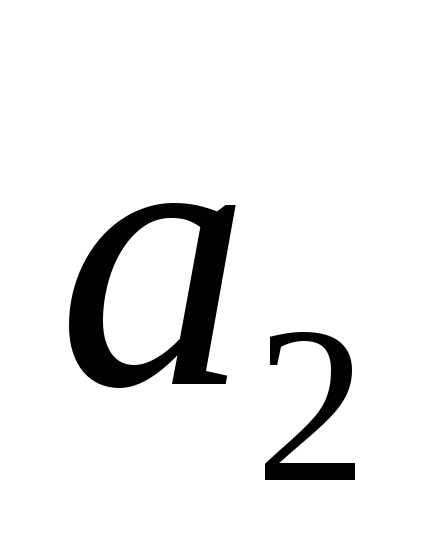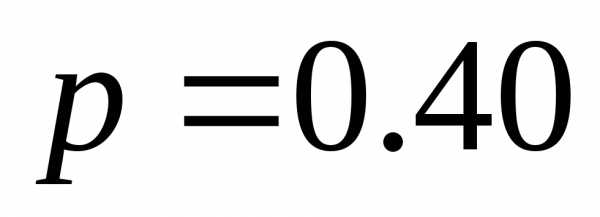
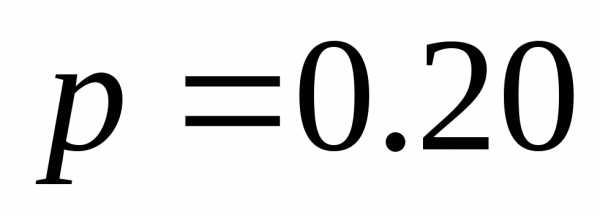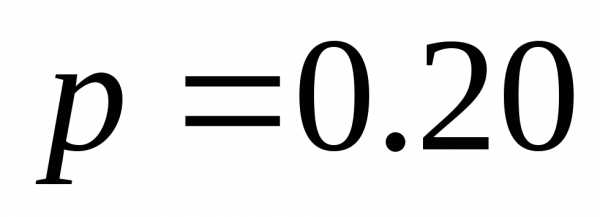
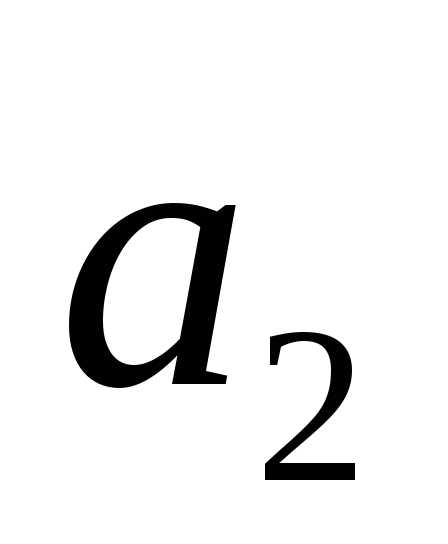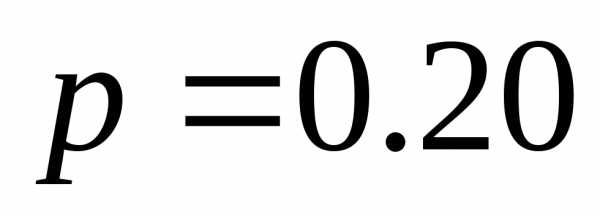
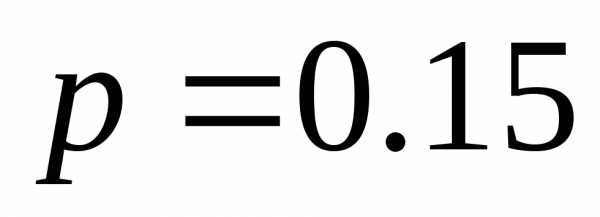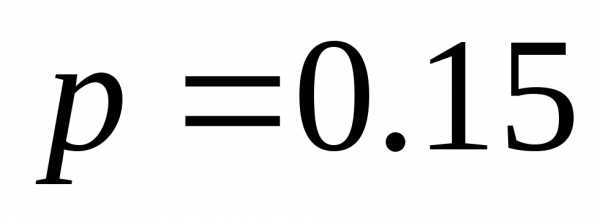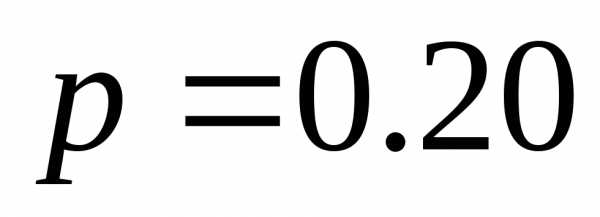
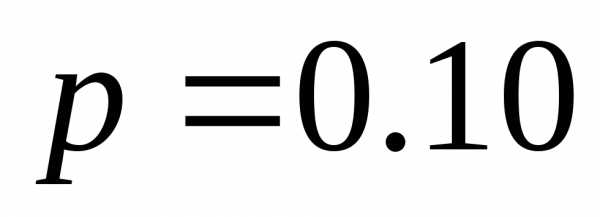