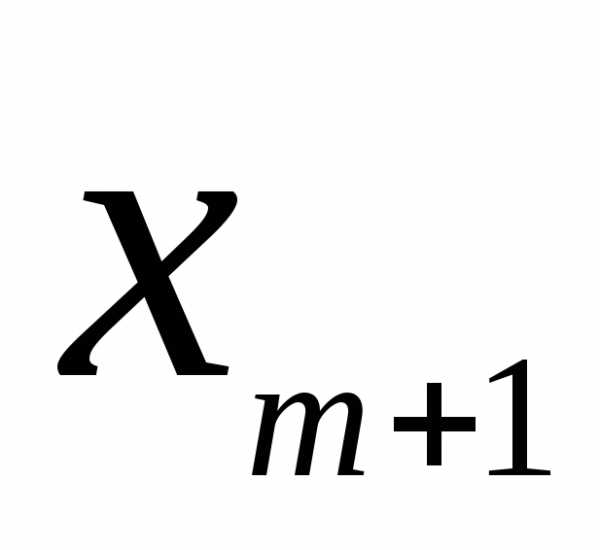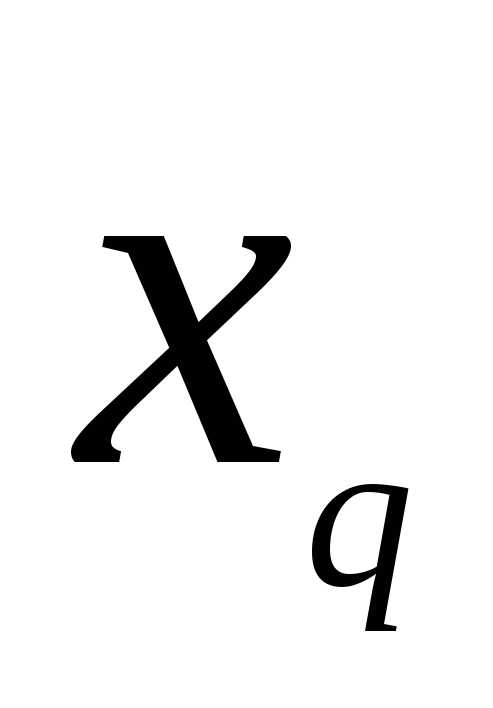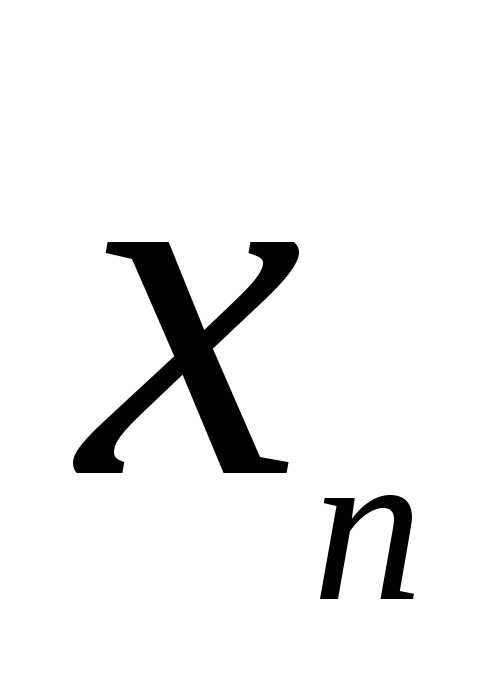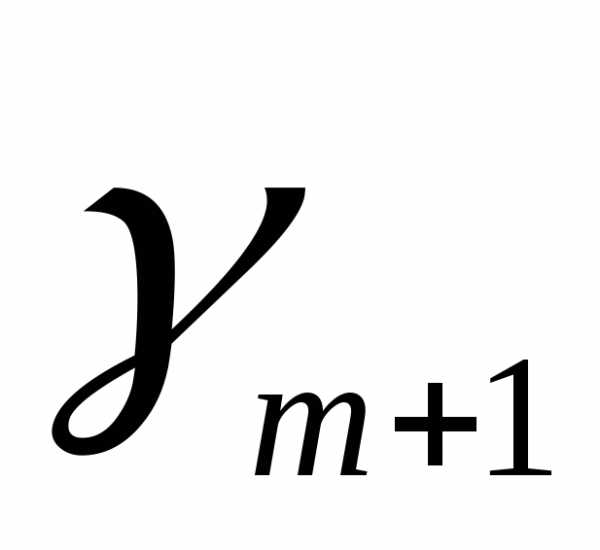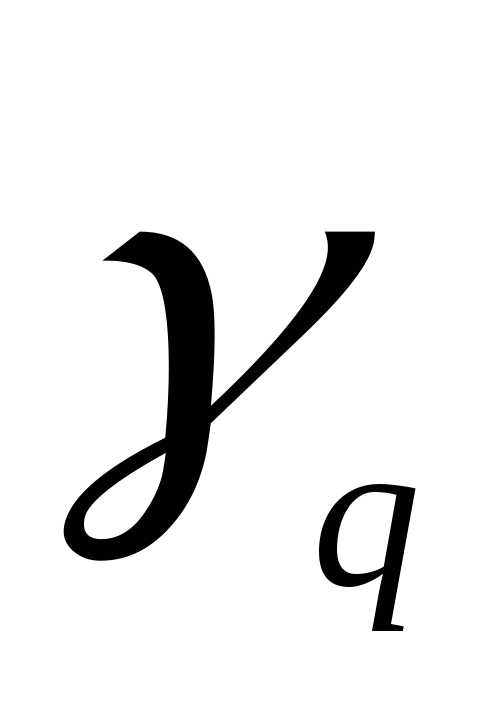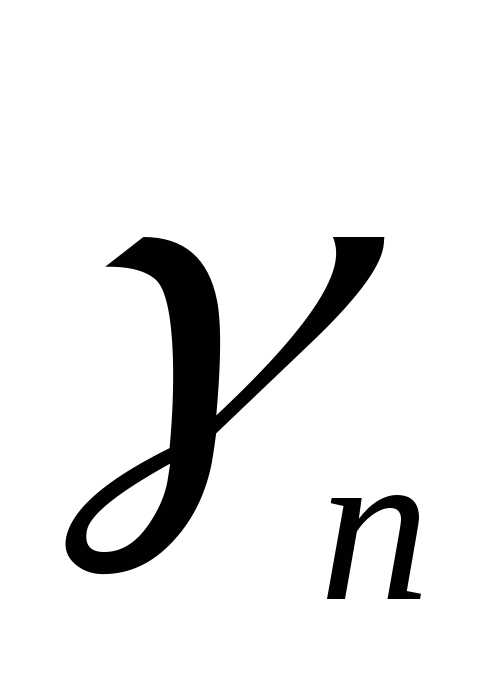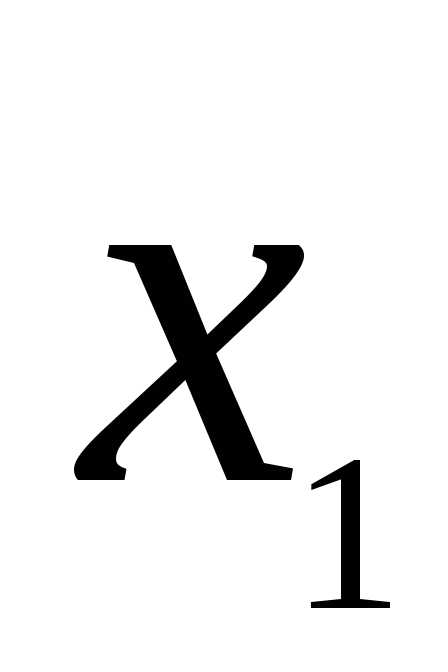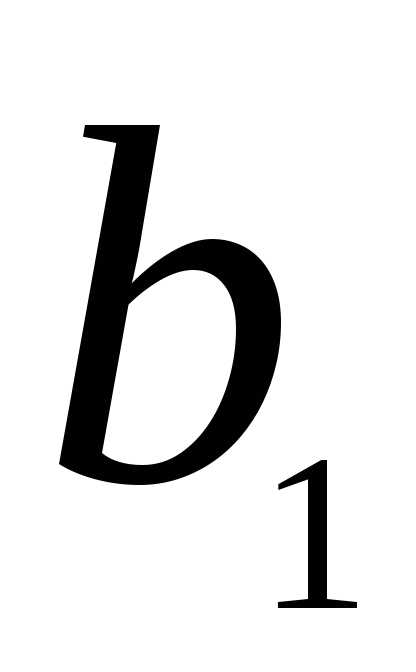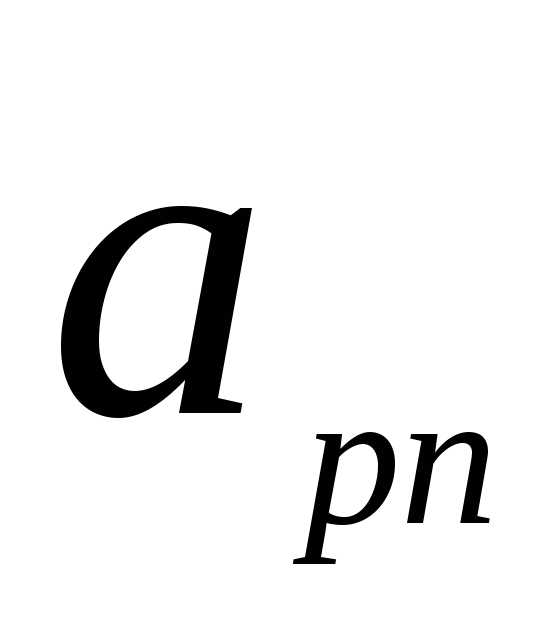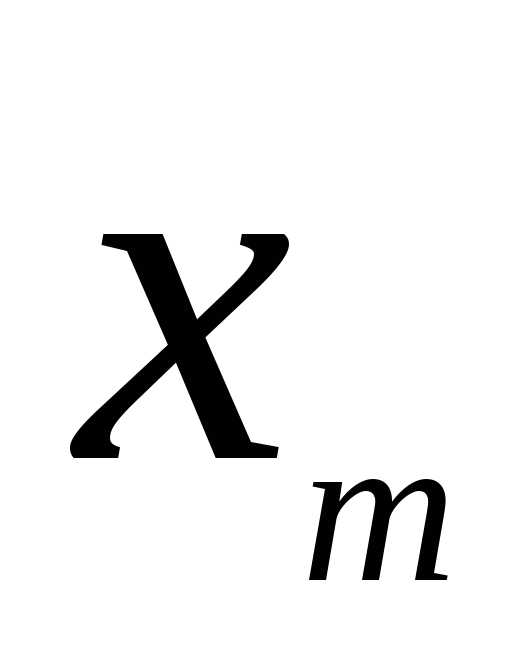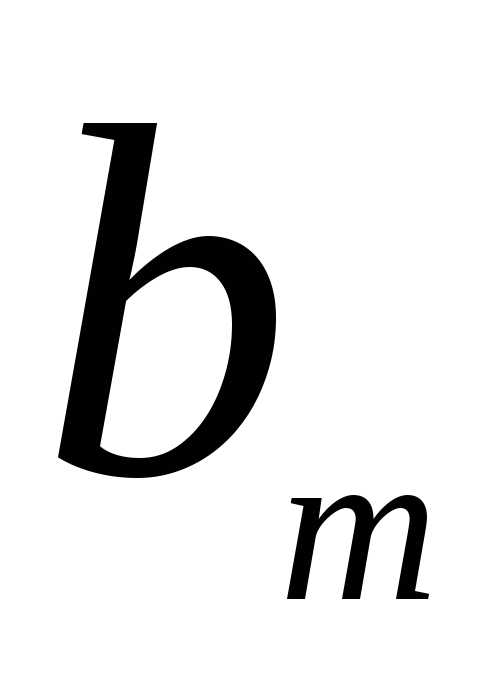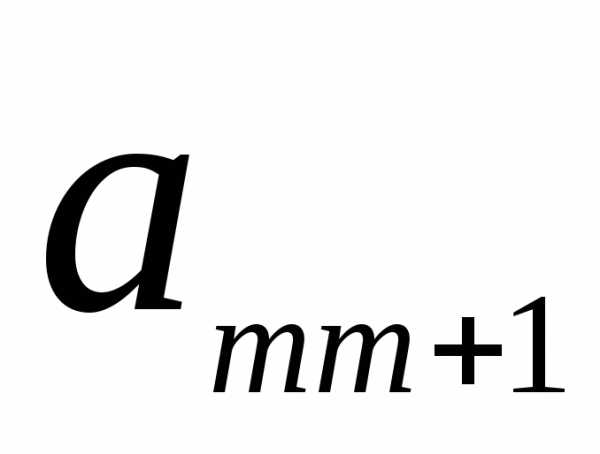Решение производственной задачи табличным симплекс-методом. Методы оптимизации симплекс метод примеры
Алгоритм и пример симплекс-метода (ММЭ). Пример решения симплекс-методом
Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.3
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности.
Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.
Таблица 5.4
Исходная симплекс-таблица
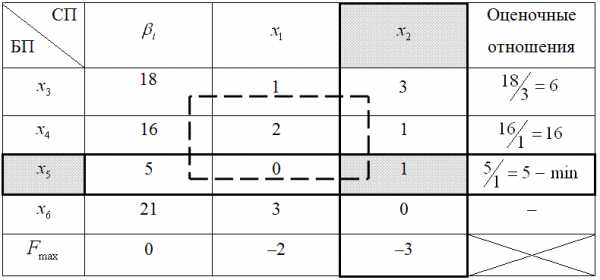
В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.
Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».
9 этап: преобразование симплекс-таблицы.
Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.
9.1. Преобразование разрешающего элемента.
Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:
Полученный результат вписываем в аналогичную клетку таблицы 5.5.
9.2. Преобразование разрешающей строки.
Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.
9.3. Преобразование разрешающей колонки.
Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.
9.4. Преобразование остальных элементов симплекс-таблицы.
Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».
К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5.4), а в числителе произведение двух других неиспользованных вершин, т.е.:
«х3»: .
Аналогично преобразуются значения других клеток:
«х3 х1»: ;
«х4»: ;
«х4 х1»: ;
«х6»: ;
«х6 х1»: ;
«»: ;
«х1»: .
В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).
II итерация:
1 этап: составление симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.5
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
–(3/1)=–3 | ||||
–(1/1)=–1 | ||||
5/1=5 | 0/1=0 | (1)–1=1 | ||
–(0/1)=0 | ||||
–(–3/1)=3 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):
.
Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.6
Симплекс-таблица II итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | 3/1=3 – min | |
11 | 2 | –1 | 11/2=5,5 | |
5 | 0 | 1 | – | |
21 | 3 | 0 | 21/3=7 | |
15 | –2 | 3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.
III итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.7
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3/1=3 | (1)–1=1 | –3/1=–3 | ||
–(2/1)=–2 | ||||
–(0/1)=0 | ||||
–(3/1)=–3 | ||||
–(–2/1)=2 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.
8 этап: определение разрешающего элемента.
8.1. Определение разрешающей колонки.
Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.
8.2. Определение разрешающей строки.
Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.
Таблица 5.8
Симплекс-таблица III итерации
СП БП | Оценочные отношения | |||
3 | 1 | –3 | – | |
5 | –2 | 5 | 5/5=1 – min | |
5 | 0 | 1 | 5/1=5 | |
12 | –3 | 9 | 12/9=1? | |
21 | 2 | –3 |
9 этап: преобразование симплекс-таблицы.
Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.
IV итерация
1 этап: построение новой симплекс-таблицы.
По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:
Таблица 5.9
Симплекс-таблица IV итерации
СП БП | Оценочные отношения | |||
–(–3/5)=3/5 | ||||
5/5=1 | –2/5 | (5)–1= | ||
–(1/5)=–1/5 | ||||
–(9/5)=–9/5 | ||||
–(–3/5)=3/5 |
2 этап: определение базисного решения.
В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:
.
3 этап: проверка совместности системы ограничений.
Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.
4 этап: проверка ограниченности целевой функции.
Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.
5 этап: проверка допустимости найденного базисного решения.
Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .
Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:
Решение:
I итерация:
1 этап: формирование исходной симплекс-таблицы.
Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:
Приведем целевую функцию к следующему виду:
На основе полученной задачи сформируем исходную симплекс-таблицу:
Таблица 5.10
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
18 | 1 | 3 | ||
16 | 2 | 1 | ||
5 | 0 | 1 | ||
21 | 3 | 0 | ||
0 | –2 | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
3 этап: проверка совместности системы ограничений ЗЛП.
На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).
4 этап: проверка ограниченности целевой функции.
На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).
5 этап: проверка допустимости найденного базисного решения.
Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.
6 этап: проверка оптимальности найденного базисного решения.
Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
7 этап: проверка альтернативности решения.
Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).
Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .
Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:
Решение:
I итерация
1 этап: составление исходной симплекс-таблицы.
Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.
Умножим (поэлементно) первую строку на –3 и сложим со второй:
.
Умножим вторую строку на :
.
Сложим вторую с первой строкой:
.
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:
.
Запишем целевую функцию в следующем виде:
.
Составим исходную симплекс-таблицу:
Таблица 5.11
Исходная симплекс-таблица
СП БП | Оценочные отношения | |||
–1 | 0 | |||
0 | 2 | |||
4 | – | –3 |
2 этап: определение базисного решения.
Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:
.
Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.
3 этап: проверка совместности системы ограничений ЗЛП.
Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.
Еще записи по теме
www.ikasteko.ru
Решение производственной задачи табличным симплекс-методом
Один из методов решения оптимизационных задач (как правило связанных с нахождением минимума или максимума) линейного программирования называется симплекс-методом. Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода.
Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи, которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.
Исходные данные задачи на симплекс-метод
Предприятие выпускает 4 вида изделий, обрабатывая их на 3-х станках.
Нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:
Фонд времени работы станков (мин.) задан в матрице B:
Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:
Цель производственной задачи
Составить такой план производства, при котором прибыль предприятия будет максимальной.
Решение задачи табличным симплекс-методом
(1) Обозначим X1, X2, X3, X4 планируемое количество изделий каждого вида. Тогда искомый план: (X1, X2, X3, X4)
(2) Запишем ограничения плана в виде системы уравнений:
(3) Тогда целевая прибыль:
То есть прибыль от выполнения производственного плана должна быть максимальной.
(4) Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7).
(5) Примем следующий опорный план:
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80
(6) Занесем данные в симплекс-таблицу:
!! В последнюю строку заносим коэффициенты при целевой функции и само ее значение с обратным знаком;
(7) Выбираем в последней строке наибольшее (по модулю) отрицательное число.
Вычислим b = Н / Элементы_выбранного_столбца
Среди вычисленных значений b выбираем наименьшее.
Пересечение выбранных столбца и строки даст нам разрешающий элемент. Меняем базис на переменную соответствующую разрешающему элементу (X5 на X1).
(8) Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b. Вот как это можно сделать:
- Сам разрешающий элемент обращается в 1.
- Для элементов разрешающей строки – aij(*) = aij / РЭ (то есть каждый элемент делим на значение разрешающего элемента и получаем новые данные).
- Для элементов разрешающего столбца – они просто обнуляются.
- Остальные элементы таблицы пересчитываем по правилу прямоугольника.
aij(*) = aij – ( A * B / РЭ )
Как видите, мы берем текущую пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A * B) делим на разрешающий элемент (РЭ). И вычитаем из текущей пересчитываемой ячейки (aij) то, что получилось. Получаем новое значение - aij(*).
(9) Вновь проверяем последнюю строку (c) на наличие отрицательных чисел. Если их нет – оптимальный план найден, переходим к последнему этапу решения задачи. Если есть – план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.
Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию вычислений.
(10) Так как в последней строке нет отрицательных элементов, это означает, что нами найден оптимальный план производства! А именно: выпускать мы будем те изделия, которые перешли в колонку «Базис» - X1 и X2. Прибыль от производства каждой единицы продукции нам известна (матрица C). Осталось перемножить найденные объемы выпуска изделий 1 и 2 с прибылью на 1 шт., получим итоговую (максимальную!) прибыль при данном плане производства.
ОТВЕТ:
X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт.
P = 48 * 32 + 33 * 20 = 2 196 руб.
Галяутдинов Р.Р.
© Копирование материала допустимо только при указании прямой гиперссылки на источник: Галяутдинов Р.Р.
galyautdinov.ru
Пример решения прямой и двойственной задачи симплекс методом
Условие задачи
Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b1 = 240, b2 = 200, b3 = 160 единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a11 = 2 единицы, ресурса второго вида в количестве a21 = 4 единицы, ресурса третьего вида в количестве a31 = 4 единицы. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a12 = 3, a13 = 6 единицы, ресурса второго вида в количестве a22 = 2, a23 = 4 единицы, ресурса третьего вида в количестве a32 = 6, a33 = 8 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно c1 = 4, c2 = 5, c3 = 4 (тыс. руб.). Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
К прямой задаче планирования товарооборота, решаемой симплекс методом, составить двойственную задачу линейного программирования. Установить сопряженные пары переменных прямой и двойственной задачи. Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.
Решение задачи симплекс методом
Пусть x1, x2, x3 - количество реализованных товаров, в тыс. руб., 1, 2, 3 - ей групп, соответственно. Тогда математическая модель задачи имеет вид:F = 4·x1 + 5·x2 + 4·x3 –>max
Решаем симплекс методом.
Вводим дополнительные переменные x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, чтобы неравенства преобразовать в равенства.
В качестве базиса возьмем x4 = 240; x5 = 200; x6 = 160.
Данные заносим в симплекс таблицу
Симплекс таблица № 1
Целевая функция:
0 · 240 + 0 · 200 + 0 · 160 = 0
Вычисляем оценки по формуле:
Δ1 = 0 · 2 + 0 · 4 + 0 · 4 – 4 = – 4Δ2 = 0 · 3 + 0 · 2 + 0 · 6 – 5 = – 5Δ3 = 0 · 6 + 0 · 4 + 0 · 8 – 4 = – 4Δ4 = 0 · 1 + 0 · 0 + 0 · 0 – 0 = 0Δ5 = 0 · 0 + 0 · 1 + 0 · 0 – 0 = 0Δ6 = 0 · 0 + 0 · 0 + 0 · 1 – 0 = 0
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ2 = – 5
Вводим переменную x2 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x2.
= 26.667
Наименьшее неотрицательное: Q3 = 26.667. Выводим переменную x6 из базиса
3-ю строку делим на 6.Из 1-й строки вычитаем 3-ю строку, умноженную на 3Из 2-й строки вычитаем 3-ю строку, умноженную на 2
Вычисляем:
Получаем новую таблицу:
Симплекс таблица № 2
Целевая функция:
0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 0 · 8/3 + 5 · 2/3 – 4 = – 2/3Δ2 = 0 · 0 + 0 · 0 + 5 · 1 – 5 = 0Δ3 = 0 · 2 + 0 · 4/3 + 5 · 4/3 – 4 = 8/3Δ4 = 0 · 1 + 0 · 0 + 5 · 0 – 0 = 0Δ5 = 0 · 0 + 0 · 1 + 5 · 0 – 0 = 0Δ6 = 0 · (–1)/2 + 0 · (–1)/3 + 5 · 1/6 – 0 = 5/6
Поскольку есть отрицательная оценка Δ1 = – 2/3, то план не оптимален.
Вводим переменную x1 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x1.
Наименьшее неотрицательное: Q3 = 40. Выводим переменную x2 из базиса
3-ю строку делим на 2/3.Из 2-й строки вычитаем 3-ю строку, умноженную на 8/3
Вычисляем:
Получаем новую таблицу:
Симплекс таблица № 3
Целевая функция:
0 · 160 + 0 · 40 + 4 · 40 = 160
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 0 · 0 + 4 · 1 – 4 = 0Δ2 = 0 · 0 + 0 · (–4) + 4 · 3/2 – 5 = 1Δ3 = 0 · 2 + 0 · (–4) + 4 · 2 – 4 = 4Δ4 = 0 · 1 + 0 · 0 + 4 · 0 – 0 = 0Δ5 = 0 · 0 + 0 · 1 + 4 · 0 – 0 = 0Δ6 = 0 · (–1)/2 + 0 · (–1) + 4 · 1/4 – 0 = 1
Поскольку отрицательных оценок нет, то план оптимален.
Решение задачи: x1 = 40; x2 = 0; x3 = 0; x4 = 160; x5 = 40; x6 = 0; Fmax = 160
Ответ
x1 = 40; x2 = 0; x3 = 0; x4 = 160; x5 = 40; x6 = 0; Fmax = 160То есть необходимо реализовать товар первого вида в объеме 40 тыс. руб. Товар 2-го и 3-го видов реализовывать не надо. При этом максимальная прибыль составит Fmax = 160 тыс. руб.
Решение двойственной задачи
Двойственная задача имеет вид:
Z = 240·y1 + 200·y2 + 160·y3 –>min
Вводим дополнительные переменные y4 ≥ 0, y5 ≥ 0, y6 ≥ 0, чтобы неравенства преобразовать в равенства.
Сопряженные пары переменных прямой и двойственной задач имеют вид:
| Основные | Дополнительные | ||||
| x1 | x2 | x3 | x4 | x5 | x6 |
| y4 | y5 | y6 | y1 | y2 | y3 |
| Дополнительные | Основные | ||||
Из последней симплекс таблицы № 3 прямой задачи, находим решение двойственной задачи:
Zmin = Fmax = 160;y1 = Δ4 = 0; y2 = Δ5 = 0; y3 = Δ6 = 1; y4 = Δ1 = 0; y5 = Δ2 = 1; y6 = Δ3 = 4;
Ответ
y1 = 0; y2 = 0; y3 = 1; Zmin = 160;Автор: Олег Одинцов. Опубликовано: 08-12-2011
1cov-edu.ru
Симплекс-метод, примеры решения задач
Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. Первая задача содержит знаки неравенства только " ≤ " (задача с начальным базисом), вторая может содержить знаки " ≥ ", " ≤ " или " = " (задача с искусственным базисом), они решаются по разному.
Симплекс-метод, решение задачи с начальным базисом
1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений " ≤ ").
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является системой с базисом (базис s1, s2, s3, каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 - свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: -система ограничений должна быть системой уравнений с базисом; -свободные члены всех уравнений в системе должны быть неотрицательны.
Полученная система - система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь "БП" означает столбец базисных переменных, «Решение» - столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.
симплекс-метод итерация 0
| БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
| z | -4 | -6 | 0 | 0 | 0 | 0 | - |
| s1 | 2 | 1 | 1 | 0 | 0 | 64 | 64/1=64 |
| s2 | 1 | 3 | 0 | 1 | 0 | 72 | 72/3=24 |
| s3 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Для улучшения решения перейдем к следующей итерации симплекс-метода, получим следующую симплекс-таблицу. Для этого надо выбрать разрешающий столбец, т.е. переменную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x2 (коэффициент -6).
Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца "Решение" к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 20).
Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следовательно, на следующей итерации симплекс-метода переменная x2 заменит в базисе s1. Заметим, что в z-строке отношение не ищется, там ставится прочерк " - ". В случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.
Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований - превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).
1)Вычисление строки х2 таблицы "Итерация 1". Сначала делим все члены разрешающей строки s3 таблицы "Итерация 0" на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x2 в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s3 таблицы "Итерация 0" будет совпадать со строкой х2 таблицы "Итерация 1". Строку x2 таблицы "Итерации 1" мы получили 0 1 0 0 1 20, остальные строки таблицы "Итерация 1" будут получены из этой строки и строк таблицы "Итерация 0" следующим образом:
2) Вычисление z-строки таблицы "Итерация 1". На месте -6 в первой строке (z-строке) в столбце х2 таблицы "Итерация 0" должен быть 0 в первой строке таблицы "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на 6, получим 0 6 0 0 6 120 и сложим эту строку с первой строкой (z - строкой) таблицы "Итерация 0" -4 -6 0 0 0 0, получим -4 0 0 0 6 120. В столбце x2 появился ноль 0, цель достигнута. Элементы разрешающего столбца х2 выделены красным цветом.
3) Вычисление строки s1 таблицы "Итерация 1". На месте 1 в s1 строке таблицы "Итерация 0" должен быть 0 в таблице "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 - строкой таблицы "Итерация 0" 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.
4) Вычисление строки s2 таблицы "Итерация 1". На месте 3 в s2 строке таблицы "Итерация 0" должен быть 0 в таблице "Итерация 1". Для этого все элементы строки х2 таблицы "Итерация 1" 0 1 0 0 1 20 умножим на -3, получим 0 -3 0 0 -3 -60 и сложим эту строку с s1 - строкой таблицы "Итерация 0" 1 3 0 1 0 72, получим строку 1 0 0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице "Итерация 1" стал единичным, он содержит одну 1 и остальные 0.
Строки таблицы «Итерация 1» получаем по следующему правилу:
Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).
Например для z-строки имеем:
Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).
Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.
симплекс-метод итерация 1
| БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
| z | -4 | 0 | 0 | 0 | 6 | 120 | - |
| s1 | 2 | 0 | 1 | 0 | -1 | 44 | 44/2=22 |
| s2 | 1 | 0 | 0 | 1 | -3 | 12 | 12/1=12 |
| x2 | 0 | 1 | 0 | 0 | 1 | 20 | - |
Разрешающий столбец х1, разрешающая строка s2, s2 выходит из базиса, х1 входит в базис. Совершенно аналогично получим остальные симплекс-таблицы, пока не будет получена таблица со всеми положительными коэффициентами в z-строке. Это признак оптимальной таблицы.
симплекс-метод итерация 2
| БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
| z | 0 | 0 | 0 | 4 | -6 | 168 | - |
| s1 | 0 | 0 | 1 | -2 | 5 | 20 | 20/5=4 |
| x1 | 1 | 0 | 0 | 1 | -3 | 12 | - |
| x2 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Разрешающий столбец s3, разрешающая строка s1, s1 выходит из базиса, s3 входит в базис.
симплекс-метод итерация 3
| БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
| z | 0 | 0 | 6/5 | 8/5 | 0 | 192 | - |
| s3 | 0 | 0 | 1/5 | -2/5 | 1 | 4 | - |
| x1 | 1 | 0 | 3/5 | -1/5 | 0 | 24 | - |
| x2 | 0 | 1 | -1/5 | 2/5 | 0 | 16 | - |
В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1 = 24, x2 = 16, zmax = 192.
studfiles.net
2.2. Алгоритм симплекс-метода для задачи на минимум
Шаг 0. Подготовительный этап.
Приводим задачу ЛП к специальной форме (15).
Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме:
| B |
| … |
| … |
| |
| L |
|
| … |
| … |
|
|
|
|
| … |
| … |
|
| .. | .. | ………… | ||||
|
|
|
| … |
| … |
|
| .. | .. | ………… | ||||
|
|
|
| … |
| … |
|
Заметим, что этой таблице соответствует допустимое базисное решение задачи (15). Значение целевой функции на этом решении
Шаг 2. Проверка на оптимальность
Если среди элементов индексной строки симплекс – таблицы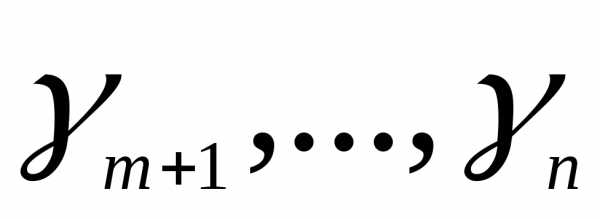 
нет ни одного положительного элемента то, оптимальное решение задачи ЛП найдено:. Алгоритм завершает работу.
Шаг 3. Проверка на неразрешимость
Если среди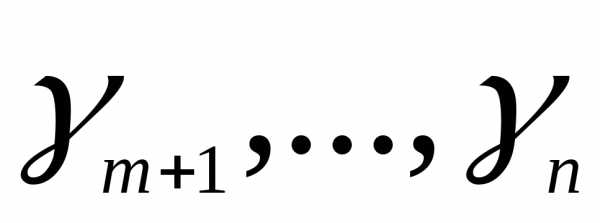 
есть положительный элемент
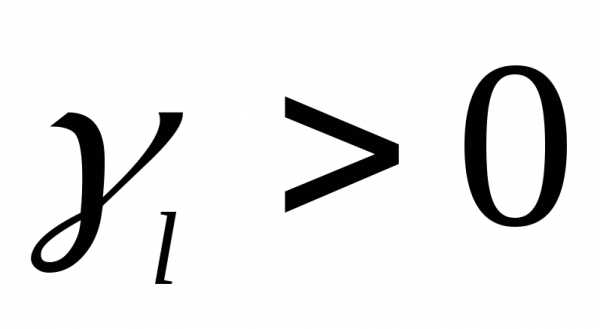, а в соответствующем столбценет ни одного положительного элемента, то целевая функцияL является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует. Алгоритм завершает работу.
Шаг 4. Выбор ведущего столбца q
Среди элементов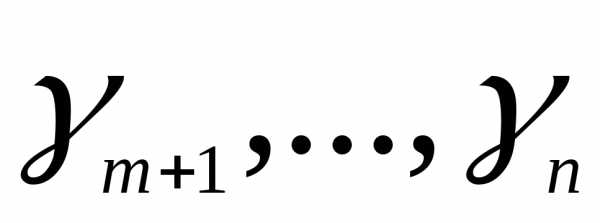 
выбираем максимальный положительный элемент
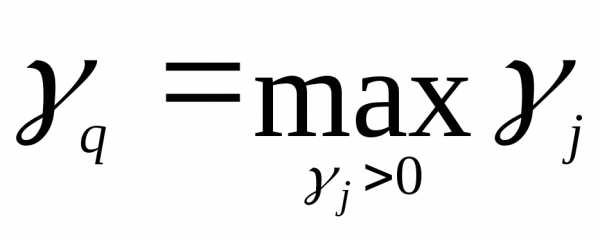.Этот столбец объявляем ведущим (разрешающим).
Шаг 5. Выбор ведущей строки p
Среди положительных элементов столбца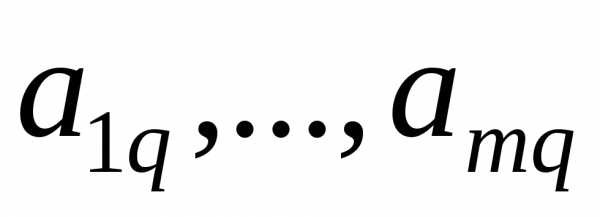 
находим элемент
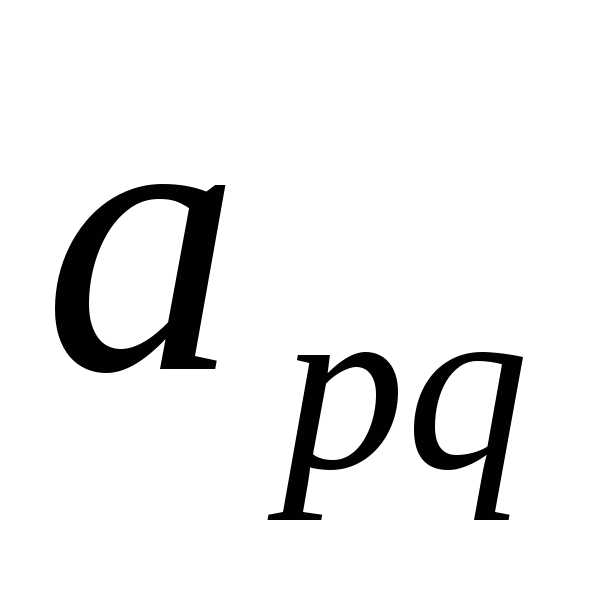, для которого выполняется равенство
.
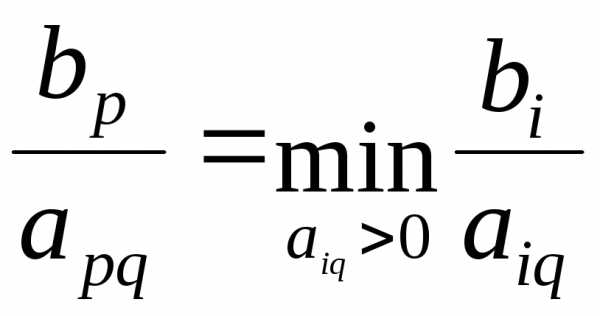Строку p объявляем ведущей (разрешающей). Элемент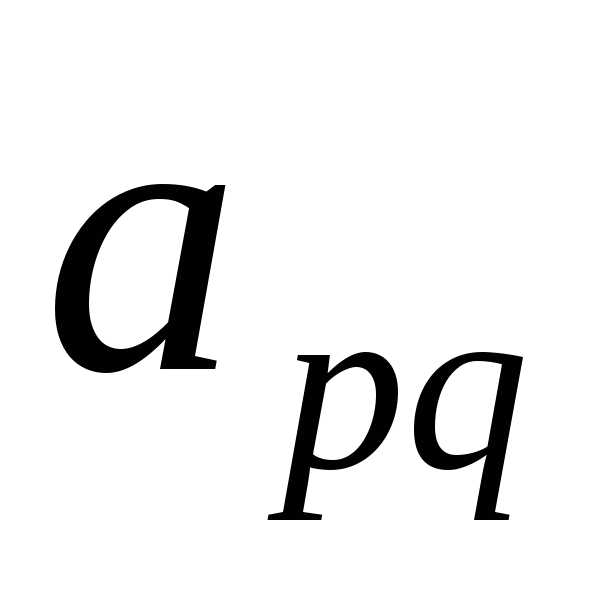 
объявляем ведущим (разрешающим).
Шаг 6. Преобразование симплексной таблицы
Составляем новую симплекс-таблицу, в которой:
а) вместо базисной переменной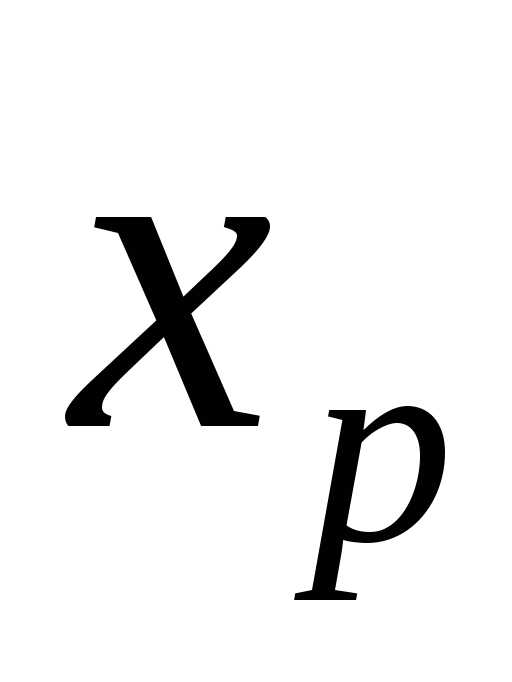 
записываем
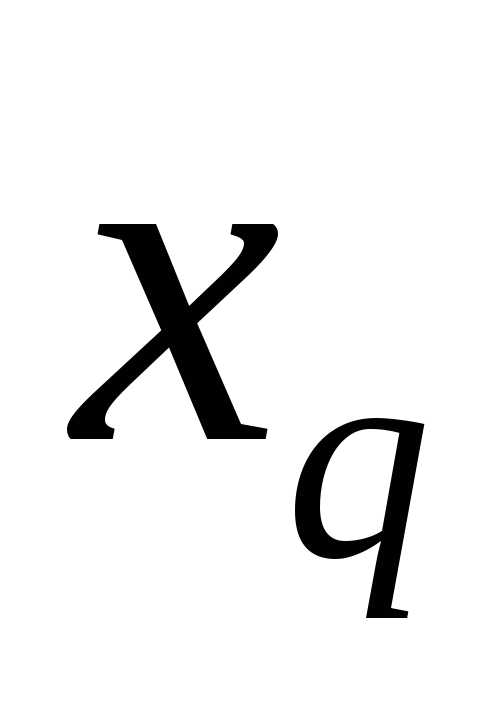, вместо небазисной пере менной
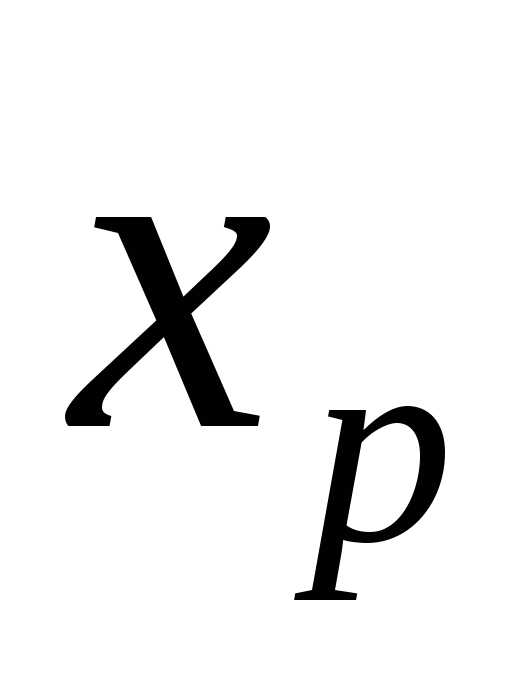записываем
;
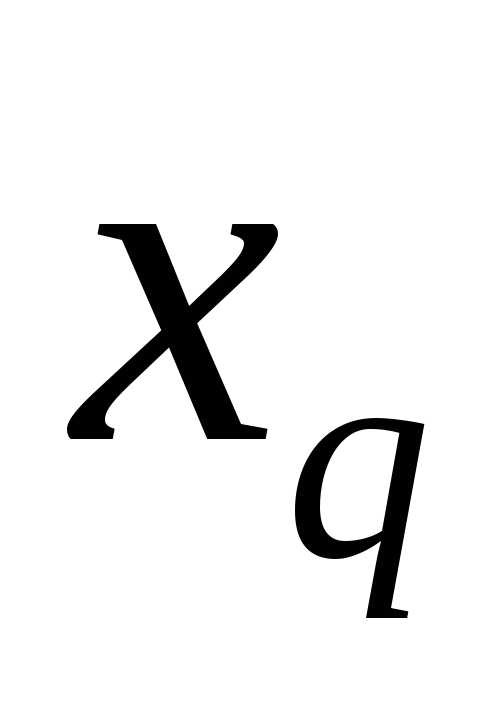б) ведущий элемент заменяем обратной величиной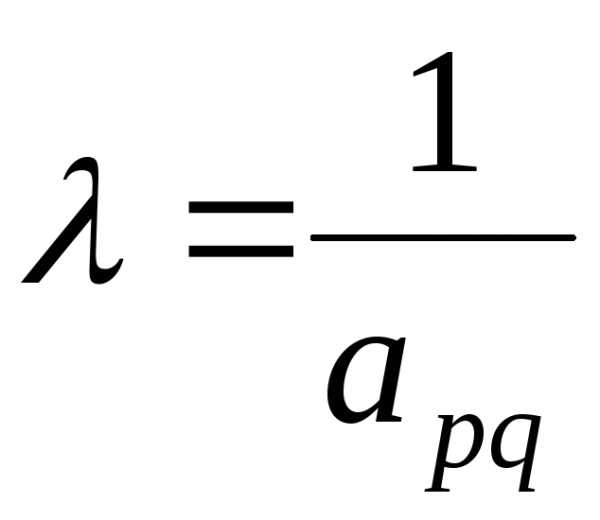 
;
в) все элементы ведущего столбца (кроме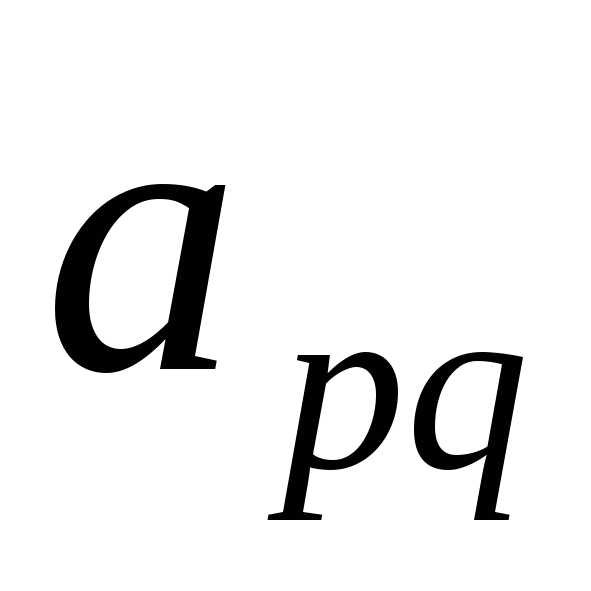 
) умножаем на 
;
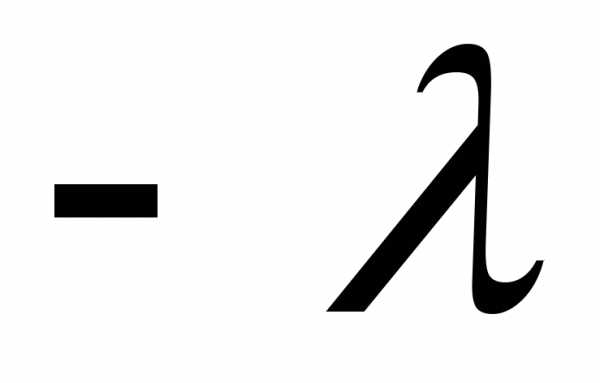г) все элементы ведущей строки (кроме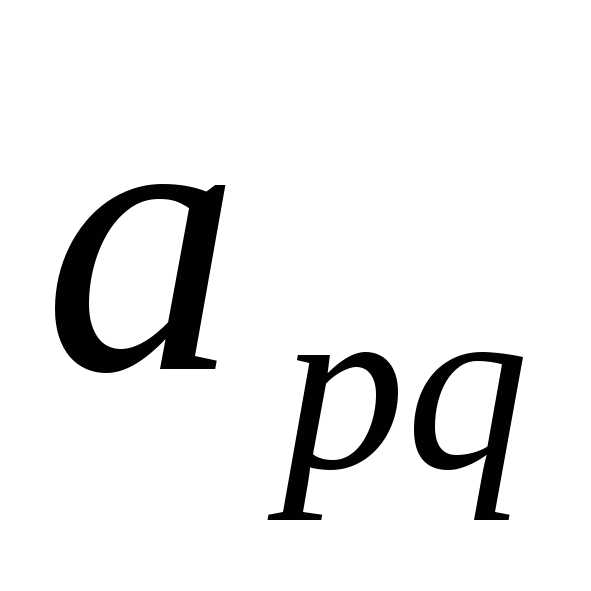 
) умножаем на
;
д) оставшиеся элементы симплексной таблицы преобразуются по следующей схеме «прямоугольника».
Из элемента вычитается произведение трех сомножителей:
первый – соответствующий элемент ведущего столбца;
второй – соответствующий элемент ведущей строки;
третий – обратная величина ведущего элемента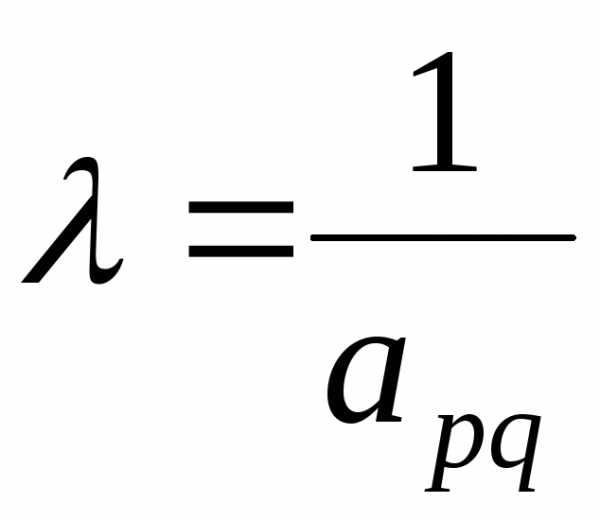 
.
Преобразуемый элемент и соответствующие ему три сомножителя как раз и являются вершинами «прямоугольника».
Шаг 7. Переход к следующей итерации осуществляется возвратом к шагу 2.
2.3. Алгоритм симплекс-метода для задачи на максимум
Алгоритм симплекс-метода для задачи на максимум отличается от алгоритма для задачи на минимум только знаками индексной строки коэффициентов в целевой функции , а именно:
На шаге 2: :
На шаге 3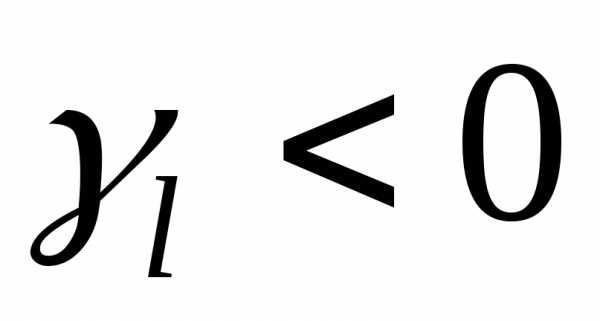 
. Целевая функция является неограниченной сверху на допустимом множестве.
На шаге 4: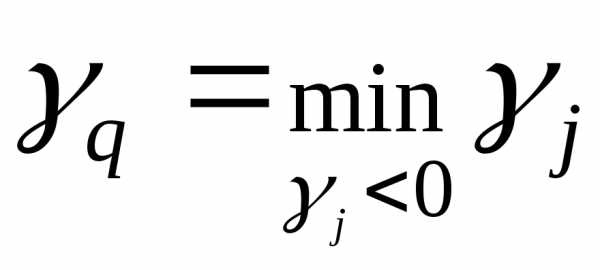 
.
2.4. Пример решения задачи симплекс-методом
Решить задачу, записанную в виде (15).
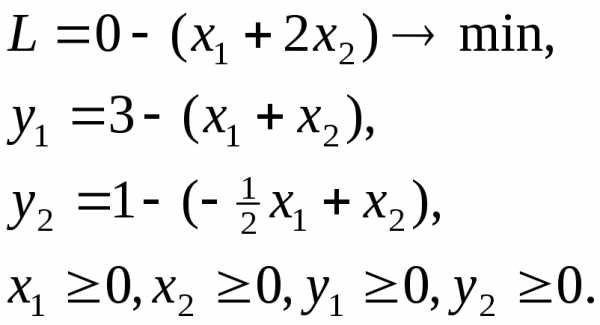
Составим симплексную таблицу:
Так как коэффициенты строки целевой функции неотрицательны, то начальное базисное решение не является оптимальным. Значение целевой функции для этого базисаL=0.
Выбираем ведущий столбец – это столбец, соответствующий переменной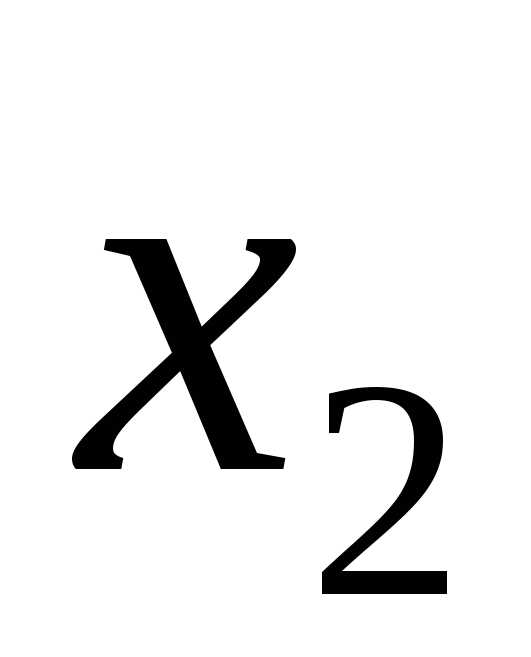 
.
Выбираем ведущую строку. Для этого находим . Следовательно, ведущая строка соответствует переменной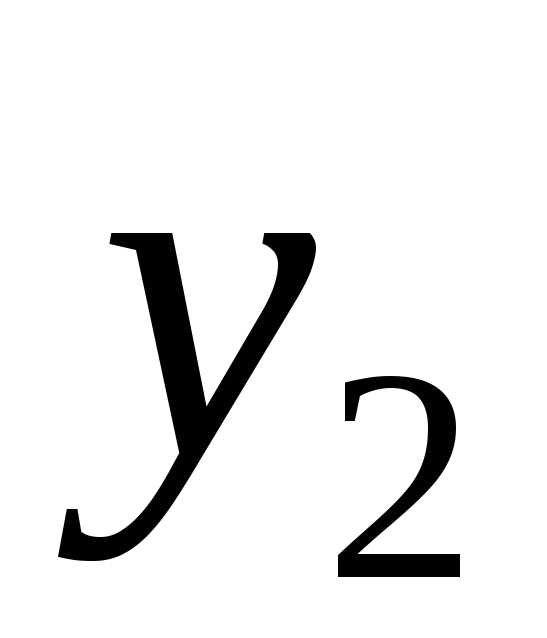
.
Проводим преобразование симплексной таблицы, вводя переменную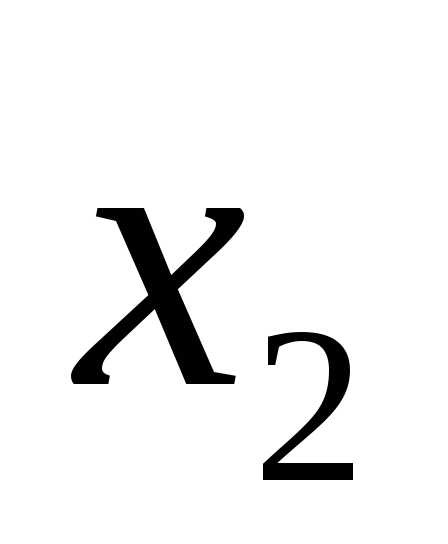 
в базис и выводя переменную
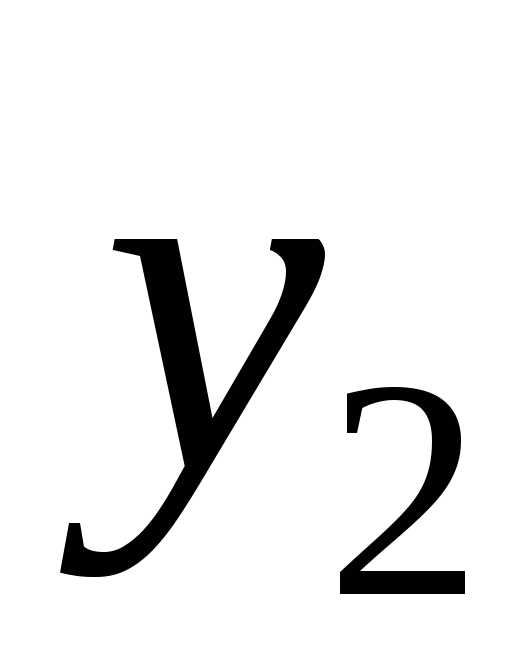из базиса. Получим таблицу:
Одна итерация метода завершена. Переходим к новой итерации. Полученная таблица неоптимальная. Базисное решение, соответствующее таблице, имеет вид . Значение целевой функции на этом базисеL= -2.
Ведущий столбец здесь – столбец, соответствующий переменной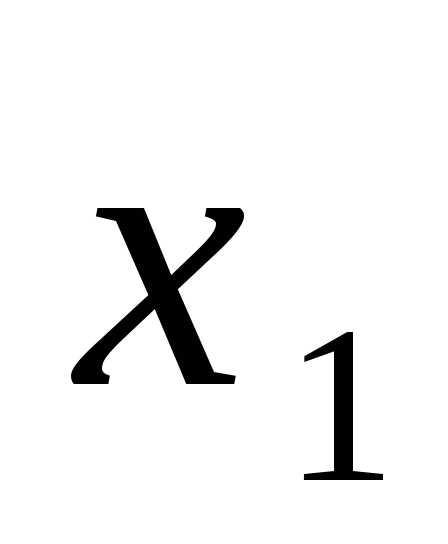 
. Ведущая строка – строка, соответствующая переменной
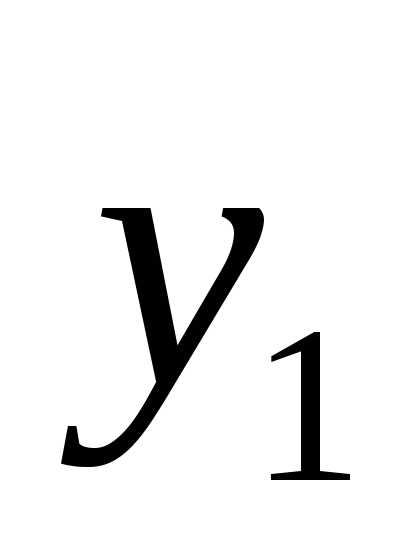. После проведения преобразований получим симплексную таблицу:
Еще одна итерация завершена. Переходим к новой итерации.
Строка целевой функции не содержит положительных значений, значит, соответствующее базисное решение является оптимальным, и алгоритм завершает работу.
studfiles.net
Симплекс метод онлайн
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку "Вычислить". Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
| Количество ограничений: m= | 1234567891011121314151617181920 |
| Количество переменных : n= | 1234567891011121314151617181920 |
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные , а свободные переменные :
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4 под переменными нет отрицательных элементов.
Решение можно записать так: .
Значение целевой функции в данной точке: F(X)=.
Пример 2. Найти максимум функции
при условиях
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1:
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . Все следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
при условиях
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы следовательно, все элементы в столбцах ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор Сделаем исключение Гаусса для столбца учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными нет отрицательных элементов.
Решение исходной задачи можно записать так:
| . |
Значение целевой функции в данной точке:
| . |
Пример 2. Найти оптимальный план задачи линейного программирования:
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
matworld.ru
Математическое программирование. Графический и симплекс метод. Примеры решения задач
Графический и симплекс метод
Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течении 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа.
Для производства единицы изделия В оборудование первого типа используется в течении 2 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час.На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 32 часа, оборудование второго типа – 60 часов, оборудование третьего типа – 50 часов.
Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.1) Составить математическую модель задачи
2) Решить графическим методом
3)Решить симплекс-методом путем преобразования симплекс-таблиц
Решение
Перед нами – классическая задача линейного программирования. Под планом производства понимается ответ на простой вопрос: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна.Прибыль рассчитывается по формуле: .
Запишем математическую модель задачи:
Чтобы проиллюстрировать применение симплекс-метода решения этой задачи, решим ее графически.Для этого построим на плоскости области, описываемые ограничениями-неравенствами, и прямую , которая называется целевой функцией.
Три записанных выше неравенства ограничивают на плоскости многоугольник (построен красным цветом), ограниченный слева и снизу координатными осями (т.к. искомое количество изделий положительно).
График целевой функции (построен синим цветом) передвигается в направлении, обозначенном стрелкой (по-научному – в направлении своего градиента), до тех пор, пока не достигнет граничной точки многоугольника – в нашем случае это точка – (15 ; 5). В этой точке целевая функция будет достигать максимума.
А теперь решим эту задачу симплекс-методом. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам, введя дополнительные переменные .
Симплекс-таблица составляется так: В графе Базис записываются вектора переменных, принимаемые за базисные. На первом этапе это – A3, A4, A5. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных. В следующий столбец записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной. Под столбцом свободных членов записывается начальная оценка
Остальные оценки записываются под столбцами соответствующих векторов .Следует отметить, что оценки для базисных векторов всегда равны нулю.
Преобразование симплекс-таблицы ведется следующим образом:
Шаг 1: Проверяется критерий оптимальности, суть которого состоит в том, что все оценки должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
Шаг 2: Для отрицательных оценок вычисляются величины:
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае минимально, поэтому в качестве так называемого разрешающего элемента выбирается третий элемент первого столбца – 3 (выделен в таблице).
Шаг 3: Третья строка таблицы делится на 3 и вычитается из первой и второй строк. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса. Таким образом, новыми базисными переменными становятся A3, A4, A1.
Возвращаемся к шагу 1 и повторяем весь процесс.Под столбцом свободных членов записывается начальная оценка
Остальные оценки записываются под столбцами соответствующих векторов .Следует отметить, что оценки для базисных векторов всегда равны нулю.
Опять проверяется критерий оптимальности. Отрицательная оценка только одна – в столбце А2.
Вычисляем:
Разрешающим элементом будет второй элемент второго столбца – 2/3.
Новыми базисными переменными становятся A3, A2, A1 Делим вторую строку на 2 и вычитаем из третьей.Умножаем вторую строку на 5/2 и вычитаем из первой.
На этот раз отрицательных оценок нет, т.е. критерий оптимальности выполнен.
Таким образом, получается искомое значение целевой функции F(15; 5; 7; 0; 0) = 70, т.е. возвращаясь к системе неравенств, получаем:
Ответы, полученные различными методами, совпадают.
www.matem96.ru
