4.7.4. Методы однопараметрической оптимизации. Методы оптимизации поиска
4.7.4. Методы однопараметрической оптимизации
(одномерного поиска)
Методы однопараметрической оптимизации используются:
при исследовании влияния отдельных параметров на показатель оптимальности;
для определения длины шага вдоль выбранного направления поиска в многопараметрических задачах оптимизации.
Методы однопараметрической оптимизации по объему информации, используемой в каждой точке поиска можно разделить на два класса алгоритмов. Алгоритмы одного класса учитывают при определении длины шага только признак возрастания (убывания) показателя оптимальности в нескольких последовательно выбираемых точках поиска. К этому классу относятся методы:
общего поиска;
деления интервала пополам;
дихотомии;
«золотого сечения»;
Фибоначчи и др.
Алгоритмы другого класса учитывают при определении длины шага изменения числовых значений целевой функции в одной или нескольких итерациях. (Итерация – лат. iteratio – повторение – результат неоднократно повторяемого применения какой-либо математической операции). Сюда относится метод квадратичной аппроксимации и др.
При решении задачи оптимизации предполагается, что исследуемая целевая функция y = F(x) является «унимодальной», т.е. в рассматриваемом интервале изменения значений х (а х b) существует только один экстремум. Других сведений о целевой функции не имеется.
Вводится понятие «интервал неопределенности» – это интервал значений х, в котором заключен оптимум. В начале процесса оптимизации этот интервал имеет длину L или (b - a) – начальный интервал неопределенности. Задача оптимизации состоит в систематическом сужении интервала неопределенности до такой величины, в которой находится экстремум с заданной точностью. Оценка положения экстремума получается интервальной, а не точечной.
1. Метод общего поиска (равномерного поиска)
В этом методе расположение точек, в которых проводятся опыты, выбирается до проведения первого испытания. Интервал неопределенности (отрезок а – b) делится на N + 1 равных частей, где N – число испытаний на отрезке [а, b]. В 1-й серии опытов определяются значения целевой функции в узлах полученной сетки (рис. 4.17): N = 5.
На рисунке обозначены: L – начальный интервал неопределенности; М – суженный интервал неопределенности (до двух шагов сетки).
Число испытаний можно уменьшить на одно, если остановиться в точке 4.
Новый интервал неопределенности М опять делят на N1 + 1 равных частей, но в два раза меньших, чем в 1-й серии опытов (N1 = 3). Процедура повторяется до получения нужной точности.
F(x) L
М
0 а 1 2 3 4 5 b
Рисунок 4.17.
Дробление интервала неопределенности характеризуется коэффициентом дробления
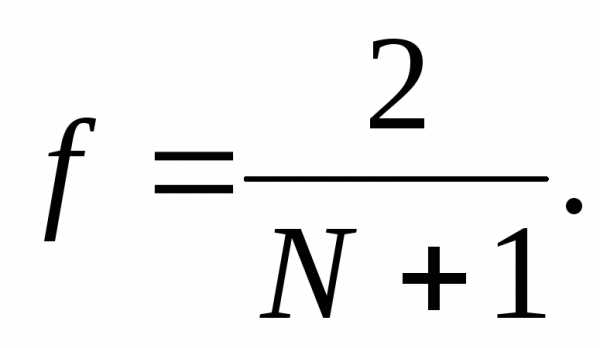
Чтобы получить f = 0,01 потребуется целевую функцию определить в 199 точках, а при f = 0,001 – в 1999 точках. Следовательно, эффективность метода быстро падает при уменьшении интервала неопределенности.
studfiles.net
Методы оптимизации поиска - Структуры и алгоритмы обработки данных.
Всегда можно говорить о некотором значении вероятности поиска того или иного элемента в таблице. Считаем, что в таблице данный элемент существует. Тогда вся таблица поиска может быть представлена как система с дискретными состояниями, а вероятность нахождения там искомого элемента - это вероятность p(i) i - го состояния системы.
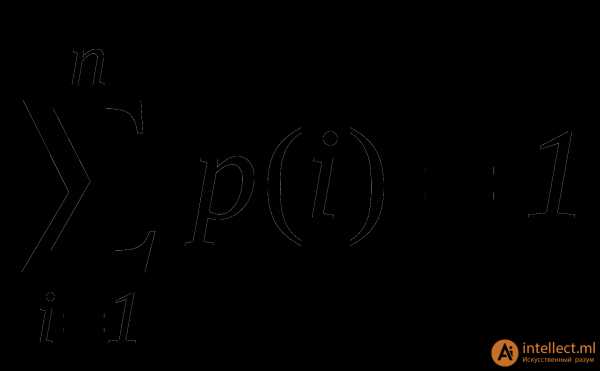
Количество сравнений при поиске в таблице, представленной как дискретная система, представляет собой математическое ожидание значения дискретной случайной величины, определяемой вероятностями состояний и номерами состояний системы.
Z=Q=1p(1)+2p(2)+3p(3)+…+np(n)
Желательно, чтобы p(1)³p(2) ³p(3) ³…³p(n).
Это минимизирует количество сравнений, то есть увеличивает эффективность. Так как последовательный поиск начинается с первого элемента, то на это место надо поставить элемент, к которому чаще всего обращаются (с наибольшей вероятностью поиска).
Наиболее часто используются два основных способа автономного переупорядочивания таблиц поиска. Рассмотрим их на примере односвязных списков.
5.5.1 Переупорядочивание таблицы поиска путем перестановки найденного элемента в начало списка
Суть этого метода заключается в том, что элемент списка с ключом, равным заданному, становится первым элементом списка, а все остальные сдвигаются.Этот алгоритм применим как для списков, так и для массивов. Однако не рекомендуется применять его для массивов, так как на перестановку элементов массива затрачивается гораздо больше времени, чем на перестановку указателей.
Алгоритм переупорядочивания в начало списка:
| Псевдокод: q=nil p=table while (p <> nil) do if key = k(p) then if q = nil then 'перестановка не нужна' search = p return endif nxt(q) = nxt(p) nxt(p) = table table = p search = p return endif q = p p = nxt(p) endwhile search = nil return |
Паскаль: q:=nil; p:=table; while (p <> nil) do begin if key = p^.k then begin if q = nil then 'перестановка не нужна' search := p; exit; end; q^.nxt := p^.nxt; p^.nxt := table; table := p; exit; end; q := p; p := p^.nxt; end; search := nil; exit; |
5.5.2. Метод транспозиции
В данном методе найденный элемент переставляется на один элемент к голове списка. И если к этому элементу обращаются часто, то, перемещаясь к голове списка, он скоро окажется на первом месте.р - рабочий указатель
q - вспомогательный указатель, отстает на один шаг от р
s - вспомогательный указатель, отстает на два шага от q
Алгоритм метода транспозиции:
| Псевдокод: s=nil q=nil p=table while (p <> nil) do if key = k(p) then ‘ нашли, транспонируем if q = nil then ‘ переставлять не надо search=p return endif nxt(q)=nxt(p) nxt(p)=q if s = nil then table = p else nxt(s)=p endif search=p return endif endwhile search=nil return |
Паскаль: s:=nil; q:=nil; p:=table; while (p <> nil) do begin if key = p^.k then ‘ нашли, транспонируем begin if q = nil then begin ‘переставлять не на- до search:=p; exit; end; q^.nxt:=p^.nxt; p^.nxt:=q; if s = nil then table := p; else begin s^.nxt := p; end; search:=p; exit; end; end; search:=nil; exit; |
Этот метод удобен при поиске не только в списках, но и в массивах (так как меняются только два стоящих рядом элемента).
5.5.3. Дерево оптимального поиска
Если извлекаемые элементы сформировали некоторое постоянное множество, то может быть выгодным настроить дерево бинарного поиска для большей эффективности последующего поиска.Рассмотрим деревья бинарного поиска, приведенные на рисунках a и b.Оба дерева содержат три элемента - к1, к2, к3, где к1<к2<к3. Поиск элемента к3требует двух сравнений для рисунка 5.6 a), и только одного - для рисунка 5.6 б).
Число сравнений ключей, которые необходимо сделать для извлечения некоторой записи, равно уровню этой записи в дереве бинарного поиска плюс 1.
Предположим, что:
p1 - вероятность того, что аргумент поиска key = к1
р2 - вероятность того, что аргумент поиска key = к2
р3 - вероятность того, что аргумент поиска key = к3
q0 - вероятность того, что key < к1
q1 - вероятность того, что к2 > key > к1
q2 - вероятность того, что к3 > key > к2
q3 - вероятность того, что key > к3
C1 - число сравнений в первом дереве рисунка 5.6 a)
C2 - число сравнений во втором дереве рисунка 5.6 б)
Тогда ×р1+×р2+×р3+×q0+×q1+×q2+×q3 = 1
Ожидаемое число сравнений в некотором поиске есть сумма произведений вероятности того, что данный аргумент имеет некоторое заданное значение, на число сравнений, необходимых для извлечения этого значения, где сумма берется по всем возможным значениям аргумента поиска. Поэтому
C1 = 2×р1+1×р2+2×р3+2×q0+2×q1+2×q2+2×q3
C2 = 2×р1+3×р2+1×р3+2×q0+3×q1+3×q2+1×q3
Это ожидаемое число сравнений может быть использовано как некоторая мера того, насколько "хорошо" конкретное дерево бинарного поиска подходит для некоторого данного множества ключей и некоторого заданного множества вероятностей. Так, для вероятностей, приведенных далее слева, дерево из a) является более эффективным, а для вероятностей, приведенных справа, дерево из б) является более эффективным:
P1 = 0.1 P1 = 0.1
P2 = 0.3 P2 = 0.1
P3 = 0.1 P3 = 0.3
q0 = 0.1 q0 = 0.1
q1 = 0.2 q1 = 0.1
q2 = 0.1 q2 = 0.1
q3 = 0.1 q3 = 0.2
C1 = 1.7 C1 = 1.9
C2 = 2.4 C2 = 1.8
Дерево бинарного поиска, которое минимизирует ожидаемое число сравнений некоторого заданного множества ключей и вероятностей, называется оптимальным. Хотя алгоритм создания дерева может быть очень трудоемким, дерево, которое он создает, будет работать эффективно во всех последующих поисках. К сожалению, однако, заранее вероятности аргументов поиска редко известны.
intellect.ml
Оптимизация. Методы многомерного поиска
Министерство образования Республики Беларусь
Учреждение образования “Гомельский государственный университет им.Ф. Скорины”
Математический факультет
Кафедра ВМ и П
“Оптимизация. Методы многомерного поиска”
Выполнили
студентки группы М - 51, М - 52
Лаптева Е.Н., Кулай Н.В.
Научный руководитель
Орлов В.В.
Гомель 2002
Содержине
Введение
1. Основы теории оптимизации
1.1 Проектные параметры
1.2 Целевая функция
1.3 Поиск минимума и максимума
1.4 Пространство проектирования
1.5 Ограничения - равенства
1.6 Ограничения - неравенства
1.7 Локальный оптимум
1.8 Глобальный оптимум
2. Методы многомерного поиска
3. Метод покоординатного подъема
4. Метод исключения областей
5. Метод случайного поиска
6. Градиентные методы
6.1 Ступенчатый наискорейший подъем
Литература
Методы оптимизации позволяют выбрать наилучший вариант конструкции из всех возможных вариантов. В последние годы этим методам уделялось большое внимание, и в результате был разработан целый ряд высокоэффективных алгоритмов, позволяющих найти оптимальный вариант конструкции при помощи ЭЦВМ. В данной методической разработке излагаются основы теории оптимизации, рассматриваются принципы, лежащие в основе построения алгоритмов оптимальных решений, описываются наиболее известные алгоритмы, анализируются их достоинства и недостатки.
Термином "оптимизация" в литераторе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего, или "оптимального", решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.
Рассматривая некоторую произвольную систему, описываемую т уравнениями с n неизвестными, можно выделить три основных типа задач. Если т= n, задачу называют алгебраической. Такая задача обычно имеет одно решение. Если т> n, то задача переопределена и, как правило, не имеет решения. Наконец, при т< n задача недоопределена и имеет бесконечно много решений. В практике проектирования чаще всего приходится иметь дело с задачами третьего типа. При этом инженеру помогает интуиция, позволяющая сформулировать условия для выбора оптимального варианта. Очевидно, что изделие или технологический процесс, выгодно отличающееся от аналогичных изделий и процессов, будет пользоваться на рынке большим спросом. В этом и состоит смысл поиска оптимальных решений.
Прежде чем приступить к обсуждению вопросов оптимизации, введем ряд определений.
Этим термином обозначают независимые переменные параметры, которые полностью и однозначно определяют решаемую задачу проектирования. Проектные параметры - неизвестные величины, значения которых вычисляются в процессе оптимизации. В качестве проектных параметров могут служить любые основные или производные величины, служащие для количественного описания системы. Так, это могут быть неизвестные значения длины, массы, времени, температуры. Число проектных параметров характеризует степень сложности данной задачи проектирования. Обычно число проектных параметров обозначают через n, а сами проектные параметры через x с соответствующими индексами. Таким образом n проектных параметров данной задачи будем обозначать через x ,x ,x , …x .
Это - выражение, значение которого инженер стремится сделать максимальным или минимальным. Целевая функция позволяет количественно сравнить два альтернативных решения. С математической точки зрения целевая функция описывает некоторую (n+1) - мерную поверхность. Ее значение определяется проектными параметрами M= M ( x ,x ,x , …x ).
Примерами целевой функции, часто встречающимися в инженерной практике, являются стоимость, вес, прочность, габариты, КПД. Если имеется только один проектный параметр, то целевую функцию можно представить кривой на плоскости (рис.1).
Продолжительность эксплуатации
(проектный параметр)
Рис.1. Одномерная целевая функция
Если проектных параметров два, то целевая функция будет изображаться поверхностью в пространстве трех измерений. При трех и более проектных параметрах поверхности, задаваемые целевой функцией, называются гиперповерхностями и не поддаются изображению обычными средствами. Топологические свойства поверхности целевой функции играют большую роль в процессе оптимизации, так как от них зависит выбор наиболее эффективного алгоритма.
Целевая функция в ряде случаев может принимать самые неожиданные формы. Например, ее не всегда удается выразить в замкнутой математической форме, в других случаях она может представлять собой кусочно-гладкую функцию. Для задания целевой функции иногда может потребоваться таблица технических данных (например, таблица состояния водяного пара) или может понадобиться провести эксперимент. В ряде случаев проектные параметры принимают только целые значения. Примером может служить число зубьев в зубчатой передаче или число болтов во фланце. Иногда проектные параметры имеют только два значения - да или нет. Качественные параметры, такие как удовлетворение, которое испытывает приобретший изделие покупатель, надежность, эстетичность, трудно учитывать в процессе оптимизации, так как их практически невозможно охарактеризовать количественно. Однако в каком бы виде ни была представлена целевая функция, она должна быть однозначной функцией проектных параметров.
В ряде задач оптимизации требуется введение более одной целевой функции. Иногда одна из них может оказаться несовместимой с другой. Примером служит проектирование самолетов, когда одновременно требуется обеспечить максимальную прочность, минимальный вес и минимальную стоимость. В таких случаях конструктор должен ввести систему приоритетов и поставить в соответствие каждой целевой функции некоторый безразмерный множитель. В результате появляется "функция компромисса", позволяющая в процессе оптимизации пользоваться одной составной целевой функцией.
Одни алгоритмы оптимизации приспособлены для поиска максимума, другие - для поиска минимума. Однако независимо от типа решаемой задачи на экстремум можно пользоваться одним и тем же алгоритмом, так как задачу минимизации можно легко превратить в задачу на поиск максимума, поменяв знак целевой функции на обратный.
Так называется область, определяемая всеми n проектными параметрами. Пространство проектирования не столь велико, как может показаться, поскольку оно обычно ограничено рядом условий, связанных с физической сущностью задачи. Ограничения могут быть столь сильными, что задача не будет иметь ни одного удовлетворительного решения. Ограничения делятся на две группы: ограничения - равенства и ограничения - неравенства.
Ограничения - равенства - это зависимость между проектными параметрами, которые должны учитываться при отыскании решения. Они отражают законы природы, экономики, права, господствующие вкусы и наличие необходимых материалов. Число ограничений - равенств может быть любым. Они имеют вид C
(x ,x , …x ) =0,C (x ,x , …x ) =0, C (x ,x , …x ) =0.Если какое-либо из этих соотношений можно разрешить относительно одного из проектных параметров, то это позволяет исключить данный параметр из процесса оптимизации. Тем самым уменьшается число измерений пространства проектирования и упрощается решение задачи.
Это особый вид ограничений, выражаемых неравенствами. В общем случае их может быть сколь угодно много, причем все они имеют вид
mirznanii.com
Методы поисковой оптимизации - часть 2
Каждая из формул (2.6), (2.7) является векторным соотношением, включающим n уравнений. Например, с учетом Хk+1 = ( x1k+1 , x2. k+1 ,…,xnk+1 ), Хk = ( x1k , x2. k ,…,xnk ) формула (2.6) примет вид:
или в скалярном виде
В общем виде (2.9) можно записать:
В качестве условия прекращения поиска во всех градиентных методах используется, как правило, комбинация двух условий: ç Ф(Xk+1 ) - Ф(X k ) ç £ e или

В градиентном методе можно несколько сократить число итераций, если научиться избегать ситуаций, когда несколько шагов поиска выполняются в одном и том же направлении.
3.3. Градиентный метод с дроблением шага
В градиентном методе с дроблением шага процедура подбора величины шага на каждой итерации реализуется следующим образом.
Исходными данными являются требуемая точность e, начальная точка поиска Х0 и начальная величина шага поиска h (обычно h = 1). Получение новых точек производится по формуле:
где hk – величина шага на k-ой итерации поиска, при hk должно выполняться условие:
Если величина hk такова, что неравенство (2.13) не выполнено, то производится дробление шага до тех пор, пока данное условие не будет выполнено. Дробление шага выполняется по формуле hk = hk ×a, где 0 < a < 1.Такой подход позволяет сократить число итераций, но затраты на проведение одной итерации при этом несколько возрастают.
3.4. Метод наискорейшего спуска
В методе наискорейшего спуска на каждой итерации градиентного метода выбирается оптимальный шаг в направлении градиента.
Исходными данными являются требуемая точность e, начальная точка поиска Х0 .
Получение новых точек производится по формуле:
то есть выбор шага производится по результатам одномерной оптимизации по параметру h.
Основная идея метода наискорейшего спуска заключается в том, что на каждой итерации метода выбирается максимально возможная величина шага в направлении наискорейшего убывания целевой функции, то есть в направлении вектора-антиградиента функции Ф(Х) в точке Хk ( рис. 2. 4).
При выборе оптимальной величины шага необходимо из множества ХМ = { Х½ Х = Хk – h×grad Ф(Хk ), hÎ[0,¥) } точек, лежащих на векторе градиенте функции Ф(Х), построенном в точке Хk , выбрать ту, где функция Ф(h) = Ф(Хk – h ×grad Ф(Хk )) принимает минимальное значение.
На практике целевые функции являются гораздо более сложными, линии уровня также имеют сложную конфигурацию, но в любом случае справедливо следующее: из всех градиентных методов в методе наискорейшего спуска наименьшее число итераций, но некоторую проблему представляет поиск оптимального шага численными методами, так как в реальных задачах, возникающих при проектировании РЭС, применение классических методов нахождения экстремума практически невозможно.

4. Методы поиска второго порядка
Несмотря на простоту реализации, метод наискорейшего спуска не рекомендуется в качестве “серьезной” оптимизационной процедуры для решения задачи безусловной оптимизации функции многих переменных, так как для практического применения он работает слишком медленно. Причиной этого является тот факт, что свойство наискорейшего спуска является локальным свойством, поэтому необходимо частое изменение направления поиска, что может привести к неэффективной вычислительной процедуре. Более точный и эффективный метод решения задачи параметрической оптимизации (1.5) можно получить, используя вторые производные целевой функции (методы второго порядка). Они базируются на аппроксимации (то есть приближенной замене) функции Ф(Х) функцией j(Х),
mirznanii.com
Безградиентные методы оптимизации поиска — Мегаобучалка
До сих пор рассматривались методы поиска оптимума, в которых производился предварительный анализ производных функций цели по всем независимым переменным для определения направления и величины шага поиска. Это связано с необходимостью выполнения большого объёма вычислений, что приводит к увеличению времени поиска.
Кроме того, при оптимизации объекта в условиях отсутствия его математического описания, погрешность вычисления производной как разности значений и критерия оптимальности может достигать до сотен процентов из-за неизбежных погрешностей при измерений величин, характеризующих этот критерий. Причём это может иметь место даже при небольшой относительной погрешности вычислений значения критерия оптимальности. Это может привести к существенным ошибкам в определении направления движения к оптимуму с помощью градиентных методов.
Существует другая группа методов – безградиентные методы, использующие в процессе поиска информацию, получаемую не при анализе производных, а от сравнительной оценки критерия оптимальности в результате выполнения очередного шага. К ним относятся методы сканирования, покоординатного спуска (Гаусса- Зейделя), симплекса.
Метод сканирования
Идея алгоритма перебора крайне проста. Вычисляют значения функции в конечном числе точек области Dx (в узлах координатной сетки).Из вычисленных значений выбирают наименьшее (наибольшее) . Координаты соответствующего узла сетки – это координаты экстремума, определённые с точностью до , где – h шаг сетки (рис. 6.10).
Рисунок 3.11 – Поиск оптимума на сетке переменных
Точность определения точки минимума, причем глобального, зависит от плотности наполнения области Dx дискретным множеством , то есть от величины шага h координатной сетки, тем выше точность определения положения оптимума, однако при уменьшении h быстро растёт объём вычислений. Если интервал изменения каждой переменной разбить К равных частей, то h равно
,
При этом необходимое количество вычислений I(x) равно .
Поэтому эффективное применение данного метода ограничивается задачами невысокой размерности (n=2-3). При большой размерности вектора требуется выполнение большого объёма вычислительной работы.
Пусть область Dx – геперкуб:
,
в котором ищется .Точность определения координат вектора , минимизирующего , положим равной 0,1. Тогда интервалы следует разбить на 10 частей с шагом h=0,1 плоскостями, ортогональными и вычислить во всех точках перечисления плоскостей значения . Всего потребуется вычислить в 11n точках. Пусть для нахождения I в каждой точке требуется примерно 102n арифметических операций. Тогда общее число арифметических операций алгоритма перебора примерно 11(n+2)n и при n=10 на ЭВМ с быстродействием 109 oп/c требуется примерно 104 с, т.е. примерно 167 минут непрерывной работы ЭВМ.
Иногда поиск осуществляется с переменным шагом сканирования. Вначале величина h выбирается достаточно большой, выполняется грубый поиск для локализации экстремума, а поиск в районе оптимума осуществляется с меньшим шагом.
Достоинства метода – возможность определения глобального оптимума и независимость поиска от вида оптимизируемой функции.
Метод Гаусса-Зейделя
Метод Гаусса-Зейделя, называемый также методом покоординатного спуска, аналогичен методу релаксации. Отличие заключается лишь в том что, в этом методе не определяется осевое направление, вдоль которого значение изменяется наиболее сильно. Поочерёдно изменяются все переменные.
Алгоритм поиска минимума следующий. Пусть ищется минимум . Устанавливается очерёдность изменения – и начальная точка поиска. Затем все переменные фиксируются на уровне , изменяется по алгоритму
; ; ; (3.22)
где – шаг изменяется , обычно не зависит от k.
После каждого шага вычисляется , сравнивается с предыдущим значением, критерия шаги продолжаются до достижения частного оптимума по xj = x1. В этой точке величина фиксируется и изменяется x2 до достижения оптимума по x2 и т.д. После того как достигается оптимум по последней переменной xn, снова изменяется x1 и весь цикл повторяется до тех пор, пока не будет найдена точка оптимума.
На рисунке 3.11 показан алгоритм поиска минимума для функции двух переменных.
Рисунок 3.12 – Траектория движения к оптимуму в методе координатного спуска
Заметим что для функции двух переменных методы релаксации и Гаусса-Зейделя совпадают.
Если первый шаг изменения xj не улучшает значение критерия, т.е. , а , то выполняется шаг по xj в обратном направлении , т. е. Первый шаг пробный. Если и этот шаг неудачный, то переходят к изменению xj+1 и т.д.
Поиск заканчивают когда достигается точка , из которой при движении в любом осевом направлении улучшение критерия не наблюдается.
Рассмотрим вопрос улучшения алгоритма поиска .
Пусть в области допустимых решений D задано нулевое приближение .
Рассматриваем функцию при фиксированных значениях как функцию одной переменной x1, т. е.
(3.23)
Минимизируя находим значение , доставляющее минимум функцию (3.23):
;
.
Далее при фиксированных значениях рассматриваем как функцию одной переменной x2. Находим её минимум
;
.
Продолжая эту процедуру последовательно, после n шагов получаем точку , в которой выполняется условие
.
В результате одного шага покоординатного спуска происходит переход из начальной точки в точку . Если при этом оказывается, что
,
то начальная точка – точка, доставляющая минимум функцию .
Если ,то выполняется следующий шаг поко-ординатного спуска, в котором за начальную точку принимается , получаем и т.д. Этот процесс продолжается до тех пор, пока не выполнится какое-либо условие окончания поиска, например такое
, (3.24)
где – заданная точность.
или
(3.25)
Таким образом, поиск минимума функции одной переменной занимает центральное место в рассматриваемом алгоритме покоординатного спуска.
Простота метода и сравнительно небольшой объём вычислений обусловили его распространение в автоматических системах поиска.
megaobuchalka.ru
Поисковые методы одномерной оптимизации — Мегаобучалка
Общие сведения
Поисковые методы оптимизации составляют класс методов нелинейного программирования. Вспомним еще раз постановку задачи оптимизации:
(3.1)
при условиях
(3.2)
Часто критерий не имеет явного выражения, либо функции(3.1), (3.1) являются трудно вычислимыми нелинейными функциями. Задачи такого типа составляют предмет нелинейного программирования.
Как правило, решение задач нелинейного программирования может быть найдено только численными методами. В настоящее время для решения надобных задач разработано значительное число методов. Однако все еще не предоставляется возможным отдать предпочтенное какому-либо одному из них. Поисковые методы оптимизации основаны на постоянном перемещении в пространстве переменных в направлении к оптимальному значению функции . Различные методы поиска отличаются способом определения направления движения к оптимуму, размером шага и продолжительного поиска вдоль найденного направления, критериями окончания поиска, простотой алгоритмизации для ЭВМ.
Нормирование переменных. Переменные в конкретных задачах могут иметь самый различный физический смысл и разные единицы измерения. Поэтому при решении оптимальных задач численными методами целесообразно оперировать с их безразмерными нормализованными значениями.
Обычно для нормализации применяется возможный диапазон изменения значений независимых переменных
.
Вводя безразмерные переменные
; , (3.3)
исходную задачу (3.1), (3.2) выражают через них, решают преобразованную задачу, определяют оптимальное значения нормированных переменных , а через них оптимальные значения исходных переменных, :
;
при
Линии уровня. В соответствии с (3.1) критерий может рассматриваться как функция, определенная n-мерном пространстве переменных Поскольку наглядное графическое изображение n-мерного пространства отсутствует, обычно используется прием представления на плоском чертеже. Все методы оптимизации сводятся к тому, чтобы найти минимум или максимум, т.е. впадину или вершину на поверхности, описываемой уравнением . Эта поверхность называется поверхностью отклика. Линии, вдоль которых целевая функция сохраняет постоянное значение при изменении входящих в нее переменных, называются контурными линиями или линиями уровня.
Примеры линией уровня показаны на рис.3.1 (при отсутствии ограничений), на рис.3.2 (при наличии ограничений) и на рис.3.3 (в окрестности седловой точки).
Рисунок 3.2 – Линии уровня без ограничений
Рисунок 3.3 – Линии уровня с ограничениями
Рисунок 3.4 – Линии уровня в окрестностях седловой точки
Точки, в которых на одним направлениям имеет минимум, а по другим – максимум, называются Седловыми точками функции . В этой точке хотя выполняется необходимое условие экстремума функции в ней нет. Линии уровня, соответствующие разным значениям , не пересекаются. Внутри линии уровня, соответствующие числам I, больше, чем I, в случае максимума и меньше, чем I, в случае минимума.
Поисковые методы оптимизации основаны на постоянном перемещении в пространстве переменных в направление к оптимальному значению функции .
Различные методы поиска отличаются способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, критерия окончания поиска, простой алгоритмизации для ЭВМ.
Вычисление производных и градиента. В основу градиентных методов поиска оптимума положены вычисления и анализ производных , , вычисляются аналитически, если это не представляет особого труда, либо численным методом по приближенному соотношению, основанному на замене частных производных в точке отношениями конечных приращений. Для этого в точке поочерёдно изменяют переменные и вычисляют соответствующие приращения в точке
, , (3.4)
где
При применении нормализованных переменных в алгоритме оптимизации необходимо учесть соотношение (3.3) при вычислении , если она выражена через значения исходных физических переменных :
. (3.5)
Для вычисления производных удобно давать одно и то же приращение но всем независимым переменным , т.е.
,
тогда
,
Формула (3.4) дает лишь приближенное значение производной . Точность этого приближения зависит от приращения независимой переменной . Априорных способов предсказания наилучшего значения не существуют. Можно лишь заметить, что допустимое приращение по максимуму ограничено кривизной целевой функции в исследуемой точке (которая заранее не известна), а по минимуму- погрешностью вычисления значения функции (которая тоже заранее не известна и может существенно отличаться от погрешности задания значений в процессе поиска).
На практике для определения приемлемого значения (в особенности в начале поиска, когда произведение еще ни разу не находилось) используют метод дробления . Вычисляют значение производной с приращением . Расчет повторяют с . Если полученные значения производных различаются существенно, расчет повторяется с и т.д., пока не будет найдено приемлемое значение приращения . На последующих шагах это значение может уточняться.
Градиент в точке равен .
megaobuchalka.ru
Методы оптимизации поисковые - Энциклопедия по машиностроению XXL
Сущность оптимизации при выбранной комплексной целевой функции сводится к отысканию при наложенных ограничениях таких значений параметров механизма, которые дают максимум (минимум) целевой функции, характеризующей комплексную эффективность проектируемой машины. При этом используются математические методы оптимизации, позволяющие осуществить непрерывный поиск направления улучшения внутренних параметров механизма за счет количественного изменения их значений. Так как комплексная целевая функция, получаемая сверткой векторных критериев, определяется неявным образом от внутренних параметров синтеза, что не позволяет оценить ее свойства (выпуклость, вогнутость и т. д.), то решение задач оптимизации ведется с помощью поисковых методов, получивших название методов математического программирования. В настоящее время нет экономичного, универсального метода, дающего высокую гарантию получения наилучшей совокупности внутренних параметров машины и механизма, пригодного для решения любой задачи оптимизации. В зависимости от класса решаемых задач из имеющихся в наличии программ, входящих в программное обеспечение методов оптимизации, выбирают такую, которая дает наиболее высокую вероятность отыскания оптимальной совокупности определяемых параметров с наименьшими затратами машинного времени. [c.316] Наиболее распространенным приемом, позволяющим отстроиться от локальности направленных методов поиска, является организация алгоритмов, в которых на первом этапе применяется пассивный поиск, а в дальнейшем — один из методов направленного поиска. Такое комби нирование методов оптимизации позволяет вести направленный обзор области поиска из нескольких начальных точек (как это показано в примере на рис. 5.21), которые могут формироваться методами сканирования или статистических испытаний. Важно отметить, что начальные точки должны находиться в области допустимых значений параметров. Схема организации комбинированного алгоритма поисковой оптимизации, дающего возможность определять приближения к глобальному экстремуму функции цели, представлена на рис. 5.28. [c.164]Такая универсальная характеристика рассматриваемых методов оптимизации, как затраты на поиск, и может быть принята для сравнительной оценки эффективности всей группы методов поисковой оптимизации. [c.169]
Основными методами оптимизации в САПР являются поисковые методы, которые основаны на пошаговом изменении управляемых параметров [c.157]
Научно-техническая база ОС включает результаты фундаментальных, поисковых и прикладных научных исследований, открытия и изобретения, принятые к реализации, методы оптимизации параметров объектов стандартизации и прогнозирования потребностей народного хозяйства и населения в данной продукции. ОС проводится на основе целевого подхода одновременно с НИОКР по созданию систем, комплексов и семейств машин, оборудования, механизмов и приборов, решением важнейших экономических и социальных проблем, систематическим изысканием путей повышения технического уровня, качества и конкурентоспособности изделий на международном рынке, с ускорением реализации результатов фундаментальных, прикладных исследований, открытий и изобретений. [c.327]
При построении поисковых алгоритмов оптимизации следует учесть, что многообразие методов оптимального проектирования ЭМП требует их сравнительной оценки и выбора из них наиболее эффективных для решения конкретных задач. Однако достаточно полные критерии теоретической оценки методов пока не разработаны и поэтому оценка осуществляется обычно с помощью вычислительного эксперимента. Анализ работ по оптимальному проектированию ЭМП показывает, что все основные методы программирования получили практическую апробацию. Так, методы упорядоченного перебора использованы для проектирования асинхронных двигателей [42], методы случайного перебора — для проектирования асинхронных двигателей и синхронных генераторов [24], методы градиента, покоординатного поиска, динамического программирования— для проектирования синхронных машин [8], методы случайного направленного поиска —для проектирования асинхронных машин (22] и т. д. [c.144]
Поисковые методы динамического программирования основаны на численных методах решения уравнения (3.75). Общая вычислительная схема на первом этапе сводится к решению задачи одномерной оптимизации ДЯо по параметру Azi, при фиксированной точке Zo и заданной функции /p-i(Zi). Аналитический вид этой функции, как правило, неизвестен, но для численных [c.254]
Методы и алгоритмы поисковой оптимизации [c.153]
Как уже отмечалось, в задачах оптимизации ЭМУ часто приходится иметь дело с параметрами оптимизации, которые могут изменяться, только дискретно. Такие задачи принято называть задачами смешанного целочисленного программирования. Все рассмотренные ранее поисковые методы (за исключением сканирования) позволяют решать такие задачи только при искусственной замене в процессе поиска дис- [c.161]
В результате знакомства с рассмотренными методами поисковой оптимизации нетрудно увидеть, что методы направленного поиска обладают рядом органически присущих им недостатков. [c.162]
Понятие эффективности весьма многообразно. В данном случае речь может идти о сложности алгоритмов и программ, реализующих различные методы, или о возможностях этих программ в решении практических задач. Частично особенности построения алгоритмов поисковой оптимизации, позволяющие судить об их относительной сложности, были рассмотрены ранее. Здесь обсудим вопрос эффективности применения готовых алгоритмов в виде соответствующих программ для рещения задач оптимизации ЭМУ. [c.169]
Таким образом различные методы поиска имеют определенные сферы действия в решении задач оптимизации проектных решений. Поэтому при разработке САПР целесообразно включать в ее состав комплекс алгоритмов и программ поисковой оптимизации. [c.173]
Вводится некоторая уступка Д01 по основному критерию, определяется область поиска по параметрам, и ЭМУ оптимизируется поочередно по всем неосновным функциям цели 02, Од. при условии, что ограничения на другие функции, кроме основной, не принимаются во внимание. Поиск оптимального варианта по различным функциям цели осуществляется с использованием методов поисковой оптимизации. Определяются лучшее и худшее значения каждого неосновного критерия и соответствующие им значения параметров оптимизации. [c.215]
Поиск оптимальных значений параметров управления проводился методами поисковой оптимизации с учетом заданных ограничений по току и потребляемой мощности. При определении параметров двигателя на каждой частоте вращения учитывалось влияние насыщения магнитной цепи по алгоритму, представленному в 6.4. [c.226]
Приведенный пример показывает возможности применения ранее рассмотренных методов и алгоритмов поисковой оптимизации для решения задач оптимального управления. [c.226]
Таким образом, методы и алгоритмы поисковой оптимизации при определенных условиях могут рассматриваться как универсальное средство выявления лучших вариантов проекта с учетом не только внутренних параметров ЭМУ, но и алгоритмов их управления. [c.229]
Кроме того, известно, что допуски на целый ряд параметров (например, на геометрические размеры) регламентируются системой ква-литетов, а следовательно, изменяются дискрета. Для реализации общего подхода к решению задачи оптимизации и соответствующей унификации применяемых алгоритмов целесообразно заменить в первом приближении дискретно изменяемые параметры их непрерывными аналогами. Эта операция, в частности, позволяет применять при определении допусков практически всю совокупность методов и алгоритмов поисковой оптимизации. После получения оптимальных значений допусков они могут быть скорректированы с учетом дискретности изменения допусков на ряд параметров. [c.247]
В составе подсистемы Оптимизация рассматриваемой САПР нашли применение несколько методов поисковой оптимизации. В частности, разработан алгоритм экстраполяционного поиска, предусматривающий генерацию ряда состояний в окрестности каждой текущей точки с определением целевой функции и ограничений, а также их многомерную линейную аппроксимацию. Для решения задач целочисленного программирования, к которым часто сводится оптимизация электрических машин, применяется алгоритм последовательного улучшения функции [c.287]
Метод отжига - метод поисковой оптимизации, в котором для увеличения вероятности выхода из областей притяжения локальных минимумов допускается переход в точки с худшим значением целевой функции с некоторой вероятностью Метод распространения ограничений - метод решения задач условной оптимизации, основанный на сокращении интервалов значений управляемых переменных (или мощности множеств значений этих переменных) благодаря учету исходных ограничений. Сокращенные интервалы в явном виде определяют подмножество допустимых решений [c.312]
Если для выбора динамически оптимального закона движения у(х) наиболее уместны вариационные методы, то для определения дискретных параметров оптимизации целесообразно использовать поисковые методы [50]. Поскольку настоящая par бота посвящена в основном использованию вариационных методов в задачах динамической оптимизации механизмов машин- [c.84]
Таким образом, задача оптимального управления сводится к применению методов прямого поиска. Если имеются граничные условия, то, применяя метод штрафных функций, решение можно свести к решению обычной задачи поисковой оптимизации. [c.310]
Алгоритмы, реализующие методы случайного поиска, обладают большей универсальностью, чем алгоритмы, основанные на регулярных поисковых процедурах, поскольку общая структура таких алгоритмов в принципе не зависит от свойств данной конкретной модели оптимизации и определяется свойствами класса моделей в целом. Это весь.ма существенное достоинство алгоритмов случайного поиска обеспечивается возможностью эффективной адаптации всех без исключения параметров поиска, позволяющей гибко перестраивать тактику и даже стратегию поиска в зависимости от конкретных свойств поисковой ситуации, т. е. свойств функций оптимизационной модели в окрестности текущей точки поиска хь. [c.216]
При структурной оптимизации структура объекта подлежит оптимизации (например, тип металлической конструкции коробчатая или решетчатая). При этом производится параметрическая оптимизация каждой из структур, полученные оптимальные варианты сравниваются между собой и из них выбирается удовлетворяющий наилучшим образом условиям поставленной задачи. Если требуется проанализировать много структур объекта оптимизации, возможен метод машинного поиска решений (автоматизация поискового конструирования) [70 ]. [c.337]
Для методов поисковой оптимизации типичен выбор направления поиска оптимума по результатам последовательных вычислений целевой функции. По способу выбора точки испытания целевой функции поисковые методы безусловной оптимизации делятся на детерминированные методы поиска и методы случайного поиска. В детерминированных методах процесс перехода из точки в точку происходит в соответствии с некото- [c.156]
Таким образом, содержанием любого метода или алгоритма поисковой оптимизации должны быть способы выбора направления поиска gii величины шага /г формул для нормирования управляемых параметров критерия окончания поиска. Эффективность поиска зависит от того, как сделан этот выбор. Составляющими эффективности являются надежность, точность, экономичность. Надежность определяется как вероятность достижения заданной е-окрест-ности экстремальной точки при применении данного метода точность характеризуется гарантированным значением е экономичность отождествляется с потерями на поиск. Потери на поиск выражают трудоемкость процедуры оптимизации, которую в большинстве случаев оценивают количеством обращений к ММ объекта. [c.71]
Существующие алгоритмы для ряда других проектных процедур не приспособлены для крупноблочного распараллеливания. Это относится ко всем вычислительным процедурам, сводящимся к рекуррентным вычислениям. Так, не распараллеливаются процессы, относящиеся к разным шагам численного интегрирования систем дифференциальных уравнений или поисковой оптимизации. Это не означает, что моделирование динамических процессов, поисковая оптимизация и другие подобные им задачи невозможно решать на основе крупноблочного распараллеливания. Такое решение становится возможным по мере разработки соответствующих методов и алгоритмов параллельных вычислений. [c.313]
Таким образом формируется единичный процесс, полученный по аналогии с существующими процессами. Обычно такой процесс не является оптимальным (в структурном отношении), так как основан на использовании случайных процессов, далеко не самых лучших. Оптимизация режимов резания не дает большой экономии, поскольку основной эффект достигается от структурной оптимизации. Поэтому данный метод можно назвать методом случайных аналогий. Качество процесса зависит от результатов поиска детали-аналога — от эффективности работы ИПС технологического назначения. Поиск деталей-аналогов затруднен тем, что детали — это объекты со сложной структурой, и поэтому точность поиска зависит, во-первых, от возможностей информационно-поискового языка, необходимого для формулировки требования на поиск, а во-вторых, от степени детализации описания объектов, хранимых в базе данных. Если хранить лишь описание общих характеристик деталей, то ИПС будет выдавать много лишних деталей из-за невозможности точного задания детали-аналога. Хранение полного описания детали теоретически возможно, но создание базы данных с полным описанием всей номенклатуры деталей чрезвычайно трудоемко. [c.442]
Решение задач параметрического синтеза в САПР выполняется методами поисковой оптимизации (основана на последовательных приближениях к оптимальному решению). Каждая итерация представляет собой шаг в пространстве управляемых параметров. Основными характеристиками метода оптимизации являются способы определения направления, в котором производится шаг в пространстве ХП, величины этого шага и момента окончания поиска. Эти характеристики наряду с особенностями математических моделей оптимизируемых объектов и формулировки задач как задач математического лрограм.мировапия определяют показатели эф-фективпос ги поиска — надежность отыскания экстремальной точки, точность попадания в окрестности этой точки, затраты вычислительных ресурсов па поиск. [c.68]
Числовой подход к решению задачи требует применения ЭВМ и поисковых методов оптимизации. При решении данного примера в качестве параметров оптимизации приняты высота полюсного наконечника hp, высота hm и ширина Ьт полюсного сердечника, высота ярма hj. Однако независимыми являются только параметры Лт и bm, так как hj жестко связан с Ьт, а Ар однозначно определяется одним из равенств а р = Одоп или,Вкр = Вдсл. Они обусловлены тем, что возникающее в процессе оптимизации стремление увеличить окно обмотки возбуждения приводит к превращению соответствующих неравенств в равенства. Все остальные исходные данные расчета индуктора с учетом предыдущих этапов расчета генератора предполагаются фиксированными. Для поиска оптимальных решений использованы градиентный метод и метод локального динамического программирования. Числовое решение рассматриваемой задачи не достигает конечной цели, т. е. не приводит к уравнениям расчета оптимальных значений параметров оптимизации. Конечную цель можно достичь только при сочетании числовых результатов с методами планирования эксперимента. При этом в качестве единичного эксперимента следует рассматривать отдельное оптимальное решение рассматриваемой задачи, полученное для конкретного набора исходных данных. В качестве факторов можно рассматривать любые независимые исходные данные. [c.105]
Во многих случаях задача оптимизации, особенно это относится к задачам нелинейного программирования, решается в несколько этапов. На каждом этапе используется свой метод оптимизации. Например, сначалй используется метод поиска области глобального экстремума. Далее с помощью одного из поисковых методов область, в которой находится экстремальная точка, уменьшается. Если эффективность поисковых методов вблизи оптимума падает, необходимо использовать более точный метод оптимизации. [c.198]
В большинстве задач проектирования при отсутствии аналитического задания целевых функций проверка F( ) на выпуклость или вогнутость, как правило, невозможна, поэтому для решения задач оптимального проектирования используют методы поисковой оптимизации, основанные на исследовании малой окрестности отимальной точки в допустимой области. Основные требования, предъявляемые к методу поиска,— высокая алгоритмическая надежность, приемлемые затраты машинного времени и требуемой памяти. [c.281]
Попытка такой перестройки осуществлена в разработанном нами экспериментальном курсе пространственного эски-зирования, теоретическое обоснование которого приведено в данной работе. В основу экспериментального курса положен метод пространственно-графического моделирования, как наиболее точно соответствующий идее системного подхода к развитию творческого мышления. Реализация этого метода осуществляется в поисковой деятельности оптимизации структуры ( ормы во взаимосвязи с наложенными на структуру условиями. Учебный процесс в этом случае вполне согласуется с информационными требованиями автоматизации профессиональной деятельности инженера, развития у него кибернетического мышления. В учебных заданиях, построенных по новым принципам, моделируется не структура изделия (узла, детали), а структура процесса его образования (изготовления детали, конструктивной увязки деталей в сборочную единицу, проектирования целостной формы, удовлет-воряющей заданным функциональным требованиям). Концеп-) [c.180]
Методы покоординатного поиска. Типичными представителями группы многоэтапных методов поисковой оптимизации являются метод Гаусса—Зейделя и созданный на его основе метод Пауэлла [30]. В соответствии с методом Гаусса-Зейделя поиск на каждом этапе ведется по одному параметру при зафиксированных значениях всех остальных. Пример поиска по методу Гаусса-Зейделя в пространстве двух параметров показан на рис. 5.25. В примере сначала фиксируется значение параметра х, =х, ив этом сечении определяется значение параметрах , дающее лучшее значение Q. Затем фиксируется параметр Хг на уровне Х2 и находится значение первого параметра х", соответствующее лучшему значению Q в сечении Х2 =Х2 = onst. В дальнейшем действия по. поиску экстремума Q повторяются в той же последовательности. [c.161]
Приведенные выше соображения позволяют дать лишь некоторые качественные оценки эффективности двух групп методов поисковой оптимизации. Однако, очевидно, что эти оценки весьма приблизительны и не дают возможности выбирать конкретные методы при решени практических задач для того или иного класса объектов. В то же время особенности математического описания объектов проектирования могут значительно повлиять на оценку эффективности. Поэтому наиболее корректную сравнительную оценку эффективности различных методов поисковой оптимизации можно получить в результате проведения специально организованньк вычислительных экспериментов, когда разные методы в сравнимых условиях применяются для оптимизации одного и того же объекта. [c.170]
Результаты одного из таких вычислительных экспериментов, выйол-ненных с помощью пакета программ, реализующего алгоритмы поисковой оптимизации и разработанного при участии авторов пособия, приведены в табл. 5.7. В качестве объекта был выбран асинхронный гиродвигатель. При его оптимизации принимались во внимание технологические ограничения по выполнимости пазов, зубцов и спинок статора и ротора, а также ограничения на рабочие показатели КПД в номинальном режиме > 0,5, кратность пускового момента к > > 1,2, пусковой ток / время разгона tp [c.170]
Другой важнейшей задачей, достаточно часто встречающейся на этапе вторичной обработки информации, является задача оптимизации [5, 34], т е. нахождение такой комбинации влияющих факторов, при которой выбранный показатель оптимальности принимает экстремальное значение. При экспериментальном решении задачи оптимизации, когда экстремум находится при наличии случайных шумов, наибольшее распространение имеют поисковые процедуры как градиентные (методы градиента, наискорейшего спуска, сопряженных градиентов), так и неградиентные (прямой поиск, симплексный метод, метод Гаусса—Зейделя, случайный поиск, комплекс-метод). [c.458]
Несмотря на ряд очевидных преимуществ, методы случайного поиска не исключают необходимости использования в процессе численной реализации оптимизационных задач регулярных поисковых процедур. Так, если с11тл свойства функций моделей оптимизации достаточно просты, регулярный поиск по сравнению со случайным оказывается более быстродействующим. Особенно в таких задачах, где градиенты функций могут быть вычислены по аналитическим выражениям. Таким образом, наиболее эффективным и универсальным средством численной реализации задач оптимизации несущих конструкций следует считать алгоритмы, которые рационально, т. е. с учетом особенностей и свойств решаемого класса задач, сочетают достоинства как случайных, так и регулярных методов поиска. Данный вывод является итогом обобщения практического опыта решения задач оптимизации несущих конструкций из композитов (см. заключительные главы книги). При решении указанных задач использованы алгоритмы, содержащие как регулярные поисковые процедуры (метод проекции градиента Розена, метод скользящего допуска и др.), так и методы случайного поиска (поиск по наилучшей пробе и метод статистических испытаний (Монте-Карло)). Отдельные задачи решены методами теории планирования многофакторных экспериментов. Все использованные методы достаточно хорошо известны и подробно обсуждены в тех публикациях, на которые сделаны соответствующие ссылки. [c.217]
Многообразие поисковых задач, особенности объектов контроля, специфические условия применения аппаратурных средств, высокие требования по функциональным возможностям, чувствительности, надежности, весогабаритным и эксплуатационным характеристикам практически исключают возможность использования д ля их решения технических средств интроскопии общепромышленного назначения. Напротив, в большинстве случаев для решения конкретных поисковых задач требуется целенаправленный анализ вариантов их решения, поиск и оптимизация физического метода или их комбинаций, разработка алгоритма работы и структурнофункциональной схемы, исследование физических и технико-технологических возможностей построения аппаратуры. [c.627]
Теоретической основой для такого подхода явилось проведение аналогии между характеристиками и параметрами АС в низкочастотной области и характеристиками соответствующих фильтров верхних частот (т. е. фильтров, АЧХ которых претерпевает спад в сторону низких частот — см. гл. 3). Это позволило построить математическую модель АС для низких частот, т. е. идентифицировать ее передаточной дробио-рациоиальной функцией соответствующего фильтра верхних частот [4.6]. Появление единого системного подхода к анализу и синтезу низкочастотного оформления АС послужило основой для создания методов его оптимального проектиро вания с использованием ЭВМ [4.7, 4.8]. Суть этих методов состоит в том, что иа ЭВМ рассчитывают реальные характеристики акустической системы в области низких частот, являющиеся функцией электромеханических параметров низкочастотного громкоговорителя и конструктивных параметров корпуса, и путем целенаправленного изменения значений параметров системы, с учетом наложенных на них ограничений, минимизируется разница между реальными и желаемыми характеристиками системы. Благодаря применению методов нелинейного программирования и поисковой оптимизации определяются нанлучшне, т. е. потенциально достижимые в смысле выбранных критериев оптимальности, электромеханические и конструктивные параметры системы, что практически невозможно при традиционных методах проектирования. [c.104]
mash-xxl.info