Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы" (стр. 7 из 12). Методы оптимизации лабораторный практикум

Методы оптимизации функций одной переменной - Лабораторный практикум

Метод равномерного поиска

Этот метод основан на том, что переменной x присваиваются значения x+∆x с шагом ∆x = const и вычисляются значения F(x). Если F(x n+1)>F(xn), переменной x даётся новое приращение. Как только F(xn+1)станет меньше F(x) поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Метод поразрядного приближения

Этот метод является разновидностью метода равномерного поиска и реализуется следующим алгоритмом:

Задаём начальное приближение x=x₀ слева от максимума F(x) и вычисляем F(x₀). Задаём D=h, где h=∆x – начальный шаг поиска.
Полагаем, что G=F(xn), где вначале F(xn)=F(x₀), задаём x=x+D и вычисляем F(x n+1)=F(x).
Проверяем условие F(x n₊₁)>G; если оно выполняется, идём к п.2, если нет, то к п.4.

Полагаем D=-D/4. Проверяем условие |D|>E/4, где E – заданная погрешность вычисления xn в точке максимума. Если оно выполняется, идём к п.2, т.е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполняется, процесс вычисления заканчиваем.

Метод дихотомии

Метод дихотомии (деление интервала поиска [a, b] пополам) реализуется следующим алгоритмом:

Проверяем условие |b-a|n. Если это условие выполняется, идём к п.6; если не выполняется, идём к п.2.
Делим интервал поиска [a, b] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки

x=(a + b)/2

x1=(a + b - E)/2 и x2=(a + b + E)/2

Для этих значений x вычисляем F(x₁)>F(x₂).
Проверяем условие F(x₁)>F(x₂). Если оно выполняется, полагаем b=x₂ и идём к п.1. Если не выполняется, идём к п.5.
Полагаем a=x₁ и идём к п.1.
Выводим на печать xn=(a+b)/2 и вычисляем F(xn).

Метод Фибоначчи

В методе Фибоначчи точка деления интервала исследования определяется с каждым новым расчётом (в методе дихотомии необходимо на каждом шаге выполнять два расчёта). В интервал исследования попадет предыдущий расчёт и для продолжения поиска достаточно произвести расчёт симметрично имеющемуся.

Допустим, задано число расчётов (шагов) N. Необходимо их произвести так, чтобы интервал, в котором лежит оптимум, был минимальным. Числа Фибоначчи, используемые в этом методе, определяются следующим образом:

FN=FN-1+FN-2

F0=F1=1

Алгоритм метода Фибоначчи состоит из следующих этапов:

Изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают 1=X₀/FN, или если задана длина l, в котором лежит оптимум, находят его на исходном интервале длиной X₀. Для этого, разделив X₀ на 1, находят ближайшее большее число Фибоначчи FN,а по нему определяют N – число необходимых расчётов для определения интервала.
Расставляют первые две точки и на интервале исследования X0 на расстоянии FN-2 от конца b.
Вычисляют значение целевой функции в этих точках для сужения интервала исследования. Пусть > , тогда интервал [, FN] исключается из рассмотрения.
На новом интервале исследования снова расставляют две точки и , но в одной из них уже известно значение целевой функции = .

Переходят к этапу 3 и т.д., пока не достигают искомого интервала, в котором находится значение переменной, максимизирующее её целевую функцию.

На рис. 6 показан процесс сужения интервала исследования:

Рис. 6. Процесс сужения интервала исследования.

Последний N–й расчёт определяет интервал длиной l, в котором находится экстремум целевой функции.

topuch.ru

Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

2.2 Анализ программных средств

В наше время практически никакой, даже самый маленький проект в программировании выполняется с помощью специализированных сред пограммирования. Для создания программного продукта в рамках архитектуры клиент-сервер необходимо подобрать программные средства, которые будут использоваться в дипломной работе.

Выбор основывается на способности программной среды выполнять поставленные задачи в рамках выбранной архитектуры.

2.2.1 Свободное программное обеспечение

В дипломном проекте используется свободное (свободно распространяемое) программное обеспечение. В последнее время в мире все большее развитие получило движение за свободное программное обеспечение. «Свободное программное обеспечение» означает свободу, а не цену. «Свобода ПО» означает право пользователя свободно запускать, копировать, распространять, изучать, изменять и улучшать его.

В настоящее время большинство создаваемых в мире программных продуктов распространяется потребителям в соответствии с условиями пользовательского соглашения. Обычно это соглашение закрепляет программный продукт как объект авторского права. Этот объект не передается в собственность потребителю, а принадлежит изговотовителю, а передается только права использовать этот продукт на определенных условиях. Эти условия, как правило, запрещают практически все другие действия с программами, кроме тех, для которых она предназначена.

Философия свободного программного обеспечения обращается не к личной выгоде разработчиков программ, а к общественной выгоде от программирования как рода деятельности. При этом приводятся убедительные доводы о том, что выгода общества от перехода к модели бесплатного программного обеспечения настаивает перевешивает ту выгоду, которую оно получает от работы по модели авторского права и собственности в этой сфере.

Основными общественными организациями, продвигающими свободное программное обеспечение, являются международные Free software foundation (FSF) и проект GNU, цель которого — создание полностью свободной операционной системы. С большим количеством материалов по данной теме можно ознакомиться на сайтах этих организаций в интернете.

2.2.2 Серверные программные средства

Для реализации клиент-серверной модели можно пойти путем создания отдельно клиентской части, отдельно серверной части и разработать протокол на уровне операционной системы, посредством которого эти части будут сообщаться.

Это наиболее прямолинейный способ, но возможно упростить задачу путем использования готовых решений, если они позволяют сократить трудозатраты.

Преимущества и недостатки этих двух подходов представлены для сравнения в таблице 2.2.

Таблица 2.2 Преимущества и недостатки готовых решений

Как можно видеть, при небольших недостатках подход с использованием готовых решений дает преимущество, заключающееся в простоте разработки и высокой надежности, которая связана с использованием известных и хорошо зарекомендовавших себя продуктов.

Из общедоступных средств разработки приложений, наиболее универсальным и простым в использовании является язык HTML. Он позволяет описывать пользовательский интерфейс стандартным способом, который можно отобразить на широком спектре устройств, в том числе на компьютерах с помощью различных программ и операционных систем.

Для передачи форм в формате HTML и программ на клиентскую сторону используется HTTP сервер, в качестве которого могут выступать программы разных производителей, в том числе свободно распространяемые. В таблице приведены наиболее распространенные программы.

Таблица 2.3 Сравнение HTTP-серверов

Как мы видим, Apache и ngnix более универсальны, но требуют более тщательной настройки. В дипломной работе используется веб-сервер Apache, но возможен переход и к другому веб-серверу, если он будет поддерживать используемые технологии.

Для реализации серверной логики используется язык программирования PHP, как универсальный язык, применимый в широком спектре задач. Язык позволяет сохранять информацию в памяти сервера во время работы клиентов с данными и сохранять отчетность на диск по завершении операций.

2.2.3 Клиентские программные средства

Для отображения пользовательского интерфейса, организации диалога с пользователем используется веб-браузер. Требования к нему заключаются в поддержке следующих технологий:

- Javascript

- CSS

- XSLT

- Cookies

Данным требованиям удовлетворяют наиболее популярные веб браузеры, созданные в последнее время, работа программ тестировалась в браузерах Mozilla Firefox версий 2 и 3 и Microsoft Internet Explorer версий 6 и 7.

Javascript — это язык программирования, единственный в настоящее время, который используется в веб-браузерах для программирования действий на HTML страницах. Язык обладает богатыми возможностями, поддерживает работу с объектами и позволяет подключать дополнительные библиотеки, реализующие в готовом виде многие требуемые операции.

При создании форм приложений в формате HTML в составе программного продукта желательно, чтобы эти страницы имели одинаковое оформление элементов управления и отображения информации. В настоящее время для этого разработана технология CSS (Cascading Style Sheets), которая описывает задание общих параметров отображения на уровнях иерархии элементов управления.

Условия задания требуют отображения составленных программой графиков, но у различных веб-браузеров до сих пор нет единой реализации набора процедур для использования возможностей рисования. Наиболее распространенная модель, SVG, работает в большинстве браузеров, но не работает в Microsoft Internet Explorer. Поскольку данный браузер широко используется на практике, то игнорирование его недопустимо. Поэтому применяется специальная библиотека Dojo, которая реализует рисование графиков в любом веб-браузере, используя технологии SVG, VML, Silverlight, когда они доступны.

Также используется библиотека Jquery, облегчающая написание кода работы с элементами управления в окнах программы и выполнение запросов на сервер.

2.3 Описание практикума

В соответствии с клиент-серверной архитектурой, основу практикума составляет серверная часть, которая хранит и передает клиентской части по требованию составленные программы и модули интерфейса пользователя.

Клиентская часть практикума обеспечивает работу пользовательского интерфейса и позволяет пользователям подключаться к серверной части и выполнять выданное им задание (рис 2.1).

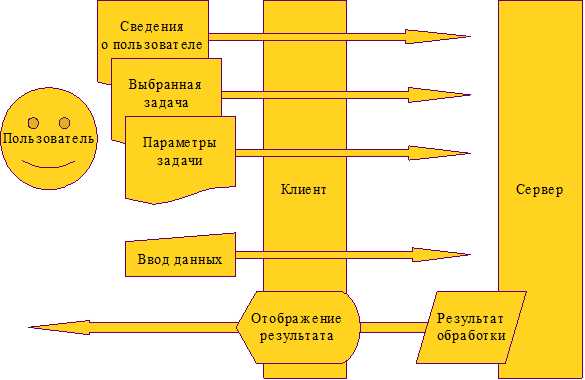
Рисунок 2.1 Клиент-серверная архитектура

Библиотека алгоритмов, использующаяся в практикуме, состоит главным образом из алгоритмов расчета методов оптимизации и алгоритмов построения линий уровня, которые хранятся в библиотеке алгоритмов. Серверная часть использует алгоритмы расчета методов оптимизации для работы методов, а клиентская часть отвечает за рисование линий уровня и использует соответствующие алгоритмы. Общая схема работы алгоритмической части представлена на рис.2.2

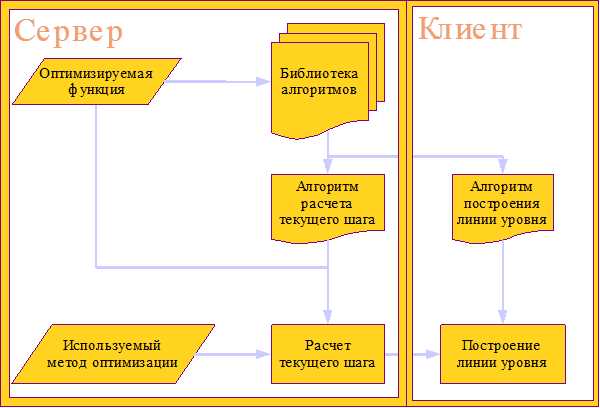
Рисунок 2.2.Алгоритмическая часть

По завершении работы пользователя с клиентской частью практикума серверная часть создает протокол работы, который записывается в базу данных протоколов для последующего анализа.

Также в состав практикума входит справочная система, содержащая основные сведения по работе с практикумом.

Общая последовательность операций при работе с практикумом представлен на рис. 2.3

Рисунок 2.3. Функциональная схема практикума

2.3.1 Описание серверной части

Серверная часть состоит из набора HTML-страниц программ на языке PHP. HTML-страницы обеспечивают отображение пользовательского интерфейса и справочной системы, а PHP-программы — хранение информации о проводимых работах, произведение математических расчетов и ведение отчетности.

mirznanii.com

Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы

Введение

В современном мире постоянно происходило совершенствование системы образования. Происходит модернизация старых, поиск новых способов обучения, способных улучшить сделать образовательный процесс более эффективным.

В настоящее время активно идут процессы внедрения в образовательный процесс компьютерных технологий. Компьютеры, разработанные первоначально для автоматизации вычислительных операций, с развитием средств мультимедиа превратились в мощнейший инструмент обработки информации различного рода. Свое применение они нашли и в сфере образования, предоставив свои возможности при работе с объемом человеческих знаний, накопленных за всю историю человечества.

Использование информационных технологий позволяет заменить часть ручного труда преподавателя трудом машинным, который, как и в других сферах, обходится дешевле, и, следовательно, более эффективен. Машины не устают, готовы к работе в любое время, не совершают арифметических ошибок и способны обладать огромными объемами памяти. Поэтому они внедряются в учебный процесс там, где это возможно.

Большое развитие компьютерные технологии получили в сфере дистанционного обучения. С появлением компьютерных сетей дистанционное обучение, подразумевающее работу обучающего с обучаемым на расстоянии, получило возможность мгновенной передачи информации между ними. Это позволило оперативно предоставлять учебные материалы и проводить контроль полученных знаний при снижении расходов на транспорт и связь.

Когда мы говорим о сетевых технологиях, то прежде всего имеем ввиду сеть интернет. Эта сеть, связывающая компьютеры по всему миру, позволяет организовать дистанционный учебный процесс практически в любой точке планеты в кратчайшие сроки.

Использование интернет-технологий также помогает в расширении виртуального образовательного пространства, ввиду того, что знания и учебные материалы из разных источников можно моментально получить в одном месте, стоит лишь правильно сформировать поисковый запрос. Данное обстоятельство несомненно способствует творческому процессу обучения и самостоятельной работе обучаемых в виртуальном образовательном пространстве.

Системы компьютерного дистанционного обучения в результате развития приняли различные формы, предназначенные для выполнения соответствующих задач, это и компьютерные учебники, содержащие учебные материалы в оптимизированной для наилучшего восприятия мультимедийной форме, и системы тестирования, обеспечивающие контроль знаний обучаемых путем анализа ответа на серии тематических вопросов, и лабораторные практикумы, обеспечивающие получение практических навыков использования полученных знаний.

В сфере информационных технологий зачастую при разработке нового продукта можно использовать готовые решения, которые поставляются в виде некоторой оболочки и наполняются содержимым по заданной тематике. Если использование готовых решений представляется затруднительным в связи с особенностями предметной области, приходится создавать новые программные продукты, позволяющие учесть эти особенности.

В направлении информатизации сферы образования работают сейчас практически все гуманитарные и технические учебные заведения разных стран. Разработки в этом направлении ведутся и в Московском авиационном институте. Кафедра «Математическая кибернетика» факультета «Прикладная математика и физика» института в течении многих лет разрабатывает учебные материалы с использованием компьютерных технологий. За это время создан комплекс компьютерных пособий и учебников, охватывающих предметы, читаемые преподавателями кафедры. Комплекс, включающий в себя более 70 компьютерных учебников, поддерживает 8 разделов курса "Теория управления", 7 разделов курса "Системный анализ", 3 раздела курса "Линейная алгебра и аналитическая геометрия", а также курсы "Теория графов", "Теория функций комплексного переменного", "Линейное программирование", "Линейные дифференциальные уравнения" и другие. Также функционирует кафедральных сайт в интернете, позволяющий студентам и преподавателям института обмениваться информацией дистанционно. В настоящее время на кафедре ведется работа по созданию других средств обучения с применением информационных технологий.

Кафедра «Математическая кибернетика» факультета «Прикладная математика и физика» института читает студентам курс «Методы оптимизации», изучающий методы оптимизации математических функций. На кафедре был создан практикум по этому курсу в среде Microsoft DOS, позволяющий студентам изучать методы на примерах, работая за компьютером в терминальном классе. В рамках дипломного проекта поставлена задача создания аналогичного практикума, работающего в сетевом режиме с целью упростить проведение работ. Также требуется расширить функционал имеющегося практикума для достижения большей наглядности примеров.

В рамках дипломного проекта требуется:

Изучить описываемые методы оптимизации и составить документацию по ним в мультимедийной форме.
Разработать архитектуру практикума
Разработать пользовательский интерфейс
Выбрать программные средства для разработки и составить алгоритмы

Раздел 1 содержит теоретические сведения о математических методах поиска безусловного экстремума функций многих переменных. Приводятся алгоритмы, графические иллюстрации и условия окончания методов.

Раздел 2 содержит описание практической части разработанного практикума. Проводится анализ современных программных архитектур, обоснование выбора клиент-серверной модели, анализ и выбор программных сред. Также приводится описание пользовательского интерфейса, форм отчетности и справочной системы практикума.

Раздел 3 содержит расчет экономических показателей, связанных с выполнением дипломного проекта.

В разделе 4 описаны вредные воздействия, возникающие при использовании информационных технологий в обучении и способы их сокращения.

1. Теоретическая часть

Решение задачи о поиске безусловного экстремума функции многих переменных с помощью необходимых и достаточных условий приводит к необходимости решать систему нелинейных уравнений с неизвестными с последующей проверкой знакоопределенности матрицы Гессе . Как правило, для достаточно сложных функций такая процедура решения задачи достаточно трудоемка и подразумевает численное решение нескольких задач. Поэтому возникает необходимость использовать так называемые прямые или численные методы безусловной оптимизации, которые позволяют найти стационарные точки функции, не используя аппарат необходимых и достаточных условий экстремума.

Компьютерный лабораторный практикум предназначен для студентов технических специальностей вузов и позволяет в наглядной и доступной форме представить численные алгоритмы отыскания экстремумов. Особенностью практикума является интерактивная форма реализации алгоритмов, при которой студент на каждой итерации принимает решение о выборе параметров методов, основываясь на числовой и графической информации о ходе процесса оптимизации.

Целью лабораторного практикума является изучение студентами прямых методов поиска безусловного экстремума двух типов функций:

Для достижения цели студент должен, изменяя параметры методов, добиться выполнения критерия окончания счета для каждого метода с одной и той же заданной точностью , из одной и той же начальной точки, за заданное для каждого метода число итераций N.

Методы, реализованные в лабораторном практикуме

Прямые методы, представленные в практикуме имеют один и тот же алгоритм

где

и отличаются друг от друга способом задания и выбором .

Алгоритм работы прямых методов схематически изображен на рис. 1.1

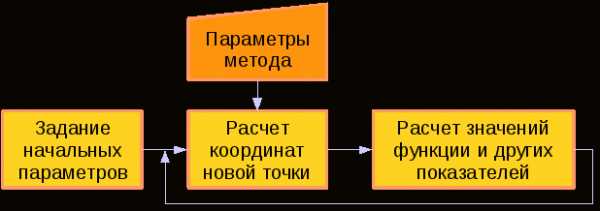
Рисунок 3.1. Алгоритм работы прямых методов

В практикуме реализованы:

методы первого порядка, использующие информацию о 1-х производных функции :
- метод градиентного спуска;
- метод наискорейшего градиентного спуска;
- метод покоординатного спуска;
- метод Гаусса-Зейделя;
- метод сопряженных градиентов.
методы второго порядка, использующие для своей реализации информацию о 1-х и 2-х производных функции :

продолжение

ua.coolreferat.com