Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 9. Методы одномерной оптимизации

Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 9

Процесс поиска продолжается до тех пор, пока , , не станут близки к нулю или пока не будет достигнута граница области задания переменных.

В алгоритме с автоматическим уточнением шага величину уточняют так, чтобы изменение направления градиента в соседних точках и улучшающей последовательности составляло (рис 3.7)

Рисунок 3.8 – Изменение направления градиента в соседних

точках

Должно быть

где – скалярное произведение векторов.

;

Если ;

если ;

если ,

где .

Критерии окончания поиска оптимума:

; (3.14)

,; (3.15)

; (3.16)

; (3.17)

где – норма вектора.

Поиск завершается при выполнении одного из условий (3.14) – (3.17).

Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции . Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.

3.2.3 Метод наискорейшего спуска

Метод наискорейшего спуска предложен американскими специалистами Дж. Боксом и К. Уилсоном как синтез лучших свойств градиентного метода и метода релаксации.

Недостатком градиентного метода заключается в том, что на каждом шаге надо вычислять все производные функции и определять направление градиента, что при большом числе переменных эта трудоемкая операция. Метод релаксации в том смысле обладает определенным достоинством, так как при движении вдоль выбранного осевого направления не требует вычислений производных после каждого шага. Однако в данном случае движение происходит не в оптимальном направлении, поскольку градиент в общем случае не совпадает с осевым направлением.

Метод наискорейшего спуска (крутого восхождения) сочетает основные идеи методов релаксации и градиента и заключается в следующем. Так же как в градиентном методе, в начальной точке определяет направление градиента и перемещается в этом (при поиске максимума) или в противоположном (при поиске минимума) направлении. Однако перемещаются не на один шаг, а несколько шагов (как в методе релаксации). После каждого шага оценивается только величина критерия , производные не вычисляются (рис. 3.8)

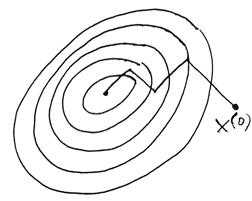
Рисунок 3.9 – Траектория движения к оптимуму в методе наискорейшего спуска

, , (3.18)

где – вектор точки, в которой последний раз вычислялся градиент .

В алгоритме (3.18) знак “+” – принимается при поиске максимума, а знак “-” – при поиске минимума. В направлении градиента выполняют шаги пока выполняется условие (при поиске минимума)

(3.19)

При нарушении условия (3.19) в последней точке определяют новое направление градиента и процедуру поиска повторяют.

Критерием окончания поиска может служить одно из условий (6,14) – (6,17) градиентного спуска.

Рассмотрим возможность улучшения алгоритма поиска Итерационный поиск (6.18) в векторной форме в точке имеет вид

(3.20)

С учетом этого можно определить значение в точке :

(3.21)

Поскольку и определены, то значение целевой функции в следующей точке

оказывается функцией только одного параметра – шага спуска (рис. 6.9). Применяя какой-нибудь метод однометрической оптимизации определяем величину оптимального шага

и координаты новой точки

Рисунок 3.10 – Характер зависимости целевой функции от величины шага поиска

Аналогично находим:

Вычислив в новой точке градиент , имеем

Эта процедура повторяется до выполнения одного из условий (3.14) – (3.17)

Заметим, что центральным звеном рассматриваемого алгоритма является поиск минимума функции одной переменной, что существенно увеличивает быстродействие алгоритма поиска оптимума методом наискорейшего спуска.

Этот метод, также как и другие методы градиентного спуска, определяет локальный минимум функции . Это связано с зависимостью всего пути спуска . Для определения других локальных минимумов необходимо производить поиск из других начальных точек.

3.3. Безградиентные методы оптимизации поиска

До сих пор рассматривались методы поиска оптимума, в которых производился предварительный анализ производных функций цели по всем независимым переменным для определения направления и величины шага поиска. Это связано с необходимостью выполнения большого объёма вычислений, что приводит к увеличению времени поиска.

Кроме того, при оптимизации объекта в условиях отсутствия его математического описания, погрешность вычисления производной как разности значений и критерия оптимальности может достигать до сотен процентов из-за неизбежных погрешностей при измерений величин, характеризующих этот критерий. Причём это может иметь место даже при небольшой относительной погрешности вычислений значения критерия оптимальности. Это может привести к существенным ошибкам в определении направления движения к оптимуму с помощью градиентных методов.

Существует другая группа методов – безградиентные методы, использующие в процессе поиска информацию, получаемую не при анализе производных, а от сравнительной оценки критерия оптимальности в результате выполнения очередного шага. К ним относятся методы сканирования, покоординатного спуска (Гаусса- Зейделя), симплекса.

3.3.1 Метод сканирования

Идея алгоритма перебора крайне проста. Вычисляют значения функции в конечном числе точек области Dx (в узлах координатной сетки).Из вычисленных значений выбирают наименьшее (наибольшее) . Координаты соответствующего узла сетки – это координаты экстремума, определённые с точностью до , где – h шаг сетки (рис. 6.10).

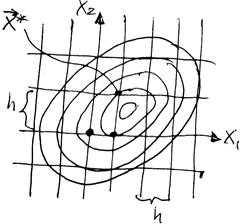
Рисунок 3.11 – Поиск оптимума на сетке переменных

Точность определения точки минимума, причем глобального, зависит от плотности наполнения области Dx дискретным множеством , то есть от величины шага h координатной сетки, тем выше точность определения положения оптимума, однако при уменьшении h быстро растёт объём вычислений. Если интервал изменения каждой переменной разбить К равных частей, то h равно

При этом необходимое количество вычислений I(x) равно .

vunivere.ru

Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 3

где e – заданная погрешность определения экстремума, то задачу отыскания экстремума можно считать выполненной. При этом x*=x1+Δx.

Если же условие (1.11) не соблюдается, то это означает, что исходное предположение о квадратичности целевой функции не выполняется и следует продолжать процесс поиска, то есть выполнить следующий цикл, но построение модели производить в окрестности точки x*=x1. Эта процедура повторяется до тех пор, пока не выполнится условие (1.11).

Вполне очевидно, что критерием окончания процесса поиска экстремума может служить выполнение условия

(1.15)

Таким образом, с помощью итерационной процедуры значение x* уточняется до получения его с заданной погрешностью e.

2 Методы одномерной оптимизации на основе преобразования задач

Многие инженерные задачи связаны с оптимизацией при наличии различного вида ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. Однако, несмотря на это, процесс оптимизации становится более сложным, поскольку известные критерии оптимальности решения задачи безусловной оптимизации нельзя использовать при наличии ограничений. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом. Часто оптимум достигается в точке, не являющейся стационарной точкой функции. Указанные трудности наталкивают на мысль использовать безусловную оптимизацию вспомогательных функций, составленных с учётом ограничений, для отыскания точки условного оптимума.

Идея преобразования задачи с ограничениями в последовательность задач без ограничений представляется эффективной в связи с наличием надёжных методов безусловной оптимизации. Это позволяет отыскать условный оптимум с приемлемой точностью путём решения относительно небольшого числа не слишком сложных задач.

Ниже рассматривается задача нелинейного программирования следующего вида:

, , (2.1)

при ограничениях

, , ; (2.2)

, . (2.3)

Начнём рассмотрение с краткого обсуждения метода классического анализа поиска экстремума функции многих переменных без ограничений. Этот метод часто является неотъемлемой частью методов решения преобразованной задачи оптимизации.

2.1 Метод классического анализа.

Пусть целевая функция является непрерывной дифференцируемой функцией

(2.4)

Необходимые условия экстремума:

, . (2.5)

Решением этой системы уравнений определяют точки , соответствующие «подозрительным» экстремумам.

Чтобы сформировать достаточные условия рассмотрим матрицу вторых производных в точке (матрицу Гессе)

;

(2.6)

Поскольку

матрица Гессе симметрична относительно главной диагонали.

Обозначим определители диагональных миноров матрицы (2.6) через Δ1, Δ2,…, Δn

;

и т.д.

В общем случае определитель Δк имеет вид:

(2.7)

Чтобы установить тип экстремума достаточно определить знаки диагональных миноров (условие Сильвестра).

В точке функция имеет минимум, если

, , (2.8)

или максимум, если

,. (2.9)

Если же условия (2.8) и (2.9) не выполняются, но все определители Δк, , отличны от нуля (Δк ≠0, ), то в исследуемой точке функция не имеет экстремума. При обращении в нуль хотя бы одного из определителей Δк тип экстремума не определён, вопрос о наличии экстремума в исследуемой точке решается сложнее, с использованием производных более высокого порядка.

На практике обычно используют лишь необходимые условия – условия первого порядка совместно с некоторыми физическими соображениями, относящимися к конкретной задаче, ввиду сложности проверки достаточных условий – условий второго порядка.

В отдельных случаях может оказаться эффективным непосредственное вычисление в окрестности стационарных точек, где выполняются необходимые условия.

Эффективно использовать методы исследования функции – классического анализа когда относительно просто можно найти аналитическое выражение критерия оптимальности. Применение этих методов оказывается так же полезным при предварительном анализе и более сложных задач в первоначальном, относительно грубом приближении. Поэтому эти методы не теряют своего значения в теории оптимальных процессов по мере дальнейшего его развития.

2.2 Метод исключения переменных

Рассмотрим задачу оптимизации, в которой требуется найти экстремум критерия оптимальности

(2.10)

при ограничении в виде равенства

. (2.11)

Экстремум, который достигается функцией с учётом выполнения соотношения (2.11), связывающего между собой независимые переменные, называется условным или относительным в отличие от безусловного экстремума, имеющего место при отсутствии ограничений.

Поставленную задачу можно решить следующим образом. Можно решить уравнение (2.11) относительно какой-либо переменной, например хn, выразив его через остальные n-1 переменных х1, х2, …, хn-1

(2.12)

Подставляя затем это выражение в (2.10), получим функцию, которая будит зависеть только от переменных хί, , не связанных дополнительными условиями

(2.13)

Таким образом, устраняя ограничивающее условие(2.11), удалось и уменьшить размерность исходной оптимальной задачи и свести задачу с ограничениями к эквивалентной задаче безусловной оптимизации, что позволяет применить для решения методы классического анализа.

Часто имеется несколько ограничений в виде равенств

, . (2.14)

vunivere.ru

Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 7

Поисковые методы оптимизации составляют класс методов нелинейного программирования. Вспомним еще раз постановку задачи оптимизации:

(3.1)

при условиях

(3.2)

Часто критерий не имеет явного выражения, либо функции(3.1), (3.1) являются трудно вычислимыми нелинейными функциями. Задачи такого типа составляют предмет нелинейного программирования.

Как правило, решение задач нелинейного программирования может быть найдено только численными методами. В настоящее время для решения надобных задач разработано значительное число методов. Однако все еще не предоставляется возможным отдать предпочтенное какому-либо одному из них. Поисковые методы оптимизации основаны на постоянном перемещении в пространстве переменных в направлении к оптимальному значению функции. Различные методы поиска отличаются способом определения направления движения к оптимуму, размером шага и продолжительного поиска вдоль найденного направления, критериями окончания поиска, простотой алгоритмизации для ЭВМ.

Нормирование переменных. Переменные в конкретных задачах могут иметь самый различный физический смысл и разные единицы измерения. Поэтому при решении оптимальных задач численными методами целесообразно оперировать с их безразмерными нормализованными значениями.

Обычно для нормализации применяется возможный диапазон изменения значений независимых переменных

Вводя безразмерные переменные

; , (3.3)

исходную задачу (3.1), (3.2) выражают через них, решают преобразованную задачу, определяют оптимальное значения нормированных переменных , а через них оптимальные значения исходных переменных, :

;

при

Линии уровня. В соответствии с (3.1) критерий может рассматриваться как функция, определенная n-мерном пространстве переменных Поскольку наглядное графическое изображение n-мерного пространства отсутствует, обычно используется прием представления на плоском чертеже. Все методы оптимизации сводятся к тому, чтобы найти минимум или максимум, т.е. впадину или вершину на поверхности, описываемой уравнением . Эта поверхность называется поверхностью отклика. Линии, вдоль которых целевая функция сохраняет постоянное значение при изменении входящих в нее переменных, называются контурными линиями или линиями уровня.

Примеры линией уровня показаны на рис.3.1 (при отсутствии ограничений), на рис.3.2 (при наличии ограничений) и на рис.3.3 (в окрестности седловой точки).

Рисунок 3.2 – Линии уровня без ограничений

Рисунок 3.3 – Линии уровня с ограничениями

Рисунок 3.4 – Линии уровня в окрестностях седловой точки

Точки, в которых на одним направлениям имеет минимум, а по другим – максимум, называются Седловыми точками функции . В этой точке хотя выполняется необходимое условие экстремума функции в ней нет. Линии уровня, соответствующие разным значениям , не пересекаются. Внутри линии уровня, соответствующие числам I, больше, чем I, в случае максимума и меньше, чем I, в случае минимума.

Поисковые методы оптимизации основаны на постоянном перемещении в пространстве переменных в направление к оптимальному значению функции .

Различные методы поиска отличаются способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, критерия окончания поиска, простой алгоритмизации для ЭВМ.

Вычисление производных и градиента. В основу градиентных методов поиска оптимума положены вычисления и анализ производных , , вычисляются аналитически, если это не представляет особого труда, либо численным методом по приближенному соотношению, основанному на замене частных производных в точке отношениями конечных приращений. Для этого в точке поочерёдно изменяют переменные и вычисляют соответствующие приращения в точке

, , (3.4)

где

При применении нормализованных переменных в алгоритме оптимизации необходимо учесть соотношение (3.3) при вычислении , если она выражена через значения исходных физических переменных :

. (3.5)

Для вычисления производных удобно давать одно и то же приращение но всем независимым переменным , т.е.

тогда

Формула (3.4) дает лишь приближенное значение производной . Точность этого приближения зависит от приращения независимой переменной . Априорных способов предсказания наилучшего значения не существуют. Можно лишь заметить, что допустимое приращение по максимуму ограничено кривизной целевой функции в исследуемой точке (которая заранее не известна), а по минимуму- погрешностью вычисления значения функции (которая тоже заранее не известна и может существенно отличаться от погрешности задания значений в процессе поиска).

На практике для определения приемлемого значения (в особенности в начале поиска, когда произведение еще ни разу не находилось) используют метод дробления . Вычисляют значение производной с приращением . Расчет повторяют с . Если полученные значения производных различаются существенно, расчет повторяется с и т.д., пока не будет найдено приемлемое значение приращения . На последующих шагах это значение может уточняться.

Градиент в точке равен .

3.2 Градиентные методы оптимизации

3.2.1 Метод релаксации

Алгоритм метода заключается в отыскании осевого направления, вдоль которого целевая функция уменьшается наиболее сильно ( при поиске минимума). Рассмотрим задачу безусловной оптимизации

(3.6)

Для определения осевого направления в начальной точке поиска из области определяются производные , , по всем независимым переменным. Осевому направлению соответствует наибольшая по модулю производная .

Пусть – осевое направление, т.е. .

Если знак производной отрицательный, функция убывает в направлении оси, если положительный – в обратном направлении:

vunivere.ru

1. Прямые методы одномерной оптимизации. Сравнительный анализ методов оптимизации

Методы одномерной оптимизации - Доклад - Методы одномерной оптимизации

приобрестиДоклад - Методы одномерной оптимизациискачать (319.5 kb.)Доступные файлы (1):

n1.doc

Методы одномерной оптимизации.Постановка: требуется оптимизировать х (формальная постановка) - функция одной переменной

- целевая функция.Решение: найти х, при котором принимает оптимальное значение.

2 варианта:

минимизировать – задача минимизации;
максимизировать – задача максимизации.

Рассмотрим случай минимизации2 способа:

аналитический
численный

В аналитическом задается в виде формулы, в численном задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке. Пусть функция определена в некоторой области S (), в случае одномерной оптимизации S – интервал :

точка называется глобальным минимумом, если для
точка называется строгим глобальным минимумом, если для
точка называется локальным минимумом, если для
точка называется строгим локальным минимумом, если для

Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.

Аналитический способ нахождения локального минимума. - дифференцируема

- необходимое условие точки локального минимума.

Численные методы.Пусть функция задана на интервале , при этом существует такая точка , что на – монотонно убывает, а на – монотонно возрастает, то функция унимодальная.

а bЕсли из того что следует, что , то функция называется монотонно возрастающей. Если из того что следует, что , то функция называется монотонно убывающей.

Методы одномерного поиска.Разобьем и вычислим значение функции в каждой точке.

искомый минимумВ результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.

2) - после выполнения n шагов сокращение исходного интервала

- точность с которой надо найти решение задачи.N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).

Метод золотого сечения.Точки должны быть расположены на равном расстоянии.

а b

; ; ;

; - золотое сечение.а

- величина сокращения на каждом шаге

число итераций растет как логарифм функции.

Одномерная оптимизация с использованием производных.. Пусть целевая функция дифференцируема .

Методы для нахождения корня уравнения функции 1-ой производной от исходной. Нахождение локального минимума или максимума сводится к нахождению корней первой производной от данной

f’(x)=0Если f’(x) представляет собой многочлен, то уравнение называется алгебраическим (полиномиальным), если f’(x) представлена тригонометрическими, логарифмическими, показательными и т.п. функциями, то уравнение называется трансцендентным.( вдальнйшем вместо f’(x) будем употреблять f(x) )

Решение уравнения вида разбивается на два этапа:

отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;
вычисление выделенного корня с заданной точностью.

На первом этапе может помочь построение приближенного графика функции f(x) или, если функция достаточно сложная, то можно попытаться представить уравнение в виде и построить два графика и , тогда корнями уравнения будут абсциссы точек пересечения этих кривых.

Выбор интервалов, в которых имеется один и только один корень производится на основании известных свойств непрерывных функций:

Для вычисления выделенного корня существует множество приближенных методов. Все они вычисляют значение корня уравнения с заданной степенью точности , т.е. заданное количество цифр после запятой. Рассмотрим следующие методы:

половинного деления;
Ньютона.

Метод половинного деления

Суть метода половинного деления (дихотомии) заключается в следующем.

Отрезок делится пополам и за первое приближение корня принимается точка c, которая является серединой отрезка, т.е.. Если , это корень уравнения. Если нет, то далее выбирается тот из отрезков [a, c] или [c, b], на концах которого функция имеет разные знаки. Полученный отрезок снова делится пополам, и проводятся те же рассуждения. Деление продолжается до тех пор, пока длина отрезка не станет меньше заданного .

Графическая интерпретация метода представлена на рис. 1.1. Метод половинного деления реализуется в виде следующего алгоритма:

Если f(a)f(c) a, c], если нет, то корень лежит на интервале [c, b].

Если величина интервала не превышает некоторое достаточно малое число е, то найден корень с точностью е, иначе возврат к п.1.

Несмотря на простоту, этот метод требует слишком большого количества вычислений и не всегда позволяет найти решение с заданной точностью.

Блок-схема алгоритм решения уравнения методом деления пополам.

Метод Ньютона (метод касательной):Идея метода касательных состоит в следующем. Возьмем некоторую точку , участка , например, и проведем касательную к графику функции в точке . Уравнение касательной в точке имеет вид:

В качестве начального приближения корня уравнения примем абсциссу точки пересечения этой касательной с осью Ох. Тогда, полагая в уравнении касательной , можно найти абсциссу точки пересечения:

Это значение можно принять за следующее приближение . Далее касательная проводится через точку , абсцисса пересечения которой с осью Ох даст второе приближение корня , и так далее, пока не будет достигнута точность .

Алгоритм, реализующий метод касательных, можно представить так:

Уточняется значение корня по формуле .

Если абсолютное значение функции в найденной точке не превышает некоторое достаточно малое число , то найден корень с точностью , иначе возврат к п.2.

Алгоритм решения уравнения методом Ньютона

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРЗОВАНИЯ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

РЕФЕРАТ

По теме:

«Методы одномерной оптимизации »Выполнил: ********************

Руководитель: *************

г. Уфа. 2008 г.

Методы одномерной оптимизации

nashaucheba.ru

Методы одномерной оптимизации. Методы одномерной оптимизации на основе преобразования задач. Поисковые методы одномерной оптимизации, страница 10

Поэтому эффективное применение данного метода ограничивается задачами невысокой размерности (n=2-3). При большой размерности вектора требуется выполнение большого объёма вычислительной работы.

Пусть область Dx – геперкуб:

в котором ищется .Точность определения координат вектора , минимизирующего , положим равной 0,1. Тогда интервалы следует разбить на 10 частей с шагом h=0,1 плоскостями, ортогональными и вычислить во всех точках перечисления плоскостей значения . Всего потребуется вычислить в 11n точках. Пусть для нахождения I в каждой точке требуется примерно 102n арифметических операций. Тогда общее число арифметических операций алгоритма перебора примерно 11(n+2)n и при n=10 на ЭВМ с быстродействием 109 oп/c требуется примерно 104 с, т.е. примерно 167 минут непрерывной работы ЭВМ.

Иногда поиск осуществляется с переменным шагом сканирования. Вначале величина h выбирается достаточно большой, выполняется грубый поиск для локализации экстремума, а поиск в районе оптимума осуществляется с меньшим шагом.

Достоинства метода – возможность определения глобального оптимума и независимость поиска от вида оптимизируемой функции.

3.3.2 Метод Гаусса-Зейделя

Метод Гаусса-Зейделя, называемый также методом покоординатного спуска, аналогичен методу релаксации. Отличие заключается лишь в том что, в этом методе не определяется осевое направление, вдоль которого значение изменяется наиболее сильно. Поочерёдно изменяются все переменные.

Алгоритм поиска минимума следующий. Пусть ищется минимум . Устанавливается очерёдность изменения – и начальная точка поиска. Затем все переменные фиксируются на уровне , изменяется по алгоритму

; ; ; (3.22)

где – шаг изменяется , обычно не зависит от k.

После каждого шага вычисляется , сравнивается с предыдущим значением, критерия шаги продолжаются до достижения частного оптимума по xj = x1. В этой точке величина фиксируется и изменяется x2 до достижения оптимума по x2 и т.д. После того как достигается оптимум по последней переменной xn, снова изменяется x1 и весь цикл повторяется до тех пор, пока не будет найдена точка оптимума.

На рисунке 3.11 показан алгоритм поиска минимума для функции двух переменных.

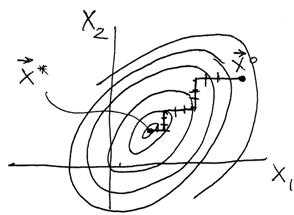
Рисунок 3.12 – Траектория движения к оптимуму в методе координатного спуска

Заметим что для функции двух переменных методы релаксации и Гаусса-Зейделя совпадают.

Если первый шаг изменения xj не улучшает значение критерия, т.е. , а , то выполняется шаг по xj в обратном направлении , т. е. Первый шаг пробный. Если и этот шаг неудачный, то переходят к изменению xj+1 и т.д.

Поиск заканчивают когда достигается точка , из которой при движении в любом осевом направлении улучшение критерия не наблюдается.

Рассмотрим вопрос улучшения алгоритма поиска .

Пусть в области допустимых решений D задано нулевое приближение .

Рассматриваем функцию при фиксированных значениях как функцию одной переменной x1, т. е.

(3.23)

Минимизируя находим значение , доставляющее минимум функцию (3.23):

;

Далее при фиксированных значениях рассматриваем как функцию одной переменной x2. Находим её минимум

;

Продолжая эту процедуру последовательно, после n шагов получаем точку , в которой выполняется условие

В результате одного шага покоординатного спуска происходит переход из начальной точки в точку . Если при этом оказывается, что

то начальная точка – точка, доставляющая минимум функцию .

Если ,то выполняется следующий шаг поко-ординатного спуска, в котором за начальную точку принимается , получаем и т.д. Этот процесс продолжается до тех пор, пока не выполнится какое-либо условие окончания поиска, например такое

, (3.24)

где – заданная точность.

или

(3.25)

Таким образом, поиск минимума функции одной переменной занимает центральное место в рассматриваемом алгоритме покоординатного спуска.

Простота метода и сравнительно небольшой объём вычислений обусловили его распространение в автоматических системах поиска.

3.3.3 Метод поиска по симплексу

Рассмотрим задачу

(3.26)

Симплексный метод является безградиентным методом, реализует процедуру прямого поиска оптимума на основе вычисления значения целевой функции. Предполагается, что непрерывна, а может как существовать, так и не существовать, поскольку соответствующие числовые значения не используются. Однако следует отметить, что симплексный метод можно применить для решения задач, в которых существует, но представляет собой сложную векторную функцию управляемых переменных. Наконец, предполагается, что функция унимодальна в рассматриваемой области. Если же метод применяется для анализа мультимодальных функций, то приходится ограничиваться идентификацией локальных оптимумов.

Симплексный метод относится к категории эвристических, которые реализуют процедуры поиска с помощью интуитивных геометрических представлений.

Первые попытки решения оптимизационных без ограничений на основе прямого поиска связаны с использованием процедуры сканирования, что является непригодной для решения задач с числом переменных превышающим 2.

Более полезная идея заключается в выборе базовой точки и оценивания значений в точках, окружающих базовую точку. Например, при решении задач с двумя переменными можно воспользоваться квадратным образцом (рис. 3.12), который является частным случаем кубического образца. В вершинах образца и базовой точке вычисляется значение .

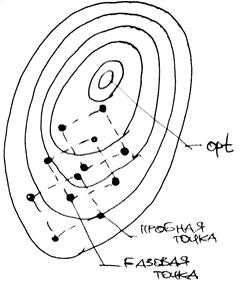
Рисунок 3.13 – Использование квадратного образца для поиска оптимума

Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Этот тип эволюционной оптимизации был использован Боксом и другими исследователями США для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой.

vunivere.ru