Справочник химика 21. Методы лагранжа методы оптимизации

5.2 Метод Лагранжа

Суть метода Лагранжа заключается в сведении задачи на условный экстремум к решению задачи безусловного экстремума. Рассмотрим модель нелинейного программирования:

(5.1)

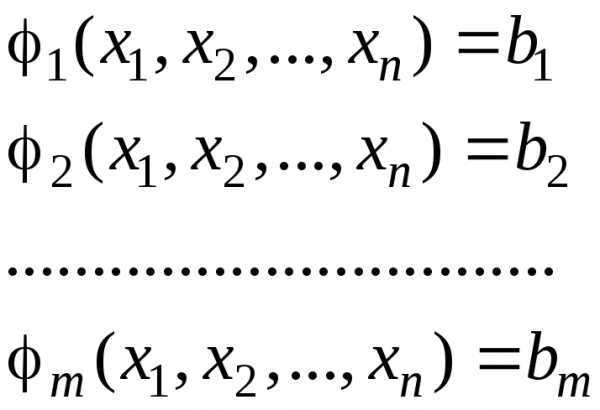(5.2)

где – известные функции,

а – заданные коэффициенты.

Отметим, что в данной постановке задачи ограничения заданы равенствами, отсутствует условие неотрицательности переменных. Кроме того, полагаем, что функции непрерывны со своими первыми частными производными.

Преобразуем условия (5.2) таким образом, чтобы в левых или правых частях равенств стоял ноль:

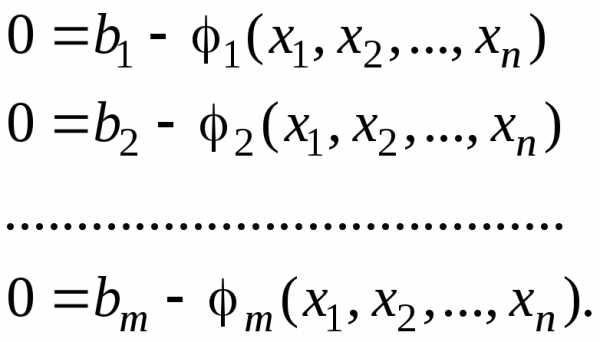(5.3)

Составим функцию Лагранжа. В нее входит целевая функция (5.1) и правые части ограничений (5.3), взятые соответственно с коэффициентами . Коэффициентов Лагранжа будет столько, сколько ограничений в задаче.

(5.4)

Точки экстремума функции (5.4) являются точками экстремума исходной задачи и наоборот: оптимальный план задачи (5.1)-(5.2) является точкой глобального экстремума функции Лагранжа.

. (5.5)

Действительно, пусть найдено решение задачи (5.1)-(5.2), тогда выполняются условия (5.3). Подставим планв функцию (5.4) и убедимся в справедливости равенства (5.5).

Таким образом, чтобы найти оптимальный план исходной задачи, необходимо исследовать на экстремум функцию Лагранжа. Функция имеет экстремальные значения в точках, где ее частные производные равны нулю. Такие точки называютсястационарными.

Определим частные производные функции (5.4)

После приравнивания нулю производных получим системуm+n уравнений сm+n неизвестными

,(5.6)

. (5.7)

В общем случае система (5.6)-(5.7) будем иметь несколько решений, куда войдут все максимумы и минимумы функции Лагранжа. Для того чтобы выделить глобальный максимум или минимум, во всех найденных точках вычисляют значения целевой функции. Наибольшее из этих значений будет глобальным максимумом, а наименьшее – глобальным минимумом. В некоторых случаях оказывается возможным использование достаточных условий строгого экстремуманепрерывных функций (см. ниже задачу 5.2):

пусть функция 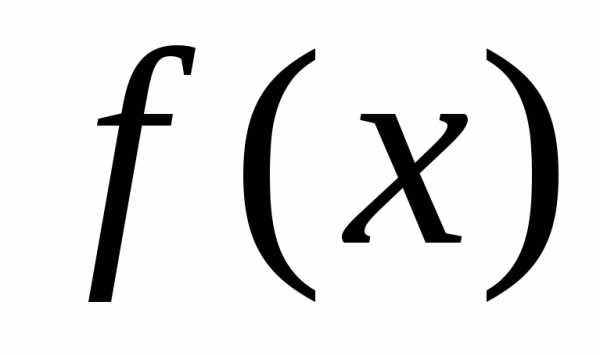непрерывна и дважды дифференцируема в некоторой окрестности своей стационарной точки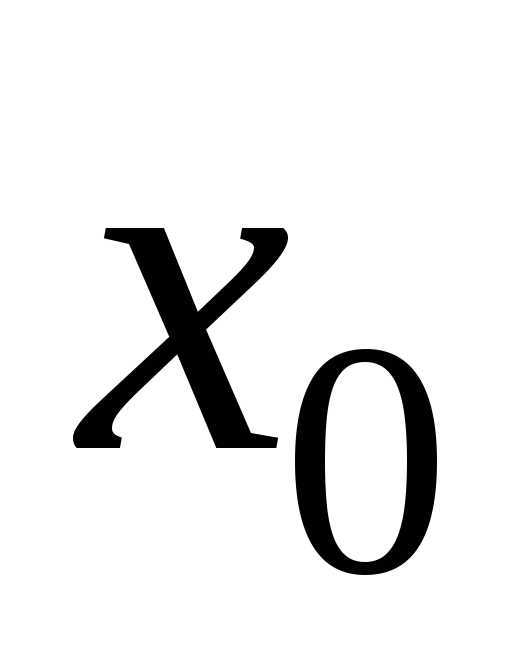( т.е.) ). Тогда:

а) если ,(5.8)

то 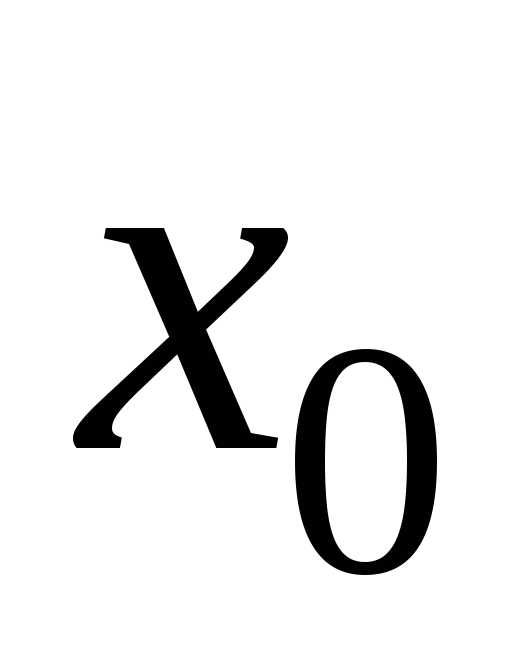– точка строгого максимума функции;

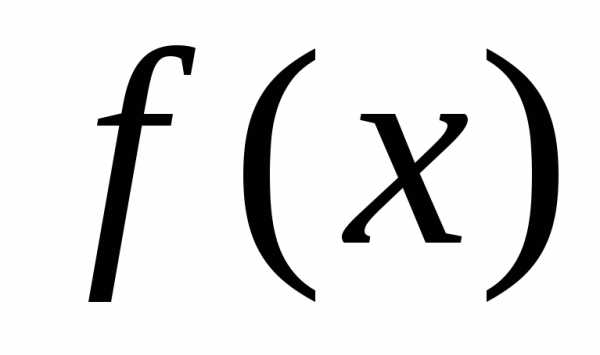б) если ,(5.9)

то 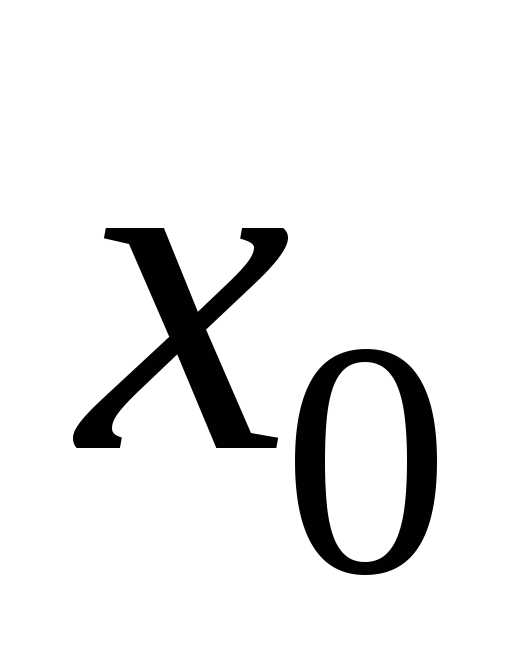– точка строгого минимума функции;

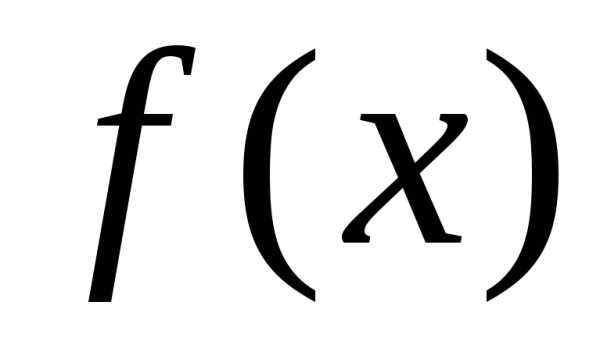г) если ,

то вопрос о наличии экстремума остается открытым.

Кроме того, некоторые решения системы (5.6)-(5.7) могут быть отрицательными. Что не согласуется с экономическим смыслом переменных. В этом случае следует проанализировать возможность замены отрицательных значений нулевыми.

Экономический смысл множителей Лагранжа. Оптимальное значение множителяпоказывает на сколько изменится значение критерияZ при увеличении или уменьшении ресурсаjна одну единицу, так как

Метод Лагранжа можно применять и в том случае, когда ограничения представляют собой неравенства. Так, нахождение экстремума функции при условиях

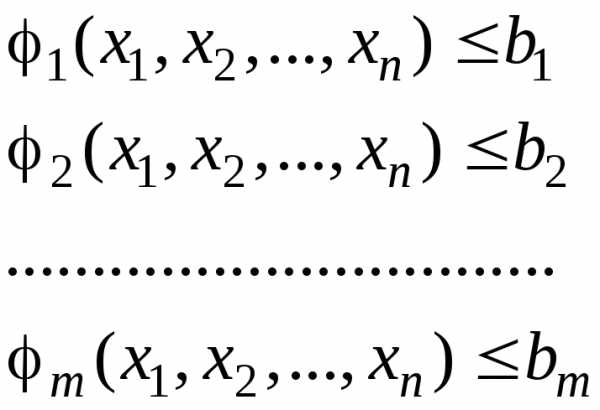выполняют в несколько этапов:

1. Определяют стационарные точки целевой функции, для чего решают систему уравнений

2. Из стационарных точек отбирают те, координаты которых удовлетворяют условиям

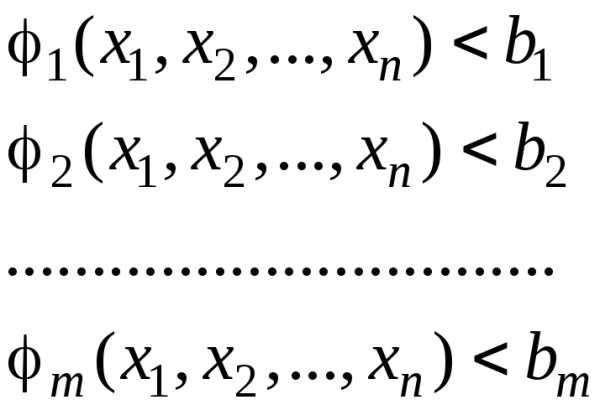
3. Методом Лагранжа решают задачу с ограничениями-равенствами (5.1)-(5.2).

4. Исследуют на глобальный максимум точки, найденные на втором и третьем этапах: сравнивают значения целевой функции в этих точках – наибольшее значение соответствует оптимальному плану.

Задача 5.1Решим методом Лагранжа задачу 1.3, рассмотренную в первом разделе. Оптимальное распределение водных ресурсов описывается математической моделью

Составим функцию Лагранжа

Найдем безусловный максимум этой функции. Для этого вычислим частные производные и приравняем их к нулю

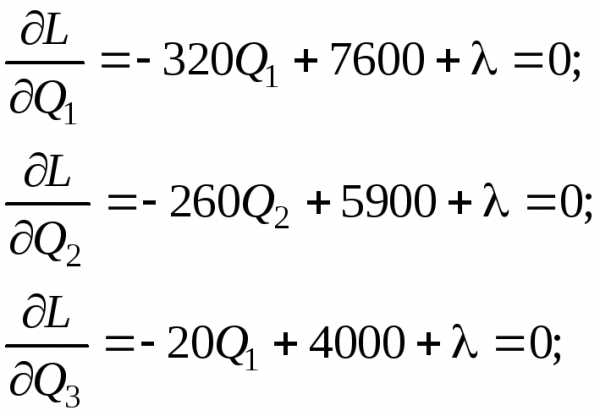Таким образом, получили систему линейных уравнений вида

Решение системы уравнений представляет собой оптимальный план распределения водных ресурсов по орошаемым участкам

, .

Величины 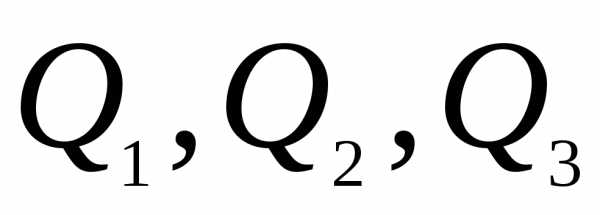измеряются в сотнях тысяч кубических метров. - величина чистого дохода на одну сотню тысяч кубических метров поливной воды. Следовательно, предельная цена 1 м3 оросительной воды равна ден. ед.

Максимальный дополнительный чистый доход от орошения составит

-160·12,262+7600·12,26-130·8,552+5900·8,55-10·16,192+4000·16,19=

= 172391,02 (ден. ед.)

Задача 5.2 Решить задачу нелинейного программирования

Ограничение представим в виде:

Составим функцию Лагранжа и определим ее частные производные

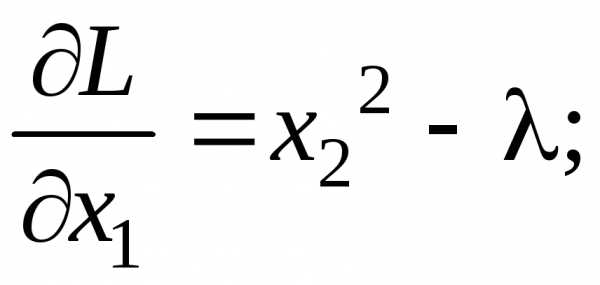
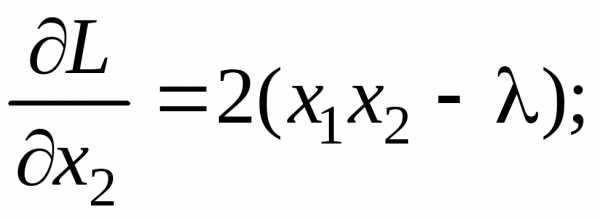
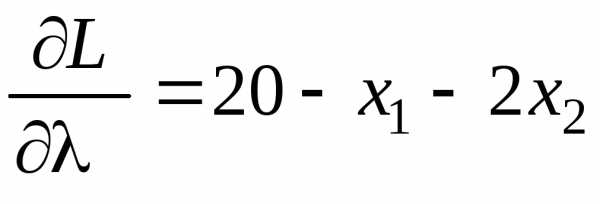Чтобы определить стационарные точки функции Лагранжа, следует приравнять нулю ее частные производные. В результате получим систему уравнений

Из первого уравнения следует

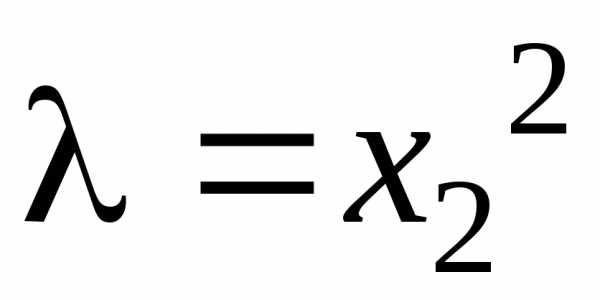. (5.10)

Выражение подставим во второе уравнение

откуда следует два решения для :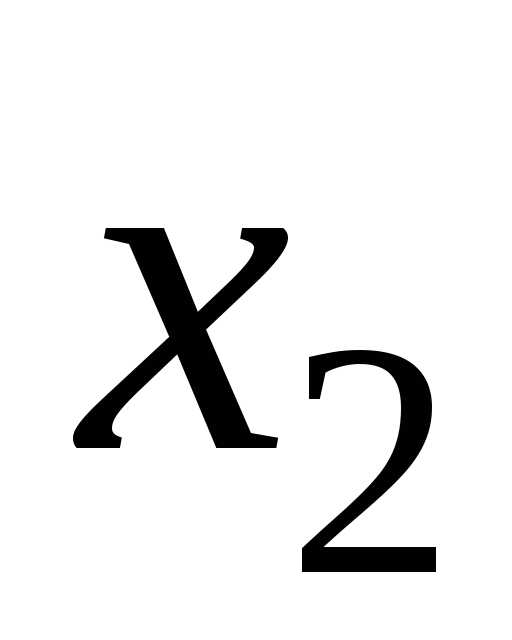

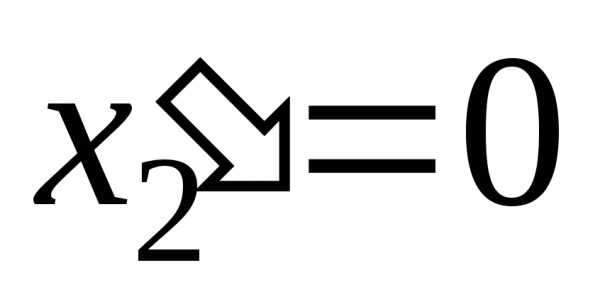и 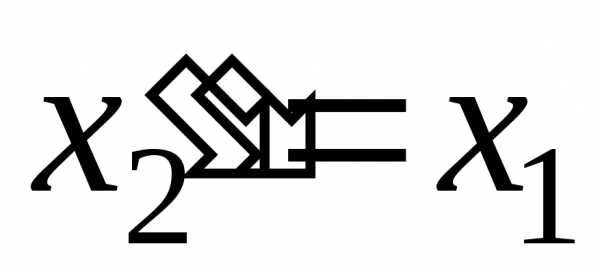. (5.11)

Подставив эти решения в третье уравнение, получим

, .

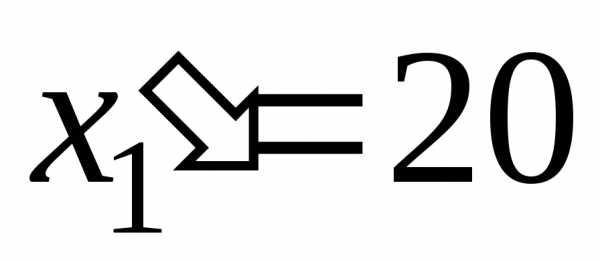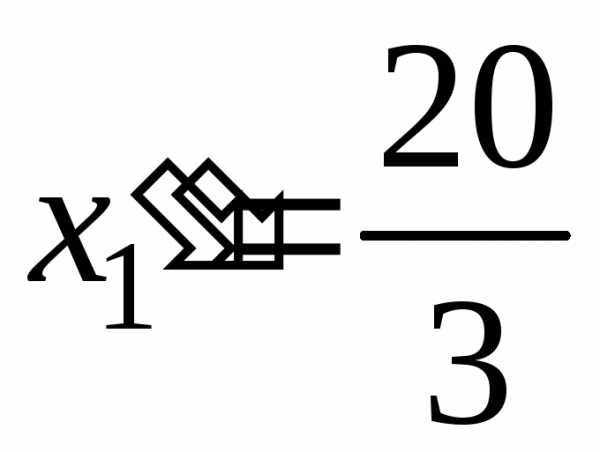Значения множителя Лагранжа и неизвестной 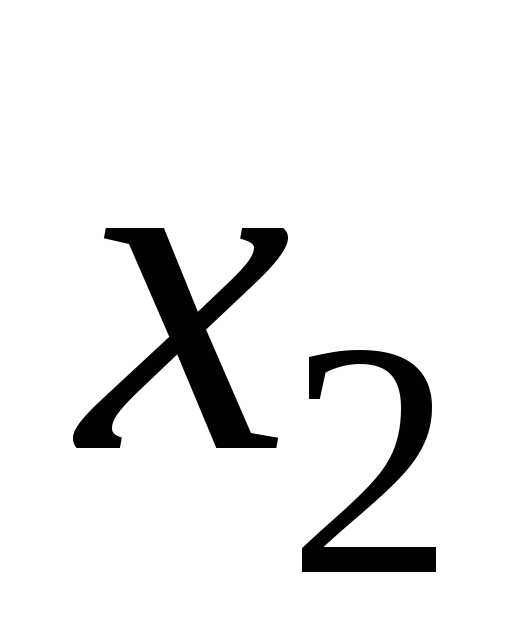вычислим по выражениям (5.10)-(5.11):

, ,,.

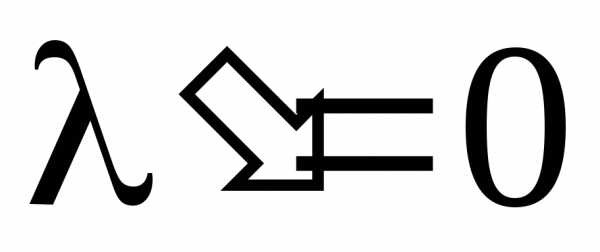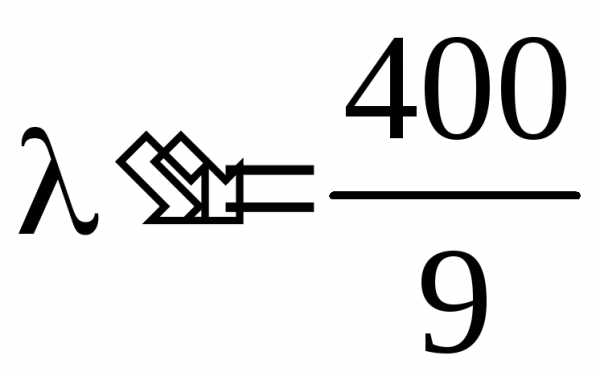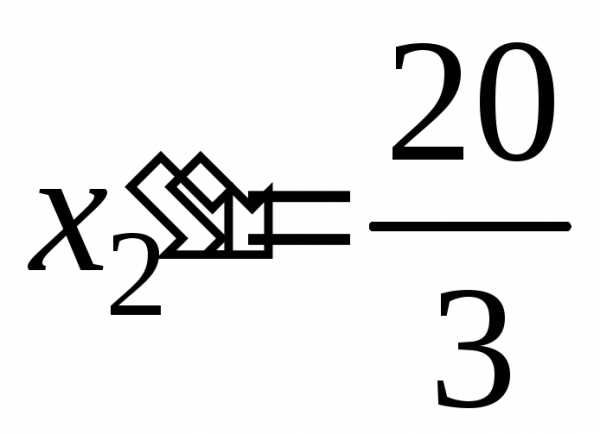Таким образом, получили две точки экстремума:

; .

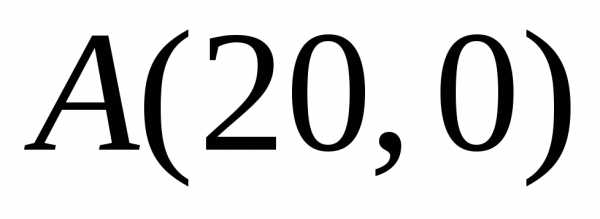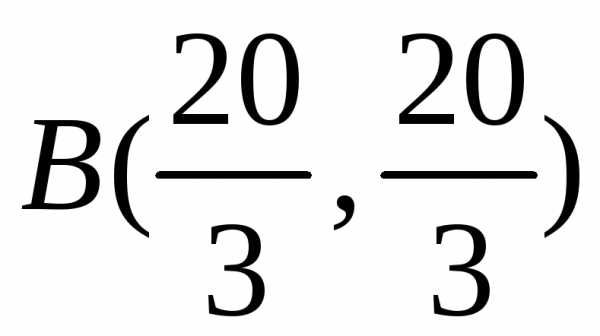Для того чтобы узнать являются ли данные точки точками максимума или минимум, воспользуемся достаточными условиями строгого экстремума (5.8)-(5.9). Предварительно выражение для 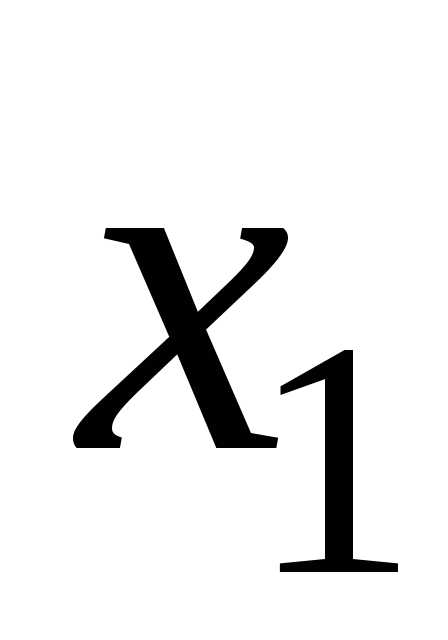, полученное из ограничения математической модели, подставим в целевую функцию

. (5.12)

Для проверки условий строгого экстремума следует определить знак второй производной функции (5.11) в найденных нами экстремальных точках 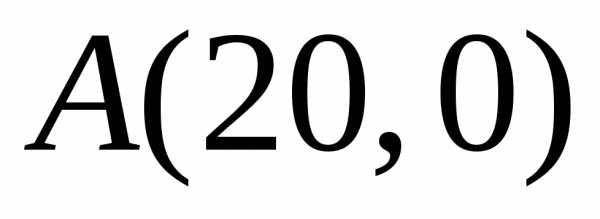и.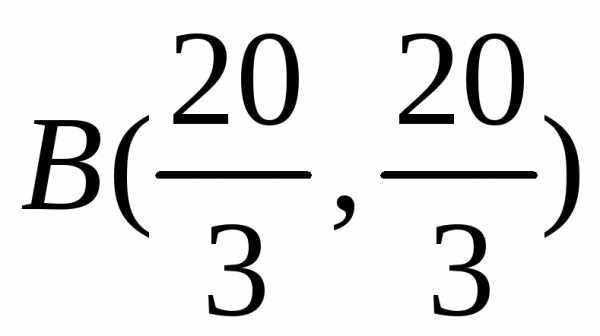

, ;

Таким образом, (·)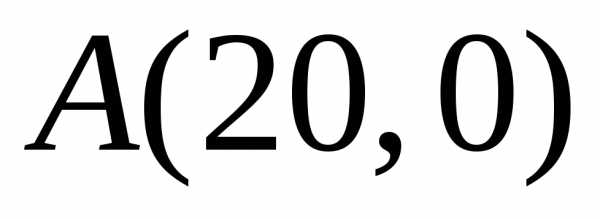является точкой минимума исходной задачи (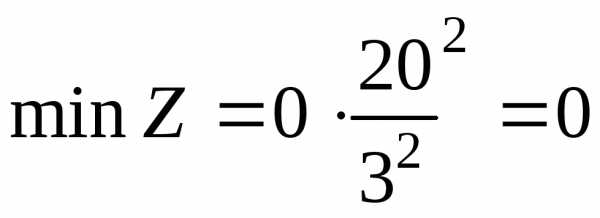), а (·)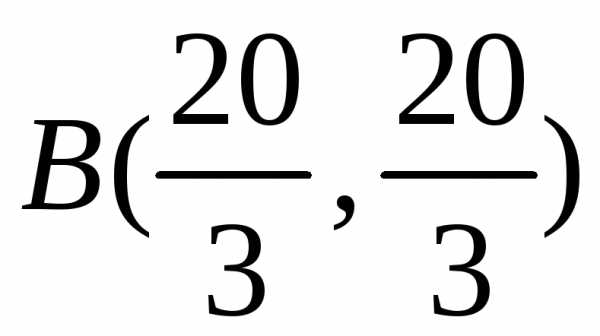– точкой максимума.

Оптимальный план:

, ,,

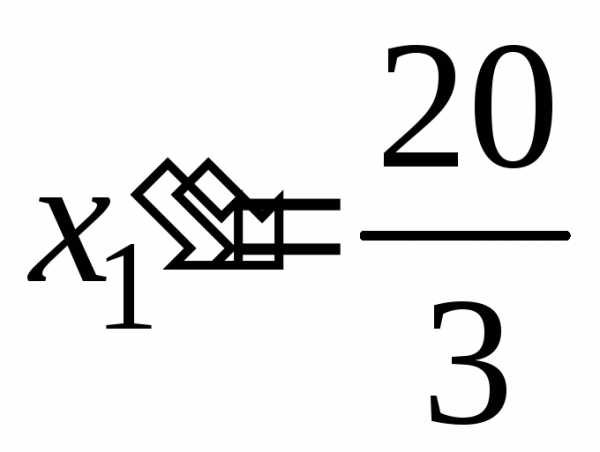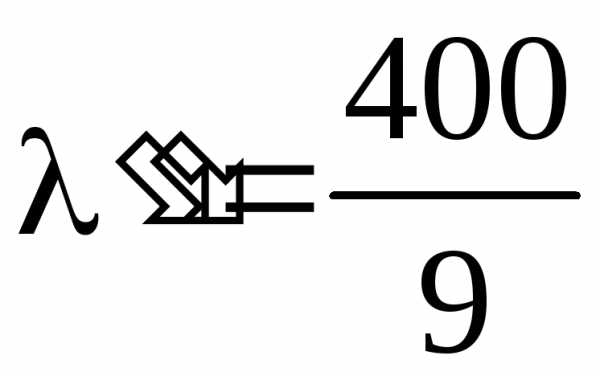studfiles.net

Множителей Лагранжа метод - Энциклопедия по экономике

Метод множителей Лагранжа состоит в получении условий оптимальности в несколько измененной, но эквивалентной форме. [c.46] В последние несколько десятилетий основные идеи метода множителей Лагранжа удалось перенести и на задачи с ограничениями типа неравенств, которые, как мы увидим в дальнейшем, более естественны для экономико-математических моделей. Сформулируем необходимое условие максимума функции U(x), где х е= Еп, при наличии ограничений [c.48]

Используем метод множителей Лагранжа для решения чрезвычайно простой линейной задачи оптимизации [c.49]

Как видно, описанный здесь метод решения, основанный на полном переборе вершин, является значительно более простым л эффективным, нежели непосредственное использование метода множителей Лагранжа. В то же время не следует считать, что решение задач линейного программирования является простым делом, состоящим просто в полном переборе вершин множества допустимых значений переменных. Для того чтобы понять это, достаточно заметить, что вершина множества допустимых точек (в том случае, когда это множество имеет внутренние точки) в задаче (4.22) — (4.24) связана с обращением в равенства п ограничений из их совокупности (4.23), (4.24). Таким образом, вообще говоря, число вершин множества (4.23), (4.24) может равняться числу различных сочетаний по п ограничений из общего числа т + п. Число различных сочетания [c.51]

Можно доказать и более общее утверждение о свойствах двойственных переменных. При описании метода множителей Лагранжа для задач с ограничениями типа равенств мы показали, что множитель Лагранжа равен производной критерия по правой части равенства. Этим же свойством множители Лагранжа обладают и в задачах линейного программирования [c.56]

Если и(у) >0 только при у > 0, то для решения задачи у имеем у > 0 и модель можно проанализировать при помощи описанного в 4 гл. 1 метода неопределенных множителей Лагранжа. Выпишем функцию Лагранжа для задачи (6.9) [c.119]

Для решения задачи (1.2) — (1.4), т. е. выбора такого варианта распределения ресурса Xi (i = 1,. . ., п) и соответствующих плановых заданий yt (i = 1,. . ., д), связанных с xi соотношением (1.2), можно использовать метод множителей Лагранжа, описанный в 4 гл. 1. Функция Лагранжа имеет вид [c.339]

Воспользуемся методом множителей Лагранжа. Функция Лагранжа в данном случае имеет вид [c.128]

Применяя метод множителей Лагранжа, получим [c.106]

Эта задача легко решается с применением метода множителей Лагранжа. [c.14]

Применяя метод множителей Лагранжа, обозначим [c.92]

Применяя метод множителей Лагранжа, находим [c.28]

Из метода множителей Лагранжа получаем условие оптималь- [c.88]

Для задач типа 1 и 2, применяя метод множителей Лагранжа, [c.89]

Применяя метод множителей Лагранжа, получаем, что реше- [c.95]

Применяя метод множителей Лагранжа, убеждаемся, что оп- [c.106]

Для решения таких задач могут быть использованы методы дифференцирования, множителей Лагранжа, численные методы, математическое программирование и др. [c.193]

Метод множителей Лагранжа используется, когда целевая функция находится при функциональных ограничениях. Задача решается следующим образом. [c.194]

Со + Мо, i=M0 можно решить с помощью метода множителей Лагранжа [c.19]

Теорема Лагранжа устанавливает метод (известный как метод множителей Лагранжа ) нахождения необходимых условий экстремума при наличии ограничений типа равенств. Определим сначала функцию Лагранжа ф [c.179]

Пользуясь методом множителей Лагранжа, показать, что минимум достигается в точке (0,0) при А = 1. Рассмотреть функцию Лагранжа [c.183]

Решить следующие задачи методом множителей Лагранжа [c.183]

В тех случаях, когда у нельзя выразить явно через ж, применяют так называемый метод множителей Лагранжа, сущность которого состоит в следующем. [c.319]

Второй способ решения. Определим теперь точку условного экстремума, пользуясь методом множителей Лагранжа. [c.320]

Метод множителей Лагранжа может быть использован и при исследовании на экстремум функции большего числа переменных. [c.321]

Указанная задача может быть решена методом множителей Лагранжа. [c.112]

Приведенные выше рассуждения, разумеется, не являются доказательством сформулированного здесь утверждения они лишь помогают понять существо метода составляющая kg(X) в составе функции Лагранжа должна уравновешивать возможное увеличение максимального значения функции f(X) при малом отклонении (на единицу) значений функции g(X) от нуля. Это обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла множителя Лагранжа. [c.591]

Мукштадт [180] предложил решать исходную задачу (11.3.1) с помощью двух аппроксимаций для запасов в депо и множителя Лагранжа. Метод опирается на тот факт, что число дефицитов в каждом пункте в практически интересных ситуациях хорошо приближается экспоненциальной функцией максимального запаса Sjj. [c.342]

Метод множителей Лагранжа. Рассмотрим слеиующую задачу Найти максимум U(xt, х2), где Xi и х2 — скалярные переменные, при условии g(xi, х2) = b. [c.46]

Для построения двойственной задачи обратимся к методу множителей Лагранжа, который хотя и не эффективен при решении задач линейного программирования, но полезен для их качественного анализа. Функция Лаграижа для задачи (4.22) — (4.24) имеет вид [c.53]

Способ решения задачи зависит от вида функции /. При линейной функции методом решения будет линейное программирование, при нелинейной фиункции — возможно привлечение метода множителей Лагранжа либо динамического программирования. [c.105]

Так как Y = -L, то Y = 10 и X = 10. Максимальное произведение 10 10= 100. Метод множителей Лагранжа был продемонстрирован для двух переменных и одной 01раничительной функции. Метод можно также применять, когда есть более чем две переменные и более чем одна ограничительная функция. Далее для примера следует форма для поиска экстремума, когда есть три переменные и две ограничительные функции [c.187]

Таким образом, мы можем утверждать, что эффективные границы портфелей с неограниченной суммой весов содержат одинаковые портфели с разным уровнем заемных средств (с разным плечом). Портфель, в котором меняется величина плеча для получения заданного уровня прибыли Е, когда снято ограничение суммы весов, будет иметь второй множитель Лагранжа, равный нулю, при сумме весов, равной 1. Теперь мы можем достаточно просто определить, каким будет наш неограниченный геометрический оптимальный портфель. Сначала найдем портфель, который имеет нулевое значение для второго множителя Лагранжа, когда сумма весов ограничена 1,00. Одним из способов поиска такого портфеля является процесс итераций. Получившийся в результате портфель поднимается (или опускается) рычагом в зависимости от выбранного Е для неограниченного портфеля. Значение Е, удовлетворяющее любому уравнению с (7.Оба) по (7.06г), и будет тем значением, которое соответствует неограниченному геометрическому оптимальному портфелю. Для выбора геометрического оптимального портфеля на эффективной границе AHPR для портфелей с неограниченными весами, можно использовать первый множитель Лагранжа, который определяет положение портфеля на эффективной границе. Вспомните (см. главу 6), что одним из побочных продуктов при определении состава портфеля методом элементарных построчных преобразований является первый множитель Лагранжа. Он выражает мгновенную скорость изменения дисперсии по отношению к ожидаемой прибыли (с обратным знаком). Первый множитель Лагранжа, равный - 2, означает, что в этой точке дисперсия изменяется по отношению к ожидаемой прибыли со скоростью 2. В результате, мы получим портфель, который геометрически оптимален. (7.06д) L1 = - 2, [c.218]

Применяя метод множителей Лагранжа, из(11)и(12) получа- [c.205]

См. также Ассортиментные задачи, Базисное решение, Блочное программирование, Булево линейное программирование, Ведущий столбец, Ведущая строка, Вершина допустимого многогранника, Вырожденная задача, Гомори способ, Граничная точка, Двойственная задача, Двойственность в линейном программировании, Дифференциальные ренты, Дополняющая нежесткостъ, Жесткость и нежесткость ограничений ЛП, Задача диеты, Задача о назначениях, Задача о раскрое, Задачи размещения, Исходные уравнения, Куна— Таккера условия, Множители Лагранжа, Область допустимых решений, Опорная прямая, Оптимальное распределение ресурсов, Распределительные задачи, Седловая точка, Симплексная таблица, Симплексный метод, Транспортная задача. [c.173]

МНОЖИТЕЛИ ЛАГРАНЖА [Lagrange multipliers] — дополнительные множители, преобразующие целевую функцию экстремальной задачи выпуклого программирования (в частности, линейного программирования) при ее решении одним из классических методов — методом разрешающих множителей (методом Л агранжа). Полученная функция носит название лагранжиан, или функция Лагранжа. Подробнее об этом методе см. в ст. "Лагранжиан". [c.202]

economy-ru.info

Метод множителей Лагранжа — Мегаобучалка

Рассмотрим частный случай общей задачи НЛП.

Предполагая, что сумма ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных и функции , а так же функции непрерывные вместе со своими частными производными (это классическая задача оптимизации):

Что бы найти решение этой задачи водят набор переменных называются множителями Лагранжа, тогда функция Лагранжа:

Далее находят все частные производные функции Лагранжа

Затем рассматриваем систему уравнений с неизвестными

Решив систему уравнений получают все точки, в которых функция может иметь экстремальные значения. Дальнейшее исследование найденных точек производят так же, как и в случае безусловного экстремума.

Пример. Найти точки экстремума функции

при условиях

З переменных:

Таким образом, в точке данная функция может иметь условный экстремум

Используя вторые частные производные можно показать, что в этой точке функция имеет условный минимум и

Метод множителей Лагранжа можно применять и когда условие связи представляет собой неравенство. Если нужно найти экстремум функции при , то следует сначала найти точки безусловного экстремума функций из уравнений производных .

Затем, среди этих точек отобрать те, координаты которых удовлетворяют условию связи , а так же определить точки, удовл. системе уравнений

Точки, найденные в результате решения системы вместе с точками определенными на І этапе, а также удовлетворяя условиям подлежат дальнейшему исследованию как и при нахождение безусловного экстремума. Особым классом задач ИО являются задачи выпуклого программирования для которых разработано много эффективных решений.

Задача является задачей выпуклого программирования, если целевая функция будет либо выпуклой, либо вогнутой.

К методам решения задач ВП относят:

· метод Франка - Вульфа;

· метод штрафных функций;

· метод Эрроу – Гурвица;

Эти методы являются градиентными методами и методы использования сепарабельные функции:

· функция

Функция сепарабельная, если она может быть представлена в виде суммы функции, каждая из которых является функцией одной переменной

Если целевая функция и функции в системе ограничений – сеперабельное то приблизительно решение такой задачи можно найти используя кусочно – линейную аппроксимацию.

Пример: Джек студент – первокурсник, он пришел к выводу, что одна только учеба без ежедневной игры в баскетбол плохо влияет на его умственное, моральное и физическое развитие, поэтому он решил распределить своё время примерно 10 часов для учебы и игры в баскетбол. Привлекательность игрового времени он оценивает в два раза больше чем привлекательность времени затраченного на учебу. Но имея совесть и чувство долга Джек решил что время для игры не превышает времени на учебу, кроме того он заметил что если выполнять все учебные задания, на игру останется не более 4 часов в день. Распределить время так что бы Джек получал максимальное удовольствие от игры и от работы.

х1 – время на игру

х2 – время на учебу

х1 + х2 ≤ 10

х1 ≤ х2

х1 ≤ 4

х1 + х2 + S1 = 10

х1 - х2 + S1 = 0

х1 + S1 = 4

z = 2х1 + х2

Базис	z	х2	х2	S1	S2	S3	Реш.
z			-1
S1							10 10
S2			-1				0 0
S3							4 4

z	-3
S1		-1	10 5
x1	-1		0 -0
S3		-1	4 4

z	-1
S1		-2	2 2
x1			4 ∞
x2	-1		4 -4

Базис	z	х1	х2	S1	S2	S3	Реш.
z
S2						-2
x1
x2						-1

x1 = 4

x2 = 6

z = 14

Задачи ЛП и НЛП решаются за 1 шаг. Такие задачи называются одношаговыми (однотипные). Задачи Дин. Пр. называются многошаговыми – на каждом шаге определяется решение некой частей задачи обусловленной исходной задачей.

Общая постановка задачи ДП. Пусть некоторая физическая система S находится в некотором начальном состоянии S0 Є Sнач. и является управляемой. Благодаря некоторому упр. U данная система переходит из начального состояния S0 в конечное состояние Sкон., Sкон Є Sк.

При этом качестве каждого из управлений U характеризуется соответствующим значением функции W(U).

Задача состоит в том чтобы из множества управлений найти такое, при котором функция W(U) принимает экстремальное значение.

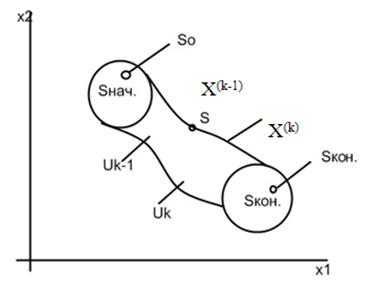
Решение задач ДП осуществляется по схеме:

Будем считать, что состояние рассматриваемой системы S на каком то k-m шаге, причем k = 1…n определяется совокупностью чисел Х(k) = (x1(k), x2(k), … xn(k)), которые получены в результате реализации управления Uk, обеспечивающего переход системы Sиз состояния Х(k-1) в состояние Х(k).

При этом считается что состояние Х(k) зависит от состояния Х(k-1) и выбранного управления Uk, но не зависит от того каким образом система S перешла в это состояние.

Врез. реализации К-го шага был получен выигрыш состояния зависящий от пред. состояния (Х(k-1)) и уравнения Uk.

Общий вклад при этом будет составлять:

F = ∑ Wk (Х(k-1), Uk)

k=1

Решения задач ДП по подобной схеме осуществляется в рамках принципа оптимальности Беллмона.

Формулировка: каково бы не было состояние системы перед очередным шагом надо на следующем шаге выбирать управление так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимален.

megaobuchalka.ru

Лагранжа метод - Справочник химика 21

МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА (МЕТОД ЦЕН) [c.174]

Кривая зависимости Су = Су Т) приведена на рис. 9. Затем для расчета соответствующих производных к кривым в точке 1 проводят касательные. По тангенсу угла наклона касательных к оси абсцисс рассчитывают численное значение производной. Производные можно также рассчитывать с помощью интерполяционного полинома Лагранжа, методом неопределенных коэффициентов, с помощью разностных формул численного дифференцирования с применением ЭВМ. [c.43]

Таким образом, в рассматриваемой системе для целей оптимизации ХТС комплексно используются идеи линейного программирования, методы однопараметрического и многопараметрического поисков и методы учета ограничений (метод модифицированной функции Лагранжа, метод приведенного градиента). [c.236]

Исследование, приводящее к уравнению (9. 8), так же, как и то, которое было использовано в гл. 3 и 5 при выводе интегральных уравнений сохранения, основано на рассмотрении потоков, направленных наружу и внутрь фиксированного в пространстве элемента постоянной величины, причем масса, заключенная в элементе, переменна. Такой подход часто называют методом Эйлера. С другой стороны, вывод уравнения (9. 14) основан на рассмотрении фиксированной массы жидкости, движущейся в пространстве, причем объем, занятый этой массой, может меняться. Такой метод называется методом Лагранжа. Метод Лагранжа удобен и будет использован в двух следующих главах при выводе уравнений энергии и импульсов. [c.88]

На базе описанной общей схемы ниже обсуждены два декомпозиционных метода, один из которых основан на применении метода множителей Лагранжа (методом цен [40]), а другой — на принципе закрепления входных и выходных переменных блоков схемы [41]. Кроме того, кратко рассмотрены метод подоптимизации [8, с. 199], а также общий подход к построению одного класса декомпозиционных методов. [c.174]

Важным и полезным для исследования задач условной оптимизации является понятие о расширении экстремальной задачи. Оно позволяет подчеркнуть взаимосвязь таких различных подходов, как метод Лагранжа, метод штрафов, переход к осред-ненной постановке и др. Основное внимание будет уделено изложению и пояснению методики перехода от условий задачи (критерия оптимальности, связей и ограничений) к условиям, выделяющим оптимальные решения. Конструкции, которые будут приведены, позволяют провести такой переход по определенным правилам для произвольной задачи из очень широкого класса задач оптимизации. Важно и то обстоятельство, что изменения в постановке задачи легко учесть при составлении условий оптимальности решения. [c.47]

chem21.info