Метод Фибоначчи поиска экстремума. Метод фибоначчи метод оптимизации

Метод Фибоначчи

В этом разделе рассматривается метод Фибоначчи. Этот метод довольно часто используется не только в случае одномерной оптимизации, но и в процессе решения задач математического программирования, например, в многомерных задачах минимизации по заданному направлению.

С помощью численной процедуры, описанной в данном учебном курсе, непосредственно ищется минимум функции в некотором интервале, в котором предположительно лежит этот минимум. При этом метод Фибоначчи относятся к методам исключения интервалов, на которых заведомо отсутствует оптимум исследуемой функции. Кроме того в данных методах предполагается, что оптимизируемая функция является унимодальной.

В процессе применения методов исключения интервалов можно выделить две фазы:

Фаза установления границ интервала, на котором реализуется процедура поиска. Это могут быть границы достаточного широкого интервала заведомо содержащего точку оптимума. В поисковых задачах оптимизации отрезок, на котором находится точка минимума, называют интервалом неопределённости.
Фаза уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины (точности поиска экстремума).

На втором этапе, этапе уменьшения интервала, как раз и применяется метод Фибоначчи. В общем виде задача оптимизации ставится следующим образом: «Найти минимум унимодальной функции на замкнутом интервалепри заданном числе вычислений функции».

Краткое описание метода Фибоначчи

Предположим, что нужно определить минимум как можно точнее, т.е. с наименьшим интервалом неопределённости, но при этом можно выполнить только вычислений функции. Как следует расположить этиточек? Ясно, что надо сделать так, чтобы в последующих итерациях использовались точки, использованные на предыдущих итерациях. Предположим, что на интервалеизвестно значение функции в точке. Если можно вычислить значение функции только один раз (т.е.), то где поместить точку, для того чтобы получить наименьший интервал неопределённости после отбрасывания интервала, в котором оптимум не расположен?

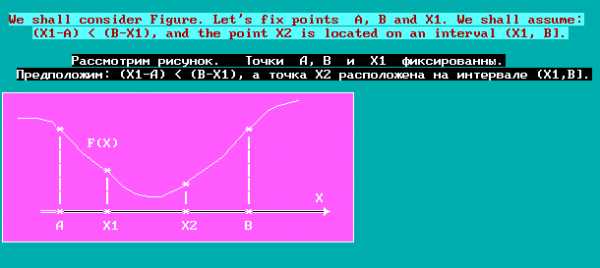
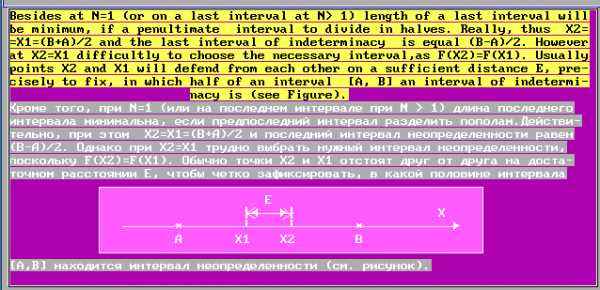
Рассмотрим рисунок. Точки фиксированы. Предположим, что, а точкарасположена на интервале. Возможны два случая:

Поскольку не известно, какая ситуация справедлива, точку надо выбрать так, чтобы минимизировать наибольшую из длин:или. Достигнуть этого можно, сделав эти длины равными, т.е. поместивсимметрично относительно точки(в любом другом случае новый интервал будет большей величины).

Кроме того, при (прина последнем интервале) длина последнего интервала минимальна, если предпоследний интервал разделить пополам. Действительно, при этоми последний интервал неопределённости равен. Однако притрудно выбрать нужный интервал неопределённости, поскольку. Обычно точкииотстоят друг от друга на достаточном расстоянии, чтобы чётко зафиксировать, в какой точке интерваланаходится интервал неопределенности.

Предположим теперь, что можно вычислить значение функции раз. В этом случае стратегия поиска ясна с самого начала. Нужно поместить следующую точку внутри интервала симметрично относительно уже находящейся там точки. Парадоксально, но, чтобы понять, как следует начинать процедуру вычисления, необходимо разобраться в том, как следует кончать её.

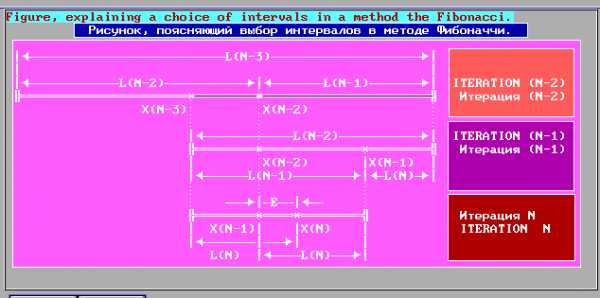
Уже было показано, что на последнем -ом вычислении -ю точку (на поясняющем рисунке) следует поместить симметрично по отношению кточке (точке) на расстояниеиз условия различимостив этих точках.– это интервал нечувствительности на последней итерации, т.е. разница между аргументамиидвух экспериментов, при которых можно отличить значения функцийи.

Замечание: на первом этапе можно считать и точкурасположить в середине отрезка, а затем точкурасположить справа или слева от первой точки на достаточно малом расстояниине равном 0.

Из рисунка следует, что интервал неопределённости имеет длину . Тогда. На предыдущем этапе точкиидолжны быть смещены симметрично внутри интервалана расстояниеот концов. Следовательно,. Аналогично показывается, что. В общем случае, при. Таким образом:

В общем случае , где,- последовательность чисел Фибоначчи, определяемая как:для.

Если начальный интервал , то конечный:. Следовательно, произведявычислений функции, начальный интервалуменьшается враз (пренебрегая малой величиной). Это наилучший результат. Если поиск начат с начальным интервалом, то его несложно продолжить, используя правило симметрии: на отрезкенеобходимо найти положение первой точки, которая размещается на расстоянииот правого конца интервала(ближе к точке), а вторая точка (точка) – на таком же расстоянииот левого конца интервала (ближе к точке). Значениеравно.

После того как найдено положение точек и, числа Фибоначчи больше не нужны. Используемое значениеможет определяться из практических соображений, но в любом случае должно выполняться:В противном случае на вычисление функциибудет напрасно тратиться время.

studfiles.net

Методичка 171 - Глава 1.4

1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

1.4. Метод поиска с использованием чисел Фибоначчи [1,3-6]

Последовательность чисел Фибоначчи определяется соотношением:

(8)

и имеет вид:

144

233

и т.д.

Подобно методу золотого сечения процедура поиска с использованием чисел Фибоначчи требует два вычисления функции на первом шаге, а на каждом последующем - только по одному. Однако, в отличие от метода золотого сечения, в этой процедуре общее число S вычисления функции должно быть выбрано заранее. Кроме того, сокращение интервала неопределенности не остается постоянным, а меняется от шага к шагу: на k-ом шаге длина интервала неопределенности сжимается с коэффициентом

Первые два вычисления проводятся в точках:

расположенных симметрично относительно середины отрезка [a,b]. Если f(x1)<f(x2), то новым отрезком локализации минимума является [a, x2], в случае f(x1)≥f(x2)-[x1, b]. Каждая следующая точка выбирается симметрично относительно середины полученного отрезка к лежащей внутри этого отрезка точке уже проведенного вычисления (x1 или x2). При этом любая внутренняя точка делит отрезок локализации в отношении, двух последовательных чисел Фибоначчи.

Взаимное расположение точек первых трех вычислений в случае f(x1)<f(x2) показано на рис. 7.

Первый шаг

Второй шаг

Рис. 7.

После (S-1)-го шага точка проведенного вычисления оказывается в середине отрезка локализации. Точка последнего, S-го, шага выбирается на расстоянии δ от середины этого отрезка, где δ - заранее фиксированное малое положительное число (константа различимости).

После S вычислений функции длина отрезка локализации составляет (с точностью до δ):

(9)

Сравнение (9) и (7) показывает, что при одном и том же S метод Фибоначчи дает меньший интервал неопределенности, чем метод золотого сечения, т.е. является более эффективным. Однако для достаточно больших S значение стремится к (0,618)S-1 , так что эти методы становятся почти идентичными.

В том случае; когда при использовании метода Фибоначчи задан .конечный интервал неопределенности ε, число S можно определить из условия:

(10)

Алгоритм минимизации функции f(x) с использование, чисел Фибоначчи.

1. По заданной точности рассчитывается вспомогательное число

2. Для полученного значения N находится такое число Фибоначчи FS, для которого выполняется неравенство:

4. По формуле (9) определяется длина конечного интервала неопределенности l.

5. Вычисляются значения x1=a+l∙FS-2, x2=b-l∙FS-2.

6. В зависимости от соотношения f(x1) и f(x2) выбирается новый интервал локализации минимума.

7. Внутри полученного интервала находится новая точка (x1 или x2), симметричная к уже имеющейся точке и отстоящая от конца интервала на величину l∙FS-1-k , где k - номер шага. В этой точке рассчитывается значение f(x). Затем вычисления повторяются, начиная с пункта 5, до тех пор, пока k не станет равно S-1. Тогда переходят к пункту 7.

8. Полагают x2=x1+δ, находят f(x2). Если f(x2)>f(x1)то минимум реализуется на интервале (a, x1), в противном случае - на интервале (x1 , b).

Блок-схема описанного алгоритма приведена на рис.8.

Рис. 8. Блок – схема алгоритма поиска минимума функции f(x) использованием чисел Фибоначчи

Пример.

С помощью метода Фибоначчи найти минимум функции f(x)=x2+2x на интервале (-3,5). Длина конечного интервала неопределенности не должна превосходить 0,2.

Решение.

Примем δ=0,01.

Найдем необходимое число вычислений функции:

F8<40<F9

Итак, S =9.

Первый шаг. a=-3; b=5.

x1=a+l∙F7= 0.0555; f(x1) =0,1141;

x2 = b-l∙F7=1,9445; f(x2) =7,6701;

f(x1)<f(x2). Новый отрезок [-3; 1,9445].

Второй шаг. a=-3; b=5.

x1=a+l∙F6= -1.1085; f(x1) =-0,9882;

x2 =0,0555; f(x2) =0,1141;

f(x1)<f(x2). Новый отрезок [-3; 0,0555].

Дальнейшие расчеты приведены в таблице 2. Значения f(x) вычисленные на каждом шаге, помечены звездочкой.

Таблица 2
№ шага	a	b	b-a	x1	x2	f(x1)	f(x2)
1	-3,000	5,000	8,000	0,0555	1,9445	0,1141*	7,6701*
2	-3,000	1,9445	4,9445	-1,1085	0,0555	-0,9882*	0,1141
3	-3,000	0,0555	3,0555	-1,8360	-1,1085	-0,3011*	-0,9882
4	-1,8360	0,0555	1,8915	-1,1085	-0,6720	-0,9882	-0,8924*
5	-1,8360	-0,6720	1,1640	-1,3995	-1,1085	-0,8404*	-0,9882
6	-1,3995	-0,6720	0,7275	-1,1085	-0,9630	-0,9882	-0,9986*
7	-1,1085	-0,6720	0,4365	-0,9630	-0,8175	-0,9986	-0,9667*
8	-1,1085	-0,8175	0,2910	-0,9630	-0,9630	-0,9986	-0,9986
9	-1,1085	-0,9630	0,1455	-0,9630	-0,9530	-0,9986	-0,9978*

Поскольку для k = 9 f(x1)<f(x2), конечный интервал неопределённости равен (-1,1085; -0,9630), длина его составляет 0,1455. В качестве приближенного значения точки минимума выберем середину этого отрезка -1,0358; f(-1,0358) = -0,9987. Напомним, что при использовании, метода золотого сечения при S = 9 длина интервала неопределенности была равна 0,176.

dit.isuct.ru

Алгоритм метода Фибоначчи

Шаг 1.

Задаётся точность и число вычислений функции.

Шаг 2.

Вычисляется длина начального интервала и число(– число вычислений функцииизменяется отдо).

Шаг 3.

Вычисляем , где- числа Фибоначчи. Вычисляемв начальной точке.

Если величина не задана, рекомендуется выбирать её из условия.

Шаг 4.

Находим и вычисляем.

Шаг 5.

5.1

Если и, то исключается интервал, а остаётся интервал. Полагаем. Если условие 5.1 выполнено, переходим к шагу 6.

5.2

Если и, то исключается интервал, а остаётся интервал. Полагаем. Переходим к шагу 6.

5.3

Если и, то остаётся интервал. Полагаем. Переходим к шагу 6.

5.4

Если и, то остаётся интервал. Полагаем. Переходим к шагу 6.

Шаг 6.

Увеличиваем и проверяем условия 6.1 и 6.2

6.1

Если , то переходим к шагу 4.

6.2

Если , то работа окончена и последний интервал, где расположен оптимум, найден. Переход к шагу 7.

Шаг 7.

Интервал неопределённости . В качестве оптимального значенияможно принять:

Пример

Методом Фибоначчи минимизировать функцию на интервалеприи.

Поскольку из таблицы чисел Фибоначчи выбереми.

Итерация 1

Шаг 1.

Шаг 2.

Шаг 3.

Вычисляем .

Шаг 4.

Находим

Шаг 5.

Сравнение . Следовательно, выполняется пункт 5.1 и надо исключить интервал. Оставляем интервал. Переприсвоение:.

Шаг 6.

Увеличиваем . Проверяем условие. Т.к.переходим ко второй итерации и делаем шаг 4.

Итерация 2

Шаг 4.

Находим .

Шаг 5.

Сравниваем . Согласно шагу 5.1 остаётся интервал. Переприсвоение:.

Шаг 6.

. Сравниваем. Переходим к итерации 3.

Итерация 3

Шаг 4.

Находим .

Шаг 5.

Сравниваем и. Согласно шагу 5.3 остаётся интервал. Переприсвоение:. Переходим к шагу 6.

Шаг 6.

Сравниваем, поэтому переходим к шагу 7.

Шаг 7.

Найденный интервал неопределённости . В качестве оптимального значенияможно принять, например, середину интервала неопределённости:. Точное значение аргумента, при котором достигается минимум, равно.

Метод дихотомии

Методы поиска, которые позволяют определить оптимум функции одной переменной путём последовательного исключения подинтервалов и, следовательно, путём уменьшения интервала поиска, носят название методов исключения интервалов. Метод дихотомии – один из методов исключения интервалов. В процессе применения методов исключения интервалов можно выделить две фазы:

Фаза установления границ интервала, на котором реализуется процедура поиска. Это могут быть границы достаточного широкого интервала заведомо содержащего точку оптимума. В поисковых задачах оптимизации отрезок, на котором находится точка минимума, называют интервалом неопределённости.
Фаза уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины (точности поиска экстремума).

Первый этап может отсутствовать, если интервал, заведомо содержащий экстремум функции, уже задан. Вторая фаза, фаза установления интервала, реализуется различными методами уменьшения интервала:

Методом дихотомии
Методом золотого сечения
Методом Фибоначчи

Суть метода дихотомии состоит в последовательном разбиении интервала, содержащего экстремум (его называют интервалом поиска), на подинтервалы и исключении одного из них, заведомо не содержащего экстремум. Величина подинтервала, исключаемого на каждом шаге, зависит от расположения пробных точек ивнутри интервала поиска. Поскольку местонахождение точки оптимума заранее не известно, целесообразно предположить, что размещение пробных точек должно обеспечивать уменьшение интервала в одном и том же отношении на каждом шаге. В методе дихотомии это отношение равно, т.е. интервал неопределённости делится на каждом шаге пополам и отбрасывается часть, где минимум заведомо быть не может.

studfiles.net

Метод чисел Фибоначчи - это... Что такое Метод чисел Фибоначчи?

Метод чисел Фибоначчи

Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации.

Описание метода

Пусть задана функция . Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки и такие, что:

Иллюстрация выбора промежуточных точек метода золотого сечения.

, где — пропорция золотого сечения.

Таким образом:

То есть точка делит отрезок в отношении золотого сечения. Аналогично делит отрезок в той же пропорции. Это свойство и используется для построения итеративного процесса.

Алгоритм

На первой итерации заданный отрезок делится двумя симметричными относительно его центра, точками и рассчитываются значения в этих точках. После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают. На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку. Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Формализация

Шаг 1. Задаются начальные границы отрезка и точность , рассчитывают начальные точки деления: и значения в них целевой функции: .
Шаг 2.
- Если , то .
- Иначе .
Шаг 3.
- Если , то и останов.
- Иначе возврат к шагу 2.

Метод чисел Фибоначчи

В силу того, что в асимптотике , метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итерации строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.

Алгоритм

Шаг 1. Задаются начальными границами отрезка и числом итераций , рассчитывают начальные точки деления: и значения в них целевой функции: .
Шаг 2. .
- Если , то .
- Иначе .
Шаг 3.
- Если , то и останов.
- Иначе возврат к шагу 2.

Литература

Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.

См. также

Wikimedia Foundation. 2010.

Метод функционала плотности
Методи Андонов-Ченто

Смотреть что такое "Метод чисел Фибоначчи" в других словарях:

Метод золотого сечения — метод поиска значений действительно значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации Содержание 1 Описание… … Википедия
Метод Фибоначчи поиска экстремума — Метод золотого сечения метод поиска значений действительно значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации … Википедия
Метод Нелдера-Мида — Последовательные симплексы в методе Нелдера Мида для функции Розенброка (англ.) (вверху) и функции Химмельблау (англ.) (внизу) Не путать с «симплекс методом» из линейного программирования методом оптимизации линейной системы с ограничениями.… … Википедия
Метод деформируемого многогранника — Последовательные симплексы в методе Нелдера Мида для функции Розенброка (англ.) (вверху) и функции Химмельблау (англ.) (внизу) Не путать с «симплекс методом» из линейного программирования методом оптимизации линейной системы с ограничениями.… … Википедия
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
Фибоначчи числа — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Метод Фибоначчи с запаздываниями — (Lagged Fibonacci generator) один из методов генерации псевдослучайных чисел. Особенности распределения случайных чисел, генерируемых линейным конгруэнтным алгоритмом, делают невозможным их использование в статистических алгоритмах, требующих… … Википедия
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Чисел теория — Теория чисел, или высшая арифметика, раздел математики, изучающий целые числа и сходные объекты. В зависимости от используемых методов теорию чисел подразделяют на несколько подтеорий. Содержание 1 Элементарная теория чисел 2 Аналитическая теория … Википедия
Числа Фибоначчи — Числа Фибоначчи элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух… … Википедия

dic.academic.ru

Метод Фибоначчи поиска экстремума - это... Что такое Метод Фибоначчи поиска экстремума?

Метод Фибоначчи поиска экстремума

Описание метода

Иллюстрация выбора промежуточных точек метода золотого сечения.

, где — пропорция золотого сечения.

Таким образом:

Алгоритм

Формализация

Шаг 1. Задаются начальные границы отрезка и точность , рассчитывают начальные точки деления: и значения в них целевой функции: .
Шаг 2.
- Если , то .
- Иначе .
Шаг 3.
- Если , то и останов.
- Иначе возврат к шагу 2.

Метод чисел Фибоначчи

Алгоритм

Шаг 1. Задаются начальными границами отрезка и числом итераций , рассчитывают начальные точки деления: и значения в них целевой функции: .
Шаг 2. .
- Если , то .
- Иначе .
Шаг 3.
- Если , то и останов.
- Иначе возврат к шагу 2.

Литература

Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.

См. также

Wikimedia Foundation. 2010.

Метод Симпсона
Метод Фоля

Смотреть что такое "Метод Фибоначчи поиска экстремума" в других словарях:

Фибоначчи числа — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Метод золотого сечения — метод поиска значений действительно значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации Содержание 1 Описание… … Википедия
Метод чисел Фибоначчи — Метод золотого сечения метод поиска значений действительно значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации … Википедия
Метод Нелдера — Мида — Последовательные симплексы в методе Нелдера Мида для функции Розенброка (англ.) (вв … Википедия
Метод Хука — Дживса (англ. Hooke Jeeves), также как и алгоритм Нелдера Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две… … Википедия
Метод сопряжённых градиентов — Метод сопряженных градиентов метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в минимум находится за шагов. Содержание 1 Основные понятия … Википедия
ФИБОНАЧЧИ МЕТОД — разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию требование строгой унимодальности на заданном интервале. При… … Математическая энциклопедия
Метод Нелдера-Мида — Последовательные симплексы в методе Нелдера Мида для функции Розенброка (англ.) (вверху) и функции Химмельблау (англ.) (внизу) Не путать с «симплекс методом» из линейного программирования методом оптимизации линейной системы с ограничениями.… … Википедия
Метод деформируемого многогранника — Последовательные симплексы в методе Нелдера Мида для функции Розенброка (англ.) (вверху) и функции Химмельблау (англ.) (внизу) Не путать с «симплекс методом» из линейного программирования методом оптимизации линейной системы с ограничениями.… … Википедия
Числа Фибоначчи — Числа Фибоначчи элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух… … Википедия

dic.academic.ru

Метод Фибоначчи

Метод Фибоначчи является процедурой линейного поиска минимума унимодальной функции f(x) на замкнутом интервале [a, b], отличающейся от процедуры золотого сечения тем, что очередная пробная точка делит интервал локализации в отношении двух последовательных чисел Фибоначчи. Последовательность чисел Фибоначчи задаётся условиями F0 = F1 = 1, Fk+1 = Fk + Fk-1, k = 1,2,... Начальными членами последовательности будут 1, 1, 2, 3, 5, 8, 13,... Стратегия поиска Фибоначчи требует заранее указать n - число вычислений минимизируемой функции и e - константу различимости двух значений f(x). Рассмотрим один из возможных вариантов метода.

Алгоритм Фибоначчи-1

Начальный этап

(1) Задать константу e, начальный интервал [a1, b1], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1)/Ln.

(2) Взять две пробные точки l1 = a1 + (Fn-2/Fn)(b1 - a1) и m1 = a1 + (Fn-1/Fn)(b1-a1). Положить k = 1.

Основной этап

Шаг 1. Сократить текущий интервал локализации:

(1) Если f(lk) < f(mk), то положить ak+1 = ak, bk+1 = mk,mk+1 =lk и вычислить новую точку lk+1 = ak+1 + (Fn-k-2/Fn-k)Lk+1, где Lk+1 = bk+1 - ak+1; перейти на шаг 2.

(2) Если f(lk)>> f(mk),то положить ak+1 =lk, bk+1 = bk, lk+1 = mk и вычислить mk+1 = ak+1 + (Fn-k-1/Fn-k) Lk+1.

Шаг 2. Проверить критерий окончания поиска:

(1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1.

Шаг 3. Найти аппроксимирующий минимум х(*):

(1) Положить mk = lk + e.

(2) Если f(lk) > f(mk), то x(*) = (lk + bk)/2. В противном случае - x(*) = (ak + mk)/2.

Алгоритм Фибоначчи-2

Начальный этап

(2) Выбрать одну пробную точку . Положить

k = 1.

Основной этап

Шаг 1. Проверить критерий окончания поиска: если k=n, то остановиться и положить x*=x2.

Шаг 2. Сократить текущий интервал локализации рассмотрением 4-х ситуаций, аналогично методу золотого сечения-2.

Метод средней точки (метод Больцано)

Данный метод является вариантом метода деления интервала пополам. Последовательные сокращения интервала неопределенности производятся на основе оценки производной минимизируемой функции в центре текущего интервала.

Начальный этап. Для запуска метода необходимо:

(1) задать [a1,b1]- начальный интервал локализации минимума, на границах которого знаки производных различны, т.е. f'¢(a1)f'¢(b1)<0; e - малое положительное число;

(2) положить к=1 и перейти к основному этапу.

Основной этап

Шаг 1. Взять пробную точку хk в центре текущего интервала и проверить критерий окончания поиска: (1) xk = (ak + bk)/2; (2) если ½f'¢(xk)½ ≤ e и Lk= ½bk - ak½≤ e, то остановиться (хk = х* -аппроксимирующий минимум).

Шаг 2. Сократить текущий интервал:

(1) Если f ¢(xk) > 0, то положить ak+1 = ak и bk+1 =xk, в противном случае - ak+1 =xk, bk+1 =bk;

(2) заменить k на k+1 и вернуться на шаг 1.

Метод квадратичной интерполяции – экстраполяции

Данный метод относится к классу прямых методов, опирающихся на идею построения аппроксимирующего полинома второго порядка на основании информации о значениях функции в n+1 точке – узлах интерполяции.

Начальный этап

Выбрать произвольную точку x1ÎRn
Задаться величиной шага h=0.001
Определить погрешность
Положить счётчик числа итераций равным 1, а также b=x1

Основной этап

Шаг 1. Вычислить fi в 3-х точках: a, b и с – центральной (b) и двух соседних: a=b-h, c=b+h. Затем, по формуле

(1)

или

(2)

найти аппроксимирующий минимум d

Шаг 2. Проверить критерий близости 2-х точек b и d

Если оба условия выполняются – фиксируем аппроксимирующий минимум

и останавливаемся. Если оба критерия не выполняются, полагаем b=d и возвращаемся на шаг 1.

studfiles.net

Метод Фибоначчи поиска экстремума Википедия

Метод золотого сечения — метод поиска экстремума действительной функции одной переменной на заданном отрезке. В основе метода лежит принцип деления отрезка в пропорциях золотого сечения. Является одним из простейших вычислительных методов решения задач оптимизации. Впервые представлен Джеком Кифером в 1953 году.

Описание метода

Пусть задана функция f(x):[a,b]→R,f(x)∈C([a,b]){\displaystyle f(x):\;[a,\;b]\to \mathbb {R} ,\;f(x)\in \mathrm {C} ([a,\;b])}. Тогда для того, чтобы найти неопределённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} такие, что:

Иллюстрация выбора промежуточных точек метода золотого сечения.

b−ab−x1=b−ax2−a=Φ=1+52=1.618…{\displaystyle {\frac {b-a}{b-x_{1}}}={\frac {b-a}{x_{2}-a}}=\Phi ={\frac {1+{\sqrt {5}}}{2}}=1.618\ldots }, где Φ{\displaystyle \Phi } — пропорция золотого сечения.

Таким образом:

x1=b−(b−a)Φx2=a+(b−a)Φ{\displaystyle {\begin{array}{ccc}x_{1}&=&b-{\frac {(b-a)}{\Phi }}\\x_{2}&=&a+{\frac {(b-a)}{\Phi }}\end{array}}}

То есть точка x1{\displaystyle x_{1}} делит отрезок [a,x2]{\displaystyle [a,\;x_{2}]} в отношении золотого сечения. Аналогично x2{\displaystyle x_{2}} делит отрезок [x1,b]{\displaystyle [x_{1},\;b]} в той же пропорции. Это свойство и используется для построения итеративного процесса.

Алгоритм

На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках.
После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают.
На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку.
Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Формализация

Шаг 1. Задаются начальные границы отрезка a,b{\displaystyle a,\;b} и точность ε{\displaystyle \varepsilon }.
Шаг 2. Рассчитывают начальные точки деления: x1=b−(b−a)Φ,x2=a+(b−a)Φ{\displaystyle x_{1}=b-{\frac {(b-a)}{\Phi }},\quad x_{2}=a+{\frac {(b-a)}{\Phi }}} и значения в них целевой функции: y1=f(x1),y2=f(x2){\displaystyle y_{1}=f(x_{1}),\;y_{2}=f(x_{2})}.
- Если y1≥y2{\displaystyle y_{1}\geq y_{2}} (для поиска max изменить неравенство на y1≤y2{\displaystyle y_{1}\leq y_{2}}), то a=x1{\displaystyle a=x_{1}}
- Иначе b=x2{\displaystyle b=x_{2}}.
Шаг 3.
- Если |b−a|<ε{\displaystyle |b-a|<\varepsilon }, то x=a+b2{\displaystyle x={\frac {a+b}{2}}} и останов.
- Иначе возврат к шагу 2.

Алгоритм взят из источника: Джон Г.Мэтьюз, Куртис Д.Финк. "Численные методы. Использование MATLAB". — М, СПб: "Вильямс", 2001. — 716 с.

Простейшая реализация данного алгоритма на языке F# (содержит лишние вычисления минимизируемой функции):

let phi = 0.5 * (1.0 + sqrt 5.0) let rec minimize f eps a b = if abs(b - a) < eps then 0.5 * (a + b) else let t = (b - a) / phi let x1, x2 = b - t, a + t if f x1 >= f x2 then minimize f eps x1 b else minimize f eps a x2 // Примеры вызова: minimize cos 1e-6 0.0 6.28 // = 3.141592794; число итераций: 33; функция f вызвана 64 раза. minimize (fun x -> (x - 1.0)**2.0) 1e-6 0.0 10.0 // = 1.000000145; число итераций: 35; функция f вызвана 68 раз.

Метод чисел Фибоначчи

В силу того, что в асимптотике Φ=limn→∞Fn+1Fn{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}}, метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.

Алгоритм

Шаг 1. Задаются начальные границы отрезка a,b{\displaystyle a,\;b} и число итераций n{\displaystyle n}, рассчитывают начальные точки деления: x1=a+(b−a)Fn−2Fn,x2=a+(b−a)Fn−1Fn{\displaystyle x_{1}=a+(b-a){\frac {F_{n-2}}{F_{n}}},\quad x_{2}=a+(b-a){\frac {F_{n-1}}{F_{n}}}} и значения в них целевой функции: y1=f(x1),y2=f(x2){\displaystyle y_{1}=f(x_{1}),\;y_{2}=f(x_{2})}.
Шаг 2. n=n−1{\displaystyle n=n-1}.
- Если y1>y2{\displaystyle y_{1}>y_{2}}, то a=x1,x1=x2,x2=b−(x1−a),y1=y2,y2=f(x2){\displaystyle a=x_{1},\;x_{1}=x_{2},\;x_{2}=b-(x_{1}-a),\;y_{1}=y_{2},\;y_{2}=f(x_{2})}.
- Иначе b=x2,x2=x1,x1=a+(b−x2),y2=y1,y1=f(x1){\displaystyle b=x_{2},\;x_{2}=x_{1},\;x_{1}=a+(b-x_{2}),\;y_{2}=y_{1},\;y_{1}=f(x_{1})}.
Шаг 3.
- Если n=1{\displaystyle n=1}, то x=x1+x22{\displaystyle x={\frac {x_{1}+x_{2}}{2}}} и остановка.
- Иначе возврат к шагу 2.

Литература

Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю. М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю. А., Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю. А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575—576.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1973. — С. 832 с илл..
Джон Г. Мэтьюз, Куртис Д. Финк. Численные методы. Использование MATLAB. — 3-е издание. — М., СПб.: Вильямс, 2001. — С. 716.

См. также

wikiredia.ru