Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы" (стр. 2 из 12). Лабораторный практикум методы оптимизации

Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы

Введение

В современном мире постоянно происходило совершенствование системы образования. Происходит модернизация старых, поиск новых способов обучения, способных улучшить сделать образовательный процесс более эффективным.

В настоящее время активно идут процессы внедрения в образовательный процесс компьютерных технологий. Компьютеры, разработанные первоначально для автоматизации вычислительных операций, с развитием средств мультимедиа превратились в мощнейший инструмент обработки информации различного рода. Свое применение они нашли и в сфере образования, предоставив свои возможности при работе с объемом человеческих знаний, накопленных за всю историю человечества.

Использование информационных технологий позволяет заменить часть ручного труда преподавателя трудом машинным, который, как и в других сферах, обходится дешевле, и, следовательно, более эффективен. Машины не устают, готовы к работе в любое время, не совершают арифметических ошибок и способны обладать огромными объемами памяти. Поэтому они внедряются в учебный процесс там, где это возможно.

Большое развитие компьютерные технологии получили в сфере дистанционного обучения. С появлением компьютерных сетей дистанционное обучение, подразумевающее работу обучающего с обучаемым на расстоянии, получило возможность мгновенной передачи информации между ними. Это позволило оперативно предоставлять учебные материалы и проводить контроль полученных знаний при снижении расходов на транспорт и связь.

Когда мы говорим о сетевых технологиях, то прежде всего имеем ввиду сеть интернет. Эта сеть, связывающая компьютеры по всему миру, позволяет организовать дистанционный учебный процесс практически в любой точке планеты в кратчайшие сроки.

Использование интернет-технологий также помогает в расширении виртуального образовательного пространства, ввиду того, что знания и учебные материалы из разных источников можно моментально получить в одном месте, стоит лишь правильно сформировать поисковый запрос. Данное обстоятельство несомненно способствует творческому процессу обучения и самостоятельной работе обучаемых в виртуальном образовательном пространстве.

Системы компьютерного дистанционного обучения в результате развития приняли различные формы, предназначенные для выполнения соответствующих задач, это и компьютерные учебники, содержащие учебные материалы в оптимизированной для наилучшего восприятия мультимедийной форме, и системы тестирования, обеспечивающие контроль знаний обучаемых путем анализа ответа на серии тематических вопросов, и лабораторные практикумы, обеспечивающие получение практических навыков использования полученных знаний.

В сфере информационных технологий зачастую при разработке нового продукта можно использовать готовые решения, которые поставляются в виде некоторой оболочки и наполняются содержимым по заданной тематике. Если использование готовых решений представляется затруднительным в связи с особенностями предметной области, приходится создавать новые программные продукты, позволяющие учесть эти особенности.

В направлении информатизации сферы образования работают сейчас практически все гуманитарные и технические учебные заведения разных стран. Разработки в этом направлении ведутся и в Московском авиационном институте. Кафедра «Математическая кибернетика» факультета «Прикладная математика и физика» института в течении многих лет разрабатывает учебные материалы с использованием компьютерных технологий. За это время создан комплекс компьютерных пособий и учебников, охватывающих предметы, читаемые преподавателями кафедры. Комплекс, включающий в себя более 70 компьютерных учебников, поддерживает 8 разделов курса "Теория управления", 7 разделов курса "Системный анализ", 3 раздела курса "Линейная алгебра и аналитическая геометрия", а также курсы "Теория графов", "Теория функций комплексного переменного", "Линейное программирование", "Линейные дифференциальные уравнения" и другие. Также функционирует кафедральных сайт в интернете, позволяющий студентам и преподавателям института обмениваться информацией дистанционно. В настоящее время на кафедре ведется работа по созданию других средств обучения с применением информационных технологий.

Кафедра «Математическая кибернетика» факультета «Прикладная математика и физика» института читает студентам курс «Методы оптимизации», изучающий методы оптимизации математических функций. На кафедре был создан практикум по этому курсу в среде Microsoft DOS, позволяющий студентам изучать методы на примерах, работая за компьютером в терминальном классе. В рамках дипломного проекта поставлена задача создания аналогичного практикума, работающего в сетевом режиме с целью упростить проведение работ. Также требуется расширить функционал имеющегося практикума для достижения большей наглядности примеров.

В рамках дипломного проекта требуется:

Изучить описываемые методы оптимизации и составить документацию по ним в мультимедийной форме.
Разработать архитектуру практикума
Разработать пользовательский интерфейс
Выбрать программные средства для разработки и составить алгоритмы

Раздел 1 содержит теоретические сведения о математических методах поиска безусловного экстремума функций многих переменных. Приводятся алгоритмы, графические иллюстрации и условия окончания методов.

Раздел 2 содержит описание практической части разработанного практикума. Проводится анализ современных программных архитектур, обоснование выбора клиент-серверной модели, анализ и выбор программных сред. Также приводится описание пользовательского интерфейса, форм отчетности и справочной системы практикума.

Раздел 3 содержит расчет экономических показателей, связанных с выполнением дипломного проекта.

В разделе 4 описаны вредные воздействия, возникающие при использовании информационных технологий в обучении и способы их сокращения.

1. Теоретическая часть

Решение задачи о поиске безусловного экстремума функции многих переменных с помощью необходимых и достаточных условий приводит к необходимости решать систему нелинейных уравнений с неизвестными с последующей проверкой знакоопределенности матрицы Гессе . Как правило, для достаточно сложных функций такая процедура решения задачи достаточно трудоемка и подразумевает численное решение нескольких задач. Поэтому возникает необходимость использовать так называемые прямые или численные методы безусловной оптимизации, которые позволяют найти стационарные точки функции, не используя аппарат необходимых и достаточных условий экстремума.

Компьютерный лабораторный практикум предназначен для студентов технических специальностей вузов и позволяет в наглядной и доступной форме представить численные алгоритмы отыскания экстремумов. Особенностью практикума является интерактивная форма реализации алгоритмов, при которой студент на каждой итерации принимает решение о выборе параметров методов, основываясь на числовой и графической информации о ходе процесса оптимизации.

Целью лабораторного практикума является изучение студентами прямых методов поиска безусловного экстремума двух типов функций:

Для достижения цели студент должен, изменяя параметры методов, добиться выполнения критерия окончания счета для каждого метода с одной и той же заданной точностью , из одной и той же начальной точки, за заданное для каждого метода число итераций N.

Методы, реализованные в лабораторном практикуме

Прямые методы, представленные в практикуме имеют один и тот же алгоритм

где

и отличаются друг от друга способом задания и выбором .

Алгоритм работы прямых методов схематически изображен на рис. 1.1

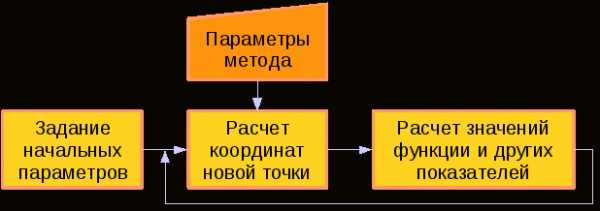
Рисунок 3.1. Алгоритм работы прямых методов

В практикуме реализованы:

методы первого порядка, использующие информацию о 1-х производных функции :
- метод градиентного спуска;
- метод наискорейшего градиентного спуска;
- метод покоординатного спуска;
- метод Гаусса-Зейделя;
- метод сопряженных градиентов.
методы второго порядка, использующие для своей реализации информацию о 1-х и 2-х производных функции :

en.coolreferat.com

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Казанский государственный технологический университет»

Нижнекамский химико-технологический институт

МЕТОДЫ ОПТИМИЗАЦИИ

Лабораторный практикум

2006

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Казанский государственный технологический университет»

Нижнекамский химико-технологический институт

МЕТОДЫ ОПТИМИЗАЦИИ

Лабораторный практикум

Казань 2006

Методы оптимизации: лабораторный практикум/ Э.Р. Галеев, В.В. Елизаров, В.И. Елизаров; Казан. гос. технол. ун-т. Казань, 2006. 64с.

Приведены лабораторные работы по разделам курса «Методы оптимизации»: линейное программирование, нелинейное программирование, принцип максимума.

Предназначено для студентов, обучающихся по направлениям «Информатика и вычислительная техника», «Автоматизированные технологии и производства».

Подготовлено на кафедре АТПП Нижнекамского химико-технологического института КГТУ.

Печатается по решению методической комиссии по циклу дисциплин систем автоматизации, электротехники и электропривода Нижнекамского химико-технологического института КГТУ.

Рецензенты: к.т.н., доц. А.В. Садыков

к.ф-м.н. О.В. Шемелова

Содержание

Введение 4

Работа 1. Решение транспортной задачи симплексным методом линейного программирования 5

1.1. Сведение задачи с ограничениями типа неравенств к задаче с ограничениями типа равенств 7

1.2. Симплексный метод решения задач линейного программирования 8

1.3. Постановка транспортной задачи 11

1.4. Порядок выполнения работы 18

Работа 2. Оптимизация реактора идеального смешения методами нелинейного программирования 20

2.1. Градиентные методы 22

2.2. Безградиентные методы детерминированного поиска 29

2.3. Методы случайного поиска 34

2.4. Поиск при наличии «оврагов» целевой функции 39

2.5. Постановка задачи оптимизации реактора идеального смешения 42

2.6. Порядок выполнения работы 43

Работа 3. Оптимизация реактора идеального вытеснения на основе принципа максимума 46

3.1. Формулировка принципа максимума в задаче со свободным правым концом 48

3.2. Постановка задачи оптимизации реактора идеального вытеснения 56

3.3. Порядок выполнения работы 61

Библиографический список 64

Введение

Оптимизацией в самом широком смысле этого слова называется получение наилучших результатов в тех или иных условиях. Оптимальное управление является одной из наиболее активно разрабатываемых областей техники и нашло большое число применений в космонавтике, химии, энергетике и других отраслях промышленности.

Современная теория управления решает задачи исследования многомерных систем, систем с ограничениями на фазовые переменные и управления, стохастических и больших систем с запаздыванием.

Исходным положением современной теории управления является система уравнений состояния, описывающих поведение системы.

При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать метод, который приводил бы к конечным результатам, обеспечивающим получение оптимального значения критерия оптимальности. Выбор того или иного метода определяется постановкой задачи и используемой математической моделью объекта оптимизации.

Для решения задачи оптимизации применяют в основном следующие методы: методы исследования функций классического анализа; линейное, нелинейное программирование; методы, основанные на использовании неопределенных множителей Лагранжа; вариационное исчисление; динамическое программирование; принцип максимума.

Предлагаемый лабораторный практикум направлен на освоение некоторых методов линейного и нелинейного программирования и принципа максимума.

studfiles.net

Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы" (стр. 1 из 12)

Введение

В рамках дипломного проекта требуется:

- Изучить описываемые методы оптимизации и составить документацию по ним в мультимедийной форме.

- Разработать архитектуру практикума

- Разработать пользовательский интерфейс

- Выбрать программные средства для разработки и составить алгоритмы

Раздел 3 содержит расчет экономических показателей, связанных с выполнением дипломного проекта.

1. Теоретическая часть

Решение задачи о поиске безусловного экстремума функции многих переменных

с помощью необходимых и достаточных условий приводит к необходимости решать систему нелинейных уравнений с неизвестными с последующей проверкой знакоопределенности матрицы Гессе . Как правило, для достаточно сложных функций такая процедура решения задачи достаточно трудоемка и подразумевает численное решение нескольких задач. Поэтому возникает необходимость использовать так называемые прямые или численные методы безусловной оптимизации, которые позволяют найти стационарные точки функции, не используя аппарат необходимых и достаточных условий экстремума.

· квадратичной функции 2-х переменных:

· овражной функции

1.1 Методы, реализованные в лабораторном практикуме

Прямые методы, представленные в практикуме имеют один и тот же алгоритм

где

- текущая точка последовательности, причем – задается из физического содержания задачи или произвольно;

- последующая точка последовательности;

- приемлемое направление перехода из точки в точку – направление спуска. Приемлемым при решении задачи поиска минимума функции будет только то направление, для которого , что обеспечивается выполнением условия ;

- шаг (число >0),

и отличаются друг от друга способом задания

и выбором .

Алгоритм работы прямых методов схематически изображен на рис. 1.1

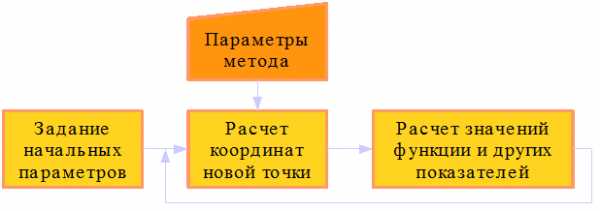
Рисунок 1.1. Алгоритм работы прямых методов

В практикуме реализованы:

- методы первого порядка, использующие информацию о 1-х производных функции

mirznanii.com

Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

· метод градиентного спуска;

· метод наискорейшего градиентного спуска;

· метод покоординатного спуска;

· метод Гаусса-Зейделя;

· метод сопряженных градиентов.

- методы второго порядка, использующие для своей реализации информацию о 1-х и 2-х производных функции

· метод Ньютона;

· метод Ньютона-Рафсона;

· метод Марквардта

- Методы нулевого порядка, представленные в практикуме, позволяют производить поиск безусловного экстремума функций с помощью заданной последовательности операций. Повторение этих операций производится до тех пор, пока не будет выполнен критерий окончания, определяемый используемым методом.

В практикуме реализованы следующие методы нулевого порядка:

· метод случайного поиска

· метод деформируемого многогранника

· метод конфигураций

1.1.1 Метод градиентного спуска

Алгоритм метода:

здесь:

- направление антиградиента функции;

- шаг выбирается из условия убывания функции в точках последовательности

Геометрическая интерпретация метода:

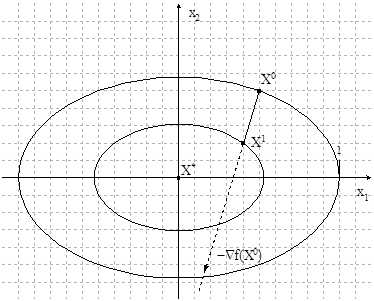
Рисунок 1.2. Геометрическая интерпретация метода

Основной критерий окончания метода:

Построение последовательности заканчивается в точке, для которой

где

- заданное малое положительное число, здесь

Начальные параметры метода:

Изменяемый параметр метода: величина шага

Особенности реализации алгоритма. Вопрос о величине шага на каждой итерации решается пользователем, причем шаг может быть, как уменьшен, если не выполняется условие

, так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя).

Рекомендации по выбору параметров метода. Согласно алгоритму метода, каждая последующая точка

в методе градиентного спуска ищется в направлении направлении антиградиента функции, построенном в текущей точке . Поэтому, если направление антиградиента в текущей точке приблизительно совпадает с направлением на минимум (согласно чертежу), шаг следует увеличить, чтобы ускорить процесс сходимости, если же направление антиградиента сильно отличается от направления на минимум, шаг уменьшают, в противном случае функция может уменьшиться несущественно или даже возрасти.

1.1.2 Метод градиентного наискорейшего спуска

Алгоритм метода:

здесь

- направление антиградиента функции

- шаг вычисляется из условия наибольшего убывания функции в точках последовательности:

Геометрическая интерпретация метода

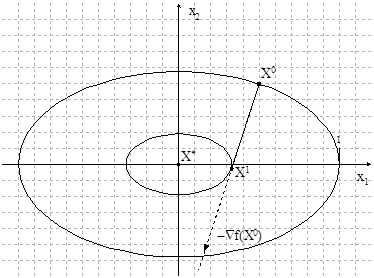
Рисунок 1.3. Геометрическая интерпретация метода

В методе наискорейшего градиентного спуска последующая точка

минимизирующей последовательности также ищется в направлении - направлении антиградиента функции, построенном в текущей точке, но условия вычисления шага позволяют определить наилучшее положение точки на этом направлении. Как видно из чертежа, точка принимает на направлении спуска предельное положение, которое характеризуется тем, что линия уровня, проходящая через точку , касается направления спуска, а, следовательно, в точках минимизирующей последовательности, построенной по методу градиентного наискорейшего спуска, выполняется условие:

Основной критерий окончания метода:

Начальные параметры метода:

Изменяемые параметры метода: отрезок для уточнения шага

Особенности реализации алгоритма. При решении задачи поиска оптимального шага

, функция становится функцией одой переменной , т.к. , а и известны. Следовательно, задача о поиске оптимального шага - это задача , которая в лабораторной работе решается численно методом дихотомии на отрезке с заданной точностью . Вопрос о границах отрезка на каждой итерации решается пользователем.

Рекомендации по выбору параметров метода. При задании на каждой итерации отрезка

для уточнения шага, следует помнить, что искомое решение может лежать как внутри, так и на границе интервала .

Проиллюстрируем ситуацию, при которой шаг

вычисляется численно методом дихотомии. Для этого построим график функции , которая в случае если является квадратичной функцией, имеет вид: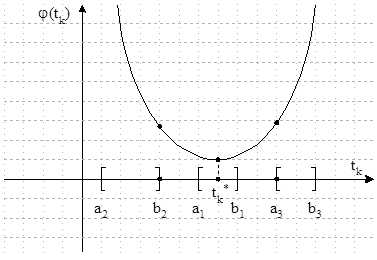

Рисунок 1.4 Метод дихотомии

Для вычислений по методу дихотомии должен быть задан отрезок для уточнения оптимального значения шага.

Как видно из чертежа, если в качестве отрезка будет выбран

, оптимальное значение шага, при котором функция принимает минимальное значение, окажется внутри отрезка, и метод с заданной точностью отыщет это значение. Если же отрезок будет , в качестве результата счета по методу дихотомии будет получено значение - как дающее наименьшее значение функции на отрезке, аналогично при выборе отрезка будет получено значение .

Таким образом, отрезок для уточнения оптимального шага должен быть достаточно большим, чтобы гарантировано включать искомое значение шага. Признаками неверного задания отрезка

являются: отсутствие касания траектории спуска из точки и линии уровня функции через точку , а также равенство величины оптимального шага величине одной из границ отрезка.

mirznanii.com

Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

Рисунок 1.17. Неудачная система пробных точек (слева - возможна повторная попытка, справа - необходимо уменьшить радиус)

5) Процедура 2)-4) повторяется до выполнения критерия окончания счета.

Основной критерий окончания метода:

Дополнительные критерии окончания метода:

- при выполнении предельного числа итераций:

- при однократном или двукратном одновременном выполнении двух условий:

где

- малое положительное число.

Алгоритм работы метода случайного поиска схематически изображен на рис. 1.18

Рисунок 1.18. Диаграмма работы метода случайного поиска

1.1.12 Метод конфигураций (Хука-Дживса)

Метод представляет собой комбинацию исследующего (исследовательского) поиска с циклическим изменением переменных и ускоряющего поиска по образцу.

Процесс поиска минимума функции всегда начинается с исследующего поиска.

Исследующий поиск осуществляется вдоль координатных направлений, результатом его являются так называемые точки базиса, в которых вычисляется значение функции

Поиск по образцу осуществляется в направлении, соединяющем де последующие точки базиса. В точках полученных «по образцу» значение функции не вычисляется, они служат лишь для проведения в них исследующего поиска.

Алгоритм метода:

1) Задается начальная точка

и начальные значение приращений. Точка называется точкой старого базиса.

2) Проводится исследующий поиск, в результате которого каждая координата новой точки

вычисляется по алгоритму:

В результате исследующего поиска получается точка

Если при этом

, то - точка нового базиса.

Если

, то исследующий поиск неудачен. В этом случае необходимо уменьшить значения приращений и повторить исследующий поиск.

Рисунок 1.19. Исследующий поиск (слева — удачный, справа - неудачный)

- точка старого базиса - точка нового базиса

3) Из точки нового базиса может быть:

· продолжен исследующий поиск со старыми или новыми значениями приращений (шаг 2) алгоритма)

· проведен поиск по образцу по алгоритму:

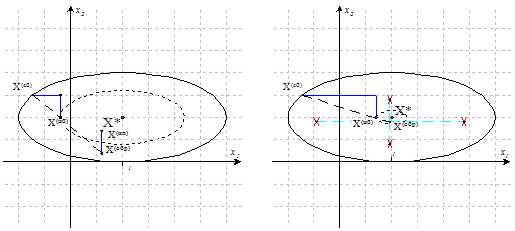
Рисунок 1.20. Поиск по образцу (слева — удачный, справа - неудачный)

В точке

значение функции не вычисляется, из этой точки проводится исследующий поиск, в результате которого получается точка . Если , то точка становится точкой нового базиса, а - точкой старого базиса.

Если

, то поиск по образцу считается неудачным, точки - аннулируются, при этом точка остается точкой нового базиса, а - точкой старого базиса.

4) Процедура 3) повторяется до выполнения критерия окончания счета.

Основной критерий окончания метода:

Дополнительные критерии окончания метода:

- при выполнении предельного числа итераций:

- при однократном или двукратном одновременном выполнении двух условий:

где

- малое положительное число.

Алгоритм работы метода конфигураций схематически изображен на рис. 1.21

Рисунок 1.21. Диаграмма работы метода конфигураций

Создание любого программного изделия, как и любая другая деятельность, делится на несколько взаимосвязанных этапов. В данном случае мы имеем дело с построением некоторой системы, которая будет выполнять определённые задачи. Значит, нам нужно определить, какие средства нам понадобятся для выполнения этих задач.

Во-первых, разрабатываемая система должна иметь определённую структуру, которая определяет механизм её работы. Для определения структуры необходимо рассмотреть современные виды архитектуры, использующиеся в сходных проектах. Затем нужно сравнить эти модели и выбрать на основании этого сравнения такую модель, которая в наибольшей степени будет соответствовать предъявляемым требованиям.

После выбора вида архитектуры программы, требуется выбрать программные средства, которые будут использоваться в проекте для реализации программных механизмов. От выбора программных средств зависит то, какая квалификация потребуется для дальнейшей работы над проектом, а также для его внедрения, и, в некоторых случаях, использования.

После выбора программных средств, производится непосредственно разработка архитектуры системы и написание текстов программ, составляющих её, написание текстов документации.

2.1 Анализ архитектур

В программировании архитектурой программного продукта является совокупность общих принципов работы программ, входящих в программный продукт и принципов взаимосвязи этих программ в единое целое. Архитектура программного продукта определяется на ранней стадии разработки, желательно до того, как будут выбраны конкретные программные среды, в которых будут разрабатываться составные части проекта, хотя не исключена ситуация, когда программная среда определена заранее, и требуется разрабатывать программы уже в предопределённых условиях.

В случае, когда сначала разрабатывается архитектура программы, то затем выбор программных сред ведётся, как правило, с учётом приспособленности этих сред не только к решению данной задачи в общем, но и к построению программного продукта в рамках выбранной архитектуры.

При выборе архитектуры программного продукта нужно руководствоваться тем, какие задачи необходимо решить с его помощью. Использование какой-либо одной архитектуры во всех проектах не оправдано, так как различные архитектуры лучше способствуют решению различных классов задач, и, если какая-либо архитектура покажет себя хорошо при решении одного класса задач, то нельзя с уверенностью сказать, что удастся с её помощью эффективно решить и любую другую задачу.

Правильно выбранная архитектура способствует прежде всего облегчению работ над проектом различными путями, а также придает программному продукту целостный вид, простоту и удобство в использовании.

В настоящее время существует несколько основных типовых архитектур, которые широко применяются в разработке программных продуктов в мире.

Локальная архитектура подразумевает монолитную программу, в которой все вычисления производятся в одном общем программном модуле.

Клиент-серверная архитектура содержит две части — клиент, где происходит диалог с пользователем и сервер, где производится обработка данных.

При большом количестве данных используется многозвенная архитектура, когда в клиент-серверной модели добавляются дополнительные серверы, которые обслуживают центральный сервер.

Сервисно-ориентированная архитектура, которая опирается на набор стандартизированных сервисов, взаимодействующих между собой.

Архитектура одноранговой сети характеризуется наличием нескольких программ, выполняющих сходные функции и соединяющихся между собой для взаимного обмена информацией.

mirznanii.com

Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы

1.	Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы В современном мире постоянно происходило совершенствование системы образования. Происходит модернизация старых, поиск новых способов обучения, способных улучшить сделать образовательный процесс более эффективным.В настоящее время активно идут процессы внедрения в образовательный процесс компьютерных технологий. Компьютеры, разработанные первоначально для автоматизации вычислительных операций, с развитием средств мультимедиа превратились в мощнейший инструмент обработки информации различного рода. Свое применение они нашли и в сфере образования, предоставив свои возможности при работе с объемом человеческих знаний, накопленных за всю историю человечества. В работе есть: введение, заключение, таблицы более 10 шт., приложения 1 шт., рисунки более 10 шт., выводы 1 шт.	ДипломРазмер: 5.77 мб.Язык: русскийРазместил (а): mangoпросмотреть
2.	Классические методы безусловной оптимизации . Как известно, классическая задача безусловной оптимизации имеет вид. . Существуют аналитические и численные методы решения этих задач Прежде всего вспомним аналитические методы решения задачи безусловной оптимизации В работе есть: рисунки более 10 шт.	РефератРазмер: 258.22 кб.Язык: русскийРазместил (а): Zeusпросмотреть
3.	Проблема формирования исследовательских умений при проведении лабораторных практикумов Сочетание традиционной репродуктивной методики проведения практикума с новыми подходами. Сочетание современного лабораторного практикума с информационными технологиями. Интеграция теоретических и эмпирических знаний. В работе есть: содержание, введение, приложения 1 шт.	РефератРазмер: 37.07 кб.Язык: русскийРазместил (а): incognitoпросмотреть
4.	Методы оптимизации функций многих переменных Методы условной и безусловной нелинейной оптимизации. Исследование функции на безусловный экстремум. Численные методы минимизации функции. Минимизация со смешанными ограничениями. Седловые точки функции. В работе есть: содержание, введение, приложения 3 шт., рисунки более 10 шт., сноски 1 шт., выводы 1 шт.	Лабораторная работаРазмер: 0.61 мб.Язык: русскийРазместил (а): Maddy1990просмотреть
5.	Теоретические основы фундаментальной естественнонаучной подготовки студентов технического вуза Модель естественнонаучной подготовки в компьютерной обучающей среде. Методика компьютерного сопровождения учебных занятий направленная на развитие творческой активности студентов при проведении лабораторного практикума с элементами автоматизации. В работе есть: приложения 1 шт., рисунки 5 шт.	РефератРазмер: 150.67 кб.Язык: русскийРазместил (а): opit prepodпросмотреть
6.	Разработка виртуальных лабораторных работ средствами эмулятора Emu8086 Виртуальный лабораторный практикум в инженерном образовании. Особенности лабораторного практикума для естественнонаучных дисциплин. Программный эмулятор виртуальный пк Emu Вывод значения байта в десятеричной системе счисления методика выполнения. В работе есть: содержание, введение, таблицы 3 шт., приложения 5 шт., рисунки более 10 шт., выводы 10 шт.	ДипломРазмер: 458.74 кб.Язык: русскийРазместил (а): Викторпросмотреть
7.	Численные методы решения систем линейных уравнений Численные методы линейной алгебры. Матричный метод. Методы Крамера и Гаусса. Интерации линейных систем. Интерации Якоби и Гаусса Зейделя. Листинг программы. Численные методы в электронных таблицах Excel и программе Mathcad Microsoft Visual Basic II Практическая часть III Польза введения расчётов. Источники: 8 шт. 1982-2004гг. В работе есть: содержание, введение, таблицы 2 шт., рисунки более 10 шт., выводы 3 шт.	КурсоваяРазмер: 334.3 кб.Язык: русскийРазместил (а): Танюшкапросмотреть
8.	Численные методы вычисления интегралов Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса. 1. Численные методы вычисления интегралов. Постановка задачи. Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам В работе есть: рисунки более 10 шт., выводы 1 шт.	РефератРазмер: 88.99 кб.Язык: русскийРазместил (а): Сергей Степановичпросмотреть
9.	Методы синтеза и оптимизации Программирование численных методов одномерной оптимизации. Решение одномерных задач оптимизации методами последовательного поиска. Градиентные методы и их применение для оптимизации на ЭВМ математических моделей объектов. В работе есть: таблицы 1 шт., рисунки более 10 шт., сноски 3 шт., выводы 4 шт.	Контрольная работаРазмер: 279.68 кб.Язык: русскийРазместил (а): Евгенийпросмотреть
10.	Разработка и отладка программного обеспечения виртуальной лаборатории Программирование микроконтроллерных Концепция построения виртуальной лаборатории вл Программирование микроконтроллерных систем. Принцип построения лабораторного практикума. Архитектура аппаратного обеспечения ВЛ. Аппаратные способы реализации генератора сигналов произвольной формы. Источники: 2 шт. 2001-2002гг. В работе есть: содержание, введение, рисунки 7 шт., выводы 2 шт.	Магистерская работаРазмер: 0.69 мб.Язык: русскийРазместил (а): RMeпросмотреть
11.	Численные методы Программа-калькулятор на Pascal Теория чисел как одно из направлений математики изучающее свойства натуральных чисел. Разработка программы-калькулятора CalcKurs на языке программирования Pascal. Основные функции реализованные в программе. В работе есть: содержание, введение, приложения 2 шт., рисунки более 10 шт., сноски 7 шт.	КурсоваяРазмер: 1.97 мб.Язык: русскийРазместил (а): Антонпросмотреть
12.	Численные методы и их реализация в Excel на тему: ‘’Численные методы и их реализация в. Кыргызский Государственный Национальный Университет. Институт Интеграции Международных Образовательных. Программ. Кыргызско - Американский факультет Компьютерных технологий и ИНТЕРНЕТ. В работе есть: рисунки более 10 шт.	РефератРазмер: 0.91 мб.Язык: русскийРазместил (а): Олег Бабаевпросмотреть
13.	Численные методы 5 Численные методы представляют собой набор алгоритмов позволяющих получать приближенное численное решение математических задач. Два вида погрешностей возникающих при решении задач. Нахождение нулей функции. В работе есть: рисунки более 10 шт.	ЛекцияРазмер: 85.48 кб.Язык: русскийРазместил (а): ftpпросмотреть
14.	Сравнительный анализ численных методов Численные методы Численные методы решения задач сводящиеся к арифметическим и некоторым логическим действиям над числами к действиям которые выполняет ЭВМ. Решение нелинейных системы линейных алгебраических обыкновенных дифференциальных уравнений численными методами. Источники: 4 шт. 1972-2004гг. В работе есть: содержание, введение, заключение, таблицы 1 шт., рисунки более 10 шт., выводы 2 шт.	ДипломРазмер: 1.48 мб.Язык: русскийРазместил (а): Натальяпросмотреть
15.	Разработка бизнес плана компьютерного клуба Характеристика нового бизнеса открытия компьютерного клуба. Виктория и его услуг. Прогноз и расчеты коньюктуры рынка. Стратегия маркетинга компьютерного клуба. Виктория обоснование стратегии. Организация работы и финансирование. В работе есть: план, таблицы 6 шт., приложения 6 шт., рисунки 2 шт., сноски 2 шт.	Бизнес-планРазмер: 39.89 кб.Язык: русскийРазместил (а): Ольгапросмотреть
16.	Численные методы решения обыкновенных дифференциальных уравнений Обыкновенным дифференциальным уравнением порядком уравнения. Уравнение с начальными условиями. Лабораторная работа. Численные методы решения обыкновенных дифференциальных уравнений (4 часа). в котором называется. В работе есть: рисунки более 10 шт.	ЗадачаРазмер: 56.27 кб.Язык: русскийРазместил (а): Palonпросмотреть
17.	Численные методы решения типовых математических задач Метод Гаусса. Численные методы решения типовых математических задач. Курсовая работа. по дисциплине Вычислительная математика. 1. Решение систем линейных алгебраических уравнений методом простой итерации. 1.1 Постановка задачи. В работе есть: рисунки более 10 шт., сноски более 10 шт., выводы 3 шт.	КурсоваяРазмер: 0.87 мб.Язык: русскийРазместил (а): Дениспросмотреть
18.	Сравнительный анализ методов оптимизации Математическая задача оптимизации. Минимум функции одной и многих переменных. Унимодальные и выпуклые функции. Прямые методы безусловной оптимизации и минимизации их практическое применение. Методы деления отрезка пополам дихотомия и золотого сечения. Источники: 3 шт. 1978-1986гг. В работе есть: содержание, введение, заключение, таблицы 2 шт., рисунки более 10 шт.	КурсоваяРазмер: 2.14 мб.Язык: русскийРазместил (а): Натальяпросмотреть
19.	Ряды Фурье. Численные методы расчета коэффициентов Ряды Фурье. Численные методы расчета коэффициентов. 1. Таковы например, сила и напряжение переменного тока или пример паровой машины путь, скорость и ускорение крейцкопфа, давление пара, касательное усилие в пальце кривошипа и т. д В работе есть: приложения 4 шт., рисунки более 10 шт., сноски 4 шт., выводы 2 шт.	КурсоваяРазмер: 118.9 кб.Язык: русскийРазместил (а): МаляВопросмотреть
20.	Разработка проекта оптимизации платежей по налогу на прибыль организации Сущность виды принципы и методы оптимизации налоговых платежей уклонение от их уплаты. Анализ финансово-хозяйственной деятельности и учетной политики предприятия. Создание резерва на ремонт основных средств и выбор оптимального способа амортизации. В работе есть: таблицы 9 шт., приложения более 10 шт., рисунки 2 шт., выводы 2 шт.	ДипломРазмер: 1.16 мб.Язык: русскийРазместил (а): Марияпросмотреть
21.	Элективный курс Биохимия в школьном курсе химии Сущность структура и функции белков нуклеиновых кислот углеводов и липидов. Место биохимии в школьном курсе химии. Методика проведения интегрированных уроков биологии и химии по темам: Химия крови и Лекарства с применением лабораторного практикума. В работе есть: введение, приложения более 10 шт., рисунки более 10 шт., выводы 2 шт.	КурсоваяРазмер: 0.78 мб.Язык: русскийРазместил (а): ларисапросмотреть
22.	Численные методы интегрирования и оптимизации сложных систем Изучение численных методов решения нелинейных уравнений. Построение годографа афчх графиков ачх и фчх с указанием частот. Практическое изучение численных методов интегрирования дифференциальных уравнений высокого порядка метод. В работе есть: таблицы 1 шт., приложения 5 шт., рисунки более 10 шт., выводы 2 шт.	КурсоваяРазмер: 416.26 кб.Язык: русскийРазместил (а): Селапросмотреть
23.	Кибернетические методы в праве Математическая логика, теория вероятностей, вычислительная математика, теория информации, теория кодирования, теория алгоритмов, теория случайных процессов, теория игр, теория статистических решений и т д данных. В работе есть: рисунки 1 шт.	РефератРазмер: 47.85 кб.Язык: русскийРазместил (а): Павел Воляпросмотреть
24.	Численные методы Программа-калькулятор на Pascal Разработка программы-калькулятора Разработка программы-калькулятора CalcKurs на языке программирования Pascal реализующую функции: решение уравнений с целочисленными коэффициентами нахождение нод и нок представление рациональной дроби в виде цепной и цепной дроби в виде рациональной. В работе есть: приложения 2 шт., рисунки более 10 шт., сноски 7 шт.	КурсоваяРазмер: 2.11 мб.Язык: русскийРазместил (а): Тузов Игорьпросмотреть
25.	Методы моделирования и оптимизации решений Всероссийский заочный ФИНАСОВО-ЭКОНОМИЧЕСКИЙ. Филиал в г. Брянске по дисциплине. Вариант Методы моделирования и оптимизации решений. ВЫПОЛНИЛ(А). СТУДЕНТ(КА). СПЕЦИАЛЬНОСТЬ. ЗАЧ. КНИЖКИ. ПРЕПОДАВАТЕЛЬ.	ТестыРазмер: 21.55 кб.Язык: русскийРазместил (а): Олег Бабаевпросмотреть

www.coolreferat.com

Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы

1.	Разработка компьютерного лабораторного практикума Теория оптимизации и численные методы В современном мире постоянно происходило совершенствование системы образования. Происходит модернизация старых, поиск новых способов обучения, способных улучшить сделать образовательный процесс более эффективным.В настоящее время активно идут процессы внедрения в образовательный процесс компьютерных технологий. Компьютеры, разработанные первоначально для автоматизации вычислительных операций, с развитием средств мультимедиа превратились в мощнейший инструмент обработки информации различного рода. Свое применение они нашли и в сфере образования, предоставив свои возможности при работе с объемом человеческих знаний, накопленных за всю историю человечества. В работе есть: введение, заключение, таблицы более 10 шт., приложения 1 шт., рисунки более 10 шт., выводы 1 шт.	ДипломРазмер: 5.77 мб.Язык: русскийРазместил (а): mangoпросмотреть
2.	Классические методы безусловной оптимизации . Как известно, классическая задача безусловной оптимизации имеет вид. . Существуют аналитические и численные методы решения этих задач Прежде всего вспомним аналитические методы решения задачи безусловной оптимизации В работе есть: рисунки более 10 шт.	РефератРазмер: 258.22 кб.Язык: русскийРазместил (а): Zeusпросмотреть
3.	Проблема формирования исследовательских умений при проведении лабораторных практикумов Сочетание традиционной репродуктивной методики проведения практикума с новыми подходами. Сочетание современного лабораторного практикума с информационными технологиями. Интеграция теоретических и эмпирических знаний. В работе есть: содержание, введение, приложения 1 шт.	РефератРазмер: 37.07 кб.Язык: русскийРазместил (а): incognitoпросмотреть
4.	Методы оптимизации функций многих переменных Методы условной и безусловной нелинейной оптимизации. Исследование функции на безусловный экстремум. Численные методы минимизации функции. Минимизация со смешанными ограничениями. Седловые точки функции. В работе есть: содержание, введение, приложения 3 шт., рисунки более 10 шт., сноски 1 шт., выводы 1 шт.	Лабораторная работаРазмер: 0.61 мб.Язык: русскийРазместил (а): Maddy1990просмотреть
5.	Теоретические основы фундаментальной естественнонаучной подготовки студентов технического вуза Модель естественнонаучной подготовки в компьютерной обучающей среде. Методика компьютерного сопровождения учебных занятий направленная на развитие творческой активности студентов при проведении лабораторного практикума с элементами автоматизации. В работе есть: приложения 1 шт., рисунки 5 шт.	РефератРазмер: 150.67 кб.Язык: русскийРазместил (а): opit prepodпросмотреть
6.	Разработка виртуальных лабораторных работ средствами эмулятора Emu8086 Виртуальный лабораторный практикум в инженерном образовании. Особенности лабораторного практикума для естественнонаучных дисциплин. Программный эмулятор виртуальный пк Emu Вывод значения байта в десятеричной системе счисления методика выполнения. В работе есть: содержание, введение, таблицы 3 шт., приложения 5 шт., рисунки более 10 шт., выводы 10 шт.	ДипломРазмер: 458.74 кб.Язык: русскийРазместил (а): Викторпросмотреть
7.	Численные методы решения систем линейных уравнений Численные методы линейной алгебры. Матричный метод. Методы Крамера и Гаусса. Интерации линейных систем. Интерации Якоби и Гаусса Зейделя. Листинг программы. Численные методы в электронных таблицах Excel и программе Mathcad Microsoft Visual Basic II Практическая часть III Польза введения расчётов. Источники: 8 шт. 1982-2004гг. В работе есть: содержание, введение, таблицы 2 шт., рисунки более 10 шт., выводы 3 шт.	КурсоваяРазмер: 334.3 кб.Язык: русскийРазместил (а): Танюшкапросмотреть
8.	Численные методы вычисления интегралов Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса. 1. Численные методы вычисления интегралов. Постановка задачи. Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам В работе есть: рисунки более 10 шт., выводы 1 шт.	РефератРазмер: 88.99 кб.Язык: русскийРазместил (а): Сергей Степановичпросмотреть
9.	Методы синтеза и оптимизации Программирование численных методов одномерной оптимизации. Решение одномерных задач оптимизации методами последовательного поиска. Градиентные методы и их применение для оптимизации на ЭВМ математических моделей объектов. В работе есть: таблицы 1 шт., рисунки более 10 шт., сноски 3 шт., выводы 4 шт.	Контрольная работаРазмер: 279.68 кб.Язык: русскийРазместил (а): Евгенийпросмотреть
10.	Разработка и отладка программного обеспечения виртуальной лаборатории Программирование микроконтроллерных Концепция построения виртуальной лаборатории вл Программирование микроконтроллерных систем. Принцип построения лабораторного практикума. Архитектура аппаратного обеспечения ВЛ. Аппаратные способы реализации генератора сигналов произвольной формы. Источники: 2 шт. 2001-2002гг. В работе есть: содержание, введение, рисунки 7 шт., выводы 2 шт.	Магистерская работаРазмер: 0.69 мб.Язык: русскийРазместил (а): RMeпросмотреть
11.	Численные методы Программа-калькулятор на Pascal Теория чисел как одно из направлений математики изучающее свойства натуральных чисел. Разработка программы-калькулятора CalcKurs на языке программирования Pascal. Основные функции реализованные в программе. В работе есть: содержание, введение, приложения 2 шт., рисунки более 10 шт., сноски 7 шт.	КурсоваяРазмер: 1.97 мб.Язык: русскийРазместил (а): Антонпросмотреть
12.	Численные методы и их реализация в Excel на тему: ‘’Численные методы и их реализация в. Кыргызский Государственный Национальный Университет. Институт Интеграции Международных Образовательных. Программ. Кыргызско - Американский факультет Компьютерных технологий и ИНТЕРНЕТ. В работе есть: рисунки более 10 шт.	РефератРазмер: 0.91 мб.Язык: русскийРазместил (а): Олег Бабаевпросмотреть
13.	Численные методы 5 Численные методы представляют собой набор алгоритмов позволяющих получать приближенное численное решение математических задач. Два вида погрешностей возникающих при решении задач. Нахождение нулей функции. В работе есть: рисунки более 10 шт.	ЛекцияРазмер: 85.48 кб.Язык: русскийРазместил (а): ftpпросмотреть
14.	Сравнительный анализ численных методов Численные методы Численные методы решения задач сводящиеся к арифметическим и некоторым логическим действиям над числами к действиям которые выполняет ЭВМ. Решение нелинейных системы линейных алгебраических обыкновенных дифференциальных уравнений численными методами. Источники: 4 шт. 1972-2004гг. В работе есть: содержание, введение, заключение, таблицы 1 шт., рисунки более 10 шт., выводы 2 шт.	ДипломРазмер: 1.48 мб.Язык: русскийРазместил (а): Натальяпросмотреть
15.	Разработка бизнес плана компьютерного клуба Характеристика нового бизнеса открытия компьютерного клуба. Виктория и его услуг. Прогноз и расчеты коньюктуры рынка. Стратегия маркетинга компьютерного клуба. Виктория обоснование стратегии. Организация работы и финансирование. В работе есть: план, таблицы 6 шт., приложения 6 шт., рисунки 2 шт., сноски 2 шт.	Бизнес-планРазмер: 39.89 кб.Язык: русскийРазместил (а): Ольгапросмотреть
16.	Численные методы решения обыкновенных дифференциальных уравнений Обыкновенным дифференциальным уравнением порядком уравнения. Уравнение с начальными условиями. Лабораторная работа. Численные методы решения обыкновенных дифференциальных уравнений (4 часа). в котором называется. В работе есть: рисунки более 10 шт.	ЗадачаРазмер: 56.27 кб.Язык: русскийРазместил (а): Palonпросмотреть
17.	Численные методы решения типовых математических задач Метод Гаусса. Численные методы решения типовых математических задач. Курсовая работа. по дисциплине Вычислительная математика. 1. Решение систем линейных алгебраических уравнений методом простой итерации. 1.1 Постановка задачи. В работе есть: рисунки более 10 шт., сноски более 10 шт., выводы 3 шт.	КурсоваяРазмер: 0.87 мб.Язык: русскийРазместил (а): Дениспросмотреть
18.	Сравнительный анализ методов оптимизации Математическая задача оптимизации. Минимум функции одной и многих переменных. Унимодальные и выпуклые функции. Прямые методы безусловной оптимизации и минимизации их практическое применение. Методы деления отрезка пополам дихотомия и золотого сечения. Источники: 3 шт. 1978-1986гг. В работе есть: содержание, введение, заключение, таблицы 2 шт., рисунки более 10 шт.	КурсоваяРазмер: 2.14 мб.Язык: русскийРазместил (а): Натальяпросмотреть
19.	Ряды Фурье. Численные методы расчета коэффициентов Ряды Фурье. Численные методы расчета коэффициентов. 1. Таковы например, сила и напряжение переменного тока или пример паровой машины путь, скорость и ускорение крейцкопфа, давление пара, касательное усилие в пальце кривошипа и т. д В работе есть: приложения 4 шт., рисунки более 10 шт., сноски 4 шт., выводы 2 шт.	КурсоваяРазмер: 118.9 кб.Язык: русскийРазместил (а): МаляВопросмотреть
20.	Разработка проекта оптимизации платежей по налогу на прибыль организации Сущность виды принципы и методы оптимизации налоговых платежей уклонение от их уплаты. Анализ финансово-хозяйственной деятельности и учетной политики предприятия. Создание резерва на ремонт основных средств и выбор оптимального способа амортизации. В работе есть: таблицы 9 шт., приложения более 10 шт., рисунки 2 шт., выводы 2 шт.	ДипломРазмер: 1.16 мб.Язык: русскийРазместил (а): Марияпросмотреть
21.	Элективный курс Биохимия в школьном курсе химии Сущность структура и функции белков нуклеиновых кислот углеводов и липидов. Место биохимии в школьном курсе химии. Методика проведения интегрированных уроков биологии и химии по темам: Химия крови и Лекарства с применением лабораторного практикума. В работе есть: введение, приложения более 10 шт., рисунки более 10 шт., выводы 2 шт.	КурсоваяРазмер: 0.78 мб.Язык: русскийРазместил (а): ларисапросмотреть
22.	Численные методы интегрирования и оптимизации сложных систем Изучение численных методов решения нелинейных уравнений. Построение годографа афчх графиков ачх и фчх с указанием частот. Практическое изучение численных методов интегрирования дифференциальных уравнений высокого порядка метод. В работе есть: таблицы 1 шт., приложения 5 шт., рисунки более 10 шт., выводы 2 шт.	КурсоваяРазмер: 416.26 кб.Язык: русскийРазместил (а): Селапросмотреть
23.	Кибернетические методы в праве Математическая логика, теория вероятностей, вычислительная математика, теория информации, теория кодирования, теория алгоритмов, теория случайных процессов, теория игр, теория статистических решений и т д данных. В работе есть: рисунки 1 шт.	РефератРазмер: 47.85 кб.Язык: русскийРазместил (а): Павел Воляпросмотреть
24.	Численные методы Программа-калькулятор на Pascal Разработка программы-калькулятора Разработка программы-калькулятора CalcKurs на языке программирования Pascal реализующую функции: решение уравнений с целочисленными коэффициентами нахождение нод и нок представление рациональной дроби в виде цепной и цепной дроби в виде рациональной. В работе есть: приложения 2 шт., рисунки более 10 шт., сноски 7 шт.	КурсоваяРазмер: 2.11 мб.Язык: русскийРазместил (а): Тузов Игорьпросмотреть
25.	Методы моделирования и оптимизации решений Всероссийский заочный ФИНАСОВО-ЭКОНОМИЧЕСКИЙ. Филиал в г. Брянске по дисциплине. Вариант Методы моделирования и оптимизации решений. ВЫПОЛНИЛ(А). СТУДЕНТ(КА). СПЕЦИАЛЬНОСТЬ. ЗАЧ. КНИЖКИ. ПРЕПОДАВАТЕЛЬ.	ТестыРазмер: 21.55 кб.Язык: русскийРазместил (а): Олег Бабаевпросмотреть