Решение многошаговых задач оптимизации методом динамического программирования. Динамическое программирование это метод оптимизации многошаговых задач в условиях

Тест с ответами: Динамическое программирование

В процессе динамического программирования раньше всех планируетсяпервый шагпоследний шаг +как сказано в условии задачипредпоследний шаг

В задачах динамического программирования шаговое управление должно выбиратьсяс учетом последствий в будущем +с учетом предшествующих шагови то, и другоенаилучшим для данного шагалучше, чем предыдущее

Задача о загрузке рюкзака является задачей …. Программированиянелинейногопараметрическогодинамического +линейногоцелочисленного

В задачах теории игр говорят, что игра имеет седловую точку, еслинижняя цена игры меньше верхнейнижняя цена игры равна верхней +нижняя цена игры больше верхнейнижняя цена игры не больше верхнейнижняя цена игры не меньше верхней

Игра называется игрой с нулевой суммой, есливыигрыш игрока А равен 0выигрыш игрока В равен 0сумма выигрышей игроков равна 0 +выигрыш переходит от одного игрока другомувыигрыш приходит извне игры

В задачах теории игр та стратегия, которая соответствует нижней цене игры, называетсяМаксиминной +минимакснойоптимальнойнижнейлучшей

В задачах теории игр элементы платежной матрицыположительныецелыедробные +любыенеотрицательные

В играх с «природой» критерий, учитывающий возможность как наихудшего, так и наилучшего для человека поведения природы, называется критериемВальдаСэвиджаГурвица +вероятностным критерием

Динамическое программирование – это метод оптимизации многошаговых задач в условияхотсутствия обратной связи (последействия) и аддитивности целевой функции +учета обратной связи (последействия) и аддитивности целевой функцииотсутствия обратной связи (последействия) и неаддитивности целевой функции

Метод динамического программирования применяется для решениямногошаговых задач +задач, которые нельзя представить в виде последовательности отдельных шаговтолько задач линейного программированиязадач макроэкономики

Динамическое программирование не характеризуется следующими условиямизадача оптимизации определяется как многошаговый процесс управлениявыбор управления на каждом шаге зависит только от состояния системы до этого шага без влияния на предыдущие шагисостояние системы после k-ого шага управления зависит только от предшествующего состояния на k-1 шаге и управления на k-ом шагецелевая функция всей задачи равна сумме целевых функций на каждом шагена каждом шаге управление зависит от конечного числа управляющих переменных, а состояние – от конечного числа параметровнахождение многоугольника допустимых решений +

Путь в сетевом графике – этолюбая непрерывная последовательность работ и событий +последовательность работ и событий, начинающаяся от исходного события и заканчивающаяся завершающим событиемсовокупность работ и событий,начинающаяся с какого-либо начального события и заканчивающаяся каким-либо конечным событием

Полный путь сетевого графика – этопоследовательность работ и событий, начинающаяся от исходного события и заканчивающаяся завершающим событием +любая непрерывная последовательность работ и событийсовокупность работ и событий, начинающаяся с какого-либо начального события и заканчивающаяся каким-либо конечным событием

Критический путь сетевого графика – этополный путь с максимальной продолжительностью +полный путь с минимальной продолжительностьюрасчетный полный путь со средней продолжительностью

Исходное событие сетевого графика – этособытие, не имеющее предшествующих работ и событий +любое начальное событиемомент начала какого-либо процесса

Завершающее событие – этособытие не имеющее последующих работ и событий +любое конечное событиемомент завершения какого-либо процесса

Начальное событие – этомомент завершения какого-либо процесса, начиная с которого происходит выполнение одной или нескольких работ +исходное событиемомент завершения какого-либо процесса с определенным результатом

Конечное событие – этомомент завершения одной или нескольких работ, предшествующих событию +завершающее событиесобытие, определяющее конец полного пути

Система массового обслуживания включает следующие элементывходящий поток требований или заявок на обслуживаниеочередьобслуживающее устройствовыходящий поток, обслуженных требованийвходящий поток требований или заявок на обслуживание, очередь, обслуживающее устройство, выходящий поток, обслуженных требований +

Средняя доля пришедших заявок, обслуживаемых системой, называетсяинтенсивность потока обслуживанийабсолютная пропускная способностьотносительная пропускная способность +интенсивность нагрузки

Поток, в котором одновременное появление двух или более заявок невозможно, называетсястационарнымординарным +простейшимбез последствий

Поток, характеризующийся тем, что вероятность поступления определенного количества требований (заявок) в течение некоторого промежутка времени зависит только от длины этого промежутка, называетсяСтационарным +ординарнымпростейшимбез последствий

Если значение коэффициента Q (относительная пропускная способность) равно 0,78, это значит, чтов единицу времени обслуживается 78 заявокобслуживается 78% поступающих заявок +78% заявок получают отказ в обслуживанииобслуживается 0,78% поступающих заявок

Среднее число заявок, обслуживаемых системой в единицу времени называетсяинтенсивность потока обслуживанийабсолютная пропускная способность +относительная пропускная способностьинтенсивность нагрузки

Корреляция ценных бумаг на риск портфеля ценных бумагВлияет +не влияетоднозначно сказать нельзя

Корреляция ценных бумаг на эффективность портфелявлияетне влияет +однозначно сказать нельзя

Возникает необходимость в операции «short sale», если вектор долей рисковых ценных бумаг есть ценные бумагипервого и второго видатолько первого видатолько третьего вида +

Проведение операции «short sale» с ценными бумагами означаетинвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги 2-го вида (вместе с доходом, который они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает ценные бумаги 1-го вида и получает по ним доход +инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги 1-го вида (вместе с доходом, который они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает ценные бумаги 2-го вида и получает по ним доход

Утверждение о том, что при полной прямой корреляции ценных бумаг (все коэффициенты корреляции равны 1) диверсификация портфеля не дает никакого эффекта – риск портфеля равен среднему арифметическому рисков составляющих его ценных бумаг и к нулю не стремится при росте числа видов ценных бумагВерно +невернонельзя проверить, т. к. для утверждения о том верно оно или нет недостаточно информации

Задача управления запасами состоит вопределении такой стратегии пополнения и расхода запасов, при которой суммарные издержки на создание и хранение (функция затрат) являются минимальными +обеспечении такого объема запасов, который позволяет осуществлять бесперебойныйпроизводственный процессуправлении дефицитом

Для простейшего (Пуассоновского) потока требований как потока событий характерным являетсястационарность, т.е. его вероятностные характеристики не зависят от временито, что он является потоком без последствия, т.е. если для любых двух непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другиеординарность, т.е. вероятность попадания на малый (элементарный) участок времени двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного событиястационарность, ординарность, поток без последействия +

testdoc.ru

5. Динамическое программирование

В ряде реальных экономических и производственных задач необходимо учитывать изменение моделируемого процесса во времени и влияние времени на критерии оптимальности. Для решения указанных задач используется метод динамического планирования (динамическое программирование). Этот метод более сложен по сравнению с методами расчета статических оптимизационных задач, изложенных выше. Также не простым делом является процесс построения для реальной задачи математической модели динамического программирования.

5.1. Постановка задачи динамического программирования. Основные условия и область применения

Пусть рассматривается задача, распадающаяся на 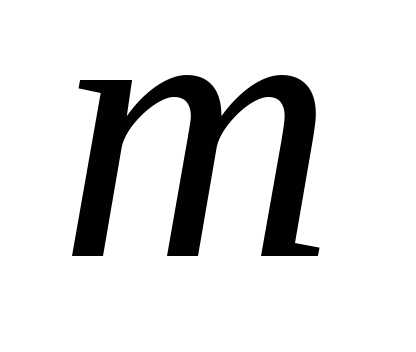шагов или этапов, например планирование деятельности предприятия на несколько лет, поэтапное планирование инвестиций, управление производственными мощностями в течение длительного срока. Показатель эффективности задачи в целом обозначим через W, а показатели эффективности на отдельных шагах – через ,

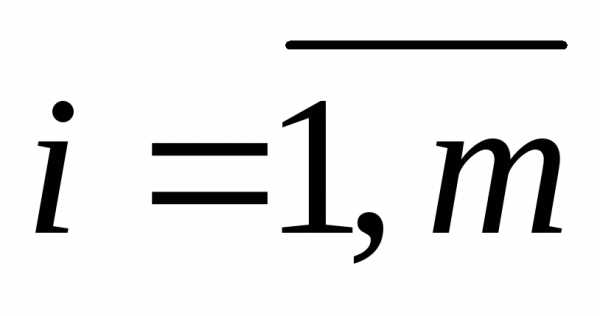
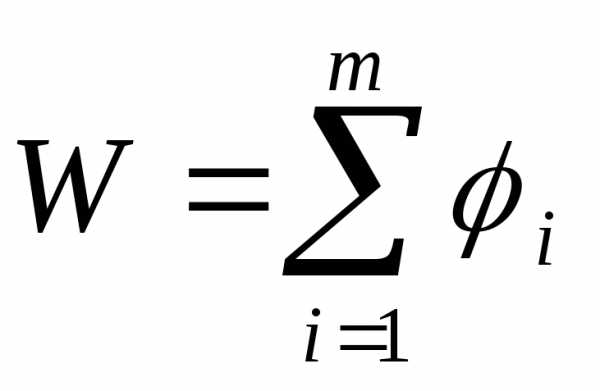. Если W обладает свойством аддитивности, т.е.

, (5.1.1)

то можно найти оптимальное решение задачи методом динамического программирования.

Таким образом, динамическое программирование – это метод оптимизации многошаговых или многоэтапных процессов, критерий эффективности которых обладает свойством (5.1.1). В задачах динамического программирования критерий эффективности называется выигрышем. Данные процессы управляемые, и от правильного выбора управления зависит величина выигрыша.

Определение 5.1.1. Переменная 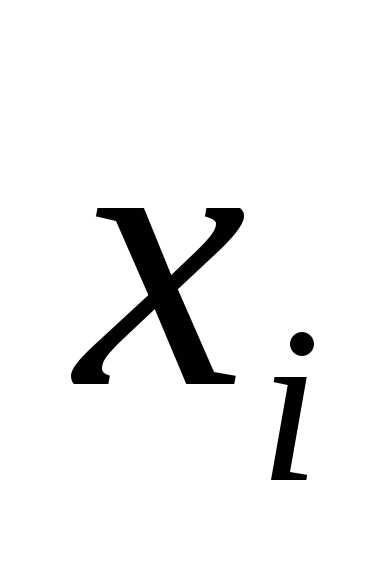, от которой зависят выигрыш на-м шаге и, следовательно, выигрыш в целом, называется шаговым управлением,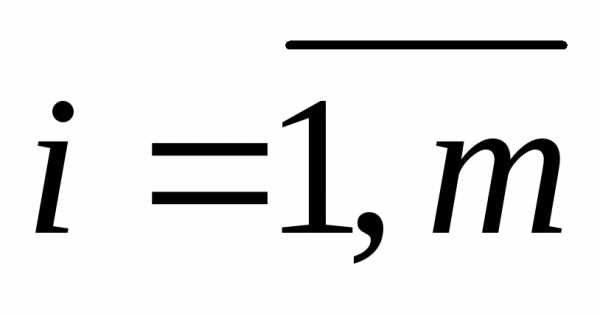

Определение 5.12. Управлением процесса в целом (х) называется последовательность шаговых управлений .

Определение 5.1.3. Оптимальное управление х* – это значение управления х, при котором значение W(x* ) является максимальным (или минимальным, если требуется уменьшить проигрыш)

, (5.1.2)

где Х - область допустимых управлений.

Оптимальное управление х* определяется последовательностью оптимальных шаговых управлений

В основе метода динамического программирования лежит принцип оптимальности Беллмана, формулирующийся следующим образом: управление на каждом шаге надо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.

Поясним это правило. При решении задачи динамического программирования на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Бели считать все шаги независимыми друг от друга, то оптимальным шаговым управлением будет то управление, которое приносит максимальный выигрыш именно на данном шаге. Но, например, при покупке новой техники взамен устаревшей на ее приобретение затрачиваются определенные средства. Поэтому прибыль от ее эксплуатации вначале может быть небольшой. Однако в следующие годы новая техника будет приносить большую прибыль. И наоборот, если руководитель примет решение оставить старую технику для получения прибыли в текущем году, то в дальнейшем это приведет к значительным убыткам. Данный пример демонстрирует следующий факт: в многошаговых процессах все шаги зависят друг от друга, и, следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс.

Другой момент, который следует учитывать при выборе управления на данном шаге, – это возможные варианты окончания предыдущего шага: Эти варианты определяют состояние процесса. Например, при определении количества средств, вкладываемых в предприятие в 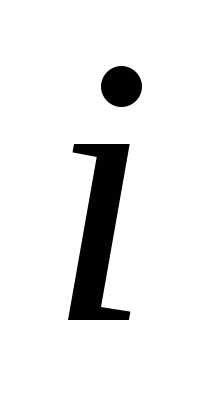-м году, необходимо знать, сколько средств осталось в наличии к этому году и какая прибыль получена в предыдущем(

)-м году. Таким образом, при выборе шагового управления необходимо учитывать: 1) возможные исходы предыдущего шага и 2) влияние управления на все оставшиеся до конца процесса шаги.

В задачах динамического программирования первый пункт учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго пункта обеспечивается тем, что в задачах динамического программирования условная оптимизация проводится от конца процесса к началу. Сперва оптимизируется последний -й шаг, на котором не надо учитывать возможные воздействия выбранного управления 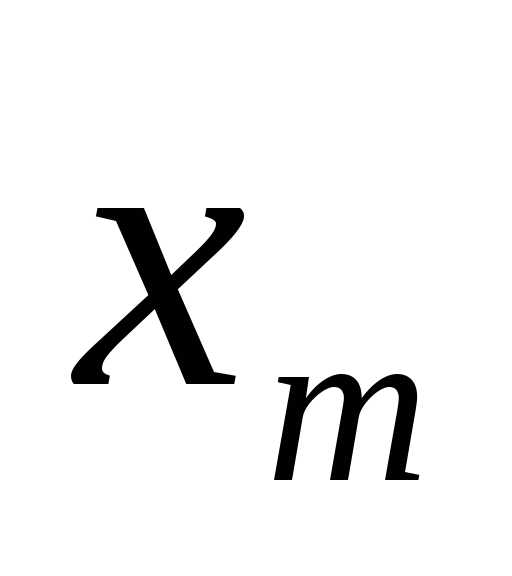на все последующие шага, так как эти шаги просто отсутствуют. Делая предположения об условиях окончания (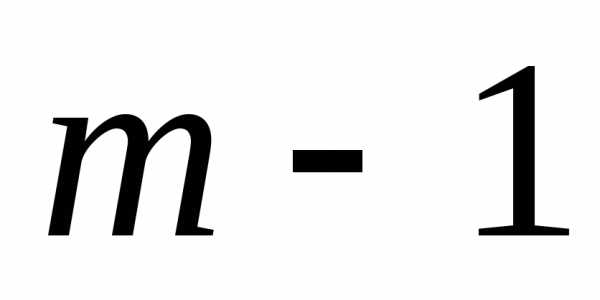)-гo шага, для каждого из них проводят условную оптимизацию -го шага и определяют условное оптимальное управление . Аналогично поступают для ()-го шага, делая предположения об исходах окончания (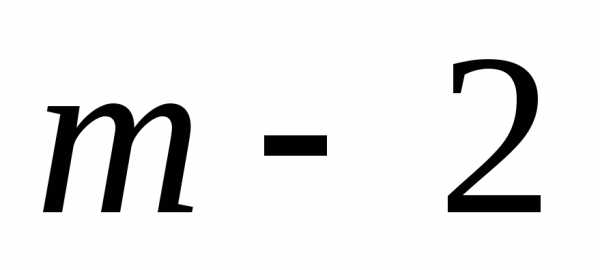)-го шага и определяя условное оптимальное управление на (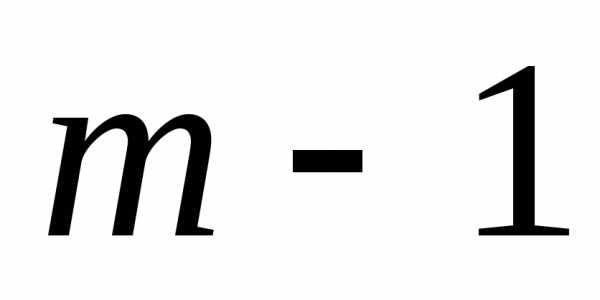)-м шаге, приносящее оптимальный выигрыш на двух последних шагах – (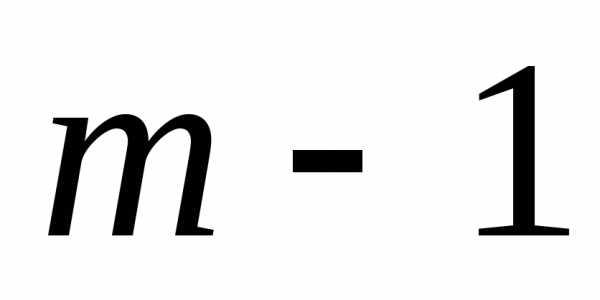)-м и 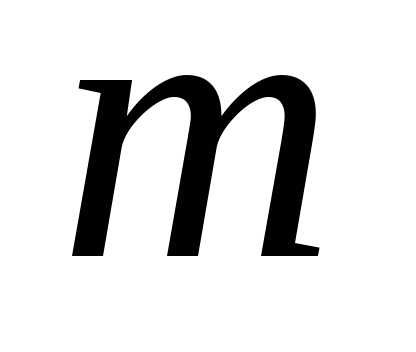-м. Так же действуют на всех остальных шагах до первого. На первом шаге, как правило, не надо делать условных предположений, так как состояние системы перед первым шагом обычно известно.

Для этого состояния выбирают оптимальное шаговое управление, обеспечивающее оптимальный выигрыш на первом и всех последующих шагах. Это управление является безусловным оптимальным управлением на первом шаге и, зная его, определяются оптимальное значение выигрыша и безусловные оптимальные управления на всех шагах. Ниже это будет пояснено на примерах.

studfiles.net

Решение многошаговых задач оптимизации методом динамического программирования

Во многих динамических задачах время рассматривается непрерывно, или как дискретная величина. Задачи такого типа называются многошаговыми (многоэтапными) задачами оптимизации. Их можно решать методом динамического программирования.

В многошаговых задачах оптимизации время принимает дискретные значения: .

Состояние системы в момент времени задается вектором: , где , .

В уравнении в момент времени задается дискретными значениями.

Рассмотрим простейшую многошаговую систему - одношаговую систему. Начальное состояние системы записывается известным вектором состояния . Выбор некоторого управления определяет переход системы из в состояние . Этот переход описывается соотношениями: .

Для многошаговых систем будем иметь

, где ; (11)

– вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управления .

Блок-схема многошагового процесса имеет вид (Рис.2):

X( -1)

X( )

…

Рис.2

Здесь вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управляющих параметров.

Предполагаем, что заданное начальное состояние - фиксированное. Требуется найти такую последовательность векторов фиксированной области управления , где , которая максимизирует целевую функцию

Таким образом, данная задача аналогична задачи оптимального управления с непрерывным временем – дискретная задача – многошаговая задача оптимального управления.

Подход динамического программирования в данном случае состоит в том, что решаемая задача “погружается ” в более широкий класс задач, описываемых рядом параметров, и вслед за этим, используя принцип оптимальности Беллмана, определяется основное рекуррентное соотношение.

Первый подход.

Возьмем в качестве параметров многошаговой задачи оптимизации начальный момент времени и начальное состояние . Тогда функция оптимального поведения равна оптимальному значению целевой функции J задачи с начальным состоянием и начальным моментом времени . Тогда оптимальное значение целевой функции исходной задачи равно: . Согласно принципу оптимальности Беллмана:

, где , .

Это означает, что оптимальное значение целевой функции с наименьшим состоянием и наименьшим моментом времени равно оптимальному значению функции в момент времени и оптимальному значению функции оптимального поведения в момент времени . Можно представить все рекуррентные соотношения в виде:

Для этого соотношения граничное условие будет: - – показывает, что оптимальное значение целевой функции с начальным состоянием в момент времени равно (совпадает) со значением функции конечных параметров, рассчитанных при . Данная задача аналогична задачи оптимального управления с непрерывным временем.

Второй подход.

Тогда ФОП – которая представляет собой оптимальное значение целевой функции с начальным состоянием , разворачивающаяся в промежутке протяженностью . Оптимальное значение целевой функции исходной задачи соответственно равно: – когда . В этом случае последовательность решений определяется методом динамического программирования в порядке, обратном тому, который рассматривается до сих пор.

Первым членом этой последовательности является: , то есть оптимальное значение целевой функции с временным промежутком нулевой протяженности, начинающейся (и заканчивающейся) в . Оптимальное значение целевой функции этой задачи равно функции конечных параметров: .

Рассмотрим – оптимальное значении целевой функции, задачи с промежутком равным одной единице времени , начинающегося в . Эта задача называется первым шагом.

Оптимальное значение в этой задачи определяется как максимум значения суммы той части целевой функции, которая соответствует указанному времени, и оптимальное значение задачи с моментом времени с управляющим вектором :

Используя уравнение перехода: , получаем

Данный выбор управления на первом шаге согласуется с принципом оптимальности Беллмана, поскольку управление - оптимально, то по отношению к состоянию , которое достигается в результате предыдущих выборов управляющих векторов.

Аналогично этому, на втором шаге (в задаче с промежутком равным двум промежуткам времени) получим

Общее рекуррентное соотношение на шаге с номером выглядит следующим образом

В рассмотренной задаче, оптимальное значение равно: – является оптимальным значением последней задачи в последовательности одношаговых задач оптимизации, описываемых функциональным уравнением, при , с граничным условием: . Вместо того, что бы решать эту задачу методом НЛП (выбирать сразу ), то здесь мы решаем последовательность одношаговых задач оптимизации.

Пример решения задачи оптимизации методом динамического программирования

В качестве примера применения подхода динамического программирования к многошаговым задачам оптимизации, в которых требуется найти набор из неотрицательных чисел максимизируем сепарабельную функцию (функция называется сепарабельной, если она представляет собой сумму функций, каждая из которых зависит только от одной переменной), при условии, что сумма этих чисел равна фиксированном числу .

Постановка задачи.

Найти ,

при ограничениях

Решение:

Будем решать данную задачу методом динамического программирования. В данной задаче можно интерпретировать постоянную как общий уровень имеющихся ресурсов и рассматривать ее в качестве параметра задачи. Обозначим через – функцию оптимального поведения для процесса развертывания в момент времени с общим запасам ресурсов .

Для процесса на временном промежутке протяженностью равной нулю и заканчивающегося для будет

Для одношагового процесса заканчивающегося в , при этом надо распределять ресурсы между огласно принципу оптимальности

Общее рекуррентное соотношение имеет вид

Решение задачи отыскивается с помощью общего рекуррентного соотношения, последовательно начиная с граничного условия , вплоть до шага (длина шага ) (C).

cyberpedia.su

Решение многошаговых (многоэтапных) задач оптимизации методом динамического программирования.

Во многих задачах динамического программирования время рассматривается непрерывно или как дискретная величина. Задачи такого типа называются многошаговыми (многоэтапными) задачами оптимизации. Их можно решать методом динамического программирования.

В многошаговых задачах оптимизации время принимает дискретные значения: .

Состояние системы в момент времени задается вектором: , где , .

В уравнении в момент времени задается дискретными значениями. Рассмотрим простейшую многошаговую систему (одношаговая система). Начальное состояние системы записывается известным вектором . Выбор некоторого управления определяет переход системы из в состояние . Этот переход описывается соотношениями: .

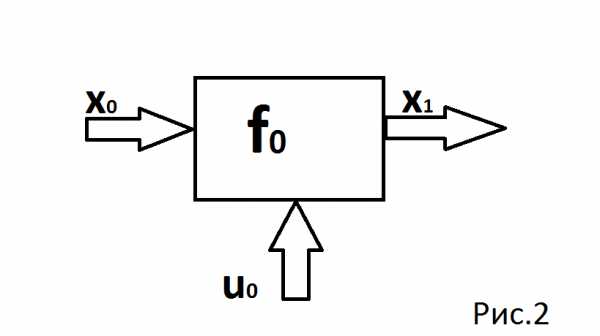
На рисунке 2 показан пример дискретной одномерной системы.

Для многошаговых систем:

, где ; , (11)

вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управления . Процесс перехода в координатной форме будет:

Блок схема многошагового процесса показана на рисунке 3:

Предполагаем, что задано начальное состояние . Требуется найти такую последовательность векторов фиксированной области управления , где . Эта последовательность, которая максимизирует целевую функцию:

, (A)

Таким образом, данная задача аналогична задачи оптимального управления (с непрерывным временем), (Смотри(11)).

Пункт А:

Возьмем в качестве параметров многошаговой задачи оптимизации начальный момент времени и начальное состояние . Тогда ФОП равна оптимальному значению целевой функции (A)задачи с начальным состоянием и начальным моментом времени , ( ). Тогда оптимальное значение целевой функции рассматриваемой задачи равно: . Согласно принципу оптимальности Беллмана:

, где , .

Это означает, что оптимальное значение целевой функции задачи с начальным состоянием и начальным моментом времени оптимальному максимальному значению суммы двух слагаемых функции в момент времени и оптимальному значению в момент времени . Используя уравнение (11)можно представить:

Граничное условие будет: – показывает, что оптимальное значение целевой функции с начальным состоянием в момент времени равно (совпадает) со значением функции конечных параметров, рассчитанных при . Данная задача аналогична задачи оптимального управления с непрерывным временем.

Пункт В:

Другой подход при решении многошаговых задач оптимизации состоит в том, что в качестве характеристических параметров выбираются не начальные состояния и не начальный момент времени, а начальное состояние и промежуток времени, остающийся до конечного момент времени. Тогда ФОП – которая представляет собой оптимальное значение целевой функции с начальным состоянием , разворачивающаяся в промежутке протяженностью .Оптимальное значение целевой функции исходной задачи (A)соответственно равно: – когда . В этом случае последовательность решений определяется методом динамического программирования в порядке, обратном тому, который рассматривается до сих пор. Первым членом этой последовательности является: , то есть оптимальное значение целевой функции с временным промежутком нулевой протяженности, начинающейся (и заканчивающейся) в . Оптимальное значение целевой функции этой задачи равно функции конечных параметров: .

Используя уравнение перехода: , получаем:

Данный выбор управления на первом шаге согласуется с принципом оптимальности Беллмана.

Аналогично этому, на втором шаге (в задаче с промежутком равным двум промежуткам времени) получим:

Общее рекуррентное соотношение на шаге с номером выглядит следующим образом:

В рассмотренной задаче, оптимальное значение равно: – является оптимальным значением последней задачи в последовательности одношаговых задач оптимизации, описываемых функциональным уравнением, при , с граничным условием: . Вместо того, что бы решать эту задачу методом НЛП (выбирать сразу ), то здесь мы решаем последовательность многошаговых задач оптимизации.

stydopedia.ru

Лекция 7,8. Метод динамического программирования.

Вопросы: 1. Основные понятия. Общая постановка задачи ДП.

2. Принцип оптимальности. Функциональные уравнения Беллмана.

3. Задача оптимального распределения ресурсов.

4. Задача о замене.

5. Задача управления производством и запасами.

1.Основные понятия. Общая постановка задачи динамического программирования.

Динамическое программирование - метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы, шаги.

Такие операции называются многошаговыми. Многие экономические процессы расчленяются на шаги естественным образом. Это процессы планирования и управления, развиваемые во времени. Естественным шагом может быть год, квартал, месяц и т.д. Т.о., если управление сводится к однократному принятию решения, то соответствующая задача называется одноэтапной или одношаговой. Ранее решаемые задачи линейного и нелинейного программирования – примеры подобных задач.Если управление требует некоторой последовательности принятых решений, то такая задача называется многоэтапной или многошаговой.

Рассмотрим некоторую управляемую систему, характеризующуюся определенным набором параметров, задающих ее состояния. Система под влиянием управления переходит из начального состояния в конечное. Введем обозначения.

1. xi–многомерный вектор, компоненты которого определяют состояние системы на

i-том шаге. Дальнейшее изменение состояния зависит только от данного состояния и не

зависит от того, каким путем система перешла в него (процесс без последствия).

2.На каждом шаге выбирается одно решение,управление ui, под действием которого

система переходит из предыдущего состояния xi-1 в новое xi. Это новое состояние

является функцией состояния на начало шага xi-1и принятого в начале решенияui, т.е.

xi=xi(xi-1,ui).

3. Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью)

или потерей (издержками), которые зависят от состояния на начало шага и принятого

решения. Fi – приращение целевой функции задачи в результате i-того шага,

аналогично, Fi = Fi ( xi-1 , ui ).Тогда значение целевой функции при переходе системы

из начального состояния в конечное за nшагов

4.На векторы состояния хiи управленияuiмогут быть наложены ограничения,

объединение которых составляет область допустимых решений uU.

5.Требуется найти такое допустимое управлениеu* = (u1* ,…,un* ) (для каждого шага),

чтобы получить экстремальное значение функции цели F* за всеnшагов.

Любая последовательность действий для каждого шага, переводящая систему из начального состояния в конечное, называется стратегией управления.

Допустимая стратегия управления, доставляющая функции цели экстремальное значение, называется оптимальной.

2. Принцип оптимальности. Функциональные уравнения Беллмана.

Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, т.к. управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом.

Принцип оптимальности: если некоторая последовательность решений оптимальна, то на любом шаге последующие решения образуют оптимальную стратегию по отношению к результату предыдущих решений.

Другими словами, каково бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге (проигрыш) плюс оптимальный выигрыш (проигрыш) на всех последующих шагах был бы максимальным (минимальным). На основе принципа оптимальности Беллмана строится схема решения монгошаговой задачи, состоящая из 2-х частей:

1) Обратный ход:от последнего шага к первому получают множество возможных оптимальных («условно-оптимальных») управлений.

2) Прямой ход:от известного начального состояния к последнему из полученного множества «условно-оптимальных» управлений составляется искомое оптимальное управление для всего процесса в целом.

Оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага.

Чтобы можно было использовать принцип оптимальности практически, необходимо записать его математически. Обозначим через z1(xn-1),z2(xn-2),…,zn(x0) условно-оптимальные значения приращений целевой функции на последнем шаге, двух последних,…, на всей последовательности шагов, соответственно.

Тогда для последнего шага:

z1(xn-1) =(min) {Fn(xn-1,un)},

где un– множество допустимых (возможных) управлений наn-ом шаге,xn-1– возможные состояния системы передn-ым шагом.

Для двух последних шагов:

z2(xn-2) =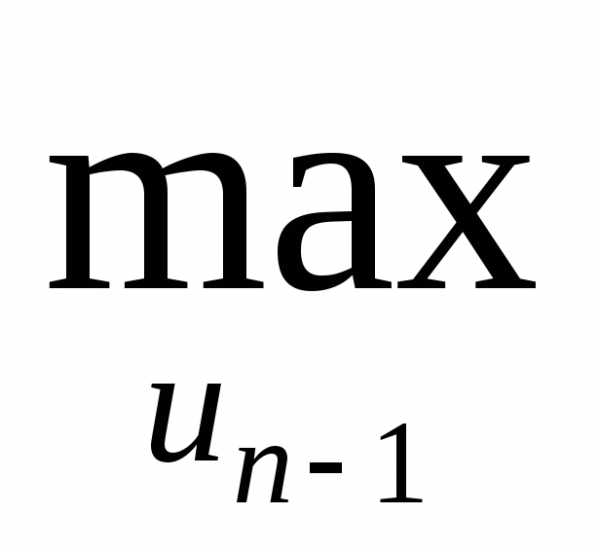(min) {Fn-1(xn-2,un-1) +z1(xn-1)}.

Для k последних шагов:

zk(xn-k) = (min) {Fn-k+1(xn-k, un-k+1) + zk-1(xn-k+1)}.

Для всех n шагов:

zn(x0) = (min) {F1(x0, u1) + zn-1(x1)}.

Полученные рекуррентные соотношения называют функциональными уравнениями Беллмана.

При этом согласно определению zn(x0) =F*.

studfiles.net

Динамическое программирование

⇐ ПредыдущаяСтр 4 из 6Следующая ⇒

В большом числе оптимизационных задач процесс принятия решений может быть разбит на отдельные этапы. Для решения многошаговых задач оптимизации разработан метод динамического программирования.

В основе метода динамического программирования лежит принцип оптимальности, формулировка которого дана Р. Беллманом.

Каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.

Рассмотрим управляемую систему, которая под влиянием управления переходит из начального состояния ε0 в конечное состояние εn. Пусть процесс управления можно разбить на n шагов и ε1, ε2, ... ,εn – состояния системы после первого, второго и т.д. шага.

Последовательное преобразование системы на каждом шаге осуществляется с помощью управление u1, u2,…, un.. Предполагается, что состояние системы в конце k-го шага зависит только от предшествующего состояния системы εk-1 и управления uk на данном шаге.

Варьируя управление u=(u1, u2,…, un), можно изменять эффективность процесса, которую будем оценивать количественно целевой функцией, зависящей от начального состояния и выбранного управления.

Z=Z(ε0 ; u) (8.1)

В рассматриваемой задаче целевая функция разбивается на сумму показателей эффективности каждого этапа.

(8.2)

Задача пошаговой оптимизации формулируется следующим образом: определить совокупность допустимых управлений u1, u2, …, un, переводящих систему из начального состояния ε0 в конечное состояние εn и максимизирующих или минимизирующих показатель эффективности (8.2). Управление, при котором достигается экстремум целевой функции (1.3), называется оптимальным управлением и обозначается через u*=(u*1, u*2, …, u*n).

Сущность метода динамического программирования заключается в следующем. Если система в начале k-го шага находится в состоянии εk-1 и мы выбираем управление uk, то система придет в новое состояние и дальнейшие управления uk+1,…,un должны выбираться оптимальными относительно состояния εk. Это означает, что при таких управлениях оптимизируется показать эффективности на последующих до конца процесса шагах k+1,…, n, то есть величина

Обозначим через Zk показатель, характеризующий суммарную эффективность от данного k-го до последнего n-го шага, то есть

(8.3)

Если мы выберем оптимальное управление u*k на всех этапах, начиная с k-го, то получим величину

, (8.4)

которая зависит только от εk-1. Величина Zk* ( εk-1 ) называется условным максимумом (минимумом). Согласно принципу оптимальности, какое бы uk мы ни выбрали на последующих шагах, управление должно выбираться так, чтобы показатель эффективности Zk+1, достигая экстремального значения Z*k+1(εk), приводил бы к экстремуму показателя эффективности на всех шагах, начиная с k-го.

Это положение записывается в виде соотношения, называемого функциональным уравнением Беллмана

(8.5)

Уравнения Беллмана позволяют свести решение исходной задачи оптимизации функции и переменных (8.2) к решению последовательности n задач уравнениями (8.5), каждая из которых является задачей оптимизации функции переменной uk.

Применим метод динамического программирования к решению задачи.

Дана ориентированная сеть, содержащая 10 узлов. Найти кратчайший путь из точки 1 в точку 10. Расстояния между узлами приведены на рисунке.

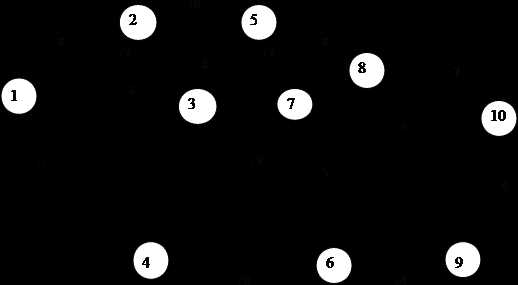
Рис. 8.1

Обозначим через Zi* минимальный путь из узла i в конечный путь узел 10. Пусть из узла i можно перейти в узел l, расстояние между узлами равно ail. Обозначим минимальный путь из l в десятый узел через Zl*. Тогда согласно принципу Беллмана узел l выбирается из условия минимума суммы ail+zl*. В результате имеем уравнение Беллмана:

Очевидно, что из 1 в 10 можно попасть не более, чем за 5 шагов. Разделим все узлы сети на 5 множеств. К множеству ε0 отнесем все узлы, из которых можно попасть в десятый узел не более чем за 5 шагов. Оно включает начальный узел сети. В множество ε1 попадут узлы 2, 3 и 4, из которых можно попасть в конечный узел не более, чем за 4 шага. К ε2 отнесем точки из которых можно попасть в пункт 10 не более чем за 3 шага. Это узлы 5 и 6. Множество ε3 составляет узел 7, из которого можно достичь узла 10 не более чем за 2 шага. Из точек 8 и 9 в конечный пункт можно попасть не более, чем за один шаг. Они составляют множество ε4 .

Условные оптимальные маршруты, начинающиеся в узле i, будем изображать дополнительной стрелкой, идущей от узла i к узлу l, а условные минимальные пути от i до 10 записывать в скобках рядом с узлом. Будем обозначать через uk*(i)- узел, в который осуществляется оптимальный переход из i. Сначала найдем , где узел s входит в ε4 . z6*(l)=0 - оптимальный путь за 0 шагов. В 10 можно попасть из точек 8 и 9.

Тогда z5*(8)=7, при u5*(8)=10 z5*(9)=4, при u5*(9)=10

Далее определим z4*(ε3). Рассмотрим точку . Из седьмого узла можно сразу попасть в 10, а можно сначала в 8. В одном случае путь равен 13, в другом 8+7=15.

Следовательно, z*4=13, u*4 (7)=10.

Найдем z3*(ε2). Множество ε2 составляют узлы 5 и 6. Из пункта 5 можно переместиться в 7 и 8.

При этом уравнение Беллмана

; s ε2

принимает вид

Мы считаем z4*(8)=z5*(8)=7-минимальный путь из 8 узла в конечный. Таким образом, z3*(5)=15; u3*(5)=8.

Для узла 6 уравнение Беллмана записывается аналогично

Здесь также считаем z4*(9)=z5*(9)=4.

Тогда z3*(6)=18; u3*(6)=7 или u3*(6)=9. На этом этапе получено два оптимальных управления u3*(6).

На следующем этапе исследуем множество εl, состоящее из узлов 2,3,4. Из пункта 2 можно попасть только в пункт 5.

Значит .

Из узла 3 можно попасть в пункт 5 и 6.

Z*2(3)=min .

Из узла 4 возможен переход в узел 6.

Следовательно, z2*(4)=min =12+18;u2*(4)=6.

На последнем этапе рассмотрим ε0. Оно состоит из одного элемента-узла 1, из которого можно попасть в 4 пункта-второй, третий, четвертый и пятый.

Z*1(1) =min .

В окончательном виде задачу можно изображать на схеме.

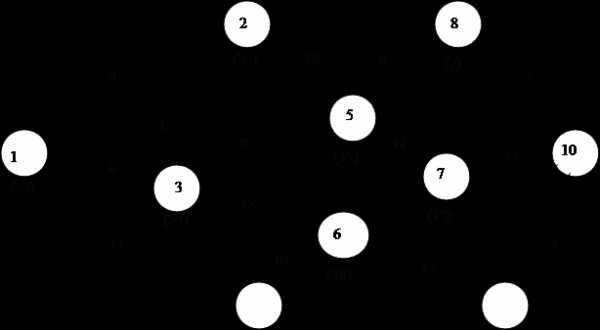
Оптимальный маршрут проходит через узлы 1, 3, 5, 8, 10. При этом путь минимален и равен 29.

Решим с помощью метода динамического программирования задачу об оптимальном распределении ресурсов.

Пусть имеется некоторое количество ресурсов x, которое необходимо распределить между n различными предприятиями, объектами, работами и т.д. так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения.

Пусть xi – количество ресурсов, выделенных i- му предприятию ;

gi(xi) – величина дохода от использования ресурса xi, полученного i-м предприятием;

fk (x) – наибольший доход, который можно получить при использовании ресурса x от первых k различных предприятий.

Запишем сформулированную задачу в математической форме:

при ограничениях:

Для решения задачи необходимо получить рекуррентное соотношение, связывающее и .

Обозначим через xk количество ресурса, используемого k-м способом , тогда для способов остается величина ресурсов, равная . Наибольший доход, который получается при использовании ресурса (x -xk) от первых (k-1) способов, составит fk-1 ( x – xk ). Для максимизации суммарного дохода от k-го и первых способов необходимо выбрать xk таким образом, чтобы выполнялись соотношения:

, , k=

Рассмотрим конкретную задачу по распределению инвестиций для эффективного использования потенциала предприятия.

Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме.

Для модернизации предприятий совет директоров инвестирует средства в объеме 250 млн. р. с дискретностью 50 млн. р. Прирост выпуска зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице.

Инвестиции, млн.р.	Прирост выпуска продукции, млн. р.
Предприятие 1	Предприятие 2	Предприятие 3	Предприятие 4

Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.

Решение задачи разобьем на 4 этапа по количеству предприятий, на которые предполагается осуществить инвестиции.

Рекуррентные соотношения будут иметь вид:

для предприятия № 1 , для всех остальных предприятий , .

1-й этап.

Инвестиции проводим только первому предприятию. Тогда f1 (50)=12; f1(100)=17; f1(150)=23; f1(200)=34; f1(250)=42.

2-й этап.

Инвестиции выделяем первому и второму предприятиям. Рекуррентное соотношение для 2го этапа имеет вид .

Тогда при x=50

при x=100

при x=150

при x=200

при x=250

Таким образом, получили

3-й этап.

Инвестиции выделяем только первому, второму и третьему предприятиям .

Тогда при x=50

при x=100

при x=150

при x=200

при x=250

Таким образом, f3(50)=13; f3(100)=25; f3(150)=36; f3(200)=41; f3(250)=48.

4-й этап.

Инвестиции в объеме 250 млн.р. распределяем между четырьмя предприятиями .

при x=250

Вернемся от 4-го этапа к 1-му этапу. Максимальный прирост выпуска в 54млн.р. получен на 4-омэтапе как 18+36, т.е. прирост продукции 18 млн. р. соответствует выделению 100млн.р. четвертому предприятию (см.табл.).

Согласно 3-му этапу 36 млн. р. получено как 11 + 25, т.е. прирост продукции 11млн. р. соответствует выделению третьему предприятию 50 млн.р. Согласно 2-му этапу 25 млн. р. получено как 13 + 12, т.е. прирост 13 млн. р. соответствует выделению второму предприятию 50 млн. р, а прирост 12 млн. р. соответствует выделению первому предприятию 50 млн. р.

Таким образом, инвестиции в объеме 250 млн.р. целесообразно выделить первому, второму и третьему предприятиям по 50 млн.р., а четвертому -100 млн.р., при этом прирост продукции будет максимальным и составит 54 млн.р.

Рекомендуемые страницы:

lektsia.com

Динамическое программирование

(Беллман, 1960г)

Метод динамического программирования применим к оптимизации многошаговых процессов, в которых решение принимается в последовательные моменты времени.

Время может быть непрерывным и дискретным. В первом случае получаем непрерывное динамическое программирование и его рассматривают в теории автоматического управления.

Рассматриваем дискретное динамическое программирование. Время будет меняться по тактам (шагам) и решения принимается на каждом таком такте. Такты будем нумеровать целыми числами от 1 до n.

Другая особенность задач динамического программирования: целевая функция аддитивна, то есть результирующий эффект от процесса складывается из частных эффектов, полученных на каждом шаге.

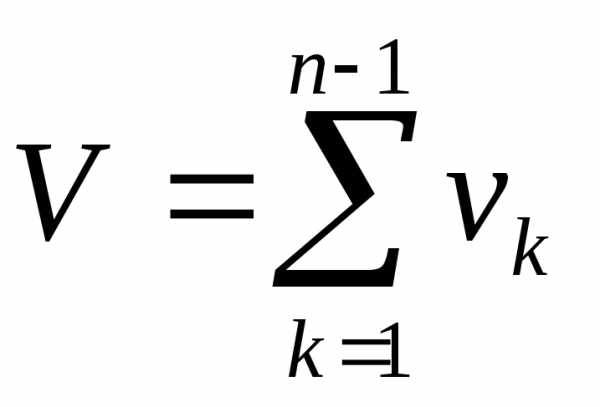В задачах динамического программирования фигурируют следующие объекты

1. Множества шагов на каждом из которых, кромеn.-го, принимается решение.

2. Множества состояний системы .

3. Множество вариантов принятия решений (управлений) .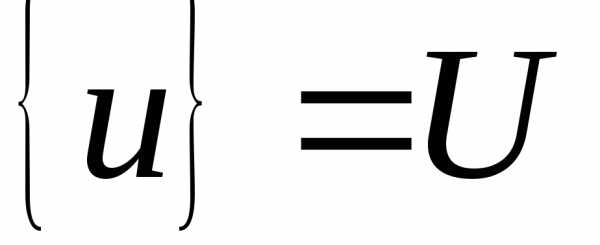

4. Две функции:

функция локального эффекта на i-ом шаге ;

функция перехода в новое состояние ,

где 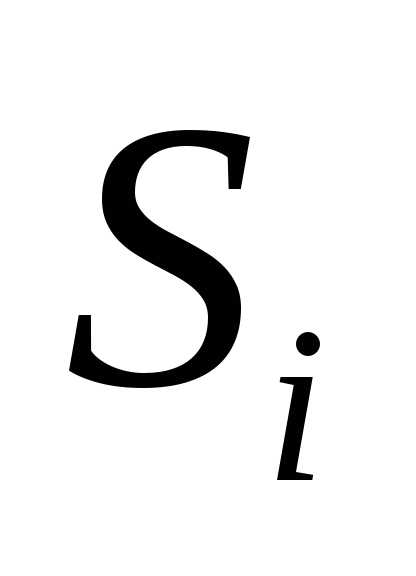- состояние системы,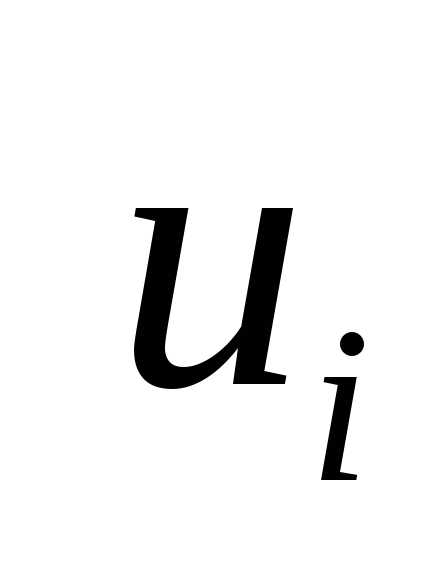- управление наi-ом шаге.

Прежде чем сформулировать задачу оптимизации промоделируем процесс функционирования этой системы.

Пусть на начальном такте (i=1) система находилась в состоянии S1. Выберем последовательность управлений и проследим, как при этом по тактам изменяется состояние системы и как формируется результирующий эффект.

Поскольку в начале процесса эффект равен нулю, то после первого такта текущий эффект окажется таким

Состояние системы на втором такте окажется равным .

После второго такта текущий эффект окажется равным

Состояние системы на третьем такте .

Вообще, после k тактов будет достигнут эффект

а состояние на (k+1)-ом такте окажется равным

В конце процесса общий эффект достигнет следующей величины

Из сказанного ясно, что результат целиком и полностью определяется начальным состоянием системы S1 и последовательностью управлений , то есть

. (*)

Однако в приложениях начальное состояние не доступно для выбора ЛПР и в лучшем случае лишь известно ему. Поэтому задача ЛПР заключается в том, чтобы для каждого начального состояния S1 найти такую последовательность управлений , чтобы функция цели (*) была максимальной.

То значение эффекта, которое будет при этом достигнуто, будем обозначать через .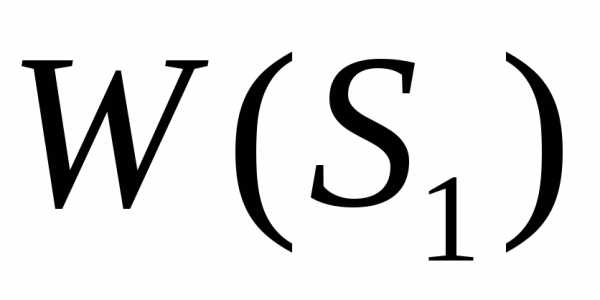

Итак, 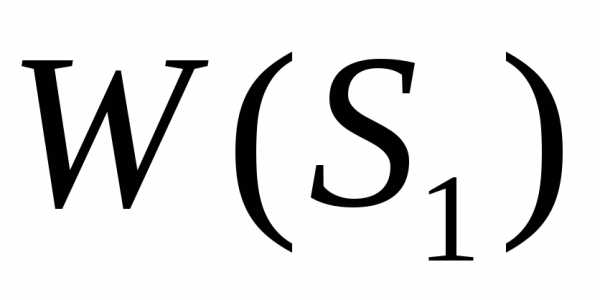- это оптимальное значение эффекта, которое может быть достигнуто из начального состоянияS1.

В силу конечности множества всех последовательностей принципиально эту задачу возможно решить методом перебора. Однако с увеличением числа тактовn и числа возможных управлений m трудоемкость этой процедуры нарастает весьма быстро. Действительно, мощность указанного множеств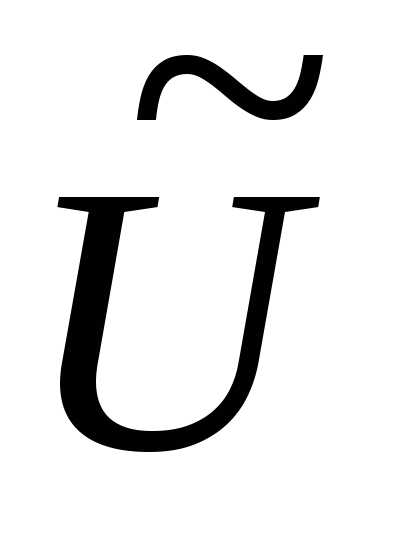а равна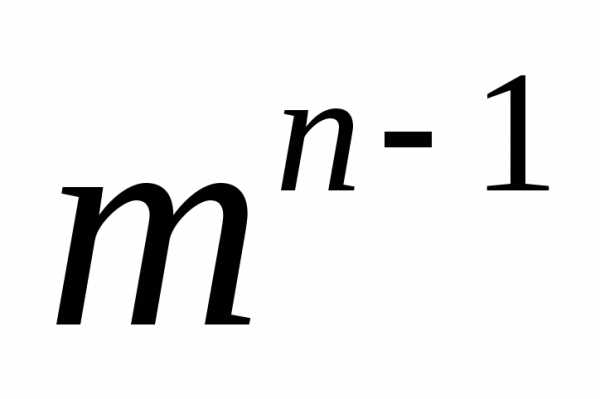. Например, если число возможных управлений равно 3 (как у витязя на распутье), а число тактов равно 10, то это число равно 39 = 19 683, но уже при четырех вариантах управления это число будет больше 16 миллионов.

Таким образом, необходимо так упорядочить перебор, чтобы снизить трудоемкость расчетов, что и происходит при применении метода динамического программирования.

В методе динамического программирования ключевым объектом является функция - функция имеющая тот же смысл, что и введенная выше функция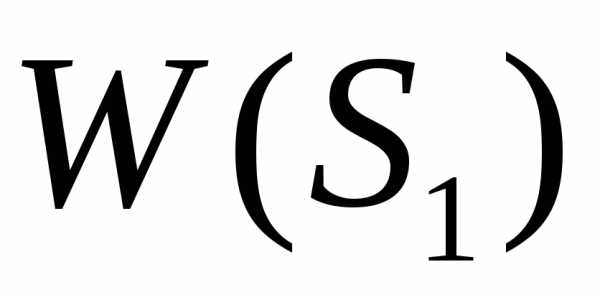, то есть это оптимальное значение эффекта, которое может быть достигнуто кn-такту (к концу процесса), но при движении не из первого такта, а из i-го такта. Эта функция в отличие от функции 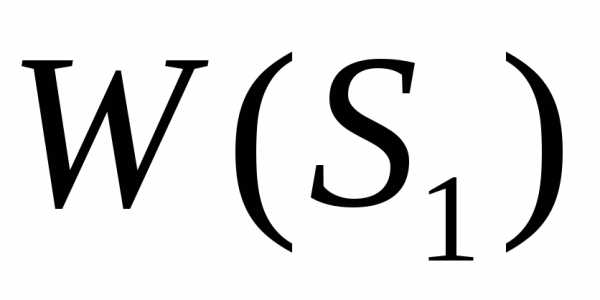зависит от двух аргументов – начального состояния и номера такта.

Функция 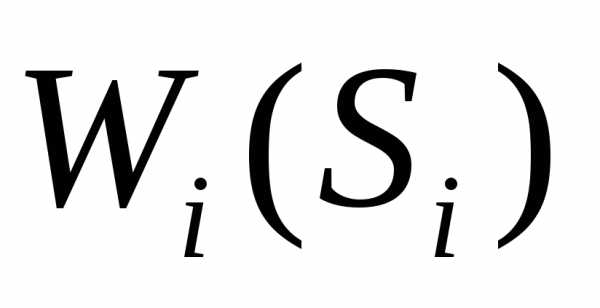удовлетворяет следующему знаменитому уравнению Беллмана, которое называется Принципом оптимальности.

.,(**)

где

Тот, кто играет в шахматы, легко согласится с этой формулой. На некотором ходу в позиции противник может предложить вам жертву и , если вы ее примете (выберете управлениеui), то получите значительный локальный эффект в виде взятой фигуры. Однако при этом вы попадаете в такую позицию 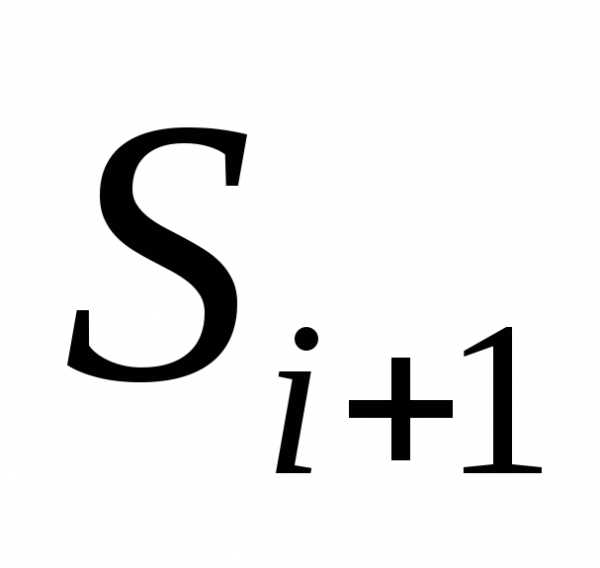, что достичь хорошего результата дальнейшей игры (большого значения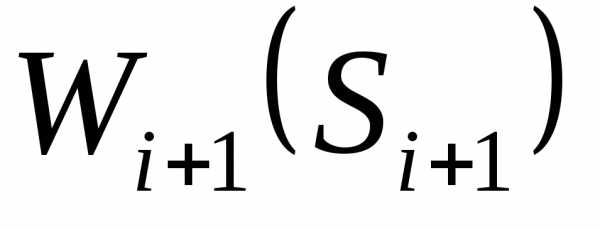) вы не сможете и, следовательно, будет плох и результат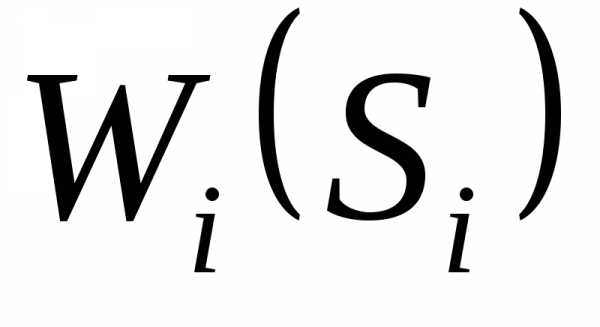. Если же вы не такой жадный, то выберете другое управлениеuj, для которого 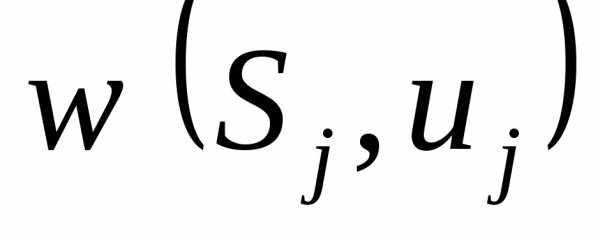не так велик, но позиция не так плоха и общий результат будет лучше.

В качестве примера применения метода динамического программирования рассмотрим так называемую задачу о рюкзаке.

studfiles.net