Энциклопедия по машиностроению XXL. Блочный метод оптимизации
Блочная оптимизация, метод - Справочник химика 21
Для испытания катализаторов в условиях, близких к промышленным, решения задач оптимизации технологического режима, а также для исследования кинетики процессов в условиях метода идеального вытеснения предложена конструкция блочного изотермического реактора, моделирующего промышленный, с контролем изотермичности и градиентов концентраций вдоль слоя контакта. [c.29]
Для устранения недостатков обычных реакторов проточного метода нами предложена конструкция блочного многоканального изотермического реактора, моделирующего промышленный конвертор, с длиною слоя катализатора 150—300 см. Благодаря высокой теплопроводности металла, из которого изготовлен блок, поддерживается изотермичность по длине и сечению слоя катализатора. Условия катализа в реакторе соответствуют методу идеального вытеснения. Возможность определения концентрации реагентов в десяти точках по длине слоя катализатора позволяет получить вид кинетического уравнения и решать задачи оптимизации. Кроме того, разработана конструкция блочного капсульного однорядного реактора метода идеального вытеснения, предложенного М. И. Темкиным с сотрудниками [3, 4]. Реактор представляет собой металлический блок, размером 7X7 см, с семью каналами, в которые помещаются капсулы из того же металла. В каналах капсул в один ряд располагаются зерна исследуемого контакта и теплоносителя. В однорядном слое контакта контролируется изотермичность и определяются градиенты концентраций, что позволяет определять вид кинетических уравнений. [c.102]
Одно из направлений научного управления в добыче газа — применение методов оптимизации для поиска оптимальных режимов эксплуатации установок газопромысловой технологии. Данное направление, безусловно, относится к перспективным, поскольку экономически оправдано, так как в процессе эксплуатации объектов ГДП система управления стремится к достижению поставленной перед ней цели. Одновременно повышается оперативность принятия решений по управлению установками обработки природного газа и ГДП в целом. Такой принцип многоуровневого управления базируется на системном подходе, позволяющем увязать локальные критерии управления процессами газопромысловой технологии таким образом, чтобы реализовывался глобальный критерий оптимальности ГДП. Сформулированные задачи оптимизации относятся к классу задач оптимального управления качеством промысловой обработки природного газа, которое должно удовлетворять требованиям ОСТ 51.40—83. В связи с этим один из важнейших путей повышения качества промысловой обработки газа — создание на ГДП автоматизированных систем управления технологическими процессами (АСУ ТП), позволяющих на базе широкого применения средств вычислительной техники, систем телемеханики и средств автоматизации решать задачи оптимизации процессов газопромысловой технологии. Поскольку обустройство ГДП в настоящее время осуществляется индустриальными методами на основе типовых блочно-модульных автоматизированных технологических установок, то расчеты, проводимые в промысловых условиях, тоже носят типовой характер. Приведенные в книге алгоритмы оптимизации являются типовыми как по постановкам задач, так и по алгоритмам их решения, что в значительной мере сокращает сроки внедрения их на тех ГДП, где эксплуатируются ЭВМ. [c.193]
Гюбой метод оптимизации сложных систем, как мы уже указы-вали, качественно представляет собой по существу совместное решение двух задач — расчета оптимальных режимов блоков и согласования работы блоков системы. В некоторых методах оптимизации сложных систем эти две задачи по существу не разъединены (см., например методы первого порядка, метод принципа максимума). В других методах как-то стремятся разъединить указанные задачи. К ним относятся методы блочной оптимизации. Под блоком в данной главе будем понимать один аппарат, либо совокупность некоторых аппаратов схемы. [c.298]
Так как штрафная добавка обычно разрушает сепарабельность целевой функции, задача 1а не распадается в сумму блочных задач. Следовательно, для достижения декомпозиционности в схеме метода штрафов нужно организовать выполнение процедуры нижнего уровня, чтобы решение задачи 1а получалось в результате оптимизации отдельных блоков. Этого можно добиться несколькими способами. [c.243]
По мере развития метода заводнения широкое распространение получили активные блоковые системы с трехрядным размещением добывающих скважин по сеткам 600x600, 700x700, 800x800 м и т.д. Создаются и внедряются избирательное, очаговое, площадное (пятиточечные, семиточечные и девятиточечные) блочно-квадратные и другие системы заводнения. С начала 70-х годов широкое развитие принимают работы по оптимизации плотностей сеток скважин в зависимости от послойной и зональной неоднородностей пласта, соотношения вязкостей нефти и закачиваемой воды и от других факторов. По многим месторождениям плотность сетки принимается 24-36 га/скв. [c.75]
chem21.info
Последовательность блоков оптимизация, метод - Справочник химика 21
Первый способ. Задача 1а решается методом группового покоординатного спуска. В отличие от обычного метода покоординатного спуска, в котором оптимизация ведется последовательно по каждой переменной, в групповом методе покоординатного спуска оптимизация осуществляется последовательно по группам переменных. В качестве отдельных групп переменных в данном случае берутся переменные, относящиеся к отдельным блокам. При применении данного способа на /-ом шаге проводится оптимизация /-го блока на множестве 0 по соответствующему критерию [c.243] Из изложенного следует, что в рассматриваемом случае задача расчета производных в замкнутой схеме является достаточно сложной и трудоемкой. Поэтому изложим сейчас другой метод оптимизации схемы с рециклом , который в ряде случаев может привести к существенному уменьшению количества вычислений. Разберем последовательность блоков 1, 2,. . ., N, служащую частью схемы (сдг. рис. 42). [c.198]Программа позволяет генерировать системы уравнений и допускает использование различных подпрограмм. Она состоит из трех основных блоков, которые используются последовательно один за другим. Первый блок формирует уравнения из структуры ХТС в форме / (д ) = 0. Второй блок определяет оптимальную совокупность выходных переменных с учетом одного из критериев минимального числа итерируемых переменных или критерия чувствительности. Третий блок предназначен для решения систем уравнений (в том числе и уравнений для элементов ХТС с распределенными параметрами) методами простой итерации с модификациями или методом Гаусса— Ньютона. В этом же блоке имеются подпрограммы для оптимизации ХТС и расчета ХТС с учетом неопределенности некоторых параметров математических описаний ХТС. [c.108]
Декомпозиционные методы оптимизации позволяют свести глобальную задачу оптимизации ХТС большой размерности к последовательности локальных задач оптимизации отдельных блоков или совокупностей отдельных блоков ( суперблоков ) существенно меньшей размерности, При конструировании подобных методов главная проблема состоит в ликвидации или учете взаимного влияния блоков ХТС при формировании локальных задач оптимизации. В связи с этим был разработан принцип закрепления П10, с. 302—308], на основе которого был создан декомпозиционный метод закрепления [1, с. 302 [c.169]
Реконструкция установок применение горячей воды для обессоливания реализация прямых связей по сырью с последующими установками оптимизация теплообмена на основе пинч-ана-лиза (определение оптимальной поверхности теплообмена по отношению к стоимости сэкономленного тепла и к требуемым затратам) установка дополнительных теплообменников и применение параллельной схемы подогрева сырой нефти вместо общепринятой последовательной (обеспечивается повышение температуры нефти до 285°С на атмосферном и вакуумном блоках) применение усовершенствованных методов регулирования расходов нефти в параллельных теплообменниках применение усовершенствованной системы регулирования (минимизации расходов пара при отпарке в боковых стриппингах), применение стриппингов с ребойлерами отказ от подачи сухого пара оптимизация распределения тепловых нагрузок циркулирующего орошения в некоторых случаях — использование предварительного эвапоратора сырья применение электродвигателей с регулируемым числом оборотов. [c.445]
Для оптимизации сложных систем, каковыми являются производства, часто применяют декомпозиционный метод, который сводит решение общей задачи к последовательному решению задач оптимизации отдельных блоков системы по соответствующим критериям. [c.76]
Предположим, что ХТС разбита на подсистемы (блоки), каждая из которых описывается уравнениями типа 2.34—2.48. Для оптимизации ХТС может быть выбран, например, двухуровневый декомпозиционный метод. Первому уровню будет соответствовать алгоритм локальной оптимизации отдельных блоков ХТС, а второму уровню - алгоритм коррекции локальных задач оптимизации. При решении задачи оптимизации необходимо прежде всего учесть взаимное влияние блоков ХТС при проведении оптимизации отдельных частей или подсистем на первом уровне. Для этого можно использовать алгоритм, который сводит задачи условной минимизации к последовательности задач безусловной минимизации. [c.77]
Очевидно, что применение рассмотренного выборочного метода в этом случае не позволит уменьшить среднее время поиска, поскольку нет оснований для того, чтобы заключить, какой из элементов следует проверять раньше других. Для оптимизации поиска в данном случае можно использовать связь между элементами. Это позволит проверить элементы не по одному, а группой, и в процессе проверки планомерно исключать из рассмотрения целые группы элементов. Как правило, метод средней точки используют для поиска неисправностей в тех узлах, блоках, в которых элементы соединены последовательно. Тогда, проверяя одну группу элементов, можно быть уверенным, что другие группы элементов не влияют на результаты этой проверки. [c.163]
Декомпозиционными методами оптимизации сложных химикотехнологических схем (СХТС) обычно называют методы, которые сводят задачу оптимизации схемы к последовательности задач оптимизации ее отдельных блоков но соответствующим критериям (12, с. 172 127—129]. Идея такого подхода естественным образом возникает из аддитивности глобального критерия и сепарабельной структуры системы. [c.227]
ПОТОК возвращаемый на вход схемы с выхода блока изомеризации. Рецикл можно учесть двумя способами на уровне расчета схемы при итерациях по Xi [см. задачу 1, выражения (I, 64)—(I, 66) ] и при оптимизации, рассматривая его как ограничение типа равенства на разрываемую переменную Xi [см. задачу 4, выражения (I, 79)— (1,81)]. При решении был применен второй способ. Оптимизация проводилась с применением методов последовательной безусловной минимизации метода модифицированной функции Лагранжа (AL) и штрафных функций (PEN), на нижнем уровне которых использовались квазиньютоновские алгоритмы DFP, SSVM. Расчет производных выполнялся разностным способом [см. выражение (1,49)]. В процессе оптимизации для удержания значений варьируемых переменных Xi (напомним, что лг — коэффициенты разделения газовых потоков) между нулем и единицей применялись замены переменных с использованием функции ar tg. Функции, участвующие в постановке задачи оптимизации, наиболее чувствительны (в окрестности л ) к изменению Xi, Xs, л ,. В связи с этим для повышения стабильности получаемых результатов применялось преобразование сжатия по осям л .,, Xi, Xj, Хв, что можно сравнить с процедурой [11, с. 82—83]. В табл. 23 приведены результаты решения рассматриваемой задачи [c.140]
Однако применение метода нодонтимизации в данном случае осложняется тем, что вследствие наличия рециркуляционной цепи при варьировании управляющих переменных в г-ой последовательности меняют входные переменные x (0),, у всех остальных последовательностей . Поэтому, хотя алгоритм оптимизации здесь останется таким же, как и в предыдущем случае, но при поиске оптимальных значений и ( ) . в А -ой последовательности необходимо решать уравнения блоков во всех остальных последовательностях . В данном случае это значительно снижает эффективность метода. [c.201]
chem21.info
Выбор метода оптимизации - Справочник химика 21
Наибольшее распространение при оптимизации ХТС в настоящее время получает вторая группа методов оптимизации ХТС— декомпозиционные методы (блок В). Декомпозиционные методы сводят задачу оптимизации схемы в известном смысле к взаимосвязанным задачам оптимизации отдельных подсистем ХТС. Взаимосвязь отдельных задач оптимизации, как уже указывалось, обусловлена взаимодействием подсистем, учитываемым тем или иным приемом децентрализации и декомпозиции общей проблемы оптимизации. Прямые декомпозиционные методы (блок F), такие, как методы цен (блок 7 1), метод закрепления переменных (блок fU) и их модификации, строятся- по общему принципу, основанному на внесении соотношений связи между подсистемами в критерий оптимизации с последующим разбиением общей проблемы оптимизации на ряд подзадач. Эта группа обладает большим достоинством, связанным со свободой выбора метода оптимизации из группы А для решения локальных задач оптимизации. [c.180] Выбор метода оптимизации и оптимальный расчет. [c.299]Оптимизация БТС осуществляется с использованием известных методов оптимизации сложных систем [14, 17], реализация которых включает общий анализ задачи оптимизации определение критерия оптимизации и выбор оптимизирующих параметров анализ влияния параметров математической модели на критерий оптимизации организацию оптимальной стратегии оптимизации выбор метода оптимизации и проведение оптимального расчета. Качество и эффективность функционирования БТС при этом в значительной степени зависит от обоснованного выбора показателя эффективности — критерия оптимизации системы. [c.25]
Отметим, что ДГ-оптимизация характеризуется разбиением множества Мг на логически связанные множества а М (что соответствует разбиению комбината на блоки и регионы), составлением множества 8г а 3 (связи между регионами), установлением глобального критерия 2дг, соответствующего данному разбиению, и выбором метода оптимизации. Короче говоря, при ДГ-оптимизации ищется оптимум критерия Z работы регионов М при связи выбранным методом. При этом каждый регион из множества М рассматривается как своего рода черный ящик , т. е. задаются зависимости выходных переменных от управляемых и входных переменных региона без учета всех его внутренних процессов и особенностей. Поэтому если Х . — есть вектор выходных переменных v-гo региона, Yrv — вектор его входных переменных, А Ату — матрица преобразования, то зависимости между этими переменными в линейном варианте могут быть представлены в следующем виде [c.160]
Пожалуй, наилучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различных методов оптимизации. В последующих главах будут рассмотрены перечисленные выше математические методы решения оптимальных задач и примеры их использования. Здесь же дана лишь краткая характеристика указанных методов и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для решения -конкретной оптимальной задачи. [c.30]
При выборе метода оптимизации необходимо учитывать могущие возникнуть вычислительные трудности объем вычислений, сложность самого метода, размерность задачи и т. п. Целесообразно производить по возможности предварительные оценки положения оптимума какой-либо конкретной задачи. Для этого необходимо рассмотреть исходные и основные соотношения между переменными. Для сокращения размерности задачи часто используется прием выделения наиболее существенных переменных. [c.141]
Не представляется возможным изложить твердые правила упрощения задач для всех возможных случаев необходимо каждый раз подходить к выбору метода оптимизации и решению задачи, исходя из конкретного существа самой задачи. Ниже излагаются основные принципы различных методов оптимизации, наиболее широко используемых в химии и химической технологии. [c.141]
Удачно выбранный метод оптимизации должен привести к конечным результатам с наименьшими затратами на вычисления или же к получению наибольшего объема информации об искомом решении. Чем сложнее объект оптимизации, тем труднее выбрать метод решения оптимальной задачи. При выборе метода оптимизации для рассматриваемой задачи нужно проанализировать известные решения других задач и исходить из опыта их решения и конкретного существа самой задачи. Следует отметить, что некоторые методы специально разработаны для решения оптимальных задач объектов, которые описываются математическими моделями определенного вида. [c.246]
Выбор метода оптимизации и осуществление оптимального расчета. [c.17]
ВЫБОР МЕТОДА ОПТИМИЗАЦИИ [c.280]
Выбор метода оптимизации, пригодного для принятого критерия. [c.183]
На выбор метода оптимизации решающее влияние оказывает вид математической модели и целевой функции. В результате проведения расчетов по оптимизации устанавливаются значения параметров, которые позволяют добиться конечных результатов с наименьшими затратами. [c.174]
Целесообразно применять однотипные вычислительные схемы. Применение вычислительных машин позволяет упростить расчеты благодаря использованию стандартных подпрограмм, поскольку в таких случаях лишь для целевых функций приходится создавать специальные программы (например, при динамическом программировании). Изложить твердые правила упрощения задачи для всех возможных случаев не представляется возможным при выборе метода оптимизации и решения задачи необходимо каждый раз исходить из конкретного существа самой задачи. Ниже излагаются основные принципы различных методов оптимизации, наиболее широко используемых в химии и химической технологии [10, 11]. [c.203]
При выборе метода оптимизации необходимо учитывать могущие возникнуть вычислительные трудности объем вычислений, сложность самого метода, размерность задачи и т. п. [c.117]
В связи со сказанным выше представляется целесообразным находить оптимальные условия проведения ионообменных процессов, используя математические модели. Это расширяет возможности решения задачи оптимизации, так как варьирование параметров проводится не экспериментально, а на математической модели, записанной в виде программы для ЭВМ [2, 3]. В этом случае варьируются все параметры опыта в широком диапазоне их изменения с любой заданной точностью. В настоящей статье излагаются принцип и результат оптимизации некоторых типичных ионообменных процессов, которые реализуются в следующем порядке 1) формулировка критерия оптимальности 2) выбор параметров оптимизации и обоснование ограничений 3) выбор метода оптимизации 4) обоснование математической модели процесса. [c.169]
chem21.info
Метод локальной оптимизации - Энциклопедия по машиностроению XXL
Преимущественное применение для решения охарактеризованного вьппе класса задач получили методы следующих двух групп, иногда в сочетании с методами локальной оптимизации. [c.208]Рассмотрим идею отжига применительно к методу локальной оптимизации. [c.209]
Метод локальной оптимизации - итерационный метод оптимизации, основанный на поиске локального экстремума в ограниченной окрестности текущей точки поиска на каждой итерации и перемещении текущей точки в найденную точку локального экстремума [c.312]
Сформулирована задача построения оптимальных (по интегральному критерию качества) законов движения манипуляторов при выполнении ими транспортных и технологических операций и показано, что ее можно свести к известным задачам вариационного исчисления. Применительно к плоскому манипулятору с тремя степенями свободы оптимальные движения построены в явном виде. Приводится сравнительный анализ оптимальных решений для транспортной и технологической операций и сопоставление этих результатов с приближенным решением, полученным методом локальной оптимизации. [c.181]Методы локальной оптимизации и поиска с запретами [c.182]
Особенность безградиентных методов состоит в том, что для определения направления поиска не применяется анализ чувствительности целевой функции к изменениям управляемых параметров. Наиболее простым с алгоритмической точки зрения, но крайне неэкономичным является метод сканирования, практически совпадающий с методом матричных испытаний, рассмотренным в 3 гл. 1 как экспериментальный метод оптимизации. С помощью этого метода можно найти глобальный экстремум. Остальные рассматриваемые здесь методы относятся к методам локальной оптимизации. [c.156]
Дискретная оптимизация сложнее непрерывной. Комбинаторная задача общего вида относится к N9 полным, и сложность ее точного решения является экспоненциальной. Эффективные точные методы дискретной оптимизации существуют лишь для отдельных классов задач, поэтому для задач целочисленного линейного программирования и нелинейного дискретного программирования в САПР применяются приближенные методы локальной оптимизации и ветвей и границ. [c.76]
С точки зрения конечной цели поиска первый подход более естествен и предпочтителен, так как не требует избыточной информации о локальных оптимумах. Однако известно, что методы поиска глобального оптимума (методы перебора и динамического программирования) имеют на практике ограниченное применение из-за большого машиносчетного времени. Поэтому при решении практических задач часто более эффективными оказываются алгоритмы, включающие в себя поиск локальных оптимумов. Обобщения по использованию методов локального поиска для решения задач глобальной оптимизации даны в [71]. [c.133]
Время поиска существенно уменьшается при стремлении к локальному оптимуму. В этом случае соотношение (П.43) принципиально сохраняет свою силу, однако значения N существенно уменьшаются и не являются постоянными. Количество расчетов Но на каждом этапе определяется принятым методом одномерной оптимизации и начальной точкой, с которой начинается поиск на данном этапе. Поэтому N изменяется при повторной оптимизации на данном этапе. На основе стратегии динамического программирования построены алгоритмы локальной оптимизации, обеспечивающие значительно меньшее время поиска по сравнению с глобальной оптимизацией [4, 8]. [c.255]
При описании комплексной целевой функции нелинейными зависимостями от внутренних параметров задача оптимизации решается методами линейного программирования если же целевая функция является линейной функцией от внутренних параметров, то имеет место задача линейного программирования. В общем случае целевая функция может иметь несколько экстремумов, отличающихся по абсолютной величине. В зависимости от типа экстремума, в котором заканчивается поиск оптимального решения, различают методы поиска локального и глобального экстремума. Если на значение определяемых параметров наложены некоторые ограничения, то решение задачи синтеза механизмов осуществляется методами условной оптимизации. В противном случае (при отсутствии ограничений) при синтезе механизмов для поиска значений определяемых параметров используют методы безусловной оптимизации. [c.316]
Среди методов поиска локального экстремума методы безусловной оптимизации составляют наиболее многочисленную группу. Сущность этих методов заключается в том, что строится такая последовательность значений вектора внутренних параметров х , Хц Х.2, при которой в случае поиска минимума целевой функции в [c.316]
Наибольшее распространение в задачах автоматизированного проектирования получили градиентные метода i оптимизации [ 2]. Особенность этих методов заключается в поиске локальных экстремумов целевой функции с использованием первых и вторых производных этой функции. Если в качестве целевой функции выбрано отклонение от желаемого выходного сигнала, то для оптимизации удобно пользоваться результатами анализа чувствительности конструктивных параметров. [c.31]
Как генетический, так и локальный поиск по отдельности недостаточно эффективны. Эффективность решения задач синтеза повышается при использовании локально-генетического метода. В соответствии с этим методом применяется локальная оптимизация по отношению к каждой хромосоме, порождаемой в результате кроссовера. Она заключается в случайном поиске лучшего решения в окрестностях хромосомы потомка (при этом расстояния между хромосомами измеряются числом позиций с неодинаковыми значениями). [c.240]
Метод отжига - метод поисковой оптимизации, в котором для увеличения вероятности выхода из областей притяжения локальных минимумов допускается переход в точки с худшим значением целевой функции с некоторой вероятностью Метод распространения ограничений - метод решения задач условной оптимизации, основанный на сокращении интервалов значений управляемых переменных (или мощности множеств значений этих переменных) благодаря учету исходных ограничений. Сокращенные интервалы в явном виде определяют подмножество допустимых решений [c.312]
Разработанные в последнее время методы построения движений исполнительных органов манипуляторов [1, 2], основанные на локальной оптимизации некоторого функционала от траектории системы, сводят задачу к интегрированию системы дифференциальных уравнений, связывающих законы изменения обобщенных коор- [c.8]
Более того, решение задачи выбора оптимального варианта построения орбитальной структуры СНС с точки зрения обеспечения точности определения навигационных параметров потенциальных потребителей вообще делает проблематичной возможность получения решения методами численной оптимизации. Это связано с тем, что, во-первых, для однократного вычисления оптимизируемой функции необходимо усреднение значений искомых параметров, характеризующих орбитальное построение СНС, приблизительно в 10 точках временной и географической сетки во-вторых, оптимизация должна производиться по числу данных параметров, исчисляемых десятками в-третьих, оптимизируемая функция в этом случае будет иметь большое число локальных экстремумов, нахождение среди которых глобального — пока еще неразрешимая проблема. [c.222]
Методы оптимизации. Для оптимизации оптических систем в настоящее время применяются почти исключительно методы локального спуска, сущность которых заключается в том, что из начальной точки данного -го шага определяется направление, двигаясь по которому мы предполагаем уменьшить оценочную функцию, т. е. спуститься от исходной точки. Вдоль этого направления производится спуск до некоторой конечной точки х данного шага, которая затем принимается за начальную точку следующего шага. Таким [c.215]
Отметим, Что методы локального спуска приводят только к ближайшему от исходной точки минимуму и не позволяют найти самый глубокий, т. е. глобальный минимум оценочной функции, обеспечивающий самую лучшую конструкцию оптической системы. Опыт оптимизации показывает, что часто небольшие изменения начальной конструкции, параметров оптимизации, оптимизируемых функций неожиданно приводят к другому более глубокому минимуму, чем ранее найденный. Поэтому задача построения глобальных методов оптимизации представляется очень заманчивой. К сожалению, в настоящее время отсутствуют сведения [c.218]
Методы поиска экстремума классифицируются по следующим признакам в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции — методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а в методах нулевого порядка производные не используют. [c.281]
К выбору коэффициента Xk для градиентных методов можно подойти двояко. Если учесть локальный характер аппроксимации (П.15), то шаг Д2),, а следовательно, Хк надо выбирать достаточно малым. Это приводит к увеличению количества шагов в процессе поиска и снижает его эффективность. Поэтому часто ki, выбирают из условия оптимизации АНок, решая одномерную зада- [c.245]
Прежде всего рассмотрим возможности классических или аналитических методов оптимизации, основанных на применении средств дифференциального и вариационного исчислений для определения экстремума функции цели. Эти методы позволяют определить лишь необхо-. димые признаки относительного или локального экстремума, для чего используются частные производные функции цели по параметрам. Применение классических методов возможно только при условии дифференцируемости указанной функции. Как известно, в точке экстремума все частные производные функции обращаются в нуль, т. е. [c.149]
Еще более проблематичным представляется применение аналитических методов при отыскании условных экстремумов функции цели, что характерно для реальных задач оптимизации ЭМУ при наличии многочисленных ограничений. Ограничения, накладываемые на область определения функции цели, приводят к возможному несовпадению условных и локальных экстремумов, а поэтому уравнения (5.38) в данном случае вообще нельзя рассматривать в качестве необходимых условий для определения точек экстремума. [c.149]
Наиболее распространенным приемом, позволяющим отстроиться от локальности направленных методов поиска, является организация алгоритмов, в которых на первом этапе применяется пассивный поиск, а в дальнейшем — один из методов направленного поиска. Такое комби нирование методов оптимизации позволяет вести направленный обзор области поиска из нескольких начальных точек (как это показано в примере на рис. 5.21), которые могут формироваться методами сканирования или статистических испытаний. Важно отметить, что начальные точки должны находиться в области допустимых значений параметров. Схема организации комбинированного алгоритма поисковой оптимизации, дающего возможность определять приближения к глобальному экстремуму функции цели, представлена на рис. 5.28. [c.164]
Генетические алгоритмы и методы отжига. Генетические алгоритмы относятся к наиболее универсальным подходам к решению сложных задач структурного синтеза и подробно обсуждаются далее. Методы отжига можно рассматривать как реализацию идеи повышения вероятности определения глобального экстремума в других статистических методах оптимизации, таких, как генетические или локальные методы поиска, [c.208]
Гибридный алгоритм - алгоритм, в котором для рещения задачи используются принципы и приемы, характерные для разных подходов и методов, например, особенности локального и генетического методов для поиска экстремума целевой функции в задачах оптимизации [c.311]
Рассмотрим такой метод, основанный на переходе от глобальной оптимизации к локальной. Иначе говоря, вместо оптимизации функционала (1) траектории системы будем стремиться к минимизации подынтегральной функции F (ф, ф) в каждый момент времени. Естественно, в такой процедуре и информация о двигательной задаче должна иметь локальный характер (не учитывать движения системы до рассматриваемого момента и после него). Например, для технологических операций такая информация со- [c.32]
Допуская, что область D может быть несвязной, целесообразно рекомендовать решение задачи на основе ЛП-поиска в сочетании с локальными методами оптимизации [4, 5]. [c.43]
Методы локальной оптимизации. Эти методы успешно используются для поиска локальных экстремумов в метризованных пространствах. К сожалению, велика вероятность застревания текущей точки на траектории поиска вдали от глобального экстремума. Чтобы уменьшить эту вероятность, применяют поиск с запретами (tabu sear h), в котором запрещается переход в некоторые точки, в том числе в точки, пройденные на нескольких последних итерациях поиска. Спуск происходит в лучшую из пройденных на очередной итерации точек, даже если эта точка хуже результата предьщущей итерации. Тем самым облегчается выход из локальных экстремумов. [c.208]
При оптимизации аналогом энергии является целевая функция и для увеличения вероятности выхода из областей притяжения локальных минимумов нужно, в отличие от базового метода локальной оптимизации, разрешить переход в точки с худшим значением целевой функции с вероятностьюр, определяемой по формуле (2.1). При этом Е иЕ - значения целевой функции в исследуемой и принятой точках поиска, Т - параметр поиска. [c.209]
Среди других приближенных методов решения задачи ДМП отметим метод локальной оптимизации. Так как пространство D метризовано, то можно использовать понятие а-окрестности S (X ) текущей точки поиска Х . Вместо перебора точек во всем пространстве D осуществляется перебор точек только в S (X). Если F(X ) > F(XJ для всех X е S (ХЛ, то считается, что [c.180]
Метод локальной оптимизации характеризуется тем, что один его шаг заключается в исследовании е-окрестности текущей точки поиска X при значении е, обеспечивающем нахождение в этой окрестносги по крайней мере еще одной точки. Если Г(Х ) / (Ху), где X/ — любая точка в исследуемой е-окрестности, то Хй принимается в качестве точки локального экстремума. Если же найдется точка с лучшим значением целевой функции, то она становится новой текущей точкой поиска и происходит переход к следующему шагу. Д.тя реализации метода локальной оптимизации нужно установить способы выбора начальной точки поиска, величины е, правила возможного изменения е в процессе поиска и т. п. При больших е увеличивается трудоемкость поиска, при малых е — снижается надежность определения глобального экстремума. [c.76]
Числовой подход к решению задачи требует применения ЭВМ и поисковых методов оптимизации. При решении данного примера в качестве параметров оптимизации приняты высота полюсного наконечника hp, высота hm и ширина Ьт полюсного сердечника, высота ярма hj. Однако независимыми являются только параметры Лт и bm, так как hj жестко связан с Ьт, а Ар однозначно определяется одним из равенств а р = Одоп или,Вкр = Вдсл. Они обусловлены тем, что возникающее в процессе оптимизации стремление увеличить окно обмотки возбуждения приводит к превращению соответствующих неравенств в равенства. Все остальные исходные данные расчета индуктора с учетом предыдущих этапов расчета генератора предполагаются фиксированными. Для поиска оптимальных решений использованы градиентный метод и метод локального динамического программирования. Числовое решение рассматриваемой задачи не достигает конечной цели, т. е. не приводит к уравнениям расчета оптимальных значений параметров оптимизации. Конечную цель можно достичь только при сочетании числовых результатов с методами планирования эксперимента. При этом в качестве единичного эксперимента следует рассматривать отдельное оптимальное решение рассматриваемой задачи, полученное для конкретного набора исходных данных. В качестве факторов можно рассматривать любые независимые исходные данные. [c.105]
Простейшим но структуре алгоритмом глобального поиска является независимый поиск (методы Монте-Карло), оенованный на случайном переборе точек в ограниченном пространстве Gp варьируемых параметров [51, 90]. Характерной особенностью методов Монте-Карло является постоянная в течение всего поиска нлот-пость распределепия зондирующих точек. Поэтому для решения этими методами задач оптимизации машинных агрегатов с многомерными векторами Р варьируемых параметров обычно необходимо выполнить значительное число проб. Выгодным для задач динамического синтеза машинных агрегатов свойством метода случайного поиска е равномерным распределением пробных точек является возможность одновременного онределения нескольких оптимальных решений, соответствующих различным критериям эффективности. Это свойство независимого глобального поиска особенно важно для задач параметрической оптимизации машинных агрегатов, оперирующих с неприводимыми к единой мере локальными критериями эффективности. Такая ситуация характерна для параметрического синтеза динамических моделей машинных агрегатов по критериям эффективности, отражающим, ианример, общую несущую способность силовой цепи по разнородным факторам динамической нагругкепности ее отдельных звеньев (передаточного механизма п рабочей машины). Аналогичная ситуация возникает также при оптимизации характеристик управляемых систем машинных агрегатов по критериям устойчивости и качества регулирования. [c.274]
Общий метод построения движений манипуляторов был предложен в работе [1], где сформулирован критерий оптимизации движения и рассмотрен вопрос построения оптимальных движепий-на основе принципа локальной оптимизации. Для изучения основных свойств и особенностей предложенного метода был разработан реализующий его алгоритм и составлена программа построения движений четырехзвенного манипулятора с пятью степенями свободы [2], кинематическая схема которого приведена на рисунке. При построении оптимальных движений в [1] не учитывались возможные ограничения подвижности в кинематических парах манипулятора. Соответственно в [2] предполагалось, что все пять вращательных пар манипулятора допускают неограниченные изменения обобщенных координат ф . Учет ограничений подвижности Б кинематических парах приводит к усложнению алгоритма построения оптимальных движений манипулятора. [c.56]
Однотипность простых повторяющихся вычислительных операций делает метод локальных вариаций удобным для реализации на ЭВМ и позволяет при решении нелинейной пространственной задачи термоупругости избежать многократного решения громоздкой системы линейных алгебраических уравнений вида (6.40), хотя для поиска достаточно точного решения требуется обычно большое число итераций. Поскольку для устойчиво деформируемого материала dajde >0, минимумы функционалов (6.77) и (6.78) единственные (см. 1.4), что позволяет помимо метода локальных вариаций для поиска решения эффективно применять различные методы оптимизации и, в частности, градиентные методы. [c.253]
В книге рассматриваются современные модели расчета и методы параметрической оптимизации несущей способности оболочек вращения из композитов двумерной и пространственной структур армирования. Основное внимание при этом уделено оболочкам, работающим на статическую устойчивость или в режиме колебаний, эффективные деформативные характеристики которых определяются методами теории структурного моделирования композита. В задачах, содержащих оценки предельных состояний оболочек по прочности, используется феноменологическая структурная модель прочностных характеристик слоистого композита, параметры которой получены экспериментально. Подробно анализируются особенности постановки задач пара.метрической оптимизации оболочек из композитов. Показана взаимосвязь векторной и скалярной моделей задач оптимизации в случае формализуемых локальных критериев качества проекта. Значительное место отведено изложению и примерам приложения нового метода решения задач оптимизации оболочек из. многослойных композитов — метода обобщенных структурных параметров, применение которого позволяет получить наиболее полную информацию об опти.чальных проектах широкого класса практически важных задач оптимизации. Содержащиеся в книге результаты могут быть использованы для инженерного проектирования оболочек из волокнистых композитов. Табл. 23, ил. 58, библиогр. 181 назв. [c.4]
Рассматриваемые методы являются методами поиска локальных экстремумов. Это основные методы в САПР, так как методов глобальной оптимизации, обеспечивающих нахождение глобального экстремума с приемлемыми потерями на поиск, для задачи математического программирования общего вида (3.3) не существует. В САПР поиск глобального экстремума осуществляется путем локальной оптимизации из нескольких исходных точек, выбираемых случайным образом в пределах области, задаваемой прямыми ограничениями. В многоэкстремальных задачах возможно получение нескольких локальных экстремумов, из которых выбирается наилучший. Вероятность определения глобального экстремума при подобном подходе тем меньше, чем меньше объем области притяжения глобального экстремума. Малый объем этой области, как правило, свидетельствует и о низкой стабильности выходных параметров в точке экстремума, следовательно, глобальный экстремум может оказаться малополезным. Поэтому оптимизация на основе небольшого числа вариантов локального поиска является достаточной. [c.71]
Следует указать на группу ЧМ-процедур, полученных в результате применения к задаче (1) адаптивных методов рандомизации и сглаживания. При данном подходе.исходная мнргокритер иалЬная задача формулируется в виде задачи стохастической оптимизации, для решения которой используется метод локальных улучшений [55]. Предложенные варианты процедур используют информацию ЛПР как в виде Уц(г), так и /лпр — 2л>2в (альтернатива А предпочтительнее альтернативы В). В [56, 57] рассмотрены вопросы повышения скорости сходимости и повышения качества ЧМ-процедур этого типа. [c.38]
Для поиска локальных оптимумов используются однопарамвтрические методы оптимизации (метод покоординатного спуска в сочетанжи с методом золотого сечения), Функщюнально-технические огранячендя на систему пластин целесообразно учитывать методом штрафных функций fij. Тогда алгоритм оптимизации заключается в минимизации функции [c.131]
Вводя понятия скользящего допуска и эквиваленхного ограничения и не останавливаясь на способах задания последовательности (П.38), можно получить следующую стратегию поиска. Начальная точка Zo задается произвольно и проверяется условие (П.37). При этом возможны два варианта. Если условие (П.37) не удовлетворяется, то производится минимизация функции T(Zo) любым из приемлемых методов поиска до тех пор, пока условие (П.37) будет выполнено. Если условие (П.37) удовлетворяется, то переходят к оптимизации функции Wo(Zo) также с помощью любого подходящего метода поиска. Как обычно, определяется направление Sg и совершается переход в точку 2i, где все предыдущие процедуры повторяются. Поиск заканчивается, когда дальнейшее улучшение Ha(Zk) становится невозможным или величина d становится меньше наперед заданной минимальной погрешности. Процесс поиска сходится к локальному оптимуму. [c.253]
В зависимости от характера экст ремума различают методы условной и безусловной, а также локальной и оощей оптимизации. Наиболее удобно и просто реализовать на ЭВМ методы поиска безусловных локальных экстремумов. [c.30]
Заметим прежде всего, что выбор метода расчета зависит от вида целевых функций (7.54). Если целевая функция непрерывно дифференцируема и имеет один экстремум в рассматриваемой односвязной и выпуклой области допустимых конструктивных параметров, для приближенного нахождения экстремума можно с успехом использовать многие численные локальные методы [264, 312]. Однако, как отмечалось выше, целевые функции в задачах акустической оптимизации являются сложными функциями параметров и, помимо ярко выраженной овражности , обладают обычно многими экстремумами, а области допустимых значений параметров в общем случае невынуклы и многосвязны. [c.269]
Выше отмечалось, что функции цели, возникающие в задачах акустической оптимизации машинных конструкций, как правило, овражисты . Это их свойство затрудняет применение на этом этапе многих локальных методов, в частности градиентных [289, 312], заключающихся в движении от заданной начальной точки в сторону наибольшего убывания (возрастания) целевой функции. Рис. 7.43 иллюстрирует эту трудность на примере функции двух переменных параметров J а, г). На линиях без стрелок функция /( 1, аг) имеет постоянные значения. Отрезками со стрелками показано движение от одного приближенного значения параметров 1 и 2 к другому при применении одного из градиентных методов. Последовательпость приближенных точек снабжена порядковыми числами, показывающими число шагов при счете, которые необходимо сделать, чтобы попасть в эту точку, начиная от первоначальной (нулевой). На рис. 7.43, а функция /(ai, 2) убывает (возрастает) примерно одинаково во всех на-нравлеппях от экстремума и градиентный метод дает возможность в несколько шагов перейти от начальной точки О в ближайшую окрестность экстремума. На рис. 7.43, б изображена [c.271]
Если J [а], al) > J ( 1, aJ), то вращение па ДО продолжается до тех нор, пока следующее значение не станет меньше предыдущего или равно ему. На рис. 7.44 такой точкой стала четвертая по счету. После этого начинает вращаться точка О вокруг точки 4 и т. д. Как видно из рисунка, в этом алгоритме последовательность точек приближения спускается в овраг и движется вдоль него до минимума. Метод движения но оврагу легко обобщается на случай многих переменных параметров (см, [125]). Он также позволяет обойтн еще одну трудность, возникающую при необходимости находить локальные экстремумы в задачах акустической оптимизации машин. Трудность заключается в том, что целевые функции часто содержат абсолютные значения комплексных выражении, зависящих от параметров а,, и поэтому не [c.272]
Прежде всего изложенные методы, как детерминированные, так и случайные, являются по существу локальными, т. е. они обеспечивают (с заданной точностью) попадание в точку локального экстремума, в зоне притяжения которого находится начальная точка поиска В то же время, как показывает анализ, критерии качества при оптимизации параметров теплообменных аппаратов являются сложными и, главное, многоэкстремальными функциями оптимизируемых параметров. Таким образом, для решения поставленной задачи необходим метод, который бы позволял находить глобальный экстремум функции качества. [c.202]
mash-xxl.info
Тема 09. Оптимизация математической модели хтп.
Вернуться к списку лекций
Оглавление
§1. Постановка задачи оптимизации.
§2. Характеристика оптимизирующих переменных.
§3. Численные методы оптимизации.
3.1. Экспериментально-статистический метод оптимизации
3.2. Движение к экстремуму методом крутого восхождения
3.3. Уточнение положения экстремума в почти стационарной области
§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.
Задания для самопроверки
§1. Постановка задачи оптимизации.
Оптимизация – это процедура нахождения наилучших условий проведения химического процесса.
Задача оптимизации рассматривается как математическая задача поиска экстремального значения функции многих переменных.
Формулировка задачи оптимизации для многих переменных:
Необходимо найти такие значения оптимизирующих переменных 
(ресурсов оптимизации) из допустимой области их определения 
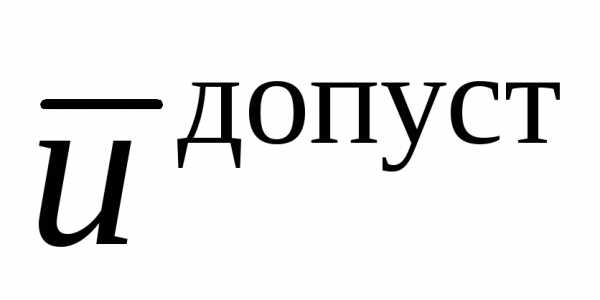, которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.
В результате задачу оптимизации можно представить в следующим виде:
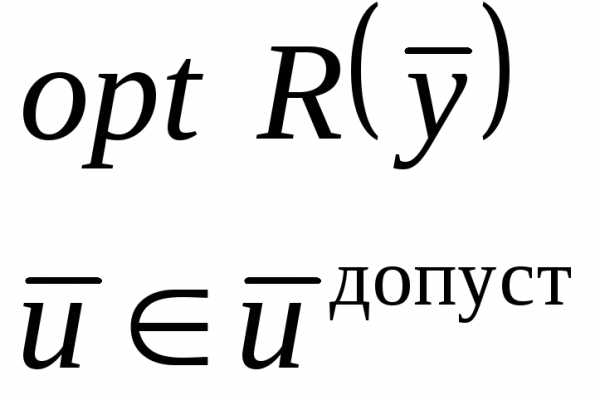
Связь выходных переменных 
с другими переменными задаётся отображением с физико-химическим оператором:
где входные переменные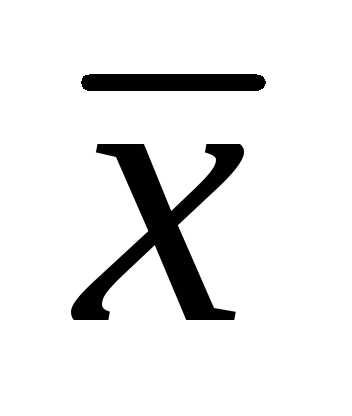 
, определяющие состояние моделируемого объекта, разбиваются на две группы переменных: 
- оптимизирующие переменные, которые можно контролировать и регулировать и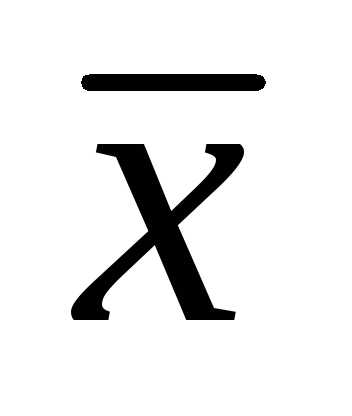 
- контролируемые, но не регулируемые переменные (не могут использоваться как ресурсы оптимизации).
В результате задача оптимизации представляется в следующем виде:
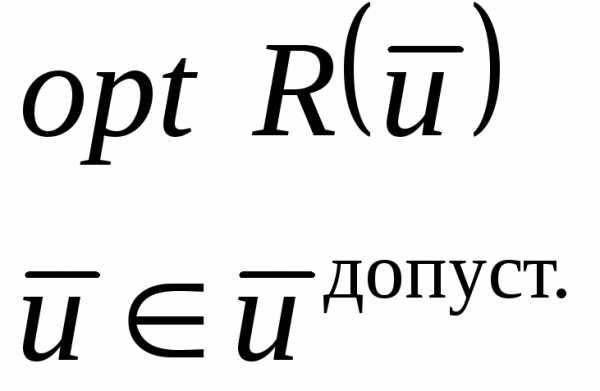
На оптимизирующие переменные 
и выходные переменные 
могут накладываться ограничения (возможность изменения переменных только в определённых пределах).
На практике выходные переменные 
при решении задачи оптимизации определяются либо из экспериментальных данных – экспериментально-статистический метод оптимизации, либо с помощью математических моделей процессов – численный метод оптимизации.
Математические модели в этом случае формализуются с помощью отображения с функциональным оператором:
Замена вектора выходных переменных 
на вектор оценок выходных переменных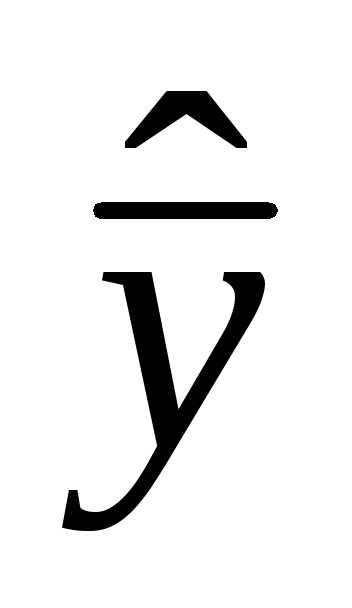 
, полученных при расчёте по математической, модели позволяет рассматривать задачу оптимизации как математическую задачу поиска экстремума функции многих переменных на компьютере.
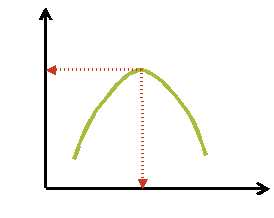
Задача: определение максимума функции R = R( u )
Результат решения: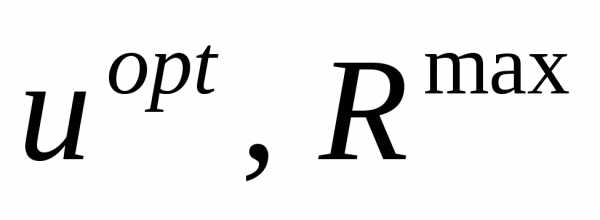 
.
Пример:
Для последовательной реакции A → P → S , изменение концентраций компонентов которой представлено ниже на рисунке, можно сформулировать следующую задачу оптимизации: найти оптимальное время реакции ( topt ), при котором концентрация промежуточного продукта Р будет максимальной.
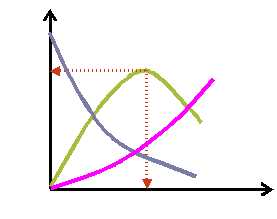
Для решения задачи оптимизации необходимо:
Критерий оптимальностиявляется количественной характеристикой качества функционирования процесса.
Различают физико-химические (концентрация целевого продукта, примеси, выход продукта) и экономические (себестоимость, прибыль, рентабельность) критерии оптимальности.
Значение критерия оптимальности зависит от выходной переменной , рассчитываемой с помощью математической модели (численный метод оптимизации). Предполагается, что при оптимизации применяются математические модели, для которых предварительно решена задача идентификации. Соответственно коэффициенты модели не показаны в равенстве:
Если адекватную математическую модель процесса построить не удаётся, то значение выходной переменной 
в уравнении:
определяется из опытов (экспериментально-статистический метод оптимизации). В этом случае реализуется оптимальная стратегия проведения эксперимента (активный эксперимент).
Требования к критерию оптимальности:
критерий оптимальности должен быть количественным
критерий оптимальности должен быть единственным
критерий оптимальности должен монотонно изменяться в зависимости от оптимизирующих переменных.
Таким образом, при выборе критерия оптимальности необходимо стремиться к тому, чтобы его функция была унимодальной с одним экстремумом и не содержала точек разрыва.
Оглавление
studfiles.net
