Виды оптимизации: Недопустимое название — Самая полная в Рунете энциклопедия интернет-маркетинга

Содержание

Виды и методы оптимизации сайта. Блог Web-студии РостСайт

SEO-оптимизация — это ряд мероприятий, которые направлены на улучшение позиций в поисковой системе. Говоря простыми словами, специалисты производят настройку сайта таким образом, чтобы именно его рекомендовал Гугл или Яндекс, когда пользователь будет искать необходимую ему информацию, услугу или товар. Чем выше положение веб-ресурса в выдаче, тем больше вероятность получить внимание потенциального потребителя. Как показывает практика, дальше 3 страницы в поиске — никто не ходит, поэтому даже самый полезный и качественный продукт может потеряться.

Для чего нужно SEO

Оптимизация сайта — это своего рода комплекс различных решений, которые помогают добиться нужного результата. Раньше можно было просто вписать ключевые слова в текст, закупиться ссылками и быстро заслужить внимание от поисковой системы. Однако с развитием новых брендов, появлением новых компаний — возросла в сотни раз конкуренция. Теперь стандартные методы в единичном использовании не работают. Контекстная реклама, сотрудничество с блогерами, таргетинг, улучшение юзабилити ресурсов, адаптация под мобильные устройства, чтобы страницы грузились быстрее (проверить показатели можно через pagespeed) — это все относится к поисковой оптимизации SEO .

Статистика от Гугл и Яндекс показывает, что около 70% всего трафика потенциальных клиентов доходит только до 3 строки в поисковой выдачи. Далее интерес пользователей теряется, они переписывают запрос и начинают поиск заново. Остальная часть отдает свое внимание и доверие компаниям, которым удалось выбиться в строки лидеров. Решить самостоятельно проблемы работы ресурсов в Тильде, WordPress не всегда получается. Потеря времени сказывается на снижении доходов. Специалисты в период работы будут разбирать каждую проблему по шагам, поэтому получение даже базовых знаний в области раскрутки известных платформ (Тильда, Joomla и другие) гарантировано.

Что входит в услуги SEO-оптимизации сайтов

Специалисты компании РостСайт предлагают комплексные методы раскрутки, которые помогут быстро наверстать необходимый трафик для увеличения прибыльности бизнеса.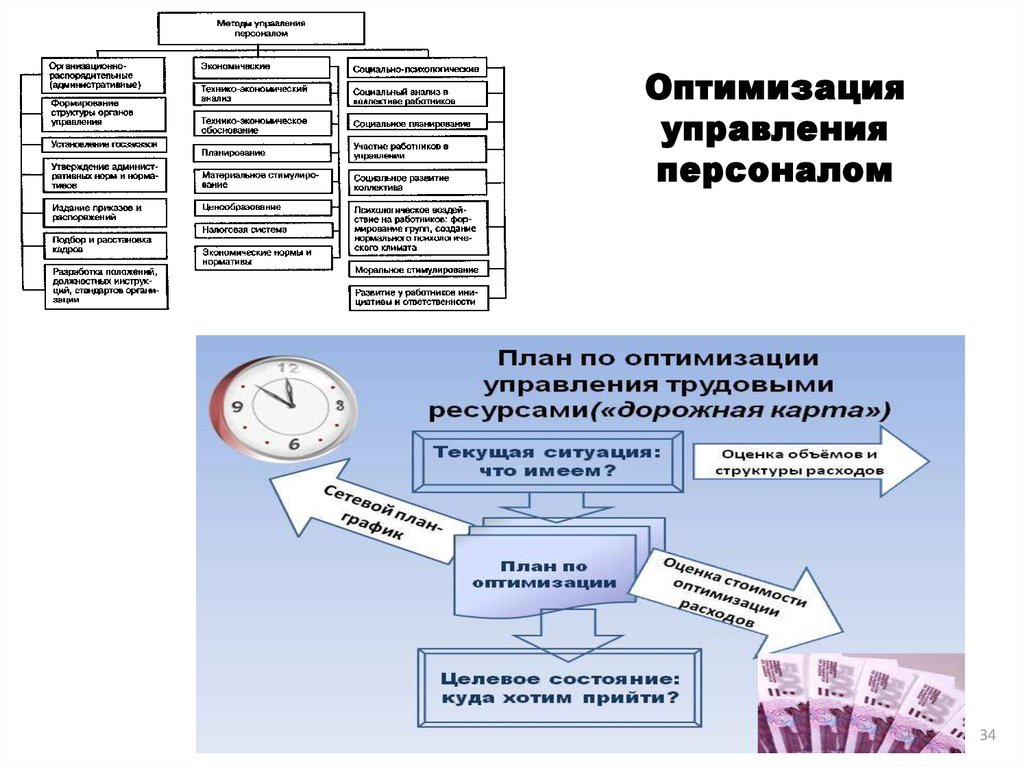 Что входит:

производят анализ текущего спроса — по шагам изучают статистику переходов, основываясь на опыте конкурентов в предложенном сегменте;
разрабатывают семантическое ядро для естественного продвижения;
производят внутреннюю оптимизацию, которая положительно скажется на общей работе ресурса (сейчас большая часть клиентов ищет информацию через мобильные устройства, многие ресурсы еще не адаптированы к этому), проверить можно через page speed;
проводят работу, которая касается увеличения частоты цитирования в сети;
также проводят анализ поведения пользователей (как увидят выдачу, как отображается информация на самих ресурсах), что крайне важно для продвижения;
отслеживают результаты трафика, производят корректирующие работы для достижения постоянного и максимального результата.

Чтобы проводить глобальную работу, необходимо подключать большое количество специалистов, выполнить манипуляции самостоятельно едва получится.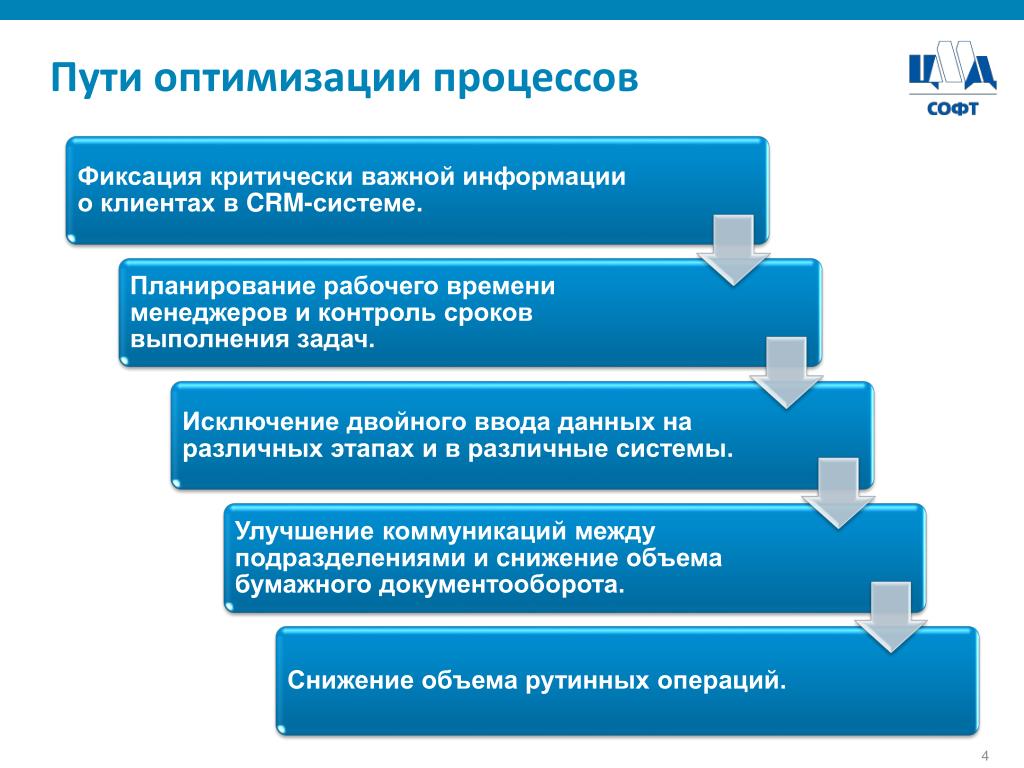 Сегодня обращение в агентство является наиболее приемлемым решением для оптимизации бизнес ресурса, который может приносить еще больше доходов своему владельцу.

/Og (Виды глобальной оптимизации) | Microsoft Learn

Twitter

LinkedIn

Facebook

Адрес электронной почты

Статья

01/10/2023

Чтение занимает 2 мин

Не рекомендуется. Обеспечивает локальную и глобальную оптимизацию, автоматическое выделение регистров и оптимизацию цикла. Вместо этого рекомендуется использовать параметр/O1 (Свернуть размер) или /O2 (Максимальная скорость).

Синтаксис

/Og

Параметр /Og использовать не рекомендуется. Эти оптимизации теперь включены по умолчанию при включении любой оптимизации. Дополнительные сведения об оптимизации см. в разделе /O1, /O2 (Минимизация размера, Максимальная скорость) или /Ox (Включение оптимизации большинства скоростей).

В разделе /Ogдоступны следующие оптимизации:

Устранение локальных и глобальных общих вложенных выражений
В этой оптимизации значение общего подэкспрессии вычисляется один раз. В следующем примере, если значения b и c не изменяются между тремя выражениями, компилятор может назначить вычисление b + c временной переменной и использовать эту переменную для b + c:
```
a = b + c;
d = b + c;
e = b + c;
```
Для оптимизации локальных общих выражений компилятор проверяет короткие разделы кода на наличие общих вложенных выражений. Для глобальной оптимизации общих выражений компилятор выполняет поиск общих вложенных выражений во всех функциях.
Автоматическое выделение регистров
Такая оптимизация позволяет компилятору хранить часто используемые переменные и вложенные выражения в регистрах. Ключевое register слово игнорируется по умолчанию и вызывает диагностику в или /std:c++17 более поздней версии.
Оптимизация цикла
Эта оптимизация удаляет инвариантные вложенные выражения из тела цикла. Оптимальный цикл содержит только выражения, значения которых изменяются при каждом выполнении цикла. В следующем примере выражение x + y не изменяется в тексте цикла:
```
i = -100;
while( i < 0 ) {
    i += x + y;
}
```
После оптимизации вычисляется один раз, x + y а не каждый раз при выполнении цикла:
```
i = -100;
t = x + y;
while( i < 0 ) {
    i += t;
}
```
Оптимизация цикла гораздо эффективнее, если компилятор не может предполагать псевдонимы, заданные с __restrictпомощью , noaliasили restrict.
Примечание
Вы можете включить или отключить глобальную оптимизацию на основе функции с помощью optimize прагмы вместе с параметром g .

Дополнительные сведения см. в разделах/Oi (Создание встроенных функций) и /Ox (Включение большинства оптимизаций скорости).

Установка данного параметра компилятора в среде разработки Visual Studio

Откройте диалоговое окно Страницы свойств проекта. Подробнее см. в статье Настройка компилятора C++ и свойства сборки в Visual Studio.
Выберите страницу свойствC/C++>Command Lineсвойства> конфигурации.
Введите параметр компилятора в поле Дополнительные параметры .

Установка данного параметра компилятора программным способом

См. раздел AdditionalOptions.

См. также

Синтаксис командной строки компилятора MSVC

Типы задач оптимизации — Руководство по NEOS

svg»/>

Как отмечалось во Введении в оптимизацию, важным шагом в процессе оптимизации является классификация вашей модели оптимизации, поскольку алгоритмы решения задач оптимизации адаптированы к конкретному типу задач. Здесь мы даем некоторые рекомендации, которые помогут вам классифицировать вашу модель оптимизации; для различных типов задач оптимизации мы предоставляем связанную страницу с некоторой базовой информацией, ссылками на алгоритмы и программное обеспечение, а также онлайн и печатные ресурсы.

Выпуклая оптимизация по сравнению с Невыпуклая оптимизация
Непрерывная оптимизация по сравнению с Дискретная оптимизация
Некоторые модели имеют смысл, только если переменные принимают значения из дискретного набора, часто из подмножества целых чисел, тогда как другие модели содержат переменные, которые могут принимать любые действительные значения . Модели с дискретными переменными дискретная оптимизация проблемы; модели с непрерывными переменными — это задач непрерывной оптимизации . Задачи непрерывной оптимизации, как правило, легче решить, чем задачи дискретной оптимизации; гладкость функций означает, что значения целевой функции и функции ограничения в точке \(x\) могут быть использованы для получения информации о точках в окрестности \(x\). Однако усовершенствования алгоритмов в сочетании с достижениями в вычислительной технике резко увеличили размер и сложность задач дискретной оптимизации, которые можно эффективно решить. Алгоритмы непрерывной оптимизации важны в дискретной оптимизации, потому что многие алгоритмы дискретной оптимизации генерируют последовательность непрерывных подзадач.
Неограниченная оптимизация по сравнению с Ограниченная оптимизация
Другое важное различие заключается между задачами, в которых нет ограничений на переменные, и задачами, в которых есть ограничений на переменные. Неограниченная оптимизация проблемы возникают непосредственно во многих практических приложениях; они также возникают при переформулировке задач оптимизации с ограничениями , в которых ограничения заменяются штрафным членом в целевой функции. Оптимизация с ограничениями проблемы возникают из-за приложений, в которых существуют явные ограничения на переменные. Ограничения на переменные могут широко варьироваться от простых границ до систем равенств и неравенств, которые моделируют сложные отношения между переменными. Задачи оптимизации с ограничениями можно дополнительно классифицировать в соответствии с характером ограничений (например, линейные, нелинейные, выпуклые) и гладкостью функций (например, дифференцируемые или недифференцируемые).
Детерминированная оптимизация по сравнению с Стохастическая оптимизация
В детерминированной оптимизации предполагается, что данные для данной задачи известны точно. Однако для многих актуальных задач данные не могут быть точно известны по целому ряду причин. Первая причина связана с простой ошибкой измерения. Вторая и более фундаментальная причина заключается в том, что некоторые данные представляют собой информацию о будущем (например, спрос на продукт или цену за будущий период времени) и просто не могут быть известны с уверенностью. В оптимизация в условиях неопределенности или стохастическая оптимизация неопределенность включается в модель. Методы надежной оптимизации можно использовать, когда параметры известны только в определенных пределах; цель состоит в том, чтобы найти решение, приемлемое для всех данных и оптимальное в некотором смысле. Модели стохастической оптимизации используют тот факт, что распределения вероятностей, управляющие данными, известны или могут быть оценены; цель состоит в том, чтобы найти некоторую политику, применимую для всех (или почти всех) возможных экземпляров данных и оптимизирующую ожидаемую производительность модели.

Непрерывная оптимизация

В непрерывной оптимизации переменные в модели могут принимать любое значение в пределах диапазона значений, обычно действительных чисел. Это свойство переменных отличается от дискретной оптимизации , в которой некоторые или все переменные могут быть двоичными (ограниченными значениями 0 и 1), целыми (для которых разрешены только целочисленные значения) или более абстрактными объектами. взяты из множеств с конечным числом элементов.

В непрерывной оптимизации существует важное различие между задачами, в которых нет ограничений на переменные, и задачами, в которых есть ограничения на переменные. Оптимизация без ограничений проблемы возникают непосредственно во многих практических приложениях; они также возникают при переформулировке задач оптимизации с ограничениями , в которых ограничения заменяются штрафным членом в целевой функции. Оптимизация с ограничениями Проблемы возникают из-за приложений, в которых есть явные ограничения на переменные. Существует множество подполей условной оптимизации, для которых доступны специальные алгоритмы.

Дискретная оптимизация

При дискретной оптимизации некоторые или все переменные в модели должны принадлежать дискретному набору; это отличается от непрерывной оптимизации, при которой переменным разрешается принимать любое значение в пределах диапазона значений. Здесь мы рассматриваем две ветви дискретной оптимизации. В целочисленном программировании дискретное множество является подмножеством целых чисел. В комбинаторной оптимизации дискретный набор представляет собой набор объектов или комбинаторных структур, таких как назначения, комбинации, маршруты, расписания или последовательности. 9n \rightarrow \mathcal{R}\) — гладкая функция. Тогда задача неограниченной оптимизации имеет вид \[\mbox{min}_x \; е(х).\]

Проблемы оптимизации без ограничений возникают непосредственно в некоторых приложениях, но они также возникают косвенно при переформулировании задач оптимизации с ограничениями. Часто целесообразно заменить ограничения задачи оптимизации штрафными членами целевой функции и решить задачу как задачу без ограничений.

Ограниченная оптимизация

Задачи оптимизации с ограничениями Рассматривают задачу оптимизации целевой функции с учетом ограничений на переменные. В общих чертах,
\[ \begin{array}{lllll}
\mbox{минимизация} & f(x) & & & \\
\mbox{при условии} & c_i(x) & = & 0 & \forall i \in \mathcal{E} \\
& c_i(x) & \leq & 0 & \forall i \in \mathcal{I}
\end{массив}
\]
где \(f\) и функции \(c_i(x) \,\) являются гладкими вещественными функциями на подмножестве \(R^n \,\) и \(\mathcal{E}\) и \(\mathcal{I}\) — наборы индексов для ограничений равенства и неравенства соответственно. допустимое множество — это множество точек \(x\), которые удовлетворяют ограничениям.

Оптимизация в условиях неопределенности

Типы задач оптимизации, описанные в разделах «Непрерывная оптимизация» и «Дискретная оптимизация», неявно предполагают, что данные для данной задачи известны точно. Однако для многих реальных задач данные о задаче не могут быть точно известны по целому ряду причин. Первая причина связана с простой ошибкой измерения. Вторая и более фундаментальная причина заключается в том, что некоторые данные представляют собой информацию о будущем (например, спрос на продукт или цену за будущий период времени) и просто не могут быть известны с уверенностью.

Стохастическое программирование и Надежная оптимизация являются наиболее популярными платформами для явного учета неопределенности. Стохастическое программирование использует случайные величины с заданными распределениями вероятностей для характеристики неопределенности и оптимизирует ожидаемое значение целевой функции. Надежная оптимизация использует принадлежность множества для характеристики неопределенности и оптимизирует наихудший возможный случай проблемы.

Типы задач и методы оптимизации

Проблемы оптимизации

Непрерывная оптимизация и дискретная оптимизация
Неограниченная оптимизация по сравнению с ограниченной оптимизацией
Нет, одна или несколько целей
Детерминированная оптимизация по сравнению со стохастической оптимизацией
- Линейное программирование
- Квадратичное программирование

Линейное программирование
Квадратичное программирование

При обсуждении направления математики и компьютерных наук проблемы оптимизации относятся к поиску наиболее подходящего решения из всех возможных решений.

Задачу оптимизации можно определить как вычислительную ситуацию, целью которой является поиск наилучшего из всех возможных решений.

Использование оптимизации для решения проектных задач позволяет получить уникальное представление о ситуации. Модель может сравнивать текущий дизайн с лучшим из возможных и включает информацию об ограничениях и подразумеваемых затратах произвольных правил и политических решений. Хорошо разработанная оптимизационная модель также может помочь в анализе «что, если», показывая, где можно сделать улучшения, а где, возможно, придется пойти на компромиссы. Применение оптимизации к инженерным задачам охватывает несколько дисциплин.

Оптимизация делится на разные категории. Первый — это статистический метод, а второй — вероятностный метод. Математический алгоритм используется для оценки набора моделей данных и выбора наилучшего решения. Область проблемы определяется ограничениями, такими как диапазон возможных значений функции. Чтобы найти оптимальное решение, необходимо выполнить оценку функции. Оптимальные решения будут иметь минимальную ошибку, поэтому минимальная ошибка равна нулю.

Существуют различные типы задач оптимизации. Несколько простых не требуют формальной оптимизации, например задачи с очевидными ответами или без переменных решения. Но в большинстве случаев необходимо математическое решение, и целью является достижение оптимальных результатов. Большинство проблем требуют некоторой оптимизации. Цель состоит в том, чтобы уменьшить стоимость проблемы и минимизировать риск. Он также может быть многоцелевым и включать несколько решений.

Есть три основных элемента для решения задачи оптимизации: цель, переменные и ограничения. Каждая переменная может иметь разные значения, и цель состоит в том, чтобы найти оптимальное значение для каждого из них. Цель – это желаемый результат или цель проблемы.

Давайте рассмотрим различные задачи оптимизации в зависимости от различных элементов.

Непрерывная оптимизация по сравнению с дискретной оптимизацией

Модели с дискретными переменными — это задачи дискретной оптимизации, а модели с непрерывными переменными — задачи непрерывной оптимизации. Задачи постоянной оптимизации решить легче, чем задачи дискретной оптимизации. Задача дискретной оптимизации направлена на поиск объекта, такого как целое число, перестановка или граф, из счетного множества. Однако с улучшением алгоритмов в сочетании с достижениями в области вычислительной техники увеличился размер и сложность задач дискретной оптимизации, которые могут быть эффективно решены. Следует отметить, что алгоритмы непрерывной оптимизации необходимы для дискретной оптимизации, поскольку многие алгоритмы дискретной оптимизации генерируют ряд непрерывных подзадач.

Неограниченная оптимизация по сравнению с ограниченной оптимизацией

Существенное различие между задачами оптимизации заключается в том, что задачи имеют ограничения на переменные и задачи, в которых есть ограничения на переменные. Проблемы неограниченной оптимизации возникают в основном во многих практических приложениях и при переформулировке задач условной оптимизации. Проблемы с оптимизацией с ограничениями возникают в приложениях с явными ограничениями на переменные. Задачи оптимизации с ограничениями далее делятся в зависимости от характера ограничений, таких как линейные, нелинейные, выпуклые и функциональная гладкость, например, дифференцируемые или недифференцируемые.

Нет, одна или несколько целей

Хотя большинство задач оптимизации имеют одну целевую функцию, были особые случаи, когда задачи оптимизации либо не имели целевой функции, либо имели несколько целевых функций. Проблемы многокритериальной оптимизации возникают в инженерных, экономических и логистических потоках. Часто задачи с несколькими целями переформулируют как задачи с одной целью.

Детерминированная оптимизация по сравнению со стохастической оптимизацией

Детерминированная оптимизация — это когда данные для данной задачи известны точно. Но иногда данные не могут быть точно известны по разным причинам. Причиной этого может быть простая ошибка измерения. Другая причина заключается в том, что некоторые данные описывают информацию о будущем и, следовательно, не могут быть известны с уверенностью. В оптимизации в условиях неопределенности это называется стохастической оптимизацией, когда неопределенность включается в модель.

Проблемы оптимизации делятся на два типа:

Линейное программирование:

В задачах линейного программирования (ЛП) цель и все ограничения являются линейными функциями переменных решения. Поскольку все линейные функции выпуклы, решение задач линейного программирования изначально проще, чем нелинейных задач.

Квадратичное программирование:

В задаче квадратичного программирования (QP) цель является квадратичной функцией переменных решения, а все ограничения являются линейными функциями переменных. Широко используемая задача квадратичного программирования — это задача Марковица средней дисперсии оптимизации портфеля. Целью является дисперсия портфеля, а линейные ограничения определяют нижнюю границу доходности портфеля.

Мы все придерживаемся оптимизации, так как это образ жизни. Мы все хотим максимально использовать свое свободное время и сделать его продуктивным. Оптимизация находит свое применение от использования времени до решения проблем цепочки поставок. Ранее мы узнали, что под оптимизацией понимается поиск наилучших возможных решений из всех возможных решений. Оптимизацию можно разделить на Линейное программирование и Квадратичное программирование . Давайте пройдёмся.

Линейное программирование

Линейное программирование — это простой метод поиска наилучшего результата или оптимальных точек из сложных отношений, отображаемых с помощью линейных отношений. Реальные отношения могут быть намного сложнее, но их можно упростить до линейных отношений.
Линейное программирование широко используется в оптимизации по нескольким причинам, которые могут быть:

При исследовании операций сложные задачи реальной жизни могут быть выражены в виде задач линейного программирования.
Многие алгоритмы в конкретных задачах оптимизации работают, решая задачи линейного программирования как подзадачи.
Многие ключевые концепции теории оптимизации, такие как двойственность, декомпозиция, выпуклость и обобщения выпуклости, были вдохновлены или получены из идей линейного программирования.
Раннее формирование микроэкономики свидетельствует об использовании линейного программирования, и оно до сих пор используется в отделах планирования, производства, транспорта, технологий и т. д.

Квадратичное программирование

Квадратичное программирование — это метод решения конкретной задачи оптимизации, при котором оптимизируется (минимизируется или максимизируется) квадратичная целевая функция с одним или несколькими линейными ограничениями. Иногда квадратичное программирование можно назвать нелинейным программированием. Целевая функция в QP может содержать билинейные или полиномиальные члены вплоть до второго порядка. Ограничения обычно линейны и могут быть как равенствами, так и неравенствами. Квадратичное программирование широко используется в оптимизации. Причины:

Обработка изображений и сигналов
Оптимизация финансовых портфелей
Выполнение метода наименьших квадратов регрессии
Управление планированием на химических предприятиях
Решение более сложных задач нелинейного программирования
Использование в исследованиях операций и статистической работе

Существует много типов математических и вычислительных методов оптимизации. Важным шагом в методе оптимизации является категоризация модели оптимизации, поскольку алгоритмы, используемые для решения задач оптимизации, настраиваются в соответствии с характером проблемы.

Целочисленное программирование, например, является формой математического программирования. Эта техника восходит к Архимеду, который впервые описал проблему определения состава стада крупного рогатого скота. Достижения в области вычислительных кодов и теоретических исследований привели к его формальному развитию. Ниже перечислены некоторые примеры задач, которые можно решить с помощью целочисленного программирования.

Генетические алгоритмы (GAN) — еще один математический и вычислительный метод оптимизации. Эти алгоритмы используют одни и те же математические принципы для оптимизации сложных систем. Основной принцип ГА — минимизировать линейную целевую функцию при минимальных затратах. Этот тип алгоритма также основан на удовлетворении ограничений линейного неравенства. С другой стороны, нелинейные алгоритмы используют действительные числа и нелинейные функции. Эти алгоритмы часто более сложны, чем самая простая версия.

Различные формы генетических алгоритмов широко используются для расчета оптимального решения задачи. Генетические алгоритмы, например, широко использовались на протяжении десятилетий. Генетические алгоритмы (GCR), генетические алгоритмы (GMO) и оптимизация с ограничениями (LP) являются двумя наиболее часто используемыми методами. Генетические алгоритмы также произвели революцию в том, как алгоритмы решают задачи оптимизации. Они могут помочь в максимизации доходности данного продукта или услуги.

Термин оптимизация является синонимом компьютерного программирования. Область сочетает в себе изучение математической структуры задач оптимизации, изобретение методов их решения и реализацию на компьютерах. Сложность и размер задач оптимизации увеличились с развитием более быстрых компьютеров. В результате развитие этих методов шло по аналогичной схеме. Это особенно верно в отношении генетических алгоритмов, которые имеют несколько применений в биологических и химических исследованиях.

Источники
Ядав, доктор Ракхи; Камбл, мистер Сандип; Рао, доктор Д.С.; Сарадха, доктор Р.; Анусаркар, мисс Гаури. «Интеллектуальный анализ данных и бизнес-аналитика». му.ак.в. https://mu.ac.in/wp-content/uploads/2022/05/MCA-Data-Mining-and-Business-Intelligence-2.pdf (по состоянию на 4 июня 2022 г.).

Подробнее

алгоритмы
оптимизация
проблемы оптимизации

Пред.