«ОПТИМИЗАЦИОННЫЕ ЗАДАЧИ В ЭЛЕКТРОЭНЕРГЕТИКЕ». Задачи оптимизации в электроэнергетике
Оптимизационные задачи электроэнергетики
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ ЗАОЧНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ЭЛЕКТРОСНАБЖЕНИЯ
Отчет по практическому занятию
Студенты :
Специальность: 140211
Курс: 5
Шифр: вариант 9
Дата выдачи: 03.11.2011
Работу принял:
Преподаватель: Стрижова Т.А.
Санкт - Петербург
2011 год
Практическое занятие №1
Решение линейных оптимизационных задач.
Цель работы: Закрепление теоретического материала по математической формализации оптимизационных задач. Решение на персональном компьютере линейной задачи оптимального распределения ресурсов.
Задача.
Предприятие планирует выпускать продукцию, включающую три вида изделий (i = 1, 2, 3). Для изготовления каждого i-го изделия требуются три вида ресурсов: энергетические, финансовые и сырьевые (j = 1, 2, 3).
Наличие на предприятии каждого j-го ресурса ограничено величиной bj; норма расхода j-го ресурса на одно i-е изделие составляет aji; прибыль от реализации одного i-го изделия составляет zi.
Требуется определить, при каком количестве изделий каждого вида прибыль будет максимальной?
Исходные данные:
b1 =80
b2 =100
b3 =120
a11 =3
a12 =3,5
a13 =2,5
a21 =4
a22 =5
a23 =3,5
a31 =3,5
a32 =4
a33 =3
z1 =6
z2 =7
z3 =5
Математическая модель задачи:
Поскольку необходимо найти максимальную прибыль предприятия, используем экономический критерий и выражаем его целевой функцией. Прибыль от реализации изделий i-го вида есть произведение zixi.
Подлежащая максимизации суммарная прибыль от реализации трех видов изделий будет иметь вид (целевая функция):
Z=z1x1+z2x2+z3x3→max (1.1)
Составим ограничения.
На одно изделие i-го вида требуется а1i единиц энергии, на искомое количество xi потребуется a1ixiединиц энергии. Суммарный расход энергии на выпуск трех видов изделий составит a11x1+a12x2+a13x3 единиц энергии. Эта величина ограничена наличием на предприятии энергетических ресурсов в количестве b1. Ограничение по энергетическим ресурсам будет иметь вид: a11x1+a12x2+a13x3 ≤ b1
Аналогично составляем ограничениям по финансовым и сырьевым ресурсам :
a21x2+a22x2+a23x3 ≤ b2
a31x1+a32x2+a33x3 ≤ b3
Ограничение минимально суммарного количества выпускаемых изделий записываем в виде: x1+x2+x3 ≤ b4
В итоге вся система ограничений будет иметь вид:
a11x1+a12x2+a13x3 ≤ b1
a21x2+a22x2+a23x3 ≤ b2 (1.2)
a31x1+a32x2+a33x3 ≤ b3
x1+x2+x3 ≤ b4
Количество изделий любого вида не может быть отрицательным числом, граничными условиями будут неотрицательные значения искомых переменных
xi ≥ 0, i = 1,2,3 (1.3)
Выражения (1.1), (1.2) и (1.3) представляют собой математическую модель поставленной оптимизационной задачи.
Результат решения задачи на ПК
Формульное представление Таблица 1.1
| A | B | C | D | E | F | G | H | I | ||
| 1 | Исходные данные: | Переменные: | ||||||||
| 2 | Прибыль | Z1= | 6 | х1= | 0 | |||||
| 3 | Z2= | 7 | х2= | 0 | ||||||
| 4 | Z3= | 5 | х3= | 0 | ||||||
| 5 | Ресурсы: | |||||||||
| 6 | по энергии = | 80 | Целевая функция | Z= | =B2*h3+B3*h4+B4*h5 | |||||
| 7 | по финансам = | 100 | ||||||||
| 8 | по сырью = | 120 | ||||||||
| 9 | Нормы расхода: | |||||||||
| 10 | по энергии | а11= | 3 | а12= | 3,5 | а13= | 2,5 | |||
| 11 | по финансам | а21= | 4 | а22= | 5 | а23= | 3,5 | |||
| 12 | по сырью | а31= | 3,5 | а32= | 4 | а33= | 3 | |||
| 13 | ||||||||||
| 14 | Левые части ограничений: | |||||||||
| 15 | а11х1+а12х2+а13х3= | =B10*h3+D10*h4+F10*h5 | ||||||||
| 16 | а21х1+а22х2+а23х3= | = B11*h3+D11*h4+F11*h5 | ||||||||
| 17 | а31х1+а32х2+а33х3= | = B12*h3+D12*h4+F12*h5 | ||||||||
Числовое представление Таблица 1.2
| A | B | C | D | E | F | G | H | I | J | |
| 1 | Исходные данные: | Переменные: | ||||||||
| 2 | Прибыль | Z1= | 6 | х1= | 25 | |||||
| 3 | Z2= | 7 | х2= | 0 | ||||||
| 4 | Z3= | 5 | х3= | 0 | ||||||
| 5 | Ресурсы: | |||||||||
| 6 | по энергии = | 80 | Целевая функция: | Z= | 150 | |||||
| 7 | по финансам = | 100 | ||||||||
| 8 | по сырью = | 120 | ||||||||
| 9 | Нормы расхода: | |||||||||
| 10 | рпо энергии | а11= | 3 | а12= | 3,5 | а13= | 2,5 | |||
| 11 | по финансам | а21= | 4 | а22= | 5 | а23= | 3,5 | |||
| 12 | по сырью | а31= | 3,5 | а32= | 4 | а33= | 3 | |||
| 13 | ||||||||||
| | Левые части ограничений: | |||||||||
| 15 | а11х1+а12х2+а13х3= | 75 | ||||||||
| 16 | а21х1+а22х2+а23х3= | 100 | ||||||||
| 17 | а31х1+а32х2+а33х3= | 88 | ||||||||
Практическое занятие №2
studfiles.net
Оптимизационные задачи электроэнергетики
В. Н. Костин.: Оптимизационные задачи электроэнергетики: Учеб. пособие. -СПб.: СЗТУ, 2003 — 120 с.
Учебное пособие соответствует государственным образовательным стандартам высшего профессионального образования по направлению подготовки дипломированных специалистов 650900 — «Электроэнергетика» (специальность 100400 — Электроснабжение) и направлению подготовки бакалавров 551700 — «Электроэнергетика».
ОглавлениеПредисловие1. Основные понятия и определения1.1. Исходная информация1.2. Математическая модель1.3. Методы решения оптимизационных задач1.4. Выполнение вычислений1.5. Анализ оптимизационной задачи2. Линейные оптимизационные задачи2.1. Графическое решение задачи линейного программирования2.2. Алгебраические преобразования систем линейных уравнений2.3. Симплекс-метод3. Транспортные задачи электроэнергетики3.1. Постановка транспортной задачи3.2. Получение доступного решения3.3. Распределительный метод3.4. Метод потенциалов3.5. Учет пропускной способности линий3.6. Транспортная задача с транзитом мощности4. Нелинейные оптимизационные задачи4.1. Общие положения4.2. Графическая иллюстрация задачи нелинейного программирования4.3. Градиентные методы4.4. Метод неопределенных множителей Лагранжа4.5. Задача оптимального распределения активной мощности в энергосистеме4.6. Задачи оптимального распределения компенсирующих устройств в системах электроснабжения5. Оптимизационные задачи с целочисленными и дискретными переменными5.1. Задачи с целочисленными переменными5.2. Двоичные переменные5.3. Задачи с дискретными переменными6. Оптимизационные задачи при случайной исходной информации6.1. Основные понятия6.2. Математические модели стохастических задач6.3. Детерминированный эквивалент стохасгической задачи7. Оптимизационных задачи при недетерминированной исходной информации8. Многокритериальные оптимизационные задачи8.1. Определение коэффициентов веса каждого критерия8.2. Оптимизация с помощью обобщенной целевой функцииБиблиографический списокПриложенииП.1. Общие сведения об ExcelП.2. Решение задач линейного программированияП.З. Решение задач целочисленного программированияП.4. Решение задач нелинейного программированияП.5. Решение задач дискретного программированияП.6. Решение многокритериальных задачПредметный указатель
Скачать учебное пособие «Оптимизационные задачи электроэнергетики»
electrichelp.ru
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ В ЭЛЕКТРОЭНЕРГЕТИКЕ — Мегаобучалка
2.1. Введение в теорию оптимизации
Производство и распределение электрической энергии связано с большими затратами материальных средств и топлива. Необходимо их экономить за счет выбора оптимальных мест размещения электрических станций, конфигурации электрических сетей, режимов работы оборудования и т.д. Поэтому постановка и решение оптимизационных задач в деятельности инженера-электрика занимает значительное место. Важно получить хорошее представление о математическом моделировании. Полезно обстоятельно познакомиться с постановкой общей задачи программирования, как оптимизационной задачи с ограничениями.
На примере общей задачи программирования необходимо усвоить основную терминологию, а также понятия о целевой функции и критерии оптимальности, балансовых и граничных ограничениях; классификацию оптимизационных задач и методы их решения. Понимания методов классической оптимизации можно добиться при внимательном изучении постановки ряда задач на оптимизацию распределения электрических нагрузок в электрической системе и решения их методом Лагранжа.
Контрольные вопросы.
1. Что такое математическое программирование?
2. Что такое математическое моделирование?
3. Что такое целевая функция и какие критерии оптимальности используются в энергетике?
4. Что такое экстремум или оптимум функции? Понятие глобального или абсолютного и условного или относительного оптимума.
5. Напишите в общем виде функцию Лагранжа.
-8-
В условии задачи указывается литература, которую рекомендуется использовать для изучения методов их решения.
Задача 1. Вычислить определитель квадратной матрицы третьего порядка (табл.1) двумя способами: классическим и разложением по элементам строки или столбца [2].
Задача 2. Обратить классическим способом квадратную матрицу третьего порядка (табл.1) [2].
Задача 3.Для графа сети (табл.2) составить матрицы, входящие в уравнения законов Ома и Кирхгофа [1,3].
Задача 4. Для графа сети (табл.2) составить матрицы, входящие в выражения:
(1)
(2)
для определения токов в ветвях методом узловых напряжений [1,3].
Задача 5. Рассчитать потоки активной мощности в электрической сети (рис.1) методом узловых напряжений.
Указание. Расчеты выполнять приближенно, используя идею “расщепления схемы” [3], согласно которой потоки активной мощности можно распределять по реактивным сопротивлениям. Для этого в формулах (1) – (2) заменить комплексные сопротивления и проводимости на реактивные сопротивления и проводимости, комплексные токи – на активные мощности. Исходные данные задаются в табл.3.
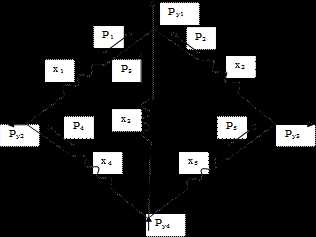
Рис. 1 X – схема электрической сети к задаче 5
Задача 6. Решить СЛУ третьего порядка (табл.4) методом обратной матрицы [2].
Задача 7. Решить СЛУ третьего порядка (табл.4) методом Гаусса. Вычисления выполнять в матричной форме [2].
-13-
При сглаживании экспериментальных зависимостей самых распространенным является метод наименьших квадратов, который следует изучить.
Особое внимание необходимо уделить методу статических испытаний (методу Монте-Карло).
Контрольные вопросы.
1. Какие основные задачи решает математическая статистика?
2. Что такое статистическая функция распределения и гистограмма?
3. Что такое критерий согласия и для чего он используется?
4. Дайте определение доверительной вероятности и доверительного интервала.
5. В чем сущность теорем Муавра-Лапласа и Бернулли?
6. Приведите выражения для определения статистических числовых характеристик случайных величин.
7. В чем сущность метода статистических испытаний (Монте-Карло) и какова область его применения?
КОНТРОЛЬНОЕ ЗАДАНИЕ
Контрольное задание служит для изучения и закрепления учебного материала по данному курсу.
Контрольное задание выполняется в тетради, на обложке которой указываются фамилия и инициалы студента, полный шифр и номер варианта.
Работа должна быть написана четко, без помарок и сокращений, с соблюдением полей. Решения всех задач и пояснения к ним должны быть достаточно подробными. При необходимости следует делать ссылки на источники, приведенные в списке использованной литературы. Буквенные обозначения в формулах, графические изображения в схемах должны соответствовать действующим ГОСТам.
После получения работы (как зачетной, так и не зачетной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан выполнить все требования рецензента и представить работу на повторное рецензирование, приложить при этом первоначально выполненную работу. Зачтенную работу студент обязан представить на экзамене.
Вариант задания определяется по двум последним цифрам номера зачетной книжки при числах от 01 до 20, при числах от 20 до 40 следует вычесть 20, при числах от 41 до 60 – число 40, при числах от 61 до 80 – число 60 и при числах от 81 до 100 – число 80. Например, следует выбрать 16 вариант.
6. Сущность прямых классических методов решения задач на относительный и абсолютный оптимум многих переменных.
7. Объясните физический смысл неопределенных множителей Лагранжа в задаче оптимального распределения мощностей в энергосистеме.
-12-
2.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
В задачах линейного программирования целевая функция и ограничения линейны. Оптимум в таких задачах определяется на выпуклом многограннике допустимых решений. На примере простейшей задачи распределения нагрузки между двумя тепловыми станциями полезно ознакомится с основной задачей ЛП, рассмотреть ее геометрическую интерпретацию. Важно усвоить наиболее строгий и универсальный симплекс-метод для решения задач ЛП.
Контрольные вопросы
1. Какие математические модели оптимизируются методами ЛП?
2. Сформулируйте основную задачу ЛП.
3. Дайте геометрическое представление области допустимых решений.
4. Как выбираются базисные переменные в симплекс-методе.
5. Алгоритм решения задачи ЛП симплекс-методом.
2.3. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Следует знать, что если хотя бы одна функция в математической модели является нелинейной, то задача относится к классу задач нелинейного программирования. В общем случае большинство задач электроэнергетики являются задачами НП. Простейшим случаем задач НП являются задачи выпуклого программирования с одним экстремумом для решения которых используется метод Лагранжа. Другим простым методом, применяемым при оптимизации режимов работы электрических систем, является градиентный метод. Важно также рассмотреть способы учета ограничений в виде равенств и неравенств при решении задач НП в электроэнергетике.
-9-
Контрольные вопросы
1. Понятие о нелинейном программировании методах решения задач НП.
2. Метод Лагранжа.
3. Понятие о градиентных методах поиска экстремума нелинейной целевой функции.
4. Метод наискорейшего спуска.
5. Метод приведенного градиента.
6. Учет ограничений в виде равенств и неравенств при решении оптимизационных задач.
megaobuchalka.ru
Задача - электроэнергетика - Большая Энциклопедия Нефти и Газа, статья, страница 1
Задача - электроэнергетика
Cтраница 1
Задача электроэнергетики состоит в том, чтобы, расширяя сферу электрификации, обеспечить максимальную механизацию и автоматизацию процессов производства и на этой основе достичь наивысшей производительности общественного труда. [1]
Большинство задач электроэнергетики являются квазистационарными; рассматриваемые в них расстояния малы по сравнению с длинами волн; так, запаздывание потенциалов при распространении магнитного поля внутри генератора или двигателя незначительно; практически электродинамические потенциалы в них не отличаются от статических потенциалов. Однако в теории длинных линий электропередачи, телеграфных и телефонных линий, в излучении и распространении радиоволн запаздывание потенциалов становится ощутительным и им пренебрегать нельзя. [2]
Следует отметить, что решение задач промышленной электроэнергетики может быть получено, как правило, несколькими техническими способами. Многовариантность задач оптимизации систем электроснабжения обусловливает проведение технико-экономических расчетов, целью которых является экономическое обоснование выбранного технического решения. [3]
Теория подобия и моделирование применительно к задачам электроэнергетики. [4]
Теория подобия и моделирования применительно к задачам электроэнергетики. [5]
Теория подобия и моделирование применительно к задачам электроэнергетики. [6]
Необходимо отметить, что решение целого ряда задач электроэнергетики может быть получено несколькими техническими способами. [7]
В е н и к о в В. А. Теория подобия и моделирования применительно к задачам электроэнергетики. [8]
Следует отметить, что с появлением ЦВМ основным методом решения многих задач, в том числе и задач электроэнергетики, стал численный метод. [9]
Интенсивное развитие электрификации бурения, добычи и транспорта нефти и газа в сложных геологических и природно-климатических условиях различных нефтегазодобывающих районов страны придает особую важность обоснованному решению таких задач промысловой электроэнергетики, как создание рациональных систем электроснабжения, разработка и внедрение энергосберегающей техники и технологии, правильный выбор типа и мощности электроприводов, разработка и внедрение в практику прогрессивных методов электропотребления и оценки эффективности мероприятий по сокращению непроизводительных энергетических затрат. [10]
Создание экономичных машин постоянного тока и начальные шаги в: развитии электрического освещения и электрического привода не могли бы внести кардинальных изменений в производственную практику, если, бы не была решена другая краеугольная задача электроэнергетики - передача электрической энергии на расстояние. [11]
При решении задач оптимизации промышленного электроснабжения возникает необходимость сравнения большого количества вариантов. Многовариантность задач промышленной электроэнергетики обусловливает проведение технико-экономических расчетов, целью которых является экономическое обоснование выбранного технического решения. Важность этого положения обосновывается тем, что более одной трети всех суммарных капиталовложений в стране расходуется на добычу, переработку, транспортировку и хранение энергетических ресурсов и генерирование, передачу, распределение и потребление всех видов энергии в народном хозяйстве. [12]
Теория подобия и моделирования применительно к задачам электроэнергетики. [13]
Упомянутые два подхода отвечают двум рассматриваемым в механике случаям устойчивости движения: устойчивости относительно координаты и устойчивости относительно траектории. Поиски его практических ( инженерных) применений служат предметом большого количества исследовательских работ, направленных на такую модификацию метода, при которой он будет отвечать задачам электроэнергетики. Современные расчеты устойчивости и переходных процессов проводятся преимущественно на цифровых вычислительных машинах ( ЦВМ) с помощью типовых алгоритмов, проходящих перед их массовым использованием специальную апробацию. Здесь применяются также расчетные модели и аналоговые машины. [14]
Одно из развивающихся направлений в исследовании устойчивости электрических систем - это проведение расчетов в процессе текущей эксплуатации, когда исходные данные получаются от работающей системы, а результаты расчетов выдаются непосредственно персоналу системы или управляющим устройствам. Таким образом, неотложными задачами электроэнергетики являются проведение расчетов установившихся режимов систем, нахождение распределения в них потоков мощностей, токов и напряжений. Для решения этих задач применяются матричные записи уравнений с использованием теории графов и элементов топологии. Установившиеся режимы рассчитываются как при детерминированных, так и при вероятностных условиях. Причем для расчета при вероятностных условиях требуется учет возможного появления случайных величин и случайных событий, для характеристики которых можно использовать стохастически заданную информацию, а иногда только неполную информацию. Еще одна задача электроэнергетики - это рассмотрение переходных режимов и анализ работы регулирующих устройств, для решения ее требуется также применение различных методов исследования дифференциальных уравнений. [15]
Страницы: 1
www.ngpedia.ru
«ОПТИМИЗАЦИОННЫЕ ЗАДАЧИ В ЭЛЕКТРОЭНЕРГЕТИКЕ» - PDF
ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ
Подробнее1. Цели и задачи дисциплины
1. Цели и задачи дисциплины Целью дисциплины является овладение знаниями в области исследования операций, что необходимо для профессиональной деятельности бакалавров и формирования у студентов самостоятельного
ПодробнееПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ
ПодробнееПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Подробнее«ОБЩАЯ ЭЛЕКТРОТЕХНИКА И РАДИОЭЛЕКТРОНИКА»
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ
ПодробнееСОЦИАЛЬНЫЕ ПРОЦЕССЫ И СИСТЕМЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО «Брянский государственный технический университет» Факультет информационных технологий Кафедра «Высшая математика» «УТВЕРЖДАЮ» Первый проректор по учебной
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Подробнее1. ЦЕЛИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
QD-6.2.2/РПД-50.(53.88) Выпуск: 14.01.2016 Версия: Стр. 2/13 1. ЦЕЛИ ОСВОЕНИЯ ДИСЦИПЛИНЫ Целью освоения дисциплины «Методы Принятия управленческих решений» является формирование теоретических знаний о
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееШифр направления
2 1 Цели и задачи дисциплины Целью изучения дисциплины «Оптимизация и принятие решений в технических системах» является формирование представлений о теоретических и алгоритмических основах классических
ПодробнееПрикладная математика
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ»
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Подробнее1. Цели и задачи дисциплины
1. Цели и задачи дисциплины Основной целью дисциплины «Методы принятия управленческих решений» является формирование у бакалавров теоретической базы по современным методам и способам принятия управленческих
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееМЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (Финансовый университет) Кафедра «Прикладная
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ПодробнееОПД.В1.1 Теория принятия решений
Автономная некоммерческая организация высшего профессионального образования «СМОЛЬНЫЙ ИНСТИТУТ РОССИЙСКОЙ АКАДЕМИИ ОБРАЗОВАНИЯ» Факультет информационных технологий Кафедра информационных систем УТВЕРЖДАЮ
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Подробнееdocplayer.ru
Оптимизационные задачи в электроэнергетике
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра электроснабжения промышленных предприятий
ОТЧЕТ ПО ПРОИЗВОДСТВЕННОЙ ПРАКТИКЕ
На тему: «Оптимизационные задачи в электроэнергетике»
Специальность 6М071800 Электроэнергетика
Выполнил К.А. Асылкожанов Группа МЭЭп 10 №104М006
Принял В.Б. Фадеев « »____________2011 г.
Алматы 2011
Содержание
Введение………………………………………………………………… | 3 | |
1 | Понятие линейного программирования………………………………. | 5 |
2 | Теоретическое описание решения оптимизационной задачи при помощи пакетов прикладных программ……………………………… |
8 |
3 | Пример решения задачи при помощи программного обеспечения… | 11 |
4 | Анализ полученного решения…………………………………………. | 21 |
5 | Задачи, решаемые в работе……………………………………………. | 32 |
Список литературы…………………………………………………….. | 33 |
Введение
В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности.
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
количество продукции - расход сырья
количество продукции - качество продукции
Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.
Типичный пример неправильной постановки задачи оптимизации:
«Получить максимальную производительность при минимальной себестоимости».
Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая: а) получить максимальную производительность при заданной себестоимости; б) получить минимальную себестоимость при заданной производительности;
В первом случае критерий оптимизации – производительность, а во втором- себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой - критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
В зависимости от своей постановки, любая из задач оптимизации может решаться различными методами, и наоборот – любой метод может применяться для решения многих задач. Методы оптимизации могут быть скалярными (оптимизация проводится по одному критерию), векторными (оптимизация проводится по многим критериям), поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.), вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.), теоретико-вероятностными, теоретико-игровыми и др. Подвергаться оптимизации могут задачи как с ограничениями, так и без них.
1.Понятие линейного программирования
Линейное программирование - один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование». Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и др. задач. Термин «линейное программирование» возник в результате неточного перевода английского «linear programming». Одно из значений слова «programming» - составление планов, планирование. Следовательно, правильным переводом «linear programming» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины.
Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми.
Итак, линейное программирование возникло после Второй Мировой Войны и стал быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а так же математической «стройности».
Можно сказать, что линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.
Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: рационального использования сырья и материалов; задачи оптимизации раскроя;
оптимизации производственной программы предприятий; оптимального размещения и концентрации производства; составления оптимального плана перевозок, работы транспорта; управления производственными запасами; и многие другие, принадлежащие сфере оптимального планирования.
Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.
Первые постановки задач линейного программирования были сформулированы известным советским математиком Л.В.Канторовичем, которому за эти работы была присуждена Нобелевская премия по экономике.
Значительное развитие теория и алгоритмический аппарат линейного программирования получили с изобретением и распространением ЭВМ и формулировкой американским математиком Дж. Данцингом симплекс-метода.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов.
В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области математического программирования. Линейное программирование тесно связано с другими методами математического программирования (например, нелинейного программирования, где целевая функция нелинейна).
Задачи с нелинейной целевой функцией и линейными ограничениями называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Если целевая функция Е - квадратичная функция, то мы имеем дело с задачей квадратичного программирования; если Е – это отношение линейных функций, то соответствующая задача носит название задачи дробно-линейного программирования, и т.д. Деление оптимизационных задач на эти классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.
Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы.
Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.
Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.
Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде в свою очередь также состоит из трех элементов:
управляемых переменных; неуправляемых переменных; формы функции (вида зависимости между ними).
Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.
Если система ограничений несовместима, то область допустимых решений является пустой.
Оптимизационные задачи решаются методами математического программирования, которые подразделяются на:
линейное программирование; нелинейное программирование; динамическое программирование; целочисленное программирование; выпуклое программирование; исследование операций; геометрическое программирование и др.
Главная задача математического программирования – это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.
В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование». Слово линейное указывает на линейный характер зависимости, как в целевой функции, так и в системе ограничений. Следует еще раз подчеркнуть, что задача обязательно носит экстремальный характер, т.е. состоит в отыскании максимума или минимума (экстремума) целевой функции.
Сущность задач оптимизации: определить значение переменных х1, х2,..., хn, которые обеспечивают экстремум целевой функции Е, с учетом ограничений, наложенных на аргументы этой функции. При этом сложность решения задач зависит:
- от вида функциональных зависимостей, то есть от связи функции Е с элементами решения;
- от размерности задачи, то есть от количества элементов решения;
- от вида и количества ограничений, накладываемых на элементы решения.
Найти оптимальное решение для реальной задачи вручную, без применения компьютера, практически невозможно из-за очень большого объёма вычислений. Наличие компьютера является необходимым, но не достаточным условием нахождения оптимального решения. Для успешного решения необходимы три составляющие:
- математическая модель;
- компьютер с соответствующим программным обеспечением;
- достоверные исходные данные.
Итак, решению задачи оптимизации предшествует построение её математической модели, представляющей собой систему алгебраических уравнений.
stud24.ru
Оптимизационные задачи в электроэнергетике
Зона рассеяния центра электрических нагрузок промышленного предприятия представляет собой эллипс.
Образование зоны рассеяния ЦЭН предприятия. Зона рассеяния центра электрических нагрузок промышленного предприятия представляет собой эллипс. Форма эллипса зависит от соотношения величин hx и Нц. При hx hy эллипс превращается в круг. Для построения зоны рассеяния ЦЭН промышленного объекта достаточно осуществить параллельный перенос осей координат так, чтобы начало новой системы совпало с величинами математических ожиданий ах, ау. Из найденного выражения ( 19 - 58) определяются значения полуосей эллипса, совпадающих по направлению с осями новой системы координат, и строится зона рассеяния координат ЦЭН.
Зона рассеяния центра электрических нагрузок на территории промышленного предприятия. В общем случае центры электрических нагрузок цеха и всего предприятия постоянно находятся в движении, перемещаясь в пределах некоторой области, которая называется областью рассеяния центра электрических нагрузок цеха или соответственно предприятия.
Описанный метод отыскания центра электрических нагрузок ( ЦЭН) отличается простотой и наглядностью, он легко реализуется на ЭВМ. Погрешность расчетов по этому методу не превышает 5 - 10 % и определяется точностью исходных данных.
Описанный метод отыскания центра электрических нагрузок отличается простотой и наглядностью, он легко машинно реализуем. Погрешность расчетов по этому методу не превышает 5 - 10 % и определяется точностью исходных данных. ПС размещают вблизи центра электрических нагрузок, в непосредственной близости к подъездным дорогам с обеспечением удобных подходов ВЛ и КЛ; на незатопляемых местах с уровнем грунтовых вод ниже уровней заложения фундаментов. Подстанции располагают вблизи центра электрических нагрузок, что сокращает протяженность распределительных сетей, уменьшает потери электроэнергии и снижает капитальные затраты. ЦРП и РП размещают на границе питаемых ими участков, с учетом расположения цеховых ТП, таким образом, чтобы не было обратных потоков энергии. Эту точку называют центром электрических нагрузок ( ЦЭН) группы приемников. Данное понятие введено в теорию электроснабжения промышленных предприятий [18] по аналогии с понятием центра тяжести системы материальных точек. В связи с этим центр электрических нагрузок описывает во времени на генеральном плане промышленного предприятия фигуру сложной формы. Показатели разброса нагрузок и центр электрических нагрузок являются взаимосвязанными простейшими характеристиками распределения нагрузок группы приемников. В связи с этим центр электрических нагрузок описывает во времени на генеральном плане промышленного предприятия фигуру сложной формы. Электростанция предприятия помещена вне центра электрических нагрузок. Зона рассеяния центра электрических нагрузок на территории промышленного предприятия. Определение области рассеяния координат центра электрических нагрузок обычно не решает полностью вопроса о выборе местоположения ГПП или ГРП, так как территория предприятия достаточно плотно покрыта цехами, железными и автомобильными дорогами, проездами, проходами, различными сооружениями. Большая удаленность КЭС от центра электрических нагрузок по сравнению с ТЭЦ ведет при прочих равных условиях к повышению а. Увеличение затрат на тепловые сети по комбинированному варианту по сравнению с раздельным приводит к некоторому снижению ачопт. Таким образом, на эффективность теплофикации большое влияние оказывает учет географического размещения генерирующих установок относительно центров электро - и теплопотребления. Ниже приводится пример определения центра электрических нагрузок по первому методу.
Методика определения зоны рассеяния центра электрических нагрузок предприятия, изложенная в § 9 - 4, предполагает наличие сведений об электрических нагрузках цехов. Однако если принять электрические нагрузки цехов предприятия за величины, неизменные во времени, равные расчетным нагрузкам, и считать их, как это обычно делается, приложенными в одной точке - центре тяжести цеха - это повлечет за собой значительную ошибку при построении зоны рассеяния ЦЭН предприятия. Внутрицеховые подстанции размещают в центре электрических нагрузок, что позволяет сократить протяженность сетей напряжением до 1 кВ и уменьшить потери мощности и энергии в них.
Расположение питающих подстанций в соответствующих центрах электрических нагрузок обеспечивает минимальные годовые приведенные затраты. Всякое смещение питающей подстанции из центра электрических нагрузок ведет к увеличению этих затрат и повышенному расходу электроэнергии. Схема электроснабжения. Площадка подстанции должна размещаться вблизи центра электрических нагрузок, автомобильных дорог ( для трансформаторов мощностью 10 MB-А и выше) и существующих инженерных сетей. Учитывается также наличие подъездных железнодорожных путей промышленных предприятий.
Генеральный план предприятия с зоной рассеяния ЦЭН. Если задана вероятность Р попадания случайных центров электрических нагрузок в зону рассеяния, то из (9.117) определяют параметр К0 и по (9.116) вычисляют полуоси эллипса.
Максимальное приближение этих подстанций к центрам электрических нагрузок обеспечивает наилучшие технико-экономические показатели по расходу электроэнергии и цветного металла. Если собственная ТЭЦ находится в центре электрических нагрузок предприятия ( или вблизи него), для распределения электроэнергии используется ГРУ 6 - 20 кВ ТЭЦ. В связи с внедрением направления по разукрупнению, подстанций ЦРП в настоящее время, как правило, не проектируются. После нахождения закона распределения случайных координат центра электрических нагрузок и его числовых характеристик определим зону рассеяния ЦЭН. Разновидности схем питающих осветительных сетей. Размещение щитков следует производить вблизи от центра электрических нагрузок, при этом необходимо обеспечить доступность их обслуживания. Не следует устанавливать щитки в горячих и сырых цехах предприятий, а также в пожароопасных помещениях. Запрещается установка щитков во взрывоопасных помещениях всех классов. На рис. 9.8 изображена зона рассеяния центра электрических нагрузок, ограниченная этим эллипсом. После нахождения закона распределения случайных координат центра электрических нагрузок и его числовых характеристик определим зону рассеяния ЦЭН. Трансформаторные подстанции устанавливаются по возможности в центре электрической нагрузки. В подстанциях монтируется трансформатор с низковольтным распределительным щитом. От щита проводят магистральные линии, преимущественно воздушные, к главным узлам потребления электроэнергии. Специфика электрической части ТЭЦ определяется расположением электростанции вблизи центров электрических нагрузок. Особенности технологической схемы ТЭЦ. 1 - сетевой насос. 2 - сетевой подогрева.| Вариант размещения основного оборудования на площадке ТЭЦ с отдельным зданием ГРУ. Специфика электрической части ТЭЦ определяется расположением электростанции вблизи центров электрических нагрузок. В этих условиях часть мощности может выдаваться в местную сеть непосредственно на генераторном напряжении. Избыток мощности выдается, как и в случае КЭС, в энергосистему на повышенном напряжении. Специфика электрической части ТЭЦ определяется положением станции вблизи центров электрических нагрузок. В этих условиях часть мощности может выдаваться в местную сеть непосредственно на генераторном напряжении. Избыток мощности выдается, как в случае 1ЭС, в систему на повышенном напряжении. Особенности технологической схемы ТЭЦ. Специфика электрической части ТЭЦ определяется положением электростанции вблизи центров электрических нагрузок. Встроенные и внутрицеховые подстанции можно максимально приблизить к центру электрических нагрузок. Для таких подстанций обычно применяют комплектные трансформаторные подстанции промышленного типа внутренней установки, которые устанавливаются в цехах открыто с использованием простейших сетчатых ограждений.
Помещение ГРЩ должно быть размещено возможно ближе к центру электрических нагрузок здания, как правило, в первом этаже здания. Допускается размещать ГРЩ в вышележащих этажах или в сухом отапливаемом подвале, исходя из планировочных и схемных соображений. Группа приемников, использованная для иллюстрации показателя е. Для группы приемников, изображенных на рис. 9.6, центр электрических нагрузок и геометрический центр (9.366) совпадают. Но стоит только изменить нагрузку или место расположения любого приемника, как сразу же происходит смещение одного центра относительно другого.
Схема электроснабжения на напряжении 35 кв. Все это приводит часто к удаленному расположению ТЭЦ от центра электрических нагрузок. Принципиальная схема ТП с двумя трансформаторами мощностью. Цеховую ТП всегда стремятся расположить как можно ближе к центру электрической нагрузки, чтобы уменьшить расход цветного металла на питающие сети от подстанции к электроприемникам. Возможность применения внутрицеховых ТП зависит от характера производства, конструкции здания и определяется противопожарными нормами.
- задачу нахождения мощности и местонахождения батарей статических конденсаторов или других источников реактивной мощности;
- задачу выбора сечения проводников;
- задачу выбора напряжения питающих и распределительных электрических сетей.
Эти задачи являются значимыми, особенно в настоящее время, когда проблема энергосбережения считается актуальной, важной и приоритетной во всем мире.
2.На базе выбранной конкретной оптимизационной задачи электроснабжения разработать ее математическую модель. Сформулировать и записать целевую функцию и ограничения. Подробно описать реализацию модели с помощью программного обеспечения MS Excel.
3.Разработать программу исследования и провести их.
Список литературы
1. Чмутов А. П. Оптимальное размещение источников питания электроэнергией. — «Электричество», 1969, № 12.
2. Каменева В. В. Определение местоположения главных понизительных или распределительных подстанций промышленных предприятий. «Электричество», 1970, № 9.
3. Федоров А. А. Основы электроснабжения промышленных предприятий. М., «Энергия», 1967 и 1972 г.
4. Бутков А. Н. Определение центра нагрузок при выборе источника питания электроэнергии. — «Электрические станции», 1957, № 6.
УДК 621.314
Магистрант
(научный руководитель доцент кафедры ЭПП Фадеев В.Б.)
ОПРЕДЕЛЕНИЕ МОЩНОСТИ БАТАРЕЙ СТАТИЧЕСКИХ КОНДЕНСАТОРОВ НА ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЯХ С ИСПОЛЬЗОВАНИЕМ МЕТОДА МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ».
Актуальность проблемы.
В настоящее время одной из наиболее актуальных проблем энергетики является проблема экономии и рационального использования энергоресурсов. По мнению специалистов, доля полезно используемых энергоресурсов от их общего количества составляет приблизительно 40 - 42%, а остальные 58 -60% идут на потери. Эти показатели свидетельствуют о том, что экономия энергоресурсов, то есть снижение доли их потерь, может существенно повлиять на развитие народного хозяйства и, в частности, обеспечить снижение себестоимости продукции. Последнее следует также из того, что в некоторых отраслях промышленности доля комплексных энергетических затрат в себестоимости продукции составляет более 50%. Кроме того, в настоящее время существует тенденция снижения уровней производства энергоресурсов, в связи с чем происходит постоянное повышение актуальности проблемы энергосбережения. При этих условиях экономия энергии может рассматриваться как источник дополнительной энергии, и поэтому она должна осуществляться во всех случаях, где затраты на энергосбережение меньше, чем затраты на добычу первичных топливно-энергетических ресурсов.
Одно из свойств электроэнергии как продукции состоит в том, что ее транспортировка осуществляется за счет ее расхода. При передаче электроэнергии от источников питания до приемников теряется в среднем 10 - 15% отпущенной с шин источников питания электроэнергии. Поэтому вопросы уменьшения потерь электроэнергии на ее транспорт являются весьма актуальными, причем в настоящее время актуальность проблемы снижения потерь электроэнергии дополнительно подтверждается различными правительственными постановлениями и законодательными актами по энергосбережению.
Для решения проблемы снижения потерь в сетях разработано множество мероприятий, которые обычно внедряются на основе предварительных расчетов потерь. Задачи расчета потерь в сетях разных напряжений и разного назначения имеют свои особенности. В частности, в отношении распределительных сетей 6 - 10 кВ указано, что эти сети характеризуются низкой достоверностью исходной информации для расчета потерь. Однако в настоящее время в распределительных сетях промышленных предприятий этого напряжения появилась тенденция значительного улучшения информационной обеспеченности расчетов потерь. Причины для этого следующие: 1). повышается степень автоматизации производства, в связи с чем уменьшаются случайные колебания нагрузок; 2). внедряются автоматизированные системы учета электроэнергии; 3). начинают проводиться энергетические обследования промышленных предприятий, которые дают много информации.
В связи с улучшением информационной обеспеченности, а также с компьютеризацией промышленных предприятий появилась возможность учета дополнительных факторов при расчете потерь и выборе мероприятий по их снижению. Одним из таких факторов является температурная зависимость сопротивления, влияние которой на потери в промышленных сетях и на результаты расчетов по их снижению на настоящий момент мало исследовано. В данной работе предлагаются методы расчета и оптимизации потерь в радиальных сетях промышленного типа, учитывающие этот фактор.
Из-за ухудшения финансовой ситуации в последние десятилетия наблюдается ухудшение состояния всего энергетического оборудования на предприятиях страны. Большинство предприятий не имеют возможности модернизировать производство, потому вынуждены использовать устаревшее оборудование, особенно это касается компенсации реактивной мощности (КРМ). А на КРМ из всех возможных способов по энергосбережению приходится около 80% возможной экономии электроэнергии в электрических сетях.
Передача реактивной мощности приводит к повышению нагрузки, перегружает линии электропередач (ЛЭП) реактивными токами, что приводит к увеличению потерь активной мощности при передаче электроэнергии к потребителям. Реактивная мощность перегружает электростанции и подстанции, приводя к снижению частоты в системе, а снижение частоты в свою очередь приводит к аварийным отключениям потребителей. Появление в сети реактивной мощности способствует перегреванию оборудования и кабельных линий, что способствует сокращению срока их службы. Из всего выше сказанного следует, что задача компенсации реактивной мощности на промышленных предприятиях необходима, актуальна и экономически оправдана.
Научная новизна диссертации состоит в разработке уточненных методов расчета и оптимизации потерь в промышленных радиальных сетях, учитывающих фактический нагрев токопроводящих частей элементов сети, а также в определении областей значений параметров режима, при которых учет нагрева при оптимизации потерь становится неэффективным. Отличие предлагаемых в работе методов от ранее известных заключается в том, что они включают расчеты температуры кабелей и обмоток трансформатора и учитывают изменение активных сопротивлений этих элементов сети во времени, а при оптимизации - также и в ходе процесса поиска оптимального варианта. Расчет температур производится методами, разработанными специально для расчета потерь и учитывающими специфику поставленных задач.
Теоретическая значимость
В данной работе предложено применение метода математического программирования для решения задачи расчета мощности КУ в системах электроснабжения промышленных предприятий. Это является новым подходом к решению задачи, поскольку существующие рекомендации по выбору КУ, используемые, например, в учебном проектировании ориентированы на применение калькулятора и безнадежно устарели.
stud24.ru